五年级数学图形面积专题训练(一)

合集下载

五年级图形面积练习题

五年级图形面积练习题一、选择题：（每题2分，共10分）1. 一个长方形的长是10厘米，宽是5厘米，其面积是多少平方厘米？A. 25B. 30C. 50D. 752. 一个正方形的边长是8米，其面积是多少平方米？A. 32B. 48C. 64D. 803. 一个平行四边形的底是12厘米，高是8厘米，其面积是多少平方厘米？A. 48B. 64C. 96D. 1004. 一个三角形的底是6厘米，高是4厘米，其面积是多少平方厘米？A. 12B. 14C. 18D. 245. 一个梯形的上底是7厘米，下底是13厘米，高是5厘米，其面积是多少平方厘米？A. 40B. 45C. 50D. 55二、填空题：（每题2分，共20分）6. 一个圆形的半径是3厘米，其面积是________平方厘米。

7. 一个长方形的长是15厘米，宽是8厘米，其面积是________平方厘米。

8. 一个正方形的边长是10厘米，其面积是________平方厘米。

9. 一个平行四边形的底是20厘米，高是10厘米，其面积是________平方厘米。

10. 一个三角形的底是9厘米，高是6厘米，其面积是________平方厘米。

三、计算题：（每题10分，共30分）11. 一个长方形花坛，长20米，宽15米，请计算花坛的面积。

12. 一个圆形水池，直径是14米，求水池的面积。

13. 一个梯形的上底是10厘米，下底是20厘米，高是8厘米，请计算梯形的面积。

四、应用题：（每题15分，共40分）14. 小明家有一个长方形的菜园，长是30米，宽是20米。

如果每平方米可以种植5棵番茄，那么这个菜园可以种植多少棵番茄？15. 学校操场上有一个正方形的花坛，边长是25米。

如果学校计划在花坛周围铺设一圈宽1米的石子路，求石子路的面积。

16. 小华要制作一个风筝，风筝的形状是一个等腰三角形，底边长是20厘米，两腰的长度都是15厘米。

如果风筝的面积是120平方厘米，那么这个风筝的高是多少厘米？五、拓展题：（每题15分，共15分）17. 一个圆环，外圆的半径是10厘米，内圆的半径是5厘米。

五年级数学多边形面积与组合图形面积(含答案)

多边形与组合图形面积精选题一.计算题（共2小题）1 .计算如图各图形的面积.1 2d m图12 .平行四边形ABCD的边BC长10厘米，直角三角形的直角边EC长8厘米.已知阴影部分的面积比三角形EGF的面积大9平方厘米.求CF的长.二.解答题（共48小题）3 .求图中阴影部分的面积.（单位：cm）4 .计算如图图形中阴影部分的面积.6I5 .如图是学校生态园的平面图，你能算出生态园的面积吗？（单位:6 .计算下面图形的面积.7 .图形由两个正方形组成，求阴影部分的面积. （单位：cm）9 .在如图中剪出一个最大的长方形，画出来并求出剩余部分的面积.m)15m8.计算阴影部分的面积.10 .求如图平面图形的面积.图211 .李大爷家有一块菜地（如图）你能用巧妙的方法算出菜地的周长和面积吗?S米23米12 . 一张长8厘米，宽4厘米的长方形纸，从下边的中点和右上角顶点连线一条线段，沿这条线段剪去一个角（如图），剩下的面积是多少？13 .用篱笆围一块菜地，如图的梯形，一边利用房屋的墙壁，已知梯形上、下底的比为3: 5,篱笆长40米，求菜地面积.14 .把一个大平行四边形分成3块，（如图）已知图形阴影部分是平行四边形，面积是12平方米，求三角形和梯形的面积各是多少？15 .如图，三角形ABC的面积是56平方米，BD=DC DE垂直于AC, AC=14米.求图中阴影部分的面积.16 .李大伯一边利用房屋干墙壁，另三边用篱笆围成一个梯形养鸡场地（如图）笆总长是36米.求这个养鸡场的面积是多少？17 .求下列图形中阴影部分的面积.* 2 f 4 ----------------- 9------------------ ► * 2+♦2-W 42 +单位:厘米18.看图计算如图图形的面积.19.认真观察，巧计算.(用两种方法计算组合图形的面积)10cm20. 一块水稻田的形状如下图.如果按照平均每穴 30平方分米插秧，大约要插多少26 cm2t>cm34dro6 cm 2.5 cm H cm ;(2)图2的面积是： __________ 21.求组合图形的面积.(1)图1的面积是:22 .如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角.求四边形ABCD的面积.23 .如图，长方形里有四个三角形，已知其中的三角形的面积，求三角形ADE的面积.24 .（如图）三角形ABC的周长为80厘米，形内有一点P到三角形三条边的距离都是8厘米，求三角形ABC的面积.25.求如图图形的面积.1三厘26 .我会计算阴影部分的面积.6cm6cm 9cm15二力27 .如图：ABCE^一个梯形，其中ABCD是长8厘米，宽7厘米的长方形,4厘米，求阴影部分的面积？28 .如图是由两个完全一样的直角三角形叠在一起而成的，求阴影部分的面积.位：厘米）29 .计算下列图形的面积.（单位：厘米）AF长是（单D C30 .如图，长方形的ABCD面积被线段AE, AF分成三等份，且三角形AEF的面积是35平方厘米，求长方形的面积.A BD F C31 .图中长方形的面积是432平方厘米，求阴影部分的面积.6cm32 .如图，已知正方形和三角形有一部分重叠，三角形乙比三角形甲面积大7平方厘米，则X=厘米.333 .用篱笆围成一个养鸡场（如图），一面靠墙，篱笆总长90米，下底长度是上底长度的3倍.求这个养鸡场的面积.34 .如图正方形ABCD的边长是4分米，长方形EFGD的长GD是5分米，求DE的长.35 .已知如图大正方形的边长是5厘米，小正方形的边长是3厘米，求阴影部分的36 .如图所示，长方形ABCD的面积是180平方厘米，CD长15厘米，ED长17厘米,求三角形ACE的面积.37 .图中的两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积.（单位：米）38 .如图ABC 皿梯形，/ A=Z B=90°, AB=12cm, BC=6cm 甲、乙两阴影面积之差为24cm 2,求ABCD 的面积.39 .有一块如图形状的菜田，算一算：①占地多少公顷？所需数据在图中选择.（单位：m ）②如果每公顷需要施化肥50千克，这块地一共要施肥多少千克? *5AB41.求组合图形的面积. 1242 .如图，一个梯形的上底是5厘米，下底是8厘米.三角形的高是4厘米，并把三角形分为面积相等的甲乙两部分，求阴影部分的面积.43 .求如图的面积或阴影面积:44 .如图，是大小两个正方形组成的图形，大正方形边长是8厘米，小正方形边长为6厘米，求阴影部分的面积.45 .如图，正方形ABCD的边AB、BC分别在三角形BEF的BE BF边上，顶点D在EF边上，点D把EF分成两段，DE=12米，DF=15米，求两个阴影三角形的面积和.B C46 .在长方形 ABCD 中，AD=15厘米，AB=8厘米，四边形EFGO 的面积是9平方厘米，阴影部分的面积是多少平方厘米？47 .如图是由两个平行四边形组成的，这个图形的面积是多少?*— 7.Scm -48 .如图，四边形 ACEH^梯形，ACEG ＞平行四边形，ABGH 是正方形，CDFG 是长方形.已知，AC=8厘米，HE=13厘米，求阴影部分的面积.49 .图中长方形的面积是180平方厘米，&的面是45平方厘米，&的面积是60平方厘米.求阴影部分的面积.50 .有一块铁皮，形状如图.如果要油饰这块铁皮的一面，每平方米用油漆0.6千克，刷完这块铁皮需要多少千克油漆？ 5m3 cm多边形与组合图形面积精选题参考答案与试题解析一.计算题（共2小题）1 .【解答】解：（1） 8X6+ 2=24（平方厘米）答：三角形的面积是24平方厘米.（2）（8+20）X 11 + 2=28X11 +2=154（平方厘米）答：梯形的面积是154平方厘米.（3）12X8+10 X 3+2=96+15=111 （平方分米）答：这个图形的面积是111平方分米. 2.【解答】解：设EF长为x厘米，则CF就是8-x厘米，根据题干分析可得方程：10X （8-x） =10X 8+2+9 80 - 10x=49 10x=31 x=3.18- 3.1=4.9 （厘米）；答：CF长为4.9厘米. 二.解答题（共48小题）3 .【解答】解:8.5 X 5 - 8.5 X 5 - 2=42.5 - 21.25=21.25 （ cm2）,答：阴影部分的面积为21.25cm2. 4.【解答］解：6X6+4X4 — 6X6 + 2 — 4X4 + 2 — 6X （6-4） +2=36+16 -18-8-6=20 （平方厘米）答：阴影部分的面积是20平方厘米.5.【解答】解：20-12=8 （米）16-10=6 （米）12X 16+8X6 + 2=192+24216 （平方米）答：生态园的面积是216平方米. 6.【解答】解：15X4=60 （平方米），答：它的面积是60平方米. 7.【解答】解：（10+8） X 10+2=18X5=90 （平方厘米）答：阴影部分的面积是90平方厘米. 8.【解答】解：30X28 + 2=30X14=420 （平方厘米）答：阴影部分的面积是420平方厘米. 9.【解答】解：如图所示，（12-6） X （10-5）+ 2=6 X 5 + 2=15 （平方厘米）答：剩余部分的面积是15平方厘10.【解答】解：（1） 15X30=450 （平方厘米）答：平行四边形的面积是450平方厘米.（2） 5X2-2+5X 3=5+15=20 （平方米）答：这个图形的面积是20平方米.11.【解答】解：周长是：（17+8+23） X2=48X 2=96 （米）面积是：（17+8） X23- （23-8） X 17=25X23- 15X17=575- 255=320 （平方米）答：周长是96米，面积是329平方米. 12.【解答】解：（8+8+2） X 4 + 2=（8+4）X4 + 2=12X4 + 2=24（平方厘米），答：剩下的面积为24平方厘米.13.【解答】解：如图:40X 弓=12 （米）（12+20） X8+2=32X 8+2=128 （平方米）答：菜地面积是128 Ur 0T 士平方米.14.【解答】解：因为大平行四边形的对边平行且相等，所以阴影部分的高=12+ 3=4（米），所以三角形的面积苦X 3X4=6（平方厘米），梯形的面积=y （3+6）X4=18 （平方厘米）.答：三角形的面积是6平方厘米，梯形的面积是18平方厘米.15 .【解答】解：因为BD=DC所以三角形ABD和三角形ADC的面积相等，因为三角形ABC的面积是56平方米，所以图中阴影部分的面积为：56+2=28 （平方米）答：阴影部分的面积是 28平方米.16.【解答】解：（36-10） X 10 + 2=26 X 10+2=130 （平方米）答：这个养鸡场的面积是 130平方米.17.【解答】解：（2+9+2） X （2+4+2） +2X2X4=13X 8- 16=104- 16=88 （平方厘米）答：阴影部分的面积是88平方厘米.18 .【解答】解：（1） 8X 3=24（平方分米）答：图形的面积是24平方分米.（2） 25X 14+ 2=25X7=175 （平方米）答：图形的面积是 175960 平方厘米.（3）（26+34） X 32+ 2=60X32+2=960 （平方分米）答：图形的面积是 960 平方分米.（4） 26X 20+ （26+30） X 5 +2=520+56X 5 + 2=520+140=660 （平方厘米）答：图形的面积是 60平方厘米.（5） 6X7+ （8-6） X （7-2.5） -2=42+2X 4.5+2=42+4.5=46.5 （平方厘米）答：图形的面积是 46.5平方厘米. 19.【解答】9cm2=40+9.5=49.5 （平方厘米）（2）如图所示， 1比m , 5X9+ （4+5） X （10-9） +2=45+4.5=49.5 （平方厘米）答：组合图形的面积是 49.5平方厘米. 20.【解答]解：8X 11+2+ （11+22） X 10+ 2=44+165=209（平方分米）209 + 30=6（穴）•••29（平方分米）6+1=7 （穴）答：大约要插7穴.21 .【解答】解：（1）24X8+10X24+ 2=192+120=312（平方米）答：组合图形的面积为312平方米.（2） 12X6+ （12+6） X 6+2=72+18X 3=72+54=126 （平方米）答：组合图形的面积为 126 平方米.故答案为：312, 126. 22.【解答】解：连接AC,就变成ADC 和ABC 两个三角形，如图：「 U '三角形ABC 已知底AB=2 （厘米）高就是 CE=6（厘米）那么三角形 ABC 面积就是2X6 +2=6 （平方厘米）三角形 ADC 已知底 DC=5（厘米）高就是AF=4（厘米）三角形ADC 面积是5X4 + 2=10（平方厘米）ABCD 面积是10+6=16 （平方厘米）答：四边形 ABCD 的面积16平方厘米. 23.【解答】A r t===：^~ TH 0 F CT"': ------ 7t E]G41 \解：如图：：一 SA ABE 面积+SA DEC 面积=（ABX EF=） +2+（DCX EG ） +2,因为AB=DC 两个三角形高的和等于 AD,所以，SA ABE 面积+S △ DEC®积=ABX AD-2=£方形面积的一半；同理，另两个三角形面积的和也是长方形面解：（1）如图所示, ,4X10+ (9+10)义(5- 4) +5 cm10cm 9cm4 cm5 cm积的一半，IPSA ABE面积+$△ EDCB 积=3\ ADE 面积+$△ BCEB 积，即SA =37+29-41=25. 24.【解答］解：如图:APB+S A APC+S A BPC=ABX BP+ 2+ACX PE+ 2+BCX PD+ 2JPDX （AB+AGB。

五年级图形的面积练习题

五年级图形的面积练习题在数学学科中，图形的面积是非常重要的一个概念。

通过计算图形的面积，我们可以更好地理解和应用数学知识。

本文将为五年级学生提供一些图形的面积练习题，帮助他们巩固和应用所学的知识。

题目一：矩形的面积计算已知一个矩形的长为8厘米，宽为4厘米，求其面积。

解析：矩形的面积可以通过长乘以宽来计算。

根据题目给出的数据，我们可以得知这个矩形的长为8厘米，宽为4厘米，那么它的面积为8乘以4，即32平方厘米。

题目二：正方形的面积计算已知一个正方形的边长为5厘米，求其面积。

解析：正方形的面积也可以通过边长的平方来计算。

根据题目给出的数据，我们可以得知这个正方形的边长为5厘米，那么它的面积为5的平方，即25平方厘米。

题目三：三角形的面积计算已知一个三角形的底边长为6厘米，高为3厘米，求其面积。

解析：三角形的面积可以通过底边长乘以高再除以2来计算。

根据题目给出的数据，我们可以得知这个三角形的底边长为6厘米，高为3厘米，那么它的面积为（6乘以3）除以2，即9平方厘米。

题目四：梯形的面积计算已知一个梯形的上底长为5厘米，下底长为9厘米，高为4厘米，求其面积。

解析：梯形的面积可以通过上底长、下底长和高来计算。

根据题目给出的数据，我们可以得知这个梯形的上底长为5厘米，下底长为9厘米，高为4厘米，那么它的面积为（5加9）乘以4再除以2，即56平方厘米。

通过以上的练习题，我们可以看到计算图形的面积需要根据不同的图形选择不同的计算公式。

对于矩形和正方形，可以直接使用边长相乘的方式；对于三角形，可以使用底边长乘以高再除以2的方式；对于梯形，可以使用上底长、下底长和高来计算。

除了熟练掌握计算公式外，还需要学会正确地读题和提取关键信息。

在解答练习题时，我们需要仔细阅读题目，理解所给的条件，并根据条件来选择合适的计算方法。

在日常生活中，图形的面积计算应用广泛。

比如，我们可以利用矩形的面积计算来确定房间的大小；利用三角形的面积计算来计算地块的面积等等。

北师大版2020-2021小学五年级数学上册六组合图形的面积单元综合训练题1(附答案)

北师大版2020-2021小学五年级数学上册六组合图形的面积单元综合训练题1（附答案）一、选择题1．r=20厘米，圆的面积是（）A．62.8平方厘米B．1256平方厘米C．19.625平方厘米D．200.96平方厘米2．下图，这个梯形的面积是（）cm2。

A．10B．25C．50D．1003．下列哪种方法不能正确得到组合图形的面积（）．A．把组合图形分割成几个基本图，再求各部分面积的和B．用线绕图形围一周，再把这段线围成一个规则的正方形，求正方形的面积C．采用割补法，把组合图形转化成基本图形再计算面积4．亚洲的面积约为4400万( )。

A．公顷B．平方千米C．平方米5．叔叔粉刷一面墙，每平方米用0.15千克的涂料，一共用去约6千克的涂料，这面墙的长和宽可能是（）。

A．10米和4米B．20米和3米C．15米和3米6．一块长方形菜地的宽是80m，长是100m，它的面积约是1( )。

A．m2B．km2C．公顷7．在长方形的四个角上各剪去一个相同的正方形后，所得的图形( )A．周长增加，面积减少B．周长减少，面积也减少C．周长不变，面积减少D．周长和面积的变化无法确定8．下图是一个房间的侧面，它的面积是( )平方米．9．下面两个是完全一样的平行四边形，涂色部分的面积（）A．甲大B．乙大C．一样大二、填空题10．50000m2＝_____公顷；0.32km2＝_____m211．下面图形的面积是________平方厘米．12．给一个三角形的底边增加5cm，三角形的面积就比原来增加15cm2。

这个三角形底边上的高是（____）cm。

13．如图，如果1个小正方形的面积是1cm2,那么整个小花瓶的面积是（_____）cm2。

14．估计下列图形的面积．(每个小方格的面积表示1cm2)约（_____）cm2约（_________）cm2约（_________）cm215．估一估下面图形的面积。

（每个小方格的面积是1平方厘米）（1）面积约为（_____）（2）面积约为（____）(3)面积约为（____）16．0.5公顷=（______）2mkm=（______）2m=（______）2km0.35217．写出下面图形的面积。

五年级图形面积练习题

五年级图形面积练习题在五年级学习数学的过程中，图形的面积计算是一个重要的内容。

通过解决各种图形面积的练习题，可以帮助学生掌握不同图形的面积计算方法，提高他们的数学运算能力和几何思维能力。

本文将通过一些有趣的练习题，帮助五年级的学生们更好地理解和应用图形面积的概念。

一、矩形和正方形的面积计算1. 假设一个矩形的长为12厘米，宽为8厘米，求其面积。

解答：矩形的面积可以通过长乘以宽来计算。

根据给定的数据，我们可以得到面积=12厘米 × 8厘米 = 96平方厘米。

2. 一个房间是一个正方形，边长为6米，求房间的面积。

解答：正方形的面积计算方法同样是边长的平方，因此房间的面积=6米 × 6米 = 36平方米。

二、三角形的面积计算1. 一个三角形的底边长度为10厘米，高为6厘米，求其面积。

解答：计算三角形面积的公式是底边乘以高再除以2。

根据给定的数据，我们可以得到面积=10厘米 × 6厘米 ÷ 2 = 30平方厘米。

2. 一个等边三角形的边长为8厘米，求其面积。

解答：等边三角形的面积计算公式为（边长的平方× √3）÷ 4。

根据给定的数据，我们可以得到面积=（8厘米 × 8厘米× √3）÷ 4 ≈ 11.71平方厘米。

三、圆的面积计算1. 一个圆的半径为5厘米，求其面积（取π≈3.14）。

解答：圆的面积计算公式为π乘以半径的平方。

根据给定的数据，我们可以得到面积=3.14 × 5厘米 × 5厘米≈ 78.5平方厘米。

2. 一个圆的直径为10厘米，求其面积。

解答：根据性质可知，圆的半径等于直径的一半，因此半径=10厘米 ÷ 2 = 5厘米。

再根据圆的面积公式，我们可以得到面积=3.14 × 5厘米 × 5厘米≈ 78.5平方厘米。

四、其他图形的面积计算1. 一个边长为6厘米的正五边形可以划分成若干个等边三角形，求其面积。

五年级下册数学试题 - 图形面积（奥数版块）北师大版

第十四讲图形问题三角形的阴影面积一、等积模型D C BA 1-a ①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．一半模型二、共角定理（鸟头定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．:():()ABC ADE S S AB AC AD AE =⨯⨯△△三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S=或者1324S S S S⨯=⨯②()()1243::AO OC S S S S=++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．S4S3S2S1ODCBA梯形中比例关系(“梯形蝴蝶定理”)：①2213::S S a b=②221324::::::S S S S a b ab ab=；③S的对应份数为()2a b+．例一、图是由两个完全一样的直角三角形重叠在一起，求阴影部分的面积。

AB CDOaS3S2S1S4练习一、图是两个完全一样的直角三角形重叠在一起，按图中的已知条件求阴影部分的面积。

（单位：厘米）练习二、图是正方形ABCD是有三个长方形拼成。

长方形EFGH的宽式正方形的一半，甲阴影部分的面积是30平方厘米。

求阴影部分的总面积。

例二、图是梯形的上底AB长20厘米，下底DC长30厘米，高15厘米，求阴影部分的面积。

练习一、图中，梯形的下底为8厘米，高为4厘米。

五年级数学平面几何图形的面积基础+拔高例题带作业(带详细答案)

平面几何图形的面积板块一：基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米，则平行四边形的面积是（24 ）平方分米，三角形的面积是（12 ）平方分米。

2、李叔叔在院子里靠着墙边围城了一个鸡笼，围鸡笼的网子长20.5米，求这个鸡笼的占地面积是多少平方米？上底+下底=20.5-8.5=12（米）梯形面积=12×8.5÷2=51（平方米）3、有一个长方形，如果宽减少2米，或长减少3米，则面积均减少24平方米，求这个长方形的是是多少平方米？32原长方形的长：24÷2=12（米）原长方形的宽：24÷3=8（米）原来长方形的面积：12×8=96（平方米）4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形，求阴影部分面积。

方法一：可以分割成两个钝角三角形第一个钝角三角形的底是4，高是4，第二个钝角三角形的高是8，底是8-4=4，所以总共的面积是：4×4÷2+8×（8-4）÷2=24（平方厘米）方法二：两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×（4+8）÷2=24（平方厘米）5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形，求阴影部分面积。

方法一：可以分割成三个钝角三角形第一个钝角三角形的底是4，高是4，面积是：4×4÷2=8（平方厘米）第二个钝角三角形的高是8，底是（8-4），面积：8×（8-4）÷2=16（平方厘米）第三个钝角三角形的高是8，底是6，面积是：6×8÷2=24（平方厘米）一共的面积：8+16+24=48（平方厘米）方法二：把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×（8-6）-（8+4）×4÷2-8×（6+8）÷2=48（平方厘米）板块二：拓展提高【例题1】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15（厘米）（15+20）×8÷2=140（平方厘米）【例题2】右图中甲的面积比乙的面积大__________平方厘米．乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=（甲+空白）-（乙+空白）=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8（平方厘米）【例3】右图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9平方厘米，求ED 的长．A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积，则：长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24（平方厘米）则三角形BCE 的面积=24-9=15（平方厘米）EC=15×2÷6=5（厘米）ED=5-4=1（厘米）【巩固】如图所示，CA=AB=4厘米，△ABE 比△CDE 的面积小2平方厘米，求CD 的长为多少厘米？A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积，则：三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8（平方厘米）则三角形BCD 的面积=8+2=10（平方厘米）CD=10×2÷4=5(厘米)【例4】一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？1215222原来的面积=15×12=180（平方分米）现在的的面积=（15-2）×（12-2）=130（平方厘米）减少的面积：180-130=50（平方厘米）【巩固】一个长方形，如果长减少5厘米，宽减少2厘米，那么面积就减少66平方厘米，这时剩下的部分恰好成为一个正方形，求原来长方形的面积？5×22566-2×5=56（平方厘米）设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长：8+5=13（厘米）原来长方形的宽：8+2=10（厘米）原来长方形的面积：13×10=130（平方厘米）【例5】下面图形中，长方形ABCD的面积是32平方厘米，EF都是所在边的中点，求三角形AEF的面积。

北师大版五年级数学上册期末复习专题组合图形的面积练习(含答案)

北师大版五年级数学上册期末复习专题组合图形的面积【知识点归纳】方法：①“割法”：观察图形，把图形进行分割成容易求得的图形，再进行相加减．②“补法”：观察图形，给图形补上一部分，形成一个容易求得的图形，再进行相加减． ③“割补结合”：观察图形，把图形分割，再进行移补，形成一个容易求得的图形．【典例分析】例1：求图中阴影部分的面积．（单位：厘米）分析：根据图所示，可把组合图形分成一个直角梯形和一个41圆，阴影部分的面积等于梯形的面积减去41圆的面积再加上41圆的面积减去三角形面积的差，列式解答即可得到答案．解：[（5+8+5）×5÷2-41×3.14×52]+（41×3.14×52-5×5÷2）， =[18×5÷2-0.785×25]+（0.785×25-25÷2）， =[90÷2-19.625]+（19.625-12.5）， =[45-19.625]+7.125， =25.375+7.125，=32.5（平方厘米）；答：阴影部分的面积为32.5平方厘米．点评：此题主要考查的是梯形的面积公式（上底+下底）×高÷2、三角形的面积公式底×高÷2和圆的面积公式S=πr 2的应用．同步测试一．选择题（共10小题）1．已知长方形和正方形的面积相等，阴影部分A和B的面积不相等是（）A．B．C．D．2．如图是一个直角梯形，图中阴影部分面积是100平方厘米，空白部分面积是（）平方厘米．A．140 B．120 C．100 D．703．如图中阴影部分的面积是60平方厘米，空白部分的面积是（）平方厘米．A．12 B．30 C．60 D．无法判断4．下面三个完全一样的直角梯形中，阴影部分的面积（）A．甲最大B．乙最大C．丙最大D．一样大5．在图的平行四边形中，E、F把AB边分成了相等的三段，平行四边形的面积是48平方厘米，阴影三角形的面积是（）A．8平方厘米B．12平方厘米C．16平方厘米D．24平方厘米6．如图，平行四边形的面积是24cm2，则阴影部分的面积是（）A．2cm2B．4cm2C．10cm2D．12cm27．两个完全一样的正方形，如果①号图形阴影部分的面积是10平方厘米，那么②号图形阴影部分的面积是（）平方厘米．A．30 B．25 C．20 D．108．下面两个是完全一样的平行四边形，涂色部分的面积（）A．甲大B．乙大C．一样大9．如图中，阴影部分面积与三角形（）的面积相等．A．BCD B．BFC C．BCE10．比较下面两个图形，说法正确的是（）A．甲、乙的面积相等，周长也相等B．甲、乙的面积相等，但甲的周长长C．甲、乙的周长相等，但乙的面积大D．甲、乙的面积相等，它们周长不一定相等二．填空题（共8小题）11．如图（单位：dm），半圆是长方形内最大的半圆，则这个长方形的面积是dm2．12．如图的面积是平方厘米．13．如果用1厘米表示如图小方格的边长，那么阴影部分的面积是平方厘米．14．如图，平行四边形的面积是20cm2，那么三角形的高是cm，面积是cm2．15．图中四边形的面积是平方厘米．16．如图，阴影部分是面积是平方厘米．（π取3.14）17．某正方形园地是由边长为1的四个小正方形组成的，现要在园地上建一个花坛（阴影部分）使花坛面积是园地面积的一半，以下图中设计不合要求的是．18．如图是一块长方形ABCD的场地，长AB＝102m，宽AD＝51m，从A、B两处入口的中路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪面积为．（A）5050m2（B）4900m2（C）5000m2（D）4998m2三．判断题（共5小题）19．图中阴影部分的面积比半圆大．．（判断对错）20．如图所示，梯形的上底长等于下底长的一半，空白面积也等于阴影部分面积的一半．（判断对错）21．图中阴影部分的面积为24cm2．（判断对错）22．如图中阴影部分的面积是14平方厘米．（判断对错）23．计算组合图形的面积时，可以把组合图形分成几个简单的图形，然后再进行计算．．（判断对错）四．计算题（共2小题）24．求阴影部分的面积．（单位：cm）25．计算下面图形的面积．五．解答题（共3小题）26．下面是一个菜园的平面图，算一算这个菜园的面积是多少平方米．27．如图，在平行四边形ABCD中，BC长10厘米，直角三角形BCE的直角边EC长8厘米，已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米，求CF的长．28．李大爷家有一块菜地．（形状如图，单位米）长方形地里种的是圆白菜，右边的梯形地里种的是茄子．（1）每棵圆白菜占地0.15平方米，一共可以种几棵？（2）茄子地一共有多少平方米？参考答案与试题解析一．选择题（共10小题）1．【分析】我们通过对每个选项给出的图形计算可知，A选项中阴影部分A的面积等于正方形的面积的，B的面积等于长方形面积的，而长方形和正方形的面积相等；所以阴影部分A和B的面积；选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积，所以相等；选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积，B的面积得出正方形减去空白部分小长方形的面积，所以不相等．选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积，所以相等；据此解答．解：A选项中阴影部分A的面积等于正方形的面积的，B的面积等于长方形面积的，而长方形和正方形的面积相等；所以阴影部分A和B的面积；选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积，所以相等；选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积，B的面积得出正方形减去空白部分小长方形的面积，所以不相等．选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积，所以相等；故选：C．【点评】本题考查了学生的观察能力，考查了学生灵活解决问题的能力．2．【分析】空白三角形、阴影三角形，以及梯形的高相等，根据三角形的面积＝底×高÷2可知，先用阴影三角形的面积乘上2，再除以它的底20厘米，即可求出它的高，再用空白三角形的底乘上高，再除以2，即可求出空白部分的面积．解：100÷20×2＝5×2＝10（厘米）14×10÷2＝140÷2＝70（平方厘米）答：空白部分的面积是70平方厘米．故选：D．【点评】本题考查了三角形的面积公式，三角形的面积＝底×高÷2，关键是得出两个三角形的高相等．3．【分析】先利用三角形的面积公式S＝ah÷2计算出三角形的高，也就等于知道了空白部分的高，从而利用三角形的面积公式进行解答即可．解：60×2÷20＝120÷20＝6（厘米）10×6÷2＝30（平方厘米）答：空白部分的面积是30平方厘米．故选：B．【点评】此题主要考查三角形的面积公式的灵活应用．4．【分析】这几个直角梯形中，阴影部分总面积都是以梯形的下底为底，以梯形的高为高的三角形的面积，由此即可判断它们面积的大小．解：三图中，阴影部分总面积都是以梯形的下底为底，以梯形的高为高的三角形的面积，因为三个梯形完全相同，由此可得：阴影部分的面积都相等．故选：D．【点评】此题主要考查等底等高的三角形面积都相等，据图即可以作出判断．5．【分析】根据图得出阴影部分的三角形，与平行四边形的等高，底是平行四边形底的，又三角形的面积是与它底等高平行四边形面积的一半，所以三角形的面积是平行四边形面积的×＝，然后解答即可．解：因为E、F把AB边分成了相等的三段，所以阴影部分三角形的底是平行四边形底的，所以三角形的面积是平行四边形面积的×＝，阴影三角形的面积是48×＝8（平方厘米）．答：阴影三角形的面积是8平方厘米．故选：A．【点评】本题关键理解以三角形的面积是与它底等高平行四边形面积的一半．6．【分析】首先根据平行四边形的面积公式：s＝ah，那么a＝s÷h，已知平行四边形的面积和高求出平行四边形的底，然后用平行四边形的底减去5就是阴影部分三角形的底，然后根据三角形的面积公式：s＝ah÷2，把数据代入公式解答．解：24÷4＝6（厘米），（6﹣5）×4÷2＝1×4÷2＝2（平方厘米），答：阴影部分的面积是2平方厘米．故选：A．【点评】此题主要考查平行四边形的面积公式、三角形的面积公式的灵活运用，关键是熟记公式．7．【分析】由正方形的特征可知，①号图中阴影部分的面积等于正方形面积的，因此正方形的面积就等于图①中阴影部分面积的4倍，已知①号图形阴影部分的面积是10平方厘米，用10乘上4即可得到正方形的面积；而②号图中阴影部分的面积是正方形面积的，因此再用正方形的面积乘上即可得到②号图形阴影部分的面积，据此解答．解：由分析知②号图形阴影部分的面积是：10×4×＝40×＝20（平方厘米）；答：②号图形阴影部分的面积是20平方厘米．故选：C．【点评】解决本题的关键是明确各个图中阴影部分的面积和正方形的面积之间的数量关系．8．【分析】甲图中阴影部分的面积可以看作与平行四边形等底等高的三角形，三角形的面积是平行四边形的面积的一半，乙图中的阴影部分面积也可以看作与平行四边形等底等高的三角形，三角形的面积是平行四边形的面积的一半，平行四边形又是完全一样，所以阴影部分的三角形的面积也是一样据此判断．解：甲图中阴影部分的面积和乙图中的阴影部分面积都可以看作与平行四边形等底等高的三角形，平行四边形的面积一样，它们的面积也一样大．故选：C．【点评】此题主要考查等底等高的三角形面积相等及平行四边形的特点．据图即可以作出判断．9．【分析】三角形的面积S＝ah，只要是三角形的底和高相等，则它们的面积相等，据此即可得解．解：由图意可知：图中3个三角形的底是相等的，要想面积与阴影部分的三角形面积相等，那么如果高与阴影部分的三角形的高相等即可；再根据平行线间的距离相等，所以△BCE的面积与阴影部分的面积相等．故选：C．【点评】解答此题的主要依据是：等底等高的三角形的面积相等．10．【分析】由图形可知，甲的面积小于长方形面积的一半，乙的面积大于长方形面积的一半，所以乙的面积大于甲的面积；因为甲的周长＝长方形的两条邻边的和+中间的曲线的长，乙的周长＝长方形的两条邻边和+中间的曲线的长，进行解答继而得出结论．解：因为甲的面积小于长方形面积的一半，乙的面积大于长方形面积的一半，所以甲的面积小于乙的面积；甲的周长＝长方形的两条邻边的和+中间的曲线的长，乙的周长＝长方形的两条邻边的和+中间的曲线的长，所以甲的周长等于乙的周长；故选：C．【点评】解答此题应根据长方形的特征，并结合周长的计算方法进行解答．二．填空题（共8小题）11．【分析】观察图形可知，长方形的长等于圆的直径是8分米，宽是半圆的半径是8÷2＝4分米，据此利用长方形的面积＝长×宽计算即可解答问题．解：8÷2＝4（分米）8×4＝32（平方分米）答：这个长方形的面积是32平方分米．故答案为：32．【点评】掌握长方形内的半圆的特征得出长方形的长与宽的值，是解决本题的关键．12．【分析】根据图示，这个组合图形可以看作由一个梯形和一个长方形拼成的图形，利用长方形和梯形面积公式求解即可．解：如图：该图形可看作一个梯形和一个长方形拼成的图形，其面积为：（12+16）×（10﹣5）÷2+16×5＝28×5÷2+80＝70+80＝150（平方厘米）答：这个图形的面积为150平方厘米．故答案为：150平方厘米．【点评】此题主要考查的是梯形的面积公式：（上底+下底）×高÷2、长方形面积公式：长×宽的应用．13．【分析】右边图形中阴影部分的面积＝最上面一行中的2个方格的面积+下面图形中的长方形的面积﹣1个方格的面积，据此即可求解．解：2+4×5﹣1＝2+20﹣1＝21（平方厘米）答：阴影部分的面积是21平方厘米．故答案为：21．【点评】解答此题的关键是：看利用小方格的边长计算简单还是利用小正方形的面积计算简单，要灵活应对．14．【分析】根据平行四边形的面积变形公式h＝S÷a，可求平行四边形的高，根据三角形面积公式S＝ah可求三角形的面积；依此即可求解．解：高：20÷5＝4（厘米）三角形的面积：3×4÷2＝12÷2＝6（平方厘米）故答案为：4，6．【点评】本题考查了学生求平行四边形、三角形面积的知识，关键是求出平行四边形的高．15．【分析】根据图意可把这个不规则的四边形，看作是2个直角三角形面积的和来进行解答，然后再根据三角形的面积公式进行计算．解：11×6÷2＝66÷2＝33（平方厘米）答：这个四边形的面积是33平方厘米．故答案为：33．【点评】本题属于求组合图形面积的问题，这种类型的题目主要明确组合图形是由哪些基本的图形构成的，然后看是求几种图形的面积和还是求面积差，然后根据面积公式解答即可．16．【分析】观察图示可知，阴影部分的面积＝梯形面积﹣圆面积的，代入数据，解答即可．解：（4+10）×4÷2﹣3.14×42×＝28﹣12.56＝15.44（平方厘米）答：阴影部分是面积是15.44平方厘米．故答案为：15.44．【点评】本题属于求组合图形面积的问题，这种类型的题目主要明确组合图形是由哪些基本的图形构成的，然后看是求几种图形的面积和还是求面积差，然后根据面积公式解答即可．17．【分析】运用面积公式、割补法求阴影部分面积，再与题目的要求比较．解：花坛面积为4m2，一半为2m2，A、阴影部分面积为2×2÷2＝2（m2）B、阴影部分面积为1×1+1×1÷2+1×2÷2＝2.5（m2）不符合要求；C、阴影部分面积为1×1÷2×4＝2（m2）D、把图中上面两个扇形移下来，刚回拼成两个小正方形，面积为2m2；故答案为：B．【点评】本题考查了阴影部分图形面积的计算方法，即规则图形用面积公式求，不规则图形用割补法求解．18．【分析】本题要看图解答．从图中可以看出剩余部分的草坪正好可以拼成一个长方形，然后根据题意求出长和宽，最后可求出面积．解：由图可知：矩形ABCD中去掉小路后，草坪正好可以拼成一个新的矩形，且它的长为：（102﹣2）米，宽为（51﹣1）米．所以草坪的面积＝长×宽＝（102﹣2）×（51﹣1）＝100×50＝5000（米2）．故答案为：C．【点评】此题考查了生活中的平移，根据图形得出草坪正好可以拼成一个长方形是解题关键．三．判断题（共5小题）19．【分析】分别计算出阴影部分和半圆的面积，再判断．解：设正方形的边长为a，则：阴影部分面积＝πa2﹣＝a2；半圆的面积为：π×═a2；所以阴影部分面积等于半圆的面积，原说法错误．故答案为：错误．【点评】解决本题的关键是计算出组合图形中相关部分的面积，再比较．20．【分析】分别运用梯形的面积公式和三角形的面积公式进行列式比较就可做出判断．解：设梯形的上底为a，高为h，则下底为2a；梯形的面积＝（a+2a）×h÷2＝3ah÷2＝ah；空白三角形的面积＝a×h÷2＝ah；则阴影部分的面积＝梯形的面积﹣空白三角形的面积＝ah﹣ah＝ah；由此可以看出：空白面积等于阴影部分面积的一半．故此题是正确的．故答案为：√．【点评】此题主要考查三角形和梯形的面积公式．21．【分析】观察图形可知，可把右侧阴影部分割补到左侧对称的位置，如下图所示：会发现阴影部分是一个上底为4cm、下底为8cm，高为4cm的梯形，利用梯形的面积公式代入数据计算即可．解：由分析知，阴影部分的面积等于上图所示梯形的面积，梯形的上底为：8﹣8÷2＝8﹣4＝4（cm），高为：8÷2＝4（cm），所以面积为：（4+8）×4÷2＝12×4÷2＝48÷2＝24（cm2）；答：图中阴影部分的面积为24cm2．所以题干说法正确．故答案为：√．【点评】本题考查了求组合图形的面积，组合图形的面积一般都是转化为规则图形的面积的和或差，再利用规则图形的面积公式进行计算．22．【分析】把这个图形分成三部分计算，上面是底4厘米、高2厘米的三角形，中间是上底2厘米、下底4厘米、高1厘米的梯形，下面是长与宽分别是3厘米、2厘米的长方形，据此计算出它们的面积，再加起来即可判断．解：4×2÷2+（2+4）×1÷2+2×3＝4+3+6＝13（平方厘米）答：阴影部分的面积是13平方厘米．故答案为：×．【点评】此题考查了不规则图形的周长与面积的计算方法，一般都是转化到规则图形中利用面积公式计算解答．23．【分析】根据组合图形的面积的计算方法可知：计算组合图形的面积时，可以把组合图形分成几个简单的图形，然后再利用规则图形的面积公式进行计算，据此即可判断．解：计算组合图形的面积时，可以把组合图形分成几个简单的图形，然后再根据简单图形的计算公式进行计算．故答案为：√．【点评】此题考查组合图形的面积的计算方法：关键是把组合图形的面积转化为我们学过的图形的面积，再利用相应的面积公式与基本的数量关系解决问题．四．计算题（共2小题）24．【分析】（1）通过旋转平移把阴影部分转化为一个半圆，根据圆的面积公式：S＝πr2，把数据代入公式解答．（2）阴影部分的面积等于圆的面积减去正方形的面积，根据圆的面积公式：S＝πr2，三角形的面积公式：S＝ah÷2，把数据代入公式解答．解：（1）3.14×42÷2＝3.14×16÷2＝50.24÷2＝25.12（平方厘米）；答：阴影部分的面积是25.12平方厘米．（2）3.14×（10÷2）2﹣10×（10÷2）÷2×2＝3.14×25﹣10×5÷2×2＝78.5﹣50＝28.5（平方厘米）；答：阴影部分的面积是28.5平方厘米．【点评】解答求阴影部分的面积关键是观察分析图形是由哪几部分组成的，是各部分的面积和、还是求各部分的面积差，再根据相应的面积公式解答．25．【分析】组合图形的面积等于底为35米，高为12米的三角形面积加上底为50米，高为33米的平行四边形的面积；根据三角形和梯形面积公式解答即可．解：33×50+35×12÷2＝1650+210＝1860（平方米）答：图形的面积是1860平方米．【点评】本题属于求组合图形面积的问题，这种类型的题目主要明确组合图形是由哪些基本的图形构成的，然后看是求几种图形的面积和还是求面积差，然后根据面积公式解答即可．五．解答题（共3小题）26．【分析】本题可用长80米、宽40米的长方形面积减去边长10米的正方形面积求出菜园的面积，长方形面积＝长×宽，正方形面积＝边长×边长．解：80×40﹣10×10＝3200﹣100＝3100（平方米）答：这个菜园的面积是3100平方米．【点评】本题主要考查了学生利用长方形的面积公式解题的能力，找出正确的计算组合图形的面积的方法是解题关键．27．【分析】根据题意：如图，已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米，则三角形EFG的面积+10平方厘米+梯形BCFG的面积＝平行四边形ABCD的面积，又因为三角形EFG的面积+梯形BCFG的面积＝三角形BCF的面积，所以三角形BCF的面积+10平方厘米＝平行四边形ABCD的面积；CF是平行四边形的高，根据平行四边形的面积＝底×高，则高CF＝平行四边形的面积÷底即可．解：（10×8÷2+10）÷10＝（40+10）÷10＝50÷10＝5（厘米）答：CF长5厘米．【点评】解决此题的关键用直角三角形的面积+10平方厘米代替平行四边形的面积，根据面积公式求出CF．28．【分析】（1）先利用长方形的面积公式S＝ab计算出圆白菜地的面积，再用它的面积除以每棵圆白菜的占地面积，即可得解；（2）依据梯形的面积公式S＝（a+b）×h÷2，代入数据即可求解．解：（1）8×4.5÷0.15＝36÷0.15＝240（棵）答：一共可以种240棵．（2）（4.8+10.5﹣4.5）×（8﹣2）÷2＝10.8×6÷2＝32.4（平方米）答：茄子地一共有32.4平方米．【点评】此题主要考查长方形和梯形的面积公式的灵活应用．。

【期末专项复习】北师大版小学五年级上册数学《组合图形的面积》期末专项强化突破卷(一)含答案

北师大版2021~2022学年上册期末专项强化突破卷（一）组合图形的面积（考试时间 90分钟全卷满分 100分）学校:___________姓名：___________班级：___________考号：___________ 题号一二三四五总分得分亲爱的同学们，学期末的智慧之旅马上就要开始了！只要你认真地分析每一道题，你一定能获得一次难忘的旅途记忆!一、选择题（满分16分）1．组合图形面积的计算方法，老师向我们介绍过的方法有（）A．分割法B．填补法C．平行移动法2．已知如图阴影部分的面积是3平方厘米，则两个正方形中较小的正方形的面积为．（）A．3平方厘米B．6平方厘米C．12平方厘米D．无法确定3．下面的面积单位中，最大的面积单位是（），最小的是（）。

A．平方千米；平方分米B．平方米；平方分米 C．公顷；平方分米D．平方分米；平方分米4．已知长方形和正方形的面积相等，阴影部分A和B的面积不相等是（）A．B．C．D．5．下图中的梯形是由等底等高的三角形和平行四边形拼成的，已知三角形的面积是20平方厘米，那么梯形的面积是( )．A ．40平方厘米B ．60平方厘米C ．80平方厘米6．一块长方形菜地，长50米，宽40米，（）块这样大的菜地面积是1公顷。

A ．5B ．50C ．207．张爷爷家的池塘占地面积约是15（）。

A ．公顷B ．平方米C ．平方千米8．一所新建学校占地面的长200米，宽150米，它的占地面积是（）。

A ．3平方千米B ．3公顷C ．3000平方米D ．3万米二、填空题（满分16分）9．一块长方形菜地，长是200米，宽是50米，面积是（________）公顷。

10．200000平方米＝（________）公顷（________）平方千米＝600公顷1个平角＝（________）个直角 70°＋（________）°＝90°11．国家休育馆（鸟巢）的占地面积约为20（______）；5个“鸟巢”的占地面积约为（______）平方千米。

（完整版）小学五年级数学三角形的面积练习题（含答案）

（完整版）小学五年级数学三角形的面积练习题（含答案）三角形的面积练习题一、填空题1、一个三角形的面积是25平方厘米，和它等底等高的平行四边形的面积是( 50 )平方厘米。

2、★在一个长9厘米，周长26厘米的长方形内画一个最大的三角形，这个三角形的面积是( 18 )平方厘米。

3、一个平行四边形的底是6厘米，高是14厘米，它的面积是（84 ）平方厘米，与它等底等高的三角形面积是（42 ）平方厘米。

4、沿着平行四边形的任一对角线剪开,分成两个完全一样的( 三角形),它们的底和平行四边形的底( 相等).它们的( 高)和平行四边形的高相等.每个三角形的面积是平行四边形面积的( 一半)。

5、一个三角形的面积是20平方厘米,它的高是8厘米,底是( 5 )厘米.6、一个三角形的底扩大2倍，高不变，这个三角形的面积扩大（ 2 ）倍7、直角三角形的两条直角边长分别为3厘米和4厘米，这个直角三角形面积是( 6 )平方厘米。

8、一个等腰直角三角形的直角边是10厘米，它的面积是（50 ）平方厘米。

9、一个三角形的底和高分别扩大4倍，它的面积扩大（16 ）倍。

10、一个等腰三角形，已知一个底角是55°，顶角是（70 ）度。

11、一个直角三角形，其中一个锐角是另一个锐角的2倍，较小的锐角是（30 ）度。

12、在一个面积是36平方米的长方形里剪一个最大的三角形，这个三角形的面积是（18 ）平方厘米。

13、一个三角形和一个平行四边形的底相等，并且平行四边形的高是三角形高的2倍。

那么平行四边形的面积是三角形的（4 ）倍。

14、270平方厘米＝（ 2.7 ）平方分米 1.4公顷＝（ 14000）平方米15、一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米，平行四边形的面积是（ 25）平方分米，三角形的面积是（ 12.5）平方分米。

16、两个完全一样的三角形可以拼成一个( 平行四边形).每个三角形的面积等于所拼图形面积的( 一半)，所以三角形的面积=( 底×高÷2 )，如果用S表示三角形的面积，用a表示三角形的底，h表示三角形的高，那么三角形的面积公式可以写成( S=0.5ah )17、一个等边三角形的周长是12厘米，高是3厘米，它的面积是( 6平方厘米).18、一个等腰三角形的周长是18分米，腰是7分米，底边上的高是3分米，它的面积是( 6平方分米).19、三角形一条边长是4分米，这条边上的高是6分米；另一条边长是3分米，则这条边上的高是( 8平方分米).20、一个等腰直角三角形，两条直角边的和是8分米，它的面积是( 8平方分米).21、一个直角三角形的面积是16平方厘米，一个直角边长是4厘米，另一个直角边长是( 8 )厘米.22、一个平行四边形和一个三角形面积相等，底边一样长，如果三角形的高是6厘米，平行四边形的高是( 3 )厘米.二、判断题1、两个面积相等的三角形可以拼成平行四边形行（×）2、等底等高的三角形面积相等（√）3、三角形的面积等于平行四边形面积的一半（×）4、用两个直角三角形可以拼成一个长方形，也可以拼成一个平行四边形（√）5、三角形的底扩大到它的2倍，高也扩大到它的3倍，面积扩大到它的6倍（√）6、两个三角形面积相等，它们的形状也一定相同（×）7、平行四边形面积等于长方形面积。

五年级数学面积练习题

五年级数学面积练习题1. 长方形面积计算：- 题目1：一个长方形的长是12厘米，宽是8厘米，求它的面积。

- 题目2：如果一个长方形的长增加了2厘米，宽减少了2厘米，面积会如何变化？2. 正方形面积计算：- 题目3：一个正方形的边长是10厘米，求它的面积。

- 题目4：如果正方形的边长扩大到原来的2倍，面积会扩大到原来的多少倍？3. 平行四边形面积计算：- 题目5：平行四边形的底是15厘米，高是10厘米，求它的面积。

- 题目6：如果平行四边形的底不变，高增加到原来的1.5倍，面积会如何变化？4. 三角形面积计算：- 题目7：一个三角形的底是14厘米，高是9厘米，求它的面积。

- 题目8：如果三角形的底不变，高增加到原来的2倍，面积会增加到原来的多少倍？5. 梯形面积计算：- 题目9：一个梯形的上底是8厘米，下底是12厘米，高是7厘米，求它的面积。

- 题目10：如果梯形的上底和下底都增加2厘米，高不变，面积会如何变化？6. 圆形面积计算：- 题目11：一个圆的半径是5厘米，求它的面积。

- 题目12：如果圆的半径增加到原来的1.5倍，面积会增加到原来的多少倍？7. 组合图形面积计算：- 题目13：一个由两个相同的长方形组成的L形图形，每个长方形的长是10厘米，宽是5厘米，求这个L形图形的面积。

- 题目14：如果将一个正方形和一个长方形组合成一个更大的长方形，正方形的边长是8厘米，长方形的长是12厘米，宽是8厘米，求组合后的长方形面积。

8. 面积单位转换：- 题目15：将1平方米转换为平方厘米。

- 题目16：如果一个房间的面积是50平方米，那么它的面积是多少平方厘米？9. 面积的实际应用：- 题目17：一块长方形的菜地，长是30米，宽是20米，如果每平方米可以种植5棵蔬菜，这块菜地可以种植多少棵蔬菜？- 题目18：一个圆形的花坛，半径是3米，如果每平方米可以种植10朵花，这个花坛可以种植多少朵花？10. 面积问题的解决策略：- 题目19：一个房间的地面是一个长方形，长是6米，宽是4米，如果要铺满整个房间需要多少平方米的地毯？- 题目20：一个三角形的风筝，底是10分米，高是8分米，如果要用布来制作这个风筝，需要多少平方分米的布？请同学们认真完成这些练习题，以加深对面积概念的理解和计算能力。

五年级下册数学试题-几何图形面积计算练习一(无答案)人教版

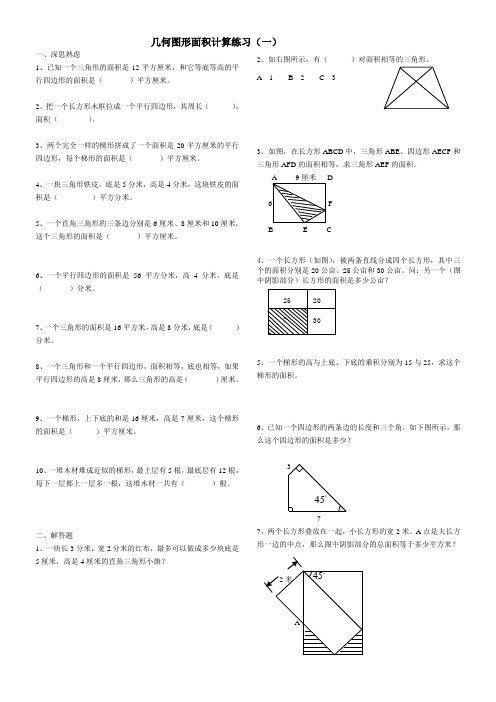
几何图形面积计算练习（一）一、深思熟虑1、已知一个三角形的面积是12平方厘米，和它等底等高的平行四边形的面积是（）平方厘米。

2、把一个长方形木框拉成一个平行四边形，其周长（），面积（）。

3、两个完全一样的梯形拼成了一个面积是20平方厘米的平行四边形，每个梯形的面积是（）平方厘米。

4、一块三角形铁皮，底是5分米，高是4分米，这块铁皮的面积是（）平方分米。

5、一个直角三角形的三条边分别是6厘米、8厘米和10厘米，这个三角形的面积是（）平方厘米。

6、一个平行四边形的面积是56平方分米，高4分米，底是（）分米。

7、一个三角形的面积是16平方米，高是8分米，底是（）分米。

8、一个三角形和一个平行四边形，面积相等，底也相等，如果平行四边形的高是8厘米，那么三角形的高是（）厘米。

9、一个梯形，上下底的和是16厘米，高是7厘米，这个梯形的面积是（）平方厘米。

10、一堆木材堆成近似的梯形，最上层有5根，最底层有12根，每下一层都上一层多一根，这堆木材一共有（）根。

二、解答题1、一块长3分米，宽2分米的红布，最多可以做成多少块底是5厘米，高是4厘米的直角三角形小旗？2、如右图所示，有（）对面积相等的三角形。

A 1B 2C 33、如图，在长方形ABCD中，三角形ABE、四边形AECF和三角形AFD的面积相等，求三角形AEF的面积。

A 9厘米 D6 FB E C4、一个长方形（如图），被两条直线分成四个长方形，其中三个的面积分别是20公亩、25公亩和30公亩。

问：另一个（图中阴影部分）长方形的面积是多少公亩？25 20? 305、一个梯形的高与上底、下底的乘积分别为15与25，求这个梯形的面积。

6、已知一个四边形的两条边的长度和三个角，如下图所示，那么这个四边形的面积是多少？34577、两个长方形叠放在一起，小长方形的宽2米。

A点是大长方形一边的中点，那么图中阴影部分的总面积等于多少平方米？。

五年级几何面积题

五年级几何面积题一、题目。

1. 一个平行四边形的底是8厘米，高是5厘米，它的面积是多少平方厘米？- 解析：根据平行四边形面积公式S = 底×高，已知底a = 8厘米，高h=5厘米，所以面积S=8×5 = 40平方厘米。

2. 三角形的底是12分米，高是8分米，求三角形的面积。

- 解析：三角形面积公式为S=(1)/(2)×底×高，底a = 12分米，高h = 8分米，那么面积S=(1)/(2)×12×8=48平方分米。

3. 一个梯形的上底是4厘米，下底是6厘米，高是5厘米，求梯形的面积。

- 解析：梯形面积公式S=((上底 + 下底)×高)/(2)，上底a = 4厘米，下底b=6厘米，高h = 5厘米，所以S=((4 + 6)×5)/(2)=25平方厘米。

4. 有一个长方形，长是10米，宽是6米，它的面积是多少平方米？- 解析：长方形面积公式S = 长×宽，长l=10米，宽w = 6米，面积S=10×6 = 60平方米。

5. 一个正方形的边长是7分米，它的面积是多少平方分米？- 解析：正方形面积公式S = 边长×边长，边长a = 7分米，所以面积S =7×7=49平方分米。

6. 平行四边形的面积是48平方厘米，底是6厘米，高是多少厘米？- 解析：由平行四边形面积公式S = 底×高可得高=(S)/(底)，已知S = 48平方厘米，底a = 6厘米，所以高h=(48)/(6)=8厘米。

7. 三角形的面积是36平方米，高是9米，底是多少米？- 解析：根据三角形面积公式S=(1)/(2)×底×高，可得底=(2S)/(高)，已知S = 36平方米，高h = 9米，所以底a=(2×36)/(9)=8米。

8. 梯形的面积是50平方厘米，上底是4厘米，下底是6厘米，高是多少厘米？- 解析：由梯形面积公式S=((上底 + 下底)×高)/(2)可得高=(2S)/(上底+下底)，已知S = 50平方厘米，上底a = 4厘米，下底b = 6厘米，所以高h=(2×50)/(4 + 6)=10厘米。

五年级数学思维《平面图形面积计算》专题训练

五年级数学思维《平面图形面积计算》专题训练一、选择题（每小题6分，共60分）1 平行四边形的底扩大到原来的3倍，高扩大到原来的3倍，它的面积（）.（A）扩大到原来的3倍（B）扩大到原来的9倍（C）扩大到原来的6倍（D）不变2 一个梯形的上、下底各扩大到原来的5倍，它的面积扩大到原来的（）倍.（A）5 （B）10 （C）25 （D）不一定3 如图，梯形中两个阴影部分的大小关系是（）．（A）①=②（B）①＞②（C）①＜②（D）无法比较4 一批钢管整齐地堆放在一起，最上层有5根，最下层有16根，每两层柜差1根．这批钢管共有（）根.（A）120 （B）126 （C）231 （D）2525 一个梯形，高是4m,若上底和下底不变，高增加2m后，面积增加8㎡，那么原来梯形的面积是（）㎡.（A）42 （B）16 （C）21 （D）326 如图，甲、乙两点分别为长方形宽的中点，那么图中面积相等的所有三角形是（）.（A）A、B和C （B）D和E （C）A和B （D）B和C7 如图，两个正方形的阴影部分的面积是26cm2，那么大正方形内的空白部分面积是（）cm2.（A）25 （B）15 （C）12.5 （D）108 如图，平行线间的三个图形，比较它们的面积是（）．（A）平行四边形大（B）三角形大（C）梯形大（D）相等9 牧羊人用15段每段长2米的篱笆，一面靠墙围成一个正方形或长方形羊圈，则羊圈的最大面积是（）平方米.（A）100 （B）108 （C）112 （D）122 10 如图，每个小方格面积为1，那么△ABC面积为（）.（A）10（B）11（C）12（D）11.5二、解答题（每题12分，共60分）11 如图，正方形的一组对边中，一条边增加17cm，另一条边减少10cm，这样就变成梯形，这时梯形的下底长是上底长的4倍．问：这个梯形的面积是多少？12 如图，将一个长方形分成一个三角形和一个梯形，其中三角形的面积比梯形的面积小60cm2，问：梯形的面积是多少？13 如图，正方形ABCD的边长为4cm，△BCF的面积比△DEF的面积多2cm2，求DE的长度.14 如图，已知△ABC的面积等于梯形BCDE的面积，求BC的长.（单位：cm）15 如图，已知长方形ABCD的长BC=l2厘米，宽DC=8厘米，并且BF=CG，三角形EFC的面积是32平方厘米，那么线段HG的长度是多少厘米？。

五年级数学平面几何图形的面积基础+拔高训练题 (带答案)

平面几何图形的面积1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米，则平行四边形的面积是（24 ）平方分米，三角形的面积是（12 ）平方分米。

方法一：可以分割成三个钝角三角形第一个钝角三角形的底是4，高是4，面积是：4×4÷2=8（平方厘米）第二个钝角三角形的高是8，底是（8-4），面积：8×（8-4）÷2=16（平方厘米）第三个钝角三角形的高是8，底是6，面积是：6×8÷2=24（平方厘米）一共的面积：8+16+24=48（平方厘米）方法二：把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×（8-6）-（8+4）×4÷2-8×（6+8）÷2=48（平方厘米）6、下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15（厘米）（15+20）×8÷2=140（平方厘米）7、右图中甲的面积比乙的面积大__________平方厘米．乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=（甲+空白）-（乙+空白）=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8（平方厘米）8、右图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9平方厘米，求ED 的长．A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积，则：长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24（平方厘米）则三角形BCE 的面积=24-9=15（平方厘米）EC=15×2÷6=5（厘米）ED=5-4=1（厘米）9、如图所示，CA=AB=4厘米，△ABE 比△CDE 的面积小2平方厘米，求CD 的长为多少厘米？A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积，则：三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8（平方厘米）则三角形BCD 的面积=8+2=10（平方厘米）CD=10×2÷4=5(厘米)10、一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？原来的面积=15×12=180（平方分米）现在的的面积=（15-2）×（12-2）=130（平方厘米）减少的面积：180-130=50（平方厘米）11、一个长方形，如果长减少5厘米，宽减少2厘米，那么面积就减少66平方厘米，这时剩下的部分恰好成为一个正方形，求原来长方形的面积？5×22566-2×5=56（平方厘米）设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长：8+5=13（厘米）原来长方形的宽：8+2=10（厘米）原来长方形的面积：13×10=130（平方厘米）12、下面图形中，长方形ABCD的面积是32平方厘米，EF都是所在边的中点，求三角形AEF的面积。

五年级数学上册图形面积(一)专题练习题

五年级数学上册图形面积(一)专题练习题一，填空题A，三角形1、两个完全一样的三角形可以拼成一个（），一个三角形的面积是这个（）形的（），所以三角形的面积＝（），字母表示（）。

2、一个三角形的底是7分米，是高的2倍，它的面积是（）平方厘米。

3、一个直角三角形，它的两条直角边分别是6cm和8cm，它的面积是（）4、一个三角形的底是4分米，高是30厘米，面积是（）平方分米。

5、两个完全一样的三角形能拼（）所以三角形的面积等于（）。

用字母表示是（）。

6、一个三角形底是5cm，高是7cm，面积是（）。

7、一个三角形和一个平行四边形面积相等，高也相等，则三角形的底是平行四边形底的（）。

一个三角形的面积是30平方厘米，底是6厘米，高是（）厘米。

8、一个三角形的高是7分米，底是8分米，和它等底等高的平行四边形的面积是（）平方分米。

9、一个三角形的面积是4.8平方米，与它等底等高的平行四边形的面积是（）10、一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米，平行四边形的面积是（）平方分米，三角形的面积（）平方分米。

11、一个三角形和一个平行四边形的面积相等，底也相等，如果三角形的高是10米，那么平行四边形的高是（）米；如果平行四边形的高是10米，那么三角形的高是（）米。

B，平行四边形1、一个平行四边形，沿它的一条高剪开，通过平移拼成长方形。

这个长方形的长与原来平行四边形的（）相等；原平行四边形的高与长方形的（）相等。

2、一个平行四边形的面积是20平方米，高是4米，它的底是（），与它等底等高的三角形面积是（）平方米。

3、一个平行四边形的面积是48厘米2 ，高是6厘米,底是（）厘米。

4、一个平行四边形的面积是48平方分米，与它等底等高的三角形的面积是（）平方分米。

5、两个完全一样的三角形可以拼成一个平行四边形，这个平行四边形的底就是（），这个平行四边形的高也就是（），因为平行四边形的面积等于（），所以三角形的面积等于（）。

【小学】五年级数学上册试题一课一练6.1《组合图形的面积》习题1 北师大版(含答案)

《组合图形的面积》习题1引领思路1．某公园有一块长2021宽15m的长方形草地，草地中有两条均匀的小路（如图1），求草地的实际面积。

想：该问题如果用一般方法解决，就要从长方形草地的面积中减去两条小路的面积，显得比较麻烦。

如果我们转换思路，用平移的方法来解决，就显得比较容易。

如图1，是两条小路把长方形草地分成了四块；如图2，是把上面的两块向（）平移了（）米；如图3，是把左面的两块地向（）平移了（）米，四块草地就拼成了一个长为（）、宽为（）的长方形，求出该长方形的面积即可。

不管哪个图形，底和高都是垂直关系的两条线段，确定了底就确定了高。

夯实基础2．计算下面各图形的面积。

（单位：厘米）3．图中大、小正方形的边长分别是10厘米和7厘米，求每个直角三角形的面积。

4 如图，一块梯形田地中间留有一条宽2米的路，求这块地的面积。

（单位：米）5．如图，有两个边长是10cm的正方形卡片叠在一起，求重叠部分的面积。

（单位：cm）参考答案引领思路1．某公园有一块长2021宽15m的长方形草地，草地中有两条均匀的小路（如图1），求草地的实际面积。

想：该问题如果用一般方法解决，就要从长方形草地的面积中减去两条小路的面积，显得比较麻烦。

如果我们转换思路，用平移的方法来解决，就显得比较容易。

如图1，是两条小路把长方形草地分成了四块；如图2，是把上面的两块向（下）平移了（1）米；如图3，是把左面的两块地向（右）平移了（ 1 ）米，四块草地就拼成了一个长为（19m ）、宽为（14m）的长方形，求出该长方形的面积即可。

不管哪个图形，底和高都是垂直关系的两条线段，确定了底就确定了高。

20215－（15×1＋2021－1×1） 19×14＝266（m²）＝300－（15＋2021）＝300－34＝266（m²）夯实基础2．计算下面各图形的面积。

（单位：厘米）（8＋4＋202116÷2－4×4 8×4＋（4＋6）×（10－8）÷2＝32×16÷2－16 ＝32＋24×2÷2＝256－16 ＝32＋24＝240（厘米²）＝56（厘米²）3．图中大、小正方形的边长分别是10厘米和7厘米，求每个直角三角形的面积。

五年级数学图形面积专题训练

五年级数学图形面积专题训练五年级数学图形面积专题训练（一）一、填空。

1、一个平行四边形的底长 8 厘米，是高的 2 倍，它的面积是（），与它等底等高的三角形面积是（）。

2、一个梯形的上底是 16 米，下底是 24 米，高30 米，它的面积是（）平方米。

3、一堆钢管，最上层有 3 根，最下层有 13 根，每相邻两层相差 1 根，这堆钢管一共有（）根。

4、一个直角三角形，三条边分别是10 厘米、8 厘米、6 厘米，它的面积是（），用两个这样的三角形拼成的长方形面积是（）。

5、一个三角形和一个平行四边形的底相等，面积也相等，已知三角形的高是32 厘米，那么平行四边形的高是（）厘米。

6、一个平行四边形的面积是 8 平方分米，高是2 分米，它的底是（）分米。

7、一个近似梯形的花坛，高 10 米，上下底之和是 16 米，面积是（）。

8、一个三角形的面积是 6 平方分米，底 3 分米，高是（）。

9、用四根硬纸条钉成一个长方形框架，将它拉成一个平行四边形后，周长（），面积（）。

------（填“不变”或“变大”、“变小”）10、三角形的底扩大3 倍，高不变，面积会（）。

11、0.45 公顷＝（）平方米。

12、两个完全一样的梯形可以拼成一个（）形。

13、一个梯形上底与下底的和是 15 厘米，高是 8.8 厘米，面积是（）平方米。

14、平行四边形的底是 2 分米 5 厘米，高是底的 1.2 倍，它的面积是（）平方厘米。

15、梯形的上底增加 3 厘米，下底减少 3 厘米，高不变，面积（）。

16、一个直角三角形的三条边分别是 6cm，8cm 和 10cm，它斜边上的高是（）。

17、当梯形的上底逐渐缩小到一点时，梯形就转化成（）；当梯形的上底增大到与下底相等时，梯形就转化成（）。

二、判断。

1、三角形面积是平行四边形的一半。

（）2、两个面积相等的三角形一定能拼成一个平行四边形。

（）3、面积相等的两个梯形，形状不一定相等。

【北师大版】五年级上册数学试题-图形的面积(一)测试卷

1二图形的面积（一） ⒈同学们，这一单元我们学习的主要内容有：平面图形面积大小的比较方法，平行四边形、三角形以及梯形的面积计算方法等。

⒉在“比较图形的面积”的情境活动中，主要是借助方格纸来比较各种不同形状图形面积的大小，我们可以从中体验到确定两个图形面积的大小，有多种比较方法。

⒊探索平行四边形、三角形以及和梯形的面积公式的推导过程时，将利用方格纸或割补等方法，我们会经历自主探索的过程，为今后形成较强的探索能力打下扎实的基础，同学们一定要用心呦！比较图形的面积⒈借助方格纸，能直接判断图形面积的大小。

⒉通过交流，知道比较图形面积大小的基本方法。

⒊体验图形形状的变化与面积大小变化的关系。

⒈数一数。

（每个小方格的边长是1cm ）图（）面积最大，图（）面积最小。

⒉ 下面图形的面积分别是多少？（每个小方格的边长都是1cm ）图⑴（）平方厘米，图⑵ ( ）平方厘米，图⑶（）平方厘米，图⑷（）平方厘米。

⒊如下图：一个梯形少了一块，你认为下面的哪个图形补上去就能使这个梯形完整了？轻松演练单元总览目标导航⑴ ⑵ ⑶ ⑷ ⑴ ⑵ ⑶ ⑷1⒋如下图，左边的两个图形，它们可以拼成右边的哪个图形？⒌下面方格图中每个小方格的面积为1平方厘米。

请你画出2个面积都是4平方厘米的不同形状的三角形。

⒍下面方格图中每个小方格的面积为1平方厘米。

请你画出3个面积都是8平方厘米的不同图形。

⒎下图是由7个边长为2厘米的正方形组成的，你知道这个图形的周长吗？通过本课的学习我能得到☆☆☆☆☆地毯上的图形面积⒈能直接在方格图上，数出相关图形的面积。

⒉能利用分割的方法，将较复杂的图形转化为简单的图形，并用较简单的方法计算面积。

⒊在解决问题的过程中，体会策略、方法的多样性。

能力提升聚沙成塔轻松演练目标导航1⒈地毯上绿色部分的面积是多少？（每个小方格的边长表示1cm ）绿色部分的面积是平方厘米 ⒉求出下面各图中涂色部分的面积。

北师大版数学五年级上册第六单元组合图形的面积达标测试卷(及答案)

北师大版数学五年级上册第六单元组合图形的面积达标测试卷一、选择题（满分16分）1．图中每个小方格的面积表示1平方厘米，估计这个米老鼠图片的面积是（）平方厘米。

A．10 B．20 C．35 D．502．计算下边组合图形的面积，列式正确的是（）。

A．（18＋20）×20＋18×（35－15）B．（18＋20）×35C．（18＋30）×20÷2＋18×15÷2 D．（18＋30）×35÷23．下面的第（）个算式是在计算右面图形的面积．A．ab+ah B．ab+bh C．ab+ah÷2 D．ab﹣ah÷24．如图，甲的周长（）乙的周长；甲的面积（）乙的面积．A．大于B．小于C．等于5．图中是由一个小正方形与8个相同的长方形拼成的大正方形．已知小正方形的面积是900平方厘米，大正方形的周长是200厘米，那么，每个长方形的长是（）厘米．A．12 B．20 C．25 D．306．下面两个图形的面积相比，（）A．①>②B．①<②C．①=②7．下面每一组中两个图形的周长相等吗？面积呢？8．用12个1平方厘米的小正方形拼成一个长方形，这个长方形的面积是（）平方厘米。

A．12 B．14 C．16二、填空题（满分16分）9．如图，两个正方形的边长分别是8厘米和10厘米，阴影部分的面积是平方厘米．10．长方形的广告牌长为20米，宽为l6米，A、B、C、D分别在四条边上，并且C比A低8米，D在B的左边5米，则四边形ABCD的面积是平方米．11．图中有大、中、小3个大小不同的正方形，其中大正方形的面积比中正方形的面积大32，大正方形的周长比小正方形的周长多16．那么大正方形的面积是．12．如图，由8个同样的小长方形拼成一个大长方形．大长方形的周长是84厘米．大长方形的面积是平方厘米．13．如图所示的直角梯形的每条边长向外作正方形，则四个正方形的面积之和是．14．一个长方形的长和宽都增加10厘米，形成的新长方形面积比原长方形的面积大400平方厘米，原来长方形的周长是厘米．15．一个长10cm，周长24cm的长方形，它的面积是（________）cm2。

五年级数学图形面积专题训练(一)

五年级图形面积练习题

五年级数学多边形面积与组合图形面积(含答案)

五年级图形的面积练习题

北师大版2020-2021小学五年级数学上册六组合图形的面积单元综合训练题1(附答案)

五年级图形面积练习题

五年级下册数学试题 - 图形面积（奥数版块） 北师大版

五年级数学 平面几何图形的面积 基础+拔高例题 带作业(带详细答案)

北师大版五年级数学上册期末复习专题组合图形的面积练习(含答案)

【期末专项复习】北师大版小学五年级上册数学《组合图形的面积 》期末专项强化突破卷(一)含答案

（完整版）小学五年级数学三角形的面积练习题（含答案）

五年级数学面积练习题

五年级下册数学试题-几何图形面积计算练习一(无答案)人教版

五年级几何面积题

五年级数学思维《平面图形面积计算》专题训练

五年级数学 平面几何图形的面积基础+拔高训练题 (带答案)

五年级数学上册图形面积(一)专题练习题

【小学】五年级数学上册试题 一课一练6.1《组合图形的面积》习题1 北师大版(含答案)

五年级数学图形面积专题训练

【北师大版】五年级上册数学试题-图形的面积(一)测试卷

北师大版数学五年级上册第六单元组合图形的面积达标测试卷(及答案)

五年级下册数学试题 - 图形面积（奥数版块）北师大版

五年级数学平面几何图形的面积基础+拔高例题带作业(带详细答案)

【期末专项复习】北师大版小学五年级上册数学《组合图形的面积》期末专项强化突破卷(一)含答案

五年级数学平面几何图形的面积基础+拔高训练题 (带答案)

【小学】五年级数学上册试题一课一练6.1《组合图形的面积》习题1 北师大版(含答案)