四皇后问题(数据结构C语言)
八皇后问题c语言代码讲解

八皇后问题c语言代码讲解八皇后问题是一个经典的回溯算法问题,要求在一个8x8的棋盘上放置8个皇后,使得它们互不攻击,即任意两个皇后都不能在同一行、同一列或同一对角线上。
下面是一个使用C语言实现八皇后问题的代码示例:c.#include <stdio.h>。
#define N 8。
int board[N][N];// 检查当前位置是否安全。
int isSafe(int row, int col) {。
int i, j;// 检查当前列是否有皇后。
for (i = 0; i < row; i++) {。
if (board[i][col] == 1) {。
return 0;}。
}。
// 检查左上对角线是否有皇后。
for (i = row, j = col; i >= 0 && j >= 0; i--, j--) {。
if (board[i][j] == 1) {。
return 0;}。
}。
// 检查右上对角线是否有皇后。
for (i = row, j = col; i >= 0 && j < N; i--, j++) {。
if (board[i][j] == 1) {。
return 0;}。
}。
return 1;}。
// 在当前行放置皇后。
int solve(int row) {。
int col;// 所有行都放置完毕,打印结果。
if (row == N) {。
for (int i = 0; i < N; i++) {。
for (int j = 0; j < N; j++) {。
printf("%d ", board[i][j]); }。
printf("\n");}。
printf("\n");return 1;}。
// 逐列尝试放置皇后。
for (col = 0; col < N; col++) {。
N皇后问题

源程序:#include<stdio.h>#include<stdlib.h>#include<math.h>#define MAXQSIZE 100 //循环队列最大元素个数//皇后问题搜索结点typedef struct qnode {int k;int* x;} QueenNode;typedef qnode QElemType;//循环队列类型typedef struct QNode{QElemType *base;int front, rear;}SqQueue;//初始化循环队列int InitQueue(SqQueue *q){q->base = (QElemType *) malloc ( MAXQSIZE * sizeof (QElemType)); //分配数组空间if(!q->base) exit(0);//初始化队头、队尾q->front = 0;q->rear =0;return 1;}//返回队列长度int QueueLength(SqQueue *q){return (q->rear - q->front + MAXQSIZE) % MAXQSIZE ;}//队列空判定int QueueEmpty(SqQueue *q){return q->front == q->rear ;}//队满判定int QueueFull(SqQueue *q){return ((q->rear +1) % MAXQSIZE) == q->front;}//入队int EnQueue(SqQueue *q, QElemType e){if (((q->rear +1) % MAXQSIZE) == q->front) return 0; //队满则出错q->base[q->rear] = e; //队尾处放入新元素q->rear=(q->rear +1) % MAXQSIZE; //循环递增队尾return 1;}//出队QElemType DeQueue(SqQueue *q){QElemType e;if (q->front == q->rear) exit(0); //队空则出错e=q->base [q->front]; //取队头元素q->front =(q->front+1) % MAXQSIZE; //循环递增队头return e;}//销毁队列int DestoryQueue(SqQueue *q){free(q->base);q->base=NULL;q->front =0;q->rear =0;return 1;}//创建新的搜索结点QueenNode NewQNode(int *x, int row, int col,int n){QueenNode e;e.k=row;e.x=(int *)malloc((n+1)*sizeof(int));for(int j=1; j<=n; j++) e.x[j]=x[j]; //复制上一步的部分解e.x[row]=col;return e;}//输出void output(QueenNode e,int n){for(int i=1; i<=n; i++) printf("%5d",e.x[i]);printf("\n");}//检查皇后i 的放置是否满足约束(与前面i-1 个皇后是否冲突)int place (QueenNode e){for(int i=1; i<e.k; i++)if ( (e.x[i]==e.x[e.k]) ||abs(i-e.k) == abs(e.x[i]-e.x[e.k]))return 0;return 1;}void queen_branch(int n){SqQueue q, *qt;QueenNode e, ec;int i, *x;int k, cnt=0;x=(int *)malloc((n+1)*sizeof(int));//初始化队列qt=&q;InitQueue(qt);//根结点无父结点,必须单独构造其部分解向量k=0;for(i=1; i<=n; i++) x[i]=0;e=NewQNode(x, k, 0,n);EnQueue(qt, e); //根结点入队while(!QueueEmpty(qt)) {e=DeQueue(qt); //取出队头结点k=e.k +1 ;if ( k>n ) {//叶结点:说明已将所有皇后放完,得到一个可行解,输出++cnt;if(cnt==1){printf("%d个皇后放置在%d×%d棋盘上的全部可行方案如下:\n 行号",n,n,n);for(i=1;i<=n;i++)printf(" %d行",i);printf("\n");}printf("方案%2d",cnt);output(e,n);}else//生成全部子结点for(i=1; i<=n; i++) {ec= NewQNode (e.x, k, i,n);if ( place(ec) ) {EnQueue(qt, ec);//printq("入队", qt);}}}if(cnt==0) printf("找不到可行的%d皇后放置方案!\n",n);else printf("[每一行所对应的数字表示该行的皇后放置的列号]\n"); }void main(void){int n;printf("请输入放置在棋盘上皇后的个数: ");scanf("%d",&n);queen_branch( n);system("pause");}运行结果:。
回溯法解皇后问题

Ch1-绪论1. 回溯法解皇后问题#include "stdio.h"#include "math.h"#include "stdlib.h"void queen(int n){ int i,j,k,jt,*q;q=malloc(n*sizeof(int));for(i=0; i<n; i++) q[i]=0;i=0; jt=1;printf("\n");printf("%d queen problem\n",n);while(jt==1){ if (q[i]<n){ k=0;while((k<i)&&((q[k]-q[i])*(fabs(q[k]-q[i])-fabs(k-i)))!=0) k=k+1;if (k<i) q[i]=q[i]+1;else{ if (i==n-1){ for(j=0; j<n; j++)printf("%5d",q[j]+1);printf("\n");q[n-1]=q[n-1]+1;}else i=i+1;}}else{ q[i]=0; i=i-1;if (i<0){ printf("\n"); free(q); return; }q[i]=q[i]+1;}}}2. 简单二分法求方程实根(1)#include "stdio.h"#include "math.h"double root(a,b,eps,f)double a,b,eps,(*f)();{ double f0,f1,c;f0=(*f)(a);while (fabs(a-b)>=eps){ c=(a+b)/2; f1=(*f)(c);if (f1==0) return(c);if (f0*f1>0) a=c;else b=c;}c=(a+b)/2;return(c);}(2)#include "root.c"main(){ double a,b,eps,f();a=1; b=2; eps=0.000001;printf("x=%7.3f\n",root(a,b,eps,f));}double f(x)double x;{ double y;y=x+log(x)-2.2;return(y);}Ch2-矩阵与线性代数方程组(1)文件头:#include "math.h"#include "stdio.h"int maqr(m,n,a,q)int m,n;double a[],q[];{ int i,j,k,l,nn,p,jj;double u,alpha,w,t;if (m<n){ printf("fail\n"); return(0);}for (i=0; i<=m-1; i++)for (j=0; j<=m-1; j++){ l=i*m+j; q[l]=0.0;if (i==j) q[l]=1.0;}nn=n;if (m==n) nn=m-1;for (k=0; k<=nn-1; k++){ u=0.0; l=k*n+k;for (i=k; i<=m-1; i++){ w=fabs(a[i*n+k]);if (w>u) u=w;}alpha=0.0;for (i=k; i<=m-1; i++){ t=a[i*n+k]/u; alpha=alpha+t*t;}if (a[l]>0.0) u=-u;alpha=u*sqrt(alpha);if (fabs(alpha)+1.0==1.0){ printf("fail\n"); return(0);}u=sqrt(2.0*alpha*(alpha-a[l]));if ((u+1.0)!=1.0){ a[l]=(a[l]-alpha)/u;for (i=k+1; i<=m-1; i++){ p=i*n+k; a[p]=a[p]/u;}for (j=0; j<=m-1; j++){ t=0.0;文件尾:for (jj=k; jj<=m-1; jj++)t=t+a[jj*n+k]*q[jj*m+j];for (i=k; i<=m-1; i++){ p=i*m+j; q[p]=q[p]-2.0*t*a[i*n+k];}}for (j=k+1; j<=n-1; j++){ t=0.0;for (jj=k; jj<=m-1; jj++)t=t+a[jj*n+k]*a[jj*n+j];for (i=k; i<=m-1; i++){ p=i*n+j; a[p]=a[p]-2.0*t*a[i*n+k];}}a[l]=alpha;for (i=k+1; i<=m-1; i++)a[i*n+k]=0.0;}}for (i=0; i<=m-2; i++)for (j=i+1; j<=m-1;j++){ p=i*m+j; l=j*m+i;t=q[p]; q[p]=q[l]; q[l]=t;}return(1);}(2)#include "stdio.h"#include "maqr.c"main(){ int i,j;static double q[4][4],a[4][3]={ {1.0,1.0,-1.0}, {2.0,1.0,0.0},{1.0,-1.0,0.0},{-1.0,2.0,1.0}};i=maqr(4,3,a,q);if (i!=0){ printf("MAT Q IS:\n");for (i=0; i<=3; i++){ for (j=0; j<=3; j++)printf("%13.7e ",q[i][j]);printf("\n");}printf("\n");printf("MAT R IS:\n");for (i=0; i<=3; i++){ for (j=0; j<=2; j++)printf("%13.7e ",a[i][j]);printf("\n");}printf("\n");}}(3)文件头:#include "stdlib.h"#include "math.h"int muav(m,n,a,u,v,eps,ka)int m,n,ka;double eps,a[],u[],v[];{ int i,j,k,l,it,ll,kk,ix,iy,mm,nn,iz,m1,ks;double d,dd,t,sm,sm1,em1,sk,ek,b,c,shh,fg[2],cs[2]; double *s,*e,*w;void ppp();void sss();s=malloc(ka*sizeof(double));e=malloc(ka*sizeof(double));w=malloc(ka*sizeof(double));it=60; k=n;if (m-1<n) k=m-1;l=m;if (n-2<m) l=n-2;if (l<0) l=0;ll=k;if (l>k) ll=l;if (ll>=1){ for (kk=1; kk<=ll; kk++){ if (kk<=k){ d=0.0;for (i=kk; i<=m; i++){ ix=(i-1)*n+kk-1; d=d+a[ix]*a[ix];}s[kk-1]=sqrt(d);if (s[kk-1]!=0.0){ ix=(kk-1)*n+kk-1;if (a[ix]!=0.0){ s[kk-1]=fabs(s[kk-1]);if (a[ix]<0.0) s[kk-1]=-s[kk-1];}for (i=文件尾:{ int i,j,p,q;double d;if (m>=n) i=n;else i=m;for (j=1; j<=i-1; j++){ a[(j-1)*n+j-1]=s[j-1];a[(j-1)*n+j]=e[j-1];}a[(i-1)*n+i-1]=s[i-1];if (m<n) a[(i-1)*n+i]=e[i-1];for (i=1; i<=n-1; i++)for (j=i+1; j<=n; j++){ p=(i-1)*n+j-1; q=(j-1)*n+i-1;d=v[p]; v[p]=v[q]; v[q]=d;}return;}static void sss(fg,cs)double cs[2],fg[2];{ double r,d;if ((fabs(fg[0])+fabs(fg[1]))==0.0){ cs[0]=1.0; cs[1]=0.0; d=0.0;} else{ d=sqrt(fg[0]*fg[0]+fg[1]*fg[1]);if (fabs(fg[0])>fabs(fg[1])){ d=fabs(d);if (fg[0]<0.0) d=-d;}if (fabs(fg[1])>=fabs(fg[0])){ d=fabs(d);if (fg[1]<0.0) d=-d;}cs[0]=fg[0]/d; cs[1]=fg[1]/d;}r=1.0;if (fabs(fg[0])>fabs(fg[1])) r=cs[1];elseif (cs[0]!=0.0) r=1.0/cs[0];fg[0]=d; fg[1]=r;return;}#include "stdio.h"#include "cgauss.c"main(){ int i;static double ar[4][4]={ {1.0,3.0,2.0,13.0},{7.0,2.0,1.0,-2.0},{9.0,15.0,3.0,-2.0},{-2.0,-2.0,11.0,5.0}};static double ai[4][4]={ {3.0,-2.0,1.0,6.0},{-2.0,7.0,5.0,8.0},{9.0,-3.0,15.0,1.0},{-2.0,-2.0,7.0,6.0}}; static double br[4]={2.0,7.0,3.0,9.0};static double bi[4]={1.0,2.0,-2.0,3.0};if (cgauss(4,ar,ai,br,bi)!=0)for (i=0;i<=3;i++)printf("b(%d)=%13.7e +j %13.7e\n",i,br[i],bi[i]); }。
四皇后问题实验报告

人工智能——四皇后问题一、问题描述四皇后问题一个4×4国际象棋盘,依次放入四个皇后,条件:每行、每列及对角线上只允许出现一枚棋子。
设:DATA=L(表) x∈L x ∈﹛i j﹜ 1≤ i, j ≤4 其中:i j 表示棋子所在行列如:24 表示第二行第四列有一枚棋子∵棋盘上可放入的棋子数为0 ~ 4 个∴L表中的元素数为0 ~ 4 个,即 Length L = 0 ~ 4 ,如图A ﹛12,24,31,43 ﹜定义规则: if 1≤ i ≤4 and Length DATA = i -1then APPEND(DATA( ij )) 1≤ j ≤4①对于任一行i , 1≤ j ≤4 表明每行有四条规则。
比如第一行:R11,R12,R13,R14②棋盘中共有四行,所以共有16条规则。
即: R11,R12,R13,R14R21,R22,R23,R24R31,R32,R33,R34R41,R42,R43,R44③ 16条规则中,哪些是当前可用规则,取决于DATA的长度,即:DATA中的元素个数。
换言之,每次只能将一个棋子放在当前行的下一行。
二、回溯法搜索策略图讨论:上述算法产生22次回溯,原因在于规则自然顺序排列,没考虑任何智能因素。
改进算法定义对角线函数:diag(i,j):过ij点最长的对角线长度值。
规定:①如果: diag(i,k) ≤ diag(i,j) 则规则排列次序为: Rik, Rij 同一行四条规则中,对角线函数值小的排在前面②如果:diag(i,k) = diag(i,j) 则规则排列次序为: Rij ,Rik j < k对角线长度相等的规则按照字母排列顺序排序讨论:①利用局部知识排列规则是有效的。
② BACKTRACK算法对重复出现的状态没有判断,所以可能造成出现死循环。
③没有对搜索深度加以限制,可能造成搜索代价太大。
三、算法描述回溯法——在约束条件下先序遍历,并在遍历过程中剪去那些不满足条件的分支。
回溯典型题目——N皇后问题剖析
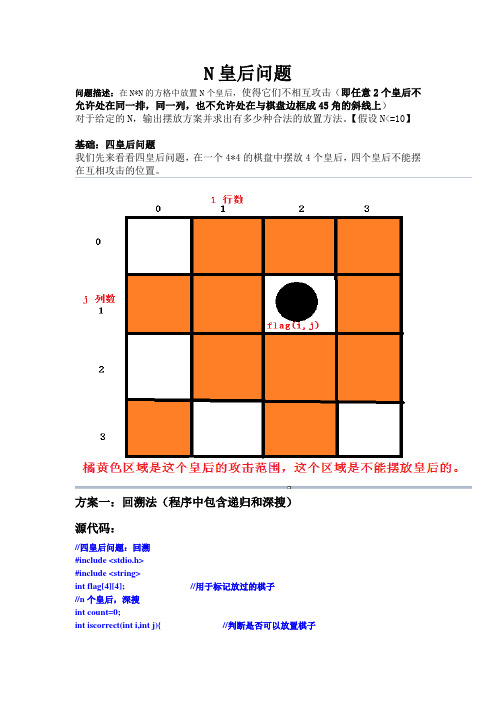
N皇后问题问题描述:在N*N的方格中放置N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上)对于给定的N,输出摆放方案并求出有多少种合法的放置方法。
【假设N<=10】基础:四皇后问题我们先来看看四皇后问题,在一个4*4的棋盘中摆放4个皇后,四个皇后不能摆在互相攻击的位置。
方案一:回溯法(程序中包含递归和深搜)源代码://四皇后问题:回溯#include <stdio.h>#include <string>int flag[4][4]; //用于标记放过的棋子//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<4;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<4;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=3;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=3&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=3&&b<=3;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==4){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已//经完成0~3的所有排布已经完成for(m=0;m<4;m++){for(n=0;n<4;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<4;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}其实从四皇后问题拓展到n皇后问题是非常简单的事情,方案一进阶到N皇后的源代码:N皇后其实只要把其中的4改成N就行了:源代码:#include <stdio.h>#include <string>int flag[10][10]; //用于标记放过的棋子int number; //表示棋子个数//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<number;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<number;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=number-1;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=number-1&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=number-1&&b<=number-1;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==number){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已经完成0~number-1的所有排布已经完成for(m=0;m<number;m++){for(n=0;n<number;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<number;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){scanf("%d",&number);memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}。
C语言题_2n皇后问题

printf("%c",NN[i][j]);
printf("\n");
for(i=1;i<=N;i++)
{
}
NN[line][i]='Q';
q[line]=i;
if(n=Cheak(line)>0)
{
}
Search(line,N);
NN[line][i]='1';
for(i=1;i<=(N+1)/2;i++)
{
}
void main()
{
//初始
int N,i,j;
q[1]=i;
NN[1][i]='Q';
Search(1,N);
NN[1][i]='1';
for(i=1;i<9;i++)
for(j=1;j<9;j++)
//如果最后一行的 Q 已经存在,则打印棋盘
//遍历此行,并通过检测查询下一行
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安,与全要过,加度并强工且看作尽护下可1都关能可于地以管缩正路小常高故工中障作资高;料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高,核中或对资者定料对值试某,卷些审弯异核扁常与度高校固中对定资图盒料纸位试,置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高,技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术,、以术来管及避架系免等统不多启必项动要方方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
c语言数据结构及算法

C语言是一种广泛应用于编程和软件开发的编程语言,它提供了一系列的数据结构和算法库,使得开发者能够在C语言中使用这些数据结构和算法来解决各种问题。
以下是C语言中常用的数据结构和算法:数据结构:1. 数组(Array):一组相同类型的元素按顺序排列而成的数据结构。
2. 链表(Linked List):元素通过指针连接而成的数据结构,可分为单向链表、双向链表和循环链表等。
3. 栈(Stack):具有后进先出(LIFO)特性的数据结构,可用于实现函数调用、表达式求值等。
4. 队列(Queue):具有先进先出(FIFO)特性的数据结构,可用于实现任务调度、缓冲区管理等。
5. 树(Tree):一种非线性的数据结构,包括二叉树、二叉搜索树、堆、A VL树等。
6. 图(Graph):由节点和边组成的数据结构,可用于表示网络、关系图等。
7. 哈希表(Hash Table):基于哈希函数实现的数据结构,可用于高效地查找、插入和删除元素。
算法:1. 排序算法:如冒泡排序、插入排序、选择排序、快速排序、归并排序等。
2. 查找算法:如线性查找、二分查找、哈希查找等。
3. 图算法:如深度优先搜索(DFS)、广度优先搜索(BFS)、最短路径算法(Dijkstra、Floyd-Warshall)、最小生成树算法(Prim、Kruskal)等。
4. 字符串匹配算法:如暴力匹配、KMP算法、Boyer-Moore 算法等。
5. 动态规划算法:如背包问题、最长公共子序列、最短编辑距离等。
6. 贪心算法:如最小生成树问题、背包问题等。
7. 回溯算法:如八皇后问题、0-1背包问题等。
这只是C语言中常用的一部分数据结构和算法,实际上还有更多的数据结构和算法可以在C语言中实现。
开发者可以根据具体需求选择适合的数据结构和算法来解决问题。
同时,C语言也支持自定义数据结构和算法的实现,开发者可以根据需要进行扩展和优化。
四皇后实验报告

篇一:四皇后问题实验报告人工智能——四皇后问题一、问题描述四皇后问题一个4×4国际象棋盘,依次放入四个皇后,条件:每行、每列及对角线上只允许出现一枚棋子。
设:data=l(表) x∈l x ∈﹛i j﹜1≤ i, j ≤4 其中:i j 表示棋子所在行列如:24 表示第二行第四列有一枚棋子∵棋盘上可放入的棋子数为0 ~ 4 个∴l表中的元素数为0 ~ 4 个,即 length l = 0 ~ 4 ,如图a ﹛12,24,31,43 ﹜定义规则: if1≤ i ≤4andlength data = i -1thenappend(data( ij )) 1≤ j ≤4①对于任一行i , 1≤ j ≤4 表明每行有四条规则。
比如第一行:r11,r12,r13,r14②棋盘中共有四行,所以共有16条规则。
即: r11,r12,r13,r14r21,r22,r23,r24r31,r32,r33,r34r41,r42,r43,r44③ 16条规则中,哪些是当前可用规则,取决于data的长度,即:data中的元素个数。
换言之,每次只能将一个棋子放在当前行的下一行。
二、回溯法搜索策略图讨论:上述算法产生22次回溯,原因在于规则自然顺序排列,没考虑任何智能因素。
改进算法定义对角线函数:diag(i,j):过ij点最长的对角线长度值。
规定:①如果: diag(i,k) ≤ diag(i,j) 则规则排列次序为: rik, rij 同一行四条规则中,对角线函数值小的排在前面②如果:diag(i,k) = diag(i,j) 则规则排列次序为: rij ,rikj < k 对角线长度相等的规则按照字母排列顺序排序讨论:①利用局部知识排列规则是有效的。
② backtrack算法对重复出现的状态没有判断,所以可能造成出现死循环。
③没有对搜索深度加以限制,可能造成搜索代价太大。
三、算法描述回溯法——在约束条件下先序遍历,并在遍历过程中剪去那些不满足条件的分支。
八皇后问题c语言代码

八皇后问题c语言代码八皇后问题是经典的回溯算法问题,下面是一个简单的C语言代码示例来解决八皇后问题:c.#include <stdio.h>。
#include <stdbool.h>。
#define N 8。
int board[N][N];void printSolution() {。
for (int i = 0; i < N; i++) {。
for (int j = 0; j < N; j++) {。
printf("%d ", board[i][j]); }。
printf("\n");}。
}。
bool isSafe(int row, int col) {。
int i, j;for (i = 0; i < col; i++) {。
if (board[row][i]) {。
return false;}。
}。
for (i = row, j = col; i >= 0 && j >= 0; i--, j--) {。
if (board[i][j]) {。
return false;}。
}。
for (i = row, j = col; j >= 0 && i < N; i++, j--) {。
if (board[i][j]) {。
return false;}。
}。
return true;}。
bool solveNQUtil(int col) {。
if (col >= N) {。
return true;}。
for (int i = 0; i < N; i++) {。
if (isSafe(i, col)) {。
board[i][col] = 1;if (solveNQUtil(col + 1)) {。
return true;}。
board[i][col] = 0;}。
树和二叉树(4N皇后(回溯法))

Backtracking
回溯 N皇后问题 跳马问题 迷宫问题 图的着色问题 0-1背包问题 装载问题 批处理作业调度 填数问题 组合输出问题 算24点问题 ACM应用
学习要点
掌握回溯的概念 掌握经典问题的回溯解决方法 掌握回溯与其它方法的异同
回溯法
有许多问题,当需要找出它的解集或者要求回答什么 解是满足某些约束条件的最佳解时,往往要使用回溯 法。 ► 回溯法的基本做法是搜索,或是一种组织得井井有条 的,能避免不必要搜索的穷举式搜索法。这种方法适 用于解一些组合数相当大的问题。 ► 回溯法在问题的解空间树中,按深度优先策略,从根 结点出发搜索解空间树。算法搜索至解空间树的任意 一点时,先判断该结点是否包含问题的解。如果肯定 不包含,则跳过对该结点为根的子树的搜索,逐层向 其祖先结点回溯;否则,进入该子树,继续按深度优 先策略搜索。
N皇后问题
递归写法: procedure try(k:byte); var i:byte; begin for i:=1 to n do if place(k) then begin x[k]:=i; if k=n then print else try(k+1); end;
分析:状态恢复(回溯)在什 么地方实现?
x
path:array[1..m] of integer; 其中,path[i]:表示第i个节点所走的方向
方向t,下一步的位置就是 (x+dx[t], y+dy[t])。
跳马问题
约束条件:
不越界: (x + dx[i] <= n) and (y + dy[i] > 0) and (y + dy[i] <= n)
x[3,1,4,2]
c++八皇后问题最简单算法

八皇后问题是一个经典的回溯算法问题。
下面是一个使用C语言实现的简单算法:c复制代码#include<stdio.h>#include<stdbool.h>#define N 8int col[N] = {0}; // 表示皇后所在的列int queens[N][N] = {0}; // 存储棋盘状态bool is_valid(int row, int col) {for (int i = 0; i < row; i++) {if (queens[i][col] || queens[i][col - (row - i)] || queens[i][col + (row -i)]) {return false;}}return true;}void backtrack(int row) {if (row == N) { // 找到了一组解for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf("%d ", queens[i][j]);}printf("\n");}return;}for (int col = 0; col < N; col++) {if (is_valid(row, col)) { // 如果当前位置是合法的,则放置皇后queens[row][col] = 1;col[row] = col; // 记录每行皇后所在的列backtrack(row + 1); // 继续放下一行的皇后queens[row][col] = 0; // 回溯,撤销当前位置的皇后}}}int main() {backtrack(0); // 从第0行开始放皇后return0;}在上面的代码中,我们使用一个一维数组col来记录每一行皇后所在的列。
在is_valid函数中,我们检查当前位置是否合法,即与前面的皇后不冲突。
实验四 皇后问题求解

实验实习名实验二皇后问题求解(以下为参考内容,具体内容要求由课程在实验实习指导书中规定。
)一、实验实习目的及要求实验题目:皇后问题求解实验目的:1)以Q-皇后问题为例,掌握回溯法的基本设计策略。
2)掌握回溯法解决Q-皇后问题的算法并实现;3)分析实验结果。
二、实验实习设备(环境)及要求(软硬件条件)实验环境:计算机、C语言程序设计环境三、实验实习内容与步骤实验内容与步骤1.用回溯法求解N-Queen,参考教材算法思想,并实现你的算法。
要求:用键盘输入N;输出此时解的个数,并统计运算时间。
2.给出N=4,5,6时,N-Queen解的个数。
3.尝试增大N,观察运行情况;并理解该算法的时间复杂度。
四、实验实习过程或算法(源程序、代码)源程序:#include<stdio.h>#include<math.h>#include <time.h>int X[10];bool PLACE (int k){int i=1;while(i<k){if (X[i]==X[k] || abs(X[i]-X[k])==abs(i-k) )return false;i=i+1;}return true;}void main(){int k=1,n;int count=0;printf("请输入一个正整数:\n");scanf("%d",&n);double duration;clock_t finish, start;start = clock();while (k>0) //对所有行执行以下语句{X[k] = X[k]+1; //移到下一列while(X[k]<=n && !PLACE(k) ){X[k] = X[k]+1; //移到下一列,再判断}if (X[k] <= n) //找到一个位置{if (k==n) //一个完整的解{//printprintf("the soution is:");for (int t=1;t<=n;t++)printf("%3d",X[t]);printf("\n");count +=1 ;}else{k=k+1;X[k]=0;} //转向下一行}elsek=k-1; //回溯}finish = clock();duration = (double)(finish - start);printf("\n the number of the solutions is %d \n", count);printf( "The count time is %2.6f seconds.\n", duration);}五、实验实习结果分析和(或)源程序调试过程(一)算法理论分析使用回溯算法求解的问题特征,求解问题要分为若干步,且每一步都有几种可能的选择,而且往往在某个选择不成功时需要回头再试另外一种选择,如果到达求解目标则每一步的选择构成了问题的解,如果回头到第一步且没有新的选择则问题求解失败。
数据结构与程序设计12八皇后问题

Post: A queen has been inserted into the square at row count and column
col; count has been incremented by 1.
*/
{
queen_square[count++][col] = true;
}
7/25/2024
for (i = 0; ok && i < count; i++)
ok = !queen_square[i][col];
// Check upper part of column
for (i = 1; ok && count - i >= 0 && col - i >= 0; i++)
Байду номын сангаас
ok = !queen_square[count - i][col - i]; // Check upper-left diagonal
}
7/25/2024
数据结构与程序设计
11
Eight-Queens Puzzle p191
bool Queens::unguarded(int col) const
/*
Post: Returns true or false according as the square in the first
数据结构与程序设计
10
Eight-Queens Puzzle
Queens::Queens(int size)
/*
Post: The Queens object is set up as an empty
数据结构课程设计-四、八、N皇后问题

计算机与软件工程学院课程设计说明书课程名称: 数据结构与算法-课程设计课程代码: 106014389题目: 四、八、N皇后问题年级/专业/班: 学生姓名: 学号: 312012********* 开始时间:年月日完成时间:年月日课程设计成绩:指导教师签名:年月日摘要解决八皇后问题主要利用了递归法、回溯法,以及对for语句、数据结构中树的灵活运用、和对栈及数组的掌握。
编程实现了在8*8的格的国际象棋上摆放八个皇后,使其不能相互攻击,即任意两个皇后都不能处于同一列、同一行、或同一条斜线上面。
编程实现了任意给定一个初始位置,输出八皇后问题的一个布局。
本次设计旨在学习各种算法,训练对基础知识和基本方法的综合运用及变通能力,增强对算法的理解能力,提高软件设计能力。
在实践中培养独立分析问题和解决问题的作风和能力。
关键词:递归法; 回溯法; 顺序栈;数组;目录1需求分析 (4)2开发及运行平台 (5)3 概要设计 (6)4 详细设计 (8)5 调试分析 (9)6 测试结果 (10)6.1 遇到的问题 (10)6.2 调试结果 (10) (11)7 结论 (12)通过这次的课程设计,让我了解了八皇后这一经典的问题。
同时让我更好地掌握了栈思想以及一维数组等等知识,以及一些书本上没有的东西,这对我以后的学习生涯以及将来步入社会起到很大的帮助。
这次课程设计虽然花了我很多时间和精力,但很值得,因为它对我能力提高起到很大帮助。
这次课程设计也提醒我以前知识的匮乏,它给我敲响了警钟,让我意识到自己基础的不扎实.当然这次实验还是有很多问题的。
比如程序设计的界面不够好,一些程序并非自己所写,而是修改某些程序而成,但这些不该,在下次课程设计时不会再发生。
(12)参考文献 (13)附录 (14)1需求分析八皇后问题是一个古老而著名的问题,该问题是十九世纪著名的数学家高斯1850年提出的,并作了部分解答。
高斯在棋盘上放下了八个互不攻击的皇后,他还认为可能有76种不同的放法,这就是有名的“八皇后”问题。
C语言题_2n皇后问题

2n皇后问题试题来自:程设09秋(徐)(程序设计基础课(清华大学徐明星老师、吴文虎老师)2009秋) 【问题描述】给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。
现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。
问总共有多少种放法?n小于等于8。
【输入格式】输入的第一行为一个整数n,表示棋盘的大小。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
【输出格式】输出一个整数,表示总共有多少种放法。
【样例输入1】41 1 1 11 1 1 11 1 1 11 1 1 1【样例输出1】2【样例输入2】41 0 1 11 1 1 11 1 1 11 1 1 1【样例输出2】分析:每行的Q的位置,保存在一个数组中Q[6],Q[1]表示第一行q的列数。
从第一行开始1到(n+1)/2遍历如果Q[1]=1,那么Q[2]==Q[1],则不符合如果Q[1]>Q[2],检测Q[2]是否在Q[1]的135度线上, Q[1]+([2]-[1])?=Q[2],Q1与Q2的Q2的列值如果Q[1]<Q[2],检测Q[2]是否在Q[1]的45度线上, Q[1]-([2]-[1])?=Q[2],Q1的列值减去Q1与Q2的行差是否等于Q2的列值如果只要求一种颜色的N皇后问题,并且没有0,1的限制,实现代码:#include<stdio.h>char NN[9][9]; //棋盘,初始设为‘-’,1表示在棋盘格为空,Q表示放置皇后int q[6]; //记录1-N行Q的列数,q[1]=3表示第一行的Q在第三列int Cheak(int line) //检测要添加的Q是否符合要求{int i;for(i=1;i<line;i++){if(q[i]-q[line]==0)return 0;else if(q[i]-q[line]>0){if(q[i]-(line-i)==q[line])return 0;}else{if(q[i]+(line-i)==q[line])return 0;}}return 1;}void Search(int line,int N){int i,j,n;if(line==N) //如果最后一行的Q已经存在,则打印棋盘for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}else //遍历此行,并通过检测查询下一行{line++;for(i=1;i<=N;i++){NN[line][i]='Q';q[line]=i;if(n=Cheak(line)>0){Search(line,N);}NN[line][i]='1';}}}void Begin(int N){int i;for(i=1;i<=(N+1)/2;i++){q[1]=i;NN[1][i]='Q';Search(1,N);NN[1][i]='1';}}void main(){//初始int N,i,j;for(i=1;i<9;i++)for(j=1;j<9;j++)NN[i][j]='-';printf("Start:(8*8)\n");for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}//输入Nscanf("%d",&N);for(i=1;i<=N;i++)for(j=1;j<=N;j++)NN[i][j]='1';printf("Now you choice N=%d:(%d*%d)\n",N,N,N);for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}//开始计算Begin(N);}上述的代码中,只实现了棋盘的打印,并未统计放法的数量,通过Begin()函数,第一行只检测一半,因为另一半是对称的(为了提高效率),然而题目要求是有0,1限制的,所以,为了实现上述要求,代码还应改动去掉对称,因为棋盘添加了0后便不是对称的了。
四、八皇后问题 C语言递归算法程序

#include<stdio.h>#include<math.h>const int NUM=4;//四皇后问题(NUM=4)static int count=0;void output(int array[][NUM]);//四皇后分布输出int judge(int array[][NUM],int row,int column);//判定函数void search(int array[][NUM],int row);//搜索函数int main(){int i,j;int box[NUM][NUM];for(i=0;i<NUM;i++){for(j=0;j<NUM;j++)box[i][j]=0;}//output(box);search(box,0);printf("四皇后分布共有%d 种。
\n",count);return 0;}void output(int array[][NUM]){int i,j;for(i=0;i<NUM;i++){for(j=0;j<NUM;j++){printf("%d ",*(*(array+i)+j));}printf("\n");}}int judge(int array[][NUM],int row,int column){int i,j;for(i=0;i<row;i++){for(j=0;j<NUM;j++){if(array[i][j]==1){if(j==column) return 0;//判断是否在同一列if(abs(row-i)==abs(column-j)) return 0;//判断是否在同一斜线上}}}return 1;}void search(int array[][NUM],int row){int j;//for(i=0;i<NUM;j++)//{for(j=0;j<NUM;j++){if(!judge(array,row,j)){//printf("%d ",judge(array,row,j));continue;}array[row][j]=1;if(row==NUM-1){//array[row][j]=1;count++;printf("四皇后分布图:%d\n",count);output(array);array[row][j]=0;continue;}elsesearch(array,row+1);array[row][j]=0;}//}return;}。
