100测评网高一数学复习附件4:2007~2008年广东卷考点在相关模块的分布
100测评网广东省华南师大附中 2008届高三综合测试

广东省华南师大附中2008届高三综合测试(四)政治试题第一部分(选择题,共76分)一、在下列各题的四个选项中,只有一项是最符合题意的。
每小题2分,共52分1.2007年12月5日,中央经济工作会议在北京闭幕。
在对明年的宏观调控政策部署中,会议明确提出,明年要实施稳健的财政政策和的货币政策。
()A.稳健B.从紧C.积极D.消极2.2007年9月13日,揭牌,马馼兼任局长。
A.国家预防腐败局 B.能源部C.发改委D.国家反腐局3.2007年5月29日,因大面积爆发蓝藻,江苏无锡市发生饮用水危机。
A.鄱阳湖B.洞庭湖C.千岛湖D.太湖4.2007年6月9日是我国第二个“文化遗产日”。
今年“文化遗产日”的主题是“”。
A.保护文化遗产,构建和谐社会B.保护文化遗产,守望精神家园C.保护文化遗产,全面建设小康社会D.保护非物质文化遗产5.2007年4月26日,第29届奥运会火炬接力传递计划路线和火炬发布仪式在北京中华世纪坛举行。
以中国传统“”符号和纸卷轴为创意的北京奥运会火炬正式亮相。
A.中国龙B.云纹C.回纹D.祥云6.12月1日,中共中央决定,由同志兼任广东省委委员、常委、书记。
()A.汪洋B.薄熙来C.张德江D.李长春7.2007年12月3日,俄罗斯中央选举委员会公布,的得票率为64.1%,成为国家杜马多数派()A.俄罗斯共产党B.自由民主党C.统一俄罗斯党D.公正俄罗斯党8.某高一学生喜欢打篮球,疯狂崇拜NBA球星麦克格雷迪,跟父母软磨硬泡一个月,买了一双价格上千元的麦迪五代篮球鞋,也觉得这样可以拉近跟偶像的距离。
在轰动一时的超女总决赛时,又有学生花掉上万元高额话费为自己的支持对象投票。
上述消费行为()A.是受从众心理影响的消费B.违背量入为出、适度消费的原则C.是重视精神享受消费的表现D.是社会消费水平提高的表现9.上图反映了()A.一年来我国居民消费价格总水平不断提高B.2007年6月,我国CPI已超过3.5%的国际警戒线,因此我国已进入通涨时代C.一年来我国价格总水平不断提高D.应对CPI的提高,我国应该适当提高利率水平10.面对我国严峻的就业形势,劳动者应该认识到,在市场竞争中,只有自身实力强才能就业机会多,即要树立()A.自主择业观B.职业平等观C.竞争就业观D.多种方式就业观11.增值税和个人所得税是我国现阶段影响最大的两个税种,从作用上,它们的共同点主要在于A.促进生产专业化发展B.调节个人收入C.促进财政收入的稳定增长D.调整生产的发展方向12.为了防止鱼场的鱼卵感染某种真菌,一些地方的少数鱼类养殖、经营户非法使用化学制剂“孔雀石绿”,引起社会的普遍关注。
广州市2007~2008学年第二学期高一数学期末测试试卷

广州市2007~2008学年第二学期高一数学期末测试试卷注意事项:1.本试卷共三大题,满分150分.考试时间120分钟.2.本试卷的所有题目的答案全部做在答卷上,写在问卷上不给分.3.考生必须将学校、班级、姓名、学号填写在答卷密封线内,并用黑色的钢笔、签字笔作答,不准使用涂改液.一、选择题:(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的,)1.6π弧度化为度是(*) A.30︒ B.60︒ C.120︒ D. 150︒ 2.2sin 3π的值为(*)A.12 C. 12- D. 3.在数列{}n a 中,已知前n 项和28n S n n =-,则5a 的值为(*)A.63-B. 15-C. 1D. 54.若向量(3,2)a =,(0,1)b =-,则向量2b a -的坐标是(*)A.(3,4)B.(3,4)-C.(3,4)-D.(3,4)-- 5.已知向量(3,1)a →=,(,3)b x →=-,且//a b →→则x =(*)A. 9B.9-C. 13-D. 136.△ABC 中,AB a =,AC b =,若0a b ⋅<, 则ABC ∆是(*)A .锐角三角形B .直角三角形C .钝角三角形D .直角三角形或钝角三角形7. 在ABC 中,1a =,b =30A =︒, 则B ∠等于(*)A.60︒B.60︒或120︒C.30︒或150︒D.120︒x8.下列各式中,值为2的是( * ) A .2sin15cos15 B .22cos 15sin 15- C .22sin 151-D .22sin 15cos 15+9.下列各二元一次不等式组能表示如图所示阴影部分的是(*)A.2240x x y ≤⎧⎨-+≤⎩ B. 02240x x y ≤≤⎧⎨-+≤⎩ C. 02240x y x y ≤⎧⎪≤⎨⎪-+≥⎩D.002240x y x y ≤⎧⎪≤≤⎨⎪-+≥⎩10.已知等比数列的公比为2,且前4项之和为1,那么前8项之和等于(*)A.15B.17C.19D.21二、填空题:(本大题共4小题,每小题5分,满分20分). 11.已知1()22P 是角α终边上的一点,则sin α= * . 12.已知等差数列{}n a 中,357324a a a a +=-=,则2a = * .13.已知,,a b c 三个数成等比数列,其中5a =+5c =-则b = * . 14.正数a ,b 满足8ab a b =++,则ab 的最小值是 * .三、解答题:(本大题共六大题,满分80分)15.(本小题满分12分)已知||2a =,(1,1)b =-且a b ⊥,求向量a 的坐标.16. (本小题满分12分)已知函数()2cos 2f x x x =- (x R ∈). (1) 求函数()f x 的最小正周期;(2) 当x 为何值时,()f x 的值最大? 最大值是多少?17. (本小题满分14分)已知: 0αβπ<<<,且4cos()5αβ-=. (1)求sin()αβ-; (2) 当4tan 3β=时, 求tan α.18. (本小题满分14分)设锐角ABC ∆的内角A 、B 、C 的对边分别为a ,b ,c , 且2sin c b C =. (1)求角B 的大小;(2)若5,a c ==b .19. (本小题满分14分)某工厂用两种不同的原料均可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可生产产品90千克;若采用乙种原料,每吨成本1500元,运费400元,可生产产品100千克.若每日预算总成本不得超过6000元,运费不得超过2000元,问此工厂每日最多可生产多少千克产品?20. (本小题满分14分)已知正整数列{}n a 的前n 项和为n S ,且对任意的正整数n满足1n a =+. (1)求数列{}n a 的通项公式; (2)设11n n n b a a +=⋅,求数列{}n b 的前n 项和n B .2007~2008学年第二学期高一数学期末考题参考答案及评 分 标 准一、选择题:(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.A 2. B 3. C 4. D 5. B 6.C 7. B 8. B 9. D 10. B二、填空题:(本大题共4小题,每小题5分,满分20分,其中13题答对一个3分,全对5分). 11. 1212. 0 13.1± 14. 16三、解答题:(本大题共六大题,满分80分) 15.(本小题满分12分)已知||2a =,(1,1)b =-且a b ⊥,求向量a 的坐标. 解:设(,)a x y =, 2分 ∵a b ⊥,∴0x y -= 4分又||2a =,则 2240x y x y ⎧+=⎨-=⎩ 解得,x y ⎧=⎪⎨=⎪⎩x y ⎧=⎪⎨=⎪⎩ 10分∴(2,2)a =或(2,a =- 12分16. (本小题满分12分)解:(1)由原式得,1()2(2cos 2)2(sin 2cos cos 2sin )2sin(2)22666f x x x x x x πππ=-=-=- 6分 ∴周期T π= 8分 (2) 当sin(2)16x π-=时,此时2262x k πππ-=+,3x k ππ=+10分()2f x =最大值 12分17. (本小题满分14分) 解: (1) 4cos()5αβ-=, 又0αβπ<<< 0παβ∴-<<< 2分3sin()5αβ∴-==- 6分l:90x+100y=0x(2)sin()3tan()cos()4αβαβαβ--==--, 8分又 4tan 3β=tan()tan 7tan tan[()]1tan()tan 24αββααββαββ-+∴=-+==-- 14分18. (本小题满分14分)解:(1)由2sin c b C =,根据正弦定理得, sin 2sin sin C B C =, 1sin 2B =4分 又ABC ∆为锐角三角形, 所以6Bπ= 6分(2)由余弦定理得,222222cos 52572b ac ac B =+-=+-⨯⨯= 12分故 b =分19. (本小题满分14分) 解:设工厂每日需用甲原料x 吨,乙原料y 吨,可生产产品z 千克,根据题意,则001000150060005004002000x y x y x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩, 即002354x y x y x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩画出可行域如图所示则不等式组(*)所表示的平面区域是四边形 的边界及其内部(如图阴影部分)由23125420x y x y +=⎧⎨+=⎩解得, 127207x y ⎧=⎪⎪⎨⎪=⎪⎩,设1220(,)77M ,90100z x y =+ 令0z =,得 ':901000l x y += 即910y x =- 由图可知把'l 平移至过点1220(,)77M 时, 即1220,77x y ==时,12209010044077z =⨯+⨯=最大值(千克) 答:工厂每日最多生产440千克产品.20. (本小题满分14分) 解:(1)∵对任意的正整数n ,1n a =+ ① 恒成立,∴当1n =时,11a =+,即21)0=,∴11a = 2分当2n ≥时,有11n a -=+ ②①2-②2, 得2211422n n n n n a a a a a --=-+-, 4分即11()(2)0n n n n a a a a --+--=∵0n a >,∴10n n a a -+>,∴12n n a a --= 6分 ∴数列{}n a 是首项为1,公差为2的等差数列. ∴1(1)221n a n n =+-⨯=- 8分(2)由(1)知121n a n +=+ ∴1111()(21)(21)22121n b n n n n ==--+-+ 10分∴12311111111111(1)()()()2323525722121n n B b b b b n n =+++⋅⋅⋅+=-+-+-+⋅⋅⋅+--+ 11(1)2212(1)nn n =-=++ 14分。
100测评网高一数学复习附件3:2007~2008年海南、宁夏卷考点在相关模块的分布
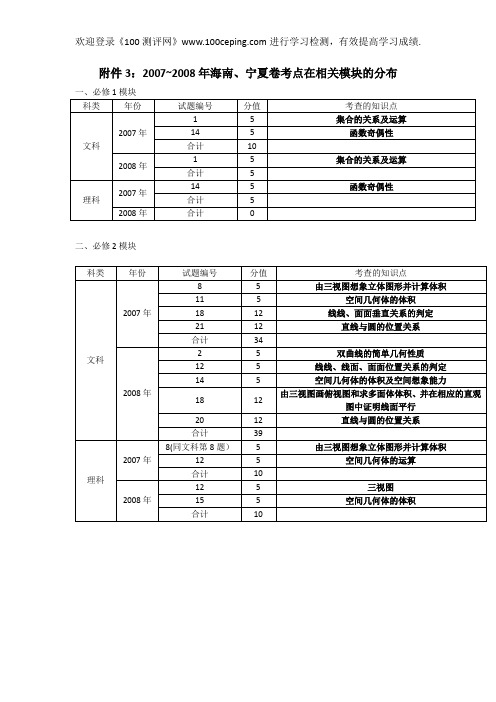
附件3:2007~2008年海南、宁夏卷考点在相关模块的分布二、必修2模块四、必修4模块六、选修1-1、1-2模块八、选修4模块(理科:从“标系与参数方程、不等式选讲选、几何证明选讲”中“3选2”;文科从“坐标系与参数方程、几何证明选讲”中“2选1”。
)===========================================================适用版本:人教版,苏教版, 鲁教版,北京版,语文A版,语文S版,冀教版,沪教版,北大师大版,人教版新版,外研版,新起点,牛津译林,华师大版,湘教版,新目标,苏科版,粤沪版,北京版,岳麓版适用学科:语文,数学,英语,科学,物理,化学,生物,政治,历史,地理适用年级:一年级,二年级,三年级,四年级,五年级,六年级,七年级,八年级,九年级,小一,小二,小三,小四,小五,小六,初一,初二,初三,高一,高二,高三,中考,高考,小升初适用领域及关键字:100ceping,51ceping,52ceping,ceping,xuexi,zxxx,zxjy,zk,gk,xiti,教学,教学研究,在线教学,在线学习,学习,测评,测评网,学业测评, 学业测评网,在线测评, 在线测评网,测试,在线测试,教育,在线教育,中考,高考,中小学,中小学学习,中小学在线学习,试题,在线试题,练习,在线练习,在线练习,小学教育,初中教育,高中教育,小升初复习,中考复习,高考复习,教案,学习资料,辅导资料,课外辅导资料,在线辅导资料,作文,作文辅导,文档,教学文档,真题,试卷,在线试卷,答案,解析,课题,复习资料,复习专题,专项练习,学习网,在线学习网,学科网,在线学科网,在线题库,试题库,测评卷,小学学习资料,中考学习资料,单元测试,单元复习,单元试卷,考点,模拟试题,模拟试卷,期末考试,期末试卷,期中考试,期中试卷===========================================================本卷由《100测评网》整理上传,专注于中小学生学业检测,练习与提升.。
人教A版数学必修一20072008高一必修1模块测试题答案

秀全中学2007学年第一学期中段考试高一数学试题参考答案一.选择题二、填空题11.60.7>0.76>log 0.76 12.____1_________13.]2,(--∞14.①,②,③ 三、解答题:15.解:由{}9A B ⋂=得29a =,所以3a =±……………………5’当3a =时,{}3,4,9B =-,此时{}4,9A B ⋂=,与题设矛盾…………………7’ 当3a =-时,{}9,2,9B =--,满足{}9A B ⋂=…………………9’ 故所求的3a =-,{}9,2,4,9A B ⋃=--……………………………………12’ 16.解(1)原式=323log 3lg(254)21+⨯++=23lg1032++ =3132322++=……………………7’(2)设1t =,则1t ≥1t =-,22()(1)2(1)1f t t t t ∴=-+-=-所以2()1(1)f x x x =-≥(没写1x ≥扣1分)………………14’17.解:设0x <时,则-x>0,22()()2()323f x x x x x -=----=+- 而f(x)为R 上的奇函数,所以f(-x)=-f(x) 所以当0x <时,2()23f x x x =--+223x x --(x>0) ()f x =0(x=0)223x x --+(x<0)(8分)简图如右(14分)18.解:由20.5()log log (2)f x x x =--得:020x x >->且,所以02x <<……………2’ 设()y f x =,则20.5log log (2)y x x =--2log (2)x x =-……………………6’ 设(2)u x x =-,则2log y u =……………………7’由22(2)2(1)1u x x x x x =-=-+=--+……………………8’所以在(0,1],(2)u x x =-单调递减,在[1,2),(2)u x x =-单调递增……………………10’ 由于2log y u =在(0,)+∞单调递增,所以函数f(x)的增区间为:[1,2); 减区间为(0,1]……………………12’19.解(1)∵3)1(=f ∴23a b+=①……………………………2’ 又∵29)2(=f ∴4(1)1922a b ++=②…………………4’ 由①、②解得a=1,b=1∴221()x f x x+=……………………7’(2)函数f (x )在区间[1,+∞)上是增函数, ……………………8’设211x x >≥,,则222121212121()()x x f x f x x x ++-=-=22211221(21)(21)x x x x x x +-+⋅=211221()(21)x x x x x x --⋅……………………12’∵x 1≥1,x 2>1,∴2x 1x 2-1>0.,x 1x 2>0.,又∵x 1<x 2,∴x 2-x 1>0.∴21()()f x f x ->0即21()()f x f x >故函数f (x )在区间[1,+∞)上是增函数.……………………14’ 20.解:(Ⅰ)x 的取值范围为10≤x ≤90;……………2分 (Ⅱ)依题意得221[2010(100)]5y x x =+-…………………………6分(10≤x ≤90);……………7分 (III )由222110040000[2010(100)]6()533y x x x =+-=-+.……………………11分 则当x =1003千米时,y 最小.……………13分答:故当核电站建在距A 城1003千米时,才能使供电费用最小.……………14分。
2007-2008年高一数学必修1人教版期末复习试卷2

2007-2008学年度第一学期期末复习试卷高一数学试题(考试时间:120分钟总分160分)注意事项:1、本试卷共分两部分,第Ⅰ卷为选择题,第Ⅱ卷为填空题和解答题。
2、所有试题的答案均填写在答题纸上(选择题部分使用答题卡的学校请将选择题的答案直接填涂到答题卡上),答案写在试卷上的无效。
公式:锥体体积V=sh;球的表面积S=4πR2;圆锥侧面积S=πrl一、填空题:1. 已知平行四边形ABCD的三个顶点坐标为A(-1,2,3),B(2,-2,3),C(1,5,1),则第四个顶点D的坐标为.2. 用“<”从小到大排列23,,,0.53.3.求值:(lg5)2+lg2×lg50=________________。
4. 已知A={(x,y)|x+y-2=0},B={(x,y)|x-2y+4=0},C={(x,y)|y=3x+b},若(A∩B)C,则b=_____5. 已知函数是偶函数,且在(0,+∞)是减函数,则整数的值是.6. 如图,假设,⊥,⊥,垂足分别是B、D,如果增加一个条件,就能推出BD⊥EF。
现有下面3个条件:①⊥;②与在内的射影在同一条直线上;③∥.其中能成为增加条件的是.(把你认为正确的条件的序号都填上)7.(1)函数的最大值是(2)函数的最小值是8.,是两个不共线的向量,已知,,且三点共线,则实数=9.已知,(),且||=||(),则.10.对于函数,给出下列四个命题:①存在(0,),使;②存在(0,),使恒成立;③存在R,使函数的图象关于轴对称;④函数的图象关于(,0)对称.其中正确命题的序号是11.函数的最小正周期是。
12.已知,,以、为边作平行四边形OACB,则与的夹角为__________二、解答题:(解答应写出必要的文字说明,证明过程或演算步骤。
)13.(14分)已知函数f(x)=(a>0,a≠1,a为常数,x∈R)。
(1)若f(m)=6,求f(-m)的值;(2)若f(1)=3,求f(2)及的值。
100测评网高三数学复习2008~2009学年度高一期末考试

2008~2009学年度高一期末考试数学试题 2009.1.16一、选择题(共10小题,共50分)1. 已知A={0,1,2},B={0,1},则下列关系不正确的是( )A . A ∩B=B B 。
∁A B ⊆BC .A ∪B ⊆AD 。
B ⊂≠ A2. 函数()()2lg 31f x x =+的定义域为( )A .1,3⎛⎫-∞- ⎪⎝⎭B 。
11,33⎛⎫- ⎪⎝⎭C 。
1,13⎛⎫- ⎪⎝⎭D 。
1,3⎛⎫-+∞ ⎪⎝⎭3.下列各组函数中,表示同一函数的是( ) A .y x =与y =B 。
ln x y e =与ln x y e =C 。
()()131x x y x -⋅+=-与3y x =+ D 。
0y x =与01y x =4.下列函数中,在区间()0,2上为增函数的是( ) A .()ln 1y x =- B。
y C 。
245y x x =-+ D 。
2y x=5.10y --=的倾斜角为( )A .30 B 。
60 C 。
120 D 。
150 6. 函数()3x f x x =+在下列哪个区间内有零点 ( )A .2,1⎡⎤⎣⎦--B .1,0⎡⎤⎣⎦-C .0,1⎡⎤⎣⎦D .1,2⎡⎤⎣⎦7. 如图所示,甲、乙、丙是三个立方体图形的三视图,甲、乙、丙对应的标号正确的是 ( )(甲)(乙)(丙)主视图左视图俯视图主视图左视图俯视图主视图左视图俯视图8. 设,,αβγ为两两不重合的平面,l ,m ,n 为两两不重合的直线,给出下列四个命题: ①若,,αγβγ⊥⊥则α∥β; ②若,,m n m αα⊂⊂∥,n β∥,β则α∥β; ③若α∥,,l βα⊂则l ∥β; ④若,,,l m n l αββγγα⋂=⋂=⋂=∥,γ则m ∥n . 其中真命题的个数是( )A .1B 。
2C 。
3D 。
49. 函数()21log f x x =+与()12x g x -+=在同一直角坐标系下的图像是如图中的( ) 10. 如果直线20ax y -+=与直线30x y b --=关于直线0x y -=对称,则有( )A .1,63a b == B 。
广东中山高三级2007—2008学年第一学期期末统一考试数学文科试题

中山市高三级2007—2008学年度第一学期期末统一考试数学科试卷(文科)本试卷分第I 卷(选择题)、第II 卷(非选择题)两部分•共100分,考试时间100分 钟•第I 卷(选择题共40分)注意事项:1 •答第I 卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在 答题卡上.[]2 •每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡 皮擦干净后,再选涂其它答案,不能答在试题上3 •考试结束,将答题卡与第n 卷交回 . 、选择题(每小题5分,共50分;每小题给出的四个选项中,只有一个选项符合题目要求,把所选项前的字母填涂在答题卡上) 1 •在复平面内复数(1 i )2对应的点位于A •一、三象限的角平分线上 C .实轴上2•条件p:x 1,条件q : x2,贝V p 是A •充分但不必要条件C .充分且必要条件 3•在 ABC 中,角 代B,C 的对边分别为a, b,c ,已知A5A.B .C . 一3664 •为了了解某地区高三学生的身体发育情况,抽查了该地区 的男生体重(kg ),得到频率分布直方图如下: 根据上图可得这100名学生中体重 在〔56.5,64.5〕的学生人数是A. 20B. 30C. 40B •二、四象限的角平分线上D .虚轴上q 的B .必要但不充分条件D . 50100名年龄为17.5岁一18岁5 .已知数列 2a n 的前n 项和S n 满足S n n 2n 1,则A . a n 2n 1 n 2n C . a n 2, 2n 1,n 2,n N a n 2n2, n 1 1,n 2,n N6.某个容器的底部为圆柱,顶部为圆锥,其正视图 A . m 3 B . C . 3 m 3 D .7.已知 f (x)是周期为 2的奇函数, 如右图所示,则这个容器的容积为 7 312 5 f (2),则b c& 设 f(x)= 2e x1,x log 3(x 2 2,A . (1, C . (1, 9.已知函数 式可以为 2x C . y 10 .若函数 (2 2 x 范围为 1)C . ( 1,2)m 30 x 1 时, f(x) C . c 则不等式 1),x 2, f(x)>2的解集为 (3, +1(.10 , +m )sin x 的图像的一部分如图⑴,B . y f 2xm)x lg x.设 af(|),b 5(10 , +1(1, 2)则图⑵的函数图像所对应的函数解析的图象如图所示,则 m 的取值B . (1,2) D . (0,2)中山市高三级2006 —2007学年度第一学期期末统一考试数学科试卷(文科)第II卷(非选择题共60分)号考考统题号-二二1516171819总分总分人复分人密、填空题(每小题5分, 共20分)名姓封线内不要答11.高二某个文科班有男同学的方法抽取10个同学参加问卷调查,则应抽取男同学10人,女同学40人,现用分层抽样_____ 人,女同学__________ 人. 12•从分别写有1, 2, 3, 4, 5的五张卡片中任取两张,求这两张卡片上的数字之和为偶数的概率为____________ .uuu uuu UULT13 .已知向量OA (3, 4), OB (6, 3),OC (5 m, 3若点A、B、C三点共线,则实数m应满足的条件为14 •下列程序框图可用来估计的值(假设函数CONRND (-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788, 则由此可估计的近似值为.(保留四位有效数字)级班校学三、解答题(共80分•解答题应写出推理、演算步骤)15.(本题满分12分)2已知函数f(x) 2cos X 2sinxcosx 1 , (x R).(I)求函数f (x)的最小正周期;(n)求函数f (x)的最大值,并求此时自变量x的集合.\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\16.(本题满分12分)如图,四棱锥P—ABCD中,PA 是直角梯形,AB丄AD , CD丄AD , CD=2AB , E为PC中点.(I) 求证:平面PDC 平面PAD;(II) 求证:BE// 平面PAD .■■■ 217 .(本题满分14分)已知向量a 1,x,向量b x x, x • r r 1(1 )已知常数m满足2 w m w 2,求使不等式a b > 4斗m成C B立的x的解集; a br r 1(2)求使不等式a b > 4子m对于一切x 0恒成立的实数m取值集合.a b18.(本题满分14 分)设某物体一天中的温度T 是时间t 的函数,已知32T(t) at bt ct d(a 0),其中温度的单位是C,时间的单位是小时•中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8: 00 相应的t=-4,下午16 : 00相应的t=4).若测得该物体在早上8:00的温度为8C,中午12:00 的温度为60 C,下午13:00的温度为58 C,且已知该物体的温度早上8:00与下午16:00有相同的变化率•(1)求该物体的温度T关于时间t的函数关系式;(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?19.(本小题满分14分)把正整数排列成如图所示的数阵.(I )求数阵中前10行所有的数的个数; (H )求第n 行最左边的数;(川)2007位于数阵的第几行的第几个数(从左往右数) 20 .(本题满分14分)设函数f x 的定义域是0,,对任意正实数m,n 恒有f (m n) f(m) f(n),且当 x 1 时,fx 0, f 211(1) 求f —的值;2(2)求证:f X 在0, 上是增函数;(3)求方程4sinx f x 的根的个数.45 6 78 9 1011 12 13 14 15中山市高三级2007—2008学年度第一学期期末统一考试数学科试卷(文科)答案一、选择题:DABCC ADCBB二、填空题:11 . 2, 8;212.513. m114. 3.1522三、解答题15 .解:T2f (x) 2 cos x 2 sin xcosx1二f(x)sin 2x cos2x\ 2 sin2x4(x R).1 x2.11(n)f (x)的 最大值为2 ,此时: 2x -2k -,即x k3-(k ).428所以, 所求x 的勺取值集合为{x |xk 3k Z }8CD AD(已知) 证明: (1 )由 PA 平面 ABCDPA CDPA AD ACD 面PADCD 面PAD平面 PDC 平面 PAD ;取1 PD 中点为 F ,连结 EF 、AF ,由 E 为 PC 中点,(I) f(x)的最小正周期为T 16 . (2) 得EF PDC 的中位线,贝U EF//CD , 又 CD=2AB ,贝U EF=AB .由 AB//CD 所以四边形ABEF 为平行四边形,则 EF//AF . 由AF 面 PAD ,EF// 面 PAD . 17 .解:T 1,x , x 2 x, CD=2EF . ,贝U EF II AB . b (1) xmxm 2 4mx 0恒成立.mx•••所求的不等式的解集为R| x 0当且仅当x 2时等号成立,•函数y要使a bm 恒成立m 恒成立,所以 m 2 .••• m的取值集合为m | m 2 .18 .解⑴因为T' =3at2+2bt+c,而T 4 T 4 故48a+8b+c=48a-8b+cT 0d60a1T -464 a16b4c d 8b0T 1a b c d58c-348a8b c48a8b c d60T t t33t60(-12 w t w 12).7分⑵T ' (t)=3t2-3=3(t2-1), 由T'(t) 0得t 1 或t 1当t在上变化时,'的变化情况如下表19 .解:(I)数阵的第n行有n个数,所以前10行的数的个数有:1+ 2+ 3+ ……+ 10= 55.一1(n)前n行所有个数为:1 + 2 + 3 + .............. +n = n(n 1)21所以,第n行最右边的数为丄n(n 1).2一1 1 2 1第n行最左边的数为n(n 1) (n 1) n n 1.2 2 21(川)又n = 63时,第63行最左边的数为:63 62+1=1954 ,21第63行最右边的数为:丄64 63= 2016 ,2所以2007位于第63行.又因为2007 —1954= 53,故2007位于第63行的第54位.20 .解(1)令m n 1,则f 1 1 f 1 f 1 f 1 0—16x-4令m111 2,n,则 f 1f 2 -f 2f222f1 f 1f 2 12(2) 设0% x , 则x 21 Q 当x 1时, f x 0f 竺0X 1f(X 2)f(X 1S =f (xj f(竺) f (xj%%f x 在 0,上是增函数(3)T y 4sin x 的图象如下所示,由图可知y 最大值为4,又Q f 4 f 2 2 2f 22, f (16)f (4 4) 2f(4) 4由y f (x)在x 0单调递增,且f(1) 0 , f (16) 4可得f (x)的图象大致形状如下所示,由图可知,y 4sinx 的图象与y f (x)的图象在 0,2 内有一个交点,在2 ,4 内有两个交点,在 4 ,5 内有两个交点,又 516 6 ,所以总共有 5个交占八、、♦ x 的根的个数是5 .y4y 4sin x方程4sin xf(x)。
100测评网高一数学试题

安庆一中2008——2009学年度第一学期期末考试高一数学试题(必修4模块检测)一、 选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合要求的,把正确答案的代号填在括号内.)1.若点P 在34π的终边上,且|OP|=2,则点P 的坐标( )A .)3,1(B .)1,3(-C .)3,1(--D .)3,1(-2.已知AB =(5,-3),C (-1,3),CD =2AB ,则点D 的坐标为(A )(11,9) (B )(4,0) (C )(9,3) (D )(9,-3)3.设向量)21,(cos α=→a 的模为22,则c os2α=( ) A.41- B.21- C.21 D.234.已知)]1(3cos[3)]1(3sin[)(+π-+π=x x x f ,则 f (1)+f (2)+……+f (2005)+f(2006)=( )A.32B.3C.1D.05.在sin sin cos cos ,ABC A B A B ∆⋅<⋅中,则这个三角形的形状是 (A )锐角三角形 (B )钝角三角形(C )直角三角形 (D )等腰三角形 6.把函数y =c os x 的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移4π个单位,则所得图形对应的函数解析式为( ) A.)421cos(π+=x y B. )42cos(π+=x yC. )821cos(π+=x yD. )22cos(π+=x y7.已知P(4,-9),Q(-2,3),y 轴与线段PQ 的交点为M ,则M 分−→−PQ 所成的比为( ) A .31 B.21 C.2 D.38.己知12,e e 是夹角为60的两个单位向量,则122a e e =+与1232b e e =-+的夹角的余弦值是(A )12 (B )12- (C )2 (D )2-9.若→→b a ,均为非零向量,则“→→⊥b a ”是“||||→→→→-=+b a b a ”的( )A .充要条件 B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件10.若函数f (x )=si nax +c os ax (a >0)的最小正周期为1,则它的图像的一个对称中心为( )A .)0,8(π- B.(0,0) C.(0,81-) D.)0,81( 11.设向量)20cos ,20(sin ),25sin ,25(cos o o o o b a ==→→,若→→→+=b t a c (t ∈R),则||→c 的最小值为( )A .2 B.1 C.22 D.21 12.已知函数f (x )=f (π-x ),且当)2,2(ππ-∈x 时,f (x )=x +sin x ,设a =f (1),b =f (2),c =f (3),则( )A.a<b<cB.b<c<aC.c<b<aD.c<a<b安庆一中2007——2008学年度第一学期期末考试高一数学试题(必修4模块检测)一 .选择题:本大题共11小题,每小题3分,共33分,在每小题给出的四个选项中,只有一项是符合题目要求的。
广东省华南师大附中2007—2008学年第一学期高三期末水平测试数学试题(文科)

A .5B .6C .7D .87.函数)(x f y =图象为C ,C 关于直线x=1对称图象为C 1,将C 1向左平移2个单位后得到图象C 2,则C 2对应函数为 ( ) A .)(x f y -=B .)1(x f y -=C .)2(x f y -=D .)3(x f y -=8.若函数b bx x x f 36)(3+-=在(0,1)内有极小值,则实数b 的取值范围是( )A .(0,1)B .(-∞,1)C .(0,+∞)D .(0,21) 9.如图,在△ABC 中,,0,212tan=⋅=BC AH C 0)(=+⋅CB CA AB ,则过点C ,以A 、H 为两 焦点的双曲线的离心率为 ( )A .2B .3C .2D .310.已知实系数一元二次方程01)1(2=+++++b a x a x 的两根分别为10,121<<x x x ,且,a bx ,则12>的取值范围是( )A .)21,1(--B .]21,1(--C .]21,2(--D .)21,2(--第二部分(非选择题 共100分)二、填空题:本大题共4小题,每小题5分,共20分.11.下图是一个物体的三视图,根据图中尺寸(单位:cm ),计算它的体积等于 cm 3.12.在平面直线坐标系xoy 中,已知△ABC 的顶点A (-4,0)和C (4,0),顶点B 在椭圆=+=+BCA y x sin sin sin 192522上,则 13.在等比数列{a n }中,若=+++-==+++4321324321111189,815a a a a a a a a a a ,则 ▲选做题:在下面两道小题中选做一题,两道都选的只计算第14题的得分. 14.已知Rt △ABC 的两直角边AC=5,BC=12,D 是BC 上一点,当AD 是∠A 的平分线时,则CD=15.在极坐标系中,O 为极点,设点)65,5(),3,4(ππ-B A ,则三角形ABO 的面积为三、解答题:本大题共6小题,共80分. 解答应给出文字说明、证明过程或演算步骤.16.(本小题满分12分)如图,正三棱柱ABC —A 1B 1C 1的所有棱长都为2,D 为CC 1中点. (Ⅰ)求证:AB 1⊥平面A 1BD ; (Ⅱ)求点B 到平面A 1B 1D 的距离.17.(本小题满分12分)甲、乙两同学下棋,胜一盘得2分,和一盘各得一分,负一盘得0分. 连下三盘,得分多者为胜,求甲获胜的概率.18.(本小题满分14分)如图,平面四边形ABCD 中,AB=13,AC=10,AD=5,AC AB DAC ⋅=∠,53cos =120. (1)求cos ∠BAD ;(2)设y x AD y AB x AC 、,求⋅+⋅=的值.19.(本小题满分14分)已知直线y x y x l 40122:2==+-与抛物线交于A 、B 两点,过A 、B 两点的圆与抛物线在A (其中A 点在y 轴的右侧)处有共同的切线. (1)求圆M 的方程;(2)若圆M 与直线y=mx 交于P 、Q 两点,O 为坐标原点,求证:OQ OP ⋅为定值.20.(本小题满分14分)如图所示,A 、B 为函数)11(32≤≤-=x x y 图象上两点,且AB//x 轴,点M (1,m )(m>3)是△ABC 边AC 的中点.(1)设点B 的横坐标为t ,△ABC 的面积为S ,求S 关于t 的函数关系式)(t f S =;(2)求函数)S 的最大值,并求出相应的点C的坐标.(tf21.(本小题满分14分)把自数按下表排列:(Ⅰ)求200在表中的位置(在第几行第几列);(Ⅱ)试求自上至下的第m行,自左至右的第n列上的数;(Ⅲ)求主对角线上的数列:1、3、7、13、21、……的通项公式和前n项和的求和公式.∴AB 1⊥平面A 1BD ………………6分(3)运用等积法求解,Rt △A 1DC 1中,A 1C 1=2,C 1D=1, ∴51=D A 同理B 1D=5 …………7分 作DE ⊥A 1B 1,则E 为A 1B 1的中点, DE=2 ∴22221211111=⋅⋅=⋅=∆DE B A S D B A …………8分 由(1) ∴AO ⊥平面BCC 1B 1,且3223=⨯=AO ∴A 1到面A 1B 1D 的距离为3,设点B 到面A 1B 1D 的距离为h , 由331311111111⋅=⋅=∆∆--D BB DB A D BB A D B A B S S V V 得………………10分3)2221(2⨯⨯⨯=∴h ,求得∴=3h 点B 到面A 1B 1D 的距离为3.……12分17.(本小题满分12分)解:甲同学的胜负情况画树图如下:………………4分每盘棋都有胜、和、负三种情况,三盘棋共有3×3×3=27种情况.…………6分。
广东省东莞市2008-2009高一数学下期末试题(含答案)

2007—2008学年度第二学期期末教学质量检查高一数学考生注意:本卷共三大题,20小题,满分150分,时间120分钟.不准使用计算器.第Ⅰ卷 选择题一、选择题(本大题共10小题,每小题5分,共50分. 每小题各有四个选择支,仅有一个选择支正确.请把正确选择支号填在答题表内.) 1.已知3cos 5θ=-,4tan 3θ=,则角θ的终边落在 A .第一象限 B .第二象限 C .第三象限 D .第四象限 2.下列给出的赋值语句中,正确的是A .2P =B .M M =-C .2B A ==D .0=+y x3.若(4,)a m = ,(2,1)b =,且//a b ,则实数m 等于 A.4 B. 3 C. 2 D. 14.在空间直角坐标系Oxyz 中,已知点(2,2,1)A ,点M 在z轴上且||AM =M 的坐标为A .)1,0,0(-B .)1,0,0(C .)3,0,0(-D .)3,0,0(5.某校有教师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n 的样本.若从女学生中抽取的人数为40,则从男学生中抽取的人数应为 A .56 B . 48 C .44 D . 406. 若200辆汽车经过某一雷达测速区时被测得的时速频率分布直方图如右图所示,则时速在[50,60)的汽车大约有 A. 20辆 B. 36辆 C. 56辆 D. 78辆 7. 要得到函数2sin(2)3y x π=+的图象,只需将函数 sin 2y x =的图象上的所有点A .向左平移32π个单位B .向右平移32π个单位C .向左平移3π个单位 D .向右平移3π个单位 8. 如果tan()34πα+=-,那么tan 2α等于A .43-B . 43C . 45- D . 459.已知圆C 的方程为,222r y x =+M 00(,)x y 为圆内不同于圆心的定点,则直线200:r y y x x l =+与圆C 的位置关系是A . 直线l 过圆心B . 直线l 与圆C 相交但不过圆心 C . 直线l 与圆C 相切D . 直线l 与圆C 相离10.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0,且AB →|AB→| ·AC →|AC →| =14 , 则△ABC 为A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形(第6题图)二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中的横线上.) 11.如右图,一张正方形的桌面被划分为九个全等的小正方形.现将一颗豆子随机扔到 桌面上,假设豆子不落在线上,则它落在 阴影区域的概率为___ _____ .12.右边的程序框图中,输出s 的值为_____ . 13. 以线段AB :20(02)x y x +-=≤≤为直径的圆的方程为 . 14. 已知4sin cos 3αα+=-,53(,)42ππα∈,则 ααcos sin -的值等于 .三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.) 15.(本小题满分13分)将B A 、两枚骰子先后各抛掷一次,观察向上的点数. (1)共有多少种不同的结果?(2)列出两枚骰子点数之和是5的倍数的所有可能结果; (3)两枚骰子点数之和是5的倍数的概率为多少? (第12题图)(第11题图)16.(本小题满分14分)已知函数()sin sin(),2f x x x x π=+-∈R .(1)求函数()f x 的最小正周期;(2)求函数()f x 的的最大值,并指出此时x 的值; (3)求函数()f x 的单调递增区间.17.(本小题满分14分)甲、乙两台机床在相同的技术条件下生产同一种零件,从中各抽出10个,测得它们的尺寸如下(单位:mm ):甲机床 10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1 乙机床 10.3 10.4 9.6 9.9 10.1 10.9 8.9 9.7 10.1 10.1 (1)分别计算上面两个样本的平均数和方差;(2)如果图纸规定零件的尺寸为10 mm ,从计算的结果来看哪台机床加工这种零件较合适? 参考公式:平均数:)(121n x x x n x +⋯++=,方差:()()[]22121x x x x ns n -+⋯⋯+-=18.(本小题满分12分)在ABC ∆中,O 为中线AM 上的动点.(1)证明:2OB OC OM +=;(2)设||2AM =,OM t AM = (01)t ≤≤,试把()OA OB OC ⋅+ 表示为t 的函数()f t ,并求当O 在AM 上何处时,()f t 的值最小,最小值是多少?已知)0,0()cos()(πϕϕ≤≤>+=w wx x f 是定义在R 上的奇函数,当43π=x 时,()f x 取得最值,且()f x 在区间]2,0[π上为单调函数.(1)求w 和ϕ的值;(2)若当∈x +∈-N a a a ],,[ππ时,函数)(x f 恰好取得2008个最大值,求正整数a 的值.已知圆C :222440,x y x y +-+-=斜率为1的直线l 交圆C 于A 、B 两点,(1)化圆C 的方程为标准方程,并指出圆心和半径;(2)是否存在直线l ,使以线段AB 为直径的圆过原点?若存在,求出直线l 的方程;若不存在,说明理由;(3)当直线l 平行移动时,求CAB ∆面积的最大值.2007—2008学年度第二学期期末教学质量自查高一数学参考答案及评分标准一、选择题(本大题共10小题,每小题5分,共50分.)二、填空题(本大题共4小题,每小题5分,共20分.) 11.31 12.14 13.22(1)(1)2x y -+-= 14.32- 三、解答题15.(本小题满分13分)解: (1)共有3666=⨯种结果. ……4分(2)若用),(b a 来表示两枚骰子向上的点数,则点数之和是5的倍数的结果有:(1,4),(4,1),(2,3),(3,2),(4,6),(6,4),(5,5),共7种. ……9分(3)两枚骰子点数之和是5的倍数的概率是:367=P . ……13分16.(本小题满分14分) 解:()sin sin()2f x x x π=+- sin cos x x =+)x x =+)4x π=+ ……4分(1))(x f 的最小正周期为ππ212==T . ……6分 (2))(x f 的最大值为2,此时224πππ+=+k x ,即Z x k x ∈+=,42ππ ……10分(3)由22422πππππ+≤+≤-k x k 得42432ππππ+≤≤-k x k , ……12分所以,函数()f x 的单调递增区间为[]Z k k k ∈+-,42,432ππππ. ……14分17.(本小题满分14分)解:(1)101001011.101.102.10101=⨯=++=)(甲 x , ……3分 10100101104.103.10101=⨯=+++=)(乙 x . ……6分 (2)[]2222101.10101.10102.10101)()()(甲-+-+-= s =0.03, ……9分 []22221所以=甲x 乙x 且2s 甲2s <乙, 因此,用甲机床比乙机床更稳定,即用甲机床加工较合适. ……14分18.(本小题满分12分)(1)证明:由AM 是中线知,M 为BC 中点,∴OM OB BM =+12OB BC =+1()2OB OC OB =+-1()2OB OC =+ . ……4分 (2)解:由OM t AM =(01)t ≤≤得,t )1(-=,∴t )1(-=. ……6分又由(1)知22OB OC OM t AM +==, ……8分结合||2AM =得()f t =()OA OB OC ⋅+(1)(2)t AM t AM =-⋅222()t t AM =-2118[()]24t =-- ……10分∴当]1,0[21∈=t ,即O 为AM 中点时,()OA OB OC ⋅+ 取得最小值,最小值为2-.…12分19.(本小题满分13分)解:(1)∵)cos()(ϕ+=wx x f 是定义在R 上的奇函数,∴)cos()(ϕ+=wx x f 的图象关于原点对称,即20ππϕ+=+⋅k w )(Z k ∈.∵πϕ≤≤0,∴2πϕ=, ……3分∴wx x f sin )(-=.又∵当43π=x 时,()f x 取得最值,∴243πππ+=⋅n w )(Z n ∈, ∴324+=n w )(Z n ∈. ……5分 由0>w 知,wx x f sin )(-=在]2,0[wπ上为减函数. 由于)(x f 在区间]2,0[π上为单调函数,∴ππ≤∴10≤<w ,从而得32=w . ……7分 (2)由(1)知x x f 32sin)(-=,最小正周期为π3=T , ……8分 在长度为一个周期的区间]49,43[ππ-内刚好有两个最大值,结合x x f 32sin )(-=的图象,要使当∈x +∈-N a a a ],,[ππ时,函数)(x f 恰好取得2008个最大值,a 应满足,1003249100349⨯++<≤⨯+T Ta T πππ ……11分即 ,1003323491003349⨯++<≤⨯+ππππππa由此得433012413011+<≤+a ,所以正整数a 的值为3012. ……13分20.(本小题满分14分)解:(1)圆C 化成标准方程为:2223)2()1(=++-y x ,所以圆心为(1,2)C -,半径3r =. ……2分(2)设以线段AB 为直径的圆为M ,且圆心M 的坐标为(,)a b .由于CM l ⊥,1CM l k k ∴⋅=-,即1112-=⨯-+a b , ∴,01=++b a ① ……3分由于直线l 过点M (,)a b ,所以l 的方程可写这为y b x a -=-,即0x y b a -+-=,因此CM =. ……4分又AB M 以为直径的圆过原点,MA MB OM ∴==. ……5分而22229MB CB CM=-=-,222OM a b =+所以222)23(9b a a b +=+-- ② ……6分由①②得:312a a ==-或. 当32a =时,52b =-,此时直线l 的方程为40x y --=;当1a =-时,0b =,此时直线l 的方程为10x y -+=.所以,所求斜率为1的直线l 是存在的,其方程为40x y --=或10x y -+=. ……8分 (3)设线段AB 中点为M ,由(2)知在CAB ∆中, 2229222CMCMCB MB AB -=-==,CM ==, ……10分 ∴CAB ∆的面积12CAB S AB CM ∆=⋅ ||||92212CM CM ⨯-⨯====2948129)1(222≤+⎥⎦⎤⎢⎣⎡---=a ……12分当⎪⎩⎪⎨⎧-==2725b a 或⎪⎩⎪⎨⎧-=-=2121b a 时,上式取等号,此时直线l 的方程为0=-y x 或06=--y x , 易知上面两直线都与圆C 相交,所以,当直线l 运动变化时,CAB ∆面积的最大值为29.…14分。
[全解全析]07-08学年第一学期期末考试卷高一物理(广东新课标)
![[全解全析]07-08学年第一学期期末考试卷高一物理(广东新课标)](https://img.taocdn.com/s3/m/89f0a426c5da50e2524d7fda.png)
2007-2008年学年第一学期期末试卷高一物理版本:广东测试范围:必修1一、单项选择题(20小题,每小题3分,共60分)1、关于质点、位移和路程,下列说法中正确的是A、只有很小的物体才能看成质点B、路程是标量,即位移的大小C、位移的大小不会比路程大D、当质点作直线运动时,路程等于位移的大小答案:C解析:选项A错误,物体是否能看成质点,不是用物体的大小来决定;选项B错误,路程是标量,但不是位移的大小;选项D错误,路程等于位移的大小时,物体做直线运动且不反向。
2、两位同学分别乘坐甲、乙两船游览珠江,甲船上的同学看到乙船在运动,那么相对河岸两船的运动情况不可能...的是A、甲船不动,乙船在运动B、甲船运动,乙船不动C、甲、乙两船都在运动D、甲、乙两船同时以相同的速度运动答案:D解析:若甲、乙两船同时以相同的速度运动,则甲船上的同学看到乙船是静止的。
3、一本书放在水平桌面上,下列说法错误..的是A、桌面受到的压力实际就是书的重力B、桌面受到的压力是由于书本发生形变产生的C、桌面对书的支持力与书的重力是一对平衡力D、桌面对书的支持力与书对桌面的压力大小相等,方向相反,是一对作用力与反作用力答案:A解析:桌面受到的压力大小等于书的重力,但不能说就是书的重力。
因为桌面受到的压力是书给的,而书的重力是地球给的,它们的施力物体不同。
所以压力不能是重力。
4、如图所示,L1、L2是劲度系数均为k的轻质弹簧,A、B两只钩码均重G,则静止时两弹簧伸长量之和为A、3G/kB、2G/kC、G/kD、G/2k答案:A解析:L1伸长二个x,L2伸长一个x,两弹簧伸长三个x。
5、如图3所示,物体静止在斜面上,若斜面倾角θ增大(物体仍静止),物体受到的斜面的支持力和摩擦力的变化情况是A、支持力增大,摩擦力增大B、支持力增大,摩擦力减小C 、支持力减小,摩擦力增大D 、支持力减小,摩擦力减小 答案:C解析:物体静止在斜面上,物体受三个力:地球给的重力、斜面给的支持力、斜面给的静摩擦力。
2007-2008学年广东省广州市育才中学高一数 学第二学期第二次月考人教版

2007-2008学年广东广州市育才中学高一数 学第二学期第二次月考(必修四、必修五)一、选择题:本大题共10小题,每小题4分,共40分.每小题恰有一项....是符合题目要求的. 1. 19sin()6π-=( ) A .12 BC .12-D .2.已知等差数列{}n a 中,247,15a a ==,则前10项的和10S = ( ). A .100 B .210 C .380 D .400 3.ABC ∆中,3A π∠=,3BC =,AB =,则C ∠= ( )A .6πB .4π C .34π D .4π或34π4.已知a,b 都为正数,则正确的是( )A.a b +>B.a b +≤C.a b +≥D.a b +<5. 设变量x y ,满足约束条件142x y x y y -≥-⎧⎪+≤⎨⎪≥⎩,则目标函数z =2x +4y 的最大值为( )A .10B .12C .13D .146.已知等差数列{}n a 的公差为2,若245,,a a a 成等比数列,则2a 的值为( ) A .-10B .-8C .-6D .-47. 已知向量(21,4)c x →=+,(2,3)d x →=-,若//c d →→,则实数x 的值等于( ). A .21-B .61- C .61 D .21 8.如果tan(α+β)=43,tan(β-4π)=21,那么tan(α+4π)的值是 ( ) A .112B . 1110C .52D .29.设数列.,}{n n S n d a 项和为前的等差数列是公差为当首项1a 与公差变化时d ,若984a a a ++是一个定值,则下列各数中也是定值的是( )A .9SB .11SC .13SD .15S10.cos(35)cos(25)sin(35)cos(65)αααα-︒⋅︒++-︒︒-等于( )A .12 BC. 12-二、填空题:本大题共4小题,每小题4分,共16分。
广东省五校2007—2008学年第一学期高三期末联考数学试题(文科)

中小学教育资源站,百万资源无需注册免费下载!广东省五校2007—2008学年第一学期高三期末联考数学试题(文科)本试卷分选择题和非选择题两部分,共4页,满分为150分,考试时间120分钟。
1) 23. A .9 B .9 C .-9 D .-94.设,)cos 21,31(),43,(sin x b x a ==→-→-且→-→-b a //,则锐角x 为 ( ) A .6π B .4π C .3π D .π125中小学教育资源站,百万资源无需注册免费下载!5.如下图,该程序运行后输出的结果为 ( ) A .1 B .2 C .4 D .166 )7A .0.18, 0.47 B .0.47, 0.18 C .0.18, 1 D .0.38, 18.已知等比数列}{n a 的首项为8,n S 是其前n 项的和,某同学经计算得1S =8,2S =20,3S =36,4S =65,后来该同学发现其中一个数算错了,则该数为 ( ) A .1S B .2S C .3S D .4S中小学教育资源站,百万资源无需注册免费下载!9.已知 则实数 时均有 当 且a x f x a x x f a a x,21)()1,1(,)(,102<-∈-=≠>的取值范围是( ) A .[)∞+⎥⎦⎤ ⎝⎛,,221 0 B .(]4,11,41 ⎪⎭⎫⎢⎣⎡ C .(]2 11,21, ⎪⎭⎫⎢⎣⎡ D .[)∞+⎥⎦⎤ ⎝⎛, 441,0 10.定义两种运算:,22b a b a -=⊕a ⊗b=2)(b a -,则函数f(x)=2)2(2-⊗⊕x x为( )A .奇函数B .偶函数 C11.函数1213.对2⎪⎪⎭⎫ ⎝⎛2d c b a 14(1|AB (2)若三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤) 15.(本题满分12分)某射手进行射击训练,假设每次射击击中目标的概率为34,且各次射击的结果互不影响.中小学教育资源站,百万资源无需注册免费下载!(1)求射手在3次射击中,3次都击中目标的概率(用数字作答); (2)求射手在3次射击中,恰有两次连续击中目标的概率(用数字作答); (3)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答).16.(本小题满分12分)在⊿ABC 中,角A 、B 、C 所对的边分别为a 、b 、c,且10103cos ,21tan ==B A (1)求tanC 的值;(2)若⊿ABC 最长的边为1,求b 。
广东省五校2007—2008学年高三第一学期期末联考试数学试题(理科)

广东省五校2007—2008学年高三第一学期期末联考试数学试题(理科)本试卷分选择题和非选择题两部分,共4页,满分为150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
第一部分 选择题(共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若集合}1|{2<=x x M ,}1|{xxy x N -==,则N M = A .M B .N C .φ D .}10|{}01|{<<<<-x x x x 2.在复平面内,复数1+i2009(1-i)2 对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限3.已知cos 0()(1)10x x f x f x x π->⎧⎪=⎨++≤⎪⎩,则)34()34(-+f f 的值等于A .2-B .1C .2D .3 4.已知三条不重合的直线m 、n 、l ,两个不重合的平面βα,,有下列命题 ①若αα//,,//m n n m 则⊂; ②若βαβα//,//,则且m l m l ⊥⊥;③若βαββαα//,//,//,,则n m n m ⊂⊂; ④若αββαβα⊥⊥⊂=⊥n m n n m 则,,,, ; 其中正确的命题个数是A .1B .2C .3D .45.已知数列{}n a 、{}n b 都是公差为1的等差数列,其首项分别为1a 、1b ,且11a +b =5,11a >b ,++11a b N (n N )、∈∈,则数列nb{a }前10项的和等于A.55B.70C.85D.100 6.定义行列式运算1234a a a a =1423a a a a -.将函数sin ()cos xf x x=的图象向左平移n (0n >)个单位,所得图象对应的函数为偶函数,则n 的最小值为A .6pB .3pC .56pD .23p 7.定义在R 上的函数()f x 的图象关于点3(,0)4-成中心对称,对任意的实数x 都有3()()2f x f x =-+,且(1)1,f -=(0)2f =-,则(1)(2)(3)(2008)f f f f +++鬃?的值为A .2-B .1-C .0D .18.对任意正整数n ,定义n 的双阶乘!!n 如下:当n 为偶数时,!!(2)(4)642n n n n =--当n 为奇数时,!!(2)(4)531n n n n =--` 现有四个命题:①(2007!!)(2006!!)2007!=, ②2006!!21003!=, ③2006!!个位数为0, ④2007!!个位数为5其中正确的个数为A.1B.2C.3D.4第二部分 非选择题(共110分)二、填空题:本大题共7小题,其中9~12题是必做题,13~15题是选做题. 每小题5分,满分30分.9.若抛物线22y px =的焦点与双曲线22163x y -=的右焦点重合,则p 的值为 . 10.设a =(sin cos )x x dx π+⎰,则二项式6(展开式中含2x 项的系数是11.在Rt △ABC 中,CA ⊥CB ,斜边AB 上的高为h 1, 则2221111CB CA h +=;类比此性质,如图,在四 面体P —ABC 中,若PA ,PB ,PC 两两垂直,底面ABC 上的高为h ,则得到的正确结论为 ;12.某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未用血清的人一年中的感冒记录作比较,提出假设0H :“这种血清不能起到预防感冒的作用”,利用22⨯列联表计算得2 3.918K ≈,经查对临界值表知2( 3.841)0.05P K ≥≈. 对此,四名同学做出了以下的判断:p :有95%的把握认为“这种血清能起到预防感冒的作用” q :若某人未使用该血清,那么他在一年中有95%的可能性得感冒r :这种血清预防感冒的有效率为95% s :这种血清预防感冒的有效率为5%则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上) (1) p ∧﹁q ; (2)﹁p ∧q ; (3)(﹁p ∧﹁q )∧(r ∨s ); (4)(p ∨﹁r )∧(﹁q ∨s ) ▲选做题:在下面三道小题中选做两题,三题都选的只计算前两题的得分.13.(坐标系与参数方程选做题) 已知圆的极坐标方程为2cos ρθ=,则该圆的圆心到直线si n 2cos 1ρθρθ+= 的距离是 .14.(不等式选讲选做题) 已知g(x)=|x-1|-|x-2|,则g(x)的值域为 ;若关于x 的不等式2()1()g x a a x R ≥++∈的解集为空集,则实数a 的取值范围是 .15.(几何证明选讲选做题) 如图:PA 与圆O 相切于A , PCB 为圆O 的割线,并且不过圆心O ,已知∠BPA=030,PA=PC=1,则圆O 的半径等于 .三、解答题:本大题共6小题,共8016.(本小题满分12分) 在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.已知a+b=5,c =7,且.272cos 2sin 42=-+C B A (1) 求角C 的大小; (2)求△ABC 的面积.17.(本小题满分12分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R 的函数:23123456f(x)=x,f(x)=x ,f(x)=x ,f(x)=sinx,f(x)=cosx,f(x)=2. (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率; (2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.BAFEDC BA GFDECBA18.(本小题满分14分) 已知梯形ABCD 中,AD ∥BC ,∠ABC =∠BAD =2π,AB=BC=2AD=4,E 、F 分别是AB 、CD 上的点,EF ∥BC ,AE = x ,G 是BC 的中点。
广东新课程2007~2008学年度第一学期期末学生学业质量监测高一数学试题(必修①和数学必修④一、三章)

2007~2008学年度第一学期期末学生学业质量监测高一数学时量:120分钟 分值:150分 .适用学校:全市各高中. 内容:数学必修①和数学必修④一、三章. 注意:本次考试不得使用计算器.一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内) 1.已知全集U =Z ,{}1012A =-,,,,{1,0}B =-,则)(B C A U ⋂为 (A){}12-,(B){}10-,(C){}01,(D){}12,2. 函数()lg(1)f x x =- (A) (1,4](B) (1,4] (C) [1,4] (D) [1,4)3. 设2log 2.0=a ,22.0=b ,2.02=c ,则 (A)a b c << (B)c b a <<(C)c a b <<(D)b a c <<4.与角619π终边相同的角是 (A)30° (B) 150° (C) 210° (D) 300°5.已知角α的终边上一点P (-,则sin tan αα+=(A )235--(B )232--(C )6-D )15- 6. ︒︒-+︒︒15sin )105cos(15cos 75sin 等于(A )0(B )12(C )2(D )17.方程226x x -+=的解所在区间是(A )(0,1) (B )(1,2) (C )(2,3) (D )(3,4) 8.下表表示一球自一斜面滚下t 秒内所行的距离s 的呎数当t=2.5时,距离s 为(注:呎是一种英制长度单位)(A )45 (B )62.5 (C )70 (D )759. 函数⎩⎨⎧≤>=ππx x x x x f ,cos ,sin )(,则=︒)240(f(A )23-(B )23(C )21- (D )2110.已知πcos 22ϕ⎛⎫+=⎪⎝⎭,且π||2ϕ<,则tan ϕ= (A)3-(B)3(C) (D11. 已知函数()x f y =是R 上的偶函数,且()x f 在),0[+∞上是减函数,若()()2-≥f a f ,则a 的取值范围是(A )2≤a (B )2≥a (C )22≥-≤a a 或 (D )22≤≤-a 12. ()3sin 2f x x π⎛⎫=- ⎪3⎝⎭的图象为C , ①图象C 关于直线1112x =π对称; ②函数()f x 在区间5ππ⎛⎫-⎪1212⎝⎭,内是增函数; ③由3sin 2y x =的图象向右平移π3个单位长度可以得到图象C . 以上三个论断中,正确论断的个数是 (A )0 (B )1 (C )2 (D )3二、填空题(本大题共6小题,每小题5分,共30分,请将正确答案填空在答卷上) 13.计算:cos 660︒= .(填数值) 14.已知函数()f x ,()g x 分别由下表给出则[(2)]f g 的值为.15.化简:sin(90)cos()cos(180)ααα︒-⋅-︒-= .(填最简形式)16.函数241()()3x f x -+=最大的单调递减区间是 .17.若0a >,253=a ,则=a 51log .18.已知定义在R 上的连续函数()f x 满足:1)在),0(+∞上单调递减;2)1)0(=f ;3))()(x f x f -=.请写出一个这样的函数的表达式: .三、解答题(本大题共5小题,每题12分,共60分.请将详细解答过程写在答卷上) 19. 已知1sin cos 3αα+=. (1)求sin 2α的值;(2)求44sin cos αα+的值.20. 已知,αβ都是锐角,35cos ,cos(),513ααβ=+=- (1)求sin α和αtan 的值;(2)求)sin(βα+ 和cos β的值.21.某大型专卖店经营一种耐用消费品.已知该种消费品的进价为每件40元;该店每月销售量q (百件)与销售价p (元/件)之间的关系用右图中的一条折线(实线)表示;职工每人每月平均工资为1200元,该店应交付的其它费用为每月13200元.若当销售价p 为52元/件时,该店正好收支平衡,求该店的职工人数。
广东深圳益田中学07-08学年度第一学期高一必修四考试

益田中学2007—2008学年度第一学期第二学段高一年级 数学必修四 模块考试试题答题注意事项:1.本试卷满分150分,第Ⅰ卷17道题,满分100分, 第Ⅱ卷7道题,满分50分,全卷共24道题;2.考试用时120分钟;3.答题时请将答案写在试卷的相应位置上.第Ⅰ卷(满分100分)一、选择题 本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有 一项符合题目的要求,请将答案填写在题后的表格中. 1.已知点P (ααcos ,tan )在第三象限,则角α在 A .第一象限B .第二象限C .第三象限D .第四象限2.函数x y 2sin -=,R x ∈是A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的奇函数D .最小正周期为2π的偶函数 3.已知a 与b 均为单位向量,它们的夹角为60︒,那么|3|a b -等于 A BC D .44.已知M 是△ABC 的BC 边上的中点,若向量AB =a ,AC = b ,则向量AM 等于A .21(a -b )B .21(b -a )C .21( a +b )D .12-(a +b ) 5.若θ是△ABC 的一个内角,且81cos sin -=θθ,则θθcos sin -的值为A .23-B .23C .25-D .25 6.已知4πβα=+,则)tan 1)(tan 1(βα++的值是A .-1B .1C .2D .47.在ABC ∆中,有如下四个命题:①BC AC AB =-; ②AB BC CA ++=0;③若0)()(=-⋅+AC AB AC AB ,则ABC ∆为等腰三角形;④若0>⋅AB AC ,则ABC ∆为锐角三角形.其中正确的命题序号是 A .① ② B .① ③ ④ C .② ③D .② ④8.函数)sin(ϕω+=x A y 在一个周期内的图象如下,此函数的解析式为 A .)322sin(2π+=x y B .)32sin(2π+=x y C .)32sin(2π-=x y D .)32sin(2π-=x y 9.下列各式中,值为12的是A .0sin15cos15 B .22cossin 1212ππ-C .6cos 2121π+ D .020tan 22.51tan 22.5- 10.已知βα,为锐角,且cos α=101,cos β=51,则βα+的值是A .π32 B .π43 C .4π D .3π二、填空题 本大题共4小题,每小题5分,共20分.请将答案填写在横线上. 11.075sin 的值为 .12.已知向量2411()(),,,a =b =.若向量()λ⊥b a +b ,则实数λ的值是 .13.若32)sin(-=-απ, 且)0,2(πα-∈, 则αtan 的值是____________.14.已知51)cos(=+βα,53)cos(=-βα,则βαtan tan 的值为.三、解答题 本大题共3小题,每小题10分,共30分.解答应写出文字说明,证明过程 或演算步骤.15.(本题满分10分)已知)2,3(),2,1(-==b a,当k 为何值时,平行?与b a b a k 3-+平行时它们是同向还是反向?16.(本题满分10分) 已知函数)2cos(cos )(π+-=x x x f ,R x ∈.(Ⅰ)求()f x 的最大值; (Ⅱ)若3()4f α=,求sin 2α的值.17.(本题满分10分)已知函数1)4()sin()2x f x x ππ-=+. (Ⅰ)求()f x 的定义域;(Ⅱ)若角α是第四象限角,且3cos 5α=,求()f α.第Ⅱ卷(满分50分)一、选择题 本大题共2小题,每小题5分,共10分.在每小题给出的四个选项中,只有 一项符合题目的要求,请将答案填写在题后的【 】中. 18.已知tan(α+β) =53 , tan(β-4π )=41 ,那么tan(α+4π)为 【 】 A .1813 B .2313 C .237 D .18319.)10tan 31(50sin 00+的值为 【 】 ABC .2D .1二、填空题 本大题共2小题,每小题5分,共10分.请将答案填写在横线上. 20.080cos 40cos 20cos 的值为_____________________________. 21.已知tan2α=2,则αtan 的值为_________;6sin cos 3sin 2cos αααα+-的值为____________.三、解答题 本大题共3小题,每小题10分,共30分.解答应写出文字说明,证明过程 或演算步骤.22.(本题满分10分) 已知函数x x x x y 22cos 3cos sin 2sin ++=,R x ∈,那么 (Ⅰ)函数的最小正周期是什么? (Ⅱ)函数在什么区间上是增函数?23.(本题满分10分)已知向量 a=(cos α,sin α),b=(cos β,sin β),|b a-|=5. (Ⅰ)求cos (α-β)的值; (Ⅱ)若0<α<2π,-2π<β<0,且sin β=-513,求sin α的值.24.(本题满分10分)已知向量]2,0[),2sin ,2(cos ),23sin ,23(cos π∈-==x x x b x x a 且,求(Ⅰ)||b a b a +⋅及;(Ⅱ)若||2)(b a b a x f+-⋅=λ的最小值是23-,求实数λ的值.益田中学2007—2008学年度第一学期第二学段高一年级 数学必修四 模块考试试题参考答案(一)本套试题命题范围:1.使用教材(人教A 版)2.命题范围(必修4 全册)3.适用学生(高一年级)(二)详细答案及评分标准:第Ⅰ卷(满分100分)一、 选择题 本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目的要求,请将答案填写在题后的表格中.二、填空题本大题共4小题,每小题5分,共20分.请将答案填写在横线上. 11.426+ 12. 3- 13.552-14.21三、解答题 本大题共3小题,每小题10分,共30分.解答应写出文字说明,证明过程或演算步骤. 15.(本题满分10分)解: 因为)22,3(+-=+k k b a k ,)4,10(3-=-b a--------------------------------2分 当平行与b a b a k3-+时,则010)22()4()3(=⨯+--⨯-k k -------------------------------------------------2分 解得:31-=k --------------------------------------------------------------------------2分 此时)4,10(3-=-b a,)22,3(+-=+k k b a k=)2)31(2,331(+-⨯--=)34,310(-=)3(31)4,10(31b a--=--.-----------------------------------------------------------2分所以b a b a k3-+与反向.---------------------------------------------------------------2分[另解:当平行与b a b a k 3-+,存在唯一实数λ,使)3(b a b a k-=+λ即)4,10()22,3(-=+-λk k 得:⎩⎨⎧-=+=-λλ422103k k解得:31,31-=-=λk , 即当31-=k ,平行与b a b a k 3-+这时因为31-=λ,所以b a b a k 3-+与反向.]16.(本题满分10分)解:(Ⅰ)(5分) x x x x x f sin cos )2cos(cos )(+=+-=π=x x cos sin +-----------------------------------1分)cos 22sin 22(2x x += )4sin(2π+=x ------------------------------2分∴)(x f 的最大值为2.--------------------------------2分(Ⅱ)(5分) 因为43)(=αf ,即43cos sin =+αα -------------------1分∴169cos sin 21=+αα --------------------------------------2分∴1672sin -=α.------------------------------------------2分17.(本题满分10分) 解:(Ⅰ)(4分)由sin()02x π+≠,得cos 0x ≠,所以f(x)的定义城为{|,}2x x k k ππ≠+∈Z .--------------------------------4分[另解:由sin()02x π+≠,得Z k k x ∈≠+,2ππ∴Z k k x ∈-≠,2ππ所以f(x)的定义城为},2{Z k k x x ∈-≠ππ](Ⅱ)(6分)xx x x f cos )2sin 2sin 4cos 2(cos 21)(ππ++==xxx cos 2sin 2cos 1++-----------------------------------------------------------1分∴21cos 2sin 22cos 2cos sin ()2(cos sin )cos cos f αααααααααα+++===+.---2分因为α是第四象限角,所以4sin 15α===-.----------2分所以342()2()555f α=-=-.----------------------------------------------------------------1分 第Ⅱ卷(满分50分)一、选择题 本大题共2小题,每小题5分,共10分.在每小题给出的四个选项中,只有一项符合题目的要求,请将答案填写在题后的【 】中. 18.C 19.D二、填空题 本大题共2小题,每小题5分,共10分.请将答案填写在横线上. 20.81 21.34-(2分); 67(3分)。
高一级2007-2008第一学期月考试卷及答案解析(原始打印版)

高一级2007-2008第一学期月考试卷(考试时间:120分钟,满分150分)班别 姓名 分数一.选择题:(共12小题,每题5分,共60分)1.圆锥的底面半径是3,高是4,则它的侧面积是( )A .152πB .12πC .15πD .30π 2.已知两个球的表面积之比为1∶9,则这两个球的半径之比为( )A 1∶3B 11∶9 D 1∶81 3.长、宽、高分别为4、3、2的长方体的外接球的体积为 ( )A. 36πB.2327π C. 29π D. 9π 4.两个平面若有三个公共点,则这两个平面 ( )A .相交B .重合C .相交或重合D .以上都不对 5.若点M 在直线b 上,b 在平面β内,则β,,b M 之间的关系可记作( )A. β∈∈b MB. β⊂∈b MC.β⊂⊂b MD.β∈⊂b M 6“直线a 经过平面α外一点P ”用符号表示为:( )A. α//,a a P ∈B. P a =⋂αC. α∉∈p A p ,D. α⊂∈a a P , 7.下列说法正确的是 ( )A .平面α和平面β只有一个公共点 B. 两两相交的三条线共面C. 不共面的四点中, 任何三点不共线D. 有三个公共点的两平面必重合 8.用平行四边形ABCD 表示平面,正确的说法是 ( )A. ACB. 平面ACC. ABD. 平面AB 9. 异面直线是指( )A .不相交的两条直线B . 分别位于两个平面内的直线C .一个平面内的直线和不在这个平面内的直线D .不同在任何一个幸而内的两条直线 10、正方体1111D C B A ABCD -中,M 、N 是棱BC 、CD 的中点,则异面直线AD 1与MN 所成的角为 ( )度 A. 30 B 45 C 60 D 9011.三条直线a 、b 、c ,有命题:(1)若a//b,b//c,则a//c; (2)若a ⊥b,c ⊥b,则a//c; (3)若a//c,c ⊥b,则b ⊥a; (4)若a 与b, a 与c 都是异面直线, 则b 与c 也是异面直线. 其中正确的命题个数是 A.1 B.2 C.3 D.4 12..下面命题正确的是( )A .过两条直线有且只有一个平面B 过一点和一条直线有且只有一个平面C 过梯形两腰所在的直线有且只有一个平面D 过三点有且只有一个平面二.填空题:(共4题,每题5分,共20分)13. 过不在同一条直线上的四点最多可以确定 ___________个平面。
广东省华南师大附中2007—2008学年度高三综合测试(三)数学试题(文科)

广东省华南师大附中2007—2008学年度高三综合测试(三)数学试题(文科)本试卷分选择题和非选择题两部分,满分150分,考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡上, 用2B 铅笔将试卷类型(A )填涂在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改 动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区 域内的相应位置上;如需改动,先划掉原来的答案,然后写上新的答案;不准使用 铅笔和涂改液,不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题,共50分)一、(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知命题p :1sin ,≤∈∀x R x ,则( )A .1sin ,:≥∈∃⌝x R x pB .1sin ,:≥∈∀⌝x R x pC .1sin ,:>∈∃⌝x R x pD .1sin ,:>∈∀⌝x R x p 2.函数xx x f 1ln )(-=的零点个数为 ( )A .0B .1C .2D .33.若xxb x g a x f b a b a ==≠≠=+)()()1,1(0lg lg 与,则函数其中的图象 ( )A .关于直线y=x 对称B .关于x 轴对称C .关于y 轴对称D .关于原点对称4.下列能使θθθtan sin cos <<成立的θ所在区间是 ( )A .)4,0(πB .)2,4(ππ C .),2(ππD .)23,45(ππ5.下列四个函数中,以π为最小正周期,且在区间),2(ππ上为减函数的是 ( )A .x y 2cos =B .x y sin 2=C .xy cos )31(=D .x y tan -= 6.已知数列{a n }中,a 1=2,前n 项和S n ,若n n a n S 2=,则a n =( )A .n2 B .14+n C .)1(2+n nD .)1(4+n n7.不等式02||2<--x x 的解集是( )A .}22|{<<-x xB .}22|{>-<x x x 或C .}11|{<<-x xD .}11|{>-<x x x 或8.已知函数1)(0,01),sin()(12=⎪⎩⎪⎨⎧≥<<-=-a f x e x x x f x ,若π,则a 的所有可能值组成的集合为( )A .}22,1{-B . {1,22}C .{-22}D .{1}9.设函数P M x f x P x f x M x ax x f ≠⊂≥'=<=--=,若,集合}0)(|{},0)(|{1)(,则实数a 的取值范围是( )A .)1,(-∞B .(0,1)C .),1(+∞D .),1[+∞10.给出下面类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集):①“若b a b a R b a =⇒=-∈0,则、”类比推出“b a b a C c a =⇒=-∈0,则、” ②“若d b c a di c bi a R d c b a ==⇒+=+∈,,则复数、、、”类比推出“d b c a d c b a Q d c b a ==⇒+=+∈,22,则、、、”③“若b a b a R b a >⇒>-∈0,则、、”类比推出“若b a b a c b a >⇒-∈0.,则、”④“若111||<<-⇒<∈x x R x ,则”类比推出“若111||<<-⇒<∈z z C z ,则” 其中类比结论正确....的个数有 ( )A .1B .2C .3D .4第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分). 11.若复数z 满足方程1-=⋅i i z ,则z= 12.在等比数列{a n }中,∏∏==+=⋅===92110131i i n nki k k ia a a a aa a ,则,若,13.已知xy y x R y x ,则,且14,=+∈+的最大值为 14.将正整数排成下表:12 3 45 6 7 8 910 11 12 13 14 15 16 ……则数表中的300应出现在第 行.三、解答题;本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分12分) 已知a>0且1≠a命题P :函数),0()1(log +∞+=在x y a 内单调递减; 命题Q :曲线x x a x y 与1)32(2+-+=轴交于不同的两点. 如果“P\/Q ”为真且“P/\Q ”为假,求a 的取值范围.16.(本小题满分12分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:17.(本小题满分14分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c. 已知.272cos 2sin 42=-+C B A a+b=5,c=7,(1)求角C 的大小; (2)求△ABC 的面积. 18.(本小题满分14分)在公差为d (d ≠0)的等差数列{a n }和公比为q 的等比数列{b n }中,已知a 1=b 1=1,a 2=b 2,a 8=b 3.(1)求数列{a n }与{b n }的通项公式;(2)令n n n b a c ⋅=,求数列{c n }的前n 项和T n .19.(本小题满分14分)如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花园AMPN ,要求B 在AM 上,D 在AN 上,且对角线MN 过C 点,|AB|=3米,|AD|=2米.(Ⅰ)要使矩形AMPN 的面积大于32平方米,则AM 的长应在什么范围内?(Ⅱ)当AM 、AN 的长度是多少时,矩形AMPN 的面积最小?并求出最小面积.20.(本小题满分14分)定义域为R 的偶函数)(ln )(0)(R a ax x x f x x f ∈-=>时,,当,方程0)(=x f 在R 上恰有5个不同的实数解. (Ⅰ)求x<0时,函数)(x f 的解析式; (Ⅱ)求实数a 的取值范围.参考答案一、选择题 1.C2.B 利用数形结合求解,令xy x y x x x x 1ln 1ln 01ln ====-与,即求函数,得的交点个数.3.C 解析:取满足2121lg lg ===+b a b a ,则的特殊值可得答案C. 4.B 解析:取答案各区间的特点值343236ππππ、、、代入检验即可. 5.D 解析:B 、C 的函数周期为2π,不合题意,A 的函数在区间),2(ππ上为增函数,不合题意6.D 解析:由a 1=2知答案A 不正确,再由a 1+a 2=S 2=4a 2322=⇒a 可得答案B 、C 不正确 7.A 解析:2||02||01||0)1|)(|2|(|02||2<⇒<-⇒>+<+-⇒<--x x x x x x x ,由 22<<-⇒x ,故选A.8.A 解析:2221221)sin(01;110a k a a a a e a a ⇒+=⇒=⇒<<-=⇒=⇒≥-ππππ时时=2k+2221-=a ,由范围得,故选A. 9.D 解析:0)(,1,1)(110)1(1)(2='=⇒≠==≥⇒≥--='x f M x x f a a x a x f φ时,,当满足}0|{),,1(1;}0|{0)(≠==>⊂⇒≠=⇒≥'≠x x P a M a P M x x P x f 时,当 P M ≠⊂,故a 的取值范围是),1[+∞,故选D.10.B 解析:①、②正确,③、④错误,因为③、④中对于虚数的情况没有大小关系,故选B. 二、填空题11.答案:1-i 解析:i z i ii z -=⇒+=-=11112.答案:81 解析:813)())()()((441016574839298765432====a a a a a a a a a a a a a a a a a a 13.答案:161 解析:∵161)24(41441,,2=+≤⋅=⋅∴∈+y y x y x y x R y x ,当且仅当81,214===y x y x 即时取等号. 14.答案:18 解析:每行的数字取值从(n -1)2+1到n 2,而172<300<182,故300在第18行.三、解答题:15.解:∵1,0≠>a a , ∴命题P 为真时1,0a <⇔命题P 为假时1>⇔a命题Q 为真时,252101,004)32(2><<≠>>--=∆⇔a a a a a 或,即,且 命题Q 为假时 2521≤≤⇔a 由“P\/Q ”为真且“P/\Q ”为假,知P 、Q 有且只有一个正确.情形(1):P 正确,且Q 不正确)1,21[252110∈⎪⎩⎪⎨⎧≤≤<<⇔a a a ,即情形(2):P 不正确,且Q 正确),25(252101+∞∈⎪⎩⎪⎨⎧><<>⇔a a a a ,即或 综上,a 取值范围是),25()1,21[+∞⋃ 另解:依题意,命题P 为真时,0<a<1曲线x x a x y 与1)32(2+-+=轴交于两点等价于04)32(2>--a , 得 2521><a a 或 故命题Q 为真时,2521><a a 或 由“P\/Q ”为真且“P/\Q ”为假,知P 、Q 有且只有一个正确.等价于P 、Q 为真时在数轴表示图形中有且只有一个阴影的部分. 由图形知a 取值范围是),25()1,21[+∞⋃ (注:如果答案中21端点取了开区间,扣2分) 16.解:设此工厂应分别生产甲、乙两种产品x 吨、y 吨. 获得利润z 万元依题意可得约束条件:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤+≤+003001032005436049y x y x y x y x作出可行域如右图利润目标函数z=6x+12y由几何意义知当直线l :z=6x+12y ,经过可行域上的点M 时,z=6x+12y 取最大值.解方程组 ⎩⎨⎧=+=+20054300103y x y x ,得M (20,24)答:生产甲种产品20t ,乙种产品24t ,才能使此工厂获得最大利润17.解:(Ⅰ)∵A+B+C=180°由272cos 2cos 4272cos 2sin422=-=-+C C C B A 得 ∴27)1cos 2(2cos 142=--+⋅C C整理,得01cos 4cos 42=+-C C 解得:21cos =C∵︒<<︒1800C ∴C=60°(Ⅱ)由余弦定理得:c 2=a 2+b 2-2abcosC ,即7=a 2+b 2-2ab ∴ab b a 3)(72-+==25-3ab 6=⇔ab∴23323621sin 21=⨯⨯==∆C ab S ABC 18.解:(1)由条件得:126,4565711-=-=⇒⎩⎨⎧==⇒⎩⎨⎧=+=+n n n b n a q d qd qd (2)123216)45(611661--++⨯+⨯+=++++=n n n n c c c c T ①∴6T n =6+6×62+11×63+…+(5n -4)6n ② ①-②:n n n n T 6)45()666(51512--++++=--n n n n n 6)1(556)45(5)61(6511---=----⋅+=-∴16)1(+-=nn n T19.解:设AM 的长为x 米(x>3)∵||||||||AM DC AN DN = ∴32||-=x xAN∴32||||2-=⋅=x x AM AN S AMPN…………3分(Ⅰ)由S AMPN >32得32322>-x x , ∵12430)12)(4(04816,32><<∴>-->+-∴>x x x x x x x 或,即即AM 长的取值范围是(3,4)),12(+∞⋃(Ⅱ)令2222)3()6(3)3(3)3(633--=---='-=x x x x x x x y x x y ,则 ∴当),6(0,6+∞>'>,即函数在y x 上单调递增,x<6,0<'y ,函数在(3,6)上单调递减∴当x=6时,322-=x x y 取得最小值即S AMPN 取得最小值24(平方米)此时|AM|=6米,|AN|=4米答:当AM 、AN 的长度分别是6米、4米时,矩形AMPN 的面积最小,最小面积是24平方米.另解:以AM 、AN 分别为x 、y 轴建立直角坐标系,设1),2,3()3(),,0(),0,(=+>by a x MN C a b N a M 的方程为直线,则 由C 在直线MN 上得 ab b a 312123-=⇔=+ ∴)31(162163232ab b a ab S AMPN-=⋅=>⇔>=124048162><⇔>+-⇔a a x a 或∴AM 的长取值范围是(3,4)),12(+∞⋃(Ⅱ)∵4,62324232231===≥⇒⋅≥+=b a ba ab b a b a ,即,当且仅当时等号成立. ∴|AM|=6米,|AN|=4米时,S AMPN 达到最小值24答:当AM 、AN 的长度分别是6米、4米时,矩形AMPN 的面积最小,最小面积是24平方米. 20.解:(1)设x<0,则-x>0∵)(x f 为偶函数, ∴ax x x f x f +-=-=)ln()()( (2)∵)(x f 为偶函数,∴)(x f =0的根关于0对称.由)(x f =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根. 且两个正根和二个负根互为相反数∴原命题)(0x f x 时当>⇔图像与x 轴恰有两个不同的交点 下面研究x>0时的情况 ∵),0(0)(01)(+∞∈>'≤∴-='x x f a a xx f ,时,当即 ),0(ln )(+∞-=在ax x x f 为单调增函数,故),0(0)(+∞=在x f 不可能有两实根 ∴a>0 令ax x f 10)(==',得 当)(0)(1)(,0)(10x f x f a x x f x f a x ,时,递增,当时,<'>>'<<递减, ∴ax x f 1)(=在处取到极大值1ln --a又当-∞→+∞→-∞→→)(,)(0x f x x f x ,当时, 要使x x f x 与时,)(0>轴有两个交点当且仅当1ln --a >0 解得e a 10<<,故实数a 的取值范围(0,e1) 方法二:(2)∵)(x f 为偶函数, ∴)(x f =0的根关于0对称.由)(x f =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根. 且两个正根和二个负根互为相反数∴原命题)(0x f x 时当>⇔图像与x 轴恰有两个不同的交点 下面研究x>0时的情况x y x f ln 0)(=⇔=的零点个数与直线ax y =交点的个数.∴当0≤a 时,x y ln =递增与直线y=ax 下降或是x 国, 故交点的个数为1,不合题意 ∴a>011 由几何意义知x y ln =与直线y=ax 交点的个数为2时,直线y=ax 的变化应是从x 轴到与x y ln =相切之间的情形. 设切点t x k t t t x 1|)(ln )ln ,(='=⇒= ∴切线方为 )(1ln t x t t y -=-由切线与y=ax 重合知e a e t t t a 1,1ln ,1==⇒== 故实数a 的取值范围为(0,e1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附件4:2007~2008年广东卷考点在相关模块的分布一、必修1模块
二、必修2模块
四、必修4模块
六、选修1-1、1-2模块
七、选修2-1、2-2、2-3模块
八、选修4模块
(理科:从“标系与参数方程、不等式选讲选、几何证明选讲”中“3选2”;文科从“坐标系与参数方程、几何证明选讲”中“2选1”。
)
===========================================================
适用版本:
人教版,苏教版, 鲁教版,北京版,语文A版,语文S版,冀教版,沪教版,北大师大版,人教版新版,外研版,新起点,牛津译林,华师大版,湘教版,新目标,苏科版,粤沪版,北京版,岳麓版
适用学科:
语文,数学,英语,科学,物理,化学,生物,政治,历史,地理
适用年级:
一年级,二年级,三年级,四年级,五年级,六年级,七年级,八年级,九年级,小一,小二,小三,小四,小五,小六,初一,初二,初三,高一,高二,高三,中考,高考,小升初
适用领域及关键字:
100ceping,51ceping,52ceping,ceping,xuexi,zxxx,zxjy,zk,gk,xiti,教学,教学研究,在线教学,在线学习,学习,测评,测评网,学业测评, 学业测评网,在线测评, 在线测评网,测试,在线测试,教育,在线教育,中考,高考,中小学,中小学学习,中小学在线学习,试题,在线试题,练习,在线练习,在线练习,小学教育,初中教育,高中教育,小升初复习,中考复习,高考复习,教案,学习资料,辅导资料,课外辅导资料,在线辅导资料,作文,作文辅导,文档,教学文档,真题,试卷,在线试卷,答案,解析,课题,复习资料,复习专题,专项练习,学习网,在线学习网,学科网,在线学科网,在线题库,试题库,测评卷,小学学习资料,中考学习资料,单元测试,单元复习,单元试卷,考点,模拟试题,模拟试卷,期末考试,期末试卷,期中考试,期中试卷
===========================================================
本卷由《100测评网》整理上传,专注于中小学生学业检测,练习与提升.。
