BKIN双线性随动强化
ANSYS弹塑性分析教程

弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:∙ 什么是塑性 ∙ 塑性理论简介∙ ANSYS 程序中所用的性选项 ∙ 怎样使用塑性 ∙ 塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也 就 是说,当 移 走 载 荷 时,其应变也完全消失。
由于屈服点和比例极限相差很小,因此在ANSYS 程序中,假定它们相同。
在应力一应变的曲线中,低于屈服点的叫作弹性部分,超过屈服点的叫作塑性部分,也叫作应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
路径相关性:即然塑性是不可恢复的,那么这种问题的就与加载历史有关,这类非线性问题叫作与路径相关的或非保守的非线性。
路径相关性是指对一种给定的边界条件,可能有多个正确的解—内部的应力,应变分布—存在,为了得到真正正确的结果,我们必须按照系统真正经历的加载过程加载。
率相关性:塑性应变的大小可能是加载速度快慢的函数,如果塑性应变的大小与时间有关,这种塑性叫作率无关性塑性,相反,与应变率有关的性叫作率相关的塑性。
大多的材料都有某种程度上的率相关性,但在大多数静 力分 析所经历的应变率范围,两者的应力-应变曲线差别不大,所以在一般的分析中,我们变为是与率无关的。
工程应力,应变与真实的应力、应变: 塑性材料的数据一般以拉伸的应力—应变曲线形式给出。
材料数据可能是工程应力(P A 0)与工程应变(∆l 0),也可能是真实应力(P/A )与真实应变(nL l l ()0)。
大应变的塑性分析一般采用真实的应力,应变数据而小应变分析一般采用工程的应力、应变数据。
什么时候激活塑性:当材料中的应力超过屈服点时,塑性被激活(也就是说,有塑性应变发生)。
而屈服应力本身可能是下列某个参数的函数。
ANSYS命令大全

ANSYS命令大全一、定义材料号及特性mp,lab, mat, co, c1,…….c4lab: 待定义的特性项目(ex,alpx,reft,prxy,nuxy,gxy,mu,dens)ex: 弹性模量nuxy: 小泊松比alpx: 热膨胀系数reft: 参考温度reft: 参考温度prxy: 主泊松比gxy: 剪切模量mu: 摩擦系数dens: 质量密度mat: 材料编号(缺省为当前材料号)c 材料特性值,或材料之特性,温度曲线中的常数项c1-c4: 材料的特性-温度曲线中1次项,2次项,3次项,4次项的系数二、定义DP材料:首先要定义EX和泊松比:MP,EX,MAT,……MP,NUXY,MAT,……定义DP材料单元表(这里不考虑温度):TB,DP,MAT进入单元表并编辑添加单元表:TBDATA,1,CTBDATA,2,ψTBDATA,3,……如定义:EX=1E8,NUXY=0.3,C=27,ψ=45的命令如下:MP,EX,1,1E8MP,NUXY,1,0.3TB,DP,1TBDATA,1,27TBDATA,2,45这里要注意的是,在前处理的最初,要将角度单位转化到“度”,即命令:*afun,deg三、单元生死载荷步!第一个载荷步TIME,... !设定时间值(静力分析选项)NLGEOM,ON !打开大位移效果NROPT,FULL !设定牛顿-拉夫森选项ESTIF,... !设定非缺省缩减因子(可选)ESEL,... !选择在本载荷步中将不激活的单元EKILL,... !不激活选择的单元ESEL,S,LIVE !选择所有活动单元NSLE,S !选择所有活动结点NSEL,INVE !选择所有非活动结点(不与活动单元相连的结点)D,ALL,ALL,0 !约束所有不活动的结点自由度(可选)NSEL,ALL !选择所有结点ESEL,ALL !选择所有单元D,... !施加合适的约束F,... !施加合适的活动结点自由度载荷SF,... !施加合适的单元载荷BF,... !施加合适的体载荷SAVESOLVE请参阅TIME,NLGEOM,NROPT,ESTIF,ESEL,EKILL,NSLE,NSEL,D,F,SF和BF命令得到更详细的解释。
[VIP专享]等向强化、随动强化理解
![[VIP专享]等向强化、随动强化理解](https://img.taocdn.com/s3/m/ae9f9b8014791711cd791726.png)
等向强化、随动强化理解1、强化、等向强化、随动强化1. 强化、等向强化、随动强化定义分析时涉及到材料的塑性变形,如果是小变形,是用BKIN还是BISO模型好,两种模型算出的结果有差别吗应力达到屈服点后,继续加载(如果切线弹模大于0),有塑形变形,应力升高,然后卸载,这时是弹性的,再加载还是弹性的,直到应力得到卸载时的应力值才开始新的屈服。
这种屈服点升高的现象称为强化。
如果材料在一个方向屈服强度提高(强化)在其它方向的屈服强度也同时提高,这样的材料叫等向强化材料。
如果材料在应该方向的屈服点提高,其它方向的屈服应力相应下降,比如拉伸的屈服强度提高多少,反向的压缩屈服强度就减少多少,这样的材料叫随动强化材料。
具体用那种强化模型要看你的材料是那种材料。
不过从上面的分析可以看出,如果你只是单向加载,(即没有加载到屈服,卸载,再反向加载到屈服)两种材料模型的效果是一样的。
2.等向强化、随动强化理解屈服面(见屈服条件)的大小、形状和位置的变化规律。
塑性变形对应于微观上的位错运动。
在塑性变形过程中不断产生新的位错,位错的相互作用提高了位错运动的阻力。
这在宏观上表现为材料的强化,在塑性力学中则表现为屈服面的变化。
各种材料的强化规律须通过材料实验资料去认识。
利用强化规律得到的加载面(即强化后的屈服面)可用来导出具体材料的本构方程。
强化规律比较复杂,一般用简化的模型近似表示。
目前广泛采用的强化模型是等向强化模型和随动强化模型。
等向强化模型假设,在塑性变形过程中,加载面作均匀扩大,即加载面仅决定于一个强化参量q。
如果初始屈服面是f*(σij)=0,则等向强化的加载面可表为:f(σij)=f*(σij)-C(q)=0,式中σij为应力分量;C(q)是强化参量q的函数。
通常q可取为塑性功或等效塑性应变式中dε为塑性应变ε的增量;式中重复下标表示约定求和。
随动强化模型假设,在塑性变形过程中,加载面的大小和形状不变,仅整体地在应力空间中作平动。
塑性理论

塑性的三个主要方面:"屈服准则"流动准则"强化准则屈服准则:对单向受拉试件,我们可以通过简单的比较轴向应力与材料的屈服应力来决定是否有塑性变形发生,然而,对于一般的应力状态,是否到达屈服点并不是明显的。
屈服准则是一个可以用来与单轴测试的屈服应力相比较的应力状态的标量表示。
因此,知道了应力状态和屈服准则,程序就能确定是否有塑性应变产生。
屈服准则的值有时候也叫作等效应力,一个通用的屈服准则是Von Mises 屈服准则,当等效应力超过材料的屈服应力时,将会发生塑性变形。
流动准则:流动准则描述了发生屈服时,塑性应变的方向。
一般来说,流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的。
这种流动准则叫作相关流动准则,如果不用其它的流动准则(从其它不同的函数推导出来)。
则叫作不相关的流动准则。
强化准则:强化准则描述了初始屈服准则随着塑性应变的增加是怎样发展的。
一般来说,屈服面的变化是以前应变历史的函数,在ANSYS程序中,使用了两种强化准则。
等向强化是指屈服面以材料中所作塑性功的大小为基础在尺寸上扩张。
对Mises屈服准则来说,屈服面在所有方向均匀扩张。
由于等向强化,在受压方向的屈服应力等于受拉过程中所达到的最高应力。
随动强化假定屈服面的大小保持不变而仅在屈服的方向上移动,当某个方向的屈服应力升高时,其相反方向的屈服应力应该降低。
在随动强化中,由于拉伸方向屈服应力的增加导致压缩方向屈服应力的降低,所以在对应的两个屈服应力之间总存一个差值,初始各向同性的材料在屈服后将不再是向同性的。
2 塑性选项ANSYS程序提供了多种塑性材料选项,在此主要介绍四种典型的材料选项可以通过激活一个数据表来选择这些选项。
"经典双线性随动强化BKIN "双线性等向强化BISO "多线性随动强化MKIN "多线性等向强化MISO 经典的双线性随动强化(BKIN)使用一个双线性来表示应力应变曲线,所以有两个斜率,弹性斜率和塑性斜率,由于随动强化的Vonmises 屈服准则被使用,所以包含有鲍辛格效应,此选项适用于遵守Von Mises 屈服准则,初始为各向同性材料的小应变问题,这包括大多数的金属。
钢筋混凝土有限元分析

钢筋混凝土有限元分析(1)首先建立有限元模型,这里我们选用ANSYS软件自带的专门针对混凝土的单元类型Solid 65,进入ANSYS主菜单Preprocessor->Element Type->Add/Edit/Delete,选择添加Solid 65号混凝土单元。
(2) 点击Element types窗口中的Options,设定Stress relax after cracking为Include,即考虑混凝土开裂后的应力软化行为,这样在很多时候都可以提高计算的收敛效率。
(3) 下面我们要通过实参数来设置Solid 65单元中的配筋情况。
进入ANSYS主菜单Preprocessor-> Real Constants->Add/Edit/Delete,添加实参数类型1与Solid 65单元相关,输入钢筋的材料属性为2号材料,但不输入钢筋面积,即这类实参数是素混凝土的配筋情况。
(4) 再添加第二个实参数,输入X方向配筋为0.05,即X方向的体积配筋率为5%。
(5) 下面输入混凝土的材料属性。
混凝土的材料属性比较复杂,其力学属性部分一般由以下3部分组成:基本属性,包括弹性模量和泊松比;本构关系,定义等效应力应变行为;破坏准则,定义开裂强度和压碎强度。
下面分别介绍如下。
(6) 首先进入ANSYS主菜单Preprocessor-> Material Props-> Material Models,在DefineMaterial Model Behavior 窗口中选择Structural-> Linear -> Elastic-> Isotropic,输入弹性模量和泊松比分别为30e9和0.2(7) 下面输入混凝土的等效应力应变关系,这里我们选择von Mises屈服面,该屈服面对于二维受力的混凝土而言精度还是可以接受的。
在Define Material Model Behavior 窗口中选择Structural-> Nonlinear->Inelastic-> Rate Independent-> Isotropic Hardening Plasticity-> Mises Plasticity-> Multilinear,输入混凝土的等效应力应变曲线如下图所示。
ANSYS培训

六个常数(Rxx, Ryy, Rzz, Rxy, Ryz, Rxz )表示 Hill 屈服准则的特性:
1
G H
R
2 xx
F H
1
R
2 yy
F G 1
R
2 zz
N
3
2
R
2 xy
3
L
2
R
2 yz
M
3
2
R
2 xz
R xx
y xx
o
R yy
y yy
o
Rz
y z
o
R xy R yz R xz
3
y xy
e1 21 2 22 3 23 1 2
式中 1 、2 和 3 是主应力。 当等效应
力超过材料的屈服e应力 y时,屈服发生:
范 • 米赛斯屈服 准则
若在 3D 主应力空间中画出, von Mises 屈服面是一个圆柱 体。
2
圆柱体以1=2=3 为轴排列。 注意如果应力状态在圆柱体内, 不发生屈服。这意味着如果材料 在静水压力下 (1=2=3), 再 大的静水压力也不会引起屈服。 从另一个角度看,偏离 (1=2=3) 轴的应力参与计算 von Mises 应力 {s}。
– 从金属的观点看,这种行为是因为延伸但没有破坏原 子间化学键。因为弹性是由于原子键的延伸,所以是 完全可恢复的。而且这些弹性应变往往是小的。
– 金属的弹性行为最常用虎克定律的应力应变关系描述:
E
塑性回顾:
• 塑性金属中也会遇到非弹性或塑性响应。
–超过屈服应力是塑性区域,塑性区域中卸载后残 留一部分永久变形。
材料属性 – 双线性随动强化:
双线性随动强化(BKIN)用双线性的应力-应变 曲线表示,包括弹性斜率和剪切模量。采用 随动强化的 Mises屈服准则,因此包括包辛
参考: 培训手册塑性基础 (6-41) 双线性随动强化 (BKIN)

• 单击 [Add Temperature] 增加另一个温度列 • T1 = 0 时 EX = 12e6 • T2 = 500 时 EX = 8e6 • 在T1 和T2时 PRXY = 0.3 • [确定]
– 或者输入如下命令: – /prep7
MPTEMP,1,0 MPTEMP,2,500 MPDATA,EX,1,1,12e6 MPDATA,EX,1,2,8e6 MPDATA,PRXY,1,1,0.3 MPDATA,PRXY,1,2,0.3
– 或输入如下命令:
FINISH
/CLEAR
/FILNAM,BKIN
• 1b. 启动 ANSYS 交互模式, 在指导者指定的工 作目录中以 “BKIN” 作为工作名
10.塑性基础
…双线性随动强化
• 2.定义弹性常数和温度表
– Preprocessor > Material Props > Material Models… – 在材料模型界面中, 依次双击 Structural … Linear …
Basic Structural Nonlinearities 11.0
• 步骤: • 1a. 清除数据库
– Utility Menu > File > Clear & Start New
• [确定] • [是]
– Utility Menu > File > Change Jobname …
• 用 “BKIN” 作为工作名 • [确定]
Training Manual
Basic Structural Nonlinearities 11.0
10.塑性基础
…双线性随动强化
ANSYS弹性及塑性分析(非常经典)

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例(GUI方法) (9)塑性分析实例(命令流方法) (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:什么是塑性塑性理论简介ANSYS程序中所用的性选项怎样使用塑性塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说,当移走载荷时,其应变也完全消失。
由于屈服点和比例极限相差很小,因此在ANSYS程序中,假定它们相同。
在应力一应变的曲线中,低于屈服点的叫作弹性部分,超过屈服点的叫作塑性部分,也叫作应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
路径相关性:即然塑性是不可恢复的,那么这种问题的就与加载历史有关,这类非线性问题叫作与路径相关的或非保守的非线性。
路径相关性是指对一种给定的边界条件,可能有多个正确的解—内部的应力,应变分布—存在,为了得到真正正确的结果,我们必须按照系统真正经历的加载过程加载。
率相关性:塑性应变的大小可能是加载速度快慢的函数,如果塑性应变的大小与时间有关,这种塑性叫作率无关性塑性,相反,与应变率有关的性叫作率相关的塑性。
大多的材料都有某种程度上的率相关性,但在大多数静力分析所经历的应变率范围,两者的应力-应变曲线差别不大,所以在一般的分析中,我们变为是与率无关的。
工程应力,应变与真实的应力、应变:塑性材料的数据一般以拉伸的应力—应变曲线形式给出。
等向强化、随动强化理解

等向强化、随动强化理解1、强化、等向强化、随动强化1. 强化、等向强化、随动强化定义分析时涉及到材料的塑性变形,如果是小变形,是用BKIN还是BISO模型好,两种模型算出的结果有差别吗应力达到屈服点后,继续加载(如果切线弹模大于0),有塑形变形,应力升高,然后卸载,这时是弹性的,再加载还是弹性的,直到应力得到卸载时的应力值才开始新的屈服。
这种屈服点升高的现象称为强化。
如果材料在一个方向屈服强度提高(强化)在其它方向的屈服强度也同时提高,这样的材料叫等向强化材料。
如果材料在应该方向的屈服点提高,其它方向的屈服应力相应下降,比如拉伸的屈服强度提高多少,反向的压缩屈服强度就减少多少,这样的材料叫随动强化材料。
具体用那种强化模型要看你的材料是那种材料。
不过从上面的分析可以看出,如果你只是单向加载,(即没有加载到屈服,卸载,再反向加载到屈服)两种材料模型的效果是一样的。
2.等向强化、随动强化理解屈服面(见屈服条件)的大小、形状和位置的变化规律。
塑性变形对应于微观上的位错运动。
在塑性变形过程中不断产生新的位错,位错的相互作用提高了位错运动的阻力。
这在宏观上表现为材料的强化,在塑性力学中则表现为屈服面的变化。
各种材料的强化规律须通过材料实验资料去认识。
利用强化规律得到的加载面(即强化后的屈服面)可用来导出具体材料的本构方程。
强化规律比较复杂,一般用简化的模型近似表示。
目前广泛采用的强化模型是等向强化模型和随动强化模型。
等向强化模型假设,在塑性变形过程中,加载面作均匀扩大,即加载面仅决定于一个强化参量q。
如果初始屈服面是f*(σij)=0,则等向强化的加载面可表为:f(σij)=f*(σij)-C(q)=0,式中σij为应力分量;C(q)是强化参量q的函数。
通常q可取为塑性功或等效塑性应变式中dε为塑性应变ε的增量;式中重复下标表示约定求和。
随动强化模型假设,在塑性变形过程中,加载面的大小和形状不变,仅整体地在应力空间中作平动。
塑性材料的有限元分析

October 17, 2000
塑性分析 – 5.7版本
5-4
塑性-预备知识
在进行塑性分析之前应先理解下列问题: • 比例极限 • 屈服点 • 应变强化 • Bauschinger 效应 • 应力偏量 • 等效应力 • 率相关性
October 17, 2000
塑性分析 – 5.7版本
5-5
比例极限与屈服点
下表总结了塑性选项,包括屈服准则,流动准则和强化准则。
October 17, 2000
塑性分析 – 5.7版本
5-24
双线性随动强化
双线性随动强化(BKIN) 使用双线段表示应力-应变曲线,其中包括 弹性模量和切向模量。 随动强化使用von Mises 屈服准则,所以包 括Bauschinger效应。此选项可用于小应变和循环加载。
October 17, 2000
塑性分析 – 5.7版本
5-30
多线性随动强化MKIN选项
MKIN选项使用 Besseling 或 内层模型(参见ANSYS 理论手册)。 MKIN 选项最多允许五个应力-应变数据点,可定义最多五条不同温 度下的曲线。MKIN 模型有下列限制:
• 每条应力-应变曲线必须 用同一组应变值。
2
3
2
3
1
2
5-11
October 17, 2000
塑性分析 – 5.7版本
率相关性
塑性应变的大小可能是施加载荷快慢的函数。如果塑性应变发生不 需考虑时间效应,这种塑性是率无关 的。相反,塑性与应变率有 关的称为率相关塑性。 本次讲解主要集中在率无关 塑性上。塑性应变假设为与时间无关 系。 ANSYS 有适用于金属成形过程的率相关模型 (Anand模型)。
等向强化、随动强化理解

等向强化、随动强化理解1、强化、等向强化、随动强化1. 强化、等向强化、随动强化定义分析时涉及到材料的塑性变形,如果是小变形,是用BKIN还是BISO模型好,两种模型算出的结果有差别吗应力达到屈服点后,继续加载(如果切线弹模大于0),有塑形变形,应力升高,然后卸载,这时是弹性的,再加载还是弹性的,直到应力得到卸载时的应力值才开始新的屈服。
这种屈服点升高的现象称为强化。
如果材料在一个方向屈服强度提高(强化)在其它方向的屈服强度也同时提高,这样的材料叫等向强化材料。
如果材料在应该方向的屈服点提高,其它方向的屈服应力相应下降,比如拉伸的屈服强度提高多少,反向的压缩屈服强度就减少多少,这样的材料叫随动强化材料。
具体用那种强化模型要看你的材料是那种材料。
不过从上面的分析可以看出,如果你只是单向加载,(即没有加载到屈服,卸载,再反向加载到屈服)两种材料模型的效果是一样的。
2.等向强化、随动强化理解屈服面(见屈服条件)的大小、形状和位置的变化规律。
塑性变形对应于微观上的位错运动。
在塑性变形过程中不断产生新的位错,位错的相互作用提高了位错运动的阻力。
这在宏观上表现为材料的强化,在塑性力学中则表现为屈服面的变化。
各种材料的强化规律须通过材料实验资料去认识。
利用强化规律得到的加载面(即强化后的屈服面)可用来导出具体材料的本构方程。
强化规律比较复杂,一般用简化的模型近似表示。
目前广泛采用的强化模型是等向强化模型和随动强化模型。
等向强化模型假设,在塑性变形过程中,加载面作均匀扩大,即加载面仅决定于一个强化参量q。
如果初始屈服面是f*(σij)=0,则等向强化的加载面可表为:f(σij)=f*(σij)-C(q)=0,式中σij为应力分量;C(q)是强化参量q的函数。
通常q可取为塑性功或等效塑性应变式中dε为塑性应变ε的增量;式中重复下标表示约定求和。
随动强化模型假设,在塑性变形过程中,加载面的大小和形状不变,仅整体地在应力空间中作平动。
Ansys材料非线性理论概述

4.1 材料非线性概述许多与材料有关的参数可以使结构刚度在分析期间改变。
塑性、非线性弹性、超弹性材料、混凝土材料的非线性应力—应变关系,可以使结构刚度在不同载荷水平下(以及在不同温度下)改变。
蠕变、粘塑性和粘弹性可以引起与时间、率、温度和应力相关的非线性。
膨胀可以引起作为温度、时间、中子流水平(或其他类似量)函数的应变。
ANSYS程序应可以考虑多种材料非线性特性:1.率不相关塑性指材料中产生的不可恢复的即时应变。
2.率相关塑性也可称之为粘塑性,材料的塑性应变大小将是加载速度与时间的函数。
3.材料的蠕变行为也是率相关的,产生随时间变化的不可恢复应变,但蠕变的时间尺度要比率相关塑性大的多。
4.非线性弹性允许材料的非线性应力应变关系,但应变是可以恢复的。
5.超弹性材料应力应变关系由一个应变能密度势函数定义,用于模拟橡胶、泡沫类材料,变形是可以恢复的。
6.粘弹性是一种率相关的材料特性,这种材料应变中包含了弹性应变和粘性应变。
7.混凝土材料具有模拟断裂和压碎的能力。
8.膨胀是指材料在中子流作用下的体积扩大效应。
4.2 塑性分析4.2.1 塑性理论简介许多常用的工程材料,在应力水平低于比例极限时,应力—应变关系为线性的。
超过这一极限后,应力—应变关系变成非线性,但却不一定是非弹性的。
以不可恢复的应变为特征的塑性,则在应力超过屈服点后开始出现。
由于屈服极限与比例极限相差很小,ANSYS程序在塑性分析中,假设这二个点相同,见图4-1。
图4-1 弹塑性应力-应变曲线塑性是一种非保守的(不可逆的),与路径相关的现象。
换句话说,荷载施加的顺序,以及什么时候发生塑性响应,影响最终求解结果。
如果用户预计在分析中会出现塑性响应,则应把荷载处理成一系列的小增量荷载步或时间步,以使模型尽可能附合荷载—响应路径。
最大塑性应变是在输出(Jobname.OUT)文件的子步信息中打印的。
在一个子步中,如果执行了大量的平衡迭代,或得到大于15%的塑性应变增量,则塑性将激活自动时间步选项[ AUTOTS ](GUI:Main Menu>Solution> Sol"n Control:Basic Tab 或Main Menu>Solution>Unabridged Menu> Time /Frequenc>Time and Substps)。
ANSYS本构关系

于二维和三维结构分析,后者对杆系结构分析比较适用。裂缝的处理
方式有离散裂缝模型、分布裂缝模型和断裂力学模型,后者目前尚处
研究之中,主要应用的是前两种。离散裂缝模型和分布裂缝模型各有
特点,可根据不同的分析目的选择使用。随着计算速度和网格自动划
分的快速实现,离散裂缝模型又有被推广使用的趋势。
就ANSYS而言,可以考虑分离式模型(solid65+link8,认为混
资料仅供参考
在混凝土到达其屈服面之前,SOLID65单 元可以具有线弹性属性、多线性弹性或者是其他 的塑性特性。本构关系有等强硬化模型、随动硬 化模型和Drucker-Prager模型。但如果超出了混 凝土的屈服面,则将丧失混凝土屈服性能。通过 路径MainMenu>Preprocessor>Material Props>Material Models
资料仅供参考
资料仅供参考
资料仅供参考
资料仅供参考
ANSYS中混凝土本构关系
一、关于模型
资料仅供参考
钢筋混凝土有限元模型根据钢筋的处理方式主要分为三种,即分
离式、分布式和组合式模型。考虑钢筋和混凝土之间的粘结和滑移,
则采用引入粘结单元的分离式模型;假定混凝土和钢筋粘结很好,不
考虑二者之间的滑移,则三种模型都可以;分离式和分布式模型适用
(4)多线性等向强化资(料仅供参M考 ISO) 使用多线性来表示使用Von Mises屈服准则
的等向强化的应力-应变曲线,它适用于比例加 载的情况和大应变分析。 需要输入最多100个应力-应变曲线,最多可以 定义20条不同温度下的曲线。 其材料特性的定义步骤如下: 1.定义弹性模量 2.定义MISO数据表 3.为输入的应力-应变数据指定温度值 4.输入应力-应变数据 5.画材料的应力-应变曲线 与MKIN 数据表不同的是,MISO的数据表对不同 的温度可以有不同的应变值,因此,每条温度曲 线有它自己的输入表。
ANSYS应用实例:钢筋混凝土简支梁数值模拟
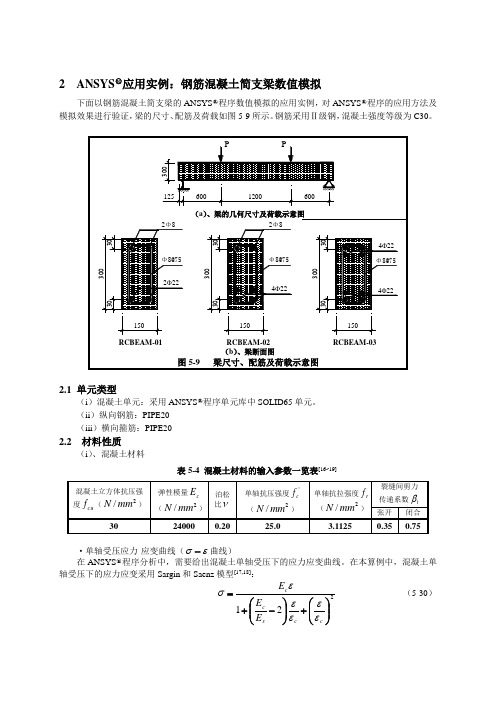
(ii )纵向钢筋:PIPE20 (iii )横向箍筋:PIPE202.2 材料性质(i )、混凝土材料表5-4 混凝土材料的输入参数一览表[16~19]·单轴受压应力-应变曲线(εσ-曲线)在ANSYS ○R程序分析中,需要给出混凝土单轴受压下的应力应变曲线。
在本算例中,混凝土单轴受压下的应力应变采用Sargin 和Saenz 模型[17,18]:221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-+=c c s c c E E E εεεεεσ (5-30)式中取4'4')108.0028.1(c c c f f -=ε;断面图配筋图断面图配筋图断面图配筋图RCBEAM-01 RCBEAM-02 RCBEAM-03图5-12 各梁FEM模型断面图(a)单元网格图(b)钢筋单元划分图图5-13 算例(一)的FEM模型图2.4 模型求解在ANSYS○R程序中,对于非线性分析,求解步的设置很关键,对计算是否收敛关系很大,对于混凝土非线性有限元分析,在计算时间容许的情况下,较多的求解子步(Substeps)或较小的荷载步和一个非常大的最大子步数更容易导致收敛[2]。
在本算例中,设置了100个子步。
最终本算例收敛成功,在CPU为P41.6G、内存为256MB的微机上计算,耗时约为8小时。
2.5 计算结果及分析2.5.1 荷载—位移曲线图5-14为ANSYS○R程序所得到的各梁的荷载-跨中挠度曲线,从图中可以看出:(i)、梁RCBEAM-01:曲线形状能基本反映钢筋混凝土适筋梁剪切破坏的受力特点,而且荷载-跨中挠度曲线与钢筋混凝土梁的弯剪破坏形态非常类似,即当跨中弯矩最大截面的纵筋屈服后,由于裂缝的开展,压区混凝土的面积逐渐减小,在荷载几乎不增加的情况下,压区混凝土所受的正应力和剪应力还在不断增加,当应力达到混凝土强度极限时,剪切破坏发生,荷载突然降低。
(ii)、梁RCBEAM-02:荷载-跨中挠度曲线与超筋梁的试验荷载-跨中挠度曲线很相似,在荷载达到极限情况下,没有出现屈服平台,而是突然跌落。
ANSYS中典型的非线性材料模型

ANSYS中典型的非线性材料模型:双线性随动强化(BKIN)双线性等向强化(BISO)多线性随动强化(MKIN)多线性等向强化(MISO)双线性随动强化(Bilinear Kinematic Hardening Plasticity)、双线性等向强化(Bilinear Isotropic Hardening Plasticity)均属于双线性模型。
双线性模型通过两个直线段来模拟弹塑性材料的本构关系,即认为材料在屈服以前应力—应变关系按照弹性模量成比例变化,屈服以后,按比弹性模量小的另一个模量(切线模量)变化。
模型有两个斜率:弹性斜率和塑性斜率。
对于服从Mises屈服准则,初始为各向同性材料的小应变非线性问题,一般采用双线性随动强化模型,这种材料包括大多数的金属材料。
而对于初始各向同性材料的大应变问题则采用等向强化模型。
需要输入的常数是屈服应力s y和切向斜率ET。
(理想弹塑性材料ET=0)多线性随动强化(Multilinear Kinematic Hardening Plasticity)、多线性等向强化(Multilinear Isotropic Hardening Plasticity)属于多线性模型。
多线性模型与双线性模型类似,只是使用多条直线段来表示模拟弹塑性材料的本构关系,即认为材料在屈服以前应力—应变关系按照弹性模量成比例变化,屈服以后,则按照其位置不同,以不同的、小于弹性模量的另一个模量变化。
例1:MP,EX,1,30E6!定义第1类材料的弹性模量EX=30E6MP,NUXY,1,0.3!定义第1类材料的泊松比为NUXY=0.3TB,BKIN,1!激活数据表,应用经典双线性随动强化准则,并为第1类材料指定1个参考温度。
TBTEMP,70!在数据表中为输入的应力—应变数据指定参考温度值TEMP=70TBDATA,1,36000,0!在数据表中从第1个空格开始填入数据,屈服应力36000,塑性斜率0 (红色为塑性选项)例2:定义双线性随动强化模型的标准过程MPTEMP,1,0,500!定义杨氏弹性模量对应的温度MPDATA,EX,1,,12E6!定义杨氏模量的取值MPDATA,EX,1,,8E6TB,BKIN,1,2!激活数据表,应用经典双线性随动强化准则,并为第1类材料指定2个参考温度。
ANSYS中典型的非线性材料模型

ANSYS中典型的非线性材料模型:双线性随动强化(BKIN)双线性等向强化(BISO)多线性随动强化(MKIN)多线性等向强化(MISO)双线性随动强化(Bilinear Kinematic Hardening Plasticity)、双线性等向强化(Bilinear Isotropic Hardening Plasticity)均属于双线性模型。
双线性模型通过两个直线段来模拟弹塑性材料的本构关系,即认为材料在屈服以前应力—应变关系按照弹性模量成比例变化,屈服以后,按比弹性模量小的另一个模量(切线模量)变化。
模型有两个斜率:弹性斜率和塑性斜率。
对于服从Mises屈服准则,初始为各向同性材料的小应变非线性问题,一般采用双线性随动强化模型,这种材料包括大多数的金属材料。
而对于初始各向同性材料的大应变问题则采用等向强化模型。
需要输入的常数是屈服应力s y和切向斜率ET。
(理想弹塑性材料ET=0)多线性随动强化(Multilinear Kinematic Hardening Plasticity)、多线性等向强化(Multilinear Isotropic Hardening Plasticity)属于多线性模型。
多线性模型与双线性模型类似,只是使用多条直线段来表示模拟弹塑性材料的本构关系,即认为材料在屈服以前应力—应变关系按照弹性模量成比例变化,屈服以后,则按照其位置不同,以不同的、小于弹性模量的另一个模量变化。
例1:MP,EX,1,30E6!定义第1类材料的弹性模量EX=30E6MP,NUXY,1,0.3!定义第1类材料的泊松比为NUXY=0.3TB,BKIN,1!激活数据表,应用经典双线性随动强化准则,并为第1类材料指定1个参考温度。
TBTEMP,70!在数据表中为输入的应力—应变数据指定参考温度值TEMP=70TBDATA,1,36000,0!在数据表中从第1个空格开始填入数据,屈服应力36000,塑性斜率0 (红色为塑性选项)例2:定义双线性随动强化模型的标准过程MPTEMP,1,0,500!定义杨氏弹性模量对应的温度MPDATA,EX,1,,12E6!定义杨氏模量的取值MPDATA,EX,1,,8E6TB,BKIN,1,2!激活数据表,应用经典双线性随动强化准则,并为第1类材料指定2个参考温度。
等向强化、随动强化理解

等向强化、随动强化理解1、强化、等向强化、随动强化1. 强化、等向强化、随动强化定义分析时涉及到材料的塑性变形,如果是小变形,是用BKIN还是BISO模型好,两种模型算出的结果有差别吗应力达到屈服点后,继续加载(如果切线弹模大于0),有塑形变形,应力升高,然后卸载,这时是弹性的,再加载还是弹性的,直到应力得到卸载时的应力值才开始新的屈服。
这种屈服点升高的现象称为强化。
如果材料在一个方向屈服强度提高(强化)在其它方向的屈服强度也同时提高,这样的材料叫等向强化材料。
如果材料在应该方向的屈服点提高,其它方向的屈服应力相应下降,比如拉伸的屈服强度提高多少,反向的压缩屈服强度就减少多少,这样的材料叫随动强化材料。
具体用那种强化模型要看你的材料是那种材料。
不过从上面的分析可以看出,如果你只是单向加载,(即没有加载到屈服,卸载,再反向加载到屈服)两种材料模型的效果是一样的。
2.等向强化、随动强化理解屈服面(见屈服条件)的大小、形状和位置的变化规律。
塑性变形对应于微观上的位错运动。
在塑性变形过程中不断产生新的位错,位错的相互作用提高了位错运动的阻力。
这在宏观上表现为材料的强化,在塑性力学中则表现为屈服面的变化。
各种材料的强化规律须通过材料实验资料去认识。
利用强化规律得到的加载面(即强化后的屈服面)可用来导出具体材料的本构方程。
强化规律比较复杂,一般用简化的模型近似表示。
目前广泛采用的强化模型是等向强化模型和随动强化模型。
等向强化模型假设,在塑性变形过程中,加载面作均匀扩大,即加载面仅决定于一个强化参量q。
如果初始屈服面是f*(σij)=0,则等向强化的加载面可表为:f(σij)=f*(σij)-C(q)=0,式中σij为应力分量;C(q)是强化参量q的函数。
通常q可取为塑性功或等效塑性应变式中dε为塑性应变ε的增量;式中重复下标表示约定求和。
随动强化模型假设,在塑性变形过程中,加载面的大小和形状不变,仅整体地在应力空间中作平动。
【2017年整理】等向强化、随动强化理解

等向强化、随动强化理解1、强化、等向强化、随动强化1. 强化、等向强化、随动强化定义分析时涉及到材料的塑性变形,如果是小变形,是用BKIN还是BISO模型好,两种模型算出的结果有差别吗应力达到屈服点后,继续加载(如果切线弹模大于0),有塑形变形,应力升高,然后卸载,这时是弹性的,再加载还是弹性的,直到应力得到卸载时的应力值才开始新的屈服。
这种屈服点升高的现象称为强化。
如果材料在一个方向屈服强度提高(强化)在其它方向的屈服强度也同时提高,这样的材料叫等向强化材料。
如果材料在应该方向的屈服点提高,其它方向的屈服应力相应下降,比如拉伸的屈服强度提高多少,反向的压缩屈服强度就减少多少,这样的材料叫随动强化材料。
具体用那种强化模型要看你的材料是那种材料。
不过从上面的分析可以看出,如果你只是单向加载,(即没有加载到屈服,卸载,再反向加载到屈服)两种材料模型的效果是一样的。
2.等向强化、随动强化理解屈服面(见屈服条件)的大小、形状和位置的变化规律。
塑性变形对应于微观上的位错运动。
在塑性变形过程中不断产生新的位错,位错的相互作用提高了位错运动的阻力。
这在宏观上表现为材料的强化,在塑性力学中则表现为屈服面的变化。
各种材料的强化规律须通过材料实验资料去认识。
利用强化规律得到的加载面(即强化后的屈服面)可用来导出具体材料的本构方程。
强化规律比较复杂,一般用简化的模型近似表示。
目前广泛采用的强化模型是等向强化模型和随动强化模型。
等向强化模型假设,在塑性变形过程中,加载面作均匀扩大,即加载面仅决定于一个强化参量q。
如果初始屈服面是f*(σij)=0,则等向强化的加载面可表为:f(σij)=f*(σij)-C(q)=0,式中σij为应力分量;C(q)是强化参量q的函数。
通常q可取为塑性功或等效塑性应变式中dε为塑性应变ε的增量;式中重复下标表示约定求和。
随动强化模型假设,在塑性变形过程中,加载面的大小和形状不变,仅整体地在应力空间中作平动。
ANSYS本构关系

2021/10/10
5
(4)多线性等向强化(MISO) 使用多线性来表示使用Von Mises屈服准则
的等向强化的应力-应变曲线,它适用于比例加 载的情况和大应变分析。 需要输入最多100个应力-应变曲线,最多可以 定义20条不同温度下的曲线。 其材料特性的定义步骤如下: 1.定义弹性模量 2.定义MISO数据表 3.为输入的应力-应变数据指定温度值 4.输入应力-应变数据 5.画材料的应力-应变曲线 与MKIN 数据表不同的是,MISO的数据表对不同 的温度可以有不同的应变值,因此,每条温度曲 线有它自己的输入表。
率,弹性斜率和塑性斜率,由于随动强化的Von mises屈 服准则被使用,所以包含有鲍辛格效应,此选项适用于遵 守Von Mises 屈服准则,初始为各向同性材料的小应变问 题,这包括大多数的金属。
需要输入的常数是屈服应力和切向斜率,可以定义高 达六条不同温度下的曲线。 注意: 1.使用MP命令来定义弹性模量 2.弹性模量也可以是与温度相关的 3.切向斜率Et不可以是负数,也不能大于弹性模量 在使用经典的双线性随动强化时,可以分下面三步来定义 材料特性。 1.定义弹性模量 2.激活双线性随动强化选项 3.使用数据表来定义非线性特性
2021/10/10
3
(2)双线性等向强化(BIS0)
也是使用双线性来表示应力-应变曲线,在此选 项中,等向强化的Von Mises 屈服准则被使用, 这个选项一般用于初始各向同性材料的大应变问 题。需要输入的常数与BKIN选项相同。 举例如下: MP,EX,1,200e9 MP,NUXY,1,0.25 MP,GXY,1,150e9 TB,BISO,1
变关系,而开裂和压碎后采用其给出的本构关系。但屈服准则尚可另
