最新七年级下几何证明题
七年级数学(下册)几何典型题
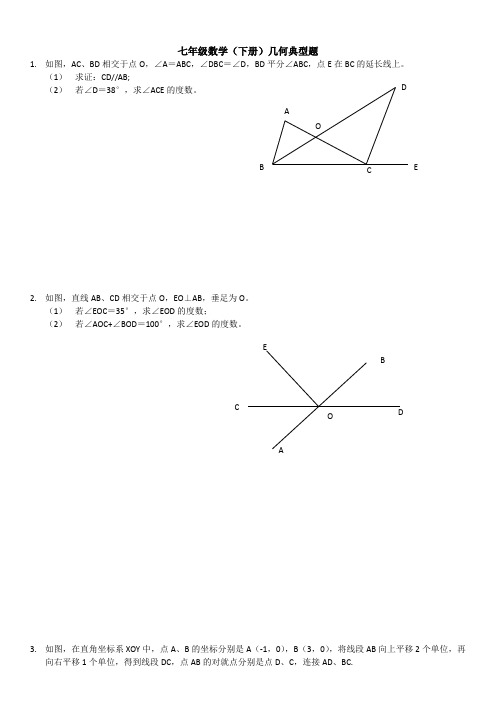
七年级数学(下册)几何典型题1. 如图,AC 、BD 相交于点O ,∠A =ABC ,∠DBC =∠D ,BD 平分∠ABC ,点E 在BC 的延长线上。
(1) 求证:CD//AB;(2) 若∠D =38°,求∠ACE 的度数。
2. 如图,直线AB 、CD 相交于点O ,EO ⊥AB ,垂足为O 。
(1) 若∠EOC =35°,求∠EOD 的度数;(2) 若∠AOC+∠BOD =100°,求∠EOD 的度数。
3. 如图,在直角坐标系XOY 中,点A 、B 的坐标分别是A (-1,0),B (3,0),将线段AB 向上平移2个单位,再向右平移1个单位,得到线段DC ,点AB 的对就点分别是点D 、C ,连接AD 、BC.(1) 直接写出点C 、D 的坐标; (2) 求四边形ABCD 的面积;(3) 点P 为线段BC 上任意一点(与点B 、C 不重合),连接PD 、PO.求证:∠CDP+∠BOP=∠OPD.4. 如图,直接EF 分别与直线AB ,CD 相交于点P 和点Q ,PG 平分∠APQ, QH 平分∠DQP ,并且∠1=∠2,说出图中哪些直线平行。
5. 平面内的两条直线有相交和平行两种位置关系。
(1) 如图1,若AB//CD ,点P 在AB 、CD 内部,∠B =50°,∠D =30°,求∠BPD 的度数。
(2) 如图2,将点P 移到AB 、CD 外部,则∠BPD 、∠B 、∠D 之间有何数量关系?请写出你的结论并加以证6. 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A (1,2),解答以下问题。
(1) 请在图中建立适当的直角坐标系,并写出图书馆(B )的位置坐标。
(2) 若体育馆位置坐标为C (-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC ,求△ABC 的面积。
7. 如圖,CE ⊥AB 于E ,DF ⊥AB 于F ,AC ∥A CE FB8. 如图,在平面直角坐标系中,已知点A (-3,3),B (-5,1),C (-2,0),P (a,b )是△ABC 的边AC 上任意一点,△ABC 经过平移后得到△A ’B ’C ’,点P 的对应点为P ’(a+6,b-2). (1) 直接写出点C ’的坐标; (2) 在图中画出△A ’B ’C ’; (3) △AOA ’的面积。
人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题(含答案)

人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题1、如图,已知∠2=∠3,∠C=∠D,求证:∠A=∠F.证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3.∴DB∥CE.∴∠DBA=∠C.∵∠D=∠C,∴∠D=∠DBA.∴DF∥AC.∴∠A=∠F.2、如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).3、如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.求证:AB∥CD,EG∥FH.证明:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,∴∠FCD=∠3.∴AB∥CD.∵∠2=50°,∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,∴∠GEF=12∠NEF=65°.∴∠GEF=∠3.∴EG∥FH.4、如图,已知∠B=∠D,∠E=∠F,判断BC与AD的位置关系,并说明理由.解:BC∥AD,理由:∴BE∥FD.∴∠B=∠BCF.又∵∠B=∠D,∴∠BCF=∠D.∴BC∥AD.5、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.证明:∵AD⊥BC,EG⊥BC,∴∠ADC=∠EGC=90°.∴AD∥EG.∴∠1=∠2,∠E=∠3.∵∠E=∠1,∴∠2=∠3.∴AD平分∠BAC.6、如图,B,C,E三点在一条直线上,A,F,E三点在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.证明:∵AB∥CD,∴∠4=∠BAE.∴∠3=∠BAE.∵∠1=∠2,∴∠1+∠CAF=∠2+∠CAF,即∠BAE=∠CAD.∴∠3=∠CAD.∴AD∥BE.7、如图,已知AB∥CD,试判断∠B,∠BED和∠D之间的关系,并说明理由.解:∠BED=∠B+∠D.理由如下:过点E作EF∥AB,则∠B=∠BEF.∵AB∥CD,∴EF∥CD.∴∠DEF=∠D.∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D.8、如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?解:平行.理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∴∠AEF -∠1=∠EFD -∠2,即∠GEF =∠HFE.∴EG ∥HF.9、如图,A ,B ,C 三点在同一直线上,∠1=∠2,∠3=∠D ,试判断BD 与CF 的位置关系,并说明理由.解:BD ∥CF.理由如下:∵∠1=∠2,∴AD ∥BF.∴∠D =∠DBF.∵∠3=∠D ,∴∠3=∠DBF.∴BD ∥CF.10、如图,∠ABC =∠ADC ,BF ,DE 分别是∠ABC ,∠ADC 的平分线,∠1=∠2,试说明:DC ∥AB.解:∵BF ,DE 分别是∠ABC ,∠ADC 的平分线,∴∠3=12∠ADC ,∠2=12∠ABC. ∵∠ABC =∠ADC ,∴∠3=∠2.∵∠1=∠2,∴∠1=∠3.∴DC∥AB.11、如图,AD平分∠BAC,AD⊥BC于D,点E,A,C共线,∠DAC=∠EFA,延长EF 交BC于点G.求证:EG⊥BC.证明:∵AD平分∠BAC,∴∠DAC=∠DAB.又∵∠DAC=∠EFA,∴∠DAB=∠EFA.∴AD∥EG.∴∠ADC=∠EGD.∵AD⊥BC,∴∠ADC=90°.∴∠EGD=90°.∴EG⊥BC.12、已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.13、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′和C′的位置上,ED′与BC的交点为G.若∠EFG=50°,求∠1,∠2,∠3的度数.解:根据折叠的性质可知,∠DEF=∠D′EF,∠EFC=∠EFC′.∵∠EFG=50°,∴∠EFC=180°-50°=130°.∴∠EFC′=∠EFC=130°.∴∠3=∠EFC′-∠EFG=130°-50°=80°.∵AD∥BC,∴∠DEF=∠EFG=50°.∴∠DED′=2∠DEF=100°.∴∠1=180°-∠DED′=180°-100°=80°.∵AD∥BC,∴∠1+∠2=180°.∴∠2=180°-∠1=100°.故∠1=80°,∠2=100°,∠3=80°.14、如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D =∠3+60°,∠CBD =70°,∴∠3=25°.∵AB ∥CD ,∴∠C =∠3=25°.15、(1)如图1,AB ∥CD ,则∠E +∠G 与∠B +∠F +∠D 有何关系?(2)如图2,若AB ∥CD ,又能得到什么结论?请直接写出结论.解:(1)过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥CD. ∵AB ∥CD ,∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1=∠B ,∠2=∠3,∠4=∠5,∠6=∠D.∴∠1+∠2+∠5+∠6=∠B +∠3+∠4+∠D ,即∠BEF +∠FGD =∠B +∠EFG +∠D.(2)∠B +∠F 1+∠F 2+…+∠F n -1+∠D =∠E 1+∠E 2+…+∠E n .16、已知E ,F 分别是AB ,CD 上的动点,P 也为一动点.(1)如图1,若AB ∥CD ,求证:∠P =∠BEP +∠PFD ;(2)如图2,若∠P =∠PFD -∠BEP ,求证:AB ∥CD ;(3)如图3,AB ∥CD ,移动E ,F ,使∠EPF =90°,作∠PEG =∠BEP ,则∠AEG∠PFD =2.证明:(1)过点P作PG∥AB,则∠EPG=∠BEP.∵AB∥CD,∴PG∥CD.∴∠GPF=∠PFD.∴∠EPF=∠EPG+∠FPG=∠BEP+∠PFD.(2)过点P作PQ∥AB,则∠QPE=∠BEP.∵∠EPF=∠PFD-∠BEP,∴∠PFD=∠EPF+∠BEP=∠EPF+∠QPE=∠FPQ. ∴DC∥PQ.∴AB∥CD.。
七年级数学典型几何证明50题
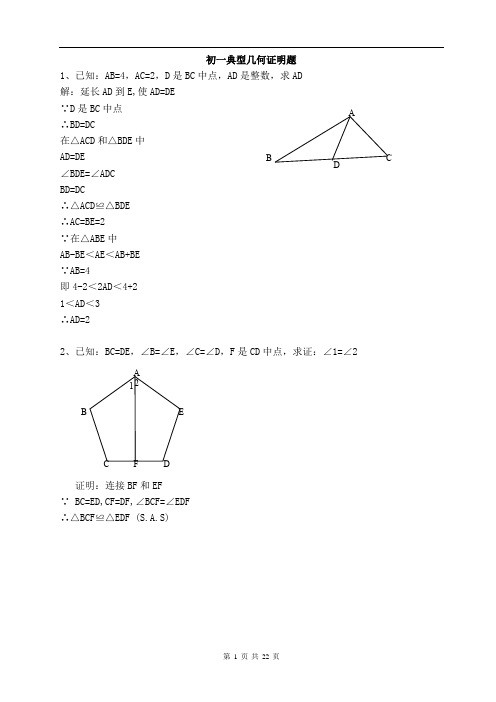
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
七年级下册数学期末考试几何大题证明必考题
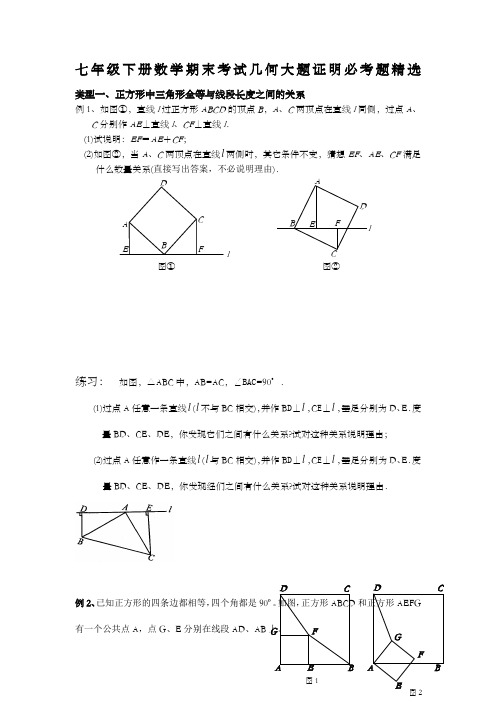
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
A E B 图1D CG FA BD CG FE图2(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE(1)BD 与CE 相等吗?请说明理由.A BCFDE GP32B(2)你能求出BD与CE的夹角∠BFC的度数吗?(3)若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连结BE、DG交点记为点M(如图).请直接写出线段BE和DGF例3、正方形四边条边都相等,四个角都是90o.如图,已知正方形ABCD在直线MN 的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明理由;②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.图 2FG DA图 1FDA类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.CBAPDE2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形,将一块含30o 角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立C图1吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
七年级下几何证明题(精华版)

几何证明题专项练习 1、直接根据图示填空:(1)∠α=_________ (2)∠α=_________ (3)∠α=_________ (4)∠α=_________ (5)∠α=_________ (6)∠α=_________α38°62°20°α°30°25°150°α(1) (2) (3)70°α°70°60°20°α20°135°45°α(4) (5) (6) 2、填空完成推理过程: 如图,∵AB ∥EF ( 已知 )∴∠A + =1800( ) ∵DE ∥BC ( 已知 )∴∠DEF= ( )2. ∠ADE= ( ) 3. 已知:如图,∠ADE =∠B ,∠DEC =115°. 求∠C 的度数.4. 已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.3.5.已知AB ∥CD ,∠1=70°则∠2=_______,∠3=______,∠4=______5.4321A CDB4.ACD E FBDEB CAHG 2 1 FE DC B A EDBAC21FEDBA Ca34126. 已知:如图4, AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数 6.7.8.7.直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.8. 如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.9.如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.12.9.10.10.如图,已知:21∠∠=, 50=D ∠,求B ∠的度数。
初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
(完整版)七年级几何证明题训练(含答案)

1. 已知:如图11所示,∆ABC 中,∠=C 90于E ,且有AC AD CE ==。
求证:DE =122. 已知:如图 求证:BC =3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14【试题答案】1. 证明:取AC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,∴∠=∠=∴≅∴=∴=4312AC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截CB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ,3. 证明:延长PM CQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线AD BC AD AEBC AE AD⊥∴<∴=>,22()AB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。
几何推理题七年级

以下是一道适合七年级学生的几何推理题:
题目:证明等边三角形的三个内角都等于60度。
已知:三角形ABC是等边三角形,即AB=BC=CA。
求证:三角形ABC的三个内角都等于60度。
证明:
第一步,由于三角形ABC是等边三角形,所以∠A = ∠B = ∠C(等边三角形的性质,等边三角形的三个内角相等)。
第二步,由于三角形内角和等于180度(三角形内角和定理),因此∠A + ∠B + ∠C = 180度。
第三步,将第一步的结论代入第二步的等式,可得:
3∠A = 180度
第四步,解这个方程,可得:
∠A = 60度
所以,三角形ABC的三个内角都等于60度(由于第一步的结论,因此∠B = ∠C = 60度)。
七年级下几何证明题
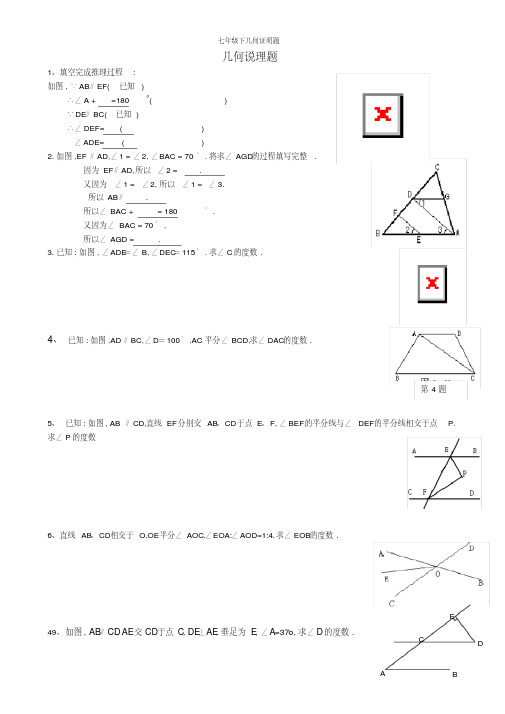
第4题几何说理题1、填空完成推理过程:如图,∵AB ∥EF( 已知 )∴∠A + =1800( )∵DE ∥BC( 已知 )∴∠DEF= ( ) ∠ADE= ( )2.如图,EF ∥AD,∠1 =∠2,∠BAC = 70°.将求∠AGD 的过程填写完整.因为EF ∥AD,所以∠2 = . 又因为∠1 = ∠2,所以∠1 = ∠3. 所以AB ∥ . 所以∠BAC + = 180°.又因为∠BAC = 70°, 所以∠AGD = .3.已知:如图,∠ADE =∠B,∠DEC =115°.求∠C 的度数.4、已知:如图,AD ∥BC,∠D =100°,AC 平分∠BCD,求∠DAC 的度数.5、已知:如图, AB ∥CD,直线EF 分别交AB 、CD 于点E 、F,∠BEF 的平分线与∠DEF 的平分线相交于点P.求∠P 的度数6、直线AB 、CD 相交于O,OE 平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB 的度数.49、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37o,求∠D 的度数.ABCDEHG 21FEDCBA50、如图,已知:,,求的度数。
51、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数、52、AB//CD,EF ⊥AB 于点E,EF 交CD 于点F,已知∠1=600、求∠2的度数、53、如图,AB ∥CD,BF ∥CE,则∠B与∠C有什么关系?请说明理由.54、如图,已知:DE ∥BC,CD 就是∠ACB 的平分线,∠B =70°,∠ACB =50°,求∠EDC与∠BDC 的度数.55、如图AB∥CD,∠NCM =90°,∠NCB =30°,CM 平分∠BCE,求∠B的大小.56、如图,AB ⊥BD ,CD ⊥MN ,垂足分别就是B 、D 点,∠FDC=∠EBA . (1)判断CD 与AB 的位置关系;第11题图(2)BE 与DE 平行不?为什么?57、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行不?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 不?为什么.58、如图,已知:E 、F 分别就是AB 与CD 上的点,DE 、AF 分别交BC 于G 、H ,A =D ,1=2,求证:B =C .59、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.60、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数、61、如图,点D 就是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)
![[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)](https://img.taocdn.com/s3/m/e2aed845c4da50e2524de518964bcf84b8d52d05.png)
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)试题部分一、选择题:1. 在下列几何图形中,哪一个图形可以通过旋转90度后与自身重合?()A. 矩形B. 等边三角形C. 正方形D. 梯形2. 下列哪个条件可以证明两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等3. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个条件可以证明两个角相等?()A. 两角的度数相等B. 两角的对边相等C. 两角的邻边相等D. 两角的余角相等5. 若一个等腰三角形的底边长为10cm,腰长为13cm,则该三角形的周长为()A. 32cmB. 42cmC. 46cmD. 52cm6. 在平行四边形ABCD中,若AB=6cm,BC=8cm,则对角线AC的取值范围是()A. 2cm < AC < 14cmB. 2cm < AC < 6cmC. 2cm < AC < 8cmD. 6cm < AC < 14cm7. 下列哪个条件可以证明两个平行四边形全等?()A. 一组对边平行且相等B. 两组对边平行C. 一组对边平行,另一组对边相等D. 一组对边平行且相等,另一组对边也相等8. 在三角形ABC中,若AB=AC,∠B=60°,则三角形ABC的周角为()A. 120°B. 180°C. 240°D. 360°9. 下列哪个图形是轴对称图形?()A. 等腰梯形B. 直角梯形C. 等腰三角形D. 一般四边形10. 若一个正方形的对角线长为10cm,则该正方形的面积是()A. 50cm²B. 100cm²C. 200cm²D. 500cm²二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
七年级下几何证明题(精选)

七年级下几何证明题(精选)第一篇:七年级下几何证明题(精选)七年级下几何证明题学了三角形的外角吗?(三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于和它不相邻的任何一个内角) 角ACD>角BAC>角AFE角ACD+角ACB=180度角BAC+角ABC+角ACB=180度所以角ACD=角BAC+角ABC所以角角ACD>角BAC同理:角BAC>角AFE所以角ACD>角BAC>角AFE解∶﹙1﹚连接AC∴五边形ACDEB的内角和为540°又∵∠ABE+∠BED+∠CDE=360°∴∠A+∠C=180°∴AB∥CD﹙2﹚过点D作AB的垂线DE∵∠CAD=∠BAD,∠C=∠AEDAD为公共边∴Rt△ACD≌Rt△AED∴AC=AE,CD=DE∵∠B=45°∠DEB=90°∴∠EDB=45°∴DE=BEAB=AE+BE=AC+CD﹙3﹚∵腰相等,顶角为120°∴两个底角为30°根据直角三角形中30°的角所对的边为斜边的一半∴腰长=2高=16﹙4﹚根据一条线段垂直平分线上的点到线段两个端点的距离相等∴该交点到三角形三个顶点的距离相等解∶﹙1﹚先连接AC∴五边形ACDEB的内角和为540°∵∠ABE+∠BED+∠CDE=360°∴∠A+∠C=180°∴就证明AB∥CD♂等鴏♀栐薳2010-05-3017:33(1)解:过E作FG∥AB∵FG∥AB∴∠ABE+∠FEB=180°又∵∠ABE+∠CDE+∠BED=360°∴∠FED+∠CDE=180°∴FG∥CD∴AB∥CD(2)解:作DE⊥AB于E∵AD平分∠CAB,CD垂直AC,DE垂直AB∴CD=DE,AC=AE又∵AC=CB,DE=EB,AC⊥CB,DE⊥EB∴∠ABC=∠EDB=45°∴DE=EB∴AB=AE+EB=AC+CD(3)16CM(4)3个顶点如图已知在四边形ABCD中,∠BAD为直角,AB=AD,G为AD 上一点,DE⊥BG交BG的延长线于E,DE的延长线与BA的延长线相交于点F。
七年级数学典型几何证明50题

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收集于网络,如有侵权请联系管理员删除
第4题
几何说理题
1、填空完成推理过程: 如图,∵AB ∥EF ( 已知 )
∴∠A + =1800
( ) ∵DE ∥BC ( 已知 )
∴∠DEF= ( ) ∠ADE= ( ) 2.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°.将求∠AGD 的过程填写完整.
因为EF ∥AD ,所以 ∠2 = . 又因为 ∠1 = ∠2,所以 ∠1 = ∠3. 所以AB ∥ .
所以∠BAC + = 180°. 又因为∠BAC = 70°, 所以∠AGD = .
3.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.
4. 已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.
5. 已知:如图, AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数
6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.
7、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.
A
C
D E F
B
D
E B C
A
A
B
C
D E
收集于网络,如有侵权请联系管理员删除
H G
2
1
F
E
D
C B
A
2
1
F
E
D
B
A
C
8、如图,已知:21∠∠=, 50=D ∠,求B ∠的度数。
9、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
10、AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600
.求∠2的度数.
11、如图,AB∥CD,BF∥CE,则∠B 与∠C 有什么关系?请说明理由.
12.如图,已知:DE∥BC,CD 是∠ACB 的平分线,∠B=70°,∠ACB=50°,求∠EDC 和∠BDC 的度数.
13.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM 平分∠BCE,求∠B 的大小.
14、如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;
(2)BE 与DE 平行吗?为什么?
第11题图
A
B C
D E
E N
M C
D B
A
N
M
F
E D
C
B
A
b
a
341
2
收集于网络,如有侵权请联系管理员删除
15、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?
(3)BC 平分∠DBE 吗?为什么.
16、如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .
2 A
B
E
C
F
D H
G 1
17、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.
18、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数.
19、如图,点D 是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
20、如图,BC ⊥DE 于O ,∠A =27°,∠D =20°,求∠B 与∠ACB 的度数。
F
E
D
C B
A F
E
2
1
D
C
B
A
1题
C
收集于网络,如有侵权请联系管理员删除
B
22、如图,B 、D 、F 在AN 上,C 、E 在AG 上,且AB =BC =CD ,EC =ED =EF ,∠A =20°,求∠FEG 的大小。
23、已知:如图,AB =AC ,BD 平分∠ABC ,交AC 于D ,DE ∥BC ,交AB 于E 。
试说明:DE =DC 。
24、已知:如图在ΔABC 中,∠BAC =90°,DA ⊥BC 于点D ,∠ABC 的平分线BE 交AD 于F ,试说明AE =AF 。
25、如图,ED ∥BC ,E D ∠=∠,那么BD EC =吗?为什么?
26、如图,△ABC 中,AB =AC ,DE ⊥BC 于E ,交AC 于F ,交BA 的延长线于D ,判断△ADF 是什么三角形?并说明理由。
C
E E
A C
B
B
A E
F
D
仓库管理制度
根据餐饮业务实际储备量和需求来确定仓库面积,一般把维持两个星期营业的原材料储备作为前提。
(一)仓库的温度、湿度要求
1.干货仓库:不需供热和制冷设备,最佳湿度为15℃至20℃,选择比较清爽凉快的地点。
2.肉类冷冻库:冻藏的温度应在-18℃,而且要稳定,冻藏原材料的保存也不是无限期的,
它们一般不超过三个月。
货仓的最佳湿度为15至20℃左右。
湿度也会影响食品原材料储存时间的长短和质量的高低,湿度太大,微生物容易繁殖,原材料回迅速变质;
湿度过小,会引起食物干缩、失鲜。
不同原材料对湿度的要求也不一样。
(二)仓库的照明要求
强烈的光照对原材料的保存不利,仓库如有玻璃门窗,应尽量使用毛玻璃。
在选用人工照明时,应尽可能选用冷光灯,亮度每平方米2-3瓦为宜。
(三)仓库的通风要求
仓库应保持空气的流通。
不管何种仓库,原材料的存放都不能贴墙,也不能直接堆放在地上或堆放过密。
(四)对设备、器材的要求
1.货架:货架应有一定的高度以提高单位面积使用效率。
干货仓库
收集于网络,如有侵权请联系管理员删除。
