相似三角形A字型

合集下载

相似三角形”A“字模型(含详细答案解析)~经典

相似三角形”A“字模型(含详细答案)-经典.docx

教师辅导教案授课日期：年月日授课课时：课时△ ABC与厶AB C ■相似，AH是厶ABC中BC边上的高线，AH ■是△ ABC ■中BC ■边上的高线，则有AB _ BC AB^BCAC AHk =AC AH（k为相似比）.进而可得S∆ ABCS∆ ABC1BC AH211BC AH2BC AH 2kBC AH、相似三角形的判定1.平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似.2•如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似•可简单说成：两角对应相等，两个三角形相似.3•如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似.4. 如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似.可简单地说成：三边对应成比例，两个三角形相似.5. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.6•直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底三、相似证明中的基本模型A字形图①A字型，DE//BC ;结论: AD _ AE _ DE AB 一AC 一BC，【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（）已知：如图，在∆ABC中，点D, E, F分别在边AB, AC, BC上，且DE// BC, DF// AC, 求证：∆ADEs∆ DBF.证明：①又∙∙∙DF//AC,②∙∙∙DE// BC,③∙∙∙∠ A= ∠ BDF,④∙∙∙∠ ADE=∠ B,A.③②④①B.②④①③C.③①④②D.②③④①【解答】证明：②I DE// BC,④∙∠ADE=∠ B,①又∙∙∙DF// AC,③∙∠A= ∠ BDF,•••△ ADE^∆DBF.故选：B.故选：A .【练1】如图，在△ ABC 中，∠ ACB=90, BC=16cm, AC=12cm ,点P 从点B 出发，以2cm∕秒的速度向点 C 移动，同时点Q 从点C 出发，以1cm∕秒的速度向点 A 移动，设运动时间为与厶ABC 相似.【解答】解：CP 和CB 是对应边时，△ CPQ^△ CBA 所以，C e ICB CA即-■ -I --t1512解得t=4.8;CP 和CA 是对应边时，△ CPQ^△ CAB, 所以，丄二二，CA CBIMtt 12^16 解得t=-综上所述，当t=4.8或斤一时，△ CPQ 与厶CBA 相似. 故答案为4.8或〒二.AE AD DE 图②反A 字型，∠ ADE ∠ B 或∠仁∠B 结论：==AC AB BCt 秒，当t= 4.8或空秒时，△ CPQ---------- 11-【例2】如同，在△ ABC 中，点D , E 分别在边AB , AC 上，下列条件中不能判断厶 ABC^△ AED 的是（）AD AE AB =AC AD AC-'AB【解答】解：τ∠ DAE=∠ CAB,•••当∠ AED=∠ B 或∠ ADE=∠ C 时，△ ABC ^△ AED; AD .AC'AE∙≠∙件二 ι∙WA . B.C.∠ ADE=∠ C D .∠ AED=∠ B时，△ ABC ^△ AED. 当—昱L 二一―即【例3】如图，P 是厶ABC 的边AB 上的一点.（不与A 、B 重合）当∠ ACP=∠ B 时，△ APC 与厶ABC 是否相似；当 AC AP 、AB 满足丄二丄时，△ ACP 与厶ABC 相似.— AC AB-【解答】解：τ∠ A= ∠ A ,∠ ACP=∠ B ,故答案为：B ；寺二二【练习1】如图，D 、EABC 的边AC 、AB 上的点，当 ∠ ADE=∠ B 时，△ ADE ^△ ABC.其中D 、E 分别对应B 、C.（填一个条件）. 【解答】解：当∠ ADE=∠ B ,∙∠ EAD=∠ CAB,• △ ADE ^△ ABC. 故答案为∠ ADE=∠ B .【练习2】如图，在△ ABC 中，D E 分别在AB 与AC 上，且AD=5, DB=7, AE=6, EC=4 求证：△ ADE ^△ ACB.【解答】证明：• AD=5, DB=7, AE=6, EC=4, • AB=5+7=12, AC=6+4=10,.AD = 5 _1 AE = 6 _1 • AC 10 T r AB 12 = 2， .AP =Ag• AC AB ，又∙∠ A= ∠ A , • △ ADE ^△ ACB.【练习3】如图，AB=AC, ∠ A=36° , BD 是∠ ABC 的角平分线，求证：△ ABC^△ BCD. 【解答】证明：• AB=AC, ∠ A=36°, ∙∠ ABC=∠ C=72 , • BD 是角平分线，∙∠ ABD=∠ DBC=36 , ∙∠ A= ∠ CBD, 又∙∠ C=∠ C, • △ ABC^△ BCD.•丄二丄''[I∠ A= ∠ A ,【练习4】已知：如图，△ ABC 中，∠ ACD=∠ B ,求证：△ ABC^△ ACD. 【解答】证明：τ∠ ACD=∠ B ,∠ A= ∠ A ,【例4】如图，在△ ABC 中，D ，E 分别是AB ，AC 上的点，∠ AED=∠ ABC,∠ BAC 的平分线 AF 交DE 于点G ,• △ ABC^△ AED.τ∠ AED=∠ ABC,∠ EAG=∠ BAF,• △ AEG^△ ABF.【练习5】如图，已知 AD?AC=AB?AE 求证：△ ADE^△ ABC. 【解答】证明：I AD?AC=AE?AB— =AEAB AC在厶ABC 与厶ADE 中 ■: 一.AEAB AC• △ ABC^△ ADE.【练习6】已知：如图，在厶ABC 中，D , E 分别为AB 、AC 边上的点，且AD 匚AE,连接DE.若AC=4, AB=5.求证：△ ADE ^△ ACB【解答】证明：∙∙∙ AC=3, AB=5, ADjL 匕,5.AC _ AB厂-Λ,τ∠ A= ∠ A ,• △ ADE ^△ ACB.图③双A 字型交BC 于点F .(1)试写出图中所有的相似三角形，并说明理由.3'2BC的值. 【解答】解：(1 )∙∙∙∠ AED=∠ ABC,∠ EAD=∠ BAC,,∠ A= ∠ A , R3(2)若,求小τ∠ EDG=∠ ACF, ∠ DAG=∠ CAF , •••△ ADG sA ACF.•••△ ADG sA ACF,」丄 .A.-. 3GF 5【练习1】如图，在△ ABC 中，D 、E 分别是 AB 、AC 上的点，AE=4, AB=6, AD : AC=2: 3,A ABC 的角平分线AF 交DE 于点G ，交BC 于点F .(1) 请你直接写出图中所有的相似三角形； (2) 求AG 与GF 的比.【解答】解：(1 )△ ADG sA ACF △ AGE^A AFB,A ADE sA ACB;(2).• AE _4」2 AD _2(∙ TiTE =可，疋=可胚. -AE)AB '又 τ∠ DAE=∠ CAB,• △ ADE sA ACB,∙∠ ADG=∠ C ,∙∙∙ AF 为角平分线，∙∠ DAG=∠ FAE• △ ADG sA ACF,AG. 3GF 2(2)AG . Ar 2 ^^' AC 3 =2.AG GF图④内含正方形 A 字形，结论AH a=_^ ( a 为正方形边长) AH BC【例5】如图，△ ABC ,是一张锐角三角形的硬纸片， AD 是边BC 上的高，BC=40cm,AD=30cm ,从这张硬纸片上剪下一个长 HG 是宽HE 的2倍的矩形EFGH 使它的一边EF 在BC 上，顶点 G 、H 分别在 AC, AB 上，AD 与HG 的交点为 M .(2)的周长;(3)是否存在一个实数 a ,当HEFa 时从三角形硬纸片上剪下的矩形面积最大？若存在,请说明理由.【解答】(1)证明：•••四边形 HEFG 为矩形, ∙∙∙ HG // EF, 而 AD ⊥ BC,∙ AM 丄 BC, •••△ AHGsA ABC,AJfl HGAD - S BC(2)解：设 HE=X HG=2X,•这个矩形 EFGH 的周长=2x+4x=6x=72 (Cm );(3) 存在.AD BC(1)求证:30-x i 2x30 - _40,解得x=12,则30-a . .HG 30当HE=a,则• HG=- 430_ 2X 〔申即当HEF Cm 时从三角形硬纸片上剪下的矩形面积最大.4• S 矩形 HEFG Fa (- a+30) F -a 2+30a ,当a=- 454时，S 矩形HEFG 最大, 试求出a ；若不存在,【练习1】如图，△ ABC ,是一张锐角三角形的硬纸片， AD 是边BC 上的高，BC=80cm , AD=60cm ,从这张硬纸片上剪下一个长 HG 是宽HE 的2倍的矩形EFGH 使它的一边 EF 在BC 上，顶点G 、H 分别在AC, AB 上,AD 与HG 的交点为M .(2)求这个矩形 EFG H 的面积.∙∙∙ EF// GH, ∙∙∙∠ AHG=∠ ABC,又 τ∠ HAG=∠ BAC,AJI L L … ADBC(2)解：设 HE=XCm, MD=HE=xcm , ■/ AD=60cm ,• AM= (60 - x ) Cm , ∙∙∙ HG=2HE, • HG=2xcm,AD ~BC'解得，x=24, 故 HE=24, HG=2x=48, 则矩形 EFGH 的面积=24 × 12=1152cm 2.【例6】如图，在△ ABC 中，D 为AC 上一点，E 为CB 延长线上一点，且求证：AD=EB【解答】证明：过D 点作DH / BC 交AB 于H,如图, ∙/ DH // BC, • △ AHD ^△ ABC,∙/ DH // BE ,M L .HG AD BC的理由;(1)试说明:&0-x. -2x60 ' SO可得【解答】(1)证明：I 四边形 EFG H 为矩形,AD DH AC CS B CAD ACBC,即GH5DED-2.-EF HD DP , AC EFBC ' -Il =■> DF ADHD DH,∙∙∙ AD=EB.【例7】如图，在△ ABC中，∠ BAC=90, BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证：AE=EF?ED【解答】解：τ∠BAC=90 ,∙∠B+∠ C=90, ∠ D+∠ C=90 ,∙∠B=∠ D,∙∙∙ BC的垂直平分线交BC于点E,∠ BAC=90 .• BE=EA∙∠B=∠ BAE∙∠D=∠ BAEτ∠FEA=∠AED,• △ FEA^△ AED,.恆=DE•EP =AE•AE=EF?ED旋转型”相似三角形，如图•若图中∠仁∠ 2,∠ B=∠ D（或∠ C=∠ £）,则厶ADE∞^ABC,该图可看成把第一个图中的△ADE绕点A旋转某一角度而形成的.【例8】如图，在厶ABC与厶ADE中，∠ BAC=∠ D,要使△ ABC与厶ADE相似，还需满足下列条件中的（）AC AB AD=AE AC BC AD==DE【解答】解：τ∠BAC=∠D, • △ ABC^△ ADE.AC ABAD=DEAC ABADAC BCAE ==AEA. B.C D.E故选：C.【练习1】如图所示，在厶ABC 与厶ADE 中，AB?ED=AE?BC 要使△ ABC 与厶ADE 相似，还需要添加一个条件, 这个条件是∠ B=∠ E （答案不唯一）（只加一个即可）并证明.【解答】解：条件①，∠ B=∠ E 证明：∙∙∙ AB?ED=AE?BCAEECAD•••△ ABC^△ AED.故答案为：∠ B=∠ E （答案不唯一）【练习 2】如图，已知：∠ BAC=∠ EAD, AB=20.4, AC=48, AE=17, AD=40. 求证：△ ABC^△ AED.【解答】证明：I AB=20.4, AC=48, AE=17, AD=40. • AB =20. 4 =1 2 AC 座=1 2• AE .,而 40 .， •塑座'二=「，∙∙∙∠ BAC=∠ EAD,• △ ABC^△ AED.【练习3】如图，在△ ABC 和厶ADE 中，已知∠ABC^△ ADE.【解答】解：如图，τ∠ BAD=∠ CAE, ∙∠ BAD+ ∠ BAE=∠ CAE+ ∠ BAE , 即 ∠ DAE=∠ BAC. 又τ∠ B= ∠ D ,• AB - BCAE F.C∙∙∙∠ B= ∠ E ,• △ ABC^△ AED.条件②, AD==AEAC证明：•• • AB? ED=AE?BC• AB = BCAE EC-AE --- ,AC AB AB =BC = AC B= ∠ D ,∠ BAD=∠ CAE 求证：△C• △ABC^△ADE.【练习4】如图，△ ABC △ DEP是两个全等的等腰直角三角形，∠BAC=∠ PDE=90 .(1)若将△ DEP的顶点P放在BC上(如图1) , PD PE分别与AC、AB相交于点F、G.求证:(2)若使△ DEP的顶点P与顶点A重合(如图2), PD、PE与BC相交于点F、似吗？为什么？【解答】(1)证明：如图1,•••△ ABC △ DEP是两个全等的等腰直角三角形,∙∙∙∠B=∠ C=∠ DPE=45 ,∙∙∙∠BPG+∠ CPF=135,在厶BPG 中，τ∠B=45,∙∠BPG+∠ BGP=135 ,∙∠BGP=∠ CPF,τ∠B=∠C,•••△ PBG∞^ FCP(2)解：△ PBG与厶FCP相似.理由如下：如图2, •••△ ABC △ DEP是两个全等的等腰直角三角形,∙∠B=∠C=∠DPE=45 ,∙∙∙∠ BGP=∠C+∠CPG=45 + ∠CAG,∠CPF=Z FPGF ∠CAG=45 + ∠CAG,∙∠AGP=∠CPF,τ∠B=∠C,•••△ PBG∞^ FCP.课堂小结: △ PBG∞^ FCPG.试问△ PBG与厶FCP还相。

中考数学几何专项——相似模型(相似三角形)

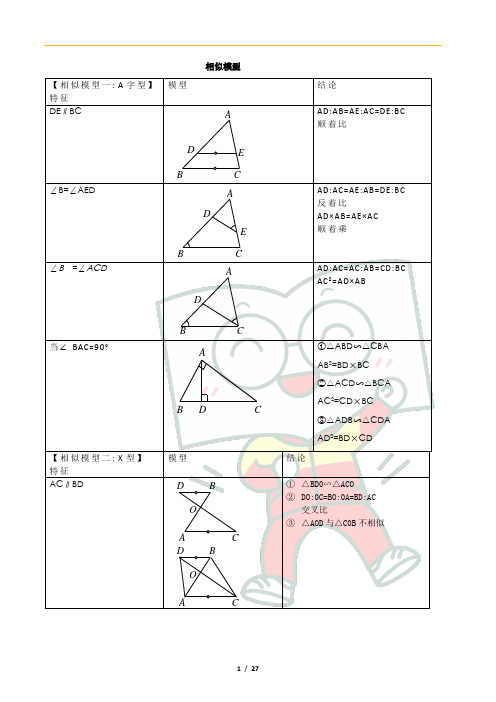
相似模型【相似模型一: A 字型】特征模型结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB C BDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD【相似模型二: X 型】特征模型结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C（也叫蝴蝶型相似）A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D ③ 顺着比, 交叉乘 ④ △BOC∽△DOA【相似模型三: 旋转相似】特征模型结论成比例线段共端点① △ABC ∽△ADE ② △ABD∽△ACE【相似模型四: 三平行模型】特征模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=【相似模型五: 半角模型】特征模型结论ECD BAA BDC EEDCBA90度, 45度； 120度, 60度 120度，60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六: 三角形内接矩形模型】特征模型结论矩形EFGH 或正方形EFGH 内接与三角形H GFED C BA【相似模型七: 十字模型】特征模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE, 则AF=BE,②若AF ⊥BE ，则AF=BE,长方形PEAB CD矩形ABCD 中, CE ⊥BD, 则△CDE ∽△BCD,平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中, AB ＝AC,AB ⊥AC, ①D 为中点, ②AE ⊥BD, ③BE ：EC ＝2：1, ④∠ADB ＝∠CDE, ⑤∠AEB ＝∠CED,⑥∠BMC ＝135°, ⑦ , 这七个结论中, “知二得五”【A 型, X 型, 三平行模型】1.如图, 在△ABC 中, EF ∥DC, ∠AFE=∠B, AE=6, ED=3, AF=8, 则AC=_________, _________．F E DCBABCDE FA2. 如图, AB ∥CD, 线段BC, AD 相交于点F, 点E 是线段AF 上一点且满足∠BEF=∠C, 其中AF=6, DF=3, CF=2, 则AE=_________.3.如图, 在Rt △ABD 中, 过点D 作CD ⊥BD, 垂足为D, 连接BC 交AD 于点E, 过点E 作EF ⊥BD 于点F, 若AB=15, CD=10, 则BF:FD=_____________.FEBCD AN MEDCBA4.如图, 在□ABCD中, E为BC的中点, 连接AE, AC, 分别交BD于M, N, 则BM:DN=_____________.5.如图所示, AB∥CD, AD, BC相交于点E, 过E作EF∥AB交BD于点F．则下列结论：①△EFD∽△ABD；②；③；④．其中正确的有___________．F EDCBA图26.在△ABC中, AB=9, AC=6, 点M在边AB上, 且AM=3, 点N在AC边上.当AN= 时, △AMN与原三角形相似.7.如图, 在△ABC中, ∠C=90°, AC=8, BC=6, D是边AB的中点, 现有一点P位于边AC上, 使得△ADP与△ABC相似, 则线段AP的长为.8.如图, 已知O是坐标原点, 点A.B分别在轴上, OA=1, OB=2, 若点D在轴下方, 且使得△AOB与△OAD相似, 则这样的点D有个.9.如图, 在Rt△ACB中, ∠C=90°, AC=16cm, BC=8cm, 动点P从点C出发, 沿CA方向运动；动点Q同时从点B出发, 沿BC方向运动,如果点P的运动速度均为4cm/s, Q点的运动速度均为2cm/s, 那么运动几秒时, △ABC与△PCQ相似.10.将△ABC的纸片按如图所示的方式折叠, 使点B落地边AC上, 记为点B＇, 折叠痕为EF, 已知AB=AC=8, BC=10,若以点B＇.F.C为顶点的三角形与△ABC相似, 那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图, 四边形中, 平分, , , 为的中点.（1）求证: ；（2）与有怎样的位置关系？试说明理由；（3）若, , 求的值.13.如图, 在中, 为上一点, , , , 于, 连接．（1）求证：；（2）找出图中一对相似三角形, 并证明．14.如图, 在中, , 分别是, 上的点, , 的平分线交于点, 交于点.（1）试写出图中所有的相似三角形, 并说明理由（2）若, 求的值．15.如图, 在平行四边形ABCD中, 对角线AC.BD交于点O. M为AD中点, 连接CM交BD于点N, 且ON=1.（1）求BD的长；（2）若△DCN的面积为2, 求四边形ABNM的面积.16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB = _________.19.如图所示, AD=DF=FB, DE∥FG∥BC,则=__________.20.如图, 在矩形ABCD中, 对角线AC, BD相交于点O, OE⊥BC于点E, 连接DE交OC于点F, 作FG⊥BC于点G, 则线段BG与GC的数量关系是___.21.如图, 已知点C为线段AB的中点, CD⊥AB且CD=AB=4, 连接AD, BE⊥AB, AE是∠DAB的平分线, 与DC相交于点F, EH⊥DC于点G, 交AD 于点H, 则HG的长为 .22.如图1, 在△ABC 中, 点D.E 、Q 分别在边AB.AC.BC 上, 且DE ∥BC, AQ 交DE 于点P. （1）求证: ；（2）如图, 在△ABC 中, ∠BAC=90°, 正方形DEFG 的四个顶点在△ABC 的边上, 连接AG 、AF, 分别交DE 于M 、N 两点. 如图2, 若AB=AC=1, 直接写出MN 的长；如图3, 求证MN2=DM【母子型】1.已知: 如图, △ABC 中, ∠ACB=90°, CD ⊥AB 于D, S △ABC=20, AB=10。

相似三角形A字形

①∠ABC=∠ADE．求证：AB·AE=AC·AD
②△ABC中，AB=AC，△DEF是等边三角形
求证：BD?CN=BM?CE．
③等边三角形ABC中，P为BC上任一点，AP的垂直平分线交AB、AC于M、N两点。
求证：BP?PC=BM?CN
?有射影，或平行，等比传递我看行
①在Rt△ABC中，∠BAC=90°，AD⊥BC于D，E为AC的中点，求证：AB?AF=AC?DF
②ቤተ መጻሕፍቲ ባይዱ证其它三角形相似——创造边、角条件
相似判定条件：两边成比夹角等、两角对应三边比
相似终极策略：
遇等积，化比例，同侧三点找相似；
四共线，无等边，射影平行用等比；
四共线，有等边，必有一条可转换；
两共线，上下比，过端平行条件边。
彼相似，我角等，两边成比边代换。
（3）等比代换：若是四条线段，欲证，可先证得（是两条线段）然后证，这里把叫做中间比。
试说明△EBC∽△DEB
②已知 ∽ ，求证： ∽ ．
③D为△ABC内一点，连接BD、AD，以BC为边在△ABC外作∠CBE=∠ABD，∠BCE=∠BAD，求证：△DBE∽△ABC。
④D、E分别在△ABC的AC、AB边上，
且AE?AB=AD?AC，BD、CE交于点O.
求证：△BOE∽△COD.
⑥△ABC中，AC=BC，F为底边AB上的一点，（m、n＞0），取CF的中点D，连结AD并延长交BC于E.（1）的值.（2）如果BE=2EC，那么CF所在直线与边AB有怎样的位置关系？证明你的结论；（3）E点能否为BC中点？如果能，求出相应的的值；如果不能，证明你的结论。?彼相似，我条件，创造边角再相似①AE2＝AD·AB，且∠ABE＝∠BCE，

相似三角形”A“字模型(含详细问题详解)-经典

教师辅导教案授课日期：年月日授课课时：课时ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）． 4．相似三角形周长的比等于相似比． ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++． 5．相似三角形面积的比等于相似比的平方．ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．二、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似． 4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．三、相似证明中的基本模型A 字形图①A 字型，DE//BC ;结论：AD AE DEAB AC BC==，【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（）已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，求证：△ADE∽△DBF．证明：①又∵DF∥AC，②∵DE∥BC，③∴∠A=∠BDF，④∴∠ADE=∠B，∴△ADE∽△DBF．A．③②④① B．②④①③ C．③①④② D．②③④①【解答】证明：②∵DE∥BC，④∴∠ADE=∠B，①又∵DF∥AC，③∴∠A=∠BDF，∴△ADE∽△DBF．故选：B．【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t= 4.8或秒时，△CPQ与△ABC相似．【解答】解：CP和CB是对应边时，△CPQ∽△CBA，所以，，即，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，，即，解得t=．综上所述，当t=4.8或时，△CPQ与△CBA相似．故答案为4.8或．图②反A字型，∠ADE=∠B或∠1=∠B结论：AE AD DE==AC AB BC【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B【解答】解：∵∠DAE=∠CAB，∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；当=即=时，△ABC∽△AED．故选：A．【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．【解答】解：∵∠A=∠A，∠ACP=∠B，∴△ACP∽△ABC；∵，∠A=∠A，∴△ACP与△ABC；故答案为：B；．【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽△ABC．其中D、E分别对应B、C．（填一个条件）．【解答】解：当∠ADE=∠B，∵∠EAD=∠CAB，∴△ADE∽△ABC．故答案为∠ADE=∠B．【练习2】如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．求证：△ADE∽△ACB．【解答】证明：∵AD=5，DB=7，AE=6，EC=4，∴AB=5+7=12，AC=6+4=10，∴====，∴=，又∵∠A=∠A，∴△ADE∽△ACB．【练习3】如图，AB=AC，∠A=36°，BD是∠ABC的角平分线，求证：△ABC∽△BCD．【解答】证明：∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，∵BD是角平分线，∴∠ABD=∠DBC=36°，∴∠A=∠CBD，又∵∠C=∠C，∴△ABC∽△BCD．【练习4】已知：如图，△ABC中，∠ACD=∠B，求证：△ABC∽△ACD．【解答】证明：∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD．【练习5】如图，已知AD•AC=AB•AE．求证：△ADE∽△ABC．【解答】证明：∵AD•AC=AE•AB，∴=在△ABC与△ADE 中∵=，∠A=∠A，∴△ABC∽△ADE．【练习6】已知：如图，在△ABC中，D，E分别为AB、AC边上的点，且AD=AE，连接DE．若AC=4，AB=5．求证：△ADE∽△ACB．【解答】证明：∵AC=3，AB=5，AD=，∴，∵∠A=∠A，∴△ADE∽△ACB．图③双A字型【例4】如图，在△ABC中，D，E分别是AB，AC上的点，∠AED=∠ABC，∠BAC 的平分线AF交DE于点G，交BC于点F．（1）试写出图中所有的相似三角形，并说明理由（2）若=，求的值．【解答】解：（1）∵∠AED=∠ABC，∠EAD=∠BAC，∴△ABC∽△AED．∵∠AED=∠ABC，∠EAG=∠BAF，∴△AEG∽△ABF．∵∠EDG=∠ACF，∠DAG=∠CAF，∴△ADG∽△ACF．（2）∵=，∴=，∵△ADG∽△ACF，∴==．【练习1】如图，在△ABC中，D、E分别是AB、AC上的点，AE=4，AB=6，AD：AC=2：3，△ABC的角平分线AF交DE于点G，交BC于点F．（1）请你直接写出图中所有的相似三角形；（2）求AG与GF的比．【解答】解：（1）△ADG∽△ACF，△AGE∽△AFB，△ADE∽△ACB；（2）∵==，=，∴=，又∵∠DAE=∠CAB，∴△ADE∽△ACB，∴∠ADG=∠C，∵AF为角平分线，∴∠DAG=∠FAE∴△ADG ∽△ACF ， ∴==，∴=2．图④内含正方形A 字形，结论AH a aAH BC-=（a 为正方形边长）【例5】如图，△ABC ，是一张锐角三角形的硬纸片，AD 是边BC 上的高，BC=40cm ，AD=30cm ，从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ，使它的一边EF 在BC 上，顶点G 、H 分别在AC ，AB 上，AD 与HG 的交点为M ．（1）求证：=；（2）求这个矩形EFGH 的周长；（3）是否存在一个实数a ，当HE=a 时从三角形硬纸片上剪下的矩形面积最大？若存在，试求出a ；若不存在，请说明理由．【解答】（1）证明：∵四边形HEFG 为矩形， ∴HG ∥EF ，而AD ⊥BC ， ∴AM ⊥BC ，。

相似三角形A字型模型

相似三⻆形模型A 字型⼀正⽉型A条件BCN DE 7ADFUA ABCD Mi E结论㗊㖚夞⼆箭相似⽐Bic㗊笓AM MNSAADESAABc 相似⽐2找相似三⻆形g 如图点三是⼝ABCD 的边13延⻓线上⼀点EA 分别交织BD 的延⻓线于点EF G 则图中相似三⻆形共有6对B AA1311C F AEB n FEC ADG Fu AB GA CF DAD 11CE ADF n A ECF AAG Dcs AE GB GtADFGAE BA全等BDCIA DBA相似的基础计算g 如图在A ABC 中B C 20B Bz ⼀138C CzC 8分别是AB AE 的九等分点则B ci ⼗Bzczt 1388的值为80ABCBzCzˋB A CBAGAABCUAAB ci AB AB ⼆AC ACBiG⼀号管B C ⼆本BC 138的同理可得132G GBC⼀138G98B CB CB C ⼗132C z ⼗⼀⼀⼗138C 8i B C92BC⼗⼗g B C4B C 80g如图⼀张三⻆形纸⽚ABC边AB⻓为10cm AB边上的⾼为15cm在三⻆形内从左到右叠放边⻓为2的正⽅形⼩纸⽚第⼀次⼩纸⽚的⼀条边在仍上依次这样往上叠放则最多能叠放的正⽅形的个数是14个C第⼀层能放的个数取决于AB的⻓Az P132A B7由A ACB n AA CB得A B管h s A131552X10ii21334第⼀层能放4个第⼆层能放的个数取决于名及的⻓华号⼆点A2132⼆⽉54x103223222j3第⼆层能放3个同理第三层个数393第四层个数372第五层个数351第六层个数331第七层个数3⼆0总数433-1211141个利⽤相似转化⽐例91在四边形ABCD中⼆是对⻆线13⼝上⼀点EF HAD EM NBC则ǕtǜIAEM NBC EDM as A BDC了烮㗊D EF HAD s EBFU DBA髿品EF MEit烮成t i迎113c92如图所示在梯形ABCD中仍11CD A B12CD⼆9过对⻆线交点0作EFHCD交AD BC 于点EF D CE Fl求证E O F002求EF的⻓A B1i ABHEF2AA OB is ACODin A ABDU A EOD A ABC n A OFC䂟f B43⼀官⼆品官⼆品㗊⼆品品P的ODA1311CD AB⼆BD⼆千⼋A013n A COD EOÌAB⼆千i㗊实则分i2E0ic官⼆窍即的⼆的最值问题转化⾼g如图13⼆8AH上BC AH6PMN⼜为矩形没吓x①PM⼆成⽤ㄨ表示A②求S队吸最⼤值P F M①AA PM n A ABC B T CQ H N只召AFAHPM⼆箭B CÌx②SPMNQEPM FM⼆Ìx6-X J x3212最⼤值为12egz LA900B C10SAAB c25D为A B上任意点不与A13重合DEHBC DE x将AADEU DE为折痕向下翻折得AA DE与四边形DE CB重叠部分S记为4A求吗ㄨ的关系ˇB CA①当A在13上⽅或BE上时D N E即0X S5AB7CAM2台竺5Mi BCHDE iAABC2ADE焁朤A N B5Ìxy t AN DE⼆ÌÍX x f x2②当A在13下⽅时A即5x10De N E同上AM⼆5AN X B TMF G CA M⼆2AN AM x5AYAA FG n ADE⾦煚主⾦华2全⽂2ii SAAF a x52y SAADE SAAF az x2-X52jx2tlox25综上yÌx0x5-43x210X255x10⼀斜A型⼀A条件LADE A C B AD En AA CB结论管㖌夞D EB CA⺟⼦型相似条件LABD LACB AABD A AE BD结论㗊焽A BEAD ACB cA条件AB LAC ADL BCˇ结论A D2B D n CDA132⼆BD BC7c A C CD BCB D基础计算g如图在ABC中ㄥA C B900D为A上⼀点DE LAB于点E A C4BE3C 1求证ADE n A ABC D2当DE⼆DC时求AD的⻓A E Bl LA ED⼆LA CB L DAE BACADE is A ABC2设17E D C X A D4-X器器品⾼解得X23AD592如图在A ABC中A1613C20点⼝E分别在边AC BE上AD6 LB t LA DE1800连结AE AD 4求证EDC n A ABC2求BE的⻓B c③若A B12求A ABE的⾯积El E L Bt LA DE1800LCDEt LA DE1800ㄥB CDE⼜iㄥCㄥCi A EDC n A ABC AA2D A C A D10ˋEDC n A ABCi䇮贸CE jㄨ168BE B C C E123i AB4ACEBC2iLBACqiSAABCIIAB.AE96SAABF.IS tABc BEiBC35SA.ABEfSAABcf8eg3如图在ABC中点D E分别在边AB.AE上LACD B.DE BCAl求证2ACDz若㕵6BE10求线段们的⻓D E lˋDE NBC B c LADE B A CD⼜i LDAE CADAADEnAACDlzi.DEBCnLCDE sBCD⼜A CD13只怨⼆泉即CDEBC.DE60⼈CD EnABCD CD⼆215。

相似三角形A字形

A 字形，A ’形，8字形，蝴蝶形，双垂直,旋转形双垂直结论:射影定理：①直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项⑴△ACD ∽△CDB →AD:CD=CD:BD →CD2=AD •BD ⑵△ACD ∽△ABC →AC:AB=AD:AC →AC2=AD •AB ⑶△CDB ∽△ABC →BC:AC=BD:BC →BC2=BD •AB 结论：⑵÷⑶得AC2:BC2=AD:BD 结论：面积法得AB •CD=AC •BC →比例式证明等积式(比例式)策略直接法：找同一三角形两条边变化：等号同侧两边同一三角形三点定形法 2、间接法： ⑴3种代换 ①等线段代换； ②等比代换； ③等积代换；⑵创造条件 ①添加平行线——创造“A ”字型、“8”字型②先证其它三角形相似——创造边、角条件相似判定条件：两边成比夹角等、两角对应三边比相似终极策略：遇等积，化比例，同侧三点找相似；四共线，无等边，射影平行用等比；四共线，有等边，必有一条可转换；两共线，上下比，过端平行条件边。

彼相似，我角等，两边成比边代换。

（3）等比代换：若d c b a ,,,是四条线段，欲证d cb a =，可先证得feb a =（f e ,是两条线段）然后证d c f e =，这里把fe叫做中间比。

①∠ABC=∠ADE ．求证：AB ·AE=AC ·AD②△ABC 中，AB=AC ，△DEF 是等边三角形求证：BD •CN=BM •CE ．③等边三角形ABC 中，P 为BC 上任一点，AP 的垂直平分线交AB 、AC 于M 、N 两点。

求证：BP •PC=BM •CNEA B EACBADECF EDABC☞有射影，或平行，等比传递我看行①在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于D ，E 为AC 的中点，求证：AB •AF=AC •DF斜边上面作高线，比例中项一大片②ABCD③梯形ABCD 中，AD求证：DE2=BE ·CE.☞两共线，上下比，过端平行条件边。

相似三角形中的“A”字模型(4种题型)-2023新九年级数学核心知识点与常见题型(沪教版)(解析版)

重难点专项突破：相似三角形中的“A”字模型（4种题型）【知识梳理】【考点剖析】题型一：直接利用“A”字模型解题例1.如图，E是▱ABCD的边BA延长线上一点，CE与AD相交于点F，AE＝1，AB＝2，BC＝3，那么AF＝．【分析】利用A字模型相似三角形进行计算即可解答．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAF＝∠B，∠EFA＝∠ECB，∴△EAF∽△EBC，∴EAEB =AFBC，∴13=AF3，∴AF＝1，故答案为：1．【点评】本题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握A字模型相似三角形是解题的关键．例2．（2022秋•静安区期末）在△ABC中，AB＝6，AC＝5，点D、E分别在边AB、AC上，当AD＝4，∠ADE＝∠C时，＝．【分析】首先判定△ADE∽△ACB，然后利用该相似三角形的对应边成比例解答．【解答】解：∵∠ADE＝∠C，∠A＝∠A，∴△ADE∽△ACB．∴＝．∵AC＝5，AD＝4，∴＝．故答案为：．【点评】本题考查的是相似三角形的判定与性质，相似三角形是相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．题型二：添加辅助线构造“A”字模型解题例3.如图，在△ABC中，∠C＝90°，BC＝2，AB=2√5，点D在边AC上，CD：AD＝1：3，联结BD，点E 在线段BD上，如果∠BCE＝∠A，那么CE＝．【分析】根据已知∠BCE＝∠A，想到构造这两个角所在的三角形相似，所以过点E作EF⊥BC，垂足为F，可得△ABC∽△CEF，进而可得CF＝2EF，然后设EF为a，则CF为2a，BF为2﹣2a，最后再证明A字模型相似△BFE∽△BCD，从而解答即可．【解答】解：过点E作EF⊥BC，垂足为F，∵∠ACB ＝90°，BC ＝2，AB =2√5，∴AC =√AC 2−BC 2=√(2√5)2−22=4，∵CD ：AD ＝1：3，∴CD ＝1，∵∠BCE ＝∠A ，∠ACB ＝∠CFE ＝90°，∴△ABC ∽△CEF ，∴AC BC =CF EF =42=2，∴设EF 为a ，则CF 为2a ，BF 为2﹣2a ，∵∠ACB ＝∠BFE ＝90°，∠CBD ＝∠FBE ，∴△BFE ∽△BCD ，∴BF BC =EF CD ，∴2−2a 2=a 1， ∴a =12，∴EF =12，CF ＝1，∴CE =√EF 2+CF 2=√(12)2+12=√52，故答案为：√52．【点评】本题考查了相似三角形的判定与性质，勾股定理，熟练掌握A 字模型相似是解题的关键．例4．如图，已知ABC ∆中，AD 、BE 相交于G ，:3:1BD DC =，:1:2AG GD =．求:BG GE 的值．【答案】11．【解析】点G 作//GM BC 交AC 于点M ．//GM BC ∴AG GM AD CD =，EG GM EB CB =；:1:2AG GD =， ∴13AG GM AD CD ==，:3:1BD DC =，∴14DC BC =，∴112GM BC =， ∴112GE EB =，∴:BG GE 的值为11．【总结】本题考查了三角形一边的平行线知识，要学会构造平行基本模型．例5．如图，在ABC ∆中，点D 在线段BC 上，75BAD ∠=︒，30CAD ∠=︒，AD = 2，BD = 2DC ，求AC 的长．【答案】3．【解析】过点D 作//DM AB 交AC 于点M ．//DM AB， ∴75BAD ADM ∠=∠=；又180ADM AMD DAM ∠+∠+∠=，30CAD ∠=∴75AMD∠=，∴AMD ADM∠=∠，∴2AD AM==．//DM AB，∴AM BDAC BC=．又2BD DC=，∴23BD AMBC AC==．∴3AC=．【总结】本题考查了三角形一边的平行线及等腰三角形的相关知识．题型三：“AX”字型解题例6.如图，ABC∆中，//DE BC，3AE=，4DE=，2DF=，5CF=，求EC的长．【答案】92EC=．【解析】//DE BC，25DE DF AEBC CF AC∴===，即3235EC=+，求得：92EC=．【总结】相似三角形中“A”字型和“X”字型的综合应用，可得到相等比例关系式．例7.如图，在梯形ABCD中，//AD BC，对角线AC、BD交于点O，点E在AB上，且//EO BC，已知3AD=，6BC=．求EO的长．【答案】2．【解析】由//AD BC ，可得：3162AO AD CO BC ===，故13AO AC =，由//EO BC ，13EO AO BC AC ==，求得2EO =．【总结】相似三角形中“A ”字型和“X ”字型的综合应用，可得到相等比例关系式．题型四：双A 字模型例8.如图，AB ⊥BD ，CD ⊥BD ，垂足分别为B 、D ，AC 和BD 相交于点E ，EF ⊥BD ，垂足为F ．求证：111AB CD EF+=．【解析】AB ⊥BD ，CD ⊥BD ，EF ⊥BD ，∴////AB CD EF∴EF DF AB DB =，EF BF CD DB = ∴1EF EF AB DC +=，即111AB CD EF +=．【总结】本题考查了三角形一边的平行线知识的应用．【过关检测】一．选择题（共3小题）1．（2023•嘉定区二模）如图，已知点D 、E 分别在△ABC 的边AB 、AC 上，DE ∥BC ，AD ：DB ＝1：3，那么S △DEC ：S △DBC 等于（）AB CDEFA．1：2B．1：3C．2：3D．1：4【分析】根据题意可得AD：AB＝1：4，再证明△ADE∽△ABC，得，即BC＝4DE，根据平行线间的距离处处相等可得C到DE的距离为等于点D到BC的距离，以此即可求解．【解答】解：∵AD：DB＝1：3，∴AD：AB＝1：4，∵DE∥BC，∴△ADE∽△ABC，∴，∴BC＝4DE，设点C到DE的距离为h1，点D到BC的距离为h2，∵DE∥BC，∴h1＝h2，∴，即S△DEC：S△DBC＝1：4．故选：D．【点评】本题主要考查平行线的性质、相似三角形的判定与性质，灵活运用相关知识解决问题是解题关键．2．（2022秋•徐汇区期末）如图，在△ABC中，DE∥FG∥BC，AD：AF：AB＝1：2：5，则S△ADE：S四边形DEGF：S四边形FGCB＝（）A．1：2：5B．1：4：25C．1：3：25D．1：3：21【分析】由DE∥FG∥BC，可得△ADE∽△AFG∽△ABC，又由AD：AF：AB＝1：2：5，利用相似三角形的面积比等于相似比的平方，即可求得S△ADE：S△AFG：S△ABC＝1：4：25，然后设△ADE的面积是a，则△AFG和△ABC的面积分别是3a，21a，即可求两个梯形的面积，继而求得答案．【解答】解：∵DE∥FG∥BC，∴△ADE∽△AFG∽△ABC，∴AD：AF：AB＝1：2：5，∴S△ADE：S△AFG：S△ABC＝1：4：25，设△ADE的面积是a，则△AFG和△ABC的面积分别是4a，25a，则S四边形DFGE＝S△AFG﹣S△ADE＝3a，S四边形FBCG＝S△ABC﹣S△AFG＝21a，∴S△ADE：S四边形DFGE：S四边形FBCG＝1：3：21．故选：D．【点评】此题考查了相似三角形的判定与性质．此题难度适中，解题的关键是掌握相似三角形面积的比等于相似比的平方．3．（2022秋•奉贤区期中）在△ABC中，点D、E在边AB、AC上，，要使DE∥BC，可添加下列条件中的（）A．B．C．D．【分析】先求出比例式，再根据相似三角形的判定得出△ADE∽△ABC，根据相似推出∠ADE＝∠B，根据平行线的判定得出即可【解答】解：只有选项D正确，理由是：∵AD：BD＝3：2，∴AD：AB＝3：5，∴AE：AC＝3：5，∵∠DAE＝∠BAC，∴△ADE∽△ABC，∴∠ADE＝∠B，∴DE∥BC，根据选项A、B、C的条件都不能推出DE∥BC，故选：D．【点评】本题考查了平行线分线段成比例定理，相似三角形的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．二．填空题（共13小题）4．（2023春•普陀区期中）如图，在梯形ABCD中，AD∥BC，E、F分别是AB、DC上的点，EF∥BC，如果，AD＝4，BC＝9，那么EF的长为．【分析】延长BA，与CD的延长线交于点G，易证明△GAD∽△GBC，得到，进而得到，再证明△GEF∽△GBC，利用相似三角形的性质即可解答．【解答】解：延长BA，与CD的延长线交于点G，如图，∵AD∥BC，AD＝4，BC＝9，∴△GAD∽△GBC，∴，∵，∴，，∵EF∥BC，∴△GEF∽△GBC，∴，∵BC＝9，∴EF＝6．故答案为：6．【点评】本题主要考查相似三角形的判定与性质，熟知相似三角形的对应边成比例是解题关键．5．（2023•普陀区一模）如图，△ABC中的一边BC与双边平行且单位相同的刻度尺的一边重合，边AB、AC 分别与刻度尺的另一边交于点D、E，点B、C、D、E在刻度尺上的读数分别为0、5、1、3，如果刻度尺的宽度为3，那么△ABC的面积是．【分析】过点A作AF⊥DE，垂足为G，并延长AG交BC于点H，根据题意得：DE＝2，BC＝5，GH＝3，DE ∥BC，从而可得∠ADE＝∠ABC，∠AED＝∠ACB，然后证明A字模型相似三角形△ADE∽△ABC，从而利用相似三角形的性质求出AH的长，最后利用三角形的面积公式进行计算，即可解答．【解答】解：过点A作AF⊥DE，垂足为G，并延长AG交BC于点H，由题意得：DE＝2，BC＝5，GH＝3，DE∥BC，∴∠ADE＝∠ABC，∠AED＝∠ACB，∴△ADE∽△ABC，∴＝，∴＝，解得：AH＝5，∴△ABC的面积＝BC•AH＝×5×5＝，故答案为：．【点评】本题考查了相似三角形的判定与性质，三角形的面积，平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．6．（2023•静安区校级一模）在△ABC中，AB＝6，AC＝5，点D、E分别在边AB、AC上，当AD＝4，∠ADE＝∠C时，＝．【分析】首先判定△ADE∽△ACB，然后利用该相似三角形的对应边成比例解答．【解答】解：∵∠ADE＝∠C，∠A＝∠A，∴△ADE∽△ACB．∴＝．∵AC＝5，AD＝4，∴＝．故答案为：．【点评】本题考查的是相似三角形的判定与性质，相似三角形是相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．7．（2023•青浦区一模）如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC，EF∥AB，CF＝3BF．如果S△ADE＝1，那么S四边形DBCE＝．【分析】根据题意可得，四边形DEFB为平行四边形，则，易证明△ADE∽△ABC，根据相似三角形的性质得，以此求出S△ABC＝16，由S四边形DBCE＝S△ABC﹣S△ADE 即可解答．【解答】解：∵CF＝3BF，∴，∵DE∥BC，EF∥AB，∴四边形DEFB为平行四边形，∴DE＝BF，△ADE∽△ABC，∴，∴，∵S△ADE＝1，∴S△ABC＝16，∴S四边形DBCE＝S△ABC﹣S△ADE＝15．故答案为：15．【点评】本题主要考查平行四边形的判定与性质、相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解题关键．8．（2022秋•黄浦区期中）如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则S△DMN：S四边形DBCM＝．【分析】由DE为三角形ABC的中位线，利用中位线定理得到DE平行于BC，且DE等于BC的一半，再由M 为DE的中点，得到DM为DE的一半，可得出DM为BC的四分之一，由DM与BC平行，得到两对同位角相等，进而确定出三角形DMN与三角形NBC相似，由相似三角形面积之比等于相似比的平方，求出三角形DMN与三角形NBC面积之比，即可求出四边形DBCM与三角形DMN的面积之比．【解答】解：∵DE为△ABC的中位线，∴DE∥BC，DE＝BC，∴∠NDM＝∠B，∠NMD＝∠NCB，∴△NDM∽△NBC，∵M为DE的中点，∴DM＝DE＝BC，即相似比为1：4，∴S△NDM：S△NBC＝1：16，则S△DMN：S四边形DBCM＝1：15．故答案为：1：15．【点评】此题考查了相似三角形的判定与性质，以及三角形的中位线定理，熟练掌握相似三角形的判定与性质是解本题的关键．9．（2022秋•宝山区期中）在梯形ABCD中，AD∥BC，AD＝2，BC＝5，点E、F分别在边AB、CD上，且EF∥BC，如果AE：EB＝2：1，那么EF的长为．【分析】连接AC交EF于点P，先利用平行线分线段成比例定理求出、，再利用相似三角形的性质求出EP、FP EF．【解答】解：如图，连接AC交EF于点P．∵AD∥BC，EF∥BC，∴AD∥EF∥BC．∴＝＝．∴＝，＝．∵AD∥EF∥BC，∴△AEP∽△ABC，△CFP∽△CDA．∴＝＝，＝＝．∵AD＝2，BC＝5，∴EP＝，PF＝．∵EF＝EP+PF＝+＝4．故答案为：4．【点评】本题主要考查了相似三角形的性质和判定，掌握“平行线分线段成比例定理”、相似三角形的判定和性质是解决本题的关键．10．（2022秋•嘉定区期中）如图，AD∥BC∥EF，AE：AB＝2：3，AD＝8，BC＝14则EF＝．【分析】过点A作AH∥DC，交EF于点G，利用平行四边形的判定可得四边形AGFD和四边形AHCD都是平行四边形，从而可得AD＝GF＝8，AD＝CH＝8，进而可得BH＝6，然后证明A字模型相似三角形△AEG∽△ABH，从而利用相似三角形的性质可得EG＝4，最后进行计算即可解答．【解答】解：过点A作AH∥DC，交EF于点G，∵AD∥BC∥EF，∴四边形AGFD是平行四边形，四边形AHCD是平行四边形，∴AD＝GF＝8，AD＝CH＝8，∵BC＝14，∴BH＝BC﹣CH＝6，∵EG∥BH，∴∠AEG＝∠B，∠AGE＝∠AHB，∴△AEG∽△ABH，∴＝，∴＝，∴EG＝4，∴EF＝EG+FG＝4+8＝12，故答案为：12．【点评】本题考查了相似三角形的判定与性质，平行四边形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．11．（2022秋•浦东新区期中）如图、在△ABC，CD平分∠ACB，DE∥BC，AD＝2，BD＝3，BC＝5，则CE ＝．【分析】根据平行线的性质可得∠ADE＝∠B，∠AED＝∠C，从而可得△ADE∽△ABC，然后利用相似三角形的性质进行计算可得DE＝2，最后再根据角平分线的定义和平行线的性质可得△EDC是等腰三角形，即可解答．【解答】解：∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴△ADE∽△ABC，∴＝，∴＝，∴DE＝2，∵DE∥BC，∴∠EDC＝∠DCB，∵CD平分∠ACB，∴∠DCB＝∠ACD，∴∠EDC＝∠ACD，∴ED＝EC＝2，故答案为：2．【点评】本题考查了相似三角形的判定与性质，等腰三角形的判定与性质，平行线的性质，熟练掌握根据角平分线的定义和平行线的性质可得等腰三角形是解题的关键．12．（2022秋•徐汇区校级月考）如图，AM：MB＝AN：NC＝1：3，则MN：BC＝．【分析】首先根据已知条件可以证明MN∥BC，然后证明△AMN∽△ABC即可求解．【解答】解：∵AM：MB＝AN：NC＝1：3，∴MN∥BC，AM：AB＝1：4，∴△AMN∽△ABC，∴MN：BC＝AM：AB＝1：4．故答案为：1：4．【点评】此题主要考查了相似三角形的性质与判定，熟练掌握相似三角形的性质是解题的关键．13．（2022秋•虹口区校级月考）如图，矩形DEFG为△ABC的内接矩形，点G，F分别在AB，AC上，AH 是BC边上的高，BC＝10，AH＝6，EF：GF＝2：5，则矩形DEFG的面积为．【分析】据矩形的性质可得出GF∥BC，进而可得出△AGF∽△ABC，设EF＝2x，则GF＝5x，根据相似三角形的性质即可得出关于x的一元一次方程，解之即可得出x的值，再利用矩形的面积公式即可求出矩形DEFG 的面积．【解答】解：设EF＝2x，则GF＝5x．∵GF∥BC，AH⊥BC，∴AK⊥GF．∵GF∥BC，∴△AGF∽△ABC，∴＝．∵AH＝6，BC＝12，∴＝．解得x＝．∴EF＝，GF＝6，∴矩形DEFG的面积为．故答案为：．【点评】本题考查了相似三角形的判定与性质、矩形的性质以及解一元一次方程，根据相似三角形的性质列出关于x的一元一次方程是解题的关键．14．（2022春•青浦区校级期末）已知：如图，在△ABC中，AC＝6，BC＝8，AB＝10，点D位于边AB上，过点D作边BC的平行线交边AC于点E，过点D作边AC的平行线交边BC于点F，设AE＝x，四边形CEDF的面积为y，则y关于x的函数关系式是．（不必写定义域）【分析】根据已知可证四边形DECF是平行四边形，然后利用勾股定理的逆定理证明△ABC是直角三角形，从而可得∠C＝90°，进而可得四边形DECF是矩形，再证明A字模型相似三角形△AED∽△ABC，从而利用相似三角形的性质可得DE＝x，最后根据矩形的面积公式进行计算即可解答．【解答】解：∵DE∥BC，DF∥AC，∴四边形DECF是平行四边形，在△ABC中，AC＝6，BC＝8，AB＝10，∵AC2+BC2＝62+82＝100，AB2＝102＝100，∴AC2+BC2＝AB2，∴△ABC是直角三角形，∴∠C＝90°，∴四边形DECF是矩形，∵DE∥BC，∴∠AED＝∠C＝90°，∵∠A＝∠A，∴△AED∽△ABC，∴＝，∴＝，∴DE＝x，∴矩形CEDF的面积＝DE•CE，∴y＝x（6﹣x）＝﹣x2+8x，故答案为：y＝﹣x2+8x．【点评】本题考查了相似三角形的判定与性质，勾股定理的逆定理，函数关系式，熟练掌握A字模型相似三角形是解题的关键．15．（2021秋•金山区期末）如图，E是▱ABCD的边BA延长线上一点，CE与AD相交于点F，AE＝1，AB ＝2，BC＝3，那么AF＝．【分析】利用A字模型相似三角形进行计算即可解答．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAF＝∠B，∠EFA＝∠ECB，∴△EAF∽△EBC，∴＝，∴＝，∴AF＝1，故答案为：1．【点评】本题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握A字模型相似三角形是解题的关键．16．（2021秋•嘉定区期末）如图，在△ABC中，∠C＝90°，BC＝2，，点D在边AC上，CD：AD＝1：3，联结BD，点E在线段BD上，如果∠BCE＝∠A，那么CE＝．【分析】根据已知∠BCE＝∠A，想到构造这两个角所在的三角形相似，所以过点E作EF⊥BC，垂足为F，可得△ABC∽△CEF，进而可得CF＝2EF，然后设EF为a，则CF为2a，BF为2﹣2a，最后再证明A字模型相似△BFE∽△BCD，从而解答即可．【解答】解：过点E作EF⊥BC，垂足为F，∵∠ACB＝90°，BC＝2，，∴AC＝＝＝4，∵CD：AD＝1：3，∴CD＝1，∵∠BCE＝∠A，∠ACB＝∠CFE＝90°，∴△ABC∽△CEF，∴＝＝＝2，∴设EF为a，则CF为2a，BF为2﹣2a，∵∠ACB＝∠BFE＝90°，∠CBD＝∠FBE，∴△BFE∽△BCD，∴＝，∴＝，∴a＝，∴EF＝，CF＝1，∴CE＝＝＝，故答案为：．【点评】本题考查了相似三角形的判定与性质，勾股定理，熟练掌握A字模型相似是解题的关键．三．解答题（共5小题）17．（2022秋•奉贤区期中）如图，已知在四边形ABCD中，AD∥BC．E为边CB延长线上一点，联结DE 交边AB于点F，联结AC交DE于点G，且＝．（1）求证：AB∥CD；（2）如果AE2＝AG•AC，求证：＝．【分析】（1）由AD∥BC，得到△ADG∽△CEG，根据相似三角形的性质即可得到结论；（2）由AE2＝AG•AC易得△AEG∽△ACE，所以∠AEG＝∠ACE＝∠DAG，可得△ADG∽△EDA，再根据相似三角形的性质可得结论．【解答】证明：（1）∵AD∥BC，∴△ADG∽△CEG，∴＝，∵＝，∴＝，∴AB∥CD；（2）∵AE2＝AG•AC，∴＝，∵∠EAG＝∠CAE，∴△AEG∽△ACE，∴∠AEG＝∠ACE，∵AD∥BC，∴∠ACE＝∠DAG，∴∠DAG＝∠AEG，∵∠ADG＝∠EDA，∴△ADG∽△EDA，∴，即＝．【点评】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．18．（2022秋•杨浦区期中）如图，点D、E分别在△ABC的边AB、AC上，DE∥BC．如果S△ADE＝2，S△BCE＝7.5．求S△BDE．【分析】设S△BDE＝x，则可得出△ABE△BCE的面积之比，再将x的值代入即可得出答案；【解答】解：（1）设S△BDE＝x．∴＝，∴＝．∵DE∥BC，∴＝，∵S△ADE＝2，S△BCE＝7.5，∴＝，解得：x1＝﹣5（舍），x2＝3．∴S△BDE＝3．【点评】本题考查了平行线分线段成比例定理以及分式方程的应用，难度较大．19．（2022秋•奉贤区期中）如图，在△ABC中，点D在边AB上，点F、E在边AC上，且DF∥BE，．（1）求证：DE∥BC；（2）如果＝，S△ABC＝12，求S△ADE的值．【分析】（1）由DF∥BE得比例，结合已知比例，利用过渡比得出＝，证明结论；（2）首先可以证明＝，然后证明△ADE∽△ABC，最后利用相似三角形的面积比等于相似比的平方求解．【解答】（1）证明：∵DF∥BE，∴＝，∵＝，∴＝，∴DE∥BC；（2）解：∵＝，∴＝，∴＝，∵DE∥BC，∴△ADE∽△ABC，∴＝＝（）2＝，∵S△ABC＝12，∴S△ADE＝．【点评】本题考查了相似三角形的判定与性质，平行线的性质，平行线分线段成比例．关键是利用平行线得出相似三角形及比例，利用相似三角形的面积比等于相似比的平方解题．20．（2023•青浦区一模）如图，在平行四边形ABCD中，点F在边AD上，射线BA、CF相交于点E，DF＝2AF．（1）求EA：AB的值；（2）如果，，试用、表示向量．【分析】（1）根据平行四边形的性质可得AB∥CD，AB＝CD，易证△AEF∽△DCF，则＝，由DF ＝2AF即可求解；（2）先算出，再根据即可求解．【解答】解：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴△AEF∽△DCF，∴，∴，∵DF＝2AF，∴，∴；（2）∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵DF＝2AF，∴，∵，，∴，，∴．【点评】本题主要考查相似三角形的判定与性质、平行四边形的性质、平面向量，熟练掌握平面向量的运算法则是解题关键．21．（2021秋•普陀区期末）如图，在△ABC中，边BC上的高AD＝2，tan B＝2，直线l平行于BC，分别交线段AB，AC，AD于点E、F、G，直线l与直线BC之间的距离为m．（1）当EF＝CD＝3时，求m的值；（2）将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，延长EP交线段CD于点Q．①当点P恰好为△ABC的重心时，求此时CQ的长；②联结BP，在∠CBP＞∠BAD的条件下，如果△BPQ与△AEF相似，试用m的代数式表示线段CD的长．【分析】（1）根据＝tanB＝2，可得：BD＝1，再由EF＝CD＝3，DG＝m，可得：BC＝4，AG＝2﹣m，利用EF∥BC，可得＝，建立方程求解即可；（2）①由翻折可得：BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，进而得出：AG＝，推出DP＝GP，再由EF∥BC，可得出EG＝，利用ASA证明△PQD≌△PEG，即可求得答案；②分两种情况：Ⅰ．当△BPQ∽△FAE时，由△FAE∽△CAB，推出△BPQ∽△CAB，建立方程求解即可；Ⅱ．当△BPQ∽△AFE时，由△AFE∽△ACB，推出△BPQ∽△ACB，建立方程求解即可．【解答】解：（1）如图1，在△ABC中，边BC上的高AD＝2，tanB＝2，∴＝tanB＝2，∴BD＝1，∵EF＝CD＝3，DG＝m，∴BC＝BD+CD＝4，AG＝AD﹣DG＝2﹣m，∵EF∥BC，∴＝，即＝，解得：m＝，∴m的值为；（2）①如图2，∵将△AEF沿着EF翻折，点A落在△ABC的重心点P处，∴BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，∴AG＝GP＝AP＝，∴DP＝GP，∵EF∥BC，∴∠PGE＝∠PDQ＝90°，△AEG∽△ABD，∴＝，即＝，∴EG＝，在△PQD和△PEG中，，∴△PQD≌△PEG（ASA），∴DQ＝EG＝，∴CQ＝CD﹣DQ＝1﹣＝，∴此时CQ的长为；②在Rt△ABD中，AB＝＝，∵将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，∴∠PBQ＜∠ABD，∵EF∥BC，∴∠AEF＝∠ABD，∴∠PBQ＜∠AEF，∵∠CBP＞∠BAD，∴∠BAD＜∠PBQ＜∠AEF，∵GP＝AG＝2﹣m，DG＝m，∴DP＝DG﹣GP＝m﹣（2﹣m）＝2m﹣2，∴m＞1，∴1＜m＜2，∵∠AEF＝∠ABD，∴＝tan∠AEF＝tan∠ABD＝2，∴＝2，∴EG＝，∵EF∥BC，∴△PEG∽△PQD，∴＝，即＝，∴DQ＝m﹣1，∴BQ＝BD+DQ＝m，∵∠AEF＝∠PEG＝∠BQP，∠PBQ＜∠AEF，∴△BPQ与△AEF相似，则△BPQ∽△FAE或△BPQ∽△AFE，Ⅰ．当△BPQ∽△FAE时，∵△FAE∽△CAB，∴△BPQ∽△CAB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝；Ⅱ．当△BPQ∽△AFE时，∵△AFE∽△ACB，∴△BPQ∽△ACB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝，综上，线段CD的长为或．【点评】本题考查了全等三角形判定和性质，相似三角形的判定和性质，勾股定理，三角函数，翻转变换的性质等，熟练掌握全等三角形判定和性质、相似三角形的判定和性质等相关知识，运用分类讨论思想和方程思想思考解决问题是解题关键．22．（2023•奉贤区一模）已知：如图，在梯形ABCD中，AD∥BC，点E在对角线BD上，∠EAD＝∠BDC．（1）求证：AE•BD＝AD•DC；（2）如果点F在边DC上，且，求证：EF∥BC．【分析】（1）利用平行线的性质证明∠ADB ＝∠DBC ，然后利用已知条件可以证明△ADE ∽△DBC ，由此即可解决问题；（2）利用（1）的结论和已知条件可以证明△DEF ∽△DBC ，接着利用相似三角形的在即可求解．【解答】证明：（1）∵AD ∥BC ，∴∠ADB ＝∠DBC ，又∵∠EAD ＝∠BDC ，∴△ADE ∽△DBC ，∴AE ：AD ＝DC ：BD ，∴AE •BD ＝AD •DC ；（2）∵AE ：AD ＝DC ：BD ，且，∴＝，而∠EDF ＝∠BDC ，∴△DEF ∽△DBC ，∴∠DEF ＝∠DBC ，∴EF ∥BC ．【点评】此题主要考查了相似三角形的性质与判定，同时也利用了平行线的性质，比例的基本性质，有一定的综合性．23.如图，在平行四边形ABCD 中，E 是AD 上一点，CE 与BD 相交于点O ，CE 与BA 的延长线相交于点G ，已知2DE AE =，10CE =，求GE 和CO 的长．【答案】56GE CO ==，．【解析】四边形ABCD 是平行四边形，//AD BC AD BC ∴=，．又2DE AE =，13GE AE AE GC BC AD ∴===，23EO DE OC BC ==，即13GE GE EC =+，23EC CO CO −=，代入即可求得56GE CO ==，．【总结】考查利用三角形一边平行线的性质构造“A ”字型和“X ”字型，进行比例线段的综合应用．24.如图，在ABC ∆中，设D 、E 是AB 、AC 上的两点，且BD CE =，延长DE 交BC 的延长线于点F ，:3:5AB AC =，12cm EF =，求DF 的长．【答案】20cm ．【解析】过点D 作//DH AC 交BC 于H ，则有35BD AB DH AC ==，又BD CE =，则有35CE DH =，由//CE DH ，得35EF CE DF DH ==，代入计算得：125320DF cm =⨯÷=．【总结】作平行线，构造出与所求线段相关的“A ”字型或“X ”字型，比例转化．25.如图，已知ABC ∆中，点D 、E 分别在边AB 、AC 上，且:3:2AD DB =，:1:2AE EC =，直线ED和CB 的延长线交于点F ，求:FB FC ． FE DC B A【答案】1:3．【解析】过点B 作//BG FE 交AC 于G ．根据三角形一边平行线的性质定理，可得：32AE AD EG DB ==，又:1:2AE EC =，故13EG EC =，由//BG FE ，可得：::1:3FB FC EG EC ==．【总结】作平行线，构造出与所求线段相关的“A ”字型或“X ”字型，比例转化． G F EDCB A。

相似专题四相似三角形的基本模型A字型及其变形初中数学模型

A．4 B．4 2 C．6 D．4 3
3．如图，在△ABC中，点D，E分别在边AB，AC上，请添加一个条件： ________∠__A_E_D__＝__∠__B_(_答__案__不__唯__一__) _，使△ABC∽△AED.
4．如图，在▱ABCD中，点P在BC的延长线上，连接AP，交BD于点M，交DC于点 N.求证：AM2＝MN·MP.
专题(四) 相似三角形的基本模型(一)——A字型及其变形
Hale Waihona Puke 【模型展示】(1)A 字型
如图 1，已知：DE∥BC.
结论：△ADE∽△ABC⇒
AD AB
＝AAEC
＝DBCE
.
(2)反 A 字型(共角)
如图 2，已知：∠AED＝∠C.
结论：△ADE∽△ABC⇒
AD AB
＝AAEC
＝DBCE
.
(3)反 A 字型(共边共角) 如图，已知：∠ABD＝∠C. 结论：①△ABD∽△ACB； ②AADB ＝AABC ＝DBCB ； ③AB2＝AD·AC.
【对应训练】
1．(2022·凉山州)如图，在△ABC 中，点 D，E 分别在边 AB，AC 上．若 DE∥BC，
AD DB
＝23
，DE＝6 cm，则 BC 的长为(
C
)
A．9 cm B．12 cm C．15 cm D．18 cm
2．如图，在△ABC 中，AD 是中线，BC＝8，∠B＝∠DAC.则线段 AC 的长为 ( B)
解：(1)∵DE∥BC，∴AAEC ＝AADB ＝23 ， ∵AE＝4，∴AC＝6，∴EC＝6－4＝2
(2)∵M 是 BC 的中心，∴S△ABM＝12 S△ABC＝18，又∵DE∥BC，∴△ADN∽△ABM，

(挑战压轴)专项27.2 相似三角形种A字型(2种类型)(原卷版)

（挑战压轴）专项27.2 相似三角形种A 字型（2种类型）【方法技巧】有一个公共角（图①、图②）或角有公共部分（图③，∠BAC 及∠DAE 有公共部分∠DAF ），此时需要找另一对角相等，另外若题中未明确相似三角形对应顶点，则需要分类讨论，如图③中可找条件∠D ＝∠C 或∠D ＝∠B.1.如图，在△ABC 中，DE ∥BC ，DE ＝2，BC ＝5，则S △ADE ：S △ABC 的值是（）A ．B ．C ．D ．2.如图，在△ABC 中，点E 、F 分别在AB 、AC 上，EF ∥BC ，＝，四边形BCFE 的面积为21，则△ABC 的面积是（）A ．B ．25C ．35D ．633.如图，在△ABC 中，点D ，E 分别是AB ，AC 的中点，若△ADE 的面积是4cm 2，则四边形BDEC 的面积为（）A ．4cm 2B ．8cm 2C ．12cm 2D ．16cm 24．（2019•梁平区模拟）如图，△ABC ∽△ADE ，且BC ＝2DE ，则的值为（）A ．B ．C ．D ．5．（2021•绥化）两个相似三角形的最短边分别为5cm 和3cm ，它们的周长之差为12cm ，那么大三角形的周长为（）A ．14 cmB ．16 cmC ．18 cmD ．30 cm6．（2022•漳州模拟）如图，在△ABC 中，点D ，E 分别是AB ，AC 的中点，若△ADE 的面积是4cm 2，则四边形BDEC 的面积为（）A ．4cm 2B ．8cm 2C ．12cm 2D ．16cm 27．如图，直线l 1∥l 2∥l 3，直线AC ，DF 分别交l 1，l 2，l 3于点A ，B ，C 和点D ，E ，F ，连结AF ，作BG ∥AF ，若＝，BG ＝6，则AF 的长为（）A ．8B ．9C ．10D ．118.如图，有一块三角形余料ABC ，BC ＝120mm ，高线AD ＝90mm ，要把它加工成一个矩形零件，使矩形的一边在BC 上，点P 、M 分别在AB ，AC 上，若满足PM ：PQ ＝2：1，则PQ的长为（）A．36mm B．40mm C．50mm D．120mm9.已知：如图，在△ABC中，∠ADE＝∠C，则下列等式成立的是（）A．＝B．＝C．＝D．＝10．（2022•馆陶县模拟）如图，有一块等腰三角形材料，底边BC＝80cm，高AD＝120cm，现要把它加工成正方形零件，使其一边在BC边上，其余两个顶点分别在AB、AC上，则这个正方形零件的边长为（）A．36cm B．40cm C．48cm D．60cm 11．（2022春•任城区校级期末）如图，有一块三角形余料ABC，BC＝120mm，高线AD＝90mm，要把它加工成一个矩形零件，使矩形的一边在BC上，点P、M分别在AB，AC 上，若满足PM：PQ＝2：1，则PQ的长为（）A．36mm B．40mm C．50mm D．120mm12.已知：如图，在△ABC中，AC＝6，BC＝8，AB＝10，点D位于边AB上，过点D作边BC的平行线交边AC于点E，过点D作边AC的平行线交边BC于点F，设AE＝x，四边形CEDF的面积为y，则y关于x的函数关系式是　．（不必写定义域）13．（2021•镇江）如图，点D，E分别在△ABC的边AC，AB上，△ADE∽△ABC，M，N分别是DE，BC的中点，若＝，则＝．14．如图，E为▱ABCD的边CD延长线上的一点，连结BE交AC于点O，交AD点F．（1）求证：△AOB∽△COE；（2）求证：BO2＝EO•FO．15．如图，在△ABC中，点D，E，F分别在AB，BC，AC上，DE∥AC，EF∥AB．（1）求证：△BDE∽△EFC．（2）若＝，△EFC的面积为9，求△ABC的面积．16．（2022秋•宜兴市月考）有一块三角形的余料ABC，要把它加工成矩形的零件，已知BC ＝12cm，高AD＝8cm，矩形EFGH的边EF在BC边上，G、H分别在AC、AB上，设HE的长为ycm、EF的长为xcm．（1）写出y与x的函数关系式；（2）当x取多少时，EFGH是正方形．17．如图，在菱形ABCD中，DE⊥BC交BC的延长线于点E，连结AE交BD于点F，交CD于点G，连结CF．（1）求证：AF＝CF；（2）求证：AF2＝EF•GF；（3）若菱形ABCD的边长为2，∠BAD＝120°，求FG的长．。

八年级上册数学a字模型

八年级上册数学a字模型一、A字模型的概念。

在三角形中，A字模型是一种常见的相似三角形模型。

它类似字母“A”的形状，通常由一条与三角形一边平行的直线所截得的图形构成。

（一）基本图形结构。

1. 在三角形ABC中，DE平行于BC，这样就形成了一个典型的A字模型。

- 其中三角形ADE和三角形ABC相似。

- 对应角相等，即∠ADE = ∠ABC，∠AED = ∠ACB，∠A是公共角。

2. 相似比。

- 根据相似三角形的性质，相似三角形对应边成比例。

在这个A字模型中，(AD)/(AB)=(AE)/(AC)=(DE)/(BC)。

二、A字模型的性质及应用。

（一）求线段长度。

1. 例1：在三角形ABC中，DE平行于BC，AD = 2，DB = 3，AC = 10，求AE的长度。

- 因为DE平行于BC，所以三角形ADE相似于三角形ABC。

- 根据相似三角形对应边成比例，(AD)/(AB)=(AE)/(AC)。

- 首先求AB的长度，AB = AD+DB = 2 + 3 = 5。

- 设AE=x，则(2)/(5)=(x)/(10)，通过交叉相乘可得5x = 20，解得x = 4，即AE = 4。

2. 例2：已知三角形ABC中，EF平行于BC，AF = 3，FC = 2，BC = 10，求EF 的长度。

- 由于EF平行于BC，三角形AEF相似于三角形ABC。

- 此时(EF)/(BC)=(AF)/(AC)。

- 先求AC的长度，AC = AF+FC = 3+2 = 5。

- 设EF = y，则(y)/(10)=(3)/(5)，解得y = 6，即EF = 6。

（二）求比例关系。

1. 例3：在三角形ABC中，DE平行于BC，若AD:DB = 1:2，求三角形ADE与四边形DBCE的面积比。

- 因为DE平行于BC，三角形ADE相似于三角形ABC。

- 已知AD:DB = 1:2，那么AD:AB = 1:(1 + 2)=1:3。

- 根据相似三角形面积比等于相似比的平方，S_ ADE:S_ ABC=((AD)/(AB))^2 = ((1)/(3))^2=(1)/(9)。

相似三角形的基本模型(A字型)(原卷版)(人教版) -九年级数学下册

专题04相似三角形的基本模型（A 字型）【模型说明】“A ”字模型图形（通常只有一个公共顶点）的两个三角形有一个“公共角”（是对应角），再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．图1图2图31）“A ”字模型条件：如图1，DE ∥BC ；结论：△ADE ∽△ABC ⇔AD AB ＝AE AC ＝DE BC.2）反“A ”字模型条件：如图2，∠AE D ＝∠B ；结论：△ADE ∽△ACB ⇔AD AC ＝AE AB ＝DE BC.3）同向双“A ”字模型条件：如图3，EF ∥BC ；结论：△AEF ∽△ABC ，△AEG ∽△ABD ，△AGF ∽△ADC ⇔EG FG AG BD CD AD==【例题精讲】例1．（基本模型1）如图，已知D 是BC 的中点，M 是AD 的中点．求:AN NC 的值．A．24B．12【变式训练2】．如图，在Rt ABC BC上，连接C D AE，交于点F【变式训练4】．如图，△ABO AO 边的三等分点M 、N 分别作的值为（）A ．9【变式训练5】．如图，把边长为使点B 和D 重合，求折痕课后训练1．如图，,AB CD AE FD ∥∥，A ．DH CH FH BH =B ．GE DF3．如图，在三角形ABC中，点折至三角形ABC平面内，使得=与AD交于点O，若AH CH4．在平面直角坐标系中，已知，另一直角边交直角边构造直角ABC小值为．5．已知，平行四边形ABCD中，7．一块直角三角形木板的面积为21.5m，一条直角边AB为1.5m，怎样才能把它加工成一个面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用学过的知识说明哪位木匠的方法符合要求（加工损耗忽略不计，计算结果中的分数可保留）．8．如图，在平行四边形ABCD中，AD＝AC，∠ADC＝α，点E为射线BA上一动点，且AE ＜AB，连接DE，将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H，DE所在直线与射线CA交于点G．（1）如图1，当α＝60°时，求证：△ADH≌△CDG；（2）当α≠60°时，①如图2，连接HG，求证：△ADC∽△HDG；②若AB＝9，BC＝12，AE＝3，请直接写出EG的长．9．在等腰三角形ABC 中，AB AC =，作CM AB ⊥交AB 于点M ，BN AC ⊥交AC 于点N ．（1）在图1中，求证：BMC CNB ≌；（2）在图2中的线段CB 上取一动点P ，过P 作//PE AB 交CM 于点E ，作//PF AC 交BN 于点F ，求证：①PE PF BM +=；②OM BN AM PF AM PE ⋅-⋅=⋅．10．在矩形ABCD 中，6AB =，8AD =，点E 是边AD 上一点，EM EC ⊥交AB 于点M ，点N 在射线MB 上，且AE 是AM 和AN 的比例中项．（1）如图1，求证：ANE DCE ∠=∠；（2）如图2，当点N 在线段MB 之间，联结AC ，且AC 与NE 互相垂直，求MN 的长；（3）联结AC ，如果AEC ∆与以点E 、M 、N 为顶点所组成的三角形相似，求DE 的长．（1）求证：DB AB=；（2）点E在BC边上，连接AE交BD于点F 度数．△（3）在（2）的条件下，若16BC=，ABF。

相似三角形A字形

(2)若AF:FC=2:7，BD:DC=4:3，求AE:ED.
（3）BD:CD=2:3,AE:ED=3:4
求:AF:FC
⑤在△ABC中，D、E分别为BC的三等分点，AC边上的中线BM交AD于P，交AE于Q，若BM=10cm，试求BP、PQ、QM一点，（m、n＞0），取CF的中点D，连结AD并延长交BC于E.（1）的值.（2）如果BE=2EC，那么CF所在直线与边AB有怎样的位置关系？证明你的结论；（3）E点能否为BC中点？如果能，求出相应的的值；如果不能，证明你的结论。?彼相似，我条件，创造边角再相似①AE2＝AD·AB，且∠ABE＝∠BCE，
试说明△EBC∽△DEB
②已知 ∽ ，求证： ∽ ．
③D为△ABC内一点，连接BD、AD，以BC为边在△ABC外作∠CBE=∠ABD，∠BCE=∠BAD，求证：△DBE∽△ABC。
④D、E分别在△ABC的AC、AB边上，
且AE?AB=AD?AC，BD、CE交于点O.
求证：△BOE∽△COD.
求证：AB:AC=BD:CD.
②在△ABC中，AB=AC，
求证：DF:FE=BD:CE.
③在△ABC中，AB>AC，D为AB
上一点，E为AC上一点，AD=AE，
直线DE和BC的延长线交于点P，
求证：BP:CP=BD:CE.
④ 在△ABC中，BF交AD于E.
(1)若AE:ED=2:3，BD:DC=3:2，求AF:FC；
①Rt△ABC中四边形DEFG为正方形。
求证：EF2=BE?FC
②△ABC中，AB=AC，AD是BC边上的中线，CF∥BA，求证：BP2=PE·PF。
③ AD是△ABC的角平分线，EF垂直平分AD，
交BC的延长线于E，交AB于F.

相似三角形A字形

FA 字形，A ’形，8字形，蝴蝶形，双垂直,旋转形双垂直结论:射影定理：边的比例中项⑴△ACD ∽△CDB →AD:CD=CD:BD →CD2=AD?BD⑵△ACD ∽△ABC →AC:AB=AD:AC →AC2=AD?AB⑶△CDB ∽△ABC →BC:AC=BD:BC →BC2=BD?AB结论：⑵÷⑶得AC2:BC2=AD:BD结论：面积法得AB?CD=AC?BC →比例式证明等积式(比例式)策略直接法：找同一三角形两条边变化：等号同侧两边同一三角形三点定形法 2、间接法： ⑴3种代换 ①等线段代换； ②等比代换； ③等积代换；⑵创造条件 ①添加平行线——创造“A ”字型、“8”字型②先证其它三角形相似——创造边、角条件相似判定条件：两边成比夹角等、两角对应三边比相似终极策略：遇等积，化比例，同侧三点找相似；四共线，无等边，射影平行用等比；四共线，有等边，必有一条可转换；两共线，上下比，过端平行条件边。

彼相似，我角等，两边成比边代换。

（3）等比代换：若d c b a ,,,是四条线段，欲证d c b a =，可先证得feb a =（f e ,是两条线段）然后证d c fe =，这里把f e叫做中间比。

①∠ABC=∠ADE ．求证：AB ·AE=AC ·AD②△ABC 中，AB=AC ，△DEF 是等边三角形求证：BD?CN=BM?CE ．③等边三角形ABC 中，P为BC 上任一点，AP 的垂直平分线交AB 、AC 于M 、N 两点。

求证：BP?PC=BM?CN ?有射影，或平行，等比传递我看行 ①在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于D ，E 为AC 的中点，求证：AB?AF=AC?DF斜边上面作高线，比例中项一大片②ABCD③梯形ABCD 中，AD//BC ，作BE//CD, 求证：OC2=OA.OE?四共线，看条件，其中一条可转换；①Rt △ABC 中四边形DEFG 为正方形。

相似三角形的a型结构

相似三角形的a型结构相似三角形是初中数学中一个重要的概念，它是指具有相同形状但大小不同的两个三角形。

在相似三角形中，它们的对应角度相等，而对应边的长度成比例。

其中，a型结构是一种特殊的相似三角形，它的三个内角分别为a°、(180-2a)°和(a+30)°。

相似三角形a型结构在几何学中有着重要的应用。

首先，我们来看一下它的特点和性质。

在a型结构中，角a°是两个相似三角形的对应角，而角(a+30)°是两个相似三角形的内角和角。

根据角度和定理，我们可以得出：对于两个相似三角形，它们的对应角度相等。

接下来，我们来讨论相似三角形a型结构的应用。

在实际问题中，我们经常会遇到需要求解未知长度的情况。

通过相似三角形的性质，我们可以利用已知条件求解未知长度。

例如，已知两个相似三角形的对应边长比为1:2，求解未知边长的方法如下：首先，我们设未知边长为x，已知边长为y。

根据相似三角形的性质，我们可以得出以下比例关系：x/y=1/2。

通过求解这个比例关系，我们可以得出未知边长的值。

除了求解未知边长外，相似三角形a型结构还可以用于解决一些实际问题。

例如，已知两个相似三角形的一个角度为30°，求解另一个角度的方法如下：首先，我们设另一个角度为x°。

根据相似三角形的性质，我们可以得出以下角度关系：x+30=180-2x。

通过求解这个方程，我们可以得出另一个角度的值。

相似三角形a型结构常常出现在几何证明中。

在证明相似三角形的过程中，我们可以利用a型结构的特点来推导结论。

例如，已知两个相似三角形的一个角度为a°，我们可以通过a型结构的特点推导出它们的对应角度相等。

这样一来，我们就可以利用已知条件来证明相似三角形的性质。

相似三角形a型结构还可以应用于三角函数的计算中。

在三角函数中，我们经常需要计算三角形的各个内角的正弦、余弦和正切值。

通过相似三角形a型结构的特点，我们可以将一个角度的三角函数值转化为另一个角度的三角函数值。

相似三角形A字形

相似三角形A字形(总2页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2A 字形，A ’形，8旋转形双垂直结论:射影定理：①直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项⑴△ACD ∽△CDB →AD:CD=CD:BD →CD2=AD?BD⑵△ACD ∽△ABC →AC:AB=AD:AC →AC2=AD?AB⑶△CDB ∽△ABC →BC:AC=BD:BC →BC2=BD?AB结论：⑵÷⑶得AC2:BC2=AD:BD结论：面积法得ABCD=ACBC→比例式证明等积式(比例式)策略直接法：找同一三角形两条边变化：等号同侧两边同一三角形三点定形法2、间接法： ⑴3种代换 ①等线段代换； ②等比代换； ③等积代换；⑵创造条件 ①添加平行线——创造“A ”字型、“8”字型②先证其它三角形相似——创造边、角条件相似判定条件：两边成比夹角等、两角对应三边比相似终极策略：遇等积，化比例，同侧三点找相似；四共线，无等边，射影平行用等比；四共线，有等边，必有一条可转换；两共线，上下比，过端平行条件边。

彼相似，我角等，两边成比边代换。

3F ED AB C（3）等比代换：若d c b a ,,,是四条线段，欲证dc b a =，可先证得fe b a =（fe ,是两条线段）然后证d cf e =，这里把f e 叫做中间比。

①∠ABC=∠ADE ．求证：AB ·AE=AC ·AD②△ABC 中，AB=AC ，△DEF 是等边三角形求证：BDCN=BMCE ．③等边三角形ABC 中，P 为BC 上任一点，AP 的垂直平分线交AB 、AC 于M 、N 两点。

求证：BPPC=BMCN有射影，或平行，等比传递我看行①在Rt △ABC 中，∠BAC=90°，AD ⊥BC 于D ，E为AC 的中点，求证：ABAF=ACDF斜边上面作高线，比例中项一大片②ABCD③梯形ABCD 中，AD两共线，上下比，过端平行条件边。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相似三角形判定A 字型与8字型．
平行线分线段成比例定理：
= = =
一．复习引入：
1、相似三角形的定义：对应角相等，对应边成比例的两个三角形叫做相似三角形。

2、相似三角形的预备定理：如果一条直线平行于三角形的一条边，且这条直线与原三角形的两条边（或其延长线）分别相交，那么所构成的三角形与原三角形相似。

3、判定定理1：两角对应相等，两三角形相似。

4、判定定理2：两边对应成比例且夹角相等，两三角形相似。

5、判定定理3：三边对应成比例，两三角形相似。

6．相似三角形中的基本图形．（1）平行型：（A 型，8型）
= = = = =
（2）交错型：
（3）旋转型：（4）母子三角形：
1．已知2
1=b a ，则b a a
+的
值为（）
A B
C D E
A B C D E A B C D E A B C D D
A B
C D A B C
E
F
A B C
D E a b c
A B C D E
（A ）
21 （B ）32 （C ）31 （D ）4
3
2．如图，D ，E 分别是△ABC 的边AB ，AC 上的点，DE ∥BC ，如果
2
3
=DB AD ，AE=15，那么EC 的长是（）
（A ） 10 （B ） 22. 5 （C ） 25 （D ） 6
3．如图，DE 是三角形ABC 的中位线，△ADE 的面积为3cm 2
，则梯形DBCE 的面积为（）
A 、6cm 2
B 、9cm 2
C 、12cm 2
D 、24cm 2
4．如图，E 是平行四边形ABCD 的边AD 上的点，AE ＝2
1
ED ，BE 交AC 于F ，则
FC
AF
＝（） A 、21 B 、31 C 、32 D 、4
1
5．如图FD ∥BC ，FB ∥AC ，5
3=BC FE ，则
FB AD
＝（） A 、5
2 B 、5
3 C 、32
D 、85
6．梯形ABCD 的两腰AD 和BC 延长相交于点E ，若两底的长度分别为12和8，梯形ABCD 的面积等于90，则△DCE 的面积为（）
A 、50
B 、64
C 、72
D 、50
7．如图，E 是AC 的中点，C 是BD 的中点，则
ED
FE
＝（） A 、21 B 、31 C 、32 D 、4
1
8．如图，在梯形ABCD 中，AB ∥CD ，AB ＝3CD ，E 为对角线AC 的中点，直线BE 交AD 于
点F ，则AF ∶FD 的值等于（） A 、2 B 、
35 C 、2
3
D 、1
9.若G 为BC 中点,EG 交AB 于点F,且EF:FG=2:3,求AF:FB 的值.
A
B
C
D
E
A B
C
D
E
F
E
C A
D
B E
F
D C
B
A
F
E D
C
B
A
D
F
E
C
B A。