云南省楚雄州普通高中2015-2016学年高二下学期期末考试数学文试题 Word版(含答案)
云南省楚雄彝族自治州高二下学期期末数学试卷

云南省楚雄彝族自治州高二下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共16分)1. (3分) (2019高二上·柳林期末) 命题“存在实数x、y,使得2x+3y≥2”,用符号表示为________;此命题的否定是________(用符号表示)是________(选填“真”或“假”)命题.2. (1分) (2016高一上·宜春期中) 函数f(x)= 的定义域为________.3. (1分)设全集I={x||x|<4且x∈Z},S={-2,1,3},若∁IP⊆S,则这样的集合P共有________个.4. (1分)三位同学参加跳高、跳远、铅球项目的比赛.若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是________.5. (1分) (2016高二上·沭阳期中) 命题“p:x﹣1=0”是命题“q:(x﹣1)(x+2)=0”的________条件.(填:“充分不必要”、“必要不充分”、“充要条件”、“既不充分也不必要”)6. (1分)若函数f(x)=x2﹣lnx+1在其定义域内的一个子区间(a﹣1,a+1)内存在极值,则实数a的取值范围________7. (1分) (2017高二上·乐山期末) 已知命题p:方程 + =1表示焦点在y轴上的椭圆,命题q:双曲线﹣ =1的离心率e∈(,),若命题p、q中有且只有一个为真命题,则实数m的取值范围是________8. (1分) (2019高一上·惠来月考) 已知函数对于任意实数满足条件,若,则 f(7) ________.9. (1分) (2019高二下·吉林期中) 函数的最大值为________.10. (1分) (2019高一上·吐鲁番月考) 已知函数,求的最大值________.11. (1分)已知函数的图像与直线相切,则实数的值为________12. (1分)已知函数 ,若 ,则实数的取值范围是________13. (1分)若在区间[0,1]上存在实数x使2x(3x+a)<1成立,则a的取值范围是________14. (1分)已知函数f(x)=有两个零点,则实数a的取值范围是________二、解答题 (共10题;共95分)15. (5分) (2016高一上·呼和浩特期中) 已知集合A={x|x2﹣5x+6=0},B={x|mx﹣1=0},且A∩B=B,求由实数m所构成的集合M,并写出M的所有子集.16. (5分)函数f(x)=x2﹣x﹣2,x∈[﹣5,5],设任意x0∈[﹣5,5]使f(x0)≤0的概率为P,求P的值.17. (10分)(2020·甘肃模拟) 设椭圆的右焦点为,离心率为,过点且与轴垂直的直线被椭圆截得的线段长为 .(1)求椭圆的方程;(2)若上存在两点,椭圆上存在两个点满足:三点共线,三点共线,且,求四边形的面积的最小值.18. (10分) (2016高一下·漳州期末) 随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2 ,人行道的宽度分别为4m和10m.(1)若休闲区的长A1B1=x m,求公园ABCD所占面积S关于x的函数S(x)的解析式;(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?19. (15分) (2018高三上·信阳期中) 已知函数f(x)=log2(1+x)+alog2(1﹣x)(a∈R)的图象关于y 轴对称.(1)求函数f(x)的定义域;(2)求a的值;(3)若函数g(x)=x﹣2f(x)﹣2t有两个不同的零点,求实数t的取值范围.20. (10分) (2016高三上·洛宁期中) 已知函数f(x)=lnx﹣有两个零点x1、x2 .(1)求k的取值范围;(2)求证:x1+x2>.21. (5分)函数f(x)= +lnx是[1,+∞)上的增函数.(Ⅰ)求正实数a的取值范围;(Ⅱ)若函数g(x)=x2+2x,在使g(x)≥M对定义域内的任意x值恒成立的所有常数M中,我们把M的最大值M=﹣1叫做f(x)=x2+2x的下确界,若函数f(x)= +lnx的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.(Ⅲ)设b>0,a>1,求证:ln >.22. (10分)(2020·江苏模拟) 对有个元素的总体进行抽样,先将总体分成两个子总体和(是给定的正整数,且),再从每个子总体中各随机抽取2个元素组成样本.用表示元素和同时出现在样本中的概率.(1)求的表达式(用m,n表示);(2)求所有的和.23. (10分) (2018高二下·抚顺期末) 某校从6名学生会干部(其中男生4人,女生2人)中选3人参加青年联合会志愿者。
楚雄高二期末考试卷子

楚雄高二期末考试卷子一、语文部分1. 阅读理解:阅读以下文章,回答文后问题。
(文章内容略)问题:(1)请概括文章的主要内容。
(2)文章中作者通过哪些细节描写来表现主人公的性格特点?(3)文章的结尾部分有何深意?请结合全文进行分析。
2. 作文:请以“我眼中的家乡”为题,写一篇不少于800字的作文。
要求内容真实,情感真挚,能够反映出家乡的自然风光、人文特色或社会发展。
二、数学部分1. 选择题:(1)下列哪个选项是二次方程的根?A. 1B. -1C. 2D. 32. 解答题:(1)证明:若a,b,c为实数,且满足a^2 + b^2 = c^2,则a,b,c构成直角三角形的三边。
三、英语部分1. 阅读理解:阅读以下短文,回答文后问题。
(文章内容略)问题:(1)What is the main idea of the passage?(2)According to the passage, what are the characteristics of a good leader?2. 写作:Write an essay on the topic "The Importance of Learning English". Your essay should be at least 200 words and include an introduction, body and conclusion.四、物理部分1. 选择题:(1)下列关于牛顿第二定律的描述,哪个是正确的?A. F=maB. F=mvC. F=ma^2D. F=ma^32. 实验题:设计一个实验,验证牛顿第三定律。
请描述实验的步骤,并解释实验结果。
五、化学部分1. 选择题:(1)下列哪个反应是氧化还原反应?A. 2H2O + O2 → 2H2O2B. 2H2 + O2 → 2H2OC. 2CO + O2 → 2CO2D. 2H2O + CO2 → H2CO3 + H2O2. 计算题:给定一个化学反应方程式:2H2 + O2 → 2H2O。
2015─2016学年下学期高二期末考试数学试卷(文科含答案)

2015─2016学年高二下学期期末考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集}5,4,3,2,1{=U ,集合}5,3,1{=A ,集合}4,3{=B ,则B A C U )(=( ) A .}3{ B .}4{ C .}4,32{, D .}5,4,31{, 2.若复数z 满足i i z 2)1(=-(i 为虚数单位),则||z =( ) A .1 B .2 C .3 D .2 3.一个球的体积是π36,那么这个球的表面积为( ) A .π8 B .π12 C .π16 D .π36 4.设抛物线的顶点在原点,准线方程为x =2,则抛物线的方程是( ) A .x y 82-= B .x y 42-= C .x y 42= D .x y 82=5.若R y x ∈,,且⎪⎩⎪⎨⎧≥≥+-≥x y y x x 0321,则y x z -=2的最小值等于 ( )A .1-B .0C .1D .36.将两个数5=a ,12=b 交换,使12=a ,5=b ,下面语句正确一组是 ( )7.某三棱锥的三视图如右图示,则该三棱锥的体积是( )A .8B .332C .340D . 328.已知下表是x 与y 之间的一组数据:则y 与x 的线性回归方程为a bx y+=ˆ必过点( ) A .)(3,23 B .)(4,23C .)3,2(D . )(4,29.已知某函数图象的一部分如右图示,则函数的解析式可能是( )A .y =cos(2x -错误!)B .y =sin (2x -错误!)C .y =cos(4x -错误!)D .y =sin (x +错误!)10.已知双曲线)0,0(12222>>=-b a b y a x 的离心率为26,则其渐近线方程为( )A .x y 21±= B .x y 22±= C .x y 2±= D . x y 2±= 11.将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每涨价1元,其销售量就要减少20个,为了获得最大利润,每个售价应定为( ) A .95元 B .100元 C .105元 D . 110元 12.已知数列}{n a 各项均不为0,其前n 项和为n S ,且对任意*N n ∈都有n n pa p S p -=-)1(的常数)为大于(1p ,则n a = ( )A .1)12(--n p p B .1)12(--n pp p C .1-n p D .n p 第Ⅱ卷二、填空题:(本大题共4小题,每小题5分,共20分)13.圆042422=-+-+y x y x 的圆心和半径分别是____________________;14.在等比数列}{n a 中,若2a ,10a 是方程091132=+-x x 的两根,则6a 的值是______; 15.已知向量),4(m a =,)2,1(-=b ,若b a ⊥,则=-||b a ____________; 16.己知)(x f y =是定义在R 上的奇函数,当0<x 时,2)(+=x x f ,那么不等式01)(2<-x f 的解集是______________.三、解答题:(本大题共6小题, 17~21题每题12分,22题10分,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)已知a 、b 、c 是△ABC 中A 、B 、C 的对边,S 是△ABC 的面积.若a =4,b =5, S =53,求c 的长度.18.(本小题满分12分)为了了解云南各景点在大众人群中的熟知度,随机对15~65岁的人群抽取了n 人回答问题“云南省有哪几个著名的旅游景点?”统计结果如下图表所示.(1)分别求出表中a ,b ,x ,y 的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.组号分组回答正确的人数 回答正确的人数 占本组的频率第1组 [15,25) a 0。
云南省楚雄州普通高中高二数学下学期期末教学质量检测试题文

2015年楚雄州普通高中学年末教学质量检测高二文科数学试题(考试时间:120分钟)第Ⅰ卷(选择题60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) (1)若集合{1234}A =,,,,{2478}{1,3,4,5,9}B C ==,,,,,则集合A ∩C=(A) {2,4} (B) {1,3,4} (C) {4} (D) {1,2,3,4,5,9} (2)复数21i-化简的结果为 (A )1i + (B )1i -+ (C )1i - (D )1i -- (3)已知2(2,1),(1,1)a a b k =+=-,则“k=2”是“a b ⊥”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件(4)若实数x ,y 满足则y+2x 的最大值是(A )7 (B ) 6 (C ) 4 (D ) 3(5)执行如图所示程序框图所表达的算法,若输出的x 值为48,则输入的x 值为(A )3 (B )6 (C ) 8 (D )12(6根据上表,得回归直线方程为=10.5x+a ,则a= (A )1 (B )1.5 (C )2 (D )2.5(7)抛物线y=8x 2的准线方程是(A)=-2x (B)=-y 2 (C)=-116X (D)=-1y 32(8)函数y=x 3﹣x 2﹣x 的单调递增区间为(A) 1,13⎡⎤-⎢⎥⎣⎦ (B)⎡⎤⎢⎥⎣⎦1-1,3(C)1,3⎛⎤-∞- ⎥⎝⎦,或[)∞1,+ (D)(],-∞-1,或13⎡⎫∞⎪⎢⎣⎭,+(9)如图,已知网格纸上所有小正方形的边长为1,粗实线画出的是某多面体的三视图,则该几何体的体积为 (A) 64 (B)1603 (C) 80 (D) 1763(10)已知△ABC 的三顶点坐标为A (3,0),B (0,4),C (0,0),D 点的坐标为(2,0),向△ABC 内部投一点,那么点落在△ABD 内的概率为(A )16 (B )12 (C )14 (D )31 (11)在△ABC 中,若3t a n 4A =,则s i n ()s i n ()c o s (2)c o s ()=22BC B C ππππ-++-- (A )45 (B )45-(C )35(D )35-(12)已知定义域为R 的奇函数)(x f y =的导函数为)(x f y '=,当0≠x 时,0)()(>+'x x f x f ,若)21(21f a =,)2(2--=f b ,)21(ln )21(ln f c =,则c b a ,,的大小关系正确的是(A) a>b>c (B) a>c>b (C) c>a>b (D) b>c>a第Ⅱ卷(非选择题90分)二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上)(13)双曲线y 2-x 2=1的渐近线方程是 . (14) 设f (x )=,则f (f (5))= .(15) 在等差数列{a n }中,2632a a π+=,则= .(16) 设a 为实数,函数x a ax x x f )3()(23-++=的导函数为)('x f ,且)('x f 是偶函数,则曲线)(x f y=在点))2(,2(f 处的切线方程为 .三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤)(17)(本小题满分10分) 在平面直角坐标系xOy 中,以坐标原点为极点,以x 轴的非负半轴为极轴,建立极坐标系,已知直线l 的参数方程为⎩⎨⎧=+=ty tx 2(t 为参数),圆C 的极坐标方程为ρ=1.(Ⅰ)求直线l 与圆C 的公共点的个数;(Ⅱ)在平面直角坐标中,圆C 经过伸缩变换⎩⎨⎧='='yy xx 2得到曲线C ',设M (),y x 为曲线C '上一点,求422y xy x ++的最大值,并求相应点M 的坐标.(18)(本小题满分12分2是1a 和318a -的等差中项. (I )求数列{}n a 的通项公式;(II )若数列{}n a 是递减数列,且2log n n n b a a =+,求数列{}n b 的前n 项和n S .(19)(本小题满分12分)已知多面体ABCDE 中,DE ⊥平面ACD ,AB ∥DE ,AC=AD=CD=DE =2,AB =1,O 为CD 的中点.(I )求证:AO ⊥平面CDE ; (II )求证:AO ∥平面BCE.(20)(本小题满分12分) 为让消费者发现最值得信赖的商家,使消费者享受超低折扣的优质服务,“美团网”对某地随机抽查100户商家一个月的销售状况和质量进行调查。
云南省楚雄彝族自治州高二下学期数学期末考试试卷

云南省楚雄彝族自治州高二下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2016高二下·佛山期末) 设集合A={x|0≤x≤6},集合B={x|3x2+2x﹣8≤0},则A∪B=()A . [0, ]B . [﹣2, ]C . [0,6]D . [﹣2,6]2. (2分)已知扇形的周长是4cm,则扇形面积最大是()A . 2B . 1C .D . 33. (2分) (2015高二下·遵义期中) 复数z=1﹣i,则 =()A .B .C .D .4. (2分)对于函数,下列命题:①函数图象关于直线对称; ②函数图象关于点(,0)对称;③函数图象可看作是把y=sin2x的图象向左平移个单位而得到;④函数图象可看作是把y=sin(x+)的图象上所有点的横坐标缩短到原来的倍(纵坐标不变)而得到;其中正确的命题的个数是()A . 0B . 1C . 2D . 35. (2分) (2017·惠东模拟) 在△ABC中,,,则的值为()A . 3B . ﹣3C .D .6. (2分)已知映射f:A→B,其中B=R,对应法则:f:x→y=log0.5(2﹣x)﹣,对于实数k∈B,在集合A中不存在原象,则k的取值范围是()A . k>0B . k<1C . k<0D . 以上都不对7. (2分) (2015高二下·思南期中) (1+3x)n(其中n∈N且n≥6)的展开式中x5与x6的系数相等,则n=()A . 6B . 7C . 8D . 98. (2分)(2017·黑龙江模拟) 设函数f(x)满足2x2f(x)+x3f′(x)=ex , f(2)= ,则x∈[2,+∞)时,f(x)()A . 有最大值B . 有最小值C . 有最大值D . 有最小值9. (2分)在直角坐标系中,直线的倾斜角是()A .B .C .D .10. (2分)已知函数的图像在点A(1,f(1))处的切线l与直线平行,若数列的前项和为,则的值为()A .B .C .D .二、填空题 (共7题;共7分)11. (1分) (2019高一下·阜新月考) 如图,在矩形ABCD中,边AB=5,AD=1,点P为边AB上一动点,当∠DPC 最大时,线段AP的长为________.12. (1分) (2019高一上·新疆月考) 已知是定义在上的偶函数,且时,,则 ________.13. (1分)(2017·山东模拟) 已知等腰直角三角形BCD中,斜边BD长为2 ,E为边CD上的点,F为边BC上的点,且满足:,,若 = ,则实数λ=________.14. (1分)设随机变量X的分布列为P(X=k)= ,其中k=1,2,3,…,n,则常数a等于________15. (1分) (2016高二上·杨浦期中) 以AB为直径的半圆,| |=2,O为圆心,C是上靠近点A的三等分点,F是上的某一点,若∥ ,则 =________.16. (1分) (2019高一上·金华期末) 已知函数,若存在实数,使得成立,则实数的取值范围是________.17. (1分) (2016高一下·义乌期末) 已知函数f(x)=x2﹣mx+1﹣m2 ,若|f(x)|在[0,1]上单调递增,则实数m的取值范围________.三、解答题 (共5题;共45分)18. (5分)设函数f(x)=sinx+cosx(x∈R).求函数f(x)的最小正周期和最值;19. (10分) (2016高二下·三门峡期中) 某学校为了丰富学生的业余生活,以班级为单位组织学生开展古诗词背诵比赛,随机抽取题目,背诵正确加10分,背诵错误减10分,只有“正确”和“错误”两种结果,其中某班级的正确率为,背诵错误的概率为,现记“该班级完成n首背诵后总得分为Sn”.(1)求S6=20且Si≥0(i=1,2,3)的概率;(2)记ξ=|S5|,求ξ的分布列及数学期望.20. (10分) (2016高一上·六安期中) 若函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)写出函数f(x)(x∈R)的解析式.(2)若函数g(x)=f(x)+(4﹣2a)x+2(x∈[1,2]),求函数g(x)的最小值h(a).21. (10分) (2015高二下·福州期中) 已知a1= (n∈N*)(1)求a2,a3,a4并由此猜想数列{an}的通项公式an的表达式;(2)用数学归纳法证明你的猜想.22. (10分)已知函数f(x)=lnx+x.(1)求函数f(x)在点(1,f(1))处的切线方程;(2)若方程f(x)=mx在区间[1,e2]内有唯一实数解,求实数m的取值范围.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共45分) 18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。
2016-2017学年云南省楚雄州高二下学期期末考试数学(文)试题-解析版

云南省楚雄州2016-2017学年高二下学期期末考试数学(文)试题一、选择题1.设集合U={-1,0,1,2,3,4,5}, A={1,2,3}, B={-1,0,1,2},则A∩(C U B)= A. {1,2,3} B. {3} C. {1,2} D. {2} 【答案】B【解析】{}{}{}1,0,1,2,3,4,5,?1,2,3,?1,0,1,2U A B =-==-.{}3,4,5U C B =, (){}3U A C B ⋂=.故选B.2.已知i 为虚数单位,则复数1ii+= A. 1+i B. 1-i C. 12i + D. 12i - 【答案】B 【解析】()211111i i i ii i i ++-+===-+-. 故选B.3.设:12,:21xp x q <,则p 是q 成立的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】A【解析】试题分析:由指数函数的性质可知,当必有,所以的充分条件,而当时,可得,此时不一定有,所以的不必要条件,综上所述,的充分而不必要条件,所以正确选项为A.考点:充分条件与必要条件. 【方法点睛】判断p 是不是q 的充分(必要或者充要)条件,遵循充分必要条件的定义,当p 成立时, q 也成立,就说p 是q 的充分条件,否则称为不充分条件;而当q 成立时, p 也成立则p 是q 的必要条件,否则称为不必要条件;当p 能证明q 的同时q 也能证明p ,则p 是q 的充分条件.4.已知抛物线24x y =上一点A 纵坐标为4,则点A 到抛物线焦点的距离为( ) A.10 B. 4 C. 5 D. 15【答案】C【解析】抛物线24x y =的准线方程为1y =-,点A 到准线的距离为5,根据抛物线定义可知点A 到焦点的距离为5.故选择C.5.正项数列{a n }成等比数列,a 1+a 2=3,a 3+a 4=12,则a 4+a 5的值是 A. -24 B. 21 C. 48 D. 24 【答案】D【解析】正项数列{a n }成等比数列,234124a a q a a +==+,所以2q =.()345123824a a a a q +=+=⨯=.故选D. 6.已知,2x ππ⎛⎫∈ ⎪⎝⎭,tanx =-43,则 cos (-x-2π)等于A.35 B. -35 C. 45 D. -45【答案】D 【解析】4 3tanx =-, ,2x ππ⎛⎫∈ ⎪⎝⎭,所以45sinx =. 4cos 25x sinx π⎛⎫--=-=- ⎪⎝⎭.故选D.7.设f′(x )是函数f (x )的导函数,y=f′(x )的图象如图所示,则y=f (x )的图象最有可能的是( )A. B.C. D.【答案】C【解析】试题分析:先根据导函数的图象确定导函数大于0 的范围和小于0的x 的范围,进而根据当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减确定原函数的单调增减区间.解:由y=f'(x )的图象易得当x <0或x >2时,f'(x )>0,故函数y=f (x )在区间(﹣∞,0)和(2,+∞)上单调递增;当0<x <2时,f'(x )<0,故函数y=f (x )在区间(0,2)上单调递减; 故选C .考点:函数的单调性与导数的关系. 8.关于函数()[]()22cos 3sin 0,2xf x x x π=+∈,下列结论正确的是 A. 有最大值3,最小值-1 B. 有最大值2,最小值-2 C. 有最大值2,最小值0 D. 有最大值3,最小值0 【答案】D【解析】函数()223132sin 126x f x cos sinx cosx sinx x π⎛⎫=+=++=++ ⎪⎝⎭ []70,,?,666x x ππππ⎡⎤∈+∈⎢⎥⎣⎦.1sin ,162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦.[]2sin 10,36x π⎛⎫++∈ ⎪⎝⎭. 所以有最大值3,最小值0,故选D.9.执行如图程序框图,输出的为( )A. B. C. D. 【答案】A【解析】时,否,所以, 是 ,否,所以,是,, 是,,是, ,否,所以,是, ,否,所以, 是, , 是,,否,输出 ,故选A.10.若函数f(x) = x 3-ax-2在区间(1,+∞)内是增函数,则实数a 的取值范围是A. (],3-∞B. (],9-∞ C. (-1, +∞) D. (-∞,3) 【答案】A【解析】若函数f(x) = x 3-ax-2在区间(1,+∞)内是增函数, 则()230f x x a '=-≥在区间(1,+∞)上恒成立.只需()3?0min f x a =-≥',解得3a ≤.故选A.点睛:利用函数的导数研究函数的单调性有两种题型,一种是求单调区间,只需令导数大于0求增区间,令导数小于0求减区间;另一种是已知函数的单调性求参数,若已知函数单增,只需函数导数在区间上恒大于等于0即可,若已知函数单减,只需函数导数小于等于0即可.注意等号!11.如图,三棱柱A 1B 1C 1 - ABC 中,侧棱AA 1丄底面A 1B 1C 1,底面三角形A 1B 1C 1是正三角形,E 是BC 中点,则下列叙述正确的是A. CC 1与B 1E 是异面直线B. AC 丄平面ABB 1A 1C. A 1C 1∥平面AB 1ED. AE 与B 1C 1为异面直线,且AE 丄B 1C 1 【答案】D【解析】A 不正确,因为CC 1与B 1E 在同一个侧面中,故不是异面直线;B 不正确,由题意知,上底面ABC 是一个正三角形,故不可能存在AC ⊥平面ABB 1A 1;C 不正确,因为A 1 C 1所在的平面与平面A B 1E 相交,且A 1 C 1与交线有公共点,故A 1 C 1∥平面A B 1E 不正确;D 正确,因为AE , B 1 C 1为在两个平行平面中且不平行的两条直线,故它们是异面直线; 故选C.12.过椭圆C: 22221(0)x y a b a b+=>>的左顶点A 且斜率为k 的直线交椭圆C 于另一点B ,且点B 在x 轴上的射影恰好为右焦点F 2,若1132k <<,则椭圆C 的离心率的取值范围是 A. 10,2⎛⎫⎪⎝⎭ B. 12,23⎛⎫⎪⎝⎭ C. 2,13⎛⎫⎪⎝⎭ D. 10,2⎛⎫ ⎪⎝⎭∪2,13⎛⎫ ⎪⎝⎭【答案】B【解析】如图所示: 2222,a c AF a c BF a-=+=,所以()22222tan BF a c k BAF AF a a c -=∠==+, 又因为1132k <<,所以()221132a c a a c -<<+,即2111312e e -<<+,解得1223e <<. 故选B.点睛:一般来说,求椭圆(或双曲线)的离心率的取值范围,通常可以从两个方面来研究:一是考虑几何的大小,例如线段的长度、角的大小等;二是通过设椭圆(或双曲线)点的坐标,利用椭圆(或双曲线)本身的范围,列出不等式.二、填空题13.已知向量a =(1,-1) , b =(6,-4).若a 丄(t a +b),则实数t 的值为____________.【答案】-5【解析】向量a =(1,-1) , b =(6,-4),t a +()t 6,t 4b =+-- .若a 丄(t a+b),则()0a ta b +=,即t 6t 40+++=, 解得: t 5=-.14.若x , y∈ R,且满足1{230 x x y y x≥-+≥≥,则z=2x+3y 的最大值等于_____________.【答案】15【解析】由约束条件作出可行域如图,联立1{230 x x y y x≥-+≥≥,解得B (3,3),化目标函数z =2x +3y 为233z y x =-+, 由图可知,当直线过B 时,直线在y 轴上的截距最大,z 有最大值为2×3+3×3=15.故答案为:15.点睛:本题是常规的线性规划问题,线性规划问题常出现的形式有:①直线型,转化成斜截式比较截距,要注意z 前面的系数为负时,截距越大, z 值越小;②分式型,其几何意义是已知点与未知点的斜率;③平方型,其几何意义是距离,尤其要注意的是最终结果应该是距离的平方;④绝对值型,转化后其几何意义是点到直线的距离. 15.已知ABC ∆三内角,,A B C 对应的边长分别为,,a b c ,且23B π=,又边长3b c =,那么sin C = __________. 【答案】36【解析】根据正弦定理变形3sin 3sin b c B C =⇔=,所以sin 3sin 36B C ==. 16.已知函数()()3,0{1,0x x f x ln x x ≤=+>,若()()22f x f x ->,则实数x 的取值范围是____________.【答案】(-2,1)【解析】∵当x =0时,两个表达式对应的函数值都为零 ∴函数的图象是一条连续的曲线∵当x ⩽0时,函数f (x )= 3x 为增函数;当x >0时,f (x )=ln(x +1)也是增函数 ∴函数f (x )是定义在R 上的增函数因此,不等式()()22f x f x ->等价于22x ->x ,即2x +x −2<0,解之得−2<x <1, 答案为:(-2,1)三、解答题17.选修44-:坐标系与参数方程选讲在直角坐标系xoy 中,直线l 的参数方程为232{ 252x t y t=-=+(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为25sin ρθ=.(Ⅰ)求圆C 的圆心到直线l 的距离;(Ⅱ)设圆C 与直线l 交于点A B 、,若点P 的坐标为()3,5,求PA PB +.【答案】(1)530x y +--=,(2)32 .【解析】(Ⅰ)∵:25sin C ρθ= ∴2:25sin C ρρθ= ∴22:250C x y y +-=,即圆C 的标准方程为()2255x y +-=.直线l 的普通方程为530x y +--=.所以,圆C 的圆心到直线l 的距离为05533222+--=. (Ⅱ)由2(5{53y x y x +==-++,解得1{52x y ==+或2{51x y ==+()()()()2222315523255132PA PB +=-+--+-+--=18.在等差数列{a n }中,a 1 =-2,a 12 =20. (1)求数列{a n }的通项a n ; (2)若b n =12a a a n n+++ ,求数列{3n b}的前n 项和.【答案】(1)24n a n =-;(2)3118n n S -=.【解析】试题分析:(1)先求出公差,再利用等差数列通项公式求解即可; (2)计算等差数列{a n }的前n 项和a 1+a 2+…+a n =n(n-3),得b n =12a a a nn+++ = n-3,令c n =3n b =3n-3,利用等比数列求和公式求和即可. 试题解析:(1)因为a n =-2+(n-1)d ,所以a 12=-2+11d=20,所以d=2,所以24n a n =-. (2)因为24n a n =-,所以a 1+a 2+…+a n =n(n-3),所以b n =12a a a nn+++ = n-3.令c n =3n b,则c n =3n-3,显然数列{c n }是等比数列,且c 1=3-2,公比q=3,所以数列{3nb }的前n 项和为3118n n S -=.19.如图所示,已知AB 丄平面BCD ,M 、N 分别是AC 、AD 的中点,BC 丄 CD.(1)求证:MN//平面BCD;(2)若AB=1,BC=3,求直线AC与平面BCD所成的角.【答案】(1)见解析;(2)30°.【解析】试题分析:(1)由中位线定理可得MN∥CD,进而得线面平行;(2)由AB⊥平面BCD,知∠ACB为直线AC与平面BCD所成的角,在直角△ABC中求解即可.试题解析:证明:(1)∵M,N分别是AC,AD的中点,∴MN∥CD.∵MN⊄平面BCD且CD⊂平面BCD,∴MN∥平面BCD.(2)∵AB⊥平面BCD,∴∠ACB为直线AC与平面BCD所成的角.在直角△ABC中,AB=1,BC=3,∴tan∠ACB=33ABBC.∴∠ACB=30°.故直线AC与平面BCD所成的角为30°.点睛:求直线和平面所成角的关键是作出这个平面的垂线进而斜线和射影所成角即为所求,有时当垂线较为难找时也可以借助于三棱锥的等体积法求得垂线长,进而用垂线长比上斜线长可求得所成角的正弦值,当空间关系较为复杂时也可以建立空间直角坐标系,利用向量求解.20.某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在20〜60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.年龄分组抽取份数答对全卷的人数答对全卷的人数占本组的概率[20,30)40280.7 [30,40)n270.9 [40,50)104b [50,60]20a0.1(1)分别求出n , a , b , c 的值;(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率. 【答案】(1)30,2,0.4,0.02n a b c ====;(2)35. 【解析】试题分析:(1)根据频率直方分布图,通过概率的和为1,求求出n ,a ,b ,c 的值,(2)年龄在[40,50)中答对全卷的4人记为A ,B ,C ,D ,年龄在[50,60]中答对全卷的2人记为a ,b ,分别列举出所有的基本事件,根据概率公式计算即可. 试题解析:(1)因为抽取总问卷为100份,所以n=100-(40+10+20)=30.年龄在[)40,50中,抽取份数为10份,答对全卷人数为4人,所以b=410=0.4. 年龄在[]50,60中,抽取份数为20份,答对全卷人数占本组的概率为0.1,所以20a=0.1,得2a =.根据频率直方分布图,得(0.04+0.03+c+0.01)×10=1,解得0.02c =.(2)因为年龄在[)40,50与中答对全卷的人数分别为4人与2人.年龄在[)40,50中答对全卷的4人记为1a , 2a , 3a , 4a ,年龄在中答对全卷的2人记为1b , 2b ,则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是: ()12,a a , ()13,a a , ()14,a a , ()11,a b , ()12,a b , ()23,a a , ()24,a a ,()21,a b , ()22,a b , ()34,a a , ()31,a b , ()32,a b , ()41,a b , ()42,a b , ()12,b b ,共15种(8分). 其中所抽取年龄在的人中至少有1人被授予“环保之星”的情况是: ()11,a b ,()12,a b , ()21,a b , ()22,a b , ()31,a b , ()32,a b , ()41,a b , ()42,a b , ()12,b b 共9种.故所求的概率为.21.已知椭圆C 1: ,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率.(1)求椭圆Q 的方程;(2)设0为坐标原点,点A ,B 分别在椭圆C 1和C 2上,,求直线AB 的方程.【答案】(1);(2)或.【解析】(1)由已知可设椭圆C 2的方程为=1(a >2),其离心率为,故=,解得a =4.故椭圆C 2的方程为=1.(2)A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ), 由=2及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入+y 2=1中,得(1+4k 2)x 2=4,所以.将y =kx 代入=1中,得(4+k 2)x 2=16,所以.又由=2,得,∴,解得k =±1.故直线AB 的方程为y =x 或y =-x .22.已知函数()()3xf x a bx e =-, ()ln xg x x=,且函数()f x 的图象在点()1,e 处的切线与直线210ex y +-=平行. (1)求,a b ;(2)求证:当()0,1x ∈时, ()()2f x g x ->. 【答案】(1)a 2,b 1==;(2)见解析. 【解析】试题分析:第一问考查导数几何意义,利用()()12,1f e f e '=-=,第二问证明题转化为函数最值问题,注意指对分离,利用左侧函数最小值大于右侧函数最大值. 解:(1)∵()1f e =,故()a b e e -=,故1a b -=,①依题意, ()'12f e =-,又()()23'32xf x x x e =--+,故42a b -=-②联立①②解得2a =, 1b =(2)证明:要证()()2f x g x ->,即证3ln 22x x x e e x x->+令()32xx h x e e x =-11 ∴()()()()322'32122x x h x e x x e x x x =--+=-++-故当()0,1x ∈时, 0,10x ex -+; 令()222p x x x =+-,∵()p x 的对称轴为1x =-,且()()010p p ⋅<故存在()00,1x ∈,使得()00p x =故当()00,x x ∈时, ()2220p x x x =+-<, 故()()()2'1220x h x e x x x =-++->,即()h x 在()00,x 上单调递增当()0,1x x ∈时, ()2220p x x x =+->,故()()()2'1220x h x ex x x =-++-<即()h x 在()0,1x 上单调递减又∵()02h =, ()1h e =故当()0,1x ∈时, ()()02h x h >= 又当()0,1x ∈时,ln 0x x <, ∴ln 22x x+< ∴3ln 22x x x e e x x ->+,即()()2f x g x ->. 点睛:证明函数()()2f x g x ->,可转化为证明3ln 22x x x e e x x->+,证左侧最小值大于右侧最大值,巧妙地进行指对函数分离.。
2015年楚雄州普通高中高二物理

………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○…………2015年楚雄州普通高中学年末教学质量检测高二物理试题第I 卷(选择题)一、选择题:本大题共12小题,共40分。
在每小题给出的四个选项中,第1-8题只有一项符合题目要求,第9-12题有多项符合题目要求。
第1-8题选对的得3分,选错或不选的得0分,第9-12题全部选对的得4分,选对但不全的得2分,选错或不选的得0分)1、将两个分别带有电荷量-2Q 和+5Q 的相同金属小球A 、B 分别固定在相距为r 的两处(均可视为点电荷),它们间库仑力的大小为F .现将第三个与A 、B 两小球完全相同的不带电小球C 先后与A 、B 相互接触后拿走,A 、B 间距离保持不变,则两球间库仑力的大小为( )A .F B.15F C.910F D.14F2、如图所示,实线为不知方向的三条电场线,从电场中M 点以相同速度垂直于电场线方向飞出a 、b 两个带电粒子,仅在电场力作用下的运动轨迹如图中虚线所示.则( )A .a 一定带正电,b 一定带负电B .a 的速度将减小,b 的速度将增加C .a 的加速度将减小,b 的加速度将增加D .两个粒子的动能,一个增大、一个减小3、一个带正电的质点,电荷量为q =2.0×10-9C ,在静电场中由a 点移到b 点,在这个过程中,除静电力做功外,其他力做的功为 6.0×10-5J ,质点的动能增加了8.0×10-5J ,则a 、b 两点间的电势差U ab 为( )A .3×104V B .1×104V C .4×104V D .7×104V 4、半径为r 的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A 点以速度v 0垂直于磁场方向射入磁场中,并从B 点射出.∠AOB =120°,如图所示,则该带电粒子在磁场中运动的时间为( )A.2πr 3v 0 B.23πr 3v 0 C.πr 3v 0 D.3πr3v 05、如图所示,有一个有界匀强磁场区域,磁场方向垂直纸面向外,一个闭合的矩形导线框abcd ,沿纸面由位置1(左)匀速运动到位置2(右),则( )A .导线框进入磁场时,感应电流的方向为a →b →c →d →aB .导线框离开磁场时,感应电流的方向为a →d →c →b →aC .导线框离开磁场时,受到的安培力水平向右D .导线框进入磁场时,受到的安培力水平向左6、在竖直方向的匀强磁场中,水平放置一圆形导体环。
云南省楚雄州2015-2016学年高二下学期期末数学试卷(文科) 含解析

2015-2016学年云南省楚雄州高二(下)期末数学试卷(文科)一、选择题(本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)2.=( )A.1+2i B.﹣1+2i C.1﹣2i D.﹣1﹣2i3.已知命题p、q,“¬p为真”是“p∧q为假”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.已知=(1,﹣1),=(﹣1,2)则(2+)•=()A.﹣1 B.0 C.1 D.25.等差数列{a n}的公差为2,若a2,a4,a8成等比数列,则{a n}的前10项和S10=()A.110 B.99 C.55 D.456.某三棱锥的三视图如图所示,则该三棱锥的体积是()A.B. C. D.17.过抛物线y=2x2的焦点且垂直于它的对称轴的直线被它切得的弦长为()A.2 B.1 C.0。
25 D.0.58.一个算法程序如图所示,则输出的n的值为()A.6 B.5 C.4 D.39.已知函数f(x)=x2﹣2x+b在区间(2,4)内有唯一零点,则b的取值范围是( )A.R B.(﹣∞,0)C.(﹣8,+∞)D.(﹣8,0)10.若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是( )A.(﹣∞,﹣2] B.(﹣∞,﹣1]C.[2,+∞)D.[1,+∞)11.设F1,F2是双曲线(a>0,b>0)的两个焦点,点P在双曲线上,若•=0 且||||=2ac(c=),则双曲线的离心率为()A.B. C.2 D.12.已知函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f(﹣x)•x>0的解集是( )A.(﹣1,0)∪(0,1)B.(﹣1,1)C.(﹣3,﹣1)∪(0,1)D.(﹣1,0)∪(1,3)二、填空题(本大题共4个小题,每小题5分,共20分。
云南省楚雄彝族自治州高二下学期期末数学试卷(文科)

云南省楚雄彝族自治州高二下学期期末数学试卷(文科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)“”是“”的()A . 充要条件B . 必要而不充分条件C . 充分而不必要条件D . 既不充分也不必要2. (2分)集合,,则()A .B .C .D .3. (2分) (2019高二上·开封期中) 设命题若函数是减函数,则,命题若函数在上是单调递增,则 .那么下列命题为真命题的是()A .B .C .D .4. (2分) (2016高一上·金台期中) 设a=log36,a=log510,a=log714,则()A . a>b>cB . a>c>bC . c>a>bD . c>b>a5. (2分)已知函数f(x)=kax﹣a﹣x(a>0且a≠1)在R上是奇函数,且是增函数,则函数g(x)=loga (x﹣k)的大致图象是()A .B .C .D .6. (2分) (2016高一上·普宁期中) 幂函数y=f(x)经过点(3,),则f(x)是()A . 偶函数,且在(0,+∞)上是增函数B . 偶函数,且在(0,+∞)上是减函数C . 奇函数,且在(0,+∞)是减函数D . 非奇非偶函数,且在(0,+∞)上是增函数7. (2分) (2016高一上·济南期中) 已知定义在R上的奇函数f(x)满足f(x+2)=﹣f(x),则,f(2016)的值为()A . ﹣1B . 0C . 1D . 28. (2分)已知函数f(x)=lnx﹣x+﹣1,g(x)=x2﹣2bx+4,若对任意的x1∈(0,2)存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是()A . [,+∞)B . (﹣∞,]C . (﹣∞,2]D . [2,+∞)9. (2分) (2018高三上·长春期中) 设函数f ′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf ′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是()A . (-∞,-1)∪(0,1)B . (-1,0)∪(1,+∞)C . (-∞,-1)∪(-1,0)D . (0,1)∪(1,+∞)10. (2分)(2017·成都模拟) 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)在区间(a,b)内的极小值点的个数为()A . 1B . 2C . 3D . 411. (2分) (2017高一上·吉林月考) 如果函数在区间上是减函数,那么实数的取值范围是()A .B .C .D .12. (2分)函数,下列结论不正确的()A . 此函数为偶函数.B . 此函数是周期函数.C . 此函数既有最大值也有最小值.D . 方程f[f(x)]=1的解为x=1.二、填空题 (共4题;共4分)13. (1分)已知函数f(x)=lgx,若f(ab)=1,则f(a2)+f(b2)=________14. (1分)已知函数 f(x)=ax3+f'(2)x2+3,若 f'(1)=﹣5,则a=________.15. (1分)用二分法求函数y=f(x)在区间[2,4]上零点的近似解,经验证有f(2)•f(4)<0.取区间的中点为x1=3,计算得f(2)•f(x1)<0,则此时零点x0∈________(填区间)16. (1分) (2016高三上·巨野期中) 对于函数f(x)= ,有下列5个结论:①任取x1 ,x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;②函数y=f(x)在区间[4,5]上单调递增;③f(x)=2kf(x+2k)(k∈N+),对一切x∈[0,+∞)恒成立;④函数y=f(x)﹣ln(x﹣1)有3个零点;⑤若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1 , x2 ,则x1+x2=3.则其中所有正确结论的序号是________.(请写出全部正确结论的序号)三、解答题 (共6题;共55分)17. (15分) (2019高一上·淮南月考) 已知函数 .(1)求函数的值域;(2)设,,,求函数的最小值;(3)对(2)中的,若不等式对于任意的时恒成立,求实数的取值范围.18. (10分)已知a是实数,函数f(x)=x2(x﹣a).(1)若f′(1)=3,求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;(2)若,求f(x)在区间[0,2]上的最大值.19. (5分) (2016高一上·盐城期中) 有甲、乙两种商品,经销这两种商品所获的利润依次为p(万元)和q(万元),它们与投入的资金x(万元)的关系,据经验估计为:p=﹣x2+4x,q=2x今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?20. (10分)(2019·湖北模拟) 设函数 .(1)若函数在区间(为自然对数的底数)上有唯一的零点,求实数的取值范围;(2)若在(为自然对数的底数)上存在一点,使得成立,求实数的取值范围.21. (10分) (2016高三上·宝安模拟) 在平面直角坐标系中,圆C的方程为(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).(1)当m=3时,判断直线l与C的位置关系;(2)当C上有且只有一点到直线l的距离等于时,求C上到直线l距离为2 的点的坐标.22. (5分)(2017·河西模拟) [选修4-4:坐标系与参数方程]在直角坐标系xoy中,曲线C1的参数方程为(β为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ.(Ⅰ)将曲线C1的方程化为极坐标方程;(Ⅱ)已知直线l的参数方程为(<α<π,t为参数,t≠0),l与C1交与点A,l与C2交与点B,且|AB|= ,求α的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9、答案:略10-1、11-1、12、答案:略二、填空题 (共4题;共4分)13、答案:略14-1、15-1、16-1、三、解答题 (共6题;共55分)17-1、17-2、17-3、18-1、18-2、19-1、20-1、20-2、21-1、21-2、22-1、。
2015-2016学年云南省楚雄州高二(下)期末数学试卷(理科)(解析版)

2015-2016学年云南省楚雄州高二(下)期末数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)若集合A={1,2,3,4},B={2,4,7,8},C={1,3,4,5,9},则集合(A ∪B)∩C的子集个数是()A.3B.6C.8D.92.(5分)已知i为虚数单位,且复数z满足z(1+2i)=11+2i,则|z|=()A.5B.C.25D.103.(5分)已知命题p,q,“¬p为假”是“p∨q为真”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(5分)某几何体的三视图如图所示,则它的体积为()A.B.C.2πD.5.(5分)若(ax2﹣)6的展开式中x3的系数是20,则实数a=()A.2B.1C.1或﹣1D.﹣16.(5分)若非零向量,满足||=||,且(﹣)⊥(3+2),则与的夹角为()A.πB.C.D.7.(5分)执行如图所示的程序框图,输出的i的值为()A.3B.4C.5D.68.(5分)函数f(x)=lnx﹣x+2的零点所在的区间为()A.(4,5)B.(1,2)C.(2,3)D.(3,4)9.(5分)在△ABC中,tan B=2,tan C=3,则A=()A.B.C.D.10.(5分)已知等差数列{a n}的前n项和为S n,且S4=32,S8=96,则a3和a11的等比中项为()A.15B.17C.±15D.±1711.(5分)抛物线y2=2px(p>0)的焦点为F,准线为L,A、B是抛物线上的两个动点,且满足∠AFB=.设线段AB的中点M在L上的投影为N,则的最大值是()A.B.1C.D.12.(5分)已知函数f(x)=(x2+ax+b)e x,当b<1时,函数f(x)在(﹣∞,﹣2),(1,+∞)上均为增函数,则的取值范围是()A.(﹣2,]B.[﹣,2)C.(﹣∞,]D.[﹣,2]二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上)13.(5分)若函数f(x)=,则f(f(3))=.14.(5分)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)下面的临界值表供参考:(参考公式K2=其中n=a+b+c+d)则在犯错的概率不超过0.025的前提下认为视觉和空间能力与性别(填“有关”或“无关”).15.(5分)已知a>0,b>0且实数x、y满足条件.若ax+by的最大值为4,则+的最小值为.16.(5分)设F1、F2是双曲线﹣=1(a>0,b>0)的两个焦点,P在双曲线上,若•=0,||•||=2a,则双曲线的离心率为.三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤)17.(10分)已知数列{a n}的前n项和为S n,且S n+2=2a n(n∈N*).(I)求数列{a n}的通项公式;(Ⅱ)设b n=log2a n,数列{}的前n项和为T n,证明:T n<1.18.(12分)在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.(I)根据这500个数据的频率分布直方图,求出这批日光灯管的平均寿命;(Ⅱ)某人从这个批次的灯管中随机地购买了4个进行使用,若以上述频率作为概率,用X表示此人所购买的灯管中优等品的个数,求X的分布列和数学期望.19.(12分)已知平面向量=(sin x,﹣cos x),=(cos x,cos x),函数f(x)=2•+λ,λ∈R.将f(x)的图象向左平移个单位后得到函数g(x)的图象,且g(x)的最大值为.(I)求实数λ的值;(II)在△ABC中,若g(A)=1,a=2且△ABC的面积为2,求b+c的值.20.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面P AB⊥底面ABCD,P A=2,PB=2.(I)求证:AC⊥平面PBD;(II)若∠DAB=60°,求二面角B﹣PD﹣C的余弦值.21.(12分)已知F1、F2分别是离心率为的椭圆C:+=1(a>b>0)的左、右焦点,过F2的直线l交椭圆C于A、B两点,且△ABF1的周长为4.(I)求椭圆C的方程;(II)若△ABF1的面积为,求直线l的方程.22.(12分)已知函数f(x)=﹣x3+x2﹣2x(a∈R).(I)当a=3时,求函数f(x)的单调区间;(II)若过点(0,﹣)可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.2015-2016学年云南省楚雄州高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【解答】解:集合A={1,2,3,4},B={2,4,7,8},C={1,3,4,5,9},∴集合(A∪B)={1,2,3,4,7,8},集合(A∪B)∩C={1,3,4},∴集合(A∪B)∩C的子集个数是23=8.故选:C.2.【解答】解:∵z(1+2i)=11+2i,∴z(1+2i)(1﹣2i)=(11+2i)(1﹣2i),∴5z=15﹣20i,化为z=3﹣4i.则|z|==5.故选:A.3.【解答】解:若¬p为假,则p为真,则p∨q为真,即充分性成立,当p假q真时,满足p∨q为真,但¬p为真,则必要性不成立,则“¬p为假”是“p∨q为真”的充分不必要条件,故选:A.4.【解答】解:由三视图可得,该几何体是由圆锥与半球的组合体,体积为=.故选:B.5.【解答】解:(ax2﹣)6的展开式中的通项公式为T r+1=•a6﹣r•(﹣1)r•x12﹣3r,令12﹣3r=3,求得r=3,可得x3的系数是﹣•a3=20,则实数a=﹣1,故选:D.6.【解答】解:设与的夹角为θ,∵(﹣)⊥(3+2),||=||,∴(﹣)•(3+2)=3﹣﹣2=3•﹣•||cosθ﹣2=0,∴cosθ=,∴θ=,故选:D.7.【解答】解:模拟执行程序,可得a=172,b=﹣84,i=1,a=44,b=﹣20,满足条件|a﹣b|>1,执行循环体,i=2,a=12,b=﹣4满足条件|a﹣b|>1,执行循环体,i=3,a=4,b=0满足条件|a﹣b|>1,执行循环体,i=4,a=2,b=1不满足条件|a﹣b|>1,退出循环,输出i的值为4.故选:B.8.【解答】解:∵f(1)=ln1+1>0,f(2)=ln2>0,f(3)=ln3﹣1>0,f(4)=ln4﹣2<0,f(5)=ln5﹣3<0,∴函数f(x)=lnx﹣x+2的零点所在的区间为(3,4);故选:D.9.【解答】解:△ABC中,∵tan B=2,tan C=3,∴tan(B+C)===﹣1,∴B+C=,则A=π﹣B﹣C=,故选:A.10.【解答】解:设等差数列{a n}的公差为d,∵S4=32,S8=96,∴4a1+d=32,d=96,解得a1=5,d=2.∴a n=5+2(n﹣1)=2n+3.设a3和a11的等比中项为x,则x2=(2×3+3)×(2×11+3)=152,解得x=±15,故选:C.11.【解答】解:设|AF|=a,|BF|=b,连接AF、BF,由抛物线定义,得|AF|=|AQ|,|BF|=|BP|,在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.由余弦定理得,|AB|2=a2+b2﹣2ab cos60°=a2+b2﹣ab,配方得,|AB|2=(a+b)2﹣3ab,又∵ab≤()2,∴(a+b)2﹣3ab≥(a+b)2﹣(a+b)2=(a+b)2得到|AB|≥(a+b).∴≤1,即的最大值为1.故选:B.12.【解答】解:由f′(x)=[x2+(a+2)x+a+b]e x 函数f(x)在(﹣∞,﹣2),(1,+∞)增函数,∴x2+(a+2)x+a+b>0恒成立,,∴,∴b=(z﹣1)a﹣2z,设y=(z﹣1)x﹣2z,,由图象可知在点B(﹣1,﹣1)取最大值为z=,在点A(1,1)取最小值z=﹣2的取值范围为(﹣2,],故答案选:A.二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上)13.【解答】解:∵f(3)=23=8,∴f(f(3))=f(8)=log48==,故答案为:.14.【解答】解:由观测值K2=≈6.349>5.024,∴在犯错的概率不超过0.025的前提下认为视觉和空间能力与性别由关,故答案为:有关.15.【解答】解:画出满足条件的平面区域,如图示:,由,解得:A (1,1),显然直线z =ax +by 过A (1,1)时z 取到最大值4, 此时:a +b =4,+=(+)(a +b )=(2+)≥(2+2)=1,当且仅当a =b =2时“=”成立, 故答案为:1. 16.【解答】解:由题意,⊥,设||=m ,||=n (m >n ),则mn =2ac ,∵m ﹣n =2a ,m 2+n 2=4c 2, ∴4c 2﹣4ac =4a 2, ∴e ﹣2e ﹣1=0, ∵e >1, ∴e =.故答案为:.三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤) 17.【解答】解:(I )由S n +2=2a n , 当n =1时,a 1+2=2a 1,解得a 1=2;当n ≥2时,S n ﹣1+2=2a n ﹣1有a n =2a n ﹣2a n ﹣1,即a n =2a n ﹣1, 所以数列{a n }是以2为首项,2为公比的等比数列, 数列{a n }的通项公式为a n =2×2n ﹣1=2n.(Ⅱ)证明:由(I )得b n =log 22n=n ,所以T n=+++…+=+++…+=﹣+﹣+﹣+…+﹣=1﹣<1.18.【解答】解:(I)根据这500个数据的频率分布直方图,这批日光灯管的平均寿命为50×0.05+150×0.1+250×0.15+350×0.3+450×0.15+550×0.2+650×0.05=392.5天;(Ⅱ)X的所有取值为0,1,2,3,4.由题意,购买一个灯泡,且这个灯泡是次品的概率为0.1+0.15=0.25,从本批次灯泡中购买4个,X表示4个灯泡中次品的个数,则X~B(4,0.25),∴P(X=0)=C40×(1﹣0.25)4=,P(X=1)=C41×0.25×(1﹣0.25)3=,P(X=2)=C42×0.252×(1﹣0.25)2=,P(X=3)=C43×0.253×(1﹣0.25)=P(X=4)=C44×0.254×(1﹣0.25)0=∴随机变量X的分布列为:X的数学期望E(X)=0×+1×+2×+3×+4×=1.19.【解答】解:(I)∵=(sin x,﹣cos x),=(cos x,cos x),函数f(x)=2•+λ,λ∈R.∴f(x)=2•+λ=2sin x cos x﹣2cos2x+λ=sin2x﹣cos2x+λ﹣1=sin(2x﹣)+λ﹣1,∵将f(x)的图象向左平移个单位后得到函数g(x)的图象,、∴g(x)=f(x+)=sin(2x+)+λ﹣1,∵g(x)的最大值为.∴λ﹣1=0,可得:λ=1.(II)∵由(I)可得g(x)=sin(2x+),∴sin(+)=1,解得:sin(+)=,可得:sin+cos=1,两边平方,利用二倍角公式可得:sin3A=0,解得:A=kπ,k∈Z,∵0<A<π,∴A=,或.∵a=2且△ABC的面积为2,∴当A=时,由余弦定理可得:(2)2=b2+c2﹣2bc,可得:12=b2+c2﹣bc=(b+c)2﹣3bc,又2==×,解得:bc=8,可得:b+c=6.当A=时,由余弦定理可得:(2)2=b2+c2+2bc,可得:12=b2+c2+bc=(b+c)2﹣bc,又2==×,解得:bc=8,可得:b+c=2.20.【解答】(I)证明:∵P A=2,PB=2,AB=2,∴PB2+AB2=P A2,∴PB⊥BA,∵侧面P AB⊥底面ABCD,侧面P AB∩底面ABCD=AB,∴PB⊥底面ABCD,∴PB⊥AC∵底面ABCD是边长为2的菱形,∴AC⊥BD,∵PB∩BD=B,∴AC⊥平面PBD;(II)解:作OE⊥PB,连接CE,则CE⊥PB.∴∠CEO是二面角B﹣PD﹣C的平面角在△PCD中,P二面角B﹣PD﹣C的C=PD=2,CD=2,∴,∴CE=,∵CO=,∴OE=,∴cos∠CEO==.21.【解答】解:由离心率e==,即a2=2c2,△ABF1的周长为4.即4a=4.∴a=,c=1,由b2=a2﹣b2=2﹣1=1,∴椭圆方程为:;(2)当斜率不存在时,当x=1时,y=±,丨AB丨=,△ABF1的面积S=×2c×丨AB丨=,不成立,当斜率存在,过点F2(1,0)直线AB的方程为x=ny+1,将直线方程代入椭圆方程,得(2+n2)y2+2ny﹣1=0,设A(x1,y1),B(x2,y2),∴y1+y2=,y1•y2=﹣,丨y1﹣y2丨==,△ABF1的面积S=×2c×丨AB丨=×2×=,=,整理得:2n4﹣n2﹣1=0,解得:n2=1,n=±1,故直线方程为y﹣x+1=0或﹣y﹣x+1=0.22.【解答】解:(Ⅰ)当a=3时,f′(x)=﹣x2+3x﹣2=﹣(x﹣1)(x﹣2),当1<x<2时,f′(x)>0,函数f(x)单调递增;当x<1或x>2时,f′(x)<0,函数f(x)单调递减,所以函数f(x)的单调递增区间为(1,2),单调递减区间为(﹣∞,1)和(2,+∞);(Ⅱ)设点A(t,﹣t3+t2﹣2t)是函数f(x)图象上的切点,则过点A的切线斜率k=﹣t2+at﹣2,所以过点A的切线方程为y+t3﹣t2+2t=(﹣t2+at﹣2)(x﹣t),因为点(0,﹣)在该切线上,所以﹣+t3﹣t2+2t=(﹣t2+at﹣2)(0﹣t),即t3﹣at2+=0,若过点(0,﹣)可作函数y=f(x)图象的三条不同切线,则方程t3﹣at2+=0三个不同的实数根,令g(t)=t3﹣at2+=0,则函数y=g(t)的图象与x轴有三个不同的交点,g′(t)=2t2﹣at=0,解得t=0或t=,因为g(0)=,g()=﹣a3+,所以令g()=﹣a3+<0,即a>2,所以实数a的取值范围是(2,+∞).。
云南省楚雄州民族中学2015-2016学年高二数学下学期期中试题 文(无答案)

云南省楚雄州民族中学2015-2016学年高二数学下学期期中试题 文(无答案)满分 150分 考试时间 120分钟一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.并将最终答案填涂在答题卡上)1.已知集合A={0,l,3},B={0,3},则A B=( ) (A) {0) (B) {0,1} (C) {0,3} (D) {0,1,3} 2.已知z=212ii+-(i 为虚数单位),则复数z=( ) (A) -1 (B) l (C) i (D) -i3.cos18cos78sin18sin78⋅+⋅等于( )(A) 12-124.对变量x ,y 有观测数据(x i ,y i )(i =1,2,…,10),得散点图1;对变量u ,v 有观测数据(u i ,v i )(i =1,2,…,10),得散点图2.由这两个散点图可以判断( )(A )变量x 与y 正相关,u 与v 正相关 (B )变量x 与y 正相关,u 与v 负相关 (C )变量x 与y 负相关,u 与v 正相关 (D )变量x 与y 负相关,u 与v 负相关5.下列命题,真命题是( ) (A )0a b -=的充要条件是1ab= (B )∈∃0x R ,0||0x ≤ (C )0x ∀>,22x x > (D )若p q ∧为假,则p q ∨为假 6.下表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知用水量y 与月份x 之间有较好的线性相关关系,其回归方程是0.7y a x =-,则a 等于( ) (A) 10.5 (B) 5.15 (C) 5.2 (D) 5.25 7.在等差数列}{n a 中,12=a ,54=a 则}{n a 的前5项和5S =( )(A ) 7 (B ) 15 (C ) 20 (D ) 258.在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示,则此机械部件的表面积为( )ππ(C)227ππ+6 9.若双曲线221:128x y C -=与22222:1(0,0)x y C a b a b-=>>的渐近线相同,且双曲线C 2的焦距为b=( ) (A) 2 (B) 4 (C) 6 (D) 810.下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列;{}2:n p na 数列是递增数列; 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列;{}4:3n p a nd +数列是递增数列; 其中的真命题为( ) (A) 12,p p(B) 34,p p(C) 23,p p(D) 14,p p11.已知等边△ABC 的边长为2,若3,,BC BE AD DC BD AE ==⋅则等于( ) (A) -2 (B) 一103 (C) 2 (D) 10312.直线x=t 分别与函数f(x)=e x+1的图像及g(x)=2x-l 的图像相交于点A 和点B ,则|AB|的最小值为( ) (A) 2 (B) 3 (C) 4-21n2 (D) 3-21n2二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置上. 13.曲线2()ln f x x x =+在(1,(1))f 处的切线的斜率为14.在区间[-1,2]上随即取一个数x ,则x ∈[0,1]的概率为15.如图是一个程序框图,则输出的S 的值是______.16.已知圆C 的方程为228150x y x +++=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的取值范围为三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17(本小题满分12分)在ABC ∆中,60BC A =∠=.(Ⅰ)若cos 3B =,求AC 的长度; (Ⅱ)若2AB =,求ABC ∆的面积.18. (本小题满分12分)某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下表:(Ⅰ)试根据上述数据,求这个班级女生阅读名著的平均本数;(Ⅱ)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率; (Ⅲ)试判断该班男生阅读名著本数的方差21s 与女生阅读名著本数的方差22s 的大小. (注:方差2222121[()()()]n s x x x x x x n=-+-++-,其中x 为1x 2x ,…… n x 的平均数)19.(本小题满分12分)如图,四棱锥P -ABCD 的底面ABCD 为直角梯形,其中BA ⊥AD ,CD ⊥AD ,CD =AD =2AB ,PA ⊥底面ABCD ,E 是PC 的中点.(1)求证:BE∥平面PAD ;(2)若AP =2AB ,求证:BE ⊥平面PCD .20.(本小题满分12分)已知椭圆1C :22221(0)x y a b a b +=>>抛物线2C :22(0)x py p =>的焦点F 是椭圆1C 的顶点. (Ⅰ)求1C 与2C 的标准方程;(Ⅱ)若2C 的切线交1C 于P ,Q 两点,且满足0FP FQ ⋅=,求直线PQ 的方程.21、(本小题满分12分)已知函数32()ln ,()2f x x x g x x ax x ==+-+(Ⅰ)若函数()g x 的单调递减区间为1(,1)3-,求函数()g x 的解析式; (Ⅱ)在(Ⅰ)的条件下,求函数()g x 的图像在点(1,1)P -处的切线方程; (Ⅲ)若不等式2()()2f x g x '≤+恒成立,求实数a 的取值范围.22、(本小题满分10分)在极坐标系中,曲线1C 的极坐标方程是2cos 2sin ρθθ=+,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,曲线2C 参数方程是2cos (sin x y ααα=+⎧⎨=⎩为参数)(1)求曲线1C 的平面直角坐标方程和曲线2C 的普通方程; (2)点P 是曲线2C 上一动点,求点P 到直线sin()33πρθ-=的最小距离.。
云南省楚雄彝族自治州数学高二下学期文数期末模拟卷

云南省楚雄彝族自治州数学高二下学期文数期末模拟卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2017·榆林模拟) 若集合A={x|y= },B={x|x≥﹣1},则A∩B等于()A . [﹣1,0]B . [﹣1,1)C . (﹣1,+∞)D . (0,1]2. (2分)下列实验中最适合用分层抽样法抽样的是()A . 从一箱3 000个零件中抽取5个入样B . 从一箱3 000个零件中抽取600个入样C . 从一箱30个零件中抽取5个入样D . 从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样3. (2分)(2019·肇庆模拟) 若复数满足,则()A .B .C .D .4. (2分) (2017高二下·夏县期末) 某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果你在该游戏中,猜得珠子从口3出来,那么你取胜的概率为()A .B .C .D . 都不对5. (2分)设F1和F2为双曲线的两个焦点,点P在双曲线上,且满足∠F1PF2=900 ,则⊿F1PF2的面积是()A . 1B . 2C . 3D . 46. (2分)关于空间两条直线a、b与平面,下列命题正确的是()A . 若,则B . 若,则C . 若,则D . 若则7. (2分)(2018·辽宁模拟) 已知x,y满足约束条件,则的最大值为A . 2B . 0C .D .8. (2分) (2019高三上·沈河月考) 已知函数的图象与的图象关于直线对称,则的图象的一个对称中心可以为()A .B .C .D .9. (2分)设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有恒成立,则不等式的解集是()A . (-2,0) ∪(2,+∞)B . (-2,0) ∪(0,2)C . (-∞,-2)∪(2,+∞)D . (-∞,-2)∪(0,2)10. (2分)(2018·银川模拟) 阅读如图所示的程序框图,运行相应的程序,输出的的值等于()A .B .C .D .11. (2分) (2015高一下·湖州期中) 在△ABC中,内角A,B,C的对边分别为a,b,c,且b2+c2+bc﹣a2=0,则 =()A . ﹣B .C . ﹣D .12. (2分) (2016高一上·遵义期中) 直线y=2与曲线y=x2﹣|x|+a有四个交点,则a的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2018高二下·甘肃期末) 已知向量,满足,且,则向量与的夹角是________.14. (1分) (2018高二上·睢宁月考) 若直线与直线与直线互相平行,则实数 ________.15. (1分)(2018·广东模拟) 若,且,则 ________.16. (1分) (2015高三上·保定期末) 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为2的正方体.三、解答题 (共7题;共60分)17. (10分)(2020·武汉模拟) 若等比数列{an}的前n项和为Sn ,满足a4﹣a1=S3 , a5﹣a1=15.(1)求数列{an}的首项a1和公比q;(2)若an>n+100,求n的取值范围.18. (5分)如图,在四棱柱P﹣ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥AD.(Ⅰ)求证:PC∥平面BED;(Ⅱ)若CD=1,BC=PC=PD=2,求三棱锥P﹣BCD的体积.19. (10分) (2018高二下·双流期末) 近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出条较为详细的评价信息进行统计,车辆状况的优惠活动评价的列联表如下:对优惠活动好评对优惠活动不满意合计对车辆状况好评对车辆状况不满意合计参考数据:参考公式:,其中 .(1)能否在犯错误的概率不超过的前提下认为优惠活动好评与车辆状况好评之间有关系?(2)为了回馈用户,公司通过向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了张骑行券,其中只有张是一元券.现该用户从这张骑行券中随机选取张转赠给好友,求选取的张中至少有张是一元券的概率.20. (10分) (2018高二上·深圳期中) 已知椭圆的标准方程为,该椭圆经过点,且离心率为.(1)求椭圆的标准方程;(2)过椭圆长轴上一点作两条互相垂直的弦.若弦的中点分别为,证明:直线恒过定点.21. (10分)(2017·晋中模拟) 已知函数f(x)=2a2lnx﹣x2 , g(x)=﹣x2+2a3x+ .(1)讨论函数f(x)在(1,e2)上零点的个数;(2)若h(x)=f(x)﹣g(x)有两个不同的零点x1,x2,求证:x1•x2>2e2.(参考数据:e取2.8,ln2取0.7,取1.4)22. (5分)(2017·黑龙江模拟) 在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为.(Ⅰ)求圆C的圆心到直线l的距离;(Ⅱ)设圆C与直线l交于点A、B.若点P的坐标为(3,),求|PA|+|PB|.23. (10分) (2017高二下·牡丹江期末) 已知函数 .(1)若,解不等式;(2)若存在实数,使得不等式成立,求实数的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共60分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、23-1、23-2、。
2015年楚雄州普通高中学年末教学质量检测
2015年楚雄州普通高中学年末教学质量检测
高二物理试题
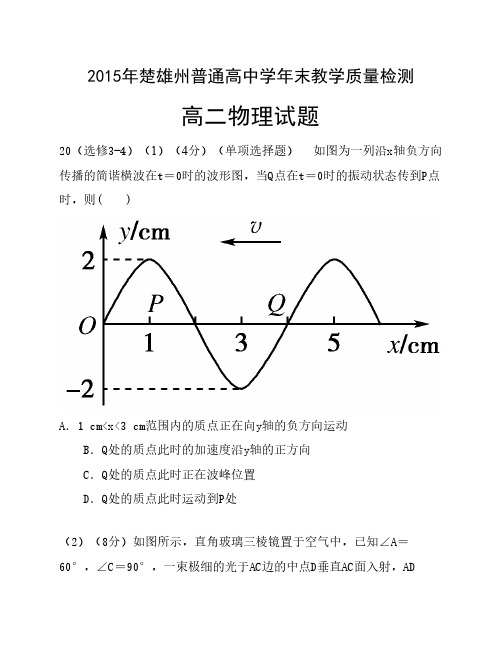
20(选修3-4)(1)(4分)(单项选择题)如图为一列沿x轴负方向传播的简谐横波在t=0时的波形图,当Q点在t=0时的振动状态传到P点时,则( )
A.1 cm<x<3 cm范围内的质点正在向y轴的负方向运动
B.Q处的质点此时的加速度沿y轴的正方向
C.Q处的质点此时正在波峰位置
D.Q处的质点此时运动到P处
(2)(8分)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC边的中点D垂直AC面入射,AD
=a,棱镜的折射率n=.求:(1)光从棱镜第一次射入空气时的折射角;
(2)光从进入棱镜到它第一次射入空气所经历的时间.(设光
在真空中的传播速度为c)
19、 (1)(4分)B
(2)(1)如图所示,i1=60°,设玻璃对空气的临界角为C,
则sin C== C=45°
i1>45°,发生全反射
i2=i1-30°=30°<C,由折射定律有:=,
所以γ=45°.
(2)镜中光速v== ,所求时间:
t=+=.
答案:(每问4分) (1)45° (2)。
云南省楚雄彝族自治州数学高二(重点班)下学期文数期末考试试卷

云南省楚雄彝族自治州数学高二(重点班)下学期文数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高三上·郑州期中) 具有相关关系的两个量、的一组数据如下表,回归方程是,则()A .B .C .D .2. (2分)已知复数(且≠),且为实数,则()A .B .C .D .3. (2分)如图所示程序框图中,其中不含有的程序框是()A . 终端框B . 输入、输出框C . 判断框D . 处理框4. (2分) (2017高二下·咸阳期末) 已知变量x,y之间具有线性相关关系,其散点图如图所示,则其回归方程可能为()A . =1.5x+2B . =﹣1.5x+2C . =1.5x﹣2D . =﹣1.5x﹣25. (2分) (2017高二下·中山月考) 下列说法正确的是()A . 由归纳推理得到的结论一定正确B . 由类比推理得到的结论一定正确C . 由合情推理得到的结论一定正确D . 演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确6. (2分) (2015高二下·九江期中) 已知a、b、c是△ABC的三边长,A= ,B= ,则()A . A>BB . A<BC . A≥BD . A≤B7. (2分)(2016·青海) 若函数图像上的任意一点的坐标满足条件,则称函数具有性质,那么下列函数中具有性质的是()A .B .C .D .8. (2分) (2018高二上·闽侯期中) 下列结论正确的是()A . 若,则B . 若,则C . 若,则D . 若,则9. (2分) (2019高二下·太原月考) 过点(4,0),与极轴垂直的直线的极坐标方程为()A .B .C .D .10. (2分) (2019高三上·西湖期中) 设全集,集合,则下列关系中正确的是()A .B .C .D .11. (2分)有如下几个结论:①相关指数越大,说明残差平方和越小,模型的拟合效果越好;②回归直线方程:一定过样本点的中心;③残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适;④在独立性检验中,若公式中的|ad-bc|的值越大,说明“两个分类变量有关系”的可能性越强.其中正确结论的个数有()个.A . 1B . 3C . 2D . 412. (2分) (2019高一上·山丹期中) 已知集合,,则下列关系中正确的是()A .B .C .D .二、填空题 (共4题;共5分)13. (1分) (2016高一上·宿迁期末) 已知集合A={﹣1,0},B={0,2},则A∪B=________.14. (1分)(2017·怀化模拟) 若命题p:“∀x∈(﹣∞,0),x2≥0”,则¬p为________.15. (1分) (2018高二上·东至期末) 若“ ”是“ ”的充分不必要条件,则实数的取值范围是________.16. (2分) (2016高二上·湖州期末) 已知x,y为正实数,且x+2y=1,则的最大值是________,的最小值是________.三、解答题 (共5题;共40分)17. (10分)(2017·西宁模拟) 已知:x、y、z是正实数,且x+2y+3z=1,(1)求的最小值;(2)求证:x2+y2+z2≥ .18. (5分) (2017高二下·黄山期末) 解答下面两个问题:(Ⅰ)已知复数,其共轭复数为,求;(Ⅱ)复数z1=2a+1+(1+a2)i,z2=1﹣a+(3﹣a)i,a∈R,若是实数,求a的值.19. (5分)已知正实数a、b、c满足条件a+b+c=3,(Ⅰ)求证:;(Ⅱ)若c=ab,求c的最大值.20. (10分)全集U=R,若集合A={x|3≤x<10},B={x|1<x﹣1≤6},则(1)求A∩B,A∪B;(2)若集合C={x|x>a},满足C∪A=C时,求a的取值范围.(结果用区间或集合表示)21. (10分)写出下列命题的否定,并判断其真假:(1):;(2)至少有一个实数,使得 .参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共5题;共40分) 17-1、17-2、18-1、19-1、20-1、20-2、21-1、21-2、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年楚雄州普通高中学年末教学质量检测高二文科数学试题 (考试时间:120分钟)第Ⅰ卷(选择题60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)(1)已知集合A={x|﹣1<x <2},B={x|0<x <3},则A∪B=(A)(﹣1,3) (B)(﹣1,0) (C)(0,2) (D)(2,3) (2)131ii+-= (A )1+2i (B )﹣1+2i (C )1﹣2i (D )﹣1﹣2i (3)已知命题p 、q ,“¬p 为真”是“p∧q 为假”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件(4)已知a r =(1,﹣1),b r=(﹣1,2)则2+a b a r r r g ()=(A )﹣1 (B )0 (C )1 (D )2(5)等差数列{a n }的公差为2,若a 2,a 4,a 8成等比数列,则{a n }的前10项和S 10=(A )110 (B )99 (C )55 (D )45 (6)某三棱锥的三视图如图所示,则该三棱锥的体积是(A )16 (B )13 (C )23(D )1(7)过抛物线y=2x 2的焦点且垂直于它的对称轴的直线被它切得的弦长为(A)2 (B)1 (C)0.25 (D)0.5 (8)一个算法程序如图所示,则输出的n 的值为(A) 6 (B)5 (C)4 (D)3(9)已知函数f (x )=x 2﹣2x+b 在区间(2,4)内有唯一零点,则b 的取值范围是(A) R (B)(﹣∞,0) (C)(﹣8,+∞) (D)(﹣8,0)(10)若函数f (x )=kx ﹣lnx 在区间(1,+∞)单调递增,则k 的取值范围是(A )(﹣∞,﹣2] (B )(﹣∞,﹣1] (C )[2,+∞) (D )[1,+∞)(11)设1F 、2F 是双曲线22221(0,0)x y a b a b-=>>的两个焦点,P 在双曲线上,若120PF PF ⋅=,12||||2PF PF ⋅=,则双曲线的离心率为(A(B(C )2 (D(12)已知函数f (x )是定义在(﹣3,3)上的奇函数,当0<x <3时,f (x )的图象如图所示,则不等式f (﹣x )﹒x >0的解集是(A)(﹣3,﹣1)∪(0,1) (B)(﹣1,1)(C)(﹣1,0)∪(0,1) (D)(﹣1,0)∪(1,3)第Ⅱ卷(非选择题90分)二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上) (13)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是 .(14) 若x ,y 满足约束条件,则z=2x+y 的最大值为 .(15) 已知y 与x 之间具有很强的线性相关关系,现观测得到(x,y)的四组观测值并制作了相应的对照表,由表中数据粗略地得到线性回归直线方程为y=bx+60,其中b 的值没有写上.当x=5-时,预测y 的值为 .(16) 在数列{a n }中,a n =﹣n 2+λn ,且{a n }为递减数列,则λ的取值范围为 .三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤)(17)(本小题满分10分) 已知直线l 的参数方程是(t 为参数),圆C 的极坐标方程为ρ=2cos (θ+4π). (Ⅰ)求圆心C 的直角坐标;(Ⅱ)由直线l 上的点向圆C 引切线,求切线长的最小值.(18)(本小题满分12分) 已知向量m u r =(cosx ,﹣1),n r =(sinx ,﹣32),()f x =(m u r ﹣n r )•m u r.(Ⅰ)求函数f (x )的单调增区间;(Ⅱ)已知锐角△ABC 中角A ,B ,C 的对边分别为a ,b ,c .其面积()8f A π-=,a=3,求b+c 的值.(19)(本小题满分12分)M 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.(Ⅰ)求男生成绩的中位数及女生成绩的平均值;(Ⅱ)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?(20)(本小题满分12分) 如图,五面体中,四边形ABCD 是矩形,DA ⊥面ABEF ,且DA=1,AB ∥EF ,AB=12AF=BE=2,P 、Q 、M 分别为AE 、BD 、EF 的中点.(Ⅰ)求证:PQ ∥平面BCE ; (Ⅱ)求证:AM ⊥平面ADF .(21)(本小题满分12分) 设椭圆E:()222210x y a b a b+=>>过M (、N)两点,O 为坐标原点.(I )求椭圆E 的方程;(II )若直线()40y kx k =+>与圆2283x y +=相切,并且与椭圆E 相交于两点A 、B ,求证:OA OB ⊥ .(22)(本小题满分12分) 已知函数1()()ln f x a x x x=--.(Ⅰ)若a =1,求曲线y=()f x 在点(1,()f x )处的切线方程; (Ⅱ)若函数()f x 在其定义域内为增函数,求a 的取值范围;2016年楚雄州普通高中学年末教学质量检测 高二文科数学试题参考答案与评分标准一、选择题:本大题共12小题。
每小题5分,共60分。
二、填空题:本大题共4小题,每小题5分,共20分。
三.解答题:本大题共6个小题,共70分。
(17) (本小题满分10分)解:(I )∵,∴,∴圆C 的直角坐标方程为,即,∴圆心直角坐标为(5分)。
(II )∵直线l 的普通方程为,圆心C 到直线l 距离是,∴直线l 上的点向圆C 引的切线长的最小值是(10分)。
(18) (本小题满分12分)解:(Ⅰ)∵m u r =(cosx ,﹣1),n r =(sinx ,﹣),∴m u r ﹣n r=(cosx ﹣sinx ,), ∴f (x )=(m u r ﹣n r )•m u r=(cosx - sinx )cosx -=(4分), 由,得,k ∈Z 。
所以函数的单调性递增区间为:,k ∈Z (6分)。
(Ⅱ)∵,∴,又∵0,∴0<2A <π,∴,即A=(8分),∴S=,∴bc=4(10分)。
由余弦定理得a 2=b 2+2﹣2bccos A ,∴9=b 2+c 2﹣bc ,∴(b+c )2=b 2+c 2+2bc=9+3bc=21, ∴b+c=(12分)。
(19) (本小题满分12分)解:(Ⅰ)男生共14人,中间两个成绩是175和176,它们的平均数为175.5, 所以男生成绩的中位数是175.5(2分)。
女生的平均成绩==181(4分)(Ⅱ)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取5人,每个人被抽中的概率是=。
根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人。
所以选中的“甲部门”人选有=2人,“乙部门”人选有=3人(8分)。
记选中的“甲部门”的人员为A 1,A 2,选中的“乙部门”人员为B ,C ,D 。
从这5人中选2人的所以可能情况为:(A 1,A 2),(A 1,B ),(A 1,C ),(A 1,D ),(A 2,B ),(A 2,C ),(A 2,D ),(B ,C ),(B ,D ),(C ,D ),共10种。
其中至少有1人是“甲部门”人选的结果有7种。
因此,至少有1人是“甲部门”人选的概率是(12分)。
(20)(本小题满分12分)证明:(Ⅰ)连接AC .∵四边形ABCD 是矩形,Q 为BD 的中点,∴Q 为AC 的中点。
又在△AEC 中,P 为AE 的中点,∴PQ ∥EC 。
∵EC ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE (6分)。
(Ⅱ)∵M 是EF 的中点,∴EM=AB=,又∵EF ∥AB ,∴四边形ABEF 是平行四边形, ∴AM ∥BE ,AM=BE=2,又∵AF=2,MF=,∴AM 2+AF 2=MF 2,∴∠MAF=90°,∴MA ⊥AF 。
∵DA ⊥平面ABEF ,∴DA ⊥AM 。
又∵AF∩AD=A,∴AM ⊥平面ADF (12分) (21) (本小题满分12分)解:(I )因为椭圆E: 22221x y a b+=(a>b>0)过M (2,,1)两点,所以2222421611a b a b +=+=⎧⎪⎪⎨⎪⎪⎩解得22118114a b ⎧=⎪⎪⎨⎪=⎪⎩所以2284a b ⎧=⎨=⎩ , 所以椭圆E 的方程为22184x y +=(4分)(II )设()11y x A ()22y x B ,由题意得:5,362142==+=k k d (6分) 联立⎪⎩⎪⎨⎧=++=1484522y x x y ,024516112=++x x 化简得, 所以1124,511162121=-=+x x x x 所以OA OB uuu r uu u rg=()()16)(5464545212121212121+++=+++=+x x x x x x x x y y x x =0 。
OB OA ⊥∴(12分)(22) (本小题满分12分)解:(Ⅰ)当a=1时,函数,所以f(1)=1﹣1﹣ln1=0,(4分),曲线f(x)在点(1,f(1))处的切线的斜率为f′(1)=1+1﹣1=1。
从而曲线f(x)在点(1,f(1))处的切线方程为y﹣0=x﹣1,即y=x﹣1(6分)。
(Ⅱ)(8分)。
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立.即ax2﹣x+a≥0,得恒成立(10分)。
因为,所以,所以。
所以f(x)在(0,+∞)内为增函数,实数a的取值范围是(12分)。
