第七章 机械的运动及其速度波动的调节
第7章机械运转速度波动的调节

m V Dm HB
选定飞轮的材料和比值 H/B 之后,可得飞轮轮缘 的截面尺寸。
§7-3 飞轮主要尺寸的确定 二、实心圆盘式飞轮
1 D mD2 J m 2 2 8
2
D
选定圆盘直径D,可得 飞轮的质量:
m V
B
D 2
4
B
选定飞轮的材料之后,可得飞轮的宽度B。
原动机2的输入功与供 汽量的大小成正比。
当负荷突然减小时,原动 机 2 和工作机 1 的主轴转速升高。 由圆锥齿轮驱动的调速器主轴 的转速也随着升高,重球因离 心力增大而飞向上方,带动圆 筒 N 上升,并通过套环和连杆 将节流阀关小,使蒸汽输入量 减少。
1
工作机
原动机
2
N
蒸汽
图7-2 离心调速机构
§7-1 机械运转速度波动调节的目的和方法 二、非周期性速度波动
§7-2 飞轮设计的近似方法 对于不同的机器,因工作性质不同而取不同的值[δ]。 比如:发电机,冲床、破碎机
设计时要求:δ≤[δ] 表7-1 机械运转速度不均匀系数δ的取值范围
机械名称
[δ]
机械名称
[δ]
机械名称
[δ]
1/60~1/100
碎石机
1/5~1/20 汽车拖拉机 1/20~1/60 造纸织布 1/40~1/50 切削机床 1/30~1/40 纺纱机 发电机 1/100~1/300
反之,若负荷突然增 加,原动机及调速器主轴 转速下降,飞球下落,节 流阀开大,使供汽量增加。
1
工作机
原动机
2
用这种方法使输入功 和负荷所消耗的功(包括 摩擦损失)达成平衡,以 保持速度稳定。
N
蒸汽
机械原理第七章机械的运转及其速度波动的调节

一个单自由度机械系统的运动, 可以等效为一个具有等效转动 惯量Je(),在其上作用有等效 力矩 Me(,,t) 的假想简单构件 的运动,该假想的构件称为 等
效构件,也称为原机械系统的
等效动力学模型。
B A
N
的函数。
其特征曲线可以用一条通过N点和 C点的直线近似代替。直线方程为:
直流电机机械特性曲线
M
Md Mn 0 / 0 n
O
n
0
Mn: 电动机的额定转矩;
C
——驱动力是转动速度的函数。
直流串 激电机
O
直流并 激电机
n:电动机的额定角速度; o:电动机的同步角速度; Md、 :任意点的驱动力矩 M F dt 1 1 3 1
Je
等效转动惯量 J e J e (1 )
M e 等效力矩
Me Me (1 , 1 , t )
用等效转动惯量( Je)和等效力矩( Me)表示的机械运动方程式 的一般表达式为
ω
度逐渐减速,直到
停止。
起动 稳定运转 图11-1 停车
功(率)特征:Wd-Wc= -Wc
动能特征:E= Wd-Wc= -Wc<0 速度特征:i+1< i
ω
三.作用在机械上的力
1. 作用在机械上力的的种类 2. 驱动力和生产阻力
内 外
力 ——反力、摩擦力 驱 动 力 力 生产阻力 重 力
停车
1. 起动阶段——原动件的速度由零逐渐上升到开始稳定的过程。
功(率)特征:外力对系统做正功Wd-Wc>0 动能特征:系统的动能增加E=Wd-Wc>0 速度特征:系统的速度增加 =0 m
第7章机械的运转及其速度波动的调节

当移动构件为等效构件时,
Fe=∑[Ficosαi(vi /v)±Mi(ωi /v)] me=∑[mi(vSi /v)2+JSi(ωi /v)2]
16
18
第7章机械的运转及其速度 波动的调节
§7-1 概述 §7-2 机械的运动方程式 §7-3 机械运动方程式的求解 §7-4 稳定运转状态下机械的周期性速度
波动及其调节 §7-5 机械的非周期性速度波动及其调节
3
§7-1 概述 一、 机械运转的三个阶段
1.起动阶段(starting period )
= 575 (Nm)
c -100 +550
a
e +125
d -500 f
Wmax g +25 -50
-50
h
b
47
2. 900 Wmax
JF = [d]p2 nm2 = 900×575 0.06×2×1202 = 60.159453 (kgm2) ≈60.5 (kgm2)
48
讨论
如果因某种原因,转化件轴上无法安装质量较大 的飞轮,只能装在第i构件的轴上,其飞轮的转
等效力矩是作用在等效构件上的一个假想力矩,其瞬时功率 应等于作用在原机械系统上的所有外力在同一瞬时的功率之和。
把具有等效转动惯量,其上作用有等效力矩的等效构件就称为 原机械系统的等效动力学模型。
14
2.取移动构件为等效构件
令
me等效质量
Fe等效力
15
等效转动惯量(等效质量)和等效力矩(等效力) 的一般计算公式为:
第七章 机械的运转及其速度波动的调节

第七章 机械的运转及其速度波动的调节一.学习指导与提示在做机械的运动分析和受力分析时,都认为原动件的运动规律是已知的并且做等速运动。
实际上,原动件的真实运动规律与作用在机械上的外力、原动件的位置和所有构件的质量、转动惯量等因素有关,因而在一般条件下,原动件的速度和加速度是随着时间而变化的。
因此设计机械时,如果对执行构件的运动规律有比较严格的要求,或者需要精确地进行力的计算和强度计算时,就需要首先确定机械在外力作用下的真实运动规律。
1、以角速度ω作定轴转动的等效构件的等效参量的计算如等效构件以角速度ω作定轴转动,其动能为:E J e =122ω组成机械系统的各构件或作定轴转动,或作往复直线移动,或作平面运动,各类不同运动形式的构件动能分别为:E J i si i =122ωE m v i i si =122 E J i si i =122ω+122m v i si整个机械系统的动能为:E J i n si i ==∑1212ω + i n i si m v =∑1212式中:ωi 为第i 个构件的角速度;m i 为第i 个构件的质量;J si 为第i 个构件对其质心轴的转动惯量;v si 为第i 个构件质心处的速度。
由于等效构件的动能与机械系统的动能相等,则有:122J e ω = i n si i J =∑1212ω+ i n i si m v =∑1212 方程两边统除以122ω,可求解等效转动惯量:J e = i n si i J =∑12(ωω) +21)(ωsi i n i v m ∑=2.周期性速度波动调节与非周期性速度波动调节机械在某段工作时间内,若驱动力所作的功大于阻力所作的功,则出现盈功;若驱动力所作的功小于阻力所作的功,则出现亏功。
盈功和亏功将引起机械动能的增加和减少,从而引起机械运转速度的波动。
机械速度波动会使运动副中产生附加的动压力,降低机械效率,产生振动,影响机械的质量和寿命。
第7章机械运转速度波动及其调节

例如:汽车和拖拉机车轮上、 例如:汽车和拖拉机车轮上、汽、柴油机上,冲 柴油机上, 剪床上,以及发电机上均有飞轮的应用。 床、剪床上,以及发电机上均有飞轮的应用。
盈功:输入功大于输出功。 盈功:输入功大于输出功。 亏功:输入功小于输出功。 亏功:输入功小于输出功。 机械动能的增减是形成机械运转速度波动的原因
盈功 亏功
起动
稳定运行
停车
速度波动的危害:产生a和附加力,机械效率↓ ,工作 速度波动的危害: 和附加力,机械效率↓ 效率↓ 附带机械振动,影响零件强度和寿命。 效率↓ ,附带机械振动,特点:机械主轴的角速度作周期性变化
周期T内 驱动力作功等于阻力作功。 在一个运转周期 在一个运转周期 内,驱动力作功等于阻力作功。 E0=ET,△ET= E0-ET=0.→ω0=ωT,△ωT=ω0 -ω T =0。 △ 。 但在该周期内的任一瞬时, 但在该周期内的任一瞬时,ω1≠ω2。 运转周期T可以是机械主轴回转一转 或数转( 可以是机械主轴回转一转, 运转周期 可以是机械主轴回转一转,或数转(整转 数倍)。 数倍)。 速度周期波动的调节方法: 速度周期波动的调节方法 安装飞轮——转动惯量很大的回转构件。 转动惯量很大的回转构件。 安装飞轮 转动惯量很大的回转构件 飞轮的调速原理(相当能量存储器): 飞轮的调速原理(相当能量存储器): 当机械运转速度变化时, 当机械运转速度变化时,飞轮的动能变化 ∆E =J(ω2-ω02) /2;
最大盈亏功: 最大盈亏功:
概述机械原理 第七章 机械的运转及其速度波动的调节.ppt

/ 2)
Me
即
Je
d(2 / 2) d
2
2
dJe
d
Me
式中
d(2 / 2) d(2 / 2) dt d 1 d
d
dt d dt dt
代入便可得机械运动方程式的力矩形式
Je
d
dt
2
2
dJ e
0d.0
Me
12
此外还可得到机械运动方程式的动能形式
1
2
J e
2
1 2
J
e0
2 0
0 M e d
解 Je J1(1 /2)2 J2 m3(v3 /2)2 m4(v4 /2)2
v3 vC 2l
v4 vC sin 2 2l sin 2
故 Je J1(z2 / z1)2 J2 m3(2l /2)2 m4(2l sin2 /2)2
9J1 J 2 m3l 2 m4l 2 sin 2 2
J 112
1 2
m2
v
2 S2
1 2
J
S
2
2 2
1 2
m3v32 )
(M 11
F3v3 )dt
二.机械系统的等效动力学模型 1 1
d
12
2
J1
m2
(
vS2
1
)2
J
S
2
(
2 1
)2
m3
(
v3
1
)
2
1
M
1
F3
( v3
1
)dt
又令
Je
J1
m2
(
vS2
1
)2
J
S
机械原理 第七章 机械的运转及其速度波动的调节

第7章
机械的运转及其速度波动的调节
一、机械运动方程的一般表达式:
于是曲柄滑块机构的运动方程式为:
2 2 2 dE d ( J 1 12 / 2 m 2v S 2 / 2 JS 2 2 / 2 m 3v 3 / 2) ( M 1 1 F 3v 3 )dt 对于由 n个活动构件组成的机构
第7章
机械的运转及其速度波动的调节
二、机械运转的三个阶段:
从机器开始运动到终止运动所经历的时间内,机器的工作过 程一般都要经历启动阶段、稳定运转阶段、停车阶段三个阶段。
Northwest A&F University
第7章
机械的运转及其速度波动的调节
二、机械运转的三个阶段:
1.启动阶段:原动件的速度从零逐渐上升到开始稳定运转的 过程 。
一、机械运动方程的一般表达式:
现以曲柄滑块机构为例说明运动方程式的建立方法。
已知曲柄1作为原动件,其角速度为ω 1。
曲柄1的质心S1在O点,其转动惯量为J1,连
杆2的角速度为ω 2 ,质量为m2,其对质心S2 的转动惯量为JS2,质心S2的速度为VS2,滑块
3的质量为m3,其质心S3在B点,速度为V3。
Northwest A&F University
第7章
机械的运转及其速度波动的调节
第二节
机械的运动方程式
一、机械运动方程的一般表达式: 在研究机械的运转问题时,需要建立的作用在机械上 的力、构件的质量、转动惯量和其运动参数之间的函数关 系,称为机械的运动方程式。
对于只有一个自由度的机械,描述它的运动规律只需要
第七章 机械运动速度波动的调节
第一节 第二节 第三节 第四节 概述 机械的运动方程式 运动方程式的求解 稳定状态下机械周期性速度波动及其调节Fra bibliotek第五节
机械设计第7章机械速度波动与调节
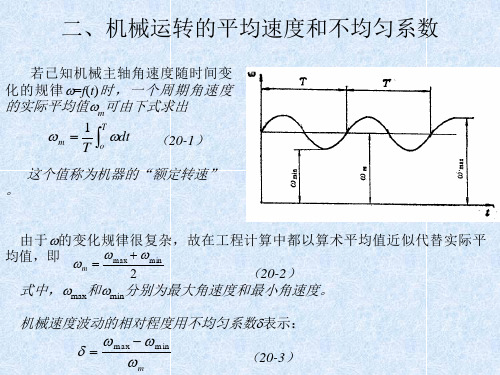
若已知机械主轴角速度随时间变
化 的 规 律 =f(t) 时 , 一 个 周 期 角 速 度
的实际平均值m可由下式求出
m
1 T
T
dt
o
(20-1)
这个值称为机器的“额定转速” 。
由于的变化规律很复杂,故在工程计算中都以算术平均值近似代替实际平
均值,即
m
max
min
2
(速度和最小角速度。
机械速度波动的相对程度用不均匀系数表示:
max min m
(20-3)
三、飞轮设计方法
1.转动惯量的计算
动能的最大变化量即最大剩余功为:
Amax
Emax
E m in
1 2
J
2 max
2 min
J 2m
式中Amax为最大剩余功,或最大盈亏功。
图20-4飞轮结构示意图
因此,有
J Amax 900 Amax
m2 2 n 2
(20-4)
图20-3 转动惯量与 不均匀系数的关系
2.飞轮尺寸确定
般飞轮的轮毂和轮辐的质量很小,近似计算时认为飞轮质量m集中于平均直 径为Dm轮缘上。因此,转动惯量可以写成
J
m
Dm
2
mDm2
2 4
(20-6)
当按照机器的结构和空间位置选定轮缘的平均直径Dm之后,由式(20-6)便 可求出飞轮的质量m。选定飞轮的材料与高宽比H/B后,按轮缘为矩形端面求出 轮缘截面尺寸,见图20-4。
07机械设计基础第七章机械运转速度波动的调节

第一节 速度波动调节的目的和方法
周期性速度波动的调节方法
在机械中加上一个转动惯量很大的回转件——飞轮
飞轮的动能变化
E
1 2
J( 2
- 02 )
显然动能变化相同时,飞轮的转动惯量越大,速度波动越小。
第一节 速度波动调节的目的和方法
三、非周期性速度波动
机械的运转速度变化是非周期性的,完全随机的,不能依靠飞轮对其进行速 度波动的调节。
第二节 飞轮设计的近似方法
Ea Eo Aoa Eo M [S1] Eb Ea Aab Ea M [S2 ] Ec Eb Abc Eb M [S3 ] Ed Ec Acd Ec M [S4 ] Eo Ed Ado Ed M [S5 ]
Amax
Emax
Emin
1 2
J (m2ax
2 min
)
Jm2
飞轮转动惯量 Amax用绝对值表示
J Amax
m2
第二节 飞轮设计的近似方法
由上式可知:
1)当Amax与ω 2m一定时 ,J-δ 是
一条等边双曲线。
J ∆J
当δ 很小时, δ ↓→ J↑↑
过分追求机械运转速度的平稳性,将使飞轮过于笨重。
2)当J与ω m一定时 , Amax-δ 成正比。即Amax越大,∆δ
机械运转速度越不均匀。
J
Amax
m2
δ
3) 由于J≠∞,而Amax和ω m又为有限值,故δ 不可能
为“0”,即使安装飞轮,机械总均转速越高,所需飞轮
的转动惯量越小。一般应将飞轮安装在高速轴上。
飞轮设计的基本问题:已知作用在主轴上的驱动力矩和阻力矩的变化规律,
第7章机械的运转及速度波动的调节

变量分离:
dt=Jedω/ Me (ω)
积分得: 2020/5/3
t t0
Je
0
d M e ( )
17
若 t=t0=0, ω0=0 则:
t Je 0 可求得ω=ω(t),
d M e ( )
加速度为:α=dω/dt,
由dφ=ωdt积分得位移:
-0=
t t0
(t
)dt
若 t=t0, φ0=0
Fer ) ,则有:
2020/5/3
Me= Med –Mer Fe= Fed –Fer
14
三、运动方程式的推演
1.把表达式:
d[1 2
Je 2
]
M ed
或
d[
1 2
mev2
]
Feds
称为能量微分形式的运动方程式。
2.若已知初始条件:
t=t0时,φ=φ0,ω=ω0, Je=Je0, v=v0, me=me0 则对以上两表达式积分得:
me=me (φ)
Je=Je (φ)
而Fi , Mi可能与φ、ω、t有关,因此,等效力Fe和等效力矩Me 也是这些参数的函数:
也可将驱动力F和e=F阻e(力φ,分ω,t别) 进行等M效e处=M理e(,φ,ω得,t出) 等效驱动力矩
Med ( 或 等 效 驱 动 力 Fed ) 和 等 效 阻 力 矩Mer( 或 等 效 阻 力
为vi。则瞬时功率为: n
n
n
N Ni Fivi cosi Mii
i 1
i 1
i 1
式中αi为Fi与vi之间的夹角,Mi与ωi方向相同时取“+”, 相反时取“-”。
机器运动方程的一般表达式为:
d[
7《机械原理》机械的运转及其速度波动的调节

7《机械原理》机械的运转及其速度波动的调节机械原理是研究机械的运转原理和调节方法的学科,其中之一的问题是机械的运转及其速度波动的调节。
机械的运转是指机械设备在正常工作状态下的运动情况,而速度波动则是指机械设备在运转过程中出现的速度变化。
为了保证机械设备的正常运转和提高工作效率,必须对机械的运转及其速度波动进行调节。
机械的运转及其速度波动的调节包括两个方面的内容,一是机械运动的平稳性,二是机械的速度调节。
1.机械运动的平稳性机械的运动平稳性是指机械设备在运转过程中存在的速度波动较小,加速、减速过程缓慢、稳定,不产生冲击和振动的特性。
机械的运动平稳性对机械设备的工作效果、使用寿命和安全性有重要影响。
要实现机械运动的平稳性,可以采取以下措施:(1)合理进行动平衡。
机械设备在运转过程中,受到各种力的作用,容易产生振动。
通过对机械设备进行动平衡处理,可以减小机械设备的振动,提高运动平稳性。
常见的动平衡方法有静质量的调整和加装动平衡块。
(2)减小摩擦与浮动间隙。
摩擦与浮动间隙是机械设备中常见的能量损失和产生振动的原因之一、通过合理设计和制造,减小摩擦与浮动间隙,可以提高机械设备的运动平稳性。
(3)采用减速装置。
在机械设备的运转过程中,经常需要对速度进行调节。
为了保证机械设备的平稳运行,可以在机械设备中加入减速装置,通过减小输入轴的速度,降低机械设备的运转速度,提高运行平稳性。
2.机械的速度调节机械的速度调节是指对机械设备的运转速度进行调节,以适应不同的工作需要。
机械设备的速度调节对于工作效率的提高、负荷均衡和能耗的节约等方面有着重要的意义。
要实现机械的速度调节,可以采取以下措施:(1)采用变速装置。
变速装置是实现机械设备速度调节的主要手段之一、通过变速装置,可以改变机械设备的传动比,从而实现速度的调节。
常见的变速装置有齿轮传动、皮带传动、液力变矩器等。
(2)采用调速电机。
调速电机是一种可以通过电信号调节转速的电机。
7《机械原理》机械的运转及其速度波动的调节

7《机械原理》机械的运转及其速度波动的调节《机械原理》是研究机械的运转及其速度波动调节的一门学科。
机械的运转及其速度波动的调节对于机械的工作效率和精度具有重要影响,因此掌握机械原理是非常重要的。
机械的运转是指机械在工作过程中的各种运动状态。
机械的运转方式可以分为平动、回转、滚动等多种形式,这些运动方式在机械工程中被广泛应用。
机械的运转是通过将输入能量转化为输出能量来完成各种工作任务的过程。
机械的速度波动是指机械在运转中由于各种原因引起的速度变化。
速度波动会对机械的工作效率和工作质量产生不利影响,因此需要对机械的速度波动进行调节和控制。
机械的速度波动调节可以通过多种方式实现,下面介绍几种常见的调节方法。
首先,可以通过改变机械的结构设计来减小速度波动。
例如,在一些机械中可以设置减震装置,用以减轻机械在运转时产生的震动和冲击,从而减小速度波动。
其次,可以通过加装速度波动控制装置来调节机械的速度波动。
这种控制装置可以根据机械运转时的速度波动情况进行自动调节,使得机械的速度保持在一个较为稳定的范围内。
此外,还可以通过改变机械的驱动方式来调节速度波动。
例如,在一些机械中可以采用变频调速的方法,通过改变电机的转速来调节机械的运转速度和速度波动。
另外,还可以通过使用精密传感器和控制系统来实现速度波动的调节。
这些传感器可以实时监测机械的运转速度,并将实时数据传输给控制系统,控制系统根据这些数据进行运算,从而实现对机械速度波动的调节。
在进行机械的运转及其速度波动调节时,需要注意以下几点。
首先,需要对机械的运转过程进行全面的分析和研究,了解机械在不同运转状态下的速度波动情况,为调节提供依据。
其次,需要对机械的结构和工作原理进行深入了解,以便能够根据具体情况选择适合的调节方法和措施。
最后,进行调节时需要进行实际测试和实验,以确保调节效果的准确性和可靠性,同时也需要对调节过程中的安全性和可行性进行充分考虑。
总之,机械的运转及其速度波动调节是机械工程中的重要内容,通过合理的调节方法和措施可以改善机械的工作效率和精度,提高机械的整体性能和可靠性。
《机械设计基础》第7章 机械的运转及其速度波动的调节

二、飞轮设计的基本原理
飞轮设计的基本问题是:已知作用在主轴上的驱动力 矩M′和阻力矩M″的变化规律,要求在机械的速度不均匀 系数δ的容许范围内,确定安装在主轴上的飞轮的转动惯 量J。
2、非周期性速度波动 机械运转中随机的、不规则的、没有一定周期的速
度变化称为非周期性速度波动。 这种速度波动不能依靠飞轮来进行调节,需要采用
专用装置——调速器来进行调节。
§7—2 飞轮设计的近似方法 一、平均角速度ωm和速度不均匀系数δ
图7-1所示为机械主轴角速度 随时间的变化规律ω=f (t)。
Aab= 400(Nm) (-) Abc=750(Nm) (+) Acd= 450(Nm) (-) Ade= 400(Nm)(+) Aea ′ =300(Nm) (-)
取比例尺μA=20Nm/mm,作能量指示图。 Amax =Lmax μA=37.5 ×20= 750(Nm)
J =900Amax/(π2n2 δ) =900 × 750/(π2× 1202 ×0.06) =79.2(kgm 2 )
在一般机械中,其他构件所具有的动能与飞轮相比, 其值甚小,因此,近似设计中可以认为飞轮的动能就是整 个机械的动能,即其他构件的转动惯量可忽略不计。
如图所示为作用在某机械主轴 上的驱动力矩M′和阻力矩M″的变 化曲线及机械功能E的变化情况。 由图可见:
当E=Emax时,即c点处,ω=ωmax; 当E=Emin时,即b 点处,ω=ωmin。
二、速度波动调节的目的
由于速度波动会导致在运动副中产生附加的作用力, 从而降低机械效率和工作可靠性;并引起机械的振动,影 响零件的强度和寿命;还会降低机械的精度和工艺性能, 使产品质量下降。因此,对机械运转速度的波动必须进行 调节,以便使波动程度限制在许可的范围内,从而来减轻 所产生的上述不良影响。 三、速度波动调节的方法
机械原理第七章机械的运转及其速度波动的调节

n
n
n
由两者功率相等 N Me
Ni Fivi cosi M ii
i 1
i 1
i 1
求得等效力矩:
Me
n i 1
Fi
vi 湘co潭s大学i专用 n
i 1
Mi
i
由两者动能相等
E
1 2
J e 2
n
i 1
Ei
n i 1
1 2
mivc2i
n i 1
1 2
J
2
ci i
得等效转动惯量:Je
y
ω1
1
O
A
2
M1
φ1
ω2
s2 v2 B v3
3
x
F2
(a)
等效替换的条件:
v3
me Fe v3 me Fe
(b)
(d)
1.等效力或力矩所作的功与原系统所有外力和外力矩所作的功相等:
Ne=ΣNi
2.等效构件所具有的动能应等于原系统所有运动构件的动能之和。
Ee=ΣEi
一般结论:取转动构件作为等效构件:
Fe=Fe(φ,ω,t)
Me=Me(φ,ω,t)
也可将驱动力和阻力分别进行等效处理,得出等效驱动力矩 Med或等效驱动力Fed和等效阻力矩Mer和等效阻力Fer,则有:
Me= Med –Mer Fe= Fed –Fer
三、运动方程的推演
称把为表能达量式微:分形d[式12 J的e运2 ]动 方M程湘ed潭式大学。专用或
为vi。则瞬时功率为n :
n
n
N Ni Fivi cosi Mii
i 1
i 1
i 1
式中αi为Fi与vi之间的夹角,Mi与ωi方向相同时取“+”, 相反时取“-”。
07机械设计基础第七章 机械运转速度波动的调节

选定圆盘直径D后,便可求出飞轮的质量m,由
m V
可确定飞轮的宽度B
D2
4
B
飞轮的转速越高,其轮缘材质产生的离心力越大。当轮缘材料所受离心力超过 其材料的强度极限时,轮缘便会爆裂,为了安区起见,在选择Dm和D时,应使 飞轮外缘的圆周速度不大于以下安全数值: 对铸铁飞轮:
vmax 36m / s
飞轮设计的基本问题:已知作用在主轴上的驱动力矩和阻力矩的变化规律, 在[δ ]的范围内,确定安装在主轴上的飞轮的转动惯量 JF 。 在一般机械中,其他构件所具有的动能与飞轮相比,其值甚小,因此,近似 设计中可以认为飞轮的动能就是整个机械的动能,当主轴处于最大角速度 ωmax时,飞轮具有最大动能Emax,反之,当主轴处于最小角速度ωmin时, 飞轮具有最小动能Emin, Emax与Emin之差即为一个周期内动能的最大变化量, 它是由最大盈亏功Amax转化来的。
第二节
定义:
飞轮设计的近似方法
max min m
为机器运转速度不均匀系数,它表示了机器速度波动的程度。
由ω m=(ω max +ω min)/2 以及上式可得:
ω max=ω m(1+δ /2) ω min=ω m(1-δ /2)
ω max-ω min 表示了机器主轴速度波动范围的大小,称为绝对不均匀度。
飞轮设计的近似方法
Ea Eo Aoa Eo M [ S1 ] Eb Ea Aab Ea M [ S 2 ] Ec Eb Abc Eb M [ S3 ] Ed Ec Acd Ec M [ S 4 ] Eo Ed Ado Ed M [ S5 ]
可知,当ω m一定时,δ 愈小,则差值ω max-ω min也愈小,说明机器的 运转愈平稳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械运动方程式:
2 2 2 d ( 1 J S112 1 m2vS 2 1 J S 22 1 m3v3 ) ( M11 F3v3 )dt 2 2 2 2
二.机械系统的等效动力学模型
选曲柄1的转角 1 为独 立的广义坐标(单自由度
系统),可将上式改写。
2 2 2 d ( 1 J S112 1 m2vS 2 1 J S 22 1 m3v3 ) ( M11 F3v3 )dt 2 2 2 2
N
的函数。
其特征曲线可以用一条通过N点和 C点的直线近似代替。直线方程为:
直流电机机械特性曲线
M
Md Mn 0 / 0 n
O
n
0
Mn: 电动机的额定转矩;
C
——驱动力是转动速度的函数。
直流串 激电机
O
直流并 激电机
n:电动机的额定角速度; o:电动机的同步角速度; Md、 :任意点的驱动力矩和角速度
起动
稳定运转 图11-1
ω
停车
① 常数,但在正常工作速度的平均值 m上下作周期性速度 波动——周期变速稳定运转
② =常数——等速稳定运转
功(率)特征:Wd-WcT=0 动能特征:E= Wd-WcT=0 速度特征:T=T+1
3. 停车阶段 ——
驱动力为零 ,机械 系统由正常工作速
n 2 2
v3 vC 2l vD v4 vC sin 2 2l sin 2 vC vD vCD 故 J e J1 ( z2 / z1 )2 J 2 m3 ( 2l / 2 )2 m4 ( 2l sin 2 / 2 )2
n 2 2
等效条件:
1)me (或Je)的等效条件——等效构件的动能应等于原机械系 统的总动能。 2)Fe (或Me)的等效条件——等效力Fe (或等效力矩Me)的瞬 时功率应等于原机构中所有外力在同一瞬时的功率代数和。
一般意义的等效动力学模型
等效质量 (转动惯量) 等效力(矩)
v J e mi Si J Si i i 1 2 n vi M e Fi cos i M Si i i 1
曲柄滑块机构中: 已知: J1;m2、 JS2; m3;M1、F3 。 设: 1、 2、vs2、 v3 。
2 2 2 dE d ( 1 J S112 1 m2vS 2 1 J S 22 1 m3v3 ) 2 2 2 2
dW ( M11 F3v3 )dt Pdt
第七章 机械的运动及其速度波动 的调节
本章教学内容
◆ 机械的运动方程式 ◆ 机械运动方程式的求解 ◆ 稳定运转状态下机械的周期性速 度
本章重点:
等效质量、等效转动惯
量、等效力、等效力矩
的概念及其计算方法; 机械运动产生速度波动 的原因及其调节方法。
波动及其调节
◆ 机械的非周期性速度波动及其调 节
n 2 2
2)取移动构件为等效构件 等效质量
等效力
v me mi S i J Si i v v i 1 n v Fe Fi cos i i M i i i 1
构件相对于等效构件的速度比有关;
无关。 件的速度比平方有关; 速度无关。
等效力(矩)与机械系统驱动构件的真实速度 质量(转动惯量)与机械系统驱动构件的真实
例:已知z1= 20、z2 = 60、 J1、 J2、 m3、 m4、M1、F4及曲柄长为l,现 取曲柄为等效构件。求图示位置时 的 Je、Me。 解
v J e mi Si J Si i 等效转动惯量 i 1 Je J1 (1 / 2 )2 J2 m3 (v3 / 2 )2 m4 (v4 / 2 )2 2 n vi 等效力矩 M e Fi cos i M Si i i 1 Me M1 (1 / 2 ) F4 cos180 (v4 / 2 )
惯性力
驱动力——由原动机产生。其变化规律决定于原动机的 机械特性。 原动机的机械特性:原动机发出的驱动力与运动参数(位移、
速度或时间)之间的关系称为原动机的机械特性。
F f (v ) M f ( )
或
不同的原动机具有不同的机械特性。
交流异步电动机机械特性
曲线——驱动力是转动速度
M
B A
内燃机的机械 特性曲线
——驱动力是转动位置的函数。 M
工作阻力——机械工作时需要克服的工作负荷, 它决定于机械的工艺特性。 1)生产阻力常数
2)生产阻力是位移的函数
3)生产阻力是速度的函数
4)生产阻力是时间的函数
§7-2 机械的运动方程式
一.机械运动方程式的一般表达式
机械运动方程式——机械上的力、构件的质量、转动惯量和 其运动参数之间的函数关系。
2
用等效转质量(me)和等效力(Fe)表示的机械运动方程式的一 般表达式为 2 d[ 1 me ( s3 )v3 ] Fe ( s3 , v3 , t )v3dt 2
等效质量、等效力也是机构位置的函数,与 注意! 速比有关,与机构的真实速度无关。
曲柄滑块机构 等效力学模型
2 m vS 2 m v3 2 3 J e J S1 J S 2 1 1 1 M M F v3 1 3 e 1
Je
等效转动惯量 J e J e (1 )
M e 等效力矩
Me Me (1 , 1 , t )
用等效转动惯量(Je)和等效力矩(Me)表示的机械运动方程式 的一般表达式为
2 d[ 1 J e ( 1 )1 ] M e ( 1 , 1 , t )1dt 2
一个单自由度机械系统的运动, 可以等效为一个具有等效转动 惯量Je(),在其上作用有等效 力矩Me(,,t)的假想简单构件 的运动,该假想的构件称为等
本章教学目的
◆ 了解机器运动和外力的定量关系
难点:
盈亏功的计算。
◆ 了解机器运动速度波动的原因、特点、 计算飞轮转动惯量时最大 危害 ◆ 掌握机器运动速度波动的调节方法
一.研究目的和内容
§7-1 概述
运动分析时,都假定原动件作匀速运动,实际上是多个参 数的函数。
1、由于机械的运动规律是由各构件的质量、转动惯量和作用 力等因素决定的,随时间变化而变化,要对机械进行精确的运 动分析和力分析,就要研究在外力作用下,机械的真实运动规 律。
1 J 2 n 1 m v2 n 1 J 2 1 m v2 E Ei Si i 2 Si i 2 i Si 2 i Si i 1 i 1 i 1 i 1 2
n n
Байду номын сангаас
机构在dt时间内的动能增量:
2 dE d 1 J Si i2 1 mi vSi 2 i 1 2
效构件,也称为原机械系统的
等效动力学模型。
等效转动惯量、等效力矩是机构位置的函数, 注意! 与速比有关,与机构的真实速度无关。
等效构件也可选用移动构件。在上图所示的曲柄滑块机构中,如 选取滑块3为等效构件(其广义坐标为滑块的位移s3),运动方程式 可改写成下列形式:
v3 1 ) 2 m ( vS 2 ) 2 J ( 2 ) 2 m v M 1 F d t d J ( 2 S2 3 3 1 3 2 S1 v 3 v3 v3 v3 Fe me 等效力 Fe Fe ( s3 , v3 , t ) 等效质量 me me ( s3 )
n 2 2
等效力(矩)的特征:
等效力(矩)是一个假想力(矩);
质量(转动惯量)的特征:
等效质量(转动惯量)是一个假想质量(转动
等效力(矩)为正,是等效驱动力(矩),反之, 惯量); 为等效阻力(矩); 等效质量(转动惯量)不仅与各构件质量和转 动惯量有关,而且与各构件相对于等效构 等效力(矩)不仅与外力(矩)有关,而且与各
n n i 1
机构上所有外力在dt时间内作的功:
dW [ ( Fi vi cos i M i i )]dt
机械运动方程式的一般表达式
n
1 m v 2 1 J 2 )] [ n ( F v cos M )]dt d[ ( i i i Si Si i i i i 2 i 1 2 i 1
ω
度逐渐减速,直到
停止。
起动 稳定运转 图11-1 停车
功(率)特征:Wd-Wc= -Wc
动能特征:E= Wd-Wc= -Wc<0 速度特征:i+1< i
ω
三.作用在机械上的力
1. 作用在机械上力的的种类 2. 驱动力和生产阻力
内 外
力 ——反力、摩擦力 驱 动 力 力 生产阻力 重 力
2、由于机械在运动过程中会出现速度波动,导致运动副产生
附加动压力,并引起振动,从而降低机械使用寿命、效率和工
作质量,因此需研究机械运转过程中,速度的波动及其调节方
法。
二.机械运转的三个阶段
根据动能定理 Wd-Wc=E
ω
稳定运转 图11-1 ω
驱动功
阻抗功 输出功 Wr和损 失功Wf 之和
动能
起动
停车
1. 起动阶段——原动件的速度由零逐渐上升到开始稳定的过程。
功(率)特征:外力对系统做正功Wd-Wc>0 动能特征:系统的动能增加E=Wd-Wc>0 速度特征:系统的速度增加 =0 m
