离散数学ch1-2
离散数学1-1,1-2

(疑4)问你句今:年提暑出假问题去的旅句行子吗,句?末(用疑问问号。句) (感5)叹克句里:特带岛有人浓说厚感:情“的克句里子特,岛句末人用是感说叹谎号话。者”。
(悖论)
悖:相反。悖论:自相矛盾的陈述。
h)我们要努力学习。
第十五页,共52页。
离散数学
解:
Hale Waihona Puke a),c),e)是原子命 题,f)是复合命题。
a)离散数学是计算机科学系的一门必修课。 是命题, 真值为T。
b)小李有空吗? 疑问句,不是命题。 c)明天我去看电影。 是命题,真值要根据具体情况 确定。
d)请勿随地吐痰! 祈使句,不是命题。 e)不存在最大质数。 是命题,真值为T。 f)如果我掌握了英语、法语,那么学习其他欧洲语 言就容易的多。 是命题,真值为T。 g)x=3 不是命题,x=3的真假由x确定,当x取3时句 子为真,当x取其他值时句子为假。 h)我们要努力学习。 祈使句,不是命题。
第二十一页,共52页。
离散数学
2/7
与“和”有相同意义的汉字还有“与”、“以及”、 “并且”、“而且”等。
例:P:今天下雨。
Q:明天下雨。
上述命题的合取为
P∧Q:今天下雨而且明天下雨。
P∧Q:今天与明天都下雨。 P∧Q:这两天都下雨。 显然只有当“今天下雨”与“明天下雨”都是真时, “这两天都下雨”才是真的。
祈使句、疑问句、感叹句 等都不能作为命题,悖论
无真值,也不能作为命题。
语句(7)—(11)都不是 命题。
第十三页,共52页。
离散数学
3、分类
离散数学(1.2逻辑联接词)资料

P
┐P
F
T
T
F
4
第一章 命题逻辑(Propositional Logic) 1.2逻辑
联结词(Logical Connectives)
例1. P: 天津是一个城市. Q: 3是偶数.
于是: ┐P: 天津不是一个城市. ┐Q: 3不是偶数.
例2. P:苏州处处清洁. Q:这些都是男同学. ┐P:苏州不处处清洁 (注意,不是处处不清洁). ┐Q:这些不都是男同学.
联结词“ ”的定义真值表
P
Q
PQ
F
F
T
F
T
F
T
F
F
T
T
T
18
第一章 命题逻辑(Propositional Logic) 1.2逻辑
联结词(Logical Connectives)
注:(1)P仅当Q 可译为P→Q P当Q 可译为Q→P P当且仅当Q 译为P Q
(2)“ ”属于二元(binary)运算符。 (3) 双条件命题P Q所表达的逻辑关系是, P与Q互
(5)如果 2+2=4, 则太阳从东方升起。 (P →Q, T)
P
Q
如果 2+2=4, 则太阳从西方升起。 (P →R, F)
R
如果 2+2 4, 则太阳从东方升起。 (┐P →Q , T) 如果 2+2 4, 则太阳从西方升起。 (┐P →R, T)
注意: (1)与自然语言的不同:前件与后件可以没有任何内在联系! (2) 在数学中,“若P则Q”往往表示前件P为真,则后件Q为真的
(2) ”“ 属于二元(binary)运算符。
例5. 将下列命题符号化。 (1)天不下雨,则草木枯黄。 P:天下雨。 Q:草木枯黄。 则原命题可表示为: ┐P→Q。
ch1-2

A
B
= 0. 4 + (1- 0. 3 ) - 0. 3 = 0. 8 ;
会利用概率的性质计算事件 的概率
例8 (P12 例8) 设 P(A)= P(B)= P(C)= 1/4 , P(AC)= P(BC)= 1/6 , P(AB)= 0, 求事件 A , B, C 全不发生的概率. 余概公式 解 P( A B C ) P ( A B C )
包含, 相等, 互斥, 对立
样本空间 —— 所有基本事件构成的集合 基本事件 事件的关系及运算 —— 四种关系和三种仅关心试验中会出现哪些事件,或者某事件 发生的可能性大不大, 即只有一个定性的描述是不够的, 准确了 解事件发生的可能性即概率的大小,对人们的生活有重要意义. 更重要的是对事件出现的可能性的大小有一个定 量的描述.这就需要有一个度量事件发生可能性大小的 数量指标. 事件的概率就是事件发生可能性大小的一个数值度量.
对偶律
例9 设 P(A)=0.6, P(B)=0.7,问在何条件下P(AB)取得最 最大值 大(小)值?最大(小)值是多少? 解 P ( AB ) P ( A ) P ( B ) P ( A B ) P ( A ) P ( B ) 1 0.3 , 即 当 P ( A B ) 1 时, P(AB)取得最小值 0.3 ; 最小值 最大值 又 P ( AB ) P ( A) 0. 6, 即 当 P ( A B ) P ( A ) 时P(AB) 取得最大值 0. 6. 如果将回答改成: A B 时, P(AB)取得最小值 0.3 是否正确? 这个命题并不成立! 这相当于问如下命题是否正确:
二、概率
离散数学ch

布尔代数的性质
定理11.8 设<B,∧,∨, , 0, 1>是布尔代数, 则 (1) a∈B, (a) = a . (2) a,b∈B, (a∧b) = a∨b, (a∨b) = a∧b (德摩根律)
证 (1) (a)是a的补元, a也是a的补元. 由补元惟一性得(a)=a. (2) 对任意a, b∈B有
例7 考虑下图中的格. 针对不同的元素,求出所有的补元.
16
解答
(1) L1中 a 与 c 互为补元, 其中 a 为全下界, c为全上界, b 没有 补元.
(2) L2中 a 与 d 互为补元, 其中 a 为全下界, d 为全上界, b与 c 也互为补元.
(3) L3中a 与 e 互为补元, 其中 a 为全下界, e 为全上界, b 的补 元是 c 和 d ; c 的补元是 b 和 d ; d 的补元是 b 和 c ; b, c, d 每个元素都有两个补元.
定理11.1 设<L, ≼>是格, 则运算∨和∧适合交换律、结合 律、 幂等律和吸收律, 即 (1) a,b∈L 有
a∨b = b∨a, a∧b = b∧a (2) a,b,c∈L 有
(a∨b)∨c = a∨(b∨c), (a∧b)∧c = a∧(b∧c) (3) a∈L 有
a∨a = a, a∧a = a (4) a,b∈L 有
(4) 显然
a∨(a∧b)≽ a
由 a ≼a, a∧b ≼ a 可得
由式(5)和(6) 可得 根据对偶原理,
a∨(a∧b) ≼a a∨(a∧b) = a, a∧(a∨b) = a
(5) (6)
7
格的性质:序与运算的关系
定理11.2 设L是格, 则a,b∈L有 a ≼ b a∧b = a a∨b = b
离散数学第2章ppt课件

C
n
A k A 1A 2 A n
k 1
二、集合的并 (Union)
3、性质
1)幂等律 A∪A =A
2)零律
A∪U =U
3)同一律 A∪ =A
4)交换律 A∪B =B∪A
5)结合律 A∪(B∪C) =(A∪B)∪C
二、集合的并 (Union)
3、性质
, 6)
若A⊆B,C⊆D,则A∪C
是集合,没有元素
有1个元素的集合
2) ∈{}, {}
五、特殊集合
1、空集
定理 空集是任一集合A的子集,即 ⊆A。
下列命题是否为真。
1)√⊆;
2) ∈ ; 3) ⊆{}; 4) ∈{} 。
√
√
五、特殊集合
1、空集
推理 空集是唯一的。(绝对唯一)
证明: 设1,2是两个空集, 则1 2,且2 1,
证明唯一性 一般采用反
1、符号表示法
通常用大写字母A, B, C, …代表集合; 用小写字母a, b, c, …代表元素。
1)如果a是集合A的一个元素, 则记为 a∈A, 读做“a属于A”,或 “a在集合A中”。
2)如果a不是集合A的一个元素, 则记为 a∈A, 读做“a不属于A”,或 “a不在集合A中”。
注:任一元素, 对某一集合而言, 或属于该集合, 或不属于该集合, 二者必居其一, 且只居其一。
1) 若b∈A,则b是不给自己刮脸的人, 而由题意,b只给集合A中的人刮脸。 ∴b 要给b 刮脸, 即b ∈ A。
理发师问题
在一个很僻静的孤岛上,住着一些人家,岛上只 有一位理发师,该理发师专给那些并且只给那些自己 不刮脸的人刮脸。那么,谁给这位理发师刮脸?
离散数学知识点总结

离散数学知识点总结离散数学是数学的一个分支,主要研究离散的数学结构和离散的数学对象。
它包括了许多重要的概念和技术,是计算机科学、通信工程、数学和逻辑学等领域的基础。
本文将对离散数学的一些核心知识点进行总结,包括命题逻辑、一阶逻辑、图论、集合论和组合数学等内容。
1. 命题逻辑命题逻辑是离散数学的一个重要分支,研究命题之间的逻辑关系。
命题是一个陈述语句,要么为真,要么为假,而且不能同时为真和为假。
命题逻辑包括逻辑运算和逻辑推理等内容,是离散数学的基础之一。
1.1 逻辑运算逻辑运算包括与(∧)、或(∨)、非(¬)、蕴含(→)和双条件(↔)等运算。
与、或和非是三种基本的逻辑运算,蕴含和双条件则是基于这三种基本运算得到的复合运算。
1.2 逻辑等值式逻辑等值式是指在命题逻辑中具有相同真值的两个复合命题。
常见的逻辑等值式包括德摩根定律、双重否定定律、分配率等。
1.3 形式化证明形式化证明是命题逻辑的一个重要内容,研究如何利用逻辑规则和等值式来推导出给定命题的真值。
形式化证明包括直接证明、间接证明和反证法等方法,是离散数学中的常见技巧。
2. 一阶逻辑一阶逻辑是命题逻辑的延伸,研究命题中的量词和谓词等概念。
一阶逻辑包括量词、谓词逻辑和形式化证明等内容,是离散数学中的重要部分。
2.1 量词量词包括全称量词(∀)和存在量词(∃),用来对命题中的变量进行量化。
全称量词表示对所有元素都成立的命题,而存在量词表示至少存在一个元素使命题成立。
2.2 谓词逻辑谓词逻辑是一阶逻辑的核心内容,研究带有量词的语句和谓词的逻辑关系。
谓词是含有变量的函数,它可以表示一类对象的性质或关系。
2.3 形式化证明形式化证明在一阶逻辑中同样起着重要作用,通过逻辑规则和等值式来推导出给定命题的真值。
一阶逻辑的形式化证明和命题逻辑类似,但更复杂和抽象。
3. 图论图论是离散数学中的一个重要分支,研究图和图的性质。
图是由节点和边组成的数学对象,图论包括图的表示、图的遍历、最短路径、最小生成树等内容,是离散数学中的一大亮点。
离散数学第一二章定义概念

二、谓词逻辑Predicate Logic●个体和谓词3 是偶数4 是偶数用P(x)来表示x 是偶数,那么两个命题就可以用P(3), P(4) 来表示,这里P(x) 是一元谓词,3,4是个体●一般用小写字母表示个体,大写字母表示谓词●谓词可以是多元的。
如用P(x,y)表示x>y,那么P(4,3)就表示命题4>3;也可以用Q(x)表示x>3,那么Q(4)也表示命题4>3●命题可以看成0元谓词量词●全称量词(任意)●存在量词●量词只作用到个体变元上,谓词和量词结合,可以构成意思完整的命题如任何整数都是偶数这一命题可以如下表示。
●P(x) : x是整数;Q(x): x 是偶数●注意:量词只作用到个体变元上,不作用到谓词变元上。
所以我们这里介绍的谓词逻辑更准确地也叫一阶逻辑(First-order Logic),区别于高阶谓词逻辑。
●谓词逻辑的公式(1)P, P(a),P(x,y) 等是公式(2)若A是公式,则¬A是公式(3)若A和B都是公式,A^B, AvB, A B,A B都是公式(4) 若a是公式,则都是公式量词的作用域自由变元和约束变元●量词的作用域是跟在量词后最小的命题公式●受量词限制的变元是约束变元●不受量词限制的为自由变元●例子:闭区间上的连续函数可积。
g(x)在闭区间[a,b]上连续。
所以,g(x)在闭区间[a,b]上可积。
●P(f,a,b)表示f(x)是[a,b]的连续函数。
Q(f,a,b)表示f(x)在[a,b]上可积。
●谓词公式的赋值:把(自由)个体变元用特定的个体代替,把谓词变元用确定的谓词代替。
●若对所有的赋值,谓词公式的真值都为真,则称为有效的。
(类似于命题公式的永真式)●若存在一种赋值使得谓词公式为真,则称为可满足的。
等价式与蕴涵式●若A↔B是有效的,就称A和B是等价的。
记作A⇔B●若A →B是有效的,称公式A蕴涵公式B,记作A⇒B量词与否定联结词●P(a,b) 表示a>b●C(a,b,c) 表示|a-b|<c●那么极限不存在应该如何说呢?量词的分配二元关系Binary Relation有序对●有序对(x1,y1)和(x2,y2)相等的充分必要条件是●x1=x2 并且y1=y2笛卡尔乘积●给定集合A和B,它们的笛卡尔乘积定义为(二元)关系●A,B是两个集合,则AxB的子集●R 称为从A到B的一个(二元)关系。
ch1-1,2,3

离散数学-lecture1
20
实例
Example1 写出下列命题的否定命题 (a) P:上海是一个大城市。 :上海是一个大城市。 ﹁P:上海不是一个大城市。 :上海不是一个大城市。 上海是一个不大的城市。 上海是一个不大的城市。 (b) P: 昨天张三去看球赛了。 : 天张三去看球赛了。 ﹁P:昨天张三没有去看球。 :昨天张三没有去看球。
离散数学-lecture1
2
数理逻辑的产生
创建了逻辑学,逻辑是探索、 亚里士多德 创建了逻辑学,逻辑是探索、阐述和确立有效推 理原则的学科。 理原则的学科。 布莱尼次 提出用数学研究推理的思想 英国数学家布尔 发表了《逻辑的数学分析》,建立了“布尔 发表了《逻辑的数学分析》 建立了“ 代数” 创造一套符号系统, 代数”,创造一套符号系统,利用符号来表示逻辑中的各种 概念, 概念,奠定了数理逻辑的基础 出版了《数论的基础》一书, 德国数学家弗雷格 出版了《数论的基础》一书,使得数理逻 辑的符号系统更加完备 美国人皮尔斯著作中引入了逻辑符号 美国人皮尔斯著作中引入了逻辑符号
离散数学-lecture1 12
实例(三) 实例(
Example3 下列句子中哪些是命题? 下列句子中哪些是命题? (a) 好大的雪啊! 好大的雪啊! (b) 8大于 吗? 大于12吗 大于 (c) 请勿吸烟. 请勿吸烟 (d) 本页这一行的这句话是假话。 本页这一行的这句话是假话。 (e) x-y=y-x (f) 如果 2=0,那么 如果A ,那么A=0. (1)是感叹句 是疑问句 是祈使句 和(6)缺少上 是感叹句,(2)是疑问句 是祈使句,(5)和 缺少上 是感叹句 是疑问句,(3)是祈使句 下文,(4)是悖论 是悖论。 下文 是悖论。
离散数学的定义精简版

图1.每个无向图所有结点度总和等于边数的2倍.2每个无向图中,奇数度的结点必为偶数个.3G=<V ,E>是有向图, 则G 的所有结点的出度之和等于入度之和.4无向完全图Kn, 有边数 5有n 个结点的有向简单完全图有边数为n(n-1).6有n 个结点的有向完全图, 有边数 n2.12 两个图同构的必要条件:1.结点个数相等. 2.边数相等.3.度数相同的结点数相等. 4. 对应的结点的度数相等.17 在一个有n 个结点的图中,如果从结点vi 到vj 存在一条路,则从vi 到vj 必存在一条长度不多于n-1的路.19 连通分支:令G=<V ,E>是无向图, R 是V 上连通关系, 设R 对V 的商集中有等价类V1,V2,V3,…, Vn ,这n 个等价类构成的n 个子图分别记作G(V1),G(V2),G(V3),…, G(Vn),并称它们为G 的连通分支. 并用W(G)表示G 中连通分支数.28 如果从u 到v 不可达,则d<u,v>=∞29 图的直径: G 是个有向图, 定义D=max{d<u,v>} u,v ∈V 为图G 的直径.30强连通、单侧连通和弱连通:在简单有向图G 中,如果任何两个结点间相互可达, 则称G 是强连通. 如果任何一对结点间, 至少有一个结点到另一个结点可达, 则称G 是单侧连通. 如果将G 看成无向图后(即把有向边看成无向边)是连通的,则称G 是弱连通.31一个有向图G 是强连通的,当且仅当G 中有一个回路, 此回路至少包含每个结点一次. 32一. 邻接矩阵这是以结点与结点之间的邻接关系确定的矩阵.1.定义:设G=<V ,E>是个简单图,V={v1,v2,v3,…,vn }, 一个n ×n 阶矩阵A=(aij)称为G 的邻接矩阵. 其中:aij ={ 1 vi 与vj 邻接, 即(vi,vj)∈E 或 < vi,vj >∈E0 否则33从邻接矩阵看图的性质:无向图:每行1的个数=每列1的个数=对应结点的度有向图:每行1的个数=对应结点的出度每列1的个数=对应结点的入度34在(A(G1))2 中a342 =2 表示从v3到v4有长度为2的路有2条:在(A(G1))3中a233 =6 表示从v2到v3有长度为3的路有6条:设G=<V ,E>是简单图,令V={v1,v2,v3,…,vn}, G 的邻接矩阵(A(G))k 中的第 i 行第j 列元素aijk=m, 表示在图G 中从vi 到vj 长度为k 的路有m 条.35二.可达性矩阵1.定义:设G=<V ,E>是个简单图,V={v1,v2,v3,…,vn }, 一个n ×n 阶矩阵P=(pij)称为G 的可达性矩阵. 其中: pij ={1 vi 到vj 可达, (至少有一条路)0 否则)1(21 n n37三.完全关联矩阵此矩阵是按照结点与边之间的关联关系确定的矩阵.1.无向图的完全关联矩阵1).定义:设G=<V,E>是个无向图,V={v1,v2,v3,…,vm },E={e1,e2,e3,…,en },一个m×n阶矩阵M=(mij)称为G的完全关联矩阵. 其中:mij ={ 1 vi与ej关;0 否则2).从关联矩阵看图的性质:a)每列只有二个1.(因为每条边只关联两个结点)b)每行中1的个数为对应结点的度数.c)如果两列相同,则说明对应的两条边是平行边.2.有向图的完全关联矩阵1).定义:设G=<V,E>是个简单有向图,V={v1,v2,v3,…,vm },E={e1,e2,e3,…,en },一个m×n阶矩阵M=(mij)称为G的完全关联矩阵. 其中: mij ={1 vi是ej的起点;-1 vi是ej的终点;0 vi与ej不关联2).从关联矩阵看图的性质:a)每列只有一个1和一个-1.(每条边有一个起点一个终点)b)每行中1的个数为对应结点的出度.-1个数是结点入度38关键路径:就是各个结点的缓冲时间均为0的路径.39 欧拉路:在无孤立结点的图G中,如果存在一条路,它经过图中每条边一次且仅一次, 称此路为欧拉路.40 欧拉回路:在无孤立结点的图G中,若存在一条回路,它经过图中每条边一次且仅一次,称此回路为欧拉回路.41有欧拉路与有欧拉回路的判定:无向图G具有欧拉路,当且仅当G是连通的,且有零个或两个奇数度的结点.42无向图G具有欧拉回路,当且仅当G是连通的,且所有结点的度都是偶数.43汉密尔顿图:定义:设G=<V,E>是个无向有限图,汉密尔顿路:通过G中每个结点恰好一次的路.汉密尔顿回路(H回路):通过G中每个结点恰好一次的回路.汉密尔顿图(H图):具有汉密尔顿回路(H回路)的图.44汉密尔顿图的判定:到目前为止并没有判定H图的充分和必要条件.(充分条件):G是完全图,则G是H图.(充分条件)设G是有n个结点的简单图,若G中每对结点度数之和大于等于n-1(n),则G 有一条H路(H回路)注意:上述条件只是充分条件,而不是必要条件,即不满足这个条件的, 也可能有H路.45 (必要条件) 若图G=<V,E>有H回路,则对V的任何非空子有限集S, 均有W(G-S)≤|S|, 其中W(G-S)是从G中删去S中所有结点及与这些结点关联的边所得到的子图的连通分支数. 48完全二部图:令G=<V,E>是以V1,V2为互补的结点子集的二部图,如果V1中的每个结点都与V2中每个结点相邻接,则称G是完全二部图. 如果|V1|=m, |V2|=n 则G记作Km,n 49.二部图的判定: 定理G=<V,E>是二部图当且仅当它的所有回路的长度都是偶数.52两个重要的非平面图:K5和K3,353 欧拉公式G是个连通的平面图, 设v、e、r分别表示G中结点数、边数、面数, 则有v-e+r=2. 称此式为欧拉公式.54 平面图的判定(必要条件) 设G是有v 个结点、e条边的连通简单平面图, 若v≥3, 则e ≤3v-6.55一个图是平面图的充分且必要条件是它不含有任何与K5、K3,3在2度结点内同构的子图.56如果G1和G2是同构的,或者通过反复插入或删去度数为2的结点, 使得它们变成同构的图, 称G1和G2 是在2度结点内同构.树1度数为1的结点,称为叶结点. 分支结点(内结点):度数大于1的结点.2无回路且e=v-1 其中e是T的边数,v是T的结点数.3如果图G的生成子图是树,则称此树为G的生成树.4图G中,不在其生成树里的边,称作弦. 所有弦的集合,称为该生成树的补.5连通图至少有一棵生成树. 寻找生成树的方法:深度优先;广度优先.6一棵生成树中的所有边的权之和称为该生成树的权. 具有最小权的生成树,称为最小生成树.7根树:如果一棵有向树,恰有一个结点的入度为0,其余所有结点的入度均为1,则称此树为根树. 1.树根:入度为0的结点. 2.叶:出度为0的结点. 3.分支结点(内结点):出度不为0的结点. 8在有向树中,如果规定了每一层上的结点的次序,称之为有序树.9 1.m叉树:在根树中,如果每个结点的出度最大是m, 则称此树是m叉树.2.完全m叉树:在根树中,如果每个结点的出度都是m或者等于0, 则称此树是完全m叉树.3. 正则m叉树:在完全m叉树中,如果所有树叶的层次相同, 则称之为正则m叉树.10 T是棵完全m叉树, 有t个叶结点, i个分支结点,则(m-1)i=t -1 .11 m叉有序树转化成二叉树:方法是:1.每个结点保留左儿子结点, 剪掉右边其它分支. 被剪掉的结点如下处理.2.同一个层次的结点, 从左到右依次画出.12 1.先序遍历⑴访问根结点.⑵先序遍历左子树⑶先序遍历右子树2.中序遍历⑴中序遍历左子树⑵访问根结点.⑶中序遍历右子树3.后序遍历⑴后序遍历左子树⑵后序遍历右子树⑶访问根结点.代数系统20 <X,★>和<X,★, ο>是代数系统, ★,ο是二元运算:1.封闭性:∀x,y∈X, 有x★y∈X。
图论及其应用ch1-2详解

几个有趣的图论问题
Kö nigsberg七桥背后的故事
Graph Theory
/图论
Kö nigsberg七桥位于前苏联的加里宁格勒,历史上 曾是德国东普鲁士省的省会,霹雷格尔横 穿城堡,河中有两个小岛B与C,并有七座桥连接岛与 河岸及岛与岛(见图)。是否存在一种走发,从四块 陆地中的任意一块开始,通过每一座桥恰好一次再回 到起点。这就是著名的Kö nigsberg七桥问题,即一笔 画问题;也是图论的起源。
Graph Theory
/图论
在一个图G (V (G ), E (G ), G )中, 如果 G (e ) uv , 则说边e 连接 顶点u, v , 称u, v为e的端点 ,称u和v是 相邻的,而称u(或v )与e 关联。 与同一个顶点关联的若 干条边称为相邻的 。 两个端点重合为一个顶 点的边称为环; 关联于同一对顶点的两 条或以上的边称为 多重边 。
有
实际上,有向图即将无向图中的无序对看成有序对. 其中有向图对应的无向图称为有向图的基础图。 其中V(G)称为顶点集,E(G)称为边集(A(D)又称为 弧集).令p(G)=|V(G)|,q(G)=|E(G)|, 分别称为图的 阶和边数。举例说明。
11/19/2018 10:03 PM Li-Li Zhang 14
11/19/2018 10:03 PM Li-Li Zhang 12
1.2 图的定义
Graph Theory
/图论
生活中,人们常常需要考虑一些对象之间的某种特定 的关系 . 如某区域内,两城市之间有无交通线;一群 人中,两个人之间相识或不相识等等 . 这种关系是对 称的,即如果甲对于乙有某种关系,则乙对于甲也有 这种关系 . 可以用一个图形来描述给定对象之间的某 个关系:我们用平面上的点分别表示这些对象,若 对象甲和乙有关系,就用一条线连接表示甲和乙的 两个点 . 这种由一些点与连接其中某些点对的线所构 成的图形就是图论中所研究的图. 图/Graph:可直观地表示离散对象之间的相互关系, 研究它们的共性和特性,以便解决具体问题。
《离散数学》第二章 一阶逻辑 讲稿

2.1 一阶逻辑基本概念一、本节主要内容基本概念——个体词、谓词、量词命题符号化二、教学内容个体词(个体): 所研究对象中可以独立存在的具体或抽象的客体,它可以是一个具体的事物,也可以是一个抽象的概念. 表示主语的词(名词或代词):苏格拉底,2,黑板,自然数,思想,定理.个体常项:具体的或特定的个体词,用a, b, c表示个体变项:抽象的或泛指的个体词,用x, y, z表示个体域: 个体变项的取值范围有限个体域,如{a, b, c}, {1, 2}无限个体域,如N, Z, R, …全总个体域: 宇宙间一切事物组成基本概念谓词: 表示个体词的性质或相互之间关系的词谓词常项:表示具体性质或关系的谓词F: …是人,F(a):a是人G:…是自然数,F(2):2是自然数谓词变项:表示抽象的或泛指的谓词F: …具有性质F,F(x):x具有性质F元数:谓词中所包含的个体词数一元谓词: 表示事物的性质多元谓词(n元谓词, n 2): 表示个体词之间的关系如L(x,y):x与y有关系L,L(x,y):x比y高2厘米注意:多元谓词中,个体变项的顺序不能随意改动个体变项和谓词的联合体,F(x),L(x,y),也称为谓词n元谓词L(x1, x2,…, xn)可看作一个函数,定义域为个体变项的个体域,值域为{0,1}n元谓词L(x1, x2,…, xn)的真值不确定,不是命题, 如:L(x,y)如果L(x,y)表示“x小于y”,谓词部分已经是常项,但还不是命题.考虑L(2,3)和L(3,2)L(x1, x2,…, xn)是命题:只有当L是常项,x1, x2,…, xn是个体常项0元谓词: 不含个体变项的谓词, 如L(a, b)如L的意义明确,则0元谓词都是命题一阶逻辑中命题符号化例1 用0元谓词将命题符号化要求:先将它们在命题逻辑中符号化,再在一阶逻辑中符号化(1) 墨西哥位于南美洲在命题逻辑中, 设p: 墨西哥位于南美洲符号化为p, 这是真命题在一阶逻辑中, 设a:墨西哥,F(x):x位于南美洲符号化为F(a)例1(续)(2) 是无理数仅当是有理数在命题逻辑中, 设p:是无理数,q:是有理数.符号化为p → q, 这是假命题在一阶逻辑中, 设F(x): x是无理数, G(x): x是有理数符号化为(3) 如果2>3,则3<4在命题逻辑中, 设p:2>3,q:3<4.符号化为p→q, 这是真命题在一阶逻辑中, 设F(x,y):x>y,G(x,y):x<y,符号化为F(2,3)→G(3,4)(4)如果张明比李民高,李民比赵亮高,则张明比赵亮高.在命题逻辑中, 设p:张明比李民高,q:李民比赵亮高, r:张明比赵亮高.符号化为:p ∧ q → r在一阶逻辑中, 设F(x,y):x比y高a:张明,b:李民,c:赵亮符号化为:F(a, b) ∧ F(b, c) → F(a, c)基本概念(续)量词: 表示数量的词例如(1)所有的人都要死的;(2)有的人活一百岁以上;全称量词∀: 表示任意的, 所有的, 一切的等∀x 表示对个体域中所有的个体,∀x F(x)表示个体域中所有的个体都有性质F.∀x F(x),其中F(x):x是要死的,个体域为人类集合存在量词∃: 表示存在着, 有的, 有一个,至少有一个等∃x 表示存在个体域中的个体,∃x F(x)表示存在着个体域中的个体具有有性质F ∃x G(x),其中G (x):x活一百岁以上,个体域为人类集合如果个体域D为全总个体域,则∀x F(x),其中F(x):x是要死的,表示宇宙间的一切事物都要死的.∃x G(x),其中G (x):x活一百岁以上,表示宇宙间的一切事物中存在活一百岁以上的. 特性谓词:M(x): x是人符号化为:(1)∀x (M(x) → F(x))(2)∃x (M(x) ∧ G(x))考虑:(1)∀x (M(x) ∧ F(x))(2)∃x (M(x) → G(x))一阶逻辑中命题符号化(续)例2 在一阶逻辑中将下面命题符号化(1) 人都爱美; (2) 有人用左手写字分别取(a) D为人类集合, (b) D为全总个体域.解:(a) (1) 设G(x):x爱美, 符号化为∀x G(x)(2) 设G(x):x用左手写字, 符号化为∃x G(x)(b) 设F(x):x为人,G(x):同(a)中(1) ∀x (F(x)→G(x))(2) ∃ x (F(x)∧G(x))这是两个基本公式, 注意这两个基本公式的使用.一阶逻辑中命题符号化(续)例3 在一阶逻辑中将下面命题符号化(1) 正数都大于负数(2) 有的无理数大于有的有理数解注意: 题目中没给个体域, 一律用全总个体域(1) 令F(x): x为正数, G(y): y为负数, L(x,y): x>y∀x(F(x)→∀y(G(y)→L(x,y))) 或∀x∀y(F(x)∧G(y)→L(x,y)) 两者等值(2) 令F(x): x是无理数, G(y): y是有理数,L(x,y):x>y∃x(F(x)∧∃y(G(y)∧L(x,y)))或∃x∃y(F(x)∧G(y)∧L(x,y)) 两者等值一阶逻辑中命题符号化(续)几点注意:1元谓词与多元谓词的区分无特别要求,用全总个体域量词顺序一般不要随便颠倒例:对任意x,存在着y,使得x+y=5. 个体域为实数集.符号化为:∀x ∃y H(x,y), 其中H(x,y):x+y=5考虑∃y ∀x H(x,y) 否定式的使用例:在一界逻辑中命题符号化①没有不呼吸的人②不是所有的人都喜欢吃糖③不是所有的火车都比所有的汽车快①⌝∃x( F(x)∧⌝G(x))其中F(x):x是人,G(x):x呼吸或者:∀x( F(x) →G(x))②⌝∀x( F(x) →G(x))其中F(x):x是人,G(x):x喜欢吃糖或者:∃x( F(x)∧⌝G(x))③⌝∀x( F(x) →∀y (G(y) →H(x,y)) )或者:∃x( F(x)∧∃y (G(y) ∧⌝ H(x,y)) )例:在一界逻辑中命题符号化①一切人都不一样高②每个自然数都有后继数③有的自然数无先驱数①∀x ∀y( F(x) ∧F(y) ∧ G(x,y) →⌝H(x,y))其中F(x):x是人,G(x,y) :x和y不是同一个人,H(x,y):x和y一样高或者:⌝∃x ∃y( F(x) ∧F(y) ∧ G(x,y) ∧H(x,y))②∀x( F(x) →∃y(G(y) ∧ H(x,y))其中F(x):x是自然数,H(x,y) :y是x的后继数或者:∀x( F(x) →L(x)) ,L(x) :x有后继数③∃x( F(x) ∧∀y(G(y) →⌝ H(x,y))或者:∃x( F(x)∧⌝L(x) ) ,L(x) :x有先驱数2.2 一阶逻辑公式及解释一、本节主要内容字母表合式公式(简称公式)个体变项的自由出现和约束出现解释永真式(逻辑有效式)矛盾式(永假式)可满足式二、教学内容字母表定义字母表包含下述符号:(1) 个体常项:a, b, c, …, ai, bi, ci, …, i ≥1(2) 个体变项:x, y, z, …, xi, yi, zi, …, i ≥1(3) 函数符号:f, g, h, …, fi, gi, hi, …, i ≥1(4) 谓词符号:F, G, H, …, Fi, Gi, Hi, …, i ≥1(5) 量词符号:∀, ∃(6) 联结词符号:⌝, ∧, ∨, →, ↔(7) 括号与逗号:( , ), ,项定义项的定义如下:(1) 个体常项和个体变项是项.(2) 若ϕ(x1, x2, …, xn)是任意的n元函数,t1,t2,…,tn是任意的n个项,则ϕ(t1, t2, …, tn) 是项.(3) 所有的项都是有限次使用(1), (2) 得到的.例:a,b,x,y,f(x,y)=x+y,g(x,y)=x-y都是项f(a, g(x,y))=a+ (x-y)是项其实, 个体常项、变项是项,由它们构成的n元函数和复合函数还是项原子公式定义设R(x1, x2, …, xn)是任意的n元谓词,t1,t2,…, tn是任意的n个项,则称R(t1, t2, …, tn)是原子公式.其实,原子公式是由项组成的n元谓词.例如,F(x,y), F(f(x1,x2),g(x3,x4))等均为原子公式合式公式定义合式公式(简称公式)定义如下:(1) 原子公式是合式公式.(2) 若A是合式公式,则(⌝A)也是合式公式(3) 若A, B是合式公式,则(A∧B), (A∨B), (A→B),(A↔B)也是合式公式(4) 若A是合式公式,则∀xA, ∃xA也是合式公式(5) 只有有限次地应用(1)~(4)形成的符号串才是合式公式(谓词公式).个体变项的自由出现与约束出现定义在公式∀xA和∃xA中,称x为指导变元,A为相应量词的辖域. 在∀x和∃x的辖域中,x的所有出现都称为约束出现,A中不是约束出现的其他变项均称为是自由出现的.例如, 在公式∀x(F(x,y)→G(x,z)) 中,A=(F(x,y)→G(x,z))为∀x的辖域,x为指导变项, A中x的两次出现均为约束出现,y与z均为自由出现.闭式: 不含自由出现的个体变项的公式.例1:∀x(F(x)→∃y H(x,y) )∃y H(x,y)中,y为指导变项,∃的辖域为H(x,y),其中y为约束出现的,x为自由出现的. 在整个合式公式中,x为指导变项,∀的辖域为(F(x)→∃y H(x,y) ),其中x与y都是约束出现的,x约束出现2次,y约束出现1次.例2:∀x ∀y(R(x,y) ∨L(y,z) ) ∧∃x H(x,y)∀x ∀y(R(x,y) ∨L(y,z) )中,x,y都是指导变项,辖域为(R(x,y) ∨L(y,z) ),x与y都是约束出现的,z为自由出现的.∃x H(x,y)中,x为指导变项,∃的辖域为H(x,y),其中x为约束出现的,y为自由出现的在此公式中,x为约束出现的,y为约束出现的,又为自由出现的. z为自由出现的.换名规则将量词辖域中出现的某个约束出现的个体变项及对应的指导变项,改成另一个辖域中未出现过的个体变项符号,公式中的其余部分不变。
Ch 1.2 集合概念及集合之间的关系

第一编 集合论
2
集合结构
离散数学的大部分内容是研究离散结构,表现离 散对象。
很多重要的离散结构是用集合来构造的,即对象 的联合。
例如 自然数集:{0, 1, 2, …} 关系:序偶集合,用来表现元素间关系; 图:结点和联结结点的边的集合。
第一编 集合论
3
集合论的起源
集合论(Set Theory)是现代数学的基础.它的起源可追 溯到16世纪末,主要是对数集进行卓有成效的研究.
成A的子集B 。
这样 B 与该二进制数 b 一一对应,有多少个不同 n 位二进制 就有多少个不同的子集。
例如:S={a,b,c},
P(S)={Si | i∈J}, J={i | i是二进制数且00…0≤i≤11…1}
例如 S3=S011={b,c}, S6=S110={a,b}等。
一般地 P(S ) {S0 , S1,
子集、相等、真子集 空集、全集 幂集、n元集、有限集 集族
第一编 集合论
18
子集(Subset)
定义1.1 集合B的每个元素都是集合A中的元素, 称B是A的子集,也称 B包含于A, A包含B: B⊆A ⇔ ∀x(x∈B x∈A)
B不是A的子集: B A ⇔ ∃x(x∈B∧x ∉A)
Ch 1.2 集合概念与集合间关系
集合的概念 集合之间的关系
第一编 集合论
1
集合论(Set Theory)
十九世纪数学最伟大成就之一 集合论体系
朴素(naive)集合论 公理(axiomatic)集合论
创始人康托(Cantor) Georg Ferdinand Philip Cantor (1845 ~ 1918) 德国数学家, 集合论创始人.
离散数学1-2
q
1 0 1 0
┐p∨┐q
0 1 1 1
┐p∨q
1 0 1 1
p∨┐q
1 1 0 1
p∨q
1 1 1 0
<
>
《离散数学》
第二章
命题逻辑等值演算
第二节 析取范式与合取范式
为了便于记忆,将两个命题变项的极大、小项列于下表:
极小项 公式 p∧q p ∧┐q ┐p ∧ q ┐p∧┐q 成真赋值 1 1 1 0 0 1 0 0 编码 m3 m2 m1 m0 公式 p∨q p ∨┐q ┐p ∨ q ┐p∨┐q
《离散数学》
第二章
命题逻辑等值演算
第一节
等值式
等值置换规则:
1、子公式: 定义:如果X是命题公式A的一部分,且X也是命题公式, 则称X是命题公式A的子公式。 2、等值置换定理: 定理:若X是命题公式A的子公式,X⇔Y,则若将A中的 X用Y来置换,所得公式B与A等值,即A⇔B。
证:因为对命题变项的任一赋值,X与Y真值相同,所以以Y 取代X后,公式B与公式A对命题变项的任一赋值也相同, 所以A⇔B。
《离散数学》
第二章
命题逻辑等值演算
第一节
等值式
第二章
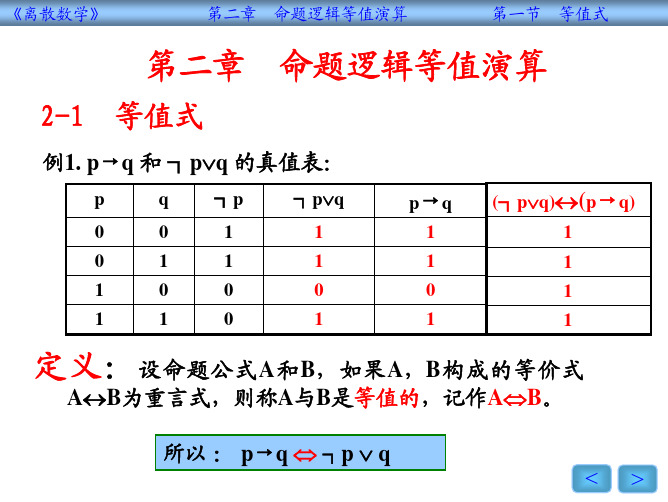
2-1
p 0 0 1 1
命题逻辑等值演算
等值式
q 0 1 0 1 ┐p 1 1 0 0 ┐p∨q 1 1 0 1 p→ q 1 1 0 1 (┐p∨q)↔(p→q) 1 1 1 1
例1. p→q 和 ┐p∨q 的真值表:
定义: 设命题公式A和B,如果A,B构成的等价式
否 否 是
<
>
《离散数学》
第二章
命题逻辑等值演算
离散数学-ch1

1.1 命题与命题联结词
• 给定命题 给定命题P→Q , 我们把 我们把Q→P, ﹁P→﹁Q , ﹁ , ﹁
Q→﹁P分别叫作命题 ﹁ 分别叫作命题 分别叫作命题P→Q的逆命题,反命题和逆 的逆命题, 的逆命题 反命题。 反命题。
• 注意:由定义知,一切没有判断内容的句子 注意:由定义知,
如命令,感叹句,疑问句,祈使句, 如命令,感叹句,疑问句,祈使句,二义性 的陈述句等都不能作为命题。 的陈述句等都不能作为命题。
11/73
1.1 命题与命题联结词
• 例1-2:下列句子哪些是命题,判断命 :下列句子哪些是命题,
题的真假。 题的真假。
15/73
1.1 命题与命题联结词
• 定义 :设P ﹑Q是任意两个命题,复合命题“P 定义1.3: 是任意两个命题, 是任意两个命题 复合命题“
并 且 Q” ( 或 “ P 和 Q” ) 称 为 P 与 Q 的 合 取 式 (Conjunction),记作P ∧ Q,“∧ ”为合取联 ) 记作 , 结词。 为真当且仅当P, 同为真 同为真。 结词。 P ∧ Q为真当且仅当 ,Q同为真。 为真当且仅当 例,P:2是素数,Q:2是偶数。则P ∧ Q:2是素 : 是素数, : 是偶数。 : 是素 是素数 是偶数 数并且是偶数。 数并且是偶数。
第七章 代数系统 第八章 群论
5/73
引言
•教学内容
第三部分 代数结构
第九章 环与域 第十章 格与布尔代数
6/73
第一部分 数理逻辑
• 逻辑学
– 是一门研究思维形式和规律的科学。分为辩证逻 是一门研究思维形式和规律的科学。 辑和形式逻辑两种。思维的形式结构包括了概念 辑和形式逻辑两种。思维的形式结构包括了概念 判断和推理之间的结构和联系 其中概念 之间的结构和联系, 概念是思 ﹑判断和推理之间的结构和联系,其中概念是思 维的基本单位, 维的基本单位,通过概念对事物是否具有某种属 性进行肯定或否定的回答,就是判断 判断。 性进行肯定或否定的回答,就是判断。由一个或 几个判断推出另一判断的思维形式就是推理 推理。 几个判断推出另一判断的思维形式就是推理。
离散数学课件:CH1-集合

1930年,哥德尔(Godel)给出了连续统假设与选择公理是相容 的,从而证明了连续统假设不会错。
1963年,科恩(Cohen)证明了选择公理与连续统假设是相互 独立的,从而给出了:证明连续统假设成立是不可能的。由此 得到,在使用的公理系统中,连续统假设是不能判定的。
十九世纪末到二十世纪初,数学的各个分支的一个普遍的思潮 就是建立公理化系统。
集合论最初是一门研究数学基础的学科,它从一个比“数”更 简单的概念——集合出发,定义数及其运算,进而发展到整个 数学领域,在此方面它取得了极大的成功。
17
集合论的起源可以追溯到19世纪末期,为了追寻微积分的坚实 基础,开始时人们主要是对数集进行了卓有成效的研究。
1874年,29岁的德国数学家康托(Georg Cantor)在“数学杂 志”上发表了关于无穷集合论的第一篇革命性文章。
4
五、如何学好离散数学
离散数学是计算机学科的专业基础课程,它对学生计算机科学 理论水平的提高起着非常重要的作用。但是,在该课程的学习 过程中,学生对离散数学的重要性以及与其它课程的联系似乎 是雾里看花,模糊不清。当然,这是很自然的事情,因为处在 现有的知识结构中,学生不可能对所学的知识具有全面和深刻 的认识,就象古诗中描述的那样:“不识庐山真面目,只缘身 在此山中”。处在一个环境中难以看清该环境中的一切事物是 很正常的。所以,在学习离散数学的过程中,学生不必过分关 注它的用处以及它在计算机学科中所起的作用,而应从以下几 个方面入手,力争学好本课程的全部内容。
9
读书时追求细腻。反复读书是学好离散数学不可缺少的一 环。读书时,应该读懂每一个细节,理解每一个符号和每 一句话。很多时候,初学者会跳过一些难以理解的步骤, 特别是证明过程中的某些细节,这实际上是放弃了提高各 方面能力的机会。理解能力、推理技能、抽象思维以及意 志品质等各方面素质的提高都溶于数学概念的每一个细节 之中。著名数学家华罗庚先生有句名言:“一本书应先把 它读厚,再把它读薄”。重视细节、追求细腻也许就是读 厚一本书的方法吧。
《离散数学》ch

C(4+6-1, 6) (可以直接套用公式)
Remark: Please use this theorem to consider example 2 (page 336):
C(3+4-1, 6)
n! / ( n1!×n2!......nk! ) Proof: similar to example 2.
整理课件
5. Distributing Objects into Boxes (把物体 放入盒子)
(1) Example 9 (page 341) How many ways are there to
distinguishable objects into k distinguishable boxes so that ni objetcs are placed into box i, i=1,2, …, k, equals
n! / ( n1!×n2!......nk! )
整理课件
Exercises
distribute hands of 5 cards of four player from the standard of deck of 52 cards. Solution: C(52,5)×C(47,5) ×C(42,5) ×C(37,5)
整理课件
(5) Theorem 4 (page 341) The number of ways to distribute n
SUCCESS
Solution: Success-------3 Ss, 2 Cs, 1 U, 1 E
整理课件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这三类公式间有如下关系: 1. 公式A永真, 当且仅当 ¬A永假。 2. 公式A可满足, 当且仅当 ¬A非永假。 3. 不是可满足的公式必永假。4. 不是永假的公式必可满足。
二、 代入规则 A是一个公式, 对A使用代入规则得公式B, 若A是重言式, 则B也是重言式。 为保证重言式经代入规则仍得到保持, 要求: 1. 公式中被代换的只能是命题变元(原子 命题), 而不能是复合命题。 2. 对公式中某命题变项施以代入,必须对 该公式中出现的所有同一命题变项代换同 一公式。
Translating English Sentences
“You can access the internet from the campus if you are a computer science major or you are not a freshman .” 2. “You can access the internet from the campus only if you are a computer science major or you are not a freshman.” Solution: a------”You can access the internet from the campus.” b------”You are a computer science major.” c------”You are a freshman.” 1. (c \/ ¬f) → a 2. a →(c \/ ¬f) 1.
第五节 简单自然句的形式化 推理问题的描述,需首先把自然语句形式化成逻辑语言, 即以符号表示的逻辑公式。要注意自然语句中某些 联结词的逻辑含义。 1. 北京不是村庄。 P表示“北京是村庄”,于是1可表示为 ¬P。 2. 李明既聪明又用功。 令P表示“李明聪明”,Q表示“李明用功”,于是 2可表为P∧Q。
说明
这是递归(归纳)的定义。在定义中使用了 所要定义的概念。
条件4说明了哪些不是合式公式,而1、2和3 说明不了这一点。
优先次序 为了减少圆括号的数量,可以引入一些约定,可按 ¬ , ∧ , ∨,→,↔ 的排列次序安排优先的级别,多个同一联结词按从左到右的优 先次序。 (P→(Q∨R)) 可写成 P→(Q∨R) 或 P→Q∨R。
3. A: 今晚我在家里看电视。 B: 今晚我去体育场看球赛。 C: 今晚我在家里看电视或去体育场看球赛。 问题:C与A∨B是否表达的是同一命题呢?
Translating English Sentences
“You can access the internet from the campus if you are a computer science major or you are not a freshman .” 2. “You can access the internet from the campus only if you are a computer science major or you are not a freshman .” Solution: a------”You can access the internet from the campus.” b------”You are a computer science major.” c------”You are a freshman.” 1. ? 2. ? 1.
Summary of logical operators
Alternative notations
第三节 合式公式 合式公式的定义: 1. 简单命题是合式公式。 2. 如果A是合式公式, 那么¬A也是合式公式。 3. 如果A、B是合式公式, 那么(A∧B), (A∨B), (A→B)和(A↔B)是合式公式。 4. 当且仅当经过有限次地使用1.2.3所组成的符号 串才是合式公式。 这个定义给出了建立合式公式的一般原则,也给出 了识别一个符号串是否是合式公式的原则。 使用圆括号来区分运算的先后次序。
第一章 命题逻辑的基本概念 (二)
第二节 命题联接词及真值表 第三节 合式公式 第四节 重言式 第五节 简单自然句的形式化 第六节 波兰表达式
四、 蕴涵词→ P→Q, 读作如果P则Q, 或读作P蕴涵Q, 如果P那么Q, 其中P称前件(前项、条件), Q称后件(后项、结论)。 规定只有当P=T而Q=F时, P→Q= F。否则P→Q=T。 P Q P→Q
P→Q同 ¬P∨Q有相同的真值(在所有任意解 释下), 于是可记作 P→Q = ¬P∨Q, 或P→Q ¬P∨Q 这也说明→可由 ¬、∨来表示, 从逻辑上看"如 果P则Q"同"非P或Q"是等同的两个命题。
五、 双条件词 P↔Q, 读作P当且仅当Q, 或读作P等值Q。 只有当两个命题P、Q的真值相同或说P = Q时, P↔Q=T,否则P↔Q =F。
以代数的例子来说明,如对 (a + b)2 = a2 + 2ab + b2 可以a = cd代入,等式仍成立。 但不能a + b以cd代入,结果左端得(cd)2,而 右端无法代入cd,不能保持等式成立了。 如 P∨¬ P, 以Q∨¬Q代入P得 (Q∨¬Q) ∨ ¬(Q∨¬Q) 仍是重言式。 若将 ¬P以Q代之得 P∨Q,就不是重言式了。
(P→(P→R)) 可写成 P→(P→R)。
第四节 重言式 • 如果一个公式,对于它的任一解释下其真值都为 真,就称为重言式(永真式)。 P∨ ¬P • 一个公式,如在某个解释下该公式真值为真, 则 称这公式是可满足的。如P∨Q。 重言式当然是可满足的。 • 一个公式,对于它的任一解释下真值都是假,便 称是矛盾式(永假式或不可满足的) 。 P∧ ¬P
P T T F F
Q T F T F
P↔Q T F F T
P↔Q与P=Q的区别: • ↔是联结词, P↔Q是一命题,它有真值,其值由P与 Q的值决定。 • P=Q不是命题。= 表示P与Q的关系,即它们的值相 等。 问题:填写真值表 P
T F
Q
T F
(P→Q)∧(Q→P)
F
T
T
F
问题 1 如果P与Q有以下关系:P=Q,则P↔Q的值为? 2 P: △ABC是等腰三角形 Q: △ABC中有两个角相等 P↔Q的值为?
T T F F
T F T F
T F T T
使用P→Q能描述推理。 即P→Q为真时, 只要P为真必有Q真, 而不能出 现P真而Q假就够了。 至于P为假时, Q取真取假, 并不违背P为真时Q 必真。
例: 竞选人A:如果我当选议员,我将使政府减税。 选民认为上面的承诺何时为假?
真值相同的等值命题以等号联结。
