2021-2021学年高中数学苏教版必修二课件.ppt.ppt
合集下载
高中数学必修二课件:圆的一般方程(42张PPT)
此方程表示以(1,-2)为圆心,2为半径长的圆.
问题2:方程x2+y2+2x-2y+2=0表示什么图形?
提示:对方程x2+y2+2x-2y+2=0配方得
(x+1)2+(y-1)2=0,即x=-1且y=1. 此方程表示一个点(-1,1). 问题3:方程x2+y2-2x-4y+6=0表示什么图形? 提示:对方程x2+y2-2x-4y+6=0配方得 (x-1)2+(y-2)2=-1. 由于不存在点的坐标(x,y)满足这个方程,所以这 个方程不表示任何图形.
3.若方程x2+y2+2mx-2y+m2+5m=0表示圆,求 (1)实数m的取值范围; (2)圆心坐标和半径.
解:(1)根据题意知D2+E2-4F=(2m)2+(-2)2- 1 4(m +5m)>0,即4m +4-4m -20m>0,解得m<5,
2 2 2
1 故m的取值范围为(-∞,5).
(2)将方程x2+y2+2mx-2y+m2+5m=0写成标准 方程为(x+m)2+(y-1)2=1-5m, 故圆心坐标为(-m,1),半径r= 1-5m.
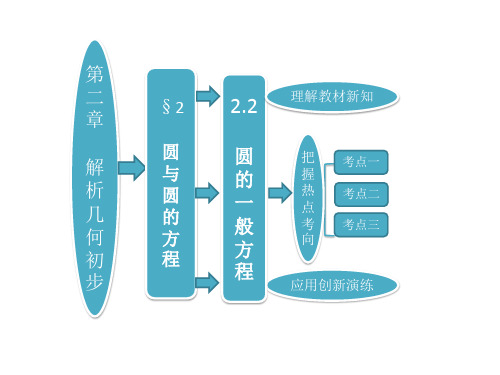
第 二 章 解 析 几 何 初 步
§2 圆 与 圆 的 方 程
2.2
圆 的 一 般 方 程
理解教材新知
把 握 热 点 考 向
考点一 考点二 考点三
应用创新演练
把圆的标准方程(x-a)2+(y-b)2=r2展开得,x2+y2 -2ax-2by+a2+b2-r2=0,这是一个二元二次方程的形 式,那么,是否一个二元二次方程都表示一个圆呢? 问题1:方程x2+y2-2x+4y+1=0表示什么图形? 提示:对x2+y2-2x+4y+1=0配方得 (x-1)2+(y+2)2=4.
1.若x2+y2-x+y-m=0表示一个圆的方程,则m的取值 范围是 1 A.m>-2 1 C.m<-2 1 B.m≥-2 D.m>-2 ( )
8.3正态分布课件-2021-2022学年高二下学期数学苏教版(2019)选择性必修第二册

面积,则称随机变量X服从参数m和s 2的正态分布, 简记为X ~ N(m,s 2)。
y
O
ab
x
数学应用 类型一 正态分布的特征的应用
例1、设两个正态分布N(m1,s12)(s1>0)和N(m2,s22)(s2>0)
的密度函数图象如图所示, 则有( A )
(A) m1<m2,s1<s2 (B) m1<m2,s1>s2 (C) m1>m2,s1<s2 (D) m1>m2,s1>s2
落在区间(μ-3σ, μ+3σ)内的概率约为99.7%;
P(μ-3σ<X<μ+3σ)=0.9974
数学建构
6、正态分布中随机变量在相关区间取值概率的大小
若X ~ N(m,s 2),则随机变量X在m的附近取值的概率 很大,在离m很远取值的概率很小。
具体地,
P(μ-σ<X<μ+σ)=0.6826
P(μ-2σ<X<μ+2σ)=0.9544
O 20 40 60 80 100 x
P(μ-σ<X<μ+σ)=0.6826
变式拓展
若 X~N(5,1),求 P(6<X<7)。
解:由 X~N(5,1) 知 m=5,s =1
∴P(51<X<5+1)=0.6826 则 P(5<X<6)0.3413 同理P(52<X<5+2)=0.9544, ∴ P(5<X<7)0.4772 于是得P(6<X<7)=P(5<X<7)-P(5<X<6)
变式拓展
已知随机变量x 服从正态分布 N(0,s2),若P(x >2)=0.023, 则 P(-2≤x ≤ 2)等于( C )
y
O
ab
x
数学应用 类型一 正态分布的特征的应用
例1、设两个正态分布N(m1,s12)(s1>0)和N(m2,s22)(s2>0)
的密度函数图象如图所示, 则有( A )
(A) m1<m2,s1<s2 (B) m1<m2,s1>s2 (C) m1>m2,s1<s2 (D) m1>m2,s1>s2
落在区间(μ-3σ, μ+3σ)内的概率约为99.7%;
P(μ-3σ<X<μ+3σ)=0.9974
数学建构
6、正态分布中随机变量在相关区间取值概率的大小
若X ~ N(m,s 2),则随机变量X在m的附近取值的概率 很大,在离m很远取值的概率很小。
具体地,
P(μ-σ<X<μ+σ)=0.6826
P(μ-2σ<X<μ+2σ)=0.9544
O 20 40 60 80 100 x
P(μ-σ<X<μ+σ)=0.6826
变式拓展
若 X~N(5,1),求 P(6<X<7)。
解:由 X~N(5,1) 知 m=5,s =1
∴P(51<X<5+1)=0.6826 则 P(5<X<6)0.3413 同理P(52<X<5+2)=0.9544, ∴ P(5<X<7)0.4772 于是得P(6<X<7)=P(5<X<7)-P(5<X<6)
变式拓展
已知随机变量x 服从正态分布 N(0,s2),若P(x >2)=0.023, 则 P(-2≤x ≤ 2)等于( C )
高中数学必修二课件:概率的基本性质

一次购物 1至4件 5至8件
量
9至 12件
13至 16件
顾客数(人)
x
30
25
ቤተ መጻሕፍቲ ባይዱ
y
结算时间
1
1.5
2
2.5
(分钟/人)
已知这100位顾客中一次购物量超过8件的顾客占55%.
17件 及以上
10
3
①确定x,y的值,并求顾客一次购物的结算时间的平均值;
②求一位顾客一次购物的结算时间不超过2分钟的概率(将频率视为概率).
错解:因为P(A)=36=12,P(B)=36=12, 所以P(A∪B)=P(A)+P(B)=1. 错因分析:由于事件A与事件B不是互斥事件,更不是对立事件,因此 P(A∪B)=P(A)+P(B)不成立.因此解答此题应从“A∪B”这一事件出发求解. 答:因为A∪B包含4种结果,即出现1,2,3和5,所以P(A∪B)=46=23.
②由于A,AB型血不能输给B型血的人,故“任找一个人,其血不能输给小 明”为事件A′+C′,根据互斥事件的概率加法公式,得P(A′+C′)=P(A′) +P(C′)=0.28+0.08=0.36.
(2)某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集
了在该超市购物的100名顾客的相关数据,如下表所示.
(2)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号为0,1,2, 3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的 编号之和等于7,则中一等奖,等于6或5,则中二等奖,等于4,则中三等奖, 其余结果不中奖.
①求中二等奖的概率; ②求不中奖的概率.
【解析】 从五个小球中一次任意摸出两个小球,不同的结果有(0,1), (0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共 10种.记两个小球的编号之和为x.
高中数学必修二ppt课件

高中数学必修二ppt课 件
CONTENTS 目录
• 引言 • 平面解析几何初步 • 立体几何初步 • 圆的性质与定理 • 圆锥曲线与方程 • 单元复习与习题解答
CHAPTER 01
引言
课程目标与重要性
课程目标
使学生掌握高中数学必修二的基本概 念、原理和解题方法,培养数学思维 和解决问题的能力。
圆锥曲线的概念和标准方程
理解圆锥曲线的概念和标准方程,包 括椭圆、双曲线和抛物线的标准方程 ,掌握各参数的意义。
圆锥曲线的几何性质
掌握圆锥曲线的几何性质,如焦点、 准线、离心率等,能够根据已知条件 求出相应圆锥曲线的几何量。
圆锥曲线的实际应用
了解圆锥曲线在实际问题中的应用, 如行星运动轨迹的计算、光学透镜的 设计等。
椭圆的参数方程
椭圆的焦点
椭圆的参数方程为 $x = a cos theta, y = b sin theta$,其中 $theta$ 是参数。
椭圆的焦点到椭圆上任意一点的距离之和 等于长轴的长度。
双曲线与方程
双曲线的标准方程
双曲线的标准方程为 $frac{x^2}{a^2} frac{y^2}{b^2} = 1$ 或 $frac{y^2}{b^2} frac{x^2}{a^2} = 1$,其中 $a$ 和 $b$ 是双曲 线的半实轴和半虚轴。
CHAPTER 05
圆锥曲线与方程
椭圆与方程
椭圆的标准方程
椭圆的性质
椭圆的标准方程为 $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$,其中 $a$ 和 $b$ 是椭圆的半长轴和半短轴。
椭圆具有对称性,即关于x轴、y轴和原点 都是对称的。此外,椭圆上任意一点到两 焦点的距离之和等于长轴的长度。
CONTENTS 目录
• 引言 • 平面解析几何初步 • 立体几何初步 • 圆的性质与定理 • 圆锥曲线与方程 • 单元复习与习题解答
CHAPTER 01
引言
课程目标与重要性
课程目标
使学生掌握高中数学必修二的基本概 念、原理和解题方法,培养数学思维 和解决问题的能力。
圆锥曲线的概念和标准方程
理解圆锥曲线的概念和标准方程,包 括椭圆、双曲线和抛物线的标准方程 ,掌握各参数的意义。
圆锥曲线的几何性质
掌握圆锥曲线的几何性质,如焦点、 准线、离心率等,能够根据已知条件 求出相应圆锥曲线的几何量。
圆锥曲线的实际应用
了解圆锥曲线在实际问题中的应用, 如行星运动轨迹的计算、光学透镜的 设计等。
椭圆的参数方程
椭圆的焦点
椭圆的参数方程为 $x = a cos theta, y = b sin theta$,其中 $theta$ 是参数。
椭圆的焦点到椭圆上任意一点的距离之和 等于长轴的长度。
双曲线与方程
双曲线的标准方程
双曲线的标准方程为 $frac{x^2}{a^2} frac{y^2}{b^2} = 1$ 或 $frac{y^2}{b^2} frac{x^2}{a^2} = 1$,其中 $a$ 和 $b$ 是双曲 线的半实轴和半虚轴。
CHAPTER 05
圆锥曲线与方程
椭圆与方程
椭圆的标准方程
椭圆的性质
椭圆的标准方程为 $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$,其中 $a$ 和 $b$ 是椭圆的半长轴和半短轴。
椭圆具有对称性,即关于x轴、y轴和原点 都是对称的。此外,椭圆上任意一点到两 焦点的距离之和等于长轴的长度。
最新-2021学年高中数学必修二精讲优练课件:第二章 点、直线、平面之间的位置关系 2.1.1 精品

公理
文字语言
如果两个不重合的平
面有一个公共点,那么 公理3
它们有且只有一条过
该点的_公__共__直__线__
图形语言
符号语言
P∈α且P∈β⇒
_________ α∩β=l, ______ 且P∈l
【即时小测】 1.思考下列问题: (1)一个平面能把空间分成几部分? 提示:因为平面是无限延展的,一个平面把空间分成两部分. (2)若A∈a,a⊂α,是否可以推出A∈α? 提示:根据直线在平面内的定义可知,若A∈a,a⊂α,则A∈α.
(2)平面的画法.
常常把水平的平面画成一个_平__行__四__边__形__,并且 其锐角画成_4_5_°__,且横边长等于邻边长的_2_倍.
一个平面被另一个平面遮挡住,为了增强立体 感,被遮挡部分用_虚__线__画出来.
(3)平面的表示方法. ①用希腊字母表示,如平面α,平面β,平面γ. ②用表示平面的平行四边形的四个顶点的大写字母表示,如平面ABCD. ③用表示平面的平行四边形的相对的两个顶点表示,如平面AC,平面BD.
【解题探究】典例中梯形ABCD的两腰分别是什么?其延长后的交点位 于什么地方? 提示:结合题意可知梯形ABCD的两腰分别是AB,CD,它们延长后的交点 既在平面α内又在平面β内.
【证明】因为梯形ABCD中,AD∥BC, 所以AB,CD是梯形ABCD的两腰. 因为AB,CD必定相交于一点. 设AB∩CD=M. 又因为AB⊂α,CD⊂β,所以M∈α,M∈β. 所以M∈α∩β. 又因为α∩β=l,所以M∈l. 即AB,CD,l共点(相交于一点).
【总结提升】 1.公理1、2、3的意义和作用 (1)公理1. 意义:说明了平面与曲面的本质区别.通过直线的“直”来刻画平面的 “平”,通过直线的“无限延伸”来描述平面的“无限延展性”. 作用:既是判断直线在平面内,又是检验平面的方法.
2021年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件6苏教版必修2

【解】 (1)将直线方程化为一般式为 x-y-3=0, 由点到直线的距离公式,得 d1= |112-+2(--31|)2=2 2.
(2)法一:直线方程化为一般式为 y+1=0, 由点到直线的距离公式,得 d2= |20+2+11| 2=3. 法二:∵y=-1 平行于 x 轴(如图所示), ∴d2=|-1-2|=3. (3)法一:y 轴的方程为 x=0, 由点到直线的距离公式,得 d3=|1+120++002|=1. 法二:如图所示,可知 d3=|1-0|=1.
|4×4-3a-1| |15-3a| 解析 d= 42+-32 = 5 ≤3,|3a-15|≤15, ∴-15≤3a-15≤15,0≤a≤10.
解析答案
3.假设点P到直线5x-12y+13=0和直线3x-4y+5=0的距离 相等,那么点P的坐标应满足的方程是 什么?
解析 设点P的坐标为(x,y), |5x-12y+13| |3x-4y+5|
解析答案
解 假设直线l1,l2的斜率存在,设直线l1与l2的斜率为k,
由斜截式得l1的方程为y=kx+1,即kx-y+1=0;
由点斜式可得l2的方程为y=k(x-5),
即kx-y-5k=0.
在直线l1上取点A(0,1), |1+5k|
则点 A 到直线 l2 的距离 d= 1+k2=5,
∴25k2+10k+1=25k2+25,∴k=152. ∴l1的方程为12x-5y+5=0, l2的方程为12x-5y-60=0.
分析:由平面几何知识可知:过点的直线只有过AB 的中点时或平行于AB时,两点到直线距离相等。
l例3:求过点M〔-2,1〕且与A〔-1,2〕,B〔3,0〕 两点距离相等的直线的方程?
解:(1)假设L//AB,那么直线L方程为x+2y=0 (2)假设L过AB的中点N〔1,1〕,那么直 线的方程为y=1.
(2)法一:直线方程化为一般式为 y+1=0, 由点到直线的距离公式,得 d2= |20+2+11| 2=3. 法二:∵y=-1 平行于 x 轴(如图所示), ∴d2=|-1-2|=3. (3)法一:y 轴的方程为 x=0, 由点到直线的距离公式,得 d3=|1+120++002|=1. 法二:如图所示,可知 d3=|1-0|=1.
|4×4-3a-1| |15-3a| 解析 d= 42+-32 = 5 ≤3,|3a-15|≤15, ∴-15≤3a-15≤15,0≤a≤10.
解析答案
3.假设点P到直线5x-12y+13=0和直线3x-4y+5=0的距离 相等,那么点P的坐标应满足的方程是 什么?
解析 设点P的坐标为(x,y), |5x-12y+13| |3x-4y+5|
解析答案
解 假设直线l1,l2的斜率存在,设直线l1与l2的斜率为k,
由斜截式得l1的方程为y=kx+1,即kx-y+1=0;
由点斜式可得l2的方程为y=k(x-5),
即kx-y-5k=0.
在直线l1上取点A(0,1), |1+5k|
则点 A 到直线 l2 的距离 d= 1+k2=5,
∴25k2+10k+1=25k2+25,∴k=152. ∴l1的方程为12x-5y+5=0, l2的方程为12x-5y-60=0.
分析:由平面几何知识可知:过点的直线只有过AB 的中点时或平行于AB时,两点到直线距离相等。
l例3:求过点M〔-2,1〕且与A〔-1,2〕,B〔3,0〕 两点距离相等的直线的方程?
解:(1)假设L//AB,那么直线L方程为x+2y=0 (2)假设L过AB的中点N〔1,1〕,那么直 线的方程为y=1.
2021_2022学年新教材高中数学第二章一元二次函数方程和不等式2.2第2课时基本不等式的应用课件

【加固训练】 已知 a,b,c 为正实数,且 a+b+c=1, 求证:1a-1 b1-1 1c-1 ≥8.
【解析】因为 a,b,c 为正实数,且 a+b+c=1,
所以a1
-1=1-a a
=b+a c
≥2
bc a
.
同理,1b
-1≥2
ac b
,c1
-1≥2
ab c
.
上述三个不等式两边均为正,相乘得:
130
130
x2
130
【解析】(1)设所用时间为 t= x ,则 y= x ×2×2+360 +14× x ,
50≤x≤100.
所以,这次行车总费用 y 关于 x 的表达式是
130×18 y= x
2×130 + 360
x,50≤x≤100或y=23x40+1138x,50≤x≤100
.
(2)y=130× x 18 +2×361030 x≥26 10 , 当且仅当130× x 18 =2×361030 x, 即 x=18 10 时等号成立. 故当 x=18 10 千米/时时,这次行车的总费用最低,最低费用的值为 26 10 元.
bc ca ab 当且仅当 a = b = c ,即 a=b=c 时取等号.
已知 x,y,z 都是正数,求证:(x+y)(y+z)(z+x)≥8xyz. 【证明】因为 x,y,z 都是正数,x+y≥2 xy ,y+z≥2 yz ,x+z≥2 xz , 所以(x+y)(y+z)(z+x)≥8xyz.
方法二:由 xy=24,得 x=2y4 . 所以 l=4x+6y=9y6 +6y=61y6+y
16 ≥6×2 y ·y =48. 当且仅当1y6 =y,即 y=4 时,等号成立,此时 x=6. 故每间虎笼长 6 m,宽 4 m 时,可使钢筋网总长最小.
新版高中数学必修2课件:8.4.1平面

平面个数是 1 或 3,如果交于不共线的三点,可以确定的平面个数 是 1,所以空间两两相交的三条直线,可以确定的平面个数是 1 或
3. 答案:B
2.如图所示的两个相交平面,其中画法正确的是( )
解析:对于①,图中没有画出平面 α 与平面 β 的交线,另外图 中的实线、虚线也没有按照画法原则去画,因此①的画法不正确.同 样的道理,可知②③的画法不正确,④中画法正确.
方法归纳 证明三点共线,可以证明三点都在两平面的交线上或第三点在 两点所确定的直线上.
微点 2 线共点问题 例 3 在四面体 ABCD 中,E,G 分别是 BC,AB 的中点,点 F 在 CD 上,点 H 在 AD 上,且 DF:FC=DH:HA=2:3.求证:EF,GH, BD 交于一点.
证明:如图,连接 GE、HF 因为 E,G 分别是 BC,AB 的中点,所以 GE∥AC,GE=12AC. 又 DF:FC=DH:HA=2:3, 所以 FH∥AC,FH=25AC,所以 FH∥GE,FH≠GE, 所以 E,F,H,G 四点共面,且四边形 EFHG 是一个梯形. 延长 GH 和 EF 交于一点 O, 因为 GH⊂平面 ABD,EF⊂平面 BCD, 所以 O∈平面 ABD,O∈平面 BCD, 所以点 O 在这两个平面的交线上, 而这两个平面的交线是 BD,且交线只有这一条,所以点 O 在 直线 BD 上. 所以 EF,GH,BD 交于一点.
(3)根据已知符号语言或文字语言画相应的图形时,要注意实线 和虚线的区别.
跟踪训练 1 根据如图所示,在横线上填入相应的符号或字母: A___∈_____平面 ABC,A____∉____平面 BCD,BD___⊄_____平面 ABC,平面 ABC∩平面 ACD=___A__C___.
高中数学必修二课件:余弦定理

要点2 适宜用余弦定理解决的两类基本的解三角形问题 (1)已知两边及其夹角,解三角形; (2)已知三边,解三角形. 要点3 推论 在△ABC中(1)c2=a2+b2⇔C为__直_角___; (2)c2>a2+b2⇔C为___钝_角___; (3)c2<a2+b2⇔C为__锐__角___.
1.判断下列命题是否正确. (1)勾股定理是余弦定理的特例. (2)余弦定理每个公式中均涉及三角形的四个元素. (3)在△ABC中,已知两边及夹角时,△ABC不一定唯一.
课后巩固
1.一个三角形的两边长分别为5和3,它们夹角的余弦值是-
3 5
,则三角形
的第三边长为( B )
A.52
B.2 13
C.16
D.4
解析 设第三边长为x,则x2=52+32-2×5×3×-35=52,∴x=2 13.
2.在△ABC中,a=3,b= 7,c=2,那么B等于( C )
A.30°ቤተ መጻሕፍቲ ባይዱ
解析 ∵c2=a2+b2-2abcos C, ∴( 3)2=a2+12-2a×1×cos 2π 3 , ∴a2+a-2=0,即(a+2)(a-1)=0. ∴a=1或a=-2(舍去).∴a=1.
5.在△ABC中,a2+abb2c+c2(coas A+cobs B+cocs C)=____12____.
a2+c2-b2
a2+b2-c2
(2)推论:cos A=____2_b_c____,cos B=____2_a_c____, cos C=____2_a_b____.
(3)余弦定理的另一种常见变形:b2+c2-a2=2bccos A,a2+c2-b2=2accos
B,a2+b2-c2=2abcos C.
高中数学必修二《 点到直线的距离》ppt课件

.
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
2021_2022学年高中数学第1章导数及其应用1.1.2瞬时变化率——导数课件苏教版选修2_2

所以切线方程为 y-2=4(x-1),即 4x-y-2=0.]
1.瞬时速度、瞬时加速度即为当 Δt→0 时的ΔΔyt的极限值. 2.导数的几何意义:曲线上某点的导数即为该点处切线的斜率. 3.在求切线方程时,要注意“过点”与“在点”的区别,求切 线方程的关键是求切点坐标.
当堂达标 固双基
1.判断(正确的打“√”,错误的打“×”) (1)函数 y=f(x)在 x=x0 处的导数值与 Δx 值的正、负无关.( ) (2)导函数 f′(x)的定义域与函数 f(x)的定义域相同.( ) (3)直线与曲线相切,则直线与已知曲线只有一个公共点.( ) (4)函数 f(x)=0 没有导函数.( )
2.曲线在某点处的切线是否与曲线只有一个交点? [提示] 不一定,切线只是一个局部概念,是该点处的割线的极 限位置,在其他地方可能还有一个或多个公共点. 3.函数在某点处的导数与导函数有什么区别和联系? [提示] 区别:函数在某点处的导数是一个定值,导函数是一个 函数.
联系:函数 f(x)在 x0 处的导数就是导函数 f′(x)在 x=x0 时的函数 值.
(2)设斜率为-13的切线的切点为 Qa,1a, 由(1)知,k=f′(a)=-a12=-13,得 a=± 3.
所以切点坐标为
3, 33或-
3,- 33.
故满足斜率为-13的曲线的切线方程为
y- 33=-13(x- 3)或 y+ 33=-13(x+ 3), 即 x+3y-2 3=0 或 x+3y+2 3=0.
【例 1】 (1)以初速度 v0(v0>0)垂直上抛的物体,t 秒时的高度为 s(t)=v0t-12gt2,则物体在 t0 时刻的瞬时速度为__________.
(2)某物体的运动方程为 s=2t3,则物体在第 t=1 时的瞬时速度是 __________.
1.瞬时速度、瞬时加速度即为当 Δt→0 时的ΔΔyt的极限值. 2.导数的几何意义:曲线上某点的导数即为该点处切线的斜率. 3.在求切线方程时,要注意“过点”与“在点”的区别,求切 线方程的关键是求切点坐标.
当堂达标 固双基
1.判断(正确的打“√”,错误的打“×”) (1)函数 y=f(x)在 x=x0 处的导数值与 Δx 值的正、负无关.( ) (2)导函数 f′(x)的定义域与函数 f(x)的定义域相同.( ) (3)直线与曲线相切,则直线与已知曲线只有一个公共点.( ) (4)函数 f(x)=0 没有导函数.( )
2.曲线在某点处的切线是否与曲线只有一个交点? [提示] 不一定,切线只是一个局部概念,是该点处的割线的极 限位置,在其他地方可能还有一个或多个公共点. 3.函数在某点处的导数与导函数有什么区别和联系? [提示] 区别:函数在某点处的导数是一个定值,导函数是一个 函数.
联系:函数 f(x)在 x0 处的导数就是导函数 f′(x)在 x=x0 时的函数 值.
(2)设斜率为-13的切线的切点为 Qa,1a, 由(1)知,k=f′(a)=-a12=-13,得 a=± 3.
所以切点坐标为
3, 33或-
3,- 33.
故满足斜率为-13的曲线的切线方程为
y- 33=-13(x- 3)或 y+ 33=-13(x+ 3), 即 x+3y-2 3=0 或 x+3y+2 3=0.
【例 1】 (1)以初速度 v0(v0>0)垂直上抛的物体,t 秒时的高度为 s(t)=v0t-12gt2,则物体在 t0 时刻的瞬时速度为__________.
(2)某物体的运动方程为 s=2t3,则物体在第 t=1 时的瞬时速度是 __________.
新版高中数学必修2课件:10.1.3古典概型

2.在古典概型中,每个基本事件发生的可能性都相等,称这 些基本事件为等可能基本事件.
[教材答疑]
1.教材P233思考 在10.1.1节中,我们讨论过彩票摇号试验、抛掷一枚均匀硬币 的试验及掷一枚质地均匀骰子的试验.它们的共同特征有哪些? 提示:共同特征:(1)有限性:样本空间的样本点只有有限 个; (2)等可能性:每个样本点发生的可能性相等.
(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5), (3,6),(4,5),(4,6),(5,6)},共有15个样本点.
(1)从口袋中的6个球中任取2个球,所取的2个球都是白球包含 的样本点共有6个,分别为(1,2),(1,3),(1,4),(2,3),(2,4), (3,4).
(A,B,C,D)共11种,选对的概率为111.
4.教材P236思考 在例8中,为什么要把两枚骰子标上记号?如果不给两枚骰子 标记号,会出现什么情况?你能解释其中的原因吗?
提示:如果不给两枚骰子标记号,则不能区分所抛掷出的两
个点数分别属于哪枚骰子,如抛掷出的结果是1点和2点,有可能 第一枚骰子的结果是1点,也有可能第二枚骰子的结果是1点.这 样,(1,2)和(2,1)的结果将无法区别.
(1)如果小球是不放回的,按抽取顺序记录结果(x,y).则x有 10种可能,y有9种可能,共有可能结果10×9=90种.因此,事件 A的概率是1980=15.
(2)如果小球是有放回的,按抽取顺序记录结果(x,y),则x有 10种可能,y有10种可能,共有可能结果10×10=100种,因此, 事件A的概率是11080=590.
Ω={(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),(0,1,0), (0,0,1),(0,0,0)},
[教材答疑]
1.教材P233思考 在10.1.1节中,我们讨论过彩票摇号试验、抛掷一枚均匀硬币 的试验及掷一枚质地均匀骰子的试验.它们的共同特征有哪些? 提示:共同特征:(1)有限性:样本空间的样本点只有有限 个; (2)等可能性:每个样本点发生的可能性相等.
(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5), (3,6),(4,5),(4,6),(5,6)},共有15个样本点.
(1)从口袋中的6个球中任取2个球,所取的2个球都是白球包含 的样本点共有6个,分别为(1,2),(1,3),(1,4),(2,3),(2,4), (3,4).
(A,B,C,D)共11种,选对的概率为111.
4.教材P236思考 在例8中,为什么要把两枚骰子标上记号?如果不给两枚骰子 标记号,会出现什么情况?你能解释其中的原因吗?
提示:如果不给两枚骰子标记号,则不能区分所抛掷出的两
个点数分别属于哪枚骰子,如抛掷出的结果是1点和2点,有可能 第一枚骰子的结果是1点,也有可能第二枚骰子的结果是1点.这 样,(1,2)和(2,1)的结果将无法区别.
(1)如果小球是不放回的,按抽取顺序记录结果(x,y).则x有 10种可能,y有9种可能,共有可能结果10×9=90种.因此,事件 A的概率是1980=15.
(2)如果小球是有放回的,按抽取顺序记录结果(x,y),则x有 10种可能,y有10种可能,共有可能结果10×10=100种,因此, 事件A的概率是11080=590.
Ω={(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),(0,1,0), (0,0,1),(0,0,0)},
高中数学必修二全册课件ppt人教版

解析答案
反思与感悟
解 (1)∵这个几何体的所有面中没有两个互相平行的面,∴这个几何体不是棱柱. (2)在四边形ABB1A1中,在AA1上取E点,使AE=2;在BB1上取F点,使BF=2;连接C1E、EF、C1F,则过C1、E、F的截面将几何体分成两部分,其中一部分是棱柱ABC—EFC1,其侧棱长为2;截去部分是一个四棱锥C1—EA1B1F,该几何体的特征为:有一个面为多边形,其余各面都是有一个公共顶点的三角形.
①③
1.在理解的基础上,要牢记棱柱、棱锥、棱台的定义,能够根据定义判断几何体的形状.2.各种棱柱之间的关系(1)棱柱的分类
棱柱
(2)常见的几种四棱柱之间的转化关系
3.棱柱、棱锥、棱台在结构上既有区别又有联系,具体见下表:
名称
底面
侧面
侧棱
高
平行于底面的截面
棱柱
斜棱柱
平行且全等的两个多边形
平行四边形
第一 章 § 1.1 空间几何体的结构
第1课时 多面体的结构特征
1.认识组成我们的生活世界的各种各样的多面体;2.认识和把握棱柱、棱锥、棱台的几何结构特征;3.了解多面体可按哪些不同的标准分类,可以分成哪些类别.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
如图棱柱可记作:棱柱
相关概念:底面(底):两个互相 的面侧面: 侧棱:相邻侧面的顶点: 的公共顶点
互相平行
四边形
互相平行
平行
其余各面
公共边
侧面与底面
ABCDEF—
A′B′C′D′E′F′
答案
分类:①依据:底面多边形的 ②类例: (底面是三角形)、 (底面是四边形)……
高中数学必修二课件:总体离散程度的估计

3 10
标准差是____1_0 ___.
【解析】 由方差公式 s2=(x1--x )2+(x2--xn)2+…+(xn--x )2,得
s2=(x12+x22+…+xn2)-2-xn(x1+x2+…+xn)+n-x 2
=x12+x22+n …+xn2--x 2.由已知得
n=40,x12+x22+…+x402=56,-x =
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
根据这组数据判断应该选择哪一种小麦进行推广.
【思路】 本题主要考查平均数和方差的概念和计算以及实际应用.从平均 数和方差两个角度去考虑.
【解析】 甲种冬小麦的平均单位面积产量 -x 甲=9.8+9.9+105.1+10+10.2=10, 乙种冬小麦的平均单位面积产量 -x 乙=9.4+10.3+150.8+9.7+9.8=10, 则甲、乙两种冬小麦平均单位面积产量相同.
练成绩(单位:环),结果如下:
运动员 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次
甲
87
91
90
89
93
乙
89
90
91
88
92
则成绩较为稳定(方差较小)的那位运动员成绩的方差为___2_____.
【解析】 本题考查统计中的方差计算. -x 甲=90,且 s 甲 2=15[(87-90)2+(91-90)2+(90-90)2+(89-90)2+(93-90)2] =4, -x 乙=90,且 s 乙 2=15[(89-90)2+(90-90)2+(91-90)2+(88-90)2+(92-90)2] =2. 所求方差为 2.
标准差是____1_0 ___.
【解析】 由方差公式 s2=(x1--x )2+(x2--xn)2+…+(xn--x )2,得
s2=(x12+x22+…+xn2)-2-xn(x1+x2+…+xn)+n-x 2
=x12+x22+n …+xn2--x 2.由已知得
n=40,x12+x22+…+x402=56,-x =
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
根据这组数据判断应该选择哪一种小麦进行推广.
【思路】 本题主要考查平均数和方差的概念和计算以及实际应用.从平均 数和方差两个角度去考虑.
【解析】 甲种冬小麦的平均单位面积产量 -x 甲=9.8+9.9+105.1+10+10.2=10, 乙种冬小麦的平均单位面积产量 -x 乙=9.4+10.3+150.8+9.7+9.8=10, 则甲、乙两种冬小麦平均单位面积产量相同.
练成绩(单位:环),结果如下:
运动员 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次
甲
87
91
90
89
93
乙
89
90
91
88
92
则成绩较为稳定(方差较小)的那位运动员成绩的方差为___2_____.
【解析】 本题考查统计中的方差计算. -x 甲=90,且 s 甲 2=15[(87-90)2+(91-90)2+(90-90)2+(89-90)2+(93-90)2] =4, -x 乙=90,且 s 乙 2=15[(89-90)2+(90-90)2+(91-90)2+(88-90)2+(92-90)2] =2. 所求方差为 2.
(新教材)2020-2021学年高中苏教版数学必修2课件:14.4.4 百分位数

2.下列关于一组数据的50百分位数的说法正确的是
()
A.50百分位数就是中位数
B.总体数据中的任意一个数小于它的可能性一定是50%
C.它一定是这组数据中的一个数据
D.它适用于总体是离散型的数据
【解析】选A.由百分位数的意义可知选项B,C,D错误.
3.(教材二次开发:例题/习题改编)数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1的 30百分位数是________. 【解析】数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1是按照从小到大的顺序排列 的,因为8×30%=2.4,故30百分位数是第三项数据8.4. 答案:8.4
3.四分位数 中位数即为50百分位数,我们也把中位数、25百分位数和75百分位数称为四分 位数.
【思考】 (1)p百分位数有什么特点? 提示:总体数据中的任意一个数小于或等于它的可能性是p. (2)某组数据的p百分位数在此组数据中一定存在吗?为什么? 提示:不一定.因为按照计算p百分位数的步骤,第2步计算所得的i=n×p%如果是 整数,则p百分位数为第i项与第(i+1)项数据的平均数,若第i项与第(i+1)项数据 不相等,则p百分位数在此组数据中就不存在.
【思路导引】(1)依据题设条件,分段写出函数解析式; (2)依据题设条件结合频率直方图,利用方程思想解决; (3)利用百分位数的定义结合频率直方图直接求解.
【变式探究】 根据典例的(2)题中求得的数据计算用电量的15百分位数. 【解析】设15百分位数为x,因为用电量低于100千瓦时的所占比例为0.001× 100=10%,用电量不超过200千瓦时的占30%,所以15百分位数在[100,200)内,所 以0.1+(x-100)×0.002=0.15,解得x=125千瓦时,即用电量的15百分位数为125千 瓦时.
