2010年中考适应性练习数学试题

合集下载

福建省2010年九年级数学适应性练习人教版

某某省2010年适应性练习数学(一) (答题时间120分钟满分150分)一, 选择题(本大题共10小题,每小题4分,共40分)1. 2010相反数是 ( )2.下列运算正确的是（）A ．523a a a =+B ．632a a a =⋅C ．22))((b a b a b a -=-+Ｄ．222)(b a b a +=+3.用配方法解一元二次方程542=-x x 的过程中，配方正确的是（）A ．（1)22=+xB ．1)2(2=-xC ．9)2(2=+xD ．9)2(2=-x4.计算()4323b a --的结果是 ( )（Ａ）12881b a （B ）7612b a （C ）7612b a -（D ）12881b a -5.如图所示，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠EFB ＝65°，则∠AED ′等于（）（A ） 70°（B ） 65° （C ） 50°（D ） 25°6.盒子里有3支红色笔芯，2支黑色笔芯，每支笔芯除颜色外均相同．从中任意拿出一支笔芯，则拿出黑色笔芯的概率是（）A ．23B ．15C ．25D ． 357.将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为（）EDBC′ FCD ′A （第5题图）A10cm B30cm C40cm D 300cm8．若n （0n ≠）是关于x 的方程220x mx n ++=的根，则m +n 的值为（）A1 B2 C -1 D -29.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（）10.若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式．．．．．，如a b c ++就是完全对称式.下列三个代数式：①2)(b a -；②ab bc ca ++；③222a b b c c a ++．其中是完全对称式的是( )A ．①②B ．①③C ．②③D ．①②③二，填空题（本大题共7小题，每小题3分，共21分）11若关于x 的方程mx 2－mx ＋2＝0有两个相等的实数根，则m ＝__________． 12.请你写出一个图象在第一、三象限的反比例函数．答：．13.随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果为：13=甲x ，13=乙x ，5.72=甲S ，6.212=乙S ，则小麦长势比较整齐的试验田是(填“甲”或“乙”)14.如图，三角板ABC 中，︒=∠90ACB ，︒=∠30B ，6=BC ．三角板绕直角顶点C 逆时针旋转，当点A 的对应点'A 落在AB 边的起始位置上时即停止转动，则点B 转过的路径长为15.在四边形ABCD 中，已知AB 与CD 不平行，∠ABD ＝∠ACD ，请你添加一个条件：，使得加上这个条件后能够推出AD ∥BC 且AB ＝CD . 16.将三角形纸片（△ABC ）按如图所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝3，BC ＝4，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是．17.6月1日起，某超市开始有偿．．提供可重复使用的三种环保购物袋，每只售价分别为1元、（第14题）B C DAO（第15题）E（第16题图）AB ′C FB2元和3元，这三种环保购物袋每只最多分别能装大米3公斤、5公斤和8公斤．6月7日，小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20公斤散装大米，他们选购的3只环保购物袋至少．．应付给超市元．三，解答题（本大题共8小题，共89分） 18.（1）解方程：212111x x-=+-（2）．计算：20)6()15(3--+-．19.解不等式组⎩⎪⎨⎪⎧2－x ＞0，5x ＋12＋1≥2x －13，并把解集在数轴上表示出来．20.如图，⊙O 的直径AB =4，C 为圆周上一点，AC =2，过点C 作⊙O 的切线l ，过点B 作l 的垂线BD ，垂足为D ，BD 与⊙O 交于点 E ． (1) 求∠AEC 的度数；（2）求证：四边形OBEC 是菱形．21.某中学对全校学生60秒跳绳的次数进行了统计，全校平均次数是100次．某班体育委员统计了全班50名学生60秒跳绳的成绩，列出的频数分布直方图如下（每个分组包括左端点，不包括右端点）：（第20题图）求：（1）该班60秒跳绳的平均次数至少是多少？是否超过全校平均次数？（2）该班一个学生说：“我的跳绳成绩在我班是中位数”，请你给出该生跳绳成绩的所在X 围．（3）从该班中任选一人，其跳绳次数达到或超过校平均次数的概率是多少？ 22.如图，斜坡AC 的坡度（坡比）为1:3，AC ＝10米．坡顶有一旗杆BC ，旗杆顶端B 点与A 点有一条彩带AB 相连，AB ＝14米．试求旗杆BC 的高度．23.在“某某地震”灾民安置工作中，某企业接到一批生产甲种板材240002m 和乙种板材120002m 的任务．（1）已知该企业安排140人生产这两种板材，每人每天能生产甲种板材302m 或乙种板材（第19题图）ABC （第22题图）D202m ．问：应分别安排多少人生产甲种板材和乙种板材，才能确保他们用相同的时间完成各自的生产任务？（2）某灾民安置点计划用该企业生产的这批板材搭建A B ，两种型号的板房共400间，在搭建过程中，按实际需要调运这两种板材．已知建一间A 型板房和一间B 型板房所需板材及能安置的人数如下表所示：问：这400间板房最多能安置多少灾民？24.定义：到凸四边形一组对边距离相等，到另一组对边距离也相等的点叫凸四边形的准内．．点．．如图1，PH PJ =，PI PG =，则点P 就是四边形ABCD 的准内点．（1）如图2，AFD ∠与DEC ∠的角平分线,FP EP 相交于点P ．求证：点P 是四边形ABCD 的准内点．（2）分别画出图3平行四边形和图4梯形的准内点．（作图工具不限，不写作法，但要有必要的说明）（3）判断下列命题的真假，在括号内填“真”或“假”． ①任意凸四边形一定存在准内点．（） ②任意凸四边形一定只有一个准内点．（）③若P 是任意凸四边形ABCD 的准内点，则PD PC PB PA +=+或PD PB PC PA +=+．( )（第23题）图2图4F EDC B A P G HJ I 图1B J IH GDC AP25.如图，已知直线交坐标轴于B A ，两点，以线段AB 为边向上作正方形ABCD ，过点C D ，A ，的抛物线与直线另一个交点为E ．（1）请直接写出点D C ,的坐标；（2）求抛物线的解析式；（3）若正方形以每秒5个单位长度的速度沿射线AB 下滑，直至顶点D 落在x 轴上时停止．设正方形落在x 轴下方部分的面积为S ，求S 关于滑行时间t 的函数关系式，并写出相应自变量t 的取值X 围；（4）在（3）的条件下，抛物线与正方形一起平移，同时D 停止，求抛物线上E C , 两点间的抛物线弧所扫过的面积．（第25题）y x121+-=x y某某省2010年适应性练习数学(一)答案应为原创试题，选择题和填空题无答案，望请谅解三，解答题20.1）解：在△AOC中，AC=2，∵AO＝OC＝2，∴△AOC是等边三角形．………2分∴∠AOC＝60°，∴∠AEC＝30°．…………………4分（2）证明：∵OC⊥l，BD⊥l．∴OC∥BD．……………………5分∴∠ABD＝∠AOC＝60°．∵AB为⊙O的直径，∴△AEB为直角三角形，∠EAB＝30°．…………………………7分∴∠EAB＝∠AEC．∴四边形OBEC 为平行四边形．…………………………………8分又∵OB＝OC＝2．∴四边形OBEC是菱形．…………………………………………9分21.解：（1）该班60秒跳绳的平均次数至少是：＝100.8．因为100.8>100，所以一定超过全校平均次数．…………………3分（2）这个学生的跳绳成绩在该班是中位数，由4+13+19=36，所以中位数一定在100～120X 围内．…………………………………………6分（3）该班60秒跳绳成绩大于或等于100次的有：19+7+5+2=33（人），……………………………………………………………………………8分．所以，从该班任选一人，跳绳成绩达到或超过校平均次数的概率为0.66．……… 9分 22.解：延长BC 交AD 于E 点，则CE ⊥AD ．……1分在Rt △AEC 中，AC ＝10，由坡比为1: 可知：∠CAE ＝30°，………2分 ∴ CE ＝AC ·sin30°＝10× ＝5，………3分 AE ＝AC ·cos30°＝10× ＝．……5分在Rt △ABE 中，BE ＝＝ =11．……………………………8分 ∵ BE ＝BC ＋CE ，∴ BC ＝BE －CE ＝11-5＝6（米）．答：旗杆的高度为6米． …………………………………………10分 23.1）设安排x 人生产甲种板材，则生产乙种板材的人数为(140)x -人．由题意，得24000120003020(140)x x =-，解得：80x =．经检验，80x =是方程的根，且符合题意．答：应安排80人生产甲种板材，60人生产乙种板材．（2）设建造A 型板房m 间，则建造B 型板房为(400)m -间，由题意有：5478(400)240002641(400)12000m m m m +-⎧⎨+-⎩≤≤，．解得300m ≥．又0400m ≤≤，300400m ∴≤≤．这400间板房可安置灾民58(400)33200w m m m =+-=-+．∴当300m =时，w 取得最大值2300名．答：这400间板房最多能安置灾民2300名．24.（1）如图2，过点P 作AD PJ CD PI BC PH AB PG ⊥⊥⊥⊥,,,，∵EP 平分DEC ∠， ∴PH PJ =．……………3分同理 PI PG =．…………………………………1分 ∴P 是四边形ABCD 的准内点．…………………1分（2）……………………………………………………………………………4分平行四边形对角线BD AC ,的交点1P 就是准内点，如图3（1）. 或者取平行四边形两对边中点连线的交点1P 就是准内点，如图3（2）；梯形两腰夹角的平分线与梯形中位线的交点2P 就是准内点．如图4.（3）真；真；假．……………………………………………………………………3分（各1分，若出现打“√”“×”或写“对”“错”同样给分．）25.（1）)3,1(),2,3(D C ；…………………………………………………2分（2）设抛物线为c bx ax y ++=2，抛物线过),1,0()3,1(),2,3(，⎪⎩⎪⎨⎧=++=++=.239,3,1c b a c b a c 解得5,617,61.a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩…………………………………………………2分 ∴1617652++-=x x y ．……………………………………………………………1分（3）①当点A 运动到点F 时，,1=t当10≤<t 时，如图1， ∵'OFA GFB ∠=∠， ,21tan ==∠OF OA OFA ∴,215''''tan ===∠t GB FB GB GFB ∴,25't GB = ∴2'4525521''21t t t GB FB S G FB =⨯⨯=⨯=∆；……2分 ②当点C 运动到x 轴上时，2=t ，图3（1）图4图3（2）DCB AABCDGD CBA F E EG HF 1P1P2P图1当21≤<t 时，如图2，22''215,A B AB ==+=∴,55'-=t F A ∴255'-=t G A ， ∵25't H B =， ∴''1'')''2A B HG S A G B H A B =+⨯梯形（5)25255(21⨯+-=t t 4525-=t ；…………（2分）③当点D 运动到x 轴上时，3=t ，当32≤<t 时，如图3， ∵255'-=t G A ， ∴25532555'tt GD -=--=， ∵1,12121==⨯⨯=∆OA S AOF ， AOF ∆∽'GD H ∆∴2')'(OAGD S S AOF H GD =∆∆，∴2')2553(t S H GD -=∆， ∴22'''3555)2GA B C H t S -=-五边形（）（图2图3word 11 / 11 =425215452-+-t t ．………（2分）（解法不同的按踩分点给分）（4）∵3=t ,53''==AA BB , ∴''''BB C C AA D D S S S ==阴影矩形矩形………………………………………………（2分） ='AA AD ⨯=15535=⨯．……………………………………………………………（1分）图4。

2010年中考适应性练习数学试题

第6题图2010年中考适应性练习数学试题考生注意：1．本卷共6页，三大题26小题，满分150分．考试时间为120分钟． 2．一律在《答题卡》相应位置作答，在试题卷上答题视为无效． 3．可以使用科学计算器．一、选择题（共10小题，每小题4分，满分40分） 1．的相反数是（）.A ．5B ．C ．D ．2．五边形的内角和是（）.A ．180°B ．360°C ．540°D ．720° 3．下列运算正确的是（）. A ．B ．C ．Ｄ．4．在如图所示的四个剪纸图案中，形如轴对称图形的图案是( ).A ．B ．C ．D ．5．我国部分城市今年五月某一天最高温度如下表，这些数据的中位数是（）.城市北京上海重庆杭州苏州广州武汉最高温度（℃）24273125293030A ．30B ．29C ．28D ．25 6．一副三角板按如图所示叠放在一起，则图中∠的度数是（）． A ．60° B.75° C.90° D.105°7．不等式组的解集在数轴上表示为（）.A ．B ．C ．D ．1 2 3－1 0 1 2 3－1 0第14题图第10题图第16题图8．如图，点A 、B 、C 是⊙O 上三点，∠C ＝20°，则∠AOB 的度数是（）．A ．10° B.20° C.40° D.60° 9．下列事件中，是确定事件的为（）. A ．在一个装着白球和黑球的袋中摸球，摸出红球B ．打开电视体育频道，正在播放NBA 球赛C ．掷6枚相同的硬币，3枚正面向上3枚正面向下D ．射击运动员射击一次，命中十环10．如图，是一个棱长分别为2、3、4的长方体，一只蜘蛛在顶点A处，一只小昆虫在顶点B 处，则蜘蛛接近小昆虫时所爬行的最短路线的长是（）. A ．B ．7C ．D ．6二、填空题（共8小题，每小题3分，满分24分） 11．.计算：＝______________．12．.分解因式：____________________．13．.如图，在□ABCD 中，已知AD ＝8厘米，AB ＝6厘米，DE 平分∠ADC 交BC 边于点E ，则BE 等于_______厘米.14．.如图，天平中放有苹果、香蕉、砝码，且两个天平都平衡.若一个苹果的重量是210克，则一个香蕉的重量是______克.15．.如图所示几何体（a ）的一个视图（b ）的名称是________． 16．如图，挂钟指示的时间是10点10分钟，若分针的固定点到分针针尖的距离为9厘米，则到10点30分钟时，分针的针尖转过的路线长是______厘米﹙结果保留﹚．17．如图，正方形OEFG 和正方形ABCD 是位似图形，点F 的坐标是（1，1），点C 的坐标是（4，2），则这两个正方形位似中心432第15题图正面（b）（a）ABCDE第13题图第8题图的坐标是_______．18．如图所示的运算程序中，若开始输入的值是93，我们发现第1次输出的结果是96，第2次输出的结果是48，…，第2010次输出的结果是_____．三、解答题（满分86分） 19．（每小题8分，满分16分）⑴ 先化简，再求值：，其中．⑵解方程：.20．（本小题满分8分）已知：如图，AB ∥DE ，∠A ＝∠D ，且A B ＝D E ，求证：BE ＝C F .21．（本小题满分8分）如图1，是一张关于“2009年中央政府投资预算”的新闻图片．请你根据图1给出的信息，解答下列问题：第18题图输入+3输出为偶数为奇数第17题图今年中央政府投资预算已安排下达5553亿元 2009年中央政府投资预算已安排下达5553亿元占总预算的61% 四大类重点项目的投资预算共下达：2348亿元保障性安居工程农田水利等农村民生工程教育和卫生等社会事业技术改造和技术创新49.23% 18.19%15%17.58%图1200400 600 800 1000 1200 1156352 427A C（）（） A ：农田水利等农村民生工程 B ：教育和卫生等社会事业 C ：技术改造和技术创新 D ：保障性安居工程2009年中央四大类重点项目的投资预算统计图项目（亿元）（1）2009年中央政府总投资预算为多少元？（用科学记数法表示，保留4位有效数字）（2）“教育与卫生等社会事业”项目在扇形统计图中对应的圆心角的度数是多少？（3）如图2，是根据图2中的扇形统计图转换成的条形统计图（未完成），请补全图2的条形统计图，并将项目的代码填在相应的括号内.22．（本小题满分8分）如图，有4张形状、大小、质地均相同的卡片，正面分别写有一个实数，背面完全相同．现－将这4张卡片洗匀后正面向下放在桌子上，⑴从中随机抽取一张，则抽出卡片正面的实数是有理数的概率是__________.⑵从中随机抽取一张，记下卡片正面的实数，放回洗匀，再抽取一张，记下卡片正面的实数，求两次抽出卡片正面的实数相加结果是有理数的概率.23．（本小题满分8分）如图，有一段斜坡长为10米，坡角，为方便残疾人的轮椅车通行，现准备把坡角降为5°． ⑴求坡高；⑵求斜坡新起点到原起点的距离（精确到0.1米）．24．（本小题满分12分）“五一”期间，国美电器商城推出了两种优惠方式：第一种是打折优惠，凡是在该商城购买家用电器的客户均可享受八折优惠；第二种是赠送购物券，凡在商城三天内购买家用电器的金额满400元且少于600元的，赠购物券100元；不少于600元的，所赠购物券是购买电器金额的，另再送．．50．．元现金．．．.（注：每次购买电器时只能使用其中一种优惠方式） ⑴在第二种促销方式中，设购买电器的金额为x ﹙x ≥400﹚元，优惠券金额为a 元，则可用如下形式表达：①当x ＝500时，a ＝______； ②当x ≥600时，a ＝_________；⑵如果小张想一次性购买金额为x ﹙400≤x ＜600﹚元的电器，在上面的两种促销方式中，试通过计DCB A－3－2图2算帮他确定一种比较合算的方式？⑶如果小张在三天内在此商城先后两次购买电器时都得到了优惠券（且第二次购买时未使用第一次的优惠券），所得优惠券金额累计达800元，设他购买电器的金额为元，至少．．应为多少？（=支付金额－所送现金金额）25．（本小题满分13分）已知，如图，矩形中，AD =6，DC =7，菱形的三个顶点分别在矩形的边上，，连接．⑴若DG=2，求证四边形为正方形；⑵若DG=6，求的面积；⑶当DG 为何值时，的面积最小．26．（本题满分13分）已知：如图，直线：经过点一组抛物线的顶点（为正整数）依次是直线上的点，这组抛物线与轴正半轴的交点依次是：（为正整数），设⑴求的值； ⑵若，求经过点的抛物线的解析式；⑶定义：若抛物线的顶点与轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为：“美丽抛物线”．探究：当的大小变化时，这组抛物线中是否存在美丽抛物线？若存在，请你求出相应的的值．参考公式：抛物线的顶点坐标为，对称轴．yOM xl123…。

2010年中考模拟数学卷参考答案

2010年中考模拟试卷数学参考答案及评分标准三、解答题（本题有8小题，第17～19题每题6分，第20～21题8分，第22～23题每题10分，第24题12分，共66分） 17、（本题满分6分）解：∵方程2233x mx x -=--无解∴方程2233x mx x -=--有增根x=3------------2分∴方程两边同乘以（x-3）,得：26x m -=------------2分∴当x=3时，m =分 18、（本题满分6分）解：过C 点作BA 的延长线交于点E ，------------1分∵AB ＝AC ＝10，∠B ＝022.5 ∴∠EAC ＝045∴△EAC 为等腰直角三角形------------1分设AE ＝EC ＝X,则AB ＝AC ＝10∴x =∴111022S A B E C ∆=⋅=⨯⨯=≈35.42m ------------2分又∵53.610⨯2cm ＝362m ＞35.42m ------------1分 ∴预订草皮够用------------1分19、（本题满分6分）解：答案不唯一，酌情给分。

20、（本题满分8分）解：（1）18 0.55------------各1分（2）图略--------------共4分（虚设组不设各扣1分）（3）0.55±0.1均为正确------------2分 21、（本题满分8分）解：（1）正确的结论：①②③------------2分（2）错误理由：当a ＞0时，只有1x ＞2x ＞0或2x ＜1x ＜0时，1y ＜2y 而2x ＜0＜1x 时，1y ＞2y ------------4分改正：当a ＞0时，在同一象限内，函数a y x=，y 随x 增大而减小-----2分22、（本题满分10分）解：（1）如右图------------共6分（030，045角，线段a 各1分，余酌情给分）（2）设AB ＝x,则R t △ABC 中，OB ＝x ，由题意得：6+ x ------------1分得，1)x =≈8米------------2分答：旗杆高度约为8米。

2010年初中数学中考模拟试卷.doc

2010年初三中考模拟(一)数学试卷时间：120分钟总分：120一、选择题（本大题共有5小题，每小题3分，共15分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号涂在答题卡相应位置．．．．．．．上） 1、平面直角坐标系内，点A （-2，-3）在（）A.第一象限 B 第二象限 C.第三象限 D 。

第四象限 2．下列图形中，既是．．轴对称图形又是．．中心对称图形的是( )3．下列事件中最适合使用普查方式收集数据的是（）A ．了解某班同学的身高情况B ．了解全国每天丢弃的废旧电池数C ．了解一批炮弹的杀伤半径D ．了解我国农民的年人均收入情况 4.下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )5、如图，平面直角坐标系中，在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周，则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是（）二、填空题（共12小题，每小题2分，共24分。

请将答案写在答题卡相应位置．．．．．．．上）1 2 3 412ys O 1 2 3 4 1 2 y s O s 1 2 3 4 1 2 y sO 1 2 3 4 1 2 y O A B .C .D . DC B A A B C DABC DE 第16题图6计算：2332x x ∙ ，()322x。

7、分解因式：228x -= 。

8、已知数据：2，1-，3，5，6，5，则这组数据的众数是，极差是。

9 函数21+=x y 中，自变量x 的取值范围是．10．如图5，∠1，∠2，∠3，∠4是五边形ABCDE 的外角，且∠1=∠2=∠3=∠4=070，则∠AED 的度数是_________________ .第10题第12题第13题 11、已知双曲线xky =过点（-2，3），则k = 。

12、AB ∥CD ，AC ⊥BC ，∠BAC ＝65°，则∠BCD ＝______________度。

2010年中考模拟试卷数学

2010年中考模拟试卷数学考生须知：1．本试卷分试题卷和答题卷两部分。

满分120分，考试时间100分钟。

2．答题前，必须在答题卷的左上角填写校名、姓名和班级、学号、试场号、座位号。

3．所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应。

4．考试结束后，上交试题卷和答题卷。

试题卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内，注意可以用多种不同的方法来选取正确答案。

1、（原创）已知△ABC 中，∠C ＝90︒，SinA=21，则tanB 的值是（▲）A. 33 B. 2 C. 1 D. 32、萧山历史上规模最大、投资最多、涉及面最广的交通基础设施工程 “12881”工程就是争取用三年时间，在全区范围内推进“一桥两隧八纵八横一绕”工程建设，完成交通道路投资428.6亿元,新建、改建道路273公里，到2011年基本形成“城乡贯通、区间快速、主次分明、东网加密”的全区交通道路网络体系。

将428.6亿元用科学记数法表示为（▲）A ．910286.4⨯元 B 、11104286.0⨯元 C 、1010286.4⨯元 D 、10104286.0⨯元3、图中BOD ∠的度数是（▲） A 、550 B 、1100 C 、1250 D 、15004、（原创）将211292.0128，，，，化简成最简二次根式后，随机抽取其中一个根式，与 2 被开方数相同的概率是（▲）A.15B.25C.35D.455、（改编）若干杯奶茶摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆奶茶共有（▲）A.5杯B. 6杯C.9杯D.12杯D(第8题)(第5题)6、（原创）已知），），（，2211(yxyx是反比例函数xy1-=图象上两点，且210xx，则21yy-的值是(▲)A.正数B.负数C.非正数D.非负数7、小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能．．．是(▲)A B C D8、如图，已知矩形ABCD中，AB＝8，BC＝π5．分别以B、D为圆心，AB为半径画弧，两弧分别交对角线BD于点E、F，则图中阴影部分的面积为（▲）A．π4 B．π5 C．π8 D．π109、（原创）如图是一次函数y=kx+b和y=mx+n的图像,则不等式组的解是(▲）A.x≤1B.x≤1或 x≥4C.1≤x≤4D.0≤x≤4y10、（改编）如图，在平面直角坐标系中，点A1是以原点O为圆心，半径为2的圆与过点（0，1）且平行于x轴的直线l1的一个交点；点A2是以原点O为圆心，半径为3的圆与过点（0，2）且平行于x轴的直线l2的一个交点；……按照这样的规律进行下去，点A n的坐（▲）A．(1,12++nn) B.(nn,12+) C.(nn,2) D.(nn,12-)二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案。

2010年中考模拟数学试卷和答案

2010年中考模拟试卷数学考生须知：1.本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟 .2.答题时，应该在答题卷指定位置内写明校名，姓名和准考证号 .3.所有答案都必须做在答题卷标定的位置上，请务必注意试题序号和答题序号相对应 .4.考试结束后，上交试题卷和答题卷试题卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的 .注意可以用多种不同的方法来选取正确答案 .1. 如果0=+b a ，那么a ，b 两个实数一定是（）A.都等于0B.一正一负C.互为相反数D.互为倒数2. 要了解全校学生的课外作业负担情况，你认为以下抽样方法中比较合理的是（）A.调查全体女生B.调查全体男生C.调查九年级全体学生D.调查七、八、九年级各100名学生 3. 直四棱柱，长方体和正方体之间的包含关系是（）4. 有以下三个说法：①坐标的思想是法国数学家笛卡儿首先建立的；②除了平面直角坐标系，我们也可以用方向和距离来确定物体的位置；③平面直角坐标系内的所有点都属于四个象限 .其中错误的是（）A.只有①B.只有②C.只有③D.①②③ 5. 已知点P （x ，y ）在函数x xy -+=21的图象上，那么点P 应在平面直角坐标系中的（）A.第一象限B. 第二象限C. 第三象限D. 第四象限6. 在一张边长为4cm 的正方形纸上做扎针随机试验，纸上有一个半径为1cm 的圆形阴影区域，则针头扎在阴影区域内的概率为（）A.161 B.41 C.16π D.4π 7. 如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（） A.只有1个 B.可以有2个 C.有2个以上，但有限 D.有无数个8. 如图，在菱形ABCD 中，∠A=110°，E ，F 分别是边AB 和BC的中点，EP ⊥CD 于点P ，则∠FPC=（） A.35° B.45° C.50° D.55°9. 两个不相等的正数满足2=+b a ，1-=t ab ，设2)(b a S -=，则S 关于t 的函数图象是（）A.射线（不含端点）B.线段（不含端点）C.直线D.抛物线的一部分10. 某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点)(k k k y x P ，处，其中11=x ，11=y ，当k≥2时，⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ，[a ]表示非负实数a 的整数部分，例如[2.6]=2，[0.2]=0 .按此方案，第2009棵树种植点的坐标为（）A.（5，2009）B.（6，2010）C.（3，401） D （4，402）二. 认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案 11. 如图，镜子中号码的实际号码是___________ .12. 在实数范围内因式分解44-x = _____________________ . 13. 给出一组数据：23，22，25，23，27，25，23，则这组数据的中位数是___________；方差（精确到0.1）是_______________ .14. 如果用4个相同的长为3宽为1的长方形，拼成一个大的长方形，那么这个大的长方形的周长可以是______________ .15. 已知关于x 的方程322=-+x mx 的解是正数，则m 的取值范围为______________ . 16. 如图，AB 为半圆的直径，C 是半圆弧上一点，正方形DEFG 的一边DG 在直径AB 上，另一边DE 过ΔABC 的内切圆圆心O ，且点E 在半圆弧上 .①若正方形的顶点F 也在半圆弧上，则半圆的半径与正方形边长的比是______________；②若正方形DEFG 的面积为100，且ΔABC 的内切圆半径r =4，则半圆的直径AB = __________ .三. 全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤 .如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以 . 17. （本小题满分6分）如果a ，b ，c 是三个任意的整数，那么在2b a +，2c b +，2ac +这三个数中至少会有几个整数？请利用整数的奇偶性简单说明理由 .18. （本小题满分6分）如图，，有一个圆O 和两个正六边形1T ，2T .1T 的6个顶点都在圆周上，2T 的6条边都和圆O 相切（我们称1T ，2T 分别为圆O 的内接正六边形和外切正六边形） . （1）设1T ，2T 的边长分别为a ，b ，圆O 的半径为r ，求a r :及b r :的值；（2）求正六边形1T ，2T 的面积比21:S S 的值 .如图是一个几何体的三视图 . （1）写出这个几何体的名称；（2）根据所示数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B 出发，沿表面爬到AC 的中点D ，请你求出这个线路的最短路程 .20. （本小题满分8分）如图，已知线段a .（1）只用直尺（没有刻度的尺）和圆规，求作一个直角三角形ABC ，以AB 和BC 分别为两条直角边，使AB=a ，BC=a 21（要求保留作图痕迹，不必写出作法）；（2）若在（1）作出的RtΔABC 中，AB=4cm ，求AC 边上的高 .学校医务室对九年级的用眼习惯所作的调查结果如表1所示，表中空缺的部分反映在表2的扇形图和表3的条形图中.（1）请把三个表中的空缺部分补充完整；（2）请提出一个保护视力的口号（15个字以内）.22. （本小题满分10分）如图，在等腰梯形ABCD中，∠C=60°，AD∥BC，且AD=DC，E、F分别在AD、DC的延长线上，且DE=CF，AF、BE交于点P .（1）求证：AF=BE；（2）请你猜测∠BPF的度数，并证明你的结论.在杭州市中学生篮球赛中，小方共打了10场球 .他在第6，7，8，9场比赛中分别得了22，15，12和19分，他的前9场比赛的平均得分y 比前5场比赛的平均得分x 要高 .如果他所参加的10场比赛的平均得分超过18分（1）用含x 的代数式表示y ；（2）小方在前5场比赛中，总分可达到的最大值是多少？（3）小方在第10场比赛中，得分可达到的最小值是多少？24. （本小题满分12分）已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ，又有定点P （2，0） . （1）若0>a ，且tan ∠POB=91，求线段AB 的长；（2）在过A ，B 两点且顶点在直线x y =上的抛物线中，已知线段AB=38，且在它的对称轴左边时，y 随着x 的增大而增大，试求出满足条件的抛物线的解析式；（3）已知经过A ，B ，P 三点的抛物线，平移后能得到259x y =的图象，求点P 到直线AB 的距离 .2010年中考模拟试卷数学参考答案一、仔细选一选（每小题3分，芬30分）二. 认真填一填（本题有6个小题，每小题4分，共24分） 11、326512.)2)(2)(2(2-++x x x 13、23；2.614、14或16或2615、46-≠->m m 或16、①5∶2 ；②21三. 全面答一答（本题有8个小题，共66分） 17、（本题6分）至少会有一个整数 .因为三个任意的整数a,b,c 中，至少会有2个数的奇偶性相同，不妨设其为a ，b ，那么2ba +就一定是整数 . 18、（本题4分）（1）连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点，得以圆O 半径为高的正三角形，所以r ∶b=3∶2;（2） T 1∶T 2的连长比是3∶2，所以S 1∶S 2=4:3):(2=b a .19、（本题6分）（1）圆锥；（2）表面积S=πππππ164122=+=+=+r rl S S 圆扇形（平方厘米）（3）如图将圆锥侧面展开，线段BD 为所求的最短路程 . 由条件得，∠BAB ′=120°，C 为弧BB ′中点，所以BD =33 .20、（本题8分）（1）作图如右，ABC ∆即为所求的直角三角形；（2）由勾股定理得，AC =52cm ，设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421，所以554=h 21、（本题8分）（1）补全的三张表如下：（表一）（2）例如：“象爱护生命一样地爱护眼睛！”等 . 22、（本题10分）（1）∵BA=AD ，∠BAE=∠ADF ，AE=DF ， ∴△BAE ≌△ADF ，∴BE=AF ；（2）猜想∠BPF=120° .∵由（1）知△BAE ≌△ADF ，∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ，而AD ∥BC ，∠C=∠ABC=60°， ∴∠BPF=120° . 23、（本题10分）（1）9191215225++++=x y ；（2）由题意有x x >++++9191215225，解得x ＜17，所以小方在前5场比赛中总分的最大值应为17×5－1=84分；（3）又由题意，小方在这10场比赛中得分至少为18×10 + 1=181分，设他在第10场比赛中的得分为S ，则有81+（22+15+12+19）+ S ≥181 .解得S≥29，所以小方在第10场比赛中得分的最小值应为29分 .24、（本题12分）（1）设第一象限内的点B （m,n ），则tan ∠POB 91==m n ，得m=9n ，又点B 在函数xy 1=的图象上，得m n 1=，所以m =3（－3舍去），点B 为)31,3(，而AB ∥x 轴，所以点A （31，31），所以38313=-=AB ；（2）由条件可知所求抛物线开口向下，设点A （a , a ），B （a 1，a ），则AB =a1－ a =38, 所以03832=-+a a ，解得313=-=a a 或 .当a = －3时，点A （―3，―3），B （―31，―3），因为顶点在y = x 上，所以顶点为（－35，－35），所以可设二次函数为35)35(2-+=x k y ，点A 代入，解得k= －43,所以所求函数解析式为35)35(432-+-=x y .同理，当a = 31时，所求函数解析式为35)35(432+--=x y ；（3）设A （a , a ），B （a 1，a ），由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为：)2)1()(2(59++--=aa x x y .点A （a , a ）代入，解得31=a ，1362=a ，所以点P 到直线AB 的距离为3或136.。

2010—2011九年级数学试卷

2010～2011学年度适应性测试九年级数学试题（满分：150分考试时间：120分钟）友情提醒：本卷中的所有题目均在答题卡上作答，在本卷中作答无效。

一、选择题（本大题共8小题，每小题3分，共24分．每题的四个选项中，只有一个选项是符合要求的．） 1．若3)2(⨯-=x ，则x 的相反数是 A ．61-B ．61C ．－6D ．62．下列运算正确的是A ．236·a a a =B ． 221-=-C 4=±D ．|6|6-=3．图中圆与圆之间不同的位置关系有 A ．2种 B ．3种 C ．4种 D ．4.5．为了解某小区居民的日用电情况，居住在该小区的一名同学随机抽查了l5户家庭的日用电量，结果如下表：则关于这l5户家庭的日用电量，下列说法错误的是A 众数是6度B 平均数是6.8度C 中位数是6度D 极差是5度 6．在平面直角坐标系中，对于平面内任一点（m,n ），规定以下两种变换：①(,)(,)f m n m n =-，如(2,1)(f =-；②(,)(,g m n m n =--，如(2,1)(g =--。

按照以上变换有：()()()3,43,43,4f g f =--=-⎡⎤⎣⎦，那么B ． C ． D ．BD AC 第7题图 B 1()3,2g f -⎡⎤⎣⎦等于A.（3，2）B.（3，-2）C.（-3，2）D.（-3，-2）7. 如图，利用四边形的不稳定性改变矩形ABCD 的形状，得到□A 1BCD 1，若□A 1BCD 1的面积是矩形ABCD 面积的一半，则∠ABA 1的度数是A ．15°B ．30°C ．45°D ．60°8．已知：如图，点P 是正方形ABCD 的对角线AC 上的一个动点(A 、C 除外)，作AB PE ⊥于点E ，作BC PF ⊥于点F ，设正方形ABCD 的边长为x ，矩形PEBF 的周长为y ，在下列图象中，大致表示y 与x 之间的函数关系的是二、填空题（本大题共10题，每题3分，共30分．把答案填在答题卡中对应的横线上）．9．请写出一个图象在第一、三象限的反比例函数：。

2010-2011年九年级数学期中适应性试题

2010/11学年度第一学期期中教学质量检测九年级数学适应性试题温馨提示：本试卷共分三大题，计23小题，时间120分钟，满分150分。

请把答案写在规定的位置。

一、单项选择题（下列各题的四个选项中，只有一个是符合题意要求的，请将正确答案写在题后的答题卡内；计10小题，每小题4分，共40分）1．下列各式中，一定是二次根式的是A ．4-B ．1-xC ．32a D.32+x2．下列图形中，既是轴对称，又是中心对称的图形是3．下列关于x 的一元二次方程中，有两个不相等的实数根的方程是A ．012=+xB ．012=-+x xC ．0322=++x x D. 01442=+-x x4．若()()822222=-++b a b a ，则=+22b a （） A ．－2 B. 4 C.4或－2 D .－4或25．等腰三角形的底和腰是方程0862=+-x x 的两根，则这个三角形的周长为A.8或10B.8C.10D.不能确定6．如果关于x 的一元二次方程()011222=++-x k x k 有两个不相等的实数根，那么 k 的取值范围是A ．k ＞41-且k ≠0B ．k ＞41-C ．k ＜41-D ．k ≥41-且k ≠0 7．如右图所示的Rt △ABC 向右翻滚，下列说法正确的有（1）①→②是旋转（2）①→③是平移（3）①→④是平移（4）②→③是旋转A. 1种B. 2种C. 3种D. 4种8．如图，图中的两个圆中的一个圆是由另一个圆旋转而得到的，问它的旋转中心有A.1个B.2个C. 无数个D.无法确定9．定义：如果一元二次方程 ax 2＋b x ＋c=0(a ≠0）满足a ＋b ＋c=0，那么我们称这个方程为“凤凰”方程．己知ax 2+bx+c=0（a ≠0）是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是A.a=cB.a=bC.b=c D ．a=b=c10．轴对称与平移、旋转的关系不正确．．．的是 A ．经过两次翻折（对称轴平行）后的图形可以看作是原图形经过一次平移得到的B ．经过两次翻折（对称轴不平行）后的图形可以看作是原图形经过一次平移得到的C ．经过两次翻折（对称轴不平行）后的图形可以看作是原图形经过旋转得到的D ．经过几次翻折（对称轴有偶数条且平行）后的图形可以看作是经过一次平移得到的二、填空题（本大题共4小题，每小题5分，共20分）11．在实数范围内因式分解=-44x ______________________________.12．把方程2x 2＋4x －l=0配方后得（x ＋m ）2=k ，则m=_______,k=_______.13．符号“f ”表示一种运算，它对一些数的运算结果如下：()()()()() ,34,23,12,011====f f f f() ,5)51(,4)41(,3)31(,2)21(2====f f f f利用以上规律计算：()=-)20091(2009f f _____________________. 14．己知平面直角坐标系上的三个点O(0,0）、A （－2,2）、B （－2,0），将△ABO 绕O 按顺时针方向旋转135°，则点A,B 的对应点A 1,B 1的坐标分别是A 1(_____,_____)，B l （______，______）．三、解答题（本大题共9小题，共90分）15．（8分）计算()2)31(21243122++⋅--16．(8分）解方程x 2＋5=3(x ＋l)17．(8分）在正数范围内定义某种运算“⊗”，作如下规定：a ⊗b=a 2＋a b －b 2求方程 x ⊗(x ＋l)=0的解．18．（8分）先化简121111122+-+÷--+x x x x x ,然后从1,1,13--中选取一个你认为合适．．的数作为 x 的值代入求值．19．（10分）如下图，己知△ABC 的三个顶点的坐标分别为A （－2,3）、B （－6,0）、C （－l,0).（1）请直接写出点A 关于y 轴对称的点坐标；（2）将△ABC 绕坐标原点O 旋转180°画出图形，直接写出点A 的对应点的坐标；（3）请直接写出：以A 、B 、C 为顶点的平行四边形的第四个顶点D 的坐标．20．（10分）含山县县城为改善居民的住房条件，每年都新建一批住房，人均住房面积逐年增加，该开发区2005年至2007年，每年年底人口总数和人均住房面积的统计结果分别如图所示，请根据两图所提供的数据解答下列问题：（1）该区2006年和2007年两年中，哪一年比上一年增加的住房面积多？多增加了多少万平方米？（2）由于经济发展需要，预计到2009年底，该区人口总数量将比2007年底增加2万，为使到2009年底该区人均住房面积达到11平方米/人，试求2008年和2009年这两年该区住房总面积的年平均增长率应达到百分之几？21．（12分）如下图，在4×3的网格上，由个数相同的白色方块与黑色方块组成的一幅图案，请仿照此图案，在下列网格中分别设计出符合要求的图案（注：①不得与原图相同；②黑、白方块的个数要相同）（1）是轴对称图形，又是中心对称图形；（2）是轴对称图形，但不是中心对称图形；（3）是中心对称图形，但不是轴对称图形。

2010年南通通州中考适应性考试—数学

2010年中考适应性测试（满分150分，答卷时间120分钟）一、选择题：本大题共8小题；每小题3分，共24分。

下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的。

请将正确选项的代号填在左边的括号里。

2 3（X2）3•小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是得分评卷人-32的值是—6 B . 6下列运算正确的是-9C. X-22=x2 -44.如图，在等边三角形ABC 中,AED为AC的中点，竺EB1，则和△ AED （不包含△ AED ）3相似的三角形有（A . 1个B . 2个5 .如图，已知O是四边形ABCDC . 3个内一点，OA=OB = OC,Z ABC =Z ADC =65° ,则/ DAO +/ DCO的度数是130 °C. 262.5第4题图a, b在数轴上对应点的位置如图所示，则必有B . a - b ：： 0a 门D . 0b第5题图6 .实数A. a b 0C . ab 0b -1 0 a1第6题图第8题图 5 7时间（分钟）【】1.A CB. 230°O D. 165 °【】7•已知某反比例函数的图象经过点（m, n），则它一定也经过点1】8•—名考生步行前往考场，5分钟走了总路程的丄，估计步行不能准时到达，于是他改乘出租车6赶往考场，他的行程与时间关系如图所示（假定总路程为1,出租车匀速），则他到达考场所花的时间比一直步行提前了9•写出一个大于-2的负无理数： __________ . _______10. 截至2010年，南通市绿化总面积达到4103.7万平方米。

这个数据用科学记数法表示为平方米.11. ___________________________________________________ 二次函数y = x • 3 2 - x取得最大值时，x = •12. 将点M向左平移3个单位，再向下平移2个单位得到M ' （—2, —3）,则点M的坐标是__________ •13. 若等腰三角形的一个外角为_____________ 150°,则它的底角为度•214. 数学家发明了一个魔术盒，当任意实数对（a, b）进入其中时，会得到一个新的实数： a b 1 •例如2把（3, -2）放入其中，就会得到3■ （-2）• 1 = 8 .现将实数对（m,-2m ）放入其中得到实数4，则主视图左视图m = _________ •15. 如图，长方体的主视图和左视图如图所示（单位：cm），则其俯视图的面积为_______ cm2•第15题图16•在△ ABC中，BC边不动，改变点A的位置，使得• A减少：•度，• B增加［度，• C增加度, 则〉，-, 三者之间的等量关系是C3 - A 45CC1B2B1C2B3 B 4B • (m, - n)C • (_m, n)D • (m ,n)A • 18分钟E. 20分钟 C. 24分钟 D • 28分钟得分评卷人3分，共30分。

枣阳市2010年中考适应性考试数学答案

枣阳市2010年中考适应性考试数学答案一.选择题：（每小题3二.填空题：（每小题3＞-1且k ≠0 15.221x y -=3 17.82 三、解答题：（共69分）18.解：原式＝y x y x +-2·y x xy 2-·y x xy +（2分）＝2222y x y x -（3分）当x=2+3，y=2－3时，原式＝2416（6分）.19.(1)120人；（1分）补全统计图略（2分）；（2）C 组内（3分）；（3）300180×16000=9000（人）（4分）；达到规定体育锻炼活动时间的约为9000人。

（5分）20. （1）列表如下：（（2）从上表可以看出，所有可能出现的等可能结果有12种（4分），其中小明能得满分的结果有4种，故这次实验操作小明得满分的概率是31.（6分） 21.解：（1）画图（略）2分（2）∵tan ∠AOB=33,且∠AOB 为锐角， ∴∠AOB=30°(4分)，∵△OAB 绕点O 旋转90°到△OA ＇B ＇,∴OA ＇=OA,A ＇B ＇=AB,∠OA ＇B ＇=90°,∠AOA ＇=90°,∴∠AOB ＇=∠AOA ＇+∠A ＇OB ＇=90°+30°=120°(5分)（3）S 四边形OAA ＇B ＇=S △OAA ＇+S △OA ＇B ＇=29+233.（6分）22.解：设台布各边垂下的长度为x 米，则（6+2x ）(4+2x)=2×4×6整理，得0652=-+x x解之，得 61-=x ，12=x .61-=x 不合题意，舍去.∴1=x .862=+x （米） 642=+x （米）答：这块台布的长和宽分别为8米，6米.（6分）23.解：（1）连结OC.∵OC 切⊙O 于C ，∴∠OCD ＝90°.（1分）又∵∠ACD=120°，∴∠ACO=∠ACD-∠OCD=120°-90°=30°.（2分）∵OC=OA ，∴∠A=∠ACO=30°，∴∠COD=60°，∴∠D=30°，∴∠COD=60°，∴∠D=30°.∴CA=DC.（4分）（2）∵sin ∠D=OD OC =BD OB OC +=BDOB OB +,(5分) sin ∠D=sin30°=21,∴10+OB OB =21.(6分) 解之，得OB=10，经检验OB=10是原方程的解.即⊙O 的半径为10.（7分）24.解：（1）由题意，装运C 种水果的车辆数为（20-x-y ），则有6x+5y+4(20-x-y)=200 （2分）整理，得 y=-2x+20 （3分）（2）由（1）知，装运A 、B 、C 三种水果的车辆数分别为x,-2x+20,x ，由题意，得（4分）解之，得 4≤x ≤8.(5分)因为x 为整数，因此x 的值为4，5，6，7，8，所以安排的方案共有5种.（6分）（3）设利润为W 百元，则W=-28x+1400.（7分）（4≤x ≤8）∵K=-28＜0，∴W 值随x 的增大而减小.要使利润W 最大，则x=4.故选装运A 种水果4车，B 种水果12车，C 种水果4车这种方案.（8分） W 最大=1288（百元）=12.88（万元）.（9分）答：当装运A 种水果4车，B 种水果12车，C 种水果4车时，可获得最大利润，最大利润为12.88万元.25.解：（1）四边形ACED 是等腰梯形.（1分） ∵四边形ABCD 是矩形，∴CE=BC=AD ，∠AEC=∠B=∠ADC=90°，AE=AB=CD.（2分）AC=AC ，∴Rt △ADC ≌Rt △CEA. 过D 作DG ⊥AC 于G ，过E 作EH ⊥AC 于H ∴DG=EH, ∴四边形DGHE 是矩形.（3分）∴DE ∥∠ADC ＞∠ECD ，∴AD 与CE 不平行.∴四边形ACED 是等腰梯形.（4分）（2）在Rt △ADC 中，21×DG ×AC=21AD ·DC. DG =512（5分）， EH=512 AG=CH=59. DE=GH=57. S 梯形ACED =25192（6分） L 梯形ACED =562（7分）（3）若CP=CQ ，则5-AP=AP ，AP=25.（8分）若CQ=PQ ，过Q 作QM ⊥AC 于M ，则MP=MC ，△CQM ∽△CEH.AP=1125.（9分）若PQ=PC ，过P 作PN ⊥CE 于N ，则△PCN ∽△CAE ，AP=1340. ∴AP=25或1125或1340. 26.（1）解方程x 2+8x+48=0,得x 1=-12,x 2=4.(1分)∴B （-12，0），C （4，0）.∵BC 为直径，∴∠BAC=Rt ∠.又AO ⊥BC ， ∴∠BCA+∠CAO=90° ∠CAO+∠OAB=90° ∴∠BCA=∠OAB∴Rt △COA ∽Rt △AOB.（3分） ∴OA OC =OBOA ∴OA 2=OB ·OC 即OA 2=48。

2010年初中毕业生适应性考试数学试卷

2010年初中毕业生适应性考试数学试卷（考试时间：120分满分：150分）温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！参考公式：二次函数y =ax 2+bx +c 的顶点坐标是)44,2(2ab ac a b -- 卷Ⅰ一、选择题（本大题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）1、如果a 与－2互为倒数，那么a 是（ ▲ ）A 、－2B 、－12C 、12D 、22、嫦娥一号飞行1小时的行程约28 600 000m ，用科学记数法可表示为（ ▲ ）A 、0.286×108mB 、2.86×107mC 、28.6×106mD 、2.86×105m 3、下右图是一根钢管的直观图，则它的三视图为（ ▲ ）4、如图，在△ABC 中，∠C ＝90O 。

AB ＝2，BC ＝1，那么cos B 的值是（ ▲ ）A 、12B、2CD5、方程2440x x -+=根的情况是（ ▲ ）A 、有两个不相等的实数根B 、有两个相等的实数根C 、有一个实数根D 、没有实数根6、欣欣榨菜公司购买了甲、乙、丙三台包装机，同时分别包装质量为150g 的榨菜，从它们各自包装的榨菜中分别随机抽取10袋，测得它们的实际质量的方差如下表所示。

根据表中数据，可以认为三台包装机中，包装榨菜质量最稳定的是包装机（ ▲ ）A 、甲 B、乙C 、丙D 、甲与丙7、端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只五芳斋粽子：一只大肉粽、一只豆沙粽、两只蛋黄粽。

四只粽子除内部馅料不同外其他一切均相同，小明喜欢吃蛋黄粽，小明吃到两个粽子都是蛋黄粽的概率是（ ▲ ）A 、12B 、13C 、14D 、16第4题图8、如果圆锥的母线长为5cm 、高为3cm ，那么这个圆锥的侧面积是（ ▲ ）A 、10πcm 2B 、15πcm 2C 、20πcm 2D 、25πcm 2 9、反比例函数ky x=在第一象限的图象如图所示，则k 的值可能是（ ▲ ） A 、1B 、2C 、3D 、410、已知三个边长分别为2，3，5的三个菱形如图排列，菱形的较小锐角为60O ，则图中阴影部分的面积为（ ▲ ）A 、158BCD 、154卷Ⅱ二、填空题（本题共6小题，每小题5分，共30分） 11、分解因式：22m m +＝ ▲ 。

2010中考模拟试卷数学试题卷参考答案

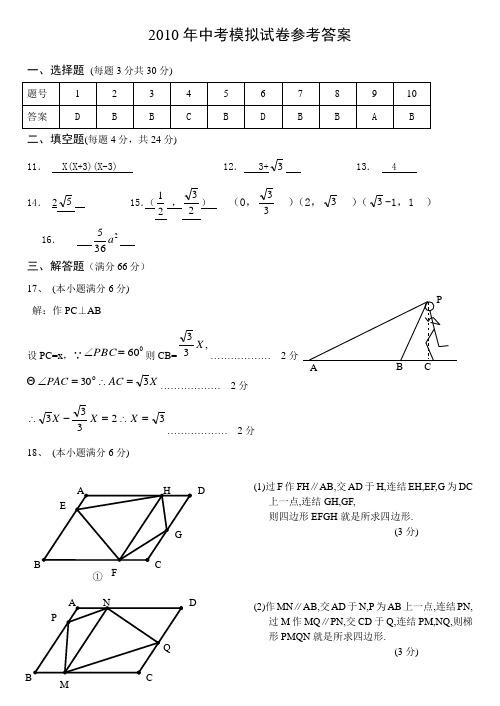
2010年中考模拟试卷参考答案一、选择题 (每题3分共30分)题号 1 2 3 4 5 6 7 8 9 10 答案DBBCBDBBAB二、填空题(每题4分，共24分)11． X(X+3)(X-3) 12． 3+3 13． 414． 25 15．（21 ，23）（0，33 ）（2，3 ）（3-1，1 ）16．2365a三、解答题（满分66分）17、 (本小题满分6分) 解：作PC ⊥AB设PC=x ，∵060=∠PBC 则CB=,33X ……………… 2分X AC PAC 330=∴=∠……………… 2分32333=∴=-∴X X X ……………… 2分18、 (本小题满分6分)(1)过F 作FH ∥AB,交AD 于H,连结EH,EF,G 为DC 上一点,连结GH,GF, 则四边形EFGH 就是所求四边形.(3分)①(2)作MN ∥AB,交AD 于N,P 为AB 上一点,连结PN,过M 作MQ ∥PN,交CD 于Q,连结PM,NQ,则梯形PMQN 就是所求四边形.(3分)PAB CA B C D HFG E MA BCD N P Q②(工具不限,画得有理就给满分,画图正确但无画法每个扣一分) 19、（本小题满分8分）（1）A （2,2）;B(-2,-2);C (23,23)-.………………3分(2)作AD ⊥x 轴于D ,连结AC 、BD 和OC 。

∵A 的坐标为（2,2）, ∴∠AOD=45°,AO=22………………1分∵C 在O 的东南45°方向上, ∴∠AOC=45°+45°=90°,∵AO=BO,∴AC=BC , 又∵∠BAC=60°,∴△ABC 为正三角形………………2分∴AC=BC=AB=2AO=42. ∴OC=3·42262=………………1分由条件设:教练船的速度为3m,A 、B 两船的速度均为4m.则教练船所用的时间为: 263m ,A 、B 两船所用的时间均为：424m =2m .∵263m =243m ，2m =183m ，∴263m >2m ，所以教练船不是最先赶到。

初三中考模拟考试数学试卷 2010

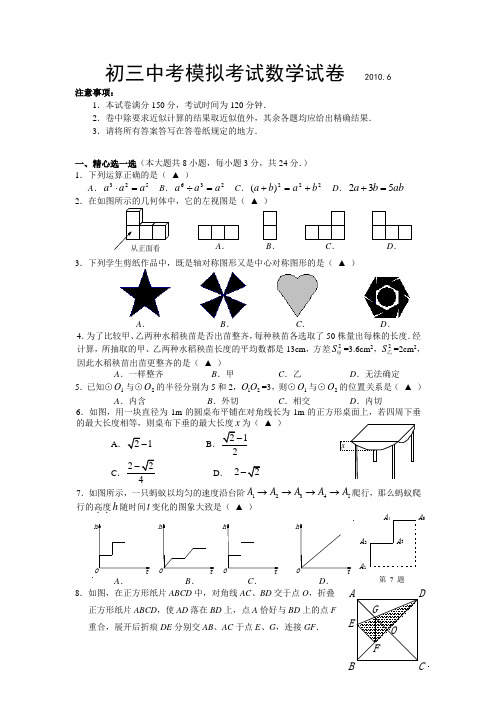
AG DBCOEF初三中考模拟考试数学试卷 2010.6注意事项：1．本试卷满分150分，考试时间为120分钟．2．卷中除要求近似计算的结果取近似值外，其余各题均应给出精确结果． 3．请将所有答案答写在答卷纸规定的地方．一、精心选一选（本大题共8小题，每小题3分，共24分．） 1．下列运算正确的是（ ▲ ）A ．523a a a =⋅ B ．236a a a =÷ C ．222)(b a b a +=+ D ．ab b a 532=+ 2▲ ）3．下列学生剪纸作品中，既是轴对称图形又是中心对称图形的是（ ▲ ）A ．B ．C ．D ．4．为了比较甲、乙两种水稻秧苗是否出苗整齐，每种秧苗各选取了50株量出每株的长度．经计算，所抽取的甲、乙两种水稻秧苗长度的平均数都是13cm ，方差2S 甲=3.6cm 2，2S 乙=2cm 2，因此水稻秧苗出苗更整齐的是（ ▲ ）A ．一样整齐B ．甲C ．乙D ．无法确定5．已知⊙1O 与⊙2O 的半径分别为5和2，12O O =3，则⊙1O 与⊙2O 的位置关系是（ ▲ ） A ．内含 B ．外切 C ．相交 D ．内切6．如图，用一块直径为1m 的圆桌布平铺在对角线长为1m 的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x 为（ ▲ ）A 1B ．12C ．24D ． 27．如图所示，一只蚂蚁以均匀的速度沿台阶1A 2345A A A A →→→→爬行，那么蚂蚁爬行的高度．．h 随时间t 变化的图象大致是（ ▲ ）A ．B ．C ．D ．8．如图，在正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB 、AC 于点E 、G ，连接GF ．A 1A 2A 3A 4A 5第7题A ．B ． D ．C ．ADCB E下列结论 ①∠ADG =22.5°；②tan ∠AED =2；③AGD OGD S S ∆∆=；④四边形AEFG 是菱形；⑤BE =2OG ．其中正确的结论有（ ▲ ） A ．①④⑤ B ．①②④ C ．③④⑤ D ．②③④二、细心填一填（本题共有10小题，每小题3分，共30分．） 9．9的平方根是 ▲ ．10．因式分解：32a ab -= ▲ ．11．2008年北京奥运会火炬在全球传递里程约为137000km ，该数用科学记数法表示为 ▲ km ． 12．函数y =x 的取值范围为 ▲ ．13．如图，点A 、B 、C 都在⊙O 上，若∠C =35°，则∠AOB = ▲ °． 14．如果点（3，―4）在反比例函数ky x=的图象上，则k = ▲ ． 15．已知圆锥的底面半径为9cm ，母线长为30cm ，则圆锥的侧面积为 ▲ cm 2． 16．如图，在四边形ABCD 中，若∠A=∠C =90°，∠B =62°，则∠D = ▲ °． 17．如图，将矩形纸ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，若EH =1cm ，EF =2cm ，则边AD 的长是 ▲ cm ．18．如图，在由24个边长都为1的小正三角形组成的正六边形网格中，以格点P 为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长 ▲ ．三、认真答一答（本题共8小题，共72分．解答需写出必要的文字说明、演算步骤或证明过程） 19．（本题共2小题，每题4分，满分8分）⑴计算： 101(1)4sin 602π-⎛⎫+︒- ⎪⎝⎭⑵解方程：213x x =-20．（本题满分8分）如图，在梯形ABCD 中，AD ∥BC ，∠D =90°，BE ⊥AC ，E 为垂足，AC =BC ． ⑴求证：CD =BE ． ⑵若AD =3，DC =4，求AE ．OABC第13题A BD CH FE G 第17题P第18题第16题类别80 320报名参加排球项目报名参加篮球项目报名参加排球项目并在测试中没有达到满分的占20%⑴请在如图所示的网格图中，将△ABC 向上平移5格，再向右平移7格，得△A 1B 1C 1，再将△A 1B 1C 1绕点B 1按顺时针方向旋转90°，得△A 2B 1C 2；（在网格图中画出这两个三角形并标注相应的顶点字母） ⑵若在网格图的适当位置建立直角坐标系后，点A 、C 的坐标分别为（－5，1）、（－1，－3），则在这个直角坐标系中，点A 2、C 2的坐标分别为：A 2（）、C 2（）．22．（本题满分8分）我市对2009届初中毕业生体育考试报名参加篮、排球项目情况作了一个抽样测试，并根据收集到的数据绘制了如下的统计图，试解答以下问题：⑴本次测试调查了多少名学生？被调查的学生中，有多少人报名排球项目并得到了满分？⑵我市2009届初中毕业生共有42000名，请你估计目前报名排球项目但还不能拿满分23．（本题满分10分）有一个不透明的盒子，盒中有四张分别写有数字1、－2、3、4的卡片，卡片除数字外完全相同．小张从盒中随机取出两张卡片，并按照抽取的先后顺序依次将卡片上的数字作为点P 的横坐标和纵坐标．请你用画树状图或列表的方法解答下列问题：⑴求点P 落在第四象限的概率；⑵求点P 落在反比例函数3y x的图像上的概率． 24．（本题满分10分）某校组织学生到外地进行社会实践活动，共有680名学生参加，并携带300件行李．学校计划租用甲、乙两种型号的汽车共20辆．经了解，甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李．⑴如何安排甲、乙两种汽车可一次性地将学生和行李全部运走？有哪几种方案？⑵如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元，请你选择最省钱的一种租车方案．C B AAC B AC BAC BAC BACB在一条东西走向的公路的正南方A处，观测到公路上有一辆汽车正从位于点A北偏西60°方向上的B处，由西向东匀速行驶，15秒后，观测到该车已经行驶到位于点A北偏东45°方向上的C处．⑴请在图中标出点C的位置．（尺规作图，不必写作法，但要保留作图痕迹）⑵若该汽车行驶速度为60千米/时，试求出观测点A到公路的距离．（结果保留根号）26．（本题满分10分）现有一些形状为等腰直角三角形的边角料．如图1所示，测得∠C=90°，AC=BC=10cm．今要从这种三角形中裁剪出一种扇形，使扇形的半径都落在△ABC的边上，且扇形的弧与△ABC的其它边相切．⑴请设计出所有符合题意的方案示意图，并求出扇形的半径（只要求画出图形，并直接写出扇形半径）．⑵指出哪些方案中裁剪出的扇形的面积相等并求出该面积．（图1）（备用图）四、实践与探索（本题共2小题，满分24分）27．（本题满分12分）如图，已知二次函数图象的顶点坐标为C （1，0），直线y=x+b与该二次函数的图象交于A、B两点，其中点A的坐标为（3，4），点B在y轴上．点P为线段AB上的一个动点（点P与A、B不重合），过点P作x轴的垂线与该二次函数的图象交于点E．⑴求b的值及这个二次函数的关系式；⑵设线段PE的长为h，点P的横坐标为x，求h与x之间的函数关系式，并写出自变量x的取值范围；⑶若点D为直线AB与该二次函数的图象对称轴的交点，则四边形DCEP能否构成平行四边形？如果能，请求出此时P点的坐标；如果不能，请说明理由．⑷以PE为直径的圆能否与y轴相切？如果能，请求出点P的坐标；如果不能，请说明理由．如图，△ABC 为直角三角形，∠C =90°，BC =2cm ，∠A =30°；四边形DEFG 为矩形，DE= cm ，EF =6cm ，且点C 、B 、E 、F 在同一条直线上，点B 与点E 重合． ⑴求AC 的长度．⑵将Rt △ABC 以每秒1 cm 的速度沿矩形DEFG 的边EF 向右平移，当点C 与点F 重合时停止移动，设Rt △ABC 与矩形DEFG 重叠部分的面积为y ，请求出重叠面积y （cm 2）与移动时间x （s ）的函数关系式（时间不包括起始与终止时刻）； ⑶在⑵的基础上，当Rt △ABC 移动至重叠部分的面积323y 时，将Rt △ABC 沿边AB 向上翻折，并使点C 与点C ’重合，请求出翻折后Rt △ABC’与矩形DEFG 重叠部分的周长（可利用备用图）．备用图1 备用图2A D G CFB(E)D G FED GFE数学参考答案一、精心选一选(每小题3分)1．A；2．B；3．B ；4．C；5．D；6．C；7．B ；8．A；二、细心填一填（每空3分）9．±3；10．a(a+b)(a－b)；11．1.37⨯105；12．x≥－3；13．70︒；14．－12；15．270π；16．118︒；1718．2，4，7三、认真答一答19．⑴(π+1)0sin60︒－(12)1-⑵解方程：213x x=-=1－⨯－2…………（2分）解：x=3（x－2）……(1分)=1－2……………（3分）2x=6………………(2分)=－1 …………………………（4分）x=3………………(3分)经检验：x=3是原方程的解。

2010数学二模.doc

九年级中考适应性练习数学试卷2010年6月一、填空题：（每小题２分，共24分） 1．－3的相反数是 ▲ ；2的倒数是 ▲ . 2．16的算术平方根．．．．．是 ▲ ；－2的立方．．是 ▲ . 3．计算：(2)(1)x x +-= ▲ ；分解因式：21x -= ▲ . 4．若代数式12x x -+的值为零，则x = ▲；函数y =中，自变量x 的取值范围是 ▲ .5．若关于x 的一元二次方程042=+-k x x 有两个相等的实数根，则k 的值是 ▲ ，两个相等的根是 ▲ . 6．若函数xky =的图象经过点（－1，2），则k 的值是 ▲ ，在每个象限内y 随x 的增大而 ▲ (填“增大”或“减小”). 7．如图（1），图中的1∠= ▲ o；如图（2），已知直线12l l ∥，135∠=o，那么2∠= ▲ o.8．如图，DE 是ABC △的中位线，2DE =cm ，12AB AC +=cm ，则BC = ▲ cm ，梯形DBCE 的周长为 ▲ cm ．9．如图，⊙O 是ABC 的外接圆，AB AC =，45A ∠=o ，BD 为⊙O的直径，BD =，连结CD ，则D ∠= ▲ o，BC = ▲ .10．如图，在直角梯形ABCD 中，AD ∥BC ，∠DAB=∠ABC=90º,点E 在DC 上，且△ABE 是以AB 为底的等腰直角三角形，若AD =2cm ,BC=4cm ,则AB = ▲ cm , DC = ▲ cm .第7题图（1） 1 35o100o第7题图（2）12l 1 l 2A EC B D（第8题图）（第9题图）EDC BA （第10题图）11．在如图所示的运算流程中，若输出的数y =3，则输入的数x = ▲ .12．如图，三角板ABC 中，∠ACB =90º,∠B =30º,BC =6.三角板绕直角顶点C 逆时针旋转，当点A 的对应点A ˊ落在AB 边的起始位置上时即停止转动，则点B 转过的路径长为 ▲ .二、选择题：（每小题３分，共15分） 13．下列计算正确的是（ ▲ ）A ．43x x x =+B ．1052x x x =⋅C ．824)(x x =D ．422x x x =+ 14答对题数 7 8 9 10 人数420188根据表中数据可知，全班同学答对的题数所组成的样本的中位数和众数分别是（ ▲ ） A ．8、8 B ． 8、9 C ．9、9 D ．9、815．某市2008年第一季度财政收入为76.41亿元，用科学记数法（结果保留两个有效数字）表示为（ ▲ ）Ａ．81041⨯元Ｂ．9101.4⨯元Ｃ．9102.4⨯元Ｄ．8107.41⨯元 16．如图，一只蚂蚁从O 出发，沿着扇形OAB 的边缘匀速爬行一周，设蚂蚁的运动时间为t ，蚂蚁与点O 的距离为S ，则S 关于t 的函数图象大致是（ ▲ ）BˊAˊCBA（第12题图）（第11题图） St O A.StO B.C.St OD.StOBA第16题图图①图②17．在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如的，我们不妨把这样的牌照叫做“数字对称”牌照.如果让你负责制作只以“8”为字母“L ”后的第一个数字且有五个数字的“数字对称”牌照，那么最多可制作（ ▲ ） A ．10个B ．20个C ．100个D ．200个三、解答题：（本大题共11题，81分,解答要有必要的演算．．．．．或说理过程．．．．．） 18．（本题满分10分）（1）计算：|2|)1(82010---+ （2）化简：2211xyx y x y x y ⎛⎫+÷ ⎪-+-⎝⎭． 19．（本题满分10分）（1）解方程：x x x -=+--32332 （2）解不等式组⎪⎩⎪⎨⎧<-+≤+321)2(352x x x x 20．（本题满分6分）如图，已知E 、F 是平行四边形ABCD 的对角线AC 的点，且AE=CF . （1）连接BE 、DF ，猜想线段BE 与DF 具有怎样的数量．．关系和位置．．关系？（2）请证明你的猜想.21．（本题满分4分）图①、图②均为76⨯的正方形网格，点A B C 、、在格点上．（1）在图①中确定格点D ，并画出以A B C D 、、、为顶点的四边形，使其为轴对称图形．（画一个即可）（2）在图②中确定格点E ，并画出以A B C E 、、、为顶点的四边形，使其为中心对称图形．（画一个即可）B 等A 等38%C 等D 等22．（本题满分6分）四张扑克牌的牌面如图①所示，将扑克牌洗均匀后，如图②背面朝上放置在桌面上.（1）若随机抽取一张扑克牌，则牌面数字恰好为“5”的概率是_____________；（2）规定游戏规则如下：若同时随机抽取两张扑克牌，抽到两张牌的牌面数字之和是偶数为胜；反之，则为负.你认为这个游戏是否公平？请说明理由.23.（本题满分6分）某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A B C D ，，，四等，并绘制成下面的频数分布表和扇形统计图.（1）试直接写出x y m n ，，，的值；（2）求表示得分为C 等的扇形的圆心角的度数；（3）如果该校九年级共有男生200名，试估计这200名男生中成绩达到A 等和B 等的人数共有多少人？等第成绩（得分）频数（人数）频率 A10分70.149分 x m B8分150.307分 8 0.16 C6分40.085分y nD 5分以下3 0.06合计501.0024．（本题满分6分）如图，四边形ABCD 内接于⊙O ，BD 是⊙O 的直径，AE ⊥CD ，垂足为点E ，DA 平分∠BDE .（1）AE 是⊙O 的切线吗？请说明理由；（2）若AE =4，求BC 的长.25．（本题满分6分）阅读：设两个正整数为a 、b ，且a ≤b ．若ab=a+b ，则ab=a+b ≤b+b=2b ，所以a ≤2．若ab=a+b ，则ab=a+b ≥a+a=2a ，所以b ≥2．仔细阅读以上材料，根据阅读材料的启示，思考并解决以下问题：已知△ABC 的三边分别为a 、ｂ、ｃ.（1）若a= 2、b= 5，则c 的取值范围是；（2）若a 、ｂ、ｃ均为整数，且ａ+ｂ+ｃ＝30，ａ＜ｂ＜ｃ． ①求c 的取值范围；②列表求出满足条件的三角形有多少个？26．（本题满分6分）甲、乙两地相距720km ，一列快车和一列慢车都从甲地驶往乙地，慢车先行驶1小时后，快车才开始行驶.已知快车的速度是120km/h,以快．．车开始行驶计时．．．．．．．，设时间为x （h ），两车之间的距离为y （km ），图中的折线是y 与x 的函数关系的部分图象. 根据图象解决以下问题：（1）慢车的速度是 km/h ，点B 的坐标是；（2）线段AB 所表示的y 与x 之间的函数关系式是；（3）试在图中补全点B 以后的图象.DPF C27．（本题满分9分）如图，四边形ABCD 中，AD ＝CD ，∠DAB ＝∠ACB ＝90°，过点D 作BC 的平行线，交AC 于点F ,交AB 与点E . （1）求证：F 是AC 的中点,（2）已知AB ＝15cm ，BC ＝9cm ，P 是射线．．DE 上的动点.设DP ＝x cm （x ＞0）， ①当x = cm 时，BP ∥CD ；②若四边形BCDP 的面积为y cm 2,求y 关于x 的函数关系式； ③在②中，当x 为何值时，△PBC 的周长最小，并求出此时y 的值.28．（本题满分12分）如图，在平面直角坐标系中，点O 为坐标原点，以点A （0，－3）为圆心，5为半径作⊙A ，交x 轴于B 、C 两点，交y 轴于点D 、E 两点．（1）求点B 、C 、D 的坐标；（2）如果一个二次函数图像经过B 、C 、D 三点，求这个二次函数解析式；（3）P 为x 轴正半轴．．．上的一点，过点P 作与⊙A 相离．．并且与x 轴垂直的直线，交上述二次函数图象于点F ，当△CPF 中一个内角的正切值为21时，求点P 的坐标．。

2010年初中毕业生学业考试适应性试卷

2010年初中毕业生学业考试适应性试卷X1、若分式| X | 1无心义，则 X 的值是：（）A．0 B ．1 C．－1 D ．± 1 yy kx的图像如图2、一次函数 y=kx+b 与反比率函数 1 所示，o x 则以下说法正确的选项是：（）A．它们的函数值y 随 x 的增大而增大；B．它们的函数值y 随 x 的增大而减小；C． k<0 图 1D．它们的自变量x 的取值为全体实数。

3、在一次射击测试中，甲、乙、丙、丁的均匀环数同样，而方差分班为8.7, 6.5, 9.1,7.7 ，则这四人中，射击成绩最稳固的是：（）A．甲B ．乙 C ．丙 D ．丁4、已知三角形两边长为 2 和 6，要使这个三角形为直角三角形，则第三边的长为：（）A ． 2B ．2 10C ．42 或 2 10 D ．以上都不对5、如图 2 所示，在平面直角坐标系中，菱形ABCD的极点 A、 B的坐标分别是（ 0, 0 ），（ 2, 0 ），∠α＝ 60°，则极点 C 在第一象限的坐标是：（）A．（ 2, 2 ）， B ．（ 3, 3 ），C．（ 3, 2 ）， D ．（3＋1 , 3 ），6、一块蓄电池的电压（u）为定值，使用此蓄电池为电源时，电流I(A) 函数关系如图 3 所示，假如以此蓄电池为电源的用电器限制电流不得超出uI那么此用电器的可变电阻应（注R ）：（）A．不小于 4.8 Ω B ．不大于 4.8 ΩC．不小于 14Ω D ．不大于 14Ωk k 127、当k 5 与k 互为相反数时， k 等于：（）yDCαO (A)B x图 2与电阻 R( Ω ) 之间的10A，I(A)6O8R(Ω)6 5 3 2A．5B ．6C ．2D ．38、已知 Rt△ ABC中，∠ C=90°，若 a+b=14cm，c=10cm，则 Rt△ ABC的面积是：（）A ．24cm2B ．36cm2C ．48cm2D ．60cm2二、填空题：（本大题共 8 小题，每题 3 分，共 24 分）9、若 4x-3=1 ，则 x=_____________________ 。

2010年初中毕业生学业考试适应性试卷

2010年初中毕业生学业考试适应性试卷数学试题卷卷Ⅰ（选择题）一、选择题（本题有10小题，每题4分，共40分） 1．如果□×(－2)=1，则“□”内应填的实数是（ ▲ ）(A)21 (B)2 (C)2- (D)21- 2．下列计算错误．．的是（ ▲ ） (A)437m n mn += (B) 633a a a ÷= (C)3412()x x = (D)34a a a = 3．不等式组⎪⎩⎪⎨⎧<-≥+-010221x x 的解是（ ▲ ）(A)13<<-x (B)13<≤-x (C)1<x (D)11<≤-x 4．下列平面图形都由小正方形组成，其中不能围成正方体的是（ ▲ ）5．除2008年和2009年受全球金融危机影响外，2003到2007年，我国GDP 增长率分别为10.0％，10.1％，10.4％，11.6％，13.0％，这五年的年度GDP 增长率之间比较平稳。

“增长率之间比较平稳”说明这组数据的（ ▲ ）较小： (A)中位数 (B) 平均数 (C)众数 (D)方差6．若矩形面积为4，则它的长y 与宽x 之间的函数关系用图象大致可表示为（ ▲ ）7．如图，在直角坐标系中，已知点A (1，3)，O 是坐标原点．若连结OA ，将线段OA(A)(B)(D)(D)(A)(B)(C)(C)绕点O 逆时针旋转900得到线段OB ，则点B 的坐标是（ ▲ ）(A) (3，1-) (B) (3，1-)或(3-，1)(C) (3-，1) (D) 以上答案都不对8．下列命题：①同位角相等；②如果009045<α<，那么α>αcos sin ；③若关于x 的方程223=+-x mx 的解是负数，则m 的取值范围为m <-4；④相等的圆周角所对的弧相等．其中假．命题．．有（ ▲ ） (A) 1个 (B) 2个 (C) 3个 (D) 4个9．已知抛物线y =ax 2+bx +c (a ＞0)的对称轴为直线x =－1，与x 轴的一个交点为(x 1，0)，且0＜x 1＜1(如图为抛物线的部分图像)．下列结论：①9a －3b ＋c ＞②b ＜a ；③3a ＋c ＞0中，正确的是（ ▲ ）(A) ① (B ) ②③ (C) ①③ (D) ①②③ 10．正方形ABCD 中，点,P Q 分别是边,AB AD 上的点，连结PQ 、PC 、QC ，下列说法：①若045PCQ ∠=，则PB ＋QD ＝PQ ；②若AP =AQ =2，036=∠PCQ ，则15+=PC ； ③若PQC ∆是正三角形，则PB=1，AP =13+．其中正确的说法有（ ▲ ）(A) 3个 (B) 2个 (C) 1个 (D) 0个卷Ⅱ（非选择题）二、填空题（本题有6小题，每题5分，共30分） 11．分解因式：xy x 622-＝ ▲ ．12．整数605 490 000用科学记数法可表示为 ▲ (保留三位有效数字)．13．若1O ⊙和2O ⊙的半径分别为1cm 和3cm ，且521=O O cm ，则1O ⊙和2O ⊙的位置(第9题图)(第7题图)关系是 ▲ ．14．如图，已知AD 是ABC ∆的外接圆的直径，54sin =C ，则=∠BAD tan ▲ ．15．如图，已知双曲线)0k (xky ＞=经过直角三角形OAB 的斜边OB 的中点D ，与直角边AB 相交于点C ．当6=∙OA BC 时，k ＝ ▲ ． 16．阅读理解：符号a b c d称为二阶行列式，规定它的运算法则为：d c ba =bc ad -，例如3546=3×6－4×5=－2．问：若a c bk -=1，则akc abb kc +-22)(= ▲ ．三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）： 17．（本小题满分8分）计算：02060cos )6(41+-π--．18．（本小题满分8分）已知02000)2010(2=-+-b a ，求代数式22b a -的值．(第15题图)19．（本小题满分8分）如图，教室窗户的高度AF 为2.5米，遮阳蓬外端一点D 到窗户上椽的距离为AD (墙面与遮阳蓬、地面均垂直)，某一时刻太阳光从教室窗户射入室内，与地面的夹角BPC 为030，PE 为窗户的一部分在教室地面所形成的影子且长为3米，试求AD 的长度（结果带根号）．20．（本小题满分8分）将背面完全相同，正面上分别写有数字1、2、3、4的四张卡片混合后，小明从中随机地抽取一张，把卡片上的数字作为被减数；再将形状、大小完全相同，分别标有数字1、2、3的三个小球混合后，小华从中随机地抽取一个，把小球上的数字作为减数，然后计算出这两个数的差.（1）请你用画树状图或列表的方法，求这两数差为0的概率.（2）小明与小华做游戏，规则是：若这两数的差为非负数，则小明赢；否则，小华赢.你认为该游戏公平吗？请说明理由.如果不公平，请你修改游戏规则，使游戏公平.(第19题图)21．（本小题满分10分）2009年某市中小学生约有16万人，为开展好阳光体育运动，该市随机抽取2160名学生，做了一次内容为“每天锻炼是否超过1小时，以及锻炼未超过1小时的原因”的调查，调查所得的部分数据如图．（1）请补全频数分布直方图．（2）估计2009年全市中小学生每天锻炼未超过1小时的约有多少万人？（3）如果计划2011年该市中小学生每天锻炼未超过1小时的人数降到1.44万人，求2009年至2011年每天锻炼未超过1小时人数的年平均降低的百分率是多少？22．（本小题满分12分）将□ABCD 纸片沿EF 折叠，使点C 与点A 重合，点D 落在点G 处(如图)． (1)求证：△ABE ≌△AGF .(2)连结AC ，若□ABCD 的面积等于16，x BC EC=，y EF AC =∙，试求y 与x 之间的函数关系式.(第21题图)A BCDE FG(第22题图)超过1小时23．（本小题满分12分）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A 、B 、C ．（1）用直尺和圆规画出该圆弧所在圆的圆心M 的位置(不用写作法，保留作图痕迹)．（2）若A 点的坐标为（0，4），D 点的坐标为（7，0），求证：直线CD 是⊙M 的切线．（3）在（2）的条件下，连结MA 、MC ，将扇形AMC 卷成一个圆锥，求此圆锥的高．24．（本小题满分14分）如图，在平面直角坐标系中，已知△OAB 是等腰三角形(OB 为底边)，顶点A 的坐标是(2，4)，点B 在x 轴上，点Q 的坐标是(－6，0)， AD ⊥x 轴于点D ，点C 是AD 的中点，点P 是直线BC 上的一动点．(1)求点C 的坐标．(2)若直线QP 与y 轴交于点M ，问：是否存在点P ，使△QOM 与△ABD 相似？若存在，请求出点P 的坐标；若不存在，请说明理由．(3)以点P 为圆心、2为半径长作圆，得到动圆⊙P ，过点Q 作⊙P 的两条切线，切点分别是E 、F ．问：是否存在以Q 、E 、P 、F 为顶点的四边形的最小面积S ？若存在，请求出S 的值；若不存在，请说明理由．(第23题图)2010年初中毕业生学业考试适应性试卷(一)数学卷参考答案一．选择题(本题有10小题，每题4分，共40分)DABAD ；BCCCA二．填空题（本题有6小题，每题5分，共30分）11．)3(2y x x -；12．81005.6⨯(或6.05亿)；13．相交；14．43；15．2；16．1- 三．解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）17．(本题8分) 解：原式=22)21(121+-=41141+-=21-18.(本题8分) 解：∵02000)2010(2=-+-b a ∴2000,2010==b a∴40100)20002010)(20002010(200020102222=+-=-=-b a 19．(本题8分)解：过点E 作EG AC ∥交于PD 于G 点 (1分)tan 3031EG EP ==⨯= (2分) ∴BF =EG =1 (1分) 即 2.51 1.5AB AF BF =-=-= (1分)在Rt ABD △中，tan 303AB AD ===∴AD (1分) (解法不同时参考给分) 20．(本题8分)解：（1）画树状图(或列表)如下：(4分) (2分) (2分)(4分)(4分) (第19题图)被减数减数差由图（表）知，所有可能出现的结果有12种，其中差为0的有3种．（2分）∴ 这两数的差为0的概率为：31124p ==．（2分）（2）不公平，理由如下：由（1）知，所有可能出现的结果有12种，这两数的差为非负数的有9种，其概率为：134p =，这两数的差为负数的概率为：214p =．因为3144≠，所以该游戏不公平．（2分）游戏规则修改为：若这两数的差为正数，则小明赢；否则，小华赢．（2分） (答案不唯一，正确即可) 21．(本题10分) 解：(1) ∵2160×41=540，∴540-120-20=400 ∴因为没时间而导致锻炼未超过1小时的人数为400人 (1分) ∴补全频数分布直方图如下： (2分)400（2分）(图补对而无前述说明扣1分，补图时少400说明、明显不等于400高等均分别扣1分, 3分扣完为止) (2)∵44116=⨯∴估计2009年全市中小学生每天锻炼未超过1小时的约有4万人. (2分)(3)设年平均降低的百分率是x 则：44.1)1(42=-x (2分) 解此方程得：6.1,4.021==x x (1分)经检验：6.1=x 不符合题意，应舍去. (1分) ∴%404.0==x答：2009年至2011年每天锻炼未超过1小时人数的年平均降低．．．．．的百分率是40%. 22．(本题12分)（1）证明：∵□ABCD ∴AB =CD ，BCD BAC ∠=∠ (1分) 又根据题意得：AG =CD ，BCD EAG ∠=∠ ∴AB = AG ，EAG BAD ∠=∠ (1分) ∴GAF BAE ∠=∠ (1分) 又∵AB ∥CD ，AE ∥GF∴GFA EAF BEA ∠=∠=∠ (1分) ∴△ABE ≌△AGF (AAS) (2分) (2)解：连结CF ，由(1)得：EC =AE =AF ，而AF ∥EC ∴四边形AECF 是平行四边形 (1分) ∴□AECF 是菱形 (1分) ∴y =AC ·EF =2×菱形AECF 的面积 (1分)又∵□ABCD 的面积等于16，x BCEC= ∴△AEC 的面积等于8x (1分)∴菱形AECF 的面积等于16x ，∴x y 32= (2分) 说明：不必写出x 的取值范围，解法不同时请参考给分.23．(本题12分)解：（1）如图1，点M 就是要找的圆心。

绍兴市区2010年初中毕业生学业考试适应性检测数学试卷

九年级五月自测数学试卷一、选择题（本大题有10小题,每小题4分,共40分.） 1．－3的相反数是（） A 、－13 B 、13C 、3D 、－3 2．明天数学课要学“勾股定理”．小敏在“百度”搜索引擎中输入“勾股定理”，能搜索到与之相关的结果个数约为12 500 000，这个数用科学记数法表示为（） A ．1.25×105B ．1.25×106C ．1.25×107D ．1.25×1083．如图，已知AB ∥CD ，BC 平分∠ABE ，∠C ＝34°，则∠BED 的度数是（）A ．17°B ．34°C ．56°D ．68°4．由5个相同的正方体搭成的几何体如图所示，则它的左视图是（）A ．B ．C ．D ．5．如图，AB 为⊙O 的直径，点C 在⊙O 上．若∠C ＝16°，则∠BOC 的度数是（） A ．74° B ．48° C ．32° D ．16°6．一条排水管的截面如图所示．已知排水管的截面圆半径OB ＝10，截面圆圆心O 到水面的距离OC 是6，则水面宽AB 是（） A ．16 B ．10 C ．8 D ．67．在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是白球的概率为32，则黄球的个数为（）A ．2B ．4C ．12D ．16 8．如图，在△ABC 中，分别以点A 和点B 为圆心，大于21AB 的长为半径画弧，两弧相交于点M ，N ，作直线MN ，交BC 于点D ，连结AD ．若△ADC 的周长为10，AB ＝7，则△ABC 的周长为（） A ．7 B ．14 C ．17 D ．209.如图，在矩形ABCD 中，AB =4cm ，AD =2cm ，动点M 自点A 出发沿A →B 的方向，以每秒1cmA DBCE第3题图第6题图ABOCOA CB 第5题图 CAN M B第8题图D第4题图主视方向的速度运动，同时动点N 自点A 出发沿A →D →C 的方向以每秒2cm 的速度运动，当点N 到达点C 时，两点同时停止运动，设运动时间为x （秒），△AMN 的面积为y （cm 2），则下列图象中能反映y 与x 之间的函数关系的是( )A B C D 10．如图，在△ABC 中，∠C=90°，AC=4，BC=2，点A 、C 分别在x 轴、 y 轴上，当点A 在x 轴上运动时，点C 随之在y 轴上运动，在运动过程中，点B 到原点的最大距离是（） A ．6 B ．26 C ．25 D ．222+二、填空题（本大题有6小题,每小题5分,共30分） 11．分解因式：x 2＋x ＝．12．为备战2012年5月11日在绍兴举行的第四届全国皮划艇马拉松赛，甲、乙运动员进行了艰苦的训练，他们在相同条件下各10次划艇成绩的平均数相同，方差分别为0.23，0.20，则成绩较为稳定的是_________(填“甲”或“乙”）． 13．若点A （1，y 1），B （2，y 2）是双曲线xy 3=上的点，则y 1 y 2（填“＞”，“＜”或“＝”）．14．一个圆锥的侧面展开图是半径为4，圆心角为90°的扇形，则此圆锥的底面半径为．15、如图，在矩形ABCD 中，BC=8，AB=6，经过点B 和点D 的两个动圆均与AC 相切，且与AB 、BC 、AD 、DC 分别交于点G 、H 、E 、F ，则EF+GH 的最小值是____________16、如图，已知△ABC 是面积为3的等边三角形，△ABC ∽△ADE ， AB ＝2AD ，∠BAD ＝45°，AC 与DE 相交于点F ，则△AEF 的面积等于（结果保留根号）．三、解答题17．（1）计算：8－02）（-π＋︒45cos 2＋14-； xy 123–1123–1O xy 123–1123–1O xy 123–1123–1O xy 123–1123–1O AGBHCFDE（2）先化简，再求值：2)())((2)2(b a b a b a b a a ++-++-，其中21-=a ，1=b ．18．如图，在一个10×10的正方形DEFG 网格中有一个△ABC 。

2010年中考适应性练习数学试题

福建省2010年九年级数学适应性练习人教版

2010年中考适应性练习数学试题

2010年中考模拟数学卷参考答案

2010年初中数学中考模拟试卷.doc

2010年中考模拟试卷 数学

2010年中考模拟数学试卷和答案

2010—2011九年级数学试卷

2010-2011年九年级数学期中适应性试题

2010年南通通州中考适应性考试—数学

枣阳市2010年中考适应性考试数学答案

2010年初中毕业生适应性考试数学试卷

2010中考模拟试卷 数学试题卷参考答案

初三中考模拟考试数学试卷 2010

2010数学二模.doc

2010年初中毕业生学业考试适应性试卷

2010年初中毕业生学业考试适应性试卷

绍兴市区2010年初中毕业生学业考试适应性检测数学试卷

2010年中考模拟试卷数学

2010中考模拟试卷数学试题卷参考答案