浙江金华市社会经济发展统计年鉴数据：2018年税收收入情况统计

合集下载

合肥市社会经济发展统计年鉴指标数据：2018年省级以上开发区主要经济指标统计

76 221637
255 8592540
35841 22731
当年新批进区外商投资企业
(个)
64
当年实际利用外商直接投资额
(万美元)
194145
利用内资情况(在建亿元以上项目)
项目个数
(个)
226
到位省外境内资金额
(万元)
9005282
专利申请授权情况
专利申请量
(件)
41149
专利授权量
15773
摘编自《合肥统计年鉴2019》
2018
132282878 60062992 69777524 60877267 41812432 22376141 19869041 13490489 2443389 1438325 1005064 5605458 7545158 1490768 18628973 7492857 1647409
22645465
规模以上工业增加值
20446872
进出口总额
(万美元)
1939751
出口额
1070082
进口额
869669
税收总额
(万元)
5116155
财政收入
(万元)
8353790
土地收入
3127671
固定资产投资总额
(万元)
3427பைடு நூலகம்746
工业投资
20230153
基础设施投资
4850195
利用外商直接投资情况
指标
合肥市2018年省级以上开发区主要经济指标统计
单位
2017
全区经营(销售)收入
(万元)
147692987
规模以上工业销售收入
82904655

浙江省社会经济发展统计数据：2018年地级市市区基本情况统计(十六)

丽水市
20
62049 10.67 69.42 63.48 24.65
126.12 56.51 245359 126196 47417 33961
775 1019 20.0 4703 4175 1234 2123 565 5066 356 10948 10016 29.83 6.22 9.89 13.72 106.2 102.9 103.6 106.5 108.2 105.4
(五)生活设施年末排水管道长度年末公共供水管道长度公共供水综合生产能力公共供水总量售水量生产运营用水居民家庭用水公共服务用水供气总量(人工煤气.天然气) 居民家庭用量液化石油气供气总量居民家庭用量全社会从业人员数第一产业第二产业第三产业地区生产总值指数(上年=100) 第一产业第二产业工业第三产业人均GDP指数(上年=100)(常住)
306.5 125.52 723745 408769 136174 77561
610.17 533.36 951200 776425 75474 39187
公里公里万立方米/日万立方米万立方米万立方米万立方米万立方米万立方米万立方米吨吨万人万人万人万人 % % % % % %
浙江省2018年地级市市区基本情况统计(十万吨
处万元万元万户万户万户万户
43 227674 167760 22.14 398.29 174.06 58.85
36 39772 83076 17.62 114.35 74.64 40.05
万吨标准煤万吨标准煤万千瓦时万千瓦时万千瓦时万千瓦时
台州市
1733
40 26150 277956 43.55 342.97 282.91 87.54

温州市社会经济发展统计年鉴指标数据：历年财政收入与支出统计(2013-2018)

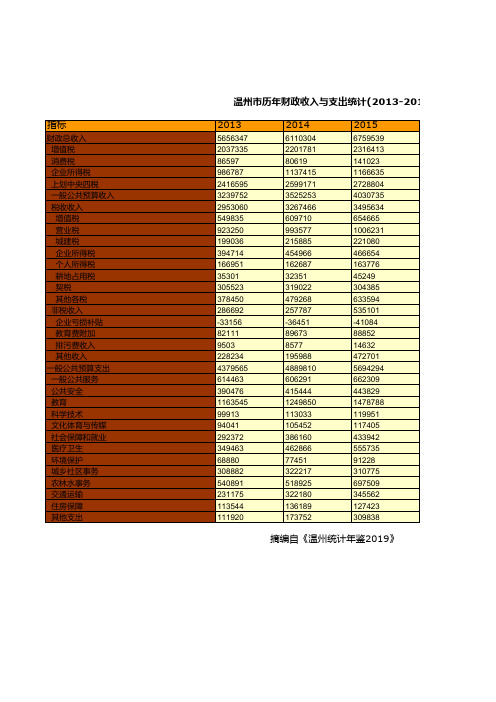
2015
6759539 2316413 141023 1166635 2728804 4030735 3495634 654665 1006231 221080 466654 163776 45249 304385 633594 535101 -41084 88852 14632 472701 5694294 662309 443829 1478788 119951 117405 433942 555735 91228 310775 697509 345562 127423 309838
摘编自《温州统计年鉴2019》
2013-2018)
2016
7219849 2770905 141545 1158519 2821105 4398744 3713776 1213739 572209 227483 463406 193700 75781 330310 637148 684968 -37960 97088 10349 615491 6667495 803075 559197 1624404 134104 141671 514657 686720 125763 490682 681217 382396 148483 375126
温州市历年财政收入与支出统计(2013-2018)
2013
5656347 2037335 86597 986787 2416595 3239752 2953060 549835 923250 199036 394714 166951 35301 305523 378450 286692 -33156 82111 9503 228234 4379565 614463 390476 1163545 99913 94041 2923721175 113544 111920

浙江省社会经济发展统计数据：2018年地级市市区基本情况统计(三)

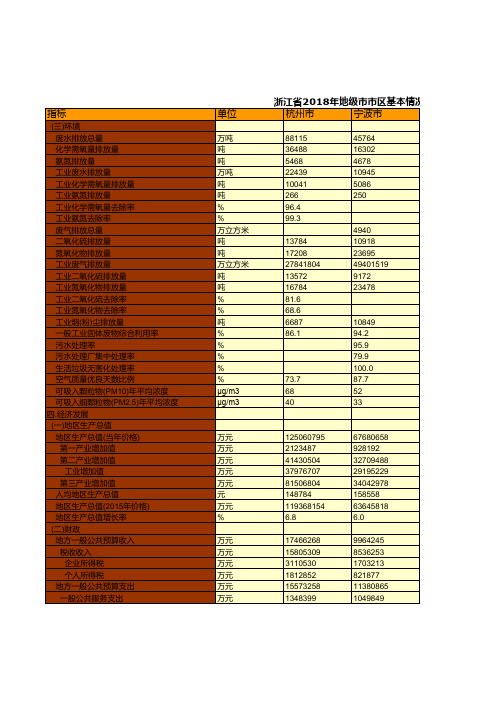
125060795 2123487 41430504 37976707 81506804 148784 119368154 6.8
17466268 15805309 3110530 1812852 15573258 1348399
67680658 928192 32709488 29195229 34042978 158558 63645818 6.0
1661555 1520889 226594 98121 2093405 185802
湖州市
11898100 455307 5274455 4640368 6168338 88371 11876502 8.1 1216618 1007679 164340 66599 1844635 184522
绍兴市
23922709 165962 9685691 7287265 14071056 79549 23692181 7.4
2336655 1971759 307027 127493 2960257 431372
12464226 246632 5869664 5281926 6347931 97720 11267506 7.4
指标
(三)环境废水排放总量化学需氧量排放量氨氮排放量工业废水排放量工业化学需氧量排放量工业氨氮排放量工业化学需氧量去除率工业氨氮去除率废气排放总量二氧化硫排放量氮氧化物排放量工业废气排放量工业二氧化硫排放量工业氮氧化物排放量工业二氧化硫去除率工业氮氧化物去除率工业烟(粉)尘排放量一般工业固体废物综合利用率污水处理率污水处理厂集中处理率生活垃圾无害化处理率空气质量优良天数比例可吸入颗粒物(PM10)年平均浓度可吸入细颗粒物(PM2.5)年平均浓度

浙江省社会经济发展统计数据：2018年地级市市区基本情况统计(八)

外国人港.澳.台同胞国际旅游(外汇)收入国内游客国内旅游收入五.科技创新 (一)科创投人 R&D人员 R&D人员全时当量 R&D经费内部支出 (二)科创成果专利申请数专利授权数发明专利六.人民生活 (一)就业从业人员期末人数(城镇单位) 第一产业(农.林.牧.渔业) 第二产业采矿业制造业电力.热力.燃气及水生产和供应业建筑业
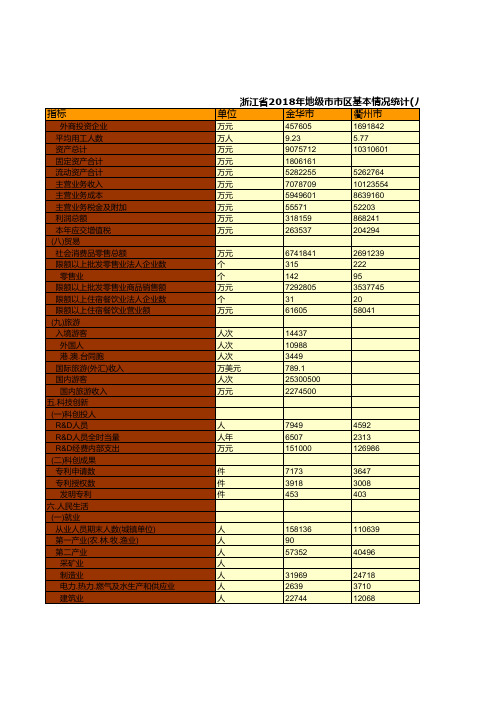
人
100694
70143
人
9770
3556
人
6752
3670
摘编自《金华统计年鉴2019》
情况统计(八) 舟山市
218722 5.19 11644547 3686843 5175310 6118119 5408767 42243 150749 124472
4169658 343 70 23272883 98 207575
浙江省2018年地级市市区基本情况统计(八)
单位
金华市
衢州市
万元
457605
1691842
万人
9.23
5.77
万元
9075712
10310601
万元
1806161
万元
5282255
5262764
万元
7078709
10123554
万元
5949601
8639160
万元
55571
52203
万元
318159
1891 26644700 2925588
14379 10783
15499 12322 1379
388353 318 235752 0 138029 4778 92945
丽水市
27664 4.10 4730130

浙江金华市社会经济发展统计年鉴数据：2018年末市区人口情况统计

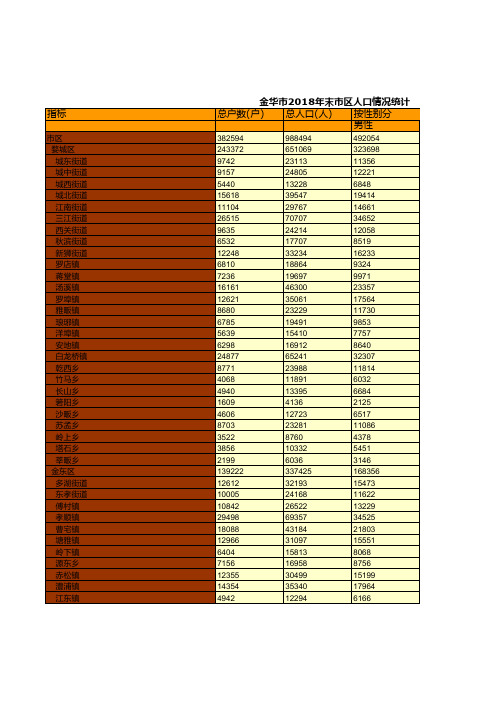
16912
8640
24877
65241
32307
8771
23988
11814
4068
11891
6032
4940
13395
6684
1609
4136
2125
4606
12723
6517
8703
23281
11086
3522
8760
4378
3856
10332
5451
2199
6036
3146
139222
337425
168356
12612
32193
15473
10005
24168
11622
10842
26522
13229
29498
69357
34525
18088
43184
21803
12966
31097
15551
6404
15813
8068
7156
16958
8756
12355
30499
15199
14354
35340
17964
按城镇和农村分农村人口
城镇人口
567376
421118
326971
324098
23113
24805
13228
39547
29767
70707
24214
17707 21297 2663 5197 7197 2496 4553 3835 1534 2791 29447
11937 16201 14500 39103 32565 18676 15656 13876 14121 35794 23988

乡村振兴战略下农民家庭经济幸福感

产经视点【基金项目】2021年金华市社会科学联合会课题（金社字〔2021〕8号），项目编号：2021408。

【作者简介】任程程（1993-），男，浙江金华人，助理研究员，从事农村经济、资本市场研究。

乡村振兴战略下农民家庭经济幸福感现状及提升路径研究———以金华市为例任程程（浙江广厦建设职业技术大学，浙江金华322103）【摘要】近年来，随着乡村振兴战略和新农村建设的持续推进，全国范围内的农村经济正在快速发展，农村地区的振兴关乎国家经济发展的大局，是党实现两个现代化和中华民族伟大复兴的历史要求。

论文以金华市为例，首先，对于乡村振兴对农民真实财富收入的影响，以恩格尔系数为统计指标研究金华市农村地区家庭经济幸福感现状。

结果显示，乡村振兴对提升农民家庭经济幸福感具有一定效果但作用有限，且提升效应比城镇弱，这表明当前乡村振兴遇到了瓶颈期，对于经济幸福感的提升作用有限。

其次，论文基于经济幸福感现状针对性地提出5种提升路径。

【关键词】经济幸福感；真实财富收入；恩格尔系数【中图分类号】F323.8【文献标志码】A【文章编号】1673-1069（2023）01-0159-031引言“三农”问题一直是关乎国家总体稳定和发展的重大问题，解决好“三农”问题也是我党面临的重大历史任务和责任，特别是在国际政治和经济局势不断变化的今天，实现乡村地区稳步健康发展是挖掘我国发展内生动力、增加新的经济增长点以及提升我国综合国力的重要途径和方式，也是实现社会主义现代化强国的必经之路。

2018年9月，中共中央、国务院印发了《乡村振兴战略规划（2018-2022年）》，并发出通知，要求各地区各部门结合实际认真贯彻落实。

自乡村振兴战略实施以来，全国各地都如火如荼地进行新农村建设并取得了一定的成效，但同时也出现了不少问题。

本文以金华地区的农民家庭为研究对象，重点研究该地区的农民家庭经济幸福感现状，探究农民家庭的实际财富是否真正增加、生活质量是否得到根本改善等问题。

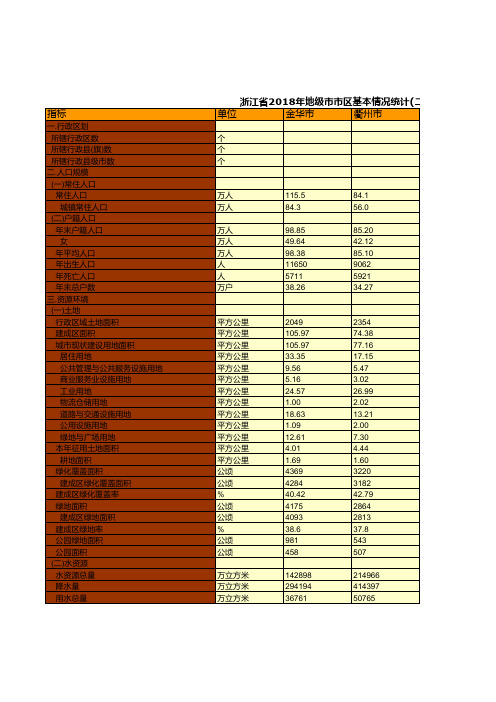
浙江省社会经济发展统计数据：2018年地级市市区基本情况统计(二)

154179 271582 51829
48.1 36.6
41.39 20.66 41.19 5441 2820 19.31
1493 39.40 39.54 12.18 6.16 2.46 4.36 0.35 4.47 5.23 4.33 1.98 0.27 1846 1752 44.46 1607 1533 38.9 422 354
91176 211698 13128
019》
12353
64012
6575
12880
197.6 Biblioteka 40.8162.50 81.19 161.96 17310 10545 50.44
1680 141.69 134.06 42.75 9.34 5.20 34.25 0.84 19.65 2.47 19.56 5.40 3.22 6596 6236 44.01 6543 6267 44.2 1971 1456
浙江省2018年地级市市区基本情况统计(二)
单位
金华市
衢州市
个个个
万人万人
万人万人万人人人万户
115.5 84.3
98.85 49.64 98.38 11650 5711 38.26
84.1 56.0
85.20 42.12 85.10 9062 5921 34.27
平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里平方公里公顷公顷 % 公顷公顷 % 公顷公顷
214966 414397 50765
规模以上工业企业取水量
万立方米
21550
摘编自《金华统计年鉴2019》
情况统计(二) 舟山市

计量经济学(庞皓)_课后习题答案

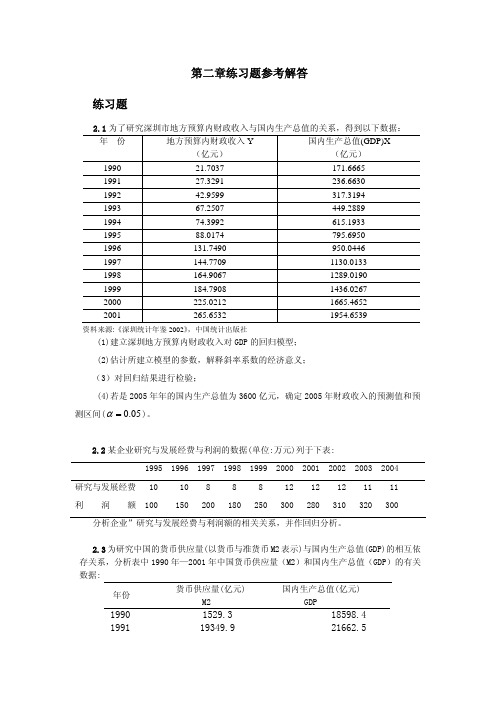
Yˆ2005 = −3.611151 + 0.134582 × 3600 = 480.884 （亿元）
区间预测：
∑ 平均值为：
xi2
=
σ
2 x
(n
−1)
=
587.26862
× (12
−1)
=
3793728.494
( X f 1 − X )2 = (3600 − 917.5874)2 = 7195337.357
1.138
18
2.98
1.092
试建立曲线回归方程 yˆ = a ebx （ Yˆ = ln a + b x ）并进行计量分析。
2.7 为研究美国软饮料公司的广告费用 X 与销售数量 Y 的关系,分析七种主要品牌软饮
料公司的有关数据2(见表 8-1)
表 8-1
美国软饮料公司广告费用与销售数量
品牌名称
449.2889
1994
74.3992
615.1933
1995
88.0174
795.6950
1996
131.7490
950.0446
1997
144.7709
1130.0133
1998
164.9067
1289.0190
1999
184.7908
1436.0267
2000
225.0212
1665.4652
2 i
=
3134543
∑Yi2 = 539512
（1）作销售额对价格的回归分析，并解释其结果。（2）回归直线未解释的销售变差部分是多少？
∑ XiYi = 1296836
2.9 表中是中国 1978 年-1997 年的财政收入 Y 和国内生产总值 X 的数据:

【沪科版】高中数学必修三期末试题(及答案)(4)

一、选择题1．有五条线段长度分别为1,3,5,7,9，从这5条线段中任取3条，则所取3条线段能构成一个三角形的概率（） A ．110B ．310C ．12D ．7102．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设D 为BE 中点，若在大等边三角形中随机取一点，则此点取自小等边三角形的概率是（）A ．17B ．14C ．13D ．4133．从2017年到2019年的3年高考中，针对地区差异，理科数学全国卷每年都命了3套卷，即：全国I 卷，全国II 卷，全国III 卷.小明同学马上进入高三了，打算从这9套题中选出3套体验一下，则选出的3套题年份和编号都各不相同的概率为（）A ．184B ．142 C ．128 D ．1144．在编号分别为(0,1,2,,1)i i n =⋅⋅⋅-的n 名同学中挑选一人参加某项活动，挑选方法如下：抛掷两枚骰子，将两枚骰子的点数之和除以n 所得的余数如果恰好为i ，则选编号为i 的同学．下列哪种情况是不公平的挑选方法（） A ．2n =B ．3n =C ．4n =D ．6n =5．执行如图所示的程序框图，则输出的S =（）A ．1-B ．2-C．2D．1 26．执行如图所示的程序框图，若输入的a，b的值分别为1，1，则输出的S是（）A．25 B．18 C．11 D．37．执行如图所示的程序框图，输出a的值为118，则的值可以是（）A．0.06B．0.03C．0.2D．0.048．元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒?”用程序框图表达如图所示，即最终输出的0x ，则一开始输入的x的值为( )A．34B．78C．1516D．31329．某校举行演讲比赛，9位评委给选手A打出的分数如茎叶图所示，统计员在去掉一个最高分和一个最低分后，算得平均分为91，复核员在复核时，发现有一个数字(茎叶图中的x)无法看清，若统计员计算无误，则数字x应该是（）A．5 B．4 C．3 D．210．某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，这与性别有关联的可能性最大的变量是（）A．成绩B．视力C．智商D．阅读量11．有200人参加了一次会议，为了了解这200人参加会议的体会，将这200人随机号为001,002，003，…，200，用系统抽样的方法(等距离)抽出20人，若编号为006,036,041,176, 196的5个人中有1个没有抽到，则这个编号是（）A．006 B．041 C．176 D．19612．已知x，y的取值如表：x2678y若x ，y 之间是线性相关，且线性回归直线方程为，则实数a 的值是A ．B ．C ．D ．二、填空题13．辛普森悖论(Simpson’sParadox)有人译为辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”.辛普森悖论为英国统计学家E .H .辛普森(E.H.Simpson)于1951年提出的，辛普森悖论的内容大意是“在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论：关于某高校法学院和商学院新学期已完成的招生情况，现有如下数据：某高校申请人数性别录取率法学院200人男50%女 70% 商学院300人男60% 女90% ①法学院的录取率小于商学院的录取率；②这两个学院所有男生的录取率小于这两个学院所有女生的录取率； ③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率； ④法学院的录取率不一定小于这两个学院所有学生的录取率. 其中，所有正确结论的序号是___________.14．天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数： 488 932 812 458 989 431 257 390 024 556 734 113 537 569 683 907 966 191 925 271据此估计，这三天中恰有两天下雨的概率近似为__________. 15．已知函数2()22f x x =-M ，(())y f f x =的定义域为P ，在M 上随机取一个数x ，则x P ∈的概率是____________．16．如图是一个算法流程图，若输入x 的值为2，则输出y 的值为_______. .17．根据如图所示的伪代码可知,输出的结果为______.18．执行如图所示的算法框图，若输入的x的值为2，则输出的n的值为__________．19．东汉·王充《论衡·宜汉篇》：“且孔子所谓一世，三十年也.”，清代·段玉裁《说文解字注》：“三十年为一世.按父子相继曰世”.“一世”又叫“一代”，到了唐朝，为了避李世民的讳，“一世”方改为“一代”，当代中国学者测算“一代”平均为25年.另据美国麦肯锡公司的研究报告显示，全球家庭企业的平均寿命其实只有24年，其中只有约30%的家族企业可以传到第二代，能够传到第三代的家族企业数量为总量的13%，只有5%的家族企业在第三代后还能够继续为股东创造价值.根据上述材料，可以推断美国学者认为“一代”应为__________年．20．一个容量为40的样本，分成若干组，在它的频率分布直方图中，某一组相应的小长方形的面积为0.4，则该组的频数是__________．三、解答题21．在流行病学调查中，潜伏期指自病原体侵入机体至最早临床症状出现之间的一段时间.某地区一研究团队从该地区500名A病毒患者中，按照年龄是否超过60岁进行分层抽样，抽取50人的相关数据，得到如下表格：潜伏期（单位：天）[]0,2(]2,4(]4,6(]6,8(]8,10(]10,12(]12,14人数60岁及以上258752160岁以下0224921（2）以各组的区间中点值为代表，计算50名患者的平均潜伏期（精确到0.1）；（3）从样本潜伏期超过10天的患者中随机抽取两人，求这两人中恰好一人潜伏期超过12天的概率.22．某大学综合评价面试测试中，共设置两类考题：A类题有4个不同的小题，B类题有3个不同的小题.某考生从中任抽取3个不同的小题解答.（1）求该考生至少抽取到2个A类题的概率；（2）设所抽取的3个小题中B类题的个数为X，求随机变量X的分布列与均值. 23．设计程序求使1210000n⨯⨯⨯<成立的最大正整数n，并画出程序框图．24．给出30个数：1，2，4，7，，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，以此类推，要计算这30个数的和，现已给出了解决该问题的算法框图（如图所示）.（1）请在图中处理框内①处和判断框中的②处填上合适的语句，使之能完成该题算法功能；（2）根据算法框图写出算法语句.25．某地级市共有200000中学生，其中有7%学生在2017年享受了“国家精准扶贫”政策，在享受“国家精准扶贫”政策的学生中困难程度分为三个等次：一般困难、很困难、特别困难，且人数之比为5:3:2，为进一步帮助这些学生，当地市政府设立“专项教育基金”，对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元.经济学家调查发现，当地人均可支配年收入较上一年每增加%n ，一般困难的学生中有3%n 会脱贫，脱贫后将不再享受“精准扶贫”政策，很困难的学生有2%n 转为一般困难学生，特别困难的学生中有%n 转为很困难学生.现统计了该地级市2013年到2017年共5年的人均可支配年收入，对数据初步处理后得到了如图所示的散点图和表中统计量的值，其中年份x 取13时代表2013年，x 取14时代表2014年，……依此类推，且x 与y （单位：万元）近似满足关系式y x βα=+.（2013年至2019年该市中学生人数大致保持不变）y521()ii yy =-∑51()()iii x x y y =--∑0.8 3.11（1）估计该市2018年人均可支配年收入为多少万元？（2）试问该市2018年的“专项教育基金”的财政预算大约为多少万元？附：对于一组具有线性相关关系的数据11(,)u υ，22(,)u υ，…，(,)n n u υ，其回归直线方程u υβα=+的斜率和截距的最小二乘估计分别为121()()()niii nii u u uu υυβ==--=-∑∑，u αυβ=-.26．某土特产销售总公司为了解其经营状况，调查了其下属各分公司月销售额和利润，得到数据如下表：分公司名称雅雨雅雨雅女雅竹雅茶月销售额(x 万元35679在统计中发现月销售额x 和月利润额y 具有线性相关关系．(Ⅰ)根据如下的参考公式与参考数据，求月利润y 与月销售额x 之间的线性回归方程； (Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元，试求估计它的月利润额是多少？(参考公式：1221ni i i n i i x y nx y b x nx==-⋅=-∑∑，a y b x =-，其中：1112ni ii x y ==∑，21200)nii x==∑．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】列出所有的基本事件，并找出事件“所取三条线段能构成一个三角形”所包含的基本事件，再利用古典概型的概率公式计算出所求事件的概率．【详解】所有的基本事件有：()1,3,5、()1,3,7、()1,3,9、()1,5,7、()1,5,9、()1,7,9、()3,5,7、()3,5,9、()3,7,9、()5,7,9，共10个，其中，事件“所取三条线段能构成一个三角形”所包含的基本事件有：()3,5,7、()3,7,9、()5,7,9，共3个，由古典概型的概率公式可知，事件“所取三条线段能构成一个三角形”的概率为310，故选：B ．【点睛】本题考查古典概型的概率计算，解题的关键就是列举基本事件，常见的列举方法有：枚举法和树状图法，列举时应遵循不重不漏的基本原则，考查计算能力，属于中等题．2．A解析：A 【分析】根据几何概型的概率计算公式，求出中间小三角形的面积与大三角形的面积的比值即可【详解】设DE x =，因为D 为BE 中点，且图形是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形所以2BE x =，CE x =，120CEB ∠=︒所以由余弦定理得：2222cos BC BE CE BE CE CEB =+-⋅⋅∠222142272x x x x x ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭即BC =，设DEF 的面积为1S ，ABC 的面积为2S因为DEF 与ABC 相似所以21217S DE P S BC ⎛⎫=== ⎪⎝⎭故选：A 【点睛】1.本题考查的是几何概型中的面积型，较简单2.相似三角形的面积之比等于相似比的平方.3．D解析：D 【分析】先计算出9套题中选出3套试卷的可能，再计算3套题年份和编号都各不相同的可能，通过古典概型公式可得答案. 【详解】通过题意，可知从这9套题中选出3套试卷共有39=84C 种可能，而3套题年份和编号都各不相同共有336A =种可能，于是所求概率为61=8414.选D. 【点睛】本题主要考查古典概型，意在考查学生的分析能力，计算能力，难度不大.4．C解析：C 【分析】首先求出两枚骰子的点数之和可能的取值对应的概率，再分别讨论四个选项中n 的取值对应的余数的概率，若每一个余数的概率都相等则是公平的，若不相等则不公平，即可得正确选项. 【详解】由题意知两枚骰子的点数之和为X ，则X 可能为2,3,4,5,6,7,8,9,10,11,12，()1236P X ==， ()2336P X ==，()3436P X ==，()4536P X ==，()5636P X == ()6736P X ==，()5836P X ==，()4936P X ==，()31036P X ==，()21136P X ==，()11236P X ==，对于选项A ：2n =时，0,1,i = ()1351023636362P i ⎛⎫==++⨯= ⎪⎝⎭，()246421136363636362P i ==++++=，所以2n =是公平的，故选项A 不正确；对于选项B ：3n =时，0,1,2i =，()254110363636363P i ==+++=，()363113636363P i ==++=， ()145212363636363P i ==+++=，所以3n =是公平的，故选项B 不正确；对于选项C ：4n =时，0,1,2,3i = ()351103636364P i ==++=，()442136369P i ==+=， ()153123636364P i ==++=，()2625336363618P i ==++= 因为概率不相等，所以4n =不公平，故选项C 正确；对于选项D ：6n =时，0,1,2,3,4,5i = ()511036366P i ==+=，()611366P i ===，()151236366P i ==+=， ()241336366P i ==+=，()331436366P i ==+=，()421536366P i ==+=，所以6n =是公平的，故选项D 不正确，故选：C 【点睛】关键点点睛：本题解题的关键点是理解题意，对于所给n 的值的每一个余数出现的概率相等即为公平，不相等即为不公平.5．D解析：D 【分析】列举出前四次循环，可知，该算法循环是以3为周期的周期循环，利用周期性可得出输出的S 的值. 【详解】第一次循环，02020k =≤成立，1112S ==--，011k =+=；第二次循环，12020k =≤成立，()11112S ==--，112k =+=；第三次循环，22020k =≤成立，12112S ==-，213k =+=；第四次循环，32020k =≤成立，1112S ==--，314k =+=；由上可知，该算法循环是周期循环，且周期为3，依次类推，执行最后一次循环，20202020k =≤成立，且202036731=⨯+，此时12S =， 202012021k =+=，20212020k =≤不成立，跳出循环体，输出S 的值为12. 故选：D. 【点睛】本题考查利用程序框图计算输出结果，推导出循环的周期性是解题的关键，考查计算能力，属于中等题.6．C解析：C 【分析】该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序的运行过程，分析循环中各变量的变化情况，即可得到答案. 【详解】模拟执行程序框图，可得：1,1,1a b n ===，第1次循环，可得3,1,3,2S a b n ====；第2次循环，可得5,3,5,3S a b n ====；第3次循环，可得11,5,11,4S a b n ====，满足判断条件，输出11S =. 故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中模拟程序框图的运行过程，逐次计算，结合判断条件求解是解答的关键，意在考查运算与求解能力，属于基础题.7．C解析：C 【分析】该程序是二分法求方程的近似解的方法，模拟执行程序框图，计算端点处的函数值，再由中点处的函数值，结合函数零点存在定理，即可得到所求值．【详解】解：该程序是二分法求方程的近似根的方法，由流程图可得()1120g =-<，()20f >，可得32m =，302f ⎛⎫< ⎪⎝⎭，可得方程的根介于(1,2)，进而介于31,2⎛⎫⎪⎝⎭，由52520416f ⎛⎫=-< ⎪⎝⎭，可得方程的根介于5(4，3)2，由118m =，1112120864f ⎛⎫=-< ⎪⎝⎭，可得方程的根介于11(8，3)2，由31110.2288-=<，可得输出的值为118，故选：C ．【点睛】本题主要考查了程序框图和算法的应用，模拟执行程序框图，考查二分法求方程近似值的方法，属于基础题．8．B解析：B 【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算输入时变量x 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得到答案. 【详解】本题由于已知输出时x 的值，因此可以逆向求解：输出0x =,此时4i =；上一步：1210,2x x -==,此时3i =；上一步：1321,24x x -==,此时2i =；上一步：3721,48x x -==,此时1i =；故选：B . 【点睛】本题考查了程序框图的循环结构，考查了学生逻辑推理和数学运算的能力，属于基础题.9．D解析：D 【解析】记分员在去掉一个最高分94和一个最低分87后，余下的7个数字的平均数是91，()89889290939291791x +++++++÷=，635=917=6372x x ，∴+⨯∴=，故选D.10．D解析：D 【解析】试题分析：由表中数据可得表1:()25262210140.00916362032K ⨯⨯-⨯=≈⨯⨯⨯；表2: ()2524201216 1.76916362032K ⨯⨯-⨯=≈⨯⨯⨯；表3: ()252824128 1.316362032K ⨯⨯-⨯=≈⨯⨯⨯；表4: ()25214302623.4816362032K ⨯⨯-⨯=≈⨯⨯⨯．其中23.48最大,所以阅读量与性别有关联的可能性最大．故D 正确．考点：独立性检验．11．B解析：B 【解析】【分析】求得抽样的间隔为10，得出若在第1组中抽取的数字为6，则抽取的号码满足104n -，即可出判定，得到答案. 【详解】由题意，从200人中用系统抽样的方法抽取20人，所以抽样的间隔为2001020=，若在第1组中抽取的数字为006，则抽取的号码满足6(1)10104n n +-⨯=-，其中n N +∈，其中当4n =时，抽取的号码为36；当18n =时，抽取的号码为176；当20n =时，抽取的号码为196，所以041这个编号不在抽取的号码中，故选B. 【点睛】本题主要考查了系统抽样的应用，其中解答中熟记系统抽样的抽取方法是解答的关键，着重考查了运算与求解能力，属于基础题.12．B解析：B 【解析】【分析】根据所给的两组数据，做出横标和纵标的平均数，写出这组数据的样本中心点，根据线性回归方程一定过样本中心点，得到线性回归直线一定过的点的坐标．【详解】根据题意可得，，由线性回归方程一定过样本中心点，．故选：B ．【点睛】本题考查线性回归方程的意义，线性回归方程一定过样本中心点，本题解题的关键是正确求出样本中心点，题目的运算量比较小，是一个基础题．二、填空题13．②④【分析】根据题意结合古典概型的概率计算公式逐项进行判定即可求解【详解】设申请法学院的男生人数为女生人数为则法学院的录取率为设申请商学院的男生人数为女生人数为则商学院的录取率为由该值的正负不确定所解析：②④ 【分析】根据题意，结合古典概型的概率计算公式，逐项进行判定，即可求解. 【详解】设申请法学院的男生人数为x ，女生人数为y ，则200x y +=，法学院的录取率为0.50.70.50.7(200)0.70.001200200x y x x x ++⨯-==-，设申请商学院的男生人数为m ，女生人数为n ，则300m n +=，商学院的录取率为0.60.90.60.9(300)0.90.001200200m n m m m ++⨯-==-，由()()0.90.0010.70.0010.20.001()0.001(200)m x m x m x ---=--=-+，该值的正负不确定，所以①错误，④正确；这两个学院所有男生的录取率为0.50.6x mx m++，这两个学院所有女生的录取率为0.70.9y ny n++，因为0.50.60.70.90.20.40.10.30()()x m y n xy xn my nmx m y n x m y n +++++-=<++++，所以②正确；③错误. 故答案为：②④. 【点睛】本题主要考查了古典概型的概率公式的应用，其中解答中正确理解题意，结合古典概型的概率计算公式求得相应的概率是解答的关键，着重考查数学阅读能力，属于基础题.14．3【分析】在20组随机数中表示三天中恰有两天下雨的可以通过列举得到共6组随机数根据概率公式得到结果【详解】由题意知模拟三天的下雨情况经随机模拟产生了20组随机数在20组随机数中表示三天中恰有两天下雨解析：3【分析】在20组随机数中表示三天中恰有两天下雨的可以通过列举得到共6组随机数，根据概率公式，得到结果．【详解】由题意知模拟三天的下雨情况，经随机模拟产生了20组随机数，在20组随机数中表示三天中恰有两天下雨的有：932、812、024、734、191、271，共6组随机数，∴所求概率为60.320P ==．故答案为：0.3 【点睛】本题主要考查了模拟方法估计概率，解题主要依据是等可能事件的概率，注意列举法在本题的应用，属于中档题．15．【分析】根据函数解析式可求得定义域和的定义域即可由几何概型概率求解【详解】函数的定义域为则的定义域为即解得即根据几何概型的概率计算公式得故答案为：【点睛】本题考查了函数定义域的求法复合函数定义域的求解析：22- 【分析】根据函数解析式，可求得()f x 定义域M 和(())y f f x =的定义域P ，即可由几何概型概率求解. 【详解】函数()f x =M ，则[1,1]M =-，(())y f f x =的定义域为P[]1,1-，解得1,22x ⎡⎤∈--⋃⎢⎥⎣⎦⎣⎦，即1,P ⎡⎤=-⋃⎢⎥⎣⎦⎣⎦．根据几何概型的概率计算公式得21222⎛⨯- ⎝⎭=．故答案为：22-. 【点睛】本题考查了函数定义域的求法，复合函数定义域的求法，几何概型概率求法，属于中档题.16．5【分析】直接模拟程序即可得结论【详解】输入的值为2不满足所以故答案是：5【点睛】该题考查的是有关程序框图的问题涉及到的知识点有程序框图的输出结果的求解属于简单题目解析：5 【分析】直接模拟程序即可得结论. 【详解】输入x 的值为2，不满足1x ≤，所以3325y x =+=+=，故答案是：5. 【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有程序框图的输出结果的求解，属于简单题目.17．72【分析】模拟程序的运行依次写出每次循环得到的的值可得当时不满足条件退出循环输出的值为72【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循环体；满足条件执行循环体;满足条件执行循环体；不解析：72 【分析】模拟程序的运行，依次写出每次循环得到的S i ，的值，可得当9i = 时不满足条件8i ＜，退出循环，输出S 的值为72. 【详解】模拟程序的运行，可得10,i S ==，满足条件8i ＜，执行循环体，39;i S ==，满足条件8i ＜，执行循环体，524i S ==，；满足条件8i ＜，执行循环体，745i S ==， ; 满足条件8i ＜，执行循环体，9i =，72S =；不满足条件8i ＜，退出循环，输出S 的值为72, 故答案为72 【点睛】本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决，属于基础题．18．2【解析】当x=2时x2﹣4x+3=﹣1＜0满足继续循环的条件故x=3n=1；当x=3时x2﹣4x+3=0满足继续循环的条件故x=4n=2；当x=4时x2﹣4x+3=3＞0不满足继续循环的条件故输出解析：2 【解析】当x=2时，x 2﹣4x+3=﹣1＜0，满足继续循环的条件，故x=3，n=1；当x=3时，x 2﹣4x+3=0，满足继续循环的条件，故x=4，n=2；当x=4时，x 2﹣4x+3=3＞0，不满足继续循环的条件，故输出的n 值为2；故答案为2．点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括顺序结构、条件结构、循环结构，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.19．20【分析】设美国学者认为的一代为年然后可得出寿命在的家族企业的频率分别为然后利用平均数公式列方程解出的值即可得出所求结果【详解】设美国学者认为的一代为年然后可得出寿命在的家族企业的频率分别为则家族解析：20 【分析】设美国学者认为的一代为x 年，然后可得出寿命在(]0,x 、(],2x x 、(]2,3x x 、(]3,4x x 的家族企业的频率分别为0.52、0.3、0.13、0.05，然后利用平均数公式列方程解出x 的值，即可得出所求结果．【详解】设美国学者认为的一代为x 年，然后可得出寿命在(]0,x 、(],2x x 、(]2,3x x 、(]3,4x x 的家族企业的频率分别为0.52、0.3、0.13、0.05，则家族企业的平均寿命为0.5(10.30.130.05) 1.50.3 2.50.13 3.50.0512.124x x x x x ⨯---+⨯+⨯+⨯==，解得20x ≈，因此，美国学者认为“一代”应为20年，故答案为20. 【点睛】本题考查平均数公式的应用，解题的关键要审清题意，将题中一些关键信息和数据收集起来，结合相应的条件或公式列等式或代数式进行求解，考查运算求解能力，属于中等题．20．16【解析】根据频率直方图的含义每组小矩形的面积就是该组数据在总体中出现的频率所以该组频数为故填16解析：16 【解析】根据频率直方图的含义，每组小矩形的面积就是该组数据在总体中出现的频率，所以该组频数为400.4=16⨯，故填16.三、解答题21．（1）200（2）10.4（天）（3）815【分析】（1）求出调查的50名A 病毒患者中，年龄在60岁以下的有20人，即得解；（2）利用平均数公式计算即得解；（3）利用古典概型的概率公式求解即可. 【详解】（1）调查的50名A 病毒患者中，年龄在60岁以下的有20人，因此该地区A 病毒患者中，60岁以下的人数估计有2050020050⨯=人.（2）()11123751071191411413251810.45050x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=⨯=（天）（3）样本潜伏期超过10天的患者共六人，其中潜伏期在10~12天的四人编号为：1，2，3，4，潜伏期超过12天的两人编号为：5，6，从六人中抽取两人包括15个基本事件：1，2；1，3；1，4；1，5；1，6；2，3；2，4；2，5；2，6；3，4；3，5；3，6；4，5；4，6；5，6.记事件“恰好一人潜伏期超过12天”为事件A ，则事件A 包括8个，所以8()15P A =. 【点睛】本题主要考查古典概型的概率公式，考查平均数的计算，意在考查学生对这些知识的理解掌握水平. 22．（1）2235；（2）分布列见解析，97EX = 【分析】（1）利用古典概率与互斥事件概率计算公式即可得出．（2）设所抽取的3个小题中B 类题的个数为X ，则X 的取值为0，1，2，3．利用超几何分布列计算公式即可得出．【详解】（1）该考生至少抽取到2个A 类题的概率213434372235P +==．（2）设所抽取的3个小题中B 类题的个数为X ，则X 的取值为0，1，2，3．34374(0)35P X ===， 21433718(1)35P X ===， 12433712(2)35P X ===， 33371(3)35P X ===， ∴随机变量X 的分布列为：均值0123353535357EX =⨯+⨯+⨯+⨯=．【点睛】本题考查古典概率与互斥事件概率计算公式、超几何分布列计算公式及其数学期望计算公式，考查推理能力与计算能力．23．见解析【分析】根据题目要求，设计出对应的程序框图，并写出程序.【详解】程序框图如图所示：程序如下：S=1n=1WHILE S<10000S=S*nn=n+1WENDPRINT n–2END【点睛】本小题主要考查设计程序框图并写出对应的程序，属于基础题.24．(1) ①处应填；②处应填 (2)见解析【解析】分析：（1）由已知中程序的功能是给出个数，其规律是：第个数是；第个数是；第个数比第个数大，第个数比第大，，依次类推，要计算区间个数的和，可以根据循环此时，循环变量的初值、步长计算出循环变量的终值，得到①中的条件；再根据累加的变化规律，得到②中累加通项的表达式；（2）利用直到型循环结构，写出程序.详解：（1）因为是求30个数的和，故循环体应执行30次，其中是计数变量，因此判断框内的条件就是限制计数变量的，故应为，算法中的变量实质是表示参与求和的各个数，由于它也是变化的，且满足第个数比其前一个数大，第个数比其前一个数大，故应有，故①处应填；②处应填. （2）根据框图，写出算法如下：点睛：本题主要考查了直到型的循环结构的算法框图，解答中循环体的循环次数=（循环终值-初值）+步长+1，确定循环的次数，其中循环次数、终值、初值、步长中，能知道其中的三个可求解另一个，对于循环结构的程序框图，判断框内的内容容易出错，做题时要注意，同时注意循环点所在的位置.25．(1) 0.10.7y x =-;(2)1624万元.【解析】分析：（1）根据表中数据，求出x ，代入公式求值，从而得到回归直线方程，代入18x =即可；（2）通过由题意知2017年时该市享受“国家精准扶贫”政策的学生共2000007%14000⨯=人.一般困难、很困难、特别困难的中学生依次有7000人、4200人、2800人，按照增长比例关系求解2017年时该市享受“国家精准扶贫”政策的学生，即可得财政预算.详解：（1）因为()11314151617155x =++++=，所以()()5222221()211210i i x x =-=-+-++=∑. 所以()()()515210ˆ.1i ii i i x x y y x x β==--==-∑∑， 0.80.1150.ˆ7ˆy x αβ=-=-⨯=-，所以0.1.7ˆ0y x =-. 当18x =时，2018年人均可支配年收入0.1180.7ˆ 1.1y=⨯-=（万元）. （2）由题意知2017年时该市享受“国家精准扶贫”政策的学生共2000007%14000⨯=人. 一般困难、很困难、特别困难的中学生依次有7000人、4200人、2800人，2018年人均可支配收入比2017年增长()()0.1180.70.1170.70.110%0.1170.7⨯--⨯-==⨯-. 所以2018年该市特别困难的中学生有()2800110%2520⨯-=人，很困难的学生有()4200120%280010%3640⨯-+⨯=人，一般困难的学生有()7000130%420020%5740⨯-+⨯=人.所以2018年的“专项教育基金”的财政预算大约为57400.136400.1525200.21624⨯+⨯+⨯=（万元）.点睛：本题考查了线性回归方程的求法及应用.26．（1）ˆ0.50.4yx =+（2）5.4万元【解析】试题分析：(1)首先由题意求得平均数6, 3.4x y ==，然后利用系数公式计算可得回归方程为0.5.4ˆ0yx =+ . (2)由题意结合(1)中的结论预测可得“雅果”分公司的月利润额是5.4万元. 试题(Ⅰ) 由已知数据计算得：5n =，6, 3.4x y ==1221511256 3.40.5,20056653.40.560.4n i ii n i i x y xy b x x a ==--⨯⨯===-⨯⨯-=-⨯=∑∑∴线性回归方程为0.5.4ˆ0yx =+ (Ⅱ)将x =10代入线性回归方程中得到0.5100.4ˆ 5.4y=⨯+=（万元） ∴估计“雅果”分公司的月利润额是5.4万元。

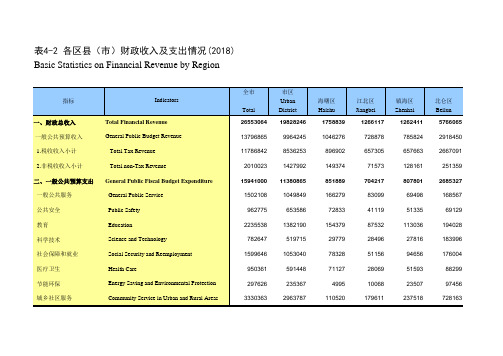
浙江宁波市社会经济发展统计年鉴指标数据：4-2 各区县(市)财政收入及支出情况(2018)

313564 2125104
207563 112672 262353 152357 236747 150169
36499 392617
奉化区 Fenghua
786135 494700 414545
80155 718765
96998 42750 130289 32878 113319 62190 14361 43996
北仑区 Beilun
5766065 2918450 2667091
251359 2685327
168567 69129
194028 183996 176004
88299 97456 728163
单位：万元(10000 yuan)
鄞州区 Yinzhou
4359081 2529936 2216372
宁海县 Ninghai
象山县 Xiangshan
1000663
712828
616311
409984
460517
360259
155794
49725
834266
686585
84130
91100
51560
43386
170050
108542
15250
33020
135942Biblioteka 7392377010
40862
13061
余姚市 Yuyao
1693652 1006321
875531 130790 1153702 121728
81003 227670
58495 214470
96198 23889 42955
慈溪市 Cixi 3317675 1800004 1554282 245722 1885582 155301 133240 347086 156167 122271 144843 13142 235657

税务年鉴全国各省市区数据：中国2018年税收收入分税种分产业收入情况统计

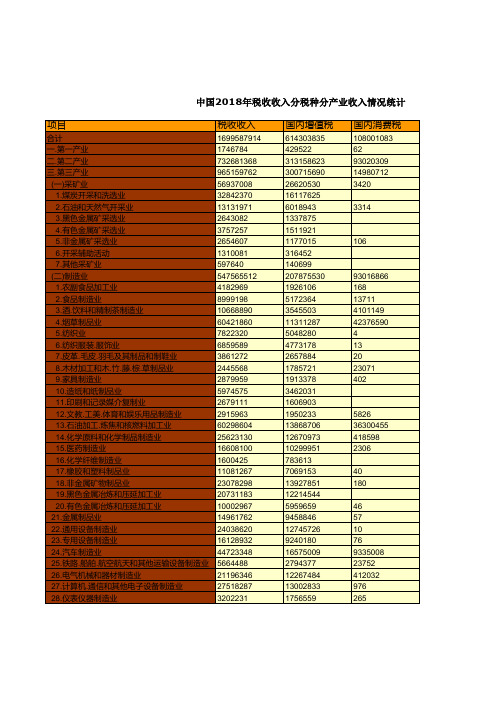
国内消费税
108001083 62 93020309 14980712 3420
3314
106
93016866 168 13711 4101149 42376590 4 13 20 23071 402
5826 36300455 418598 2306
40 180
46 57 10 76 9335008 23752 412032 976 265
单位:万元
ቤተ መጻሕፍቲ ባይዱ
中国2018年税收收入分税种分产业收入情况统计
项目
合计一.第一产业二.第二产业三.第三产业
(一)采矿业 1.煤炭开采和洗选业 2.石油和天然气开采业 3.黑色金属矿采选业 4.有色金属矿采选业 5.非金属矿采选业 6.开采辅助活动 7.其他采矿业
(二)制造业 1.农副食品加工业 2.食品制造业 3.酒.饮料和精制茶制造业 4.烟草制品业 5.纺织业 6.纺织服装.服饰业 7.皮革.毛皮.羽毛及其制品和制鞋业 8.木材加工和木.竹.藤.棕.草制品业 9.家具制造业 10.造纸和纸制品业 11.印刷和记录媒介复制业 12.文教.工美.体育和娱乐用品制造业 13.石油加工.炼焦和核燃料加工业 14.化学原料和化学制品制造业 15.医药制造业 16.化学纤维制造业 17.橡胶和塑料制品业 18.非金属矿物制品业 19.黑色金属冶炼和压延加工业 20.有色金属冶炼和压延加工业
29.其他制造业 30.废弃资源综合利用业 31.金属制品.机械和设备修理业 (三)电力.热力.燃气及水的生产和供应业 1.电力.热力生产和供应业 2.燃气生产和供应业 3.水的生产和供应业 (四)建筑业 1.房屋建筑业 2.土木工程建筑业 3.建筑安装业 4.建筑装饰和其他建筑业 (五)批发和零售业 1.批发业 2.零售业 (六)交通运输.仓储和邮政业 1.铁路运输业 2.道路运输业 3.水上运输业 4.航空运输业 5.管道运输业 6.装卸搬运和运输代理业 7.仓储业 8.邮政业 (七)住宿和餐饮业 1.住宿业 2.餐饮业 (八)信息传输.软件和信息技术服务业 1.电信.广播电视和卫星传输服务 2.互联网和相关服务 3.软件和信息技术服务业 (九)金融业 1.货币金融服务 2.资本市场服务 3.保险业 4.其他金融业 (十)房地产业 1.房地产开发经营业 2.物业管理 3.房地产中介服务 4.自有房地产经营活动 5.其他房地产业 (十一)租赁和商务服务业 1.租赁业

温州市社会经济发展统计年鉴指标数据：2018年分县(市.区)茶叶.水果和林业生产情况统计

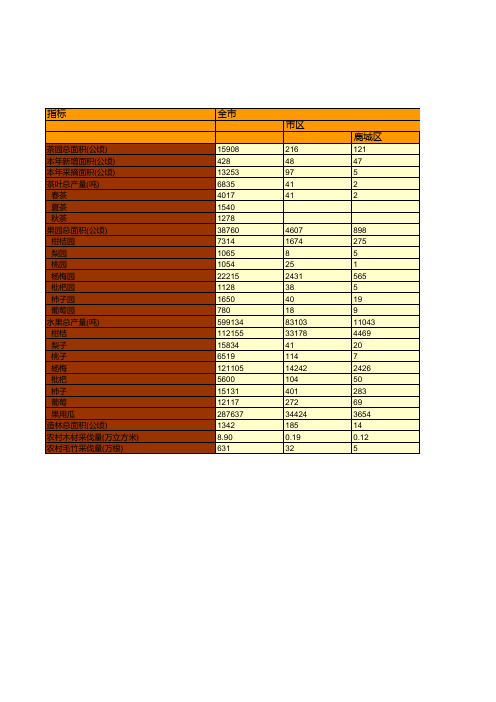
全市
15908 428 13253 6835 4017 1540 1278 38760 7314 1065 1054 22215 1128 1650 780 599134 112155 15834 6519 121105 5600 15131 12117 287637 1342 8.90 631
市区
文成县
1317
1057 474 350 50 74 6229 401 623 168 4267 83 227 29 48423 717 10493 243 17274 116 235 136 16389 35 2.20 33
泰顺县
5611 67 4613 3461 1355 1044 1062 4283 170 133 153 2543 105 102 58 30549 787 1460 945 12377 131 970 720 3426
指标
茶园总面积(公顷) 本年新增面积(公顷) 本年采摘面积(公顷) 茶叶总产量(吨)
春茶夏茶秋茶果园总面积(公顷) 柑桔园梨园桃园杨梅园枇杷园柿子园葡萄园水果总产量(吨) 柑桔梨子桃子杨梅枇杷柿子葡萄果用瓜造林总面积(公顷) 农村木材采伐量(万立方米) 农村毛竹采伐量(万根)
2.32 87
平阳县
1648 124 1389 969 672 207 90 2343 755 28 114 1085 10 14 107 76801 9440 110 1079 8909 68 124 1237 52941 364 0.37 70
苍南县
1820 66 1344 942 654 237 51 3443 1281 32 153 1293 31 37 189 84429 23341 158 1474 4856 191 202 3106 49520 466 0.79 46