五年级数学上册思维训练:倍数问题(二)
【精品奥数】五年级上册数学思维训练讲义-第9讲 倍数问题(二) 人教版(含答案)

第九讲 倍数问题(二)第一部分:趣味数学熊猫智惩小狐狸卖水果的狐狸波利在给顾客称水果时总缺斤短两,人家找来后他还不承认错误,熊猫菲菲打算惩治他一下。
这一天他来狐狸波利这儿买香蕉。
“ 香蕉一元钱一斤,您买多少啊? ” 波利很热情。
“ 我们要开个生日晚会,打算买一百斤,不过得麻烦您把它们全部剥好,我给您每斤香蕉皮 5 角钱,每斤香蕉肉 5 角钱,行吗? ” 狐狸波利想: 5 角钱加上 5 角钱,还是每斤一元钱。
便爽快地答应了。
他连忙把这一百斤香蕉全部剥好,皮与肉分开称好斤数。
熊猫菲菲迅速地把钱付了,可是狐狸波利盯着自己的钱,总感觉有问题,却又不知问题出在哪里?同学们,你能帮狐狸波利想一想问题出在哪里了吗?第二部分:奥数小练【例题1】,养鸡场的母鸡只数是公鸡的6倍,后来公鸡和母鸡各增加60只,结果母鸡只数就是公鸡的4倍。
原来养鸡场一共养了多少只鸡?【思路导航】养鸡场原来母鸡的只数是公鸡的6倍,如果公鸡增加60只,母鸡增加60×6=360只,那么,后来的母鸡只数还是公鸡的6倍。
可实际母鸡只增加了60只,比360只少300只。
因此,现在母鸡只数只有公鸡的4倍,少了2倍。
所以,现在公鸡的只数是300÷2=150只,原来有公鸡150-60=90只,一共养了90×(1+6)=630只鸡。
练习一:1.今年,爸爸的年龄是小明的6倍,再过4年,爸爸的年龄就是小明的4倍。
今年小明多少岁?2.原来食堂里存的大米是面粉的4倍,大米和面粉各吃掉80千克,大米的重量是面粉5倍。
食堂里原来存有大米、面粉各多少千克?3.饲养场的白兔只数是黑兔的5倍,后来卖掉了10只黑兔,买回来20只白兔,现在白兔的只数是黑兔的7倍。
饲养场原来养白兔和黑兔各多少只?【例题2】有1800千克的货物,分装在甲、乙、丙三辆车上。
已知甲车装的千克数正好是乙车的2倍,乙车比丙车多装200千克。
甲、乙、丙三辆车各装货物多少千克?【思路导航】如果丙车多装200千克,就和乙车装的货物同样多,这样三辆车装的总重量就是1800+200=2000千克。
北师大版五年级上册数学思维训练(二)

五年级数学思维训练(二)班级 姓名一、填空。
1、在括号里填上适当的分数。
340千克=( )吨 1米70厘米=( )米12分=( )小时 28平方分米=( )平方米2、在500克的水中加入10克的盐,盐占盐水的( );盐占水的( )。
3、如果把53的分子加上6,要使分数的大小不变,分母应( )。
4、两根10米长的绳子,第一根用去它的53,第二根用去53米 。
第( )根 用去的多。
5、把6米长的绳子剪成相等的8段,每段占总长的)()(,每段长( )米,3段 长( )米,4段占总长的)()(。
第3段占总长的)()(,第6段长( )米。
6、写出下面每组数的最小公倍数和最大公因数。
﹝7,9﹞= ﹝15,25﹞= ﹝13,91﹞=( 7,9)= (15,25)= (13,91)=7、在7a 中,a 是自然数,当 a ( )时,它是真分数;当 a ( )时, 它能化成整数。
8、如果a ÷b=0.1(a 、b 都是非0的自然数),那么,a 和b 的最大公因数是( ),最小公倍数是( )。
二、判断题。
1、方程的解就是解方程。
…………………………………………( )2、非零的自然数中,所有偶数的最大公因数是2。
……………( )3、分子与分母的最大公因数是1,这个分数是最简分数。
……( )4、把一条5米长的彩带对折两次,每段是54米。
…………… ( ) 三、列方程并解方程。
1、368除以一个数,商和余数都是8,2、一个数的2.5倍,比这个数多22.5, 这个数是多少? 这个数是多少?四、约分、通分。
1、把下面的分数约分,是假分数的化成整数或带分数 3248 824 2712 9538 1435 9139 2、通分。
43和65 83和127 94和187 6和43 153和73五、解决问题。
1、三角形的面积是72.72平方厘米,底是4.5分米。
高是多少分米?(列方程解答)2、王师傅加工93个零件,其中有3个废品,合格品占零件总数的几分之几?3、100千克花生可榨油35千克,平均每千克花生可榨油多少千克?榨1千克花生油需要多少千克花生?4、一个分数的分子比分母少24,约分之后是74,这个分数是多少?5、把一个分数约分,用2约了两次,用3约了一次,得65,原来这个分数是多少?6、一个分数,如果分子加上1,这个分数化简后结果是1,如果分母加1,化简后得87,这个分数原来是多少?7、一个最简分数分子和分母的和是25,若分子减去2,分母加上2后约分得14,这个最简分数是多少?8、张老师把全班同学平均分成了两组,并和全班同学一起为学校搬新课桌。
五年级数学思维训练 因数与倍数

五年级数学思维训练因数与倍数(最小公倍数与最大公因数二)姓名突破重难点最小公倍数与最大公因数之间的关系。
1、两个自然数分别除以它们的最大公因数,所得的商互质。
2、两个数的最小公倍数与最大公因数之积等于这两个数的乘积。
3、两个数的公因数一定是这两个数的最大公因数的因数。
例题精选例1、两个数的最大公因数是4,最小公倍数是252,其中一个数是28,另一个数是多少?例2、两个自然数的和是50,它们的最大公因数是5,求这两个数的差。
例3、两个数的最大公因数为21,最小公倍数为126,求这两个数的和。
例4、两个自然数的和是54,它们的最小公倍数与最大公因数的差是114,求这两个自然数。
加强训练1、某数与24的最大公因数是4,最小公倍数是168,这个数是多少?2、两个自然数的和是56,它们的和是56,它们的最大公因数是7,求这两个数。
3、两个自然数的最大公因数是7,最小公倍数是210,这两个数的和是77。
求这两个数。
4、两个自然数的差是30,它们的最小公倍数与最大公因数的差是450,求这两个数。
5、两个数的最大公因数是60,最小公倍数是720,其中的一个数是180,另一个数是多少?6、已知两个自然数的和为165,它们的最大公因数是15,求这两个数。
7、两个不同自然数的和是60,它们的最大公因数与最小公倍数的和也是60,满足条件的自然数共有多少组?8、已知a与b,a与c的最大公因数分别是12和15,a,b,c的最小公倍数是120,求a,b,c。
9、两个自然数的差是3,它们的最大公因数与最小公倍数的积是180,求这两个数。
10、已知a与b,a,与c,b与c的最小公倍数分别是60,90和36。
问:满足此条件的a,b,c有多少组?。
第三单元倍数与因数 思维素养篇--五年级数学上册(解析版)北师大版

目录 (3) (3)2、5和3的倍数特征(一) (4)2、5和3的倍数特征(二) (4) (5) (6) (7)【奥数拓展二】因数和倍数拓展(二) (8)2、5和3的倍数特征拓展(一) (9)2、5和3的倍数特征拓展(二) (10) (10) (11) (12) (12) (13) (13) (14) (15) (16)第三单元倍数与因数·思维素养篇【从课内到奥数】求80和144的因数各有多少个?解析:10个;15个。
【专项训练】1. 求60和90的因数各有多少个?解析:12个;12个。
2. 求196的因数有多少个?解析:9个。
3. 面积是165平方厘米的形状不同且边长是自然数的长方形共有多少种?解析:4种。
【课内精选二】因数和倍数(二)。
一只盒内共有96个棋子,如果不一次拿出,也不一个一个地拿出,但每次拿出的个数要相等,最后一次正好拿完,那么,共有多少种不同的拿法?解析:根据题意可以知道,96等于每次拿的个数与拿的次数的乘积。
96=1×96=2×48=3×32=4×24=6×16=8×12。
因为“不一次拿出,也不一个一个地拿出”,所以,1×96应该去掉,其余的每个算式都可以看作两种拿法,所以,一共有2×5=10(种)拿法。
【专项训练】1. 一只筐内共有120个苹果,如果不一次拿出,也不一个一个地拿出,但每次拿的个数要相等,最后一次正好拿完.那么,共有多少种不同的拿法?解析:14种。
2. 自然数a≥3,b≥3,a×b=195,那么,a和b的值可能是多少?解析:6种。
2、5和3的倍数特征(一)。
下面的这些数中,哪些数既是2的倍数又是5的倍数?46 63 80 39 105 120 77 2310解析:因为“一个数既是2的倍数又是5的倍数,那么它的个位数字必须是0”,所以,只有个位上是0的那些数才既是2的倍数又是5的倍数,所以,这些数中,只有80、120、2310既是2的倍数又是5的倍数。
思维拓展第3讲《倍数问题》(教案)五年级上册数学人教版

思维拓展第3讲《倍数问题》教案一、教学目标1. 让学生理解倍数概念,掌握求一个数的倍数的方法。
2. 培养学生运用倍数知识解决实际问题的能力。
3. 培养学生数学思维,提高数学素养。
二、教学内容1. 倍数的概念2. 求一个数的倍数的方法3. 倍数在实际生活中的应用三、教学重点与难点1. 教学重点:倍数的概念,求一个数的倍数的方法。
2. 教学难点:理解倍数的意义,灵活运用倍数知识解决实际问题。
四、教学过程1. 导入新课通过生活中的实例,引出倍数的概念,激发学生的学习兴趣。
2. 倍数的概念(1)讲解倍数的定义,让学生理解倍数的含义。
(2)举例说明倍数的概念,如:2的倍数有:2, 4, 6, 8, ...3. 求一个数的倍数的方法(1)讲解求一个数的倍数的方法,即用这个数分别乘以自然数1, 2, 3, ...(2)举例说明求一个数的倍数的方法,如:求5的倍数,可以分别计算5×1, 5×2, 5×3, ...4. 倍数在实际生活中的应用(1)讲解倍数在实际生活中的应用,如:计算物品的价格、长度、面积等。
(2)举例说明倍数在实际生活中的应用,如:一个苹果3元,买5个苹果需要多少钱?5. 课堂练习(1)让学生独立完成练习题,巩固所学知识。
(2)针对学生的错误,进行讲解和指导。
6. 课堂小结总结本节课所学内容,强调倍数的概念和求一个数的倍数的方法。
五、课后作业1. 完成课后练习题,巩固倍数知识。
2. 观察生活中哪些地方用到了倍数,与同学分享。
六、教学反思1. 教师要关注学生对倍数概念的理解,及时纠正学生的错误认识。
2. 在教学过程中,要注意培养学生的数学思维,提高学生解决问题的能力。
3. 针对不同学生的学习情况,进行有针对性的辅导,确保每位学生都能掌握倍数知识。
总之,本节课通过讲解倍数的概念、求一个数的倍数的方法以及倍数在实际生活中的应用,旨在培养学生数学思维,提高学生解决问题的能力。
五年级奥数倍数问题二

分析:
每小时由A站向B站开出12辆汽车,而B站 也向A站开出8辆,实际上就是每隔1小时 ,A站减少12-8=4辆汽车,而B站就增加4 辆汽车。要使B站的汽车是A站的3倍,A站 只能有(26+30)÷(1+3)=14辆,必须 减少26-14=12辆。每小时减少4辆,所以 要经过12÷4=3(小时)。
练习1:
1.今年爸爸的年龄是小明的6倍,再 过4年爸爸的年龄就是小明的4倍,小 明今年多少岁?
2. 食堂里原来存的大米重量是面
米,面粉各多少千克?
例2 有1800千克的货物,分装在
甲乙丙三辆车上。已知甲车装 的正好是乙车的2倍,乙车比丙 车多装200千克。甲乙丙三辆车 各装货物多少千克?
分析:
甲书架借出三分之一后,还剩 600÷3×2=400本。这时,甲书架的书 是乙书架的2倍还多150本,说明乙书架 还有(400-150)÷2=125本。乙书架借 出四分之三后剩下125本,则原来有 125×4=500本。
练习3:
1.某校有男生630人,选出男生人数的三分之 一和女生人数的四分之三去排练团体操,剩 下的男生人数是女生人数的2倍。这个学校共 有学生多少人?
分析: 题中出现了三个数,且关系比较复杂。我们只有
把丙数看做“1倍数”计算时才比较方便。这样,乙 就是3倍少2,而甲数比乙数的2倍多4,也就是(3倍2)×2+4=6倍。这样,三个数的和就相当于丙数的( 1+6+3)倍少2。78只要增加2就正好是丙数的10倍。 求出了丙数,就很方便求出甲数和乙数。
练习5:
差倍问题的数量是:
差数÷(倍数-1)=较小数 较小数×倍数=较大数
例1 养鸡场的母鸡只数是公鸡
的6倍,后来公鸡和母鸡各增 加60只,结果母鸡的只数就 是公鸡只数的4倍。养鸡场原 来一共养了多少只鸡?
(完整版)北师大版五年级上倍数与分解练习题

(完整版)北师大版五年级上倍数与分解练习题北师大版五年级上倍数与分解练题 (完整版)第一章:两位数的倍数知识点两位数的倍数指的是能够被10或更大的正整数整除的数字。
一个两位数的倍数一定是个两位数,被除数可以在10到99之间选择。
练题1. 用小学数学的方法,判断下列数字是否是24的倍数:1. 1442. 4563. 10084. 96答案:1. 是2. 否3. 是4. 是2. 小凯有36支笔,他想把它们放到24个笔筒中,每个笔筒中放相同的数量,问每个笔筒中应该放几支笔?答案:每个笔筒中应该放1支笔。
3. 用小学数学的方法,求下列数字的倍数:1. 15的三倍2. 20的五倍3. 27的四倍4. 41的两倍答案:1. 452. 1003. 1084. 82第二章:两位数的分解知识点两位数的分解指的是将一个两位数写成两个数的和的过程。
一个两位数可以被分解为个位数和十位数的和,例如53可以被分解为50+3。
练题1. 用小学数学的方法,将下列数字分解为两位数的和:1. 232. 473. 994. 58答案:1. 20+32. 40+73. 90+94. 50+82. 小明有27元钱,他可以买1元或2元的零食,他最多可以买多少个零食?答案:小明最多可以买13个零食。
3. 用小学数学的方法,求下列数字的和:1. 34与182. 20与303. 56与444. 24与36答案:1. 522. 503. 1004. 60。
五年级思维训练

随堂练习
第六讲 盈亏问题 教学目标:
专题简介
盈亏问题又叫盈不足问题,是指把一定数量的物品平均分给固定对象,如果按某种标 准分,则分配后会有剩余(盈);按另一种标准分,分配后又会有不足(亏),求物品的 数量和分配对象的数量。例如:把一袋饼干分给班上的小朋友,如果没人分3快,则多12 块;如果没人分4块,则少8块。小朋友有多少人?饼干有多少块?这种一盈一亏的情况, 就是我们通常说的标准的盈亏问题。 盈亏问题的基本数量关系是:(盈+亏)÷两次所分之差=人数 还有一些非标准的盈亏问题,他们被分为四类: 1、 两盈:两次分配都有余。 2、 两亏:两次分配都不够。 3、 盈适足:一次分配有余,一次分配刚好。 4、 不足适足:一次分配不够,一次分配正好。 一些非标准的盈亏问题都可以由标准的盈亏问题演变过来的,解题时我们可以记住: 1、“两亏”问题的基本数量关系是:(亏-亏)÷两次所分之差=参与分配对象的总 数。 2、“两盈”问题的基本数量关系是:(盈-盈)÷两次所分之差=参与分配对象的总 数。 3、“一盈一亏”问题的基本数量关系是:(盈+亏)÷两次所分之差=参与分配对象 的总数。
例题1:甲组有图书是乙组的3倍,
随堂练习
1、甲、乙二人加工一批帽子,甲每天比乙多加工10个。途中 乙因事休息了5天,20天后,甲加工的帽子正好是乙加工的2倍, 这时两人各加工了多少个? 2、甲、乙两车同时从A、B两地相对开出,甲车每小时比乙 车多行20千米。途中乙车因修车用了2个小时,6小时后甲车到达 两地的中点,而乙车才行驶了甲车所行路程的一半。问:A、 B 两地相距多少千米? 3、甲、乙两人承包一项工程,共得工资1120元,已知甲工作 了10天,乙工作了12天,且甲5天的工资和乙4天的工资一样多。 求甲、乙每天各得工资多少元?
五年级奥数倍数问题(二)

五年级奥数倍数问题二解决倍数问题专题简析解题关键是必须确定一个数作为标准,并根据题目中的已知条件,找出其他几个数与标准数之间的关系,再用除法求出这个标准。
由于倍数应用题中的数量关系的变化,要求同学在解题过程中注意技巧灵活解题。
倍数问题的数量关系是:倍数÷(倍数+1)=较小数较小数×倍数=较大数差倍问题的数量关系是:差数÷(倍数--1)=较小数较小数x倍数=较大数例题一养鸡场的母鸡只数是公鸡只数的6倍,后来公鸡和母鸡各增加60只,结果母鸡的只数就是公鸡只数的4倍。
养鸡场原来一共有多少只鸡?思路点拨:养鸡场原来母鸡的只数是公鸡的6倍,如果公鸡增加60只的话,母鸡增加60 x6=360只,那么,后来的母鸡只数还是公鸡只数的6倍。
可实际母鸡只数增加了60只,比360只少300只。
因此,现在母鸡的只数只有公鸡的4倍,少了2倍。
所以,现在公鸡的只数是300÷2=150只,原来有公鸡150-60=90只,一共养了90 x(1+6)=630只。
(60x6-60)÷(6-4)=150只(150-60)x(1+6)=630 只答:养鸡场原来一共养鸡630只。
举一反三1.今年爸爸年龄是小明的6倍,再过4年爸爸的年龄就是小明的4倍。
小明今年多少岁?2.食堂里原来存的大米质量是面粉的4倍,大米和面粉各吃掉89千克后大米是面粉的6倍。
食堂里原来有大米和面粉各多少千克?3.饲养场的梨白兔是黑兔的5倍,后来,卖掉了10只黑兔,买回来20只白兔,现在白兔的只数是黑兔的7倍,饲养场原来养白兔和黑兔各多少只?多装200千克例题二有1800千克的货物,分装在甲、乙、丙三辆车上。
已知甲车装的正好事乙车的2倍,乙车比丙车多装200千克,甲、乙、丙三辆车各装货物多少千克?思路点拨;从图中可以看出,如果丙车,就和乙车一样多,这样的话,三辆车装的总重就是1800+200=2000千克。
在把2000千克平均分成4份,就得到乙车的货物是500千克,甲车是装500x2=1000千克,丙车上装的是500-200=300千克。
五年级数学思维训练专题

五年级数学思维训练专题(一)小数点的妙用一、训练目标:训练学生正确理解并运用小数点向左移动或向右移动几位,表示缩小或扩大多少倍。
二、训练过程(一)创设情境,激发兴趣同学们,学习了小数加减法和小数乘除法,你觉得小数点有什么作用?(二)合作探究,解决问题甲、乙两数的和是16.5,甲数的小数点向右移动一位正好等于乙数。
你知道甲、乙两数各是多少?思路点拨:解答数学问题,首先要弄清题意。
对于这道题,较为难理解的就是“甲数的小数点向右移动一位正好等于乙数。
”这句话是什么意思呢?细细品味,甲数的小数点向右移动一位,就是甲数×10,甲数×10后才等于乙数,说明乙数是甲数10倍。
再重新理解一下题意就是这样的:甲、乙两数的和是16.5,乙数是甲数10倍。
求甲、乙两数各是多少?是一道典型的和倍问题可借助线段图:甲数:乙数:列式: 10+1=11甲数: 16.5÷11=1.5乙数: 1.5×10=15答:甲数是1.5 乙数是15.(三)归纳总结,策略点悟在小学数学中,这样的题还是比较多的,遇到这类题还是要放慢速度,仔细审题,弄清甲乙两数是什么关系?哪个数大?弄清变化前后的数量关系,再加以解决,问题便会迎刃而解。
(四)拓展应用,提升思维1.甲、乙两数的和是15.4,甲数的小数点向右移动一位正好等于乙数。
你知道甲、乙两数各是多少?2.甲、乙两数的差是13.7,甲数的小数点向左移动一位正好等于乙数。
你知道甲、乙两数各是多少?3.甲、乙两数相差是16.2,甲数的小数点向右移动一位就等于乙数。
求甲、乙两数各是多少?五年级数学思维训练专题(二)神奇的小数点训练目标:1.认识小数点的重要性,使学生学会通过移动小数点使复杂的计算简单化。
2.灵活运用一个因数扩大、另一个因数就缩小相同的倍数,积不变的性质使复杂计算简单化。
二、训练过程:(一)创设情境,提出问题。
1.引入小数点的作用。
小数点是个小不点,但它的作用却很大,不信,大家来看看。
数学思维训练(五年级上册)

数学思维训练(五年级上册)2019年9月第一讲和倍、差倍问题【知识综述】(1)已知两个数的和与两个数的倍数关系,求这两个数各是多少的应用题,我们把它叫做和倍问题。
(2)已知两个数的差与两个数的倍数关系,求这两个数各是多少的应用题,叫差倍问题。
解答和倍、差倍问题时,一般把最小的数看作“一倍”,先求出最小量,然后再分别求出其他各数。
(3)已知大小两个数的和及这两个数的差,求这两个数各是多少的应用题。
解题规律为:小数加上两数差就是大数,两数和加上两数差便是大数的2倍;大数减去两数差就是小数,两数和减去两数差是小数的2倍。
关键是:设法使两个(或若干个)大小不等的数变成两个(或若干个)相等的数。
(二)计算公式(1)和倍问题关系式小数= 两数和÷(倍数+ 1)大数= 两数和–小数小数= 两数和–大数大数= 小数×倍数小数= 大数÷倍数(2) 差倍问题关系式小数= 两数差÷(倍数-1)大数=小数+ 相差数小数= 大数–相差数大数=小数×倍数小数= 大数÷倍数(3)和差问题计算的数量关系式(和+差)÷2=大数(和-差)÷2=小数【典型例题1】和倍:小明和妈妈的年龄之和是40,妈妈的年龄是小明的4倍,求小明和妈妈各多少岁?小明和妈妈的年龄和是40,正好是小明年龄的5倍,可以求出小明8岁,进一步求出妈妈32岁.即4+1=5,40÷5=8(岁),40-8=32(岁)。
【典型例题2】差倍:一个小数,如果把它的小数点向右移动一位,就比原数多4.86,原来这个小数是多少?在小学数学中这是差倍问题,求差倍问题的方法是:两数之差除以这两个数的倍数差得到较小数,较小的数加上两数之差就是较大的数。
该题中小数点向右移动一位,这个数就扩大10倍,也就是说它们的倍数差是10-1=9,4.86是较大的数和较小的数的差。
所以4.86÷9=0.54 ,0.54+4.86=5.4,即原来的数是5.4。
最全面五年级数学上册倍数与因数知识点精讲与练习题(可编辑修改word版)(精华版)

五年级数学上册第 5 讲(倍数与因数)一、倍数和因数1、整数A 能整除整数B,A 叫作B 的倍数,B就叫做A的因数或约数,A÷B=C,A 是B的倍数,也是C的倍数,B 和C都是A 的因数。
倍数和因数不能单独说。
例题:在算式2×3=6 或6÷2=3 中,2、3 就是6 的因数。
习题1、(1)在15×4=60 中,()是()()的倍数,()和()是()的因数。
2、一个数的因数是有限的,最小因数是1,最大因数是它本身。
一个数的倍数有无限个,最小倍数是它本身,没有最大倍数。
找一个数的倍数要按照一定的顺序,用这个数分别去乘1、2、3、4 得到的积就是它的倍数。
倍数写不完用省略号代替。
但有范围要求的就不要省略号。
找一个数的所有因数也要按照一定的顺序,用除法一对一对地找。
例题:找36 的因数:36÷1=36 36÷2=18 36÷3=12 36÷4=9 36÷6=6 从小到大排列36 的因数有1、2、3、4、6、9、12、18、36.习题2:找16 的因数,并把找出的因数按从小到大的顺序排列。
二、2、3、5 的倍数特征(1)2 的倍数的特征:个位上的数是2、4、6、8 或0。
(2)5 的倍数的特征:个位上的数是 5 或0。
(3)3 的倍数的特征:各位上数的和一定是 3 的倍数。
(4)一个数既是2 的倍数又是 5 的倍数,它个位上的数是0123【例题】按要求把下列各数填入相应的括号里。
4, 12, 25, 8, 30, 45, 25,)40, 120(1)3 的倍数:((2)2 的倍数:()(2)5 的倍数:()(2)既有因数2,又有因数(3)同时是2、3、5 的倍数3:(:())习题3. 按要求把下列各数填入相应的括号里。
36,58,40, 25, 10, 83, 95, 76, 60, 15, 14, 35, 80, 554(1)2 的倍数((2)3 的倍数())(3)5 的倍数()(4)既是2 的倍数,又是 3 倍数()(5)同时是2、3、5、的倍数()。
小学五年级数学思维专题训练—因数与倍数(含答案解析)

小学五年级数学思维专题训练—因数与倍数1、由不小于30人,不大于50人的学生围成一个圆圈,由某人开始从1连续报数,如果报30和198是同一个人时,请问:这批学生一共多少人?.2、有这样一类2009位数,它们不含有数字0,任何相邻两位(按原来的顺序)组成的两位数都有一个因数和20相差1,这样的2009位数共有多少个?3、一个自然数,它的最大的因数和次大的因数和是111,这个自然数是(74 )4、筐中有60个苹果,将它们全部都取出来,分成偶数堆,使得每堆的个数相同。
问:有多少种分法?5、称一个两头(首位和末位)都是1的数为“两头蛇数”。
一个四位数的“两头蛇数”去掉两头得到一个两位数,它恰好是这个“两头蛇数”的因数,这个“两头蛇数”是。
(写出所有可能)6、你能在3×3的方格表(如下图)中填入彼此不同的9个自然数(每个格子里只填一个数),使得每行、每列、两条对角线上三个数的乘积都等于2005吗?若能,请填出一例;若不能,请说明理由)7、已知三位数240有d个不同的因数,求d的值。
8、100以内有10个因数的最小自然数是( ),它的所有因数的和是()。
9、一个正整数,它的2倍的因数恰好比它自己的因数多2个,它的3倍的数的因数恰好比自己的因数多3个。
那么这个正整数是()10、能被2145整除且恰有2145个因数的数有()个。
11、一个自然数恰好有18个因数,那么它最多有()个因数的个位是3.12、N是1,2,3,...,1995,1996,1997的最小公倍数,请问N等于多少个2与一个奇数的积?13、在下面一列数中,从第二个开始,每个数都比它前面相邻的数大7,数列如下:8,15,22,29,36.....它们前n-1个数相乘的积末尾0的个数比前n 个数相乘积的末尾0的个数少3个,求n 的最小值。
14、81,92,103, (2009)2002中,共有( )个最简分数。
15、美术老师要在一张长12分米、宽84厘米的纸上裁出同样大小的正方形手工纸若干张,且没有纸剩下,那么每张正方形纸的边长最大是( )厘米,一共能裁出( )张这样的手工纸?16、如下图所示,某公园有两段路,AB=175m,BC=125m,在这两段路上安路灯,要求A,B,C 三点各设一个路灯,相邻两个路灯间的距离都相等,则在这两段路上至少要安装多少盏灯?17、将一个数的各位数字相加得到新的一个数称为一次操作,经连续若干次这样的操作后可以变为6的数称为“好数”,那么不超过2012的“好数”的个数为( ),这些“好数”的最大公因数是()。
11.五年级奥数思维训练 倍数问题(二)

五年级奥数思维训练倍数问题(二
一、尝试练习
1. 甲、乙两人做机器零件,甲比乙多做400个,且甲做的零件个数是乙的3倍,问:甲、乙两人各做多少个零件?
2.甲比乙多存140元,如果乙取出60元,甲存入60元,那么甲的存款为乙的3倍,问:甲、乙两人原有存款各是多少元?
二、训练营地
1.大桶装水是小桶的3倍,如果从大桶倒出85千克,从小桶倒出5千克,那么剩下的水是一样多的,问:两个桶原有多少千克水?
2.某班级的同学参加活动小组,已知参加语文小组的同学比参加数学小组的多26人,且语文小组的人数比数学小组的人数的3倍少14人,问:参加两类兴趣小组的同学各有多少人?
3.有两缸金鱼,如果从第一缸取出15条放入第二缸,那么第二缸的金鱼正好是第一缸的2倍,已知第二缸原有金鱼35条,第一缸原有金鱼多少条?
4.有甲、乙两桶汽油,甲桶比乙桶重16千克,从甲桶中倒一半给乙桶,这时乙桶重80千克,原来甲桶和乙桶各有多少千克汽油?。
五年级思维训练专题——倍数问题

倍数问题(一)专题分析:倍数问题是数学竞赛中的重要内容之一,它是指已知几个数的和或者差以及几个数的倍数关系,求这几个数的应用题。
解答倍数问题,必须先确定一个数(通常选用较小的数)作为标准数,即1倍数,再根据其他几个数与这个数的关系,确定“和”或者“差”相当于这样的几倍。
最后用用除法求出1倍数。
和数÷(倍数+1)=较小数差数÷(倍数-1)=较小数例1 两根同样长的铁丝,第一根剪去18米,第二根剪去26米,余下的铁丝第一根是第二根的3倍。
原来两根铁丝各长多少米?分析解答:这两根铁丝的差保持不变,而剩下的铁丝的差依然是原来铁丝的差。
根据余下的铁丝第一根是第二根的3倍。
则余下的铁丝相差2倍。
这样很容易计算第二根余下的铁丝是:(26-18)÷(3-1)=4(厘米)则原第二根铁丝长30厘米。
随堂练习:1、两根绳子一样长,第一根用去6.5米,第二根用去0.9米,剩下部分第二根是第一根的3倍。
两根绳子原来各长多少米?2、一筐苹果和一筐梨的个数相同,卖掉40个苹果和5个梨后,剩下的梨是苹果的6倍。
原来两筐水果一共有多少个?例2 甲组有图书是乙组的3倍,若乙组给甲组6本,则甲组的图书是乙组的5倍。
原来甲组有图书多少本?分析解答:甲组的图书是乙组的3倍,若乙组拿出6本,甲组相应的也拿出6×3=18(本),则甲组仍是乙组的3倍,事实上甲组不但没有拿出18本,反而接受了乙组的6本,这样24本正好对应后来两组的(5-3=2)倍。
因此后来乙组的图书是:(6×3+6)÷(5-3)=12(本)。
则原来乙组为18本,甲组就是18×3=54(本)。
随堂练习:1、原来小明的画片是小红的3倍,后来二人个买了5张,这样小明的画片就是小红的2倍。
原来二人各有多少张画片?2、一个书架分上下两层,上层的书的本数是下层的4倍,从下层拿出5本放入上层后,上层的本数正好是下层的5倍。
小学数学思维训练四年级第八讲倍数问题(二)

倍数问题(2)和倍、差倍问题姓名:本讲讲述“倍数问题”中的“和倍问题”(即“已知两数的和以及这两数之间的倍数关系,求这两个数”)、“倍差问题”(既“已知两数的差以及这两数之间的倍数关系,求这两个数”)。
“和倍问题”的解答要点是:和÷(倍数+ 1 )= 小数小数×倍数= 大数“倍差问题”的解答要点是:差÷(倍数− 1 )= 小数小数×倍数= 大数例1、甲、乙两人做机器零件,甲比乙多做400个,且甲做的零件个数是乙的3倍,问甲、乙两人各做多少个零件?例2、哥哥比弟弟多种了2 6 棵树,哥哥中的树是弟弟的3倍。
问兄弟两人各种多少树?例3、某班的学生参加活动小组,已知参加语文小组的同学比参加数学小组的多2 6 人,且语文小组的人数比数学小组的人数的3 倍少1 4 人,问参加两类兴趣小组的同学各多少人?例4、甲比乙多存1 4 0 元。
如果乙取出6 0元,甲存入6 0元,则甲的存款是乙的三倍。
问甲、乙两人原有存款各多少元?例5、小丽有铅笔与圆珠笔若干枝,铅笔的4倍与圆珠笔的2倍相等,且圆珠笔比铅笔多十枝。
问小丽有多少枝铅笔、多少枝圆珠笔?例6、甲、乙两人分别带1 5 0 元、7 0 元去买东西。
两人买了同样的东西之后,剩下的钱数甲是乙的5倍。
问甲、乙两人身上各剩多少钱?每人身上各剩多少钱?例7、小华在读一本童话选,第二天比第一天多读了3 0 页。
第三天比第二天多读了45页。
第三天是第一天读的页数的2倍。
问三天各读了多少页?倍数问题练习题☆☆×51、小明的爸爸办了一个养鸡厂。
今年比去年多养了4000只小鸡,且今年的小鸡数比去年的3倍少2000只。
问今年、去年各养了多少只小鸡?2、水果店有苹果120千克,梨子90千克。
卖出同样多之后,苹果的重量恰好是梨子的4倍。
问两种水果各剩下多少千克?各卖出多少千克?3、大桶装水是小桶的3倍。
如果从大桶倒出85千克,从小桶倒出5千克,那么剩下的水是一样多的。
小学五年级数学上册逻辑思维第十六讲倍数问题(二)

⼩学五年级数学上册逻辑思维第⼗六讲倍数问题(⼆)⼩学五年级数学上册逻辑思维第⼗六讲倍数问题(⼆)【⼀】明明买了数学练习本和英语练习本共13本,其中数学练习本的本数⽐英语练习本的2倍多4本。
求明明买的数学练习本和英语练习本各是⼏本?练习1、姐姐和妹妹共存了540元,其中姐姐存的钱⽐妹妹的2倍还多30元,求姐妹各存了多少钱?2、已知被减数、减数与差的和为64,其中减数⽐差的2倍还多5,求减数。
【⼆】有两堆煤,第⼀堆是167千克,第⼆堆153千克,现因需要,要使第⼀堆煤的重量是第⼆堆的3倍,问:需从第⼆堆取多少千克放⼊第⼀堆?练习1、甲⽔池有⽔3830⽴⽅⽶,⼄⽔池有⽔850⽴⽅⽶。
如果甲⽔池⾥的⽔以每分钟32⽴⽅⽶的速度流⼊⼄⽔池,那么多少分钟后甲⽔池中的⽔是⼄⽔池的3倍?2、甲瓶⾥有酒精470毫升,⼄瓶⾥有酒精190毫升。
为了使甲瓶的酒精是⼄瓶酒精的2倍,应该把甲瓶的酒精倒⼊⼄瓶多少毫升?【三】养⽜场的母⽜的头数是公⽜的5倍,后来公⽜和母⽜各增加60头,结果母⽜的头数就是公⽜多的3倍。
原来养⽜场⼀共养了多少头⽜?练习1、今年,妈妈的年龄是⼩强的6倍,再过4年,妈妈的年龄就是⼩强的4倍。
今年⼩强多少岁?2、原来⾷堂⾥存的⼤⽶是⾯粉的3倍,⼤⽶和⾯粉各吃掉100千克,⼤⽶的重量是⾯粉的5倍。
⾷堂⾥原来存有⼤⽶、⾯粉各多少千克?【四】有1900千克的货物,分装在A、B、C三辆车上。
已知A车装的千克数正好是B车的2倍,B车⽐C车多装300千克。
A、B、C三辆车各装货物多少千克?练习1、三堆货物共2400箱,甲堆的箱数是⼄堆的2倍,⼄堆的箱数⽐丙堆少400箱,三堆货物各多少箱?2、A、B、C三数的和是180,如果A是B的2倍,C是A的3倍,求A、B、C三数各是多少?【五】甲、⼄两个书架,已知甲书架有书600本,从甲书架借出三分之⼀,从⼄书架借出四分之三后,甲书架的书是⼄书架的2倍还多150本。
⼄书架原来有书多少本?练习1、⽵苑⼩学有男⽣660⼈,选出男⽣⼈数的三分之⼀和⼥⽣⼈数的四分之三去排练团体操,剩下的男⽣⼈数是⼥⽣⼈数的2倍。
五年级数学思维拓展倍数与约数2

【五年级数学思维拓展】趣味入门—勇闯智慧岛(一)——约数与倍数(2)了解约数与倍数1、认识什么是约数,什么是倍数2、会利用公式和技巧解题1. 求下列各组数的最小公倍数?(a)32,24 (b)12,15,182. 动物园的饲养员给三群猴子分花生,如只分给第一群,则每只猴子可得12粒;如只分给第二群,则每只猴子可得15粒;如只分给第三群,则每只猴子可得20粒.那么平均给三群猴子,每只可得粒。
(即是该课程的课后测试)1. 简答题:什么是倍数?2. 简答题:什么是最小公倍数?3. 简答题:求解最小公倍数的方法有哪些?4. 用2、3、4、5、6、7这六个数码组成两个三位数A和B,那么A、B、540这三个数的最大公约数最大可能是___________。
5. 两个自然数的和是50,它们的最大公约数是5,试求这两个数的差?1. 答案:一个自然数a能被自然数b整除,我们就叫a是b的倍数。
2. 答案:在所有公倍数中最小的一个公倍数3. 答案:分解质因数法;短除求解法4. 答案:23540235=⨯⨯,A、B、540这三个数的最大公约数是540的约数,而540的约数从大到小排列依次为:540、270、180、135、108、90……由于A和B都不能被10整除,所以540、270、180都不是A和B的约数。
由于A和B不能同时被5整除,所以135也不是A和B的公约数。
540的约数除去这些数后最大的为108,考虑108的三位数倍数,有108、216、324、432、540、648、756、864、972,其中由2、3、4、5、6、7这六个数码组成的有324、432和756,易知当A和B一个为756、另一个为324或432时,A、B、540这三个数的最大公约数为108,所以A、B、540这三个数的最大公约数最大可能是108。
5. 答案:设这两个自然数为:5a、5b,其中a与b互质,5a+5b=50,a+b=10,经检验,容易得到两组符合条件的数:9与1或者7与3。
小学数学五年级上册第一单元思维训练 知识点
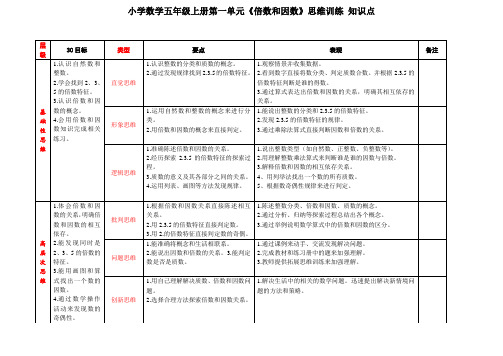
3.通过算式表达出倍数和因数的关系,明确其相互依存的关系。
形象思维
1.运用自然数和整数的概念来进行分类。
2.用倍数和因数的概念来直接判定。
1.能说出整数的分类和2.3.5的倍数特征。
2.发现2.3.5的倍数特征的规律。
4、用列举法找出一个数的所有质数。
5、根据数奇偶性规律来进行判定。
高层次思维
1.体会倍数和因数的关系,明确倍数和因数的相互依存。
2.能发现同时是2、3、5的倍数的特征。
3.能用画图和算式找出一个数的因数。
4.通过数学操作活动来发现数的奇偶性。
批判思维
1.根据倍数和因数关系直接陈述相互关系。
2.用2.3.5的倍数特征直接判定数。
3.用2.的倍数特征直接判定数的奇偶。
1.陈述整数分类、倍数和因数、质数的概念。
2.通过分析、归纳等探索过程总结出各个概念。
3.通过举例说明数学算式中的倍数和因数的区分。
问题思维
1.能准确将概念和生活相联系。
2.能说出因数和倍数的关系。3.能判定数是否是质数。
1.通过课例来动手、交流发现解决问题。
2.完成教材和练习册中的题来加强理解。
3.教师提供拓展思维训练来加强理解。
创新思维
1.用自己理解解决质数、倍数和因数问题。
2.选择合理方法探索倍数和因数关系。
1.解决生活中的相关的数学问题。迅速提出解决新情境问题的方法和策略。
3.通过乘除法算式直接判断因数和倍数的关系。
逻辑思维
1.准确陈述倍数和因数的关系。
2.经历探索2.3.5的倍数特征的探索过程。
3.质数的意义及其各部分之间的关系。
(精品word)小学数学思维训练四年级第八讲-倍数问题(二)

倍数问题(2)和倍、差倍问题姓名:本讲讲述“倍数问题”中的“和倍问题”(即“已知两数的和以及这两数之间的倍数关系,求这两个数”)、“倍差问题”(既“已知两数的差以及这两数之间的倍数关系,求这两个数”)。
“和倍问题”的解答要点是:和÷(倍数+ 1 )= 小数小数×倍数= 大数“倍差问题”的解答要点是:差÷(倍数− 1 )= 小数小数×倍数= 大数例1、甲、乙两人做机器零件,甲比乙多做400个,且甲做的零件个数是乙的3倍,问甲、乙两人各做多少个零件?例2、哥哥比弟弟多种了2 6 棵树,哥哥中的树是弟弟的3倍。
问兄弟两人各种多少树?例3、某班的学生参加活动小组,已知参加语文小组的同学比参加数学小组的多2 6 人,且语文小组的人数比数学小组的人数的3 倍少1 4 人,问参加两类兴趣小组的同学各多少人?例4、甲比乙多存1 4 0 元。
如果乙取出6 0元,甲存入6 0元,则甲的存款是乙的三倍。
问甲、乙两人原有存款各多少元?例5、小丽有铅笔与圆珠笔若干枝,铅笔的4倍与圆珠笔的2倍相等,且圆珠笔比铅笔多十枝。
问小丽有多少枝铅笔、多少枝圆珠笔?例6、甲、乙两人分别带1 5 0 元、7 0 元去买东西。
两人买了同样的东西之后,剩下的钱数甲是乙的5倍。
问甲、乙两人身上各剩多少钱?每人身上各剩多少钱?例7、小华在读一本童话选,第二天比第一天多读了3 0 页。
第三天比第二天多读了45页。
第三天是第一天读的页数的2倍。
问三天各读了多少页?倍数问题练习题☆☆×51、小明的爸爸办了一个养鸡厂。
今年比去年多养了4000只小鸡,且今年的小鸡数比去年的3倍少2000只。
问今年、去年各养了多少只小鸡?2、水果店有苹果120千克,梨子90千克。
卖出同样多之后,苹果的重量恰好是梨子的4倍。
问两种水果各剩下多少千克?各卖出多少千克?3、大桶装水是小桶的3倍。
如果从大桶倒出85千克,从小桶倒出5千克,那么剩下的水是一样多的。
