三年级数学 奥数讲座 数列规律
【奥数】三年级下册数学奥数课件-第3讲《数列找规律问题》 全国通用

练习4: 计算: (1)3+7+11+15+…+43+47 (2)3+6+9+…+30+33
答案:(1)300;(2)198
例题5:在下面12个方框中各填入一个数,使这12个数从左到右构成等差数列,其中 10 、16已经填好,这12个数的和是多少?
16
10
答案:180
PART 03
巩固提升
作业1:等差数列:5 ,9 ,13 ,17 ,… , 第 21 项是_______. 答案:85
三年级下第3讲 数列找规律问题
目录
1.知识梳理 2.例题讲解 3.巩固提升
PART 01
知识梳理
要点诠释: 定义:等差数列是指从第二项起,每一项与它前一项的差等于同一个常数的数列,这 个常数叫做等差数列的公差. 五大要素:首项、公差、项数、末项、和. 注:首项和公差确定,等差数列的每一项就固定了. 基本问题 1. 第几项是谁?首项+(项数-1)×公差 2. 谁是第几项?(该数-首项)÷公差+1 3. 公差是多少?数差÷项数差 4. 求和? 求和公式:(首项+末项)×项数÷2 ①配对求和(高斯求和) ②倒序相加
作业2:等差数列,2 ,8 ,14 ,20,… ,其中 80 是这个数列的第______项. 答案:14
作业3:等差数列计算, 2+4+6+…+58+60 =________. 答案:930
作业4:等差数列计算,6+10+14+…+50+54 答案:390
谢谢大家!
练习3: 计算: (1)3+6+9+12+15+18+21+24+27 (2)5+9+13+17+21+25+29+33
小学三年级数列中的规律与特点

小学三年级数列中的规律与特点数列是数学中的重要概念之一,也是数学与现实生活联系的桥梁。
在小学三年级数学学习中,数列是一个重要的内容。
了解数列的规律与特点,可以帮助学生发展逻辑思维和数学推理能力。
本文将探讨小学三年级数列中的规律与特点,帮助学生更好地理解和应用数列。
一、数列的定义数列是按照一定顺序排列的一系列数的集合。
数列中的每一个数称为数列的项。
通常用字母a、b、c等来表示数列的项,用n表示项的序号。
二、等差数列等差数列是指数列中的每一项与它的前一项之差都相等的数列。
例如:2,4,6,8,10就是一个等差数列,其中,公差为2。
1. 规律等差数列的规律是每一项都比前一项增加(或减少)相同的数值。
在小学三年级中,常见的等差数列有2,4,6,8,10和10,8,6,4,2等。
2. 特点等差数列的特点有:(1)数列中任意两项之间的差值始终相等。
(2)数列中每一项与第一项之间的差值等于它们的序号之差乘以公差。
三、等比数列等比数列是指数列中的每一项与它的前一项之比都相等的数列。
例如:1,2,4,8,16就是一个等比数列,其中,公比为2。
1. 规律等比数列的规律是每一项都与它的前一项成等比关系。
在小学三年级中,常见的等比数列有1,2,4,8,16和16,8,4,2,1等。
2. 特点等比数列的特点有:(1)数列中任意两项之间的比值始终相等。
(2)数列中每一项与第一项之间的比值等于公比的n-1次方(n为项的序号)。
四、斐波那契数列斐波那契数列是指数列中的每一项都是前两项之和的数列。
例如:1,1,2,3,5就是一个斐波那契数列。
1. 规律斐波那契数列的规律是每一项都等于它的前两项之和。
在小学三年级中,常见的斐波那契数列有1,1,2,3,5和3,5,8,13,21等。
2. 特点斐波那契数列的特点有:(1)数列中的每一项都是前两项之和。
(2)数列中的每一项与它的前一项之比逐渐接近黄金比例1.618。
总结:了解小学三年级数列中的规律与特点,可以帮助学生提高数学综合运算能力和逻辑思维能力。
最新小学三年级奥数【第一讲:找规律】课件PPT

准备题 观察下面各列数有什么规律?
第
一 讲
(1)1,3,5,7,9,11......
找
+2 +2 +2 +2 +2
规
律 (2)1,2,3,4,1,2,3,4,1,2,3,4.......
数列
项 1,3,5,7,9,11......
第一项 第二项 第三项
整理概念
总结概念
第
一
讲
1.数列:按一定次序排列的一列数称为数列。
第
(1) 6, 7, 8, 13, 15, 21, ( ), 36
一
讲
(2) 2, 3, 6, 11, 20 , ( )
找
规
律
(3) 11, 13, 15, 17, 19, ( ), ( )
(4) 6, 12, 18, ( ), 30, ( )
谢谢
2020年12月3日星期四
1
2 单击此处添加文本 3 单击此处添加文本 4 单击此处添加文本 5 单击此处添加文本
❖
血栓通注射液
❖ 有活血化瘀、扩张血管和改善血液循环的作用。
❖ 对脑血管的扩张作用。本品可抑制血管收缩,使 脑血流量灌注恢复正常状态。使患者脑血流平均 增加30%以上。
❖ 注意事项:100ml/h
❖
依达拉奉—必存
❖ 依达拉奉是一种脑保护剂.脑梗塞急性期患者给 予依达拉奉,可抑制梗塞周围局部脑血流量的减 少,可阻止脑水肿和脑梗塞的进展,并缓解所伴 随的神经症状,抑制迟发性神经元死亡。
银杏叶针G--金钠多 (舒血宁)
❖ 主要用于脑部,周边血流循环障碍:1.急慢性脑 机能不全,注意力不集中,记忆力衰退,老年痴 呆及脑血管硬化症状,中风后遗症。2.耳部的血 流及神经障碍,如耳鸣、眩晕和突聋。3.眼部之 血流及神经障碍,如糖尿病视网膜病变和老年黄 斑部退化。4.末稍循环障碍,如周边动脉阻塞症, 间歇破行症和手、脚的冰冷麻痹。
2020年秋季三年级奥数-第9讲找规律求和(一)(学生版)

QZ (3)第九讲 找规律求和(一)数列:按照一定次序排列的一列数叫数列。
数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项、第2 项、第3项 ..... 第〃项 ..... ;我们通常把第1项叫做首项,最后一项叫做末 项。
数列的一般形式可以写成:%、/、% ........... 勺 ........ 其中〃〃是数列的第〃项;这个数列可以简记作{凡}为非0然数)。
等差数列:如果一个数列{«,},从第2项起的每一项““与它的前一项《I 的差等 于同一个数,这个数列就叫做等差数列,这个相同的差叫做等差数列的公差,公 差通常用”表示Q 例如:1、3、5、7、9 ; da等差数列的求和公式:和二(首项+末项)X 项数.2。
字母公式:5“ =(%+”.)x 〃 + 2等差数列的通项公式:项数=(末项-首项):公差+1,字母公式:〃 = (% -卬)+ " + 11、在括号里填上合适的数。
(1) 4、6、8、10、()、(2) 28、 ( ) 、 20、 16、 12、(3) 1、3、5、7、 ( )、11、 下面的数列中,哪些是等差数列?若是,请指明公差,若不是,则说明理由。
6/0,14,18, 22, 1,23,2,3,4,5,6; 1,2,4,8,16,32,64; ④ 9,8,7,6,5,4,32; ⑤ 3,333,3,3,3,3; © 1,0,1,0,10,1,0 2、 ① ② ③8:13o3、计算:(1) 2 + 4 + 6 + 8+10+12+14(2) 5 +10 +15 + 20 + 25 + 30 + 35 + 404、等差数列:5、7、9、11、13、...... 95 o(1)项数(〃)是儿?(2)计算这个等差数列的和(篦)。
5、等差数列:1、3、5、7、9、……一共有50项,求末项是多少?拓展提高e e6、电影院的第一排有座位35个,后一排比前一排多6个座位,最后一排有83个座位,那么这个电影院共有多少个座位?7、学校礼堂共有10排座位,已知第一排是15个座位,以后每排比前一排多2个座位,那么共有多少个座位?8、下图三个图形(实线)分别是用4根、10根和16根一样长的小棍围成的。
奥数精选数列的奇妙规律

奥数精选数列的奇妙规律在数学中,数列是一系列按照特定规律排列的数字。
数列的奇妙规律一直是数学界探索与解决的难题之一。
尤其是在奥数训练中,数列问题常常出现,并需要学生通过逐步观察与总结找出其中的规律。
本文将介绍几个常见的奥数精选数列,让我们一起来探索它们的奇妙规律。
1. 等差数列等差数列是最常见的数列之一,其规律是每相邻两项之间的差值相等。
例如,1、3、5、7、9就是一个等差数列,差值为2。
在奥数中,我们常常需要根据等差数列的前几项来确定其通项公式。
一般来说,等差数列的通项公式可以表示为an = a1 + (n-1)d,其中an表示第n项,a1表示首项,d表示公差。
2. 等比数列等比数列是指数列中的每一项与其前一项的比值都相等的数列。
例如,1、2、4、8、16就是一个等比数列,比值为2。
在奥数中,我们经常需要根据等比数列的前几项来确定其通项公式。
一般来说,等比数列的通项公式可以表示为an = a1 * r^(n-1),其中an表示第n项,a1表示首项,r表示公比。
3. 斐波那契数列斐波那契数列是指数列中的每一项都是前两项之和的数列。
例如,1、1、2、3、5、8就是一个斐波那契数列。
在奥数中,斐波那契数列通常用来解决一些有趣的问题,如兔子繁殖问题、黄金分割问题等。
4. 平方数列平方数列是指数列中的每一项都是一个平方数的数列。
例如,1、4、9、16、25就是一个平方数列。
在奥数中,平方数列常常用于观察数字之间的规律,解决一些与平方数相关的问题。
5. 阶乘数列阶乘数列是指数列中的每一项都是一个数的阶乘的数列。
例如,1、1、2、6、24就是一个阶乘数列。
在奥数中,阶乘数列通常用于解决一些与排列组合相关的问题,如求解全排列、组合数等。
通过以上几个奥数精选数列的介绍,我们可以看到数列中蕴含着丰富的规律和趣味。
在奥数训练中,学生们需要通过观察、总结与推理,找出数列的奇妙规律,并运用这些规律解决问题。
通过数列问题的训练,学生们可以培养逻辑思维、分析问题的能力,以及创造性解决问题的能力。
小学三年级奥数-01找规律

单双项分组找 规律
连续型分组找规 律
1.2.2.3.3.4.(). ()……
().()……
(6)后项 由前项推导 而出:
一.().()…… 二.17.27.().()……
94. 46.22.10.().()……
三.().()…… 四.41.().()……
与项数有关
().()…… 20.().()…… 13.().()……
单击此处添加正文,文字是您思想的提炼,请尽量言简意赅地阐述观点。
02
2.8.32.128.().()…..
单击此处添加正文,文字是您思想的提炼,请尽量言简意赅地阐述观点。
1.5.25.125.().()……
03
等比数列:后项除以前项为定值的叫做等比数列。
一二.1.10.1.8.1.().()…… 一三.2.12.2.9.2.().()…… 一四.4.18.5.15.6.().()…… 一五.3.15.4.12.5.().()…… ().().10.5.12.6.14.7…… 1.15.3.13.5.11.().()……
第一讲 找规律
目录
01
数字型找规律:
02
一. 二. 三.
1,2,3,4,6…… 1,2,4,8,16…… 1,0,0,1,0 ,0, 1,0,0 ……
1、数列:
按照一定次序排列起 来的一列数,叫做数 列。
2、项:
一个数列中从左至右的第n个数,称为这个数列的第n项。数 列中的每一个数都叫做这个数列的项。第一个数叫做第1项, 第二个数叫做第2项,……第n个数就叫做第n项。
图形型找规 律:
方法:
观察图形的变化,主要从各图形的形 状、方向、数量、大小及各组成部分 的相对位置入手,从中找出变化规律。 找到每部分的相关规律是关键。
三年级奥数讲义-第一讲 找规律填数(附答案)培训讲学

三年级奥数-第一讲找规律填数【学法指导】寻找一列数的变化规律,再根据这样的规律填上适当的数,这样的问题我们叫作“找规律”。
在一般情况下,我们可以从以下几个方面来找规律:1. 从相邻两数的和、差、积、商考虑,或将和、差、积、商依次写下来成新的一列数,通过对这列数的变化规律的分析,找出规律,推断出所要填的数。
2.有时要将一列数分成两列数,分别考虑它们的变化规律。
3.对于那些分布在某些图形中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关。
这是我们解决这类问题的入手点【经典例题1】找出下面各数的排列规律,并根据规律在括号里填出适当的数。
(1)2,5,8,11,14,( ),().(2) 1,2,4,7,11,16,( ).(3) 4,12 ,36 ,108,( ) ,972.(4) 1,2,6,24,120,( ),5040.思路点拨(1)比较相邻两个数的差。
发现后一个数总比前一个数大3。
(2)比较相邻两个数的差。
发现前6个数每相邻两个数的差依次是1,2,3,4,5,由此可以推算第7个数比第6个数16大6。
(3)比较相邻两个数的商,发现后一个数总是前一个数的3倍。
(4)比较相邻两个数的商,发现前5个数每相邻两个的商依次是2,3,4,5,由此可以推算第6个数是第5个数120的6倍。
完全解题(1)2,5,8,11,14,( 17 ),( 20 ).(2) 1,2,4,7,11,16,( 22 ).(3) 4,12 ,36 ,108, ( 324 ) ,972.(4) 1,2,6,24,120,( 720 ),5040.【能力冲浪1】1.找规律填数。
(1)1,4,7,10,()(2)55,49,43,(),31,(),19.2. 找规律填数。
(1)3,4,6,9,13,18,(),(),39.(2)1,4,9,16,(),36,()。
3. 先找规律,再填数。
(1)1,3,9,27,(),().(2)1,2,6,24,(),720。
三年级奥数讲义-第一讲 找规律填数(附答案)

三年级奥数-第一讲找规律填数【学法指导】寻找一列数的变化规律,再根据这样的规律填上适当的数,这样的问题我们叫作“找规律”。
在一般情况下,我们可以从以下几个方面来找规律:1. 从相邻两数的和、差、积、商考虑,或将和、差、积、商依次写下来成新的一列数,通过对这列数的变化规律的分析,找出规律,推断出所要填的数。
2.有时要将一列数分成两列数,分别考虑它们的变化规律。
3.对于那些分布在某些图形中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关。
这是我们解决这类问题的入手点【经典例题1】找出下面各数的排列规律,并根据规律在括号里填出适当的数。
(1)2,5,8,11,14,( ),().(2) 1,2,4,7,11,16,( ).(3) 4,12 ,36 ,108,( ) ,972.(4) 1,2,6,24,120,( ),5040.思路点拨(1)比较相邻两个数的差。
发现后一个数总比前一个数大3。
(2)比较相邻两个数的差。
发现前6个数每相邻两个数的差依次是1,2,3,4,5,由此可以推算第7个数比第6个数16大6。
(3)比较相邻两个数的商,发现后一个数总是前一个数的3倍。
(4)比较相邻两个数的商,发现前5个数每相邻两个的商依次是2,3,4,5,由此可以推算第6个数是第5个数120的6倍。
完全解题(1)2,5,8,11,14,( 17 ),( 20 ).(2) 1,2,4,7,11,16,( 22 ).(3) 4,12 ,36 ,108, ( 324 ) ,972.(4) 1,2,6,24,120,( 720 ),5040.【能力冲浪1】1.找规律填数。
(1)1,4,7,10,()(2)55,49,43,(),31,(),19.2. 找规律填数。
(1)3,4,6,9,13,18,(),(),39.(2)1,4,9,16,(),36,()。
3. 先找规律,再填数。
(1)1,3,9,27,(),().(2)1,2,6,24,(),720。
小学三年级奥数找简单数列的规律【五篇】

小学三年级奥数找简单数列的规律【五篇】解答:奇数项构成数列1,3,5,7,…,每一项比前一项多2;偶数项构成数列4,8,12,…,每一项比前一项多4,所以应填:16”【第二篇:斐波那契数列】斐波那契数列为1,1,2,3,5,8,13,那么数列的第100项与前98项之和的差是多少?解答:因为第100项等于第99项与第98项之和,所以第100项与前98项之和的差等于第99项与前97项之和的差.同理第99项与前97项之和的差等于第98项与前96项之和的差,……依次类推,可得第100项与前100项之和的差等于第3项与前1项的差,即为第2项,所以第100项与前98项之和的差是【第三篇:填完数列】按照数列的变化规律在括号里填上合适的数:3,1,6,2,12,3,24,4,(),()。
【答案解析】第1个数、第3个数、第5个数、第7个数……依次为:3,6,12,24,…又组成一个新的数列,后一个数是前一个数的2倍。
所以,第9个数应填48;同样,第2个数、第4个数、第6个数、第8个数……依次为:1,2,3,4,…,也组成一个新的数列,后一个数比前一个数大1。
所以,第10个数应填5【第四篇:周期数列】小明在地上写了一列数:7,0,2,5,3,7,0,2,5,3…你知道他写的第81个数是多少吗?你能求出这81个数相加的和是多少吗?【答案解析】⑴从排列上能够看出这组数按7,0,2,5,3依次重复排列,那么每个周期就有5个数.81个数则是16个周期还多1个,第1个数是7,所以第81个数是7,81÷5=16 (1)⑵每个周期各个数之和是:7+0+2+5+3=17.再用每个周期各数之和乘以周期次数再加上余下的各数,即可得到答案.17×16+7=279,所以,这81个数相加的和是279.【第五篇:等差数列】对于数列4、7、10、13、16、19……,第10项是多少?49是这个数列的第几项?第100项与第50项的差是多少?【答案解析】能够观察出这个数列是公差是3的等差数列.根据刚刚学过的公式:第n项=首项+公差×(n-1),项数=(末项-首项)÷公差+1,第n项-第m项=公差×(n-m);第10项为:4+3×(10-1)=4+27=31,49在数列中的项数为:(49-4)÷3+1=16,第100项与第50项的差:3×(100-50)=150。
三年级奥数找规律(数列规律)
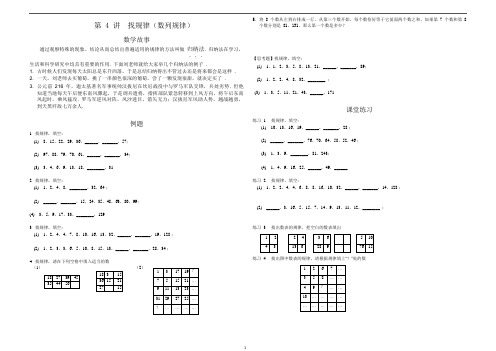
第 4 讲 找规律(数列规律)数学故事通过观察特殊的现象、结论从而总结出普遍适用的规律的方法叫做 归纳法. 归纳法在学习、...生活和科学研究中均具有重要的作用. 下面刘老师就给大家举几个归纳法的例子 . 1. 古时候人们发现每天太阳总是东升西落,于是总结归纳得出不管过去还是将来都会是这样 . 2. 一天,刘老师去买葡萄,挑了一串颜色很深的葡萄,尝了一颗发现很甜,就决定买了 .3. 公元前 216 年,迦太基著名军事统帅汉拔尼在坎尼战役中与罗马军队交锋,兵处劣势. 但他知道当地每天午后便东南风骤起,于是调兵遣将,指挥部队紧急转移到上风方向,将午后东南风起时,乘风猛攻. 罗马军逆风对阵,风沙迷目,箭矢无力;汉拔尼军风助人势,越战越勇,到天黑歼敌七万余人. 例题1. 找规律,填空:(1) 8,15,22,29,36,______,_______,57;(2) 97,88,79,70,61,______,_______,34;(3) 3,4,6,9,13,18,________,31 .2. 找规律,填空:(1) 1,2,4,8,________,32,64 ;(2) ______,_______,15,24,35,48,63,80,99;(4) 3,5,9,17,33,________,129 .3. 找规律,填空:(1) 1,2,4,4,7,8,10,16,13,32,______,_______,19,128 ;(2) 1,2,3,3,6,5,10,8,15,13,______,_______,28,34 ;4. 找规律,请在下列空格中填入适当的数 .(1)(2)1317 19 ?18 31518 27 39 457515 21 …36 152135 44 5627 1591113 23 …31 29 27 25 …? …… … …5. 将 8 个数从左到右排成一行,从第三个数开始,每个数恰好等于它前面两个数之和,如果第 7 个数和第 8个数分别是 81,131,那么第一个数是多少?【思考题】找规律,填空:(1) 1,1,2,3,5,8,13,21,______,_______,89;(2) 1,2,2,4,8,32,________ ;(3) 1,3,5,11,21,43,______,171 .课堂练习练习 1. 找规律,填空:(1) 10,13,16,19,______,_______,28 ;(2) ______,_______,76,70,64,58,52,46 ;(3) 1,3,9,________,81,243;(4) 1,4,9,16,25,______,49,______ .练习 2. 找规律,填空: (1) 1,2,2,4,4,6,8,8,16,10,32,______,_______,14,128 ;(2) ______,3,16,5,15,7,14,9,13,11,12,________ ;练习 3. 找出数表的规律,把空白的数表填出 .1224365104 313 6 28 976 15练习 4. 找出图中数表的规律,请根据规律填上“?”处的数1267 …358… …49 ? … …10 … … … … … … … … …练习5.找规律,填空:(1)______,_______,12,19,31,50,81,131,212 .(2)1,3,3,9,27,______ .(3)2,3,7,13,27,53,______,213 .我学到了什么(一)数学思想、方法小结一、数列找规律:首先、应观察数列是依次增大、依次减少还是大小上下波动.其次、再观察变动的大小有什么规律.二、数表找规律:先观察数表中的数从小到大是什么规律,再观察数表是按什么顺序排列的...三、常见的数列:1.等差数列:任何相邻两项中,后一项减去前一项的差都相等.如:1,3,5,7,9,.....2.等比数列:任何相邻两项中,后一项除以前一项的商都相等.如:1,2,4,8,16,.....3.斐波那契数列:从第三项起,每一项是前两项的和.如:1,1,2,3,5,8,13,.......我学到了什么(二)学数学,懂道理亲爱的同学们今天我们学习的从特殊现象发现一般规律的方法叫“不完全归纳法”.由不完全......归纳法的出的结论,有时候是正确的,有时候是错误的.英国著名的哲学家罗素曾用一个关于“归纳主义者火鸡”的故事来说明这一点.有一只火鸡发现,第一天上午9点钟的时候,主人给它喂食.但作为一个卓越的归纳主义者,这个火鸡并没有马上作出结论.它一直在观察在不同的情况下,比如,晴天、下雨天;星期一到星期日……主人都准时在上午9点钟来给它喂食.等到它收集到了足够多的材料时,它才最终得出了一个一般性的结论:“主人每天上午9点钟来给我喂食.”但是,在圣诞节的上午9点钟,主人没有来给它喂食,而是来把它做成了美味佳肴.今后,在高中你们会学习“数学归纳法”,由它推导出的结论则是千古不变、放诸四海皆准的.....真理.课后练习得分__________________ 1. 找规律,填空:(1)4,8,12,16,20,_________,28,______;(2)________,66,56,47,39,32,26,21,______ .2.找规律,填空:(1)2,6,18,54,______,486 ;(2)1,2,6,24,_______,720;(3)100,81,______,49,36,25,16,_____,4,1 ;(4)2,6,12,20,30,42,________,72,90,______ .3.找规律,填空:(1)40,2,37,4,34,6,31,8,______,_______,25,12;(2)5,3,7,6,9,12,11,24,_______,________,15,96 .4. 如图 5-10,5 个方格表中的数有一定的规律,请按照规律填出第 4 个方格表中的数 .1 52 73 95 1330 6 63 9 108 12 234 185. 观察数表,填出“?”处的数 .1 4 5 ?…2 3 6 ……9 8 7 ……10 ………………………6. 找规律,填空:(1)3,4,7,11,18,29,_______,________,123 .(2)3,2,5,5,8,10,13,17,21,26,_______,________ .个性化补充练习2.请你参考前面的例题和练习,自己编写数列规律填空题和数表规律填空题各2个,考考你的爸爸妈妈和好朋友?你来批改.(1)(2)。
小学三年级奥数找简单数列的规律

三一文库()/小学三年级〔小学三年级奥数找简单数列的规律〕小学三年级小学三年级奥数找简单数列的规律,供大家学习参考。
日常生活中,我们经常接触到许多按一定顺序排列的数,如:(1)自然数:1,2,3,4,5,6,7,…(2)年份:1990,1991,1992,1993,1994,1995,1996某年级各班的学生人数(按班级顺序一、二、三、四、五班排列)(3)45,45,44,46,45像上面的这些例子,按一定次序排列的一列数就叫做数列.数列中的每一个数都叫做这个数列的项,其中第1个数称为这个数列的第1项,第2个数称为第2项,…,第n个数就称为第n项.如数列(3)中,第1项是45,第2项也是45,第3项是44,第4项是46,第5项45。
根据数列中项的个数分类,我们把项数有限的数列(即第1页共3页有有穷多个项的数列)称为有穷数列,把项数无限的数列(即有无穷多个项的数列)称为无穷数列,上面的几个例子中,(2)(3)是有穷数列,(1)是无穷数列。
研究数列的目的是为了发现其中的内在规律性,以作为解决问题的依据,本讲将从简单数列出发,来找出数列的规律。
例1 观察下面的数列,找出其中的规律,并根据规律,在括号中填上合适的数.①2,5,8,11,(),17,20。
②19,17,15,13,(),9,7。
③1,3,9,27,(),243。
④64,32,16,8,(),2。
⑤1,1,2,3,5,8,(),21,34…⑥1,3,4,7,11,18,(),47…⑦1,3,6,10,(),21,28,36,().⑧1,2,6,24,120,(),5040。
⑨1,1,3,7,13,(),31。
⑩1,3,7,15,31,(),127,255。
(11)1,4,9,16,25,(),49,64。
(12)0,3,8,15,24,(),48,63。
(13)1,2,2,4,3,8,4,16,5,().(14)2,1,4,3,6,9,8,27,10,().23。
小学奥数讲座标准教案-学案-三年级第1讲 找规律

第1讲找规律奥数并不难学,我们课本上的数学好玩,数学广角,其实就是奥数知识,只要我们把基础知识打牢,养成不怕难题,勤于动脑的好习惯。
日积月累,我们就能训练出良好的数学思维,我们的解题能力就会得到较大的提高。
升入重点中学,也就不再是梦想!我们一起开始吧!按照一定次序排列起来的一列数,叫做数列。
如自然数列:1,2,3,4,……双数列:2,4,6,8,……我们研究数列,目的就是为了发现数列中数排列的规律,并依据这个规律来填写空缺的数。
按照一定的顺序排列的一列数,只要从连续的几个数中找到规律,那么就可以知道其余所有的数。
寻找数列的排列规律,除了从相邻两数的和、差考虑,有时还要从积、商考虑。
善于发现数列的规律是填数的关键。
【例题1】在括号内填上合适的数。
(1)3,6,9,12,(),()(2)1,2,4,7,11,(),()(3)2,6,18,54,(),()(1)2,8,32,128,(),()(2)1,5,25,125,(),()(3)12,1,10,1,8,1,(),()【例题2】在括号内填上合适的数。
(1)15,2,12,2,9,2,(),()(2)21,4,18,5,15,6,(),()(1)18,3,15,4,12,5,(),()(2)1,15,3,13,5,11,(),()(3)1,2,5,14,(),()【例题3】先找出规律,再在括号里填上合适的数。
(1)2,5,14,41,( ) (2)252,124,60,28,( ) (3)1,2,5,13,34,( ) (4)1,4,9,16,25,36,( )(1)2,3,5,9,17,( ),( ) (2)2,4,10,28,82,( ),( ) (3)94,46,22,10,( ),( )【例题4】根据前面图形里的数的排列规律,填入适当的数。
(1)(3)(1)(3)(2)9437148428164(2)48927682875 10 9 14 7 12 11 16 9 14 13 9 3 27 12 4 3636 12 3 7 5 981210 1412 16 148 4 16 1683232 16 645 15 12 7 21 18 9 27【例题5】按规律填数。
三年级奥数找规律(数列规律)
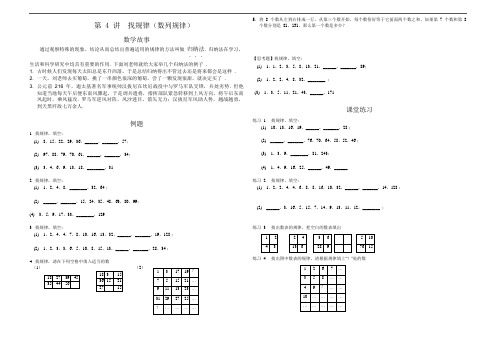
第 4 讲找规律(数列规律)数学故事通过观察特殊的现象、结论从而总结出普遍适用的规律的方法叫做归纳法.归纳法在学习、...生活和科学研究中均具有重要的作用.下面刘老师就给大家举几个归纳法的例子.1. 古时候人们发现每天太阳总是东升西落,于是总结归纳得出不管过去还是将来都会是这样.2. 一天,刘老师去买葡萄,挑了一串颜色很深的葡萄,尝了一颗发现很甜,就决定买了.3. 公元前216年,迦太基著名军事统帅汉拔尼在坎尼战役中与罗马军队交锋,兵处劣势.但他知道当地每天午后便东南风骤起,于是调兵遣将,指挥部队紧急转移到上风方向,将午后东南风起时,乘风猛攻.罗马军逆风对阵,风沙迷目,箭矢无力;汉拔尼军风助人势,越战越勇,到天黑歼敌七万余人.例题1.找规律,填空:(1)8,15,22,29,36,______,_______,57;(2)97,88,79,70,61,______,_______,34;(3)3,4,6,9,13,18,________,31 .2.找规律,填空:(1)1,2,4,8,________,32,64 ;(2)______,_______,15,24,35,48,63,80,99;(4)3,5,9,17,33,________,129 .3.找规律,填空:(1)1,2,4,4,7,8,10,16,13,32,______,_______,19,128 ;(2)1,2,3,3,6,5,10,8,15,13,______,_______,28,34 ;4.找规律,请在下列空格中填入适当的数.(1)(2)1 3 17 1918 3 1518 27 39 457 5 15 21 …36 15 2135 44 5627 15 9 11 13 23 …31 29 27 25 ……………5.将 8 个数从左到右排成一行,从第三个数开始,每个数恰好等于它前面两个数之和,如果第 7 个数和第 8个数分别是 81,131,那么第一个数是多少?【思考题】找规律,填空:(1)1,1,2,3,5,8,13,21,______,_______,89;(2)1,2,2,4,8,32,________ ;(3)1,3,5,11,21,43,______,171 .课堂练习练习 1.找规律,填空:(1)10,13,16,19,______,_______,28 ;(2)______,_______,76,70,64,58,52,46 ;(3)1,3,9,________,81,243;(4)1,4,9,16,25,______,49,______ .练习 2.找规律,填空:(1)1,2,2,4,4,6,8,8,16,10,32,______,_______,14,128 ;(2)______,3,16,5,15,7,14,9,13,11,12,________ ;练习 3.找出数表的规律,把空白的数表填出.1 2 2 4 3 6 5 104 3 13 6 28 9 76 15练习 4.找出图中数表的规律,请根据规律填上“?”处的数1 2 6 7 …3 5 8 ……4 9 ……10 ………………………练习5.找规律,填空:(1)______,_______,12,19,31,50,81,131,212 .(2)1,3,3,9,27,______ .(3)2,3,7,13,27,53,______,213 .我学到了什么(一)数学思想、方法小结一、数列找规律:首先、应观察数列是依次增大、依次减少还是大小上下波动.其次、再观察变动的大小有什么规律.二、数表找规律:先观察数表中的数从小到大是什么规律,再观察数表是按什么顺序排列的...三、常见的数列:1.等差数列:任何相邻两项中,后一项减去前一项的差都相等.如:1,3,5,7,9,.....2.等比数列:任何相邻两项中,后一项除以前一项的商都相等.如:1,2,4,8,16,.....3.斐波那契数列:从第三项起,每一项是前两项的和.如:1,1,2,3,5,8,13,.......我学到了什么(二)学数学,懂道理亲爱的同学们今天我们学习的从特殊现象发现一般规律的方法叫“不完全归纳法”.由不完全......归纳法的出的结论,有时候是正确的,有时候是错误的.英国著名的哲学家罗素曾用一个关于“归纳主义者火鸡”的故事来说明这一点.有一只火鸡发现,第一天上午9点钟的时候,主人给它喂食.但作为一个卓越的归纳主义者,这个火鸡并没有马上作出结论.它一直在观察在不同的情况下,比如,晴天、下雨天;星期一到星期日……主人都准时在上午9点钟来给它喂食.等到它收集到了足够多的材料时,它才最终得出了一个一般性的结论:“主人每天上午9点钟来给我喂食.”但是,在圣诞节的上午9点钟,主人没有来给它喂食,而是来把它做成了美味佳肴.今后,在高中你们会学习“数学归纳法”,由它推导出的结论则是千古不变、放诸四海皆准的.....真理.课后练习得分__________________ 1. 找规律,填空:(1)4,8,12,16,20,_________,28,______;(2)________,66,56,47,39,32,26,21,______ .2.找规律,填空:(1)2,6,18,54,______,486 ;(2)1,2,6,24,_______,720;(3)100,81,______,49,36,25,16,_____,4,1 ;(4)2,6,12,20,30,42,________,72,90,______ .3.找规律,填空:(1)40,2,37,4,34,6,31,8,______,_______,25,12;(2)5,3,7,6,9,12,11,24,_______,________,15,96 .4. 如图 5-10,5 个方格表中的数有一定的规律,请按照规律填出第 4 个方格表中的数 .1 52 73 9 5 1330 6 63 9 108 12 234 185. 观察数表,填出“?”1 4 5 ?…2 3 6 ……9 8 7 ……10 ………………………6. 找规律,填空:(1)3,4,7,11,18,29,_______,________,123 .(2)3,2,5,5,8,10,13,17,21,26,_______,________ .个性化补充练习2.请你参考前面的例题和练习,自己编写数列规律填空题和数表规律填空题各2个,考考你的爸爸妈妈和好朋友?你来批改.(1)(2)。
小学三年级奥数第一讲找规律专业资料

) )
律〔3〕97, 93, 89,〔 〕, 81,〔 〕
〔3〕3,4,6,9,13,18,〔24〕,〔31〕 〔3〕87,83,79,75,〔71〕,〔67 〕
(1) 6, 7, 8, 13, 15, 21, ( ), 36 〔1〕1,3,5,7,9,11.
的项。排在第一位的数称为这个数列的第
1项〔通常也叫做首项〕,排在第二位的
数称为这个数列的第2项……排在第n位的
数称为这个数列的第n项。
趁热打铁练习一下吧~
例1:指出以下数列的规律,并在〔 〕内填上适当的数
第
一观察下面各列数有什么规律?
〔1〕3,6,9,12,〔 〕,〔 〕 讲〔2〕1,7,13,19,〔25〕,〔31〕
第
一 讲
〔1〕1,3,5,7,9,11......
找
+2 +2 +2 +2 +2
规
律 〔2〕1,2,3,4,1,2,3,4,1,2,3,4.......
数列
项 1,3,5,7,9,11......
第一项 第二项 第三项
整理概念
总结概念
第
一
讲
1.数列:按一定次序排列的一列数称为数列。
找
规
律
2.项:数列中的每一个数都叫做这个数列
), ( )
〔(2)3〕21,,13,, ◆2,63我, ,5们1,1,8换,2〔0一, 〕个(,〔角度)〕,分34析一下这个数列◆
(1) 6, 7, 8, 13, 15, 21, ( ), 36
例1:指出以下数列的规律,并在〔 〕内填上适当的数
三年级数学奥数培训课程第1讲至第20讲

第1讲找规律一、知识要点按照一定次序排列起来的一列数,叫做数列。
如自然数列:1,2,3,4,……双数列:2,4,6,8,……我们研究数列,目的就是为了发现数列中数排列的规律,并依据这个规律来填写空缺的数。
按照一定的顺序排列的一列数,只要从连续的几个数中找到规律,那么就可以知道其余所有的数。
寻找数列的排列规律,除了从相邻两数的和、差考虑,有时还要从积、商考虑。
善于发现数列的规律是填数的关键。
二、精讲精练【例题1】在括号内填上合适的数。
(1)3,6,9,12,(),()(2)1,2,4,7,11,(),()(3)2,6,18,54,(),()练习1:在括号内填上合适的数。
(1)2,4,6,8,10,(),()(2)1,2,5,10,17,(),()(3)2,8,32,128,(),()(4)1,5,25,125,(),()(5)12,1,10,1,8,1,(),()【例题2】先找出规律,再在括号里填上合适的数。
(1)15,2,12,2,9,2,(),()(2)21,4,18,5,15,6,(),()练习2:按规律填数。
(1)2,1,4,1,6,1,(),()(2)3,2,9,2,27,2,(),()(3)18,3,15,4,12,5,(),()(4)1,15,3,13,5,11,(),()(5)1,2,5,14,(),()【例题3】先找出规律,再在括号里填上合适的数。
(1)2,5,14,41,()(2)252,124,60,28,()(3)1,2,5,13,34,()(4)1,4,9,16,25,36,()练习3:按规律填数。
(1)2,3,5,9,17,(),()(2)2,4,10,28,82,(),()(3)94,46,22,10,(),()(4)2,3,7,18,47,(),()【例题4】根据前面图形里的数的排列规律,填入适当的数。
(1)(3练习(1) (3)【例题5(1)187(2)练习5:(1)198,297,396,( ),( )(2) (3)(2)9437148428164(2)第2讲有余除法一、知识要点把一些书平均分给几个小朋友,要使每个小朋友分得的本数最多,这些书分到最后会出现什么情况呢一种是全部分完,还有一种是有剩余,并且剩余的本数必须比小朋友的人数少,否则还可以继续分下去。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三年级奥数讲座数列规律
1、下面是两个具有一定的规律的数列,请你按规律补填出空缺的项:
(1)1,5,11,19,29,________,55; (2)1,2,6,16,44,________,328。
解答:(1)观察发现,后项减前项的差为:6、8、10、......所以,应填41(=29+12),41+14=55符合。
(2)观察发现,6=2*(2+1),16=2*(2+6),44=2*(16+6),所以,应填120=2*(44+16),2*(120+44)=328符合。
2、有一列由三个数组成的数组,它们依次是(1,5,10);(2,10,20);(3,15,30);……。
问第99个数组内三个数的和是多少?
解答:观察每一组中对应位置上的数字,每组第一个是1、2、3、......的自然数列,第二个是5、10、15、......,分别是它们各组中第一个数的5倍,第三个10、20、30、......,分别是它们各组中第一个数的10倍;所以,第99组中的数应该是:99、99*5、99*10,三个数的和=99+99*5+99*10=1584。
3、0,1,2,3,6,7,14,15,30,________,________,________。
上面这个数列是小明按照一定的规律写下来的,他第一次先写出0,1,然后第二次写出2,3,第三次接着写6,7,第四次又接着写14,15,依次类推。
那么这列数的最后3项的和应是多少?
解答:观察发现,在0、1后写2、3,2=1*2;在2、3后面写6、7,6=3*2;在6、7后面写14、15,14=7*2;在14、15后面写30,30=15*2;所以,后三项应填31、62(=31*2)、63,和为31+62+63=156。
4、仔细观察下面的数表,找出规律,然后补填出空缺的数字。
解答:观察发现,(1)第二行的数字比第一行对应位的数字都大21,所以应该填58+21=79;(2)第一列的数字是同行中后两列的数之和,所以应该填28-9=19。
5、图5-3中各个数之间存在着某种关系。
请按照这一关系求出数a和b。
解答:图中5个圆、10个数字,其中5个数字是只属于某一个圆本身的,5个数字是每两个圆相重叠的公共区域的,观察发现,两圆重叠部分的公共区域的数字2倍,正好等于两圆独有数字之和,15*2=10+20,30*2=20+40;所以,a=2*17-10=24,b=(16+40)/2=28。
验算:20*2-16=24,符合。
6、将8个数从左到右排成一行,从第三个数开始,每个数恰好等于它前面两个数之和。
如果第7个数和第8个数分别是81,131,那么第一个数是多少?
解答:根据数列规律倒推,第6个数=131-81=50,第5个数=81-50=31,第4个数=50-31=19,第三个数=31-19=12,第2个数=19-12=7,第个数=12-7=5。
7、1,2,3,2,3,4,3,4,5,4,5,6,…。
上面是一串按某种规律排列的自然数,问其中第101个数至第110个数之和是多少?
解答:观察发现,数列的规律为三个一组、三个一组,每一组的第一个数为从1开始的自然数列,每一组中的三个数为连续自然数;101/3=33......2,说明第101个是第33+1=34组中的第二个数,那么应该是34+1=35;从101到110共有110-101+1=10个数,那么这10个数分别是:35、36,35、36、37,36、37、38,37、38;所以,他们的和为35+36+35+36+37+36+37+38+37+38=365。
8、如果把1到999这些自然数按照从小到大的顺序排成一排,这样就组成了一个多位数:12345678910111213…996997998999。
那么在这个多位数里,从左到右的第2000个数字是多少?
解答:一位数1~9共有9个;二位数10~99共有90个,占90*2=180位;一、二位数共占了189位;2000-9-180=1811,这1811个位数都是三位数,1811/3=603......2,说明第2000个数是第604个三位数的第2位,三位数从100开始,第604个应该是603,第二位就是0。
因此,从左到右的第2000个数字是0。
9、标有A,B,C,D,E,F,G记号的7盏灯顺次排成一行,每盏灯各安装着一个开关。
现在A,C,D,G这4盏灯亮着,其余3盏灯是灭的。
小方先拉一下A开关,然后拉B,C,…,直到G 的开关各一次,接下去再按从A到G顺序拉动开关,并依此循环下去。
他这样拉动了1990次后,亮着的灯是哪几盏?
解答:如果一个灯的开关被拉了2下,那么,这个灯原来是什么状态,还应该是什么状态,即原来亮着的还亮着,原来不亮的还是不亮。
现在共有7盏灯,每个拉2次的话就是14次。
也就是说,每拉14下,每个灯都和原来的情况一样。
1990/14=142......2,说明,拉1990次就相当于只拉了2次,那么就应该是A和B各被拉了一下。
A原来亮着,现在变灭;B原来不亮,现在变亮。
所以,拉1990次后亮着的灯应该有:B、C、D、G。
10、在1,2两数之间,第一次写上3;第二次在1,3之间和3,2之间分别写上4,5,得到
1 4 3 5 2。
以后每一次都在已写上的两个相邻数之间,再写上这两个相邻数之和。
这样的过程共重复了8次,那么所有数的和是多少?
解答:原来两数之和:1+2=3;操作一次:1+3+2=6=3+3;操作2次:1+4+3+5+2=15=3+3+9;操作3次:1+5+4+7+3+8+5+7+2=42=3+3+9+27;......规律是,操作n次,和为3+3^1+3^2+3^3+......+3^n,所以,操作8次的和为3+3^1+3^2+3^3+......+3^8=9843。
11、有一列数:1,1989,1988,1,1987,…。
从第三个数起,每一个数都是它前面两个数中大数减小数的差。
那么第1989个数是多少?
解答:为了找到规律,我们把这列数再往下写出一些:1,1989,1988,1,1987,1986,1,1985,1984,1,1983,1982,1,1982,…这样我们可以很容易的看出规律了,即每三个一组,第一个为1,后两个是从1989依次减1排下去;1989/3=663,共有663组,去掉每一组中的1,剩下663*2=1326个,从1989顺序递减,到最后一个应该是1989-1326+1=664。
所以,第1989个数是664。
12、在1,9,8,9后面顺次写出一串数字,使得每个数字都等于它前面两个数之和的个位数字,即得到1,9,8,9,7,6,3,9,2,1,3,4…那么这个数串的前398个数字的和是多少?
解答:同上一题所讲的思路一样,我们需要再往下写一些,以便发现规律:1,9,8,9,7,6,3,9,2,1,3,4,7,1,8,9,…这是我们已经可以发现规律了,即它们会以8,9,7,6,3,9,2,1,3,4,7,1不断循环,也即从第3个数开始,每12个数一个循环。
那么,(398-2)/12=33,即供循环33次;一个循环的数字和为8+9+7+6+3+9+2+1+3+4+7+1=60,前398个数字的和=1+9+33*60=1990。
13、有一列数:2,3,6,8,8,…从第三个数起,每个数都是前两个数乘积的个位数字,那么这一列数中的第80个数是多少?
解答:还是上面的思路,需要再往下写一些,寻找规律:2,3,6,8,8,4,2,8,6,8,8,4,2,8,…不难发现,规律是从第三个数开始,每6个数一个循环,那么,(80-2)/6=13,所以,第80个数是8。
14、1999名学生从前往后排成一列,按下面的规则报数:如果某个同学报的数是一位数,后面的同学就要报出这个数与9的和;如果某个同学报的数是两位数,后面的同学就要报出这个数的个位数与6的和。
现在让第一个同学报1,那么最后一个同学报的数是多少?
解答:按照要求,我们先写出前面的一些数,寻找规律:1,10,6,15,11,7,16,12,8,17,13,9,18,14,10,......规律是:从第2个数开始,每13个数一个循环;(1999-1)/13=153......9,所以,最后一个同学报的数是17。
15、将从1到60的60个自然数排成一行,成为111位自然数,即12345678910111213…5960。
在这111个数字中划去100个数字,余下数字的排列顺序不变,那么剩下的11位数最小可能是多少?
解答:为了使剩下的数尽可能小,那么除留下第一个1外,后面应尽可能多的留下0,1~60共有6个0,并且有一个是在最后,所以,第一个1后面只能留下5个0,也就是说,到50为止,前面除第一个1外只留下0,这时便成10000051525354555657585960;除了第一个1和6个0外,还要留下4个数,不难看出,应该留下51525354中的1234,所以,剩下的11位数最小可能是10000012340。
