重庆大学材料力学教案强度理论
材料力学强度理论

材料力学强度理论
材料力学强度理论是材料力学的一个重要分支,它研究材料在外力作用下的强
度和变形特性。
材料的强度是指材料抵抗破坏的能力,而变形特性则是指材料在外力作用下的形变行为。
强度理论的研究对于材料的设计、制备和应用具有重要意义。
首先,强度理论可以帮助我们了解材料的破坏机制。
材料在外力作用下会发生
破坏,而不同的材料在受力时表现出不同的破坏模式,比如拉伸、压缩、剪切等。
强度理论可以通过实验和理论分析,揭示材料在受力时的破坏机制,为材料的设计和选用提供依据。
其次,强度理论可以指导材料的合理使用。
在工程实践中,我们需要根据材料
的强度特性来选择合适的材料,并确定合理的使用条件。
强度理论可以帮助我们评估材料在特定工况下的承载能力,从而保证材料的安全可靠使用。
此外,强度理论还可以为材料的改进和优化提供指导。
通过对材料强度特性的
研究,我们可以发现材料的强度局限性,并提出改进的方案。
比如,可以通过合金化、热处理等手段来提高材料的强度,或者通过结构设计来减小应力集中,提高材料的抗破坏能力。
综上所述,材料力学强度理论是材料科学中的重要内容,它不仅可以帮助我们
了解材料的破坏机制,指导材料的合理使用,还可以为材料的改进和优化提供指导。
在未来的研究和工程实践中,我们需要进一步深入研究强度理论,不断提高材料的强度和可靠性,为社会发展和科技进步做出贡献。
材料力学第9章强度理论
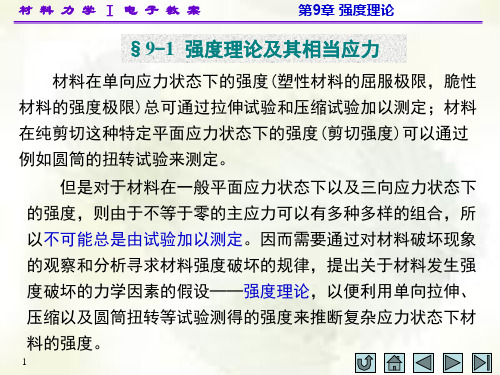
亦即
s 1 s 2 s 3 s u
s 1 s 2 s 3 s
而相应的强度条件为
按照这一理论,似乎材料在二轴拉伸或三轴拉伸应力 状态下反而比单轴拉伸应力状态下不易断裂,而这与实际 情况往往不符,故工程上应用较少。
5
材 料 力 学 Ⅰ 电 子 教 案
(3) 最大切应力理论(第三强度理论) 低碳钢在单轴拉
与翼缘交界处的强度
在Mmax和FS,max同时存在的横截面C稍稍偏左的横截面 上,该工字形截面腹板与翼缘交界点a处,正应力和切应力
分别比较接近前面求得的smax和tmax,且该点处于平面应力
状态,故需利用强度理论对该点进行强度校核。
24
材 料 力 学 Ⅰ 电 子 教 案
应力状态下,当一点处的最大拉应力(s1)达到该材料的 极限应力su时就发生脆性断裂。 第一强度理论关于脆性断裂的判据为:
s1 s u
su
在单轴拉伸试验或其它使材料发生脆性断裂的试验中测定
强度条件则是
s 1 s
其中,[s]为对应于脆性断裂的许用拉应力,[s]=su/n,
而n为安全因数。由单轴拉伸试验可得, su sb
低碳钢一类的塑性材料,纯剪切和单轴拉伸应力状态 下均发生塑性的屈服,故可用单轴拉伸许用应力[s]按第三 或第四强度理论推算许用切应力[t]。按第三强度理论,纯 剪切应力状态下的强度条件为
t--t s
可见
15
亦即
t
s
2
s t 0.5s
2
材 料 力 学 Ⅰ 电 子 教 案
1 1 s 1 s 2 2 s 2 s 3 2 s 3 s 1 2 2s s2 6E 6E
材料力学-强度理论

1 (11 1)
实践证明,该理论适合脆性材料在单向、二向或三向受 拉的情况。此理论不足之处是没有考虑其它二个主应力对材 料破坏的影响。
危险截面发生在C、D截面 MC=32KN·m QC=100KN
(二)强度校核 先绘出C截面正应力分布图和剪应力分布图。
C截面
a.正应力强度校核(K1)点
max
k1
MC WZ
32 103 237 106
135Mpa 150Mpa
b.剪应力强度校核(K2)点
C截面
max
QC
S
* Z
力横截面中性轴处的弯曲剪应力。式中的许用正应力 和许 用剪应力 是由轴向拉(压)试验和纯剪切试验所测得的极
限应力除以安全系数而得。这两类强度条件是能够直接通过试 验来建立。
然而,在工程实际中许多构件的危险点是处于复杂应力 状态下,其应力组合的方式有各种可能性。如采用拉(压) 时用的试验方法来建立强度条件,就得对材料在各种应力状 态下一一进行试验,以确定相应的极限应力,这显然是难以 实现的。
1 3 (11 3)
这一理论能较好的解释塑性材料出现的塑性流动现象。 在工程中被广泛使用。但此理论忽略了中间生应力 2的影响, 且对三向均匀受拉时,塑性材料也会发生脆性断裂破坏的事 实无法解释。
2.第四强度理论(形状改变比能理论)
这一理论认为形状改变比能是引起材料塑性流动破坏的 主要因素,即不论材料处于简单还是复杂应力状态。只要构 件危险点处的形状改变比能,达到材料在单向拉伸屈服时的 形状改变比能,就会发生塑性流动破坏。建立的强度条件为:
材料力学 第8章强度理论

同的材料,式(8.8)可演化成式(8.6)。
8.4 各种强度理论的适用范围
8.4.1 强度理论的选用原则 1. 强度理论的选用原则 (1) 脆性材料:当最小主应力大于等于 0 时,使用第一理论;当最小主应力小于 0 而
·176·
第 8 章 强度理论
·177·
最大主应力大于 0 时,使用莫尔理论。当最大主应力小于等于 0 时,使用第三或第四强度 理论。
强度条件:
相当应力表达式:
σ1
−
[σ [σ
+ −
] ]
σ
3
≤
[σ
]
(8.8)
σ rm
= σ1
−
[σ [σ
+ −
] ]
σ
3
≤ [σ
]
(8.9)
分析:莫尔强度理论考虑了材料抗拉和抗压能力不等的情况,这符合脆性材料(如岩石
混凝土等)的破坏特点,但未考虑中间主应力σ 2 的影响是其不足之处。对于 [σ + ] 和 [σ − ] 相
综合分析材料破坏的现象,认为构件由于强度不足将引发两种失效形式: (1) 脆性断裂:材料无明显的塑性变形即发生断裂,断面较粗糙,且多发生在垂直于 最大正应力的截面上,如铸铁受拉、扭,低温脆断等。关于断裂的强度理论为:最大拉应 力理论和最大伸长线应变理论。 (2) 塑性屈服(流动):材料破坏前发生显著的塑性变形,破坏断面粒子较光滑,且多发 生在最大切应力面上,例如低碳钢拉、扭,铸铁压。关于屈服的强度理论为最大切应力理 论和形状改变比能理论。 为此,对强度破坏提出了各种不同的假说。各种假说尽管各有差异,但它们都认为: 材料之所以按某种方式破坏(屈服或断裂),是由于应力、应变和应变能等诸因素中的某一 因素引起的。按照这类假说,无论单向应力状态还是复杂应力状态,造成破坏原因是相同 的,即引起破坏的因素是相同的。强度理论就是关于材料破坏现象主要原因的假设。即认 为不论是简单应力状态还是复杂应力状态,材料某一类型的破坏是由于某一种因素引起 的。据此,可以利用简单应力状态的实验结果,来建立复杂应力状态的强度条件。我们称 其为强度理论(strength theories)。
材料力学强度理论

2
2
2
u f 6E
σ1 σ 2 σ 2 σ3 σ3 σ1
将 σ1 σ s , σ 2 σ3 0 代入上式,可得材料的极限值
u fu
1 ν
6E
2
2 s
强度条件为:
1
2
2
2
2 1 2 2 3 3 1
2
2
2
2
2
设 ,则
2 2
1 2 3
由第四强度理论的计算应力 状态 (a )
r4 2 3 2
状态 (b ) r4 2 3 2
两种情况下的危险程度相等。
基本观点
构件受外力作用而发生破坏时,不论破坏的 表面现象如何复杂,其破坏形式总不外乎几种类型, 而同一类型的破坏则可能是某一个共同因素所引起的。
材料破坏的两种类型(常温、静载荷)
1. 脆断破坏: 无明显的变形下突然断裂。 2. 屈服失效: 材料出现显著的塑性变形而丧
失其正常的工作能力。
引起破坏的某一共同因素
1 3
70 2
30
2 50 MPa
70
2
30 2
402
94.72
50 20 5
MPa
5.28
r 3 89.44MPa , r 4 77.5MPa
例题 2 两种应力状态分别如图所示,试按第四强度理论, 比较两者的危险程度。
(a)
120MPa
(2)对于图 b 所示的单元体,
《材料力学》第十章 强度理论

第十章 强度理论
Theory of Strength
§10-1 强度理论的概念
The Conception of Theory of Strength
材料力学所研究的最基本问题之一——构件的强度问题。
由§1-1我们知道:构件的强度是指构件承受荷载的能力或构件抵抗
破坏的能力。在前面各章中,我们得到:
圆簇的包络线(Envelope of the family of limiting stress circles)。
简化的莫尔包络线由简单拉伸极限 应力圆和简单压缩极限应力圆的公切线, 以及简单拉伸极限应力圆的切点间轴正 向侧部分曲线构成。
§10-3 莫尔强度理论及其相当应力
Mohr’s strength theory and its equivalent stresses
P
s
P A
4 50 103
0.12 106
6.37MPa
AA s t
t
T Wn
16 7 106
0.13 109
35.65MPa
s s
1 3
6.37 2
(6.37)2 35.652 38.98 MPa
2
32.61
s1 39.0MPa,s 2 0,s 3 32.6MPa
(2)最大伸长线应变理论(The maximum tension strain theory)
认为:最大伸长线应变是使材料发生断裂破坏的主要因素
破坏条件:
e1=ejx
强度条件: бr2=б1-μ(б2+б3)≤[б]---(10-2)
((10-2)式是由虎克定律得出的,因为:e1=[б1-μ(б2+б3)]/E;单向
重庆大学材料力学教案 强 度 理 论b10

第 十 章 强 度 理 论一、教学目标和教学内容1.教学目标掌握强度理论的概念。
了解材料的两种破坏形式(按破坏现象区分)。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
2.教学内容讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点,并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
二、重点难点重点:强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
难点:常用四个强度理论的理解。
危险点的确定及其强度计算。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时3学时五、讲课提纲1、概述1.1材料在单向应力状态或纯剪切应力状态时的强度条件:轴向拉(压)杆件的最大正应力发生在横截面上各点处;而横力弯曲梁的最大正应力发生在最大弯矩横截面的上、下边缘处,如图10.1(a )、(b )所示,其应力状态皆为单向应力状态,强度条件为:拉压杆:[]σσ≤=AF N max梁:[]σσ≤=WM max 式中[]s u n /σσ=,u σ为材料破坏时的极限应力,s n 称为安全系数。
对于塑性材料,u σ=s n (屈服极限);对于脆性材料,u σ=b σ(强度极限),皆可由试验确定。
纯扭转圆轴的最大切应力发生在横截面周边各点处;而梁的最大切应力发生在最大剪力横截面的中性轴上,如图10.1(c )、(d )所示,为纯剪切应力状态,强度条件为:扭转轴:[]ττ≤=p x W M max 梁:[]ττ≤=b I S F z z Q *maxmax式中[]s u n /ττ=,s u ττ=或b τ由实验确定。
图10.11.2材料的破坏形式以上列举的强度条件,用于简单应力状态,是直接根据试验结果建立的。
材料力学-第8章 强度理论

2 3 2
材料力学-第8章 强度理论
The end!
材料力学-第8章 强度理论
§9-2 关于断裂的强度理论
根据第二强度理论,无论材料处于什么应力状态, 只要发生脆性断裂,其共同原因都是由于微元的最大 拉应变达到了某个共同的极限值。
2 1 3
max
= b
1 1 v( 2 3 ) E E
max
0 max
材料力学-第8章 强度理论
§9-2 关于断裂的强度理论
第一强度理论(最大拉应力理论) 第二强度理论(最大拉应变理论)
材料力学-第8章 强度理论
§9-2 关于断裂的强度理论
第一强度理论(最大拉应力理论)
第一强度理论又称为最大拉应力理论 (maximum tensile stress criterion),最早由英 国的兰金( Rankine . W . J . M .)提出,他认 为引起材料断裂破坏的原因是由于最大正应力达 到某个共同的极限值。对于拉、压强度不相同的 材料,这一理论现在已被修正为最大拉应力理论。
适用材料及应力状态
缺点
没有考虑 2 , 3 的影响 不适合无拉应力 1 的状态
材料力学-第8章 强度理论
§9-2 关于断裂的强度理论
第二强度理论(最大拉应变理论)
第二强度理论又称为最大拉应变理论(maximum tensile strain criterion),它也是关于无裂纹脆性材 料构件的断裂失效的理论。
1
3
失效判据 强度条件
材料力学-第8章 强度理论
§9-3 关于屈服的强度理论
畸变能理论(第四强度理论)
材料力学第九章强度理论教育研究

章节课堂
19
必须指出,即使是同一材料,在不同的应力状态下 也可以有不同的破坏形式。 无论是塑性材料或脆性材料:
在三向拉应力接近相等的情况下,都以断裂的形 式破坏,所以应采用最大拉应力理论;
在三向压应力接近相等的情况下,都可以引起塑 性变形,所以应该采用第三或第四强度理论。
如何选用强度理论,并不单纯是个力学问题。 在不同的工程技术部门中,对于在不同情况下如何 选用强度理论的问题,在看法上并不完全一致。
(1
2
)2
(
2
3
)2
(
3
1
)2
章节课堂
18
一般说来,在常温和静载的条件下,脆性材料 多发生脆性断裂,故通常采用第一、第二强度理论; 塑性材料多发生塑性屈服,故应采用第三、第四强度 理论。
影响材料的脆性和塑性的因素很多,例如:低 温能提高脆性,高温一般能提高塑性; 在高速动载 荷作用下脆性提高,在低速静载荷作用下保持塑性。
C截面
a.正应力强度校核(K1)点
max
k1
MC WZ
32 103 237 106 135Mpa
章节课堂
150Mpa
36
b.剪应力强度校核(K2)点
C截面
max
k2
FS hb
100 103 (200 22.8) 103 7 103
80.1Mpa
95Mpa
正应力和切应力强度条件均满足。
章节课堂
16
形状改变比能理论
2 1
3
=s
Uu
1
6E
2s2
U f Uu
1
2
( 1 2 )2
( 2
3)2
( 3 1 )2
7.3强度理论-单元教学设计
单元教学设计1.教案计划表2.教学实施【步骤l 】复习巩固和引入新课【步骤2】课程介绍及知识讲授单向应力状态和纯剪切应力状态下的判断,都是通过实验确定极限应力值除以相应的安全系数得到。
在工程实际中许多构件的危险点是处于复杂应力状态下(如二向或三向应力状态),同一材料不同的123σσσ、、之间的比值会对应不同的破坏应力,显然在应力比值无数组合的情况下完成试验是难以实现的。
同时大量的关于材料失效的实验结果以及工程构件失效的实例表明,复杂应力状态虽然各式各样,但是材料在各种复杂应力状态下的强度失效形式却是共同的而且是有限的,归纳起来,强度不足引起的失效现象主要是断裂和屈服两种类型。
长期以来,人们根据对材料的失效现象的分析与研究,提出了各种关于材料破坏规律的假说或学说,称为强度理论。
强度理论的假说或学说的正确性必须经受试验与实践的检验,下面将主要介绍在工程中常用的四个强度理论。
1.关于断裂的强度理论(1)最大拉应力理论(第一强度理论)。
最大拉应力理论认为:引起材料断裂的主要因素是最大拉应力,而且,不论材料处于何种应力状态,只要最大拉应力1σ达到材料单向拉伸断裂时的最大拉应力值b σ(材料的拉伸强度极限),材料即发生断裂。
考虑安全因素后,即得相应的强度条件为1bnσσ≤或 ][1σσ≤ (7-9)式中:1σ为材料危险点处的最大拉应力;][σ为材料单向拉伸时的许用应力。
铸铁等脆性材料在单向拉伸时,断裂发生于拉应力最大的横截面。
脆性材料的扭转也是沿拉应力最大的螺旋斜面断裂。
这些都与最大拉应力理论相符。
但这一理论没有考虑其它两个主应力的影响,也即认为不论三向、二向还是单向应力状态,它们的危险状态的达到并没有什么区别,这显然是不合理的。
此外对没有拉应力的状态(如单向压缩、三向压缩等)也无法应用。
(2)最大拉应变理论(第二强度理论)。
最大拉应变理论认为:引起材料断裂的主要因素是最大拉应变,而且,不论材料处于何种应力状态,只要最大拉应变1ε达到材料单向拉伸断裂时的最大拉应变u 1ε,材料即发生断裂。
材料力学大学教案

教学目标:1. 理解材料力学的基本概念和理论;2. 掌握材料力学的基本计算方法和应用;3. 培养学生的创新思维和实际操作能力;4. 提高学生的团队协作能力和沟通能力。
教学内容:一、绪论1. 材料力学的定义和发展历程;2. 材料力学的研究内容和应用领域;3. 材料力学的基本假设和模型。
二、材料力学基本理论1. 材料的应力-应变关系;2. 材料的强度理论;3. 材料的疲劳与断裂。
三、材料力学基本计算方法1. 材料的弹性力学分析;2. 材料的塑性力学分析;3. 材料的断裂力学分析。
四、材料力学应用实例1. 梁的弯曲变形与强度计算;2. 圆轴的扭转变形与强度计算;3. 材料的疲劳与断裂分析。
教学过程:一、导入1. 通过实际工程案例,让学生了解材料力学在实际工程中的应用;2. 引导学生思考材料力学的基本问题,激发学习兴趣。
二、基本理论讲解1. 讲解材料力学的定义、研究内容和应用领域;2. 讲解材料力学的基本假设和模型;3. 讲解材料的应力-应变关系、强度理论和疲劳与断裂。
三、基本计算方法讲解1. 讲解弹性力学分析、塑性力学分析和断裂力学分析的基本方法;2. 通过例题讲解,让学生掌握计算方法和步骤。
四、应用实例讲解1. 讲解梁的弯曲变形与强度计算、圆轴的扭转变形与强度计算、材料的疲劳与断裂分析;2. 通过实例分析,让学生了解材料力学在实际工程中的应用。
五、课堂练习与讨论1. 学生进行课堂练习,巩固所学知识;2. 学生分组讨论,提出问题并解答,提高团队协作能力和沟通能力。
教学评价:1. 课堂表现:观察学生在课堂上的学习态度、积极参与程度;2. 作业完成情况:检查学生作业的完成质量,了解学生的学习效果;3. 期末考试:通过考试检验学生对材料力学的掌握程度。
教学反思:1. 教师要关注学生的学习需求,及时调整教学内容和方法;2. 注重培养学生的创新思维和实际操作能力,提高学生的综合素质;3. 加强与学生的沟通,关注学生的心理需求,营造良好的学习氛围。
重庆大学材料力学教案实验i

绪 论目前,材料力学课程中开设了两类实验课程,即:材料力学性能实验及实验应力分析实验。
一、材料的力学性能实验对工程问题进行强度计算时,需要构件材料的力学性能指标,如屈服点s σ、抗拉强度b σ、疲劳强度1-σ,此外,弹性极限p σ、杨氏弹性模量E 、切变模量G 等也是设计构件的基本参数,这些量都通过材料力学性能实验来测定。
材料的力学性能,如强度极限b σ、持久极限1-σ、冲击韧度k α等,虽是材料的固有属性,但又往往随一些因素的改变而波动,如:试样的形状、尺寸、加工精度、表面粗糙度,对试样的加载速度,实验环境(实验时的温度,周围的介质情况)等。
为了使不同材料的实验结果有比较的价值,我国指定了材料力学性能实验的国家标准,国家标准对试样的取材、形状、尺寸、加工精度、试验机的安装、实验的手段和方法、数据处理等都作了规定。
我国国家标准的代号是GB ,如GB10623-89为金属力学性能实验术语、GB3102-93为量和单位、GB228-87为金属拉伸实验方法、GB6397-86为金属拉伸实验试样……GB8170-87为数值修约规则。
国际上也有相应的标准,国际标准的代号是ISO ,国际间需要做仲裁实验时,必须采用国际标准。
我国现行的国家标准与国际标准已基本接轨。
二、实验应力分析解决实验问题,特别对于形状复杂或受力复杂的构件,采用解析方法时,常常遇到数学和计算方面的困难,没有适用的理论可计算应力。
此时,常常采用实验应力分析方法或数值计算方法(如有限单元法)。
今年来,虽然有限元方法等数值方法有很大发展,但数值方法必须以正确建立数学模型为前提,否则,不能提出正确的结果。
而且,对数值计算的方法所得的结果,任需用实验方法来验证。
因此,实验应力分析方法与数值方法起到了互相不补充、互相验证的作用。
再者,对某些载荷和边界条件未知的问题,用数值方法求解时,还需采用实验方法提供必要的参数。
采用实验方法时,对边界条件没有完全确定的情况,可以从实物中获得数据。
材料力学第七章强度理论

σ
σ1 σ3
屈服准则: max jx
材料力学第七章强度理论
复杂应力状态下的最大切应力 max (1 3) / 2
单向应力状态下
jx
s
2
屈服条件
1 3 s
相应的强度条件:
1
3
s
ns
材料力学第七章强度理论
低碳钢拉伸
低碳钢扭转
材料力学第七章强度理论
适用范围: 塑性屈服
此理论较满意地解释了塑性材料的屈服现象; 并能解释材料在三向均压下不发生塑性变形或断裂的事实。 偏于安全 常用于载荷往往较不稳定的机械、动力等行业
a
C:σ≤|σ|:τ≤|τ|;
D:(σ2+4τ2)1/2≤|σ|;;
b
材料力学第七章强度理论
10、厚玻璃杯注入沸水而破裂,裂纹起始 于: 。
A:内壁; B:外壁; C:壁厚中间; D:内壁、外壁同时破裂;
式,都是由于同一种因素引起。
2
rd f (1, 2, 3)
1 3
复杂应力状态
rd
相当应力状态
[]
已有简单拉 压试验资料
强度理论
材料力学第七章强度理论
强度条件
选用原则 一、对于常温、静载、常见的单向、二向应力状态下 通常的塑性材料,如低碳钢, 弹性失效状态为塑性屈服 通常的脆性材料,如铸铁, 弹性失效状态为脆断;
材料力学第七章强度理论
二、对于常温、静载但具有某些特殊应力状态的情况 不能只看材料 必须考虑应力状态对材料弹性失效的影响
综合材料、失效状态选取适当的强度理论。 ① 塑性材料(如低碳钢)在三向拉伸应力状态下
呈脆断失效; 应选用第一强度理论; 但此时的失效应力应通过能造成材料脆断的试验获得。
重庆大学 材料力学 张晓敏 课件 07应力和应变分析强度理论

代表两个相互垂直的最大(小 切应力方位 切应力方位。 代表两个相互垂直的最大 小)切应力方位。 最大(小 切应力 切应力: ② 最大 小)切应力:
τ max =± τ min
σ x −σ y 2 + τ xy 2
同一点的应力状态可以有各种各样的描述方式: 同一点的应力状态可以有各种各样的描述方式: S平面 F 1
n
α
F
σβ τβ
1
α τα
σα
β = α + 90 o
12
目录
§7-1 应力状态概述
示例二: 示例二:
FP
S平面 平面
l/2
l/2
5 4 3 2 1
5 S平面 平面 4 3 2
目录
1
13
§7-1 应力状态概述
第七章
应力和应变分析 强度理论
1
目录
应力状态概述 二向和三向应力状态的实例 二向和三向应力状态的实例 二向应力状态分析二向应力状态分析-解析法 二向应力状态分析二向应力状态分析-图解法 三向应力状态 *位移与应变分量 *平面应变状态分析 广义胡克定律 复杂应力状态下的应变能密度 强度理论概述 四种常用强度理论 莫尔强度理论 构件含裂纹时的断裂准则
31
目录
二向应力状态分析§7-3 二向应力状态分析-解析法
(2)主应力、主平面 主应力、 σ x +σ y σx −σ y 2 2 σ max = + ( ) +τ xy 2 2
σy
τ xy
α
= 68 .3MPa
σ x σ = σ x + σ y − (σx −σ y )2 +τ 2 min xy 2 2
重庆大学材料力学教案第一章绪论

第一章绪论一、教学目标和教学内容1.教学目标明确材料力学的任务,理解变形体的的基本假设,掌握杆件变形的基本形式。
2.教学内容○1材料力学的特点○2材料力学的任务○3材料力学的研究对象○4变形体的基本假设○5材料力学的基本变形形式二、重点难点构件的强度、刚度、稳定性的概念;杆件变形的基本形式、变形体的基本假设。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时1.5学时五、讲课提纲1、材料力学的任务材料力学是研究构件强度、刚度和稳定性计算的学科。
工程中各种机械和结构都是由许多构件和零件组成的。
为了保证机械和结构能安全正常地工作,必须要求全部构件和零件在外力作用时具有一定的承载能力,承载能力表现为1.1强度强度是指构件抵抗破坏的能力。
构件在外力作用下不被破坏,表明构件具有足够的强度。
1.2刚度刚度是指构件抵抗变形的能力。
构件在外力作用下发生的变形不超过某一规定值,表明构件具有足够的刚度。
1.3稳定性稳定性是指构件承受在外力作用下,保持原有平衡状态的能力,构件在外力作用下,能保持原有的平衡形态,表明构件具有足够的稳定性。
材料力学的任务:以最经济为代价,保证构件具有足够的承载能力。
通过研究构件的强度、刚度、稳定性,为构件选择合适的材料、确定合理的截面形状和尺寸提供计算理论。
2、材料力学的研究对象2.1研究对象的几何特征构件有各种几何形状,材料力学的主要研究对象是杆件,其几何特征是横向尺寸远小于纵向尺寸,如机器中的轴、连接件中的销钉、房屋中的柱、梁等均可视为杆件,材料力学主要研究等直杆。
2.2研究对象的材料特征构件都是由一些固体材料制成,如钢、铁、木材、混凝土等,它们在外力作用下会产生变形,称变形固体。
其性质是十分复杂的,为了研究的方便,抓住主要性质,忽略次要性质材料力学中对变形固体作如下假设:♦均匀连续性假设: 假设变形固体内连续不断地充满着均匀的物质,且体内各点处的力学性质相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 十 章 强 度 理 论
一、教学目标和教学内容
1.教学目标
掌握强度理论的概念。
了解材料的两种破坏形式(按破坏现象区分)。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
2.教学内容
讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点,并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
二、重点难点
重点:强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
难点:
常用四个强度理论的理解。
危险点的确定及其强度计算。
三、教学方式
采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时
3学时
五、讲课提纲
1、概述
1.1材料在单向应力状态或纯剪切应力状态时的强度条件:
轴向拉(压)杆件的最大正应力发生在横截面上各点处;而横力弯曲梁的最大正应力发生在最大弯矩横截面的上、下边缘处,如图10.1(a )、(b )所示,其应力状态皆为单向应力状态,强度条件为:
拉压杆:[]σσ≤=A
F N max
梁:[]σσ≤=W
M max 式中[]s u n /σσ=,u σ为材料破坏时的极限应力,s n 称为安全系数。
对于塑性材料,
u σ=s n (屈服极限)
;对于脆性材料,u σ=b σ(强度极限),皆可由试验确定。
纯扭转圆轴的最大切应力发生在横截面周边各点处;而梁的最大切应力发生在最大剪力横截面的中性轴上,如图10.1(c )、(d )所示,为纯剪切应力状态,强度条件为:
扭转轴:[]ττ≤=
p x W M max 梁:[]ττ≤=b I S F z z Q *max
max
式中[]s u n /ττ=,s u ττ=或b τ由实验确定。
图10.1
1.2材料的破坏形式
以上列举的强度条件,用于简单应力状态,是直接根据试验结果建立的。
然而工程实际中许多构件的危险点都处于复杂应力状态,其破坏现象较复杂,但材料的破坏形式可分为如下二类:
脆性断裂:材料失效时未发生明显的塑性变形而突然断裂。
如:铸铁在单向拉伸和纯剪切应力状态下的破坏。
塑性屈服:材料失效时产生明显的塑性变形并伴有屈服现象。
如低碳钢在单向拉伸和纯剪切应力状态下的破坏。
注意:材料的破坏形式并不是以材料为塑性材料或脆性材料为准来区分的。
如:大理石为脆性材料,在单向压缩时发生的破坏为脆性断裂,图10.2(a );若表面受均匀经向压力,施加轴向力后出现明显的塑性变形,成为腰鼓形,显然其破坏形式为塑性屈服,图10.2(b)。
图10.2
1.3强度理论的概念
在复杂应力状态下,一点的3个主应力1σ、2σ、3σ可能都不为零,而且会出现不同的主应力组合。
此时如果采用直接试验的方法来建立强度条件,是非常困难的,原因在于:进行复杂应力状态试验的设备和加工比较复杂;不同的应力组合需要重新做试验;不同的材料需重新试验。
人们经过长期的生产实践和科学研究,总结材料破坏的规律,提出了各种不同的假说:认为材料之所以按某种形式破坏,是由于某一特定因素(应力、应变、形状改变比能)引起的;对于同一种材料,无论处于何种应力状态,当导致它们破坏的这一共同因素达到某一极限时,材料就会发生破坏。
这样的一些假说称为强度理论。
2、常用的强度理论
由于材料存在着脆性断裂和塑性屈服两种破坏形式,因而,强度理论也分为两类:一类是解释材料脆性断裂破坏的强度理论,其中有最大拉应力理论和最大伸长线应变理论;另一类是解释材料塑性屈服破坏的强度理论,其中有最大切应力理论和形状改变比能理论。
2.1第一强度理论——最大拉应力理论
该理论认为材料断裂的主要因素是该点的最大主拉应力。
即在复杂应力状态下,只要材料内一点的最大主拉应力)0(11>σσ达到单向拉伸断裂时横截面上的极限应力u σ,材料发生断裂破坏。
破坏条件为:
u σσ≥1 )0(1>σ
强度条件为:
][1σσ≤ )0(1>σ
(10-1)
式中 []σ——单向拉伸时材料的许用应力:[]s b n /σσ=。
试验表明,该理论主要适用于脆性材料在二向或三向受拉(例如铸铁、玻璃、石膏等)。
对于存在有压应力的脆性材料,只要最大压应力值不超过最大拉应力值,也是正确的。
2.2第二强度理论—最大伸长线应变理论
该理论认为材料断裂的主要因素是该点的最大伸长线应变。
即在复杂应力状态下,只要材料内一点的最大拉应变1ε达到了单向拉伸断裂时最大伸长应变的极限值u ε时,材料就发生断裂破坏。
由广义胡克定律可知
[])(13211σσυσε+-=E
单向拉伸断裂时
E b
u σε=
于是破坏条件为
()E
E b σσσυσ≥+-][1321 即: ()b σσσυσ≥+-321
所以,强度条件为
()[]σσσυσ≤+-321
(10.2)
此理论考虑了三个主应力的影响,形式上比第一强度理论完善,但用于工程上其可靠性很差,现在很少采用。
2.3第三强度理论—最大切应力理论
该理论认为材料屈服的主要因素是最大切应力。
在复杂应力状态下,只要材料内一点处的最大切应力max τ达到单向拉伸屈服时切应力的屈服极限s τ,材料就在该处发生塑性屈服。
由11章可知:复杂应力状态下最大切应力为
23
1max σστ-=
单向拉伸时
2s
s στ=
破坏条件为
s σσσ≥-31
于是强度条件为
][31σσσ≤-
(10.3)
该理论对于单向拉伸和单向压缩的抗力大体相当的材料(如低碳钢)是适合的。
2.4第四强度理论—最大形状改变比能理论
该理论认为材料屈服的主要因素是该点的形状改变比能。
在复杂应力状态下,材料内一点的形状改变比能d υ达到材料单向拉伸屈服时形状改变比能的极
限值u υ,材料就会发生塑性屈服。
由11章可知
])()()[(61213232221σσσσσσυυ-+-+-+=E
d 单向拉伸时: s σσ=1,032==σσ可得
231s u E
συυ+= 破坏条件为
221323222131])()()[(61s E
E συσσσσσσυ+≥-+-+-+ 即
s σσσσσσσ≥-+-+-])()()[(2
1213232221 于是强度条件为
[]σσσσσσσ≤-+-+-])()()[(21213232221
(10.4)
试验表明,对于塑性材料,此理论比第三强度理论更符合试验结果。
综合以上四个强度理论的强度条件,可以把它们写成如下的统一形式:
[]σσ≤r
其中r σ称为相当应力。
四个强度理论的相当应力分别为
11σσ=r
()3212σσυσσ+-=r
313σσσ-=r
])()()[(2
12132322214σσσσσσσ-+-+-=r 对于梁来讲,
2234τσσ+=r
2243τσσ+=r
注意:
1、对以上四个强度理论的应用,一般说脆性材料如铸铁、混凝土等用第一和第二强度理论;对塑性材料如低碳钢用第三和第四强度理论。
2、脆性材料或塑性材料,在三向拉应力状态下,应该用第一强度理论;在三向压应力状态下,应该用第三强度理论或第四强度理论。
3、第三强度理论概念直观,计算简捷,计算结果偏于保守;第四强度理论着眼于形状改变比能,但其本质仍然是一种切应力理论。
4、在不同情况下,如何选用强度理论,不单纯是个力学问题,而与有关工程技术部门长期积累的经验及根据这些经验制订的一整套计算方法和许用应力值[]σ有关。
*2.5莫尔强度理论
该理论认为,材料发生屈服或剪切破坏,不仅与该截面上的切应力有关,而且还与该截面上的正应力有关,只有当材料的某一截面上的切应力与正应力达到最不利组合时,才会发生屈服或剪断。
莫尔理论认为材料是否破坏取决于三向应力圆中的最大应力圆。
图10.3
在工程应用中,分别作拉伸和压缩极限状态的应力圆,这两个应力圆的直径
分别等于脆性材料在拉伸和压缩时的强度极限+b σ和-b σ。
这两个圆的公切线MN
即是该材料的包络线,如图10.3。
若一点的3个主应力1σ、2σ、3σ已知,以1σ和3σ作出的应力圆与包络线相切,则此点就会发生破坏。
由此可导出莫尔强度理论的强度条件为:
[][]
[]+
-+
≤-σσσσσ31
(10.5)
式中,[]+σ和[]-σ是脆性材料的许用拉应力和许用压应力。
对[][]-+=σσ的材料,莫尔强度条件化为:
[]σσσ≤-31
此即为最大切应力理论的强度条件。
可见莫尔强度理论是最大切应力理论的发展,它把材料在单向拉伸和单向压缩时强度不等的因素也考虑进去了。
