《长方体的体积》练习题-(1)

合集下载

小学五年级下册长方体体积计算题258题

小学五年级下册长方体体积计算题258题题目1:某长方体的长是5cm，宽是3cm，高是4cm，请计算其体积。

解答：根据长方体体积的计算公式：体积 = 长 ×宽 ×高，将给定的长、宽和高代入公式，即可计算出体积。

体积 = 5cm × 3cm × 4cm= 60立方厘米因此，该长方体的体积为60立方厘米。

题目2:一个长方体的体积是120立方米，长和高的比是2:3，求该长方体的长、宽和高。

解答：设长为2x，宽为y，高为3x。

根据长方体体积的计算公式，代入给定的体积，可以得到：120 = 2x × y × 3x化简方程可得：2x^3y = 120通过观察可以得知，120的因数有2、2、2和3，因此可以将120分解为2^3 × 3 × 5。

2x^3y = 2^3 × 3 × 5由此可得：x^3y = 2 × 5x^3y = 10为了满足题目要求的长和高的比是2:3，我们可以令x = 2，y = 5。

所以该长方体的长为2 × 2 = 4米，宽为5米，高为3 × 2 = 6米。

因此，该长方体的长、宽和高分别为4米、5米和6米。

题目3:一个长方体的体积是75立方厘米，长和宽的比是4:3，高与宽的比是2:1，求该长方体的长、宽和高。

解答：设长为4x cm，宽为3x cm，高为y cm。

根据长方体体积的计算公式，代入给定的体积，可以得到：75 = 4x × 3x × y化简方程可得：12x^2y = 75通过观察可以得知，75的因数有3和5，因此可以将75分解为3 × 5^2。

12x^2y = 3 × 5^2由此可得：4x^2y = 5^2为了满足题目要求的长和宽的比是4:3，我们可以令x = 1，y = 5。

所以该长方体的长为4 × 1 = 4厘米，宽为3 × 1 = 3厘米，高为5厘米。

长方体和正方体的体积(1)练习题及答案

第7课时长方体和正方体的体积(1)不夯实基础，难建成高楼。

1. 计算下列各形体的体积。

(单位：厘米)(1)(2)(3)2. 一个长方体的长、宽、高分别是18.5厘米、12厘米、10厘米，它的体积是多少立方厘米？3. 一个正方体，棱长是2.5分米，这个正方体的体积是多少立方分米？4. 一个铁皮油箱，从里面量它的长是12分米，宽是5分米，高是3分米，求它的容积。

重点难点，一网打尽。

5. 填一填。

(1)一个长方体框架长8厘米，宽6厘米，高4厘米，做这个框架一共有( )厘米，是求长方体框架的( )，在表面贴上塑料板，共要( )塑料板是求长方体框架的( )，在里面能盛( )升水是求长方体框架的( )，这个长方体框架有( )立方米是求( )。

(2)长方体的长是6厘米，宽是4厘米，高是2厘米，它的棱长总和是( )厘米，六个面中最大的面积是( )平方厘米，表面积是( )平方厘米，体积是( )立方厘米。

6. 下面的图形都是用体积为1cm3的正方体拼成的，它们的体积各是多少？7. 一个正方体，棱长总和是36厘米，它的体积是多少立方厘米？8. 建筑工地要挖一个长45米，宽30米，深50厘米的土坑，一共要挖出多少立方米的土？9. 一个长方体的长是6分米，宽是55厘米，高是24厘米，它的表面积和体积各是多少？10. 钢铁厂生产一种方钢，长2.8米，宽和厚都是5厘米，每立方米方钢重7.8千克，这根方钢重多少千克？举一反三，应用创新，方能一显身手！11. ”六一”儿童节前，全市的小学生代表用棱长为3厘米的正方体塑料拼插积木在广场中央搭起了一面长6米，高2.7米，厚6厘米的世博幸运墙，算一算，这块墙一共用了多少块积木？第7课时1. (1)1512立方厘米(2)1728立方厘米(3)792立方厘米2. 18.5×12×10＝2220(立方厘米)3. 2.5×2.5×2.5＝15.625(立方分米)4. 12×5×3＝180(立方分米)5. (1)72 棱长总和208平方厘米表面积0.192 容积0．000192 体积(2)48 24 88 486. 36立方厘米 64立方厘米7. 36÷12＝3(厘米) 3×3×3＝27(立方厘米)8. 50厘米＝0.5米45×30×0.5＝675(立方米)9. 表面积：12120平方厘米体积：79200立方厘米10. 0.0546千克11. 6米＝600厘米 2.7米＝270厘米600×270×6÷(3×3×3)＝36000(块)。

正方体和长方体的体积练习题目

正方体和长方体的体积练习题目正方体和长方体的体积练习题目篇一：长方体和正方体的体积练习题填空：（1）表面积和体积的意义不同，表面积是物体的（）大小，体积是物体所占的（）大小。

（2）、表面积和体积所用的计量单位不同，计量表面积常用的单位有（）（）（）相邻的两个面积单位间的进率是（）。

计量物体体积常用的单位有（）（）（）；相邻的体积单位间的进率是（）。

（3）、表面积和体积的计算方法不同。

计算正方体的体积公式是（）或（）。

计算长方体的表面公式是（）；计算长方体的体积公式是（）或（）。

（4）、一个正方体，棱长是8分米，这个正方体的棱长之和是；表面积是（）；体积（）。

（5）、一个长方体，长2米，宽5分米，高0.4分米。

这个长方体的表面积是（）；体积是（）。

（6）、一根长方体材料，宽3分米，厚2厘米，体积是0.12立方米。

这根木材的长是，放在地上占地面积最大是（）。

1．填空。

(2)用字母表示长方体的体积公式是( )。

(3)棱长2分米的正方体，一个面的面积是( )，表面积是( )，体积是( )。

(4)一个长方体长是0.4米、宽0.2米、高0.2米，它的表面积是( )，体积是( )。

(5)5立方米=( )立方分米2.8立方分米=( )立方厘米720立方分米=( )立方米32立方厘米=( )立方分米2.7立方米=( )升 1200毫升=( )立方厘米4.25立方米=( )立方分米=( )升 1.2立方米=( )升=( )毫升1、长方体有（）个面，（）条棱，（）个顶点。

2、物体所占（）的大小，叫做物体的体积。

3、一个正方体的表面积是54平方米，它的每个面的面积是（）平方米，它的棱长是（）米。

5、把棱长3cm的正方体切成棱长1cm的小正方体,可以切成( )块。

6、填上合适的单位名称。

一个文具盒的体积大小约有140（）；货车的油箱的容积是50（）数学书的封面的面积大约是300（）；一个热水瓶的容积约是2（）7、3.08 m2=（）dm2 870cm3=( )dm36.47L=( )ml=( ) dm3 489ml=( )cm3=( ) dm38、一个正方体的棱长扩大到它的4倍，面积扩大到它的（）倍，体积扩大到它的（）倍。

小学数学浙教版五年级下册第四单元长方体体积单位的换算-章节测试习题(1)

章节测试题1.【答题】一个表面积是24平方分米的正方体，它的体积是（）立方分米.A.9B.16C.14D.8【答案】D【分析】根据正方体的特征，它的6个面是完全相同的正方形，正方体的表面积，已知表面积是24平方分米，先求出1个面的面积，进而求出棱长，再根据正方体的体积，列式解答.【解答】解：24÷6=4（平方分米）；因为4是2的平方，所以正方体的棱长是2分米；2×2×2=8（立方分米）.答：它的体积是8立方分米.选D.2.【答题】如图所示，抽奖箱的长、宽、高依次为5分米、4分米、9分米，则它的体积是（）立方米.A.180B.18C.0.18【答案】C【分析】根据长方体的体积公式：，把数据代入公式解答.【解答】解：5×4×9=180（立方分米）180立方分米=0.18立方米；选C.3.【答题】小强身高1m，在儿童乐园中有一个正方体大型玩具屋，试估计该大型玩具屋的体积是（）.A.8B.16C.27D.64【答案】A【分析】根据题意，小强身高1米，约占正方体棱长的，根据已知一个数的几分之几是多少，求这个数，用除法求出正方体的棱长，再根据正方体的体积公式，列式解答.【解答】解：正方体的棱长：1÷=1×2=2（米）；正方体的体积：2×2×2=8（立方米）；答：大型玩具屋的体积是8立方米.选A.4.【答题】用长25厘米，宽20厘米，高16厘米的包装盒不能装下一个长20厘米，宽18厘米，高15厘米的玻璃盒.（）【答案】×【分析】把长方体包装箱的长、宽、高与玻璃盒的长、宽、高进行比较即可.据此判断.【解答】解：用玻璃盒的长与包装箱的长相比20厘米＜25厘米，用玻璃盒的宽与包装箱的高相比18厘米＜20厘米，用玻璃盒的高与包装箱的宽相比15厘米＜16厘米，由此可知能装下.故答案为：×.5.【答题】棱长4cm的正方体，它的表面积和体积相等.（）【答案】×【分析】根据正方体的表面积的意义、体积的意义，正方体的表面积是指它的6个面的总面积；正方体的体积是指正方体所占空间的大小；表面积与体积不是同类量，根本不能进行比较.据此判断即可.【解答】正方体的表面积是指它的6个面的总面积，表面积是：4×4×6=96（平方厘米）；正方体的体积是指正方体所占空间的大小，体积是：4×4×4=64（立方厘米）.表面积与体积不是同类量，根本不能进行比较.故本题是错误的.6.【答题】长方体的长扩大到原来的5倍，宽缩小到原来的，高不变，则体积不变.（）【答案】√【分析】根据长方体的体积公式：，再根据因数与积不变的性质，一个因数扩大到原来的5倍，另一个因数缩小到原来的，积不变.据此判断.【解答】解：由分析得：一个因数扩大5倍，另一个因数缩小5倍，积不变.因此，长方体的长扩大到原来的5倍，宽缩小到原来的，高不变，则体积不变.这种说法是正确的.故答案为：✓.7.【答题】一个长方体和一个正方体的底面积相等，高也相等，它们的体积一定相等.（）【答案】✓【分析】此题是考查体积的计算公式，求长方体、正方体的体积都可用V=sh解答．【解答】底面积和高分别相等的长方体、正方体，它们的体积都是用底面积乘高得来，所以它们的体积也一定相等，原题说法是正确的.8.【答题】正方体的棱长扩大到原来的4倍，体积就扩大到原来的16倍.（）【答案】×【分析】设正方形的棱长是a，则正方体的体积是a×a×a=，棱长扩大4倍后，棱长变为4a，体积是4a×4a×4a=64，64:=64，据此解答即可.【解答】假设正方形的棱长是a，则正方体的体积是：a×a×a=，棱长扩大到原来的4倍后，棱长变为4a，体积是4a×4a×4a=64，64:=64.所以“正方体的棱长扩大到原来的4倍，体积就扩大到原来的16倍”的说法是错误的.故本题是错误的.9.【答题】棱长是1米的正方体，也可以把它看成是棱长是10dm的正方体，它的体积就是______dm³，所以1m³＝______dm³.【答案】1000 1000【分析】此题考查的是体积单位的认识.【解答】正方体的体积是10³dm³＝1000dm³，故它的体积是1000dm³，即1立方米＝1000立方分米.故此题答案为1000、1000.10.【答题】胜利新村木材公司运回了80根长方体的木料，木料的长、宽、高分别是200cm、35cm、5.5cm，这些木料共有______立方米.（答案用小数表示）【答案】3.08【分析】此题考查的是长方体的体积公式.【解答】长方体体积＝长×宽×高.一根木料的体积为200×35×5.5＝38500（立方厘米）＝0.0385（立方米），则80根这样的体积为0.0385×80＝3.08（立方米）.答：这些木料共有3.08立方米.11.【答题】5.24m³＝______dm³.【答案】5240【分析】此题考查的是体积单位间的换算.【解答】体积间单位的换算进率是1000，即5.24×1000＝5240（dm³）.故此题答案为5240.12.【答题】一块长25厘米，宽12厘米的，厚8厘米的砖，所占的空间是______立方分米，占地面积最大是______平方厘米.（答案用小数表示）【答案】2.4 300【分析】物体的体积就是所占空间的大小，利用长方体的体积公式即可求解；最大占地面积就是求这个长方体最大面的面积.【解答】解：25×12×8=2400（立方厘米）；2400立方厘米=2.4立方分米25×12=300（平方厘米）；答：这个砖所占的空间是2400立方厘米，占地面最大是300平方厘米.故答案为：2.4、300.13.【答题】一根长2米的长方体钢材，沿横截面截成两段后，表面积增加了0.8平方米，这段长方体钢材的体积是______立方米.【答案】0.8【分析】根据长方体的面的特征，它的6个面都是长方形（特殊情况有两个相对的面是正方形），相对的面的面积相等；由题意可知，一根长2米的长方体钢材，沿横截面截成两段后，表面积增加了0.8平方米，增加了两个截面的面积，可以求出底面积是：0.8÷2=0.4（平方米），长方体的体积=底面积×高；由此解答.【解答】0.8÷2×2=0.8（立方米），这段长方体钢材的体积是0.8立方米.故答案为：0.8.14.【答题】如图，这座领奖台由四个相同的长方体拼合而成，它的前后两面涂上白色油漆，踏板和侧面铺上蓝色地毯.（单位：厘米）做这个领奖台需要木料的体积是______立方米.需要油漆部分的面积是______平方厘米.（答案用小数表示）【答案】0.096 6400【分析】（1）根据长方体的体积公式：，求出一个长方体的体积再乘4求出4个长方体的体积是多少立方厘米，然后换算成用立方米再单位即可.（2）根据长方体的特征：相对的面面积相等，它的前后两面涂上白色油漆，前后面分别是4个完全相同的长方形，长是40厘米，宽是20厘米，根据长方形的面积公式解答即可.【解答】解：（1）1立方米=1000立方分米=1000000立方厘米，40×30×20×4=24000×4=96000（立方厘米）；96000立方厘米=0.096立方米，答：做这个领奖台需要0.096立方米的木料.（2）40×20×4×2=800×4×2=3200×2=6400（平方厘米）；答：需要油漆部分的面积是6400平方厘米.15.【答题】如图所示，在一个无水的玻璃鱼缸中放入一个高3dm的假山，这个假山的体积是5.6.打开水龙头向鱼缸中注水，那么当水刚好把假山完全淹没时，鱼缸中水的实际体积是______.【答案】54.4【分析】根据题干可知，鱼缸内的水面高为3分米时，就能把这个假石山完全淹没，由此只要求出水面高为3分米时，鱼缸内的水的体积，再减去假山的体积，就是水的实际体积.【解答】解：8×2.5×3－5.6=60－5.6=54.4（立方分米）答：鱼缸中水的实际体积是54.4立方分米.16.【答题】从一个大长方体的一角挖去一个小正方体，那么剩下的物体的体积是______立方厘米.（单位：cm）【答案】88【分析】物体的体积等于大长方体的体积减去小正方体的体积即可.根据长方体的体积公式：，正方体体积公式：，代入数据即可解决问题.【解答】4×4×6－2×2×2=88（立方厘米），所以剩下的物体的体积是88立方厘米.故本题的答案是88.17.【答题】一个长方体，如果高增加3厘米，就成为一个正方体.这时表面积比原来增加了96平方厘米.原来的长方体的体积是______立方厘米.【答案】320【分析】根据题意可知，一个长方体如果高增加3厘米，就变成了一个正方体；说明长和宽相等且比高大3厘米，因此增加的96平方厘米是4个同样的长方形的面积和；由此可以求长方体的底面边长，再根据长方体的体积公式解答.【解答】增加的1个面的面积：96÷4=24（平方厘米）；长方体的长（宽）：24÷3=8（厘米）；长方体的高：8-3=5（厘米）；长方体的体积：8×8×5=320（立方厘米）.故本题的答案是320.18.【答题】如图所示，在一个无水的玻璃鱼缸中放入一个高3dm的假山，这个假山的体积是5.6.打开水龙头向鱼缸中注水，那么当水刚好把假山完全淹没时，鱼缸中水的实际体积是______.（答案用小数表示）【答案】54.4【分析】根据题干可知，鱼缸内的水面高为3分米时，就能把这个假石山完全淹没，由此只要求出水面高为3分米时，鱼缸内的水的体积，再减去假山的体积，就是水的实际体积.【解答】8×2.5×3－5.6=54.4（立方分米），所以鱼缸中水的实际体积是54.4立方分米.故本题的答案是54.4.19.【答题】学校操场的跳远场地是一个长方形沙坑，长6米，宽1.8米.共需要黄沙______吨.（答案用小数表示）【答案】6.48【分析】已知长方形沙坑的长、宽和深，可以求出长方形沙坑的体积来，然后乘每立方米的重量，就可以求出共需多少吨了.【解答】40厘米=0.4米，6×1.8×0.4×1.5=6.48（吨），所以共需要黄沙6.48吨.故本题的答案是6.48.20.【答题】计算下面图形的体积是______.（单位：cm）【答案】960【分析】这是一个长方体，它的长是12厘米，宽是10厘米，高是8厘米，根据长方体的体积=长×宽×高，进行求解即可.【解答】12×10×8=960（立方厘米），所以这个长方体的体积是960立方厘米.故本题的答案是960.。

人教五年级数学下册-第五课长方体和正方体的体积(习题)

《长方体和正方体的体积》练习一．选择题。

1、有一个长方体盒子，长8厘米，宽和高都是5厘米，这个盒子的体积是（）。

A．40平方厘米 B.200立方厘米 C.64立方厘米 D.40立方厘米2、一个长方体盛水容器的底面是一个边长6分米的正方形，高1.2分米，这个长方体容器的体积是（）A．36平方分米 B.43.2立方分米 C.7.2立方分米 D.72平方分米3、有一个小金鱼缸，长4分米、宽3分米，水深2分米，这个鱼缸的占地面积是（）。

A．12平方分米 B.24立方分米 C.8立方分米 D.6立方分米4．一个正方体的底面积是25平方分米，它的体积是（）立方分米，A．25 B．125 C.5 D.625二．填空题。

1．长方体的体积=（），正方体的体积=（）。

2. 一个长方体的体积是128立方厘米，它的长是8厘米，宽4厘米，高是（）厘米。

3.一个正方体的棱长是3分米，它的体积是（）立方分米。

4. 把一个棱长为10分米的正方体铁块，熔成一个长方体，长方体的长是8分米，宽是5分米，高是（）分米。

三．判断题。

1、ａ³＝３ａ（）2、一个正方体的底面积是２４平方厘米，它的占地面积就是２４平方厘米。

（）３、正方体的棱长扩大３倍，体积会扩大９倍。

（）４.棱长是６厘米的正方体，体积和表面积相等。

（）四．解答题。

１、修建一个正方体的蓄水池，棱长是9米，需挖土多少立方米？２、一种长方体木料，长9分米，宽6分米，高2分米。

8根这样的木料体积是多少？３、一个无盖的长方体鱼缸，长8分米，宽6分米，高7分米。

制作这个鱼缸共需玻璃多少平方分米？这个鱼缸的体积是多少？４、把一个棱长8分米的正方体铁块铸成一个长10分米，宽4分米的长方体，铸成的这个长方体铁块的高是多少分米？参考答案一．选择题。

1.答案：B解析：一个长方体盒子，长8厘米，宽和高都是5厘米，求这个盒子的体积是多少，长方体的体积＝长×宽×高，列式为８×５×５＝２００立方厘米。

(完整版)长方体的表面积和体积练习题精选

(完整版)长方体的表面积和体积练习题精选\#\# 长方体的表面积和体积练题精选1. 题目：一个长方体的长度为10 cm，宽度为6 cm，高度为4 cm。

请计算它的表面积和体积。

答案：表面积 = 2 \* (长度\*宽度 + 长度\*高度 + 宽度\*高度) = 2 \* (10\*6 + 10\*4 + 6\*4) = 2 \* (60 + 40 + 24) = 2 \* 124 = 248 cm²；体积 = 长度\*宽度\*高度 = 10\*6\*4 = 240 cm³。

2. 题目：一个长方体的表面积为600 cm²，长度为12 cm。

如果宽度是高度的两倍，那么它的体积是多少？答案：设宽度为x cm，则高度为2x cm。

根据表面积公式，可得：2 \* (12\*x + 12\*2x + x\*2x) = 600。

解方程可得：4x² + 4x² + 24x = 300。

化简得：8x² + 24x - 300 = 0。

解二次方程可得：x = (-24 ± √(24² - 4\*8\*(-300))) / (2\*8) ≈ 5.42。

因为宽度不能是负数，所以宽度约为5.42 cm。

根据体积公式，可得体积为：12\*5.42\*2\*5.42 ≈ 657.17 cm³。

3. 题目：一个长方体的体积为1000 cm³，高度为10 cm。

如果宽度是长度的1.5倍，那么它的表面积是多少？答案：设宽度为1.5x cm，则长度为x cm。

根据体积公式，可得：x\*1.5x\*10 = 1000。

解方程可得：15x³ = 1000。

化简得：x³ = 66.667。

解方程可得：x ≈ 4.15。

宽度约为6.23 cm。

根据表面积公式，可得表面积为：2 \* (x\*1.5x + x\*10 + 1.5x\*10) = 2 \*(1.5\*4.15\*4.15 + 4.15\*10 + 1.5\*4.15\*10) ≈ 204.78 cm²。

小学数学北师大版(2014秋)五年级下册第四单元长方体(二)体积单位-章节测试习题(1)

章节测试题1.【答题】普通汽水瓶的容积约是350（）.A.L B. mL 【答案】B【分析】此题考查的知识点是选择合适的容积单位.【解答】普通汽水瓶的容量大约是350mL.故选B.2.【答题】一罐饮料大约是335（）.A. 升B. 毫升 C. 立方米【答案】B【分析】此题考查的知识点是选择合适的容积单位.【解答】一罐饮料大约是335毫升.故选B.3.【答题】下列物体是用1的小木块搭成的，它的体积是______.【答案】12【分析】此题考查的知识点是体积单位的认识.【解答】由于这个图形是由1的小木块搭成的，这个图形一共有12个小正方体，不管把它们拼成什么形状，它们的体积是不会改变的，即一共有12立方厘米.故答案为12.4.【答题】下列物体是用1的小木块搭成的，它的体积______.【答案】27【分析】此题考查的知识点是体积单位的认识.【解答】从上图可以知道它是由27个1立方厘米小木块搭成的，它的体积为1×27＝27（立方厘米）.故答案为27.5.【答题】学校运动场的一个沙坑里可以放置3.5（）黄沙.A. 立方分米B. 升C. 立方米 D. 立方厘米【答案】C【分析】本题考查的是认识体积单位.【解答】在操场挖一个沙坑一般以立方米作单位，A，D选项单位太小，B选项，升是指液体的体积.选C.6.【答题】一台微波炉的体积约是40（）.A. 立方分米B. 毫升C. 立方米D. 立方厘米【答案】A【分析】本题考查的是选择合适的体积单位.【解答】由生活常识可知，一台微波炉的体积约是40立方分米.选A.7.【答题】一台洗衣机的体积约是450（）.A. 立方厘米B. 立方分米C. 立方米 D. 升【答案】B【分析】本题考查的是选择合适的体积单位.【解答】根据常识，一台洗衣机的体积约是450立方分米.选B.8.【答题】一块雪糕的体积大约是180（）.A. 立方分米B. 立方厘米C.升 D. 立方米【答案】B【分析】本题考查的是对体积单位的认识.【解答】根据生活常识可知，一块雪糕的体积大约是180立方厘米.选B.9.【答题】一块砖头的体积约是1.5（）.A. 立方厘米B. 立方分米C. 立方米D. 升【答案】B【分析】本题考查的是选择合适的体积单位.【解答】根据常识，一块砖头的体积约是1.5立方分米.选B.10.【答题】一个火柴盒的体积大约是（）.A. 20m³B.20dm³ C. 20cm³【答案】C【分析】本题考查的是选择合适的体积.【解答】由常识可知，一个火柴盒的体积大约是20cm³.选C.11.【答题】一本数学书的体积大约是220（）.A. m³B.dm³ C. cm³【答案】C【分析】本题考查的是选择合适的体积单位.【解答】根据常识可知，一本数学书的体积大约是220cm³.选C.12.【答题】一个苹果的体积大约是250（）.A. 立方厘米B. 立方分米 C. 立方米【答案】A【分析】本题考查的是选择合适的体积单位.【解答】由常识可知，一个苹果的体积大约是250立方厘米.选A.13.【答题】一个文具盒的体积是200（）.A. cm³B.dm³ C. m³【答案】A【分析】本题考查的是选择合适的体积单位.【解答】由常识可知，一个文具盒的体积是200cm³.选A.14.【答题】常见的体积单位是cm³，dm³，（）.A.m² B. m³【答案】B【分析】本题考查的是认识体积单位.【解答】常见的体积单位是cm³，dm³，m³；m²是面积单位.选B.15.【答题】一块橡皮的体积大约是10（）.A. 立方厘米B. 立方分米【答案】A【分析】本题考查的是认识体积单位.【解答】由生活常识可知，一块橡皮的体积大约是10立方厘米.选A.16.【答题】一部手机的体积大约是50（）.A. 立方厘米B. 立方分米【答案】A【分析】本题考查的是对体积单位的认识.【解答】由实际情况可知，一部手机的体积大约是50立方厘米.选A.17.【答题】一包粉笔的体积是（）.A. 1cm³B.1dm³ C. 1m³【答案】B【分析】本题考查的是认识立方分米.【解答】一包粉笔的体积通常用立方分米计量，一包粉笔的体积约是1dm³，符合实际情况.选B.18.【答题】小胖用5～6块1立方厘米的正方体积木搭出如下立体图形，体积是5立方厘米的图形是（）.A. B.C.【答案】A【分析】本题考查的是认识体积单位.【解答】由图可知，A选项由5个正方体积木搭出，体积为5立方厘米；B选项由6个正方体积木搭出，体积为6立方厘米；C选项由6个正方体积木搭出，体积为6立方厘米.选A.19.【答题】计量液体，如汽油、饮料、药水等，用（）作单位.A. 升或毫升B. 克或千克 C. 米或厘米【答案】A【分析】本题考查的是认识升和毫升.【解答】计量液体，如汽油、饮料、药水等，用升或毫升作单位.选A.20.【答题】小明爸爸的汽车油箱能装50（）汽油.A. 毫升B. 升【答案】B【分析】本题考查的是选择合适的容积单位.【解答】根据常识，小明爸爸的汽车油箱能装50升汽油.选B.。

体积应用题(一)答案.doc

体积，表面积应用题容(一)1、一个长方体木块，从上部和下部分别截去高为3厘米2厘米的长方体后，便成为一个正方体，表面积减少了120 平方厘米，原来长方体体积是多少？设长方体底边长为X,则其底边宽也为X。

减少的表面积为4X5x=120解该方程，得到x=6厘米所以原来长方体体积为6X6X (6+5)二396立方厘米。

2、一间教室长9米，宽6米，高3米。

要粉刷教室的四周和顶部，扣除门窗的面积25平方米，每平方米需要用0.4 千克的涂料。

粉刷这间教室要用多少千克的涂料？(9X3X2+6X3X2+9X6-25) X0.4=47. 6 千克3、把三个棱长都是4厘米的正方体拼成一个长方体，表面积减少了多少平方厘米，它的体积是多少立方厘米减少了4个底面积4X4X4=64平方厘米体积4X4X4X3=192立方厘米4、做一个长方体的灯箱框架，长7米，宽3米，高1米，做这个灯箱框架共需要多少铁条？铁条的长度，那么就是(长+宽+高)X4 (7+3+1) X4=44米。

5、一个长方体形状的游泳池，长50米，宽25米，高3米，池内原来水深1.2米，如果用水泵向外排水，每分钟排水2. 5立方米，那么需要几个小时排完？游泳池的四周和底部都要贴上瓷砖，求贴瓷砖的面积？50X25X1.2 = 1500 再除以 2. 5=600 分钟=10 小时50 X 3 X 2+25 X 3 X 2+50 X 25=700 平方米6、长方体容器的底面是一个边长60厘米的正方形，容器里面直立着一个高1米，底面边长是15厘米的长方体铁块，这是容器里的水深0. 5米，如果把铁块取出，容器里面的水深多少厘米？15*15*100) / (60*60) =6.25 (厘米)0. 5 米=50 厘米50-6.25=43.75 (厘米7、一根长48分米的铁丝做一个长方体的框架，使它的高为8分米，长、宽的比是1:1.再把它的五个面糊上纸，做成灯笼，糊上纸的面积是多少长=宽=(48F4-8) 4~2=2分米需要纸张8X2X4+2X2=68平方分米8、如果将4个棱长为2厘米的正方体拼成一个长方体，这个长方体表面积比4个正方体的表面积少多少？2X2X6=24cm9、从一个棱长10厘米的正方体木块上挖去一个棱长2厘米的小正方体剩下部分的表面积是多少大正方体的表面积是10X10X6=600平方厘米小正方体一个面的面积是2X2=4平方厘米600+2X2X4=616平方厘米10、在一个棱长为6厘米的大正方体木块，如果把它锯成棱长为2厘米的小正方体若干块，表面积增加了多少平方厘米？(先求大正方体，可以锯成多少小正方体)要解答过程和答案。

小学数学浙教版五年级下册第四单元长方体长方体的体积-章节测试习题(1)

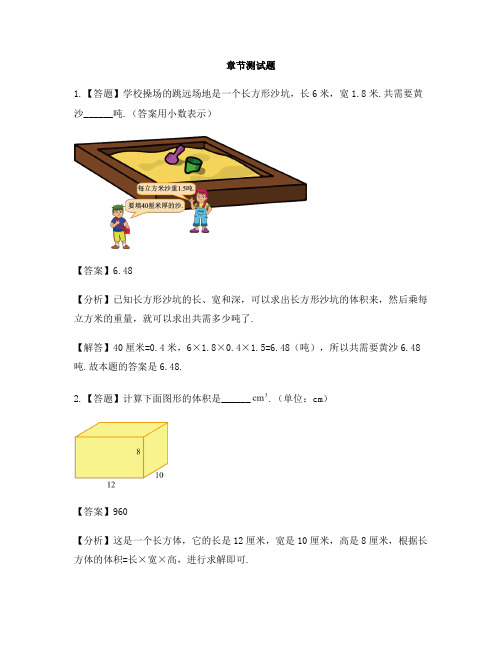
章节测试题1.【答题】学校操场的跳远场地是一个长方形沙坑，长6米，宽1.8米.共需要黄沙______吨.（答案用小数表示）【答案】6.48【分析】已知长方形沙坑的长、宽和深，可以求出长方形沙坑的体积来，然后乘每立方米的重量，就可以求出共需多少吨了.【解答】40厘米=0.4米，6×1.8×0.4×1.5=6.48（吨），所以共需要黄沙6.48吨.故本题的答案是6.48.2.【答题】计算下面图形的体积是______.（单位：cm）【答案】960【分析】这是一个长方体，它的长是12厘米，宽是10厘米，高是8厘米，根据长方体的体积=长×宽×高，进行求解即可.【解答】12×10×8=960（立方厘米），所以这个长方体的体积是960立方厘米.故本题的答案是960.3.【答题】长方体长8m，宽5m，高2m，小正方体的棱长为2m.那么下面图形的体积是______.【答案】88【分析】其体积就等于长方体的体积加上正方体的体积.根据长方体的体积公式：；正方体的体积公式：，代入数据解答即可.【解答】2×2×2+8×5×2=88（），所以此图的体积是88.故本题的答案是88.4.【答题】一个长方体的油箱，底面积是15.8dm²，高是7.2dm，它的体积是______dm³.（答案用小数表示）【答案】113.76【分析】此题考查的是长方体的体积公式.【解答】长方体的体积＝底面积×高，所以它的体积是15.8×7.2＝113.76（dm³）.答：它的体积是113.76dm³.5.【答题】牙膏盒长18cm，宽5cm，高4cm.包装箱内侧尺寸如图.这个包装箱最多能装（）盒牙膏.A. 94B. 108C.115 D. 120【答案】D【分析】根据长方形的体积公式，先求出这个包装箱的容积，再求出一个牙膏盒的体积，再利用除法的意义即可求出包装箱最多能装的盒数.【解答】40×30×36＝43200（），18×5×4＝360（），43200÷360＝120（盒），所以最多能装120盒.故选D.6.【答题】一节冷藏车厢的内部长3米，宽2.5米，高2米，这节车厢内部的体积是______立方米.【答案】15【分析】长方体容器的容积=长×宽×高，据此代入数据即可解答.【解答】3×2.5×2=15（立方米），所以这节车厢内部的体积是15立方米.故本题的答案是15.7.【答题】一个冷藏车厢，从内部量得长是2.5米，宽是2米，高是1.8米，车厢内部的容积是______立方米.【答案】9【分析】已知长方体的长、宽、高，根据长方体的体积=长×宽×高，由此进行解答即可.【解答】2.5×2×1.8＝9（立方米），所以它的容积是9立方米.故本题的答案是9.8.【答题】某游泳馆要新建一个长40米，宽25米，深30分米的游泳池.这个游泳池最多能装水______立方米.【答案】3000【分析】长方体容器的容积＝长×宽×高，把数据代入公式解答.【解答】30分米＝3米，40×25×3＝3000（立方米），所以这个游泳池最多能装水3000立方米.9.【答题】棱长为4厘米的正方体可以分成______个棱长为1厘米的小正方体.【答案】64【分析】本题考查的是求正方体的体积.【解答】棱长为4厘米的正方体的体积是4×4×4＝64（立方厘米），棱长为1厘米的小正方体的体积是1×1×1＝1（立方厘米），求棱长为4厘米的正方体可以分成多少个棱长为1厘米的小正方体用除法，列式为：64÷1＝64（个）.故本题的答案是64.10.【答题】从一个正方体木块上截下3个小正方体，剩下的表面积比原来正方体减少了8平方厘米，照这样可以截出27个小正方体.原来大正方体的体积是______立方厘米.【答案】216【分析】先计算每个小正方体的棱长，再计算小正方体的体积，最后计算大正方体的体积.【解答】从一个正方体木块上截下3个小正方体，剩下的表面积比原来正方体减少了8平方厘米，即减少了2个小正方形的面积，则1个小正方形的面积是：8÷2＝4（平方厘米）.因为2×2＝4，所以小正方形的边长是2厘米，那么小正方体的体积是：2×2×2＝8（立方厘米），照这样可以截出27个小正方体，原来大正方体的体积是：8×27＝216（立方厘米）.故本题的答案是216.11.【答题】用棱长为1厘米的正方体小木块，拼成一个大正方体，至少要4个这样的小木块.（）【答案】×【分析】本题考查的是正方体的体积计算.正方体的体积＝棱长×棱长×棱长.【解答】已知用棱长为1厘米的正方体小木块，拼成一个大正方体，那么这个大正方体的棱长至少是2厘米，体积是：2×2×2＝8（立方厘米）；原来小木块的体积是：1×1×1＝1（立方厘米）.所以至少需要这样的小木块：8÷1＝8（个）.故本题错误.12.【答题】棱长为6厘米的正方体的表面积和体积相等，都是216. （）【答案】×【分析】本题考查的是正方体的表面积和体积.【解答】棱长为6厘米的正方体的表面积为：6×6×6＝216（平方厘米），体积为：6×6×6＝216（立方厘米），单位不同，不能比较.故本题错误.13.【答题】体积相等的两个正方体，它们的表面积也一定相等. （）【答案】✓【分析】本题考查的是正方体的表面积和体积.【解答】正方体体积＝棱长×棱长×棱长.所以体积相等的两个正方体，棱长也相等.正方体表面积＝棱长×棱长×6，故它们的表面积也一定相等.故本题正确.14.【答题】正方体的棱长扩大到原来的4倍，它的表面积和体积均扩大到原来的4倍. （）【答案】×【分析】本题考查的是正方体的表面积和体积.【解答】正方体的表面积＝棱长×棱长×6，当正方体的棱长扩大到原来的4倍，则新正方体的表面积＝（4×棱长）×（4×棱长）×6＝16×棱长×棱长×6，即扩大为原来的16倍；正方体的体积＝棱长×棱长×棱长，当正方体的棱长扩大到原来的4倍，则新正方体的体积＝（4×棱长）×（4×棱长）×（4×棱长）＝64×棱长×棱长×棱长，即扩大为原来的64倍.所以正方体的棱长扩大到原来的4倍，它的表面积扩大到原来的16倍，体积扩大到原来的64倍.故本题错误.15.【答题】两个正方体的体积相等，它们的表面积不一定相等. （）【答案】×【分析】本题考查的是正方体的体积和表面积.【解答】正方体的体积＝正方体的棱长×棱长×棱长.两个正方体的体积相同，说明它们的棱长相同.正方体的表面积＝正方体的棱长×正方体的棱长×6，所以这两个正方体的表面积一定相等.故本题错误.16.【答题】正方体的棱长扩大到原来的3倍，体积扩大到原来的9倍.（）【答案】×【分析】本题考查的是正方体的体积.【解答】正方体的体积＝棱长×棱长×棱长，正方体的棱长扩大到原来的3倍，3×3×3＝27，所以它的体积扩大到原来的27倍.故本题错误.17.【答题】如果一个正方体的棱长之和是12厘米，那么它的体积是1立方厘米. （）【答案】✓【分析】本题考查的是求正方体的体积.正方体有12条棱，都相等；正方体的体积＝棱长×棱长×棱长.【解答】如果一个正方体的棱长之和是12厘米，那么每条棱长：12÷12＝1（厘米），所以它的体积是：1×1×1＝1（立方厘米）.故本题正确.18.【答题】一个正方体的棱长总和是36厘米，那么它的体积是27立方厘米. （）【答案】✓【分析】本题考查的是求正方体的体积.【解答】一个正方体的棱长总和是36厘米，那么这个正方体的棱长是36÷12＝3（厘米），体积是3×3×3＝27（立方厘米）.故本题正确.19.【答题】一块长方体合金的底面积是64平方厘米，高是50厘米.如果每立方分米该合金的质量是7.5千克，那么这块合金的质量是______千克.【答案】24【分析】本题考查的是求长方体的体积.【解答】64平方厘米＝0.64平方分米，50厘米＝5分米.一块长方体合金的底面积是0.64平方分米，高是5分米，那么体积是：0.64×5＝3.2（立方分米）.每立方分米该合金的质量是7.5千克，那么这块合金的质量是：3.2×7.5＝24（千克）.故本题的答案是24.20.【答题】一个仓库，从里面量长14.5米，宽8.4米，高3米.在这个仓库里摆放体积是1立方米的正方体大木箱，最多可以摆放______个.【答案】336【分析】本题考查的是长方体体积公式的应用.【解答】体积是1立方米的正方体，棱长是1米.仓库长14.5米，所以长的方向上可以放14个，剩下0.5米；宽为8.4米，宽的方向上可以放8个，剩下0.4米；高为3米，高的方向上可以放3个，一共是14×8×3＝336（个）.故本题的答案是336.。

五年级数学下册试题一课一练长方体和正方体的体积习题1-冀教版(含答案)

长方体和正方体的体积习题1第一课时长方体的体积1.填空题。

(1)一个长方体木箱的长是6分米,宽是5分米,高是4分米,它的棱长和是( )分米,占地面积是( )平方分米,体积是( )立方分米。

(2)一个长方体的长、宽、高分别是a米、b米、h米。

如果高增加2米,体积增加( )立方米。

2.一个长方体的长是5分米,宽是45厘米,高是24厘米,它的体积是多少立方厘米?3. 求体积。

（单位;厘米）第二课时正方体的体积1.填空题。

(1)一个正方体的棱长总和是72厘米,体积是( )立方厘米。

(2)把三个棱长都是4厘米的正方体搭成一个长方体,它的体积是( )立方厘米。

2.判断题。

(对的画“ ”,错的画“✕”)(1) 棱长为6厘米的正方体,它的表面积和体积相等。

( )(2)a3表示 a×3。

( )(3) 一个长方体(不含正方体)最多有两个面面积相等。

( )(4) 体积相等的两个正方体,它们的表面积一定相等。

( )3. 求体积。

（单位;厘米）第三课时1.在括号里填上合适的数。

873毫升=( )升 790立方分米=( )立方米1.2立方分米=( )立方厘米 354毫升=( )立方厘米2.判断题。

(对的画“√”,错的画“✕”)（1）把一块正方体橡皮泥捏成一个长方体后,虽然它的形状变了,但是它所占的空间大小不变。

( )（2）棱长为6厘米的正方体的表面积和体积相等。

( ) （3）一个箱子的体积一定比它的容积大。

( )（4）物体的体积越大,所占的空间就越大。

( )3.选择题。

(把正确答案的序号填在括号里)（1）一袋牛奶大约有250( )。

A.升B.平方厘米C.立方米D.毫升（2）一个长方体的体积是100立方厘米,它的长是10厘米,宽是2厘米,高是 ( )。

A.8厘米B.5厘米C.5平方厘米D.5米（3）用1立方分米的正方体方块摆成一个最小的正方体(不包括一块),至少需要( )块。

A.2B.4C.8D.164.求体积。

小学数学冀教版第十册长方体和正方体的体积单元综合练习-章节测试习题(1)

章节测试题1.【答题】一个长方体沙坑，占地面积是10平方米，深是2分米，填满这个沙坑需要______立方米沙子．【答案】2【分析】本题考查的是长方体体积公式的灵活应用.【解答】2分米＝0.2米，10×0.2＝2（立方米），所以填满这个沙坑需要2立方米沙子．故本题的答案是2．2.【答题】把80L水倒入一个棱长为8dm的正方体容器内，容器内水深______dm.【答案】1.25【分析】本题考查的是正方体的容积（体积）公式的灵活应用.【解答】80升＝80立方分米所以容器内水深1.25dm．故本题的答案是1.25．3.【答题】一个长方体的长、宽、高分别是8cm、6cm、4cm，这个长方体的占地面积最大是______cm2，它的体积是______cm3．【答案】48,192【分析】这个长方体的占地面积就是它的底面积，根据长方形的面积公式：S＝ab，把数据代入公式解答；再根据长方体的体积公式：V＝abh，把数据代入公式解答即可．【解答】这个长方体的占地面积最大是8×6＝48（cm2），它的体积是8×6×4＝192（cm3），故本题的答案是48，192．4.【答题】一个长方体，如果高减少2cm，就成为一个正方体.这时表面积比原来减少112cm2.原来长方体的体积是______ cm3.【答案】3136【分析】由题意知，长方体上下两个底面是正方形，减少的112cm2是四个相等的长方形的面积，求出一个长方形的面积，进而用面积除以2，得到长方体的底面边长，据此解答即可.【解答】112÷4＝28（cm2），28÷2＝14（cm），14×14×（14＋2）＝3136（cm3），所以原来长方体的体积是3136cm3.故本题的答案是3136.5.【答题】用一张长20cm，宽6cm的长方形纸围成一个长方体的侧面立在桌面上，围成的长方体，最大的体积是______cm3.（纸片的厚忽略不计）【答案】150【分析】用一张长20cm，宽6cm的长方形纸围成一个长方体的侧面立在桌面上，这个长方体只有4个侧面，没有底面，可以折成底面周长等于长方形的长，高等于长方形的宽；也可以折成底面周长等于宽，高等于长.根据长方体的体积公式，把数据代入公式计算后比较大小即可.【解答】（1）折成长方体的底面周长是20厘米，高是6厘米，底面积最大时，底面边长为20÷4＝5（厘米），体积为5×5×6＝150（立方厘米）；（2）折成长方体的底面周长是6厘米，高是20厘米，底面积最大时，底面边长为6÷4＝1.5（厘米），体积为1.5×1.5×20＝45（立方厘米）.150立方厘米＞45立方厘米，所以长方体的体积最大是150立方厘米.故本题的答案是150.6.【答题】3.05立方米＝（）.A. 305立方分米B. 3050立方分米 C. 30.5立方分米【答案】B【分析】本题考查的是体积单位之间的换算.1立方米＝1000立方米.【解答】3.05立方米＝3050立方分米.选B.7.【答题】一台长方体形状的冰箱，长是0.6米，宽是5分米，高是1.8米.这台冰箱的占地面积是（）.A. 3平方米B. 0.3平方米C. 9平方米 D. 5.4立方米【答案】B【分析】占地面积等于这个长方体的底面积，根据长方形的面积公式：S＝ab，把数据代入公式解答．【解答】5分米＝0.5米，0.6×0.5＝0.3（平方米），所以这台冰箱的占地面积是0.3平方米．选B.8.【答题】一个正方体的棱长扩大到原来的3倍，它的体积扩大到原来的（）倍．A. 3B. 6C.9 D. 27【答案】D【分析】本题考查的是正方体的体积公式与积的变化规律及应用．【解答】一个正方体的棱长扩大到原来的3倍，根据正方体的体积公式：V＝a3，3×3×3＝27，所以它的体积扩大到原来的27倍．选D.9.【答题】将长5分米、宽6分米、高0.3米的一块长方体木料，锯成棱长1分米的正方体，可以锯（）个.A. 9B. 90C.18 D. 180【答案】B【分析】本题考查的是长方体和正方体的体积计算公式.【解答】0.3米＝3分米.长方体的体积＝长×宽×高，一块长方体木料长5分米、宽6分米、高0.3米，即3分米，该长方体木料的体积为：5×6×3＝90（立方分米）；正方体的体积＝棱长×棱长×棱长，棱长1分米的正方体的体积为：1×1×1＝1（立方分米）；长方体的长、宽、高均为正方体棱长的整数倍，求可以锯多少个正方体，用除法，列式计算为：90÷1＝90（个）.选B.10.【答题】一个长方体沙坑，长6米，宽3米，深1米.用4.5立方米的黄沙铺在坑内，黄沙的平均厚度是（）.A. 4分米B. 25分米 C. 0.25米【答案】C【分析】本题考查的是长方体的体积.【解答】长方体的体积＝长×宽×高.一个长方体沙坑，长6米，宽3米，深1米，用4.5立方米的黄沙铺在坑内，黄沙的平均厚度为：4.5÷（6×3）＝0.25（米）.选C.11.【答题】下图长方体的高增加2厘米，体积比原来增加（）立方厘米.A. 2abB.2ac C. 2bc【答案】A【分析】本题考查的是长方体的体积. 长方体的体积＝长×宽×高.【解答】由图可知，长方体的长是a厘米，宽是b厘米，高是c厘米，所以高增加2厘米，体积比原来增加：a×b×2＝2ab（立方厘米）.选A.12.【答题】两个完全相同的长方体长6cm、宽5cm、高3cm，拼成一个表面积最小的长方体，拼成后的长方体的体积是（）cm3．A. 90B.120 C. 180【答案】C【分析】本题考查的是长方体体积公式的灵活应用．【解答】要使这两个长方体拼成一个表面积最小的长方体，也就是把两个长方体的最大面重合在一起，拼成一个长是6厘米，宽是5厘米，高是（3×2）厘米的长方体，6×5×（3×2）＝180（立方厘米），所以拼成后的长方体的体积是180立方厘米．选C.13.【答题】有甲、乙两个长方体水池，水池里都有部分水，它们的占地面积、水面高度和水池深度如下表：下面的说法，错误的是（）.A. 两个水池的容积相等B. 乙水池还能再装15立方米的水C. 甲水池里的水更多D. 乙水池里的水更多【答案】C【分析】本题考查的是长方体的容积（体积）公式的灵活应用．【解答】甲水池的容积：60×1.5＝90（立方米）；甲水池现有水的体积：60×1.2＝72（立方米）；乙水池的容积：50×1.8＝90（立方米）；乙水池现有水的体积：50×1.5＝75（立方米）；乙水池还可以装水的体积90－75＝15（立方米）；由此可知，A、两个水池的容积相等，此说法正确；B、乙水池还能装水15立方米，此说法正确；C、甲水池里的水多,此说法错误；D、乙水池里水多，此说法正确．选C.14.【答题】一个铁块，不管砸成什么形状，它的体积都不变. （）【答案】✓【分析】本题考查的是认识体积.【解答】一个铁块，不管砸成什么形状，它的体积都不变.故本题正确.15.【答题】当正方体的棱长是6cm时，它的表面积和体积刚好相等. （）【答案】×【分析】本题考查的是表面积和体积的意义.【解答】表面积和体积不是同类量，根本不能进行比较.故本题错误.16.【答题】长方体的长扩大为原来的2倍，宽和高不变，则体积扩大为原来的8倍. （）【答案】×【分析】本题考查的是长方体的体积公式.【解答】长方体的体积＝长×宽×高，长扩大为原来的2倍，宽和高不变，体积扩大为原来的2倍.故本题错误.17.【答题】棱长之和相等的长方体和正方体，正方体的体积和表面积都较大. （）【答案】✓【分析】本题考查的是长方体和正方体的表面积和体积.可以举例说明.【解答】假设长方体和正方体的棱长之和都为12，则正方体的棱长是1，表面积是1×1×6＝6，体积为1×1×1＝1；若长方体的长、宽、高分别为1、0.8、0.2，则长方体的表面积为（1×0.8＋1×0.2＋0.8×0.2）×2＝2.32，体积为0.8×0.2×1＝0.16.因为6＞2.32，所以正方体的表面积大；因为1＞0.16，所以正方体的体积大.所以棱长之和相等的长方体和正方体，正方体的体积和表面积都较大.故本题正确.18.【题文】求下面图形的体积.（单位：厘米）【答案】这个图形的体积是168立方厘米.【分析】图形的体积＝棱长为6厘米的正方体的体积－长为6厘米、宽为4厘米、高为2厘米的长方体的体积.【解答】所以这个图形的体积是168立方厘米.19.【题文】求下面图形的体积.（单位：厘米）【答案】这个图形的体积是215立方厘米.【分析】图形的体积＝棱长为6厘米的正方体的体积－棱长为1厘米的正方体的体积.【解答】所以这个图形的体积是215立方厘米.20.【题文】一块长方体石料，长13分米，横截面是一个边长为0.5分米的正方形.如果每立方分米石料重2.8千克，那么这块石料重多少千克？【答案】这块石料重9.1千克.【分析】本题考查的是长方体的体积公式.长方体的体积＝长×宽×高.【解答】长方体石料的体积为：13×0.5×0.5＝3.25（立方分米）这块石料的重量为：3.25×2.8＝9.1（千克）答：这块石料的重量为9.1千克.。

【小学数学】苏教版六年级数学上册第一单元《长方体、正方体的体积》解决问题专项练习

《长方体、正方体的体积》解决问题专项练习（1-4题每题3分, 5-26题每题4分, 共100分）1将一个长3米的长方体木料平均截成3段, 表面积一共增加了平方分米, 这根木料的体积是多少立方分米？2一个正方体的表面积是96平方厘米, 将它平均分成两个小长方体, 每个小长方体的体积是多少立方厘米？3用两块大小相同的正方体木块拼成长方体, 已知长方体的棱长总和是48厘米, 每块正方体木块的体积是多少？4将一个长方体平均分成了两部分, 下图是其中的一部分, 这个立体图形的体积。

单位:厘米5把下面的长方体木料切割成最大的正方体。

最多能切成多少个这样的正方体切成的每个正方体的体积是多少立方厘米6长方体的长是12厘米, 高是8厘米, 阴影部分两个面的面积和是180平方厘米。

这个长方体的体积是多少立方厘米7如图是一个长方体的空心管, 掏空部分的长方体的长为12厘米, 这根空心管的体积是多少立方厘米8. 一个长方体水池, 长100米、宽80米, 如果水泵每分钟可注入5立方米的水, 要使水深为米需注水多少小时9. 一只长方体玻璃缸, 里面长米宽米、水深10厘米, 现将一块石头完全浸入水中, 水面上升厘米, 求该石头的体积。

10把一块棱长是米的正方体钢坯, 锻成高2分米、宽4分米的长方体钢材, 锻成长方体钢材有多长？11有一个完全封闭的容器, 里面的长是2021, 宽是16厘米, 高是10厘米, 平放时里面装了7厘米深的水。

如果把这个容器侧放, 水的高度是多少厘米？12一个长方体玻璃鱼缸, 从里面量长40厘米, 宽25厘米, 高30厘米, 缸内水深12厘米。

把一块石头浸入水中后, 水面升到16厘米, 求石块的体积。

13一个底面是边长为4分米的正方形、高为5分米的长方体水箱, 里面装满水, 把它倒入棱长6分米的正方体水箱, 水面距箱口多少分米14一种油桶, 底面是边长为2分米的正方形, 高36厘米, 把这样的一桶油注入容积是72021的瓶子里, 可以装多少瓶, 宽2021的长方体玻璃缸中, 有一块棱长10cm的铁块, 这时水深15cm, 把这块铁块从玻璃缸中取出, 玻璃缸的水深多少厘米16在一个长2021, 宽15分米的水箱中, 有10分米深的水, 如果一个棱长是30cm的正方体铁块, 那么现在水箱中的水深多少分米, 水深9cm的长方体玻璃缸中, 结果水面上升到12cm水没有溢出, 这个石块的体积是多少, 水深24 厘米。

《专项提优·长方体的体积》学霸

长方体的体积典型例题例一个长方体容器里装满水，现在有大、中小三个铁球，第一次把小球沉人水中；第二次把小球取出，把中球沉人水中；第三次把中球取出，把大球和小球一起沉入水中。

已知每次从容器中溢出的水量情况是：第二次是第一次的3倍，第三次是第一次的倍，大球的体积是小球的多少倍（不计损耗）分析长方体容器里面装满水，第一次溢出的水量是小球的体积。

但当我们把小球取出时，溢出的水不会回到容积中，即容器中的水不满了。

空出的体积就是小球的体积。

因此，放入的中球的体积等于溢出水的体积＋容器中空出的体积，即等于溢出水的体积＋小球的体积。

由于第二次溢出的水量是第一次的3倍，因此中球的体积是小球体积的4倍。

同理，中球取出后，容器中空出4个小球的体积。

大球与小球的体积和是4个小球体积＋这时溢出的水体积。

这时溢出水体积是第一次的倍，所以大球和小球体积和是小球体积的倍，大球体积就是小球体积的倍。

解答设小球体积是1，根据题意，大球的体积是小球体积的1×3＋1＋1×－1＝倍。

反馈练习1.有大、中、小三个长方体水池，它们的池口都是正方形，边长分别是6dm、3dm、2dm，现在把两堆碎石分别沉入中、小水池内，这两个水池的水面分别上升了6cm 和4cm，如果把这两堆碎石都沉入大水池内，大水池的水面将升高多少厘米（得数保留整数）2.一个长方体，它的前面和上面的面积之和是209cm²，巧的是这个长方体的长、宽、高都是质数，这个长方体的体积是多少立方厘米3.李大爷准备用一块长8dm、宽4dm的长方形铁皮，焊接成一个深1dm的无盖水箱。

要使焊接的水箱容积最大，应该怎么办4.一个长方体容器底面是边长为6dm的正方形，容器里直立着一个高8dm、底面是边长为的正方形的长方体铁棒，这时容器里水深，现在将铁棒向上提起，那么，露出水面的铁棒上被水浸湿的部分长多少分米参考答案：＝ 4cm＝（3×3×＋2×2×）÷（6×6）≈（dm）＝2cm 提示：水上升的体积就是碎石的体积，算出两堆碎石的体积和除以大水池的底面积，得到水面升高的高度。

“长方体正方体的表面积和体积”应用题专项练习(一)

“长方体正方体的表面积和体积”应用题专项练习 (一）1. 长方体表面积的求法:长方体的表面积=。

如果用字母a、b、h分别表示长方体的长、宽、高,S表示它的表面积,则S=.长方体的体积=。

字母表示: 。

2。

正方体表面积的求法：正方体的表面积=。

如果用字母a表示正方体的棱长，S表示正方体的表面积，则正方体的表面积计算公式是：S=。

正方体的体积=。

字母表示：。

3、一个长方体有（）个面,他们一般都是（ )形,特殊情况下有可能有（）个面是正方形。

4、把长方体放在桌面上，最多可以看到（）个面。

5、一个长方体，长12厘米，宽和高都是8厘米，这个长方体的表面积是（）。

6、一个长方体，长8厘米,宽是5厘米，高是4厘米，这个长方体的表面积是（），棱长和是( ）。

7、一个正方体的棱长和是84厘米，它的棱长是（）,一个面的面积是（），表面积是( ).8、把三个棱长是1厘米的正方体拼成一个长方体，这个长方体的表面积是( ），比原来3个正方体表面积的和减少了（）。

9、把三个棱长是2分米的正方体拼成一个长方体，表面积是（），体积是（）。

10、用棱长为1厘米的小正方体木块拼成一个较大的正方体，至少要（）个这样的小木块才能拼成一个正方体。

11、一个正方体的棱长如果扩大2倍,那么表面积扩大（）倍，体积扩大( ）倍.12、一个无盖正方体铁桶内外进行涂漆，涂漆的是（）个面。

13、有一根长52厘米的铁丝，恰好可以焊接成一个长6厘米，宽4厘米，高（）厘米的长方体。

14、一个长方体的长宽高分别是a ,b，h，如果高增高3米，那么表面积比原来增加（）平方米,体积增加( ）立方米。

15、用4个棱长2分米的正方体拼成一个长方体,这个长方体的表面积是（）16、用27个体积是1立方厘米的小正方体粘合成一个大正方体,粘合后的大正方体的表面积是（）17、一个长15厘米，宽6厘米，高4厘米的长方体的木块,可以截成（）块棱长2厘米的正方体木块.18、有一个长方体的木料长3厘米、宽3厘米，高2厘米.把它切成1立方厘米的小方块，可以切成（）。

长方体的体积练习题-

《长方体的体积》练习题一、填空：1.一个正方体棱长5厘米，它的棱长和是（），表面积是（），体积是（）。

2.一个长方体木箱的长是6分米，宽是5分米，高是4分米，它的棱长和是（），占地面积是（），表面积是（），体积是（）。

3.一个长方体方钢，横截面积是12平方厘米，长2分米，体积是（）立方厘米。

4.一个长方体水箱，从里面量，底面积是25平方米，水深米，这个水箱能装水（）升。

5.一块正方体的钢锭，棱长是10分米，如果1立方分米的钢重千克，这块钢锭重（）千克。

6.正方体的棱长扩大3倍，棱长和扩大（）倍，表面积扩大（）倍，体积扩大（）倍。

7.用棱长5厘米的小正方体拼成一个大正方体，至少需这样的小正方体（）块。

8.一个长方体的长、宽、高分别是a米、b米、h米。

如果高增加2米，体积比原来增加（）立方米。

二、判断：1.正方体是由6个完全相同的正方形组成的图形。

（）2.棱长6厘米的正方体，它的表面积和体积相等。

（）3.a3表示a×3。

（）4.一个长方体（不含正方体），最多有两个面面积相等。

（）5.体积相等的两个正方体，它们的表面积一定相等。

（）三、操作题：右图是长方体展开图，测量所需数据，并求长方体体积。

四、解决问题：1.一个长方体铁块，长10分米，宽5分米，高4分米，每立方分米铁块重千克，这个铁块重多少千克2.一节长方体形状的铁皮通风管长2米，横截面是边长为10厘米的正方体，做这节通风管至少需要多少平方厘米铁皮3.一个无盖的长方体金鱼缸，长8分米，宽6分米，高7分米。

制作这个鱼缸共需玻璃多少平方分米这个鱼缸能装水多少升（玻璃厚度忽略不计）4.有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水。

现在把一块石头浸没到水里，水面上升2厘米。

这块石头的体积是多少立方厘米《长方体和正方体》练习题一、判断下面的说法是否正确。

（1）长方体或正方体都有6个面、12条棱、8个顶点。

（）（2）长方体的6个面中不可能有正方体。

五年级下册数学人教版课时练第3单元《3.3长方体和正方体的体积》(含答案)(1)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练3.3长方体和正方体的体积一、选择题1．一个水池能蓄水3430m，我们就说，这个水池的（）是3430m。

A．表面积B．体积C．容积2．正方体的棱长扩大到原来的2倍，体积就扩大到原来的（）倍。

A．2B．4C．83．一个长方体被挖掉一小块（如图）。

剩下部分的体积、表面积分别与原来体积、表面积相比，下面说法完全正确的是（）。

A．体积减少，表面积也减少B．体积减少，表面积增加C．体积减少，表面积不变D．体积减少，表面积增加还是减少不能确定4．计量一座粮仓的容积，应该选用最恰当的容积单位是（）。

A．毫升B．升C．立方米5．把60升水倒人棱长5分米的正方体容器中，则水面的高度是（）。

小学数学北京版五年级下册第一单元长方体和正方体体积和体积单位-章节测试习题(1)

章节测试题1.【答题】物体所占空间的大小叫做物体的体积.（）【答案】√【分析】本题考察的知识是物体的意义，物体所占空间的大小叫做物体的体积.据此判断.【解答】解：物体所占空间的大小叫做物体的体积.这种说法是正确的.故答案为：√.2.【答题】将一个正方体钢锭锻造成一个长方体的钢锭，其体积不变.（）【答案】√【分析】根据体积的意义，物体所占空间的大小叫做物体的体积.将一个正方体钢锭锻造成一个长方体的钢锭，只是形状变了，但体积不变.据此解答.【解答】解：将一个正方体钢锭锻造成一个长方体的钢锭，只是形状变了，但体积不变.故答案为：√.3.【答题】把一个长方体分割成几个小长方体后，体积变大了.（）【答案】×【分析】根据体积的意义，物体所占空间的大小叫做物体的体积.把一个长方体分割成几个小长方体后，表面积变大了，但体积不变.据此判断.【解答】解：把一个长方体分割成几个小长方体后，表面积变大了，但体积不变.因此，把一个长方体分割成几个小长方体后，体积变大了.这种说法是错误的.故答案为：×.4.【答题】找朋友.（把左边的数据和右边相应的单位名称连起来）【答案】【分析】此题考查的是体积单位的认识.【解答】一个人的身高通常用厘米计量，乐乐的身高是135cm，符合实际情况；一台液晶电视屏面积通常用平方米计量，一台液晶电视屏大约1m²，符合实际情况；一个饼干盒的体积通常用立方分米计量，一个饼干盒的体积约3dm³，符合实际情况；家用蓄水池体积通常用立方米计量，家用蓄水池体积约 1.6m³，符合实际情况.5.【答题】运货集装箱的体积约是65（）.A.B.C.【答案】C【分析】根据生活实际，一个运货集装箱的体积约是65立方米.【解答】解：运货集装箱的体积约是65.选C.6.【答题】一个铁块，不管砸成什么形状，它的体积都不变.（）【答案】✓【分析】一个铁块，不管砸成什么形状，变化的只是形状，它的体积都不会改变.【解答】一个铁块，不管砸成什么形状，它的体积都不变.原说法正确.故答案为：✓.7.【答题】游泳池注入半池水，水的体积是游泳池的容积.（）【答案】×【分析】容积是指容器所能容纳物体的体积.当游泳池注满水，此时水的体积就是游泳池的容积；而游泳池注入半池水，此时水的体积不是游泳池的容积.据此判断即可.【解答】当游泳池注满水，此时水的体积就是游泳池的容积；而游泳池注入半池水，此时水的体积不是游泳池的容积.原说法错误.故答案为：×.8.【答题】牛奶瓶里面装满的牛奶的体积就是牛奶瓶的容积.（）【答案】✓【分析】容积是指容器所能容纳物体的体积.牛奶瓶的容积就是指牛奶瓶所能容纳牛奶的多少，即装满的牛奶的体积；据此解答即可.【解答】由容积的意义可知：牛奶瓶里面装满的牛奶的体积就是牛奶瓶的容积；原说法正确.故答案为：✓.9.【答题】明明说，他家冰箱的体积和容积一样大.（）【答案】×【分析】本题考查体积和容积的定义.【解答】体积是物体所占空间的大小；容积是指容器所能容纳物体的体积，所以一个物体的容积和体积不一样.故本题是错误的.10.【答题】把一块长方体的钢材锻造成正方体的钢材，形状改变了，但体积不变.（）【答案】✓【分析】根据体积的意义，物体所占空间的大小是物体的体积.将一个长方体的钢材锻造成正方体，只是形状变了，但体积不变.【解答】把一块长方体的钢材锻造成正方体的钢材，形状改变了，但体积不变；原说法正确.故答案为：✓.11.【答题】甲杯与乙杯大小相同（如图），且都盛满了水，将①、②两块石头分别放入杯中，则______杯溢出的水多.（填“甲”或“乙”）【答案】乙【分析】根据题意可知：溢出的水的体积就是放入石头的体积，因为②石头的体积大，所以乙杯溢出的水多；由此解答即可.【解答】因为②的体积＞①的体积，所以乙杯溢出的水多.故答案为：乙.12.【答题】一卡车木料的体积约是5（）.A. m²B.m³ C. dm³【答案】B【分析】此题考查的是选择合适的体积单位.【解答】m²为面积单位，不是体积单位；一卡车木料的体积大概在5m³左右.故选B.13.【答题】下列物体是用1的小木块搭成的，它的体积是______.【答案】12【分析】此题考查的知识点是体积单位的认识.【解答】由于这个图形是由1的小木块搭成的，这个图形一共有12个小正方体，不管把它们拼成什么形状，它们的体积是不会改变的，即一共有12立方厘米.故答案为12.14.【答题】下列物体是用1的小木块搭成的，它的体积______.【答案】27【分析】此题考查的知识点是体积单位的认识.【解答】从上图可以知道它是由27个1立方厘米小木块搭成的，它的体积为1×27＝27（立方厘米）.故答案为27.15.【答题】求一个水桶能装水多少升，是求水桶的体积.（）【答案】×【分析】根据容积（是指容器所能容纳物体的体积）和体积（是指物体所占空间的大小）的意义来判断此题.【解答】求一个圆柱形水桶装多少水，实际上就是求这个水桶容纳的水的体积是多少，也就是水桶的容积.故答案为：×.16.【答题】容积的计算方法和（）的计算方法相同，但容积要从（）量长、宽、高.A. 体积，里面B. 面积，外面【答案】A【分析】本题考查的是容积的意义.【解答】体积是指物质或物体所占空间的大小，表示的是一个物体外部的大小；容积是指容器所能容纳物体的体积.所以体积和容积的计算方法相同，但是容积要从里面量长、宽、高.选A.17.【答题】（）叫做物体的容积.A. 物体所占空间的大小B. 能容纳物体的体积【答案】B【分析】本题考查的是认识容积.【解答】物体能容纳物体的体积叫做物体的容积.选B.18.【答题】蜡像厂把一个工艺品“唐老鸭”融化后，又塑造成另一个工艺品“米老鼠”，这两件工艺品的体积相比，（）.（工艺品为实心，且没有损耗）A. 唐老鸭体积大B. 唐老鸭体积小C. 它们的体积相等D. 无法比较【答案】C【分析】本题考查的是体积的认识.物体所占空间的大小叫做物体的体积.【解答】蜡像厂把一个工艺品“唐老鸭”融化后，又塑造成另一个工艺品“米老鼠”.因为“唐老鸭”融化后体积没有改变，所以“米老鼠”的体积与“唐老鸭”的体积相等，即这两件工艺品的体积相比，它们的体积相等.选C.19.【答题】将一个正方体锻造成一个长方体（不计损耗），正方体和长方体（）.A. 体积相等，表面积相等B. 体积相等，表面积不相等C. 体积不相等，表面积相等D. 体积不相等，表面积不相等【答案】B【分析】本题考查的是正方体和长方体的体积与表面积.【解答】将一个正方体锻造成一个长方体（不计损耗），则正方体和长方体体积相等，表面积不相等.选B.20.【答题】加工一个长方体油箱要用多少铁皮，是求这个油箱的（）.A. 表面积B. 体积 C. 侧面积【答案】A【分析】本题考查的是认识长方体的体积和表面积.【解答】因为长方体油箱的铁皮要包裹住这个长方体，铁皮的面积就相当于长方体的表面积.选A.。