七年级数学下册8.1角的表示检测(无答案)(新版)青岛版

合集下载

(最新)青岛版数学七年级下册《第8章角综合检测试题》(含答案解析)

第8章角单元检测试题一、选择题1.下列说法中正确的是（）A.直线是平角B.角的大小与角的两边长有关C.角的两边是两条射线D.用放大镜看一个角，角的度数变大了2.一个钝角与一个锐角的差是（）A.锐角B.钝角C.直角D.不能确定3.已知∠A=40°18′，∠B=40°17′30″，∠C=40.18°，则（）A.∠A＞∠B＞∠CB.∠B＞∠A＞∠CC.∠C＞∠A＞∠BD.∠A＞∠C＞∠B4.下列各式不正确的是（）A.18000″＜360′B.2°30′＞2.4° C.36000″＜8° D.1°10′20″＞4219″5.如图所示，AB⊥AC，AD⊥BC，垂足分别为A，D，下列说法不正确的是（）A.点A到BC的垂线段为ADB.点C到AD的垂线段为CDC.点B到AC的垂线段为ABD.点D到AB的垂线段为BD6.到直线a的距离等于2cm的点有（）个．A.0个B.1个C.无数个D.无法确定7. 如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（）A.∠A和∠B互为补角B.∠B和∠ADE互为补角C.∠A和∠ADE互为余角D.∠AED和∠DEB 互为余角8.下列说法正确的个数有（）①射线AB与射线BA表示同一条射线．②若∠1+∠2=180°，∠1+∠3=180°，则∠2=∠3．③一条射线把一个角分成两个角，这条射线叫这个角的平分线．④连结两点的线段叫做两点之间的距离．⑤40°50ˊ=40.5°．⑥互余且相等的两个角都是45°．A.1个B.2个C.3个D.4个9.α，β都是钝角，甲、乙、丙、丁计算，（α+β）的结果依次为50°，26°，72°，90°，其中有正确的结果，则计算正确的是（）A.甲B.乙C.丙D.丁10.如图，直线a，b相交于点O，若∠1等于40°，则∠2等于（）A.140°B.120°C.60°D.50°11.如图，AB、CD交于点O，∠AOE=90°，若∠AOC：∠COE=5：4，则∠AOD等于（）A.150°B.140°C.120°D.130°12.已知∠A、∠B互余，∠A比∠B大30°．则∠B的度数为（）A.30°B.40°C.50°D.60°二、填空题13.如图，直线AB、CD相交于点O，∠1=50°，则∠2=________度．14.如果∠A=34°15′，那么∠A的余角等于________15.已知∠α=72°，则∠α的余角是________，∠α的补角是________．16.已知∠1与∠2是对顶角，∠1与∠3是邻补角，则∠2+∠3＝________.17.下列说法中：①因为∠1与∠2是对顶角，所以∠1＝∠2；②因为∠1与∠2是邻补角，所以∠1＝∠2；③因为∠1与∠2不是对顶角，所以∠1≠∠2；④因为∠1与∠2不是邻补角，所以∠1+∠2≠180°.其中正确的有________（填序号）18.如图，A、O、B 三点在一条直线上，OM 是∠AOC 的平分线，ON 是∠BOC 的平分线．若∠1：∠2=1：2，则∠1=________°．19.点O是直线AB、CD的交点，OE、OF分别是∠AOC、∠BOD的平分线，则OE与OF的位置关系是________．20.角度换算：26°48′=________°．21.如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由：________．22.在同一平面内有2010条直线a1， a2，…，a2010，如果a1⊥a2， a2∥a3， a3⊥a4， a4∥a5，…，那么a1与a2010的位置关系是________．三、解答题23.在8点与9点之间，分针与时针重合的时刻是几点几分？24.如图，已知∠AOB=90°，∠EOF=60°，OE平分∠AOB，OF平分∠BOC，求∠AOC和∠COB的度数．25.如图，∠AOB=90°，∠BOC=2∠BOD，OD平分∠AOC，求∠BOD的度数．26.如图，已知AOB是一条直线，OC是∠AOD的平分线，OE是∠BOD的平分线．（1）若∠AOE=140°，求∠AOC的度数．（2）若∠EOD：∠COD=2：3，求∠COD的度数．27.如图5，O为直线AB上一点，∠AOC=48°,OE平分∠AOC, ∠DOE=90°（1）求∠BOE的度数。

七年级数学下册《8.1 角的表示》青岛版

B O1 A
A
A
O1
B
B
C
O
B
A C
D 1A
O B
D
练习2
请将图中的角用不同方法表示出来，并填写下表：
∠ABE ∠C或∠ACD
∠B
∠1
∠BED ∠A或∠BAC
∠2
∠3
练习3
如图所示，用三个大写字母表示
角，
∠AEC
∠BED
∠1为∠ABC ，∠2为∠BCE ，
∠3为，∠4为 .
⒈角是由两条具有公共端点的射线组成的图形，角的要素为顶点和边，角的大小不随边的长短而变化，即与边无关。
⒉角有四种表示方法：①可三个大写字母表示；②可用一个数字来表示；③也可用一个希腊字母来表示；④可用一个大写字母来表示。特别的，必须是在不引起混淆的情况下，才用一个大写字母来表示。
小结
当堂检测：
1.图1中，∠α、∠β用字母A、B、C 分别可以表示为 ∠CAB 、 ∠ABC .
2.图2中，以B为顶点的角有几
B
B
C
A
1
C
∠A 或∠BAC 或∠1
1
2
A
D
有三个角，分别是: ∠BAC(或∠1）， ∠CAD(或∠2）,∠BAD
角有四种表示方法：
（1）用__三_个__大_写__英_文__字_母____表示角；（2）用__一_个__大_写__英_文__字_母____表示角；（3）用__一_个__阿_拉__伯_数__字_____表示角；（4）用___一__个_希__腊_字__母_____表示角.
个？把它们表示出来.以D为
顶点的角有几个？把它们表
示出来.

青岛版七下数学第8章角测试题及答案

第8章角测试题一、选择题（共12小题，36分）1. 如图，下列各组角中，是对顶角的一组是A. 和B. 和C. 和D. 和2. 和的顶点和一边都重合，另一边都在公共边的同侧，且，那么的另一边落在的( )A. 另一边上B. 内部C. 外部D. 以上结论都不对3. 下列关于角的说法正确的个数是①角是由两条射线组成的图形；②角的边越长，角越大；③在角一边延长线上取一点；④角可以看做由一条射线绕着它的端点旋转而形成的图形．A. B. C. D.4. 画一条线段的垂线，垂足在( )A. 这条线段上B. 这条线段的端点上C. 这条线段的延长线上D. 以上都可以5. 8 点 30 分时，钟表的时针与分针的夹角为( )A. B. C. D.6. 一个角的补角是它的余角的倍，那么这个角的度数是( )A. B. C. D.7. 如图所示，，以为始边作，则的大小为A. B.C. 或D. 以上都不正确8. 点是直线外一点，，，为直线上三点，，，，则点到直线的距离( )A. 等于B. 小于C. 不大于D. 等于9. 已知，则的余角等于( )A. B. C. D.10. 如图，已知，，平分，则的度数是A. B. C. D.11. 如图所示，已知，，，，则线段的范围是A. 大于B. 小于C. 大于且小于D. 小于或大于12. 如果和互补，且，则下列表示的余角的式子中：①；②；③ ；④ ．正确的有( )A. 个B. 个C. 个D. 个二、填空题（共5小题；共15分）13. 若与互余，，则等于；若与互补，，则等于．14. 若与互为邻补角，且，那么．15. 如图，直线、、相交于点，的对顶角是，的对顶角是，如果，则，．16. 如图所示，将一副三角板叠放在一起，使直角顶点重合于点，如果，那么．17. 如图所示，是的平分线，是内的一条射线，已知比大，则的度数是．三、解答题（共8小题；共69分）18. 如图所示，比较、、、的大小．19. 如图所示，直线，，交于点，平分，且，，求的度数．20. 如图所示，点在直线上，并且，，试判断和，和的大小关系．21. 把化成度、分、秒的形式．22. 如图，建筑工人经常要测量两堵围墙所成的，但人不能进入围墙，聪明的你帮助工人师傅想想办法吧．要求：画出两种不同测量方案示意图，直接给出求的表达式．23. 写出图中符合下列条件的角．(1) 能用一个大写字母表示的角；(2) 以为顶点的角；(3) 图中所有小于平角的角（可用简便方法表示）．24. 计算：(1) ；(2) ；(3) ；(4) ．25. 如图所示，为平角，，分别是，的平分线，求的度数．答案第一部分1. B2. C3. A4. D5. B6. B7. C8. C9. C 10. B11. C 12. [1]第二部分13. ；14.15. ；；；16.17.第三部分18. (1) 它们的顶点和一条边都是重合的，由图可以看出：．19. (1) 因为，所以．因为平分，所以又因为，所以．所以．20. (1) 因为，．所以．即．同理可得．21. (1) 因为，，所以．22. (1) 方案1图：．方案2图：．23. (1) ，；23. (2) ，，，共个角；23. (3) ，，，，，，．24. (1) ．24. (2) ．24. (3) ．24. (4) ．25. (1) ，分别平分，，，．。

初中数学青岛版七年级下册第8章8.1角的表示练习题-普通用卷

初中数学青岛版七年级下册第8章8.1角的表示练习题一、选择题1.下午3:30时，钟表上的时针与分针间的夹角是()A. 40°B. 50°C. 60°D. 75°2.在上午9时到10时之间，时钟的分针与时针会重合一次，这次的重合时间是()A. 9:48～9:49B. 9:49∼9:50C. 9:50～9:51D. 9:51～9:523.在8：30这一时刻，时钟上的时针和分针之间的夹角为()A. 85°B. 75°C. 70°D. 60°4.若A在B的北偏西30º方向，那么B在A的()方向A. 北偏西30°B. 北偏西60°C. 南偏东30°D. 南偏东60°5.如图，有A，B，C三个地点，且AB⊥BC，从A地测得B地在A地的北偏东43°的方向上，那么从B地测得C地在B地的()A. 南偏西43°B. 南偏东43°C. 北偏东47°D. 北偏西47°6.如图，甲从A点出发向北偏东60°方向走到点B，乙从点A出发向南偏西20°方向走到点C，则∠BAC的度数是()A. 80°B. 100°C. 120°D. 140°7.如图，在灯塔O处观测到轮船A位于北偏东70°的方向，轮船B位于南偏东30°的方向，那么∠AOB的大小为()A. 100°B. 40°C. 80°D. 60°8.学校，电影院，公园在平面图上的标点分别是A，B，C，电影院在学校的正东方向，公园在学校的南偏西25º方向，那么平面图上的∠CAB等于()A. 25ºB. 155ºC. 115ºD. 65º9.下列说法中正确的个数是()①由两条射线组成的图形叫做角；②角的大小与边的长短无关，只与两条边张开的角度有关；③角的两边是两条射线；④把一个角放到一个放大10倍的放大镜下观看，角度数也扩大为原来的10倍．A. 1个B. 2个C. 3个D. 4个10.下列图形中，能用∠1，∠AOB，∠O三种方法表示同一个角的图形是()A. B.C. D.11.甲看乙的方向为北偏东35°，那么乙看甲的方向是()A. 南偏西35°B. 南偏东35°C. 南偏东55°D. 南偏西55°12.如图，能用∠AOB、∠O、∠1三种方法表示同一个角的图形是A. B.C. D.二、填空题13.图中一共有______个角．14.钟表上的时间指示为两点半，此时时针与分针所成的角(小于平角)的度数为______．15.如图所示，射线OA表示______ 28°方向，射线OB表示______ 方向，∠AOB=______ °.16.时钟的时间是3点30分，时钟面上的时针与分针的夹角是______．三、解答题17.观察下图，回答下列问题：(1)在图①中有几个角？(2)在图②中有几个角？(3)在图③中有几个角？(4)以此类推，如图④所示，若一个角内有n条射线，此时共有多少个角？18.按照上北下南，左西右东的规定画出表示东南西北的十字线，然后在图上画出表示下列方向的射线：(1)北偏西60∘；(2)南偏东30∘；(3)北偏东45∘；(4)西南方向19.(1)请在给定的图中按照要求画图：①画射线AB；②画平角∠BAD；③连接AC；(2)设点B、C分别表示两个村庄，它们之间要铺设燃气管道.若节省管道，则沿着线段BC铺设.这样做的数学依据是：_________________________20.钟面角是指时钟的时针与分针所成的角．(1)钟面时刻3：00时，钟面角为90°，请举一例：钟面时刻为____，钟面角为90°；(2)6：00至7：00之间，哪些时刻钟面角为90°？答案和解析1.【答案】D【解析】【分析】本题考查了钟面角，确定时针与分针相距的大格数是解题关键．根据时针与分针相距的大格数乘每个大格的度数，可得答案．【解答】解：下午3:30时时针与分针相距2+12=52个大格，每个大格是30∘，下午3:30时，钟表上的时针与分针间的夹角是30×52=75∘．故选D ． 2.【答案】B【解析】【分析】本题考查钟表时针与分针的夹角．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动(112)°，并且利用起点时间时针和分针的位置关系建立角的图形．因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30°，时钟的时针每小时转过的角是一份，即30°；分针每分钟转过的角是15分，即15×30°=6°；九点钟，时针和分针呈270°，时针1分钟走0.5°，分针一分钟走6°设九点x 分，重合，则有0.5x +270=6x ，即可解答．【解答】解：九点钟，时针和分针呈270°，时针1分钟走0.5°，分针一分钟走6°设九点x 分重合，则有0.5x +270=6x ，x =49111，故选B ． 3.【答案】B【解析】解：8：30，时针指向8与9之间，分针指向6，钟表12个数字，每相邻两个数字之间的夹角为30°，∴此时刻分针与时针的夹角正好是2×30°+15°=75°．故选：B．画出图形，利用钟表表盘的特征解答．本题考查钟表时针与分针的夹角．在钟表问题中，常利用时针与分针转动的度数关系：°，并且利用起点时间时针和分针的位置关系建立角的图形．分针每转动1°时针转动1124.【答案】C【解析】【分析】本题主要考查了方向角的定义，在叙述方向角时一定要注意以哪个图形为参照物是本题的关键．根据A在B的北偏西30º方向，是以B为标准，反之A看B的方向是以A为标准，从而得出答案．【解答】解：如图，A在B的北偏西30º方向，，那么A看B的方向是南偏东30°．故选：C．5.【答案】D【解析】解：∵AF//DE，∴∠ABE=∠FAB=43°，∵AB⊥BC，∴∠ABC=90°，∴∠CBD=47°，∴C地在B地的北偏西47°的方向上．故选：D．根据方向角的概念，和平行线的性质求解．本题主要考查了方位角，平行线的性质，正确的识别图形是解题的关键．6.【答案】D【解析】本题考查方向角，解决此题时，能准确找到方向角是解题的关键.∠BAC等于三个角的和，求出各角的度数，相加即可．【解答】解：由题意，∠BAC=(90°−60°)+90°+20°=140°．故选D．7.【答案】C【解析】解：∵在灯塔O处观测到轮船A位于北偏东70°的方向，同时轮船B在南偏东30°的方向，∴∠AOB=(90°−70°)+(90°−30°)=20°+60°=80°，故选：C．根据在灯塔O处观测到轮船A位于北偏东70°的方向，同时轮船B在南偏东30°的方向，可知∠AOB为90°减去70°与90°减去30°的和，从而可以解答本题．本题考查了方向角，解题的关键利用数形结合的思想，可以由题目中的信息得到所求角的度数．8.【答案】C【解析】【分析】本题考查了方向角.解答此类题需要从运动的角度，正确画出方向角，找准中心是做这类题的关键．根据方向角的概念，正确画出方位图表示出方向角，即可求解．【解答】解：从图中发现平面图上的∠CAB=∠1+∠2=115°．故选C．【解析】【分析】此题主要考查了角的概念，熟练根据角的组成分析得出是解题关键．根据角的定义分别分析得出答案即可．【解答】①角是由两条有公共端点的两条射线组成的图形，故①错误；②角的大小与边的长短无关，只与两条边张开的角度有关，故②正确；③角的两边是两条射线，故③正确；④把一个角放到一个放大10倍的放大镜下观看，角的度数不变，故④错误，故正确的有2个，故选：B．10.【答案】B【解析】解：A、不能用∠1，∠AOB，∠O三种方法表示同一个角，故A选项错误；B、能用∠1，∠AOB，∠O三种方法表示同一个角，故B选项正确；C、不能用∠1，∠AOB，∠O三种方法表示同一个角，故C选项错误；D、不能用∠1，∠AOB，∠O三种方法表示同一个角，故D选项错误；故选：B．根据角的表示方法和图形逐个判断即可．本题考查了角的概念．解题的关键是掌握角的表示方法的运用．11.【答案】A【解析】【分析】本题考查了方向角的知识，属于基础题，解答此类题需要从运动的角度，正确画出方位角，找准中心是解答这类题的关键，根据方位角的概念，画图正确表示出方位角，即可求解．【解答】解：如图：由题意可知∠1=35°，∵AB//CD，∴∠1=∠2，由方向角的概念可知乙在甲的南偏西35°．故选A．12.【答案】D【解析】【分析】本题考查了角的表示方法的应用，掌握角的表示方法是解题的关键．根据角的四种表示方法和具体要求回答即可．【解答】解：A.以O为顶点的角不止一个，不能用∠O表示，故A选项错误；B.以O为顶点的角不止一个，不能用∠O表示，故B选项错误；C.以O为顶点的角不止一个，不能用∠O表示，故C选项错误；D.能用∠1，∠AOB，∠O三种方法表示同一个角，故D选项正确．故选D．13.【答案】6【解析】解：图中的角有：∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD这6个，故答案为：6．根据角的定义得出图中的角即可．本题主要考查角，熟练掌握角的定义是解题的关键．14.【答案】105°【解析】解：∵时针在钟面上每分钟转0.5°，分针每分钟转6°，∴钟表上2点30分，时针与分针的夹角可以看成3×30°+0.5°×30=105°，故答案为：105°．因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30°，借助图形，找出时针和分针之间相差的大格数，用大格数乘30°即可．本题考查钟表时针与分针的夹角．在钟表问题中，常利用时针与分针转动的度数关系：)°，并且利用起点时间时针和分针的位置关系建立角的图形．分针每转动1°时针转动(11215.【答案】北偏东东南107【解析】解：射线OA表示北偏东28°方向，射线OB表示东南方向，∠AOB=(90°−28°)+45°=107°．故答案是：北偏东，东南，107．根据方向角的定义即可解答．本题考查了方向角的定义，理解定义是关键．16.【答案】75°【解析】解：根据钟面上的圆心角的度数规律得，每个大格，即两个相邻数字与圆心所成的圆心角为30°，每个小格所对应的圆心角为6°3点30分时，分针指向6的位置，时针指向3与4中间的位置，因此夹角为2.5个大格所对应的度数，因此2.5×30°=75°，故答案为75°．钟面上每一个小格所对应的圆心角为360°÷60=6°，每两个相邻数字之间所对应的圆心角为6°×5=30°，再根据3点30分时，时针、分针的位置确定几个大格，几个小格，从而确定度数．考查钟面角的特征，明确钟面上的一个小格、一个大格所对应的圆心角的度数是解决问题的关键．17.【答案】解：由分析知：=1(个)；(1)①图中有2条射线，则角的个数为：2×(2−1)2=3(个)；(2)②图中有3条射线，则角的个数为：3×(3−1)2=6(个)；(3)③图中有4条射线，则角的个数为：4×(4−1)2(4)由前三问类推，角内有n条射线时，图中共有(n+2)条射线，则角的个数为(n+1)(n+2)2个．【解析】解答此题首先要弄清楚题目的规律：当图中有n条射线时，每条射线都与(n−1)条射线构成了(n−1)个角，则共有n(n−1)个角，由于两条射线构成一个角，因此角的总数为：n(n−1)，可根据这个规律，直接求出(1)(2)(3)的结论；2在解答(4)题时，首先要弄清图中共有多少条射线，已知角内共n条射线，那么图中共有(n+2)条射线，代入上面的规律，即可得到所求的结论．解答此类规律型问题，一定要弄清题目的规律，可以从简单的图形入手进行总结，然后得到一般化结论再进行求解．18.【答案】【解析】略19.【答案】解：①如图所示：②③如图所示：(2)两点之间，线段最短．【解析】【分析】此题考查的是射线、角和线段的画法以及线段的性质，正确理解射线，线段和角的定义是关键．(1)根据射线，角的定义和线段画法作图即可；(2)根据线段性质可得结论．【解答】(1)见答案；(2)设点B 、C 分别表示两个村庄，它们之间要铺设燃气管道．若节省管道，则沿着线段BC 铺设．这样做的数学依据是：两点之间，线段最短．故答案为：两点之间，线段最短．20.【答案】解：(1)9：00(答案不唯一)；(2)解：设6点x 分时，钟面角为90°，则6点半前时，30°×(6+x 60)−6°x =90°，解这个方程，得x =18011， 6点半后时，6°x −30°×(6+x 60)=90°，解这个方程，得x =54011．答：6点18011分或者6点54011分时，钟面角为90°．【解析】【分析】本题考查了一元一次方程的应用，钟面角，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．(1)根据钟面上两格之间为30°进行解答．(2)根据分针1分钟转动6°，时针1分钟转动0.5°，根据角度之间的等量关系：角度差是90°列出方程即可求解．【解答】解：(1)如图所示，9：00时，钟面角为90°．故答案是9：00(答案不唯一)；(2)见答案．。

2019-2020学年度青岛版数学七年级下册8.1 角的表示拔高训练第十篇

2019-2020学年度青岛版数学七年级下册8.1 角的表示拔高训练第十篇➢第1题【单选题】如图所示，下列表示角的方法错误的是( )A、∠1与∠AOB表示同一个角B、∠β表示的是∠BOCC、图中共有三个角：∠AOB ，∠AOC ，∠BOCD、∠AOC也可用∠O来表示【答案】：【解析】：➢第2题【单选题】下列各式中，正确的角度互化是( )A、18°18′18″=3.33°B、46°48′=46.48°C、22.25°=22°15′D、28.5°=28°50′【答案】：【解析】：➢第3题【单选题】8点30分时，时钟的时针与分针所夹的锐角是( )A、70°B、75°C、80°D、60°【答案】：【解析】：➢第4题【单选题】如图所示，从点O出发的5条射线，可以组成的角的个数是( )．A、4B、6C、8D、10【答案】：【解析】：➢第5题【单选题】点A在点O的南偏东30°，点B在点O的北偏西70°，则OA，OB这两条射线构成的角等于( )A、140°B、100°C、80°D、40°【答案】：【解析】：➢第6题【单选题】时钟显示为8：30时，时针与分针所夹角度是( )A、90°B、120°C、75°D、84°【答案】：【解析】：➢第7题【单选题】4点10分时，时针与分针所夹的小于平角的角为( )A、55°B、65°C、70°D、以上度数都不对【答案】：【解析】：➢第8题【单选题】射线OA和射线OB是一个角的两边，这个角可记为( )．A、∠AOBB、∠BAOC、∠OBAD、∠OAB【答案】：【解析】：➢第9题【单选题】如图所示，小刚家在学校的北偏东30°方向，距离学校2 000米，则学校在小刚家的位置是( )A、北偏东30°，距离小刚家2000米B、西偏南60°，距离小刚家2000米C、西偏南30°，距离小刚家2000米D、北偏东60°，距离小刚家2000米【答案】：【解析】：➢第10题【单选题】下列关于角的说法正确的个数是( )①角是由两条有公共端点的射线组成的图形；②角的边越长，角越大；③在角一边延长线上取一点D；④角可以看作由一条射线绕着它的端点旋转而形成的图形.A、1个B、2个C、3个D、4个【答案】：【解析】：➢第11题【单选题】如图，甲从A点出发向北偏东70°走到点B，乙从点A出发向南偏西15°方向走到点C，则∠BAC的度数是( )A、125°B、160°C、85°D、105°【答案】：【解析】：➢第12题【单选题】由3点15分到3点30分，时钟的分针转过的角度是( )A、90°B、60°C、45°D、30°【答案】：【解析】：➢第13题【单选题】如果从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的( )A、南偏西30°方向B、南偏西60°方向C、南偏东30°方向D、南偏东60°方向【答案】：【解析】：➢第14题【单选题】海面上灯塔位于一艘船的北偏东40°的方向上,那么这艘船位于灯塔的( )A、南偏西50°B、南偏西40°C、北偏东50°D、北偏东40°【答案】：【解析】：➢第15题【单选题】十一点十分这一时刻，分针和时针的夹角是( )A、70°B、75°C、80°D、85°【答案】：【解析】：➢第16题【单选题】时钟9点30分时，分针和时针之间形成的角的大小等于( )A、75°B、90°C、105°D、120°【答案】：【解析】：➢第17题【填空题】∠1还可以用______表示，若∠1＝62.16°，那么62.16°＝______°______′______″．【答案】：【解析】：➢第18题【填空题】某军事行动中，对军队部署的方位，采用代码的方式来表示．例如，北偏东30°方向45km的位置与钟面相结合，以钟面圆心为基准，时针指向北偏东30°的时刻是1∶00，那么这个地点就用代码010045表示．按这种表示方式，南偏东40°方向78km的位置，可用代码表示为______.．【答案】：【解析】：➢第19题【填空题】若时钟由2点30分走到2点55分，则时针、分针转过的角度分别为______．【答案】：【解析】：➢第20题【填空题】在时钟上，当有误分时，时针与分针的夹角为______度.【答案】：【解析】：➢第21题【填空题】如图，射线OA表示北偏西36°，且∠AOB＝154°，则射线OB表示的方向是______．【答案】：【解析】：➢第22题【填空题】在时刻8：30时，时钟上时针和分针的夹角为______度．【答案】：【解析】：➢第23题【填空题】当时钟指向上午10：10时，时针与分针的夹______度．【答案】：【解析】：➢第24题【解答题】在图中一共有几个角？它们应如何表示？【答案】：【解析】：➢第25题【解答题】（1）计算：34°25′×3+35°42′（2）如图，O是直线AB上一点，OC平分∠AOD，∠BOD=42°，求∠AOC 的度数．【答案】：【解析】：➢第26题【解答题】在8点与9点之间，分针与时针重合的时刻是几点几分？【答案】：【解析】：➢第27题【作图题】如图，OA是表示北偏东30°方向的一条射线，仿照这条射线画出表示下列方向的射线，( 1 ) 南偏东25°；(2) 北偏西60°.【答案】：【解析】：➢第28题【综合题】如图，钟表的分针匀速旋转一周需要60分钟，那么：它的旋转中心是什么？分针旋转一周，时针旋转多少度？上午8点整，时针和分针的夹角是多少？8点半呢？【答案】：【解析】：➢第29题【综合题】如图，射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向，点A在点O的北偏东45°方向，点B在点O的北偏西30°方向．画出射线OB，若∠BOC与∠AOB互余，请在图1或备用图中画出∠BOC；若OP是∠AOC的角平分线，直接写出∠AOP的度数（不需要计算过程）．【答案】：无【解析】：➢第30题【综合题】如图，∠BOD=90°，∠COE=90°，解答下列问题：图中有哪些小于平角的角？用适当的方法表示出它们．比较∠AOC、∠AOD、∠AOE、∠AOB的大小，并指出其中的锐角、钝角、直角、平角．【答案】：【解析】：。

2019-2020学年度数学七年级下册第8章角8.1 角的表示青岛版习题精选三十

【答案】：
【解析】：
如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．
（1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；
（2）若图中有一艘渔船D，且∠AOD的补角是它的余角的3倍，画出表示渔船D方向的射线OD，则渔船D在货轮O的方位角
∠BOD可看作是OB绕点O逆时针方向至OD，作∠BOD的平分线OE，OE的方向是______；
在（1）、（2）、（3）的条件下，∠COE=______．
【答案】：
【解析】：
【答案】：
【解析】：
某考察队从营地P处出发，沿北偏东60°前进了3km到达A地，再向正南方向前进3km最后达C地．回答下列问题：（1）用1cm代表1千米，画出考察队行进路线图；（2）度量出C地在营地的什么方向上？（精确到1°）（3）测算出考察队此时离营地实际多远？（精确到0.1千米）
【答案】：
【解析】：
A、
B、
C、
D、
【答案】：
【解析】：
下列说法中错误的个数是( )①线段有两个端点，直线有一个端点；②角的大小与我们画出的角的两边的长短无关；③线段上有无数个点；④同角或等角的补角相等；⑤两锐角的和一定大于直角．
A、1个
B、2个
C、3个
D、4个
【答案】：
【解析】：
一副三角板如图放置，以CB为正东方向，则点D在点C的北偏西______°方向上．
【解析】：
如图，一所船停在海面上O处，从船上看灯塔A位于北偏西有误方向，港口B位于船的正东方向，港口C与O的连线刚好平分有误，那么从船上看港口C位于( )．A、南偏西方向B、 Nhomakorabea偏东方向

2022年必考点解析青岛版七年级数学下册第8章角专项测评试题(含详细解析)

青岛版七年级数学下册第8章角专项测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图所示，下列表示角的方法错误的是（）A ．∠1与∠AOB 表示同一个角B ．图中共有三个角：∠AOB ，∠AOC ，∠BOCC ．∠β+∠AOB ＝∠AOCD ．∠AOC 也可用∠O 来表示2、如图所示，AOB ∠是平角，OC 是射线，OD 、OE 分别是AOC ∠、BOC ∠的角平分线，若28COE ∠=︒，则AOD ∠的度数为（）A ．56°B ．62°C ．72°D ．124°3、如图，AB CD ⊥于点O ，OE 平分AOC ∠，若18BOF ∠=︒，则EOF ∠的度数为（）．A ．116°B ．117°C ．118°D ．127°4、在9：30这一时刻，时钟上的时针和分针之间的夹角为（）A ．105︒B ．100︒C ．90︒D ．85︒5、如图，直线AB 与CD 相交于点O ，若1280∠+∠=︒，则1∠等于（）A ．40°B ．60°C ．70°D ．80°6、如图，点P 在直线l 外，点A 、B 在直线l 上，若PA =4，PB =7，则点P 到直线l 的距离可能是（）A ．0B ．3C ．5D ．77、在灯塔O 处观测到轮船A 位于灯塔北偏西54°的方向，同时观测到轮船B 位于灯塔南偏东15°的方向，那么∠AOB 的大小为（）A．131°B．141°C．151°D．159°8、如图，O是直线AB上一点，OE平分∠AOB，∠COD=90°，则图中互余的角有（）对．A．5 B．4 C．3 D．29、小光准备从A地去往B地，打开导航显示两地距离为39.6km，但导航提供的三条可选路线长却分别为52km，53km，56km（如图）．能解释这一现象的数学知识是（）A．两点之间，线段最短B．两点确定一条直线C．垂线段最短D．过一点有且只有一条直线与已知直线垂直10、如图，已知AO⊥OC，OB⊥OD，∠COD=38°，则∠AOB的度数是（）A ．30ºB ．145ºC ．150ºD ．142º第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、已知∠1与∠2互余，∠2与∠3互补，若∠1＝33°27'，则∠2＝_____，∠3＝_____．2、已知26A ∠=︒，则A ∠的余角的度数是______．3、如图所示，直线AB 与直线CD 交于点O ．OE AB ⊥于点O ，若20BOD ∠=︒，则COE ∠的度数为________．4、一个角的补角比这个角的余角的2倍还多40°，这个角的度数是__________．5、如图，直线AB 、CD 相交于点E ，EF ⊥AB 于E ，若∠CEF ＝58°，则∠BED 的度数为______．三、解答题（5小题，每小题10分，共计50分）1、已知O 是直线AB 上一点，OC 是从点O 引出的一条射线，且∠AOC <∠BOC ，在直线AB 的上方作∠COD ，满足∠BOC -∠COD =90°．(1)如图，若OD 是∠AOC 的平分线，求∠COD 的度数；(2)若∠COD=n ，求∠BOC -∠AOD 的大小．（用含n 的式子表示）2、如图，已知∠AOB ＝∠COD ＝90°，∠BOC ＝32°，求∠AOD 的度数．3、如图，∠AOB 是平角，80AOC ∠=︒，30BOD ∠=︒，OM 、ON 外别是∠AOC 、∠BOD 的平分线，求∠MON 的度数．4、如图，直线AB 、CD 相交于点O ，AB CD ⊥，90EOF ∠=︒．(1)若30COE ∠=︒，则BOF ∠= __________．(2)从（1）的时刻开始，若将EOF ∠绕O 以每秒15的速度逆时针旋转一周，求运动多少秒时，直线AB 平分EOF ∠．(3)从（1）的时刻开始，若将EOF ∠绕O 点逆时针旋转一周，如果射线OP 是COE ∠的角平分线，请直接写出此过程中AOP ∠与BOF ∠的数量关系．（不考虑OE 与AB 、CD 重合的情况）5、如图，直线AB 和直线CD 交于O 点，EO AB ⊥，(1)若2EOC COB ∠=∠，求AOD ∠的度数．(2)作OF CD ⊥，证明：EOF COB ∠=∠．-参考答案-一、单选题1、D【解析】【分析】根据角的表示方法表示各个角，再判断即可．【详解】解：A、∠1与∠AOB表示同一个角，正确，故本选项不符合题意；B、图中共有三个角：∠AOB，∠AOC，∠BOC，正确，故本选不符合题意；C、∠β表示的是∠BOC，∠β+∠AOB=∠AOC，正确，故本选项不符合题意；D、∠AOC不能用∠O表示，错误，故本选项符合题意；故选：D．【点睛】本题考查了对角的表示方法的应用，主要检查学生能否正确表示角．2、B【解析】【分析】∠可求得∠BOC的度数，由∠AOC与∠BOC互补即可得到∠AOC的度数，由OD平分根据OE平分BOC∠AOC，即可求得∠AOD的度数．【详解】∠∵OE平分BOC∴∠BOC=2∠COE=2×28°=56°∵∠AOC+∠BOC=180°∴∠AOC=180°−∠BOC=124°∠∵OD平分AOC∴111246222AOD AOC∠=∠=⨯︒=︒故选：B【点睛】本题考查了角平分线的性质、互补等知识，角平分线的性质熟练掌握相关知识点是关键．3、B【解析】【分析】根据垂线的定义，即可得到∠AOC的度数，依据角平分线的定义，即可得到∠AOE的度数，由平角定义即可求解.【详解】解：∵AB CD⊥于点O，∴∠AOC＝90°，∵OE平分∠AOC，∴∠AOE＝12∠AOC＝12×90°＝45°，∴∠EOF＝180°−∠AOE−∠BOF＝180°−45°−18°＝117°．故选：B【点睛】本题考查了垂线的定义，角平分线的定义，熟记概念并准确识图是解题的关键．4、A【解析】【分析】根据时针与分针相距的份数乘以每份的度数，可得答案．【详解】解：9：30时针与分针相距3.5份，每份的度数是30°，在时刻9：30，时钟上时针和分针之间的夹角（小于平角的角）为3.5×30°=105°．故选：A．【点睛】本题考查了钟面角，利用时针与分针相距的份数乘以每份的度数是解题关键．5、A【解析】【分析】根据对顶角的性质，可得∠1的度数．【详解】解：由对顶角相等，得∠1=∠2，又∠1+∠2=80°，∴∠1=40°．故选：A．【点睛】本题考查的是对顶角，掌握对顶角相等这一性质是解决此题关键．6、B【解析】【分析】根据垂线段最短判断即可．【详解】解：当PA⊥AB时，点P到直线l的距离是PA=4，当PA不垂直AB时，点P到直线l的距离小于PA，故点P到直线l的距离可能是3．不可能是0，故选：B．【点睛】本题考查了点到直线的距离，解题的关键是理解题意，灵活运用所学知识解决问题．7、B【解析】【分析】根据方向角，可得∠1，∠2，根据角的和差，可得答案．【详解】解：如图，由题意，得∠1=54°，∠2=15°，由余角的性质，得：∠-∠-，3=901=9054=36由角的和差，得：∠AOB=∠3+∠4+∠2=369015=141++．故选：B．【点睛】本题考查方向角和角度的计算，熟练掌握方向角的定义是关键．8、B【解析】【分析】根据余角的定义找出互余的角即可得解．【详解】解：∵OE平分∠AOB，∴∠AOE=∠BOE=90°，∴互余的角有∠AOC和∠COE，∠AOC和∠BOD，∠COE和∠DOE，∠DOE和∠BOD共4对，故选：B．【点睛】本题考查了余角的定义，从图中确定余角时要注意按照一定的顺序，防止遗漏．9、A【解析】【分析】根据线段的性质可得答案．【详解】解：打开导航显示两地距离为39.6km，但导航提供的三条可选路线长却分别为52km，53km，56km （如图）．能解释这一现象的数学知识是两点之间，线段最短．A、故选项正确，符合题意；B、故选项错误，不符合题意；C、故选项错误，不符合题意；D 、故选项错误，不符合题意．故选：A ．【点睛】此题考查了线段的性质，解题的关键是熟记线段的性质并应用．10、D【解析】【分析】根据垂直的定义得到∠AOC =∠DOB =90°，由互余关系得到∠BOC =52°，然后计算∠AOC +∠BOC 即可．【详解】解：∵AO ⊥OC ，OB ⊥OD ，∴∠AOC =∠DOB =90°，而∠COD =38°，∴∠BOC =90°-∠COD =90°-38°=52°，∴∠AOB =∠AOC +∠BOC =90°+52°=142°．故选：D ．【点睛】本题考查了余角的概念：若两个，角的和为90°，那么这两个角互余．二、填空题1、 5633'︒ 12327'︒【解析】【分析】根据余角和补角的概念求出∠3，∠2与∠1的关系，把∠1的值代入计算即可．【详解】解：∵∠1与∠2互余，∴∠2＝90°﹣∠1，∵∠1＝33°27'，∠2＝90°﹣3327'︒896033275633'''=︒-︒=︒∵∠2与∠3互补，∴∠3＝180°﹣∠2＝180°﹣（90°﹣∠1）＝90°+∠1，∵∠1＝3327'︒，∴∠3＝12327'︒，故答案为：5633'︒，12327'︒．【点睛】本题考查了角的计算问题，掌握互余与互补的定义是解题的关键．2、64°【解析】【分析】根据余角的性质，即可求解．【详解】解：∵26A ∠=︒，∴A ∠的余角的度数是902664︒-︒=︒．故答案为：64°【点睛】本题主要考查了余角的性质，熟练掌握互余的两个角的和等于90°是解题的关键．3、70°##70度【解析】【分析】根据垂直定义和对顶角相等解答即可．【详解】解：∵OE ⊥AB ，∴∠AOE =90°，∵∠BOD =20°，∴∠AOC =∠BOD =20°，∴∠COE =∠AOE －∠AOC =90°－20°=70°，故答案为：70°．【点睛】本题考查垂直定义、对顶角相等、角的运算，熟练掌握角的运算是解答的关键．4、40°##40度【解析】【分析】根据余角（若两个角的和为90︒，则这两个角互为余角）和补角（若两个角的和为180︒，则这两个角互为补角）的定义，设这个角的度数是x ，则它的补角为()180x ︒-，余角为()90x ︒-，根据题意列出方程求解即可．【详解】解：设这个角的度数是x ，则它的补角为()180x ︒-，余角为()90x ︒-，由题意得：()()18029040x x ︒-=︒-+︒，解得：40x =︒，故答案为40︒．【点睛】本题考查了余角和补角的定义，根据角之间的互余和互补关系列出方程是解决问题的关键． 5、32°【解析】略三、解答题1、 (1)=30COD ∠︒(2)3n 或n ．【解析】【分析】（1）过点O 作OE ⊥AB ，由∠BOC -∠COD =90°可得COE COD ∠=∠，根据OD 是∠AOC 的平分线可得COD AOD ∠=∠，从而=COD AOD COE ∠=∠∠，再由++=90COD AOD COE ∠∠∠︒可得结论；（2）分OD 在OC 左右两侧讨论求解即可．(1)如图，过点O 作OE ⊥AB ，∴90BOC COE ∠-∠=︒∵90BOC COD ∠-∠=︒∴COE COD ∠=∠∵OD 是∠AOC 的平分线∴COD AOD ∠=∠∴=COD AOD COE ∠=∠∠∵++=90COD AOD COE ∠∠∠︒∴3=90COD ∠︒∴=30COD ∠︒(2)当OD 在OC 左侧时，如图，过点O 作OM ⊥AB ，∴90BOC COM ∠-∠=︒∵90BOC COD ∠-∠=︒∴COM COD n ∠=∠=∴90902AOD COD COM n ∠=︒-∠-=︒-∴90+(902)3BOC AOD n n n ∠-∠=︒-︒-=；当OD 在OC 右侧时，如图，∵90BOC COD ∠-∠=︒∴90BOD AOD ∠=∠=︒∴9090BOC AOD COD COD n ∠-∠=∠+︒-︒=∠=综上，BOC AOD ∠∠-的大小为3n 或n ．【点睛】本题主要考查了角的计算以及角平分线定义的运用，解题时注意：从一个角的顶点出发，把这个角分成两个相等角的射线叫作这个角的平分线，解决问题的关键是根据角的和差关系进行计算．2、∠AOD 的值为148°【解析】【分析】由AOC AOB BOC ∠=∠-∠得AOC ∠的值，然后根据AOD AOC COD ∠=∠+∠计算求解即可．【详解】解：∵3290BOC AOB ∠=︒∠=︒，∴58AOC AOB BOC ∠=∠-∠=︒∴5890148AOD AOC COD ∠=∠+∠=︒+︒=︒∴AOD ∠的值为148°．【点睛】本题考查了角度的计算．解题的关键在于找出角度的数量关系．3、125︒【解析】【分析】根据角平分线的定义求出,AOM BON ∠∠，再用平角减去+AOM BON ∠∠即可得到结果．【详解】解：∵∠AOB 是平角，∴180AOB ∠=︒∵OM 、ON 外别是∠AOC 、∠BOD 的平分线，且∠AOC ＝80°，∠BOD ＝30°， ∴1402AOM AOC ∠=∠=︒，1152BON BOD ∠=∠=︒， ∴∠MON ＝∠AOB -∠AOM -∠BON ＝180°-40°-15°＝125°．【点睛】本题主要考查了角的平分线的有关计算，性质、角的和差等知识点．解决本题亦可利用：∠MON =∠COD +∠COM +∠DON ．4、 (1)30°(2)11或23秒 (3)1902AOP BOF ∠=︒+∠或1902AOP BOF ∠=︒-∠ 【解析】【分析】（1）根据AB CD ⊥，30COE ∠=︒，利用余角性质得出∠EOB =90°-∠COE =90°-30°=60°，根据90EOF ∠=︒，利用余角性质得出∠BOF =90°-∠EOB =90°-60°=30°即可；（2）解分两种情形，OA 平分EOF ∠，得出1452EOA EOF ∠=∠=︒，904545FOC ∠=︒-︒=︒，设运动t秒时根据运动转过的角度列方程15304590t =++，OB 平分EOF ∠，1452EOB EOF ∠=∠=︒，根据运动转过的角度列方程153027045t =++，解方程即可；（3）分四种情况OE 在∠COB 内，OE 在∠AOC 内，OE 在∠AOD 内，OE 在∠DOB 内，根据射线OP 是COE ∠的角平分线∠COP =∠EOP ，利用角的和差计算即可．(1)解：∵AB CD ⊥，30COE ∠=︒，∴∠EOB =90°-∠COE =90°-30°=60°，∵90EOF ∠=︒，∴∠BOF =90°-∠EOB =90°-60°=30°，故答案是：30°；(2)解分两种情形，情况一∵OA 平分EOF ∠， ∴1452EOA EOF ∠=∠=︒，∴904545FOC ∠=︒-︒=︒，设运动t 秒时，OA 平分EOF ∠，根据题意得：15304590t =++，解得：11t =；情况二∵OB平分EOF∠，∴1452EOB EOF∠=∠=︒，设运动t秒时，OB平分EOF∠，根据题意得：153027045t=++，解得：23t=；综上：运动11或23秒时，直线AB平分EOF∠；(3)解：∵射线OP是COE∠的角平分线∴∠COP=∠EOP，∠AOC=∠EOF=90°，∴∠AOP=90°+∠COP=90°+∠POE，∵∠COE=∠BOF，∴∠POE=11=22COE BOF∠∠，∴1902AOP BOF∠=︒+∠，∵∠COE=∠BOF，射线OP是COE∠的角平分线，∴∠POC=11=22COE BOF∠∠，∴∠AOP=90°-∠COP=90°-11=9022COE BOF∠︒-∠，∴1902AOP BOF∠=︒-∠，∵∠COE=90°+∠COF=∠BOF，射线OP是COE∠的角平分线，∴∠POC=11=22COE BOF∠∠，∴∠AOP=90°-∠COP=90°-11=9022COE BOF∠︒-∠，∴1902AOP BOF∠=︒-∠，∵∠COE=90°+∠BOE=∠BOF，射线OP是COE∠的角平分线，∴∠POC=11=22COE BOF∠∠，∴∠AOP=90°+∠COP=90°+11=9022COE BOF∠︒+∠，∴1902AOP BOF∠=︒+∠；综上：1902AOP BOF∠=︒+∠或1902AOP BOF∠=︒-∠．【点睛】本题考查余角定义，角平分线有关的运算，一元一次方程，分类讨论思想的应用，掌握余角定义，角平分线有关的运算，一元一次方程，分类讨论思想的应用是解题关键．5、 (1)见解析(2)见解析【解析】【分析】（1）根据EO⊥AB，可得∠EOB=∠EOC+∠COB=90°，再根据2∠EOC=∠COB，即可求出AOD的度数．（2）根据EO⊥AB，FO⊥CD，可得∠EOC+∠COB=∠EOF+∠EOC=90°，即可得证∠COB=∠EOF．(1)解：∵EO⊥AB∴∠EOB=∠EOC+∠COB=90°∵2∠EOC=∠COB∴3∠EOC=90°∴∠EOC=30°∴∠AOD=∠COB=2∠EOC=60°(2)证明：∵EO⊥AB，FO⊥CD∴∠EOC+∠COB=∠EOF+∠EOC=90°∴∠COB=∠EOF【点睛】此题考查了角度的计算以及证明，解题的关键是掌握垂直的定义以及性质、对顶角相等．。

2019-2020学年度初中七年级下册数学第8章角8.1 角的表示青岛版课后练习三十六

A、69°
B、111°
C、159°
D、141°
【答案】：
【解析】：
时钟9点30分时，分针和时针之间形成的角的大小等于( )
A、75°
B、90°
C、105°
D、120°
【答案】：
【解析】：
下列说法中错误的有( )（1）线段有两个端点，直线有一个端点；（2）角的大小与我们画出的角的两边的长短无关；（3）线段上有无数个点；（4）同角或等角的补角相等；（5）两个锐角的和一定大于直角
2019-2020学年度初中七年级下册数学第8章角8.1角的表示青岛版课后练习三十六
3点30分时，时钟的时针与分针所夹的锐角是( )
A、70°
B、75°
C、80°
D、90°
【答案】：
【解析】：
一个人从A点出发向北偏东6，那么∠ABC等于( )
【答案】：
【解析】：
【答案】：
【解析】：
一货船沿北偏西62°方向航行，后因避礁先向右拐28°，再向左拐28°，这时货船沿着______方向前进．
【答案】：
【解析】：
计算：12°24′=______；56°33′+23°27′=______
【答案】：
【解析】：
如图所示，OB为正北方向，直线AD，BG，FC相交于点O，且AD与BG相互垂直，OE为南偏东25°的射线，且OE平分∠FOD，求∠COB的度数．
【解析】：
钟表在3点时，它的时针和分针所组成的角（小于180°）是( )
A、30°
B、60°
C、75°
D、90°
【答案】：
【解析】：
用量角器测得∠MON的度数，下列操作正确的是( )
A、
B、

青岛版七下数学8.1 角的表示训练题及答案

青岛版七下数学8.1 角的表示训练题及答案一、选择题（共10小题；共50分）1. 已知∠α=32∘，则∠α的补角为 ( )A. 58∘B. 68∘C. 148∘D. 168∘2. 如果α与β互为余角，则 ( )A. α+β=180∘B. α−β=180∘C. α−β=90∘D. α+β=90∘3. 已知∠A=65∘，则∠A的补角等于 ( )A. 125∘B. 105∘C. 115∘D. 95∘4. 如图所示，点O在直线AB上，∠COB=∠DOE=90∘，那么图中相等角的对数是A. 3B. 4C. 5D. 75. 如图所示，下列说法：（1）∠ECG和∠C是同一个角；（2）∠OGF和∠DGB是同一个角；（3）∠DOF和∠EOG是同一个角；（4）∠ABC和∠ACB是同一个角．其中正确的个数为A. 1B. 2C. 3D. 46. 如图所示，在∠AOB的内部有4条射线，则图中小于平角的角的个数为A. 10B. 15C. 5D. 207. 如果∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系是 ( )A. ∠1=∠3B. ∠1=180∘−∠3C. ∠1=90∘+∠3D. 以上都不对8. 若∠1，∠2互为补角，且∠1>∠2，则∠2的余角是 ( )A. 12(∠1+∠2) B. ∠1−90∘ C. 12∠1−∠2 D. 12(∠2−∠1)9. 已知∠A的余角和∠B的补角互补，则下列说法错误的是 ( )A. ∠A和∠B互余B. ∠A的补角和∠B的余角也互补C. ∠A和∠B都是锐角D. ∠A和∠B的差的绝对值为90∘10. 已知：如图所示，点A，O，B在一条直线上，∠AOC=∠BOC，若∠1=∠2，则图中互余的角共有A. 5对B. 4对C. 3对D. 2对二、填空题（共5小题；共25分）11. 从A沿北偏东60∘的方向行驶到B，再从B沿南偏西20∘的方向行驶到C，•则∠ABC=度．12. 已知∠ABC=30∘，BD是∠ABC的平分线，则∠ABD=度．13. 一个角的补角与它的余角的4倍的和等于周角的1718，则这个角为．14. 如图，在∠AOB内以点O为端点的射线有n条，则图中共有个角．15. 如图所示，在锐角∠AOB内部，画1条射线，可得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；⋯．照此规律，画6条不同射线，可得锐角个．三、解答题（共6小题；共78分）16. 如图所示，我海军的两艘军舰（分别在A，B两处）同时发现了一艘敌舰，其中A舰发现它在北偏东15∘的方向上，B舰发现它在东北方向上，试画出这艘敌舰的位置（用字母C表示）．17. 如图所示，A地和B地都是海上观测站，从A地发现它的北偏东60∘方向有一艘船，同时，从B地发现这艘船在它的北偏东30∘方向，试在图中确定这艘船的位置．18. 已知一个角的补角等于这个角的余角的4倍，求这个角的度数．19. 如图，∠A+∠B=90∘，点D在线段AB上，点E在线段AC上，DF平分∠BDE，DF与BC交于点F．(1) 依题意补全图形；(2) 若∠B+∠BDF=90∘，求证：∠A=∠EDF．证明：∵∠A+∠B=90∘，∠B+∠BDF=90∘，∴（理由：）．∵，∴∠BDF=∠EDF（理由：）．∴∠A=∠EDF．20. 如图①所示，∠AOB，∠COD都是直角．(1) 试猜想，∠AOD和∠BOC在数量上是否存在相等、互余或互补关系？你能说明你猜想的正确性吗？(2) 当∠COD绕点O旋转到如图②所示的位置时，你的猜想还成立吗？21. 一天24小时中，时钟的时针和分针共形成多少次平角？多少次周角？答案第一部分1. C2. D3. C4. C5. B6. B7. C8. B9. D 10. B第二部分11. 4012. 1513. 40∘14. (n+1)(n+2)215. 28第三部分16. (1)如图所示，分别以点A、点B为中心建立方位图，表示东北方向的射线BE与表示北偏东15∘方向的射线AD的交点C即为这艘敌舰的位置．17. (1)如图所示，作∠1=60∘，∠2=30∘，两射线相交于点P，则点P即为所求．18. (1) 设这个角为x，则它的补角为(180∘−x)，余角为(90∘−x)．由题意得180∘−x=4(90∘−x)．解得x=60∘．答：这个角的度数为60∘．19. (1)19. (2) ∠A=∠BDF，同角的余角相等；DF平分∠BDE，角平分线定义．20. (1) ∠AOD与∠BOC互补．理由如下：∵∠AOD=90∘+∠BOD，∠BOD=90∘−∠BOC，∴∠AOD=90∘+90∘−∠BOC,即∠AOD+∠BOC=180∘.所以∠AOD与∠BOC互补．20. (2) ∠AOD与∠BOC互补仍然成立．理由如下：∵∠AOB，∠COD都是直角，∴∠AOB+∠COD=180∘.∴∠AOB+∠BOC+∠COD+∠AOD=360∘，所以∠BOC+∠AOD=180∘.即∠BOC与∠AOD互补．21. (1) 一天24小时中，时钟的时针和分针共形成22次平角，22次周角．。

近年-近年学年七年级数学下册第8章角8.1角的表示作业设计(无答案)青岛版(最新整理)

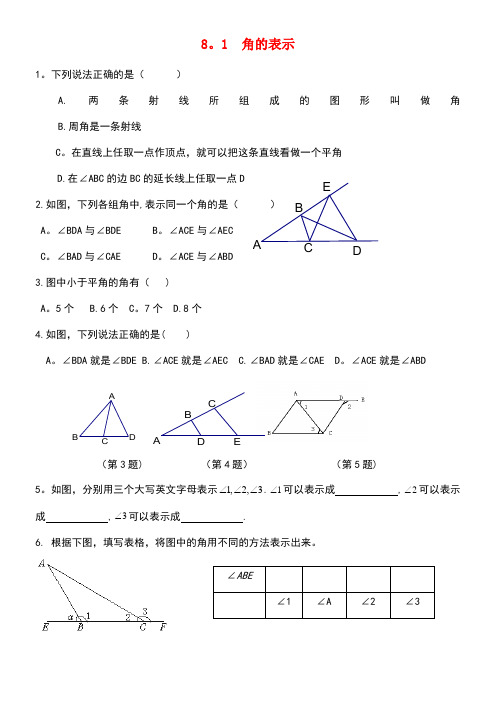
D C B A ED C B AE D C B A 8。

1 角的表示1。

下列说法正确的是（）A.两条射线所组成的图形叫做角B.周角是一条射线C 。

在直线上任取一点作顶点，就可以把这条直线看做一个平角D.在∠ABC 的边BC 的延长线上任取一点D2.如图，下列各组角中,表示同一个角的是（）A 。

∠BDA 与∠BDEB 。

∠ACE 与∠AECC 。

∠BAD 与∠CAE D 。

∠ACE 与∠ABD3.图中小于平角的角有（ )A 。

5个 B.6个 C 。

7个 D.8个4.如图，下列说法正确的是( )A 。

∠BDA 就是∠BDE B.∠ACE 就是∠AEC C.∠BAD 就是∠CAE D 。

∠ACE 就是∠ABD（第3题) （第4题）（第5题)5。

如图，分别用三个大写英文字母表示1,2,3∠∠∠.1∠可以表示成 ,2∠可以表示成 ,3∠可以表示成 .6. 根据下图，填写表格，将图中的角用不同的方法表示出来。

∠ABE∠1 ∠A ∠2 ∠37.下面各图中哪些角可以用一个大写英文字母表示?哪些角必须用三个大写英文字母表示？把它们写出来。

8。

如图,图（1)有个角,图（2）中有，图（3）中有 ,以此类推,若一个角内有n 条射线,此时共有个角.尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in ourbusy schedule. We proofread the content carefully before the release of 图(3)图(2)图(1)this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

青岛版(五四)数学七年级下8.1角的表示(同步练习)

8.1 角的表示
1.如图，若OC 平分AOB ∠，则____________AOC AOB AOC ∠=∠∠=∠，．
2. 如图，图中小于平角的角有______个，其中可以用一个大写字母表示的角有_____个，它们是_______．
3. 如图，三条直线AB CD EF 、、交于同一点O ，则图中以点O 为顶点的角(小于平角)共有( )
A ．6个
B ．8个
C ．10个
D ．12个
4.下列四个图形中，能用∠1、∠AOB 、∠O 三种方法表示同一个角的是（）
5.下列说法：
①由两条线段组成的图形叫做角；
②角的大小与边的长短无关，只与两条边张开的幅度有关；
③角的两条边是两条射线；
④把一个角放到一个可放大10倍的放大镜下观看，角的度数也扩大为原来的10倍. 其中正确的有（）
A.1个
B.2个
C.3个
D.4个
参考答案
1. 2. 3.D 4. B 5.B 初中数学试卷。

难点详解青岛版七年级数学下册第8章角专题测评练习题(精选含解析)

青岛版七年级数学下册第8章角专题测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、关于角的描述错误的是（）A．∠1与∠AOB表示同一个角B．∠AOC可以用∠O表示C．∠AOC＝∠AOB+∠BOC D．∠β表示∠BOC2、如果∠A的两边分别垂直于∠B的两边，那么∠A和∠B的数量关系是（）A．相等B．互余或互补C．互补D．相等或互补的平3、如图，已知O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，若OC是MOB分线，则下列结论正确的是（）A ．3AOM NOC ∠=∠B ．2AOM NOC ∠=∠C ．23AOM NOC ∠=∠D ．35AOM NOC ∠=∠4、若5318A '∠=︒，则A ∠的补角的度数为（）A ．3642'︒B ．3682'︒C ．12642'︒D ．12682'︒5、如图，90ACB ∠=︒，CD AB ⊥，垂足为点D ，则点C 到直线AB 的距离是（）A ．线段AC 的长度B ．线段CB 的长度C ．线段CD 的长度 D ．线段AD 的长度6、若点A 在点O 的北偏西15︒，点B 在点O 的西南方向，则AOB ∠的度数是（） A ．60︒ B ．75︒ C ．120︒ D ．150︒7、如图，∠AOC 和∠BOD 都是直角，如果∠DOC ＝38°，那么∠AOB 的度数是（）A ．128°B ．142°C ．38°D ．152°8、一个角加上20°后，等于这个角的余角，则这个角的度数是（）A ．35°B ．45°C ．60°D ．80°9、如图，∠BOC ＝90°，∠COD ＝45°，则图中互为补角的角共有（）A ．一对B ．二对C ．三对D ．四对10、下列命题：①若AC BC =，则点C 是线段AB 的中点；②若2AOB AOC ∠=∠，则射线OC 平分AOB ∠（AOB ∠小于平角）；③若12AB BC AC ==，则点B 是线段AC 的中点；④若AOC BOC ∠=∠，则射线OC 平分AOB ∠（AOB ∠小于平角），其中真命题的个数是（）A ．1B ．2C ．3D ．4第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、一块手表上午6点45分，此时时针分针所夹锐角的大小为__________度．2、将一副三角板如图所示摆放，使其中一个三角板60°角的顶点与另一个三角板的直角顶点重合，若已知25828'∠=︒，则1∠的度数是__________；3、如图，直线AB 、CD 相交于点E ，EF ⊥AB 于E ，若∠CEF ＝58°，则∠BED 的度数为______．4、已知∠α与∠β互余，且∠α=35°30′，则∠β=______度．5、9830'18︒"＝_____度，90°﹣3527'︒＝___° __'．三、解答题（5小题，每小题10分，共计50分）1、如图，O 是直线AB 上一点，COD ∠是直角，OE 平分BOC ∠．(1)若30BOD ∠=︒，则COE ∠=__________；(2)若AOC α∠=，求DOE ∠=__________（用含α的式子表示）；(3)在AOC ∠的内部有一条射线OF ，满足1()23AOC AOF AOF BOE ∠-∠=∠+∠，试确定AOF ∠与DOE ∠的度数之间的关系，并说明理由． 2、如图，直线AB ，CD 相交于点O ，OF ⊥CD ，OE 平分∠BOC ．(1)若∠BOE ＝60°，求∠DOE 的度数；(2)若∠BOD ：∠BOE ＝2：3，求∠AOF 的度数．3、如图，已知90AOB ∠=︒，60EOF ∠=︒，OE 平分AOB ∠，OF 平分BOC ∠，求AOC ∠的度数．4、若关于x ，y 的多项式()21402513m x n x y ⎛⎫-+-+-+ ⎪⎝⎭的值与字母x 取值无关． (1)求2m n -的值；(2)已知∠AOB =m °，在∠AOB 内有一条射线OP ，恰好把∠AOB 分成1：n 的两部分，求∠AOP 的度数．5、已知O 是直线AB 上一点，OC 是从点O 引出的一条射线，且∠AOC <∠BOC ，在直线AB 的上方作∠COD ，满足∠BOC -∠COD =90°．(1)如图，若OD 是∠AOC 的平分线，求∠COD 的度数；(2)若∠COD=n ，求∠BOC -∠AOD 的大小．（用含n 的式子表示）-参考答案-一、单选题1、B【解析】【分析】根据角的概念及角的表示方法即可求出答案．【详解】解：A ．1∠与AOB ∠表示同一个角，故选项正确，不符合题意．B ．由于顶点O 处，共有3个角，所以AOC ∠不可以用O ∠来表示，故选项错误，符合题意．C ．由图可知AOC AOB BOC ∠=∠+∠，故选项正确，不符合题意．D ．由图可知β∠与BOC ∠表示同一个角，故选项正确，不符合题意．故选：B ．【点睛】本题考查角的概念及角的表示方法，解题的关键是正确理解角的表示方法，本题属于基础题型．2、D【解析】【分析】由题意直接根据∠A 的两边分别垂直于∠B 的两边画出符合条件的图形进行判断即可.【详解】解：BD ⊥AD ，CE ⊥AB ，如图：∵∠A ＝90°﹣∠ABD ＝∠DBC ，∴∠A 与∠DBC 两边分别垂直，它们相等，而∠DBE＝180°﹣∠DBC＝180°﹣∠A，∴∠A与∠DBE两边分别垂直，它们互补，故选：D．【点睛】本题考查垂线及角的关系，解题关键是根据已知画出符合条件的图形．3、B【解析】【分析】BON AOM利用角平分线的定义再求解先求解21802,AOM BOC BON CON从而可得答案.180218022,【详解】MON解：90,AOM BON90,BON AOM21802,BOMOC平分,1MOC BOC MOB,2AOM BOC BON CON180218022,AOM AOM CON18018022,AOM CON2.故选B【点睛】本题考查的是角的和差运算，角平分线的定义，熟练的运用角的和差关系探究角与角之间的关系是解本题的关键.4、C【解析】【分析】根据补角的性质，即可求解．【详解】解：∵5318A '∠=︒，∴A ∠的补角的度数为180180531812642A ''︒-∠=︒-︒=︒．故选：C【点睛】本题主要考查了补角的性质，熟练掌握互为补角的两个角的和等于180°是解题的关键．5、C【解析】【分析】直线外一点到直线的垂线段的长度，叫做点到直线的距离，根据点到直线的距离的定义解答即可．【详解】∵CD AB ⊥于D ，∴点C 到直线AB 的距离是指线段CD 的长度．故选：C ．【点睛】本题考查了点到直线的距离的定义，点到直线的距离是一个长度，而不是一个图形，也就是垂线段的长度，而不是垂线段．6、C【解析】【分析】先画出符合题意的图形，如图，由题意得：15,45,,AON SOBWOB NS WO 再求解,AOW再利用角的和差关系可得答案.【详解】解：如图，由题意得：15,45,,AON SOB WOB NS WO901575,AOW 7545120,AOB 故选C【点睛】本题考查的是方向角的含义，角的和差关系，掌握“方向角的定义”是解本题的关键.7、B【解析】【分析】首先根据题意求出52AOD ∠=︒，然后根据AOB AOD BOD ∠=∠+∠求解即可．【详解】解：∵∠AOC 和∠BOD 都是直角，∠DOC ＝38°，∴903852AOD AOC DOC ∠=∠-∠=︒-︒=︒，∴5290142AOB AOD BOD ∠=∠+∠=︒+︒=︒．故选：B ．【点睛】此题考查了角度之间的和差运算，直角的性质，解题的关键是根据直角的性质求出AOD ∠的度数．8、A【解析】【分析】设这个角的度数是x ，则这个角的余角的度数是90x ︒- ，根据“一个角加上20°后，等于这个角的余角，”列出方程，即可求解．【详解】解：设这个角的度数是x ，则这个角的余角的度数是90x ︒- ，根据题意得：2090x x +︒=︒- ，解得：35x =︒ ，即这个角的度数是35°．故选：A【点睛】本题主要考查了余角的性质，一元一次方程的应用，熟练掌握互为余角的两个角的和等于90°是解题的关键．9、C【解析】【分析】根据∠BOC ＝90°，∠COD ＝45°求出∠AOC ＝90°，∠BOD ＝45°，∠AOD ＝135°，进而得出答案．【详解】解：∵∠BOC＝90°，∠COD＝45°，∴∠AOC＝90°，∠BOD＝45°，∠AOD＝135°，∴∠AOC+∠BOC＝180°，∠AOD+∠COD＝180°，∠AOD+∠BOD＝180°，∴图中互为补角的角共有3对，故选：C．【点睛】本题考查了补角的定义，理解互为补角的两角之和为180°是解题的关键．10、B【解析】【分析】线段上的一点把这条线段分成相等的两部分，称此点为线段的中点；在角的内部且经过角的顶点的射线把这个角分为相等的两个角，称此射线为角平分线；根据线段中点、角平分线的概念逐项判断即可．【详解】①当点C不在线段AB上时，则点C不是线段AB的中点，故是假命题；②当∠AOC在∠AOB的外部时，则射线OC不是AOB的平分线，故是假命题；③根据线段中点的定义知，此命题是真命题；④根据角平分线的定义知，此命题是真命题；故正确的命题有2个．故选：B．【点睛】本题考查了线段中点、角平分线的概念，掌握这两个概念是关键．二、填空题1、67.5【分析】6点45分时，分针指向9，时针在指向6与7之间，则时针45分钟转过的角度即为6时45分时，时钟的时针与分针的夹角度数，根据时针每分钟转0.5°，计算2×30°+30°-0.5°×45即可．【详解】解：∵6点45分时，分针指向9，时针在指向6与7之间，∴时针45分钟转过的角度即为6时45分时，时钟的时针与分针的夹角度数，即2×30°+30°-0.5°×45=67.5°．故答案为：67.5．【点睛】本题考查了钟面角：钟面被分成12大格，每格30°；分针每分钟转6°，时针每分钟转0.5°．2、28°28′【解析】【分析】∠=︒，求出∠EAC的度数，再根据∠1＝∠BAC−∠EAC即可得出答案．根据∠DAE＝90°，25828'【详解】∠=︒，解：∵∠DAE＝90°，25828'∴∠EAC＝31°32′，∵∠BAC＝60°，∴∠1＝∠BAC−∠EAC＝60°-31°32′＝28°28′，故答案为：28°28′．【点睛】本题主要考查了余角的概念和度分秒的换算，关键是求出∠EAC的度数，是一道基础题．【解析】略4、54.5【解析】【分析】根据90°－∠α即可求得β∠的值．【详解】解：∵∠α与∠β互余，且∠α=35°30′，∴∠β903530'=︒-︒896035305430'''=︒-︒=︒ 30300.560'==︒ 54.5β∴∠=︒故答案为：54.5【点睛】本题考查了求一个角的余角，角度进制的转化，正确的计算是解题的关键．5、 90.505 54 33【解析】【分析】根据角度的和差以及角度值进行化简计算即可【详解】解：1830.3180.330.3==0.5056060''''==︒，∴9830'18︒"90.505=︒90°﹣3527'︒896035275433'''=︒-︒=︒故答案为：90.505,54,33【点睛】本题考查了角度的和差以及角度值，掌握角度值单位的转化是解题的关键．三、解答题1、 (1)30° (2)12α(3)5∠DOE -7∠AOF =270°【解析】【分析】（1）先根据∠DOB 与∠BOC 的互余关系得出∠BOC ，再根据角平分线的性质即可得出∠COE ；（2）先根据∠AOC 与∠BOC 的互余关系得出∠BOC ，再根据角平分线的性质即可得出∠COE ，再根据∠DOE 与∠COE 的互余关系即可得出答案；（3）结合（2）把所给等式整理为只含所求角的关系式即可．(1)解：∵∠COD 是直角，∠BOD =30°，∴∠BOC =90°-∠BOD =60°，∵OE 平分∠BOC ，∴∠COE 12BOC =∠=30°， (2)∵AOC α∠=，∴180BOC α∠=-，∵OE 平分∠BOC ，∴∠COE =∠BOE 119022BOC α=∠=-，∵∠COD 是直角，∴∠DOE =90°-∠COE =12α，(3)∵()123AOC AOF AOF BOE ∠-∠=∠+∠ ∴6∠AOF +3∠BOE =∠AOC -∠AOF ，∴7∠AOF +3∠BOE =∠AOC ，∵∠COD 是直角，OE 平分∠BOC ，∴∠BOE =90°-∠DOE ，由（2）可知，∠AOC =2∠DOE∴7∠AOF +3（90°-∠DOE ）=2∠DOE∴7∠AOF +270°=5∠DOE ，∴5∠DOE -7∠AOF =270°．【点睛】本题考查角的计算；根据所求角的组成进行分析是解决本题的关键；应用相应的桥梁进行求解是常用的解题方法；注意应用题中已求得的条件．2、 (1)∠DOE =120°；(2)∠AOF =45°．【解析】（1）根据角平分线的定义，得出∠EOC=∠BOE=60°，利用邻补角定义求出∠DOE即可；（2）根据角平分线的定义，∠BOD：∠BOE=2：3，求出∠BOD，再根据对顶角可求出∠AOC，利用垂直，求出∠AOF．(1)解：∵OE平分∠BOC，∠BOE=60°，∴∠EOC=∠BOE=60°，∴∠DOE=180°-60°=120°；(2)解：∵∠BOD：∠BOE=2：3，设∠BOD=x，则∠COE＝∠BOE＝32x，∵∠COE+∠BOE+∠BOD=180°，∴x+32x+32x=180°，∴x=45°，即∠BOD=45°，∵OF⊥CD，∠AOC=∠BOD=45°，∴∠COF=90°，∴∠AOF=90°-45°=45°．【点睛】本题考查了角平分线定义，邻补角定义，对顶角性质，垂直定义，角的计算等；正确找出各个角之间的关系是正确计算的关键．3、120°【解析】根据角平分线的定义得到∠BOE =12∠AOB =45°，∠BOC =2∠BOF ，再计算出∠BOF =∠EOF -∠BOE =15°，然后根据∠BOC =2∠BOF ，∠AOC =∠BOC +∠AOB 进行计算．【详解】解：∵OE 平分∠AOB ，OF 平分∠BOC ，∴∠BOE =12∠AOB =12×90°=45°，∠BOC =2∠BOF ，∵∠BOF =∠EOF -∠BOE =60°-45°=15°，∴∠BOC =2∠BOF =30°；∠AOC =∠BOC +∠AOB =30°+90°=120°．【点睛】本题主要考查了角的计算以及角平分线的定义，正确应用角平分线的定义是解题关键．4、 (1)116(2)40°或80°【解析】【分析】（1）不含x 的项，所以40−13m =0，−n +2=0，然后解出m 、n 即可；（2）把m 和n 代入，分∠AOP ：∠BOP =1：2和∠AOP ：∠BOP =2：1两种情况讨论，列式计算即可．(1)解：由题可知：40−13m =0，−n +2=0，解得：m =120，n =2，∴m −n 2=120−22=116；(2)解：由（1）得：m =120，n =2，∴∠AOB =120°，如图①，当∠AOP ：∠BOP =1：2时，∠AOP =13∠AOB =40°；如图②，当∠AOP ：∠BOP =2：1时，∠AOP =23∠AOB =80°；综上：∠AOP =40°或80°．．【点睛】本题考查了整式的加减，一元一次方程的解，以及角的运算，熟练掌握运算法则是解本题的关键．5、 (1)=30COD ∠︒(2)3n 或n ．【解析】【分析】（1）过点O 作OE ⊥AB ，由∠BOC -∠COD =90°可得COE COD ∠=∠，根据OD 是∠AOC 的平分线可得COD AOD ∠=∠，从而=COD AOD COE ∠=∠∠，再由++=90COD AOD COE ∠∠∠︒可得结论；（2）分OD 在OC 左右两侧讨论求解即可．(1)如图，过点O 作OE ⊥AB ，∴90BOC COE ∠-∠=︒∵90BOC COD ∠-∠=︒∴COE COD ∠=∠∵OD 是∠AOC 的平分线∴COD AOD ∠=∠∴=COD AOD COE ∠=∠∠∵++=90COD AOD COE ∠∠∠︒∴3=90COD ∠︒∴=30COD ∠︒(2)当OD 在OC 左侧时，如图，过点O 作OM ⊥AB ，∴90BOC COM ∠-∠=︒∵90BOC COD ∠-∠=︒∴COM COD n ∠=∠=∴90902AOD COD COM n ∠=︒-∠-=︒-∴90+(902)3BOC AOD n n n ∠-∠=︒-︒-=；当OD 在OC 右侧时，如图，∵90BOC COD ∠-∠=︒∴90BOD AOD ∠=∠=︒∴9090BOC AOD COD COD n ∠-∠=∠+︒-︒=∠=综上，BOC AOD ∠∠-的大小为3n 或n ．【点睛】本题主要考查了角的计算以及角平分线定义的运用，解题时注意：从一个角的顶点出发，把这个角分成两个相等角的射线叫作这个角的平分线，解决问题的关键是根据角的和差关系进行计算．。

七年级数学下册第8章角单元综合测试题(无答案)(新版)青岛版

第八章角【典型例题】例 1. 如图所示，填空：（1）图中能用一个字母表示的角为__________；（2）写出以B 为顶点的角为__________；（3）写出以D 为顶点的角为__________（小于平角的角）。

A B C D E A BO C D EF例2. 如图所示，在直线AB 上有一点O ，作射线OC 、OD 、OE 、OF ，则图中共有多少个小于平角的角？例3. （1）计算：180°－（48°39′40″＋67°41′35″）＝__________；（2）比较大小：1003度__________33.3°；（3）由2点15分到2点30分，时钟的分针转过的角度是__________。

例4. （1）如果一个角的补角是120°，那么这个角的余角是（）A 。

150°B 。

90°C 。

60°D 。

30°（2）如图，将一副三角板折叠放在一起，使直角的顶点重合于点O ，则∠AOC ＋∠DOB ＝__________。

一. 选择题1. 如图所示，从点O 出发有五条射线，可以组成的角的个数是（）A. 4B. 7C. 8D. 102. 钟表上的时间指示为两点半，这时时针和分针之间形成的（小于平角）角的度数是（）A. 120°B. 150°C. 105°D. 90°3. 已知射线OA 、OB ，能判定OC 是∠AOB 的平分线的是（）A. ∠AOC ＝∠BOCB. ∠AOB ＝2∠AOCC. ∠BOC ＝12∠AOB D. A 、B 、C 都能4. 小明由A 点出发向正东方向走10米到达B 点，再由B 点向东南方向走10米到达C 点，则正确的是（）A. ∠ABC ＝22.5°B. ∠AB C ＝45°C. ∠ABC ＝67.5°D. ∠ABC ＝135°*5. 如图所示，射线OB 、OC 将∠AOD 分成三部分，下列判断错误的是（）A B C ABD12A. 如果∠AOB ＝∠COD ，那么∠AOC ＝∠BODB. 如果∠AOB ＞∠COD ，那么∠AOC ＞∠BODC. 如果∠AOB ＜∠COD ，那么∠AOC ＜∠BODD. 如果∠AOB ＝∠BOC ，那么∠AOC ＝∠BOD*6. 如图所示，若∠AOB ＝∠COD ，那么（）A. ∠1＞∠2B. ∠1＝∠2C. ∠1＜∠2D. 不确定二. 填空题1. 从一个角的顶点引出的一条射线，可以把这个角分成两个角，如果____________________，那么这条射线叫做这个角的平分线。

2019-2020年数学七年级下册第8章角8.1 角的表示青岛版巩固辅导八

2019-2020年数学七年级下册第8章角8.1 角的表示青岛版巩固辅导八第1题【单选题】如果时钟上的时针、分针和秒针都是匀速地转动，那么从3时整（3:00）开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有( )A、1次B、2次C、3次D、4次【答案】：【解析】：第2题【单选题】如图所示，由M观测N的方向是( )A、北偏西60°B、南偏东60°C、北偏西30°D、南偏东30°【答案】：【解析】：第3题【单选题】如果从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的( )A、南偏西30°方向B、南偏西60°方向C、南偏东30°方向D、南偏东60°方向【答案】：【解析】：第4题【单选题】下图中，小于平角的角有( )?A、5个B、6个C、7个D、8个【答案】：【解析】：第5题【单选题】小明在操场上从A点出发，先沿南偏东30°方向走到B点，再沿南偏东60°方向走到C点.这时，∠ABC的度数是( )A、120°B、135°C、150°D、160°【答案】：【解析】：第6题【单选题】如图所示的四条射线中，表示南偏东65°的是( )A、射线OAB、射线OBC、射线OCD、射线OD【答案】：【解析】：第7题【单选题】如果在点O北偏西60°的某处有一点A，在点O南偏西20°的某处有一点B，则∠AOB的度数是( )A、100°B、70°C、<!--{cke_protected}{C}%3C!%2D%2D%5Bif%20gte%20mso%2010%5D%3E%0A%3Cstyle%3E%0A%20%2F* %20Style%20Definitions%20*%2F%0A%20table.MsoNormalTable%0A%09%7Bmso-style-name%3A%E6%99%AE%E9%80%9A%E8%A1%A8%E6%A0%BC%3B%0A%09mso-tstyle-rowband-size%3A0%3B%0A%09mso-tstyle-colband-size%3A0%3B%0A%09mso-style-noshow%3Ayes%3B%0A%09mso-style-priority%3A99%3B%0A%09mso-style-。

精品试题青岛版七年级数学下册第8章角专题测评试题(含答案及详细解析)

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知2532'A，则A∠=︒∠的补角等于（）A．6428'︒︒D．15468'︒B．6468'︒C．15428'2、如图，将一副三角尺按不同位置摆放，下列选项的摆放方式中∠1与∠2互余的是（）A．B．C．D．3、如图，O是直线AB上一点，则图中互为补角的角共有（）A ．1对B ．2对C ．3对D ．4对4、若点A 在点O 的北偏西15︒，点B 在点O 的西南方向，则AOB ∠的度数是（）A ．60︒B ．75︒C ．120︒D ．150︒5、钟表10点30分时，时针与分针所成的角是（）A ．120︒B ．135︒C ．150︒D ．225︒6、钟表上1时30分时，时针与分针所成的角是（）A ．150︒B ．120︒C ．135︒D ．以上答案都不对7、如图所示，若90AOB ∠=︒，则射线OB 表示的方向为（）．A ．北偏东35°B ．东偏北35°C ．北偏东55°D ．北偏西55°8、一个角的度数等于6020'︒，那么它的余角等于（）A ．4040'︒B ．3980'︒C ．11940'︒D ．2940'︒9、若一个角为45°，则它的补角的度数为（）A ．55°B ．45°C ．135°D ．125°10、如图，::2:3:4AOB BOC COD ∠∠∠=，射线OM 、ON 分别平分AOB ∠与COD ∠，MON ∠是直角，则COD ∠的度数为（）A ．70°B ．62°C ．60°D ．58°第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，将一副三角板的直角顶点重合，摆放在桌面上，当∠AOC ＝__________时，AB 所在直线与CD 所在直线互相垂直．2、如图，130∠=︒，则射线OA 表示是南偏东__________︒的方向．3、冬至是地球赤道以北地区白昼最短、黑夜最长的一天，在苏州有“冬至大如年”的说法．苏州冬至日正午太阳高度角是3524'︒，3524'︒的余角为__________︒．4、如图，将一副三角尺的直角顶点O 重合在一起．若∠COB 与∠DOA 的比是2：7，OP 平分∠DOA ，则∠POC ＝_________度．5、已知3728A '∠=︒，则它的余角是______．三、解答题（5小题，每小题10分，共计50分）1、若关于x ，y 的多项式()21402513m x n x y ⎛⎫-+-+-+ ⎪⎝⎭的值与字母x 取值无关． (1)求2m n -的值；(2)已知∠AOB =m °，在∠AOB 内有一条射线OP ，恰好把∠AOB 分成1：n 的两部分，求∠AOP 的度数．2、如图① ② 所示，将两个相同三角板的两个直角顶点O 重合在一起，像图① ② 那样放置．(1)若∠BOC =60°，如图①，猜想∠AOD 的度数；(2)若∠BOC =70°，如图②，猜想∠AOD 的度数；(3)猜想∠AOD 和∠BOC 的关系，并写出理由．3、如图（1），直线AB 、CD 相交于点O ，直角三角板EOF 边OF 落在射线OB 上，将三角板EOF 绕点O 逆时针旋转180°．(1)如图（2），设AOE n ∠=︒，当OF 平分BOD ∠时，求DOF ∠（用n 表示）(2)若40AOC ∠=︒，①如图（3），将三角板EOF 旋转，使OE 落在AOC ∠内部，试确定COE ∠与BOF ∠的数量关系，并说明理由．②若三角板EOF 从初始位置开始，每秒旋转5°，旋转时间为t ，当AOE ∠与DOF ∠互余时，求t 的值．4、如图，一副三角板的两个直角顶点重合在一起，交叉摆放．(1)如图1，若35CBD ∠=︒，则ABE ∠=______︒；(2)如图1，若CBD α∠=，求ABE ∠的度数；(3)如图2，根据（2）的条件，射线BM ，射线BN 分别是ABE ∠和CBE ∠的平分线，试判断当CBD ∠的度数改变时，MBN ∠的度数是否随之改变．若改变，请说明理由；若不改变，求它的度数．5、如图，,OB OE 是AOC ∠内的两条射线，OD 平分AOB ∠，12BOE EOC ∠=∠，若55DOE ∠=︒，150AOC ∠=︒，求EOC ∠的度数．-参考答案-一、单选题1、C【解析】【分析】补角的定义：如果两个角的和是一个平角，那么这两个角互为补角，据此求解即可．【详解】解：∵2532'∠=︒A ，∴A ∠的补角等于1801802532=15428A ︒''-∠=-，故选：C ．【点睛】本题考查补角，熟知互为补角的两个角之和是180°是解答的关键．2、D【解析】【分析】由题意直接根据三角板的几何特征以及余角的定义进行分析计算判断即可．【详解】解：A．∵∠1+∠2度数不确定，∴∠1与∠2不互为余角，故错误；B．∵∠1+45°+∠2+45°=180°+180°=360°，∴∠1+∠2=270°，即∠1与∠2不互为余角，故错误；C．∵∠1+∠2=180°，∴∠1与∠2不互为余角，故错误；D．∵∠1+∠2+90°=180°，∴∠1+∠2=90°，即∠1与∠2互为余角，故正确．故选：D．【点睛】本题主要考查余角和补角，熟练掌握余角的定义即若两个角的和为90°，则这两个角互为余角是解题的关键．3、B【解析】【分析】根据补角定义解答．【详解】解：互为补角的角有：∠AOC与∠BOC，∠AOD与∠BO D，共2对，故选：B．此题考查了补角的定义：和为180度的两个角互为补角，熟记定义是解题的关键．4、C【解析】【分析】先画出符合题意的图形，如图，由题意得：15,45,,AON SOBWOB NS WO 再求解,AOW再利用角的和差关系可得答案.【详解】解：如图，由题意得：15,45,,AON SOB WOB NS WO901575,AOW 7545120,AOB 故选C【点睛】本题考查的是方向角的含义，角的和差关系，掌握“方向角的定义”是解本题的关键.5、B【解析】【分析】根据时针与分针相距的份数乘以每份的度数，可得答案．解：10点30分时的时针和分针相距的份数是4.5，10点30分时的时针和分针所成的角的度数为30°×4.5=135°，故选：B.【点睛】本题考查的知识点是钟面角，解题关键是求出时针和分针之间的格子数，再根据每个格子对应的圆心角的度数，列式解答．6、C【解析】【分析】钟表上12个大格把一个周角12等分，每个大格30°，1点30分时针与分针之间共4.5个大格，故时针与分针所成的角是4.5×30°＝135°．【详解】解：∵1点30分，时针指向1和2的中间，分针指向6，中间相差4格半，钟表12个数字，每相邻两个数字之间的夹角为30°，∴1点30分分针与时针的夹角是4.5×30°＝135°．故选：C．【点睛】本题考查钟表时针与分针的夹角．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动（112）°，并且利用起点时间时针和分针的位置关系建立角的图形．7、A 【解析】【分析】根据同角的余角相等90BOD AOD AOD AOC ∠+∠=∠+∠=︒即可得，35BOD AOC ∠=∠=︒，根据方位角的表示方法即可求解．【详解】如图，90,35AOB AOC ∠=︒∠=︒90BOD AOD AOD AOC ∠+∠=∠+∠=︒35BOD AOC ∴∠=∠=︒即射线OB 表示的方向为北偏东35°故选A【点睛】本题考查了方位角的计算，同角的余角相等，掌握方位角的表示方法是解题的关键．8、D【解析】【分析】利用90°-6020'︒计算即可．【详解】一个角的度数等于6020'︒，那么它的余角等于90°-6020'︒=2940'︒，故选D ．【点睛】本题考查了互余即两个角的和是90°，正确理解互余的意义是解题的关键．9、C【解析】【分析】根据补角的性质，即可求解．【详解】解：∵一个角为45°，∴它的补角的度数为18045135︒-︒=︒．故选：C【点睛】本题主要考查了补角的性质，熟练掌握互补的两个角的和为180°是解题的关键．10、C【解析】【分析】设∠AOB的度数为2x°，则∠BOC的度数为3x°，∠COD的度数为4x°，根据射线OM，ON分别平分∠AOB与∠COD即可得出∠BOM＝x°，∠CON＝2x°，再根据∠MON＝∠CON＋∠BOC＋∠BOM＝90°即可得出关于x的一元一次方程，解方程求出x的值，即可得【详解】解：设∠AOB＝2x°，则∠BOC＝3x°，∠COD＝4x°，∵射线OM、ON分别平分∠AOB与∠COD∴∠BOM＝1∠AOB＝x°2∠CON＝1∠COD＝2x°2∵∠MON＝90°∴∠CON＋∠BOC＋∠BOM＝90°∴2x＋3x＋x＝90解得：x＝15∴∠COD=4x=15°×4＝60°．故选C【点睛】本题主要考查了角平分线的性质和角的和差关系，能根据图形准确找出等量关系列出方程是解题的关键．二、填空题1、105°或75°【解析】【分析】分两种情况：①AB⊥CD，交DC延长线于E，OB交DC延长线于F，②AB⊥CD于G，OA交DC于H求出答案．【详解】解：①如图1，AB⊥CD，交DC延长线于E，OB交DC延长线于F，∵∠B=45°，∠BEF=90°，∴∠CFO=∠BFE=45°，∵∠DCO=60°，∴∠COF=15°∴∠AOC=90°+15°=105°；②如图2，AB⊥CD于G，OA交DC于H，∵∠A=45°，∠AGH=90°，∴∠CHO=∠AHG=45°，∵∠DCO=60°，∴∠AOC=180°-60°-45°=75°；故答案为：105°或75°．【点睛】此题考查了三角形的角度计算，正确掌握三角板的度数及各角度的关系是解题的关键．2、60【解析】【分析】如图，利用互余的含义，先求解2的大小，再根据方向角的含义可得答案.解：如图，130,∠=︒2=90160,∴ 射线OA 表示是南偏东60︒的方向.故答案为：60【点睛】本题考查的是互余的含义，方向角的含义，掌握“方向角的含义”是解本题的关键.3、5436'︒【解析】【分析】两个角的和为直角，则称这两个角互为余角，简称互余，根据余角的概念即可求得结果．【详解】9035245436''︒-︒=︒故答案为：5436'︒【点睛】本题主要考查了余角的计算，掌握余角的概念是关键．4、20【解析】根据条件可知90AOB COD ∠=∠=︒，并且180COB DOA AOB COD ∠+∠=∠+∠=︒，再根据COB ∠与DOA ∠的比是2:7，可求DOA ∠，再根据角平分线的定义和角的和差关系即可求解．【详解】解：180COB DOA COB COA COB DOB AOB COD ∠+∠=∠+∠+∠+∠=∠+∠=︒，又COB ∠与DOA ∠的比是2:7，718014027DOA ∴∠=︒⨯=︒+， OP 平分DOA ∠，70DOP ∴∠=︒，20POC ∴∠=︒．故答案为：20．【点睛】本题考查了余角与补角，角平分线的定义，正确认识COB DOA ∠+∠AOB COD =∠+∠ 180=︒ 这一个关系是解题的关键，这是一个常用的关系，需熟记．5、'5232︒【解析】【分析】根据余角的定义求即可．【详解】解：∵3728A '∠=︒，∴它的余角是90°-3728'︒='5232︒，故答案为：'5232︒．【点睛】本题考查了余角的定义，如果两个角的和等于90°那么这两个角互为余角，其中一个角叫做另一个角的余角．三、解答题1、 (1)116(2)40°或80°【解析】【分析】（1）不含x 的项，所以40−13m =0，−n +2=0，然后解出m 、n 即可；（2）把m 和n 代入，分∠AOP ：∠BOP =1：2和∠AOP ：∠BOP =2：1两种情况讨论，列式计算即可．(1)解：由题可知：40−13m =0，−n +2=0，解得：m =120，n =2，∴m −n 2=120−22=116；(2)解：由（1）得：m =120，n =2，∴∠AOB =120°，如图①，当∠AOP ：∠BOP =1：2时，∠AOP =13∠AOB =40°；如图②，当∠AOP ：∠BOP =2：1时，∠AOP =23∠AOB =80°；综上：∠AOP =40°或80°．．【点睛】本题考查了整式的加减，一元一次方程的解，以及角的运算，熟练掌握运算法则是解本题的关键．2、(1)120°(2)110°(3)∠AOD+∠BOC=180°．理由见解析【解析】【分析】（1）由图①，先求得∠AOC=30°，根据∠AOD=∠AOC+∠COD即可求得；（2）根据∠AOB+∠COD+∠BOC+∠AOD=360°，∠AOD=360°﹣∠AOB﹣∠COD﹣∠BOC即可求得；（3）结合（1）（2）分情况讨论，按（1）（2）的方法即可求得∠AOD+∠BOC=180°(1)∵∠AOB=90°，∠BOC=60°∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°又∵∠COD=90°∴∠AOD=∠AOC+∠COD=30°+90°=120°(2)∵∠AOB+∠COD+∠BOC+∠AOD=360°∠AOB =90°，∠COD =90°，∠BOC =70°∴∠AOD =360°﹣∠AOB ﹣∠COD ﹣∠BOC =360°﹣90°﹣90°﹣70°=110°(3)猜想：∠AOD +∠BOC =180°．理由：如图① ∵∠AOD =∠AOC +∠COD =∠AOC +90°，∠BOC =∠COD ﹣∠BOD =90°﹣∠BOD ，∠AOC =∠BOD ，∴∠AOD +∠BOC =180°如图②∵∠AOB +∠COD +∠BOC +∠AOD =360°，∠AOB =90°，∠COD =90°，∴∠AOD =360°﹣∠AOB ﹣∠COD ﹣∠BOC =360°﹣90°﹣90°﹣∠BOC =180°﹣∠BOC∴∠AOD +∠BOC =180°【点睛】本题考查了几何图形中角度的计算，三角尺中角度的计算，数形结合是解题的关键．3、 (1)90DOF n ∠=︒-︒(2)①130COE BOF ∠+∠=︒，理由见解析；②4秒或22秒【解析】【分析】（1）利用角的和差关系求解,BOF ∠ 再利用角平分线的含义求解DOF ∠即可；（2）①设∠=COE β，再利用角的和差关系依次求解40AOE β∠=︒-， 50AOF β∠=︒+，130BOF β∠=︒-，从而可得答案；②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒．再分三种情况讨论：如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，再利用互余列方程解方程即可.(1)解：180,90,,AOB EOF AOE n∴ 18090BOF EOF AOE n ∠=︒-∠-∠=︒-︒∵OF 平分BOD ∠∴90DOF BOF n ∠=∠=︒-︒(2)解：①设∠=COE β，则40AOE β∠=︒-，∴()904050AOF ββ∠=︒-︒-=︒+∴()180********BOF AOF ββ∠=︒-∠=︒-︒+=︒-，∴130COE BOF ∠+∠=︒②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒．如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，则90540590t t -+-=，∴4t =如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，则90554090t t -+-=，方程无解，不成立如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，则59054090t t -+-=，∴22t =综上所述4t =秒或22秒【点睛】本题考查的是角的和差运算，角平分线的定义，角的动态定义的理解，互为余角的含义，清晰的分类讨论是解本题的关键.4、 (1)145°；(2)180ABE α∠=︒-；(3)不变，45MBN ∠=︒【解析】【分析】（1）根据∠ABC 和∠DBE 都为90°进行计算；（2）根据∠ABC 和∠DBE 都为90°进行计算；（3）根据角平分线的定义以及（2）的结论解答即可．(1)解：∠ABE ＝∠ABC ＋∠DBE −∠CBD ＝90°＋90°−35°＝145°；故答案为：145；(2)解：∵90ABC ∠=︒，CBD α∠=，∴90ABD α∠=︒-，∵90DBE ∠=︒，∴9090180ABE ABD DBE αα∠=∠+∠=︒-+︒=︒-；(3)解：不变，理由如下：∵BM 平分ABE ∠， ∴()1118090222MBE ABE αα∠=∠=︒-=︒-， ∵BN 平分CBE ∠， ∴()119045222NBE CBE αα∠=∠=︒-=︒-， ∴90454522MBN MBE NBE αα⎛⎫⎛⎫∠=∠-∠=︒--︒-=︒ ⎪ ⎪⎝⎭⎝⎭ 【点睛】本题考查了余角的定义和性质以及角平分线，关键是明确同角的余角相等，灵活运用角的和差关系进行计算．5、80°【解析】【分析】设∠BOE为x°，则∠DOB=55°-x°，∠EOC=2x°，然后根据角平分线定义列方程解决求出∠BOE，可得∠EOC．【详解】解：设∠BOE=x°，则∠DOB＝55°﹣x°，∠EOC可得∠EOC＝2x°，由∠BOE＝12由OD平分∠AOB，得∠AOB＝2∠DOB，故有2x+x+2（55﹣x）＝150，解方程得x＝40，故∠EOC＝2x＝80°．【点睛】本题主要考查了角平分线的定义以及角的计算，根据角平分线的性质和已知条件列方程求解．方程思想是解决问题的基本思考方法．。