投入产出分析
统计学第十二章 投入产出分析

18
全国实物型产品投入产出模型
•直接消耗系数
–直接消耗系数矩阵
a11 a12
A
a
21
a 21
an1 an1
– 全国实物表第一部分反映的主要是列名产品之间、列名 产品与未列名产品、个别行业之间的生产技术联系。
13
全国实物型产品投入产出表
• 实物表的结构—第二部分
– 第二部分是最终产品部分。它是由第一部分的产品分配 流向表在水平方向上的延伸, 因而其主栏与第一部分的 主栏相同, 宾栏是最终产品 。
– 从第二部分行的方向看, 是最终产品分配使用表。它不 仅反映了各种列名产品年总产品中可供社会最终消费、 积累和出口等的分配与使用, 而且可具体反映各列名产 品用于消费、积累、出口的比例关系。从列的方向看, 是最终产品构成表。它反映了各项最终需求都是由哪些 列名产品构成的, 体现了国民收入的实物构成。
• 全国实物表中的平衡j yij i Qi
k 1
jn
j 1
n
qij qi yi i Qi
j 1
16
全国实物型产品投入产出模型
•直接消耗系数
– 定义第 j 种产品对第 i 种产品的直接消耗系数aij为:
aij
qij Qj
– 第二部分主要反映的是社会经济联系。
14
全国实物型产品投入产出表
• 实物表的结构
– 从全国实物表水平方向看, 第一、二两部分构成一张矩 形表, 反映了各列名产品按其使用价值(经济用途)的分 配使用去向(中间产品和最终产品)及数量, 即; 中间产品 + 最终产品一进口 = 总产品
投入产出分析原理

第二节 投入产出分析原理
2.纵向看,各产业的总产值 = 各产业消耗的中间产品价 值 + 各产业的毛附加价值。
X11 X21 Xn1 D1 V 1 M 1 X1 X12 X22 Xn2 D2 V 2 M 2 X2 X1n X2n Xnn Dn Vn Mn Xn
在(I-A)可逆时(在实践情况下一般能满足该 条件),可将矩阵形式转化为:
X=(I-A)-1 Y
其中的(I-A)-1 称为列昂惕夫逆矩阵,可以通过昂 惕夫逆矩阵进行产业感应度和影响力的分析以及波及 效果分析等。
耗量。用aij表示第j产业产品对第i产业产品的直接消耗系 数,即生产单位j产业产品所消耗的i产业产品的数量。
aij
X ij Xj
第二节 投入产出分析原理
a11 a12 a1n
实物直接消耗系数矩阵 A =
a 21
a 22
a
2
n
a
n1
an2
a
nn
a11 a12 a1n
价值直接消耗系数矩阵 A =
产值必然相等。也就是把方程组中的n个方程(i=1,2,…,
n)连加起来。
nn
nn
= ( Xij Yi
( Xji Di Vi Mi)
i1 j1
i1 j1
(i=1,2,…,n)
n
n
即:
Yi =
(Di Vi M i)
(i=1,2,…,n)
i 1
i 1
第二节 投入产出分析原理
四、直接消耗系数和完全消耗系数 (一)直接消耗系数 直接消耗是指生产单位产品对某一产业产品的直接消
X11 X12 … X1n X21 X22 … x2n
… … ……
投入产出分析

从普通I-O表到资源环境I-O表
• 常用的改进方法: • 在第Ⅲ象限下方增加资源投入、污染排放
行或矩阵,反映在当期生产过程中各类资 源的投入量和各种污染物的排放量; • 或者在第Ⅰ象限用资源部门或污染部门行 来反映资源投入、污染排放量。
2. 投入产出模型中的系数
• 直接消耗系数 • 完全消耗系数 • 完全需要系数
×最终产品 = 总用水量,
• 完全用水系数的计算中并没有重复计算的 部分。
2. 需求拉动分析
• 需求拉动分析是以投入产出的行模型,即 需求拉动模型为基础,分析最终需求变化 对总产出以及最初投入等因素之影响的一 类分析技术。
• 利用需求拉动分析,可以研究最终需求总 量与结构变化对资源消耗和污染排放数量 的影响。
• 由于资源投入和污染排放的规模和总产出 规模具有密切的关系,所以在利用基本的 需求拉动模型确定总产出以后,只需将各 部门总产出乘以各部门的直接资源投入或 污染排放系数,就可以获得最终需求变动 对资源环境的影响量,而且得到的结果具 有一般均衡的意义,是完全的度量。
• 列模型(供给驱动模型)。
• 相比行模型而言,列模型的应用范围较小 。
• 一、投入产出分析的基本原理 • 二、常用投入产出分析技术
一、投入产出分析的基本原理
• 1. 投入产出表的设计 • 2. 投入产出模型中的系数 • 3. 投入产出模型 • 4. 投入产出模型的基本假定
1. 投入产出表的设计
• 投入产出表是一张行列交织的棋盘式平衡 表,其描述对象是一个相对独立经济系统 在一定时期内所发生的投入产出关系。
?由于资源投入和污染排放的规模和总产出规模具有密切的关系所以在利用基本的需求拉动模型确定总产出以后只需将各部门总产出乘以各部门的直接资源投入或污染排放系数就可以获得最终需求变动对资源环境的影响量而且得到的结果具有一般均衡的意义是完全的度量
投入产出分析

投入产出分析,在中国也被称为投入产出法,在日本被称为产业关联法,而在前苏联和东欧国家曾经被称为部门联系平衡法。
所有这些不同的名称,抽去它们在经济理论上的不同解释,就其作为一种经济数量分析方法来说,原理是一致的。
本节主要介绍投入产出的定义、关于投入产出模型的概念,以及投入产出分析理论与实践的发展。
可以用一句话给出投入产出分析的定义:投入产出分析是研究经济系统中各个部分之间在投入与产出方面相互依存的经济数量分析方法。
这里的经“济系统” ,可以是整个国民经济,也可以是地区、部门和企业,也可以是多个地区、多个部门、多个国家。
所谓部“分” ,是指所研究的经济系统的组成部分。
一般或者是指组成经济系统的各个部门,或者是指组成经济系统的各种产品和服务。
所谓投“入” ,是指各个部门或产品在其生产或者运营过程中所必须的各种中间投入和最初投入。
例如工业部门在其生产过程中必须有资本、劳动等最初投入和原材料、燃料、劳务等中间投入。
所谓“产出”,是指各个部门或产品的的产出量的分配与使用。
例如工业部门的产出量中一部分作为本部门的投入,一部分作为其它部门的投入,一部分用于消费,一部分作为资本品用于投资,一部分用于出口。
根据上述对投“入”和产“出”的定义,可以想见,一个经济系统的各个部分之间存在着错综复杂的相互依存关系,由这些关系将经济系统的各个部分连成为一个不可分割的整体。
通过对这些相互依存关系的描述和分析,就可以揭示经济系统中包含的各种数量关系,可以使人们更深入地了解与把握经济系统。
⒈世界范围内投入产出分析的发展美国经济学家列昂捷夫(Wassily Leontief )于 1931 年开始研究投入产出分析,编制美国 1919 年、 1929 年投入产出表,并用于美国的经济结构研究; 1936 年他发表了关于投入产出分析的第一篇论文“美国经济制度中的投入产出分析” (美国《经济学与统计学评论》 1936.8. );1941 年出版专著《美国经济结构: 1919—1929 》;在 1942-1944 年间,他又主持编制了 1939 年美国投入产出表; 1966 年出版专著《投入产出经济学》。
第七讲产业关联:投入产出分析

第七讲产业关联:投入产出分析第七讲产业关联:投入产出分析里昂惕夫对产业关联理论做出了杰出贡献,他创立的投入产出法(1936)有效地揭示了产业间技术经济联系的量的比例关系。
因此,人们也将产业关联理论也称为投入产出理论。
投入产出法是产业关联分析的基本工具。
投入产出分析是一种研究国民经济体系或区域经济体系中各个产业部门间投入与产出的相互依存关系的数量分析方法。
任何一个产业部门从事生产就必须消耗一些物质和劳务,投入产出中的“投入”就是指产品生产过程中所消耗的原材料、燃料、动力、固定资产折旧和劳动力。
所有这些消耗统称为“投入”。
各个产业部门生产出产品以后,要分配出去:一是作为其他产业部门的投入,即用于生产性消费;二是作为最终使用,即用于生活性消费和积累。
投入产出中的“产出”就是指产品生产出来后所分配的趋向、流向,即使用的方向和数量,又称流量,即用于以及多少用于生产性消费、生活性消费和积累。
因此,每个产业部门,既是消耗产品(即投入)的单位,又是生产产品(即产出)的单位。
投入产出法应用于国民经济体系中的产业关联分析,就是通过编制投入产出表(即把国民经济中所有部门的投入来源和产出去向排列成一张纵横交错的棋盘式表格)和建立相应的线性代数方程体系,构建一个模拟现实国民经济各产业部门产品间的相互“流入”“流出”的经济数学模型,来分析各产业间的各种重要比例关系。
一、投入产出表运用投入产出法,是通过投入产出表、投入产出模型来对产业间“投入”与“产出”的数量比例关系进行分析。
因此,投入产出表和投入产出模型是产业关联分析的基本工具。
投入产出表包括实物型和价值型两种类型,其中使用最为广泛的是价值型分析工具。
⒈实物型投入产出表实物型投入产出表是以产品的标准单位或自然单位计量的。
它显示了国民经济各部门主要产品的投入-产出关系,即这些主要产品的生产、使用情况,以及它们之间在生产消耗上的相互联系和比例关系。
⑴实物型投入产出表的一般形式简化的一般实物型投入产出表产出投入单位中间产品最终产品总产品产产产产合品品…品…品1 2 计产品1… …产品2… ……… … … … … … ………产品………… … … … … … ………产品… …劳动力… …-表中是指a3>.第种产品生产时所消耗的第种产品的数量,或者b.第种产品提供给种产品生产时的需要量。
第一章投入产出分析

第一章 投入产出分析的基本原理 第二章 全国实物型产品投入产出模型 第三章 全国价值型产品投入产出模型 第四章 投入产出分析在经济分析中的应用 第五章 投入产出分析在计划政策模拟 和预测中的应用 第六章 地区与地区间投入产出模型及应用
第一章 投入产出分析的基本 原理
第一节 投入产出分析 一 什么是投入产出分析 (一)投入产出法的命名 1 从研究问题方法的角度命名 得:投入产出法 投入产出法 投入产出技术 投入产出分析 注:三者之间的差别在于该方法是 方法” 技术” 分析工具” “方法”、 “技术”、 “分析工具”
2从这种方法说明问的角度命名 从这种方法说明问的角度命名 得:部门联系平衡法
产业关联(或部门联系) 产业关联(或部门联系)法
(二)对“投入”与“产出”的理解 投入” 产出” 1 投入 一般意义: 一般意义:
一定时期内(通常为一年)生 产过程中的消耗。
投入产出法中的投入: 投入产出法中的投入:
除包含上述含义外,还包含各种消耗的来源。 即哪些部门向本部门提供了产品及提供了多少。
二部类等式为
1500C2 + 750V2 + 100M 2C + 50M 2V + 600M 2 = 3000
3 归纳图示 4000 C1 + 400 M 1C + 1000V1 + 100 M 1V + 500 M 1
1500C 2 + 100 M 2C + 750V2 + 50 M 2V + 600 M 2
静态开模型 静态闭模型 静态局部闭模型
动态模型 2 按模型的计量单位不同 实物型 价值型
3 按模型描述的对象不同 宏观模型 微观模型
投入产出分析

aij 虽然与 X ij 是一一对应的,但 aij 并没有双重意义,它只反映由生产技术特征决定的
投入结构,仅在列的方向可以加总; 直接消耗系数虽由宏观数据得到,但具有微观技术定额的含义,在投入产出模型中被假
定为不变常数,作为系统内不变参数处理。
完全消耗系数
• 完全消bij耗系数反映部门间的完全依存关系
第Ⅰ象限
• 假定经济系统可以分为n个部门,则第Ⅰ象 限为一个n×n的矩阵,反映货物和服务在 部门间的流量。
• 第Ⅰ象限中,元素Xij具有双重含义,一方 面它表示当期第j部门在生产过程中对第i部 门产品的消耗量,即在j部门生产过程中有 Xij数量的i部门产品作为中间投入被j部门所 消耗;另一方面它表示当期i部门产品分配 给j部门使用的数量。
直接消耗系数
aij
X ij Xj
其中, X ij 为第 j 部门在生产过程中对第 i 部门产品的消耗量, X j 为第 j 部门总产出。
aij 的含义是第 j 部门生产单位产品对第 i 部门产品的消耗量,它反映两个部门之间的直
接依存关系。n×n 个 aij 构成的矩阵称为直接消耗系数矩阵,一般记为 A。
式中, Cij 表示第 j 类最终需求中对第 i 部门产品的需求量,
F j 表示第 j 类最终需求(消费、投资、出口)的总量,
Y T 表示各类最终需求合计。 所以, S 代表最终需求构成系数,
反映各类最终需求占最终需求总量的比例;
C 代表最终需求部门组成系数,
反映用于消费、投资和出口的产品中来自各个部门的比例。 利用该式,可以计算最终需求总量发生变化的影响, 最终需求构成和最终需求部门组成等结构性因素发生变化的影响。
需求拉动分析的基础模型:
投入产出分析的公式汇总

投入产出分析的公式汇总1.投入产出关系公式:经典的投入产出模型中,存在着两个基本的关系公式:Y=AX(1)Y=C+I+G+X-M(2)其中,Y代表总产出,A代表技术系数矩阵,X代表总投入,C代表消费支出,I代表投资支出,G代表政府支出,X代表出口,M代表进口。
公式(1)表示总产出等于技术系数矩阵与总投入的乘积。
公式(2)表示总产出等于消费支出、投资支出、政府支出、净出口的总和。
2.投入产出比例关系公式:在投入产出分析中,经常使用投入产出比例关系来计算各个产业或部门的相对重要性、波及效应、乘数效应等。
直接效应:产业A的投入产出比例(a)=产业A的产出(Y_A)/产业A的投入(X_A)。
介质效应:产业A的介质投入产出比例(a_d)=产业A的介质投入(D_A)/产业A的产出(Y_A)。
波及效应:产业A对产业B的波及系数(b_AB)=产业B的投入产出比例(b)*A产出对B投入的敏感度。
乘数效应:总产出的变化(ΔY)=产出变化的总乘数(Δm)*初始投入的变化(ΔX)。
3.投入产出改进公式:当经济的投入产出关系发生变化时,可以使用改进的投入产出公式来分析这种变化。
改进的技术系数矩阵A*=D^-1*A*B^-1(3)其中,A*表示改进后的技术系数矩阵,D表示需求变化矩阵,B表示产出变化矩阵。
公式(3)表示改进后的技术系数矩阵等于需求变化矩阵、技术系数矩阵和产出变化矩阵的乘积。
4.投入产出弹性公式:投入产出弹性用于衡量投入或产出变动对整体投入产出关系的影响程度。
产出弹性,E_Y=ΔY/Y÷ΔX/X(4)投入弹性,E_X=ΔX/X÷ΔY/Y(5)其中,ΔY表示总产出的变化,Y代表总产出,ΔX表示总投入的变化,X代表总投入。
公式(4)表示产出弹性等于总产出的变化与总投入的变化之比。
公式(5)表示投入弹性等于总投入的变化与总产出的变化之比。
总结:投入产出分析的公式包括投入产出关系公式、投入产出比例关系公式、投入产出改进公式和投入产出弹性公式等。
投入产出分析经济学

投入产出分析经济学引言投入产出分析是一种经济学工具,用于评估一个国家、地区或产业的经济活动。
它通过衡量产出与投入之间的关系,揭示了经济系统的结构和运作方式。
投入产出分析广泛应用于政府决策、产业规划和经济发展的研究中。
本文将介绍投入产出分析经济学的基本概念、原理和应用,以及其在经济学研究和实践中的重要性。
基本概念投入在投入产出分析中,投入通常指的是生产过程中使用的资源和要素,包括劳动力、资本、土地和原材料等。
这些投入会被用于生产过程中,从而产生最终的产品或服务。
产出产出是指经济活动中所得到的最终产品或服务。
在投入产出分析中,产出通常指的是一个国家、地区或产业的总产出,可以用来衡量经济活动的规模和质量。
产出可以是实物产品,也可以是服务。
投入产出表投入产出表是投入产出分析的核心工具,用于描述一个经济系统中各个部门间的投入产出关系。
它包含了各个产业的投入和产出数据,可以用来计算产业间的关联度、乘数效应和经济影响等指标。
原理和方法帕累托优化投入产出分析经济学中的帕累托优化原理是指通过合理分配资源和要素,使得经济系统的产出最大化。
帕累托优化的目标是在满足资源有限的情况下,最大化社会总产出和福利。
投入产出矩阵投入产出矩阵是投入产出分析中的一个重要概念,用于描述各个产业间的投入和产出关系。
投入产出矩阵是一个方阵,其中的每一个元素表示一个产业的投入或产出量。
通过矩阵运算,可以计算产业间的关联度和乘数效应等指标。
乘数效应乘数效应是指投入产出分析中的一种经济影响指标。
它描述了一个单位的增加在一个经济系统中所能带来的总产出增加量。
乘数效应可以用来评估政府政策、产业发展和经济增长等方面的影响。
应用领域投入产出分析经济学广泛应用于各个领域的经济研究和实践中。
以下是几个主要的应用领域:政府决策投入产出分析经济学可以帮助政府制定经济政策和决策。
通过分析投入产出关系,政府可以评估政策的影响,预测经济活动的变化,并制定相应的措施和政策。
《投入产出法》

投入产出法的基本作用——通过编制投入产出表和模型, 能够清晰地揭示国民经济各部门、产业结构之间的内在联系; 特别是能够反映国民经济中各部门、各产业之间在生产过程中 的直接与间接联系,以及各部门、各产业生产与分配使用、生 产与消耗之间的平衡(均衡)关系。正因为如此,投入产出法 又称为部门联系平衡法。此外,投入产出法还可以推广应用于 各地区、国民经济各部门和各企业等类似问题的分析。当用于 地区问题时,它反映的是地区内部之间的内在联系;当用于某 一部门时,它反映的是该部门各类产品之间的内在联系;当用 于公司或企业时,它反映的是其内部各工序之间的内在联系。
这样,列昂惕夫就较大地改变了瓦尔拉斯的以论证全 部均衡理论为目的的模型体系,使投入产出模型成为一种 以技术联系为基础、以研究经济系统中各部分之间相互依 存数量关系的分析方法。同时,也使这种分析方法有了实 际应用的可能。
四、投入产出法的产生与发展
(3) 设 n 维向量 ~p 是 n 种产品的价格向量,m 维向量 w~ 是
m 种要素价格向量。即
p1
~p
p2
pn
w1
w~
w2
wm
那么可知,为了生产第 j 种产品 X j 的数量,需要第 i 种 生产要素为aij X j 数量( ( j 1,2,, n) ,所以,全部产品
n
对第 i 种生产要素的总需求量是 aij X j (i 1,2,, m) 。 j 1
在均衡的条件下,每一种生产要素的供给等于需求,由此 得到 m 个方程:
n
aij X j Ri ,i 1,2,, m
j 1
(1·1)
下面来考虑总产品 X j 的确定(简单处理,方程的思想性十分重要):
根据一般均衡的思想,第 j 种产品的需求量取决于所有产品和要素
投入产出分析

1941—1947,1961—1965 美国劳工部顾问; 1943—1945 美国战略情报局俄国经济组顾问; 1961—1962 联合国秘书长顾问; 1966年以后 美国商务部顾问; 1975年从哈佛大学退休,到纽约大学。 1964 美国计量经济学会会长; 1970 美国经济学协会会长;
1930年,里昂惕夫回到了基尔大学世界经 济研究所,继续从事他的经济和统计研究工 作。由于他的研究成果已引起美国全国经济 研究局的注意,该局主席,著名经济学家韦 斯利·密契尔等便联名写信邀请他参加该局工 作。里昂惕夫接受了这个邀请,于1931年初 同其父到了纽约,随即定居美国,后加入美 国籍。
1931年,里昂惕夫任美国全国经济研究 局研究助理,一年后,他就转到了哈佛大 学经济系工作,他在哈佛大学经济系, 1931—1932年任讲师;1933一1938年任助 理教授;1939—1945年任副教授;1946— 1974任教授。
第一章 总论
第一节 投入产出分析概述 一、投入产出分析(Input-Output Abalysis)基本概念
投入:从事经济活动耗要的原燃材料、动力设备、 劳动力以及应该交纳的税金和应该得到的利润。
产出:经济活动的成果及其分配使用去向。
投入产出表:反映投入和产出关系的表格。 投入产出模型:反映投入和产出关系的数学 模型 。 投入产出分析:利用投入产出表和相应的投 入产出模型进行经济分析和预测。
——(美)保罗.萨缪尔森
瑞典皇家科学院公告
瑞典皇家科学院已决定将1973年度纪念阿 尔弗雷德.诺贝尔经济学景金授予美国马萨楮 塞州,坎布里奇,哈佛大学的华西里. 里昂惕 夫教授。因为投入产出法的发展,并且因为 它在重要经济问题上的应用。
里昂惕夫教授是投入产出技术独一的和 没有挑战的创始人。这项重要发明给了经济 科学一种经验上有用的方法,以阐明一个社 会的生产系统中的一般相互依赖关系。特别 是,这个方法提供系统地分析一个经济中的 复杂的产业之间的交易。
投入产出分析

投入产出分析投入产出分析是一种经济学工具,用于评估生产过程中资源投入和产出之间的关系。
它可以帮助企业和政府机构决策,优化资源配置,提高生产效率。
本文将探讨投入产出分析的概念、方法和应用,并结合实际案例进行解析。
首先,我们来了解一下投入产出分析的基本概念。
投入产出分析是一种宏观经济学方法,旨在分析一个经济体中各个部门之间的关联关系和相互依赖程度。
它通过测算一个单位资源投入时所创造的产出,并以此为基础,推算整个经济体的资源配置和产出情况。
投入产出分析的核心是构建一个投入产出表,记录各个部门的资源投入和产出情况。
在具体的方法上,投入产出分析采用了线性代数和矩阵分析的技术。
首先,我们需要将经济体划分为不同的部门,例如农业、工业、服务业等。
然后,我们通过调查和统计数据,确定各个部门的资源投入和产出情况,包括劳动力、物资、资本等。
接下来,我们构建一个投入产出矩阵,将各个部门之间的关系用矩阵表示。
通过矩阵运算,我们可以计算出每个部门的资源利用率、就业效益、生产乘数等指标,从而评估整个经济体的效益和可持续发展性。
投入产出分析的应用领域广泛。
首先,它可以用于评估政府政策的效果。
政府决策往往涉及资源配置和经济发展问题,投入产出分析可以帮助政府机构预测政策的影响,优化政策设计,实现经济可持续增长。
其次,它可以用于企业的经营决策。
企业在生产过程中面临资源投入和产出之间的权衡,投入产出分析可以帮助企业优化生产方案,提高资源利用效率,增加利润。
另外,投入产出分析还可以用于评估经济发展项目的可行性,研究产业链的发展潜力,支持区域经济发展规划等。
为了更好地理解投入产出分析的实际应用,我们以汽车制造业为例进行解析。
汽车制造业是一个典型的多部门产业,涉及到冶金、机械、橡胶、塑料、电子等多个部门之间的关系。
通过投入产出分析,我们可以评估汽车制造业对其他部门的资源需求,以及对就业和产出的影响。
同时,我们还可以估算汽车制造业在整个经济体中的比重,以及其对国内生产总值和出口收入的贡献。
投入产出分析

首先,收集某产业的投入产出表,利用投入产出模型分析该产业对其他产业的波及效果 。通过计算影响力系数、感应度系数等指标,评估该产业对经济增长的贡献。其次,分 析该产业的发展趋势和潜在问题,提出针对性的政策建议,以促进该产业的可持续发展
。
案例四:不同国家或地区的投入产出比较分析
总结词
该案例对不同国家或地区的投入产出进行了 比较分析,揭示了各国或地区产业结构的差 异和经济发展水平的差距。
影响力系数与感应度系数
总结词
衡量某一部门的变化对其他部门的影响程度和感应程度。
详细描述
影响力系数用于衡量某一部门对其他部门的拉动作用,感应度系数则衡量某一 部门对其他部门的推动作用,两者结合可以反映各部门在经济发展中的地位和 作用。
投入产出表的编制方法
总结词
采用多种方法综合编制投入产出表。
详细描述
投入产出分析
汇报人:可编辑 2024-01-08
目录
• 投入产出分析概述 • 投入产出表的编制 • 投入产出分析的应用 • 投入产出分析的局限性与改进 • 投入产出分析案例研究
01
投入产出分析概述
投入产出分析概述
• 请输入您的内容
02
投入产出表的编制
直接消耗系数
总结词
衡量生产单位产出的产品对其他产品 的直接消耗量。
详细描述
选取某特定行业,收集其投入产出表,利用 投入产出模型分析该行业与其他产业的关联 程度。通过计算直接消耗系数、完全消耗系 数等指标,评估该行业对其他产业的拉动作 用和依赖程度。最后,提出促进该行业发展 的政策建议,以推动经济增长。
案例三:某产业的波及效果分析
总结词
该案例对某产业的波及效果进行了深入分析,评估了该产业对其他产业的波及影响和产 生的经济效益。
第一章 投入产出分析导论

第三节 投入产出分析的理论基础
一、 关于国民经济分类的问题 〈一〉关于社会生产两大领域的划分 物质生产和非物质生产 〈二〉关于产业级次分类 第一、二、三产业、 〈三〉关于两大部类的划分 第一部类:生产资料 第二部类:消费资料
二、关于社会总产品的理论
(一) 国内总产出的概念: 国内总产出:是指一个国家或地区在一定时期内所有常住单 位所生产的货物和劳务的总价值。 常住单位是指在一国经济领土上具有经济利益中心的经济 单位。 一国经济领土是指由该国政府控制或拥有的地理领土再 加上该国住外的使领馆、科研站等机构,并相应扣除外国住 本国的上述机构所组成的。
•在经济学的发展历程中,以国民经济部门之间的相互依
存关系为中心的最初模型可以追溯到1758年法国重农经
济学家魁奈(F.Quesnay)所发表的经济表。
•无论在理论上还是操作上,这张经济表均存在缺陷。但
它毕竟是人类第一次描绘国民经济运行的尝试。 •马克思给予了高度评价,认为它是18世纪30-60年代政治 经济学幼年时期极有天才的思想。
投入产出分析法的创立
•从此之后,投入产出分析很快推广到西方各国 和一些发展中国家,首先是日本和西欧,以后 是其他国家。现在,据不完全统计,已有近百 个国家和地区编制了投入产出表。 •联合国统计局1968年也正式规定投入产出核算作为国 民经济核算体系的重要组成部分。
三、投入产出分析在我国的应用
我国对投入产出的研究从60年代开始的,从1974---1976
投入产出分析法的创立
• 算出生产飞机所需要的铝,注意了扩大铝的生产, 但是没有预见到生产飞机要间接消耗大量的铜。 因为,炼铝要消耗大量的电力,而输电需要大量 的铜。当铜出现严重短缺时,使美国主管部门手 忙脚乱,为完成飞机生产任务不得不向国库借用 白银去代替铜。
计量地理学第五章——投入产出分析

j1
第i部门的最终产品
N个部门消 耗劳动总和
n
q0 j L
j1
一、投入产出模型的基本原理
1、实物型投入产出模型
如果令
aij
qij qj
(i, j =1,2,,n)
产品的直接消耗系数
表示生产单位数量的j类产品需 要消耗的i类产品的数量
a0 j
q0 j qj
( j 1 ,2,,n)
劳动的直接消耗系数
X (I C)-1 N
一 投入产出模型的基本原理
2、价值型投入产出模型
特点:
①计量单位统一,既可按行建立模型——反映各部门产品的产生与分 配使用情况,也可按列建立模型——反映各部门产品价值的形成过程,同时 从产品的使用价值和价值两个方面反映各个部门之间的相互联系。可根据实 际问题将部门进行合并或分解,显得更为灵活。
投入产出模型实例
例: 假设某企业在所考察的期间内,生产甲、乙两种产品。生 产过程中,甲、乙两种产品的产品量,可提供的商品量及互相提 供消耗的数量关系统计如下表。
生产 状况
消耗状况
甲
乙
商品量 总产量
甲
50t
125t
75t
250t
乙
35m3
25m3
40m3
100m3
一、投入产出模型的基本原理
1、实物型投入产出模型
j 1
产品分配方程组,表明对于每一个部门,其总产品等于 从该部门流向其它部门的产品及最终产品之和。
一、投入产出模型的基本原理
2、价值型投入产出模型
思考 : 价值型直接消耗系数的取值范围?
aij<0 aij ≥ 1
aij
xij xj
(i,j 1,2, ,n) 不符合经济规律
投入产出分析

首先分别计算农业和工业的一次间接消耗系数。
完全消耗系数计算公式的推导
图2-2(a)
农业产品对农业产品的一次间接消耗为:
完全消耗系数计算公式的推导
图2-2(b)
农业产品对工业产品的一次间接消耗为:
完全消耗系数计算公式的推导
图2-2(c) 工业产品对农业产品的一次间接消耗为:
完全消耗系数计算公式的推导
完全消耗示意图
图2-1农业对电力的完全消耗示意图
完全消耗系数
在国民经济各部门和各产品的生产中,几乎都 存在这种间接消耗和完全消耗的关系,而充分 理解各种间接消耗关系是充分理解宏观经济问 题复杂性的有力工具。例如,某些表面上看起 来毫无联系的部门或产品,实际上都有着比较 重要的间接联系。 如果能将各部门间、产品间的间接消耗和完全 消耗关系计算出来,则对了解和分析国民经济 各部门间、产品间的内在联系,搞好宏观经济 结构的分析和预测是有很大帮助的。
价值型
实物型(在模型中详细介绍)
投入产出模型
以全国实物型投入产出模型为例全 国实物型投入产出模型的任务在于系 统地反映国民经济中实物产品之间在 生产过程中发生的相互消耗、分配使 用的联系,全面揭示产品间的数量依 存关系。
实物型投入产出表
实物形态投入产出表的基本模式 实物型投入产出表的特点
直接消耗系数(重要程度:☆☆☆☆☆)又称为
投入系数或技术系数,一般用aij表示,定义为 每生产单位j产品要消耗i种产品的数量。计算 直接消耗系数是为了表明国民经济的生产技术 结构。根据定义,直接消耗系数的计算公式为:
直接消耗系数
直接消耗系数在投入产出分析中的重要性非同一般, 是最重要的基本概念。直接消耗系数是否准确,是投 入产出分析成功的基本前提。如何保证直接消耗系数 的准确性是投入产出分析始终要关注的基本问题。 引入直接消耗系数可以将物质生产中的技术联系置入 模型中,从而使模型不再局限于行向元素的数量关系 上,把行与行联结起来,是平衡数量关系得以深化。
4 投入产出分析法
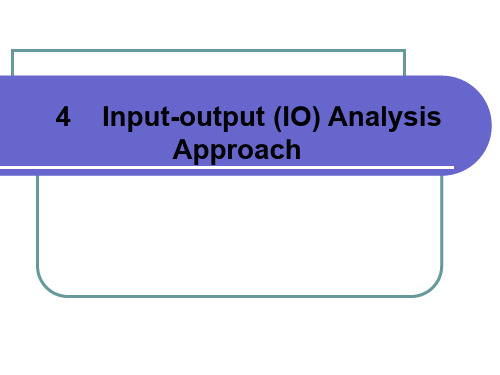
产品Ⅰ对产品Ⅲ的完全消耗系数为:
b31=a31+b31a11+b32a21+b33a31
4.2.3 完全消耗系数
b12=a12+b11a12+b12a22+b13a32 b13=a13+b11a13+b12a23+b13a33 b22=a22+b21a12+b22a22+b23a32 b23=a23+b21a13+b22a23+b23a33 b32=a32+b31a12+b32a22+b33a32 b33=a33+b31a13+b32a23+b33a33
0.250 0.079 0.005 A 0 . 125 0 . 371 0 . 216 0.125 0.154 0.200
0.750 0.500 0.270 D 0 . 500 0 . 417 0 . 108
4.2.3 完全消耗系数
由(aij) (bij) 已知 [ 完全消耗 ]=[ 直接消耗 ]+[ 各次间接消耗 ] 这是完全消耗的定义式,用其计算完全消耗系数是不可能的。 因为范围太大。
b11a11
通过产品Ⅰ对 产品Ⅰ的各次 间接消耗
+
b12a21
通过产品Ⅱ对 产品Ⅰ的各次 间接消耗
+
b13a31
通过产品Ⅲ对 产品Ⅰ的各次 间接消耗
产品Ⅰ对产品Ⅰ的完全消耗系数为: b11=a11+b11a11+b12a21+b13a31
同理得,产品Ⅰ对产品Ⅱ的完全消耗系数为:
b21=a21+b21a11+b22a21+b23a31
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章主要内容:
投入产出模型 区域经济活动的投人产出模型 资源利用与环境保护的投入产出分析
投入产出分析,又称“部门平衡”分析, 或称“产业联系”分析,最早由美国经济学家 瓦· 列昂捷夫(W. Leontief)提出。主要通过编制 投入产出表及建立相应的数学模型,反映经济 系统各个部门(产业) 之间的相互关系。自20世 纪60年代以来,这种方法就被地理学家广泛地 应用于区域产业构成分析,区域相互作用分析, 以及资源利用与环境保护研究等各个方面。在 现代经济地理学中,投入产出分析方法是必不 可少的方法之一。
即
n i 1
x
ij
v j m j x j ( j 1, , ,n) 2
上式叫做费用平衡方程组,它反映物质消 耗费用、新创造价值与产品总价值之间的
关系。
设 Nj
v j+m j
则方程组可写成:
a
i 1
n
ij
x j N j x j ( j 1, , ,n) 2
中间产品
1 2 n
最终产品 合计 消费 投资…输出 合计
总产品
x1 x2 xn
u1 u2 um
区 域 生 产 部 门 外 地 输 入 产 品 新 创 造 价 值
x11 x12 x1n
1 2 n
x21 x22 x2 n xn1 xn 2 xnn
u11 u12 u1n u 21 u 22 u 2n u m1 u m 2 u mn
第一节 投入产出模型的基本原理
实物型投入产出模型 价值型投入产出模型
按照时间概念,可以分为静态投入产出 模型和动态投入产出模型。
◆静态投入产出模型:主要研究某一个时期 各个产业部门之间的相互联系问题;按照不 同的计量单位,可以分为实物型和价值型两 种。
实物型——按实物单位计量的;
价值型——按货币单位计量。
表7.1.2 价值型投入产出表
中 间 使 用 最终产 部门 部门2 部门n 小计 品 1 y1 x x x E
11 12 1n 1
总产值
x1 x2 xn x
物 质 部门2 消 耗 部门n
部门1
x 21 x n1 C1
x 22 x n2 C2
x 2n x nn Cn
上述方程的矩阵形式为:
( I A)Q Y AQ Y Q
具体形式为:
1 a11 a12 a 21 1 a 22 ( I A) a an2 n1 a1n a2n 1 a nn
区域内外联系的投入产出模型
区域之间的投入产出模型
一般而言,一个较大的区域,如一个国家 (或者省)是由若干个较小的区域,如若干 个省(或县)构成的。区域经济活动的投入 产出模型,就是在一个较大的区域内,揭示 若干个较小区域的各个部门经济活动之间的 相互联系。
一、单一区域的投入产出模型
(一)特点:
通过求解得到各类产品的总产量:
Q ( I A) Y
实物型投入产出模型,建立了各类产品的生 产和分配使用之间的平衡关系。在模型中, 直接消耗系数矩阵A反映了生产过程的技术结 构。模型通过列昂捷夫矩阵(I-A)建立了总产 品与最终产品之间的关系,通过列昂夫逆矩 阵 ( I A) 1建立了最终产品与总产品之间的关 系。
可根据实际问题将部门进行合并或分解,显 得更为灵活。因此,应用范围更广,应用价 值更大。 ② 价值型投入产出表中的部门是“纯部门”, 是根据同类产品的原则来划分的,而不是按 行政和企业来划分的。因此,在应用价值型 投入产出模型研究有关实际问题时,数据资 料的收集和处理一定要注意这一点。
第二节 区域经济活动的投人产出模型
则有:
a
j 1
n
ij
q j y i qi (i 1, , ,n) 2
a
j 1
n
0j
qj L
若令:
a11 a12 a1n A a 21 a 22 a 2 n a a n 2 a nn n1
T T
Q q1,q 2 ,,q n , Y y1,y 2, ,y n
( I A) X Y
若假设
I A 0 ,则有: X ( I A) 1 Y
◆按列建立模型,反映各部门产品的价值
形成过程、生产与消耗之间的平衡关系。
x11 x 21 x n1 v1 m1 x1 x12 x 22 x n 2 v 2 m 2 x 2 x 1n x 2 n x nn v n m n x n
y1 y2 yn
w1 w2 wm
合计
1 2 m
合计 劳动报酬 纯收入 合计
v1 m1 v2 m2 vn mn
x1
x2
xn
(二)水平方向两种平衡关系式。
①本区域生产的产品,其生产与使用平衡方 程式为
x
即
j 1
n
ij
y i xi (i 1, , ,n) 2
a
T
W w1,w2, ,wm U u1,u 2, ,u m V v1,v 2, ,v n
T T
M m1,m2, ,mn
T
则以上各式可写成矩阵形式:
AX Y X
DX W U ˆ (C D) X V M X
若已知最终产品,由以上各式可求得中间产品, 该区域输入产品
q11 q12 q1n y1 q1 q 21 q 22 q 2 n y 2 q 2 L q n1 q n 2 q nn y n q n q 01 q 02 q 0 n
以上方程式可以写成:
q
j 1
n
ij
y i q i (i 1, , ,n) 2
q
j 1
n
0j
L
如果令
a ij
q ij qj
(i, j =1, , ,n) 2
则aij表示生产单位数量的j类产品需要消耗的i类 产品的数量,它被称为产品的直接消耗系数。 同理,劳动的直接消耗系数为:
a0 j q0 j qj ( j 1 , ,n) 2,
(I C) X N
CX N X
若|I-C|≠0,则可以建立新创造价值与总产值之间 的联系:
X ( I C )-1 N
◆特点:
与实物型投入产出模型相比,具有以下两个方 面的特点: ①计量单位统一,对价值型投入产出表,既可 按行建立模型——反映各部门产品的产生与分 配使用情况,也可按列建立模型——反映各部 门产品价值的形成过程,可同时从产品的使用 价值和价值两个方面反映各个部门之间的相互 联系。
则有:
d
j 1
n
ij
x j wi u i (i 1, , ,m) 2
(三)垂直方向有如下关系式:
x u
i 1 ij i 1
n
m
ij
v j m j x j ( j 1, , ,n) 2
a
i 1
n
ij
x j d ij x j v j m j x j ( j 1, , ,n) 2
若记:
X x1,x 2, ,x n ,Y y1,y 2, ,y n a11 a12 a1n a a 22 a 2 n A 21 a n1 a n 2 a nn
T T
则方程组可以写成矩阵形式:
AX Y X
即:
x
j 1
n
ij
yi xi (i 1, , ,n) 2
记直接消耗系数为:
a ij xij xj (i,j 1, , ,n) 2
则方程变为:
a x
j 1 ij
n
j
yi xi (i 1, , ,n) 2
上式叫做产品分配方程组,表明,对于每一 个部门,其总产品等于从该部门流向其它部 门的产品及最终产品之和。
a 为生产单位数量的j部门产品的
全部物质消耗系数。
i 1 ij
n
若将物质消耗系数矩阵记为: a 0 0
n
并记 N N1,N 2, ,N n 该模型的矩阵形式为:
T
i 1 C 0 0
i1
a
i 1
n
i2
0
0 n ain i 1
j 1xi (i 1, , ,n) 2
aij为本区域内的直接消耗系数
②来自区域以外的产品,满足平衡关系式:
u
j 1
n
ij
wi u i (i 1, , ,m) 2
令
d ij u ij xj (i 1, , ,m; j 1, , ,n) 2 2
E2 En C
y2 yn y
小计
新 创 劳动报酬 造 纯收入 价 小计 值
v1 m1 N1
v2 m2 N2
vn mn Nn
v m N0
总产值
x1
x2
xn
x
◆按横行建立数学模型:反映各部门产品的
生产与分配使用情况,描述了最终产品与总产品 之间的平衡关系。
x11 x12 x1n y1 x1 x 21 x 22 x 2 n y 2 x 2 x n1 x n 2 x nn y n x n
这两种模型最能反映投入产出特征。
