宣城市2014~2015学年度第一学期期末调研测试
2014-2015学年度第一学期期末质量检测 (1)
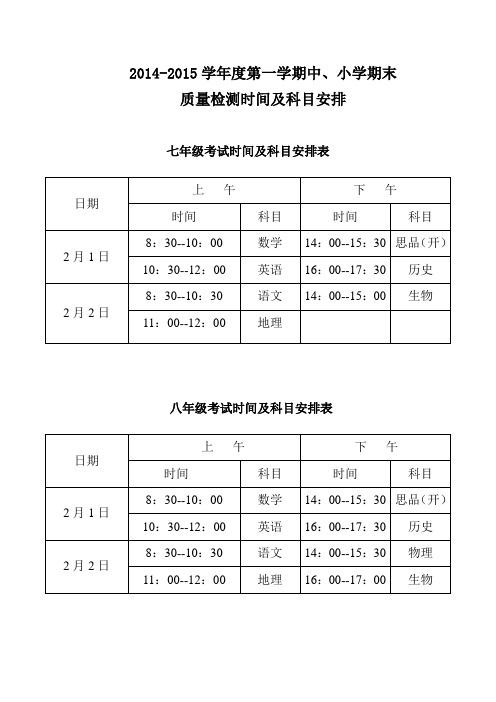
2014-2015学年度第一学期中、小学期末质量检测时间及科目安排
七年级考试时间及科目安排表
八年级考试时间及科目安排表
小学各年级考试时间及科目安排表
注意事项:
1、各学校于2015年1月31日到教研室领取试题,领到试卷后请妥善保管,切实做好保密工作,试卷在考试前半小时拆封,如造成试卷及答案泄露的,责任自负。
2、各学校统一组织,年级交叉监考、评卷,并于2015年2月5日前将各年级成绩统计表交回教研室。
3、为保证质量监测的公正性、严肃性,各中小学校长要负全责,加强领导,指定专人负责试题保密,严格遵守统一时间,任何学校不得提前或推后,如发现不按规定时间进行者,将严肃追究单位负责人的责任。
宣城市2015~2015学年度第一学期期末调研测试(整理精校版)

宣城市2015高考模拟~2015高考模拟学年度第一学期期末调研测试高考模拟试卷0209 12:41::宣城市2015高考模拟~2015高考模拟学年度第一学期期末调研测试高三语文试题【注意事项】1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
试卷满分150分,考试时间150分钟。
2.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和准考证号填写在答题卡指定区域,将条形码横贴在答题卡右上角“条形码粘贴处”。
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
4.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液£不按以上要求作答的答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回第Ⅰ卷(阅读题共66分)一、(9分)阅读下面的文字,完成1~3题。
①上世纪90年代都市文学异军突起,而这时在中国现代文学中占据主导位臵的乡土叙事似乎失去了应有的生机与活力,因此有观点认为都市叙事对乡土叙事具有超越性。
实际上,乡土叙事和都市叙事是两个独立的叙事体系,它们之间应是相互补充的。
丁帆认为,“乡土文学”与“城市文学”为世界性母题,上述现象是“在农业文明向工业文明的转换过程中,两种文明激烈冲突”的结果。
②上世纪90年代文学大潮汹涌澎湃,但都市小说中很难发现光闪闪的金子,没有出现卡夫卡、萨特和加缪式的深刻作品,也没有董桥式的反讽、幽默作品,更没看到大关心、大钟爱和大悲悯的作品,这表明都市叙事存在着一些亟待解决的问题。
而乡土叙事经历了一个多世纪的发展,已经相对成熟,可以为都市叙事的发展提供某些启示。
③在叙事对象上,可以用“他者”视角深入都市生活。
五四时期,中国开始了由传统农业文明向现代工业文明的缓慢转型。
一大批知识青年被抛出了沿袭千年的生活轨道,他们从偏远的乡村故土走入现代都市,寻求现代文明。
2014-2015学年安徽省宣城市宣州区九年级(上)期末化学试卷

2014-2015学年安徽省宣城市宣州区九年级(上)期末化学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题(本大题共10小题,共20.0分)1.物质世界充满了变化.下列变化中,属于物理变化的是()A.光合作用B.钢铁生锈C.酸雨侵蚀 D.冰山融化2.下列实验操作正确的是()A.验满氧气B.倾倒液体C.读取液体体积 D.点燃酒精灯3.二氧化锡(S n O2)可用作液晶原件电极,其中氧元素为-2价,下列有关二氧化锡的说法不正确的是()A.属于氧化物B.锡元素的化合价为+4C.含有氧分子D.具有导电性4.砷化镓(G a A s)是一种“LED”绿色节能光源材料,镓元素的相关信息如图.下列有关镓的说法错误的是()A.原子的核电荷数是31B.元素符号是G aC.属于金属元素D.相对原子质量为69.72g5.扑灭图书档案、精密仪器等火灾,不留下任何痕迹,最适宜的灭火器具是()A.高压水枪B.液态二氧化碳灭火器C.干粉灭火器D.泡沫灭火器6.“节能减排、低碳生活”的主题旨在倡导节约能源和利用清洁能源,减少温室气体二氧化碳的排放.下列措施中不符合该主题的是()A.讲究卫生,多使用一次性筷子B.回收利用废纸C.广泛使用太阳能和风能等清洁能源D.减少使用私家车次数,多乘公交车或骑自行车A.AB.BC.CD.D8.冰浮在水面,是因为水的固体密度比液体密度低.但并非所有的冰在形成时全都相同.科研人员近日揭示了一种冰的新固态阶段,这是迄今所知道的密度最小的冰.这种新形态被称为“冰XVI”,是目前发现的冰的第16个固态阶段,它有着像笼子一样的可以困住其他分子的结构.下列关于“冰XVI”说法错误的是()A.“冰XVI”是氧化物B.“冰XVI”密度小,是因为其笼形结构内部是空的C.可以用“冰XVI”在深海海底存储大量的甲烷D.“冰XVI”和水不是同一种物质A.AB.BC.CD.D10.甲醛(HCHO)是现代家居装潢产生的一种常见室内污染物,它严重危害人体健康.我国科学家研制出一种催化剂,能在室温下高效催化空气中的甲醛的氧化,其反应如下:HCHO+O2CO2+H2O,下例说法正确的是()A.反应前后各元素的化合价均不变B.该反应是分解反应C.每生成1.8g水,消耗氧气3.2gD.没有这种催化剂该反应不可能发生二、计算题(本大题共3小题,共21.0分)11.化学用语是最简明、信息丰富、国际通用的语言.请用数字和化学用语填空:(1)4个氢原子______ ;(2)2个氮气分子______ ;(3)3个亚铁离子______ ;(4)天然气的主要成分______ ;(5)地壳中含量最多的金属元素和海洋中含量最多的元素组成的化合物______ .12.水是宝贵的自然资源,在工农业生产和日常生活中有着极其广泛的运用.如图为自来水厂净水过程示意图:(1)如图吸附池内用活性炭吸附水中杂质属于______ 变化,经沉淀、过滤等净化处理后所得的水______ 纯水(填“是”或“不是”).(2)自来水厂常用的消毒剂有二氧化氯(C l O2)、漂白粉等.请完成工业上制取漂白粉的化学方程式2C12+2C a(OH)2═C a C l2+C a(C l O)2+2 ______ .二氧化氯C l O2中氯元素化合价为______ .(3)家庭生活中可以用______ 检验某水样是硬水还是软水,可用______ 方法降低水的硬度.(4)有些科学家预言:“世界上最后一滴水就是人类的眼泪”.这句话警示我们应树立保护水资源的意识:一是节约用水,二是防止水体污染.请你举一例节约用水的做法:______ .13.化学兴趣小组的同学用如图所示实验装置探究气体制取,请回答下列问题(1)图中e、f仪器的名称:e ______ ,f ______ .(2)用高锰酸钾制氧气,选用的发生装置A还需要改进地方是______ .(3)用块状石灰石固体和稀盐酸溶液常温下制取二氧化碳气体时,用C装置(多孔隔板上方用来放块状固体)代替B装置的优点是______ .观察图C装置,气体制取处于______ (填“发生”或“停止”)中,该反应方程式为______ .若用D装置来收集生成的二氧化碳,气体应从______ (填g或h)通入.(4)实验室里用双氧水和二氧化锰反应制氧气,该实验______ (填“能”或“不能”)选用C装置来控制反应发生或停止.三、填空题(本大题共1小题,共6.0分)14.某研究小组在学习氧气的化学性质时发现:铁丝燃烧没有火焰,蜡烛燃烧却有明亮的火焰.该小组同学进行了如下探究.(1)写出铁丝在氧气中燃烧的化学方程式:______ -(2)探究一:蜡烛燃烧产生火焰的原因是什么?点燃蜡烛,将金属导管一端伸入内焰,导出其中物质,在另一端管口点燃,也有火焰产生(如图所示).由此可知:蜡烛燃烧产生的火焰是由______(填“固态”或“气态”)物质燃烧形成的.(3)探究二:物质燃烧产生火焰的根本原因是什么?查阅资料由上表可知:物质燃烧能否产生火焰与其 ______ (填“熔点”或“沸点”)和燃烧时温度有关.由此推测:钠在燃烧时, ______ (填“有”或“没有”)火焰产生.(4)木炭在氧气中燃烧没有火焰,但生活中木炭燃烧时会产生火焰,其原因可能是 ______ .四、计算题(本大题共2小题,共13.0分)15.某校研究性学习小组在做“寻找新的催化剂”课题时,发现将生锈的铁钉放到过氧化氢溶液中,也可以加快过氧化氢的分解速率.于是,他们对此展开探究:【提出问题】生锈的铁钉中,哪种物质能做H 2O 2分解的催化剂?与二氧化锰相比哪种物质更适合H 2O 2做分解的催化剂?【提出猜想】猜想一:林菲同学:铁钉表面的F e 2O 3是H 202溶液分解反应的催化剂. 猜想二:小华同学:铁钉中的铁是H分解的催化剂.【分析与结论】(1)设计“实验1”的目的是 ______ .(2)由上述实验可知,猜想 ______ 错误.实验(2)反应的化学方程式为 ______ .(3)同学们讨论后认为,林菲同学的“实验2”还不能够确切的证明氧化铁就是过氧化氢分解制取氧气的催化剂,理由是: ______ .(4)小华通过仔细观察发现“实验3”中一直没有变化的试管,过了一段时间后试管中也出现了气体,小华觉得很奇怪,你能猜想其中的原因吗? ______(5)请设计实验探究F e 2O 3和M n O 2,哪种物质更适合做H 2O 2分解的催化剂? ______ .16.乙醇是一种清洁能源.但若不充分燃烧可发生以下反应:2C 2H 5OH+5O 22CO 2+2CO+6H 2O ,产生一氧化碳污染空气.求9.2g 乙醇在空气中不充分燃烧生成一氧化碳的质量.。
2014-2015年安徽省宣城市高一上学期期末物理试卷与解析

2014-2015学年安徽省宣城市高一(上)期末物理试卷一、选择题(本大题共10题。
每小题只有一个正确答案,每小题4分,共40分)1.(4分)关于物理量或物理量的单位,下列说法正确的是()A.在力学范围内,国际单位制都规定长度、质量、速度为三个基本物理量B.后人为了纪念牛顿,把“牛顿”作为力学中的基本单位C.“m”“kg”“N”都是国际单位制的单位D.1N/kg=9.8m/s22.(4分)下述说法中正确的是()A.作直线运动的物体一定能看成质点B.质点运动的位移方向和速度方向一定相同C.位移、路程、速度、加速度都是矢量D.物体速度变化越快、加速度越大3.(4分)下述说法中正确的是()A.滑动摩擦力的方向总是与物体的运动方向相反B.质点在同一平面内受到4N,6N,7N三个力的合力不可能为零C.放在桌面上的物体受到的支持力是由于桌面发生形变而产生的D.静止在斜面上的物体对斜面的压力,就是物体所受重力沿垂直斜面方向的分力4.(4分)如图所示为一质点做直线运动的v﹣t图象,下列说法中正确的是()A.整个运动过程中,BC段的加速度最大B.整个运动过程中,CE段的位移最大C.质点运动到第18s末时离出发点最远D.质点在CE段做的是匀变速运动5.(4分)在平直的公路上以72km/h的速度行驶的汽车,因发现前方有危险而进行紧急刹车,已知刹车过程中的加速度大小为5m/s2,则刹车后6.0s时间内汽车的位移为()A.30m B.40m C.216m D.342m6.(4分)如图所示,一物体放在光滑的水平板上,当缓慢提起板的一端的过程中,物体所受a支持力,b摩擦力,c下滑力,d合外力中,其中变大的力是()A.a与b B.c与d C.a与c D.b与d7.(4分)如图所示,圆弧槽半径R=30cm,质量m=1kg的小物块在沿半径方向的轻质弹簧挤压下处于静止状态,已知弹簧的劲度系数k=50N/m,弹簧原长L=40cm,一端固定在圆心O处,弹簧与竖直方向的夹角为37°,取g=10m/s2,sin37°=0.6,cos37°=0.8,则()A.物块对弹簧的拉力大小是6NB.物块对弹簧的拉力大小是15NC.物块对弹簧的摩擦力大小是6ND.槽对物块的摩擦力大小是8N8.(4分)运载火箭的用途是把卫星、飞船等送入预定轨道,则关于飞船与火箭上升的过程中,下列叙述中正确的是()A.火箭尾部向外喷气,喷出的气体反应过来对火箭产生一个反作用,从而让火箭获得了向上的推力B.火箭尾部喷出的气体对空气产生一个作用力,空气的反作用力使火箭获得飞行的动力C.火箭飞出大气层后,由于没有了空气,火箭虽然向后喷气,但也无法获得前进的动力D.火箭飞出大气层后,失去了重力9.(4分)“蹦极”是一项刺激的体育活动,某人身系弹性绳自高空P点自由下落,图中a点是弹性绳的原长位置,c是人所到达的最低点,b是人静止悬吊着时的平衡位置,人在P点下落到最低点c点的过程中()A.人在a点时的速度最大B.人在ab段做匀减速运动C.人在bc段做匀减速运动D.人在c点时的速度为零,但所受的合外力不为零10.(4分)一个物体以v0=16m/s的初速度冲上一斜面,加速度的大小为8m/s2,冲上最高点之后,又以加速度大小为4m/s2沿原路径返回,则物体()A.物体运动总时间是6s B.前3s内的位移大小为12mC.第3s末的速度大小4m/s D.4s内的平均速度大小为0二、实验题(本大题包括4题。
2014-2015学年安徽省宣城市高一(上)期末数学试卷含答案

2014-2015学年安徽省宣城市高一(上)期末数学试卷一、选择题(每小题5分,共50分)1.(5.00分)sin42°cos18°+cos42°sin18°=()A.B.C.D.2.(5.00分)下列函数中既是奇函数,又在区间(﹣1,1)上是增函数的为()A.y=e x+e﹣x B.y=|x|C.y=sinx D.y=﹣x33.(5.00分)在平行四边形ABCD中,对角线AC与BD交于点O,若+=,则λ的值为()A.2 B.1 C.D.﹣14.(5.00分)下列函数中,表示同一函数的一组是()A.f(x)=,g(x)=B.f(x)=lg(x(x+1)),g(x)=lgx+lg (x+1)C.f(x)=x﹣1(x∈R),g(x)=x﹣1(x∈N)D.f(x)=x2+x﹣1,g(x)=t2+t ﹣15.(5.00分)函数f(x)=的大致图象是()A.B.C.D.6.(5.00分)函数f(x)=lnx﹣的零点所在的区间是()A.(1,2) B.(2,3) C.(3,4) D.(e,+∞)7.(5.00分)已知a=log34,b=log43,c=log53,则a,b,c的大小关系是()A.c<a<b B.b<a<c C.a<c<b D.c<b<a8.(5.00分)已知α为第一象限角,sinα=cosα,则tan为()A.2+B.2﹣C.﹣±2 D.±29.(5.00分)若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤)的部分图象如图所示,其中A,B两点的间距为5,则()A.ω=,φ=B.ω=,φ=C.ω=,φ=D.ω=,φ= 10.(5.00分)已知函数f(x)=ln(﹣3x)+1,若f(lg(log210))=m,则f(lg(lg2))=()A.﹣m B.m C.m+2 D.2﹣m二、填空题(每小题5分,共20分)11.(5.00分)函数y=的定义域为.12.(5.00分)函数f(x)=,则f[f(16)]=.13.(5.00分)已知=(a>0),则a=.14.(5.00分)函数y=cos(2x+φ)(﹣π≤φ<π)的图象向右平移个单位后,与函数y=sin(2x+)的图象重合,则φ=.15.(5.00分)设α∈(0,π),且α≠,当∠xOy=α时,定义坐标系xOy为α﹣仿射坐标(如图),在α﹣仿射坐标系中,任意一点P的坐标这样定义“,分别是与x轴,y轴方向同向的单位向量,若向量=x+y,则记=(x,y),下列结论正确的是(写上所有正确结论的序号)①设向量=(m,n),=(s,t),若=,则有m=m,s=t;②设向量=(m,n),则||=;③设向量=(m,n)=(s,t),若,则有mt﹣ns=0;④设向量=(m,n)=(s,t),若,则有mt+ns=0;⑤设向量=(1,2)=(2,1),若与的夹角为,则有.三、解答题16.(12.00分)集合A={x|x2﹣px+15=0}和B={x|x2﹣ax﹣b=0},若A∪B={2,3,5},A∩B={3},分别求实数p、a、b的值.17.(12.00分)已知角α的终边过点P(x,﹣1),(x<0),且cosα=x.(1)求tanα的值;(2)求的值.18.(12.00分)已知向量,是夹角为的两个单位向量,=2+,=k+2,(1)若,求实数k的值;(2)若k=﹣3,求与的夹角θ.19.(12.00分)已知函数f(x)=(a>0,a≠1)(1)判定函数f(x)的奇偶性;(2)判定函数f(x)的单调性并证明你的结论.20.(13.00分)设向量=(2sin(x+),﹣1),=(2cosx,),设函数f(x)=(1)求函数f(x)的最小正周期(2)若2f(x)﹣m+1=0在[0,]内有两个相异的实根,求实数m的取值范围.21.(14.00分)根据市场调查,某商品在最近40天内的价格P与时间t的关系用图(1)中的一条折线表示,销售量Q与时间t的关系用图(2)中的线段表示(t∈N*)(1)分别写出图(1)表示的价格与时间的函数关系式P=f(t),图(2)表示的销售量与时间的函数关系式Q=g(t).(2)求这种商品的销售额S(销售额=销售量×价格)的最大值及此时的时间.2014-2015学年安徽省宣城市高一(上)期末数学试卷参考答案与试题解析一、选择题(每小题5分,共50分)1.(5.00分)sin42°cos18°+cos42°sin18°=()A.B.C.D.【解答】解:由两角和的正弦公式可得:sin42°cos18°+cos42°sin18°=sin(42°+18°)=sin60°=故选:B.2.(5.00分)下列函数中既是奇函数,又在区间(﹣1,1)上是增函数的为()A.y=e x+e﹣x B.y=|x|C.y=sinx D.y=﹣x3【解答】解:A.y=e x+e﹣x为偶函数,不满足条件.B.y=|x|为偶函数,不满足条件.C.y=sinx是奇函数,在区间(﹣1,1)上是增函数,满足条件.D.y=﹣x3是奇函数,在区间(﹣1,1)上是减函数,不满足条件.故选:C.3.(5.00分)在平行四边形ABCD中,对角线AC与BD交于点O,若+=,则λ的值为()A.2 B.1 C.D.﹣1【解答】解:如图所示,平行四边形ABCD中,对角线AC与BD交于点O,∴+==2,∴λ=2.故选:A.4.(5.00分)下列函数中,表示同一函数的一组是()A.f(x)=,g(x)=B.f(x)=lg(x(x+1)),g(x)=lgx+lg (x+1)C.f(x)=x﹣1(x∈R),g(x)=x﹣1(x∈N)D.f(x)=x2+x﹣1,g(x)=t2+t ﹣1【解答】解:对于A,f(x)==,与g(x)=的定义域不同,∴不是同一函数;对于B,f(x)=lg(x(x+1))(x<﹣1或x>0),与g(x)=lgx+lg(x+1)=lg(x (x+1))(x>0)的定义域不同,∴不是同一函数;对于C,f(x)=x﹣1(x∈R),与g(x)=x﹣1(x∈N)的定义域不同,∴不是同一函数;对于D,f(x)=x2+x﹣1(x∈R),与g(x)=t2+t﹣1(t∈R)的定义域相同,对应关系也相同,∴是同一函数.故选:D.5.(5.00分)函数f(x)=的大致图象是()A.B.C.D.【解答】解:因为﹣<0,所以f(x)在(0,+∞)上单调递减,排除选项B、C;又f(x)的定义域为(0,+∞),故排除选项D,故选:A.6.(5.00分)函数f(x)=lnx﹣的零点所在的区间是()A.(1,2) B.(2,3) C.(3,4) D.(e,+∞)【解答】解:∵f(x)=lnx﹣,则函数f(x)在(0,+∞)上单调递增,∵f(2)=ln2﹣1<0,f(3)=ln3﹣>0,∴f(2)f(3)<0,在区间(2,3)内函数f(x)存在零点,故选:B.7.(5.00分)已知a=log34,b=log43,c=log53,则a,b,c的大小关系是()A.c<a<b B.b<a<c C.a<c<b D.c<b<a【解答】解:∵a=log34>1,1>b=log43=>=log53=c,∴a>b>c.故选:D.8.(5.00分)已知α为第一象限角,sinα=cosα,则tan为()A.2+B.2﹣C.﹣±2 D.±2【解答】解:∵α为第一象限角,∴2kπ≤α≤2kπ+,k∈Z,即kπ≤≤kπ+,k∈Z,∴tan>0,已知等式sinα=cosα,整理得:tanα=,∴=,即tan2+2tan﹣1=0,解得:tan=2﹣,故选:B.9.(5.00分)若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤)的部分图象如图所示,其中A,B两点的间距为5,则()A.ω=,φ=B.ω=,φ=C.ω=,φ=D.ω=,φ=【解答】解:∵函数图象经过点(0,1),∴f(0)=2sinφ=1,可得sinφ=,又∵0≤φ≤,∴φ=.∵其中A、B两点的纵坐标分别为2、﹣2,∴设A、B的横坐标之差为d,则|AB|==5,解之得d=3,由此可得函数的周期T=6,得=6,解之得ω=.故选:C.10.(5.00分)已知函数f(x)=ln(﹣3x)+1,若f(lg(log210))=m,则f(lg(lg2))=()A.﹣m B.m C.m+2 D.2﹣m【解答】解:∵设g(x)=ln(﹣3x),∴g(﹣x)=ln(+3x),∴g(x)+g(﹣x)=ln[(﹣3x)•(﹣3x)]=ln1=0,∴g(x)=ln(﹣3x)是奇函数,∴f(x)+f(﹣x)=2,∵lg(log210)=﹣lg(lg2),∴f(lg(log210))+f(lg(lg2))=2,∴f(lg(lg2))=2﹣f(lg(log210))=2﹣m.故选:D.二、填空题(每小题5分,共20分)11.(5.00分)函数y=的定义域为[2,3)∪(3,+∞).【解答】解:∵函数y=,∴,解得,即x≥2且x≠3;∴函数y的定义域为[2,3)∪(3,+∞).故答案为:[2,3)∪(3,+∞).12.(5.00分)函数f(x)=,则f[f(16)]=8.【解答】解:∵函数f(x)=,∴f(16)==4,f[f(16)]=f(4)=2×4=8.故答案为:8.13.(5.00分)已知=(a>0),则a=.【解答】解:∵=(a>0),则a==2,∴a=.故答案为:.14.(5.00分)函数y=cos(2x+φ)(﹣π≤φ<π)的图象向右平移个单位后,与函数y=sin(2x+)的图象重合,则φ=.【解答】解:函数y=cos(2x+φ)(﹣π≤φ<π)的图象向右平移个单位后,得平移后的图象的函数解析式为y=cos[2(x﹣)+φ]=cos(2x+φ﹣π),而函数y=sin(2x+)=,由函数y=cos(2x+φ)(﹣π≤φ<π)的图象向右平移个单位后,与函数y=sin (2x+)的图象重合,得2x+φ﹣π=,解得:φ=.符合﹣π≤φ<π.故答案为.15.(5.00分)设α∈(0,π),且α≠,当∠xOy=α时,定义坐标系xOy为α﹣仿射坐标(如图),在α﹣仿射坐标系中,任意一点P的坐标这样定义“,分别是与x轴,y轴方向同向的单位向量,若向量=x+y,则记=(x,y),下列结论正确的是③⑤(写上所有正确结论的序号)①设向量=(m,n),=(s,t),若=,则有m=m,s=t;②设向量=(m,n),则||=;③设向量=(m,n)=(s,t),若,则有mt﹣ns=0;④设向量=(m,n)=(s,t),若,则有mt+ns=0;⑤设向量=(1,2)=(2,1),若与的夹角为,则有.【解答】解:.①设向量=(m,n),=(s,t),若=,则有m=s,n=t,因此不正确;②设向量=(m,n),则||=≠,因此不正确;③设向量=(m,n),=(s,t),若,则有mt﹣ns=0,因此正确;④设向量=(m,n),=(s,t),若,则有ms+nt=0,因此不正确;⑤设向量=(1,2),=(2,1),与的夹角为,则==,==,==2+2+5=4+5cosα.∴==,化为,则正确.综上可得:正确的结论为:③⑤.故答案为:③⑤.三、解答题16.(12.00分)集合A={x|x2﹣px+15=0}和B={x|x2﹣ax﹣b=0},若A∪B={2,3,5},A∩B={3},分别求实数p、a、b的值.【解答】解:因为A∩B={3},所以3∈A,从而可得p=8,所以A={3,5}(4分)又由于3∈A,且A∪B={2,3,5},,所以B={2,3}.(6分)所以方程x2﹣ax﹣b=0的二根为2和3.由韦达定理可得a=5,b=﹣6综上可知p=8,a=5,b=﹣6..(10分)17.(12.00分)已知角α的终边过点P(x,﹣1),(x<0),且cosα=x.(1)求tanα的值;(2)求的值.【解答】解:由条件知cosα=x=,解得:x=﹣2,即P(﹣2,﹣1),(1)tanα==;(2)∵P(﹣2,﹣1),∴sinα=﹣,∴原式===2sinαtanα=﹣.18.(12.00分)已知向量,是夹角为的两个单位向量,=2+,=k+2,(1)若,求实数k的值;(2)若k=﹣3,求与的夹角θ.【解答】解:(1)•=||•||•cos=,若,则=0,即(2+)•(k+2)=0,即有2k+2+(k+4)=2k+2+(k+4)=0,解得k=﹣;(2)若k=﹣3,则=﹣6+2+(﹣3+4)=﹣6+2+=﹣,||2=4++4=4+1+2=7,||2=9+4﹣12=9+4﹣6=7,则cosθ===﹣,由0≤θ≤π,解得θ=.19.(12.00分)已知函数f(x)=(a>0,a≠1)(1)判定函数f(x)的奇偶性;(2)判定函数f(x)的单调性并证明你的结论.【解答】解:(1)函数的定义域为R,则f(﹣x)==﹣=﹣f(x),即f(﹣x)=﹣f(x),则函数f(x)是奇函数;(2)设x1<x2,则f(x1)﹣f(x2)=﹣==,若a>1,则<,则f(x1)<f(x2),此时函数f(x)为单调递增函数,若0<a<1,则>,则f(x1)>f(x2),此时函数f(x)为单调递减函数.20.(13.00分)设向量=(2sin(x+),﹣1),=(2cosx,),设函数f(x)=(1)求函数f(x)的最小正周期(2)若2f(x)﹣m+1=0在[0,]内有两个相异的实根,求实数m的取值范围.【解答】解:(1)∵f(x)==4sin(x+)cosx﹣…1分=2sinxcosx+2cos2x﹣…2分=sin2x+cos2x=2sin(2x+)…4分∴T=π…6分(2)2f(x)﹣m+1=0在[0,]内有两个相异的实根,即有方程:f(x)=两个相异的实根,即y=f(x)图象与y=图象有两个交点,…8分结合函数图象,当<2或﹣2<≤﹣1,即m∈[2+1,5)∪(﹣3,﹣1]时原方程有两个相异的实根,故m∈[2+1,5)∪(﹣3,﹣1]…13分21.(14.00分)根据市场调查,某商品在最近40天内的价格P与时间t的关系用图(1)中的一条折线表示,销售量Q与时间t的关系用图(2)中的线段表示(t∈N*)(1)分别写出图(1)表示的价格与时间的函数关系式P=f(t),图(2)表示的销售量与时间的函数关系式Q=g(t).(2)求这种商品的销售额S(销售额=销售量×价格)的最大值及此时的时间.【解答】(本小题满分8分)解:(I)…(2分)…(3分)(II)当1≤t<20时,.∵t∈N*,∴t=10或11时,S的最大值为176 …(5分)当20≤t<40时,为减函数.∴t=20时,S的最大值为161,…(7分)∴t=10或11时,S的最大值为176.…(8分)。
安徽省宣城市高三数学上学期期末考试试卷 文(含解析)

2014-2015学年安徽省宣城市高三(上)期末数学试卷(文科)一、选择题(每小题5分,共50分)1.已知R是实数集,M={x|x2﹣2x>0},N={y|y=},则N∩∁U M=()A.(1,2) B. [0,2] C.∅ D. [1,2]2.已知复数z=﹣2i,则的虚部为()A. B.i C.i D.3.以下判断正确的是()A.命题“负数的平方是正数”不是全称命题B.命题“∀x∈N,x3>x2”的否定是“∃x∈N,x3<x2”C.“a=1”是“函数f(x)=cos2ax﹣sin2ax的最小正周期是π”的必要不充分条件 D.“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件4.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1) B.(﹣1,0) C.(0,1) D.(1,2)5.双曲线2x2﹣y2=1的离心率为()A. B. C. D.6.等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1=()A. B. C. D.7.执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A. 2 B. 3 C. 4 D. 58.函数y=f(x)的图象向右平移单位后与函数y=sin2x的图象重合,则y=f(x)的解析式是()A. f(x)=cos(2x﹣) B. f(x)=cos(2x+) C. f(x)=cos(2x﹣) D. f (x)=cos(2x+)9.x、y满足约束条件,若z=y﹣ax取得最大值的最优解不唯一,则实数a的值为()A.或﹣1 B. 2或 C. 2或1 D. 2或﹣110.函数y=a x+3﹣2(a>0,且a≠1)的图象恒过定点A,且点A在直线mx+ny+1=0上(m>0,n>0),则的最小值为()A. 12 B. 10 C. 8 D. 14二、填空题(每小题5分,共25分)11.已知,则= .12.设f(x)=,则f(f(2))的值为.13.三视图如图的几何体的体积为.14.已知向量=(2,3),=(﹣1,2),若与共线,则= .15.给出下列四个命题:①已知椭圆+=1的左右焦点分别为F1,F2,P为椭圆上一点,并且|PF1|=3,则|PF2|=1;②双曲线C:﹣=1的顶点到渐近线的距离为;③若⊙C1:x2+y2+2x=0;⊙C2:x2+y2+2y﹣1=0,则这两圆恰有2条公切线;④若直线l1:a2x﹣y+6=0与直线l2:4x﹣(a﹣3)y+9=0互相垂直,则a=﹣1其中正确命题的序号是.(把你认为正确命题的序号都填上)三、解答题16.在△ABC中,a,b,c分别是角A、B、C所对的边,且.(1)求边c的值;(2)求的值.重量段[80,85)[85,90)[90,95)[95,100)件数 5 a 15 b型2件,(1)从该批电器中任选1件,求其为“B”型的概率(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.18.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.(Ⅰ)证明:PA∥平面BDE;(Ⅱ)证明:AC⊥平面PBD.19.已知数列{a n}满足:a1=1,a2=a(a>0),数列{b n}满足:b n=a n a n+2(n∈N*)(1)若数列{a n}是等差数列,且b3=45,求a的值及数列{a n}通项公式;(2)若数列{a n}的等比数列,求数列{b n}的前n项和S n.20.已知函数f(x)=x3+2x2﹣ax.对于任意实数x恒有f′(x)≥2x2+2x﹣4(Ⅰ)求实数a的最大值;(Ⅱ)当a最大时,函数F(x)=f(x)﹣x﹣k有三个零点,求实数k的取值范围.21.在平面直角坐标系xOy中,已知椭圆C1:(a>b>0)的左焦点为F1(﹣1,0),且点P(0,1)在C1上.(1)求椭圆C1的方程;(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.2014-2015学年安徽省宣城市高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题(每小题5分,共50分)1.已知R是实数集,M={x|x2﹣2x>0},N={y|y=},则N∩∁U M=()A.(1,2) B. [0,2] C.∅ D. [1,2]考点:交、并、补集的混合运算.专题:集合.分析:求出集合M,N,根据集合的基本运算进行求解.解答:解:M={x|x2﹣2x>0}={x|x>2或x<0},N={y|y=}={y|y≥0},则∁U M={x|0≤x≤2},N∩∁U M={x|0≤x≤2},故选:B点评:本题主要考查集合的基本运算,求出,M,N是解决本题的关键.要求熟练掌握集合的交并补运算,比较基础.2.已知复数z=﹣2i,则的虚部为()A. B.i C.i D.考点:复数的基本概念.专题:数系的扩充和复数.分析:利用复数的运算法则、虚部的定义即可得出.解答:解:∵复数z=﹣2i,∴===的虚部为,故选:A.点评:本题考查了复数的运算法则、虚部的定义,属于基础题.3.以下判断正确的是()A.命题“负数的平方是正数”不是全称命题B.命题“∀x∈N,x3>x2”的否定是“∃x∈N,x3<x2”C.“a=1”是“函数f(x)=cos2ax﹣sin2ax的最小正周期是π”的必要不充分条件 D.“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件考点:必要条件、充分条件与充要条件的判断.专题:规律型.分析:根据含有量词的命题的性质以及充分条件和必要条件的定义进行判断即可.解答:解:A.命题“负数的平方是正数”是全称命题,∴A错误.B.命题“∀x∈N,x3>x2”的否定是“∃x∈N,x3≤x2”,∴B错误.C.f(x)=cos2ax﹣sin2ax=cos2ax,则函数的正确T=,即a=±1,∴“a=1”是“函数f(x)=cos2ax﹣sin2ax的最小正周期是π”的充分不必要条件.∴C错误.D.若函数f(x)=ax2+bx+c是偶函数,则函数f(﹣x)=ax2﹣bx+c=ax2+bx+c,即﹣b=b,解得b=0,∴“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,正确.故选:D.点评:本题主要考查充分条件和必要条件的判断以及含有量词的命题的真假关系,比较基础.4.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1) B.(﹣1,0) C.(0,1) D.(1,2)考点:函数零点的判定定理.专题:函数的性质及应用.分析:将选项中各区间两端点值代入f(x),满足f(a)•f(b)<0(a,b为区间两端点)的为答案.解答:解:因为f(0)=﹣1<0,f(1)=e﹣1>0,所以零点在区间(0,1)上,故选C.点评:本题考查了函数零点的概念与零点定理的应用,属于容易题.函数零点附近函数值的符号相反,这类选择题通常采用代入排除的方法求解.5.双曲线2x2﹣y2=1的离心率为()A. B. C. D.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:化简双曲线方程为标准方程,求出a、b、c,即可求解双曲线的离心率.解答:解:双曲线2x2﹣y2=1的标准方程为:,所以a=,b=1,c==,双曲线的离心率为:=.故选:B.点评:本题考查双曲线的离心率的求法,考查计算能力.6.等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1=()A. B. C. D.考点:等比数列的前n项和.专题:等差数列与等比数列.分析:设等比数列{a n}的公比为q,利用已知和等比数列的通项公式即可得到,解出即可.解答:解:设等比数列{a n}的公比为q,∵S3=a2+10a1,a5=9,∴,解得.∴.故选C.点评:熟练掌握等比数列的通项公式是解题的关键.7.执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A. 2 B. 3 C. 4 D. 5考点:循环结构.专题:算法和程序框图.分析:根据输入A的值,然后根据S进行判定是否满足条件S≤2,若满足条件执行循环体,依此类推,一旦不满足条件S≤2,退出循环体,求出此时的P值即可.解答:解:S=1,满足条件S≤2,则P=2,S=1+=满足条件S≤2,则P=3,S=1++=满足条件S≤2,则P=4,S=1+++=不满足条件S≤2,退出循环体,此时P=4故选:C点评:本题主要考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断.8.函数y=f(x)的图象向右平移单位后与函数y=sin2x的图象重合,则y=f(x)的解析式是()A. f(x)=cos(2x﹣) B. f(x)=cos(2x+) C. f(x)=cos(2x﹣) D. f (x)=cos(2x+)考点:函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.解答:解:函数y=f(x)的图象向右平移单位后与函数y=sin2x的图象重合,则函数y=sin2x的图象向左平移单位后与函数y=f(x)的图象重合,故f(x)=sin2(x+)=sin(2x+)=sin(2x++)=cos(2x+),故选:B.点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.9.x、y满足约束条件,若z=y﹣ax取得最大值的最优解不唯一,则实数a的值为()A.或﹣1 B. 2或 C. 2或1 D. 2或﹣1考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用目标函数的几何意义,得到直线y=ax+z斜率的变化,从而求出a的取值.解答:解:作出不等式组对应的平面区域如图:(阴影部分ABC).由z=y﹣ax得y=ax+z,即直线的截距最大,z也最大.若a=0,此时y=z,此时,目标函数只在A处取得最大值,不满足条件,若a>0,目标函数y=ax+z的斜率k=a>0,要使z=y﹣ax取得最大值的最优解不唯一,则直线y=ax+z与直线2x﹣y+2=0平行,此时a=2,若a<0,目标函数y=ax+z的斜率k=a<0,要使z=y﹣ax取得最大值的最优解不唯一,则直线y=ax+z与直线x+y﹣2=0,平行,此时a=﹣1,综上a=﹣1或a=2,故选:D点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.注意要对a进行分类讨论,同时需要弄清楚最优解的定义.10.函数y=a x+3﹣2(a>0,且a≠1)的图象恒过定点A,且点A在直线mx+ny+1=0上(m>0,n>0),则的最小值为()A. 12 B. 10 C. 8 D. 14考点:基本不等式;指数函数的单调性与特殊点.专题:不等式的解法及应用.分析:先求出定点A,将其代入直线方程即可得到n、m满足的关系式,再利用基本不等式的性质即可.解答:解:当x=﹣3时,f(﹣3)=a0﹣2=1﹣2=﹣1,∴定点A(﹣3,﹣1).∵点A在直线mx+ny+1=0上,∴﹣3m﹣n+1=0,即3m+n=1.∵m>0,n>0,∴=(3m+n)=6+=12,当且仅当m>0,n>0,3m+n=1,,即n=,时取等号.因此的最小值为12.故选A.点评:熟练掌握基本不等式的性质是解题的关键.二、填空题(每小题5分,共25分)11.已知,则= .考点:运用诱导公式化简求值.专题:计算题.分析:根据诱导公式可知=sin(﹣α﹣),进而整理后,把sin(α+)的值代入即可求得答案.解答:解:=sin(﹣α﹣)=﹣sin(α+)=﹣故答案为:﹣点评:本题主要考查了运用诱导公式化简求值的问题.属基础题.12.设f(x)=,则f(f(2))的值为 1 .考点:函数的值.专题:函数的性质及应用.分析:直接利用分段函数,由里及外求解f(f(2))的值即可.解答:解:f(x)=,则f(2)=log33=1,f(f(2))=f(1)=e1﹣1=1.故答案为:1.点评:本题考查分段函数的应用,函数值的求法,基本知识的考查.13.三视图如图的几何体的体积为 1 .考点:由三视图求面积、体积.专题:计算题.分析:通过三视图判断几何体的特征,利用三视图的数据,求出几何体的体积即可.解答:解:由三视图可知几何体是底面是上底为1,下底为2,高为1的直角梯形,一条侧棱垂直直角梯形的下底直角顶点,高为2的四棱锥,所以棱锥的体积为:=1.故答案为:1.点评:本题考查几何体的体积的求法,考查学生对三视图复原几何体的能力与计算能力.14.已知向量=(2,3),=(﹣1,2),若与共线,则= ﹣2 .考点:平面向量共线(平行)的坐标表示.专题:计算题.分析:用向量的运算法则求出向量与向量的坐标,再用向量共线的坐标形式的公式列方程解得即可.解答:解:∵向量=(2,3),=(﹣1,2),∴=(2m,3m)+(﹣n,2n)=(2m﹣n,3m+2n),=(2,3)﹣2(﹣1,2)=(4,﹣1)若与共线,∴4×(3m+2n)=n﹣2m∴14m=﹣7n∴=﹣2故答案为:﹣2.点评:考查平面向量共线(平行)的坐标表示.若=(a1,a2),=(b1,b2),则⊥⇔a1a2+b1b2=0,∥⇔a1b2﹣a2b1=0.15.给出下列四个命题:①已知椭圆+=1的左右焦点分别为F1,F2,P为椭圆上一点,并且|PF1|=3,则|PF2|=1;②双曲线C:﹣=1的顶点到渐近线的距离为;③若⊙C1:x2+y2+2x=0;⊙C2:x2+y2+2y﹣1=0,则这两圆恰有2条公切线;④若直线l1:a2x﹣y+6=0与直线l2:4x﹣(a﹣3)y+9=0互相垂直,则a=﹣1其中正确命题的序号是②③.(把你认为正确命题的序号都填上)考点:圆与圆的位置关系及其判定;直线的一般式方程与直线的垂直关系;椭圆的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:①利用椭圆的定义可得|PF1|+|PF2|=2a=8,即可判断①不正确;②利用双曲线的定义可知顶点坐标为(0,±3).渐近线方程为:y=±x,根据点到直线的距离公式可判断②正确;③首先将圆的方程转化为标准方程,根据圆心距与两圆半径的关系可判断两圆相交,从而可判断两圆恰有2条公切线;④根据两直线垂直的性质可得a2•[﹣(a﹣3)]+4×(﹣1)=0,解方程即可判断④不正确.解答:解:①由椭圆+=1可得,a=4,b=3.由椭圆的性质可知,|PF1|+|PF2|=2a=8,若|PF1|=3,则|PF2|=5.故①不正确;②由双曲线C:﹣=1可得,a=3,b=4.∴顶点坐标为(0,±3).渐近线方程为:y=±x,即3x±4y=0.∴顶点到渐近线的距离为d==.故②正确.③⊙C1:x2+y2+2x=0可化为(x+1)2+y2=1.∴圆心C1(﹣1,0),半径r1=1.⊙C2:x2+y2+2y﹣1=0可化为x2+(y+1)2=2.∴圆心C 2(0,﹣1),半径.∴圆心距|C1C2|=.∵<|C1C2|=∴两圆相交.∴两圆恰有2条公切线.故③正确.④∵直线l1:a2x﹣y+6=0与直线l2:4x﹣(a﹣3)y+9=0互相垂直,∴a2•[﹣(a﹣3)]+4×(﹣1)=0.解得a=﹣1或a=2.故④不正确.∴正确命题的序号是②③.故答案为:②③.点评:本题考查椭圆、双曲线的定义及性质,两圆位置关系的判定以及两直线垂直的性质等知识,属于中档题.三、解答题16.在△ABC中,a,b,c分别是角A、B、C所对的边,且.(1)求边c的值;(2)求的值.考点:余弦定理;两角和与差的正弦函数;正弦定理.专题:计算题.分析:(1)由a的长,及sinC=2sinA,利用正弦定理即可求出c的长;(2)利用余弦定理表示出cosA,将a,b及c的长代入求出cosA的值,再由A为三角形的内家,利用同角三角函数间的基本关系求出sinA的值,进而利用二倍角的正弦、余弦函数公式分别求出sin2A及cos2A的值,最后将所求的式子利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将sin2A和cos2A的值代入即可求出值.解答:解:(1)∵a=,sinC=2sinA,∴根据正弦定理=得:c==2a=2;(2)∵a=,b=3,c=2,∴根据余弦定理得:cosA==,又A为三角形的内角,∴sinA==,∴sin2A=2sinAcosA=,cos2A=cos2A﹣sin2A=,则sin(2A﹣)=sin2Acos﹣cos2Asin=.点评:此题考查了正弦、余弦定理,同角三角函数间的基本关系,两角和与差的正弦函数公式,以及二倍角的正弦、余弦函数公式,熟练掌握定理及公式是解本题的关键.17.对一批共50件的某电器进行分类检测,其重量(克0统计如下:重量段 [80,85) [85,90) [90,95) [95,100)件数 5 a 15 b规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件,(1)从该批电器中任选1件,求其为“B”型的概率(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.考点:根据实际问题选择函数类型.专题:应用题;概率与统计.分析:(1)由表格可知,“B”型的件数为50﹣5,即得所求的概率.(2)把5件电器行编号,写出任选2件的所有不同选法种数,查出恰有1件为“A”型的选法种数,然后直接利用古典概型概率计算公式,从而求得所求事件的概率.解答:解:(1)设“从该批电器中任选1件,其为“B”型”为事件A1,则P(A1)==;所以从该批电器中任选1件,求其为”B”型的概率为.(2)设“从重量在[80,85)的5件电器中,任选2件电器,求其中恰有1件为“A”型”为事件A2,记这5件电器分别为a,b,c,d,e,其中“A”型为a,b.从中任选2件,所有可能的情况为ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种.其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd, be,共6种.所以P(A2)==.所以从重量在[80,85)的5件电器中,任选2件电器,其中恰有1件为“A”型的概率为.点评:本题主要考查用列举法求基本事件及事件发生的概率,属于中档题.18.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.(Ⅰ)证明:PA∥平面BDE;(Ⅱ)证明:AC⊥平面PBD.考点:直线与平面平行的判定;直线与平面垂直的判定.专题:空间位置关系与距离.分析:(Ⅰ)设AC∩BD=H,连结EH.证明EH∥PA.利用直线与平面的平行的判定定理证明PA∥平面BDE.(Ⅱ)通过PD⊥平面ABCD,证明PD⊥AC.结合DB⊥AC.然后证明AC⊥平面PBD解答:(Ⅰ)证明:设AC∩BD=H,连结EH.在△ADC中,∵AD=CD,且DB平分∠ADC,∴H为AC的中点.又由题设,E为PC的中点,故EH∥PA.又EH⊆平面BDE,且PA⊄平面BDE,∴PA∥平面BDE.…(6分)(Ⅱ)证明:∵PD⊥平面ABCD,AC⊆平面ABCD,∴PD⊥AC.由(1)可得,DB⊥AC.又PD∩DB=D,故AC⊥平面PBD.…(12分)点评:本题考查直线与平面的平行的判定定理以及在与平面垂直的判定定理的应用,考查逻辑推理能力.19.已知数列{a n}满足:a1=1,a2=a(a>0),数列{b n}满足:b n=a n a n+2(n∈N*)(1)若数列{a n}是等差数列,且b3=45,求a的值及数列{a n}通项公式;(2)若数列{a n}的等比数列,求数列{b n}的前n项和S n.考点:数列的求和;数列递推式.专题:综合题;等差数列与等比数列.分析:(1)先根据{a n}是等差数列表示出通项公式,再根据b3=45求得a3a5的值从而可确定a的值,求得{a n}的通项公式.(2)先根据{a n}是等比数列表示出通项公式,进而可表示出b n的表达式,再对公比a等于1和不等于1进行讨论,即可得到最后答案.解答:解:(1)∵{a n}是等差数列,a1=1,a2=a(a>0),∴a n=1+(n﹣1)(a﹣1).又b3=45,∴a3a5=45,即(2a﹣1)(4a﹣3)=45,解得a=2或a=﹣(舍去),…(5分)∴a n=2n﹣1.…(7分)(2))∵{a n}是等比数列,a1=1,a2=a(a>0),∴a n=a n﹣1,则b n=a n a n+2=a2n.∴当a=1时,S n=n;当a≠1时,S n=.…(14分)点评:本题主要考查数列的通项公式的求法和数列求和.高考对数列的考查无外乎通项公式的求法和前n项和的求法,对经常用到的常用方法要熟练掌握.20.已知函数f(x)=x3+2x2﹣ax.对于任意实数x恒有f′(x)≥2x2+2x﹣4(Ⅰ)求实数a的最大值;(Ⅱ)当a最大时,函数F(x)=f(x)﹣x﹣k有三个零点,求实数k的取值范围.考点:利用导数研究函数的极值;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的概念及应用.分析:(1)由f′(x)=3x2+4x﹣a,对于x∈R恒有f′(x)≥2x2+2x﹣4,即x2+2x﹣a+4≥0对于x∈R恒成立得△=4﹣4(4﹣a)≤0,解得:a≤3,(2)a=3时,F(x)=f(x)﹣x﹣k有三个零点因此k=x3+2x2﹣4x,令g(x)=k,则g′(x)=3x2+4x﹣4,令g′(x)=0,解得:x=﹣2,x=,从而得到单调区间求出函数极值,进而确定k的范围.解答:解:(1)∵f′(x)=3x2+4x﹣a,对于x∈R恒有f′(x)≥2x2+2x﹣4,即x2+2x﹣a+4≥0对于x∈R恒成立∴△=4﹣4(4﹣a)≤0,解得:a≤3,∴a max=3;(2)∵a=3时,F(x)=f(x)﹣x﹣k有三个零点∴k=x3+2x2﹣4x,令g(x)=k,则g′(x)=3x2+4x﹣4,令g′(x)=0,解得:x=﹣2,x=,x,g(x),g(x)情况如下表:x (﹣∞,﹣2)﹣2 (﹣2,)(,+∞)g′(x) + 0 ﹣ 0 +g(x)单调递增极大值8 单调递减极小极﹣单调递增(10分)由上表知,当x=﹣2时g(x)取得极大值g(﹣2)=﹣8,当x=时g(x)取得极小值g()=﹣数形结合可知,实数k的取值范围为(﹣,8).点评:本题考察了函数的单调性,导数的应用,求函数的极值问题,是一道基础题.21.在平面直角坐标系xOy中,已知椭圆C1:(a>b>0)的左焦点为F1(﹣1,0),且点P(0,1)在C1上.(1)求椭圆C1的方程;(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:(1)因为椭圆C1的左焦点为F1(﹣1,0),所以c=1,点P(0,1)代入椭圆,得b=1,由此能求出椭圆C1的方程.(2)设直线l的方程为y=kx+m,由,得(1+2k2)x2+4kmx+2m2﹣2=0.因为直线l与椭圆C1相切,所以△=16k2m2﹣4(1+2k2)(2m2﹣2)=0.由此能求出直线l的方程.解答:解:(1)因为椭圆C1的左焦点为F1(﹣1,0),所以c=1,点P(0,1)代入椭圆,得,即b=1,所以a2=b2+c2=2所以椭圆C1的方程为.(2)直线l的斜率显然存在,设直线l的方程为y=kx+m,由,消去y并整理得(1+2k2)x2+4kmx+2m2﹣2=0,因为直线l与椭圆C1相切,所以△=16k2m2﹣4(1+2k2)(2m2﹣2)=0整理得2k2﹣m2+1=0①由,消去y并整理得k2x2+(2km﹣4)x+m2=0因为直线l与抛物线C2相切,所以△=(2km﹣4)2﹣4k2m2=0整理得km=1②综合①②,解得或所以直线l的方程为或.点评:本题考查椭圆方程的求法,考查直线与圆锥曲线的位置关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宣城市2014~2015学年度第一学期期末调研测试宣城市2014~2015学年度第一学期期末调研测试高三语文试题[注意事项]1.本试卷分第卷(阅读题)和第卷(表达题)两部分。
试卷满分150分,考试时间150分钟。
2.答题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和准考号填写在答题卡指定区域,将条形码横贴在答题卡右上角“条形码粘贴处”。
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
4.非选择题必须用黑色墨水的钢笔或签字笔作答,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
5.考试结束,务必将试题卷和答题卡一并上交。
第卷(阅读题共66分)一、(9分)阅读下面的文字,完成1~3题。
元杂剧作者对传统伦理道德的坚守李代宽元代初年废除科举制度后,基本上断绝了文人的进仕之路,许多文人走向社会底层,与民间艺人(如红字李二、花李郎等)相结合,组织“书会”从事杂剧创作。
但是,中国传统伦理道德等传统文化的价值观念已经深深根植于他们的心中,元杂剧作者们不可避免地要将自己接受的传统伦理道德观念融入自己所塑造的戏曲形象,这是元杂剧思想内容的主流。
钟嗣成在《录鬼簿》记述与其“相知”的“名公才人”时,多次赞赏他们的“浩然之气”,如宫天挺“豁然胸次扫尘埃”,郑光祖“名香天下”,曾瑞“乐幽闲不解趋承”,施惠“道心清静绝无尘”,钟嗣成自己也是“杜门养浩然之志”。
在两千多年的历史发展中,“仁”“义”“礼”“智”“信”等传统伦理道德因素渗透到社会生活和思想意识的方方面面,伦理道德至上的观念已内化为人们的思维模式和行为准则。
尤其是面对元代没有受到教育的绝大多数社会底层民众,杂剧就承载了更多传统伦理道德教化的功能。
李渔在《闲情偶寄·词曲部》中说:“因愚夫愚妇识字知书者少,劝使为善,诫使勿恶,其道无由,故设此种文词,借优人说法,与大众齐听。
”平民百姓热爱戏曲,重要的一条原因是他们把戏曲中传达的伦理道德因素当作社会正义舆论的引导和现实生活的规范。
从夏商周一直到元代,几千年的社会生活都在元杂剧中得到反映,上至帝王将相下到农夫商贩,各阶层人物无不笼入笔端。
《蝴蝶梦》中王老汉三个儿子,《焚儿救母》中的张屠,《冯玉兰》中的冯玉兰,《虎头牌》中的山寿马,《窦娥冤》中的窦娥,《降桑椹》中的蔡顺,都具有善良贤孝的光辉品格。
“君子笃于亲,则民兴于仁;故旧不遗,则民不偷”(《论语·泰伯》),儒家伦理道德思想的基础是“仁”。
“孝悌”是“仁”的前提,“入则孝,出则悌”(《论语·学而》)是一个人必须具备的品德,这是一个家庭、家族乃至国家关系的伦理情感纽带。
元杂剧的作者希望注重加强个人道德修养,调节好人际关系,实现家庭和睦,社会安宁的理想。
《礼记·中庸》说:“仁者,人也,亲亲为大。
”《杀狗劝夫》《老生儿》《疏者下船》实质上传达的是亲亲才能修身,亲亲才能为政,亲亲才是为人根本的观点。
《礼记·大学》说:“古之欲明明德于天下者,先治其国;欲治其国者,先齐其家。
”治家最重要的一条是教子有方,才能让子孙后代“立身行道,扬名于后世,以显父母,孝之终也。
”《孟母三移》中的孟母,《剪发待宾》中的陶母,《陈母教子》中的陈母,《九世同居》中的张公艺,《东堂老》中的东堂老无不遵循这一传统并取得成功。
《范张鸡黍》中的范式和张劭志同道合,《替杀妻》中的张千为保护朋友而宁担罪责,更彰显了“朋友有信”这一传统美德。
《豫让吞炭》《渑池会》《伊尹扶汤》《介子推》《单鞭夺槊》等杂剧塑造了豫让、廉颇、蔺相如、伊尹、介子推、尉迟恭等忠贞报国的忠臣义士形象,即使是《鲁斋郎》等杂剧中的包拯,《双献功》等杂剧中的李逵也是元杂剧作者们推崇的标杆和楷模。
《论语·里仁》里,曾子曾说:“夫子之道,忠恕而已矣”“苟利国家生死以,岂因祸福避趋之”,只有从国家和整体利益至上的原则出发,在个人对他人、对社会、对群体的关系上,“义以为上”“先义后利”才能引导一种文明不断前行,这也是中国传统伦理道德的一条主线。
元杂剧作者们坚守中国传统伦理道德这一主线,是赢得广大观众的法宝。
只有当这种深层次的文化因素深深扎根于作品之中时,才能够使戏曲观众与戏剧作品之间产生心灵的共鸣。
(选自《光明日报》2013年10月14日15版,有删改)1.下列对元杂剧创作的相关表述,不正确的一项是(3分)A.元代统治者废除科举制度后,文人们将关注点转向民间艺术,而书会这一组织的成立又有力地推动了元杂剧的发展。
B.中国传统伦理道德观念是元杂剧作者们坚守的主线,他们将这种观念融入戏曲形象中,这是元杂剧思想内容的主流。
C.元杂剧中窦娥、孟母、张千这一类的人物形象寄寓了作者们希望通过加强个人道德修养,实现家庭和睦、社会安宁的理想。
D.元杂剧题材广泛,从夏商周至元代的几千年的社会生活,帝王将相、农夫商贩等各阶层人物形象都在元杂剧中得到展现。
2.下列对原文思路的分析,不正确的一项是(3分)A.第一段首先简介元杂剧产生的背景,然后以钟嗣成《录鬼簿》记述为证总说元杂剧作者在塑造戏曲形象时将传统伦理道德观念融入作品的创作特点。
B.第二段从时代、文化的角度指出元杂剧承载着传统伦理道德教化的功能,在引导社会正义舆论和规范人们的现实生活等方面起到了积极作用。
C.三、四两段以高度概括的语言分别剖析了元杂剧中经典人物形象身上体现出来的“仁”“义”“礼”“智”“信”等伦理道德内涵。
D.第五段总结全文,强调了元杂剧作家坚守传统伦理道德的重要意义,并明确指出这是使戏曲观众与戏曲作品产生共鸣的途径。
3.下列对原文观点的概括,正确的一项是(3分)A.李渔认为,元代科举制度的废除导致绝大多数社会底层民众不识字,因此需要元杂剧这种雅俗共赏的艺术形式来完成劝人为善的教化任务。
B.在中国传统道德观念中,“孝悌”对家庭、家族乃至国家关系的维护起着重要作用,就家庭关系而言,“孝”和“教子有方”又是相辅相成的。
C.中国传统伦理道德一直强调国家和整体利益至上的原则,使“义以为上”“先义后利”成为其中最重要、最核心的部分。
D.元杂剧作家只要将传统伦理道德这种深层次的文化因素深深扎根于自己的作品中,就能使观众与作品产生共鸣,从而赢得广大观众。
二、(33分)阅读下面的文言文,完成4~7题。
耐斋记归有光万安刘先生,来教昆山学。
学有三先生,而先生所居称东斋。
先是,两斋之衙,皆在讲堂东偏,近乃徙之西,颇为深远清秘。
先生至,则扁其居曰耐斋。
予尝访先生于斋中,于时秋风飒然,黄叶满庭,户外无履迹。
独一卒衣皂衣,承迎左右,为进茗浆。
因坐语久之。
先生曰:“吾为是官,秩卑而禄微,月费廪米三石,具饘粥,养妻子,常不给,为耐贫。
上官行县,吾于职事无所辖,往往率诸生郊迎,至则随令、丞、簿拜趋唯诺,为耐辱。
久任之法不行,官无崇卑,率以期月迁徙速化,而吾官常不迁,为耐久。
有是三耐,吾是以名吾斋。
”予既别去,一日,使弟子沈孝来求《斋记》。
昔孟子论士不为道,至于为贫而仕,惟抱关击柝为宜。
夫舍学者之职业而为抱关击柝,盖亦有甚不得已者矣。
惟近代学官与书院山长之设,以待夫士之有道而不任职者,盖为贫与为道兼行而不悖。
此其法足以优天下之学士,为特愈于前世也,故当时号博士官为清高。
虽然,求为清高,而其间容有不能耐者。
夫使其不能耐,则虽博士官不可为矣。
使其能耐,如孟子所谓抱关击柝可也。
扬雄有言:“非夷、齐而是柳下惠。
”“首阳为拙,柱下为工。
”士之立身,各有所处。
夫使其能耐,虽至于大臣宰相可也。
因书其说,使孝归而质之先生云。
(选自《归有光文选》)[注]抱关击柝:守门和巡夜的人。
泛指位卑禄薄的小官。
首阳:指伯夷叔齐不食周粟而饿死在首阳山中。
老子曾在周朝任柱下史的官职。
4.对下列句子中加点词的解释,不正确的一项是(3分)A.则扁其居曰耐斋扁:做匾B.率以期月迁徙速化率:大致C.柱下为工工:聪明D.使孝归而质之先生云质:质疑5.下列各组句子中,加点词的意义和用法相同的一组是(3分)A.因坐语久之相如因持璧却立B.吾是以名吾斋忽魂季以魄动C.至于为贫而仕吾尝终日而思矣D.夫使其不能耐路漫漫其修远兮6.下列对原文有关内容的概括和分析,不正确的一项是(3分)A.本文是归有光为昆山县学训导刘先生而作,雅洁简练的文词中既有对刘先生遭际的同情,也有对其坚守的支持与鼓励。
B.全文分三个层次,第一层简介刘先生的来历和巨止,第二层记述刘先生“三耐”说的内容,第三层生发议论,洞见肺腑。
C.“秋风飒然,黄叶满庭,户外无履迹”不仅仅是环境描写,更是借此褒扬刘先生谢绝世俗往来、潜心治学的可贵品质。
D.归有光在文中以传统儒家思想为依旧,就刘先生所言“耐贫”“耐辱”“耐久”立论,引经据典,阐发了“士之立身”的原则。
7.把原文中面线的句子翻译成现代汉语。
(10分)(1)独一卒衣皂衣,承迎左右,为进茗浆。
(4分)(2)上官行县,吾于职事无所辖,往往率诸生郊迎,至则随令、丞、簿拜趋唯诺,为耐辱。
(6分)阅读下面这首词,完成8~9题。
小圣乐·骤雨打新荷元好问绿叶阴浓,遍池亭水阁,偏趁凉多。
海榴初绽,朵朵簇红罗。
老燕携雏弄语,有高柳鸣蝉相和。
骤雨过,珍珠乱撒,打遍新荷。
人生百年有几,念良辰美景,休放虚过。
穷通前定,何用苦张罗。
命友邀宾玩赏,对芳樽浅酌低歌。
且酩酊,任他两轮日月,来往如梭。
8.上阕“骤雨过,珍珠乱撒,打遍新荷”历来为人称道,请选两个角度作简要赏析。
(4分)9.有人说,本词表达诗人乐天知命的情怀,有人说是抒发了诗人失意苦闷之情。
你认为呢?请结合作品作简要分析。
(4分)10.补写出下列名篇名句中的空缺部分。
(甲、乙两题任选一题作答;如果两题都答,则按甲题计分。
)(6分)甲:而浮生若梦,为欢几何?,。
,。
,。
(李白《春夜宴从弟桃花园序》)乙:心非木石岂无感?。
(鲍照《拟行路难》)东船西舫悄无言,。
(白居易《琵琶行》),水随天去秋无际。
(辛弃疾《水龙吟·登建康赏心亭》)子曰:“见贤思齐焉,。
”(《论语十则》),赢粮而景从。
(贾谊《过秦论》),用之如泥沙?(杜牧《阿房宫赋》)三、(24分)阅读下面的文字,完成11~14题。
秋夜于德北那年深秋,佳卫突然打电话给我。
他说:“我们去郊外旅行吧。
”对于他的提议我当然高兴,可也颇为犹豫,因为深秋这个季节实在不适合去郊外旅行。
在北方,这个季节早晚已经有霜了。
但佳卫坚持。
我说:“这回怎么有时间了?”电话那端,他只是笑,没有回答。
我们所说的郊外叫土门岭,是个半丘陵地区。
我们认识住在那里的一位农民诗人,我们特别想吃他家的豆饭,烀土豆,炸辣椒酱,萝卜大葱白菜心儿。
