2021新高考数学二轮总复习第三部分专题一1.3平面向量与复数组合练课件.pptx
模块二讲重点平面向量-2021届高考数学二轮复习PPT全文课件(新高考版)

12,
3
2
,C(cosθ,sin
θ)其中∠BOC=θ,0≤θ≤π3 ,则有O→C=(cosθ,sinθ)=x12,
3
2
+y(1,0),即
2x+y=cosθ,
23x=sinθ,
解得x=
2sinθ 3
,y=cosθ-
sinθ 3
,故x
+3y= 2sin3θ +3cosθ-
3 sinθ=3cosθ-
|a||b|. 特别地,a·a=|a|2 或|a|= a·a.
(4)cos讲 重 点平面 向量-2 021届高 考数学 二轮复 习PPT 全文课 件(新 高考版 )【完 美课件 】
(5)|a·b|≤|a||b|.
平面向量数量积的坐标表示 设 a=(x1,y1),b=(x2,y2),a,b 的夹角为 θ,则 (1)a·b=x1x2+y1y2. (2)|a| = x21+y21 . 若 A(xA , yA) , B(xB , yB) , 则 | A→B | = (xA-xB)2+(yA-yB)2. (3)cosθ= x21+x1xy212+·y1xy222+y22. (4)a⊥b⇔a·b=0⇔x1x2+y1y2=0.
A→D
=
1 2
(
A→B
+
A→C
),等价于已知AD是
△ABC中BC边上的中线.
模 块 二 讲 重 点平面 向量-2 021届高 考数学 二轮复 习PPT 全文课 件(新 高考版 )【完 美课件 】
模 块 二 讲 重 点平面 向量-2 021届高 考数学 二轮复 习PPT 全文课 件(新 高考版 )【完 美课件 】
向量的夹角 (1)夹角的定义和范围:
(2)两向量的夹角分别是锐角与钝角的充要条件: ①a与b的夹角是锐角⇔a·b>0且a与b不共线. ②a与b的夹角是钝角⇔a·b<0且a与b不共线.
新高考新教材高考数学二轮复习送分考点专项练2复数平面向量pptx课件

7.(2023湖南郴州三模)若
1+i
=2-i
(其中i为虚数单位),则在复平面上所对应
的点在( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
1+i
因为 =2-i,所以
1+i
z=
2-i
(1+i)(2+i)
1
3
1
3
解析
=
= 5 + 5i,则 = 5 − 5i,
(2-i)(2+i)
1 3
即D的坐标为(1,5).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
5.(2022 新高考Ⅰ,3)在△ABC 中,点 D 在边 AB 上,BD=2DA.记=m,=n,则
=( B )
A.3m-2n
B.-2m+3n
C.3m+2n
D.2m+3n
B.x2=1-i
1
D. =i
2
解析 因为 x1=1+i 且实系数一元二次方程 x2+px+2=0 的两根为 x1,x2,
D.λμ=-1
解析 (方法一)由题意,得a+λb=(1+λ,1-λ),a+μb=(1+μ,1-μ).
∵(a+λb)⊥(a+μb),∴(1+λ)(1+μ)+(1-λ)(1-μ)=0,解得λμ=-1.故选D.
(方法二)由题意,得a2=12+12=2,b2=12+(-1)2=2,a·
b=1×1+1×(-1)=0.
平面内对应的点位于第三象限,则 =( D )
复数-2021届高三数学(新高考)一轮复习ppt完美课件(49页)

7.5复数-2021届高三数学(新高考) 一轮复 习课件( 共49张 PPT)
2.[2020·山东泰安质量检测]若复数(2-i)(a+i)的实部与虚部互为 相反数,则实数 a=( )
A.3 B.13 C.-13 D.-3 答案:D 解析:(2-i)·(a+i)=(2a+1)+(2-a)i,因为该复数的实部与虚部 互为相反数,所以(2a+1)+(2-a)=0,解得 a=-3,故选 D.
【教材提炼】
一、教材改编 1.[必修二·P94 复习参考题 7 T1(2)改编]复数i-5 2的共轭复数是 () A.i+2 B.i-2 C.-2-i D.2-i
答案:B 解析:i-5 2=2--5i22++ii=-105-5i =-2-i,其共轭复数为-2+i,故选 B.
7.5复数-2021届高三数学(新高考) 一轮复 习课件( 共49张 PPT)
7.5复数-2021届高三数学(新高考) 一轮复 习课件( 共49张 PPT)
三、走进高考 4.[2019·全国Ⅰ卷]设复数 z 满足|z-i|=1,z 在复平面内对应的点 为(x,y),则( ) A.(x+1)2+y2=1 B.(x-1)2+y2=1 C.x2+(y-1)2=1 D.x2+(y+1)2=1 答案:C 解析:由已知得,z=x+yi, ∵|z-i|=1, ∴|x+yi-i|=1, ∴x2+(y-1)2=1.
7.5复数-2021届高三数学(新高考) 一轮复 习课件则复数 z 的虚部为( ) A.16 B.-11 C.-11i D.-16
答案:B 解析:依题意,z=(3+2i)(2-5i)=6-15i+4i+10=16-11i,故 复数 z 的虚部为-11.故选 B.
2021-2022年高考数学二轮复习专题1.3三角函数与平面向量教学案
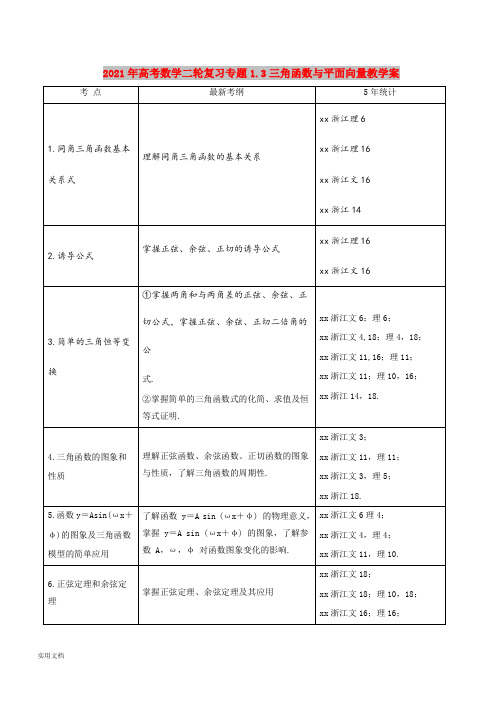
2021年高考数学二轮复习专题1.3三角函数与平面向量教学案xx浙江文16;理16; xx 浙江14. 7.平面向量的实际背景及基本概念理解平面向量及几何意义,理解零向量、向量的模、单位向量、向量相等、平行向量、向量夹角的概念。
xx·浙江理7;xx •浙江文22; xx •浙江理15; xx •浙江文理15; 8. 向量的线性运算掌握向量加法、减法、数乘的概念,并理解其几何意义。
xx·浙江7;xx •浙江文13, 理.15; xx •浙江文理15;9.平面向量的基本定理及坐标表示1.理解平面向量的基本定理及其意义,会用平面向量基本定理解决简单问题。
2.掌握平面向量的正交分解及其坐标表示。
3.掌握平面向量的加法、减法与数乘的坐标运算。
xx •浙江文22; 10.平面向量的数量积 ①理解平面向量数量积的概念及其意义,了解平面向量的数量积与向量投影的关系。
②掌握平面向量数量积的坐标运算,掌握数量积与两个向量的夹角之间的关系。
③会用坐标表示平面向量的平行与垂直。
xx •浙江文17;理7,17; xx •浙江文9;理8; xx •浙江文13;理15; xx·浙江文理15; xx •浙江10,15. 11.向量的应用会用向量方法解决某些简单的平面几何问题.xx •浙江文17;理7;xx •浙江文22; xx •浙江10.【答案】又 ,则2212{ 25sin cos 1sin cos αααα=+= ,且,可得.【对点训练】【xx 届江西省六校第五次联考】已知, ,则__________. 【答案】【解析】∵,∴cosα<0.∵7sin2α=2cosα,即14sinαcosα=2cosα,∴, 则21143127sin cos sin πααα⎛⎫-==--=- ⎪⎝⎭. 【典例2】【xx 江西省赣州厚德外国语学校上学期第一次测试】的值是( ) A. B. C. D. 【答案】D【对点训练】【xx 河南省名校联盟第一次段考】已知圆:,点,,记射线与轴正半轴所夹的锐角为,将点绕圆心逆时针旋转角度得到点,则点的坐标为__________. 【答案】【解析】设射线OB 与轴正半轴的夹角为,有已知有,所以,且,C 点坐标为 .【考向预测】对于三角恒等变换,高考命题主要以公式的基本运用、计算为主,其中多以与角的范围、三角函数的性质、三角形等知识结合考查,在三角恒等变换过程中,准确记忆公式、适当变换式子、有效选取公式是解决问题的关键.热点二 三角函数的图象和性质【典例3】【xx 课标3,理6】设函数f (x )=cos (x +),则下列结论错误的是 A .f(x)的一个周期为−2πB .y=f(x)的图像关于直线x=对称C .f(x+π)的一个零点为x=D .f(x)在(,π)单调递减【答案】D 【解析】【对点训练】【xx天津,文理】设函数,,其中,.若,,且的最小正周期大于,则(A),(B),(C),(D),【答案】【例4】【xx浙江,18】已知函数f(x)=sin2x–cos2x– sin x cos x(x R).(Ⅰ)求的值.(Ⅱ)求的最小正周期及单调递增区间.【答案】(Ⅰ)2;(Ⅱ)最小正周期为,单调递增区间为.【解析】(Ⅱ)由与得)62sin(22sin 32cos )(π+-=--=x x x x f所以的最小正周期是 由正弦函数的性质得Z k k x k ∈+≤+≤+,2236222πππππ解得Z k k x k ∈+≤≤+,326ππππ所以的单调递增区间是.【对点训练】【xx 山东,理16】设函数()sin()sin()62f x x x ππωω=-+-,其中.已知.(Ⅰ)求;(Ⅱ)将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值. 【答案】(Ⅰ).(Ⅱ)得最小值.试题解析:(Ⅰ)因为()sin()sin()62f x x x ππωω=-+-,所以31()sin cos cos 2f x x x x ωωω=--133(sin cos )22x x ωω=-由题设知, 所以,. 故,,又, 所以.【典例5】【xx 新课标2】函数()的最大值是__________. 【答案】1【解析】化简三角函数的解析式,则 ,由可得,当时,函数取得最大值1.【对点训练】【xx 湖北省部分重点中学起点】设函数,其中θ∈,则导数f ′(1)的取值范围是________. 【答案】[,2]【解析】由题【例6】【xx课标1,理9】已知曲线C1:y=cos x,C2:y=sin (2x+),则下面结论正确的是()A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2 C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2 【答案】D【解析】【对点训练】已知函数的部分图象如图所示,下面结论正确的个数是( )①函数的最小正周期是;②函数在区间上是增函数;③函数的图象关于直线对称;④函数的图象可由函数的图象向左平移个单位长度得到A. 3B. 2C. 1D. 0【答案】C【解析】根据函数f(x)=sin(ωx+φ)(ω>0)的部分图象知,=−(−)=,∴T==π,ω=2;【考向预测】几年高考在对三角恒等变换考查的同时,对三角函数(特别是)图象与性质的考查力度有所加强,往往将恒等变换与图象和性质结合考查.其中三角函数的定义域值域、单调性、奇偶性、周期性、对称性以及图象变换是主要考查对象,难度仍然以中低档为主,重在对基础知识的考查,淡化特殊技巧,强调通解通法. 特别注意:(1)解答三角函数图像变换问题的关键是抓住“只能对函数关系式中的变换”的原则.(2)对于三角函数图像平移变换问题,其移变换规则是“左加右减”,并且在变换过程中只变换其中的自变量,如果的系数不是1,就要把这个系数提取后再确定变换的单位长度和方向,另外,当两个函数的名称不同时,首先要将函数名称统一,其次要把变换成,最后确定平移的单位,并根据的符号确定平移的方向.热点三解三角形【典例7】【xx浙江,14】已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,BD=2,连结CD,则△BDC 的面积是______,cos∠BDC=_______.【答案】【解析】取BC中点E,DC中点F,由题意:,△ABE 中,,1115cos ,sin 14164DBC DBC ∴∠=-∠=-=, BC 115sin 22D S BD BC DBC ∴=⨯⨯⨯∠=△. 又2110cos 12sin ,sin 44DBC DBF DBF ∴∠=-∠=-∴∠=, 10cos sin BDC DBF ∴∠=∠=, 综上可得,△BCD 面积为,.【对点训练】【xx 届浙江省部分市学校(新昌中学、台州中学等)高三上9+1联考】设函数()22sin 2sin cos 6f x x x x π⎛⎫=++- ⎪⎝⎭.(1)求的单调递增区间;(2)若角满足, , 的面积为,求的值. 【答案】(1) , ;(2) .【典例8】【xx课标II,理17】的内角所对的边分别为,已知,(1)求;(2)若,的面积为,求.【答案】(1);(2).【解析】试题分析:利用三角形内角和定理可知,再利用诱导公式化简,利用降幂公式化简,结合求出;利用(1)中结论,利用勾股定理和面积公式求出,从而求出.【名师点睛】解三角形问题是高考高频考点,命题大多放在解答题的第一题,主要利用三角形的内角和定理,正、余弦定理、三角形面积公式等知识解题,解题时要灵活利用三角形的边角关系进行“边转角”“角转边”,另外要注意三者的关系,这样的题目小而活,备受老师和学生的欢迎。
最新-2021高考数学理天津专用二轮复习课件:13平面向量与复数 精品

1
3
(2)由 = ( + ),得 + =2 .因为 AO 是半径,连接 AO
2
并延长交圆于点 D,则 2|AO|=|AD|(直径),也就是| + |=| |,即
四边形 ABDC 是一个圆内接的平行四边形,且以直径为对角线,所以关闭
1
(1)
(2)90°
必定是一个矩形,得
(ke1+e2)=k|e1| 2+(1-2k)e 1·
e 2-2|e 2|2=k+
5
2-1
2
-2=0,解得
k= .
5
4
(1)D (2)
关闭
4
解析
答案
-16命题热点一
命题热点二
命题热点三
命题热点四
命题热点五
复数的概念及运算
【思考】 复数运算的一般思路是怎样的?
例4(1)(2016全国乙高考)设(1+i)x=1+yi,其中x,y是实数,则
数化成a+bi(a,b∈R)的形式,其次根据实部a和虚部b的符号来确定
点所在的象限.
-21命题热点一
命题热点二
命题热点三
命题热点四
命题热点五
对点训练5复数z满足(-1+i)z=(1+i)2,其中i为虚数单位,则在复平
面上复数z对应的点位于(
)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
关闭
C.1 D.2
)
关闭
4 = 0,
∵(2+ai)(a-2i)=4a+(a -4)i=-4i,∴ 2
解得 a=0.
-4 = -4,
2
2021年高考数学二轮复习专题一集合、逻辑用语、不等式等1.3平面向量与复数课件文

-2-
试题统计
(2014 全国Ⅰ,文 3)
(2014 全国Ⅰ,文 6)
(2014 全国Ⅱ,文 2)
(2015 全国Ⅰ,文 2)
(2015 全国Ⅱ,文 2)
(2016 全国Ⅰ,文 2)
(2016 全国Ⅱ,文 2)
(2016 全国Ⅲ,文 2)
(2017 全国Ⅰ,文 3)
(2017 全国Ⅱ,文 2)
命题热点三
命题热点四
2 + i
对点训练4(1)假设a为实数,且
1+i
A.-4
B.(2)(1+i)(2+i)=(
)
A.1-i B.1+3i
C.3+i D.3+3i
命题热点五
=3+i,那么a= (
答案(1)D (2)B
解析 (1)由题意,得2+ai=(3+i)(1+i)=2+4i,那么a=4.
(2)(1+i)(2+i)=2+3i+i2=1+3i,应选B.
)
-18命题热点一
命题热点二
命题热点三
命题热点四
命题热点五
复数的几何表示
【思考】 如何判断复数在复平面上的位置?
例5复平面内表示复数z=i(-2+i)的点位于(
)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 C
解析 由题意可得z=-1-2i,在复平面内对应点(-1,-2),那么该点位
于第三象限.应选C.
2 × 1 × B.-9
- -1 =-6.
2
(2)设非零向量a,b满足|a+b|=|a-b|,那么(
高考数学二轮总复习第三部分专题一3平面向量与复数组合练课件

实数 a 的值可以是-1,0,1.故选 ABC.
12/11/2021
4.(2020全国Ⅱ,理15)设复数z1,z2满足|z1|=|z2|=2,z1+z2= 3 +i,
则|z1-z2|=
.
答案 2 3
解析 设 z1=a+bi,z2=c+di,a,b,c,d∈R.∵|z1|=|z2|=2,∴a2+b2=4,c2+d2=4.
12/11/2021
考向二
平面向量的概念及线性运算
5.(多选)关于平面向量a,b,c,下列说法中不正确的是(
A.若a∥b且b∥c,则a∥c
B.(a+b)·c=a·c+b·c
C.若a·b=a·c,且a≠0,则b=c
D.(a·b)·c=a·(b·c)
12/11/2021
)
答案 ACD
解析 对于A,若b=0,因为0与任意向量平行,所以a不一定与c平行,故A不正
点C的轨迹为(
)
A.圆
B.椭圆
C.抛物线
D.直线
答案 A
解析 以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标
系.
设 C(x,y),A(-a,0),则 B(a,0),则 =(x+a,y), =(x-a,y),由 ·=1,
得(x+a)(x-a)+y2=1,整理得 x2+y2=a2+1,即点 C 的轨迹为圆.故选 A.
cos<a,a+b>=(
)
31
A.-35
19
B.-35
17
C.
35
19
D.
(通用版)2021高考数学二轮复习第一篇第2练复数与平面向量课件文

P→M=M→C,则|B→M|2 的最大值是____1_6___.
解析 答案
易错易混专项练
1.(2021·全国Ⅰ)设有下面四个命题:
p1:假设复数z满1足 ∈R,那么z∈R; z
p2:假设复数z满足z2∈R,那么z∈R; p3:假设复数z1,z2满足z1z2∈R,那z么2 z1= ;
p4:假设复数z∈R,z那么 ∈R.
解析 答案
10.如图,在△ABC 中,N 是 AC 边上一点,且A→N=12N→C,P 是 BN 上的一
点,若A→P=mA→B+29A→C,则实数 m 的值为
A.19
√B.13
C.1
D.3
解析 ∵A→N=12N→C,∴A→N=13A→C,
∴A→P=mA→B+29A→C=mA→B+23A→N. 又B,N,P三点共线,
∴m+23=1,∴m=13.
解析 答案
11.如图,在正方形 ABCD 中,M,N 分别是 BC,CD 的中点,若A→C=λA→M +μB→N,则 λ+μ 等于
A.2
8 B.3
6 C.5
√D.85
解析 答案
12.假设|a|=1,|b|=3 ,且|a-2b|=7 ,那么向量a与向量b夹角的大 小π
6
=0,且|O→A|=|A→B|,则C→A·C→B等于
3 A.2
B. 3
√C.3
D.2 3
解析 ∵O→A+A→B+O→C=0,∴O→B=-O→C,
故点O是BC的中点,且△ABC为直角三角形, 又△ABC 的外接圆的半径为 1,|O→A|=|A→B|,
∴BC=2,AB=1,CA= 3,∠BCA=30°,
应选D.
解析 答案
2.a,b∈R,i是虚数单位.假设a-i与2+bi互为共轭复数,那么(a+bi)2等
第3讲平面向量和复数-2021届高三高考数学二轮复习课件

第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
2.(2020·吉安一模)如图所示,矩形 ABCD 的对角线相交于点 O,E
为 AO 的中点,若D→E=λA→B+μA→D(λ,μ∈R),则 λ+μ 等于
( A)
A.-12
B.12
分值 10 10
10
第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
年份 卷别
Ⅰ卷 2019
Ⅱ卷 Ⅲ卷
题号 1、8
2、3 2、13
考查角度 复数的乘法运算,复数模的计算;向 量的数量积及各个向量的模,在利用 向量夹角公式求出夹角的余弦值,求 出夹角 数的运算及共轭复数;平面向量模长 的计算 复数的商的运算;复数的商的运算,
第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
● (理科)
年份 卷别 Ⅰ卷
Ⅱ卷 2020
Ⅲ卷
题号
考查角度
1
复数的运算法则和复数的模的求解
向量垂直的充分必要条件;复数模长 13、15
的求解、复数及其运算的几何意义
复数的除法运算;平面向量数量积的
2、6 计算以及向量模的计算、平面向量夹
一组基底.
第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
● 考向1 平面向量的线性运算
1.(2020·吉林省重点高中第二次月考)如图,若O→A=a,O→B=b,O→C
=c,B 是线段 AC 靠近点 C 的一个四等分点,则下列等式成立的是
第3讲平面向量和复数-2021届高三高 考数学 二轮复 习课件
【2021】浙江高考数学二轮复习:专题二 3第3讲 平面向量与复数

第3讲 平面向量与复数平面向量的概念与线性运算[核心提炼]1.在平面向量的化简或运算中,要根据平面向量基本定理选好基底,变形要有方向不能盲目转化;2.在用三角形加法法则时要保证“首尾相接”,结果向量是第一个向量的起点指向最后一个向量终点所在的向量;在用三角形减法法则时要保证“同起点”,结果向量的方向是指向被减向量.[典型例题](1)(2021·杭州模拟)如图所示,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →=( )A .a -12bB .12a -bC .a +12bD .12a +b(2)(2021·金华市十校联考)已知A 、B 、C 是平面上不共线的三点,O 是△ABC 的重心,点P 满足OP →=14(OA →+OB →+2OC →),则S △P AB S △OAB为( )A .32B .23C .2D .12(3)(2021·嘉兴七校联考)在△ABC 中,点D 满足BD →=34BC →,当点E 在射线AD (不含点A )上移动时,若AE →=λAB →+μAC →,则(λ+1)2+μ2的取值范围为________.【解析】 (1)连接CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB 且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a .(2)如图,延长CO ,交AB 中点D ,O 是△ABC 的重心,则OP →=14(OA→+OB →+2OC →)=14(2OD →+2OC →)=14(-OC →+2OC →)=14OC →,所以OP =14OC =14×23CD =16CD ;所以DP =DO +OP =13CD +16CD =12CD ,DO =13CD ;所以S △P AB S △OAB =DP DO =12CD13CD =32.(3)因为点E 在射线AD (不含点A )上,设AE →=kAD →(k >0),又BD →=34BC →,所以AE →=k (AB →+BD →)=k ⎣⎡⎦⎤AB →+34(AC →-AB →)=k 4AB →+3k 4AC →, 所以⎩⎨⎧λ=k4μ=3k4,(λ+1)2+μ2=⎝⎛⎭⎫k 4+12+916k 2=58⎝⎛⎭⎫k +252+910>1,故(λ+1)2+μ2的取值范围为(1,+∞).【答案】 (1)D (2)A (3)(1,+∞)平面向量的线性运算技巧(1)对于平面向量的线性运算,要先选择一组基底,同时注意共线向量定理的灵活运用. (2)运算过程中重视数形结合,结合图形分析向量间的关系.[对点训练]1.(2021·瑞安市四校联考)设M 是△ABC 边BC 上的点,N 为AM 的中点,若AN →=λAB →+μAC →,则λ+μ的值为( )解析:选C.因为M 在BC 边上,所以存在实数t ∈[0,1]使得BM →=tBC →. AM →=AB →+BM →=AB →+tBC →=AB →+t (AC →-AB →)=(1-t )AB →+tAC →, 因为N 为AM 的中点, 所以AN →=12AM →=1-t 2AB →+t 2AC →,所以λ=1-t 2,μ=t2,所以λ+μ=1-t 2+t 2=12,故C 正确.2.(2021·宁波诺丁汉大学附中期中考试)在△ABC 中,BC =7,AC =6,cos C =267.若动点P 满足AP →=(1-λ)AB →+2λ3AC →,(λ∈R ),则点P 的轨迹与直线BC ,AC 所围成的封闭区域的面积为( )A .5B .10C .2 6D .4 6解析:选A.设AD →=23AC →,因为AP →=(1-λ)AB →+2λ3AC →=(1-λ)AB →+λAD →,所以B ,D ,P 三点共线. 所以P 点轨迹为直线BC .在△ABC 中,BC =7,AC =6,cos C =267,所以sin C =57,所以S △ABC =12×7×6×57=15,所以S △BCD =13S △ABC =5.3.(2021·高考浙江卷)已知正方形ABCD 的边长为1.当每个λi (i =1,2,3,4,5,6)取遍±1时,|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|的最小值是________,最大值是________.解析:以点A 为坐标原点,AB 所在直线为x 轴,AD 所在直线为y 轴建立平面直角坐标系,如图,则A (0,0),B (1,0),C (1,1),D (0,1),所以λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →=(λ1-λ3+λ5-λ6,λ2-λ4+λ5+λ6),所以当⎩⎪⎨⎪⎧λ1-λ3+λ5-λ6=0λ2-λ4+λ5+λ6=0时,可取λ1=λ3=1,λ5=λ6=1,λ2=-1,λ4=1,此时|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|取得最小值0;取λ1=1,λ3=-1,λ5=λ6=1,λ2=1,λ4=-1,则|λ1AB →+λ2BC →+λ3CD →+λ4DA →+λ5AC →+λ6BD →|取得最大值22+42=2 5.答案:0 2 5平面向量的数量积[核心提炼]1.平面向量的数量积的两种运算形式(1)数量积的定义:a ·b =|a ||b |cos θ(其中θ为向量a ,b 的夹角); (2)坐标运算:a =(x 1,y 1),b =(x 2,y 2)时,a ·b =x 1x 2+y 1y 2. 2.平面向量的三个性质(1)若a =(x ,y ),则|a |=a·a =x 2+y 2.(2)若A (x 1,y 1),B (x 2,y 2),则 |AB →|=(x 2-x 1)2+(y 2-y 1)2.(3)若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角,则cos θ=a·b|a||b |=x 1x 2+y 1y 2x 21+y 21x 22+y 22.[典型例题](1)(2021·高考浙江卷)已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为π3,向量b 满足b 2-4e·b +3=0,则|a -b |的最小值是( )A .3-1B .3+1C .2D .2- 3(2)(2021·浙江新高考研究联盟)已知向量a ,b ,c 满足|a |=1,|b |=k ,|c |=2-k 且a +b +c =0,则b 与c 夹角的余弦值的取值范围是________.【解析】 (1)设O 为坐标原点,a =OA →,b =OB →=(x ,y ),e =(1,0),由b 2-4e ·b +3=0得x 2+y 2-4x +3=0,即(x -2)2+y 2=1,所以点B 的轨迹是以C (2,0)为圆心,1为半径的圆.因为a 与e 的夹角为π3,所以不妨令点A 在射线y =3x (x >0)上,如图,数形结合可知|a -b |min =|CA →|-|CB →|=3-1.故选A.(2)设b 与c 的夹角为θ,由题b +c =-a , 所以b 2+c 2+2b ·c =1.即cos θ=2k 2-4k +32k 2-4k =1+32(k -1)2-2. 因为|a |=|b +c |≥|b -c |,所以|2k -2|≤1. 所以12≤k ≤32.所以-1≤cos θ≤-12.【答案】 (1)A (2)⎣⎡⎦⎤-1,-12(1)平面向量数量积的计算①涉及数量积和模的计算问题,通常有两种求解思路 (ⅰ)直接利用数量积的定义; (ⅱ)建立坐标系,通过坐标运算求解.②在利用数量积的定义计算时,要善于将相关向量分解为图形中模、夹角和已知的向量进行计算.(2)求解向量数量积最值问题的两种思路①直接利用数量积公式得出代数式,依据代数式求最值.②建立平面直角坐标系,通过坐标运算得出函数式,转化为求函数的最值.[对点训练]1.(2021·嘉兴市高考一模)已知平面向量a 、b 满足|a |=|b |=1,a ·b =12,若向量c 满足|a-b +c |≤1,则|c |的最大值为( )A .1B . 2C . 3D .2解析:选D.由平面向量a 、b 满足|a |=|b |=1,a ·b =12,可得|a|·|b |·cos 〈a ,b 〉=1·1·cos 〈a ,b 〉=12,由0≤〈a ,b 〉≤π,可得〈a ,b 〉=π3,设a =(1,0),b =⎝⎛⎭⎫12,32,c =(x ,y ),则|a -b +c |≤1,即有⎪⎪⎪⎪⎝⎛⎭⎫12+x ,y -32≤1,即为⎝⎛⎭⎫x +122+⎝⎛⎭⎫y -322≤1, 故|a -b +c |≤1的几何意义是在以⎝⎛⎭⎫-12,32为圆心,半径等于1的圆上和圆内部分,|c |的几何意义是表示向量c 的终点与原点的距离,而原点在圆上,则最大值为圆的直径,即为2.2.如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O .记I 1=OA →·OB →,I 2=OB →·OC →,I 3=OC →·OD →,则( )A .I 1<I 2<I 3B .I 1<I 3<I 2C .I 3 < I 1<I 2D .I 2<I 1<I 3解析:选C.如图所示,四边形ABCE 是正方形,F 为正方形的对角线的交点,易得AO <AF ,而∠AFB =90°,所以∠AOB 与∠COD 为钝角,∠AOD 与∠BOC 为锐角.根据题意,I 1-I 2=OA →·OB →-OB →·OC →=OB →·(OA →-OC →)=OB →·CA →=|OB →|·|CA →|·cos ∠AOB <0,所以I 1<I 2,同理得,I 2>I 3,作AG ⊥BD 于G ,又AB =AD ,所以OB <BG =GD <OD ,而OA <AF =FC <OC ,所以|OA →|·|OB →|<|OC →|·|OD →|,而cos ∠AOB =cos ∠COD <0,所以OA →·OB →>OC →·OD →,即I 1>I 3.所以I 3<I 1<I 2.3.(2021·金华十校高考模拟)若非零向量a ,b 满足:a 2=(5a -4b )·b ,则cos 〈a ,b 〉的最小值为________.解析:非零向量a ,b 满足:a 2=(5a -4b )·b ,可得a ·b =15(a 2+4b 2)=15(|a |2+4|b |2)≥15·2|a |2·4|b |2=45|a |·|b |,即有cos 〈a ,b 〉=a ·b |a |·|b |≥45·|a |·|b ||a |·|b |=45,当且仅当|a |=2|b |,取得最小值45.答案:45平面向量与其他知识的交汇[核心提炼]平面向量具有代数形式与几何形式的“双重身份”,常与三角函数、解三角形、平面解析几何、函数、数列、不等式等知识交汇命题,平面向量的“位置”为:一是作为解决问题的工具,二是通过运算作为命题条件.[典型例题](1)如图,已知点D 为△ABC 的边BC 上一点,BD →=3DC →,E n (n ∈N *)为边AC 上的列点,满足E n A →=14a n +1·E n B →-(3a n +2)E n D →,其中实数列{a n }中,a n >0,a 1=1,则数列{a n }的通项公式为a n =( )A .3·2n -1-2 B .2n -1 C .3n -1D .2·3n -1-1(2)已知在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,向量p =(cos B +sin B ,2sin B -2),q =(sin B -cos B ,1+sin B ),且p ⊥q .①求B 的大小;②若b =2,△ABC 的面积为3,求a ,c .【解】 (1)选D.因为BD →=3DC →,所以E n C →=E n B →+BC →=E n B →+43BD →=E n B →+43(BE n →+E n D →)=-13E n B →+43E n D →.设mE n C →=E n A →,则由E n A →=14a n +1E n B →-(3a n +2)E n D →,得(14a n +1+13m )E n B →-(43m +3a n +2)E n D →=0,则-13m =14a n +1,43m =-(3a n +2),所以14a n +1=14(3a n +2),所以a n +1+1=3(a n +1).因为a 1+1=2,所以数列{a n +1}是以2为首项,3为公比的等比数列,所以a n +1=2·3n -1,所以a n =2·3n -1-1.(2)①因为p ⊥q ,所以p ·q =(cos B +sin B )(sin B -cos B )+(2sin B -2)·(1+sin B )=0,即3sin 2B -cos 2B -2=0,即sin 2B =34,又角B 是锐角三角形ABC 的内角,所以sin B =32,所以B =60°. ②由①得B =60°,又△ABC 的面积为3, 所以S △ABC =12ac sin B ,即ac =4.①由余弦定理得b 2=a 2+c 2-2ac cos B , 又b =2,所以a 2+c 2=8,② 联立①②,解得a =c =2.平面向量与其他知识的交汇点主要体现在与三角函数、立体几何、解析几何,求最值. (1)利用平面向量的知识给出三角函数之间的一些关系,解题的关键还是三角函数的知识.在解析几何中只是利用向量知识给出一些几何量的位置关系和数量关系,在解题中要善于根据向量知识分析解析几何中几何量之间的关系,最后的解题还要落实到解析几何知识上.(2)因为向量是沟通代数、几何的工具,有着极其丰富的实际背景,对于某些代数问题,可构造向量,使其转化为向量问题求解.[对点训练]1.(2021·杭州市高三二模)△ABC 中,∠C =90°,AC =4,BC =3,D 是AB 的中点,E ,F 分别是边BC 、AC 上的动点,且EF =1,则DE →·DF →的最小值等于( )解析:选B.以三角形的直角边为坐标轴建立平面直角坐标系,如图所示:则A (0,4),B (3,0),C (0,0),D ⎝⎛⎭⎫32,2. 设E (x ,0),则F (0,1-x 2),0≤x ≤1. 所以DE →=⎝⎛⎭⎫x -32,-2, DF →=⎝⎛⎭⎫-32,1-x 2-2. 所以DE →·DF →=94-32x +4-21-x 2=254-3x 2-21-x 2.令f (x )=254-3x2-21-x 2,当x ≠1时,则f ′(x )=-32+2x1-x 2 .令f ′(x )=0得x =35.当0≤x <35时,f ′(x )<0,当35<x <1时,f ′(x )>0.所以当x =35时,f (x )取得最小值f ⎝⎛⎭⎫35=154. 当x =1时,f (1)=254-32=194>154,故选B.2.(2021·浙江新高考研究联盟联考)已知向量a ,b 满足|a +b |=4,|a -b |=3,则|a |+|b |的取值范围是( )A .[3,5]B .[4,5]C .[3,4]D .[4,7]解析:选B.|a |+|b |≥max{|a +b |,|a -b |}=4, (|a |+|b |)2≤|a +b |2+|a -b |2=25,所以|a |+|b |≤5.3.(2021·江苏常州武进区高三上学期期中考试改编)已知数列{a n }中,a 1=2,点列P n (n =1,2,…)在△ABC 内部,且△P n AB 与△P n AC 的面积比为2∶1.若对n ∈N *都存在数列{b n }满足b n P n A →+12a n +1P n B →+(3a n +2)P n C →=0,求a 4.解:在线段BC 上取点D ,使得BD =2CD ,则P n 在线段AD 上, 因为b n P n A →+12a n +1P n B →+(3a n +2)P n C →=0,所以-12a n +1BP n →=b n AP n →+(3a n +2)CP n →=b n (BP n →-BA →)+(3a n +2)(BP n →-BC →),所以⎝⎛⎭⎫-12a n +1-b n -3a n -2BP n →=-b n BA →-32×(3a n +2)BD →. 因为A ,P n ,D 三点共线,所以-12a n +1-b n -3a n -2=-b n -32(3a n +2),即a n +1=3a n +2,所以a 2=3a 1+2=8,a 3=3a 2+2=26,a 4=3a 3+2=80.复 数 [核心提炼]1.复数的除法复数的除法一般是将分母实数化,即分子、分母同乘以分母的共轭复数再进一步化简. 2.复数运算中常见的结论 (1)(1±i)2=±2i ,1+i 1-i =i ,1-i1+i =-i.(2)-b +a i =i(a +b i).(3)i 4n =1,i 4n +1=i ,i 4n +2=-1,i 4n +3=-i. (4)i 4n +i 4n +1+i 4n +2+i 4n +3=0.[典型例题](1)(2021·杭州学军中学高考模拟)设复数z 满足1+z1-z =i ,则|z |=( )A .1B .2C .3D .2(2)设有下面四个命题p 1:若复数z 满足1z ∈R ,则z ∈R ;p 2:若复数z 满足z 2∈R ,则z ∈R ; p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=z 2; p 4:若复数z ∈R ,则z ∈R . 其中的真命题为( )A .p 1,p 3B .p 1,p 4C .p 2,p 3D .p 2,p 4(3)(2021·浙江新高考冲刺卷)已知复数z =1+i ,其中i 为虚数单位,则复数1+z +z 2+…+z 2 017的实部为( )A .1B .-1C .21 009D .-21 009【解析】 (1)因为复数z 满足1+z 1-z=i ,所以1+z =i -z i ,所以z (1+i)=i -1,所以z =i -1i +1=i ,所以|z |=1,故选A.(2)对于命题p 1,设z =a +b i(a ,b ∈R ),由1z =1a +b i =a -b i a 2+b 2∈R ,得b =0,则z ∈R 成立,故命题p 1正确;对于命题p 2,设z =a +b i(a ,b ∈R ),由z 2=a 2-b 2+2ab i ∈R ,得ab =0,则a =0或b =0,复数z 可能为实数或纯虚数,故命题p 2错误;对于命题p 3,设z 1=a +b i(a ,b ∈R ),z 2=c +d i(c ,d ∈R ),由z 1·z 2=(ac -bd )+(ad +bc )i ∈R ,得ad +bc =0,不一定有z 1=z 2,故命题p 3错误;对于命题p 4,设z =a +b i(a ,b ∈R ),则由z ∈R ,得b =0,所以z =a ∈R 成立,故命题p 4正确.故选B.(3)因为z =1+i , 所以1+z +z 2+…+z 2 017=1×(1-z 2 018)1-z =z 2 018-1z -1=(1+i )2 018-11+i -1=(2i )1 009-1i =(-1+21 009i )(-i )-i 2=21 009+i.所以复数1+z +z 2+…+z 2 017的实部为21 009.故选C. 【答案】 (1)A (2)B (3)C复数问题的解题思路(1)以复数的基本概念、几何意义、相等的条件为基础,结合四则运算,利用复数的代数形式列方程或方程组解决问题.(2)若与其他知识结合考查,则要借助其他的相关知识解决问题.[对点训练]1.(2021·福建省普通高中质量检查)若复数z 满足(1+i)z =|3+i|,则在复平面内,z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选A.由题意,得z =(3)2+121+i =2(1-i )(1+i )(1-i )=1-i ,所以z =1+i ,其在复平面内对应的点为(1,1),位于第一象限,故选A.2.(2021·金丽衢十二校联考)设z 是复数,|z -i|≤2(i 是虚数单位),则|z |的最大值是( ) A .1 B .2 C .3 D .4解析:选C.因为|z -i|≤2,所以复数z 在复平面内对应点在以(0,1)为圆心,以2为半径的圆及其内部.所以|z |的最大值为3.故选C. 3.(2021·高考浙江卷)复数z =11+i(i 为虚数单位),则|z |=________. 解析:通解:z =11+i=1-i 2=12-i 2,所以|z |=⎝⎛⎭⎫122+⎝⎛⎭⎫-122=22. 优解:|z |=⎪⎪⎪⎪11+i =1|1+i|=112+12=22.答案:22专题强化训练1.(2021·绍兴诸暨高考二模)已知复数z 满足z (1+i)=2i ,则z 的共轭复数z 等于( ) A .1+i B .1-i C .-1+iD .-1-i解析:选B.由z (1+i)=2i ,得z =2i 1+i =2i (1-i )(1+i )(1-i )=1+i ,则z 的共轭复数z =1-i.故选B.2.在等腰梯形ABCD 中,AB →=-2CD →,M 为BC 的中点,则AM →=( ) AB →+12AD →AB →+12AD →AB →+14AD →AB →+34AD →解析:选B.因为AB →=-2CD →,所以AB →=2DC →.又M 是BC 的中点,所以AM →=12(AB →+AC →)=12(AB →+AD →+DC →)=12(AB →+AD →+12AB →)=34AB →+12AD →,故选B.3.(2021·嘉兴一中高考模拟)复数z 满足z ·(2-i)=3-4i(其中i 为虚数单位),则复数|zi |=( )解析:选D.复数z 满足z ·(2-i)=3-4i(其中i 为虚数单位),所以z ·(2-i)(2+i)=(3-4i)(2+i),化为:5z =10-5i ,可得z =2-i.则复数|zi |=⎪⎪⎪⎪2-i i =⎪⎪⎪⎪⎪⎪-i (2-i )-i·i =|-1-2i|=|1+2i|=12+22= 5.故选D.4.在边长为2的正方形ABCD 中,E ,F 分别为BC 和DC 的中点,则DE →·BF →=( )A .-52B .32C .-4D .-2解析:选C.通过建系求点的坐标,然后求解向量的数量积.在边长为2的正方形ABCD 中,E ,F 分别为BC 和DC 的中点,以A 为坐标原点,AB ,AD 为坐标轴,建立平面直角坐标系,则B (2,0),D (0,2),E (2,1),F (1,2).所以DE →=(2,-1),BF →=(-1,2),所以DE →·BF →=-4.5.(2021·台州市书生中学检测)已知点O 是△ABC 的外接圆圆心,且AB =3,AC =4.若存在非零实数x 、y ,使得AO →=xAB →+yAC →,且x +2y =1,则cos ∠BAC 的值为( )解析:选A.设线段AC 的中点为点D ,则直线OD ⊥AC .因为AO →=xAB →+yAC →,所以AO →=xAB →+2yAD →.又因为x +2y =1,所以点O 、B 、D 三点共线,即点B 在线段AC 的中垂线上,则AB =BC =3.在△ABC 中,由余弦定理得,cos ∠BAC =32+42-322×3×4=23.故选A.6.在△ABC 中,AB =3,BC =2,∠A =π2,如果不等式|BA →-tBC →|≥|AC →|恒成立,则实数t 的取值范围是( )A .[1,+∞)B .⎣⎡⎦⎤12,1C .⎝⎛⎦⎤-∞,12∪[1,+∞) D .(-∞,0]∪[1,+∞)解析:选C.在直角三角形ABC 中,易知AC =1,cos ∠ABC =32,由|BA →-tBC →|≥|AC →|,得BA →2-2tBA →·BC →+t 2BC →2≥AC →2,即2t 2-3t +1≥0,解得t ≥1或t ≤12.7.称d (a ,b )=|a -b |为两个向量a ,b 间的“距离”.若向量a ,b 满足:①|b |=1;②a ≠b ;③对任意的t ∈R ,恒有d (a ,t b )≥d (a ,b ),则( )A .a ⊥bB .b ⊥(a -b )C .a ⊥(a -b )D .(a +b )⊥(a -b )解析:选B.由于d (a ,b )=|a -b |,因此对任意的t ∈R ,恒有d (a ,t b )≥d (a ,b ),即|a -t b |≥|a-b |,即(a -t b )2≥(a -b )2,t 2-2t a ·b +(2a ·b -1)≥0对任意的t ∈R 都成立,因此有(-2a ·b )2-4(2a ·b -1)≤0,即(a ·b -1)2≤0,得a ·b -1=0,故a ·b -b 2=b ·(a -b )=0,故b ⊥(a -b ).8.(2021·温州市高考模拟)记max{a ,b }=⎩⎪⎨⎪⎧a ,a ≥b b ,a <b ,已知向量a ,b ,c 满足|a |=1,|b |=2,a ·b =0,c =λa +μb (λ,μ≥0,且λ+μ=1,则当max{c ·a ,c ·b }取最小值时,|c |=( )解析:选A.如图,设OA →=a ,OB =b ,则a =(1,0),b =(0,2), 因为λ,μ≥0,λ+μ=1,所以0≤λ≤1. 又c =λa +μb ,所以c ·a =(λa +b -λb )·a =λ; c ·b =(λa +b -λb )·b =4-4λ. 由λ=4-4λ,得λ=45.所以max{c ·a ,c ·b }=⎩⎨⎧λ,45≤λ≤14-4λ,0≤λ<45.令f (λ)=⎩⎨⎧λ,45≤λ≤14-4λ,0≤λ<45.则f (λ)∈⎣⎡⎦⎤45,1.所以f (λ)min =45,此时λ=45,μ=15,所以c =45a +15b =⎝⎛⎭⎫45,25. 所以|c |=⎝⎛⎭⎫452+⎝⎛⎭⎫252=255.故选A. 9.(2021·绍兴市柯桥区高三期中检测)已知平面向量a ,b ,c 满足|a |=4,|b |=3,|c |=2,b ·c =3,则(a -b )2(a -c )2-[(a -b )·(a -c )]2的最大值为( )A .43+37B .47+3 3C .(43+37)2D .(47+33)2解析:选D.设OA →=a ,OB →=b ,OC →=c ,a -b 与a -c 所成夹角为θ, 则(a -b )2(a -c )2-[(a -b )·(a -c )]2 =|AB |2|AC |2-|AB |2|AC |2cos 2θ=|AB |2|AC |2sin 2θ=|AB |2|AC |2sin 2∠CAB =4S 2△ABC , 因为|b |=3,|c |=2,b ·c =3,所以b ,c 的夹角为60°, 设B (3,0),C (1,3),则|BC |=7,所以S △OBC =12×3×2×sin 60°=332,设O 到BC 的距离为h ,则12·BC ·h =S △OBC =332, 所以h =3217,因为|a |=4,所以A 点落在以O 为圆心,以4为半径的圆上, 所以A 到BC 的距离最大值为4+h =4+3217.所以S △ABC 的最大值为 12×7×⎝⎛⎭⎫4+3217 =27+332,所以(a -b )2(a -c )2-[(a -b )·(a -c )]2最大值为4⎝⎛⎭⎫27+3322=(47+33)2.故选D.10.(2021·金华市东阳二中高三月考)若a ,b 是两个非零向量,且|a |=|b |=λ|a +b |,λ∈⎣⎡⎦⎤33,1,则b 与a -b 的夹角的取值范围是( )解析:选B.因为|a |=|b |=λ|a +b |,λ∈⎣⎡⎦⎤33,1,不妨设|a +b |=1,则|a |=|b |=λ.令OA →=a ,OB →=b ,以OA 、OB 为邻边作平行四边形OACB ,则平行四边形OACB 为菱形.故有△OAB 为等腰三角形,故有∠OAB =∠OBA =θ,且0<θ<π2.而由题意可得,b 与a -b 的夹角,即OB →与BA →的夹角,等于π-θ,△OAC 中,由余弦定理可得|OC |2=1=|OA |2+|AC |2-2|OA |·|AC |·cos 2θ=λ2+λ2-2·λ·λcos 2θ,解得cos 2θ=1-12λ2.再由33≤λ≤1,可得12≤12λ2≤32,所以-12≤cos 2θ≤12,所以π3≤2θ≤2π3,所以π6≤θ≤π3,故2π3≤π-θ≤5π6,即b 与a -b 的夹角π-θ的取值范围是⎣⎡⎦⎤2π3,5π6.11.(2021·杭州市高考二模)已知复数z =1+a i i(a ∈R )的实部为1,则a =________,|z |=________.解析:因为z =1+a i i =(1+a i )(-i )-i 2=a -i 的实部为1,所以a =1,则z =1-i ,|z |= 2. 答案:1212.(2021·嘉兴一中高考适应性考试)设e 1,e 2为单位向量,其中a =2e 1+e 2,b =e 2,且a 在b 上的投影为2,则a ·b =________,e 1与e 2的夹角为________.解析:设e 1,e 2的夹角为θ,因为a 在b 上的投影为2,所以a ·b |b |=(2e 1+e 2)·e 2|e 2|=2e 1·e 2+|e 2|2=2|e 1|·|e 2|cos θ+1=2,解得cos θ=12,则θ=π3.a ·b =(2e 1+e 2)·e 2=2e 1·e 2+|e 2|2=2|e 1|·|e 2|cos θ+1=2. 答案:2π313.已知向量a ,b ,|a |=1,|b |=2.若对任意单位向量e ,均有|a ·e |+|b ·e |≤6,则a ·b 的最大值是________.解析:由题意,令e =(1,0),a =(cos α,sin α),b =(2cos β,2sin β),则由|a ·e |+|b ·e |≤6,可得|cos α|+2|cos β|≤ 6.①令sin α+2sin β=m ,②①2+②2得4[|cos αcos β|+sin αsin β]≤1+m 2对一切实数α,β恒成立,所以4[|cosαcos β|+sin αsin β]≤1,故a·b =2(cos αcos β+sin αsin β)≤2[|cos αcos β|+sin αsin β]≤12.答案:1214.(2021·温州市十五校联合体联考)已知坐标平面上的凸四边形ABCD 满足AC →=(1,3),BD →=(-3,1),则凸四边形ABCD 的面积为________;AB →·CD →的取值范围是________.解析:由AC →=(1,3),BD →=(-3,1)得AC →⊥BD →,且|AC →|=2,|BD →|=2,所以凸四边形ABCD 的面积为12×2×2=2;因为ABCD 为凸四边形,所以AC 与BD 交于四边形内一点,记为M ,则AB →·CD →=(MB →-MA →)(MD →-MC →)=MB →·MD →+MA →·MC →-MB →·MC →-MA →·MD →,设AM →=λAC →,BM →=μBD →,则λ,μ∈(0,1),且MA →=-λAC →,MC →=(1-λ)AC →, MB →=-μBD →,MD →=(1-μ)BD →,所以AB →·CD →=-4μ(1-μ)-4λ(1-λ)∈[-2,0),所以有λ=μ=12时,AB →·CD →取到最小值-2.答案:2 [-2,0)15.(2021·嘉兴一中高考适应性考试)在△ABC 中,∠ACB 为钝角,AC =BC =1,CO →=xCA →+yCB →且x +y =1,函数f (m )=|CA →-mCB →|的最小值为32,则|CO →|的最小值为________.解析:在△ABC 中,∠ACB 为钝角,AC =BC =1,函数f (m )的最小值为32. 所以函数f (m )=|CA →-mCB →| =CA →2+m 2CB →2-2mCA →·CB →=1+m 2-2m cos ∠ACB ≥32, 化为4m 2-8m cos ∠ACB +1≥0恒成立.当且仅当m =8cos ∠ACB8=cos ∠ACB 时等号成立,代入得到cos ∠ACB =-12,所以∠ACB =2π3.所以|CO →|2=x 2CA →2+y 2CB →2+2xyCA →·CB →=x 2+y 2+2xy ×cos 2π3=x 2+(1-x )2-x (1-x )=3⎝⎛⎭⎫x -122+14, 当且仅当x =12=y 时,|CO →|2取得最小值14,所以|CO →|的最小值为12.答案:1216.在△OAB 中,已知|OB →|=2,|AB →|=1,∠AOB =45°,若OP →=λOA →+μOB →,且λ+2μ=2,则OA →在OP →上的投影的取值范围是________.解析:由OP →=λOA →+μOB →,且λ+2μ=2, 则OA →·OP →=OA →·⎣⎡⎦⎤λOA →+⎝⎛⎭⎫1-λ2OB → =λOA →2+⎝⎛⎭⎫1-λ2OA →·OB →, 又|OB →|=2,|AB →|=1,∠AOB =45°, 所以由余弦定理求得|OA →|=1,所以OA →·OP →=λ+⎝⎛⎭⎫1-λ2×1×2×22=1+λ2, |OP →|=⎣⎡⎦⎤λOA →+⎝⎛⎭⎫1-λ2OB →2= λ2|OA →|2+2λ⎝⎛⎭⎫1-λ2OA →·OB →+⎝⎛⎭⎫1-λ22|OB →|2=λ22+2,故OA →在OP →上的投影OA →·OP →|OP →|=1+λ2λ22+2=22·λ+2λ2+4(*). 当λ<-2时,(*)式=-22·(λ+2)2λ2+4=-221+4λλ2+4=-221+4λ+4λ∈⎝⎛⎭⎫-22,0;当λ≥-2时,(*)式可化为22(λ+2)2λ2+4;①λ=0,上式=22; ②-2≤λ<0,上式=221+4λ+4λ∈⎣⎡⎭⎫0,22; ③λ>0,上式=221+4λ+4λ∈⎝⎛⎦⎤22,1.综上,OA →在OP →上的投影的取值范围是⎝⎛⎦⎤-22,1.答案:⎝⎛⎦⎤-22,1 17.已知OA →,OB →是非零不共线的向量,设OC →=1r +1·OA →+r r +1OB →,定义点集P =⎩⎨⎧K ⎪⎪⎪KB →·KC →|KB →|=KA →·KC →|KA →|,⎭⎪⎬⎪⎫KC →≠0,当K 1,K 2∈P 时,若对于任意的r ≥3,不等式|K 1K 2→|≤c |AB →|恒成立,则实数c 的最小值为________.解析:由OC →=1r +1·OA →+r r +1OB →,可得A ,B ,C 三点共线,由KB →·KC →|KB →|=KA →·KC →|KA →|,可得|KC →|cos ∠AKC =|KC →|cos ∠BKC ,即有∠AKC =∠BKC ,则KC 为∠AKB 的角平分线.由角平分线的性质定理可知|KA ||KB |=|AC ||BC |=r , 以AB 所在的直线为x 轴,以线段AB 上某一点为原点建立直角坐标系,设点K (x ,y ),A (-a ,0),B (b ,0),所以(x +a )2+y 2(x -b )2+y 2=r 2,化简得(1-r 2)x 2+(1-r 2)y 2+(2a +2br 2)x +(a 2-b 2r 2)=0.由方程知K 的轨迹是圆心在AB 上的圆,当|K 1K 2|为直径时最大,方便计算,令K 1K 2与AB 共线,如图,由|K 1A |=r |K 1B |,可得|K 1B |=|AB |r +1, 由|K 2A |=r |K 2B |,可得|K 2B |=|AB |r -1, 可得|K 1K 2|=|AB |r +1+|AB |r -1=2r r 2-1|AB |=2r -1r|AB |,而易知r -1r ≥3-13=83,即有|K 1K 2|≤34|AB |,即|K 1K 2||AB |≤34,即c ≥⎝⎛⎭⎫|K 1K 2||AB |max =34, 故c 的最小值为34.答案:3418.在△ABC 中,已知C =π6,向量p =(sin A ,2),q =(2,cos B ),且p ⊥q . (1)求角A 的值;(2)若BC →=2BD →,AD =7,求△ABC 的面积.解:(1)因为p ⊥q ,所以p ·q =0⇒p ·q =2sin A +2cos B =0,又C =π6,所以sin A +cos B =sin A +cos ⎝⎛⎭⎫5π6-A =0,化简得tan A =33,A ∈(0,π),所以A =π6. (2)因为BC →=2BD →,所以D 为BC 边的中点, 设|BD →|=x ,|BC →|=2x ,由(1)知A =C =π6,所以|BA →|=2x ,B =2π3,在△ABD 中,由余弦定理,得|AD →|2=|BA →|2+|BD →|2-2|BA →|·|BD →|·cos 2π3=(2x )2+x 2-2·2x ·x ·cos 2π3=7,所以x =1,所以AB =BC =2,所以S △ABC =12BA ·BC ·sin B =12×2×2×sin 2π3= 3.19.已知m =(2sin x ,sin x -cos x ),n =(3cos x ,sin x +cos x ),记函数f (x )=m ·n . (1)求函数f (x )的最大值以及取得最大值时x 的取值集合;(2)设△ABC 的角A ,B ,C 所对的边分别为a ,b ,c ,若f (C )=2,c =3,求△ABC 面积的最大值.解:(1)由题意,得f (x )=m ·n =23sin x cos x +sin 2x -cos 2x =3sin 2x -(cos 2 x -sin 2 x )=3sin 2x -cos 2x =2sin ⎝⎛⎭⎫2x -π6,所以f (x )max =2;当f (x )取最大值时,即sin ⎝⎛⎭⎫2x -π6=1,此时2x -π6=2k π+π2(k ∈Z ),解得x =k π+π3(k ∈Z ),所以x 的取值集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x =k π+π3,k ∈Z .(2)由f (C )=2,得sin ⎝⎛⎭⎫2C -π6=1,又0<C <π,即-π6<2C -π6<11π6,所以2C -π6=π2,解得C =π3,在△ABC 中,由余弦定理c 2=a 2+b 2-2ab cos C ,得3=a 2+b 2-ab ≥ab ,即ab ≤3,当且仅当a =b =3时,取等号,所以S △ABC =12ab sin C=34ab ≤334, 所以△ABC 面积的最大值为334.。
高考数学大二轮复习专题一第2讲平面向量与复数课件理

Ⅱ 1,3 复数的几何意义;平面向量数量积求参数
2016
共轭复数及复数乘除法;平面向量的夹角及坐标
Ⅲ 2,3
运算
Ⅰ 1,7 复数除法及复数的模;平面向量的线性运算
2015
Ⅱ 2,13 复数的乘法;平面向量平行
第二页,共三十九页。
命题预测
从题量上看,通常是复数、平
第2讲 平面
(píngmiàn)
第一页,共三十九页。
向量与复数
近五年高考试题统计与命题(mìng tí)预测
年份 卷别 题号 考查角度
Ⅰ 2,7 复数的几何意义;平面向量的数量积运算
2019 Ⅱ 2,3 复数的几何意义;平面向量的数量积运算
Ⅲ 2,13 复数的除法运算;平面向量的数量积运算
复数的除法运算及复数的模;平面向量的线性运
180°=-22+6+15=-1.
答案(dá àn):-1
第九页,共三十九页。
12.(2019江苏,12)如图,在△ABC中,D是BC的中点(zhōnɡ diǎn),E在边AB
上,BE=2EA,AD与CE交于点O.若
·=6·的
,则值是
第十页,共三十九页。
.
解析:如图,过点 D 作 DF∥CE,交 AB 于点 F,
(4)i4n+i4n+1+i4n+2+i4n+3=0(n∈N*).
第十四页,共三十九页。
二、平面向量的概念及线性运算
1.在平面向量的化简或运算中,要根据平面向量基本定理选好基底,变形
要有方向不能盲目转化(zhuǎnhuà);
2.在用三角形加法法则时要保证“首尾相接”,结果向量是第一个向量的起
2021高考数学二轮专题训练1.1集合复数与平面向量课件

即
a 0,
a
2
解得a=±2
8 0
,
2
综上所述,a=0或a=±2 2 ,所以C(S)=3.
答案:3
专题能力提升练
一 集合、复数与平面向量(40分钟 80分)
一、单项选择题(共8小题,每小题5分,共40分)
1.(2020·海口二模)设复数z=(2+i)(3-2i),则复数z在复平面内对应的点的坐标
【解析】选C.在△ABC中,D是AB边上的中点,
则 C BC D D BC D A D C D ( A C C D ) 2C D C A .
2.(2020·新高考全国Ⅰ卷)已知P是边长为2的正六边形ABCDEF内的一点,则
APAB的取值范围是( )
A.(-2,6)
B.(-6,2)
C.(-2,4)
【解析】选C.因为集合A={x|x(x+2)<0},B={x||x|≤1},所以A={x|-2<x<0}, B={x|-1≤x≤1},所以A∪B=(-2,1],A∩B=[-1,0),所以阴影部分表示的集合 为∁(A∪B)(A∩B)=(-2,-1)∪[0,1].
【技法点拨】提素养 解决集合运算问题的方法 在进行集合运算时,要尽可能地利用数形结合的思想使抽象问题直观化. (1)用列举法表示的集合进行交、并、补的运算,常采用Venn图法解决,此时要搞 清Venn图中的各部分区域表示的实际意义. (2)用描述法表示的数集进行运算,常采用数轴分析法解决,此时要注意“端点” 能否取到. (3)若给定的集合是点集,画出图象,采用数形结合法求解.
C.{x|1<x≤2}
D.{x|-2≤x≤2}
【解析】选D.因为函数y=ln(x-1)的值域为R,所以A=R,又集合B=[-2,2],所以
