2010年浙江省宁波市初中毕业生学业考试中考数学试卷及解析

合集下载

2010宁波中考试卷及答案(全)

宁波市2010年初中毕业生学业考试语文试题考生须知:1.全卷分试题卷和答题卷。

试题卷共6页，有四个大题，26个小题。

满分为120分，考试时间为120分钟。

2.答题必须使用黑色字迹钢笔或签字笔书写，答案必须按照题号顺序在答题卷各题目规定区域内作答，做在试题卷上或超出答题区域书写的答案无效。

3.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上。

一、书写（4分）本题根据卷面书写情况评分，请你在书写时努力做到书写正确、工整。

二、积累应用（26分）1.阅读下面文字，根据拼音写出词语。

（2分）在宁波的历史上，宁波帮不仅以其（zhuóyuè）的商业才能著称于世，亦以其丰厚的人文精神引领着时代潮流。

在各个领域，宁波籍人士承前启后，各领（fēng sāo）。

2.根据语境及括号内提示，填写合适的成语。

（任选两个作答）（2分）快乐是什么？孩子说，快乐就是和同伴一起搭积木并A(表示对某一事物发生兴趣，沉溺其中，不觉疲倦)；成人说，快乐就是和友人一起品茶而B（形容安适，愉快而满足的样子）；老人说，快乐就是和家人一起共享C（形容家庭之乐）。

我选，成语：；我再选，成语：。

3.依次填入下面这段文字横线处的词语，最恰当的一项是（）（2分）如果说命运是那破旧的花架，只要意志坚强，它可以变得；如果说命运是那漆黑的夜空，只要意志坚强，它可以变得；如果说命运是那贫瘠的土地，只要意志坚强，它可以变得。

（1）沃壤千里（2）繁花似锦（3）星光灿烂A.(1)(3)(2)B.(2)(3)(1)C.(3)(2)(1)D.(2)（1）（3）4.读下面这段话，按要求完成题目。

（2分）读书，是智慧的行为。

愚昧的人，一辈子像游走在黑暗之中，随波逐流，浑浑噩噩，最后一事无成□智慧的人，一辈子像行进在光明之中，时时清醒，步步睿智，最终怎么会不谱写出人生的美乐章？①“□”内应加的标点是②将划线句改成陈述句。

5.下面句子没有语病....的一项是（）（3分）A.世博园内的中国馆用高科技手段完善地展示了中国的强盛、城市的美好。

DA浙江省宁波市中考真题

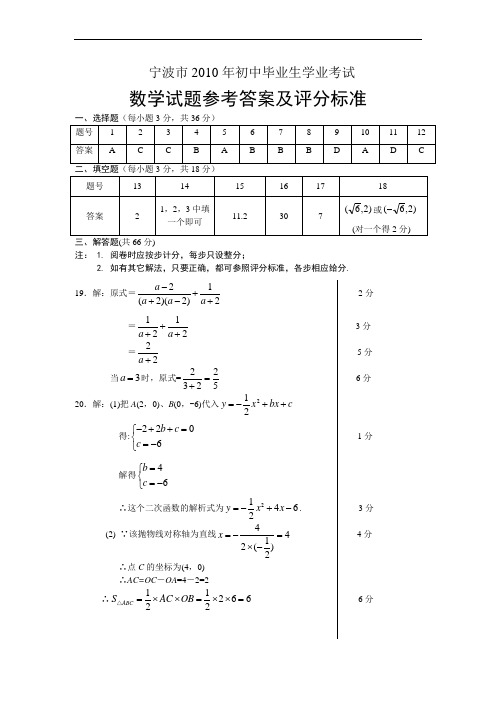
宁波市2010年初中毕业生学业考试数学试题参考答案及评分标准三、解答题(共66分)注： 1. 阅卷时应按步计分，每步只设整分；2. 如有其它解法，只要正确，都可参照评分标准，各步相应给分. 19．解：原式＝21(2)(2)2a a a a -++-+ 2分＝1122a a +++ 3分＝22a + 5分当3a =时，原式=22325=+ 6分20．解：(1)把A (2，0)、B (0，-6)代入c bx x y ++-=221得:2206b c c -++=⎧⎨=-⎩ 1分解得46b c =⎧⎨=-⎩∴这个二次函数的解析式为21462y x x =-+-. 3分 (2) ∵该抛物线对称轴为直线4412()2x =-=⨯- 4分∴点C 的坐标为(4，0) ∴AC=OC －OA =4－2=2∴1126622ABC S AC OB =⨯⨯=⨯⨯=△ 6分21．解：(1)1分周长为26 2分3分周长为22 4分 (2)6分注:画法不唯一.22．解：(1)100 2分(2)50025%89.6%112⨯⨯=。

4分5分(3)1号幼苗成活率为100%90%150⨯=， 2号幼苗成活率为85100%85%100⨯=，4号幼苗成活率为117100%93.6%125⨯=， 8分∵93.6%90%89.6%85%>>>∴应选择4号品种进行推广. 9分23．解：(1)15，4152分品种(2)由图象可知，s 是t 的正比例函数设所求函数的解析式为(0)s kt k =≠ 代入(45，4)得:445k = ，解得:445k =∴s 与t 的函数关系式为445s t =(045t ≤≤) 4分 (t 的取值范围不写不扣分)(3) 由图象可知，小聪在3045t ≤≤的时段内，s 是t 的一次函数，设函数解析式为(0)s mt n m =+≠，代入(30，4)，(45，0)得: 304450m n m n +=⎧⎨+=⎩5分解得:41512m n ⎧=-⎪⎨⎪=⎩∴412(3045)15s t t =-+≤≤ 6分 (t 的取值范围不写不扣分)令44121545t t -+=，解得1354t =7分当1354t =时， 41353454s =⨯=，答: 当小聪与小明迎面相遇时，他们离学校的路程是3千米. 8分24．解：(1)∵直径AB DE ⊥∴12CE DE == 1分 ∵DE 平分AO∴1122CO AO OE == 2分又∵90OCE ∠=︒∴30CEO ∠=︒在Rt △COE中，2cos30CEOE ===︒∴⊙O 的半径为2. 4分 (2) 连结OF .在Rt △DCP 中，∵45DPC ∠=︒ ∴904545D ∠=︒-︒=︒∴290EOF D ∠=∠=︒ 6分B∵2902360OEF S ππ=⨯⨯=扇形 1122222OEFS OE OF =⨯⨯=⨯⨯=△ 8分 ∴2OEF OEF S S S π=-=-△阴影扇形. 9分25．解：(1) 6， 6 , 2分 2V F E +-= 5分(2)20 8分(3)这个多面体的面数为x y +，棱数为243362⨯=条，根据2V F E +-=可得 24()362x y ++-=， ∴14x y +=. 10分26.解：(1) 在Rt △AOD 中，∵tan ∠DAO =3232==AO DO ， ∴ ∠DAB =60°. 2分∵四边形ABCD 是平行四边形∴∠DCB =∠DAB =60° 3分(2) ∵四边形ABCD 是平行四边形 ∴CD ∥AB∴∠DGE =∠AFE又∵∠DEG =∠AEF ，DE =AE∴△DEG ≌△AEF 4分 ∴DG =AF∵AF =OF -OA =4-2=2 ∴DG =2 ∴点G 的坐标为(2，32) 6分(3)①∵CD ∥AB∴∠DGE =∠OFE∵△OEF 经轴对称变换后得到△OEF ’∴∠OFE =∠OF ’E 7分 ∴∠DGE =∠OF ’E 在R t △AOD 中，∵E 是AD 的中点 ∴OE =21AD =AE 又∵∠EAO =60°∴∠EOA =60°， ∠AEO =60° 又∵∠EOF ’=∠EOA =60° ∴∠EOF ’=∠OEA∴AD ∥OF ’ 8分 ∴∠OF ′E =∠DEH ∴∠DEH =∠DGE 又∵∠HDE =∠EDG∴△DHE ∽△DEG 9分②点F 的坐标是F 1(113+-，0)，F 2(513--，0). 12分(给出一个得2分)对于此小题，我们提供如下详细解答，对学生无此要求. 过点E 作EM ⊥直线CD 于点M ，∵CD ∥AB∴∠EDM=∠DAB=60°∴sin 602EM DE =⋅︒==∵1122EGH S GH ME GH =⋅⋅=⋅=△∴6GH =∵△DHE ∽△DEG∴DEDH DG DE =即DH DG DE ⋅=2当点H 在点G 的右侧时，设x DG =，6+=x DH∴)6(4+=x x解得：133,13321--=+-=x x （舍）∵△DEG ≌△AEF∴AF =DG =133+-∵OF =AO +AF =1132133-=++-∴点F 的坐标为(113+-，0)当点H 在点G 的左侧时，设x DG =，6-=x DH∴)6(4-=x x解得：133,13321-=+=x x （舍）∵△DEG ≌△AEF∴AF =DG =133+∵OF =AO +AF =5132133+=++ ∴点F 的坐标为(513--，0)综上可知，点F 的坐标有两个，分别是F 1(113+-，0)，F 2(513--，0).M。

宁波中考数学试卷(解析版)

宁波中考数学试卷(解析版)宁波中考数学试卷(解析版)一、选择题1.某车站发车时间为每隔10分钟一班，小明到车站时刚好错过了一班车，他离下一班车还有多少分钟？A. 5B. 8C. 10D. 15解析：由题可知每隔10分钟一班车，小明刚好错过了一班车，所以还需要等待10分钟才能乘坐下一班车。

选C。

2.一辆汽车以每小时60公里的速度行驶，行驶了t小时后，它行驶的总距离是多少？A. 30tB. 40tC. 50tD. 60t解析：速度等于路程除以时间，汽车以每小时60公里的速度行驶，所以在t小时内，行驶的总距离为60t。

选D。

3.若a=3，b=2，则a²+3ab+b²的值等于：A. 23B. 19C. 17D. 15解析：将a、b的值代入给出的表达式，计算得到a²+3ab+b²=3²+3×3×2+2²=9+18+4=31。

选E。

4.在一个平面直角坐标系中，点A的坐标为(3,4)，点B的坐标为(7,1)，则线段AB的长度等于：A. 5B. 6C. 7D. 8解析：根据两点的坐标计算两点之间的距离：√[(7-3)²+(1-4)²]=√[4²+(-3)²]=√[16+9]=√25=5。

选A。

5.若x:y=2:3，且x=10，则y的值等于：A. 5B. 8C. 12D. 15解析：根据x:y=2:3，可得到x/y=2/3。

将已知条件x=10代入等式，得到10/y=2/3，由此可以解得y=15。

选D。

二、填空题1.已知正方形的面积是36平方厘米，那么它的周长是______厘米。

解：设正方形的边长为a，则面积为a²=36，解得a=6。

周长为4a=4×6=24。

答：24厘米。

2.在△ABC中，∠B = 45°，AB = 12 cm，BC = 9 cm，那么AC的长度是______cm。

2010年浙江省初中毕业生学业考试(温州市卷)数学试卷及解析

某班学生参加课外兴趣小组情况统计图第4题第6题h第8题CEB ．AC ．D ． 2010年浙江省初中毕业生学业考试(温州卷)数学试题卷亲爱的同学:欢迎参加考试！请你认真审题,积极思考,细心答题,发挥最佳水平．答题时,请注意以下几点: 1．全卷共4页,有三大题,24小题．全卷满分150分．考试时间120分钟． 2．答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上均无效． 3．答题前,认真阅读答题纸上的《注意事项》,按规定答题．祝你成功！参考公式:一元二次方程的ax 2＋bx ＋c ＝0的两根是:x ＝—b ±b 2—4ac2a( b 2—4ac ≥0)；二次函数的图象的顶点坐标是:y ＝ax 2＋bx ＋c (a ≠0)的顶点坐标为(—b 2a ,4ac —b 24a)．一、选择题(本题有10小题,每小题4分,共40分．每小题只有一个选项是正确的,不选、多选、错选,均不给分)1．给出四个数0,2,－12,0.3,其中最小的是()A ．0B ．2C ．－12 D ．0.32．把不等式x ＋2＞4的解表示在数轴上,正确的是()3．计算a 2·a 4的结果是()A ．a 2B ．a 6C ．a 8D ．a 164．某班学生参加课外兴趣小组情况的统计图如图所示,则参加人数最多的课外兴趣小组是()A ．书法B ．象棋C ．体育D ．美术 5．直线y ＝x ＋3与y 轴的交点坐标是()A ．(0,3)B ．(0,1)C ．(3,0)D ．(1,0)6．如图,已知一商场自动扶梯的长l 为10米,该自动扶梯到达的高度h 为 6米,自动扶梯与地面所成的解为β,则tan β的值等于() A ．34 B ．43 C ．35 D ．457．下列命题中,属于假命题的是()A ．三角形三个内角的和等于180°B ．两直线平行,同位角相等C ．矩形的对角线相等D ．相等的角是对顶角 8．如图,AC 、BD 是矩形ABCD 的对角线,过点D 作DEAC 交BC 的延长线于E ,则图中与△ABC 全等的三角形共有()第9题ABC· O第16题A C BDEK FG H Q P第18题主视方向 A ．1个 B ．2个 C ．3个 D ．4个 9．如图,在△ABC 中,AB ＝BC ＝2,以AB 为直径的⊙O 与BC 相切于点B , 则AC 等于()A ．2B ． 3C ．22D ．2 310．用若干根相同的火柴棒首尾顺次相接围成一个梯形(提供的火柴棒全部用完),下列根数的火柴棒不能．．围成梯形的是() A ．5 B ．6 C ．7 D ．8 二、填空题(本题有6小题,每小题5分,共30分) 11．分解因式:m 2－2m ＝______________．12．在“情系玉树献爱心”捐款活动中,某校九(1)班同学人人拿出自己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均每人捐款___________元． 13．当x ＝___________时,分式x ＋3x －1的值等于2． 14．若一个反比例的图象位于二、四象限,则它的解析式可能是___________(写出一个即可)．15．某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27元已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了___________支． 16．勾股定理有着悠久的历史,它曾引起很多人的兴趣．1955年希腊发行了一枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理．在右图的勾股图中, 已知∠ACB ＝90°,∠BAC ＝30°,AB ＝4,作△PQR使得∠R ＝90°,点H 在边QR 上,点D 、E 在边PR 上,点G 、F 在边PQ 上,那么△PQR 的周长等于___________．三、解答题(本题有8小题,共80分)17．(本题10分)(1)计算:2＋(2010－3)0－( 12)－1；(2)先化简,再求值:(a ＋b )(a －b )＋a (2 b －a ),其中a ＝1.5,b ＝2．18．(本题6分)由3个相同的小立方块搭成的几何体制如图所示,捐款数(元) 5 10 20 50 人数41565第19题展览馆展厅入口A入口B南出口西出口北出口第21题AB CED FQ P第22题A BxOy 19．(本题8分)2010年上海世博会某展览馆展览厅东面有两个入口A 、B ,南面、西面、北面各有一个出口,示意图如图所示．小华任选一个入口进入展览大厅,参观结束后任选一个出口离开． (1)她从进入到离开共有多少种可能的结果(要求画出树状图)？(2)她从入口A 进入展厅并从北出口或西出口离开的概率是多少？20．(本题8分)如图,在正方形ABCD 中,AB ＝4,O 为对角线BD 的中点,分别以OB 、OD 为直径作⊙O 1,⊙O 2． (1)求⊙O 1的半径； (2)求图中阴影部分的面积．21．(本题10分)如图,在□ABCD 中,EF ∥BD ,分别交BC 、CD 于点P 、Q ,交AB 、AD 的延长线于点E 、F ．已知BE ＝BP ．求证:(1)∠E ＝∠F ；(2)□ABCD 是菱形．22．(本题12分)如图,抛物线y ＝ax 2＋bx ＋c 经过点A (4,0)、B (2,2),连结OB 、AB ． (1)求该抛物线的解析式；(2)求证:△OAB 是等腰直角三角形；(3)将△OAB 绕点O 按顺时针方向旋转135°得到△OA ′B ′,写出A ′B ′的中点P 的坐标,试判断点P 是否在此抛物线上,并说明理由．23．(本题12分)在日常生活中,我们经常有目的地收集数据,分析数据,作出预测．第23题第24题A CED (1)下面是小芳家2009年全年月用电量的条形统计图．根据图中提供的信息,回答下列问题:① 2009年小芳家月用电量最小的是__________月,四个季度中用电量最大的是第__________季度； ② 求2009年5月至6月用电量的月增长率；(2)今年小芳家添置了新电器．已知今年5月份的用电量是120千瓦时,根据2009年5月至7月用电量的增长趋势,预计今年7月份的用电量将达到240千瓦时．假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,小芳家今年6月份的用电量是多少千瓦时？24．(本题14分)在Rt △ABC 中,∠ACB ＝90°,AC ＝3,BC ＝4,过点B 作射线BB 1∥AC ．动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E 从点C 出了沿射线AC 方向以每秒3个单位的速度运动．过点D 作DH ⊥AB 于H ,过点E 作EF ⊥AC 交射线BB 1于F ,G 是EF 中点,连结DG ．设点D 运动时间为t 秒(1)当t 为何值时,AD ＝AB ,并求出此时DE 的长度； (2)当△DEG 与△ACB 相似时,求t 的值；(3)以DH 所在直线为对称轴,线段AC 经轴对称变换后的图形为A ′C ′．① 当t ＞35时,连结C ′C ,设四边形ACC ′A ′的面积为S ,求S 关于t 的函数关系式；② 当线段A ′C ′与射线BB 1有公共点时,求t 的取值范围(写出答案即可)．。

2010年浙江省绍兴市初中毕业生学业考试数学试卷(word版含答案)

二、填空题（本大题有 6 小题，满分 30 分）
11． y(x + 3)(x − 3)
12. 38° 13． x < − 3 2
三、解答题（本大题有 8 小题，满分 80 分）
7．C 8. B 9. A 10. B
Байду номын сангаас
14. 1 4
15.②③
16. 1 2π
17．（本题满分 8 分）
解：(1) 原式＝ 2+1-3+1＝1．
B
C
第 8 题图
D.∠ADC 与∠ABC 互余
9.已知（x1, y1）,（x2, y2）,（x3, y3）是反比例函数 y = − 4 的图象上的三个点,且 x1＜x2＜0， x
x3＞0,则 y1,y2,y3 的大小关系是( )
A. y3＜y1＜y2
B. y2＜y1＜y3
C. y1＜y2＜y3
D. y3＜y2＜y1
15.做如下操作：在等腰三角形 ABC 中,AB= AC,AD 平分∠BAC,
交 BC 于点 D.将△ABD 作关于直线 AD 的轴对称变换,所得的
像与△ACD 重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线
第 15 题图
第 23 题图 1
第 23 题图 2
(3) 已知点 E,H,F,G 分别在矩形 ABCD 的边 AB,BC,CD,DA 上，EF,GH 交于点 O, ∠FOH＝90°,EF＝4. 直接写出下列两题的答案： ①如图 3,矩形 ABCD 由 2 个全等的正方形组成,求 GH 的长； ②如图 4,矩形 ABCD 由 n 个全等的正方形组成,求 GH 的长(用 n 的代数式表示).

中考数学试题及答案宁波

中考数学试题及答案宁波一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.33333…B. √4C. πD. 0.5答案：C2. 一个等腰三角形的底边长为6，腰长为5，那么这个三角形的周长是多少？A. 16B. 17C. 18D. 19答案：A3. 如果一个函数的图象经过点(2,3)，那么这个函数的解析式可能是？A. y = x + 1B. y = 2x - 1C. y = 3x - 6D. y = 4x + 2答案：A4. 下列哪个图形是中心对称图形？A. 等边三角形B. 矩形C. 等腰梯形D. 圆答案：D5. 一个数的相反数是-5，那么这个数是多少？A. 5B. -5C. 0D. 10答案：A6. 下列哪个选项是不等式2x - 3 > 5的解？A. x > 4B. x < 4C. x > 2D. x < 2答案：A7. 一个圆的半径是3，那么它的面积是多少？A. 9πB. 18πC. 27πD. 36π答案：B8. 一个长方体的长、宽、高分别是4、3、2，那么它的体积是多少？A. 24B. 26C. 28D. 30答案：A9. 下列哪个选项是方程x² - 5x + 6 = 0的解？A. x = 2B. x = 3C. x = 6D. x = 9答案：A10. 一个数的立方根是2，那么这个数是多少？A. 6B. 8C. 9D. 27答案：D二、填空题（每题3分，共15分）11. 如果一个数的平方是25，那么这个数可能是______。

答案：±512. 一个直角三角形的两个直角边长分别是3和4，那么它的斜边长是______。

答案：513. 一个数的绝对值是7，那么这个数可能是______。

答案：±714. 一个数的倒数是2，那么这个数是______。

答案：0.515. 一个数的平方根是4，那么这个数是______。

答案：16三、解答题（每题10分，共40分）16. 已知一个二次函数的图象经过点(1,0)和(3,0)，且顶点的横坐标为2，求这个二次函数的解析式。

宁波市2010年中考数学试卷(含答案)

（1）小聪在天一阁查阅资料的时间为__________分钟，小聪返回学校的速度为_______千米/分钟。
（2）请你求出小明离开学校的路程（千米）与所经过的时间（分钟）之间的函数关系;
（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
24、如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若，。
15、如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，引桥的坡角为，则引桥的水平距离BC的长是_________米（精确到0.1米）。
16、如图，在等腰梯形ABCD中，AD∥BC，，若，，则梯形ABCD的周长为____________。
17、若，，则 ___________。
解得：
∴ （）
令，解得
当时，
答：当小聪与小明迎面相遇时，他们离学校的路程是3千米。
24、解：（1）∵直径AB⊥DE
∴
∵DE平分AO
∴
又∵
∴
在Rt△COE中，
∴⊙O的半径为2。
（2）连结OF
在Rt△DCP中，∵
∴
∴
∵
25、解：（1）
（2）（2，）
（3）①略
②过点E作EM⊥直线CD于点M
∵CD∥AB
形的周长。
（2）沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，请在图4
中用实线画出拼成的平行四边形。
（注：上述所画的平行四边形都不能与原菱形全等）
周长为__________周长为__________
22、某生态示范园要对1号、2号、3号、4号四个品种共500株果树幼苗进行成活实验，从中选出成活率高的品种进行推广，通过实验得知，3号果树幼苗成活率为89.6％，把实验数据绘制成下列两幅统计图（部分信息未给出）

2010年宁波市学业考试数学模拟试卷

2010年宁波市学业考试数学模拟试卷考生须知：1．全卷分试题卷和答题卷．有三个大题，26个小题．满分120分，考试时间为120分钟．2. 参考公式：二次函数y=ax2+bx+c (a ≠0)的图象的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭ 一、选择题（每小题3分，共36分）1. 如果1)43(=-⨯∇，则“∇”内应填的实数是（）A.43 B.34 C. 34-D. 43-2．若21-x 没有意义，则x 的取值范围（）A . x ＞2B .x ≥ 2C . x ＜2D .x ≤23．某班有50位同学，某次月考中，有16位同学达到优秀等次，有24位同学达到良好等次，有6位同学为及格等次，其他为不及格等次。

从中任选一位同学，抽到及格等次以上的概率是（）A ．258B.2512C ．253D ．2523 4．如图所画的数轴正确的有（）A 、1条B 、2条C 、3条D 、4条5．吋是电视机常用规格之一，1吋约为拇指上面一节的长，则7吋长相当于（）A ．课本的宽度B ．粉笔的长度C ．课桌的宽度D ．黑板的高度6. 下列命题是假命题的是（）A. 单项式3423y x π-的系数是-4πB. y x <，则20082008+<+y xC. 平移不改变图形的形状和大小D. 若0)5(|2|2=-++y x 则2-=x ，5=y7．根据下列表格的对应值：实物图正视图俯视图第10题图 A B CDP P 1 11 （第9题图）判断方程02=++c bx ax (a ≠0，a ，b ，c 为常数)一个解x 的范围是（） A.3＜x ＜3.23 B.3.23＜x ＜3.24 C.3.24＜x ＜3.25 D.3.25 ＜x ＜3.268．如图，O 为矩形ABCD 的中心，将直角⊿OPQ的直角顶点与O 重合，一条直角边OP与OA 重合，使三角板沿逆时针方向绕点O 旋转，两条直角边始终与边BC 、AB 相交，交点分别为M 、N. 若AB=4，AD=6，BM=x ，AN=y ，则y 与x 之间的函数图象是（）(A) (B) (C) (D)9、在下图4×4的正方形网格中，△MNP 绕某点旋转一定的角度，得到△M 1N 1P 1，则其旋转中心可能是 ( ) A. 点AB. 点BC. 点CD. 点D（）10．如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（） A ．320cm B ．395.24 cm C ．431.76 cm D ．480 cm11..如图，把抛物线2y x =与直线1y =围成的图形OABC 绕原点O 顺时针旋转90°后，再沿x 轴向右平移1个单位得到图形1111O A B C ，则下列结论错误．．的有（．．．）个．．①点1O 的坐标是（0，1） ②点1C 的坐标是(21)-，③四边形11B OBA 是矩形 ④若连接OC ，（第8题图）AHCDEB第12题图第11题图则梯形11OCA B 的面积是3. ⑤点A 经过的路径长为3 ⑥两阴影面积的和是∏ A.2 B.3 C. 4 D.512．如图，在△ABC 中，度45=∠BAC ,AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 、CE 交于点H ，且EB EH =、小马虎在研究时得到四个结论：①∠ABC=45° ②AH=BC ③AE －BE=CH ④⊿AEC 是等腰直角三角形．你认为正确的序号是（） A ． ①②③④ B ．②③④C ．①②③D ．②③二、填空题（每小题3分，共18分）13．史诗巨片《孔子》2010年1月22日上映以来,上座率稳步攀升．上映首周末三天就拿下3800万元的票房,3800万用科学记数法表示为：元。

宁波中考数学试题及答案

宁波中考数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是最小的正整数？A. 0B. 1C. -1D. 2答案：B2. 计算下列哪个表达式等于-5？A. 3 - 8B. -3 + 2C. 5 - 10D. 7 - 12答案：A3. 一个数的平方等于9，这个数是：A. 3B. -3C. 3或-3D. 9答案：C4. 一个圆的半径是5cm，那么它的周长是：A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案：C5. 下列哪个选项是方程3x - 7 = 11的解？A. x = 2B. x = 3C. x = 4D. x = 5答案：C6. 一个数的绝对值是4，这个数可以是：A. 4B. -4C. 4或-4D. 0答案：C7. 计算下列哪个表达式等于0？A. 5 + (-5)B. 5 - (-5)C. 5 * (-1)D. 5 / 5答案：A8. 下列哪个选项是不等式2x + 3 > 5的解？A. x = 1B. x = 2C. x = 0D. x = -1答案：A9. 一个直角三角形的两条直角边分别是3cm和4cm，那么它的斜边是：A. 5cmB. 7cmC. 6cmD. 8cm答案：A10. 计算下列哪个表达式等于-2？A. 2 * (-1)B. (-2) / 2C. (-2) + 2D. (-2) - 2答案：A二、填空题（每题3分，共30分）1. 一个数的立方等于-27，这个数是_____。

答案：-32. 一个数的倒数是2，那么这个数是_____。

答案：1/23. 一个数的相反数是-5，那么这个数是_____。

答案：54. 一个数的平方根是4，那么这个数是_____。

答案：165. 如果a = 3b，那么b = _____。

答案：a/36. 计算2x - 3 = 7的解，x = _____。

答案：57. 计算3x + 6 = 0的解，x = _____。

【2010真题】浙江省宁波市初中毕业生学业考试数学中考试卷及答案

B . A .C .D .第11题宁波市2010年初中毕业生学业考试数学试题考生须知：1．全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷，试题卷共6页，有三个大题，26个小题，满分120分，考试用时120分钟2．请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上3．答题时，把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选择项位置用2B 铅笔涂黑、涂满。

将试题卷Ⅱ答案用黑色字迹钢笔或签字笔书写，答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答，做在试题卷上或超出答题卷区域内书写的答案无效。

4．允许使用计算器，但没有近似计算要求的试题，结果都不能用近似数表示。

抛物线y ＝ax 2＋bx ＋c (a ≠0)的顶点坐标为（—b2a ，4ac —b 24a）.试题卷Ⅰ一、选择题（每小题3分，共36分，在每小题给出的四个选项中，只有一项符合题目要求） 1．—3的相反数是A ．3B ．13C ．—3D ．— 132．下列运算正确的是A ．x ·x 2＝x 2B ．(xy ) 2＝xy 2C ．(x 2) 3＝x 6D ．x 2＋x 2＝x 4 3．下列各图是选择自历届世博会会徽中的图案，其中是中心对称图形的是4．据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达820亿元，其中820亿用科学记数法表示为A ．0.82×1011B ．8.2×1010C ．8.2×109D ．82×108 5．《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础. 它是下列哪位数学家的著作A ．欧几里得B ．杨辉C ．费马D ．刘微6．两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是A ．内切B ．相交C ．外切D ．外离7．从1～9这九个自然数中作任取一个，是2的倍数的概率是 A ．29 B ．49 C ．59 D ．238．如图，直线AB 与直线CD 相交于点O ，E 是∠AOD 内一点，已知OE ⊥AB 的度数是A ．125°B ．135°C ．145°D ．155°9A ．25.5厘米，26厘米B ．26厘米，25.5厘米C ．25.5厘米，25.5厘米D ．26厘米，26厘米10．如图，在△ABC 中，AB ＝AC ，∠A ＝36°，BD 、CE 分别是△ABC 、△BCD 的角平分线，则图中的等腰三角形有A ．5个B ．4个C ．3个D ．2个11．已知反比例函数y ＝1x，下列结论不正确的是A ．图象经过点（1，1）B ．图象在第一、三象限第16题A第15题B Cy图1CCCC．当x＞1时，0＜y＜1 D．当x＜0时，y随着x的增大而增大12．骰子是一种特别的数字立方体（见右图），它符合规则：相对两面的点数之和总是7．下面四幅图中可以折成符合规则骰子的是二、填空题（每小题3分，共18分）13．实数4的算术平方根是_____________________．14．请你写出一个满足不等式2x—1＜6的正整数x的值：_____________________．15．如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，引桥的坡角∠ABC为15°，引桥的水平距离BC的长是_____________________米（精确到0.1米）．16．如图，在等腰梯形ABCD中，AD∥BC，AB＝AD＝CD．若∠ABC＝60°，BC＝12，则梯形ABCD的周长为____________________．17．若x＋y＝3，xy＝1，则x2＋y2＝_________________．18．如图，已知⊙P的半径为2，圆心P在抛物线y＝12x2—1上运动，当⊙P与x轴相切时，圆心P的坐标为_________________．三、解答题（第19～21题各6分，第22题924题分，第26题12分，共66分）19．先化简，再求值：a－2a2－4＋1a＋2，其中a＝3．20．如图，已知二次函数y＝—12x2＋bx＋c的图象经过A（2，0）、B（0，—6）两点．（1）求这个二次函数的解析式；（2）设该二次函数图象的对称轴与x轴交于点C，连结BA、BC，求△ABC21．如图1，有一张菱形纸片ABCD，AC＝8，BD＝6．（1）请沿着AC剪一刀，把它分成两部分，把剪开的两部分分拼成一个平行四边形，在图2中用实线画出你所拼成的平行四边形；若沿着BD剪开，请在图3中用实线画出拼成的平行四边形；并直接写出这两个平行四边形的周长．（2）沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，请在图4中用实线画出拼成的平行四边形．（注：上述所画的平行四边形都不能与原菱形全等）22．某生态示范园要对1号、2号、3号、4号四个品种共500株果树幼苗进行成活实验，从中选择出成活率高的品种进行推广．通过实验得知，3号果树幼苗成活率为89.6%．把实验数据绘制成下列两幅统计图（部分信息未给出）：（1）实验所用的2号果树幼苗的数量是__________株；（2）请求出3号果树幼苗的成活数，并把图2的统计图补充完整；（3）你认为应选哪一品种进行推广？请通过计算说明理由．23．小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米．小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁．图中折线O→A→B→C和线段OD分别表示两人离学校的路程S（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为_________分钟，小聪返回学校的速度为_________千米/分钟；（2）请你求出小明离开学校的路程S（千米）与所经过的时间t（分钟）之间的函数关系式；（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？24．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE＝23，∠DP A＝45°．（1）求⊙O的半径；（2）求图中阴影部分的面积．25．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式请你观察下列几种简单多面体模型，解答下列问题：（1多面体顶点数（V）面数（F）棱数（E）四面体 4 4长方体8 6 12正八面体8 12正十二面体20 12 30；（2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是；（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱．设该多面体外表面三角形的个数为x个，八边形的个数为y，求x＋y的值．26．如图1，在平面直角坐标系中，O是坐标原点，□ABCD的顶点A的坐标为（－2，0），点D的坐标为（0，23），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线l与x轴交于点F，与射线DC交于点G．（1）求∠DCB的度数；（2）当点F的坐标为（－4，0），求点的坐标；（3）连结OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△OEF′，记直线EF′与射线DC 的交点为H．①如图2，当点G在点H的左侧时，求证：△DEG≌△DHE；②△若EHG的面积为33，请你直接写出点F的坐标。

2010年浙江省宁波市中考《数学》试题及答案

一、选择题（每题3分，共36分）第1题：
【正确答案】：A
第2题：
【正确答案】：C
第3题：
【正确答案】：C
第4题：
【正确答案】：B
第5题：
【正确答案】：A
第6题：
【正确答案】：B
第7题：
【正确答案】：B
第8题：
【正确答案】：B
第9题：
【正确答案】：D
第10题：
【正确答案】：A
第11题：
【正确答案】：D
第12题：
【正确答案】：C
二、填空题（每小题3分，共18分）第13题：
【参考解析】：
第14题：
【参考解析】：
第15题：
【参考解析】：
第16题：
【参考解析】：
第17题：
【参考解析】：
第18题：
【参考解析】：
三、解答题（共66分）第19题：
【参考解析】：
第20题：
【参考解析】：
第21题：
【参考解析】：
第22题：
【参考解析】：
第23题：
【参考解析】：
第24题：
【参考解析】：
第25题：
【参考解析】：
第26题：
【参考解析】：。

2010年浙江省宁波市中考数学试卷(全解全析)

Lenovo User一、填空题1、（2010•广东）﹣2的绝对值是．考点：绝对值。

分析：计算绝对值要根据绝对值的定义求解．第一步列出绝对值的表达式；第二步根据绝对值定义去掉这个绝对值的符号．解答：解：|﹣2|=2．故填2．点评：规律总结：一个正数的绝对值是它本身；一个负数的绝对值是是它的相反数；0的绝对值是0．1.2、（2010•盐城）4的算术平方根是．考点：算术平方根。

分析：如果一个非负数x的平方等于a，那么x是a的算术平方根，由此即可求出结果．解答：解：∵22=4，∴4算术平方根为2．故答案为：2．点评：此题主要考查了算术平方根的概念，算术平方根易与平方根的概念混淆而导致错误．3、（2010•宁波）请你写出一个满足不等式2x﹣1＜6的正整数x的值：．考点：一元一次不等式的整数解。

专题：开放型。

分析：首先确定不等式组的解集，然后再找出不等式的特殊解．解答：解：移项得：2x＜6+1，系数化为1得：x≤3.5，满足不等式2x﹣1＜6的正整数x的值为：1，2，3．点评：正确解不等式，求出解集是解答本题的关键，解不等式应根据不等式的基本性质．另外应掌握正整数的概念．4、（2010•宁波）如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，引桥的坡角∠ABC 为15°，则引桥的水平距离BC的长是米（精确到0.1米）．考点：解直角三角形的应用-坡度坡角问题。

分析：在Rt△ABC中，已知了铅直高度AC的长以及坡角∠ABC的度数，即可求得水平宽度BC的长．解答：解：Rt△ABC中，∠ABC=15°，AC=3，∴BC=AC÷tan15°≈11.2（米）．点评：此题主要考查学生对坡度坡角的掌握及三角函数的运用能力．5、（2010•宁波）如图，在等腰梯形ABCD中，AD∥BC，AB=AD=CD，若∠ABC=60°，BC=12，则梯形ABCD 的周长为．考点：等腰梯形的性质。