直方图及描述统计分析上机作业
直方图作业
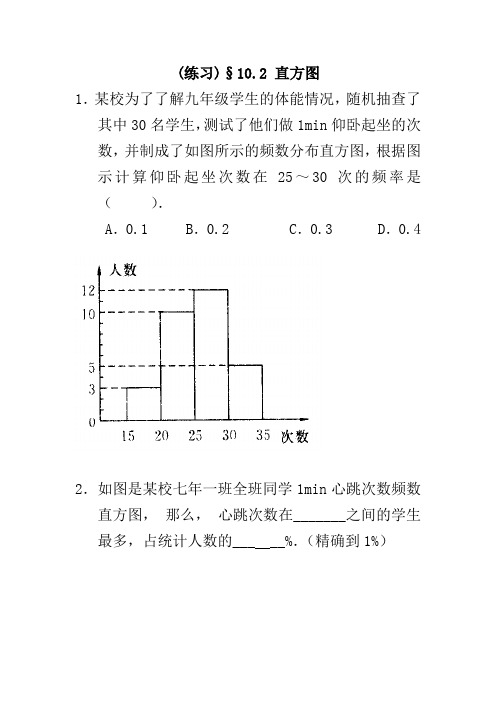
(练习)§10.2 直方图1.某校为了了解九年级学生的体能情况,随机抽查了其中30名学生,测试了他们做1min仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示计算仰卧起坐次数在25~30次的频率是().A.0.1 B.0.2 C.0.3 D.0.42.如图是某校七年一班全班同学1min心跳次数频数直方图,•那么,•心跳次数在_______之间的学生最多,占统计人数的___ __%.(精确到1%)3. 如图是某单位职工的年龄(取正整数)的频率分布直方图,•根据图中提供的信息,回答下列问题:(1)该单位共有职工多少人?(2)不小于38岁但小于44岁的职工人数占职工总人数的百分比是多少?(3)如果42岁的职工有4人,那么年龄在42岁以上的职工有几人?4.已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,•24,•26,27,28,30,以2为组距画出频数分布直方图.5.为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)•班50名学生进行1min跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下图所示.请结合图表完成下列问题.(1)表中的a=______.(2)请把频数直方图补充完整.(3)若八年级学生1min跳绳次数(x)达标要求是:x<120为不合格,120≤x<140•为合格,140≤x<160为良,x≥160为优,根据以上信息,请你给学校或八年级同学提一条合理化建议.答案1.D2.273.59.5~69.5 484.(1)4+7+9+11+10+6+3=50(人)(2)(9+10+11)÷50=60%(3)10+6+3-4=15(人)5.解:(1)计算最大值与最小值的差:32-23=9.(2)确定组数与组距:已知组距为2,则92=4.5,因此定为5组.(3)决定分点,所分的五个小组是:22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5,30.5~32.5.(4)列频数分布表:(56.(1)a=12 (2)图略(3)只要合理即可。
频数(率)分布直方图(详细解析+考点分析+名师点评)-1.doc

频数(率)分布直方图(详细解析+考点分析+名师点评)-1.doc答案与评分标准一、选择题(共20小题)1、夷昌中学开展“阳光体育活动”,九年级一班全体同学在2011年4月18日16时分别参加了巴山舞、乒乓球、篮球三个项目的活动,陈老师在此时统计了该班正在参加这三项活动的人数,并绘制了如图所示的频数分布直方图和扇形统计图.根据这两个统计图,可以知道此时该班正在参加乒乓球活动的人数是()A、50B、25C、15D、102、为了支援地震灾区同学,某校开展捐书活动,九(1)班40名同学积极参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是()A、0.1B、0.2C、0.3D、0.4考点:频数(率)分布直方图。
分析:频率=,从直方图可知在5.5~6.5组别的频数是8,总数是40可求出解.解答:解:∵在5.5~6.5组别的频数是8,总数是40,∴=0.2.故选B.点评:本题考查频数分布直方图,从直方图上找出该组的频数,根据频率=,可求出解.3、某学校为了了解九年级体能情况,随机选取20名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为()A、0.1B、0.17C、0.33D、0.4考点:频数(率)分布直方图。
专题:应用题;图表型。
分析:首先根据频数分布直方图可以知道仰卧起坐次数在25~30之间的频数,然后除以总次数(30)即可得到仰卧起坐次数在25~30之间的频率.解答:解:∵从频数率分布直方图可以知道仰卧起坐次数在25~30之间的频数为12,而仰卧起坐总次数为:3+10+12+5=30,∴学生仰卧起坐次数在25~30之间的频率为12÷30=0.4.故选D.点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.4、学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是()A、0.1B、0.15C、0.25D、0.3考点:频数(率)分布直方图。
八年级数学用直方图描述数据同步练习

12.2.2用直方图描述数据[要点再现]1.用直方图描述数据的一般步骤是:(1)收集数据;(2)求出数据中的最大值与最小值的,即求出数据的变化范围(3)按这个变化范围确定组距并把数据进行分组;(4)列频数分布表;(5)画出直方图。
2.组距和组数的确定没有固定的标准,要根据经验和研究的具体问题来决定,通常数据越多,分成的组数也越多,当数据在100个以内时,根据数据的多少通常分成个组。
[基础闯关]1.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果(1)参加这次演讲比赛的同学有人;(2)已知成绩在91~100分的同学为优胜者,那么优胜率为;(3)将成绩频数分布直方图补充完整(4)画出频数折线图,分析数据分布情况。
2.人们常用人均教育经费来反映一个地区对教育投入的情况,我国30个城市2001年人均教育经费的统计数据如下。
(单位:元)北京731南宁100长春101重庆102乌鲁木齐171青岛425深圳584合肥192武汉184上海790 兰州170呼和浩特206广州483天津440郑州197 南京292福州349洛阳127南昌117贵阳166 吉林76海口183济南205昆明234西安126 成都160哈尔滨249石家庄228长沙155沈阳237(2)画出分布直方图和折线图。
[能力提升]1.为了解某地初中三年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下表(表1):表1(1)求出表中a、m的值;(2)画出频数分布直方图和频数折线图,分析数据分布情况.12.2.1用直方图描述数据[要点再现]1.,2.[基础闯关]1、(1)20 ;(2)20% ;(3)71~80(4)(图略)(2)图略[能力提升]1.解:(1)6,0.1(2)图略。
讲直方图练习题

讲直方图练习题直方图是一种用来表示数据分布的图表形式,通过图形的高度和宽度来表示数据的频数或频率。
它通常用于描述连续数据的分布情况,可以直观地显示数据的集中程度、偏态和峰态等统计特征。
在解答直方图练习题时,我们需要了解如何构建直方图、读取直方图中的信息以及进行数据分析和解释。
本文将通过几个具体的练习题,来帮助读者掌握直方图的应用技巧。
练习题一:某班级在一次考试中,统计了学生们的成绩分布情况,得到了以下数据:分数范围频数60-70 670-80 1080-90 890-100 4请根据上述数据绘制出该班级学生考试成绩的直方图,并分析该班级学生在该次考试中的成绩分布情况。
解答:根据给定的数据,我们可以首先确定横坐标的分组区间,即分数范围。
在本题中,分数范围可取60-70、70-80、80-90和90-100四个区间。
然后,我们可以根据每个区间的频数绘制出相应的矩形条,并计算出每个矩形条的高度。
练习题二:一家电视台在某个时间段内进行了一项调查,统计了观众对于一档综艺节目的评分情况,得到了以下数据:评分区间频数5-6 106-7 157-8 208-9 309-10 25请根据上述数据绘制出该综艺节目观众评分情况的直方图,并分析观众对于该节目的评价。
解答:根据给定的数据,我们可以确定评分区间的分组范围为5-6、6-7、7-8、8-9和9-10。
然后,根据每个区间的频数绘制出相应的矩形条,并计算出每个矩形条的高度。
练习题三:某城市在连续10天内的降雨量进行了统计,得到了以下数据(单位:毫米):降雨量区间频数0-10 410-20 620-30 830-40 540-50 2请根据上述数据绘制出该城市连续10天内的降雨量分布的直方图,并分析该城市的降雨情况。
解答:根据给定的数据,我们可以确定降雨量区间的分组范围为0-10、10-20、20-30、30-40和40-50。
然后,根据每个区间的频数绘制出相应的矩形条,并计算出每个矩形条的高度。
统计学上机报告

统计学上机报告统计学上机实验报告摘要:本次实验内容是统计学上机操作,主要参考MATLAB等软件进行统计数据的处理与分析。
本文将对实验中所涉及的统计学知识进行详细介绍,包括数据描述、分布统计、假设检验等,以及分析结果和结论,为读者提供理论及实践方面的参考。
1. 实验目的本次实验旨在通过上机操作,加深对统计学理论知识的理解,并掌握MATLAB等软件进行统计数据的处理与分析能力。
2. 实验内容2.1 数据处理本次实验所涉及数据样本的处理主要包括以下几项:1. 数据输入与导入通过MATLAB等软件进行指定数据集的导入。
同时采取筛选等预处理方式,提取相应变量,过滤出目标区域内的数据。
2. 数据描述对目标区域内的数据进行统计描述,包括计算样本均值、标准差、中位数等重要参数,分析数据的特征与规律,并进行初步的可视化绘图。
2.2 假设检验假设检验是统计学中一种重要的方法,可用于检验样本中所描写的数据分布是否符合自然分布或正态分布等假设模型。
本实验中,将应用假设检验等方法,进行统计分布的检验与分析。
3. 分析结果及应用根据实验过程和结果,得出相应结论,包括:1. 数据特征与规律针对样本数据,分析其数据特征及规律,如样本均值、标准差等重要参数。
通过绘制图表等方式,对数据进行可视化处理和展示,以显著图像直观化的呈现数据分布情况。
2. 假设检验应用假设检验等方法,对数据分布进行检验,得出数据分布是否符合正态分布等相关结论,并对数据进行合理解释和分析。
4. 结论及实践意义通过本实验的学习与实践,更加深入地了解了统计学理论知识,并掌握了数据处理与分析的基本方法和技能。
同时,通过数据描述和假设检验等方法,对实践数据等进行分析和应用,完善数理统计学知识,更有助于跨学科交汇应用,提高对实际工作和科学研究的实践应用能力。
应用统计学上机
应⽤统计学上机⼯商管理学院《应⽤统计学》实验作业班级学号姓名上课教师2017年11⽉实验⼆建⽴数据⽂件1.建⽴⼀个数据⽂件记录试录⼊以下数据,并按要求进⾏变量定义。
数据:要求:将录⼊结果截图粘贴在作业题⽬答案处(变量视图和数据视图)。
(1)变量名同表格名,以“()”内的内容作为变量标签。
对性别(Sex)设值标签“男=0;⼥=1”。
(2)正确设定变量类型。
其中学号设为数值型;⽇期型统⼀⽤“mm/dd/yyyy“型号;⽣活费⽤货币型。
(3)变量值宽统⼀为10,⾝⾼与体重、⽣活费的⼩数位2,其余为0。
答案:1准备⼯作。
打开SPAA2选择变量视图,依次录⼊学号,姓名,性别等。
2.对⼤学⽣创业问题设计⼀份调查问卷。
要求格式正确,题⽬类型包括开放题、封闭题(单选、多选都有)、半封闭题三种类型,题⽬个数10-15个。
答案:3.⽤第2题得到的调查问卷进⾏模拟调查(10份),并将得到的结果录⼊到SPSS中,(1)将录⼊结果保存为xxx.sav⽂件,并将录⼊结果截图粘贴在作业题⽬答案处(变量视图和数据视图)。
答案:实验三数据的整理1. 某地区农科所为了研究该地区种植的两个⼩麦品种“中麦9号”、“豫展1号”产量的差异,从该地区的两个村庄各选5块⽥地,分别种植两个品种⼩麦,使⽤相同的⽥间管理,收获后,测得各个地块⽣产的⼩麦的千粒重(g)数据资料如表3-1所⽰。
表3-1 某地区⼩麦种植要求:量,并建⽴数据⽂件,完成分类汇总⼯作。
步骤:1.准备⼯作。
打开3-1⽂件,通过⽂件--打开,将⽂件放⼊打开窗⼝。
2.选择数据---分类汇总。
3.打开分类汇总窗⼝,将⼩麦品种放⼊分组变量对话框中,将千粒重放⼊变量摘要对话框中。
4.选择函数选项,在函数对话框中选择均值选项5.选择继续--确定,得出结果。
以此⽅式得出村对⼩麦千粒重的分类汇总。
2.某地20家企业的情况如表3-2所⽰。
表3-2 企业年产值与年⼯资总额要求:根据上述资料建⽴数据⽂件,并完成下列统计整理⼯作,并回答有关问题:(1)调⽤排序命令对企业按部门、年产值的主次顺序进⾏排序。
用直方图描述数据(含答案)
12.2.2 用直方图描述数据知识要点1.绘制频数分布表和频数分布直方图时要将一批数据分组,•组距和组数的确定没有固定的标准,通常数据越多,所分的组数也越多,当数据在100个以内时,•根据数据的多少常分成5─12组.一般地,所分的小组里含最小值,不含最大值,•即数据x满足a≤x<b.2.•频数分布表和频数分布直方图是一组数据的频数分布的两种不同表现形式,前者准确,后者直观.3.描述频数分布情况还可以用频数折线图来刻画数据的总体规律.典型例题例:刘杨阳调查了他们班50名同学的身高(单位:厘米),请你帮助他用统计图来描述所得的数据.158 157 157 157 169 155 155 141 165 144 171 •145 • •158 •145 150 150 157 168 154 168 154 168 149 150 150 154 • •155 •157 162 163 155 160 152 152 145 160 160 163 163 148 • •159 •152 159 144 160 158 162 172 155 145 168 155分析:取组距为5,将数据分成7组,绘制频数分布表、频数分布直方图和频数折图来分析数据.解:首先观察到这组数据中最大值是172,最小值是141,它们的差是31.若取组距为5,由于31÷5≈7,因此要将整个数据分为7组,用x(厘米)表示身高,则所分的组为141≤x<146,146≤x<151,151≤x<156,……,171≤x<176.•整理可得下列频数分布表:用横轴表示身高,等距离标出各组的端点141、146、151、……171、176,•用纵轴表示频数,等距离标出4、8、12、16等,以各组的频数为高画出与这一组对应的长方形,得到下面的频数分布直方图(如图1)取直方图中每一个长方形上边的中点,然后在直方图的左边取点(138.5,0),在直方图的右边取点(178.5,0),将这些点用线段依次连接起来,就得到频数折线图(如图2)(1)(2)同步练习一、选择题:1.考察50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频率是()A.20 B.0.4 C.0.6 D.302.有40个数据,其中最大值为35,最小值为15,若取组距为4,则应该分的组数是() A.4 B.5 C.6 D.7二、填空题3.绘制频数折线图时,通常要求出各个小组两个端点的平均数,•这些平均数称为_________.4.利用频数分布直方图画频数折线图时,若组距为4,•第一个小组的范围是138≤x<142,最后一个小组的范围是154≤x<158.•则折线上最左边的点的坐标是_______,最右边的点的坐标是________.三、解答题5.某班同学参加环保知识竞赛,•将学生成绩(得分都是整数)进行整理后分成5组,绘成频数分布直方图(如图),•图中从左到右各小长方形的高的比为1:3:6:4:2,最后一组的频数为6,结合直方图提供的信息解答下列问题:(1)该班有多少名同学参赛?(2)成绩落在哪组数据范围内的人数最多?是多少?(3)求成绩在60分以上(含60分)的学生占全班参赛学生人数的百分率.(4)请你直接在直方图的基础上绘制频数折线图.60(每组含最低分数但不含最高分数)频数(学生人数)分数/分1009080705006.储蓄所太多必将增加银行支出,太少又难以满足顾客的需求.为此,•银行在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:分)如下: 22 14 33 17 24 17 12 14 24 11 15 20 18 3 25 24 34 37 42 35 30 23 34 22 13 34 8 22 31 24 25 0 1 21 28 33 32 23 14 4 31 42 34 26 14 25 40 14 42 6(1)将数据适当分组,并绘制相应的频数分布直方图;(2)这50名顾客的平均等待时间是多少?根据这个数据,•你认为应该给银行提什么建议?答案:1.B 2.C 3.组中值 4.(136,0);(160,0)5.①48人;②大于等于70分而小于80分的范围内的人数最多;③93.75%;④略6.①略(答案不唯一);②平均等待的时间是22.74分.顾客平均等待的时间过长,应控制在12•分钟左右.为此,银行可以在高峰期增加办事人员,提高工作效率,加强业务训练,优化服务质量,同时可以适当的增加营业网点.。
直方图练习题

直方图练习题直方图是一种用矩形表示数据分布的图表,它对于统计和分析数据的分布非常有用。
本文将通过一些练习题来帮助读者理解和应用直方图。
练习一:某班级的学生考试成绩如下:60, 75, 85, 95, 80, 70, 90, 85, 80, 75, 65, 70, 80, 90, 85, 75, 80, 90, 95, 80请绘制成绩的直方图。
解答一:首先,我们需要确定直方图的横轴和纵轴。
在这个例子中,横轴表示成绩的区间,纵轴表示对应区间内的学生人数。
接下来,我们需要确定每个区间的范围和宽度。
根据给出的成绩数据,我们可以选择区间为10分,从60到100。
因此,我们可以将成绩分为6个区间:60-69,70-79,80-89,90-99,100。
然后,我们可以计算每个区间内的学生人数。
在这个例子中,每个区间的人数为:2,5,7,4,1。
最后,我们可以按照上述计算结果绘制直方图。
每个区间的宽度可以根据实际需求进行调整,以保证直方图的整洁美观。
练习二:一家购物网站的用户对商品的评级如下:4, 3, 5, 4, 4, 2, 3, 5, 1, 4, 3, 2, 5, 4, 3请绘制评级的直方图。
解答二:同样地,我们需要确定直方图的横轴和纵轴。
在这个例子中,横轴表示评级的等级,纵轴表示对应等级的用户数量。
接下来,我们需要确定每个等级的范围和宽度。
根据给出的评级数据,我们可以选择等级为1到5。
因此,我们可以将评级分为5个等级:1,2,3,4,5。
然后,我们可以计算每个等级对应的用户数量。
在这个例子中,每个等级的用户数量为:1,2,4,5,2。
最后,我们可以按照上述计算结果绘制直方图。
每个等级的宽度可以根据实际需求进行调整,以保证直方图的整洁美观。
练习三:某城市一周七天的降雨量数据如下:10, 5, 12, 8, 15, 2, 0请绘制降雨量的直方图。
解答三:同样地,我们需要确定直方图的横轴和纵轴。
在这个例子中,横轴表示降雨量的区间,纵轴表示对应区间内的天数。
统计学上机实验报告

福建工程学院实习报告专业国际经济与贸易班级国贸1002座号3100509209姓名蔡小强日期2012年4月20日《统计学》实验一一、实验名称:数据的图表处理二、实验日期:2012年03月27日三、实验地点:经济管理系实验室四、实验目的和要求目的:培养学生处理数据的基本能力。
通过本实验,熟练掌握利用Excel,完成对数据进行输入、定义、数据的分类与整理。
要求:就本专业相关问题收集一定数量的数据( 30),利用EXCEL进行如下操作:1.进行数据排序2.进行数据分组3.制作频数分布图、直方图和帕累托图,并进行简要解释4. 制作饼图和雷达图,并进行简要解释五、实验仪器、设备和材料:个人电脑(人/台),EXCEL 软件六、实验过程(一)问题与数据下面是一种金属零件重量的误差数据单位:g27.3 67.9 74.1 55.6 32.5表1-1(二)实验步骤1、将上表数据复制到EXCEL中;2、将上述数据调整成一列的形式;3、选择“数据-排序“得到由小到大的一列数据。
4、选择“插入-函数(fx)-数学与三角函数-LOG10”图1-1计算lg50/lg2=5.64,从而确定组数为K=1+ lg100/lg2=6.64 这里为了方便取为10组;确定组距为:(max-min)/K=(87.8-19.1)/10=6.87 取为7;5、确定接受界限为 24.0 31.0 38.0 45.0 52.0 59.0 66.0 73.0 80.0 87.0 分别键入EXCEL 表格中,形成一列接受区域;6、选“工具——数据分析——直方图”得到如下频数分布和直方图金属零件重量误差的频数分布表1-2金属零件重量误差的直方图图1-27、将其他这行删除,将表格调整为:表1-38、选择“插入——图表——柱图——子图标类型1”,在数据区域选入接收与频率两列,在图表标题中输入频率。
做出的图形如下图所示:图1-39、双击上述直方图的任一根柱子,将分类间距改为0,得到新的图.图1-410、选择“插入——图表——饼图”,得到金属零件重量的误差饼图:图1-511、选择“插入——图表——雷达图”,得到金属零件重量的误差雷达图图1-6(三)实验结果分析:从以上直方图可以发现,金属零件的重量误差大致呈对称分布,其中54.0—60.0出现的频次最多,从饼图和雷达图也能够比较清晰地看出这样的结果。
《统计学》上机实验例题(一)

• •
2010年
生成频数分布表
(列联表—Excel)
不同类型饮料和顾客性别的频数分布
绿色 健康饮品
2010年
分类数据的图示—条形图
(bar Chart)
2010年
分类数据的图示—复式条形图
(bar Chart)
• 饮料类型和顾客性别的条形图
2010年
分类数据的图示—帕累托图
(pareto chart)
(a)向上累积
非常 不满意 一般 满意 不满意 (b)向下累积
甲城市家庭对住房状况评价的累积频数分布
环形图
(例题分析)
13% 10% 7% 8% 非常不满意
15%
21% 36% 33% 不满意
一般
31% 26% 甲乙两城市家庭对住房状况的评价 满意 非常满意
用Excel制作图形
2.3 数值型数据的整理与展示 2.3.1 2.3.2 数据分组 数值型数据的图示
温度 / 0C 6 8 降雨量 /mm 25 40 产量/ ( kg/hm2 ) 2250 3450
位面积产量与降雨量 和温度等有一定关系 。为了解它们之间的 关系形态,收集数据 如表。试绘制小麦产 量与降雨量的散点图 ,并分析它们之间的 关系。
10
13 14 16 21
58
68 110 98 120
一、数值型数据:用数据分析中的直方 图编制频数分布表;绘制直方图折线图
【 例 2.5】 (
见教材38~ 42页) 表中
是某电脑公 司 2002 年 前 四个月各天 的销售量数 据(单位:台) 。试对数据 进行分组
等距分组表
(上下组限重叠)
分组数据的图示
(直方图的绘制)
统计学上机实验一、二

数据的收集、整理与显示统计数据的收集、整理与显示是统计分析的基础和初步,其中涉及到抽样方法的选择,数据的筛选、排序,数据的分类和分组以及频数分布的制作等。
本章主要介绍如何使用Excel 进行相应处理,其中第一节统计数据的收集,介绍“抽样”工具的使用;第二节数据的预处理,介绍“筛选”、“排位和百分比排位”工具的使用;第三节品质数据的整理与显示,介绍如何使用“直方图”工具制作品质型数据的频数分布;第四节数值型数据的整理与显示,介绍如何使用“直方图”工具制作数值型数据的频数分布以及多变量数据的雷达图制作。
第一节统计数据的收集数据的处理是数据整理的先前步骤,是在对数据分类或分组之前所做的必要处理,包括数据的审核、筛选、排序等。
本节主要介绍Excel中筛选和排序功能的使用。
一、数据筛选数据筛选包括两方面内容:一是将某些不符合要求的数据或有明显错误的数据予以剔除;二是将符合某种特定条件的数据筛选出来,对不符合特定条件的数据予以剔除。
下面举例说明Excel进行数据筛选的过程。
表1-28名学生的考试成绩数据单位:分表1-2是八名学生四门课程的考试成绩数据,使用Excel“筛选”命令分别找出统计成绩等于75分的学生;英语成绩前三名的学生;数学成绩大于80小于90的学生;统计成绩和数学成绩大于80分,或者英语成绩大于90分的学生。
Excel提供了两种筛选命令:“自动筛选”(适用于简单的条件)和“高级筛选”(适用于复杂的条件)。
接下先来介绍“自动筛选”的使用。
首先,将表格中的数据区域选定或者只需确保活动单元格处于数据区域既可(如表1-2所示,活动单元格为B3)。
选择“数据”菜单,并选择“自动筛选”命令。
如图1.6所示。
图1.6从“数据”菜单中选择“筛选自动”这时会在第一行(列标题)出现下拉箭头,用鼠标点击箭头会出现如下结果,如图 1.7所示。
图1.7“自动筛选”命令图1.8统计成绩75分的学生图1.9英语成绩前三名的学生图1.10数学成绩大于80小于90的学生要筛选出统计学成绩为75分的学生,可选择75,得到图1.8的结果;要筛选出英语成绩最高的前三名学生,可在英语成绩下拉箭头选项中选择“前10个”,并在对话框中输入“3”,得到如图1.9所示结果。
统计学第一章作业

第一章 描述性统计1.某生产车间50名工人日加工零件数如下(单位:个)。
试在minitabe 下画直117 122 124 129 139 107 117 130 122 125 108 131 125 117 122 133 126 122 118 108 110 118 123 126 133 134 127 123 118 112 112 134 127 123 119 113 120 123 127 135 137 1141201281241151391281241211401351301251201151101051512963日加工零件数频数(人)均值123.0标准差8.027N 50某生产车间50名工人日加工零件数1.给数据排序2.拿数据最大值减最小值,确定组数3.由于组距一般为5或10,因此确定组距为54.计算频数5.绘制直方图,再编辑横轴和纵轴的区间。
数据特征:大多数人的日加工零件数在120到125之间。
2. 为了了解车间加工零件误差与原材料供应商以及工人的关系,收集如下数据,试画多元箱线图展示该数据并进行分析 原材料供应商 员工编号1 2 3 4 5 6 7 甲 甲 乙 乙 丙 丙 丁 丁丁丙乙甲0.60.50.40.30.20.10.0原材料供应商的箱线图员工7员工6员工5员工4员工3员工2员工10.60.50.40.30.20.10.07名工人的的箱线图由原材料供应商的箱线图可知,原材料供应商的数据比较集中,差距不大,但从工人的箱线图看出,工人的数据起伏波动较大,尤其是工人2的数据,跟其他工人的数据相比有很大的差异,因此原材料供应商对加工零部件误差的影响要小于工人对加工零部件的影响。
3. 甲乙两个班各有40名学生,期末统计学考试成绩的分布如下:考试成绩 人数 甲班 乙班 优 3 6 良 6 15 中 18 9 及格 9 8 不及格 4 2(1)根据上面的数据,在Excel中画出两个班考试成绩的复合柱形图、环形图和图饼图。
概率论与数理统计上机题目及答案

实验项目一:数据整理中的统计计算一、实验要求:(1)掌握Excel中基本的数据处理方法;(2)学会使用Excel进行统计分组,能以此方式独立完成相关作业。
二、实验重点:了解数据整理的概念和内容。
掌握不同类型的统计图表。
三、实验难点:不同类型的统计图表四、实验要求:0、本实验课程要求学生已修《计算机应用基础》或类似课程。
此条为整门课程所要求,以后不再赘述。
1、已学习教材相关内容,理解数据整理中的统计计算问题;已阅读本次实验导引,了解Excel中相关的计算工具。
2、准备好一个统计分组问题及相应数据(可用本实验导引所提供问题与数据)。
3、以Excel文件形式提交实验报告(含:实验过程记录、疑难问题发现与解决记录(可选))。
此条为所有实验所要求,恕不赘述。
五、实验内容:1、在一批灯泡中随机抽取50只,测试其使用寿命,原始数据如下(单位:小时):700 716 728 719 685709 691 684 705 718706 715 712 722 691708 690 692 707 701708 729 694 681 695685 706 661 735 665668 710 693 697 674658 698 666 696 698706 692 691 747 699682 698 700 710 722进行等距分组,整理成频数分布表,并绘制频数分布图(直方图、折线图、曲线图)。
要求:(1)用MIN和MAX函数找出最小值和最大值,以50为组距,确定每组范围;(2)进行等距分组,整理成频数分布表,并绘制频数分布图(直方图、折线图、曲线图)。
3、温州市1978-2005年GDP(亿元)如下表要求:(1)作出趋势图(折线图或X-Y散点图);(2)用“添加趋势线”方法,找出一个最好的方程;(3)预测2006年、2007年温州市GDP。
4、书P140,6.4六、实验步骤与结果:1、实验项目二:数字特征的统计计算一、实验要求:学会使用Excel计算各种数字特征,能以此方式独立完成相关作业。
《统计学上机实验》课件

分析足球比赛中各队的进球情况,对球队技术和战术进行评估。
总结
1 实验的重要性
通过统计学上机实验,了解实验设计和数据处理的重要性。
2 基础知识和常用工具
掌握实验的基础知识和常用工具,提高数据分析能力。
3 对学生的意义
统计学上机实验对学生未来的发展具有重要的意义,培养数据分析思维。
《统计学上机实验》PPT 课件
统计学上机实验课程旨在介绍实验设计、数据处理和数据可视化等基础知识 及常用工具。适合初学者了解统计学实验的重要性和应用。
实验设计
实验目的和假设
定义实验目标和假设,确保实验的准确性和可重复性。
适当的实验方法
选择合适的实验方法,使实验结果具有统计学意义。
实验流程和采样方案
直方图
散点图
使用直方图将数据分布可视化, 直观显示数据的分布Байду номын сангаас况。
使用散点图展示变量之间的关 系,帮助观察相关性和趋势。
箱线图
使用箱线图显示数据的中位数、 四分位数和异常值等统计信息。
实验案例
案例一:医院药占比重
探究某医院各科室的药占比重,为医院的资源分配提供依据。
案例二:教学模式与学生成绩
研究不同教学模式对学生成绩的影响,为教学改革提供参考。
设计详细的实验流程和采样方案,确保实验的顺利进行。
数据处理
1
数据的清理和整理
对收集到的数据进行清理和整理,确保数据的准确性和完整性。
2
常见的统计分析方法
使用假设检验、方差分析等常见的统计分析方法对数据进行分析,得出相关结论。
3
数据分析工具
使用SPSS、R等数据分析工具进行统计分析,提高工作效率。
数据可视化
直方图课后作业
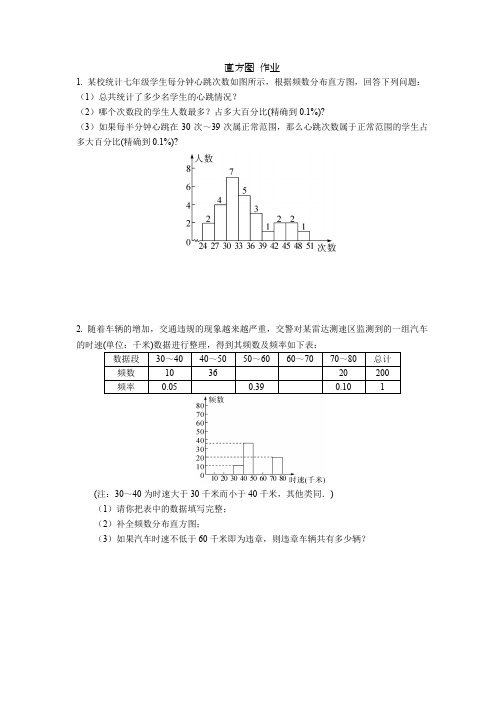
1. 某校统计七年级学生每分钟心跳次数如图所示,根据频数分布直方图,回答下列问题:(1)总共统计了多少名学生的心跳情况?
(2)哪个次数段的学生人数最多?占多大百分比(精确到0.1%)?
(3)如果每半分钟心跳在30次~39次属正常范围,那么心跳次数属于正常范围的学生占多大百分比(精确到0.1%)?
2. 随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区监测到的一组汽车的时速(单位:千米)数据进行整理,得到其频数及频率如下表:
(注:30~40为时速大于30千米而小于40千米,其他类同.)
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
1. 解:
(1)总共统计学生人数为2+4+7+5+3+1+2+2+1=27(人);
解析:小长方形的高(纵坐标)表示该组的频数,所以总频数是所有小长方形的高(纵坐标)的和
(2) 在30次~33次这个范围内的学生人数最多,共7人,所占百分比为7
27×100%≈25.9%;
(3)如果每半分钟心跳在30次~39次这个范围内属于正常范围,那么心跳属于正常范围的学生占的百分比是7+5+3
27×100%≈55.6%.
2. 解:
(1)第二列0.18,第三列78,第四列56,0.28; (2)如图所示;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有76辆.。
第14讲+让频数更直观——直方图

第14讲让频数更直观——直方图学习目标1.了解描述数据的另一种统计图——直方图;2.理解组距、频数、频数分布的意义,能绘制频数分布直方图.入门测单选题练习1.某校七年级统计30名学生的身高情况(单位cm),其中身高最大值为175,最小值为149,且组距为3,则组数为().A.7B.8C.9D.10填空题练习1.在样本的频数分布直方图中,共有9个长方形,已知中间一个长方形的面积等于其它8个长方形面积的,又已知样本总数据是100个,则中间一组的频数是.练习2.某区从近期卖出的不同面积的商品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图.从中可知卖出的110m2~130m2的商品房_____套.练习3.为了解某校八年级女生1分钟仰卧起坐的次数,从中随机揣测了50名女生参加1分钟仰卧起坐的次数测试,并绘制成一个不完整的频数分布直方图(如图),则1分钟仰卧起坐的次数在40-45的频率是______.解答题练习1.'某校抽检64个学生的体重如下,(单位:kg)列出频数分布表.'情景导入为了参加全校各年级之间的广播体操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛,为此收集到了这63名同学的身高(单位:cm)如下:要挑出身高相差不多的40名同学参加比赛,我们应该怎样整理数据?知识精讲频数分布表——组数、组距知识讲解频数分布表1.组距:把所有数据分成若干组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距。
2.组数:分成组的个数叫做组数。
例题精讲频数分布表——组数、组距例1.一组数据有若干个,最大值为125,最小值103,取组距为3,则可以分成().A.6组B.7组C.8组D.9组例2.小欢为一组数据制作频数分布表,他了解到这组数据的最大值是40,最小值是16,准备分组时取组距为4.为了使数据不落在边界上,他应将这组数据分成().A.6组B.7组C.8组D.9组频数分布表——频数知识讲解频数:各小组内的数据的个数叫做频数。
应用统计学上机操作

3、参数估计
1、Excel“数据分析”工具描述统计:勾选 “平均数置信度”,根据输出结果中的 “平均值”分别加减“平均数置信度”推 算出置信区间 分析数据特征
2、SPSS“分析” 描述统计探索
4、假设检验
单样本t检验 1、Excel“数据分析”工具:无 2、SPSS“分析” 比较均值单样本T检验 双样本t检验(配对/匹配样本) 1、Excel“数据分析”工具 t-检验:平均值 的成对二样本分析 2、SPSS“分析”比较均值配对样本T检验
1、Excel“数据分析”工具:无 2、SPSS 先“数据”加权个案(加权人数) 再“分析”描述统计 交叉表 统计量:卡方 单元格:期望值
7、相关与回归
相关分析 1、Excel“数据分析”工具相关系数 2、SPSS“分析”相关
回归分析 1、Excel“数据分析”工具回归 2、SPSS“分析”回归
• 二选一
2、定性资料统计描述
频数和频数分布(含图:条形图);老师 说不出 1、Excel“数据分析”工具直方图 2、SPSS“分析” 描述统计频率/交叉表 SPSS“图形” 旧对话框条形图
统计指标(频率、比率/相对比) 频率:频数和频数分布操作过程中已实现 比率/相对比,无相应工具,可套用公式计算
• 单样本t检验
4、假设检验
双样本t检验(独立样本)
1、Excel“数据分析”工具 t-检验:双样本等
方差假设、双样本异方差假设、z-检验:双样本 平均差检验。z-检验需事先已知总体方差,实践 里很难实现故很少使用,实践里通常用前两个, 但需要事先知道双样本是否等方差,可先通过 “数据分析”工具F-检验:双样本方差来判断。
2、SPSS“分析”比较均值独立样本T检验
直方图练习题

直方图练习题直方图是一种常用的统计图表,它用矩形条表示数据的频数或频率分布。
通过直方图,我们可以直观地了解数据的分布情况。
本文将通过几个练习题来帮助读者提高直方图的解读和绘制的能力。
练习题一:下面是某班级学生的考试成绩分布情况,请根据这些数据绘制出直方图。
分数区间频数60-70 470-80 880-90 1290-100 6解答:为了绘制直方图,我们需要将横轴分为不同的分数区间,并且每个区间的宽度一致。
然后,根据频数绘制相应高度的矩形。
首先,我们将横轴分为四个等宽的区间:60-70、70-80、80-90和90-100。
然后,根据频数绘制矩形。
分数区间60-70对应的频数为4,因此绘制4个高度相同的矩形;分数区间70-80对应的频数为8,绘制8个高度相同的矩形;分数区间80-90对应的频数为12,绘制12个高度相同的矩形;分数区间90-100对应的频数为6,绘制6个高度相同的矩形。
练习题二:某商店连续7天的销售额如下,请根据这些数据绘制出直方图。
星期一:4000元星期二:3000元星期三:5000元星期四:6000元星期五:2000元星期六:3500元星期日:4500元解答:为了绘制直方图,我们需要将横轴标记为七个星期几,并以相同的宽度绘制矩形。
首先,我们将横轴标记为星期一至星期日。
然后,根据销售额数据绘制相应高度的矩形。
星期一的销售额为4000元,绘制一个高度为4000的矩形;星期二的销售额为3000元,绘制一个高度为3000的矩形;星期三的销售额为5000元,绘制一个高度为5000的矩形;星期四的销售额为6000元,绘制一个高度为6000的矩形;星期五的销售额为2000元,绘制一个高度为2000的矩形;星期六的销售额为3500元,绘制一个高度为3500的矩形;星期日的销售额为4500元,绘制一个高度为4500的矩形。
练习题三:一份调查显示了某城市不同年龄段人群的就业率分布情况,请根据这些数据绘制出直方图。
《统计与数据分析》 数据分析实验作业

《统计与数据分析》数据分析实验作业数据来源于大肠杆菌Escherichia coli K-12 MG1655注释的4289个编码蛋白基因的长度l(单位:核苷酸,NT)及其GC含量r(%)。
其中,第1列为基因序号,第2列为基因的长度l(单位:核苷酸,NT),第3列为基因的GC含量r(%)。
试针对这一组数据完成下列统计与数据分析工作:1. 将全部4289个基因视为总体Y,请完成如下工作:(1)分别画出基因长度l和基因GC含量r的频率直方图;(2)分别求出基因长度l和基因GC含量r的均值、标准差、中位数、众数、变异系数,并检验Chebyshev定理;(3)基于总体Y,根据中心极限定理构造一个基于GC含量r值的模拟总体数据X,要求总体X为标准正态分布,且X的个体数目也为4289,取值可表示为R。
(提示:简单随机抽样的样本均值R近似服从正态分布。
)2. 基于服从标准正态分布的总体X,请完成如下工作:(1)从中进行1次简单随机抽样(容量n=61),画出R值这一样本的频率直方图,并求出样本均值和样本标准差;由此估计总体的正态分布参数(方法不限),并给出估计参数的90%置信区间;(提示:相关分布的分位数表可参考本课程讲义。
)(2)进一步地,进行100次容量为n=61的简单随机抽样,分别画出样本均值、样本标准差的频率直方图,考察同样参数估计方法所估计参数的90%置信区间的情况,并以合适的图示表示(提示:请参考本课程讲义的表示方式。
)。
3. 对于总体Y,将全部4289个基因视为从某一总体中进行1次简单随机抽样的样本(容量n=4289),给定显著性水平为10%,试考察基因长度l与GC含量r是否相互独立。
(提示:相关分布的分位数表可参考本课程讲义。
)要求:(1)本次数据分析以实验报告形式打印、装订提交,请在第一页注明学号、姓名;(2)请保证独立完成本作业,鼓励自行编程完成上述数据分析,也可使用相关软件(不限);(3)本作业占课程总成绩15%。
直方图统计练习题

直方图统计练习题在统计学中,直方图是一种用来表示数据分布情况的图表。
它将数据划分成一系列等宽的区间,并在横轴上绘制出这些区间的范围,纵轴表示数据在该区间内的频数或频率。
通过直方图,我们可以直观地观察到数据的分布形态、集中程度以及异常值等信息。
为了更好地理解和练习直方图的统计分析,下面将给出一些直方图统计练习题。
练习题1:某班级的学生体重数据如下(单位:kg):56 54 59 62 63 65 60 65 57 58 70 65 58 63 64请根据这组数据绘制出直方图,并回答以下问题:1. 该班级学生的体重数据大致呈什么样的分布形态?2. 最常见的体重区间是多少至多少kg?3. 体重在50kg至60kg之间的学生人数占总人数的百分比是多少?练习题2:一份调查统计了某国家不同年龄段的人口数量数据如下(单位:百万):0-18岁:250 18-35岁:320 35-50岁:280 50岁以上:220请根据这组数据绘制出直方图,并回答以下问题:1. 该国家人口数量在不同年龄段上的分布情况如何?2. 在哪个年龄段上,人口数量最多?3. 50岁以上的人口数量占总人口数量的百分比是多少?练习题3:一份统计调查了某公司员工的工作经验数据如下(单位:年):0-2年:20 2-5年:30 5-10年:40 10年以上:10请根据这组数据绘制出直方图,并回答以下问题:1. 该公司员工的工作经验分布情况如何?2. 在哪个工作经验区间上,员工数量最多?3. 具有5年以上工作经验的员工占总员工数量的百分比是多少?练习题4:一份调查记录了某城市不同民族的人口数量数据如下(单位:千人):汉族:900 苗族:120 壮族:300 回族:100请根据这组数据绘制出直方图,并回答以下问题:1. 该城市不同民族的人口分布情况如何?2. 哪个民族的人口数量最多?3. 除汉族外,其他民族的人口数量总和占该城市总人口数量的百分比是多少?通过以上的练习题,我们可以巩固对直方图及其统计分析的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、在某电子公司,职员实行弹性上班制度,他们每天开始工作可
7:008:309:008:007:307:308:308:307:30
8:308:308:008:007:308:307:009:008:30
通过绘制下列图表来概括这些数据:
(1)频数分布表;
(2)条形图;
(3)饼形图;
(4)你能根据该弹性上班制度数据概括出职员的偏好吗?
2、个人计算机将计算机的便利和影响力带进了家庭,但每周人们实际
0.5 1.2 4.810.3713.11612.711.6
2.28.20.797.8 2.2 1.812.812.5
15.513.612.212.512.813.5 1.3 5.55
2.5
3.9 6.5
4.28.8 2.8 2.514.416
2.89.5 1.510.5 2.27.510.514.114.9
通过编制下列表格来概括这些数据:
(1)编制频数分布表(用3小时作为组距);
(2)绘制直方图;
(3)试述数据说明了个人计算机在家庭使用的情况如何?
3、某职员每天可以有两种方法去上班:交通车和公交车。
每一种方法交通车:28293237332529
公交车:29313332343031
(1)用描述统计分析工具分别输出两种交通方法的结果;
(2)根据上一步所得到的结果,应该选择哪一种交通方法更好?
开始工作可以在上午7:00、7:30、8:00、8:30或9:00。
下面数据是职员7:00
8:00
但每周人们实际使用家用计算机的时间有多少小时呢?为了解个人计算机在家
5.1
14.1
10.8
12.4
0.3
车。
每一种方法所需要的样本时间记录如下(单位:分钟):
324134
323533
方法更好?
下面数据是职员挑选的上班开始时间的一个样本:
个人计算机在家庭中的使用情况所进行的一项研究得到了下面的数据(单位:
据(单位:小时/周):。
