质心运动定理

合集下载

2 质心质心运动定理

将质心的位置矢量 rC 对时间t求导，可得出
质心运动的速度为
dri m drC i dt vC dt m
mi v i m
由此可得
mvC mi vi
上式等号右边就是质点系的总动量
p mv C
即：质点系的总动量等于它的总质量与它的质心的运动速度的乘积。
质心、质心运动定理
质心质心运动定理
一．质心
当我们把一匀质薄三角板斜向抛出时，它的空间运动很复杂，但实际观测表明，在薄板上有一点C仍然在作抛物线运动。C点的运动规律就象把薄板的质量都集中在 C点，全部的外力也象时作用在C点一样。这个特殊点C 就是质点系统的质心。
2
质心运动定理证明：质点系的总动量等于它的总质量与它的质心的动速度的乘积。
根据牛顿第二定律的微分形式
dp dv C F m ma C dt dt
上式表明无论质点怎样运动，质点系的总质量与质心加速度的乘积总等于质点系所受全部外力的矢量和，这就是质心运动定理。它对刚体同样适用。
4

大学物理-质心质心运动定律

角动量守恒条件
当刚体绕定轴转动时，如果作用于刚体上的外力矩为零，则刚体的角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题，如陀螺仪的工作原理、天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时，刚体的角动量将发生变化。此时需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围：质心运动定律适用于任何由多个质点组成的系统，无论这些质点之间是否存在相互作用力。
02
适用条件：质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响，或者其影响可以忽略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小和方向，等于转动惯量与角速度的乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时，其质心位置保持不变，始终位于转轴上。
质心速度为零
由于质心位于转轴上，因此质心的速度为零。
质心加速度为零
由于质心速度为零，因此质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心的位置矢量称为相对位移。
性质
相对位移是描述质点系内各点相对于质心位置变化的物理量，具有矢量性。
计算方法
通过几何方法或解析方法求出各点相对于质心的位置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。

123质心运动定理理论力学

y A
A, Co
, C
, B
B mg
x
FN
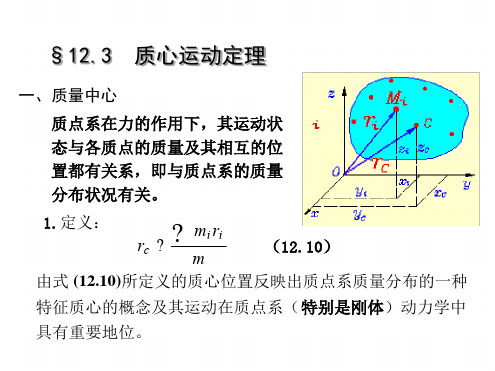
解：以均质杆AB为研究对象，并以杆AB铅直时的轴线为 y轴，建立图示坐标系。AB杆倒下过程中所受外力有：重力mg，光滑水平面的法向反力FN，杆在倒下的过程中有：
? FRex ? Fixe ? 0
即质点系动量在 x方向上守恒，
又：t=0时杆处于静止故质心运动在x方向上守恒，有：
§12.3 质心运动定理
一、质量中心
质点系在力的作用下，其运动状态与各质点的质量及其相互的位置都有关系，即与质点系的质量分布状况有关。
1.定义：
? rc ?
mi ri m
（12.10）
由式 (12.10)所定义的质心位置反映出质点系质量分布的一种
特征质心的概念及其运动在质点系（特别是刚体）动力学中
具有重要地位。
? mi ri
rc ? 2.质心的力学意义
m
① 若质点系中各质点的质量相等，则：
rc
?
m r1 ? m r2 ? ......? m m? m? ......? m
rn
? ? r1 ? r2 ? ......? rn ? n
1 n ri
1/n 与 i 无关，为公因子。
（12.11）
式中: ri系数 1/n 表示第 i个质点的质量在质点系质量中所占的比例，质心的矢径rc即为各质点的平均矢径。
（1）
x2 ? ecos? t y2 ? esin? t （2）
(3) 代入质心坐标公式得质心 c 的运动方程：
? ??
xc
?
m2 m1 ? m2
e cos?
t
?
? ??

质心运动定理讲解

质心运动定理讲解
质心运动定理指的是质点系的质心以恒定的速度沿着直线运动，
且其所受合外力等于其质量与加速度的积。

这个定理结合了牛顿第二
定律和质点系的质心公式，表达了质心运动的关键性质。

牛顿第二定律指出，物体受到的合外力等于其质量乘以加速度。

对于质点系，可以将其看成一个由若干个质点组成的系统。

此时，质
点系的质心可以看作是其所有质点质量之和的加权平均值。

因此，如
果我们知道了质点系受到的合外力，就可以计算出质点系的总加速度，从而推导出质心的运动规律。

具体来说，如果质点系受到的合外力为F，质点系的质量为M，
质心的速度为v，则根据牛顿第二定律有F=Ma。

又根据质点系的质心
公式，有Mv=Σmivi，其中Σmivi表示所有质点的质量与速度之积之和。

这里我们假设质点系并不发生转动，因此质心的速度与角速度均
为常数。

将上述两个式子联立，可以得到Mv=F/a，也就是质心的加速度与外力和质点系质量之比相等。

因此，质心的运动可以看成是一个受到
恒定加速度的匀加速直线运动，其速度随时间线性增加。

总之，质心运动定理给出了描述质点系运动的一个关键性质。

通
过计算质心的加速度，我们可以推导出质心的运动规律，从而了解整
个质点系的运动情况。

理论力学课件质心运动定理,,第十章动量矩定理

质心守恒
支承面的法向反力的最小值求得为
2
221min )(ω
e m g m m F y −+=若，则。

因此如电动机无螺栓固定，它将会跳起来。

e
m g
m m 221)(+>ω0min <N F
9.2 质心运动定理
夯体滑动而不跳起的条
件怎样建立？
问题1——运动员质心做什么运动？问题2——运动员手脚运动、肌肉收缩、关节运动是否影响质心运动？抛物线内力不影响质心运动！
跨越式翻滚式背越式
跨越式：人体质心大约在腹部，杆在双腿的下方，质心约在杆上方30cm 翻滚式：人体质心
大约在腹部，杆在
身体的下方，人体
基本上与杆平行，
质心约在杆上方
10cm
背越式：人体质心
不在身体上，可在
背部下方10cm，质
心从杆下方过杆。

1.8m-0.3m=1.5m 1.8m-0.1m=1.7m 1.8m+0.1m=1.9m
第10章动量矩定理
问题：应用动量定理和质心运动定理只能分析出其质心加速度，如何分析猫的转体？
跳水动量矩守恒
跳水运动员为什
么在空中可实现空翻
和转体的转变？
M
A。

质心质心运动定理

求: 它的质心位置。
y
d
C 0.64R
dm

x
解: 建坐标系如图
取 dl
o
M M Rd d dm dl R

x R cos y R sin
M d 0.

R sin 0 M

xc
x dm
M

R cos 0 M
说明: 质点系动量等于总质量与质心速度的积
dP 质点系动量定理 F外 d t
2. 质心的加速度及其动力学规律
质点系动量 P mv c 说明: (1)质心运动状态只取决于外力，与内力无关 (2)若 F外 0 则 ac 0 vc 常矢量
dvc F外 m mac dt
质心质心运动定理
一、质心(the center of mass) 质心位矢坐标
xc
rc
mi r i m
i i
z
mi
mx
ri
rc
r1
m1
m2
yc
m mi y i
o
y
m
i i
zc
mz m
x
对于质量连续分布的系统 rc

rdm m
例: 已知一半圆环半径为 R，质量为m ，
M
d 0
二、质心运动定理(theorem of the motion of center of mass) 1. 质心的速度 dri m dr i miv i d mi ri c d t ( ) vc m dt m m dt mv c mi v i P 质点系动量 P mv c

2_9质心与质心运动定理

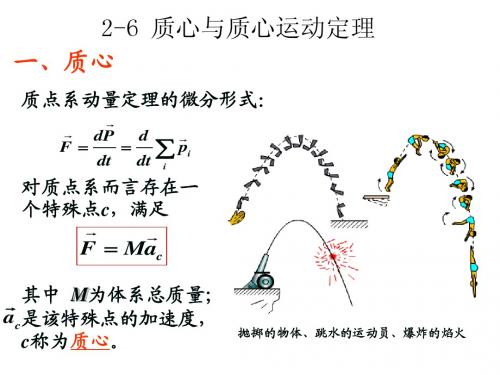
例3 有质量为2m的弹丸，从地面斜抛出去，它的落地点为xC 。如果它在飞行到最高点处爆炸成质量相等的两碎片。其中一碎片铅直自由下落，另一碎片水平抛出，它们同时落地。问第二块碎片落在何处。
解：在爆炸的前后，质心始终
只受重力的作用，因此，质心的轨迹为一抛物线，它的落地点为xc 。
m1 x1 m2 x2 xC m1 m2 mx2 xC 2m
dV r 2 dz
而
r a sin z a cos , 2 dV a sin d a cos
a 1 cos d cos
3 2
r a sin
z
z a cos x

a

0 设 u cos ，则 v z dV zdV a 4 1 1 u2 udu 2 a 3 zc 0 3 V dV
x1c R
y
O
x
1 2 小圆板质量为 m1 R， 4 质心坐标为
2
3 余下的质量为 m2 R 2，质心坐标用 x 2 c表示，则 4
1 3 2 R R R 2 x2 c 2 4 0 4 2 R
R x2c 6
例2
求半径为a的均质半圆球的质心
解：如图，以球心O为原点建立坐标系.将半球体划分为若干半径为r厚为dz的平板状薄圆，体积元为dV
令
m1r1 m2 r2 rc m1 m2
（2）n个质点系统
分量形式
xc
i
rc
mi ri
m
i
i i
i
i
m x m
i i i
i

质心运动定理公式

质心运动定理公式
《质心运动定理公式》是物理学中一个重要的定理，它描述了质点在牛顿力学中的运动规律。

它指出，在牛顿力学中，一个质点的运动轨迹是一个椭圆，其中质心是椭圆的中心，它是质点的动量的守恒定律的结果。

质心运动定理的公式为：质点的轨迹方程为：
x²/a²+y²/b²=1，其中a为椭圆的长轴，b为椭圆的短轴，x为质点的横坐标，y为质点的纵
坐标。

质心运动定理公式的发现对物理学的发展具有重要意义，它可以用来描述质点运动的轨迹，也可以用来解释物体运动的规律，比如太阳系中行星的运动轨迹就是椭圆，它们的轨迹就是质心运动定理的结果。

此外，质心运动定理公式也可以用来描述其他物理现象，比如电子在原子核中的运动轨迹也是椭圆，它们的运动轨迹也是质心运动定理的结果。

质心运动定理公式是一个重要的定理，它可以用来描述物体运动的规律，为物理学的发展做出了重要贡献。

质心运动定理讲解

质心运动定理讲解
质心运动定理是物理学中的一个重要定理，它描述了一个物体的质心在外力作用下的运动规律。

质心是一个物体的所有质点的平均位置，它是一个重要的物理量，可以用来描述物体的运动状态。

根据质心运动定理，一个物体的质心在外力作用下的运动规律可以用以下公式表示：
F = ma
其中，F表示物体所受的外力，m表示物体的质量，a表示物体的加速度。

这个公式表明，一个物体所受的外力越大，它的加速度就越大，质心的运动速度也就越快。

质心运动定理的应用非常广泛，它可以用来解释很多物理现象。

例如，当一个物体受到一个施加在它上面的力时，它的质心会向着力的方向运动。

这个现象可以用质心运动定理来解释，因为当一个物体受到外力时，它的质心会受到相同的力，从而产生加速度，导致质心运动。

质心运动定理还可以用来解释物体的旋转运动。

当一个物体旋转时，它的质心也会随着旋转，但是质心的运动速度和旋转速度是不同的。

这个现象可以用质心运动定理来解释，因为当一个物体旋转时，它的质心会受到向心力的作用，从而产生向心加速度，导致质心运动。

质心运动定理是物理学中一个非常重要的定理，它可以用来解释很多物理现象。

通过理解和应用质心运动定理，我们可以更好地理解物体的运动规律，从而更好地掌握物理学知识。

质心运动定理表达式

质心运动定理表达式
质心运动定理是一种在物理学中使用的定理，它定义了一个物体在受外力作用时，其运动轨迹对于半径等于质心处运动轨迹的投影是什么。

质心运动定理的数学表达式是：速度矢量的和等于两个外力矢量的和乘以质心距离的倒数（P2-P1）。

质心运动定理可以在物理学中应用于多种情况。

例如，在分析多部件系统的运动特性时，可以使用质心运动定理来描述它们之间的运动关系。

比如，可以用质心运动定理来求解车轮系统中每个部件的运动关系，也可以用它来研究悬挂系统中悬挂点与质心之间的运动特性。

此外，质心运动定理还可以用来描述复杂的摩擦力学系统中物体之间的运动特性；还有，它还可用来检验重力势能场和摩擦力场影响的运动特性，以及多体系统中的动力学。

另外，质心运动定理还被广泛应用于船舶分析和控制系统的设计中，并可以用来确定摇杆系统的运动特性，并对船只在自由和受控状态下的运动进行预测和模拟。

总而言之，质心运动定理是一种在多种应用领域都有重要应用的定理，可以用来查明受外力作用时物体的移动历程。

正是有了这个定理，我们才能更加清楚的掌握复杂物理问题，从而做出更好的解决方案。

质心运动定理

Newton 第三定律和动量守恒Newton 第二定律给出了任何物体的加速度与作用在它上面的力之间的关系，在这个基础上，原则上可以解决任何力学问题。

例如，为了确定几个粒子的运动，人们可以利用前面一节中所展开的数值方法。

但是我们有充分的理由来进一步研究Newton 定律。

首先，有一些十分简单的运动不仅可以用数值方法分析，也可以直接进行数学分析。

比如：虽然我们可以按数值方法计算简谐振子的位置，但是分析这个运动并找到一般解cos x t =，则更令人满意。

同样，一个行星由引力决定的绕太阳的运行固然可以用上一节的数值解法逐点地加以计算，从而找到轨道的一般形状，但能够得到准确的形状——分析表明这是一个完整的椭圆——就更好了。

因此，当存在一种简单而又更为精确的方法以得出结果时，再去用一系列麻烦的算术运算就毫无必要了。

遗憾的是，只有很少问题能够以分析方法精确求解。

例如就简谐振子来说，如果弹簧力不是正比于位置，而是更为复杂的话，人们就只得又回到数值解法上来。

或者，假如有两个天体绕太阳运行，使天体的总数是三个，那么分析法就无法得出一个简单的运动公式，实际上这个问题只能作数值解。

这就是有名的三体问题，今天，它已作为常规计算准确地按上一节所描述的方式进行充分的演算后，加以解决了。

十分有趣的是，人们曾经化了那么长时间才领悟到也许数学分析的能力是有限的，因而使用数值解法是必要的这个事实。

然而，也有一些两种方法都失效的情况：对简单的问题我们可以用分析方法，对适当困难的问题可以用数值和算术方法；但是对非常困难的问题则这两种方法都不能用了。

例如：两辆汽车的碰撞，或者甚至气体中分子的运动，就是一种复杂的问题。

在一立方厘米的气体中有数不清的粒子，而试图用这么许多变量(约个——即一万亿亿个)来作计算将是荒谬的。

任何问题，如果不是只有二、三个行星绕太阳运行，而是诸如象气体、木块、铁块中的分子或原子的运功，或在球状星团中许多恒星的运动之类这样的问题，我们就不能直接去解，因此只好借助于其他手段。

3.3 质心质心运动定理

i
F iX 0
PX 0
画系统受力图 M V X m x 0
x VX X
是m相对于小车的速度
VX m M m
X
8
第3章动量与角动量
VX
m M m
t 0
XX 来自t 0V X dt
m M m

t 0
dt X
M 例3 如图已知： , m , l ，地面光滑。 m , l mg 起初：单摆水平，静止。求：下摆至时，车的位移。 V
o
N
X
以此例即将说明动量守恒和质心速度不变是同义语。动量守恒的问题也可以利用质心速度不变来解。解：法一用动量守恒定律选 M + m 为系统
M
Mg
4

ac

i
m iai / m i
i

t2 t1
F外 d t

P P0
dP
第3章动量与角动量
讨论
F外
1）质点系动量定理微分和积分形式： t dP m a c （ F外） F d t P P0
dt

2
t1
外
2) 质心的运动，该质点集中整个系统质量，并集中系统受的外力，代替质点系整体的平动。
i
说明: 1）不太大的物体的质心与重心重合； 2）均匀分布的物体，质心在几何中心； 3）质心是位置的加权平均值，质心处不一定有质量； 4）具有可加性，计算时可分解。
2 第3章动量与角动量
例1 已知一半圆环半径为 R，质量为M。
求它的质心位置。
解建坐标系如图

质心运动定理

质心运动定理
质心运动定理是质点系动量定理的另一种形式,可由质点系动量定理直接导出。

即将P＝Mvc代入质点系动量定理dP/dt＝∑Fe，得：Mdvc/dt＝∑Fe或Mac ＝∑Fe——称为质心运动定理.(∵ac＝dvc/dt)
即：质点系的质量M与质心加速度ac的乘积等于作用于质点系所有外力的矢量和(外力主矢量)。

可见：只有外力才能改变质点系质心的运动。

定理的推论
根据这个定理可推知：
①质点系的内力不能影响它的质心的运动；例如跳水运动员自跳板起跳后，不论他在空中再做何种动作，采取何种姿势，由于外力(重力)并未改变，所以运动员的质心在入水前仍沿抛物线轨迹运动；
②如果作用于质点系上外力的矢量和始终为零，则质点系的质心作匀速直线运动或保持静止；
③若作用于质点系上外力的矢量和在某轴上的投影始终为零，则质点系质心在该轴上的坐标匀速变化或保持不变。

质心运动定律

质心运动定律
质心运动定律指的是质点系统的质心在受到外力的作用下运动
的规律。

根据牛顿第二定律，质心所受的合外力等于质点系统的总质量乘以质心的加速度。

因此，质心的运动可以看做是一个单独的质点在受力下的运动。

质心运动定律有以下几个特点：
1.质心的运动是质点系统中所有质点运动的平均化结果。

2.质心的运动状态与质点系统中的相对位置、互相作用力等无关。

3.质心的运动方向与受力方向相同或相反，具体取决于系统所受的合外力方向。

质心运动定律在工程、物理、天文学等领域有着广泛的应用。

例如，在火箭发射时，需要控制火箭的质心位置以保证火箭的稳定性。

在天文学中，质心运动定律常常被用于研究行星、恒星等天体的运动规律。

- 1 -。

质心运动定理

质心运动定理3、质心运动定理质心运动定理问题：内力是否影响质心的运动？(e)1d ()d n C ii mv F t==∑由(e)1d d n C ii v m F t ==∑得(e)1nC ii ma F ==∑或质点系的质量与质心加速度的乘积等于作用于质点系外力的矢量和.－－质心运动定理质心运动定理与动力学基本方程有何相似与不同之处？质心运动定理常量质心运动定理质心运动定理内力不能改变质心的运动汽车发动机的气体压力是原动力通过传动机构使主动轮转动地面摩擦力(e)1nC ii ma F ==∑ma F=质点系质心的运动可看成质点的运动，此质点集中了质点系的质量及其所受的力爆破山石通过质心运动轨迹，确定石块堆落地点 ma F=是公理，描述质点运动状态变化规律(e)1nC ii ma F ==∑是导出定理，描述质心运动状态变化规律质心运动守恒定律(e)Cx xma F=∑(e)Cy yma F=∑(e)Cz zma F=∑2(e)Cnv m F ρ=∑(e)C t v m F t =∑d d (e)0bF=∑在直角坐标轴上的投影式为:在自然轴上的投影式为:(e)F ∑≡若则常矢量 C v =(e)0xF∑≡若则常量 =Cxv若初始静止，质心位置不变若初始速度投影等于0，质心在该轴坐标不变质心运动定理均质曲柄AB长为r,质量为m1,假设受力偶作用以不变的角速度ω转动,并带动滑槽连杆以及与它固连的活塞D ,如图所示.滑槽、连杆、活塞总质量为m2,质心在点C .在活塞上作用一恒力F .不计摩擦及滑块B的质量,求:作用在曲柄轴A处的最大水平约束力Fx .例1t m m m m r t x a C Cxωωcos 2d d 2121222⎪⎭⎫⎝⎛++-==tm m r F F x ωωcos 2212⎪⎭⎫⎝⎛+-=⎪⎭⎫⎝⎛++=212m ax2m m r F F ω最大水平约束力为应用质心运动定理()FF a m m x Cx -=+21()21211cos cos 2m m b r m r m x C +⋅⎥⎦⎤⎢⎣⎡++=ϕϕ分析整体，受力如图所示。

质心运动定理

2 质心 质心运动定理

大学物理-质心质心运动定律

123质心运动定理理论力学

质心运动定理讲解

理论力学课件 质心运动定理,,第十章动量矩定理

质心 质心运动定理

2_9质心与质心运动定理

质心运动定理公式

质心运动定理讲解

质心运动定理表达式

质心运动定理

3.3 质心 质心运动定理

质心运动定理

质心运动定律

质心运动定理

2 质心质心运动定理

理论力学课件质心运动定理,,第十章动量矩定理

质心质心运动定理

3.3 质心质心运动定理