液体粘滞系数测定实验
粘滞系数实验报告

粘滞系数实验报告
实验目的:测定不同液体的粘滞系数,了解粘滞现象对流体运动的影响。
实验原理:粘滞系数(η)是衡量流体内部粘滞阻力大小的物理量。
根据牛顿第二定律和斯托克斯定律,流体粘滞系数可通过粘滞实验进行测定。
斯托克斯定律适用于介质为稀薄、粘滞系数不随温度和流速改变的情况,即呈牛顿流体的情况。
实验器材:粘度计、容器、不同液体样品、计时器。
实验步骤:
1. 在容器中加入待测液体,注意避免气泡的产生。
2. 将粘度计的毛细管完全浸入液体中。
3. 用计时器记录流体从A点到B点的通过时间τ。
4. 测量不同液体的通过时间,每种液体至少测量5次,取平均值。
实验数据处理:
1. 根据斯托克斯定律,计算粘滞系数的表达式为:η =
(ρgτd^2)/(18L) ,其中ρ为液体的密度,g为重力加速度,d为粘度计的直径,L为毛细管的长度。
2. 将实验得到的数据代入公式中计算粘滞系数,并计算各组数据的平均值。
实验结果和讨论:
根据实验数据计算得到的粘滞系数可以与文献中给出的数值进
行对比,判断实验结果的准确性。
同时,可以比较不同液体的粘滞系数大小,分析各液体分子间相互作用力的差异对粘滞现象的影响。
实验结论:
通过粘滞实验测得不同液体的粘滞系数,比较了液体粘滞特性的差异,进一步了解流体运动中的粘滞现象。
液体粘滞系数测定实验报告

液体粘滞系数测定实验报告实验介绍:液体粘滞系数测定实验是通过测量液体在垂直下落时的速度和时间,对液体的粘滞性进行分析和测定的实验。
液体粘滞系数是指,液体内分子间相互作用的形成的阻力大小,阻碍了分子的相对运动。
液体粘滞系数又叫做黏度,通常用希腊字母mu(μ)表示,其单位是帕秒。
液体粘滞系数是许多流体力学和化学过程的重要参数之一,因此液体粘滞系数测定实验具有非常高的实用价值。
实验原理:液体粘滞系数测定实验的原理基于斯托克斯定理。
根据斯托克斯定理,在实验介质中垂直下落的直径为d的小球,以恒定的速度υ下落的关系式为:f=6πμυd其中f是液体对小球的阻力,μ是液体的粘滞系数,在SI单位下的单位是Pa·s,υ是小球下落的恒定速度,d是小球的直径。
实验内容:实验所需的材料主要有:测量筒、滴管、计时器、小球等。
首先将测试液体倒入测量筒中,并用滴管将小球放入液体中,观察小球在液体中的运动情况并确定小球下落的恒定速度。
然后,利用计时器测量小球下落一定距离所需的时间。
在实验过程中,需要先进行预热,将测试液体倒入测量筒中,用计时器测量室温下小球下落一定距离所需的时间t1,然后将液体测温加热至70℃,用计时器测量小球下落一定距离所需的时间t2。
在实验中,需要多次重复测量,求出液体的平均时间。
利用液体平均时间及小球的下落速度,根据斯托克斯定理,可以计算液体的粘滞系数。
实验数据处理:在实验过程中,需要先计算小球的下落速度υ,通过下式计算:υ=m×g/6πRμ其中,m为小球的质量,R为小球半径,g为重力加速度,μ为液体粘滞系数。
可以求出实验所得液体的平均粘滞系数μ的值,通过求出标准偏差及误差,进一步确定实验数据的可靠性和准确性。
实验结论:通过本次液体粘滞系数测定实验,我们可以得知不同液体的粘滞系数不同,小球下落恒定速度与液体的粘滞系数成反比例关系,液体温度对粘滞系数的影响较大,液体温度升高,粘滞系数减小。
粘滞系数测定

[数据处理与分析]
• 如忽略(5-7)式分母中修正项的误差, 有
Uη = ( ∆ m + ∆Vρ0 m − Vρ 0 )2 + ( ∆ l 2 ∆t 2 ∆ d 2 ) +( ) +( ) l t d
• 其中:
∆Vρ0 = Vρ 0 ∗ (3 ∆ d 2 ∆ ρ0 2 ) +( ) d ρ0
[注意事项]
• (1) • 式中η称为粘滞系数(单位名称为帕秒,符号Pa·s)。 • 不同流体具有不同的粘滞系数,同一种流体在不同温度下其η值变化 也很大。例如蓖麻油当温度从18°C上升到40°C时粘度几乎降到原来 的1/4。 • 液体的粘滞系数是粘滞流体的主要动力学参数,也是液态物质的重要 物理、化学指标之一。精确测定粘滞系数不仅具有实用意义,而且可 以对许多学科的理论研究提供重要的依据。液体粘滞系数测定的方法 有多种,常用的有毛细管法、落球法和园筒旋转法等。通过本实验还 可以对实验技能得到多方面的训练。
•
• • • •
• •
•
[实验内容] 1.选择10个以上表面光滑及直径相同的小球,用螺旋测微计分别测 出直径d,每粒小球测一次,求其平均值d,注意个别小球直径差异 过大,应剔除不用。 2.将已测过直径的10粒以上的小球,用物理天平称衡其总质量,即 可算得每粒的质量m。 3.用游标卡尺测量量筒的内直径,算出半径R;用钢直尺测量量筒 外壁上两条标线N1、N2之间的距离l。 4.用比重计测出液体的比重,并换算密度ρ0。 5.用镊子夹住小球,先将小球在油中浸一下使小球表面完全为油所 浸湿;然后将小球放入量筒的中间液面处,用秒表测出小球匀速下降 通过路径所需的时间t,则速度 v = l t 。 6.在实验前后各测一次油的温度,以平均值作为实验时的油温T。 在进行正式测量前,必须先熟练掌握秒表的使用方法,并练习测量 2~4粒未经测量直径的小球的下落时间,在已能熟练操作后,再进行 正式测量。 7.将有关数据代入公式(6)计算粘滞系数η值,并求其不确定度。
液体粘滞系数的测定实验报告

液体粘滞系数的测定实验报告一、实验目的。
本实验旨在通过测定不同液体的粘滞系数,探究液体的流动特性,并学习粘滞系数的测定方法。
二、实验原理。
液体的粘滞系数是衡量液体黏性的重要指标,通常用于描述流体的内摩擦力。
在本实验中,我们将通过测定液体在不同条件下的流动速度和流动层厚度,利用流变学原理计算出液体的粘滞系数。
三、实验仪器与试剂。
1. 流体力学实验装置。
2. 不同液体样品(如水、甘油、汽油等)。
3. 测量工具(如尺子、计时器等)。
四、实验步骤。
1. 准备工作,将实验装置设置在水平台面上,并将不同液体样品倒入实验装置中。
2. 测定流速,打开实验装置,调节流体流动速度,并测定不同液体在相同条件下的流速。
3. 测定流动层厚度,观察液体流动时的流动层厚度,并记录下来。
4. 数据处理,根据实验数据,利用流变学原理计算出不同液体的粘滞系数。
五、实验结果与分析。
经过实验测定和数据处理,我们得到了不同液体的粘滞系数。
通过对实验结果的分析,我们发现不同液体的粘滞系数存在较大差异,这与液体的性质密切相关。
例如,甘油的粘滞系数较大,而汽油的粘滞系数较小,这与它们的分子结构和相互作用有关。
六、实验总结。
通过本次实验,我们深入了解了液体的粘滞系数测定方法,并学习了流变学原理在实验中的应用。
同时,我们也认识到了不同液体的粘滞系数反映了其内部分子结构和流动特性,这对于液体的工程应用具有重要意义。
七、实验注意事项。
1. 在实验过程中要注意操作规范,确保实验安全。
2. 实验数据的准确性对于结果的可靠性至关重要,要认真记录实验数据。
3. 在测定流速和流动层厚度时,要保持仪器的稳定,避免外界干扰。
八、参考文献。
1. 《流体力学实验方法》,XXX,XXX出版社,XXXX年。
2. 《流变学导论》,XXX,XXX出版社,XXXX年。
以上为本次液体粘滞系数的测定实验报告,谢谢阅读。
粘滞系数的测量

❖实验简介 ❖实验目的 ❖实验原理 ❖实验仪器
❖实验内容 ❖注意事项 ❖数据处理
实验简介
粘滞系数是液体的一项重要物理参数,它表征液体的 稠稀程度。粘滞系数越大液体越稠,与温度有很大关 系。不同的液体有不同的粘滞系数。
实验目的 1. 观察液体的内摩擦现象, 学会用落球法测量液体的粘滞系数。 2. 巩固基本测量仪器 (米尺、游标卡尺、 螺旋测微计、停表)的使用。
量筒,摄子、小球、停表、
米用尺游、 标3游卡.记标尺卡测录尺量和量时螺筒旋的间测内微径时计D ,眼睛必须平视标记线 。
记录时间时,眼睛必须平视标记线 。
8
粘滞系数的测量
停表测小球通过标记线A到标记线B所需的时间t。
量筒,摄子、小球、停表、
(2)量筒的上水平标准线A为什么要取在液面下一段距离处,而且要使小球从靠近液面处,从静止开始自由下落?
(3)为什么要令小球沿圆筒的中心轴线下降?
用游标卡尺测量量筒的内径D
夹起小球,使小球在量筒液面中心处释放,
【预习思考题】
(1)将小球放入液体前,为什么要将小球 在待测液体中浸一下?
(2)量筒的上水平标准线A为什么要取在 液面下一段距离处,而且要使小球从靠 近液面处,从静止开始自由下落?
(3)为什么要令小球沿圆筒的中心轴线下 降?
粘滞系数是液体的一项重要物理参数,它表征液体的稠稀程度。
停表测小球通过标记线A到标记线B所需的时间t。
粘滞系数是液体的一项重要物理参数,它表征液体的稠稀程度。
粘滞系数越大液体越稠,与温度有很大关系。
观察液体的内摩擦现象,
(1)将小球放入液体前,为什么要将小球在待测液体中浸一下?
在量筒上定出两道水平标记线A、B
实验6 落球法测液体的粘滞系数

实验6 落球法测液体的粘滞系数
落球法是用于测量液体粘滞系数的一种常见的实验方法。
它的主要原理是球体穿过液
体时,就可以测量液体的粘滞系数。
实验过程是将一个经验值圆柱形体,如铝筒,悬挂在小钢筋上方。
筒子高度为悬挂筋
的长度减去筒子长度,即可保证实验中运动的稳定性。
接着用密封容器,装入一定量的液体,调整液体温度,然后将测试体放入空气中,调整测试体的质量以保证正确的落球运动
轨道。
将测试体放入液体中,以给定的速度开始落球,记录落球的时间同时做好安全措施,以免测试过程中造成安全事故。
落球过程应尽量控制好高度和液体的温度。
测量完毕后对实验数据进行计算处理,得出液体的粘滞系数。
实验结果受多种因素的
影响,如液体粘度、液体厚度、皮带高度等,因此改变以上参数即可改变实验结果,也可
以得出正确的粘滞系数数据。
落球法测量液体的粘滞系数是简单可行的,节省金钱和精力,也有很高的准确性和稳
定性。
但同时还需要考虑一些安全因素,如防止落球设备造成危险,以及保证实验精度和
效率,避免因参数的不足而使实验结果变得不准确的情况发生。
实验13 落球法测量液体的粘滞系数

实验4 落球法测量液体的粘滞系数液体粘滞系数又叫内摩擦系数或粘度,是描述流体内摩擦力性质的一个重要物理量,它表征流体反抗形变的能力,只有在流体内存在相对运动时才表现出来。
液体在管道中的传输、机械润滑油的选择、物体在液体中的运动等与都与液体的粘滞系数有关。
液体粘滞系数可用落球法,毛细管法,转筒法等测量方法,其中落球法适用于测量粘滞系数(以下简称η)较高的液体。
η的大小取决于液体的性质与温度,温度升高η值将迅速减小。
如蓖麻油在室温附近温度改变1℃时η值改变约10%。
因此,测定液体在不同温度η值才有意义,欲准确测量液体的粘滞系数,必须精确控制液体温度。
1 [实验目的]1.1 观察液体的内摩擦现象,学会用落球法测量不同温度下蓖麻油的粘滞系数。
1.2 了解PID 温度控制的原理。
1.3练习用停表计时,用螺旋测微器测直径。
2 [实验仪器]变温粘度仪,ZKY-PID 温控实验仪,停表,螺旋测微计,钢球若干。
3 [仪器介绍]3.1落球法变温粘度仪变温粘度仪的外型如图11-1所示。
待测液体装在细长的样品管中,能使液体温度较快的与加热温达到平衡,样品管壁上有刻度线,便于测量小球下落的距离。
样品管外的加热水套连接到温控仪,通过热循环水加热样品。
底座下有调节螺钉,用于调节样品管的铅直。
3.2开放式PID 温控实验仪温控实验仪包含水箱,水泵,加热器,控制及显示电路等部分。
温控试验仪内置微处理器,带有液晶显示屏,具有操作菜单化,能根据实验对象选择PID 参数以达到最佳控制,能显示温控过程的温度变化曲线和功率变化曲线及温度和功率的实际值,能存储温度及功率变化曲线,控制精度高等特点。
开机后,水泵开始运转,显示屏显示操作菜单,可选择工作方式输入序号及室温,设定温度及PID 参数使用▲▼键选择项目,▲▼键设定参数,按确认键进入下一屏,按返回键返回上一屏。
进入测量界面后,屏幕上方的数据栏从左至右依次显示序号,设定温度,初始温度,当前温度,当前功率,调节时间等参数。
实验19 液体粘滞系数的测定
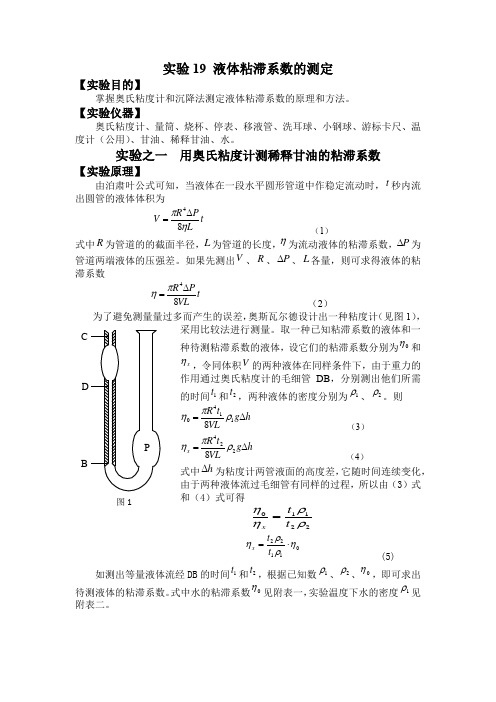
实验19 液体粘滞系数的测定【实验目的】掌握奥氏粘度计和沉降法测定液体粘滞系数的原理和方法。
【实验仪器】奥氏粘度计、量筒、烧杯、停表、移液管、洗耳球、小钢球、游标卡尺、温度计(公用)、甘油、稀释甘油、水。
实验之一用奥氏粘度计测稀释甘油的粘滞系数【实验原理】由泊肃叶公式可知,当液体在一段水平圆形管道中作稳定流动时,秒内流出圆管的液体体积为(1)式中为管道的的截面半径,为管道的长度,为流动液体的粘滞系数,为管道两端液体的压强差。
如果先测出、、、各量,则可求得液体的粘滞系数(2)奥斯瓦尔德设计出一种粘度计(见图1),采用比较法进行测量。
取一种已知粘滞系数的液体和一种待测粘滞系数的液体,设它们的粘滞系数分别为和,令同体积的两种液体在同样条件下,由于重力的作用通过奥氏粘度计的毛细管DB ,分别测出他们所需的时间和,两种液体的密度分别为、。
则(3)(4)式中为粘度计两管液面的高度差,它随时间连续变化,由于两种液体流过毛细管有同样的过程,所以由(3)式和(4)式可得(5)如测出等量液体流经DB 的时间和,根据已知数、、,即可求出待测液体的粘滞系数。
式中水的粘滞系数见附表一,实验温度下水的密度见附表二。
t tL P R V ηπ84∆=R L ηP ∆V R P ∆L tVL P R 84∆=πη0ηx ηV 1t 2t 1ρ2ρhg VLt R ∆=11408ρπηhg VL t R x ∆=2248ρπηh ∆22110ρρηηt t x =01122ηρρη⋅=t t x 1t 2t 1ρ2ρ0η0η1ρ【实验内容】(1) 用玻璃烧杯盛清水置于桌上待用,并使其温度与室温相同,洗涤粘度计,竖直地夹在试管架上。
(2) 用移液管经粘度计粗管端注入6毫升水。
用洗耳球将水压入细管刻度C 以上,用手指压住细管口,以免液面下降。
(3) 松开手指,液面下降,当夜面下降至刻度C 时,启动秒表,在液面经过刻度D 时停止秒表,记下时间。
液体粘滞系数的测定

•同一个球重复测量6次。
•换另一个半径的小钢球,重复以上实验测量6次。
大学物理实验
四. 数据处理
理 实 100% 2.求相对误差: 理
T 0.7046 实查表或 log 0.0347
1. 求实。
五.思考题 教材:
1题(实验报告)
2题(实验报告)
3题(实验报告)
大学物理实验
液体粘滞系数的测定
一.实验任务 二.测量原理与方法 三.实验内容与步骤
斯托克斯
四.数据处理
五.思考题
大学物理实验
各种流体(液体、气体)都具有不同程度的粘性。 什么是粘滞力? —液层与邻层液体间的摩擦力(非物体与液体间的摩擦力) 如何测粘滞系数? —— 本实验落球法。 粘滞系数与哪些因数有关?
L1 F f
小 球LΒιβλιοθήκη 用直尺测L1、 L2之间距离 L, 2次
用计时仪测小球 通过L1、L2之 间的时间
n
mg L2
r球 = 7800.0 kg.m-3,蓖麻油的密度:r液 = 962.0 kg.m-3 ,
量筒直径: D=6.010-2 m .
底座
•光电门1的激光在量筒中轴线距液面下方5cm处。 •用温度计测量实验前的油温T (℃), 随温度升高迅速减少。
•若v1v2=v3,则光电门1可选在其激光在圆筒中轴线处距油面
下方3cm以下的位置。
大学物理实验
3.测量粘滞系数
( r 球 r 液)d gt d d 18L(1 2.4 )(1 1.6 ) D H
2
D
用计时仪测小球通过 L1、L2之间的时 间 用螺旋测微计测量 小球直径6次
H
待测液体 r液
—— 本实验落球法。
液体粘滞系数的测量

实验三 液体粘滞系数的测定

实验三 液体粘滞系数的测定【实验目的】1. 加深对泊肃叶公式的理解;2. 掌握用间接比较法测定液体粘滞系数的初步技能。
【实验仪器】1.奥氏粘度计(加接橡皮管 ) 2.铁架及万向夹 3. 秒表 4.温度计 5.量筒 6.不同容量大小烧杯5个 7.医用橡皮吸球【实验材料】蒸馏水50ml 酒精25ml【实验原理】实际液体是有粘滞性的。
液体流动时,在本身的各个部分之间可以出现内摩擦力。
对于运动规律比较简单的流体——牛顿流体来说,内摩擦力F 是与两层流体的接触面积S 有关,与接触处的流体速度梯度dv/dx 有关的,具体表达式为:)1( dxdvS F η=即牛顿的片流关系式。
我们将比例系数η用其它物理量表示出来,得到如下公式:)2( dxdv S F=η 由此式可以看出:η代表在单位面积、单位速度梯度下的内摩擦力。
假如两种液体,它们的速度梯度及两流层接触面积相同,而摩擦力不同,则可以说它们是有不同的粘性;反过来;不同流体,它们的粘性不同,它们的比例系数η也就不同,因而称描述粘性大小比例的比例常数η为流体的粘滞系数。
测量粘滞系数的方法有很多种,本实验采用的是“间接比较法”。
由理论课的知识中,我们知道,在细管内作片流的稳定流动粘性流体,它的体积流量Q(即单位时间内流过管子一个截面的流体体积)遵从泊肃叶公式:)3(84 lP R Q ηπ∆=其中R 为细管子的半径;l 为管长;ΔP 为管两端的压强差;η为流体的粘滞系数。
在流速接近稳定的条件下,若流过细管的流体体积为V ,经过的时间为t ,则Q = V/ t ,代入公式(3)中,可得到η的表达式:)4(84 VlPt R ∆=πη可以用此式直接测定粘滞系数η,但需要测量的物理量有R 、t 、ΔP 、l 、V 等多个,各个物理量的测量也并不容易,其实也没有必要,所以,我们采用间接比较法:即控制不同的流体在某些相同的条件进行实验测量(比如:让不同的流体的相同的体积通过同一根细管),利用公式进行比较,消去相同的物理量。
液体粘滞系数的测量

(3)
m d3
6 v L
t
(4)
r d 2
式中,ρ为小球材料的密度,L为小球匀速下落的 距离,t为小球下落距离L所用的时间。
第七页,共19页
二、实验原理
实验时,待测液体盛于容器中,故不能满足无限深 广的条件,实验证明上式应该进行修正。
测量表达式为:
(液)gd2t 1
18L
(12.4d)
D
对于液体,粘滞系数与液体的性质,温度和流速 有关。液体粘滞系数的测量在工程技术上有广泛的应 用。如:机械的润滑,石油在管道中的输送,油脂涂料,
医疗和药物等方面,都需测定粘滞系数。
测量液体粘滞系数的方法有多种,如落球法、转筒法 、毛细管法等,其中落球法是最基本的一种,它可用于 测量粘度较大的透明或半透明液体,如蓖麻油、变压器 油、甘油等。
小球下落
第十四页,共19页
四、实验内容
4、启动激光计时器,将小球放入钢球导管,当小球落 下,阻挡上面的红色激光束,激光计时器开始记时,到小球 落到阻挡下面的红色激光束时,停止记时,读出下落时间。
小球下落
第十五页,共19页
四、实验内容
5、用温度计测量油温,在全部小球下落完后再测一 次油温,取其平均值。
测量油温
第十六页,共19页
四、实验内容
数据记录表格 钢球密度 =
小钢球下落距离L=
荆州本地重力加速度g=
测量次数
1
蓖麻油密度s= 容器内半径R=
测量过程前后的平均室温t=
2
3
4
5
6
平均值
小钢球直径(mm)
电子秒表记录时间 (s)
记时器记录的时间 (s)
粘滞系数η
液体粘滞系数测定实验

液体粘滞系数的测量与研究一 实验目的1.了解用斯托克斯公式测定液体粘滞系数的原理,掌握其适用条件。
2.学习用落球法测定液体的粘滞系数。
3.熟练运用基本仪器测量时间、长度和温度。
4.掌握用外推法处理实验数据。
二 实验仪器液体粘滞系数仪、螺旋测微器、游标卡尺、钢板尺、钢球、磁铁、秒表、温度计。
三 实验原理当物体球在液体中运动时,物体将会受到液体施加的与其运动方向相反的摩擦阻力的作用,这种阻力称为粘滞阻力,简称粘滞力。
粘滞阻力并不是物体与液体间的摩擦力,而是由附着在物体表面并随物体一起运动的液体层与附近液层间的摩擦而产生的。
粘滞力的大小与液体的性质、物体的形状和运动速度等因素有关。
根据斯托克斯定律,光滑的小球在无限广延的液体中运动时,当液体的粘滞性较大,小球的半径很小,且在运动中不产生旋涡,那么小球所受到的粘滞阻力f 为vd f πη3= (1)式中d 是小球的直径,v 是小球的速度,η为液体粘滞系数。
η就是液体粘滞性的度量,与温度有密切的关系,对液体来说,η随温度的升高而减少(见附表)。
本实验应用落球法来测量液体的粘滞系数。
小球在液体中做自由下落时,受到三个力的作用,三个力都在竖直方向,它们是重力r gV 、浮力r 0gV 、粘滞阻力f 。
开始下落时小球运动的速度较小,相应的阻力也小,重力大于粘滞阻力和浮力,所以小球作加速运动。
由于粘滞阻力随小球的运动速度增加而逐渐增加,加速度也越来越小,当小球所受合外力为零时,趋于匀速运动,此时的速度称为收尾速度,记为v 0 。
经计算可得液体的粘滞系数为2018)(v gd ρρη-=(2) 式中0ρ是液体的密度,ρ是小球的密度,g 是当地的重力加速度。
可见,只要测得v 0,即可由(2)式得到液体的粘滞系数。
但是注意,上述推导包括(1)、(2)式都在特定条件下方才适用(见原理的第一段黑体字部分),通过对实验仪器和实验方法的设计,这些条件大多数都可以满足或近似满足(结合本实验所用仪器和实验步骤,思考一下哪些条件被满足,是如何做到的),唯独“无限广延”在实验中是无法实现的。
液体粘滞系数实验报告

液体粘滞系数实验报告液体粘滞系数实验报告实验目的:测量不同液体的粘滞系数,并研究其影响因素。
实验仪器:液体粘度计、热水浴。
实验原理:液体的流动受到内摩擦力的阻碍,液体的粘滞性可以通过测量在单位时间内流过单位面积的液体质量当决定。
粘滞系数η是反应液体粘滞性的量,单位为帕斯卡秒(Pa·s)。
实验步骤:1. 将待测液体倒入液体粘度计中,保持液体温度恒定。
2. 慢慢旋转液体粘度计的旋钮,使其产生流动。
3. 通过目视法测量液体在粘度计中的流动时间,并记录下来。
4. 重复以上步骤,测量各种液体的粘滞系数,并进行比较分析。
实验结果:经过多次测量并计算,得到不同液体的粘滞系数如下:- 液体A的粘滞系数:0.025 Pa·s- 液体B的粘滞系数:0.035 Pa·s- 液体C的粘滞系数:0.045 Pa·s实验讨论:从实验结果可以看出,不同液体的粘滞系数有所差异。
液体C 的粘滞系数较大,说明其粘滞性较强,流动时所受到的阻力也大。
同样的流量条件下,液体C的流动速度较慢。
液体A的粘滞系数较小,粘滞性较弱,流动时所受阻力较小,流动速度较快。
液体B的粘滞系数介于液体A和液体C之间,说明其粘滞性处于中等水平。
实验结论:不同液体的粘滞系数不同,液体的粘滞性值得研究。
粘滞系数的大小取决于液体的黏度、密度、温度等因素,在实际应用中有着重要意义。
实验改进:1. 提高实验精度,增加测量次数,减小误差。
2. 扩大液体样品的种类,比较更多不同液体的粘滞系数。
3. 研究不同温度对液体粘滞系数的影响。
参考文献:1.张某某. 测量液体粘滞系数的实验方法与结果分析[J]. 化学工程, 20xx, xx(1): xx-xx.2.李某某. 液体粘滞系数的实验测定与影响因素研究[J]. 化学技术, 20xx, xx(2): xx-xx.。
液体粘滞系数的测定

液体粘滞系数的测定Determinnation of Viscosity Coefficient for Liquids[实验目的]1.了解泊肃叶公式的应用;2.用毛细管粘度计(奥氏特瓦尔德粘度计)测定液体的粘滞系数;3.了解比较法的好处。
[实验器材]奥氏粘度计、温度计、秒表、玻璃缸、洗耳球、量筒、量杯、刻度移液管(滴定管)、蒸馏水、洒精等。
[实验原理]1840年泊肃叶(Poiseulle )研究了牛顿液体在玻管中的流动,他发现流经毛细管的水的流量V 与压力差 ΔP =P 1-P 2、毛细管半径r 0的四次方及时间t 成正比,与毛细管的长度L 、液体的粘度η成反比。
其表达式是:(2一1)则(2一2)应用这一原理,奥氏特瓦尔德(1553一1932)设计制做了如图2一1所示的粘度计。
它用玻璃制成,P 泡的位置较高,为测定液体体积的球,上下各有一刻痕A 和B (A 、B 间的容器相当于量筒),在B 之下是一段截面相等的毛细管BC ;Q 泡位置较低,且比P 泡大,为储液器。
使用时竖直放置在恒温槽中。
如果我们采用直接法测量,需将一定量的液体由D 管注入,然后用洗耳球或移液管把液休吸人P 泡,高于A 线,让液体经毛细管自由下降。
液体下落到A 线时开始计时,至B 线时停止计时,时间间隔为t 秒,流经BC 的液体体积为V 。
由于该部分液体向下流动,受到的压强差是 P=ρgh ,因此有关系式(2-3)图2-1 奥氏粘度计但是在实际中h、r0、L、V都是难以测准的,尤其是h在测量过程中,随着液体重力势能的改变而正比地变化着,更无法测量。
因此用式2-3进行测算,其误差很大,实施也较为困难,因而我门通常采用比较法,即让相同体积的标准液体如蒸馏水和待测液体分别流过同一粘度计,则有(2-4)(2-5)将上述二式进行比较,可得由于相同体积的液体作用在毛细管中液体的平均液柱高度h都相同,所以(2-6)从式2-6可以看出,要测某一待测液体的粘滞系数,只要测量流经毛细管的时间t1、t2和密度ρ1、ρ2就可以了。
实验三液体粘滞系数的测定

实验三液体粘滞系数的测定方法一:用乌式粘度计测定酒精的粘滞系数[实验目的]1.1.进一步巩固和理解粘滞系数的概念。
2.2.学会一种测定粘滞系数的方法。
[实验器材]粘度计、铁架台、秒表、温度计、打气球、玻璃缸、蒸馏水、酒精、量杯。
[仪器描述]如图3-1所示,粘度计是由三根彼此相通的玻璃管A 、B 、C 构成。
A 管经一胶皮管与一打气球相连,A 管底部有一大玻璃泡,称为贮液泡;B 管称为测量管,B 管中部有一根毛细管,毛细管上有一大和一小两个玻璃泡,在大泡的上下端分别有刻线N 、N ′;C 管称为移液管,C 管上端有一乳胶管,为的是在C 管处设置夹子。
整个实验是在装满水的玻璃缸中进行。
[实验原理]一切实际液体都具有一定的“粘滞性”,当液体流动时,由于粘滞性的存在,不同的液层有不同的流速v (如图3-2),流速大的一层对流速小的一层施以拉力,流速小的一层对流速大的一层施以阻力,因而各层之间就有内磨擦力的产生,实验表明,内磨擦力的大小与相邻两层的接触面积S 及速度梯度dv /dy 成正比,即F·y vd d ·S式中的比例系数叫做粘滞系数,又叫内磨擦系数。
不同的液体具有不同的粘滞系数。
一般情况下,液体的值随温度的升高而减少。
在国际单位制中,的单位为帕·秒(Pa ·s )。
图3- 2速度梯度当粘滞液体在细管中作稳恒流动时,若管的半径为R ,管长为L ,细管两端的压强差为ΔP 1 ,液体的粘滞系数为1,则在时间t 1内液体流经细管的体积V 可依泊肃叶公式求出:11148t P LRV(3-1)同理,对于同一细管,若换用另一种粘滞系数为2的液体,并假设这时细管两端的压强差为ΔP 2,体积仍为V 的液体流经细管所需时间为t 2,则有:22248t P LR V(3-2)由(3-1)式和(3-2)式得111222t tP P (3-3)如果实验时把细管铅垂方向放置,则压强差是由重力引起的,于是121212hg h g P P (3-4)此处1及2是两种不同液体的密度,将(3-4)式代入(3-3)式,得111222t t (3-5)可见,如果一种液体的粘滞系数1为已知,且两种液体的密度1及2可查表得到,则只要测出两种液体流经同一细管的时间t 1和t 2,即可根据(3-5)式算出被测液体的粘滞系数2.本实验是已知水的1值,求待测酒精的2值。
实验4落球法测量液体的粘滞系数

实验4 落球法测量液体的粘滞系数液体粘滞系数又叫内摩擦系数或粘度,是描述流体内摩擦力性质的一个重要物理量,它表征流体反抗形变的能力,只有在流体内存在相对运动时才表现出来。
液体在管道中的传输、机械润滑油的选择、物体在液体中的运动等与都与液体的粘滞系数有关。
液体粘滞系数可用落球法,毛细管法,转筒法等测量方法,其中落球法适用于测量粘滞系数(以下简称η)较高的液体。
η的大小取决于液体的性质与温度,温度升高η值将迅速减小。
如蓖麻油在室温附近温度改变1℃时η值改变约10%。
因此,测定液体在不同温度η值才有意义,欲准确测量液体的粘滞系数,必须精确控制液体温度。
1 [实验目的]1.1 观察液体的内摩擦现象,学会用落球法测量不同温度下蓖麻油的粘滞系数。
1.2 了解PID 温度控制的原理。
1.3练习用停表计时,用螺旋测微器测直径。
2 [实验仪器]变温粘度仪,ZKY-PID 温控实验仪,停表,螺旋测微计,钢球若干。
3 [仪器介绍]3.1落球法变温粘度仪变温粘度仪的外型如图11-1所示。
待测液体装在细长的样品管中,能使液体温度较快的与加热温达到平衡,样品管壁上有刻度线,便于测量小球下落的距离。
样品管外的加热水套连接到温控仪,通过热循环水加热样品。
底座下有调节螺钉,用于调节样品管的铅直。
3.2开放式PID 温控实验仪温控实验仪包含水箱,水泵,加热器,控制及显示电路等部分。
温控试验仪内置微处理器,带有液晶显示屏,具有操作菜单化,能根据实验对象选择PID 参数以达到最佳控制,能显示温控过程的温度变化曲线和功率变化曲线及温度和功率的实际值,能存储温度及功率变化曲线,控制精度高等特点。
开机后,水泵开始运转,显示屏显示操作菜单,可选择工作方式输入序号及室温,设定温度及PID 参数使用▲▼键选择项目,▲▼键设定参数,按确认键进入下一屏,按返回键返回上一屏。
进入测量界面后,屏幕上方的数据栏从左至右依次显示序号,设定温度,初始温度,当前温度,当前功率,调节时间等参数。
实验液体粘滞系数的测定

实验液体粘滞系数的测定一、实验介绍气体和液体统称为流体。
若流体各层之间作相互运动时,相邻两层间有内摩擦力存在,则将具有此性质的流体称为粘性流体。
现实中,酒精、甘油、糖浆之类的流体都是粘性流体。
而粘性液体的粘滞性在液体(例如石油)管道输送以及医药等方面都有重要的应用。
现代医学发现,许多心脑血管疾病与血液粘滞系数有关,血液粘滞会使流入人体器官和组织的血流量减少、血流流速减缓,使人体处于供血和供氧不足的状态中,可能引发多种心脑血管疾病。
所以,血液粘滞系数的大小成了人体血液健康的重要标志之一,对于粘滞系数的测定和分析就具有非常重要的现实意义。
通常测定液体粘滞系数的方法有很多,如落球法、落针法、比较法等等。
本实验采用奥氏粘度计测量酒精的粘滞系数。
奥氏粘度计是利用比较法制成的,适用于测定液体的比较粘滞系数,即两种不同液体都采用此仪器测量,如果其中一种液体的粘滞系数已知,则通过就可获得另一种液体的粘滞系数。
此仪器是测量液体粘滞系数的常用仪器。
二、实验目的1.掌握用奥氏粘度计测定粘性流体的粘滞系数.2.了解泊肃叶公式的应用。
3.了解比较法的好处.三、实验器材奥氏粘度计、温度计、秒表、洗耳球、量筒、量杯、刻度移液管(滴定管)、蒸馏水、酒精等。
四、实验原理气体和液体统称为流体。
若流体各层之间作相互运动时,相邻两层间有内摩擦力存在,则将具有此性质的流体称为粘性流体。
现实中,酒精、甘油、糖浆之类的流体都是粘性流体。
粘性流体的运动状态有层流(laminar flow)、湍流(turbulent flow)。
所谓层流,即流体的分层流动状态。
当流体流动的速度超过一定数值时,流体不再保持分层流动状态,而有可能向各个方向运动,即在垂直于流层的方向有分速度,因而各流体层将混淆起来,并有可能形成湍流,湍流显得杂乱而不稳定,这样的流动状态称为湍流。
对于粘性流体在流动时相邻流层之间的内摩擦力又称为粘性力。
并且根据牛顿粘滞定律,粘性力f的大小与两流层的接触面积S以及接触处流层间的速度梯度dsdx成正比,具体有如下关系式:ds f S dxη= (1) 式中,比例系数η称为流体的粘度。
液体粘滞系数的测定

液体粘滞系数的测定在流动的液体中,各流体层的流速不同,则在相互接触的两个流体层之间的接触面上,形成一对阻碍两流体层相对运动的等值而反向的摩擦力,流速较慢的流体层给相邻流速较快的流体层一个使之减速的力,而该力的反作用力又给流速较慢的流体层一个使之加速的离,这一对摩擦力称内摩擦力或粘滞阻力,流体的这种性质称为粘滞性。
不同流体具有不同的粘度,同种流体在不同的温度下其粘度的变化也很大。
测定粘度在化学、医学、水利工程、材料科学、机械工业和国防建设中有着重要意义。
从实验中得到的粘滞定律:粘滞力f 的大小与所取流体层的面积S ∆和流体层之间的速度空间变化率dr du 的乘积成正比,即drdu s f ∆=η。
其中η为粘滞系数(也称内摩擦系数),它决定于液体的性质和温度,对液体而言,它随温度的升高而迅速减少。
η的国际单位:s Pa ⋅但是根据粘滞定律直接测量难度很大,一般都采用间接测量的方法。
测量液体粘滞系数的方法有很多种,如常用的落球法、落针法、转叶法。
本实验是用变温落针计测量液体在不同温度下的粘度系数。
中空长圆落针在待测液体中垂直下落,通过测量针的收尾速度确定粘度。
采用霍尔传感器和多功能秒表计测量落针的速度,并将粘度显示出来。
对待测液体进行水浴加热,通过温控装置,达到预定的温度。
巧妙的取针和提针装置,使测量过程极为简单。
本实验既适用于牛顿液体,又适于非牛顿液体,还可测定液体密度。
【实验目的】1. 用落针法测液体的粘度系数。
2. 研究液体粘度系数在不同温度下的变化规律。
【实验仪器】PH--IV 型变温粘度器、落针图1 实验仪器实图【实验原理】一个物体在液体中运动时,将受到与运动方向相反的摩擦阻力的作用,这种力即为粘滞阻力。
它是由粘附在物体表面的液层与邻近的液层相对运动速度不同而引起的,其微观机理都是分子之间以及在分子运动过程中形成的分子团之间的相互作用力。
不同的液体这种不同液层之间的相互作用力大小是不相同的。
(完整版)粘滞系数测定实验

实验 液体粘滞系数的测定当液体内各部分之间有相对运动时,接触面之间存在内摩擦力,阻碍液体的相对运动,这种性质称为液体的粘滞性,液体的内摩擦力称为粘滞力。
粘滞力的大小与接触面面积以及接触面处的速度梯度成正比,比例系数η称为粘度(或粘滞系数)。
对液体粘滞性的研究在流体力学,化学化工,医疗,水利等领域都有广泛的应用,例如在用管道输送液体时要根据输送液体的流量、压力差、输送距离及液体粘度,设计输送管道的口径。
测量液体粘度可采用落球法,毛细管法(奥氏粘滞计),转筒法等方法。
本实验根据所用方法的不同,分成两个部分,第一部分采用落球法测定变温情况下的液体(蓖麻油)粘滞系数,第二部分则是采用毛细管法测定室温下的液体粘滞系数(该方法比较适合用于生物医学应用,比如测量血液的粘度)。
实验一 落球法测变温液体的粘滞系数落球法(又称斯托克斯法)适用于测量粘度较高的液体。
一般而言,粘度的大小取决于液体的性质与温度,温度升高,粘度将迅速减小。
例如对于蓖麻油,在室温附近温度改变C 1︒,粘度值改变约10%。
因此,测定液体在不同温度的粘度有很大的实际意义,欲准确测量液体的粘度,必须精确控制液体温度。
实验中,小球在液体中下落的时间可用秒表来测量。
一、实验目的1.用落球法测量不同温度下蓖麻油的粘度。
2.了解PID 温度控制的原理。
3.练习用秒表计时,用螺旋测微计测量小球直径。
二、实验原理在稳定流动的液体中,由于各层的液体流速不同,互相接触的两层液体之间存在相互作用,流动较慢的液层阻滞着流动较快的液层运动,所以产生流动阻力。
实验证明:若以液层垂直的方向作为x 轴方向,则相邻两个流层之间的内磨擦力f 与所取流层的面积S 及流层间速度的空间变化率xv d d 的乘积成正比: S d d f x v ••η= (1) 其中η称为液体的粘滞系数,它决定液体的性质和温度。
粘滞性随着温度升高而减小。
如果液体是无限广延的,液体的粘滞性较大,小球的半径很小,且在运动时不产生旋涡,那么,根据斯托克斯定律,小球受到的粘滞力f 为:v r f •••=ηπ6 (2) 式中η称为液体的滞粘系数,r 为小球半径,v 为小球运动的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
液体粘滞系数的测量与研究一 实验目的1.了解用斯托克斯公式测定液体粘滞系数的原理,掌握其适用条件。
2.学习用落球法测定液体的粘滞系数。
3.熟练运用基本仪器测量时间、长度和温度。
4.掌握用外推法处理实验数据。
二 实验仪器液体粘滞系数仪、螺旋测微器、游标卡尺、钢板尺、钢球、磁铁、秒表、温度计。
三 实验原理当物体球在液体中运动时,物体将会受到液体施加的与其运动方向相反的摩擦阻力的作用,这种阻力称为粘滞阻力,简称粘滞力。
粘滞阻力并不是物体与液体间的摩擦力,而是由附着在物体表面并随物体一起运动的液体层与附近液层间的摩擦而产生的。
粘滞力的大小与液体的性质、物体的形状和运动速度等因素有关。
根据斯托克斯定律,光滑的小球在无限广延的液体中运动时,当液体的粘滞性较大,小球的半径很小,且在运动中不产生旋涡,那么小球所受到的粘滞阻力f 为vd f πη3= (1)式中d 是小球的直径,v 是小球的速度,η为液体粘滞系数。
η就是液体粘滞性的度量,与温度有密切的关系,对液体来说,η随温度的升高而减少(见附表)。
本实验应用落球法来测量液体的粘滞系数。
小球在液体中做自由下落时,受到三个力的作用,三个力都在竖直方向,它们是重力、浮力、粘滞阻力f 。
开始下落时小球运动的速度较小,相应的阻力也小,重力大于粘滞阻力和浮力,所以小球作加速运动。
由于粘滞阻力随小球的运动速度增加而逐渐增加,加速度也越来越小,当小球所受合外力为零时,趋于匀速运动,此时的速度称为收尾速度,记为v 0 。
经计算可得液体的粘滞系数为2018)(v gd ρρη-=(2) 式中0ρ是液体的密度,ρ是小球的密度,g 是当地的重力加速度。
可见,只要测得,即可由(2)式得到液体的粘滞系数。
但是注意,上述推导包括(1)、(2)式都在特定条件下方才适用(见原理的第一段黑体字部分),通过对实验仪器和实验方法的设计,这些条件大多数都可以满足或近似满足(结合本实验所用仪器和实验步骤,思考一下哪些条件被满足,是如何做到的),唯独“无限广延”在实验中是无法实现的。
因此,为了准确测出液体的粘滞系数,我们需要进一步对实验进行设计,下面将分别在实验上采用外推法和在理论上对计算公式进行修正进行测量,这些方法体现了实验手段和理论手段在物理实验中的作用和特点,同时反映出针对同一个问题如何在实验中层层深入,不断提高测量结果的准确程度,而这正是物理学实验的魅力所在。
四实验设计4.1 外推法的实验设计与测量4.1.1横向“无限广延”之外推h图1多管落球法测量液体粘滞系数仪用上述落球法测量出来的收尾速度与液体尺度有关,那么我们不妨在实验中就对液体尺度的依赖关系进行定量研究,如果该依赖关系存在规律,则有可能对我们的测量带来帮助或指引。
由于上述讨论中对液体的形状没有做具体要求,我们在实验中采用试管作为容器,这样得到具有轴对称性的液柱,于是我们要研究的就是液柱的尺度大小对的影响。
为简化测量,可先固定液柱的高度,改变液柱横截面积,这可以用一组直径不同的试管来实现(见图1)。
将这些试管装上同种待测液体,安装在同一水平底板上,每个管子上都用两条刻线A、B标出相等的间距,记为(上刻线A与液面间应留有适当距离,使得小球(用直径最小的球)下落经过A刻线时,可以认为小球已进入匀速运动状态)。
依次测出小球通过管中的两刻线A、B 间所需的时间,各管的直径用表示,则通过大量的实验,我们就可以得到与之间的关系。
已有的数据表明,与成线性关系。
即以为纵坐标轴,以为横坐标轴,根据实验数据可以作出一条直线(动手画画看!)。
这是个好消息,因为如果延长该直线与纵轴相交,其截距对应的是时的,而正好对应,于是我们用这种方法就可以外推出在横向“无限广延”的液体中,小球匀速下落通过距离所需的时间。
所以有(3)将(3)代入(2),即可求出液体的粘滞系数:ht d g 18)(020⋅-=ρρη (4) 若式中各量均采用国际单位,则的单位为帕•秒,记为 ,。
误差计算:ddh h t ∆+∆+∆=∆=2t E 00ηη(5) (6)最终测量结果表示成:ηηη∆±= (7)4.1.2纵向“无限广延”之外推为满足在纵向上“无限广延”这一条件,则小球的收尾速度v 还应修正为)1(0ldk v v += (8)其中,k 为常数,l 为液体的深度。
将(3)式代入(8)式,可得lv khd v h t 10⋅+=(9) (9)式中,v 、h 、k 及d 均为常量,故0t 与l1满足线性关系。
t图2 t 与1/D 图t 0根据(9)式,如果向各圆管中加入适量的液体,在保持各圆管中的液体深度均为1l 时,利用多管落球法之∞→D 时外推出的小球匀速下落距离h 所需的时间01t ,当各管中的液体深度均为2l 、3l ,…,∞→D 时,小球匀速下落距离h 所需的时间02t ,03t ,…,作lt 10-图,并进行线性拟合,延长直线与纵轴相交,纵截距为'0t ,则'0t 就是当∞→D (横向为无限广延)且∞→l (纵向为无限广延)时,小球匀速下落h 所需要的时间,故'0t hv =(10) 将(10)式代入(2)式,可得ht gd 18)('20⋅-=ρρη (11)(11)式即为当液体在横向和纵向均满足“无限广延”条件下测量液体粘滞系数的计算公式。
4.1.3 小球半径无限小之外推由于在实验中采用玻璃圆筒作为容器盛放蓖麻油,这与斯托克斯定律第二假定所要求的“在无限广延的媒质中”的环境不同。
由流体力学可知:小球在容器中的下降速度要比在广延液体中的下降速度小,两者相差一个修正因子。
密立根通过实验得到的修正因子为:)3.31)(4.21(lr R r++=β (12)式中R 和r 分别为容器和小球的半径,l 为筒中液体的深度。
可见,对同样大小的球而言,圆筒半径R 越小,液体的深度l 越小,修正因子β越大;同样,对同一圆筒及一定深度的液体,球的半径r 越大,β就越大。
于是,可以想象,当小球的直径趋于零时,器壁对小球的影响亦将t 0图2 t 0与1/l 图t 0’趋于零。
此时,量筒中的液体相对小球来说,也就可理解为“无限广延”的液体了。
但是直径趋于零的小球是无法实现的,此时如果运用外推方法,就可以帮助我们实现这种理想的状况。
由于液体的深度比量筒的直径大得多,在不考虑量筒的深度对落球的影响时,修正因子)4.21()4.21(Dd R r +=+=β (13)则,液体粘度η与量筒直径D 及小球直径d 有如下关系)4.21(0Dd +=ηη (14)式中0η是液体的真实粘滞系数,η是用落球法测量得到的粘滞系数。
从(14)式可看出,η和d 成线性关系,因此可以用不同直径的小球测出若干个η(此时,D 和l 尽可能大),并以η为纵轴,d 为横轴作出η一d 图线,再进行线性外推。
当→d 0时,直线在纵轴上的截距就是液体真实的粘滞系数。
4.2 理论修正4.2.1 边界条件的理论修正上述外推法虽然能比较准确地测量出液体的粘滞系数,但小球的运动状态也会对测量结果产生影响,得到的测量结果仍存在未知误差。
那么有无更好的方法来解决这个问题呢?让我们从头开始换个方式思考,既然容器的边界效应对球体受到的粘滞力有影响,可否一开始就从理论上将液体尺度的影响因素考虑进来?实际上是可以的,通过流体力学的分析可以证明,在其他条件不变的前提下,对于本实验中采用的是具有轴对称性的柱状液体,不考虑小球运动状态的影响时,小球在其中所受粘滞力公式(1)应修正成:)3.31)(4.21(3lrR r vd f ++=πη (15) 同样用落球法进行测量,粘滞系数应相应地表示成:())/3.31)(/4.21(11820l r D d htgd ++•-=ρρη(16)其中,为容器径,为量筒待测液体的总高度,r 为小球的半径。
4.2.2 小球运动状态的修正——雷诺数修正不仅液体的边界条件对小球在其中的运动有较大影响,物体在均匀稳定液体中的运动实际上还受到雷诺数的影响。
雷诺数是描述流体运动或物体在均匀稳定液体中运动的一个重要的无量纲参数:ηρdv R e ⋅⋅≡0 (17) 其中是液体密度,是物体运动速度或流体稳定流速,d 是运动物体的线性尺度,对本实验而言即小球直径,是液体的粘滞系数。
雷诺数的大小决定了物体在液体中的运动方式,一般当(相当于小尺度物体在低密度、高粘滞系数的液体中进行低速运动)时称低雷诺数运动,此时液体中的粘滞力起主导作用,而液体的惯性力可以忽略,运动物体感受到周围液体以层流方式流动;而当时(相当于大尺度物体在高密度、低粘滞系数的液体中进行高速运动)称物体做高雷诺数运动,此时液体的惯性力作用逐渐增强,尤其是当雷诺数超过某个阈值时(一般)液体中的粘滞力可以忽略,物体感受到周围液体以湍流方式流动,展现出非常复杂的混沌效应。
由于雷诺数对物体在液体中的运动影响很大,即便是对小雷诺数下的运动,公式(15)也需要做进一步修正,此时粘滞力在(15)式的基础上还要再乘上一个与雷诺数有关的修正项:)1080191631)(3.31)(4.21(32+-+++=e e R R l r D d vd f πη (18) 由上式可见,当较小时,可以只考虑第一级修正,随着逐渐增大,需要将第二、第三甚至更多级的修正考虑进来,而当时,公式中的修正项会变得比主项还大,这表明此时流体的运动已经产生质的变化,基于斯托克斯公式的(18)式不再适用。
在实际操作中,一般当时我们仅考虑第一级雷诺数修正(为什么?),此时粘滞系数计算公式可以写成(试着推导一下):())1631(1)/3.31)(/4.21(11820eR l r D d htgd +•++•-=ρρη(19)五 实验容1. 液体横向和纵向“无限广延”之外推法测量蓖麻油的粘滞系数提示:采用直径最小的刚球,在不同的液体深度下(约4个深度l 值),分别测量4个管子中小球下落液体高度h (15cm 左右,具体数据需要测量)所用的时间(选择5-6个刚球在同一个管子中下落,记录每个小球下落时间,该过程不可打捞落入液体中的刚球,否则会改变液体的流动状态)。
2.小球半径无限小之外推法测量蓖麻油的粘滞系数提示:在保证所用管子直径最大和所装液体最深时,利用直径不同的小球测量其在液体中下落高度h 所需的时间。
3. 利用理论修正公式(19)测量和计算蓖麻油的粘滞系数提示:管子的直径D 最大,液体的深度l 最深,小球的半径r 最小。
六 操作说明1.用螺旋测微器测量小钢球的直径d (选不同方向测量5次后取平均)。
2.用游标卡尺测量各管子的直径D (选不同方向测量5次后取平均)。
3.用钢板尺测量管子上A 、B 刻线间的距离(选不同方向测量5次后取平均)。
