4第三章相似理论
泵与风机部分思考题与习题答案.(何川_郭立君.第四版)

泵与风机(思考题答案)绪论3.泵与风机有哪些主要的性能参数?铭牌上标出的是指哪个工况下的参数?答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定工况下的各参数5.离心式泵与风机有哪些主要部件?各有何作用?答:离心泵叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能。
吸入室:以最小的阻力损失引导液体平稳的进入叶轮,并使叶轮进口处的液体流速分布均匀。
压出室:收集从叶轮流出的高速流体,然后以最小的阻力损失引入压水管或次级叶轮进口,同时还将液体的部分动能转变为压力能。
导叶:汇集前一级叶轮流出的液体,并在损失最小的条件下引入次级叶轮的进口或压出室,同时在导叶内把部分动能转化为压力能。
密封装置:密封环:防止高压流体通过叶轮进口与泵壳之间的间隙泄露至吸入口。
轴端密封:防止高压流体从泵内通过转动部件与静止部件之间的间隙泄漏到泵外。
离心风机叶轮:将原动机的机械能传递给流体,使流体获得压力能和动能蜗壳:汇集从叶轮流出的气体并引向风机的出口,同时将气体的部分动能转化为压力能。
集流器:以最小的阻力损失引导气流均匀的充满叶轮入口。
进气箱:改善气流的进气条件,减少气流分布不均而引起的阻力损失。
9.试简述活塞泵、齿轮泵及真空泵、喷射泵的作用原理?答:活塞泵:利用工作容积周期性的改变来输送液体,并提高其压力。
齿轮泵:利用一对或几个特殊形状的回转体如齿轮、螺杆或其他形状的转子。
在壳体内作旋转运动来输送流体并提高其压力。
喷射泵:利用高速射流的抽吸作用来输送流体。
真空泵:利用叶轮旋转产生的真空来输送流体。
第一章1.试简述离心式与轴流式泵与风机的工作原理。
答:离心式:叶轮高速旋转时产生的离心力使流体获得能量,即流体通过叶轮后,压能和动能都得到提高,从而能够被输送到高处或远处。
流体沿轴向流入叶轮并沿径向流出。
轴流式:利用旋转叶轮、叶片对流体作用的升力来输送流体,并提高其压力。
流体沿轴向流入叶轮并沿轴向流出。
第三章相似理论

第三章相似理论相似定律 比转速无因次性能曲线 通用性能曲线 问题的提出① 实型设计一模型设计设计任务:结构一要求:造价低、耗功少、效率高 反复设计一试验一修改一受限;② 相似设计利用优良的模型进行相似设计,设计选型的捷径 ③ 工程实际问题:不能满足要求:出力不足一改造裕量过大转速变化时进行性能的换算 一、 相似条件几何相似:通流部分对应成比例 一一前提条件; 运动相似:速度三角形对应成比例 一一相似结果;动力相似:同名力对应成比例一一根本原因。
(但Re > 105,已自模化) 二、 相似三定律1、流量相似定律(由3=con st. 表述:几何相似机泵与风机,在相似的工况下, 方、转速及容积效率的一次方成正比。
2、能头相似定律表述:直径及转速的二次方、以及流动效率(流体密度)的一次方成正比。
3、功率相似定律(由P 二〜时 1000 P—5 3 二 const D :n 3/§ 3-1§ 3-2D 2b^ 2r v q vq v2u-U1 2u ]h 及p=?gH 推得)P二 con st.Hconstj似机泵与风机, 在相似的工况D ,,其;程(或全压)与叶轮推得)其流量与叶轮直径的三次推得)表述:几何相似机泵与风机,在相似的工况下,其轴功率与流体密度的一 次方、叶轮直径五次方、转速的三次方成正比;与机械效率的一次方成反 比。
4、相似定律的几点说明:(1) 该三定律应用存在困难(原因是: V 、 h 和 m 未知) (2) 等效的相似三定律当实型和模型的几何尺度比w 5,相对转速比w 20%寸,实型和模型所对应 的效率近似相等,可得等效的相似三定律:三、相似定律的应用1、变密度「时性能参数的换算 一般产品样本的标准条件: 一般通风机:1atm=101325Pa 20 C 相对湿度:^=50% 锅炉引风机:1atm=101325Pa 200E 相对湿度:f q v = q V0, 、'石 T ,L"丿p /p0 /% 101325T 丿® P 二 P / P 。
相似原理与量纲分析
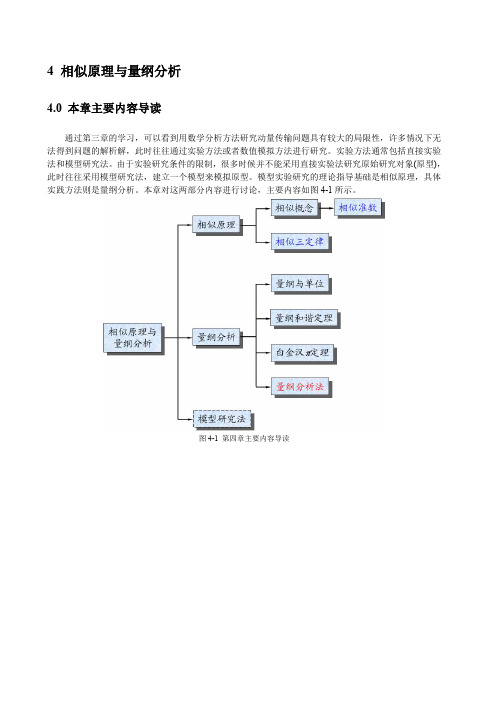
4 相似原理与量纲分析4.0 本章主要内容导读通过第三章的学习,可以看到用数学分析方法研究动量传输问题具有较大的局限性,许多情况下无法得到问题的解析解,此时往往通过实验方法或者数值模拟方法进行研究。
实验方法通常包括直接实验法和模型研究法。
由于实验研究条件的限制,很多时候并不能采用直接实验法研究原始研究对象(原型),此时往往采用模型研究法,建立一个模型来模拟原型。
模型实验研究的理论指导基础是相似原理,具体实践方法则是量纲分析。
本章对这两部分内容进行讨论,主要内容如图4-1所示。
图4-1 第四章主要内容导读4.1 相似原理4.1.1相似的基本概念遵循同一物理方程的现象称为同类现象。
如果两个同类现象对应物理量成比例(在对应的时空点,各标量物理量的大小成比例,各向量物理量大小成比例、方向相同),称这两个现象为相似现象。
对于动量传输问题,模型(model)与原型(prototype)之间必须满足如下相似条件才能成为相似现象(图4-2):(1)几何相似。
几何相似又称为空间相似,要求模型与原型外形完全一样;对应线段成比例;对应夹角相等;有粗糙度时粗糙度相似;(2)运动相似。
要求模型与原型对应流线几何相似;对应点速度大小成比例,方向相同;(3)动力相似。
又称为受力相似,要求模型与原型的两个对应流场受同种外力作用;对应点上对应作用力成比例。
上述三类相似中,几何相似是运动相似和动力相似的前提与依据,动力相似是决定二个流动相似的主导因素,运动相似则是几何相似和动力相似的表现。
相似的流动一定是同时满足几何相似、运动相似和动力相似的流动。
完全的几何相似一般并不容易达到。
例如,采用小尺寸模型模拟原型时,除非能够将模型表面加工得比原型光滑得多,否则无法按照原型的表面粗糙度成比例缩小而加工出模型的表面粗糙度;在研究沉淀物的传输时,不能将河床上的物质按比例缩小成粉末,因为细微的粉末之间有内聚力,无法模拟砂粒的特性;在研究河流流动时,水平方向的尺寸远大于垂直方向的尺寸,受实验空间的限制必须对水平方向采用较大比例尺进行缩小,如果将同样的比例尺用于垂直方向,有可能产生太浅的流动,导致毛细作用影响明显,而且河床的斜率太小会使流动保持层流。
流体力学4-3.4相似定理

l
1
p 1 m
2、弗劳德模型律
按弗劳德准则 (Fr)p=(Fr)m
g p l p g m lm
2 p 2 m
p g pl p m gmlm
1/ 2
g l
1/ 2
通常实验在地球表面进行,各地g=c
g
gp gm
1
1/ 2 l
若要同时满足Re、Fr准则
l
1
1/ 2 l
l
1
1
l
3/ 2
l 1
1/ 2 l
模型实验想做到与原型完全流动相似是困难的, 一般只能达到近似相似,就是保证对流动起主要作 用的力相似,这就是模型律的选择问题。 实际模型试验中,根据流动的特点,抓住主要矛盾。 在几何相似的基础上,只满足雷诺模型律,或者只满足 弗劳德模型律,或者两者都不满足(处于自模区,只需 满足几何相似),即可近似认为流动相似,在主要方面 满足试验要求。
2、举例说明由重力、粘滞力起主要作用的水流。
粘滞力:层流状态下的、管道、隧洞中的有压流动和 潜体绕流问题等。 重力:堰坝溢流、孔口出流及明槽流动及处于阻力平 方区的有压隧洞等。
第四章作业 2、4、6、8、 10、12
up
l t
p / t p p tm l a 2 am m / tm m t p t t
ap
3.动力相似(dynamic similarity)
指原型和模型流动相应点处质点受同名力作用,力 的方向相同,大小成比例。
分别以符号T、G、P、Tw和I代表影响流体运动的作 用力,如粘滞力、重力、压力、表面张力和惯性力,则 有 Tp Gp Pp Ip 力的比尺 F
泵与风机课后习题答案(标准版)

扬程:单位重量液体从泵进口截面到泵出口截面所获得的机械能。
流量qv:单位时间内通过风机进口的气体的体积。
全压p:单位体积气体从风机进口截面到风机出口截面所获得的机械能。
轴向涡流的定义:容器转了一周,流体微团相对于容器也转了一周,其旋转角速度和容器的旋转角速度大小相等而方向相反,这种旋转运动就称轴向涡流。
影响:使流线发生偏移从而使进出口速度三角形发生变化。
使出口圆周速度减小。
叶片式泵与风机的损失:(一)机械损失:指叶轮旋转时,轴与轴封、轴与轴承及叶轮圆盘摩擦所损失的功率。
(二)容积损失:部分已经从叶轮获得能量的流体从高压侧通过间隙向低压侧流动造成能量损失。
泵的叶轮入口处的容积损失,为了减小这部分损失,一般在入口处都装有密封环。
(三),流动损失:流体和流道壁面生摸差,流道的几何形状改变使流体产生旋涡,以及冲击等所造成的损失。
多发部位:吸入室,叶轮流道,压出室。
如何降低叶轮圆盘的摩擦损失:1、适当选取n和D2的搭配。
2、降低叶轮盖板外表面和壳腔内表面的粗糙度可以降低△Pm2。
3、适当选取叶轮和壳体的间隙。
轴流式泵与风机应在全开阀门的情况下启动,而离心式泵与风机应在关闭阀门的情况下启动。
泵与风机(课后习题答案)第一章1-1有一离心式水泵,其叶轮尺寸如下:1b =35mm, 2b =19mm, 1D =178mm, 2D =381mm, 1a β=18°,2a β=20°。
设流体径向流入叶轮,如n=1450r/min ,试画出出口速度三角形,并计算理论流量,V T q 和在该流量时的无限多叶片的理论扬程T H ∞。
解:由题知:流体径向流入叶轮 ∴1α=90° 则:1u =1n60D π=317810145060π-⨯⨯⨯= (m/s )1V =1m V =1u tg 1a β=⨯tg °= (m/s )∵1V q =π1D 1b 1m V =π⨯⨯⨯ (3m /s ) ∴2m V =122V q D b π=0.0860.3810.019π⨯⨯= (m/s ) 2u =2D 60n π=338110145060π-⨯⨯⨯= (m/s )2u V ∞=2u -2m V ctg 2a β=⨯ (m/s )T H ∞=22u u V g ∞=28.9118.529.8⨯= (m ) 1-2有一离心式水泵,其叶轮外径2D =220mm,转速n=2980r/min ,叶片出口安装角2a β=45°,出口处的轴面速度2m v =s 。
流体力学第三章(相似原理与量纲分析)

它们所反映的是没有量纲(单位)的数,称为无量纲数
l Sr 斯特劳哈尔数 tu
欧拉数
雷诺数
Vl
Re
p Eu 2 V
V2 Fr 弗劳德数 gl
25
2w 2w 2w w w w w p u v w 2 2 2 g t y z z z x x y
2伯努利方程5简单情况下的ns方程的准确解3第一节流体力学的模型实验和相似概念第二节相似判据第三节无量纲方程第四节特征无量纲数第五节量纲分析和定理主要内容第三章相似原理与量纲分析4实验数据的简化处理设计实验的基本要求理论流体力学第一二章实验流体力学普通实验数值实验5第一节流体力学的模型实验和相似概念流体力学实验
13
通常可以采用两种方法来确定动力相似判据: (一)方程分析法:描述流体的运动方程应该是一致的。 从而得到必须满足的关系式,即相似判据;
(二)量纲分析方法:以量纲分析为基础的一种方法。
14
方程分析法
动力相似判据
前提条件:假定原型流场和模型流场是满足几何相似、 时间相似和运动相似的,考虑不可压缩粘性流体的简单 情况。 首先,给出有关相似常数的定义:
此时,两个流场称之为是流场 相似或运动相似的。流场相似 也就是在两流场对应点的速度 的大小、方向成常数比例。
Q P
9
动力相似
动力相似:要求在两流场相应点上各动力学变量 成同一常数比例。 例如原型流场和模型流场在运动过程中受到的 质量力、粘性力等动力学变量成正比。
10
几何相似 时间相似 有比较清晰的关系表达式 运动相似 (可直接观测) 判断什么条件下两流场才满足动力相似??
u = U u’
流体力学相似原理和量纲分析

称为不可压缩流体定常流动的力学相似准则。
11
四、马赫数
当考虑流体压缩性时,弹性力起主要作用 F=EA
在因次上 [F ] [E][A] El2
代入(4 —10)中的 F 时,则
Enln2
nln2Vn2
Emlm2
mlm2Vm2
即 En Em
nVn2 mVm2
对可压缩流体,音速a
E
, 因此
E
1 a2
欲使雷诺数相等,将有 n lm vn m ln vm
1
1
欲使弗劳德数相等,将有
n m
ln lm
2
gn gm
2
v l
l
1 2
v
l 32
这在技术上很难甚至不可能做到。实际中,常常要对所研 究的流动问题作深入的分析找出影响流动问题的主要作用力, 满足一个主要力的相似而忽略其它次要力的相似。
15
例:对于管中的有压流动及潜体绕流等,只要流动的雷 诺数不是特别大,一般其相似条件依赖于雷诺准则数。
m gmlm3
mlm
2 2 m
简化后得
2 n
m2
(4—14)
式中
2
Fr
gnln gmlm
,称为弗劳德 Froude 数。
gl
物理意义:
惯性力与重力之比。
9
三、欧拉数
研究淹没在流体中的物体表面上的压力或压强分布时,
起主要作用的力为压力 F pA 。
在因次上为
F pA Pl 2
将其代替式(4—10)中的F时,则
纲数之间的函数式(4—22),这就是泊金汉 E.Buckingham
定理。因为经常用 表示无量纲数,故又简称 定理。
相似理论王璐2013452059

一般系统 General System
(1)系统结构相似 (2)系统功能、性能相似 (3)系统人机界面相似 (4)系统存在和演化相似
Similarity Theory
(1)连续系统动力学 (2)离散系统动力学 (3)场 (4)概率、模糊集、粗糙集 (5)图的相似
Complex System (1)非线性相似 (2)涌现性相似 (3)自治性相似 (4)突变性相似
复杂系统
Methods
(1)模式相似方法(统计决策法和句法或结 构法) (2)模糊相似方法 (3)组合相似方法(个体满足未必系统整体 满足,综合补偿处 理) (4)坐标变换相似方法(运动:飞行器、视 景系统)
Steps
Step 4 Step 3 Step 2 Step 1
根据相似第二定理 建立相似准则
1)物理模型的建立 2)模型中过程及方法 模拟
Engineering Technology
工程技术学
1)进行相似设计工程, 相 似制造工程, 相似管理工 程的研究。 2)进行相似工程机械制 造、电子、电器产品的 研制, 以及人工智能、机 器人的制造。
Systems
实物模型 Physical prototype (1)几何相似 (2)运动学相似 (3)动力相似 数学模型 Mathematical model
相似理论 Similarity Theory
主讲人:王璐
Definition
相似理论是说明自然界和工程中各相似现象 相似原理的学说。是研究自然现象中个性与共性 ,或特殊与一般的关系以及内部矛盾与外部条件 之间的关系的理论。它是模型实验的理论基础。 主要内容是相似三定理。两大分支为量纲分析法 和方程分析法。一般有这样几种类型:几何相似、 模拟、数学相似、感觉信息相似、逻辑思维相似、 生理相似等。
第三章 相似理论(1w)

Pm
Pp
ρ p q vp H pη mm η vm η hm = ρ m q vm H m η mp η vp η hp
5
功率相似定律: 功率相似定律:
D2 p = D Pm 2 m
np ρ p n ρ m m
3
η mm η mp
相似的泵与风机的功率之比: 相似的泵与风机的功率之比: 与叶轮尺寸之比的5次方成正比; 与叶轮尺寸之比的5次方成正比; 与转速的比值的3次方成正比; 与转速的比值的3次方成正比; 与流体的密度成正比 ; 与机械效率的一次方成反比. 与机械效率的一次方成反比.
D2 p = D 2m
n p η vp n η m vm
2,扬程(全压)相似定律 扬程(全压)
u2 v2u u1v1u u2 v2u H = H Tη h = ηh = ηh g g
Hp Hm
运动相似: 运动相似:
=
u2 p v2up η hp
u2 p v2up u2 m v2um
ns =
3.65n qv H
3 4
比转数应用
当ns 增加,H降低,qv 增加,D2 减小, b2增大,叶轮短而宽. 当D2/D1 降低到一定数值后,叶轮前后 盖板处的流线长度差别很大,容易引起 二次回流,必须采用斜切,使出口倾斜, 从而导致叶轮向轴流式过渡.
1,比转数作为一个综合特征数 是唯一的,对应最高效率点的 参数(从性能曲线上看,对同 一台泵,可以计算无数个ns数 值,但比转数本身是唯一的) 2,ns按单级单吸导出,当单级 双吸时,流量为qv/2;多级单吸 双吸时,流量为qv/2;多级单吸 时,扬程为H/i;多级泵第一级 时,扬程为H/i;多级泵第一级 叶轮双吸.
( H / i)
第三章相似定律(2)剖析

二、风机的无因次性能曲线
上面所得的无因次比例常数“ p ”、“ P ”、“ qv ”是 取决于相似工况点的函数,不同的相似工况点,有不同 的一组 “ ”、“ qv ”值。将这种关系, p P ”、“ 绘制成曲线,加上效率曲线,就是“无因次曲线”。
选一台 模型机 转速n 介质
p
第三章 相似理论
2018/10/24
第10页
功率系数
P c3 5 D n 3 2 p .m.
3 P 60 4 c3 2 D2 D2 n 3 4 ( ) 4 60 p . m.
P c3 A u 3 2 2 p . m.
2018/10/24 第18页
n n -q0 V qV
第三章 相似理论
二、通用性能曲线的绘制
2、理论绘制通用性能曲线 工况相似的一系列点其扬程(或全压)与流
量的平方之比为一常数,即
qVB n qVA n0
和
pB n pA n0
2
HB n HA n 0
第4页
第三章 相似理论
一、问题的提出
①已知一个风机的性能曲线,去设计一个相似的风机
作法:根据工程需要,我们可对系列化的相似风机
进行相似换算,并将其性能曲线绘制于同一张图上, 从而实现对同一系列风机性能的比较,以完成风机的 设计、选择工作。
总结:相似定律本身不能够对不同系列的风机进行换算,也就 不可能对不同系列的风机进行性能比较.
2018/10/24
第15页
第三章 相似理论
§3-4 泵与风机的通用性能曲线
一、通用性能曲线 二、通用性能曲线的绘制
第三章量纲分析和相似理论

这几个物理量的量纲是
VLT 1 RL MM FML 2 T
故有
L 1 T M 2p L M q L r T M p q L p r T 2 p
根据量纲齐次原则,必须使
p q 0 ,p r 1 , 2 p 1
解得 所以 从而
似判据:
K F ma
可以看出,对所有相似现象,其相似判据是
相同的,它是一个不变量,因此,可以用相似判
据,来确定两个相似现象中的物理量之间的关系。
K 称为相似准数。
相似第一定理,也可以用文字归纳为,对于
彼此相似的现象,其相似指标为1,或其相似判据
为一不变量,或者说相似系统的相似准数相等。
小结:
➢ 相似常数:在两相似现象中,两个相应的物理量为常数。 对于与此两现象彼此相似的第三个现象中,可以具有不 同的数值。
Cp、 C l、 C 、 C W 、 CA 为相似系数
将式(c)代入(b)式得到
1C CpC Cw l P WlCC C pAPA 将上式与(a)相比较可知,若要两现象相似,必须使
CpCl 1 CCW
Cp 1 CCA
或者
Pl Pl常数
W W
P P常数
A
写成一般形式得:
K1 PWl,K2 PA
• 物理方程量纲的均匀性:一个正确的物理方程, 式中的每项的量纲应该相同,并应采用同一度量 单位。
• 物理方程量纲的齐次性:当量度单位改变时,方 程的结构形式不变的性质。
如果已知有哪些物理量参与某一物理现象,即 可借助量纲分析方法导出某一物理现象的基本方程 式,建立它们之间的一般关系。
例如,已知物体做匀速圆周运动与物体质量M、 圆半径R,线速度V及向心力F诸物理量有关,试求其 关系。首先写出量纲表达式:
流体机械试题

第一章叶片式流体机械概述思考题1、流体具有的能量主要包括哪几个方面?2、什么是流体机械?根据什么将流体机械分为叶片式流体机械和容积式流体机械?3、什么是往复式流体机械和回转式流体机械?试分别列举几种型式。
4、往复式泵的工作原理是什么?5、泵有哪些用途?它在国民经济中的地位和作用如何?6、常用的泵有哪几种分类法?按工作原理分类,水泵有哪几种型式?叶片式水泵主要指哪几种?其作用原理如何?7、叶片泵的过流部件包括叶轮、吸水室和压水室。
不同型式、不同用途的泵,其过流部件也不同,试分别说明它们的种类和型式?8、单级单吸悬臂式离心泵叶轮上的轴向力是怎样产生的?平衡该力通常应用什么措施?多级泵叶轮上的轴向力有哪几种平衡方式,作用原理如何?9、水泵的基本性能参数有哪几个?它们是如何定义的?互相间的关系怎样?10、水泵扬程H是怎样定义的?它同水泵单位质量能Y有何区别?11、区分下述几个物理量的概念及其相互关系。
(1)水泵的工作扬程,装置扬程,泵站扬程;(2)水泵的轴功率,水泵的有效功率,电动机的输入功率、输出功率;(3)水泵效率,传动效率,机组效率,电动机效率,装置效率,泵站效率12、根据泵把原动机的能量传递给被抽送的液体,使液体能量得到增加的定义,有人认为,泵总是把液体由低处抽升到高处。
这种说法对吗?为什么?13、水泵效率包括哪三种?它们的意义是什么?根据其能量损失的原因,试述提高水泵效率的途径。
14、图1-3为一轴流泵抽水装置,试写出水泵扬程的表达式(吸水池行近流速忽略不计)。
图1-1 轴流泵抽水装置图习题一p=323.7kPa,进口真空1、某抽水装置,测得水泵流量Q=18L/s,泵出口压力表读数为d表读数为s p =39.24kPa ,表位差Z ∆=0.8m ,水泵进、出口直径分别为100mm 和75mrn ,电动机进线端功率表读数为d p =10.5kw ,电动机效率d η=95%。
求此时水泵的轴功率P 和效率η(机、泵直联传η=1)。
水轮机作业

水轮机作业第一章绪论(一)选择题1.水轮机的工作水头是()。
(A)水电站上、下游水位差(B)水轮机进口断面和出口断面单位重量水流的能量差2.水轮机的效率是()。
(A)水轮发电机出力与水流出力之比(B)水轮机出力与水流出力之比3.反击式水轮机是靠()做功的。
(A)水流的动能(B)水流的动能与势能4.冲击式水轮机转轮是()。
(A)整周进水的(B)部分圆周进水的5.喷嘴是()水轮机的部件。
(A)反击式(B)冲击式(二)填空题1.水电站中通过____________能转变成旋转机械能,再通过____________把旋转机械能转变成电能。
2.水轮机分为 _____________ 和 _____________两大类。
3.轴流式水轮机分为_____________ 和 _____________两种。
4.水轮机主轴的布置形式有_____________和_____________两种。
5.冲击式水轮机有_____________、_____________ 和_____________三种。
(三)问答题1.水轮机有哪些类型?划分类型的依据是什么?各类水轮机的适用范围是什么?2.混流式与轴流式水轮机主要不同点有哪些?其适用范围有什么不同?3.简述各类水轮机转轮区水流的流动与转轮的结构特点。
4.水轮机的基本工作参数有哪些?有何含义?它们的代表符号和单位是什么?5.反击式与冲击式水轮机各有哪些过流部件?各有何作用?6.水电站和水轮机的特征水头都有哪些?它们之间有何区别?7.冲击式水轮机的特点是什么?类型有哪些?试说明冲击式水轮机适合高水头的原因?8.反击式和冲击式水轮机在能量转换上有何区别?9.贯流式水轮机的特点是什么?类型有哪些?10.灯泡贯流式水轮机有哪些优点?简述灯泡贯流式水轮机基本组成部分。
11.灯泡贯流式机组的布置形式有几种,各自的适用条件是什么?12.灯泡贯流式机组与立式机组有何区别,相比较其优点是什么?13.喷管的作用是什么,其型式有几种?折向器和分流器的作用是什么,二者有何区别?14.水轮机的型号如何表示?各部分代表什么意义?15.解释水轮机型号:?HL160-LJ-520、ZZ560-LH-800、GD600-WP-250、2CJ30-W-120/2×10。
相似理论及应用-part11相似理论基本原理

物理规律
直接实验法 理论分析法
相
模型研究法
相似理论
似
的 基
从相似的概念入手,引入相似准数;
本 概
从相似原理和量纲分析导出相似准数的结构;
念
分析实际问题与实验模型相似的条件;
相似模型的设计
第一章 相似理论基本原理 1.1相似理论与模化
1.1相似理论与模化 1.2相似变换与相对型方程 1.3相似定律及其应用
§0 绪 论
弹药的模型实验是解决弹药工程复杂问题的重要手 段。弹药的相似设计和模拟设计是现代设计方法之一。
模型实验:通常指用简化的可控制的方法再现实际发生 的物理现象。实际发生的现象被称为原型现象,模型实验的 侧重点是再现所述现象的物理本质;只有保证模型实验和原 型中现象的物理本质相同,模型实验才是有价值的。
• 运动相似:以几何相似为前
提。流体质点流过相应的位移
所用时间成比例。
在对应瞬时, 流场速度图相 似,即相应点 速度大小成比 例,方向相同。
长度比尺llp /lm
时间比尺ttp /tm
相似
数学模拟:不同类型现象间的模拟。对应量都遵循着同样 的方程式,具有数学上的相似性。
电场模拟温度场 材料的应力场模拟有限自由度的振动系统 导热现象模拟分子的扩散现象 。。。。。。
a3 b3
L1
b1 c1
b2 c2
b3 c3
L2
c1
⑴
a1
b2
c2
⑵
a2
a a
b b
c c
CL
b3
c
⑶
3
a3
相似常数
相似定数
通过不同的相似常数来 变换相似图像的大小,称为 相似变换。
工程流体力学教学工程流体力学习题+答案(部分)之欧阳学创编

闻建龙主编的《工程流体力学》习题参考答案第一章绪论1-1 物质是按什么原则分为固体和液体两大类的?解:从物质受力和运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。
如空气、水等。
而在同等条件下,固体则产生有限的变形。
因此,可以说:流体不管是液体还是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。
与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。
1-2 何谓连续介质假设?引入连续介质模型的目的是什么?在解决流动问题时,应用连续介质模型的条件是什么?解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。
流体连续性假设是流体力学中第一个根本性假设,将真实流体看成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可看成时间和空间位置的连续函数,使我们有可能用数学分析来讨论和解决流体力学问题。
在一些特定情况下,连续介质假设是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm )内的流动。
1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水和C 020时密度为3856m kg的原油时,移动平板所需的力各为多大?题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水: 233/410416101m N u =⨯⨯=⋅=--δμτ 油: 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ 1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律是直线。
第3章_水轮机的相似理论及模型综合特性曲线

(3-7)
n1
nD1 H
(3-10)
★几点说明:
①通常用 Q1 ,n1 表示水轮机的运行工况。 当几何相似,单位流量和单位转速对应相等 时,两个水轮机工况相似。
但此为在忽略了两者之间效率上的差别,忽 略了通流部件(蜗壳、尾水管)的异形影响,以 及忽略了吸出高和汽蚀影响下得出来的,所以它 们之间的工况相似只能认为是近似相似的。
N 9.81QH 9.81aKV1
2gHs
sin 1D12
1 r
Hs r j
(1)
(1)式可改写为:
N D12 (Hs )3/ 2 j
9.81aK v1
2g sin 1
(2)
同样,对模型水轮机有:
NM D12M (HMsM )3/ 2 jM
9.81a MK v1M
2g sin 1M
(3)
3、 出力相似律 由前(1)式和(2)式整理有:
ns
ne Ne Hr5/4
也有采用最优工况下的比转速作为代表的。
★国内外大都采用比转速进行水轮机的分类,
如表3-1。
每个水轮机都有一个特征比转速,此值是在 设计工况下取得的,用来恒量水轮机的性能。
★我国颁发的水轮机型谱中,对水轮机的转 轮型号就应用ns来表示,它推荐的设计比转速与 设计水头之间的关系为:
3.2 水轮机的相似律、单位参数和比转速
一、水轮机的相似率
同一轮系的水轮机之间进行参数换算时,并不 直接应用前面讲过的相似条件来表示,而是以工况 的相似性来表示。
相似定律:两个水轮机的工况相似,则转轮中 对应点的速度三角形应是相似的,这种相似常以该 工况下的H、Q、n、N、η之间的关系来表示,这些 参数之间的固定关系称为相似律,或相似公式。
4第三章+相似理论在泵与风机中的应用

1.流量相似关系
2.扬程/全压相似关系 3.功率相似关系
Hp
qVp qV
(
Dp D
)
3
np n
Dp np 2 ( ) H D n
Pp P (
pp p
5
p Dp np
np n
(
D
n
)2
p Dp
D
) (
)3
8
第五节 相似律的实际应用
• 一、输送流体密度改变
一般产品样本的标准条件:
•为此,叶轮出口边需做成倾斜的。流动形态从离心式过渡到混流 式。极限情况,D2减小到D2/D0=1时,成为轴流式。叶轮形式引起 性能参数改变,从而导致比转数的改变。因此,可进行分类。 19
表
泵的类型 比转速ns
比转速与叶轮形状和性能曲线形状的关系
离心泵 低比转速 30<ns<80 中比转速 80<ns<150 高比转速 150<ns<300 300<ns<500 500<ns<1000 混流泵 轴流泵
叶轮形状
尺寸比D2 /D0
≈3
≈2.3
≈1.8~1.4
≈1.2~1.1
≈1
叶片形状
柱形叶片
入口处扭曲 出口处柱形
扭曲叶片
扭曲叶片
翼形叶片
性能曲线 形状 20
离心泵 泵的类型 低比 高比 中比转速 转速 转速
混流泵 轴流泵
扬程-流量曲 线特点
关死扬程为设计工 关死扬程为设计 况的1.1~1.3倍扬程随流 工 况 的 1 . 5 ~ 1 . 8 量减少而增加,变化比 倍扬程随流量减少 而增加,变化较急。 较缓慢。
( Dp )3 ; Pp P ( Dp D )5
第三讲相似理论

d─管径 l─管长
(2)物理条件相似 (即所具有具体现象都在具有一定物 理性质的介质下进行)
'' '' '' C , Cn , Cg ' ' g'
─密度 ─粘度 ─重力加速度
同济大学汽车实验室
相似第二定理
(3)边界条件相似(边界条件即所有具体现象都受到与其直 接相邻的周围情况影响) V' ' x V' ' y V' ' z Cv 即在入口及出口处的
同济大学汽车实验室
相似第三定理
相似第三定理
描述现象的关系方程式可以转变成相似准则之间的关系式。 准则关系式可表达为: 式中1,2,3, 为正整数。 F (1 , 2 , n ) 0
定理作用:提供了一种由模型实验研究来揭示原型内在规 律的方法。
只要用适当的方法求出相似准则,再用模型实验数据拟合 出 F (1 , 2 , n ) 0 ,就可获知原型的内在规律。
Cv Ct 为相似指标 CL
l Cl l
t Ct t
v Cv v
dl 代入 v dt
Ct Cv dl' v' 得: Cl dt'
即 v'
dl ' dt '
所以,当
Ct Cv 1 Cl
时(即相似指标=1)
表明两个运动能用完全相同的方程表示。
相似的两系统瞬间速度分别为 由两系统相似 :
dl' V ' dt
,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
g v Kh v z
RiRC(0.21~0.25) 层流变为湍流 RiRT(1.0) 湍流变为层流
总体理查孙数
g Rb
v (u ) 2 (v) 2
第二节
近地面层
近地面层:湍流输送占有压倒优势作用的贴 地面层,其高度约为边界层高度的1/10。常通 量层。 近地层的厚度hc 假设近地层内,流场定常、水平均匀,略去 分子粘性力作用,选择x1轴沿地面风向。则 运动方程
u 3u1 fV g sin z
注意到边界层内气压梯度力可以用地转风来代替:
z
z
u
二、温度、湿度廓线:对数律 三、推广到非中性情况:幂次律
z m u u1 ( ) z1
第四节
大气稳定度参数
非中性层结大气 必须考虑热力作用对湍流结果的影响。 1 理查孙数Ri (Richardson) 静力稳定条件下,垂直运动加速度为负,抑制湍流;而风切 变则产生湍流。为使问题简化,忽略湍流能量方程其它项的 作用,把这两项的比值称为通量理查孙数。 g g 水平均匀、水平运动 w v w v v v Rf Rf u u w u v w v u iu j i z z x j
第三节
中性近地层风温廓线
一、风廓线:对数律
中性层结,位温不随高度变化;空气微团按绝热过 程运动;垂直向湍流热通量为零。
中性层结下风随高度的分布,可以从Prandtl的混合 长理论推导。Prandtl假设:l z 由K理论: wu K u m z
u 2 2 u 将 Km l z z z
主讲人 张镭 教授
2012.10.
第三章
近地层相似理论
第一节 相似理论的基础 第二节 近地面层 第三节 中性近地层风速温度廓线 第四节 大气稳定度参数 第五节 非中性近地层风速温度廓线 第六节 近地层气象参数化
第一节
相似理论的基础
现有的基本物理知识还不足以精确得出边界层基本 规律。然而,边界层观测结果经常出现一些稳定可 重现的特征。利用有关变量可研究出一些经验关系 式。相似理论的优点是为组合这些变量提供了方法。
z1 ln z0 u1 z2 u2 ln z0
即,在z可与 z0 比拟的薄层内,考虑 z0对 l 的影响, (z z 0 ) l
u* du dz ( z z0 )
地面粗糙度z0 (roughness length),风速为零的高度。
表征地表面的几何特征,一般取凸起物的平均高度。 其典型值见表2.3.1。
am2 a1 a a2 a
21
22
a m 2 m
a
a
an a1
a a
n m ,1
a2
nm, 2
a m n m , m
根据量纲齐次性原理:
a m1 a a
a11 1 1
a12 2
a
a
a1 m m
平方,并写成差分形式:
2 2 2 u* u*0 u* fV g sin z hc
2 2 2 u* u*0 u*0 u*0 u*0 hc (10 % ~ 20 %) 2 fV g sin V g f sin u*0
f~1.2×10-4s-1 , =20 ~ 25 u*0 0.05 u*0 0.2 ~ 0.4m / s Vg hc=20 ~ 80m 如果风大(即u*很大),hc可达一、二百米。
ln
各种下垫面的z0 、u*和N的值
地面的种类 z0(cm) u*(cm/s) 16 26 36 N(cm2/s) 0.016 2.6 26
很光滑(泥面、 0.001 冰) 草地,草高1 厘米 坡地,10厘米 稀草 0.1 0.7
对数律的应用 (1)由一个高度的实测风速 lnz 求另一个高度的风速 (2)计算粗糙度 (3)计算摩擦速度 (4)求湍流切应力,空气密度 lnz0 可由状态方程求得 (5)求动量交换系数 K l 2 u 2 z 2 u u z m *
1
U 2
2
UD
3
D
8)也可以从上面的组合中重新选择得到新的组合,如:
1
U 2
2 2 3 Uz 0
1 D 3 3 z0
把1看成是与曳力系数CD完全相同的定义,而2正
好是雷诺数Re=UD/的倒数,3称为相对粗糙度。
以上仅是相似理论的第二步,下一步就是进行必要 的实验,找出无量纲组合之间的关系。
(1) 选择相关的变量。
(2) 把变量组成无量纲组应用定理。
(3) 利用实验数据,决定无量纲组的值。
(4) 使经验曲线或回归方程适合于实验数据,以便描述 无量纲组之间的关系。
相似理论并不能具体告诉无量纲组之间的方程或关 系式,必须反复实验、观察,选择定性的最佳的 方程式。如,把一组表示成另一组的幂函数、对
a=f(a1,a2,an)
(2.1.1)
ቤተ መጻሕፍቲ ባይዱ
其中:a1,a2,an为主定量(自变量)。 上述具体函数形式不确定,借助量纲分析原 理,将上述函数无量纲化,减少未知函数 的自变量数目,这是定理的基本思路。
设n个自变量中,最多有m个量纲独立的量a1,a2,am, 其余各量am+1,am+2 ,an 的量纲可用上述m个独立量 纲表示: a11 a12 a1m am1 a1 a2 am
( ) a ( D) b (U ) c
( ) d ( D) e (U ) f
z 0 ( ) g ( D) h (U ) i
6) 求解a,b,c等的幂,得到量纲相容方程。 第一个方程:ML-1T-2=(ML3)a(L)b(LT-1)C 左右量纲相等得 M:a=1 L:-3a+b+c=-1 T:-c=-2 类似,对于第二个方程和第三个方程,我们可以得到其它幂 数的值。 d=1,e=1,f=1,以及 g=1,h=1;i=0。 7) 对于各个方程,用右边除左边得到无量纲组,其数目总是对 z 于变量数减量纲数。 0
**界面的两种流动状态 取决于固体边界的几何特征(流体的物 理性质z0)和动力学特征(湍流情况/u*)。 (1)空气动力学光滑流:湍流微弱,以分子粘性为主 u* z0 0.13
边界附近必须考虑分子粘性,粘性副层以上考虑湍流粘性 宏观粘滞系数 N u* z0,它在粗糙流动中所起的作用与光滑流动 u 1 u* z ln 5.5 中粘滞率所起的作用相类似。
SL 地面总面积与粗糙元数之比,或粗糙元的地域大小
零点位移订正,位移距离d 在陆地上,如果各个粗糙元被组合得非常紧密,那么这 些粗糙元顶部的作用就类似于位移了的地面。在林冠顶 部以上,风廓线是对数增长的, u* z d u ln 中性条件下有 z0 有效高度=实际高度 +z0 – d’=实际高度 – d d’积雪厚度;d零点位移长度,可用试探法确定
a
a a a1a1 a2 2 amm
将(2.1.1)和(2.1.2)代入:
f (a1 , a 2 , a n )
a a a1a1 a 2 2 a mm
g ( a1 , a 2 , a m ; 1 , 2 n m )
上式左端为无量纲量,故右端也应为无量纲数,则: ( 1 , 2 nm )
由实验结果得知
1) 应力随雷诺数的增加而减少,直到临界雷诺数达到 2100左右为止。临界雷诺数是层流向湍流过渡的标志。 在低雷诺数(层流)时,应力不依赖于相对粗糙度。 2) 当雷诺数刚好大于临界值时,应力又重新增大。
3) 当雷诺数进一步增大时,应力又随雷诺数而减少,但 与导管粗糙度无关。 4) 当雷诺数更大时,应力是一个只依赖于相对粗糙度而 不依赖于雷诺数的常数。 大气雷诺数很大,边界层106-108。可以忽略分子粘性
z0并不等于地面上各个粗糙元的高度,但这些粗糙元 与z0之间是一一对应的关系。 z0确定后,就不随风速、稳定度或应力而改变。但如 果地面粗糙元(植被高度、范围、房屋建筑物等)发 生变化,z0也随之变化。 z0的求解方法:两个或两个高度以上的风测量结果, 即可求解z0和u*。
z0也可以根据地表情况进行估算,如果粗糙元间距均匀, 不太靠近,其高度和 * ss z 0 0.5h 形状又类似,则: S L * 粗糙元平均垂直范围;s 粗糙元平均轮廓或垂直面积 h s
2
和 u w u*2 代入得
u u* z z
u* dz du z
积分,1) 设z = z0时, u=0,则
z u ln z0
u*
若z = z1 , u = u1;z = z2 , u = u2, 显然
z z0 ln 2)设z =0, u =0, 则 u z0 u*
1
a m1
a a
a11 1
a12 2
a1m m
类似有:
2
a m 2
(2.1.2)
a a a1a21 a 2 22 a m2 m
nm an a1 n m ,1 a 2 n 0 m , 2 a mn m , m
a a a
把变量a也表示成a1,a2,am的形式:
数关系,选择方程通常包括未知系数,而未知系
数可以用实验数据回归来求解。 相似关系式常用来表示定常态(平衡),有关变量 中很少包括时间。对于随时间强烈变化的某些参 量,如边界层高度,很难用相似表达式来估计。
常利用边界层高度作为进入无量纲组的输入量以
诊断其它变量是否达到稳态。
定理
待定变量(因变量)a,满足
