16-3 一维势阱和势垒问题
量子力学-第二章-一维势阱

3
时间依赖薛定谔方程
根据能量守恒和时间演化,推导出薛定谔方程。
薛定谔方程的解析解
无限深势阱
假设粒子被限制在一个 无限深的势阱中,无法 逃逸。
波函数的边界条件
在势阱的边界处,波函 数必须满足特定的边界 条件。
波函数的对称性
在势阱中,波函数可能 具有对称或反对称的性 质。
薛定谔方程的数值解
有限差分法
含时薛定谔方程的一维势阱模型
含时薛定谔方程是一维势阱模型中描述粒子动态行为的方 程。该方程包含了时间依赖的势能项,可以描述粒子在时 间演化过程中受到的外部作用力。
含时薛定谔方程的解可以用来研究粒子在一维势阱中的动 态行为,例如粒子在受到激光脉冲作用时的运动轨迹和能 量变化。通过求解含时薛定谔方程,可以深入了解粒子在 一维势阱中的动力学性质。
01
将薛定谔方程转化为差分方程,通过迭代求解。
网格化方法
02
将连续的空间离散化为有限个网格点,对每个网格点上的波函
数进行求解。
量子隧穿效应
03
当势阱深度较小时,粒子有一定的概率隧穿势垒,从势阱中逃
逸。
03
一维势阱中的粒子行为
BIG DATA EMPOWERS TO CREATE A NEW
ERA
粒子在无限深势阱中的行为
时间依赖的一维势阱模型
时间依赖的一维势阱模型描述了粒子在一维空间中受到随时 间变化的势能作用的情况。这种模型可以用来研究粒子在时 间依赖的外部场中的动态行为,例如粒子在激光场中的运动 。
时间依赖的一维势阱模型需要求解含时薛定谔方程,该方程 描述了粒子在时间演化过程中的波函数变化。通过求解含时 薛定谔方程,可以了解粒子在时间依赖的势阱中的动态行为 。
163一维势阱和势垒问题

0,
mn mn
克罗内克符号
二、势垒穿透和隧道效应
有限高的方形势垒
数学形式:
U
(
x)
0,
U 0 ,
图形形式:
x 0(P区),x a(S区) 0 x a(Q区)
U
考虑粒子的动能 E小于势垒高
U0
度 U0的情况。( E < U0 )
E
PQ S
o ax
U (x) 0, x 0和x a
1
(0 x a)
(x 0及x a)
2
势阱内 0 < x < a
d 2 1
dx2
2E
2
1
0
势阱外 x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d 2
d x2
2E
2
0
E是粒子的总能量,E > 0,令 k
定态薛定谔方程变为
d 2
一维无限深方势阱的图形表达形式 :
∞∞
U(x)
粒子只能在宽为 a 的两个无限 高势壁间运动,这种势称为一 维无限深方势阱。
0
ax
因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。
2
2
2
U
(r)
(r )
E
(r )
————定态薛定谔方程
①列出各区域的定态薛定谔方程
若在样品与针尖之间
加一微小电压Ub电子 就会穿过电极间的势
垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变,则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。
21.7 一维势阱 势垒 隧道效应

STM的发明者 宾尼、罗雷尔和电 子显微镜的发明者 卢斯卡分享了1986 年诺贝尔物理奖。
宾尼
罗雷尔
U0
电子云重叠 U0 U0 E
样 品
d
针 尖
扫描隧道显微镜(STM)装置示意图
用STM得到的神经细胞象
液体中观察原子图象
在电解液中得到的硫酸根离子吸附在铜 单晶表面的STM图象。
“扫描隧道绘画 ” 一氧化碳“分子人”
8 n1 x n2 y n3 z ( x, y, z ) sin sin sin l1l2 l3 l1 l2 l3
三维势阱中粒子的能量:
n12 2 2 n2 2 2 2 n32 2 2 E 2 2 2 2ml1 2ml2 2ml3
处在超晶格的一维量子线和两维量子阱中的电子 就属于一维和两维势阱中的粒子,而处在金属内的电 子可看作三维势阱中的粒子。
i En t
)e
i En t
( px En t )
C 2e
( px En t )
n ( x, t ) 是由两个沿相反方向传播的平面波叠加而
③粒子在阱中的分布 经典力学的结果:均匀分布 P ( x ) 1/ a a a P ( x)dx P ( x) dx P ( x)a 1
(4) 解方程、定常数 在 0<x<a 区域,定态薛定谔方程为
令
d x 2mE 2 x 0 2 dx 2mE 2 k 2 d 2 x 2 k x 0 2 dx
2
比较谐振动方程 特解为
d2x 2 x0 2 dt
( x ) C sin(kx )
2 2 2
16-3一维势阱和势垒问题解读
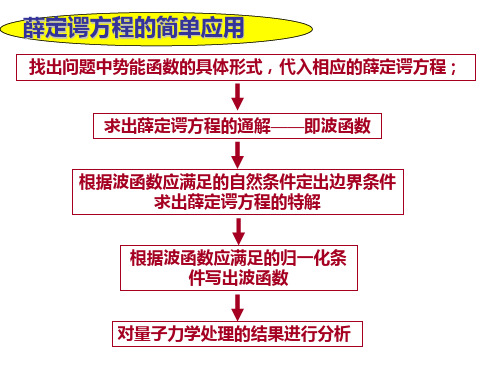
x a
a x
第k激发态(n=k+1)有k个节点。
(2)一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰:量子 经典均匀分布 0
a a n 1,x 处,几率最大 0 3 2 b n ,峰数 ,当n 时,
4
U0
II
III
o
a
x
而在微观粒子的情形,却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
(2)E<U0 从解薛定谔方程的结果来看,在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零,同时,在 x>a区域也存在波函数,所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数,由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑,粒子不可能透过阱壁,因而按照波 函数的统计诠释,要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况,即
(0) 0, (a) 0
————边界条件
(0) 0
这说明:并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件,只有当能量取上式 给出的那些分立的值 En(体系的能量本征值)时, 相应的波函数才是物理上有意义的,即本问题中体系 的能量是量子化的,亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a
【大学物理】§3-2薛定谔方程 一维势阱和势垒问题

一、一维无限深方势阱
对于一维无限深方势阱有
一维势阱和势垒问题
∞
∞
U(x)
U
(
x)
0
(0 x a) ( 0 x, x a)
势阱内U(x) = 0,哈密顿算符为
H
2
2
d2 d x2
定态薛定谔方程为
0
a
令
2E
k
薛定谔方程的解为
d 2
d x2
2E
2
0
(x) Asin(kx )
由此解得最大值得位置为
x (2N 1) a 2n
例如
n 1, N 0
最大值位置
x 1a 2
n 2, N 0,1, 最大值位置 x 1 a , 3 a Nhomakorabea44
n 3, N 0,1, 2, 最大值位置 x 1 a , 3 a , 5 a.
6 66
可见,概率密度最大值的数目和量子数n相等。
10
2m dx2
2. 波函数
(
x)
2 sin( n x), 0 x a
aa
0,
x 0或x a
3. 能量
En
n
2
22
2ma 2
n 1,2,3
4. 概率密度
(x) 2 2 sin 2 ( n π x)
a
a
4
讨论
n (x)
2 sin n x
a a
(0 x a)
1.n=0给出的波函数
1
根据 (0,)可以0确定 = 0或m,m =1,2,3,。于是上式改写为
根据 (a) 0,得
(x) Asin kx
ka = n, n = 1,2,3, ···
一维势垒问题总结

一维势垒问题总结
一维势垒问题是指在一维空间中存在一个势能障碍的物理问题。
该问题涉及到粒子的运动和势能的影响,有着广泛的应用。
一维势垒问题的主要特点是势能障碍的存在。
这个势能障碍可以是有限高度的,也可以是无限高度的。
有限高度的势能障碍表示粒子可以跨越势垒,而无限高度的势能障碍表示粒子无法穿越势垒。
在求解一维势垒问题时,需要考虑的主要因素包括粒子的动能和势能。
根据量子力学的原理,粒子在势垒两侧会存在反射和透射两种情况。
对于势能障碍的高度低于粒子的能量,粒子可以自由穿越势垒,这称为透射现象。
透射的概率可以通过隧道效应来描述,隧道效应可以用量子力学中的波函数来解释。
对于势能障碍的高度高于粒子的能量,粒子会发生反射现象。
在经典力学中,反射的概率可以通过粒子的入射能量和势垒高度之间的关系来计算。
对于无限高度的势能障碍,粒子无法穿越势垒,只能发生反射现象。
这种情况下,粒子的能量必须超过势能障碍的高度才能透过。
一维势垒问题在物理学和化学领域都有广泛的应用。
例如,它可以用于解释原子核中的核反应、电子在导体中的传输等。
总之,一维势垒问题是涉及势能障碍的物理问题,涉及粒子的运动和势能的影响。
求解该问题需要考虑粒子的动能和势能,以及透射和反射两种现象。
一维势垒问题在科学研究中具有重要的应用价值。
16-3 一维势阱和势垒问题
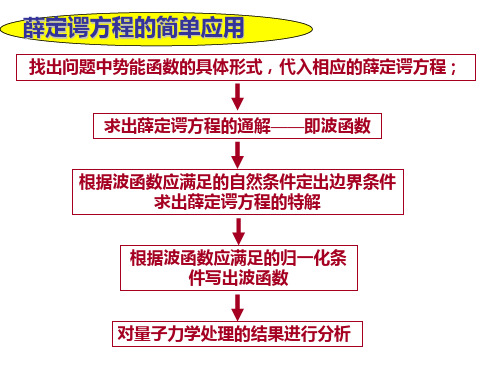
ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为:
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量,E > 0,令 是粒子的总能量, 是粒子的总能量 , 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为: 谔方程简化为: d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 :
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 : ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动, 限高势壁间运动,这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关, 因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。 态问题,可以用定态薛定谔方程进行求解。
量子力学中一维无限深势阱问题两种解题方法的比较

量子力学中一维无限深势阱问题两种解题方法的比较一维无限深势阱是量子力学中一个经典的问题,可以用两种方法进行求解:定态微扰论和定态井底近似。
1. 定态微扰论:定态微扰论是量子力学中解决简单势场问题常用的一种方法。
在无限深势阱问题中,可以将无穷深方势阱视为定态问题的微扰,将该势场加入到系统的哈密顿量中,然后使用微扰论进行求解。
定态微扰论的步骤如下:- 首先,将无限深方势阱问题的哈密顿量记为H0,并找到H0的本征函数和本征能量。
- 然后,将无穷深势阱视为微扰,将微扰项H'加入到哈密顿量。
- 使用微扰论的公式,展开本征函数和本征能量的泰勒级数,得到微扰的一阶修正项。
- 最后,将微扰项的一阶修正项加到H0的本征能量上,得到精确的能级修正。
2. 定态井底近似:定态井底近似是另一种求解一维无限深势阱问题的常用方法。
该方法的核心思想是将无穷深方势阱问题看作是薛定谔方程在势能井底附近的近似解。
定态井底近似的步骤如下:- 首先,将无限深方势阱的势能井底近似为一个宽度为a的矩阵势阱,且矩阵势阱的势垒高度为无穷大。
- 然后,将定态薛定谔方程在矩阵势阱内求解,得到在该势阱内的本征函数和本征能量。
- 最后,将势能井底趋于无穷深,即将势阱的势垒高度取极限使其趋于无穷大,此时得到的本征函数和本征能量就是无限深方势阱问题的精确解。
比较两种方法:- 定态微扰论适用于一般情况下的微扰问题,可以求得很多物理量的修正。
但是在计算过程中需要进行级数展开,需要考虑到每一阶的修正项,计算较为复杂。
- 定态井底近似是一种近似方法,适用于无穷深方势阱问题的求解。
它将无穷深方势阱问题转化为一个简单的矩阵势阱问题,简化了问题的求解过程。
- 在求解一维无限深势阱问题时,定态井底近似更加简单快速,能够直接得到问题的精确解。
而定态微扰论的应用范围更广,在求解一些复杂问题时更具有优势。
综上所述,定态井底近似适用于一维无限深势阱问题的精确解,而定态微扰论适用于更一般的微扰问题,并具有更广泛的应用范围。
一维势阱和势垒问题

1.一维无限深势阱
一维无限深方势阱是金属中自由电子的简化模型
粒子在势阱内受力为零,势能为零。在阱内自由运 动。在阱外势能为无穷大,在阱壁上受极大的斥力, 不能到阱外。
一维无限深方势阱的数学表达形式 :
0 (0 x a) U (x) (x 0及x a )
无数峰:量子 经典均匀0分布4 2
a
n4
x
0
ax
n时
量子经典
|n | 2 n很大
En
0
a
一维无限深势阱
En n
n(x)
En ( x)
h2 8ma 2
n2
n (x)
2 sin n x
aa
n(x)
2 sin2( n
aa
x)
0
ax
例1: 证明无限深方势阱中,不同能级的粒子波函数 具有正交性:
0 x a;
0,
x 0, x a.
讨论:
① 粒子的能量
En
2k 2
2
22n2
2 a2
,
n 1,2,3,
粒子的最低能量状态称为基态,则一维无限深方势 阱的基态能量为:
E1
22 2a2
0
————零点能
与零点能相对应的,应存在零点运动。这与经典粒
子的运动是相矛盾的。零点能是微观粒子波动性的表 现,因为“静止的波”是没有意义的。
② 图形
一维无限深方势阱中粒子的能级、波函数和几率密度
(2 sin nx , 0 x a;
a a
0,
x 0, x a. 0
除端点外,
《一维无限深势阱》课件

解题方法与工具
薛定谔方程、波函数公式和 边界条件的应用。
应用前景
在多个领域有很多实际应用。
计算激发态的概率
利用特定能级的波函数计算激发态的概率;以及其他相关问题的解答。
应用
材料科学领域
解决纳米材料中的物理、化学和 力学问题
量子信息领域
利用量子特性加速数据处理;破 译密码和设计新型电池。
纳米技术领域
研究光电、信息、能源等相关的 量子力学现象。
总结
一维无限深势阱的特殊 性质
简单而重要的模型,可用于 探究更复杂的问题。
基本概念
势能与波函数
势能定义粒子所在位置的势场, 波函数描述粒子位置的可能性 幅度。
薛定谔方程
描述粒子的术语,包括势能、 动量被发现 在特定位置的可能性。
波函数的物理意义
波函数描述粒子的位置、动量 和能量等物理量的概率分布。
解法
1
波函数公式
《一维无限深势阱》PPT 课件
欢迎来到我们的演示文稿。我们将一起探讨令人兴奋的量子力学现象,发现 一维无限深势阱的概念、解法和应用。让我们开始!
简介
什么是一维无限深势阱?
描述了一维粒子在具有无限 深势阱的区域内的性质。
为什么要研究它?
简单而重要的模型可用于探 索更复杂的问题。
研究它有什么应用?
了解电子和纳米材料中的量 子现象,以及量子信息学和 计算机领域中的应用。
每个薛定谔方程的解都对应一个特定能量的粒子状态并对应一个单独的波函数。
能级图谱
制作不同能级下对应的波函数图像,形成能级图谱。
典型问题
1
求解基态能量和波函数
应用波函数公式,从特定势能中解出基本能级的能量和波函数。
一维有限深方势阱和势垒贯穿汇编

从一维无限深方势阱 理解有限深方势阱
k2
2mE
2
V (x)
ka n n 1,2,3,
o
En
2 2
2ma 2
n2
n 1,2,3,
V (x) 0,
V (x) ,
ax
0 xa x 0, x a
E1
2 2
2ma2
1 2
2 2
ma2
,
微观能量尺度可以选取 2 2
ma2
微观动量尺度
ka = n
-a/2 a/2 x
对于参考书p47页说明
a)不在讨论为什么势能对称,波函数也对称了。 b) 公式29和30实质上是利用
c) 估计一下公式32的数值大小? d)纵轴取决于势阱高度,横轴取决于能量,此处
是势阱内部动能。我们让动能变化,看看什 么时候能冲破势阱束缚。
公式右面=
U0 22
U0
2 2
2
STM样品必须具有一定程度的导电性; 在恒流工作模式下有时对表面某些沟 槽不能准确探测。任何一种技术都有 其局限性。
dx2
V0 2
(x)
E2 (x),
定态薛定谔方程 的解又如何呢?
0 xa
2 2m
d
23 (x)
dx2
E3
( x),
xa
令:
k
2
Байду номын сангаас
2mE 2
k12
2m(V0 2
E)
三个区间的薛定谔方程化为:
V
V0
d
21(
dx2
x)
k
21
(
x)
0,
x0
I
d
154一维势阱与势垒

E 37.7 n2eV
E (2n 1)37.7eV
在这种情况下,相邻能级间的距离是非常大 的,这时电子能量的量子化就明显的表现出来。
29
当n>>1 时 ,能级的相对间隔近似为
En En
2n
h2 8ma2
n2
h2 8ma2
2 n
可见能级的相对间隔 En 随着n的增加成反比地减小。
U
在P区和S区薛定谔方程的形式为
U0
其中
d2 (x)
dx2
k
2
(x)
0
k 2 2E
2
E PQ S
o ax
在Q区粒子应满足下面的方程式
d2 (x)
dx2
2
(x)
0
式中
2
2
2
(U 0
E)
34
用分离变量法求解,得
1 A1eikx B1eikx 2 A2ex B2ex
3 A3eikx
(P区) (Q区) (S区)
nx
A sin( )
x)
2
dx
a 1,得
A 2/a
归一化波函数为
n(x)
2 sin nx , aa
n 1,2,3,
一维无限深方势阱中粒子的能级、波函数和几率密度
n4 E4
n3
E3
n2
E2
E1
x0
n 1
xa
o
(a) n (x) 稳定的驻波能级
(b)
n (x) 2
ax
27
例题 1 设想一电子在无限深势阱,如果势阱宽度分别 为1.0×10-2m和10-10m 。试讨论这两中情况下相邻能 级的能量差。
一维势阱
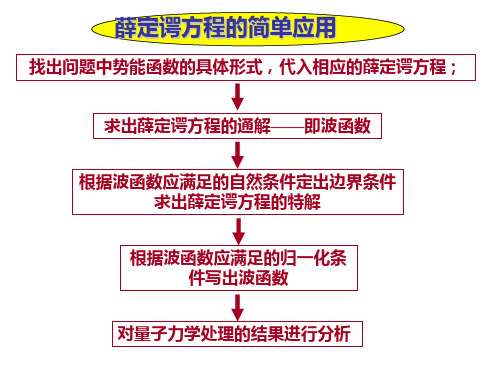
, n = 1, 2, 3, …
试计算n = 1时,在 x1 = a/4 →x2 = 3a/4 区间找到粒子的 概率.
解:找到粒子的概率为
3a / 4
2 2 x ( x) 1 ( x) d x sin d x a a a/4 a/4
* 1
3a / 4
2 x ) 3 a 1 cos( 1 1 a 4 a dx a 2 π 4
0,
讨论:
2 k 2 22n2 ① 粒子的能量 E n , n 1,2,3, 2 2 2 a
粒子的最低能量状态称为基态,则一维无限深方势 阱的基态能量为:
E1 2 0 2 a
2 2
————零点能
与零点能相对应的,应存在零点运动。这与经典粒 子的运动是相矛盾的。零点能是微观粒子波动性的表 现,因为“静止的波”是没有意义的。
3 n 3
4
n4
x a
a x
第k激发态(n=k+1)有k个节点。
(2)一维无限深势阱的粒子位置概率密度分 布 2
1
n 1
0 2
2
x a n2 x a
a x
0 n3 3
2
0 4 0
2
n4
x a
n时
量子经典
|n | 2
n很大
En
0
a
一维无限深势阱
En n
n ( x)
h 2 En ( x ) n 2 8ma
2 n n ( x) sin x a a
2ห้องสมุดไป่ตู้
2 2 n n ( x ) sin ( x ) a a
0
a
x
例1: 证明无限深方势阱中,不同能级的粒子波函数 具有正交性:
高二物理竞赛课件:一维无限深方势阱

得
Hˆ (x, y, z) i
1
df (t)
=E
(x, y, z)
f (t) dt
i
1 df (t) E, f (t) dt
其解
f
(t)
e
i
Et
Hˆ
2
2 U
另一方程: Hˆ (x, y, z) E (x, y, z) 2m
2 2 (x, y, z) U (x, y, z) E (x, y, z) (17-32)
2m
若势能U不显含时间t ,则
(x, y, z,t) (x, y, z) f (t)
Hˆ (x, y, z,t) i (x, y, z,t)
t
Hˆ (x, y, z) f (t) i (x, y, z) f (t)
t
将上式两端除以 (x, y, z) f (t), 并注意到
Hˆ 2 2 U 2m
2m
上式称为定态薛定谔方程。
波函数:
(
x,
y,
z,
t
)
(
x,
y,
z)e
i
Et
概率密度: (x, y, z,t) 2 (x, y, z) 2
概率密度不随时间而改变,是一种稳定状态,即为 定态。
0 0xa
U(x)
U (x)
x 0, x a
o
ax
图17-3
2 2m
d
2 (x)
dx2
U
(x)
Ψ(r, , ) =R(r)()Φ()
(17-47)
在E<0(束缚态)的情况下求解上述方程,可得如下 结论:
1. 能量量子化 为使波函数满足标准条件,电子(或说是整个原 子)的能量只能是
势垒和势阱名词解释

提升训练三融入社会肩负使命第六课参与政治生活一、单选题(下列各题4个备选答案中,只有1个是最符合题意的。
请选出正确答案并将其序号填入题后的括号内。
)1. (山东省)分析右边的漫画,可以看出(C )①法制建设是我国现代化建设的中心工作②我国法律是构建社会主义和谐社会、维护国家长治久安的可靠保障③我国社会主义法律体系已十分健全完善④构建和谐社会是全面建设小康社会的重要目标A. ②③ B .①④C.②④ D .①③2. (福建•福州)我国的根本政治制度是( D )A. 民族区域自治制度B. 政治协商制度C. 基层群众自治制度D. 人民代表大会制度3. (福建•福州)2008年2月28日,《中国的法治建设》白皮书发表。
白皮书强调把坚持党的领导与坚持宪法和法律至上、维护宪法和法律的权威统一起来。
这说明( C )A. 法律和宪法都是国家的根本大法B. 法治建设是我国一切工作的中心C. 依法治国是党领导人民治理国家的基本方略D. 白皮书是关于国际能源的纲领性文件4•(云南省)2007年11月15日,国务院新闻办公室发表《中国的政党制度》白皮书指出,中国实行的政党制度是(C)A •民族区域自治制度B .人民代表大会制度C •中国共产党领导的多党合作和政治协商制度D. 基层群众自治制度5. (云南省)我国宪法是国家的根本大法,从效力上看(A)A宪法具有最高的法律效力B. 宪法规定国家生活中的根本问题C. 宪法的制定和修改比普通法律更严格D. 宪法规定公民的基本权利和义务6. (贵州•贵阳)2007年12月4日是第7个全国法制宣传日,主题是“弘扬法治精神,推进依法治国”。
依法治国的前提是:(A)A、有法可依B、有法必依C违法必究7. (福建•晋江)国家法定节假日调整方案出台前曾在网上公布,广泛征求各界意见。
对此理解正确的有(A)①这一形式方便了人民的参与②它是公民行使民主权利的具体体现③我国公民行使权利的途径更加广泛④它表明我国公民可以随意表达意愿A. ①②③ B .①③④ C.①②④ D .②③④& (广西•贵港)2008年5月1日起施行的《中华人民共和国政府信息公开条例》明确规定:行政机关应当主动公开涉及国家秘密、商业秘密和个人隐私以外的政府信息,并通过政府公报、政府网站、新闻发布会以及报刊、广播、电视等便于公众知晓的方式公开。
势阱,势垒及原子结构

本征值
本征函数
4. 讨论解的物理意义
即求| |2,得出粒子在空间的概率分布。
粒子在一维无限深势阱中的波函数
2 n x i Et
Ψ (x) sin e (n 1,2,3,...; 0 x a) aa
Ψ (x) 0
(x 0, x a)
注意:解为驻波形式
5.讨论解的物理意义
强度不等,粒子出现的概率不相同.
Ψ (x,t)
2 n x i Et
sin e
aa
Ψ x,t
|Ψ (x,t) |2 | (x) |2 2 sin2 n x
a
a
x 2
E4 16E1
n=4
n= 4
E3 9E1
E2 4E1
E1
o
n=3 n= 2 n=1
ax o
n= 3
n= 2 n= 1
ax
波长量子化 n 2a n, n 1, 2,3,......
z l0
ml 0
z
l2
ml 0
z
l2 ml 1
x
x
x
电子在核外不是按一定的轨道运动的,量子力学不能断言电 子一定出现在核外某确切位置,而只给出电子在核外各处出现 的概率,其形象描述——“电子云”
1s 2 p(ml 0) 3p(ml 1)
4 f (ml 1) 5 f (ml 1)
——每瞬间氢原子核外电子照片的叠加 电子出现概率大处:雾点密度大
电子出现概率小处:雾点密度小
量子理论与玻尔理论的比较:
玻尔理论:电子只能在一些量子化的轨道上运动, 只有在这些轨道上才能发现电子。 量子理论:电子并不沿轨道运动,在空间任一点都可 能发现电子。
一维势垒问题总结

一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数,对以上的透射系数的总结,推出了对于任意势垒中透射系数, 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中,遇到的问题和 值得注意的地方。
在求方势垒波 函数中,首先要知道这是一个什 么样问题,满足什么样的方程, 方程可以写成什么样的形式,在 求解方程中,波函数的形式应该怎样需要怎样的分段,分段的过程中,特别要强调的边界条件问题。
并且验证了概率流密度。
在量子力学中,粒子在势垒附近发生的现象是不一样的,能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射,而能量小于0u 的粒子也会有部分穿过势垒,这在经典力学中是不会发生的。
下面讨论的是一维散射(即在非束缚态下问题,在无穷远处波函数不趋于零)。
重点讨论的是粒子通过势垒的透射和反射,重点在于求出波函数,这就必须求解薛定谔方程,由于)(x U 是与时间无关的,此处是定态薛定谔方程。
定态薛定谔方程通式:ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域:⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h (1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注: 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时,通解xq xq eC e C y ---+=21,当0>q 时,通解xq ixq ie C e C y -+=21方程(1)的解可以表示为:⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ (2)定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-,可以看到式子(2)的三式,第一项是左向右传播的平面波,第二项是由右向左传播的平面波,即入射波和反射波。
量子力学一维势阱

III
(x)
2
2
(U
E )
III
(x)
0
xa
方程可 简化为:
d2
dx
2
I
2 I
0
d2
dx
2
II
2 II
0
d2
dx
2
III
2 III
0
U(x)
I
II
-a 0
III a
U(x)
I
II
-a 0
III
a
1 单值,成立; 2 有限:
当x - ∞ , ψ 有限条件要求
C2=0。
d2
(x)
2
2
[U ( x)
E ]
(x)
0
β2
势V(x)分为三个区域, 用 I 、II 和 III 表达, 其上旳波函数分别为 ψI(x),ψII(x) 和 ψIII (x)。则方程为:
d2
dx 2
I
(x)
2
2
(U
E )
I
(x)
0
x a
d2 dx 2
II
(x)
2
2
E
II
(x)
0
a xa
d2
dx 2
(r , t) (r , t)
称波函数具有偶宇称;
(r , t) (r , t)
称波函数具有奇宇称;
(3)假如在空间反射下,
(r , t) (r , t)
则波函数没有拟定旳宇称
(四)讨论
一维无限深 势阱中粒子 旳状态
(1)n = 1, 基态,
0
n
1
n
sin
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波: 由 x > a 处无反射波: B 3 = 0 令 A1 = 1(以入射波强度为标准) 以入射波强度为标准) 由波函数的 标准条件得 O 可解得
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立:微观粒子被局限于某区域中, 模型的建立:微观粒子被局限于某区域中,并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如: 例如: 金属中自由电子 受规则排列的晶格点阵作用 简化:交换动量) 简 相互碰撞 (简化:交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习: 练习
已知: 已知:
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞
得:
∞
2
∞
A =
1
π
1 ψ (x ) = π (1 + ix )
2. 概率分布函数为: 概率分布函数为:
P =ψ
3. 令: 得:
(x)
2
1 = ψ ( x ) ⋅ψ ( x ) = π 1+ x2
U U
o
U
a
∞
o
a
求解问题的步骤: 求解问题的步骤: 1. 写出具体问题中势函数 写出具体问题中势函数U(r)的形式,代入一维定态 的形式, 的形式 薛定谔方程的一般形式,得本问题中的薛定谔方程。 薛定谔方程的一般形式,得本问题中的薛定谔方程。 设粒子在一维无限深方势阱运动 势函数 U(x) = 0 (0 < x < a) )
30 2 17 2 p = ∫ |ψ | d x = ∫ 5 x ( L − x ) d x = = 0 .21 L 81 0 0
A 练习: 设粒子沿 x 方向运动,其波函数为 ψ (x) = 方向运动, 1 + ix
1.将此波函数归一化; 将此波函数归一化; 将此波函数归一化 2.求出粒子按坐标的概率分布函数; 求出粒子按坐标的概率分布函数; 求出粒子按坐标的概率分布函数 3.在何处找到粒子的概率密度最大? 在何处找到粒子的概率密度最大? 在何处找到粒子的概率密度最大 解: 1. 由归一化条件
(0)
a
x
ψ 1 (0) = ψ 2 (0) dψ 1 dψ 2
dx dx ψ 2 (a ) = ψ 3 (a ) (0) =
A2 , A3 B1 , B2
dψ 2 dψ 3 (a ) = (a ) dx dx
U
入射波+反射波 入射波 反射波
U0 透射波
O 经典
E > U0
a 量子
x
越过势垒, 越过势垒,只透 射,不反射 不能越过势垒, 不能越过势垒, 只反射, 只反射,不透射
*
(
)
d 2 ψ (x ) = 0 dx
x=0
处粒子的概率密度最大。 即在 x = 0 处粒子的概率密度最大。
二、势垒穿透和隧道效应 模型: 模型:金属表面的势能墙不是 无限高,而是有限值。 无限高,而是有限值。 势函数: 势函数: 0 x < 0, x > a
U (x ) =
U
U0
代入 得
d 2 ψ 2m + 2 ( E − U )ψ = 0 2 dx ℏ
2 1
d2ψ + k12ψ = 0 2 dx
d2ψ 2 + k 2ψ = 0 d x2
2m 2mE 2 令 k = 2 k2 = 2 (E −U0 ) ℏ ℏ ik1x −ik1x ψ1 = A1 e + B1 e ( x < 0)
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
− ik 2 x
1
(0 ≤ x ≤ a )
( x > a)
E i ( k1 x − t ) ℏ
ψ 3 = A3 eik x + B3 e − ik x
乘e
i − Et ℏ
第一项: 第一项:向x方向传播的波 [例 A1 e 方向传播的波 例
]
第二项: 第二项:向-x方向传播的波 [例 B1 e 方向传播的波 例
E −i ( k1x+ t ) ℏ
Ψ( x , t ) =
i nπx − ℏ Et 2 2 2 2 2 nπx sin e |Ψ (x, t) | =|ψ(x) | = sin a a a a
Ψ(x , t )
E 4 = 16 E 1
ψ ( x)
n=4 n=3 n=2 n=1
2
n=4 n=3 n=2 n=1
E3 = 9E1
E2 = 4E1
既透射, 既透射,也反射
( B1 ≠ 0 )
E < U0
既透射, 既透射,也反射
( A3 ≠ 0 )
U
入射波+反射波 入射波 反射波
U0 透射波
x O a 隧道效应: 总能量E小于势垒高度 小于势垒高度U 隧道效应: 总能量 小于势垒高贯穿系数: 贯穿系数:
e
E
ikx
Ae ik ′x + Be − ik ′x − ikx V0 + Re
(透射波 ) 透射波
Te
0
ikx
a
x
隧道电流 I ∝ U b e − A φ x 隧道电流对针 尖与样品表面之间的距离x非常敏感 非常敏感。 尖与样品表面之间的距离 非常敏感。 电子显微镜的分辨率为: 电子显微镜的分辨率为:0.3 ~ 0.5nm 扫描隧道显微镜的分辨率为: 扫描隧道显微镜的分辨率为: 横0.1n m 纵0.01n m
d 2 ψ 2mE + 2 ψ =0 2 dx ℏ
d 2 ψ 2m + 2 ( E − U 0 )ψ = 0 2 dx ℏ
U0
0≤ x≤a
O (x<0 x > a)
a
x
(0 ≤ x ≤ a )
d2 ψ 2mE + 2 ψ =0 2 dx ℏ
( x < 0, x > a)
(0 ≤ x ≤ a )
d2 ψ 2m + 2 ( E − U0 )ψ = 0 2 dx ℏ
2 2
−∞
∫
| ψ |2 d x = 1
2 A= a
于是: 于是:
nπ x 2 sin ψ ( x) = a a
i − Et ℏ
(n = 1,2,3,...)
(n = 1,2,3⋯)
2 nπ x Ψ ( x, t ) = sin ⋅e a a
注意: 注意: 解为驻波形式
4.讨论解的物理意义 .讨论解的物理意义 1) 无限深势阱中粒子的能量量子化 无限深势阱中粒子的能量量子化 nπ 由 k 2 = 2mE k= 2 a ℏ k 2ℏ 2 n 2π 2ℏ 2 得 E= = = n 2 E1 ( n = 1,2,3,...) 2 2m 2ma
E只能取一系列分离值 E1 只能取一系列分离值 n π 2ℏ 2 式中
2
E n=4 n=3 n=2 n=1
式中
E1 =
2ma
2
E , 最小能量 1即零点能
粒子不可能静止不动
o 满足不确定关系
a
x
由
k ℏ nπ ℏ E= = = n 2 E1 2 2m 2ma
2 2 2 2 2
( n = 1,2,3,...)
| Ψ |2 相同,量子 → 经典 相同,
归一化条件, 归一化条件,曲线下面积相等
练习: 练习
粒子在宽度为a的一维无限深势阱中运动, 粒子在宽度为 的一维无限深势阱中运动,处于 的一维无限深势阱中运动 a n=1状态, 状态, 状态 求在0 ~ 区间发现该粒子的概率 。 4 2 2πx 2 解: |ψ | = sin a a
U
Asinka = 0
(n = 1,2,3⋯)
o
a
x
nπ ψ ( x ) = A sin x a
( n = 1,2,3,...)
nπ ψ ( x ) = A sin x a
∞
(n = 1,2,3,...)
由归一化条件
∞ a *
nπ x ∫∞ψ ⋅ψ d x = ∫ A sin a d x = 1 − 0
E1
o
a
x
o
a
x
Ψ (x , t )
E
4
ψ (x )
2
= 16 E
1
n=4 n=3 n=2 n=1 a x
n=4 n=3 n=2 n=1 a x
E
3
= 9E
1
E
2
= 4E
1
E1
o
o
