2020-2021学年广西陆川中学高一下周测5理科数学试卷
广西陆川县中学2020-2021学年高三下学期第二次质量检测数学试卷含解析〖附16套高考模拟卷〗
广西陆川县中学2020-2021学年高三下学期第二次质量检测数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD ,在点E ,F 处各放一个目标球,表演者先将母球放在点A 处,通过击打母球,使其依次撞击点E ,F 处的目标球,最后停在点C 处,若AE=50cm .EF=40cm .FC=30cm ,∠AEF=∠CFE=60°,则该正方形的边长为( )A .2cmB .2cmC .50cmD .6cm2.已知点()2,0A 、()0,2B -.若点P 在函数y x =PAB △的面积为2的点P 的个数为( ) A .1B .2C .3D .43.从集合{}3,2,1,1,2,3,4---中随机选取一个数记为m ,从集合{}2,1,2,3,4--中随机选取一个数记为n ,则在方程221x y m n +=表示双曲线的条件下,方程221x y m n+=表示焦点在y 轴上的双曲线的概率为( ) A .917B .817C .1735D .9354.执行下面的程序框图,如果输入1995m =,228n =,则计算机输出的数是( )A .58B .57C .56D .555.设函数()210100x x x f x lgx x ⎧++≤⎪=⎨>⎪⎩,,若关于x 的方程()()f x a a R =∈有四个实数解()1234i x i =,,,,其中1234x x x x <<<,则()()1234x x x x +-的取值范围是( )A .(]0101, B .(]099,C .(]0100,D .()0+∞,6.设复数z 满足z ii z i-=+,则z =( ) A .1B .-1C .1i -D .1i +7.阅读如图的程序框图,运行相应的程序,则输出的a 的值为( )A .2-3B .3-2C .52D .258.在ABC 中,AD 为BC 边上的中线,E 为AD 的中点,且||1,||2AB AC ==,120BAC ∠=︒,则||EB =( )A 19B .114C 3D .749.如图,2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )A .22B .3 C .212+ D .312+ 10.已知随机变量X 的分布列如下表: X1-0 1P ab c其中a ,b ,0c >.若X 的方差()13D X ≤对所有()0,1a b ∈-都成立,则( ) A .13b ≤B .23b ≤C .13b ≥D .23b ≥11.已知函数()[]f x x x =-,其中[]x 表示不超过x 的最大正整数,则下列结论正确的是( ) A .()f x 的值域是[]0,1 B .()f x 是奇函数 C .()f x 是周期函数D .()f x 是增函数12.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A ⋃B ,则集合中的元素共有( ) A .3个B .4个C .5个D .6个二、填空题:本题共4小题,每小题5分,共20分。
2020-2021学年广西陆川县中学秋季期高一9月考试题数学答题卡

18、解:(1)由题意得y 3x 2 2 3 2
…………..3 分
x2
x2
x2 0
2 0 x2
3 2 3 …….4 分 x2
y 3
…………..5 分
综上所述: y 3x 8的值域是y | y 3, y R ……..6 分
x2
(2) 设 x 2 t,则x t 2 2 t 0, ……………..2 分
f
1 2
1
f
2
1
…………….3 分
(2) 令0
x1
x2时,则
x2 x1
1
……………4 分
当x
0时,f
x
0
f
x2 x1
0
又 f mn f m f n
…………..5 分
f
x2
f x1
f
x1
x2 x1
f
x1
f
x1
f
x2 x1
f
x1
f
x2 x1
当 B 时,m 1 2m 1 m 2
………………..7 分
m 1 2m 1 当 B 时,m 1 2
2m 1 5
m 2 m 3
m 3
………………10 分
2 m 3 综上所述实数 m 的取值范围:m 3
……………………11 分 ……………………12 分
20、解: f x x2 2x 1 x 12 2
又 f x在区间0,+上是增函数
………………9 分
x
12 x4
x 0
12
0
x4
x 6
2 x 4或x 6
x 0
……………..11 分
x
广西陆川县中学2020-2021学年高一下学期开学考试(理)数学试题 答案和解析

广西陆川县中学【最新】高一下学期开学考试(理)数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}{}10,1,2,3,2,k A B n n k A -===∈,则A B =A .{}1,2,3B .{}1,2C .{}1D .{}32.已知()224f x x x -=-,那么()f x = ( ) A .284x x -- B .24x x --C .28x x +D .24x -3.22sin10sin 80cos 35sin 35⋅-的值为( ) A .12-B .12C .1D .1-4.已知ABC ∆的三边,,a b c 满足222a b c ab +=+,则ABC ∆的内角C 为( ) A .150︒B .120︒C .60︒D .305.设函数2log ,0()2,0x x x f x x ->⎧=⎨≤⎩,则2(2)(log 3)f f +-的值为( )A .4B .43C .5D .66.若sin 63πα⎛⎫-=⎪⎝⎭,则sin 26πα⎛⎫+ ⎪⎝⎭的值为( ) A .59 B .59-C .79D .79-7.已知2()sin 2cos f x x x =+,则()f x 的最大值为( ) A .1-B .0C .1D .28.已知函数()21cos 2f x x =-,则下列说法正确的是( ) A .()f x 是周期为2π的奇函数 B .()f x 是周期为2π的偶函数 C .()f x 是周期为π的奇函数 D .()f x 是周期为π的偶函数9.已知()f x 是定义在R 上的偶函数,且满足(6)()f x f x +=,当(0,3)x ∈时,2()f x x =,则(64)f =( )A .4-B .4C .98-D .2r10.函数()()sin (0,0,)2f x A x A πωφωφ=+>><的图象如图所示,为了得到()5sin 34g x x π⎛⎫=+⎪⎝⎭的图象,只需将()f x 的图象( )A .向右平移π个单位长度B .向左平移π个单位长度C .向右平移3π个单位长度 D .向左平移3π个单位长度 11.奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式[()()]0x f x f x -->的解集为( ) A .(1,0)(0,1)-B .(,1)(0,1)-∞-C .(,1)(1,)-∞-+∞D .(1,0)(1,)12.将函数()()2sin 2()2f x x πφφ=+<的图象向左平移2π个单位长度之后,所得图象关于直线4x π=对称,且()00f >,则φ=( )A .8π B .38π C .8π-D .38π-二、填空题 13.如果1cos 3α=,且α是第四象限的角,那么cos 2πα⎛⎫+ ⎪⎝⎭=______________.14.函数()21f x x mx =+-在[]1,3-上是单调函数,则实数m 的取值范围是____.15.化简:(4010sin tan ︒︒= ________.16.函数22()sin 2sin )f x x x x =-的图象为C ,如下结论: ①图象C 关于直线1112x π=对称; ②图象C 关于点(23π,0)对称;③函数()f x 在区间(5(,)1212ππ-内是增函数;④由2sin 2y x =的图角向右平移3π个单位长度可以得到图象C .其中正确结论的序号是_________.三、解答题17.已知圆22:8120C x y y +-+=,直线:20l ax y a ++=.(1)当a 为何值时,直线与圆C 相切.(2)当直线与圆C 相交于A 、B 两点,且AB =时,求直线的方程.18.如图,在三棱锥V C -AB 中,平面V AB ⊥平面C AB ,V ∆AB 为等边三角形,C C A ⊥B 且C C A =B =O ,M 分别为AB ,V A 的中点.(1)求证:V //B 平面C MO ; (2)求证:平面C MO ⊥平面V AB ; (3)求三棱锥V C -AB 的体积.19.已知直线l 过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于12. (1)求直线l 的方程.(2)求圆心在直线l 上且经过点(2,1)M ,(4,1)N -的圆的方程.20.如图,直四棱柱ABCD –A 1B 1C 1D 1中,AB //CD ,AD ⊥AB ,AB =2,AD ,AA 1=3,E 为CD 上一点,DE =1,EC =3. (1)证明:BE ⊥平面BB 1C 1C ; (2)求点B 1到平面EA 1C 1的距离.21.如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆C 的方程为2268210x y x y +--+=,点P 为圆上的动点.(1)求过点A 的圆C 的切线方程.(2)求22||||AP BP +的最大值及此时对应的点P 的坐标.22.三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A AB ,AC =2,A 1C 1=1,12BD DC =. (1)证明:BC ⊥A 1D ;(2)求二面角A -CC 1-B 的余弦值.参考答案1.B 【解析】集合{}{}10,1,2,3,2,k A B n n k A -===∈= 1,1,2,42⎧⎫⎨⎬⎩⎭,则A B ⋂={}1,2,故选B.点睛: 1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍. 2.D 【解析】因为()224f x x x -=-=()224x --,则()24f x x =-,故选D.点睛: 本题考查函数的表示方法,属于基础题目.求函数解析式的一般方法主要有:待定系数法,配凑法,换元法,构造方程组法,赋值法等.已知函数类型时,比如一次函数,二次函数,反比例函数以及指数函数或者对数函数时,往往使用待定系数法设出函数的表达式,再利用已知条件带入求出参数的值. 3.B 【解析】原式=1sin 20sin10cos1012cos70sin 202︒︒︒==︒︒,故选B. 4.C 【解析】原式可化为2221cos 22a b c C ab +-==,又()0,C π∈,则C=60︒,故选C.5.A 【解析】()()2log 3221,log 323f f =-==,则()()22log 3f f +-的值为4,故选A.6.A【解析】 【分析】 把26πα+表示为226ππα⎛⎫-- ⎪⎝⎭,再利用诱导公式和二倍角公式计算sin 26πα⎛⎫+ ⎪⎝⎭的值. 【详解】因为sin 2sin 2cos 26266ππππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以25sin 212sin 669ππαα⎛⎫⎛⎫+=--= ⎪ ⎪⎝⎭⎝⎭,故选A .【点睛】三角函数的化简求值中,注意角与角的关系,有时他们的和或差是特殊角,有时要求的角可以用已知的角来表示,有时他们之间有倍数关系等,找到它们的关系后再用三角变换求值. 7.D 【解析】函数()2sin 2cos f x x x =+=21cos 2cos x x -+,令cosx=t ∈[-1,1],则221y t t =-++,二次函数开口向下,对称轴为1t =,则当1t =时, max 2y =,即()f x 的最大值为2,故选D. 8.D 【解析】函数()21cos 2f x x =-= 12cos2x,则()f x 是周期为π的偶函数,故选D. 9.B 【解析】由()()6f x f x +=知,()f x 周期为6,且()f x 是定义在R 上的偶函数,则()64f =()()()261122224f f f ⨯-=-===,故选B.10.D 【解析】 【分析】先由题设中的图像求出函数的解析式为()sin 34f x x π⎛⎫=+ ⎪⎝⎭,再把()5sin 34g x x π⎛⎫=+ ⎪⎝⎭变形为()sin 334g x x ππ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦,从而可得平移的方向和平移的长度. 【详解】由图像可以得到1A =,且46T π=,故3ω=,所以()()sin 3f x x φ=+. 又5112f π⎛⎫=-⎪⎝⎭,所以53242k ππφπ+=+即2,4k k Z πφπ=+∈, 根据2πφ<得到4πφ=,所以()sin 34f x x π⎛⎫=+⎪⎝⎭. 而()5sin 3sin 3434g x x x πππ⎡⎤⎛⎫⎛⎫=+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故只需将()f x 的图象向左平移3π个单位长度可得()g x 的图像,故选D . 【点睛】已知()sin y A x ωφ=+的图像,求其解析式时可遵循“两看一算”,“两看”指从图像上看出振幅和周期,“一算”指利用最高点或最低点的坐标计算φ. 11.C 【解析】由奇函数()f x , 不等式()()0x f x f x ⎡⎤-->⎣⎦可化简为()2?0xf x >,即()00x f x >⎧⎨>⎩或()0x f x <⎧⎨<⎩,又()f x 在()0+∞,上为增函数,且()()101f f ==-,则x∈()(),11,-∞-⋃+∞,故选C.12.B 【分析】先根据题设条件得到()f x 的图像关于34x π=对称,从而得到,28k k Z ππφ=-∈,再根据()00f >及2πφ<得到φ的值.【详解】()f x 的图像关于34x π=对称,所以3242k ππφπ+=+即,28k k Z ππφ=-∈,因2πφ<,故8πφ=-或者38πφ=,因()00f >,故sin 0φ>,故38πφ=,选B . 【点睛】形如()()sin f x A x =+ωϕ的函数,如果其图像的对称轴为0x x =,则有()0f x A =±,如果其图像的对称中心为()0,0x ,则()00f x =.13.3【解析】解:因为1cos 5α=且α是第四象限的角,那么cos()sin 2παα+=-= 14.(][),62,-∞-+∞【解析】 【分析】就对称轴的位置分1,322m m-≤--≥两种情况讨论即可. 【详解】因为()f x 在[]1,3-是单调函数,故12m -≤-或32m-≥,所以6m ≤-或者2m ≥,故填(][),62,-∞-+∞.【点睛】本题考察二次函数的单调性,是基础题. 15.-1 【解析】原式sin10sin?40?(cos10=︒︒︒()sin402sin40 sin1?0?0cos10cos10︒︒︒︒︒︒==(1sin1?0?0)2︒︒ 2sin40sin80cos?401cos10cos10-︒-︒︒︒︒===-.故答案为1-【点睛】本题的关键点有: 先切化弦,再通分; 利用辅助角公式化简;16.①②③ 【解析】函数())22sin2cos sin sin222sin 23f x x x x x x x π⎛⎫=-==-⎪⎝⎭. ①∵111132222121232f sin sin ππππ⎛⎫⎛⎫=⨯-==- ⎪ ⎪⎝⎭⎝⎭, 因此图象C 关于直线1112x π=对称,正确; ②∵2420333f sin πππ⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭, 因此图象C 关于点(23π,0)对称对称,正确; ③由x ∈5,1212ππ⎛⎫-⎪⎝⎭,得到2,322x πππ⎛⎫⎛⎫-∈- ⎪ ⎪⎝⎭⎝⎭,因此函数f (x )在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数,正确;④由y =2sin2x 的图角向右平移3π个单位长度得到图象2222222333y sin x sin x sin x πππ⎛⎫⎛⎫⎛⎫=-=-≠- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因此不正确.综上可知:只有①②③正确. 故答案为①②③.点睛:函数y =A sin(ωx +φ)(A >0,ω>0)的性质: (1)对称性:求对称轴只需令π2,2x k k Z ωϕπ+=+∈,求解即可,求对称中心只需令,x k k Z ωϕπ+=∈.(2)周期性:y =A sin(ωx +φ)存在周期性,其最小正周期为T =2πω.(3)单调性:由-2π+2k π≤ωx +φ≤2π+2k π(k ∈Z)得单调增区间;由2π+2k π≤ωx +φ≤32π+2k π(k ∈Z)得单调减区间. 17.(1)34a =-;(2)20x y -+=或7140x y -+=.(1)将圆C 的方程化为标准形式,得出圆C 的圆心坐标和半径长,利用圆心到直线的距离等于半径,可计算出实数a 的值;(2)利用弦长的一半、半径长和弦心距满足勾股定理可求得弦心距,利用点到直线的距离公式可求得实数a 的值,进而可得出直线l 的方程. 【详解】(1)圆C 的标准方程为()2244x y +-=,圆心C 的坐标为()0,4,半径长为2,当直线l 与圆C2=,解得34a =-;(2)由题意知,圆心C 到直线l的距离为d ==由点到直线的距离公式可得d ==整理得2870a a ++=,解得1a =-或7-.因此,直线l 的方程为20x y -+=或7140x y -+=. 【点睛】本题考查直线与圆的位置关系,考查利用直线与圆相切求参数以及根据弦长求直线方程,解答的核心就是圆心到直线的距离的计算,考查计算能力,属于中等题. 18.(1)见解析;(2)见解析;(3)3. 【解析】试题分析:(Ⅰ)利用三角形的中位线得出OM ∥VB ,利用线面平行的判定定理证明VB ∥平面MOC ;(Ⅱ)证明OC ⊥平面V AB ,即可证明平面MOC ⊥平面V AB ;(Ⅲ)利用等体积法求三棱锥A-MOC 的体积即可试题解析:(Ⅰ)证明:∵O ,M 分别为AB ,V A 的中点, ∴OM ∥VB ,∵VB ⊄平面MOC ,OM ⊂平面MOC , ∴VB ∥平面MOC ;(Ⅱ)证明:∵AC=BC ,O 为AB 的中点, ∴OC ⊥AB ,又∵平面V AB ⊥平面ABC ,平面ABC∩平面V AB=AB ,且OC ⊂平面ABC ,∴OC ⊥平面VAB ,∵OC ⊂平面MOC ,∴平面MOC ⊥平面V AB(Ⅲ)在等腰直角三角形ACB中,AC BC ==所以2,1AB OC ==.所以等边三角形V AB的面积VAB S ∆=又因为OC ⊥平面V AB ,所以三棱锥C V -AB的体积等于13VAB OC S ∆⨯⨯=. 又因为三棱锥V C -AB 的体积与三棱锥C V -AB 的体积相等,所以三棱锥V C -AB的体积为3. 考点:平面与平面垂直的判定;直线与平面平行的判定;用向量证明平行19.(1)10x y +-=;(2)22(2)(1)4x y -++=【解析】【详解】试题分析: (1)设所求的直线方程为:1x y a b+=,(0,0)a b >>,将P 点坐标带入,再根据图象写出三角形面积,得到关于a,b 的方程组,解出即可;(2) 设圆心坐标(),1a a -+,又圆经过()2,1M ,()4,1N -,则M,N 到圆心的距离相等,列出方程求出a 值,进而求出圆心和半径,写出圆的方程.试题解析:(1)设所求的直线方程为:1x y a b+=,(0,0)a b >>, ∵过点()1,2P -且与两坐标轴的正半轴所围成的三角形面积等于12,∴1211122a b ab -⎧+=⎪⎪⎨⎪=⎪⎩,解得1a b ==,故所求的直线方程为:x+y-1=0.(2)设圆心坐标(),1a a -+,则∵圆经过()2,1M ,()4,1N -,∴()()()()2222211411a a a a -+-+-=-+-++, ∴2a =,圆心()2,1-,圆半径2r ,∴()()22214x y -++=.20.(1)详见解析;(2)5. 【分析】(1)过B 作CD 的垂线交CD 于F ,则1,2BF AD EF AB DE FC ===-==,在Rt BFE ∆中和Rt BFC ∆中利用勾股定理证明BE BC ⊥,再证明1BE BB ⊥,即可证明11BE BB C C ⊥平面;(2)先求得11A C E S ∆的面积,设点B 1到平面11EA C 的距离为d,用d 表示111B EAC -三棱锥的体积,列式计算即可.【详解】(1)过B 作CD 的垂线交CD 于F,则1,2BF AD EF AB DE FC ===-==在Rt BFE BE Rt BFC BC ∆∆中,中,在2229BCE BE BC EC ∆+中,因为==,故BE BC ⊥由1111BB ABCD BE BB BE BB C C ⊥⊥⊥平面,得,所以平面(2)111111113A B C E A B C V AA S ∆-⋅三棱锥的体积=11111Rt A D C AC ∆=在中, 同理,1EC =1EA =因此11A C E S ∆=.设点B 1到平面11EA C 的距离为d,则111B EAC -三棱锥的体积1113A EC V d S ∆⋅⋅=,5d == 21.(1)3x-4y-3=0或x=1;(2)详见解析.【解析】试题分析: (1)当k 存在时,设过点A 切线的方程为()1y k x =-,由圆心到直线的距离等于半径列出方程,求出k 值,即可得到切线方程; 当k 不存在时方程1x =也满足;(2) 设点(),P x y ,则由两点之间的距离公式知()22222||222||2AP BP x y OP +=++=+,即所求的最大值可转化为2||OP 最大值, 又P 为圆上点,所以()max OP OC r =+,再联立此时的直线OC 与圆方程求出对应的P 点坐标.试题解析:(1) 当k 存在时,设过点A 切线的方程为()1y k x =-,∵圆心坐标为()3,4,半径2r =,∴2=,计算得出34k =, ∴所求的切线方程为340x y -=; 当k 不存在时方程1x =也满足,综上所述,所求的直线方程为3430x y --=或1x =.(2)设点(),P x y ,则由两点之间的距离公式知()22222||222||2AP BP x y OP +=++=+, 要22||AP BP +取得最大值只要使2||OP 最大即可, 又P 为圆上点,所以()max 27OPOC r =+==, ∴()222max ||272100AP BP +=⨯+=,此时直线4:3OC y x =,由224368210y x x y x y ⎧=⎪⎨⎪+--+=⎩,计算得出95125x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)或215285x y ⎧=⎪⎪⎨⎪=⎪⎩,∴点P 的坐标为.22.(1)详见解析;(2). 【详解】 试题分析: (1)由线面垂直的性质定理可得1A A BC ⊥,在Rt ABC △中,根据长度比例可得DBA ABC ∽,可推出AD BC ⊥,再由线面垂直的判定定理推出BC ⊥平面1A AD ,根据定义得出结论成立;(2) 作1AE C C ⊥交1C C 于E 点,连接BE ,由线面垂直得到线线垂直,找到二面角的平面角, 过1C 作1C F AC ⊥交AC 于F 点,在三角形中求出1C CF ∠,再从Rt AEC △和Rt BAE △中分别求出AE 和BE,代入公式即可.试题解析:(1) 1A A ⊥平面ABC BC ,⊂平面ABC ,∴ 1A A BC ⊥.在Rt ABC △中,2AB AC BC ==∴=, :1:2BD DC =,3BD ∴=,又3BD AB AB BC==, DBA ABC ∴∽,90ADB BAC ∴∠=∠=,即AD BC ⊥.又1A A AD A =,BC ∴⊥平面1A AD , 又A 1D ⊂平面1A AD .BC ∴⊥A1D.(2)如图,作1AE C C ⊥交1C C 于E 点,连接BE ,由已知得AB ⊥平面11ACC A .∴AB┴CC1,又CC 1AE=E,∴CC 1┴平面AEB, ∴CC 1┴BE,AEB ∴∠为二面角1A CC B --的平面角.过1C 作1C F AC ⊥交AC 于F 点,则1CF AC AF =-=,11C F A A =, 160C CF ∴∠=.在Rt AEC △中,sin6022AE AC ==⨯= 在Rt BAE △中,AB=, AE=, ∴BE=.即二面角1A CC B --的余弦值为.。
广西陆川县中学2024届高一数学第二学期期末达标测试试题含解析

广西陆川县中学2024届高一数学第二学期期末达标测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.已知向量(),2m a =,()1,1n a =+,若//m n ,则实数a 的值为( ) A .23-B .2或1-C .2-或1D .2-2.若(3,4)AB =,A 点的坐标为()2,1--,则B 点的坐标为( ) A .()1,3B .()5,5C .()1,5D .()5,43.设0x >,0y >,24x y +=,则()()121x y xy++的最小值为( )A .2B .4C .72D .924.在空间直角坐标系中,点P (3,4,5)关于yOz 平面的对称点的坐标为( ) A .(−3,4,5) B .(−3,−4,5) C .(3,−4,−5) D .(−3,4,−5)5.函数()cos 3f x x πω⎛⎫=+ ⎪⎝⎭的最小正周期为π,则()f x 的图象的一条对称轴方程是( ) A .12x π=-B .6x π=-C .6x π=D .3x π=6.某林区改变植树计划,第一年植树增长率,以后每年的植树增长率都是前一年植树增长率的,若成活率为,经过年后,林区的树木量是原来的树木量的多少倍?( ) A .B .C .D .7.函数()cos f x x x x =+在[],ππ-上的图像大致为( )A .B .C .D .8.已知实数满足250x y ++=,22x y +的最小值为( )A 5B .5C .25D .559.为了得到函数sin(2)3y x π=-的图像,只需把函数sin(2)6y x π=+的图像A .向左平移4π个长度单位 B .向右平移4π个长度单位C .向左平移2π个长度单位D .向右平移2π个长度单位10.角α的终边经过点321⎛⎫ ⎪ ⎪⎝⎭,那么tan α的值为( ) A .12B .3C .3D .3二、填空题:本大题共6小题,每小题5分,共30分。
广西省陆川县中学高一数学下学期周测 新人教A版必修3
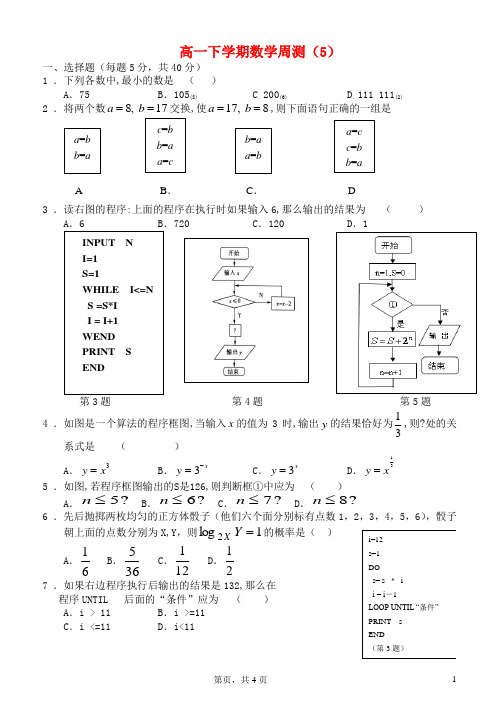
高一下学期数学周测(5)一、选择题(每题5分,共40分) 1 .下列各数中,最小的数是 ( )A .75B .105(8)C .200(6)D .111 111(2) 2 .将两个数8, 17a b ==交换,使17, 8a b ==,则下面语句正确的一组是3 .读右图的程序:上面的程序在执行时如果输入6,那么输出的结果为 ( )720 C .120 D .1第4题 第5题 4 .如图是一个算法的程序框图,当输入x 的值为3时,输出y 的结果恰好为13,则?处的关系式是 ( )A .3y x = B .3xy -= C .3xy = D .13y x = 5 .如图,若程序框图输出的S 是126,则判断框①中应为 ( )A .?5≤nB .?6≤nC .?7≤nD .?8≤n6 .先后抛掷两枚均匀的正方体骰子(他们六个面分别标有点数1,2,3,4,5,6),骰子朝上面的点数分别为X,Y ,则1log 2=Y X 的概率是( )A .61 B .365 C .121 D .217 .如果右边程序执行后输出的结果是132,那么在程序UNTIL 后面的“条件”应为 ( ) A .i > 11 B .i >=11 C .i <=11 D .i<11INPUT NI=1 S=1WHILE I<=N S =S*I I = I+1 WEND PRINT S ENDa =b b =ac =b b =a a =c b =aa =b a =cc =b b =a AB .C .Di=12 s=1 DO s= s ﹡ i i = i -1LOOP UNTIL “条件” PRINT s END (第3题)Read xIf x >0 Then1y x ←+Else1y x ←-End If Print y8 .甲、乙两人相约在某地见面,没有安排确定的时间,但都要在晚上7点到8点之间到达,先到的人等待10分钟,若没有见到另一人则离开,那么他们能见面的概率是(A .23B .1136C .13D .169 .如图,汉诺塔问题是指有3根杆子A .B .C ,B 杆上有若干碟子,把所有碟子从B 杆移到C 杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面。
人教版数学高一-广西陆川县中学高一下学期周测(6)数学(理)试题

陆川中学2015级高一(下)数学(理)周测(6)2016年4月17日一、选择题(请将选择题的答案填写在后面答题卡的对应题号的表格内)1 .直线2y=与正切曲线tan 3y x =相交的相邻两点间的距离是( )A .πB .23πC .3π D .6π 2 .已知1sin 123πα⎛⎫+= ⎪⎝⎭,则7cos 12πα⎛⎫+ ⎪⎝⎭的值等于 ( )A .13 B.3 C .13-D.3-3 .函数y =的定义域是 ( )A .2,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦B .2,2()66k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦C .22,2()33k k k Z ππππ++∈⎡⎤⎢⎥⎣⎦D .222,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦4 .将函数()sin()6f x x πω=+的图象关于6x π=对称,则ω的值可能是( )A .12B .32C .5D .25 .已知7sin cos (0)13αααπ+=<<,则tan α=( )A .125-B .512-C .512D .125-或512-6=( )其中,2πθπ⎛⎫∈ ⎪⎝⎭( )A .sin θ-cos θB .cos θ-sin θC .±(sin θ-cos θ)D .sin θ+cos θ7 .已知αsin 是方程06752=--x x 的根,且α是第三象限角,则()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛--απαπαπαππα2sin 2co tan 23co 23sin 2s s = ( ) A .169 B .169-C .43 D .43-8 .在ABC ∆中,角,A B 均为锐角,且cos sin A B >,则ABC ∆的形状是( )A .锐角三角形B .直角三角形C .等腰三角形D .钝角三角形9 .已知sin sin αβ>,那么下列命题成立的是( )A .若,αβ是第一象限角,则cos cos αβ>;B .若,αβ是第二象限角,则tan tan αβ>;C .若,αβ是第三象限角,则cos cos αβ>;D .若,αβ是第四象限角,则tan tan αβ>10.关于)42sin(3)(π+=x x f 有以下命题,其中正确的个数①若0)()(21==x f x f ,则)(21Z k k x x ∈=-π;②)(x f 图象与)42cos(3)(π-=x x g 图象相同;③)(x f 在区间]83,87[ππ--上是减函数;④)(x f 图象关于点)0,8(π-对称.( )A .0B .1C .2D .311.定义在R 上的偶函数)(x f 在(,0]-∞上是减函数,βα,是钝角三角形的两个锐角,则下列不等式关系中正确的是 ( )A .(sin )(cos )f f αβ>B .(cos )(cos )f f αβ<C .(cos )(cos )f f αβ>D .(sin )(cos )f f αβ<二、填空题(请将填空题的答案填写在答题卡对应题号的横线上)12.函数sin(2)6y x π=-的单调减区间是__________________13.若函数()2sin (0)3f x x πωω⎛⎫=-> ⎪⎝⎭的图象两相邻对称轴之间的距离为3,则(0)(1)(2)(2016)f f f f ++++= .14.函数1cos 21cos 2-+=x x y的值域为 .15.已知函数()cos(3)3f x x π=+,其中[,]6x m π∈,若()f x 的值域是[1,2--,则m 的取值范围是 .陆川中学2015级高一(下)数学(理)周测(6)答题卡姓名__________ 班级_________ 座号_________ 分数_________一、选择题(每小题5分,满分55分)题号 1 2 3 4 5 6 7 8 9 10 11 答案二、填写题(每小题5分,满分20分)12. 13. 14. ;15. . 三、解答题(每小题12分)16.设(0,4),(0,4)x y ∈∈.(1)若,x N +∈y N +∈以,x y 作为矩形的边长,记矩形的面积为S ,求4S <的概率; (2)若,,x R y R ∈∈求这两数之差不大于2的概率.17.已知函数()2sin 23f x x π⎛⎫=+⎪⎝⎭(1)求函数()f x 的最小正周期和单调增区间; (2)当[,]33x ππ∈-时,求()f x 的最值,并指明相应x 的值. (3)在给出的直角坐标系中,画出函数()y f x =在区间[0,]π上的图象.陆川中学2015级高一(下)数学(理)周测(6)参考答案一、选择题1. C 解析:直线2y =与正切曲线tan 3y x =相交的相邻两点间的距离就是函数tan 3y x =的最小正周期3π,故选C. 2. C 提示:71cos cos sin 12122123ππππααα⎛⎫⎛⎫⎛⎫+=++=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故选择C. 3. D 提示:由01cos 2≥+x 得21cos -≥x ,∴222233k x k πππ-≤≤π+,Z k ∈. 4. D 解析:试题分析:根据正弦型函数的性质及已知条件,有()662k k Z ωππππ+=+∈,取0k =,得2ω=满足条件,选D5. A分析:由7sin cos 13αα+=可得2249sin 2sin cos cos 169αααα++=即4912sin cos 169αα+=,也就是1202sin cos 169αα=-,因为0απ<<,所以sin 0,cos 0αα><,且222120289(sin cos )sin 2sin cos cos 1169169αααααα-=-+=+=,所以17sin cos 13αα-==,联立方程7sin cos 1317sin cos 13αααα⎧+=⎪⎪⎨⎪-=⎪⎩,解得12sin 135cos 13αα⎧=⎪⎪⎨⎪=-⎪⎩,所以sin 12tan cos 5ααα==-,故选A. 6. A 提示:=== sin cos θθ=-又,2πθπ⎛⎫∈ ⎪⎝⎭,∴sin 0,cos 0θθ><= sin θ-cos θ,故选A7. B 提示:因为根据诱导公式可知原式化简为22cos (sin )tan tan sin cos α-αα=-ααα,343sin cos tan 554α=-∴α=-∴α=,因此选B8. D.提示:cos sin ,sin sin ,2A B A B π⎛⎫>∴-> ⎪⎝⎭又角,A B 均为锐角,则0,0,222B A A B πππ<<-<∴<+<且ABC ∆中,,2A B C C πππ++=∴<<,故选D.9. D 提示:A 错误,例如060,30,cos cos ;αβαβ==<B 错误,例如00120,145,tan tan ;a βαβ==< C 错误,例如0210,240,cos cos ;αααβ==< D 正确,,(2,2)(),2k k k Z παβππ∈-∈正弦函数sin y x =在(2,2)2k k πππ-上是增函数,22,2k k ππβαπ∴-<<<又正切函数tan y x =在(2,2)2k k πππ-上是增函数,所以tan tan .αβ>故选D10. D. 分析:①:∵)42sin(3)(π+=x x f ,0)()(21==x f x f ,∴)(221Z k k x x ∈=-π,∴①错误; ②:∵)42sin(]2)42sin[()42cos(ππππ+=+-=-x x x ,∴②正确;③:当]83,87[ππ--∈x 时,]2,23[42πππ--∈+x ,∴)(x f 在区间]83,87[ππ--上是减函数,③正确;④:当8π-=x 时, 042=+πx ,∴0)8(=-πf ,∴④正确.11. D 提示:因为,αβ是钝角三角形的两个锐角,所以090αβ︒<+<︒,即090αβ︒<<︒-,所以0sin sin(90)cos 1αββ<<︒-=<,因为定义在R 上的偶函数)(x f 在(,0]-∞上是减函数,所以)(x f 在()∞+,0上单调递增.所以(sin )(cos )f f αβ< 二、填空题 12. ,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦提示:因为,sin(2)6y x π=-=sin(2)6x π--,所以,由222,262k x k k z πππππ-≤-≤+∈,得,,63k x k k z ππππ-≤≤+∈,故函数sin(2)6y x π=-的单调减区间是,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.13.6T=,所以263ππωω=⇒=,所以()2sin 33f x x ππ⎛⎫=-⎪⎝⎭所以(0)(1)(2)(2016)336((0)(1)(2)(3)(4)(5))(0)f f f f f f f f f f f ++++=⨯++++++3362002sin 3π⎛⎛⎫⨯⨯+-+-= ⎪ ⎝⎭⎝⎭ 14.此为dx c bx a y-+=cos cos 型的三角函数求最值问题,分子、分母的三角函数同名、同角,这类三角函数一般先化为部分分式,再利用三角函数的有界性去解.或者也可先用反解法,再用三角函数的有界性去解.解法一:原函数变形为1cos ,1cos 221≤-+=x x y ,可直接得到:3≥y 或.31≤y解法一:原函数变形为()()∴≤-+∴≤-+=,1121,1cos ,121cos y y x y y x 3≥y 或.31≤y15.解析:因为[,]6x m π∈,所以533633x m πππ≤+≤+,当5336x ππ+=即6x π=时,()62f π=-而()f x 的值域是[1,2--,故可得72525333636918m m m πππππππ≤+≤⇒≤≤⇒≤≤,故m 的取值范围是25[,]918ππ. 三、解答题16. (1)59.(2)222423()44P II -==提示:(1)x=1,2,3.y=1,2,3.所以把所有的结果表示出来.然后再从这些结果当中找出事件发生的结果.再利用古典概型概率计算公式计算即可. (2) 所有的结果的区域为{}(,)|04,04,x y x y Ω=<<<<两个之差不大于2的所有结果的区域为{}(,)|04,04,||2,II x y x y x y =<<<<-≤分别求出对应区域的面积,然后求面积比即可.(1)若,x N +∈则(,)x y 所有的结果为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共9个,满足4S <的(,)x y 所有的结果为1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),共5个,故4S <的概率为59. (2)所有的结果的区域为{}(,)|04,04,x y x y Ω=<<<<两个之差不大于2的所有结果的区域为{}(,)|04,04,||2,II x y x y x y =<<<<-≤则222423()44P II -== 17. 分析:(1)先利用三角恒等变换公式对函数的解析式进行化简,用二倍角公式和两个角的和的正弦公式,再根据化简后的解析式求三角函数的周期;(2)在所给的区间上找出函数值域的几个特殊点:最大值和最小值点,再列出表格,在坐标系中描出点画出函数图像. 解析: (1) ()2sin 23f x x π⎛⎫=+ ⎪⎝⎭所以f(x)的最小正周期T=ππ=22. 由2k π-2π<2x+3π<2kπ+2π得125ππ-k <2x+3π<12ππ+k所以f(x)的单调增区间为]12,125[ππππ+-k k (k ∈Z).(2)由23333x x πππππ-≤≤⇒≤+≤所以当23x ππ+=即3x π=时,()f x 取得最小值()2sin 03f ππ==当232x ππ+=即12x π=时,()f x 取得最大值()2sin2122f ππ==.(3)列表:x 012π 3π 127π 65π π2x+3π 3π 2π π 23π 2π 37π f(x)32-23描点连线得图象,如图所示.。
【数学】广西陆川县2020学年高一下学期期末考试理科数学试题版含答案

【关键字】数学广西陆川县中学2017年春季期高一期末考试卷理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M={-1,1},N={x|{x<0或x>},则下列结论正确的是()A.N⊆MB.N∩M=∅C.M⊆ND.M∪N=R2.设=(2,-1),=(-3,4),则2+等于()A.(3,4)B.(1,2)C.-7D.33.若cos>0,sin <0,则角的终边在( ).A.第一象限B.第二象限C.第三象限D.第四象限4.sin 20°cos 40°+cos 20°sin 40°的值等于( ).A.B.C.D.5. 已知0<A<,且cos A=,那么sin 等于( ).A.B.C.D.6. 若,则()A.-3 B.C.-D.7. 已知,则()A.B.C.D.8. 函数的周期,振幅,初相分别是()A.,,B. ,,C. ,,D. ,,9.要得到函数y=sin(2x-)的图象,只要将函数y=sin2x的图象( )A.向左平行移动个单位B.向左平行移动个单位C.向右平行移动个单位D.向右平行移动个单位10.函数是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数11.已知是定义在R上的偶函数,且,当时,,则()A .0B .C .-D .3.512. 函数y=Asin(ωx+φ)(A >0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )12题图A.2B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13. 半径为的半圆卷成一个圆锥,则圆锥的体积为 .14. 设,若,则的最小值为 .15. 在正四面体中,分别是和的中点,则异面直线和所成角为__________.16. 数列是正数列,且,则= .三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17、(本小题满分10分,(1)小问5分,(2)小问5分)已知全集,函数的定义域为集合,集合(1)求; (2)求.18、(本小题满分12分,(1)小问6分,(2)小问6分)在平面直角坐标系中,若角的始边为轴的非负半轴,其终边经过点.(1)求的值; (2)求的值.19、(本小题满分12分,(1)小问6分,(2)小问6分)已知二次函数,且满足.(1)求函数的解析式;(2)若函数的定义域为,求的值域.20、(本小题满分12分,(1)小问6分,(2)小问6分)已知函数 ,且的最小正周期为.(1)求的值; (2)求函数在区间上的单调增区间.21、(本小题满分12分,(1)小问7分,(2)小问5分)已知函数 是奇函数.(1)判断函数在上的单调性,并用定义法证明你的结论;(2)若对于区间[]5,2上的任意x 值,使得不等式n x f x+≤2)(恒成立,求实数n 的取 值范围.22、(本小题满分12分,(1)小问4分,(2)小问8分) 已知函数12sin 94)cos sin ()(--+=x x x a x f ,若9132)4(-=πf (1)求a 的值,并写出函数)(x f 的最小正周期(不需证明);(2)是否存在正整数k ,使得函数)(x f 在区间[]πk ,0内恰有2017个零点? 若存在,求出k 的值,若不存在,请说明理由.理科数学答案1-6CBDBD D 7-12ACDBBC13. 3R 14. 4 15. 4π 16. 226n n + 17解:(1)由题意可得:⎩⎨⎧>-≥-01003x x ,则 {}103|<≤=x x A .........….5分(2){}75|≥<=x x x B C U 或........….8分{}10753|)(<≤<≤=x x x A B C U 或 ........…10分18解:(1)由任意角三角函数的定义可得:224tan ==α........….6分 (2)ααααcos sin cos sin 2++=原式.....…8分 1tan 1tan 2++=αα.....…10分 351214=++=.....…12分 19解:(1))3()1(f f =-由可得该二次函数的对称轴为1=x .....…2分即124=-m从而得2-=m ....…4分 所以该二次函数的解析式为142)(2++-=x x x f ....…6分(2)由(1)可得()312)(2+--=x x f ....…9分 所以(](]3,15-2,2)(上的值域为在-x f ....…12分20解:(1)x x x x f ωωω2cos 212sin 322cos 1)(-+-=....…3分2162sin 2+⎪⎭⎫ ⎝⎛-=πωx ....…5分 由题意得πωπ=22 即可得1=ω....…6分 (2)由(1)知2162sin 2)(+⎪⎭⎫ ⎝⎛-=πx x f 则由函数单调递增性可知:Z k k x k ∈+≤-≤-,226222πππππ 整理得Z k k x k ∈+≤≤-,36ππππ........9分所以()π,0)(在x f 上的增区间为⎥⎦⎤ ⎝⎛3,0π,⎪⎭⎫⎢⎣⎡ππ,65...........12分 21解:(1)由条件可得0)()(=+-x f x f ,即 0121log 121log 22=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛---x mx x mx 化简得222411x x m -=-,从而得2±=m ;由题意2-=m 舍去,所以 2=m 即x x x x f -⎪⎭⎫ ⎝⎛-+=1221log )(2...........2分 ⎪⎭⎫ ⎝⎛+∞∈,21)(x x f 在上为单调减函数...........3分 证明如下:设+∞<<<2121x x ,则 22221112211221log 1221log )()(x x x x x x x f x f +⎪⎪⎭⎫ ⎝⎛-+--⎪⎪⎭⎫ ⎝⎛-+=- 因为+∞<<<2121x x ,所以012>-x x ,012,01221>->-x x ;所以可得1211212212211>+-⋅-+x x x x ,所以0)()(21>-x f x f ,即)()(21x f x f >;所以函数)(x f 在⎪⎭⎫ ⎝⎛+∞∈,21x 上为单调减函数...........7分 (2)设x x f x g 2)()(-= ,由(1)得)(x f 在⎪⎭⎫ ⎝⎛+∞∈,21x 上为单调减函数, 所以x x f x g 2)()(-=在[]5,2上单调递减;所以x x f x g 2)()(-=在[]5,2上的最大值为()6log 2352-=g ...........10分由题意知()x g n ≥在[]5,2上的最大值,所以6log 352-≥n ...........12分22解:(1) π==T a ,1……………4分(2)存在n =504,满足题意……5分理由如下:当⎥⎦⎤⎢⎣⎡∈2,0πx 时,12sin 94)cos (sin )(--+=x x x x f ,设x x t cos sin +=,则 []2,1∈t ,12sin 2-=t x ,则9594)(2-+-=t t t g ,095942=-+-t t 可得 1=t 或45=t ,由x x t cos sin +=图像可知, x 在⎥⎦⎤⎢⎣⎡2,0π上有4个零点满足题意…8分 当),2(ππ∈x 时,12sin 94)cos (sin )(---=x x x x f ,x x t cos sin -=,则 (]2,1∈t ,212sin t x -=,91394)(2-+=t t t h ,0913942=-+t t ,1=t 或413-=t ,因为(]2,1∈t ,所以x 在⎪⎭⎫ ⎝⎛ππ,2上不存在零点。
广西壮族自治区玉林市陆川实验中学2021-2022学年高一数学理月考试题含解析

广西壮族自治区玉林市陆川实验中学2021-2022学年高一数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知点(3,m)到直线x+y﹣4=0的距离等于,则m=()A.3 B.2 C.3或﹣1 D.2或﹣1参考答案:C【考点】点到直线的距离公式.【分析】由题意可得=,解之可得.【解答】解:由题意可得=,即|m﹣1|=2,解得m=3,或m=﹣1故选C【点评】本题考查点到直线的距离公式,属基础题.2. 已知直线l:x+ay﹣1=0(a∈R)是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C 的一条切线,切点为B,则|AB|=()A.2 B.4C.2D.6参考答案:D【考点】圆的切线方程.【分析】求出圆的标准方程可得圆心和半径,由直线l:x+ay﹣1=0经过圆C的圆心(2,1),求得a 的值,可得点A的坐标,再利用直线和圆相切的性质求得|AB|的值.【解答】解:∵圆C:x2+y2﹣4x﹣2y+1=0,即(x﹣2)2+(y﹣1)2 =4,表示以C(2,1)为圆心、半径等于2的圆.由题意可得,直线l:x+ay﹣1=0经过圆C的圆心(2,1),故有2+a﹣1=0,∴a=﹣1,点A(﹣4,﹣1).∵AC==2,CB=R=2,∴切线的长|AB|==6.故选:D.3. 在中,若=1,C=, =则A的值为 ( )A. B. C. D.参考答案:A略4. 设,若对任意的时,不等式恒成立,则的取值范围是()A. B. C. D.参考答案:B略5. 函数的图象大致是()A B CD参考答案:A6. 已知等比数列{a n}中,各项都是正数,且成等差数列,则等于()A. B. C. D.参考答案:C【分析】由条件可得a3=a1+2a2 ,即a1q2=a1+2a1q,解得q=1.代入所求运算求得结果.【详解】∵等比数列{a n}中,各项都是正数,且a1,a3,2a2成等差数列,故公比q不等于1.∴a3=a1+2a2 ,即a1q2=a1+2a1q,解得q=1.∴3+2,故选:C.【点睛】本题主要考查等差中项的性质,等比数列的通项公式,考查了整体化的运算技巧,属于基础题.7. 已知数列是等差数列,若,,且数列的前项和有最大值,那么取得最小正值时等于A. B. C. D.参考答案:c试题分析:由等差数列的性质和求和公式可得又可得:而,进而可得取得最小正值时.考点:等差数列的性质8. 若实数a、b满足条件a>b,则下列不等式一定成立的是A. B. a2>b2 C. ab>b2 D. a3>b3参考答案:D【分析】根据题意,由不等式的性质依次分析选项,综合即可得答案.【详解】根据题意,依次分析选项:对于A、,时,有成立,故A错误;对于B、,时,有成立,故B错误;对于C、,时,有成立,故C错误;对于D、由不等式的性质分析可得若,必有成立,则D正确;故选:D.【点睛】本题考查不等式的性质,对于错误的结论举出反例即可.9. 化简的结果为( )A.5 B.C.﹣D.﹣5参考答案:B【考点】方根与根式及根式的化简运算.【专题】计算题.【分析】利用根式直接化简即可确定结果.【解答】解:===故选B【点评】本题考查根式的化简运算,考查计算能力,是基础题.10. 已知中,角的对边分别为,,则()A. B. C. D.参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b 有三个不同的根,则m 的取值范围是.参考答案:(3,+∞)【考点】根的存在性及根的个数判断.【分析】作出函数f(x)=的图象,依题意,可得4m﹣m2<m(m>0),解之即可.【解答】解:当m>0时,函数f(x)=的图象如下:∵x>m时,f(x)=x2﹣2mx+4m=(x﹣m)2+4m﹣m2>4m﹣m2,∴y要使得关于x的方程f(x)=b有三个不同的根,必须4m﹣m2<m(m>0),即m2>3m(m>0),解得m>3,∴m的取值范围是(3,+∞),故答案为:(3,+∞).12. 已知函数,若对任意都有()成立,则的最小值为__________.参考答案:4π【分析】根据和的取值特点,判断出两个值都是最值,然后根据图象去确定最小值.【详解】因为对任意成立,所以取最小值,取最大值;取最小值时,与必为同一周期内的最小值和最大值的对应的,则,且,故. 【点睛】任何一个函数,若有对任何定义域成立,此时必有:,.13. 若函数的零点为,则满足且k为整数,则k= ▲.参考答案:214. 将正偶数排列如下表,其中第行第个数表示为,例如,若,则▲ .参考答案:6115. 给出函数,若对一切成立,则________。
广西陆川县中学2020学年高一数学5月月考试题 理
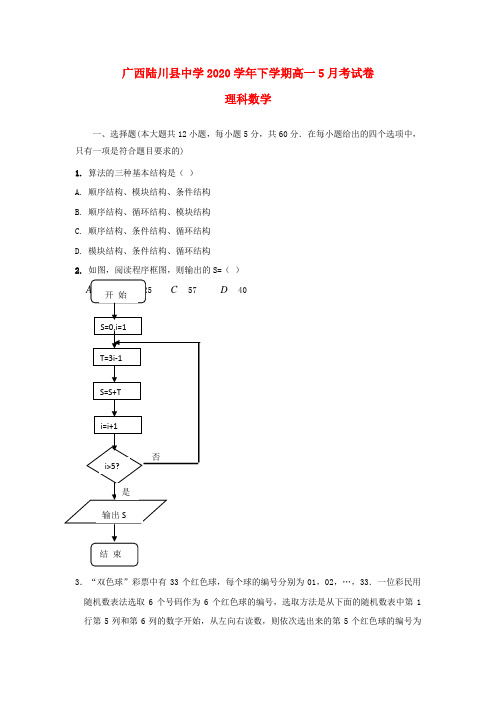
广西陆川县中学2020学年下学期高一5月考试卷理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.算法的三种基本结构是()A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2.如图,阅读程序框图,则输出的S=()D403.“双色球”彩票中有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第5列和第6列的数字开始,从左向右读数,则依次选出来的第5个红色球的编号为( )7816 6572 0802 6314 0214 4319 9714 0198 3204 9234 4936 8200 3623 4869 6938 7181 A. 01B. 02C. 14D. 194.下列函数的最小值为2的是( )A. 1lg lg y x x =+B. y =C. 22xxy -=+ D. 1sin (0)sin 2y x x x π=+<< 5.第二次数学周练题比较难,姚老师对本班学生的12道选 择题答题情况进行了统计分析,出错的人数用茎叶图表示, 如下图所示,则该组数据的中位数、众数、极差分别是( ) A. 18,12,29B. 19,22,29 第5题图C. 18,22,29D. 19,12,6.执行如图所示的程序语句,输出的结果为( ) A. 3025- B. 1009- C. 10097.从装有大小材质完全相同的1个白球,2个黑球和3个红球的 不透明口袋中,随机摸出两个小球,则两个小球同色的概率 是( ) A. 15B.415C.25D.138.若(0,)απ∈,且,则cos 2α=( ).A D 0 1 31 2 2 8 6 2 0 2 3 2 2 3 0xyO 1 2 2-A B9. 要得到函数y sin(2x 4π)的图象,只需将函数y cos2x 的图象( ).A .向左平移8π个单位 B .向右平移8π个单位长度C .向左平移4π个单位长度 D .向右平移4π个单位长度 10.如图所示,为函数()()2sin f x x ωϕ=+(0,2πωϕπ>≤≤)的部分图象,其中,A B 两点之间的距离为5,则()=1f ( ). A .3 B .3- C .1 D .1-11. 已知函数21xy -=m x --有两个零点,则实数m 的取值范围是( )A .(-2,2)B .(-1,1)C . 2)D .]22[,-12. 过点(3,1)作圆(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为( ) A .2x +y -3=0 B .2x -y -3=0 C .4x -y -3=0 D .4x +y -3=0二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.=(2,3),=(-3,5)a b ,则在a b 方向上的投影为_________.14.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE →·BD →=________.15.若直线3450x y -+=与圆222(0)x y r r +=>相交于,A B 两点,且0120AOB ∠=()O 为坐标原点,则r =_________.16.已知函数1tan sin )(++=x b x a x f ,满足(5)7f =,则)5(-f =_________.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (10分)若2cos 3α=,α是第四象限角,求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值.18. (12分)用“五点法”画出函数3sin(2)3y x π=-在 7,66x ππ⎡⎤∈⎢⎥⎣⎦的简图.19.(12分)全世界越来越关注环境保护问题,某监测站点于2020年8月某日起连续n 天监测空气质量指数(AQI ),数据统计如下:(1)根据所给统计表和频率分布直方图中的信息求出n ,m 的值,并完成频率分布直方图. (2)由频率分布直方图,求该组数据的平均数与中位数.20.(12分) 已知角的终边经过点,且α为第二象限角.(1)求实数m 和的值;空气质量指数(μg/m 3)0﹣50 51﹣100 101﹣150 151﹣200 201﹣250 空气质量等级空气优 空气良 轻度污染中度污染 重度污染天数2040m105(2)若,求βαβαπβαπβαsin sin 3)cos()cos(sin )2cos(3cos sin --+-+的值.21.(12分)已知函数22()44f x x ax b =-+,{|13}A x x =≤≤,{|14}B x x =≤≤. (1)若a ,b 都是从集合A 中任取的整数,求函数()y f x =有零点的概率.(2)若a ,b 都是从集合B 中任取的实数,求函数()y f x =在区间[2,4]上为单调函数的概率.22.(12分)在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使MA =2MO ,求圆心C 的横坐标a 的取值范围.理科数学答案1 C2 D3 A4 C5 B6 B7B 8 A 9 B 10D 11. C 12. A13.9343414.2 15. 2 16.-5 17、25. 18.略。
【满足】广西陆川县2020学年高一数学下学期期中试题理

【关键字】满足广西陆川县2016-2017学年高一数学下学期期中试题理一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知五个数成等比数列,则的值为()A.3 B.C.D.2.已知,则()A.B.C.D.3.已知向量,且,则()A.B.C.D.4.在数列中,,则()A.B.C.D.5.在下列区间中,函数的零点所在大致区间为()A. B.C.()D()6、若函数对于任意实数恒有,则等于()A、 B、 C、 D、7、函数是定义在上为增函数,且,则实数的取值范围是()A、 B、 C、 D、8、函数的零点所在的大致区间是()A、 B、 C、 D、9、下列四种说法:①函数在R上单调递加;②若函数在上单调递减,则;③若,则;④若是定义在R上的奇函数,则,其中正确的序号是()A、① ②B、②③C、③ ④D、②④资*源%库10、函数,其中,若动直线与函数的图象有三个不同的交点,它们的横坐标分别为,则的取值范围是()A、B、C、D、11.设等差数列满足,公差,当且仅当时,数列的前项和取得最大值,求该数列首项的取值范围( )A.B.C.D.12.在锐角三角形中,,,分别是角,,的对边,=,则的取值范围为( )A .B .C .D .二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13. 函数的图像关于 对称.14.已知是奇函数,,且则 .15. 若函数的值域是 .16.对于函数,定义域为,以下命题正确的是 (只要求写出命题的序号) ①若,则是上的偶函数;②若对于任意,都有,则是上的奇函数;③若函数在上具有单调性且,则是上的递减函数;④若,则是上的递加函数。
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (本小题满分10分.)已知等差数列中,.等比数列的通项公式.(I )求数列的通项公式;(II )求数列的前项和.18、(12分)设(1)求的值及的定义域;(2)求在区间上的最大值19.(本题满分12分)已知函数(1)求函数的最小正周期和函数的单调递加区间; (2)已知中,角的对边分别为,若,求.20. (本小题满分12分.)已知(1)若;(2)若函数)(x f 在区间()1,+∞上是增函数,求实数的取值范围.21.(本小题满分12分.)如图,,A B 是海面上位于东西方向相距5(33)+海里的两个观测点,现位于A 点北偏东045,B 点北偏西060的D 点有一艘轮船发出求救信号,位于B 点南偏西060且与B 点相距3C 点的救援船立即前往营救,其航行速度为30海里/小时,则该救援船达到D 点需要多长时间?22. (本小题满分12分.)已知函数()()2lg 12++++=a x a x x f ,()2-≠a (1)若()x f 能表示成一个奇函数()x g 和一个偶函数()x h 的和,求()x g 和()x h 的解析式;(2)若()x f 和()x g 在区间()()21,+∞-a 上都是减函数,求a 的取值范围; (3)在(2)的条件下,比较()1f 和61的大小. 理科数学答案1-5.BAACB 6-10ABADA 11.C 12.B 13.y 轴14.6 15. ()(),22,-∞+∞16. ②③17.解(I )由题知517149613=+=⎧⎨=+=⎩a a d a a d , 解得112a d =⎧⎨=⎩, 所以21,n a n n N *=-∈.(II )由(I )知,()1212n n n a b n -+=-+,…………….6分所以()()()()0121123252212n n s n -⎡⎤=+++++++-+⎣⎦ ()()112121212n n n ⨯-+-⎡⎤⎣⎦=+-,从而221n n S n =+-.18、(1)()2,22log 2log )1(,21=∴=+=∴=a f f a a -----2分题21图若函数有意义需满足31,0301<<-∴⎩⎨⎧>->+x x x ------3分所以函数的定义域为()3,1------(2)()()⎥⎦⎤⎢⎣⎡∈-+=32,0,31log )(2x x x x f ,设()()()4131)(2+--=-+=x x x x g 当32=x 时,9354132)(2max =+⎪⎭⎫ ⎝⎛--=x g --------10分 所以)(x f 在⎥⎦⎤⎢⎣⎡∈32,0x 的最大值为935log 2-----12分 19.(本题满分12分)解:(1)()sin(2)sin(2)cos 2166f x x x x ππ=++-++3sin 2cos21x x =++ …………………………………………1分=2sin(2)16x π++…………………………………………3分 )(x f ∴的最小正周期ππ==22T ……………………………4分 要使()f x 函数的单调递增-()36k x k k Z ππππ∴≤≤+∈ ………………………………………5分故函数()f x 的单调递增区间[,]()36k k k Z ππππ-+∈ ………………6分(2)()2sin(2)1,()36f x x f A π=++=sin(2)16A π+= ………………………………………………7分132666A πππ<+<又 ……………………………………………8分2,626A A πππ∴+=∴= ………………………………………………9分在ABC ∆中,由正弦定理得:c sin sin a A C =,即12=…………………………………………11分2b =,即=2AC b = ………………………………12分 20. 解析:(1)(1)21,f a ==由得(2)()1212,1,,,x x x x ∈+∞<任取且1<因为函数)(x f 在区间()1,+∞上是增函数所以()1212120x x a x x x x --•< 由12,x x <1<得120x x -<,120x x >所以120x x a ->在()1,+∞上恒成立,即12a x x <在()1,+∞上恒成立,又因为121x x >,所以1a ≤所以实数a 的取值范围为(],1-∞21.解:在ABD ∆中,0006045105ADB ∠=+=,由正弦定理可得:0sin sin 45AB BD ADB =∠,sin 45BD BD =⇒= ...................5分 在BCD ∆中,060CBD ∠=,由余弦定理可知:2222cos CD BD CB BD CB CBD =+-⋅⋅⋅∠,即22202cos60900CD =+-⋅=,故30CD =....................10分所以130CD t ==(小时),救援船到达D 点需要1小时时间. ...........12分 22.(1)()(),1x a x g += ()2lg 2++=a x x h(2)a 的取值范围⎪⎭⎫⎢⎣⎡--1,23 (3)()2lg 21+++=a a f ,∈a ⎪⎭⎫⎢⎣⎡--1,23 函数2lg 2+++=a a y 在∈a ⎪⎭⎫⎢⎣⎡--1,23为增函数,此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
广西壮族自治区玉林市陆川县第七中学2021年高一数学理模拟试题含解析

广西壮族自治区玉林市陆川县第七中学2021年高一数学理模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设不等式4x﹣m(4x+2x+1)≥0对于任意的x∈[0,1]恒成立,则实数m的取值范围是()A.(﹣∞,] B.[] C.[] D.[,+∞)参考答案:A【考点】指数函数综合题.【专题】计算题;函数思想;综合法;函数的性质及应用.【分析】把已知不等式变形,分离参数m,然后结合指数式的值域,利用配方法求得的范围得答案.【解答】解:由4x﹣m(4x+2x+1)≥0,得m(4x+2x+1)≤4x,即m≤=,∵x∈[0,1],∴∈[,1],则∈[],∴∈[],则m.故选:A.【点评】本题考查恒成立问题,考查了分离变量法,训练了利用配方法求函数的最值,是中档题.2. 已知集合,,那么P∪Q= A.{-1,1} B.{1} C.{-1,0,1} D.{0,1}参考答案:C,,所以,选C3. 盒中有3个白球,2个红球,从中任取两个球,则至多有一个白球的概率为()A. B. C. D.参考答案:B4. (4分)设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β均为非零实数,若f=﹣1,则f等于()A.﹣1 B. 1 C.0 D.2参考答案:B考点:运用诱导公式化简求值.专题:三角函数的求值.分析:把x=2012,f=﹣1代入已知等式求出asinα+bcosβ的值,再将x=2013及asinα+bcosβ的值代入计算即可求出值.解答:由题意得:f=asin+bcos=asinα+bcosβ=﹣1,则f=asin+bcos=﹣(asinα+bcosβ)=1,故选:B.点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.5. 已知,则的值为()A. B. C. D.参考答案:C6. 已知角θ的终边经过点P ()则角θ的正弦值为_____A. B.± C. D.±参考答案:D7. 已知,向量与垂直,则实数的值为( )A.B.C.D.参考答案:A略8. 在等差数列中,,则参考答案:B9. 与共线的单位向量是()A. B.C. 和D. 和参考答案:C略10. 已知△ABC的一个内角为120°,并且三边长构成公差为2的等差数列,则△ABC的周长为()A. 15B. 18C. 21D. 24参考答案:A 【分析】设三角形的三边分别为a、b、c,且a>b>c>0,设公差为d=2,推出a﹣b=b﹣c=2,a=c+4,b =c+2,利用余弦定理能求出三边长,从而得到这个三角形的周长.【详解】解:不妨设三角形的三边分别为a、b、c,且a>b>c>0,设公差为d=2,三个角分别为、A、B、C,则a﹣b=b﹣c=2,a=c+4,b=c+2,∵A=120°.∴cos A.∴c=3,∴b=c+2=5,a=c+4=7.∴这个三角形的周长=3+5+7=15.故选:A.【点睛】本题考查三角形的周长的求法,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.注意余弦定理的合理运用,是中档题.二、填空题:本大题共7小题,每小题4分,共28分11. 给出下面四个命题,不正确的是:.①若向量、满足,且与的夹角为,则在上的投影等于;②若等比数列的前项和为,则、、也成等比数列;③常数列既是等差数列,又是等比数列;④若向量与共线,则存在唯一实数,使得成立。
广西壮族自治区玉林市陆川县第五中学2021-2022学年高一数学文模拟试题含解析

广西壮族自治区玉林市陆川县第五中学2021-2022学年高一数学文模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 在△ABC中,D是BC中点,E是AB中点,CE交AD于点F,若,则λ+u=()A.B.C.D.1参考答案:B【考点】平面向量的基本定理及其意义.【分析】由于本题是选择题,不妨设△ABC为等边三角形,由题意可得F是△ABC的重心,即可得到==﹣+,继而求出λ,μ的值,问题得以解决.【解答】解:不妨设△ABC为等边三角形,D是BC中点,E是AB中点,CE交AD于点F,∴F是△ABC的重心,∴==(+)=(+﹣)=﹣+,∵,∴λ=﹣,μ=,∴λ+μ=,故选:B.2. 已知两个非零向量,满足,则下面结论正确的是().A. B.C. D.参考答案:B试题分析:,所以,故选B。
3. 设a=(),b=(),c=(),则()A.a<b<c B.c<a<b C.b<c<a D.b<a<c参考答案:D【考点】指数函数的单调性与特殊点.【分析】利用幂函数y=x,单调递增,指数函数y=()x,单调递减,即可得出结论.【解答】解:考查幂函数y=x,单调递增,∵,∴a>b,考查指数函数y=()x,单调递减,∵,∴c>a,故选D.【点评】本题考查幂函数、指数函数的单调性,考查学生的计算能力,比较基础.4. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A. 32B.C. 16D.参考答案:D【分析】根据三视图判断出几何体是由一个三棱锥和一个三棱柱构成,利用锥体和柱体的体积公式计算出体积并相加求得几何体的体积.【详解】由三视图可知该几何体的直观图是由一个三棱锥和三棱柱构成,该多面体体积为.故选D.【点睛】本小题主要考查三视图还原为原图,考查柱体和锥体的体积公式,属于基础题.5. 以T1,T2,T3分别表示函数tan,| cos x |,sin( sin+ cos)的最小正周期,那么()(A)T1 < T2 < T3(B)T3 < T2 < T1(C)T2 < T1 < T3 (D)T2 < T3 < T1参考答案:C6. (5分)一个几何体的三视图中的正(主)视图、侧(左)视图、俯视图均是大小形状完全相同的图形,那么这个几何体可能是()A.球B.圆柱C.三棱柱D.圆锥参考答案:A考点:由三视图还原实物图.专题:空间位置关系与距离.分析:利用几何体的形状判断三视图的情况,找出满足题意的选项.解答:解:球的三视图,都是圆,满足几何体的三视图中的正(主)视图、侧(左)视图、俯视图均是大小形状完全相同的图形,所以A正确;圆柱的三视图中正(主)视图、侧(左)视图、相同,俯视图是圆,不满足题意,B不正确.三棱柱的三视图,可能三个视图都不相同,不满足题意,C不正确;圆锥的三视图中正(主)视图、侧(左)视图、相同,俯视图是圆,不满足题意,D不正确.故选:A.点评:本题考查三视图的应用,基本知识的考查.7. ① 0∈{0},②Φ{0},③{0,1}{(0,1)},④{(a,b)}={(b,a)}A. 1B. 2C. 3D. 4参考答案:B8. 已知对数函数f(x)过点(2,4),则f()的值为()A.﹣1 B.C.D.1参考答案:D【考点】求对数函数解析式.【专题】函数的性质及应用.【分析】设出对数函数的解析式,求解即可.【解答】解:设对数函数为:f(x)=log a x,对数函数f(x)过点(2,4),可得4=log a2,解得a=,对数函数为:f(x)=log x,f()==1.故选:D.【点评】本题考查对数函数的解析式的求法,函数值的求法,考查计算能力.9. 等比数列的前n项和,则()(A) (B) (C) 0 (D)参考答案:D略10. 下列各组函数是同一函数的是()①与;②与;③与;④与。
2019-2020学年广西壮族自治区玉林市陆川实验中学高一数学理模拟试题含解析

2019-2020学年广西壮族自治区玉林市陆川实验中学高一数学理模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知矩形ABCD中,AB=2,BC=1,O为AB的中点,在矩形ABCD内随机取一点,取到的点O的距离大于1的概率为()A. B. C. D.参考答案:A2. 已知P是边长为2的正三角形ABC边BC上的动点,则的值()A.是定值6 B.最大值为8C.最小值为2 D.与P点位置有关参考答案:A【考点】9R:平面向量数量积的运算.【分析】先设=, =, =t,然后用和表示出,再由=+将=、=t代入可用和表示出,最后根据向量的线性运算和数量积运算可求得的值,从而可得到答案.【解答】解:设===t则=﹣=﹣,2=4=2?=2×2×cos60°=2=+=+t﹙﹣﹚=﹙1﹣t﹚+t+=+?﹙+﹚=﹙﹙1﹣t﹚+t﹚?﹙+﹚=﹙1﹣t﹚2+[﹙1﹣t﹚+t] +t2=﹙1﹣t﹚×4+2+t×4=6故选A.3. △ABC中,AB边上的高为CD,若,,,,,则A. B. C.D.参考答案:D由,,可知4. 关于不同直线与不同平面,有以下四个命题:①若且,则;②若且,则; ③若且,则;④若且,则.其中真命题有 ( )A.1个B.2个C.3个D.4个参考答案:B5. 设,,在,,…,中,正数的个数是()A.25 B.50 C.75 D.100参考答案:D由于的周期,由正弦函数性质可知,m且但是单调递减,都为负数,但是,∴中都为正,而都为正同理都为正,都为正,故选D.6. 已知关于x的不等式(且)的解集为,则a=( )A. B. C. D. 2参考答案:A【分析】对进行分类讨论,结合临界情况的取值,即可容易求得.【详解】当时,显然恒成立,不符合题意;当时,是单调减函数,是单调增函数,根据不等式的解集可知:,解得.故选:A.【点睛】本题考查指数函数和对数函数的单调性,属基础题.7. 下列说法正确的是( ).A.掷一枚硬币,出现正面朝上的概率是0.5,因此掷一枚硬币10次,恰好出现5次正面向上;B.连续四次掷一颗骰子,都出现6点是不可能事件;C.某厂一批产品的次品率为,则任意抽取其中10件产品一定会发现一件次品D.若P(A+B)=1,则事件A与B为对立事件参考答案:D略8. 要得到函数的图像,只需将函数的图像()A.向左平移个单位B.向左平移个单位C. 向右平移个单位D.向右平移个单位参考答案:B∵,∴要得到函数的图像,只需将函数的图像向左平移个单位.选B.9. 若是偶函数,其定义域为,且在上是减函数,则的大小关系是A.>B.<C.D.参考答案:A10. 将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )(A)(B)(C)(D)参考答案:C略二、填空题:本大题共7小题,每小题4分,共28分11. 设点A(2,0),B(4,2),点P在直线AB上,且||=2||,则点P的坐标为____________.参考答案:(3,1)或(1,-1)12. 已知,若,则= .参考答案:-313. 已知实数满足则实数的取值范围为__________。
广西陆川县中学2020学年高二数学5月月考试题 理

广西陆川县中学2020学年下学期高二5月考试卷理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.复数3i2iz -+=+的共轭复数是 A. 2i +B. 2i -C. 1i -+D. 1i --2.0cos xdx π⎰=A. 1B. 2-C. 0D. π3.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( ) A .0.6 B .0.4 C .0.3 D .0.24.某厂家为了解广告宣传费与销售轿车台数之间的关系,得到如下统计数据表:根据数据表可得回归直线方程ˆˆˆybx a =+,其中ˆ 2.4b =, ˆˆa y bx =-,据此模型预测广告费用为9万元时,销售轿车台数为 ( )A. 17B. 18C. 19D. 205. “微信抢红包”自2020年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为10元,被随机分配为1.49元,1.81元,2.19元,3.41元,0.62元,0.48元,共6份,供甲、乙等6人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( ) A.12 B. 14 C. 13 D. 166.某种子每粒发芽的概率都是0.9,现播种了100粒,对于没有发芽的种子,每粒需要再补种2粒,补种的种子数记为X ,则X 的数学期望为( )A .90B . 10C .180D .207.在的展开式中,只有第5项的二项式系数最大,则展开式中常数项是( )A .-7B .-28C .7D .288.已知函数2()2(2)55f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线方程为( ) A. y x =B. 23y x =-+C. 34y x =-+D.2y x =-9.有 5名学生进行知识竞赛.笔试结束后,甲、乙两名参赛者去询问成绩,回答者对甲说:“你们5人的成绩互不相同,很遗憾,你的成绩不是最好的”;对乙说:“你不是最后一名”.根据以上信息,这5人的笔试名次的所有可能的种数是( )A. 54B. 72C. 78D. 96 10.定义在区间[0,1]上的函数()f x 的图象如图所示,以0(0))A f (,、1(1))B f (,、())x f x C (,为顶点的ABC 的面积记为函数()S x ,则函数()S x 的导函数()S x '的大致图象为( )11.给你一个正方体纸盒的展开图(如图所示)和六个不同的复数:1,-1,,,,.要求将这六个复数分别填入展开图的六个正方形中,使得按虚线折叠成一个封闭纸盒后,纸盒相对面上的两个复数的模相等,则这样的不同填法共有( ) A .144种 B .216种 C .24种 D .48种12.给出定义:若函数()f x 在D 上可导,即()f x '存在,且导函数()f x '在D 上也可导,则称()f x 在D 上存在二阶导函数,记()()()'f x f x =''',若()0f x ''<在D 上恒成立,则称()f x 在D 上为凸函数,以下四个函数在0,2π⎛⎫⎪⎝⎭上不是凸函数的是( ) A. ()sin cos f x x x =+ B. ()ln 2f x x x =- C. ()321f x x x =-+- D. ()xf x xe-=-二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.已知,则.14. 已知的分布列为且设 ,则 的方差 .15. 如图所示的电路有 ,, 三个开关,每个开关开或关的概率都是 ,且是相互独立的,则灯泡甲亮的概率为 .16. 若函数在区间上单调递减,则实数的取值范围是 .三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)4个不同的红球和6个不同的白球放入同一个袋中,现从中取出4个球.(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法?(2)取出一个红球记2分,取出一个白球记1分,若取出4个球总分不少于5分,则有多少种不同的取法?18.(本小题满分12分)已知,R m ∈复数2(2i)(1i)z m m =+--(12i)-+(其中i为虚数单位).(1)当实数m 取何值时,复数z 是纯虚数;(2)若复数z 在复平面上对应的点位于第四象限,求实数m 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【最新】广西陆川中学高一下周测5理科数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A 、B 、C 关系是( ) A .B=A∩CB .B ∪C=CC .A ⫋CD .A=B=C2.已知α角与0120角的终边相同,那么3α的终边不可能落在( )A .第一象限B .第二象限C .第三象限D .第四象限 3.已知α是第三象限角,且cos cos22αα=-,则2α是( ) A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角4.已知tan 3α=,则222sin 4sin cos 9cos αααα+-的值为( )A .130B .13C .2110D .35.已知一扇形的周长为20 cm ,当这个扇形的面积最大时,半径R 的值为( )A .4cmB .5cmC .6cmD .7cm6.设0tan 35,cos55,sin 23a b c ===,则( )A .a b c >>B .b c a >>C .c b a >>D .c a b >> 7)A .sin 2cos2+B .cos2sin 2-C .sin 2cos2--D .sin 2cos2-8.若角α∈(−π,−π2),则√1+sinα1−sinα−√1−sinα1+sinα=( )A .−2tanαB .2tanαC .−tanαD .tanα 9.已知01cos(60)3α+=,且0018090α-<<-,则0cos(30)α-的值为( ) A. BC. D10.已知角α的终边上有一点(1,3)P ,则sin()sin()22cos(2)ππαααπ--+-的值为( )A .1B .45-C .-1D .-4 11.已知角α的终边上一点坐标为77(sin ,cos )1111ππ,则角α的最小正值为( )A .711πB .1511πC .4122πD .1811π二、填空题12.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是 . 13.已知θ是第三象限角,且2sin 2cos 5θθ-=-,则sin cos θθ+=________. 14.(cos )cos5f x x =,则(sin )f x =_________. 15.设函数23()()4f x x mx m R =++∈,对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值,则实数m 的取值范围是_________.三、解答题16.(1)若2cos θ=,求sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ------的值.(2)求函数2()lg(2cos 1)49f x x x =-+-的定义域.17.在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,060BAD ∠=,PA ⊥面ABCD , 3PA =,,E F 分别为,BC PA 的中点.(1)求证://BF 面PDE ;(2)求二面角D PE A --的大小的正弦值; (3)求点C 到面PDE 的距离.参考答案1.B 【解析】 【分析】由集合A ,B ,C ,求出B 与C 的并集,判断A 与C 的包含关系,以及A ,B ,C 三者之间的关系即可. 【详解】 由题B ⊆A ,∵A ={第一象限角},B ={锐角},C ={小于90°的角}, ∴B ∪C ={小于90°的角}=C ,即B ⊆C ,则B 不一定等于A ∩C ,A 不一定是C 的真子集,三集合不一定相等, 故选B . 【点睛】此题考查了集合间的基本关系及运算,熟练掌握象限角,锐角,以及小于90°的角表示的意义是解本题的关键,是易错题 2.C 【解析】试题分析:因为α角与0120角的终边相同,所以360120,k k Z α=⋅+∈,从而12040,3k k Z α=⋅+∈,所以3α可能落在第一、二、三象限,故选择C.考点:终边相同的角、象限角. 3.B 【分析】由α是第三象限角,知2α在第二象限或在第四象限,再由cos cos 22αα=-,知cos 02α≤,由此能判断出2α所在象限. 【详解】α是第三象限角,()180360270360k k k Z α∴+⋅<<+⋅∈, ()901801351802k k k Z α∴+⋅<<+⋅∈.当k 是偶数时,设()2k n n =∈Z ,则()903601353602n n n Z α+⋅<<+⋅∈,此时2α为第二象限角; 当k 是奇数时,设()21k n n Z =+∈,则()2703603153602n n n Z α+⋅<<+⋅∈,此时2α为第四象限角. 综上所述,2α为第二象限角或第四象限角,coscos22αα=-,cos02α∴≤,2α∴为第二象限角.故选:B . 【点睛】本题考查角所在象限的判断,属于基础题,关键在于由所在的象限,得出关于α的不等式,再求出2α的范围. 4.C 【解析】 【分析】利用同角三角函数的基本关系把原式的分母“1”变为sin 2α+cos 2α,然后给分子分母求除以cos 2α,把原式化为关于tanα的关系式,把tanα的值代入即可求出值. 【详解】 因为tanα=3,所以222222249249sin sin cos cos sin sin cos cos sin cos αααααααααα+-+-=+ 2224921110tan tan tan ααα+-==+. 故选C . 【点睛】本题是一道基础题,考查学生灵活运用同角三角函数间的基本关系化简求值的能力,做题的突破点是“1”的灵活变形.5.B 【解析】试题分析:设扇形的圆心角为α,由题意可得:220r r α+=202rrα-⇒=,所以扇形的面积:22221120210(5)2522r S r r r r r rα-==⨯⨯=-=--+,所以当5r =时,扇形的面积最大,故选择B.考点:扇形的弧长公式、面积公式. 6.A 【解析】试题分析:由题可知,00cos55sin 35b ==,00sin 35sin 23>,有b c >,利用三角函数线比较0tan 35,sin 35,如图,单位圆中35AOB ∠=,AB 是35的正切线,CD 是正弦线,通过比较三角函数可知,00tan35sin35>,则有a b >,综上,a b c >>.故选A.x考点:1、三角函数大小比较;2、三角函数线. 7.D 【解析】试题分析:本题可先利用三角函数诱导公式对原式进行等价变形,再结合sin 2,cos 2的大小关系,即可得出所需结果.因为==24ππ<<,所以原式sin 2cos2=-.故选D. 考点:三角函数诱导公式. 8.A【解析】试题分析:√1+sinα1−sinα−√1−sinα1+sinα= √(1+sinα)21−sin 2α−√(1−sinα)21−sin 2α =|1+sinα|−|1−sinα||cosα|,因为α∈(−π,−π2),所以cosα<0,1±sinα≥0,所以原式=(1+sinα)−(1−sinα)−cosα=2sinα−cosα=−2tanα,故选A.考点:三角函数恒等变形与化简. 9.A 【解析】试题分析:因为0018090α-<<-,所以()60120,30α+∈--,再由01cos(60)3α+=,可得()sin 60α+=,从而0cos(30)α-()()2cos 9060sin 60αα⎡⎤=-+=+=-⎣⎦,故选A. 考点:诱导公式、三角变换. 10.A 【解析】试题分析:根据三角函数的定义可知tan 3α=,根据诱导公式和同角三角函数关系式可知:sin()sin()22cos(2)ππαααπ--+-sin cos 1131tan 12cos 222αααα--==-==,故选A.考点:1、三角函数的定义;2、诱导公式和同角三角函数关系.【方法点晴】本题是一个三角函数的定义、三角函数诱导公式及同角三角函数关系式方面的综合性问题,属于中档题.解决本题的基本思路及其切入点是,首先根据三角函数的诱导公式将被求式进行整理与化简,再由点(1,3)P 的坐标,根据三角函数的定义求出角α的有关三角函数值,进而可得到所求结果. 11.C 【解析】试题分析:由于角α的终边上一点坐标为77(sin ,cos )1111ππ,且7sin 011π>,7cos 011π<,因此点77(sin,cos )1111ππ位于第四象限,而7cos7734111tan cot tan()tan()tan()7112112222sin 11ππππππαπ===-=-=,所以角α的最小正值为4122π,故选C.考点:坐标法求三角函数值.【思路点晴】本题是一个已知角的终边上一点的坐标,用坐标法求三角函数值方面的问题,属于中档题.解决本题的基本思路是:首先应根据角α的终边上一点的坐标确定角α所在的象限,再利用坐标法定义的三角函数的计算方法求出角α的一个三角函数值,进而在[)0,2π内得到角α的唯一的一个角,也求是角α的最小正值,从而使问题得到解决. 12.2π- 【解析】试题分析:设扇形的半径R ,弧长l ,根据题意2R l R π+=,解得2lRπ=-,而圆心角2lR απ==-.故答案填2π-. 考点:扇形的弧长、圆心角. 13.3125-【分析】由题意,联立两个方程2sin 2cos 5θθ-=-和22sin cos 1θθ+=,解得cos θ,进而求出sin θ,由此能求出结果. 本题应注意θ是第三象限角.【详解】∵θ是第三象限角,且2sin 2cos 5θθ-=-代入22sin cos 1θθ+=,解得7cos 25θ=-或3cos 5θ=(舍),∴24sin 25θ=-,∴31sin cos 25θθ+=-,故答案为3125-. 【点睛】本题主要考查三角函数得化简求值,掌握同角三角函数间的关系是解题的关键. 14.sin5x 【解析】试题分析:因为sin cos 2x x π⎛⎫=- ⎪⎝⎭,而(cos )cos5f x x =,所以5(sin )(cos())cos5()cos(5)sin 5222f x f x x x x πππ=-=-=-=.考点:同角三角函数间的关系及诱导公式.【方法点晴】本题是一个同角三角函数间的关系及诱导公式方面的问题,属于中当题.解决本题的基本思路及切入点是,紧紧围绕着“结构式”(cos )cos5f x x =,因此要求(sin )f x 的值,首先要将其化为形如“()cos f θ”的结构,结合诱导公式sin cos 2x x π⎛⎫=- ⎪⎝⎭,转化不难实现,问题得以解决. 15.[2,2]- 【解析】试题分析:因为关于x 的二次函数23()()4f x x mx m R =++∈的判别式为223434m m ∆=-⨯=-,①当0∆≤即230m m -≤⇔≤≤()0f x ≥恒成立,满足:对任意的00,()x R f x ∈和0(1)f x +至少有一个为非负值;②当0∆>即230m m ->⇔2304x mx ++=的两个根分别为12,x x ,则有1212{34x x m x x +=-=,此外由对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值可知211x x -≤,故22212121()1()41x x x x x x -≤⇔+-≤2231422m m m ⇔-≤⇔≤⇔-≤≤,结合前提条件m <或m >2m -≤<2m <≤,综上可知所求实数m 的取值范围为[2,2]-.考点:二次函数的三个“二次”之间的关系.【思路点晴】本题是一个关于二次函数的图象、一元二次不等式的解、一元二次方程的根,三个“二次”方面的综合性问题,属于中档题.解决本题的基本思路是:首先考察二次函数的图象与x 轴之间的关系,也就是对二次方程的判别式进行讨论,然后再将问题“对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值”进行转化,从而可求出实数m 的取值范围.16.(1)3±;(2)55{|77}3333x x x x ππππ-≤<--<<<≤或或. 【解析】试题分析:对于问题(1)先根据诱导公式将被求式进行化简,再由cos 3θ=,即可求出结论;对于问题(2和()lg 2cos 1x -各自有意义的x 的取值集合,再求其交集即可得到函数()f x 的定义域. 试题解析:(1)因为sin(5)cos()cos(8)(sin )sin cos 2sin 3cos (sin )3sin()sin(4)2πθπθπθθθθθπθθθθπ----===±----. (2)由题意可知:21cos 2490x x ⎧>⎪⎨⎪-≥⎩,解得:22,3377k x k k Zx ππππ⎧-<<+∈⎪⎨⎪-≤≤⎩, 得:573x π-≤<-或33x ππ-<<或573x π<≤. 故函数的定义域为55{|77}3333x x x x ππππ-≤<--<<<≤或或.考点:1、三角函数式化简及诱导公式;2、函数的定义域.【思路点晴】本题是一个关于三角函数诱导公式、三角恒等变换与化简,以及函数定义域、二次不等式、三角不等式方面的综合性问题,属于中档题.解决本题的基本思路是:对于问题(1)先根据诱导公式将被求式进行化简,再由cos 3θ=,即可求出结论;对于问题(2)和()lg 2cos 1x -各自有意义的x 的取值集合,再求其交集即可得到函数()f x 的定义域.17.(1)证明见解析;(2)7;(3)7. 【解析】试题分析:(1)要证明线面平行,可以通过构造平行四边形先证明线线平行,进而证明线面平行;(2)根据二面角的定义,先作出二面角D PE A --的平面角,再进行论证,最后进行计算,从而求得其正弦值;(3)可根据等体积法由P CDE C PDEV V--=即可求得点C到面PDE的距离.试题解析:(1)如图所示,取PD中点G,连结,GF GE,因为,E F分别为,BC PA的中点,所以可证得//FG BE,FG BE=,所以四边形BFGE是平行四边形,所以//BF EG,又因为EG⊂平面PDE,BF⊄平面PDE,所以//BF平面PDE;(2)作DH AE⊥于H点,作HI PE⊥于I点,连结DI,易证DH⊥平面PAE,所以DH PE⊥,又因为PE HI⊥,HI DH H=,所以PE⊥平面DIH,所以PE DI⊥,所以DIH∠即为二面角D PE A--的平面角,在Rt DIH∆中,23102sin107721DHDIHDI∠==⋅=;(3)因为P CDE C PDEV V--=,所以1133CDE PDES PA S h∆∆⨯=⨯3321217372CDEPDES PAhS∆∆⨯⇒===考点:1、线面平行;2、二面角;3、点到平面的距离.【思路点晴】本题是一个关于线面平行、二面角、点到平面的距离方面的综合性问题,属于难题.解决本题的基本思路是:对于问题(1)要证明线面平行,可以通过构造平行四边形先证明线线平行,进而证明线面平行;对于问题(2)根据二面角的定义,先作出二面角D PE A--的平面角,再进行论证,最后进行计算,从而求得其正弦值;对于问题(3)可本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
