新北师大版九年级数学(上)第四章图形的相似分节练习
北师大版九年级上数学《第四章图形的相似》专题练习(含答案)

图形的相似专题练习1.已知△ABC∽△DEF,AB=1,BC=3,EF=5,则△ABC与△DEF的面积比是()A.1∶9 B.1∶25C.9∶25 D.3∶52.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OB∶OB′=2∶3,则四边形ABCD与四边形A′B′C′D′的面积比为()图2A.4∶9 B.2∶5C.2∶3 D.2∶ 33.如果3A=2B(AB≠0),那么下列比例式中正确的是()A.ab=32B.ba=23C.a2=b3D.a3=b24.如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥B C.若AD=5,BD=10,AE=3,则CE的长为()图4A.3 B.6C.9 D.125.在下面的图形中,相似的一组是(),A) ,B),C) ,D)图56.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是(),A) ,B),C) ,D)图67.为测量某河的宽度,小在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E,如图所示.若测得BE=90 m,EC=45 m,CD=60 m,则这条河的宽AB等于()图7A.120 m B.67.5 mC.40 m D.30 m8.如图,在△ABC中,∠A=70°,AB=4,AC=6,将△ABC沿图中的虚线剪开,则剪下的阴影三角形与原三角形不相似的是(),A) ,B),C) ,D)图89.如图,在△ABC 中,D ,E 两点分别在AB ,AC 边上,DE ∥B C .如果ADDB =32,AC =10,那么EC =________.图910.如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P 处放一水平的平面镜,光线从点A 出发经平面镜反射后刚好到古城墙CD 的顶端C 处.已知AB ⊥BD ,CD ⊥BD ,测得AB =2米,BP =3米,PD =15米,那么该古城墙的高度CD 是_________米.图1011.如图,比例规是一种画图工具,它由长度相等的两脚AD 和BC 交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA =3OD ,OB =3OC ),然后张开两脚,使A ,B 两个尖端分别在线段l 的两个端点上,若CD =3.2 cm ,则AB 的长为_________ cm.图1112.如图,已知矩形纸片ABCD 中,AB =1,剪去正方形ABEF ,得到的矩形ECDF 与矩形ABCD 相似,则AD 的长为__________.图1213.如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为___________.图1314.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,-2).(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的位似比为2∶1,并分别写出点A,B的对应点A1,B1的坐标;(2)画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2,并写出点A,B的对应点A2,B2的坐标;(3)△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心M,并写出点M的坐标.图1415.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC =90°.(1)求证:△ADE∽△BEC;(2)若AD=1,BC=3,AE=2,求AB的长.图1516.如图,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.(1)求证:△ABF∽△BGC;(2)若AB=2,G是CD的中点,求AF的长.图1617.如图,BD,CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F,H,求证:(1)DG2=BG·CG;(2)BG·CG=GF·GH.图1718.如图,一圆柱形油桶,高1.5 m,用一根2 m长的木棒从桶盖小口斜插桶内,至另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2 m,求桶内油面高度.图1819.如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC,DE,两杆相距30米.测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H,B,F,D,G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度.图1920.如图1,把两块全等的含45°角的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合.把三角板ABC 固定不动,让三角板DEF绕点D旋转,两边分别与线段AB,BC相交于点P,Q,易说明△APD∽△CDQ.根据以上内容,回答下列问题:(1)如图2,将含30°角的三角板DEF(其中∠EDF=30°)的锐角顶点D与等腰△ABC(其中∠ABC=120°)的底边中点O重合,两边DF,DE分别与边AB,BC 相交于点P,Q.写出图中的相似三角形__△APD∽△CDQ__(直接填在横线上);(2)其他条件不变,将三角板DEF旋转至两边DF,DE分别与边AB的延长线、边BC相交于点P,Q.上述结论还成立吗?请你在图3上补全图形,并说明理由;(3)在(2)的条件下,连接PQ,△APD与△DPQ是否相似?请说明理由;(4)根据(1)(2)的解答过程,你能否将两三角板改为更一般的三角形,使得(1)中的结论仍然成立?若能,请说明两个三角形应满足的条件;若不能,请简要说明理由.,图1),图2),图3)图20参考答案【过关训练】1.C2.A3.C4.B5.C6.A7.A8.D 9.__4__10.__10__11._9.6__12._1+52__13.(-2,0)_14.解:(1)如答图,△OA1B1为所作,点A1,B1的坐标分别为(4,2),(2,-4);(2)如答图,△O2A2B2为所作,点A2,B2的坐标分别为(0,2),(-1,-1);(3)△OA1B1和△O2A2B2是位似图形,如答图,点M为所,位似中心M的坐标为(-4,2).15.[解:(1)证明:∵AD∥BC,AB⊥BC,∴AB⊥AD,∠A=∠B=90°,∴∠ADE+∠AED=90°.∵∠DEC=90°,∴∠AED+∠BEC=90°,∴∠ADE=∠BEC,∴△ADE∽△BE C.(2)∵△ADE∽△BEC,∴BEAD=BCAE,即BE1=32,∴BE=3 2,∴AB=AE+BE=7 2.16.解:(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠BCG=90°.∵BF⊥AE,∴∠BAE+∠ABF=90°,∠CBG+∠ABF=90°,∴∠BAE=∠CBG,∴△ABF∽△GB C.(2)∵△ABF∽△BG C.∴ABBG=AFBC.∵AB=2,G是CD的中点,四边形ABCD是正方形,∴BC=2,CG=1,∴BG=BC2+CG2=5,∴25=AF2,解得AF=45 5.17.证明:(1)∵BD⊥AC,DG⊥BC,∴∠BDC=∠DGC=90°,∴∠DBC+∠DCG=∠GDC+∠DCG,∴∠GDC=∠DBC,∴△BDG∽△DCG,∴BG∶DG=DG∶CG,即DG2=BG·CG.(2)同(1)中的方法,同理可证△BGH∽△FGC,∴BG∶GF=GH∶CG,∴BG·CG=GF·GH.18.解:∵DE∥BC,∴△ADE∽△ABC,∴AEAC=ADAB,即AE1.5=1.22,解得AE=0.9 m,∴EC=1.5-0.9=0.6(m),即油面高0.6 m. 19.解:设AH=x,BH=y,由题意知,△AHF∽△CBF,△AHG∽△EDG,∴BFHF=CBAH,DGHG=DEAH,∴3x=1.5×(y+3),5x=1.5×(y+30+5),解得x=24.则旗杆AH的高度为24 m.20.__△APD∽△CDQ__解:(2)成立,如答图.理由如下:∵AB=BC,∴∠BAC=∠BC A.∵∠ABC=120°,∴∠BAC=∠BCA=30°,∴∠ADP+∠APD=180°-30°=150°.∵∠EDF=30°,∴∠ADP+∠CDQ=150°,∴∠APD=∠CDQ,∴△APD∽△CDQ. (3)△APD∽△DPQ.理由如下:∵△APD∽△CDQ,∴APCD=DPDQ.∵点D为AC的中点,∴CD=AD,∴APAD=DPDQ,即APDP=ADDQ.又∵∠P AD=∠PDQ=30°,∴△APD∽△DPQ.(4)△DEF满足∠EDF=α,△ABC满足顶角为(180°-2α)的等腰三角形即可.理由:∵∠ABC=180°-2α,∴∠A=∠C=α.∵∠ADP+∠APD=180°-α,∠ADP+∠QDC=180°-α,∴∠APD=∠CDQ.又∵∠A=∠C,∴△APD∽△CDQ.。
北师大版九年级数学上第四章图形的相似同步练习含答案解析

第四章图形的相似同步练习(45分钟100分)一、选择题(每小题4分,共28分)1.下面四组线段中,能成比例的是( )A.3,6,7,9B.3,6,9,18C.2,5,6,8D.1,2,3,4【解析】选B.3∶6=9∶18.2.如图,有两个形状相同的星形图案,则x的值为( )A.15cmB.12cmC.10cmD.8cm【解析】选D.根据对应边成比例得:=,解得x=8cm.3.如图,AB∥CD,=,则△AOB的周长与△DOC的周长比是( )A. B. C. D.【解析】选D.由AB∥CD可得△AOB∽△DOC,又=,△AOB的周长与△DOC的周长比是.4.如图,AB∥CD∥EF,则图中相似三角形的对数为( )A.4对B.3对C.2对D.1对【解析】选 B.∵AB∥CD∥EF,∴△ACD∽△AEF,△ECD∽△EAB,△ADB ∽△FDE.∴图中共有3对相似三角形.5.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的图形是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是( )A.- aB.-(a+1)C.-(a-1)D.-(a+3)【解析】选D.过点B和点B′分别作x轴的垂线,垂足分别是点D和点E,∵点B′的横坐标是a,点C的坐标是(-1,0).∴EC=a+1,又∵△A′B′C的边长是△ABC的边长的2倍,∴DC=(a+1),∴DO=(a+3),∴B点的横坐标是-(a+3).6.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线交AD于E,点F是AB的中点,连接EF,则S△AEF∶S四边形BDEF为( )A.3∶4B.1∶2C.2∶3D.1∶3【解析】选D.∵DC=AC,CE平分∠ACB,∴AE=DE(等腰三角形“三线合一”).∵点F是AB的中点,∴EF是△ABD的中位线,∴EF∥BD,EF=BD,∴△AFE∽△ABD,则S△AEF∶S△ADB===,∴S△AEF∶S四边形BDEF=1∶3.7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )A.(6,0)B.(6,3)C.(6,5)D.(4,2)【解析】选B.由题意得Rt△ABC的边AB=6,BC=3,AC=3,△CDE中CD=2,若CD的对应边为AB时C,D,E为顶点的三角形与△ABC相似,则点E的坐标是(6,0)或(6,2)或(4,0)或(4,2),不可能为(6,3);若CD的对应边为BC时,C,D,E为顶点的三角形与△ABC相似,则点E的坐标是(6,5)或(6,-3)或(4,5)或(4,-3);若CD的对应边为AC时C,D,E为顶点的三角形与△ABC相似;也可直接从网格上按上面的对应边来判断四个选项,易得点E的坐标不可能是(6,3),故选B.二、填空题(每小题5分,共25分)8.如图,直线A1A∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段B1C1的长【解析】∵A1A∥BB1∥CC1,∴=.∵AB=8,BC=4,A1B1=6,∴B1C1=3.答案:39.如图,A,B两点被池塘隔开,在AB外任选一点C,连接AC,BC分别取【解析】∵M,N分别为AC,BC的三等分点,∴==,又∠C为公共角,∴△CMN∽△CAB,∴=,∴AB=3MN=114m.答案:11410.如图,P为平行四边形ABCD边AD上一点,E,F分别是PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2,若S=2,则【解析】由于E,F分别是PB,PC的中点,根据中位线性质EF∥BC,EF= BC,易得△PEF∽△PBC,面积的比是1∶4,由S=2,得△PBC的面积为8.又根据平行四边形的性质,把S1+S2看作整体,求得S1+S2=△PBC的面积=8.答案:811.已知点D是线段AB的黄金分割点,且线段AD的长为2厘米,则最【解析】当线段BD最短时,由题意得=,解得BD=-1.答案:-112.如图,已知直线l:y=x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l 于N1,过点N1作直线l的垂线交x轴于M2,……按此作法继续下去,则点M10的坐标为.【解析】根据题意可知N的坐标为(2,2),所以OM=2,MN=2,因为△OMN和△NMM1相似,所以=,所以MM1=6.所以OM1=2+6=8,因此M1的坐标为(8,0).同理,可求得M2(32,0),M3(128,0),……,由此可得M n的横坐标满足(22n+1,0),所以当n=10时,代入(22n+1,0)中,得M10的坐标为(221,0).答案:(221,0)三、解答题(共47分)13.(10分)如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),在第一象限内,画出以原点为位似中心,与原四边形ABCD相似比为的位似图形A1B1C1D1,并写出各点坐标.【解析】如图所示:各点的坐标分别为:A1(1,3),B1(2,1),C1(3,1),D1(3,2).14.(12分)(2013·徐州中考)如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上的某一点D处,折痕为EF(点E,F分别在边AC,BC上).(1)若△CEF与△ABC相似,①当AC=BC=2时,AD的长为;②当AC=3,BC=4时,AD的长为.(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由. 【解析】(1)①;②1.8或2.5.(2)相似.连接CD,与EF交于点O,∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B.由折叠知,∠COF=∠DOF=90°,∴∠DCB+∠CFE=90°,∵∠B+∠A=90°,∴∠CFE=∠A.又∵∠C=∠C,∴△CEF∽△CBA.15.(12分)(2014·宁波慈溪实验期中)如图,点E是矩形ABCD中CD 边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.(1)求证:△ABF∽△DFE.(2)若△BEF也与△ABF相似,请求出∠BEC的度数.【解析】(1)如图,∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°.∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,∴∠3+∠1=180°-∠BFE=90°.又∵∠3+∠2=90°,∴∠1=∠2,∴△ABF∽△DFE.(2)∵由(1)知,∠1+∠3=90°,∴△BEF与△ABF相似,分两种情况:△ABF∽△FBE;△ABF∽△FEB.①当△ABF∽△FBE时,∠2=∠4.∵∠4=∠5,∠2+∠4+∠5=90°,∴∠2=∠4=∠5=30°,∴∠BEC=90°-30°=60°.②当△ABF∽△FEB时,∠2=∠6,∵∠4+∠6=90°,∴∠4+∠2=90°,这与∠2+∠4+∠5=90°相矛盾,∴△ABF∽△FEB不成立.综上所述,∠BEC的度数是60°.16.(13分)(2013·永州中考)如图,已知AB⊥BD,CD⊥BD.(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似?若存在,求BP 的长;若不存在,请说明理由.(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似?并求BP的长.(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似?并求BP的长.(4)若AB=m,CD=n,BD=l,请问在m,n,l满足什么关系时,存在以P,A,B 三点为顶点的三角形与以P,C,D三点为顶点的三角形相似的一个P点?两个P点?三个P点?【解析】(1)存在P点满足题意.设BP=x,则DP=10-x, 如果是△ABP∽△CDP,则=,即=,解得x=.如果是△ABP∽△PDC,则=,即=,得方程:x2-10x+36=0,方程无解;所以BP=.(2)存在两个P点满足题意.设BP=x,则DP=12-x,如果是△ABP∽△CDP,则=,即=,解得x=.如果是△ABP∽△PDC,则=,即=,得方程:x2-12x+36=0,解得x=6;所以BP=6或.(3)存在三个P点满足题意.设BP=x,则DP=15-x,如果是△ABP∽△CDP,则=,即=,解得x=.如果是△ABP∽△PDC,则=,即=,得方程:x2-15x+36=0,解得x=3或12. 所以BP=,3或12.(4)设BP=x,则DP=x-x,如果是△ABP∽△CDP,则=,即=xx-l,解得x=mm n+l.如果是△ABP∽△PDC,则=,即mx-l=,得方程:x2-l x+mn=0,Δ=l2-4mn.当Δ=l2-4mn<0时,存在以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似的一个P点;当Δ=l2-4mn=0时,存在以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似的两个P点;当Δ=l2-4mn>0时,存在以P,A,B三点为顶点的三角形与以P,C,D三点为顶点的三角形相似的三个P点.。
九年级数学上册第四章图形的相似单元清新版北师大版(含答案)

九年级数学上册新版北师大版:检测内容:第四章 图形的相似得分________ 卷后分________ 评价________一、选择题(每小题3分,共30分)1.下列结论不正确的是( C )A .所有的等腰直角三角形都相似B .所有的正方形都相似C .所有的矩形都相似D .所有的正八边形都相似2.若X 3 =Y 4 =Z 5 ,则4X +3Y -2Z X +Y +Z =( B ) A .-76 B .76 C .-67 D .673.如图,已知AD ∥BE ∥CF ,那么下列结论正确的是( B )A .BE CF =DE DFB .DE EF =AB BC C .BE CF =AB ACD .EF DE =AB BC第3题图 第5题图 第6题图4.已知△ABC ∽△A ′B ′C ′ ,AD 和A ′D ′是它们的对应中线,若AD =10,A ′D ′=6,则△ABC 与△A ′B ′C ′的周长比是( C )A .3∶5B .9∶25C .5∶3D .25∶95.如图,在△ABC 中,DE ∥BC ,AD AB =35 ,则S △ADE S 梯形DBCE的值是( B ) A .35 B .916 C .53 D .16256.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A ,再在河的这一边选点B 和点C ,使得AB ⊥BC ,然后再在河岸上选点E ,使得EC ⊥BC ,设BC 与AE 交于点D ,如图所示,测得BD =120 m ,DC =60 m ,EC =50 m ,那么这条河的大致宽度是( C )A .25 mB .75 mC .100 mD .120 m7.如图,在平面直角坐标系中,四边形ABCD 与四边形A ′B ′C ′D ′是位似图形.位似中心是( C )A .(8,0)B .(8,1)C .(10,0)D .(10,1)第7题图 第8题图 第9题图第10题图8.(邓州期中)如图,在△ABC 中,AB =AC =10,BC =12,正方形DEFG 的顶点E ,F 在△ABC 内,顶点D ,G 分别在AB ,AC 上,AD =AG ,DG =3,则点F 到BC 的距离为( A )A .3B .2C .53D .52 9.如图,点E ,F 分别在菱形ABCD 的边AB ,AD 上,且AE =DF ,BF 交DE 于点G ,延长BF 交CD 的延长线于点H ,若AF DF =2,则HF BG的值为( B ) A .23 B .712 C .12 D .51210.如图,在正方形ABCD 中,△BPC 是等边三角形,BP ,CP 的延长线分别交AD 于点E ,F ,连接BD ,DP ,BD 与CF 相交于点H ,给出下列结论:①BE =2AE ;②△DFP ∽△BPH ;③△PFD ∽△PDB ;④DP 2=PH ·PC .其中正确的是( C )A .①②③④B .②③C .①②④D .①③④二、填空题(每小题3分,共15分)11.在△ABC 中,AB =8,AC =6,在△DEF 中,DE =4,DF =3,要使△ABC 与△DEF 相似,则需要添加一个条件是__∠A =∠D (答案不唯一)__.(写出一种情况即可)12.如图,AB ∥CD ,AD 与BC 相交于点O ,OA =4,OD =6,则△AOB 与△DOC 的周长比是__2∶3__.第12题图 第13题图 第14题图 第15题图13.如图,在平面直角坐标系中,△ABC 和△A ′B ′C ′是以坐标原点O 为位似中心的位似图形,且点B (3,1),B ′(6,2),若点A ′(5,6),则A 的坐标为__(2.5,3)__.14.如图是一山谷的横断面的示意图,宽AA ′为15 m ,用曲尺(两直尺相交成直角)从山谷两侧测量出OA =5 m ,OB =10 m ,O ′A ′=3 m ,O ′B ′=12 m(A ,O ,O ′,A ′在同一条水平线上),则该山谷的深度h 为__20_m__.15.如图,在Rt △ABC 中,BC =3,AC =4,点D ,E 分别是线段AB ,AC 上的两个动点(不与点A ,B ,C 重合).沿DE 翻折△ADE ,使得点A 的对应点F 恰好落在直线BC 上,当DF 与Rt △ABC 的一条边垂直时,线段AD 的长为__209 或_207__. 三、解答题(共75分)16.(6分)已知△ABC ∽△DEF ,△ABC 和△DEF 的周长分别为20 cm 和25 cm ,且BC =5 cm ,DF =4 cm ,求EF 和AC 的长.解:∵△ABC ∽△DEF ,∴AC DF =BC EF =C △ABC C △DEF,∴AC 4 =5EF =2025 ,∴AC =165 cm ,EF =254cm17.(8分)如图,已知点O 是坐标原点,B ,C 两点的坐标分别为(3,-1),(2,1).(1)以点O 为位似中心在y 轴的左侧将△OBC 放大到原图的2倍(即新图与原图的相似比为2),画出对应的△OB ′C ′;(2)若△OBC 内部一点M 的坐标为(a ,b ),则点M 对应点M ′的坐标是__(-2a ,-2b )__;(3)求出变化后△OB ′C ′的面积.解:(1)如图,△OB ′C ′为所作(2)点M 对应点M ′的坐标为(-2a ,-2b )(3)△OB ′C ′的面积=4S △OCB =4×(2×3-12 ×2×1-12 ×2×1-12×3×1)=1018.(8分)如图,矩形ABCD 为台球桌面,AD =260 cm ,AB =130 cm ,球目前在E 点位置,AE =60 cm ,如果小丁瞄准BC 边上的点F 将球打过去,经过反弹后,球刚好弹到D 点位置.(1)求证:△BEF ∽△CDF ;(2)求CF 的长.解:(1)证明:由对称性可知∠EFG =∠DFG ,又∵GF ⊥BC ,∴∠EFB =∠DFC .又∵在矩形ABCD 中,∠B =∠C =90°,∴△BEF ∽△CDF(2)由(1)可知△BEF ∽△CDF ,∴BE CD =BF CF ,∴70130 =260-CF CF,∴CF =169 cm19.(10分)(桐柏县月考)如图,E 为▱ABCD 的边CD 延长线上的一点,连接BE 交AC 于点O ,交AD 于点F .(1)求证:△AOB ∽△COE ;(2)求证:BO 2=EO ·FO . 证明:(1)∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴△AOB ∽△COE(2)∵△AOB ∽△COE ,∴OE OB =OC OA .∵AD ∥BC ,∴△AOF ∽△COB ,∴OB OF =OC OA,∴OB OF =OE OB,即OB 2=OF ·OE20.(10分)如图,在△ABC 中,点D ,E 分别在边BC 和AC 上,点G 是BE 上的一点,连接AD ,AG ,DG ,且∠BAD =∠BGD =∠C ,求证:(1)BD ·BC =BG ·BE ;(2)∠BGA =∠BAC .证明:(1)∵∠BGD =∠C ,∠GBD =∠CBE ,∴△BDG ∽△BEC ,∴BD BE =BG BC,∴BD ·BC =BG ·BE(2)∵∠BAD =∠C ,∠ABD =∠CBA ,∴△ABD ∽△CBA ,∴BD AB =AB BC,∴AB 2=BD ·BC .又由(1)知BD ·BC =BG ·BE ,∴AB 2=BG ·BE ,∴BG AB =AB BE.又∵∠GBA =∠ABE ,∴△GBA ∽△ABE ,∴∠BGA =∠BAC21.(10分)如图,为测量山峰AB 的高度,在相距50 m 的D 处和F 处竖立高均为2 m 的标杆DC 和FE ,且AB ,CD 和EF 在同一平面内,从标杆DC 退后2 m 到G 处可以看到山峰A 和标杆顶点C 在同一直线上,从标杆FE 退后4 m 到H 处可以看到山峰A 和标杆顶点E 在同一直线上,求山峰AB 的高度及山峰与标杆CD 的水平距离BD 的长.解:∵AB ⊥BH ,CD ⊥BH ,EF ⊥BH ,∴AB ∥CD ∥EF ,∴△CDG ∽△ABG ,△EFH ∽△ABH ,∴CD AB =DG DG +BD ,EF AB =FH FH +DF +BD.又∵CD =DG =EF =2 m ,DF =50 m ,FH = 4 m ,∴2AB =22+BD ,2AB =450+4+BD ,∴22+BD =44+50+BD,解得BD =50 m ,∴2AB =22+50,解得AB =52 m22.(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的“完美分割线”.(1)如图①,在△ABC 中,∠A =48°,CD 是△ABC 的“完美分割线”,且△ACD 为等腰三角形,求∠ACB 的度数;(2)如图②,在△ABC 中,AC =2,BC =2 ,CD 是△ABC 的“完美分割线”,且△ACD 是以CD 为底边的等腰三角形,求“完美分割线”CD 的长.解:(1)由题意得△BDC ∽△BCA ,∴∠BCD =∠A =48°.①当AD =CD 时,∠ACD =∠A =48°,∴∠ACB =∠ACD +∠BCD =96°;②当AD =AC 时,∠ACD =∠ADC =180°-∠A 2 =180°-48°2=66°,∴∠ACB =∠ACD +∠BCD =114°;③当AC =CD 时,∠ADC =∠A =48°=∠BCD ,这与∠ADC =∠BCD +∠B 相矛盾,舍弃,∴∠ACB =96°或114°(2)由已知可知AC =AD =2,∵△BCD ∽△BAC ,∴BC BA =BD BC =CD AC.设BD =x ,则BA =x +2,由BC 2=BD ·BA 得(2 )2=x (x +2),解得x =3 -1或x =-3 -1(舍去),∴CD =BD BC ×AC =3-12×2=6 -223.(13分)如图,在△ABC 和△ADE 中,BA =BC ,DA =DE ,且∠ABC =∠ADE =α,点E 在△ABC 的内部,连接EC ,EB 和BD ,并且∠ACE +∠ABE =90°.(1)如图①,当α=60°时,线段BD 与CE 的数量关系为__BD =CE __,线段EA ,EB ,EC 的数量关系为__EA 2=BE 2+EC 2__;(2)如图②,当α=90°时,请写出线段EA ,EB ,EC 的数量关系,并说明理由;(3)在(2)的条件下,当点E 在线段CD 上时,若BC =25 ,请直接写出△BDE 的面积.图① 图② 备用图 答图解:(1)点拨:∵BA =BC ,DA =DE ,∠ABC =∠ADE =60°,∴△ABC ,△ADE 都是等边三角形,∴AD =AE ,AB =AC ,∠DAE =∠BAC =60°,∴∠DAB =∠EAC ,∴△DAB ≌△EAC (SAS),∴BD =EC ,∠ABD =∠ACE .又∵∠ACE +∠ABE =90°,∴∠ABD +∠ABE =90°,∴∠DBE =90°,∴DE 2=BD 2+BE 2.又∵EA =DE ,BD =EC ,∴EA 2=BE 2+EC 2(2)EA 2=EC 2+2BE 2,理由如下:∵BA =BC ,DA =DE ,∠ABC =∠ADE =90°,∴△ABC ,△ADE 都是等腰直角三角形,∴∠DAE =∠BAC =45°,AD AE =22 ,AB AC =22,∴∠DAB =∠EAC ,AD AE =AB AC ,∴△DAB ∽△EAC ,∴DB EC =AB AC =22,∠ACE =∠ABD .∵∠ACE +∠ABE =90°,∴∠ABD +∠ABE =90°,∴∠DBE =90°,∴DE 2=BD 2+BE 2.又∵EA=2 DE ,BD =22 EC ,∴12 EA 2=12EC 2+BE 2,∴EA 2=EC 2+2BE 2 (3)如答图,∵∠AED =45°,∴∠AEC =135°.又∵△ADB ∽△AEC ,∴∠ADB =∠AEC =135°.又∵∠ADE =∠DBE =90°,∴∠BDE =∠BED =45°,∴BD =BE ,∴DE =2 BD .∵EC =2 BD ,∴AD =DE =EC .设AD =DE =EC =x ,∵AB =BC =25 ,∴AC =210 .∵AD 2+DC 2=AC 2,∴x 2+4x 2=40,∴x =22 (负根已经舍弃),∴AD =DE =22 ,∴BD=BE =2,∴S △BDE =12×2×2=2。
北师大版数学九年级上册第四章图形的相似复习练习

初中数学试卷 第四章图形的相似一、单选题1.如图,l 1,l 2,l 3,l 4是一组平行线,l 5,l 6与这组平行线依次相交于点A ,B ,C ,D和E ,F ,G ,H .若AB ∶BC ∶CD=2∶3∶4,EG=10,则EH 的长为( )A .14B .16C .18D .202.如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD 内,点E 是AB 的黄金分割点,BE >AE ,若AB =2a ,则BE 长为( )A .( +1)aB .(﹣1)a C .(3﹣)a D .(﹣2)a3.如图,已知AB ∥CD ,AC 与BD 交于点O ,则下列比例中成立的是( )A .O C O A O DO B=B .OC O B OD O D =C .O C O D A CO B=D .B D OC A CO D=4.如图,小明为了测量一凉亭的高度AB (顶端A 到水平地面BD 的距离),在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE ( 0.5m D E B C == ,A ,C ,B 三点共线),把一面镜子水平放置在平台上的点G 处,测得 15m C G = ,然后沿直线 C G 后退到点E 处,这时在镜子里恰好看到凉亭的顶端A ,测得 3m E G = .若小明身高1.6m ,则凉亭的高度AB 约为( )A .8.5mB .9mC .9.5mD .10m5.如图,ABC 与DEF 位似,点O 是位似中心,若OE=3OB ,A B CS =4,则D E FS=( )A .9B .12C .16D .366.如图,A B C 与D E F 位似,位似中心为点O ,A B C 与D E F 的周长之比为49∶,则A O O D ∶的比为( )A .2:3B .2:5C .4:9D .4:137.如图,在ΔABC 中,D 、E 分别是AB 、AC 边上的中点,连接DE ,那么ΔADE 与ΔABC 的面积之比是( )A .1:16B .1:9C .1:4D .1:28.已知:如图,在△ABC 中,B E A C ⊥于点G ,C D A B ⊥于点F ,B A B E =,C A CD =,以下结论:①DE ∠=∠,②DFG E =,③A F A C A GA B=,④D FE G C FB G=,其中正确的是( )A.①②③B.①②④C.①③④D.②③④9.如图,△OAB与△OCD是以点0为位似中心的位似图形,相似比为1:2,∠OCD=90 ︒,CO=CD.若B(2,0),则点C的坐标为()A.(2,2)B.(1,2)C.(,2 )D.(2,1)10.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的14,那么点B'的坐标是()A.(3,2)B.(-2,-3)C.(2,3)或(-2,-3)D.(3,2)或(-3,-2)二、填空题11.已知△ABC∽△A'B'C',AD和A'D'是它们的对应角平分线,若AD:A'D'=4:3,△ABC的周长为16,则△A'B'C'的周长是.12.如图,////A C E FB D,若:2:3A E E B=,10C D=,则C F=.13.如图,将矩形O A B C置于平面直角坐标系中,4=,点D在B C边O A=,O C m上,且1D C=,将矩形O A B C沿A D折叠,使点B对应点E落在坐标平面内(1)当3m=时,O E的长度为.(2)若点E恰好落在x轴上,则m的值为.14.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=.15.已知线段AB=4,点P是线段AB的黄金分割点,则AP的长为.三、解答题16.如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.17.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.18.如图(图形不全),等边三角形A B C中,3A B=,点D在直线B C上,点E在直线A C上,且B A DC B E∠=∠,当1B D=时,求A E的长.几位同学通过探究得出结论:此题有多种结果.有同学已经得出两个符合题意结论:①当点D在边B C上、点E在边A C上时,2A E=;②当点D在边B C上、点E在A C的延长线上时,92A E=.要求:请针对其它情况,继续求出A E的长,并写出总的正确结论.19.如图,在矩形ABCD中,AB=18,AD=12,点M是边AB的中点,连结DM,DM与AC交于点G。
北师大版九年级数学上册第四章 图形的相似练习题

北师大版九年级数学上册第四章图形的相似练习题选择题已知2x=3y(y≠0),则下面结论成立的是()A. B. C. D.【答案】A【解析】试题解析:A、两边都除以2y,得,故A符合题意;B、两边除以不同的整式,故B不符合题意;C、两边都除以2y,得,故C不符合题意;D、两边除以不同的整式,故D不符合题意;故选A.选择题如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是()A. 2:3B.C. 4:9D. 8:27【答案】C【解析】试题分析:两个相似三角形面积的比是=4:9.故选C.选择题下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是()A. B. C. D.【答案】B【解析】试题分析:可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.解:根据勾股定理,AB=,BC=,所以,夹直角的两边的比为,计算各选项,只有B选项三角形符合,与所给图形的三角形相似。
故选:B.选择题如图,在△ABC中,DE∥BC,,BC=12,则DE的长是()A.3 B.4 C.5 D.6【答案】B.【解析】试题分析:∵DE∥BC,∴△ADE∽△ABC,∴=,∵BC=12,∴DE=BC=4.故选B.选择题如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是16:25,则OB′:OB为()A. 2:3B. 3:2C. 4:5D. 4:9【答案】A【解析】根据位似变换的概念得到△A′B′C′∽△ABC,根据相似三角形的性质计算.∵△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,∴△A′B′C′∽△ABC,∵△A′B′C′的面积与△ABC的面积比是16:25,∴△A′B′C′与△ABC的相似比为4:5,即OB′:OB=4:5,故选C.选择题如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为()A.P1 B.P2 C.P3 D.P4【答案】C.【解析】试题∵∠BAC=∠PED=90°,,∴当=时,△ABC ∽△EPD时.∵DE=4,∴EP=6.∴点P落在P3处.故选C.填空题已知AB∥CD,AD与BC相交于点O.若,AD=10,则AO=_____.【答案】4【解析】∵AB∥CD,解得,AO=4,故答案是:4.填空题如图,在中,,分别为边、AC上的点,,,点为边上一点,添加一个条件:___________,可以使得与相似.(只需写出一个)【答案】∠A=∠BDF答案不唯一【解析】因为,, ,所以,欲使与相似,只需要与相似即可,则可以添加的条件有:∠A=∠BDF,或者∠C=∠BDF,等等,答案不唯一.填空题如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是______米.【答案】18.【解析】试题解析:∵BE⊥AC,CD⊥AC,∴△ABE∽△ACD,解得:故答案为:18.填空题如图,四边形ABCD与四边形EFGH位似,位似中心点是O,,则=_____.【答案】【解析】解:∵四边形ABCD与四边形EFGH位似,∴△OEF∽△OAB,△OFG∽△OBC,∴,∴.故答案为:.解答题如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.【答案】见解析【解析】根据:两组对应边成比例且夹角相等的两个三角形相似.可证明三角形相似.证明:∵AB=20.4,AC=48,AE=17,AD=40,∴==1.2,==1.2,∴=.又∵∠BAC=∠EAD,∴△ABC∽△AED.解答题如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).(1)画出△ABC关于x对称的△A1B1C1;(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.【答案】(1)作图见解析;(2)作图见解析,28.【解析】试题分析:(1)画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题;(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;试题解析:解:(1)如图所示,△A1B1C1就是所求三角形;(2)如图所示,△A2B2C2就是所求三角形.如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,∴A2(﹣2,4),B2(4,2),C2(8,10),∴=8×10﹣×6×2﹣×4×8﹣×6×10=28.解答题如图,在▱ABCD中,过点A作AE⊥DC,垂足为E,连接BE,F 为BE上一点,且∠AFE=∠D.(1)求证:△ABF∽△BEC;(2)若AD=5,AB=8,AE∶AD=4∶5,求AF的长.【答案】(1)见解析;(2)2.【解析】(1)由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,证出∠C=∠AFB,即可得出结论;(2)由勾股定理求出BE,由AE∶AD=4∶5,求出AE,再由相似三角形的性质求出AF的长.(1)证明:∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∴∠D+∠C=180°,∠ABF=∠BEC.∵∠AFB+∠AFE=180°,∠AFE=∠D,∴∠C=∠AFB,∴△ABF∽△BEC.(2)∵AE⊥DC,AB∥DC,∴∠AED=∠BAE=90°.∵AD=5,AE∶AD=4∶5,∴AE=AD×=5×=4,在Rt△ABE中,根据勾股定理,得BE===4.在▱ABCD中,BC=AD=5.由(1)得△ABF∽△BEC,∴=,即=,∴AF=2.。
北师大数学九年级上册:第四章《图形的相似》专题练习

第四章《图形的相似》专题练习选择题1.若 4x=7八5z, 2x+y=z,那么 x : y : z 的值为()A. 2: 1: (一3)B. 2: 1: 3C. 2: (-1) : 3D. 3: 2: 13 .如果a : 6=3: 2,且。
是a 、。
的比例中项,那么b : c 等于( )4 .如图,ZVIBC 中,4(2, 4)以原点为位似中心,将△48C 缩小后得到△/?&;若。
(1, 2),△田7的面积为4,则△A8C 的面积为()5 .如图,直线4〃。
〃总直线4C 和站被儿/2,4所截,48=5, 30=6, EF=4,贝lj " 的长为()AE.川分别交8c 于点G 、H, 则下列结论中错误的是(GE JG而不D.型里AG FAC. 410A. 4: 3B. 3: 4C. 2: 3D. 3: 26.如图,已知N4?P=N8,若〃=6, AD=4,宓=10,则缈长为( )A♦" B. 7 C. 8 D. 937.如图,在△n8c中,距平分N847交仇?于点。
,点£在4?上,如果N48E=NC, AE=2ED、那么祐与△4DC的周长比为( )A. 1: 2B. 2: 3C. 1: 4D. 4: 98.如图,在平面直角坐标系中,已知点力(-3, 6)、8(-9, -3),以原点。
为位似中心,相似比为之把△480缩小,则点8月、BA. (-3,-1)C. (-9, 1)或(9, -1)cn q9.如图,在△48C中,DE//AB,且黑=亮, D Uz ;的对应点&的坐标是( )B. (-1, 2)D. (-3, -1)或(3, 1) 则普的值为()10 .如图,点力在线段劭上,在8。
的同侧作等边△48C和等边如,CD分别与监AE交于点P、M.对于下列结论:①△%%Zk/O②"=华① ③AB・AD= BP,其中正确的是(C.①③D.①②③填空题11 .如图,在△48C中,/8=9, AC=6、/?=12,点"在四边上,且力的=3,过点制作直线椒与行边交于点花使截得的三角形与原三角形相似,则郴=.A12 .如图,在中,尸是和延长线上一点,连接81交DC于点£则图中的位似三角形共有对.13 .如图,已知AADE S AABC,且4P=3, DC=49 AE=2,贝lj 8£=DE14 .如图,在△»8C中,DE//BC,若彳。
九年级数学上册(北师大版)第四章 图形的相似 单元过关练习

九年级数学上册(北师大版)第四章图形的相似单元过关练习第四章图形的相似单元练习一、填空题1.如图,Rt△ABC中,∠ACB=90∘,∠ABC= 60∘,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为________.2.如图:在Rt△ABC中,∠C为直角,CD⊥AB 于点D,BC=3,AB=5,写出其中的一对相似三角形是________ 和________.3.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是________.4.如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…M n分别为边B1B2,B2B3,B3B4,…,B n B n+1的中点,△B1C1M1的9.如图在四边形ABCD中,E是对角线BD上一点,EF // AD,EM // BC,则EFAD +EMBC=________.10.如图,已知线段a、b、c,求作线段x,使x=abc.(不写作法,保留作图痕迹)________.二、选择题11.如图,点D、E分别在△ABC的AB、AC边上,下列条件中不能判定DE // BC的是()A.ADAB =AEACB.ADDB=AEECC.DBAB =ECACD.ADAB=DEBC12.在比例尺为1:10000的地图上,相距8cm的A、B两地的实际距离是()A.800cmB.800dmC.800mD.800km13.两个相似三角形的面积比是4:9,其周长之比为()A.4:9B.2:3C.5:4D.1:214.已知如图,一张矩形报纸ABCD的长AB= acm,宽BC=bcm,E、F分别为AB、CD的中点.若矩形AEFD与矩形ABCD相似,则a:b等于()A.√2:1B.1:√2C.√3:1D.1:√315.已知在△ABC中,点D、E、F分别在边AB、AC和BC上,且DE // BC,DF // AC,那么下列比例式中,正确的是()A.AEEC =DEBCB.AEEC=CFFBC.DFAC =DEBCD.ECAC=FCBC16.如图,∠1=∠2=∠3,AC,DE交于M,图中相似三角形共有()A.3对B.4对C.5对D.6对17.下列说法中不正确的是()A.所有的等边三角形都相似B.所有正方形都相似C.所有的等腰直角三角形都似D.所有的等腰梯形都相似18.如图,△ABC中,DE // BC,ADAB =13,DE=3,则BC边的长是()A.6B.7C.8D.919.三角形三边的长度之比为3:5:7,与它相似的三角形的最长边是21cm,另两边的长度之和是()A.15 cmB.18 cmC.21 cmD.24 cm20.在夏季某天的中午,八年级一班的综合实践活动小组为了测量学校旗杆的高度,先将2米的竹竿直立在地面上,测得竹竿的影长为0.6米,同时测得旗杆的影长为5.4米.那么旗杆的高度是()A.10.8米B.16米C.18米D.18.8米三、解答题21.△ABC∽△A′B′C,顶点A、B、C分别与A′、B′、C′对应,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,求BC、AC、A′B′、A′C′的长度.22.如图,在△ABC中,D为AC边上一点,∠DBC=∠A.(1)求证:△ACD∽△ABC;(2)如果BC=√6,AC=3,求CD的长.23.如图,是一块学生用的直角三角板ABC,其中∠A=30∘,斜边AB=8cm,里面空心△DEF 的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.(1)判断四边形EMBN的形状,并说明理由;(2)求△DEF的周长.24.如图,K是△ABC内的任一点,过点K的直线DE // AC于D,交BC于E;又MN // AB,交AC于M,交BC于N;又PQ // BC,交AB于P,交AC于Q.求证:MNAB +DEAC+PQBC=2.25.如图所示,在△ABC中,点D是AB上一点,连接CE,△ABC∽△ACD且AD=4,BD=5.求△ACD与△ABC的相似比.26.如图是人民公园中的荷花池,现要测量此荷花池两端A、B两棵树之间的距离(不能直接测量),请你根据所学知识,以卷尺和测角仪为测量工具,设计一种测量方案.要求:(1)画出你设计的测量平面图;(2)简述测量方法,并写出测量数据(长度用a,b,c,…表示,角用α,β,γ,…表示);(3)根据测量的数据,求出A、B两棵树之间的距离.答案1.4或7或92.△ABC△CBD3.②③4.14(2n−1)5.16.537.88.29.110.如图11-20: DCBAB BDDDC21.BC、AC、A′B′、A′C′的长度分别为:20cm,25cm,18cm,30cm.22.(1)证明:∵∠DBC=∠A,∠C=∠C,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴BCAC =CDBC,∴√63=√6,∴CD=2.23.解:(1)∵空心△DEF的各边与△ABC的对应边平行,∴EM // BN,EN // MB,∴四边形EMBN是平行四边形;(2)连接BE,作EH⊥BC,FG⊥BC,则CG= 1cm.∵直角△ABC中,∠A=30∘,∴BC=12AB=12×8=4.∵E到AB与到BC的距离相等,∴BE平分∠ABC.∴∠EBN=30∘在直角△BHE中,tan∠EBH=EHBH.∴BH=EHtan30∘=√3EH=√3.∴EF=NG=4−BH−CG=4−√3−1=3−√3.在直角△DEF中,∠D=30∘,∴DE=2EF=6−2√3,DF=√3EF=3√3−3.∴△DEF的周长是EF+DE+DF=3−√3+6−2√3+3√3−3=6.24.证明:过点K的直线DE // AC于D,交BC于E;又MN // AB,交AC于M,交BC于N;又PQ // BC,交AB于P,交AC于Q,MN AB +DEAC+PQBC=KM+KNAB+BDAB+APAB=KM+BP+BD+APAB=AD+BP+BD+APAB=AD+DP+BP+BD+ADAB=AB+ABAB=225.解:∵△ABC∽△ACD,∴ACAB =ADAC,∵AD=4,BD=5,∴AC2=AB×AD=36,则AC=6,故△ACD与△ABC的相似比为:69=23.26.解:(1)测量平面图如图所示.(2)先测出AC=b米,BC=c米,再找出AC的中点D,BC的中点E,最后再测量出DE=a米.(3)∵CDCA =CECB=12,∠C=∠C,∴△CDE∽△CAB,∴DEAB =CDCA=12,∴AB=2DE=2a(米).。
北师大版九年级上册数学第四章 图形的相似含答案
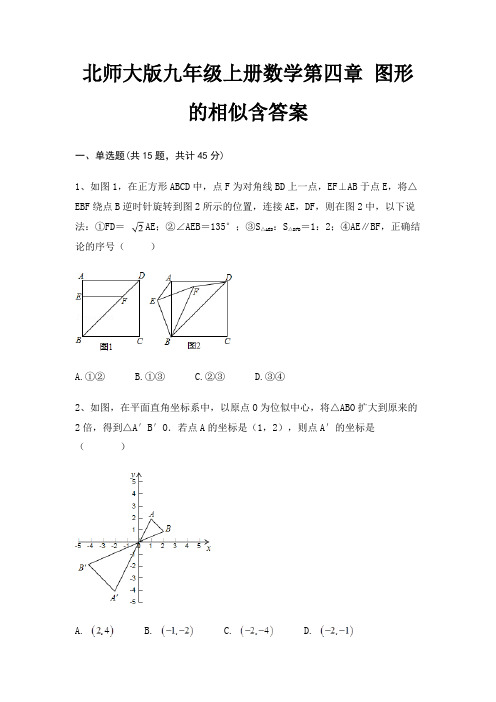
北师大版九年级上册数学第四章图形的相似含答案一、单选题(共15题,共计45分)1、如图1,在正方形ABCD中,点F为对角线BD上一点,EF⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,则在图2中,以下说法:①FD=AE;②∠AEB=135°;③S△AEB :S△DFB=1:2;④AE∥BF,正确结论的序号()A.①②B.①③C.②③D.③④2、如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是()A. B. C. D.3、下列判断正确的是A.所有等腰三角形都相似B.所有直角三角形都相似C.所有菱形都相似D.所有等边三角形都相似4、△ABC∽△A1B1C1,且相似比为,△A1B1C1∽△A2B2C2,且相似比为,则△ABC与△A2B2C2的相似比为()A. B. C. 或 D.5、下列各组长度的线段(单位:)中,成比例线段的是()A.1,2,3,4B.1,2,3,5C.2,3,4,5D.2,3,4,66、如图,与是位似图形,点是位似中心,若,,则等于()A.6B.8C.9D.127、已知,a+2b=16,则c的值为()A. B. C.8 D.28、已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出()个A.1个B.2个C.4个D.无数个9、如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE~△ECH;其中,正确的结论有( )A.1个B.2个C.3个D.4个10、如图,四边形ABCD是矩形,点E和点F是矩形ABCD外两点,AE⊥CF于点H,AD=3,DC=4,DE=,∠EDF=90°,则DF长是()A. B. C. D.11、如图,ΔABC中,∠C=90°,CD⊥AB,DE⊥AC,则图中与ΔABC相似的三角形有()A.4个B.3个C.2个D.1个12、两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为( )A.48cmB.54cmC.56cmD.64cm13、如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,其中正确的有()个.A.1B.2C.3D.414、如图,如图,A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,如果△RPQ∽△ABC ,那么点R应是甲、乙、丙、丁四点中的()A.甲B.乙C.丙D.丁15、如果一个三角形能够分成两个与原三角形都相似的三角形,我们把这样的三角形称为孪生三角形,那么孪生三角形是()A.不存在B.等腰三角形C.直角三角形D.等腰三角形或直角三角形二、填空题(共10题,共计30分)16、在平面直角坐标系xOy中,点A、B的坐标分别为(2,﹣1)、(3,0),以原点O为位似中心,把线段AB放大,点B的对应点B′的坐标为(6,0),则点A的对应点A′的坐标为________17、如图,小明将矩形纸片ABCD绕点A逆时针旋转得到矩形AEGH,点E恰好落在AC上,EG交AD于点F.若AB=3,tan∠ACB=,则FG的长为________.18、如图,以点O为位似中心,将△ABC缩小得到△A′B′C,若AA′=2OA′,则△ABC与△A′B′C′的周长比为________.19、如图,在矩形ABCD中,BC=6,AB=2,Rt△BEF的顶点E在边CD或延长线上运动,且∠BEF=90°,EF=BE,DF=,则BE=________.20、如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于________.21、如图,线段两个点的坐标分别为,,以原点为位似中心,将线段缩小得到线段,若点的坐标为,则点的坐标为________.22、如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2,则地面上的阴影面积是________ m2.23、如图,△ABC内接于⊙O,D是上一点,E是BC的延长线上一点,AE 交⊙O于点F,若要使△ADB∽△ACE,还需添加一个条件,这个条件可以是________ .24、如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为________25、已知,则的值为________.三、解答题(共5题,共计25分)26、已知=k,求k2-3k-4的值.27、如图,在中,AB=AC,D、E、B、C在同一条直线上,且.求证:∽.28、如图,在中,,在边上取一点,使,过作交于, .求的长.29、如图,操场上有一根旗杆AH.为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?30、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九(上) 第四章图形的相似 分节练习第1节 成比例线段1、 在某市城区地图(比例尺1:9000)上,新安大街的图上长度与光华大街的图上长度分别是16 cm 和10 cm . ★(1)新安大街与光华大街的实际长度各是多少米?(2)新安大街与光华大街的图上长度之比是多少?它们的实际长度之比呢? 2、【基础题】已知P 是线段AB 上的一点,且AP :PB =2:5,则AB :PB =______. ★★★ 3、【基础题】已知a ,b ,c ,d 是成比例线段,其中a =3 cm ,b =2 cm ,c =6 cm ,求线段d 的长. ★3.1【基础题】已知DCBD EA BF =,且3=BD ,2=DC ,4=EA ,则BF =______. ★★★ 4、【基础题】 (1)已知2=b a ,求b b a +; (2)已知25=b a ,求b a ba +-. ★★★5、【基础题】 若2===fed c b a ,且4=++f d b ,则=++e c a ______. ★5.1已知k cba b c a a c b =+=+=+ (0≠c b a ++),那么函数k kx y +=的图象一定不经过第______象限. ★6、【综合题】若235cb a ==,且8=+-c b a ,则a =______. ★ 6.1【提高题】已知151110ac c b b a +=+=+,求a :b :c ☆第2节 平行线分线段成比例7、【基础题】如图,321l l l ∥∥,两条直线被它们所截, AB =2,BC =3,EF =4,求DE. ★7.1【综合题】如图,321////l l l ,AM =2,MB =3,CD =4.5,则ND =______,CN =______. ★8、如图,ABC △中,DE BC ∥,2AD =,3AE =,4BD =,则AC =______. ★★★8.1、【综合题】如图,在△ABC 中,EF ∥CD ,DE ∥BC ,求证:AF ·BD = AD ·FD ★l 3l 2l 1FE D CBA第3节 相似多边形 9、【基础题】下列各组图形中,两个图形形状不一定相同的是( ) ★ A 、两个等边三角形 B 、有一个角是35°的两个等腰三角形 C 、两个正方形 D 、两个圆 9.1、【综合题】下列各组图形中相似的图形是( ) ★ A 、对应边成比例的多边形 B 、四个角都对应相等的两个梯形 C 、有一个角相等的两个菱形 D 、各边对应成比例的两个平行四边形 10、【基础题】以正方形各边中点为顶点,可以组成一个新正方形,求新正方形与原正方形的相似比. ★10.1、【综合题】两个正六边形的边长分别为a 和b ,请问它们是否相似?不相似请说明理由,相似求出相似比. ★ 11、【基础题】已知矩形草坪长20 m ,宽10 m ,沿草坪四周外围有1 m 宽的环形小路,小路内外边缘所成的矩形相似吗?为什么? 11.1【综合题】如图有一张矩形纸片,折成一半后形成的矩形与原矩形相似,则原矩形的长、宽的比是多少?12、六边形ABCDEF ∽六边形111111F E D C B A ,ο62=B ∠,则1B ∠=______.第4节 探索三角形相似的条件 13、【基础题】从下面这些三角形中,选出相似的三角形. ★★★13.1【基础题】如图,在下列每个图形中(每个图形都各自独立),是否存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据. ★★★ 14、【基础题】如图,D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD =2,BD =3,DE =4,求BC 的长. ★★★14.1【基础题】如图,BD 和EC 相交于点A ,ED ∥BC ,BD =12, AD =4,EC =9,则AC =______. ★★★14.2、【基础题】如图,在△ABC 中,点D 、E 在BC 上,且FD ∥AB ,FE ∥AC ,那么△ABC 和△FDE是否相似,为什么? ★★★14.3【基础题】如右上图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗? ★★★14.4【综合题】如图,△ABC 为等边三角形,双向延长BC 到D 、E ,使得∠DAE =120°,求证:BC 是BD 、CE 的比例中项. ★15、【基础题】如右上图在Rt △ABC 中, ∠ACB =90°,CD ⊥AB 于D .(1)请指出图中所有的相似三角形; (2)你能得出AD CD =2·DB 吗?15.1、【综合题】如右图,正方形ABCD 的边长为2,AE =EB ,MN =1, 线段MN 的两端在CB 、CD 上滑动,当CM= 时, ΔAED 与N ,M ,C 为顶点的三角形相似. ★16、【综合题】右边四个三角形,与左边的三角形相似的是( ) ★★★16.1、【综合题】如右图,在大小为4×4的正方形网格中,是相似三角形的是 ( ) ★★★A. ①和②B. ②和③C. ①和③D. ②和④17、【综合题Ⅱ】如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,点F 为线段DE 上一点,且∠AFE=∠B (1)求证:△ADF ∽△DEC ;(2)若AB=8,AD=6,AF=4,求AE 的长.黄金分割 18、【综合题Ⅰ】如图,点C 是线段AB 的黄金分割点(AC >BC ),已知AB =2 cm ,求AC 的长度和ABAC的值. ★18.1【基础题】已知M 是线段AB 的黄金分割点,且AM >BM . (1)写出AB 、AM 、BM 之间的比例式;(2)如果AB =12 cm ,求AM 与BM 的长. ★18.2【基础题】一支铅笔长16 cm ,把它按黄金分割后,较长部分涂上橘红色,较短部分涂上浅蓝色,那么橘红色部分的长是 _____ cm ,浅蓝色部分的长是 ____ cm . (结果保留一位小数) ★第5节 相似三角形判定定理的证明 19、【综合题Ⅰ】如图,BCAE AB DE AC AD ==. 求证:AE AB =. ★ 20、【综合题Ⅲ】如图,在等边三角形ABC 中,点D 、E 、F 分别是三边上的点,且AE =BF =CD ,那么△ABC 与△DEF 相似吗?请说明理由. ☆21、【综合题Ⅲ】如图,在ABC △中(∠B ≠∠C ),AB =8 cm ,BC =16 cm ,点P 从点A 开始沿边AB 向点B 以2 cm/s 的速度移动,点Q 从点B 开始沿边BC 向点C 以4 cm/s 的速度移动,如果点P 、Q 分别从点A 、B 同时出发,经几秒钟△PBQ 与△ABC 相似?试说明理由. ★第6节 利用相似三角形测高 22、【基础题】高4 m 的旗杆在水平地面上的影子长6 m ,此时测得附近一个建筑物的影长24 m ,求该建筑物的高.★★★22.1、【基础题】旗杆的影子长6米,同时测得旗杆顶端到其影子顶端的距离是10米,如果此时附近的小树影子长3米,那么小树有多高? ★22.2【综合题Ⅰ】如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度3m CD =,标杆与旗杆的水平距离15m BD =,人的眼睛与地面的高度 1.6m EF =,人与标杆CD 的水平距离2m DF =,人的眼睛E 、标杆顶点C 和旗杆顶点A 在同一直线,求旗杆AB 的高度. ★★★22.3、【综合题Ⅲ】张明同学想利用树影测校园内的树高。
他在某一时刻测得小树高为1.5米时,其影长为1.2米。
当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在教学楼的墙上. 经测量,大树在地面部分的影长为6.4米,墙上影长为1.4米,那么这棵大树高约 _____ 米. ☆ 23、【基础题】如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1 AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房MN 的高度.(精确到0.1m ). ★★★24、【基础题】如图,为了测量池塘的宽DE ,在岸边找到点C ,测得CD =30 m ,在DC 的延长线上找一点A ,测得AC =5 m ,过点A 作AB ∥DE 交EC 的延长线于B ,测出AB =6 m ,则池塘的宽DE 为( ) A .25 m B .30 m C .36 mD .40 m24.1【基础题】 已知AB 是斜靠在墙壁上的长梯,梯脚B 距墙80 cm ,梯上点D 距墙70 cm ,BD 长55 cm ,求梯子AB 的长. ★★★第7节 相似三角形的性质 25、【基础题】(1)已知△ABC ∽△DEF ,如果∠A =75°,∠B =25°,则∠F =______.(2)等腰直角三角形ABC 与等腰直角三角形A′B′C′相似,相似比为3:1,斜边AB =5 cm ,求:△A′B′C′的斜边A′B′的长和斜边A′B′边上的高. (3)两个相似三角形一组对应角平分线的长分别是2 cm 和5 cm ,那么这两个三角形的相似比是______;如果在这两个三角形的一组对应中线中,较短的中线是3 cm ,那么较长的中线是______.26、【基础题】如左下图,已知△ACD ∽△BCA ,若CD =4,CB =9,则AC =______. ★★★26.1、【基础题】如中上图,△ABC 中,DE ∥BC ,AD =1,DB =2,AE =2,则EC =______. ★★★AB ∥DC ,AC 交BD 于点O ,已知53=CO AO ,BO =6,则DO =26.2、【基础题】如右上图______.26.3【综合题Ⅰ】在四边形ABCD 中,对角线AC 与BD 相交于点E ,且∠CAB =∠CBD . 已知AB =4,AC =6,BC =3,BD =5.5,求DE 的长.★26.4【基础题】如图是小孔成像原理示意图,根据图中尺寸,蜡烛在暗盒中所成的像CD的长是()A.16cm B.13cmC.12cm D.1cm26.5、【综合题Ⅱ】如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15 cm,BC边上的高是10 cm,求正方形的面积. ★27、【基础题】如图,Rt△ABC ∽Rt△EFG,EF=2AB,BD和FH分别是它们的中线,那么△BDC与△FHG是否相似?如果相似,试确定其周长比和面积比. ★★★27.1【综合题】如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为. ★27.2、【综合题Ⅰ】两个相似三角形的相似比为2:3,它们周长的差是25,则较大三角形的周长是_____. 28、【提高题】已知:AM∶MD=4∶1,BD∶DC=2∶3,则AE∶EC=______.第8节图形的位似29、【基础题】关于对位似图形的表述,下列命题正确的是_________.(只填序号)①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.29.1【基础题】下列说法错误的是()A.位似图形一定是相似图形B.相似图形不一定是位似图形C.位似图形上任意一对对应点到位似中心的距离之比等于位似比D.位似图形中每组对应点所在的直线必相互平行30、【基础题】如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2 P A=3 P A1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )A、32.B、23.C、53.D、35.30.1【基础题】如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O是位似中心,位似比为2:1. 若五边形ABCDE的面积为17 cm2,周长为20 cm,那么五边形A′B′C′D′E′的面积为______,周长为______.30.2【综合题Ⅰ】如右上图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与_______是位似图形,ME FDCB A位似比为______;△OAB与________是位似图形,位似比为______. ★31、【基础题】如右图,以O为位似中心,作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.★★★如图:四边形ABCD中,AB=AD,对角线AC、BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD 于点F。
