2016初三线上收心课-数学-第2讲_89
初中数学九年级培优教程整理(全)

初中数学九年级培优目录第1讲二次根式的性质和运算(P2----7)第2讲二次根式的化简与求值(P7----12)第3讲一元二次方程的解法(P13----16)第4讲根的判别式及根与系数的关系(P16----22) 第5讲一元二次方程的应用(P23----26)第6讲一元二次方程的整数根(P27----30)第7讲旋转和旋转变换(一)(P30----38)第8讲旋转和旋转变换(二)(P38----46)第9讲圆的基本性质(P47----51)第10讲圆心角和圆周角(P52----61)第11讲直线与圆的位置关系(P62----69)第12讲圆内等积证明及变换((P70----76)第13讲弧长和扇形面积(P76----78)第14讲概率初步(P78----85)第15讲二次函数的图像和性质(P85----91)第16讲二次函数的解析式和综合应用(P92----98) 第17讲二次函数的应用(P99----108)第18讲相似三角形的性质(P109----117)第19讲相似三角形的判定(P118-----124)第20讲相似三角形的综合应用(P124-----130)每天进步一点点!坚持就是胜利!第1讲 二次根式的性质和运算考点·方法·破译1.了解二次根式、最简二次根式、同类二次根式的定义,能准确进行辨析; 2.掌握二次根式有关性质,并能熟练运用性质进行化简;3.会根据二次根式的性质挖掘题中隐含条件,求参数的值(或取值范围).经典·考题·赏析【例1】 (荆州)下列根式中属最简二次根式的是( )A.【解法指导】判断式子是否为最简二次根式的条件有两点:①被开方式中不能含分母;②被开方式中不能有可开尽方的数或式子. B 中含分母,C 、D 含开方数4、9,故选A.【变式题组】1.⑴(中山)下列根式中不是最简二次根式的是( )A.A .①,②B .③,④C .①,③D .①,④【例2】(黔东南)方程480x -=,当y >0时,m 的取值范围是( )A .0<m <1B .m ≥2C .m <2D .m ≤2【解法指导】本题属于两个非负数的代数和问题,隐含两个代数式均为0的结论.由题意得4x -8=0,x -y -m =0.化为y =2-m ,则2-m >0,故选C.【变式题组】2.(宁波)若实数x 、y 2(0y -=,则xy 的值是__________.3.2()x y =+,则x -y 的值为( )A .- 1B .1C .2D .34.(鄂州)使代数式4x -有意义的x 的取值范围是( ) A .x >3B .x ≥3C .x >4D .x ≥3且x ≠45.(怀化)22(4)0a c --=,则a -b -c =________.是同类二次根式的是( )A BC D【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式,再看被开方数是否一样. A=; B不能化简;=D==.故本题应选D.【变式题组】6a =________. 7.在下列各组根式中,是同类二次根式的是( ) ABCD8.已知最简二次根式ba =_______,b =______. 【例4】下列计算正确的是( ) A=B4=C= D.(11-=【解法指导】正确运用二次根式的性质①2(0)a a =≥;②(0)0(0)(0)a a a a a a ⎧⎪===⎨⎪-⎩><;③0,0)a b =≥≥0,0)b a =≥> 进行化简计算,并能运用乘法公式进行计算.A 、B 中的项不能合并.D. 2(111+=-=-.故本题应选C.【变式题组】9. (聊城)下列计算正确的是( ) A.= B=C3=D3=-10.计算:200720074)(4⋅=_____________ 11.22-=_____________12.(济宁)已知a) A .a B .-aC .-1D .013.已知a >b >0,a +b =的值为( )AB .2CD .12【例5】已知xy >0,化简二次根式的正确结果为( )A BC .D .【解法指导】先要判断出y <0,再根据xy >0知x <0. 故原式=选D. 【变式题组】14.已知a 、b 、c 为△AB C 三边的长,则化简a b c --_______.15===,算果中找出规律,并利用这一规律计算:1)++⋅=L _________.16.已知,则0<x <1=_________.【例6】(辽宁)⑴先化简吗,再求值:11()ba b b a a b ++++,其中a =b =⑵已知x =,y =值为________. 【解法指导】对于⑴,先化简代数式再代入求值;对于⑵,根据已知数的特征求xy 、x +y 的值,再代入求值.【解】⑴原式=22()()()()ab a a b b a b a b ab a b ab a b ab +++++==++,当a =,b =ab =1,a +b⑵由题意得:xy =1,x +y =10, 10199=-. 【变式题组】17.(威海)先化简,再求值:(a +b )2+(a -b)(2a +b)-3a 2,其中2a =-2b =-.18.(黄石)已知a 是4的小数部分,那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________.【例7】已知实数x 、y 满足(2008x y =,则3x 2-2y 2+3x -3y -2007的值为( )A .-2008B .2008C .-1D .1【解法指导】对条件等式作类似于因式分解的变形,找出a 、b 的关系,再代入求值.解:∵(2008x y =,∴(x =y =(y =x =,由以上两式可得x =y .∴(2008x =, 解得x 2=2008,所以3x 2-2y 2+3x -3y -2007=3x 2-2x 2+3x -3x -2007=x 2-2007=1,故选D.【变式题组】19.若a >0,b >0=的值.演练巩固·反馈提高01.若4m =,则估计m 的值所在的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <502.n 的最大值为( )A .12B .11C .8D .303.(黄石)下列根式中,不是..最简二次根式的是( )A.04.(贺州)下列根式中,不是最简二次根式的是( )A.05.下列二次根式中,是最简二次根式的是( )A.06.(常德)设a =20, b =(-3)2, c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是( )A .c <a <d <bB .b <d <a <cC .a <c <d <bD .b <c <a <d07.(十堰)下列运算正确的是( )A =B =C .21)31=-D 53=-08.如果把式子(1a -根号外的因式移入根号内,化简的结果为( )A .B C .D .09.2x -化简的结果为2x -3,则x 的取值范围是( )A .x ≤1B .x ≥2C .1≤x ≤2D .x >010.(怀化)函数y =________.11.(湘西)对于任意不相等的两个数a ,b ,定义一种运算a ※b =32=-那么12※4=________.12.(荆州)先化简,再求值:22321121a a a a a a-+÷-+-,其中a =13.(广州)先化简,再求值:((6)a a a a +--,其中12a =. 培优升级01.(凉山州)已知一个正数的平方根是3x -2和5x +6,则这个数是________.02.已知a 、b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有________对.03.(全国)设a =,则5432322a a a a a a a+---+=-________. 04.(全国)设x =a 是x 的小数部分,b 是x 的小数部,则a 3+b 3+3ab =________.05.(重庆)已知2y =,则x 2+y 2=________.06.(全国)已知1a =,a =2a =,那么a 、b 、c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .c <a <b07.(武汉)已知y =+(x ,y 均为实数),则y 的最大值与最小值的差为( )A 3B .3C 3D08.(全国)已知非零实数a 、b 满足24242a b a -++=,则a +b 等于( ) A .-1B .0C .1D .209.(全国) )A .5-B .1C .5D .110.已知0(0,0)x y x y -=>>的值为( )A .13 B .12C .23 D .3411.已知152a b c +-=-,求a +b +c 的值.12.已知9+9-a 和b ,求ab -3a +4b +8的值.第2讲 二次根式的化简与求值考点·方法·破译1.会灵活运用二次根式的运算性质化简求值.2.会进行二次根式的有理化计算,会整体代入求值及变形求值. 3.会化简复合二次根式,会在根式范围内分解因式.经典·考题·赏析【例1】2=的值等于__________ 【解法指导】通过平方或运用分式性质,把已知条件和待求式的被开方数都用1x x+表示或化简变形. 解:两边平方得,124x x ++=,12x x+= ,两边同乘以x 得,212x x += ,∵2315x x x ++=,29111x x x ++=,∴原式111.若14a a +=(0<a <1)=________ 2=) A .1a a-B .1a a-C .1a a+D .不能确定【例2】(全国)满足等式=2003的正整数对(x ,y )的个数是( ) A .1 B .2 C .3 D .4【解法指导】对条件等式作类似于因式分解的变形,将问题转化为求不定方程的正整数解.0=,∴0=0>0=,则xy =2003,且2003是质数,∴正整数对(x ,y )的个数有2对,应选B . 【变式题组】3.若a >0,b >0=的值.【例3】1)a =<<,求代数式22632x x x x x x +-+÷-. 【解法指导】视x -2,x 2-4x=a 的代数式表示x -2,x 2-4x ,注意0<a <1的制约.解:平方得,12x a a =++,∴12x a a -=+,2221442x x a a-+=++, 222142x x a a -=+-,∴化简原式=(3)(2)(2)3x x x x x x +--+g =2211()1()211()a a a a a a a a a a a++-+-=++--4.(武汉)已知32x x +=+,求代数式35(2)242x x x x -÷----的值.5.(五羊杯)已知1m =+1n =22(714)(367)8m m a n n -+--=,则a 的值等于( )A .-5B .5C .-9D .9【例4】(全国)如图,点A 、C都在函数0)y x =>的图像上,点B 、D 都在x 轴上,且使得△OAB 、△BCD 都是等边三角形,则点D 的坐标为________.【解法指导】解:如图,分别过点A 、C 作x 轴的垂线,垂足分别为E 、F .设OE=a ,BF=b ,则,CF,所以,点A 、C 的坐标为(aa )、(2a +bb ),所以2(2)a b =+=a b ⎧=⎪⎨=⎪⎩因此,点D的坐标为() 【变式题组】6.(邵阳)阅读下列材料,然后回答问题. 在进行二次根式化简时,我们有时会碰上如1323235+,,一样的式子,其实我们还可以将其进一步化简: 335333535=⨯⨯=; (一) 36333232=⨯⨯=; (二) ()()()131313132132-=-+-⨯=+; (三) 以上这种化简的步骤叫做分母有理化,132+还可以用以下方法化简:()()()13131313131313131322-=+-+=+-=+-=+; (四)(1)请你用不同的方法化简352+;①参照(三)试得:352+=_____________________________;(要有简化过程)②参照(四)试得:352+=_____________________________;(要有简化过程)(2+L【例5】(五羊杯)设a 、b 、c 、d 为正实数,a <b ,c <d ,bc >ad.【解法指导】虽然不能用面积公式求三角形面积(为什么?)a 、c 为直角边的直角三角形的斜边,从构造图形入手,将复杂的根式计算转化为几何问题加以解决.解:如图,作长方形ABCD ,使AB =b -a ,AD =c ,延长DA 至E ,使DE =d ,延长DC 至F ,使DF=b ,连结EF 、FB 、EB ,则BF=,EF=,BE ,从而知△BEF 就是题设的三角形,而S △BEF =S 长方形ABCD +S △BCF+S △ABE -S △DEF =(b -a )c +12(d -c )(b -a )-12bd =12(bc -ad )【变式题组】7.(北京)已知a 、b 均为正数,且a+b =2,求U演练巩固·反馈提高01.已知x =,y =值为__________ 02.设1a =,则32312612a a a +--=( )A . 24B .25C.10D.1203.(天津)计算2001200019991)1)1)2001--+=__________ 04.(北京)若有理数x 、y 、z 1()2x y z =++,则2()x yz -=__________05.(北京)正数m 、n 满足430m n +-==__________06.(河南)若1x=,则32(2(15x x x -+++的值是( )A .2B .4C .6D .807.已知实数a 满足2000a a -=,那么22000a -的值是( )A .1999B .2000C .2001D .200208.设a =b =c =a 、b 、c 之间的大小关系是( )A .a <b <cB .c <b <aC .c <a <bD .a <c <b09.已知1x =培优升级01.(信利)已知1x =+2111242x x x +-=+--__________025==__________03.(江苏)已知(2002x y =,则2234x xy y --6658x y --+=__________04.7x =,则x =__________05.已知x =,y =,那么22y x x y +=__________06.(武汉)如果a b +=a b -=,3333b c b c +=-,那么333a b c -的值为( )A .B .2001C .1D .007.(绍兴)当x =32003(420052001)x x --的值是( ) A .0 B .-1C .1D .20032-08.(全国)设a 、b 、c 为有理数,且等式a +=则29991001a b c ++的值是( )A .1999B .2000C .2001D .不能确定09.计算:(1(2(3+L(410.已知实数a 、b 满足条件1b a b a -=<,化简代数式11()a b-,将结果表示成不含b 的形式.11.已知21(0)a x aa +=>12.已知自然数x 、y 、z 0=,求x +y +z 的值.第3讲一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程;3.会应用一元二次方程解实际应用题。
最新九年级初三数学假期尖子生学习课外提高学习讲义

例 5.二次函数 y (x 1)2 (x 3)2 与 y (x a)2 (x b)2 的图象关于 y 轴对称,则 (a 1)2 (1 b)2 的值为
()
A.9
B.10
C.20
D.25
例 6.如图,在平面直角坐标系中,抛物线 y 1 x2 经过平移得到抛物线 y 1 x2 2x ,其对称轴与两段抛
D. y x2 x 2
6.如图,把抛物线 y 1 x2 平移得到抛物线 m ,抛物线 m 经过点 A(6, 0) 和原点 O(0, 0) ,它的顶点为 P , 2
它的对称轴与抛物线 y 1 x2 交于点 Q ,则图中阴影部分的面积为 . 2
7.如图,抛物线 y1 x2 2 向右平移 1 个单位得到抛物线 y2 ,回答下列问题:
最新九年级初三数学假期尖 子生学习课外提高学习讲义
目录
第 1 讲 二次函数的图像性质…………………………………………03 第 2 讲 二次函数的应用………………………………………………16 第 3 讲 实际问题应用题………………………………………………28 第 4 讲 二次函数几何综合……………………………………………40 第 5 讲 圆的基本性质与定理…………………………………………49 第 6 讲 圆有关的位置与切线…………………………………………75 第 7 讲 圆有关计算……………………………………………………90 第 8 讲 圆相关重难点…………………………………………………112
为底的等腰三角形,则点 P 的坐标为
.
四.二次函数图象与几何变换 1.平移规律:“左加右减,上加下减”
2.对称规律:通过顶点以及开口方向判断 关于 x 轴对称,顶点横坐标不变,纵坐标互为相反数,开口相反; 关于 y 轴对称,顶点横坐标互为相反数,纵坐标不变,开口相同;
学而思初三数学秋季班第2讲.方程与函数思想.目标班.学生版
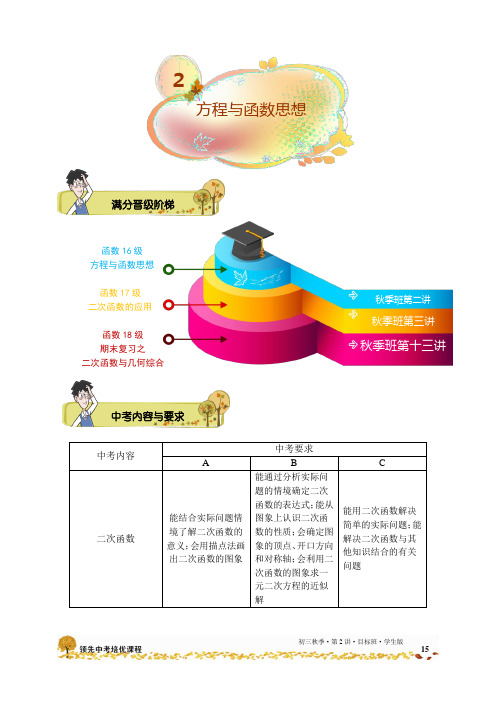
15初三秋季·第2讲·目标班·学生版中考内容中考要求A BC二次函数能结合实际问题情境了解二次函数的意义;会用描点法画出二次函数的图象 能通过分析实际问题的情境确定二次函数的表达式;能从图象上认识二次函数的性质;会确定图象的顶点、开口方向和对称轴;会利用二次函数的图象求一元二次方程的近似解能用二次函数解决简单的实际问题;能解决二次函数与其他知识结合的有关问题中考内容与要求满分晋级阶梯2方程与函数思想函数18级 期末复习之 二次函数与几何综合函数17级 二次函数的应用 函数16级 方程与函数思想16 初三秋季·第2讲·目标班·学生版二次函数在北京中考中属于必考考点,并且都以压轴题形式出现,是中考的难点,也是同学们失分最高的一部分。
这部分内容要求学生们⑴能用数形结合、归纳等数学思想,根据二次函数的表达式确定二次函数的开口方向、对称轴和顶点坐标;⑵综合运用方程、几何、函数等知识解决实际问题。
年份 2011年 2012年 2013年 题号 7,8,23 8,23 10,23 分值11分11分9分考点抛物线顶点坐标;函数图象;二次函数和一次函数解析式(函数图象与坐标轴交点、函数图象交点坐标),二次函数与一元二次方程(判别式、求根)函数图象;二次函数的对称性;二次函数和一次函数解析式(函数图象与坐标轴交点、函数图象交点坐标);二次函数图象平移,利用函数图象求取值范围二次函数函数图象的性质;二次函数和一次函数解析式(函数图象与坐标轴交点、函数图象交点坐标),二次函数图像的对称性知识互联网中考考点分析17初三秋季·第2讲·目标班·学生版抛物线()20y ax bx c a =++≠与y 轴的交点抛物线与y 轴必有一个交点()0c ,.抛物线()20y ax bx c a =++≠与x 轴的交点当240b ac ∆=->时,抛物线与x 轴有两个不同的交点. 当240b ac ∆=-=时,抛物线与x 轴有一个交点. 当240b ac ∆=-<时,抛物线与x 轴没有交点.直线()0y kx b k =+≠(或直线y m =或直线x n =)与抛物线()20y ax bx c a =++≠的交点问题,可运用方程思想联立方程2y kx b y ax bx c =+⎧⎨=++⎩(或2y my ax bx c=⎧⎨=++⎩或2x n y ax bx c =⎧⎨=++⎩)求出方程组的解,从而得到交点坐标. 比如抛物线()20y ax bx c a =++≠与x 轴的交点联立方程组为2y y ax bx c =⎧⎨=++⎩,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根,则抛物线与x 轴交于两点()()1200A x B x ,,,.【引例】 已知关于x 的二次函数()222134y x m x m m =--+++.探究二次函数y 的图象与x 轴的交点的个数,并写出相应的m 的取值范围.【解析】 令0y =时,得:()2221340x m x m m --+++=()()22214341615m m m m ∆=--++=--,以下分三种情况讨论:①当0∆>时,方程有两个不相等的实数根,即16150m -->∴1516m <-,此时,y 的图象与x 轴有两个交点②当0∆=时,方程有两个相等的实数根,即16150m --=∴1516m =-,此时,y 的图象与x 轴只有一个交点③当0∆<时,方程没有实数根,即16150m --<例题精讲思路导航题型一:方程思想18 初三秋季·第2讲·目标班·学生版∴1516m >-,此时,y 的图象与x 轴没有交点 综上所述:当1516m <-时,y 的图象与x 轴有两个交点;当1516m =-时,y 的图象与x 轴只有一个交点;当1516m >-时,y 的图象与x 轴没有交点.【例1】 1. 抛物线与x 轴的交点.⑴二次函数2y ax bx c =++与x 轴的两个交点坐标为()10-,、()50,,则一元二次方程20ax bx c ++=的两根为 .⑵二次函数n x x y +-=62的部分图象如图所示,若关于x 的一元二次方程062=+-n x x 的一个解为11=x ,则另一个解=2x .⑶二次函数2134y x x n =++-的图象与x 轴只有一个交点;另一个二 次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交于两点,这两个交点的横坐标都是整数,且m 是小于5的整数. 求:① n 的值;② 二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交点的坐标.2. 抛物线与直线y m =的交点.典题精练xy1O19初三秋季·第2讲·目标班·学生版图中抛物线的解析式为2y ax bx c =++,根据图象判断下列方程根的情况. ⑴ 方程20ax bx c ++=的两根分别为 . ⑵ 方程230ax bx c ++-=的两根分别为 . ⑶ 方程22ax bx c ++=的根的情况是 . ⑷ 方程24ax bx c ++=的根的情况是 .3. 抛物线与直线()0y kx b k =+≠的交点⑴直线6y ax =-与抛物线243y x x =++只有一个交点,则a = .⑵当m 取何值时,抛物线2y x =与直线y x m =+:① 有公共点;② 没有公共点.【例2】 在平面直角坐标系xOy 中,抛物线22y mx mx n =-+与x 轴交于A 、B 两点,点A的坐标为(2,0)-. (1) 求B 点坐标;20 初三秋季·第2讲·目标班·学生版(2) 直线n m x y ++=421经过点B . ① 求直线和抛物线的解析式;② 点P 在抛物线上,过点P 作y 轴的垂线l ,垂足为(0,)D d .将抛物线在直线l 上方的部分沿直线l 翻折,图象的其余部分保持不变,得到一个新图象G .请结合图象回答:当图象G 与直线n m x y ++=421只有两个公共点时,d 的取值范围是 .21初三秋季·第2讲·目标班·学生版【例3】 在平面直角坐标系xOy 中,抛物线22y mx mx n =-+与x 轴交于A 、B 两点,点A的坐标为(2,0)-. (1)求B 点坐标; (2)直线y =12x +4m +n 经过点B . ①求直线和抛物线的解析式;②点P 在抛物线上,过点P 作y 轴的垂线l ,垂足为(0,)D d .将抛物线在直线l 上方的部分沿直线l 翻折,图象的其余部分保持不变,得到一个新图象G .请结合图象回答:当图象G 与直线y =12x +4m +n 只有两个公共点时,d 的取值范围是 .22 初三秋季·第2讲·目标班·学生版【例4】 已知关于m 的一元二次方程221x mx +-=0.(1) 判定方程根的情况;(2) 设m 为整数,方程的两个根都大于1-且小于32,当方程的两个根均为有理数时, 求m 的值.抛物线()20y ax bx c a =++≠的重要结论0<Δx当0a >时,图象落在x 轴的上方, 无论x 为任何实数,都有0y >.思路导航题型二:函数思想23初三秋季·第2讲·目标班·学生版x当0a <时,图象落在x 轴的下方, 无论x 为任何实数,都有0y <.0=Δmx当0a >,x m =时,则0y =;当x m ≠时,则0y >.mx当0a <,x m =时,则0y =;当x m ≠时,则0y <.0>Δnmx当0a >, x m <或x n >时,则0y >;当x m =或x n =时,则0y =;当m x n <<时,则0y <.nmx当0a <,x m <或x n >时,则0y <;当x m =或x n =时,则0y =;当m x n <<时,则0y >.【引例】1. 如图,函数2y ax bx c =++的图象如图所示:⑴ 当x 时, 0y =; ⑵ 当x 时, 0y >; ⑶ 当x 时, 0y <.2. 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点()10A -,、点()30B ,和点()03C -,次函数的图象与抛物线交于B 、C 两点.⑴ 二次函数的解析式为 .⑵ 当自变量 时,两函数的函数值都随x 增大而增大. ⑶ 当自变量 时,一次函数值大于二次函数值. ⑷ 当自变量 时,两函数的函数值的积小于0.【解析】 1. ⑴ 1x =或3x =;⑵ 3x >或1x <; ⑶ 13x <<.2. ⑴ 223y x x =--;⑵ 1x >;⑶ 03x <<;⑷ 1x <-.例题精讲典题精练yxO -331-1CB A yx31O24 初三秋季·第2讲·目标班·学生版【例5】 ⑴下列命题:①若0a b c ++=,则240b ac -<;②若23b a c =+,则一元二次方程20ax bx c ++=有两个不相等的实数根;③若240b ac ->,则二次函数2y ax bx c =++的图象与坐标轴的公共点的个数是2或3.④若b a c >+,则一元二次方程20ax bx c ++=有两个不相等的实数根.正确的是( )A .②④B .①③C .②③D .③④⑵若m 、n (m n <)是关于x 的方程()()10x a x b ---=的两根,且a b <,则a 、b 、m 、n 的大小关系是( )A .m a b n <<<B .a m n b <<<C .a m b n <<<D .m a n b <<<⑶方程2310x x +-=的根可视为函数3y x =+的图象与函数1y x=的图象交点的横坐标,那么用此方法可推断出方程3210x x +-=的实根0x 所在的范围是( ) A .010x -<<B .001x <<C .012x <<D .023x <<【例6】 已知:关于x 的方程()2240x ax a ++-=①有两个实数根是1x 、2x (12x x <),若关于x的另一个方程220x ax k ++=②的两个实数根都在1x 和2x 之间.试比较:代数式4k +、a 、24a +之间的大小关系.【例7】 在平面直角坐标系xOy 中,抛物线()2220y mx mx m =--≠与初三秋季·第2y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)设直线l 与直线AB 关于该抛物线的对称轴对称,求直线 l 的解析式;(3)若该抛物线在21x -<<-这一段位于直线l 的上方,并且 在23x <<这一段位于直线AB 的下方,求该抛物线的解析式.训练1. 二次函数()20y ax bx c a =++≠的部分图象如图所示,根据图象解答下列问题:⑴写出x 为何值时,y 的值大于0;思维拓展训练(选讲)26 初三秋季·第2讲·目标班·学生版⑵写出x 为何值时,y 随x 的增大而增大;⑶若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.训练2. 已知二次函数22(21)y x m x m m =--+-(m 是常数,且0m ≠).⑴证明:不论m 取何值时,方程22(21)0x m x m m --+-=总有两个不相等的实数根;⑵设二次函数与x 轴两个交点的横坐标分别为1x ,2x (其中1x >2x ),当m的取值满足什么条件时2112xx -≤.训练3. 已知函数()20y x bx c x =++≥,满足当1x =时,1y =-,且当0x =与4x =时的函数值相等.⑴求函数()20y x bx c x =++≥的解析式并画出它的图象(不要求列表);⑵若()f x 表示自变量x 相对应的函数值,且2 (0),() 2 (0),x bx c x f x x ⎧++=⎨-<⎩≥ 又已知关于x 的方程()f x x k =+有三个不相等的实数根,请利用图象直接写出实数k 的取值范围.27初三秋季·第2讲·目标班·学生版训练4. 设二次方程()22120x a x a +-+-=有一根比1大,另一根比1-小,试确定实数a 的范28 初三秋季·第2讲·目标班·学生版题型一 方程思想 巩固练习【练习1】 已知二次函数2y x bx c =-++的图象如图所示,解决下列问题:⑴关于x 的一元二次方程20x bx c -++= 的解为 ; ⑵x 取何值时,函数值2y ≤?【练习2】 已知:关于x 的二次函数2(1)(1)2y a x a x =--++.⑴当a 取何值时,方程2(1)(1)20a x a x --++=有两个不相等的实数根; ⑵整数a 取何值时,二次函数与x 轴的交点都是正整数.复习巩固yx31O29初三秋季·第2讲·目标班·学生版【练习3】 如图是二次函数2()y x m k =++的图象,其顶点坐标为()14M -,.⑴ 求出图象与x 轴的交点A ,B 的坐标;⑵ 在二次函数的图象上是否存在点P ,使54PAB MAB S S =△△,若存在,求出P 点的坐标;若不存在,请说明理由;⑶ 将二次函数的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线(1)y x b b =+<与此图象有两个公共点时,b 的取值范围.题型二 函数思想 巩固练习【练习4】 ⑴不论x 为何值时,2y ax bx c =++永远是正值的条件是( )A .0a >,0∆<B .0a >,0∆≥C .0a >,0∆>D .0a <,0∆< ⑵若抛物线()2123y m x mx m =-+++位于x 轴上方,则m 的取值范围是( )A .1m >B .32m >C .32m ≥D .312m << ⑶二次函数2y ax bx c =++对于x 的任何值都恒为负值的条件是( ) A .0a >,0∆> B .0a >,0∆< C .0a <,0∆> D .0a <,0∆<【练习5】 已知关于x 的一元二次方程20ax bx c ++=,如果0a >,a c b +<,那么方程20ax bx c ++=的根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .没有实数根D .必有一个根为0初三秋季·第2讲·目标班·学生版巴雷尼与诺贝尔奖巴雷尼小时候因病成了残疾,母亲的心就像刀绞一样,但她还是强忍住自己的悲痛。
初三数学总复习开放探究(二)课件

加强学生运用数学知识解决实际问题的能力,培养其数学应用意识。
复习要求
复习内容应系统全面,同时针对学生薄弱环节进行有针对性的强化。
在复习过程中,应将数学理论与实践相结合,提高学生的实际应用能力。
鼓励学生自主学习,同时倡导合作学习,通过互相交流和讨论提高学习效果。
初三数学总复习开放探究(二课件
contents
目录
复习目标与要求 知识梳理与总结 开放性问题探究 典型例题解析 复习策略与建议 习题与巩固
01
复习目标与要求
知识整合
解题能力
思维能力
应用能力
复习目标
01
02
03
04
帮助学生整合初中三年所学的数学知识,形成完整的知识体系。
提高学生的数学解题能力,特别是解决综合题和难题的能力。
在保证复习质量的同时,也要注重提高复习效率,合理安排复习进度和难度。
系统性与针对性
理论与实践结合
自主与合作结合
质量与效率并重
02
知识梳理与总结
掌握代数式的概念、性质和运算,理解代数式与整式、分式的联系与区别。
代数式
理解方程的基本性质,掌握一元一次方程、一元二次方程和二元一次方程组的解法。
方程与方程组
基础习题训练
提升解题能力
总结词
提高习题训练是在学生掌握基础知识的前提下,进一步提高解题能力。这些题目难度适中,需要学生具备一定的思维能力和解题技巧。通过练习提高习题,学生可以逐步提高自己的解题水平,为解决更复杂的题目打下基础。
详细描述
提高习题训练
总结词
培养综合能力
详细描述
综合习题训练是为了培养学生的综合能力,这些题目通常涉及多个知识点,需要学生综合运用所学知识来解决问题。通过练习综合习题,学生可以提高自己的分析能力、推理能力和创新能力,有助于在数学学习中取得更好的成绩。
初三直播兴趣班数学讲义(PDF版,无答案)
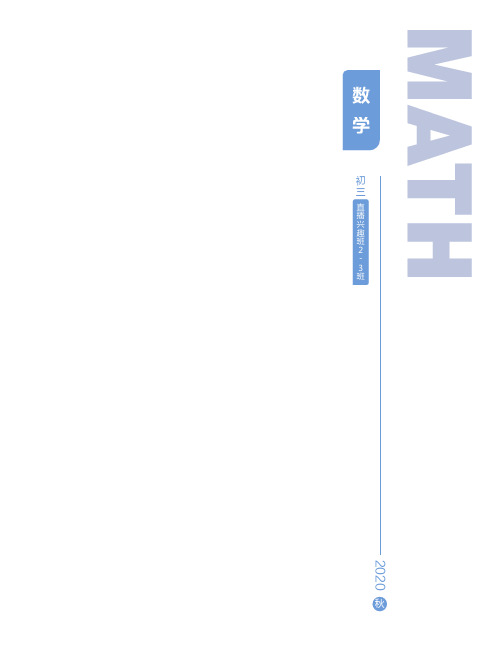
同理可证 a = c ,因此 a = b = c
sin A sinC
sin A sin B sinC
⑵ 利用平面几何知识证明正弦定理: 如图所示,
设 O 为 △ABC 的外接圆的圆心,连 BO 并延长交 ⊙O 于 A′,连 A′C,则 A′ = A,
∴sin A
=
sin A′
=
BC A′B
=
a ,即 2R
Part 1 数学逻辑推理的相关知识
110
第 10 讲 抽屉原理及应用
Part 1 抽屉原理及其应用
122
第 11 讲 数学归纳法初步
Part 1 数学归纳法
136
第 12 讲 极端原理及应用
Part 1 极端原理的相关知识
148
Part 2 无穷递降法
153
第 13 讲 比赛问题
Part 1 比赛问题
;
③ 当该三角形为钝角三角形,求 x 的值或取值范围为
.
第1讲
(2)已知 △ABC 中,AB = 1, BC = 2,则 ∠C 的取值范围是
.
(3)已知三角形的三边长为三个连续自然数,且最大角是钝角.求这个三角形三边的长.
9
【例 6】
x2
+
xy
+
1 3
y2
=
25
正数
x,y,z
满足方程组
z132y+2 +xzz+2
1
Part 1 正弦定理与解三角形
知识点睛
在 △ABC 中的三个内角 A,B,C 的对边分别用 a,b,c : 1. 解三角形: 三角形的三个角 A、B、C 和它们的对边 a,b,c 叫做三角形的元素.已知三角形的几个元素求其他元素 的过程叫做解三角形. 2. 正弦定理: 在三角形中,各边的长和它所对的角的正弦的比相等,且等于该三角形外接圆的直径,即 a =
北师大版九年级数学上册第2章 阶段方法技巧训练(一)专训1一元二次方程与三角形的综合

北师大版九年级数学上册第2章阶段方法技巧训练(一)专训1一元二次方程与三角形的综合名师点金:一元二次方程是初中数学重点内容之一,常常与其他知识结合,其中一元二次方程与三角形的综合应用就是非常重要的一种,主要考查一元二次方程的根的概念、根的判别式的应用、一元二次方程的解法及与等腰三角形、直角三角形的性质等知识的综合运用.一元二次方程与三角形三边关系的综合1.三角形的两边长分别为4和6,第三边长是方程x2-7x+12=0的解,则第三边的长为( )A.3 B.4 C.3或4 D.无法确定2.根据一元二次方程根的定义,解答下列问题.一个三角形两边长分别为3 cm和7 cm,第三边长为a cm,且整数a满足a2-10a+21=0,求三角形的周长.解:由已知可得4<a<10,则a可取5,6,7,8,9.(第一步)当a=5时,代入a2-10a+21,得52-10×5+21≠0,故a=5不是方程的根.同理可知a=6,a=8,a=9都不是方程的根,a=7是方程的根.(第二步)∴三角形的周长是3+7+7=17(cm).上述过程中,第一步是根据_______________________________________________________ ________________________________________________________________________ _________________,第二步应用的数学思想是______________,确定a值的大小是根据______________.一元二次方程与直角三角形的综合3.已知一个直角三角形的两条直角边的长恰好是方程x2-17x +60=0的两个根,则这个直角三角形的斜边长为________.4.已知a,b,c分别是△ABC的三边长,当m>0时,关于x的一元二次方程c(x2+m)+b(x2-m)-2ax=0有两个相等的实数根,试判断△ABC的形状,并说明理由.一元二次方程与等腰三角形的综合5.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.(1)求证:方程有两个不相等的实数根;(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.一元二次方程与动态几何的综合6.如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm.点P 从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿。
北师大版初中九年级下册数学全册特级教师辅导视频免费名师教学讲解毕业班总温习

北师大版初中九年级下册数学全册特级教师辅导视频免费名师教学讲解毕业班总温习北师大版初中九年级下册数学全册特级教师辅导视频免费名师教学讲解毕业班总温习家教录像上课实录、课堂实录教学视频教师多媒体优质课公布课示范课研讨课视频录像、观摩课音频精品课例名师教学实录、在线视频免费下载播放由绿色圃教育网整理,提供中学初二八年级北师大版初中数学科教案课后练习题试题答案PPT课件试卷教学设计导学案教学反思说课稿听课评课稿!北师大版初中九年级下册数学《直角三角形的边角关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《从梯子的倾斜程度谈起》特级教师辅导视频名师讲解北师大版初中九年级下册数学《30°45°60°角的三角函数值》特级教师辅导视频北师大版初中九年级下册数学《三角函数的有关计算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《船有触礁的危险吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学《测量物体的高度》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第二章二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《结识抛物线》特级教师辅导视频名师讲解北师大版初中九年级下册数学《刹车距离与二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《温习二次函数y=ax2+bx+c》特级教师辅导视频名师讲解北师大版初中九年级下册数学《用三种方式表示二次函数》特级教师辅导视频讲解北师大版初中九年级下册数学《何时取得最大利润》特级教师辅导视频名师讲解北师大版初中九年级下册数学《最大面积是多少》特级教师辅导视频名师讲解北师大版初中九年级下册数学《二次函数与一元二次方程》特级教师辅导视频北师大版初中九年级下册数学《第三章圆(一)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的对称性》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆周角和圆心角的关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《确信圆的条件》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第三章圆(二)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《直线和圆的位置关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的性质》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的判定》特级教师辅导视频名师讲解北师大版初中九年级下册数学《弧长与扇形面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆锥的侧面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第四章统计与概率》特级教师辅导视频名师讲解北师大版初中九年级下册数学《哪一种方式更合算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《游戏公平吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学期末《总温习》特级教师辅导视频名师讲解北师大版初中九年级下册数学全册特级教师辅导视频免费名师教学讲解毕业班总温习家教录像上课实录、课堂实录教学视频教师多媒体优质课公布课示范课研讨课视频录像、观摩课音频精品课例名师教学实录、在线视频免费下载播放由绿色圃教育网整理,提供中学初二八年级北师大版初中数学科教案课后练习题试题答案PPT课件试卷教学设计导学案教学反思说课稿听课评课稿!北师大版初中九年级下册数学《直角三角形的边角关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《从梯子的倾斜程度谈起》特级教师辅导视频名师讲解北师大版初中九年级下册数学《30°45°60°角的三角函数值》特级教师辅导视频北师大版初中九年级下册数学《三角函数的有关计算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《船有触礁的危险吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学《测量物体的高度》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第二章二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《结识抛物线》特级教师辅导视频名师讲解北师大版初中九年级下册数学《刹车距离与二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《温习二次函数y=ax2+bx+c》特级教师辅导视频名师讲解北师大版初中九年级下册数学《用三种方式表示二次函数》特级教师辅导视频讲解北师大版初中九年级下册数学《何时取得最大利润》特级教师辅导视频名师讲解北师大版初中九年级下册数学《最大面积是多少》特级教师辅导视频名师讲解北师大版初中九年级下册数学《二次函数与一元二次方程》特级教师辅导视频北师大版初中九年级下册数学《第三章圆(一)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的对称性》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆周角和圆心角的关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《确信圆的条件》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第三章圆(二)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《直线和圆的位置关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的性质》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的判定》特级教师辅导视频名师讲解北师大版初中九年级下册数学《弧长与扇形面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆锥的侧面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第四章统计与概率》特级教师辅导视频名师讲解北师大版初中九年级下册数学《哪一种方式更合算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《游戏公平吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学期末《总温习》特级教师辅导视频名师讲解北师大版初中九年级下册数学全册特级教师辅导视频免费名师教学讲解毕业班总温习家教录像上课实录、课堂实录教学视频教师多媒体优质课公布课示范课研讨课视频录像、观摩课音频精品课例名师教学实录、在线视频免费下载播放由绿色圃教育网整理,提供中学初二八年级北师大版初中数学科教案课后练习题试题答案PPT课件试卷教学设计导学案教学反思说课稿听课评课稿!北师大版初中九年级下册数学《直角三角形的边角关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《从梯子的倾斜程度谈起》特级教师辅导视频名师讲解北师大版初中九年级下册数学《30°45°60°角的三角函数值》特级教师辅导视频北师大版初中九年级下册数学《三角函数的有关计算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《船有触礁的危险吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学《测量物体的高度》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第二章二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《结识抛物线》特级教师辅导视频名师讲解北师大版初中九年级下册数学《刹车距离与二次函数》特级教师辅导视频名师讲解北师大版初中九年级下册数学《温习二次函数y=ax2+bx+c》特级教师辅导视频名师讲解北师大版初中九年级下册数学《用三种方式表示二次函数》特级教师辅导视频讲解北师大版初中九年级下册数学《何时取得最大利润》特级教师辅导视频名师讲解北师大版初中九年级下册数学《最大面积是多少》特级教师辅导视频名师讲解北师大版初中九年级下册数学《二次函数与一元二次方程》特级教师辅导视频北师大版初中九年级下册数学《第三章圆(一)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的对称性》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆周角和圆心角的关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《确信圆的条件》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第三章圆(二)》特级教师辅导视频名师讲解北师大版初中九年级下册数学《直线和圆的位置关系》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的性质》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆的切线的判定》特级教师辅导视频名师讲解北师大版初中九年级下册数学《弧长与扇形面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《圆锥的侧面积》特级教师辅导视频名师讲解北师大版初中九年级下册数学《第四章统计与概率》特级教师辅导视频名师讲解北师大版初中九年级下册数学《哪一种方式更合算》特级教师辅导视频名师讲解北师大版初中九年级下册数学《游戏公平吗》特级教师辅导视频名师讲解北师大版初中九年级下册数学期末《总温习》特级教师辅导视频名师讲解。
九年级数学上册 第2章 解直角三角形 2.5 解直角三角形的应用(第1课时)课件 (新版)青岛版

精选ppt
5
为了测量东方明珠塔的高 度,小亮和同学们在距离东方 明珠塔200 米处的地面上,用 高1.20 米的测角仪测得东方明 珠塔顶的仰角为60°48 ′.
根据测量的结果,小亮画 了一张示意图,其中 AB 表示 东方明珠塔, DC 为测角仪 的支架,DC= 1.20 米,
CB= 200米,∠ADE=60°48.'
根据在前一学段学过的长 D 方形对边相等的有关知识,你 C 能求出AB 的长吗?
精选ppt
A
E B
6
解:根据长方形对边相等,EB=DC,DE=CB. A
在Rt△ABC中,∠AED=90°, ∠ADE= 60°48′. 由tan ∠ADE = AE ,得
DE AE=DE·tan ∠ADE =200·tan60°48 ′
9
1.如图,在电线杆上离地面6 米处用拉
C
线固定电线杆,拉线和地面之间的夹角 为60° , 求拉线AC 的0 . 1 米).
AC≈5.2米 AD=3.0米
A
D
B
2.如图,一架梯子斜靠在墙上,梯子顶端 到地面的距离BC = 3.2 米,底端到墙根的距 离AC = 2.4 米. (1)求梯子的长度和梯子与地面所成角的大 小(精确到1 ' ) ; AB=4.0米, ∠BAC≈53°8′ (2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?
11
1.利用直角三角形的三角比解决实际问题 2.完成习题2.5的相关习题
精选ppt
12
α
A
C
解:设经过B点的水平线为BC,作AC⊥BC,垂足为C . 在Rt△ABC中,AC=1500 米,∠ABC=∠α= 18°23 ' .
华师大版数学九年级上册2中位线同步课件

E
F
O
M
N
B
C
5.求证:顺次连结四边形四条边的中点所得的四边形是平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= 1 AC.
求证:GCEE
GD AD
1. 3
A
证明:连结ED.
∵D、E分别是边BC、AB的中点,
∴DE//AC
,
DE AC
=
1. 2
(三角形的中位线平行于第
E
三边,并且等于第三边的一半).
G
∴△ACG∽△DEG,
∴
GE = GD DE 1 . GC GA AC 2
∴ GE = GD 1 . CE AD 3
B
C
D
如果在上图中,取AC的中点F,假设BF与AD交于G',
如下图,那么我们同理有,G'D G'F 1
所以有
GD
G'D
1
AD BF 3
,即两图中的点G与G'是重合的.
AD AD 3
于是我们有以下结论:
B
1. 三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
2. 三角形重心的性质:三角形的重心与一边中点的 连线的长是对应中线长的 1 .
AB与AC 的中点.根据画出的图形,
C
可以猜想:
DE // BC,且DE = 1 BC.
2
对此,我们可以用演绎推理给出证明.
九年级数学反比例函数2

核心素养回归教材(二)-北师大版九年级数学上册课件(共16张PPT)

【思想方法1】0 解-决翻1.折问题,通常会使用到翻折带来的垂直关系、相等关系,从而可以使用勾股定理对边的长度进行计算.
[2019·滨州]如图,在矩形 ABCD 中,点 E 在边 CD 上,将△BCE 沿 BE 折叠,点 C 落在 AD 边上的点 F 处,过点 F 作 FG∥CD 交 BE 于点 G,连接 CG. (1)求证:四边形 CEFG 是菱形; (2)若 AB=6,AD=10,求四边形 CEFG 的面积.
图1
图2
(1)证明:如答图,连接 OM.
∵AB=CD,BC=DA,
∴四边形 ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AM⊥MC,BM⊥MD,
∴∠AMC=∠BMD=90°,
答图
∴OM=12 BD,OM=12 AC,∴BD=AC,
∴四边形 ABCD 是矩形.
(2)解:∵四边形 ABCD 是矩形,∴∠B=90°. ∵∠BEG=60°,∴∠BGE=30°. ∵点 E 是 AB 的中点,∴AE=BE. 由折叠的性质得 EH=BE=AE,∠HEG=∠BEG=60°, ∠BGE=∠HGE=30°, ∴∠BGH=60°,∠AEH=180°-60°-60°=60°, ∴△AEH 是等边三角形, ∴∠AEH=∠EAH=∠AHE=60°, ∴图中与∠BEG 相等的所有的角有∠AEH,∠EAH, ∠AHE,∠GEH,∠BGH.
【思想方法】 解决翻折问题,通常会使用到翻折带来的垂直关系、相等关系,从而可以使用勾股定理对边的长度进行计算.
【思想方则法】A解′决C翻的折问长题的,通最常会小使值用到是翻折带1来0的垂-直1关.系、相等关系,从而可以使用勾股定理对边的长度进行计算.
BS北师大版 初三九年级数学 下册第二学期春季(导学案)第一章 锐角三角函数 1.1 第2课时 正弦与余弦

1.1 锐角三角函数第2课时 正弦与余弦学习目标:1.经历探索直角三角形中边角关系的过程,理解正弦和余弦的意义.2.能够运用sinA 、cosA 表示直角三角形两边的比.3.能根据直角三角形中的边角关系,进行简单的计算.4.理解锐角三角函数的意义.学习重点:1.理解锐角三角函数正弦、余弦的意义,并能举例说明.2.能用sinA 、cosA 表示直角三角形两边的比.3.能根据直角三角形的边角关系,进行简单的计算.学习难点:用函数的观点理解正弦、余弦和正切.学习方法:探索——交流法.学习过程:一、正弦、余弦及三角函数的定义想一想:如图(1)直角三角形AB 1C 1和直角三角形AB 2C 2有什么关系? (2) 211122BA C A BA C A 和有什么关系? 2112BA BC BA BC 和呢? (3)如果改变A 2在梯子A 1B 上的位置呢?你由此可得出什么结论?(4)如果改变梯子A1B 的倾斜角的大小呢?你由此又可得出什么结论?请讨论后回答.二、由图讨论梯子的倾斜程度与sinA 和cosA 的关系:三、例题:例1、如图,在Rt △ABC 中,∠B=90°,AC =200.sinA =0.6,求BC 的长.例2、做一做:如图,在Rt △ABC 中,∠C=90°,cosA =1312,AC =10,AB等于多B A C少?sinB 呢?cosB 、sinA 呢?你还能得出类似例1的结论吗?请用一般式表达.四、随堂练习:1、在等腰三角形ABC 中,AB=AC =5,BC=6,求sinB ,cosB ,tanB.2、在△ABC 中,∠C =90°,sinA =54,BC=20,求△ABC 的周长和面积.3、在△ABC 中.∠C=90°,若tanA=21,则sinA= .4、已知:如图,CD 是Rt △ABC 的斜边AB 上的高,求证:BC 2=AB ·BD.(用正弦、余弦函数的定义证明)五、课后练习:1、在Rt△ABC 中,∠ C=90°,tanA=34,则sinB=_______,tanB=______. 2、在Rt△ABC 中,∠C=90°,AB=41,sinA=941,则AC=______,BC=_______. 3、在△ABC 中,AB=AC=10,sinC=45,则BC=_____. 4、在△ABC 中,已知AC=3,BC=4,AB=5,那么下列结论正确的是( ) A.sinA=34 B.cosA=35 C.tanA=34 D.cosB=355、如图,在△ABC 中,∠C=90°,sinA=35,则BC AC等于( ) A.34 B.43 C.35 D.456、Rt△ABC 中,∠C=90°,已知cosA=35,那么tanA 等于( ) A.43 B.34 C.45 D.54DB A C7、在△ABC 中,∠C=90°,BC=5,AB=13,则sinA 的值是A .135B .1312C .125D .512 8、已知甲、乙两坡的坡角分别为α、β, 若甲坡比乙坡更徒些, 则下列结论正确的是( )A.tan α<tan βB.sin α<sin β;C.cos α<cos βD.cos α>cos β9、如图,在Rt△ABC 中,CD 是斜边AB 上的高,则下列线段的比中不等于sinA 的是( ) A.CD AC B.DB CB C.CB AB D.CD CB 10、某人沿倾斜角为β的斜坡前进100m,则他上升的最大高度是( )m A.100sin β B.100sin β C.100cos β D. 100cos β 11、如图,分别求∠α,∠β的正弦,余弦,和正切.12、在△ABC 中,AB=5,BC=13,AD 是BC 边上的高,AD=4.求:CD,sinC.13、在Rt△ABC 中,∠BCA=90°,CD 是中线,BC=8,CD=5.求sin∠ACD,cos∠ACD 和tan∠A CD.14、在Rt△ABC 中,∠C=90°,sinA 和cosB 有什么关系?15、如图,已知四边形ABCD 中,BC=CD=DB,∠ADB=90°,cos ∠ABD=45.求:s △ABD :s △BCDBD AC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 学习寄语:
相似三角形作为初中几何的重点和难点是有其客观原因的。一方面,对图形的 分析会大量的使用全等三角形的分析技巧, 但由于两个相似三角形大小不同, 因此, 找相似找全等更难;另一方面,关于比例式的运算也给我们的代数技巧做出新的要 求。 锐角三角函数在初中考试中难度不大,但由于是新的东西,希望各位同学通过 简单的练习对基本公式进行熟悉,并加以运用。
A.
B.
C.
D.4
【例 3】如图,已知 EC∥AB,∠EDA=∠ABF. (1)求证:四边形 ABCD 是平行四边形; 2 (2)求证:OA =OE•OF.
【例 4】如图,△ABC 中,AD⊥BC,垂足是 D,若 BC=14,AD=12,tan∠BAD=
,求 sinC 的值.来自3二、 学习要求:
熟练掌握相似三角形的证明。 熟练运用相似的基本模型进行边角关系的证明。 熟练掌握锐角三角函数的公式及变换。
三、 知识点:
1. 平行线分线段成比例定理及其推论 (1)定理:两条直线被一组平行线所截,截得的对应线段的长度成比例。 (2)推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的 对应线段成比例。 2. 相似三角形的定义、性质 (1)定义:三边成比例且三角相等的两个三角形叫做相似三角形。 (2)性质: ① 相似三角形对应角相等,对应边成比例。 ② 相似三角形周长的比等于相似比。 ③ 相似三角形面积的比等于相似比的平方。 ④ 相似三角形的对应高、 对应中线、 对应角平分线的比等于相似比。 (需 证明) 3. 相似三角形的判定 (1) 两角分别对应相等的两个三角形相似。 (2) 两边成比例且夹角相等的两个三角形相似。 (3) 三边成比例的两个三角形相似。 4. 三角函数的基本公式 a (1) sin A c b (2) cos A c a (3) tan A b
2
D.10cm,25cm,30cm 或 12cm,30cm,36cm (2) 如图, P 为平行四边形 ABCD 边 AD 上一点, E、 F 分别是 PB、 PC (靠近点 P) 的三等分点, △PEF、 △PDC、△PAB 的面积分别为 S1、S2、S3,若 AD=2,AB=2 ,∠A=60°,则 S1+S2+S3 的值为( )
(2)如图,在△ABC 中,点 D 是 AB 边的三等分点(AD<BD) ,DE∥BC 交 AC 于点 E,DF∥AC 交 BC 于 点 F,求 的值.
【例 2】 (1)已知△ABC 的三条长分别为 2cm,5cm,6cm,现将要利用长度为 30cm 和 60cm 的细木条 各一根,做一个三角形木架与△ABC 相似,要求以其中一根作为这个三角形木架的一边,将另一根 截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形 木架的三边长度分别为( ) A.10cm,25cm,30cm B.10cm,30cm,36cm 或 10cm,12cm,30cm C.10cm,30cm,36cm
1
5. 特殊三角函数
30° sin 45° 60°
1 2
2 2
3 2
1 2
cos
3 2 3 3
1
2 2
tan
3
四、 课上例题
【例 1】 (1)如图,点 D、E 分别在 AB、AC 上,以下能推得 DE∥BC 的条件是( )
A.AD:AB=DE:BC C.AD:DB=AE:EC
B.AD:DB=DE:BC D.AE:AC=AD:DB
