光纤通信课后习题解答 第2章习题参考答案
光纤通信 课后答案 人民邮电出版社

《光纤通信》人民邮电出版社课后答案第一章基本理论1、阶跃型折射率光纤的单模传输原理是什么?答:当归一化频率V小于二阶模LP11归一化截止频率,即0<V<2.40483时,此时管线中只有一种传输模式,即单模传输。
2、管线的损耗和色散对光纤通信系统有哪些影响?答:在光纤通信系统中,光纤损耗是限制无中继通信距离的重要因素之一,在很大程度上决定着传输系统的中继距离;光纤的色散引起传输信号的畸变,使通信质量下降,从而限制了通信容量和通信距离。
3、光纤中有哪几种色散?解释其含义。
答:(1)模式色散:在多模光纤中存在许多传输模式,不同模式沿光纤轴向的传输速度也不同,到达接收端所用的时间不同,而产生了模式色散。
(2)材料色散:由于光纤材料的折射率是波长的非线性函数,从而使光的传输速度随波长的变化而变化,由此引起的色散称为材料色散。
(3)波导色散:统一模式的相位常数随波长而变化,即群速度随波长而变化,由此引起的色散称为波导色散。
5、光纤非线性效应对光纤通信系统有什么影响?答:光纤中的非线性效应对于光纤通信系统有正反两方面的作用,一方面可引起传输信号的附加损耗,波分复用系统中信道之间的串话以及信号载波的移动等,另一方面又可以被利用来开发如放大器、调制器等新型器件。
6、单模光纤有哪几类?答:单模光纤分为四类:非色散位移单模光纤、色散位移单模光纤、截止波长位移单模光纤、非零色散位移单模光纤。
12、光缆由哪几部分组成?答:加强件、缆芯、外护层。
*、光纤优点:巨大带宽(200THz)、传输损耗小、体积小重量轻、抗电磁干扰、节约金属。
*、光纤损耗:光纤对光波产生的衰减作用。
引起光纤损耗的因素:本征损耗、制造损耗、附加损耗。
*、光纤色散:由于光纤所传输的信号是由不同频率成分和不同模式成分所携带的,不同频率成分和不同模式成分的传输速度不同,导致信号的畸变。
引起光纤色散的因素:光信号不是单色光、光纤对于光信号的色散作用。
色散种类:模式色散(同波长不同模式)、材料色散(折射率)、波导色散(同模式,相位常数)。
光纤通信技术(第2版)答案

6.试推导渐变型光纤子午线的轨迹方程 答:P15 如式:2-2-18 7. 什么是单模光纤?其单模传输条件是什么? 答:单模光纤是在给定的工作波长上,只传输单一基模的光纤 在阶跃单模光纤中,只传输LP01 (或称HE11 )模。因为 LP01 模的归一化截至频率为
Vc(LP11)=2.40483
而模式的传输条件是V>Vc 可传,V≤Vc 截至,因此,要保证光纤中只传输LP01 一个模式则必须要求:
代入数据可得:
0
V 2 n1k0 a
2
2 n1k0 a 2.40483
0 2 0.01 1.5
0 得: 0 a 2.36358 ( m)
a 2.40483
18.渐变型光纤的折射指数分布为
求出光纤的本地数值孔径 解: NA( r ) n 2 ( r ) n 2 ( a )
9.简述EDFA的工作原理 答: P81-P82 (2)EDFA的工作原理中内容 10. EDFA的主要特征指标是什么?说明其含义。 答: P83 “3.EDFA的主要特征参数” 这一部分 11.为什么说F-P腔型滤波器具有频率选择性? 答: P91 第六段 由于两反射镜的反射系数…… 12.简述光定向耦合器、光隔离器、光环行器以及光开关在光纤通信系统中的作用 答: 光定向耦合器:P88 倒数第二段 光隔离器:P89 倒数第二段 光环行器:P90 最后一段 13.试用图说明光波长转换器的工作原理。 答: P92 图3-45 P93 图3-46 14.什么是波分复用技术? 答:P93 第一段 15.简述光波分复用器的工作原理。 答:P94 “(1)光波分复用器的工作原理”的内容 16.简述RFA的工作原理。 答:P86 “(2)RFA的工作原理”的内容 17.RFA具有哪些特点? 答:P85 “1.RFA的特点”的内容
《光纤通信》课后习题及答案

1.光纤通信的优缺点各是什么?答:优点有:带宽资源丰富,通信容量大;损耗低,中继距离长;无串音干扰,保密性好;适应能力强;体积小、重量轻、便于施工维护;原材料来源丰富,潜在价格低廉等。
缺点有:接口昂贵,强度差,不能传送电力,需要专门的工具、设备以及培训,未经受长时间的检验等。
2.光纤通信系统由哪几部分组成?各部分的功能是什么?答:光纤通信系统由三部分组成:光发射机、光接收机和光纤链路。
光发射机由模拟或数字电接口、电压—电流驱动电路和光源组件组成。
光源组件包括光源、光源—光纤耦合器和一段光纤(尾纤或光纤跳线)组成。
模拟或数字电接的作用是实现口阻抗匹配和信号电平匹配(限制输入信号的振幅)作用。
光源是LED或LD,这两种二极管的光功率与驱动电流成正比。
电压—电流驱动电路是输入电路与光源间的电接口,用来将输入信号的电压转换成电流以驱动光源。
光源—光纤耦合器的作用是把光源发出的光耦合到光纤或光缆中。
光接收机由光检测器组件、放大电路和模拟或数字电接口组成。
光检测器组件包括一段光纤(尾纤或光纤跳线)、光纤—光检波器耦合器、光检测器和电流—电压转换器。
光检测器将光信号转化为电流信号。
常用的器件有PIN和APD。
然后再通过电流—电压转换器,变成电压信号输出。
模拟或数字电接口对输出电路其阻抗匹配和信号电平匹配作用。
光纤链路由光纤光缆、光纤连接器、光缆终端盒、光缆线路盒和中继器等组成。
光纤光缆由石英或塑料光纤、金属包层和外套管组成。
光缆线路盒:光缆生产厂家生产的光缆一般为2km一盘,因而,如果光发送与光接收之间的距离超多2km时,每隔2km将需要用光缆线路盒把光缆连接起来。
光缆终端盒:主要用于将光缆从户外(或户内)引入到户内(或户外),将光缆中的光纤从光缆中分出来,一般放置在光设备机房内。
光纤连接器:主要用于将光发送机(或光接收机)与光缆终端盒分出来的光纤连接起来,即连接光纤跳线与光缆中的光纤。
3.假设数字通信系统能够在高达1%的载波频率的比特率下工作,试问在5GHz的微波载波和 1.55μm的光载波上能传输多少路64kb/s的音频信道?解:根据题意,求得在5GHz的微波载波下,数字通信系统的比特率为50Mb/s,则能传输781路64kb/s的音频信道。
光纤通信课后答案

全书习题参考答案第1章概述1.1 填空题(1)光导纤维(2)掺铒光纤放大器(EDFA) 波分复用(WDM) 非零色散光纤(NIDSF) 光电集成(OEIC)(3)0.85µm 1.31µm 1.55µm 近红外(4)光发送机 光接收机 光纤链路(5)光纤 C=BW×log2(1+SNR) 信道带宽(6)大 大(7)带宽利用系数(8)可重构性可扩展性透明性兼容性完整性生存性1.2 解:利用光导纤维传输光波信号的通信方式称为光纤通信。
即以光波为载频,以光纤为传输介质的通信方式称为光纤通信。
1.3 解:(1)传输频带宽,通信容量大(2)传输距离长(3)抗电磁干扰能力强,无串音(4)抗腐蚀、耐酸碱(5)重量轻,安全,易敷设(6)保密性强(7) 原料资源丰富1.4 解:在光纤通信系统中,最基本的三个组成部分是光发送机、光接收机和光纤链路。
光发送机由电接口、驱动电路和光源组件组成。
其作用是将电信号转换为光信号,并将生成的光信号注入光纤。
光接收机是由光检测器组件、放大电路和电接口组成。
其作用是将光纤送来的光信号还原成原始的电信号。
光纤链路由光纤光缆、光纤光缆线路(接续)盒、光缆终端盒、光纤连接器和中继器等构成。
光纤光缆用于传输光波信息。
中继器主要用于补偿信号由于长距离传送所损失的能量。
光缆线路盒:将光缆连接起来。
光缆终端盒:将光缆从户外引入到室内,将光缆中的光纤从光缆中分出来。
光纤连接器:连接光纤跳线与光缆中的光纤。
1.5解:“掺铒光纤放大器(EDFA)+波分复用(WDM)+非零色散光纤(NIDSF)+光电集成(OEIC)”正成为国际上光纤通信的主要发展方向。
1.6 解:第一阶段(1966~1976年),实现了短波长(0.85µm)、低速(45或34 Mb/s)多模光纤通信系统,无中继传输距离约10km。
第二阶段(1976~1986年),光纤以多模发展到单模,工作波长以短波(0.85um)发展到长波长,实现了波长为1.31µm、传输速率为140~165Mb/s的单模光纤通信系统,无中继传输距离为50~100km。
光纤通信课后习题解答参考答案

思考题参考答案1、SDH帧由哪几部分组成?SDH有哪些显著特点?答:SDH帧由净负荷,管理单元指针和段开销三部分组成。
SDH主要优点有:高度标准化的光接口规范、较好的兼容性、灵活的分插功能、强大的网络管理能力和强大的自愈功能。
其缺点有:频带利用率不如PDH高、设备复杂性增加、网管系统的安全性能要求高。
2、根据帧结构,计算STM-1、STM-4的标称速率。
解:STM-1的标称速率:一帧的比特数:9×270×8=19440(比特),传送一帧所用时间为125μs,故标称速率为:19440/(125×10-6)=155520(kb/s)。
STM-4的标称速率:STM-4帧为9行,270×4列,传送一帧所用时间为125μs。
可以看出STM-4的列数是STM-1的4倍,其余都一样,所以:STM-4的标称速率为:155520×4=622080(kb/s)3、STM-N帧长、帧频、周期各为多少?帧中每个字节提供的通道速率是多少?答:STM-N帧长为9×270N×8比特,帧频8000帧/秒,周期为125μs。
帧中每个字节提供的通道速率为:8比特/帧×8000帧/秒=64kb/s。
4、段开销分几部分?每部分在帧中的位置如何?作用是什么?答:段开销分为再生段开销和复用段开销两部分。
再生段开销位于STM-N帧中的1~3行的1~9×N列,用于帧定位,再生段的监控、维护和管理。
复用段开销分布在STM-N帧中的5~9行的1~9×N列,用于复用段的监控、维护和管理。
5、管理单元指针位于帧中什么位置?其作用是什么?答:管理单元指针存放在帧的第4行的1~9×N列,用来指示信息净负荷的第一个字节在STN-N帧内的准确位置,以便正确地分出所需的信息。
6、简述2.048Mbit/s信号到STM-1的映射复用过程。
答:2.048Mbit/s信号经过C-12、VC-12、TU-12、TUG-2、TUG-3、VC-4、AU-4和AUG-1映射复用成STM-1的成帧信号。
《光纤通信》课后习题答案

习题二1.光波从空气中以角度1θ=33°投射到平板玻璃表面上,这里的1θ是入射光与玻璃表面之间的夹角。
根据投射到玻璃表面的角度,光束一部分被反射,另一部分发生折射,如果折射光束和反射光束之间的夹角正好为90°,请问玻璃的折射率等于多少?这种玻璃的临界角又是多少?解:入射光与玻璃表面之间的夹角1θ=33°,则入射角57i θ=°,反射角57r θ=°。
由于折射光束和反射光束之间的夹角正好为90°,所以折射角33y θ=°。
由折射定律sin sin i i y y n n θθ=,得到sin /sin sin67/sin33y i y n θθ==(自己用matlab 算出来)其中利用了空气折射率1i n =。
这种玻璃的临界角为1arcsinc yn θ=(自己用matlab 算出来) 2.计算1 1.48n =及2 1.46n =的阶跃折射率光纤的数值孔径。
如果光纤端面外介质折射率 1.00n =,则允许的最大入射角max θ为多少?解:阶跃光纤的数值孔径为max sin 0.24NA θ=允许的最大入射角()max arcsin 0.24θ=自己用matlab 算出来3.弱导阶跃光纤纤芯和包层折射率分别为1 1.5n =,2 1.45n =,试计算(1)纤芯和包层的相对折射率∆;(2)光纤的数值孔径NA 。
解:阶跃光纤纤芯和包层的相对折射率差为2212210.032n n n -∆=≈光纤的数值孔径为0.38NA =4.已知阶跃光纤纤芯的折射率为1 1.5n =,相对折射(指数)差0.01∆=,纤芯半径25a m μ=,若01m λμ=,计算光纤的归一化频率V 及其中传播的模数量M 。
解:光纤的归一化频率002233.3V a n ππλλ==⋅=光纤中传播的模数量25542V M ≈=5.一根数值孔径为0.20的阶跃折射率多模光纤在850nm 波长上可以支持1000个左右的传播模式。
光纤通信课后习题答案.docx
光纤通信课后答案1-1 用光导纤维进行通信最早在哪一年由谁提出答:1966年7月英籍华人高锟提出用光导纤维可进行通信。
1-2 光纤通信有哪些优点光纤通信具有许多独特的优点,他们是: 1. 频带宽、传输容量大; 2. 损耗小、中继距离长; 3. 重量轻、体积小; 4. 抗电磁干扰性能好; 5. 泄漏小、保密性好;6.节约金属材料,有利于资源合理使用。
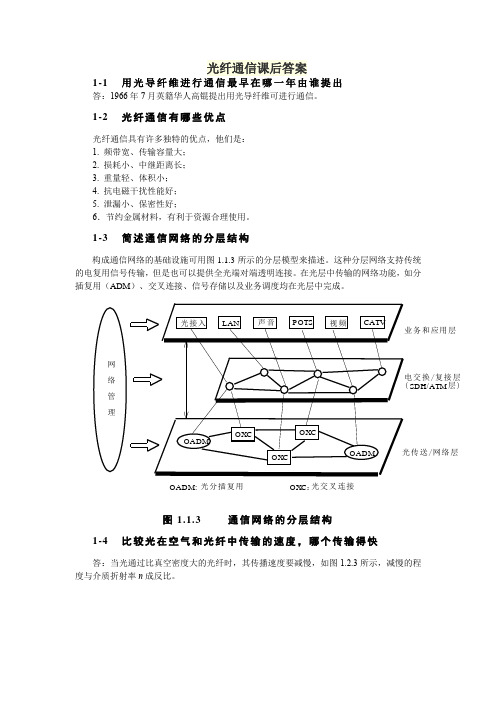
1-3 简述通信网络的分层结构构成通信网络的基础设施可用图1.1.3所示的分层模型来描述。
这种分层网络支持传统的电复用信号传输,但是也可以提供全光端对端透明连接。
在光层中传输的网络功能,如分插复用(ADM )、交叉连接、信号存储以及业务调度均在光层中完成。
电交换/复接层( 层)LAN POTS CATVOXCOXCOXC业务和应用层光传送/网络层光接入声音视频网络管理OADMOADMOADM: OXC :光分插复用光交叉连接SDH/ATM图1.1.3 通信网络的分层结构1-4 比较光在空气和光纤中传输的速度,哪个传输得快答:当光通过比真空密度大的光纤时,其传播速度要减慢,如图1.2.3所示,减慢的程度与介质折射率n 成反比。
图1.2.3 光通过密度大的介质时传播速度要减慢1-5 简述抗反射膜的工作原理。
答:当光入射到光电器件的表面时总会有一些光被反射回来,除增加耦合损耗外,还会对系统产生不利的影响,为此需要在器件表面镀一层电介质材料,以便减少反射,如图1.3.6所示。
在该例中,空气折射率11=n ,器件材料是硅,5.33=n ,电介质材料选用43N S i ,其折射率9.12≈n ,在空气和硅器件折射率之间。
当入射光到达空气和抗反射膜界面时,标记为A 的一些光被反射回来,因为它是外反射,所以反射光与入射光相比有180o 的相位变化。
该光波在电介质材料中传播,当到达抗反射膜和器件界面时,除大部分光进入器件外,一些光又被反射回来,标记为B 。
因为23n n >,还是外反射,B 光仍有180o 的相位变化,而且当它从抗反射膜出来时,已经受了2d 距离的传输延迟,d 为抗反射膜的厚度。
光纤通信原理参考答案
光纤通信原理参考答案光纤通信原理参考答案第⼀章习题1-1 什么是光纤通信?光纤通信是利⽤光导纤维传输光波信号的通信⽅式。
1-2 光纤通信⼯作在什么区,其波长和频率是什么?⽬前使⽤的通信光纤⼤多数采⽤基础材料为SiO2的光纤。
它是⼯作在近红外区,波长为0.8~1.8µm,对应的频率为167~375THz。
1-3 BL积中B和L分别是什么含义?系统的通信容量⽤BL积表⽰,其含义是⽐特率—距离积表⽰,B为⽐特率,L为中继间距。
1-4 光纤通信的主要优点是什么?光纤通信之所以受到⼈们的极⼤重视,是因为和其他通信⼿段相⽐,具有⽆以伦⽐的优越性。
主要有:(1) 通信容量⼤(2) 中继距离远(3) 抗电磁⼲扰能⼒强,⽆串话(4) 光纤细,光缆轻(5) 资源丰富,节约有⾊⾦属和能源。
光纤还具有均衡容易、抗腐蚀、不怕潮湿的优点。
因⽽经济效益⾮常显著。
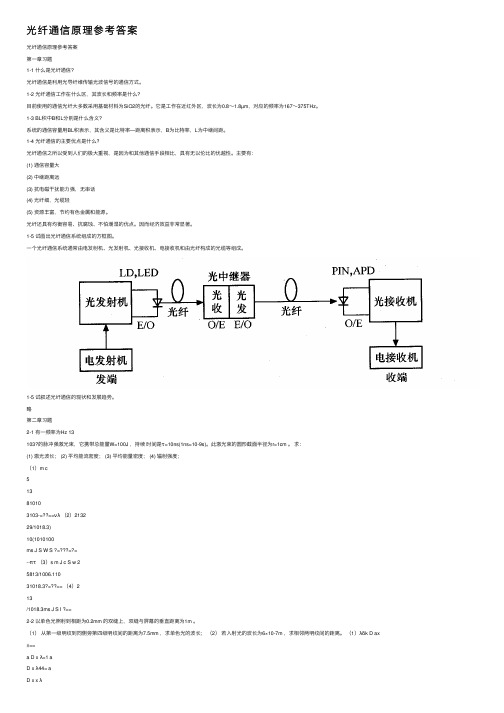
1-5 试画出光纤通信系统组成的⽅框图。
⼀个光纤通信系统通常由电发射机、光发射机、光接收机、电接收机和由光纤构成的光缆等组成。
1-5 试叙述光纤通信的现状和发展趋势。
略第⼆章习题2-1 有⼀频率为Hz 13103?的脉冲强激光束,它携带总能量W=100J ,持续时间是τ=10ns(1ns=10-9s)。
此激光束的圆形截⾯半径为r=1cm 。
求:(1) 激光波长; (2) 平均能流密度; (3) 平均能量密度; (4) 辐射强度;(1)m c513810103103-=??==νλ(2)213229/1018.3)10(1010100ms J S W S ?==?=--πτ(3)s m J c S w 25813/1006.11031018.3?=??== (4)213/1018.3ms J S I ?==2-2 以单⾊光照射到相距为0.2mm 的双缝上,双缝与屏幕的垂直距离为1m 。
(1)从第⼀级明纹到同侧旁第四级明纹间的距离为7.5mm ,求单⾊光的波长;(2)若⼊射光的波长为6×10-7m ,求相邻两明纹间的距离。
《光纤通信》课后习题答案

(2)若取芯径 a = 5m m ,保证单模传输时,则
8
1 λ0 V 1 λ0 2.405 = ∆ < ≈ 0.002 2 2π n1a 2 2π n1a
2
2
8.渐变光纤的折射指数分布为
a r = − ∆ n r n 0 1 2 ( ) ( ) a
2π
λ1
2 = a n12 − n2
2π
λ1
a ⋅ NA ,得到纤芯直径为
a=
2M 1 0.85 2000 λ1 V1 λ ⋅ = 1 ⋅ = ≈ 30.27 2π NA 2π 2π 0.20 NA
(2)当 λ2 = 1.31m m ,有
2M 1 λ2 2M 2 λ1 ⋅ =⋅ 2π 2π NA NA
2π
λ0
= ∆ 33.3 a ⋅ n1 2
光纤中传播的模数量
M≈ V2 = 554 2
5.一根数值孔径为 0.20 的阶跃折射率多模光纤在 850nm 波长上可以支持 1000 个左右的传播模式。试问: (1)其纤芯直径为多少? (2)在 1310nm 波长上可以支持多少个模? (3)在 1550nm 波长上可以支持多少个模? 解: (1)由 V1=
/10 = Po Pi 10−α L= 150 × 10
2 n12 − n2 ≈ 0.38
4.已知阶跃光纤纤芯的折射率为 n1 = 1.5 ,相对折射(指数)差 ∆ =0.01 ,纤芯 半径 a = 25m m ,若 λ0 = 1m m ,计算光纤的归一化频率 V 及其中传播的模数量 M 。 解:光纤的归一化频率
= V 2π
λ0
2 a n12 −= n2
θ r = 57 °。由于折射光束和反射光束之间的夹角正好为
梁瑞生《现代光纤通信技术及应用》课后习题及参考答案

第1章概述1-1、什么是光纤通信?参考答案:光纤通信(Fiber-optic communication)是以光作为信息载体,以光纤作为传输媒介的通信方式,其先将电信号转换成光信号,再透过光纤将光信号进行传递,属于有线通信的一种。
光经过调变后便能携带资讯。
光纤通信利用了全反射原理,即当光的注入角满足一定的条件时,光便能在光纤内形成全反射,从而达到长距离传输的目的。
1-2、光纤通信技术有哪些特点?参考答案:(1)无串音干扰,保密性好。
(2)频带极宽,通信容量大。
(3)抗电磁干扰能力强。
(4)损耗低,中继距离长。
(5)光纤径细、重量轻、柔软、易于铺设。
除以上特点之外,还有光纤的原材料资源丰富,成本低;温度稳定性好、寿命长等特点。
1-3、光纤通信系统由哪几部分组成?简述各部分作用。
参考答案:光纤通信系统最基本由光发送机、光接收机、光纤线路、中继器以及无源器件组成。
其中光发送机负责将信号转变成适合于在光纤上传输的光信号,光纤线路负责传输信号,而光接收机负责接收光信号,并从中提取信息,然后转变成电信号,最后得到对应的话音、图象、数据等信息。
(1)光发送机:由光源、驱动器和调制器组成,实现电/光转换的光端机。
其功能是将来自于电端机的电信号对光源发出的光波进行调制,成为已调光波,然后再将已调的光信号耦合到光纤或光缆去传输。
(2)光接收机:由光检测器和光放大器组成,实现光/电转换的光端机。
其功能是将光纤或光缆传输来的光信号,经光检测器转变为电信号,然后,再将这微弱的电信号经放大电路放大到足够的电平,送到接收端的电端机去。
(3)光纤线路:其功能是将发信端发出的已调光信号,经过光纤或光缆的远距离传输后,耦合到收信端的光检测器上去,完成传送信息任务。
(4)中继器:由光检测器、光源和判决再生电路组成。
它的作用有两个:一个是补偿光信号在光纤中传输时受到的衰减;另一个是对波形失真的脉冲进行整形。
(5)无源器件:包括光纤连接器、耦合器等,完成光纤间的连接、光纤与光端机的连接及耦合。
光通信原理第二章课后题答案 (2)

lev=1.602*10−19 J
代入数据得:Eg (eV)=1.459 eV
当 λ = 1.3μm时 Eg (eV)=0.954 eV 当 λ = 1.55μm时 Eg (eV)=0.800eV 2.光源有哪些主要类型?试简述他们的主要特性。 光源主要分为两大类:激光器(LD)和发光二极管(LED) 。 ①激光器的发光功率大,与光纤的耦合效率高,单色性好,光源谱 宽窄,主要用在长距离、大容量的传输系统中。 ②发光二极管发光功率小, 与光纤的耦合效率较低, 光源谱宽较宽, 主要用在短距离、小容量的传输系统中。 3.半导体激光器特性: (1)P-I 特性:当激光器诸如电流增加时,受激发射量增加,一旦超 过 P-N 结中光的吸收损耗, 激光器就开始震荡, 于是光输出功率急 剧增大。 (2)微分量子效率ηd 激光器输出光子数的增量与注入电子数的增
2 1
式中,P(0)是零频率时 LED 的发射功率;P(ω)是频率为ω时 LED 的发射功率;τ是有源区载流子的寿命时间,一般为10−8 比 LD 大一个数量级。
量之比,定义为微分量子效率: ηd =
ΔP/hf ΔI/e
=
ΔP 0 ΔI
e hf
(3 光谱线型宽度是衡量器件发光单色性的一个物理量。激光器发射 光谱的宽度取决于激发的纵模数目,对于存在的若干纵横的光谱 特性可画出包络线,其谱线宽度定义为输出光功率峰值下降 3dB
是的半功率点对应的宽度。 对于高速率系统采用的单纵模激光器, 则以光功率峰值下降 20dB 时的功率点对应的宽度评定。 (4)温度特性;半导体激光器的阈值电流随温度增加而加大,尤其 是工作于 2 长波段的 InGaAsP 激光器,阈值电流对温度更敏感。 7.发光二极管特性 (1)光输出特性 也即 P-I 特性当注入电流较小时发光二极管的输 出功率曲线基本是线性的当电流过大时,由于 P-N 结发热而出现 饱和状态。 (2)光谱特性:发光二极管的发射光谱比半导体激光器宽很多。发 光二极管对光纤传输带宽的影响比半导体激光器大。 (3)温度特性:温度对发光二极管的光功率影响比半导体激光器要 小。 (4)发光管的频率调制特性:LED 的调制特性可表示为 P= P(0) {1 + (ωτ) }2
《光纤通信》课后习题及答案

1.光纤通信的优缺点各是什么?答:优点有:带宽资源丰富,通信容量大;损耗低,中继距离长;无串音干扰,保密性好;适应能力强;体积小、重量轻、便于施工维护;原材料来源丰富,潜在价格低廉等。
缺点有:接口昂贵,强度差,不能传送电力,需要专门的工具、设备以及培训,未经受长时间的检验等。
2.光纤通信系统由哪几部分组成?各部分的功能是什么?答:光纤通信系统由三部分组成:光发射机、光接收机和光纤链路。
光发射机由模拟或数字电接口、电压—电流驱动电路和光源组件组成。
光源组件包括光源、光源—光纤耦合器和一段光纤(尾纤或光纤跳线)组成。
模拟或数字电接的作用是实现口阻抗匹配和信号电平匹配(限制输入信号的振幅)作用。
光源是LED或LD,这两种二极管的光功率与驱动电流成正比。
电压—电流驱动电路是输入电路与光源间的电接口,用来将输入信号的电压转换成电流以驱动光源。
光源—光纤耦合器的作用是把光源发出的光耦合到光纤或光缆中。
光接收机由光检测器组件、放大电路和模拟或数字电接口组成。
光检测器组件包括一段光纤(尾纤或光纤跳线)、光纤—光检波器耦合器、光检测器和电流—电压转换器。
光检测器将光信号转化为电流信号。
常用的器件有PIN和APD。
然后再通过电流—电压转换器,变成电压信号输出。
模拟或数字电接口对输出电路其阻抗匹配和信号电平匹配作用。
光纤链路由光纤光缆、光纤连接器、光缆终端盒、光缆线路盒和中继器等组成。
光纤光缆由石英或塑料光纤、金属包层和外套管组成。
光缆线路盒:光缆生产厂家生产的光缆一般为2km一盘,因而,如果光发送与光接收之间的距离超多2km时,每隔2km将需要用光缆线路盒把光缆连接起来。
光缆终端盒:主要用于将光缆从户外(或户内)引入到户内(或户外),将光缆中的光纤从光缆中分出来,一般放置在光设备机房内。
光纤连接器:主要用于将光发送机(或光接收机)与光缆终端盒分出来的光纤连接起来,即连接光纤跳线与光缆中的光纤。
3.假设数字通信系统能够在高达1%的载波频率的比特率下工作,试问在5GHz的微波载波和 1.55μm的光载波上能传输多少路64kb/s的音频信道?解:根据题意,求得在5GHz的微波载波下,数字通信系统的比特率为50Mb/s,则能传输781路64kb/s的音频信道。
《光纤通信》第二版刘增基课后习题答案

1-1光纤通信的优缺点各是什么?答与传统的金属电缆通信、微波无线电通信相比,光纤通信具有如下优点:(1) 通信容量大.首先,光载波的中心频率很高,约为2 X10^14Hz ,最大可用带宽一般取载波频率的10 %,则容许的最大信号带宽为20 000 GHz( 20 THz ) ;如果微波的载波频率选择为20 GHz ,相应的最大可用带宽为2 GHz。
两者相差10000 倍.其次,单模光纤的色散几乎为零,其带宽距离(乘)积可达几十GHz·km ;采用波分复用(多载波传输)技术还可使传输容量增加几十倍至上百倍.目前,单波长的典型传输速率是10 Gb /s。
,一个采用128 个波长的波分复用系统的传输速率就是1 . 28 Tb / s .( 2 )中继距离长。
中继距离受光纤损耗限制和色散限制,单模光纤的传输损耗可小千0 . 2 dB / km ,色散接近于零.( 3 )抗电磁干扰.光纤由电绝缘的石英材料制成,因而光纤通信线路不受普通电磁场的干扰,包括闪电、火花、电力线、无线电波的千扰.同时光纤也不会对工作于无线电波波段的通信、雷达等设备产生干扰。
这使光纤通信系统具有良好的电磁兼容性。
( 4 )传输误码率极低。
光信号在光纤中传输的损耗和波形的畸变均很小,而且稳定,.噪声主要来源于t 子噪声及光检测器后面的电阻热噪声和前置放大器的噪声.只要设计适当,在中继距离内传输的误码率可达10^-9甚至更低。
此外,光纤通信系统还具有适应能力强、保密性好以及使用寿命长等特点。
当然光纤通信系统也存在一些不足:( 1 )有些光器件(如激光器、光纤放大器)比较昂贵。
( 2 )光纤的机械强度差,为了提高强度,实际使用时要构成包声多条光纤的光缆,光统中要有加强件和保护套。
( 3 )不能传送电力.有时需要为远处的接口或再生的设备提供电能,光纤显然不能胜任。
为了传送电能,在光缆系统中还必须额外使用金属导线.(4)光纤断裂后的维修比较困难,需要专用工具。
《光纤通信》课后习题答案..

1.光纤通信的优缺点各是什么?答:优点有:带宽资源丰富,通信容量大;损耗低,中继距离长;无串音干扰,保密性好;适应能力强;体积小、重量轻、便于施工维护;原材料来源丰富,潜在价格低廉等。
缺点有:接口昂贵,强度差,不能传送电力,需要专门的工具、设备以及培训,未经受长时间的检验等。
2.光纤通信系统由哪几部分组成?各部分的功能是什么?答:光纤通信系统由三部分组成:光发射机、光接收机和光纤链路。
光发射机由模拟或数字电接口、电压—电流驱动电路和光源组件组成。
光源组件包括光源、光源—光纤耦合器和一段光纤(尾纤或光纤跳线)组成。
模拟或数字电接的作用是实现口阻抗匹配和信号电平匹配(限制输入信号的振幅)作用。
光源是LED或LD,这两种二极管的光功率与驱动电流成正比。
电压—电流驱动电路是输入电路与光源间的电接口,用来将输入信号的电压转换成电流以驱动光源。
光源—光纤耦合器的作用是把光源发出的光耦合到光纤或光缆中。
光接收机由光检测器组件、放大电路和模拟或数字电接口组成。
光检测器组件包括一段光纤(尾纤或光纤跳线)、光纤—光检波器耦合器、光检测器和电流—电压转换器。
光检测器将光信号转化为电流信号。
常用的器件有PIN和APD。
然后再通过电流—电压转换器,变成电压信号输出。
模拟或数字电接口对输出电路其阻抗匹配和信号电平匹配作用。
光纤链路由光纤光缆、光纤连接器、光缆终端盒、光缆线路盒和中继器等组成。
光纤光缆由石英或塑料光纤、金属包层和外套管组成。
光缆线路盒:光缆生产厂家生产的光缆一般为2km一盘,因而,如果光发送与光接收之间的距离超多2km时,每隔2km将需要用光缆线路盒把光缆连接起来。
光缆终端盒:主要用于将光缆从户外(或户内)引入到户内(或户外),将光缆中的光纤从光缆中分出来,一般放置在光设备机房内。
光纤连接器:主要用于将光发送机(或光接收机)与光缆终端盒分出来的光纤连接起来,即连接光纤跳线与光缆中的光纤。
3.假设数字通信系统能够在高达1%的载波频率的比特率下工作,试问在5GHz的微波载波和 1.55μm的光载波上能传输多少路64kb/s的音频信道?解:根据题意,求得在5GHz的微波载波下,数字通信系统的比特率为50Mb/s,则能传输781路64kb/s的音频信道。
《光纤通信》习题解答(陈柏年)

《光纤通信》习题解答浙江传媒学院陈柏年第一章概述1、1.1什么是光纤通信?简述光纤通信的发展历程?•解:光纤通信:以光波作为信号载体,以光纤作为传输媒介的通信方式。
光纤通信是以光波作为传输信息的载波、以光纤作为传输介质的一种通信方式。
也就是说,光纤通信是将待传送的语音、图像和数据等信号调制在光载波上,然后通过光纤进行传输的一种通信方式。
•光纤通信的发展粗略分为如下几个阶段:(1)第一阶段(1966-1976年),从基础研究到商业应用的开发时期。
在这个时期,实现了短波长(0.85μm)低速率(45-140Mb/s)多模光纤通信系统,无中继传输距离约10km。
(2)第二阶段(1976-1986年),这是以提高传输速率和增加传输距离为研究目标和大力推广应用的大发展时期。
在这个时期,光纤从多模发展到单模,工作波长从短波长发展到长波长(1.31μm和1.55μm),实现了工作波长为1.31μm、传输速率为140-565Mb/s的单模光纤通信系统,无中继传输距离为10-50km。
(3)第三阶段(1986-1996年),这是以超大容量超长距离为目标、全面深入开展新技术研究的时期。
在这个时期,实现了1.55μm色散移位单模光纤通信系统。
采用外调制技术,传输速率可达 2.5-10Gb/s,无中继传输距离可达100-150km。
(4)第四阶段(1996年-至今),开展研究光纤通信新技术。
采用光放大器增加中继距离和采用波分复用增加传输容量。
现在10Gb/s、40Gb/s的系统也已商用化。
1.2 光纤通信为什么能够成为一种主要的通信方式?•解:光纤通信能够成为现代的主要通信方式,是归因于光纤通信具有以下突出的优点:①通信速率高(单波长速率已达10Gb/s以上),传输容量大(光波具有很高的频率,约1014Hz,一根光纤可同时传输几十个波长) ;②损耗低(单模已低达0.2dB/km)、传输距离远(中继距离可达50-100Km);③抗干扰能力强(抗强电、雷电和核辐射干扰),保密性好(光纤由石英玻璃制成,由于是绝缘材料,不受电磁场干扰;在光纤中传输的光泄漏非常微弱);④质量轻(是传输相同信息量电缆重量的1/10-1/30),体积小(是相同容量电缆外径的1/3-1/4),敷设方便;⑤耐腐蚀,耐高温(石英玻璃熔点在2000 °C以上),可在恶劣环境中工作,寿命长;⑥节约金属材料,有利于资源合理使用(制造同轴电缆和波导管的铜、铝、铅等金属材料,在地球上的储存量是有限的;而制造光纤的石英(SiO2)在地球上基本上是取之不尽的材料)1.3 光纤通信系统的组成主要包括哪些部分?试画出简图予以说明。
光纤通信课后习题解答第2章习题参考答案

第二章 光纤和光缆1.光纤是由哪几部分组成的?各部分有何作用?答:光纤是由折射率较高的纤芯、折射率较低的包层和外面的涂覆层组成的。
纤芯和包层是为满足导光的要求;涂覆层的作用是保护光纤不受水汽的侵蚀和机械擦伤,同时增加光纤的柔韧性。
2.光纤是如何分类的?阶跃型光纤和渐变型光纤的折射率分布是如何表示的?答:(1)按照截面上折射率分布的不同可以将光纤分为阶跃型光纤和渐变型光纤;按光纤中传输的模式数量,可以将光纤分为多模光纤和单模光纤;按光纤的工作波长可以将光纤分为短波长光纤、长波长光纤和超长波长光纤;按照ITU-T 关于光纤类型的建议,可以将光纤分为G .651光纤(渐变型多模光纤)、G .652光纤(常规单模光纤)、G.653光纤(色散位移光纤)、G.654光纤(截止波长光纤)和G.655(非零色散位移光纤)光纤;按套塑(二次涂覆层)可以将光纤分为松套光纤和紧套光纤。
(2)阶跃型光纤的折射率分布 () 21⎩⎨⎧≥<=ar n ar n r n 渐变型光纤的折射率分布 () 2121⎪⎩⎪⎨⎧≥<⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∆-=ar n a r a r n r n cm α 3.阶跃型光纤和渐变型光纤的数值孔径NA 是如何定义的?两者有何区别?它是用来衡量光纤什么的物理量?答:阶跃型光纤的数值孔径 2sin 10∆==n NA φ 渐变型光纤的数值孔径 ()() 20-0sin 220∆===n n n NA c φ两者区别:阶跃型光纤的数值孔径是与纤芯和包层的折射率有关;而渐变型光纤的数值孔径只与纤芯内最大的折射率和包层的折射率有关。
数值孔径是衡量光纤的集光能力,即凡是入射到圆锥角φ0以内的所有光线都可以满足全反射条件,在芯包界面上发生全反射,从而将光线束缚在纤芯中沿轴向传播。
4.简述光纤的导光原理。
答:光纤之所以能够导光就是利用纤芯折射率略高于包层折射率的特点,使落于数值孔径角)内的光线都能收集在光纤中,并在芯包边界以内形成全反射,从而将光线限制在光纤中传播。
光纤通信简明教程部分参考答案

第一章习题1-1 什么是光纤通信? 目前使用的通信光纤大多数采用基础材料为SiO 2的光纤,它是工作在电磁波的哪个区?波长范围是多少?对应的频率范围是多少? 光纤通信是利用光导纤维传输光波信号的通信方式。
目前使用的通信光纤大多数采用基础材料为SiO 2的光纤。
它是工作在近红外区,波长为0.8~1.8μm ,对应的频率为167~375THz 。
1-2 试画出光纤通信系统组成的方框图。
一个光纤通信系统通常由电发射机、光发射机、光接收机、电接收机和由光纤构成的光缆等组成。
1-3 通信系统的容量用BL 积表示,B 和L 分别是什么含义?系统的通信容量用比特率—距离积表示,B 为比特率,L 为中继间距。
1-4 光纤通信的主要优点是什么?光纤通信之所以受到人们的极大重视,是因为和其他通信手段相比,具有无以伦比的优越性。
(1) 通信容量大 (2) 中继距离远(3) 抗电磁干扰能力强,无串话 (4) 光纤细,光缆轻(5) 资源丰富,节约有色金属和能源。
光纤还具有均衡容易、抗腐蚀、不怕潮湿的优点。
因而经济效益非常显著。
1-5 请查阅最新资料论述光纤通信的发展趋势。
略第二章习题2-1 一个频率为Hz 的光14106⨯源,其发射功率为10W ,它一秒内发射多少个光子? 解:191434141052.210610626.610106,10⨯=⨯⨯⨯==⨯==-ννh P N HzW P2-2 如下两种光纤,临界角满足什么条件可以保持光在纤芯中传播? (1) 对于石英光纤,纤芯的折射率48.11=n ,包层的折射率46.12=n 。
(2) 对于塑料光纤,纤芯的折射率495.11=n ,包层的折射率402.12=n 。
解:由 12sin n n c =ϑ 得 121sin n n c -=ϑ (1)︒==-57.8048.146.1sin1c ϑ (2)︒==-94.73495.1402.1sin 1c ϑ2-3 一单色光垂直照在厚度均匀的薄油膜上。
光纤通信课后第2章习题答案
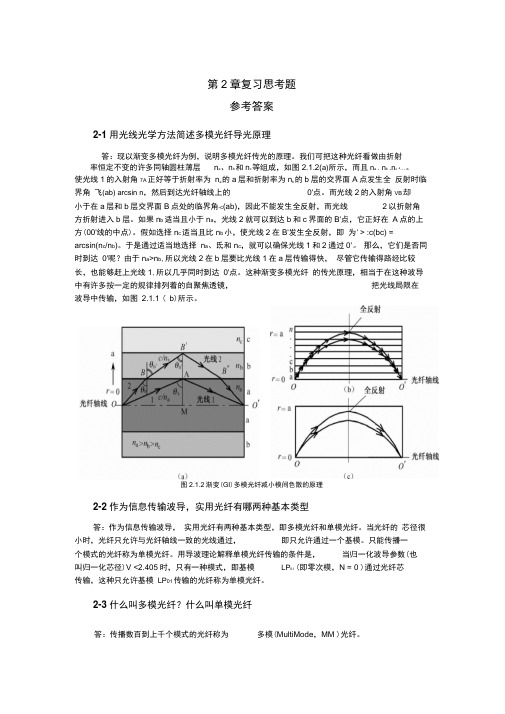
答:传播数百到上千个模式的光纤称为多模(MultiMode ,MM )光纤。
第2章复习思考题参考答案2-1 用光线光学方法简述多模光纤导光原理答:现以渐变多模光纤为例,说明多模光纤传光的原理。
我们可把这种光纤看做由折射 率恒定不变的许多同轴圆柱薄层 n a 、n b 和n c 等组成,如图2.1.2(a)所示,而且n a . n b .n c •…。
使光线1的入射角7A 正好等于折射率为 n a 的a 层和折射率为n b 的b 层的交界面A 点发生全 反射时临界角 飞(ab) arcsin n ,然后到达光纤轴线上的0'点。
而光线2的入射角VB 却小于在a 层和b 层交界面B 点处的临界角-c (ab),因此不能发生全反射,而光线2以折射角方折射进入b 层。
如果n b 适当且小于n a ,光线2就可以到达b 和c 界面的B'点,它正好在 A 点的上方(00'线的中点)。
假如选择n c 适当且比n b 小,使光线2在B'发生全反射,即 为'> :c(bc) = arcsin(n c /n b )。
于是通过适当地选择 n a 、氐和n c ,就可以确保光线1和2通过0'。
那么,它们是否同时到达 0'呢?由于n a >n b ,所以光线2在b 层要比光线1在a 层传输得快, 尽管它传输得路经比较长,也能够赶上光线1,所以几乎同时到达 0'点。
这种渐变多模光纤 的传光原理,相当于在这种波导中有许多按一定的规律排列着的自聚焦透镜, 把光线局限在波导中传输,如图 2.1.1 ( b )所示。
图2.1.2渐变(GI )多模光纤减小模间色散的原理2-2 作为信息传输波导,实用光纤有哪两种基本类型答:作为信息传输波导, 实用光纤有两种基本类型,即多模光纤和单模光纤。
当光纤的 芯径很小时,光纤只允许与光纤轴线一致的光线通过, 即只允许通过一个基模。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 光纤和光缆1.光纤是由哪几部分组成的?各部分有何作用?答:光纤是由折射率较高的纤芯、折射率较低的包层和外面的涂覆层组成的。
纤芯和包层是为满足导光的要求;涂覆层的作用是保护光纤不受水汽的侵蚀和机械擦伤,同时增加光纤的柔韧性。
2.光纤是如何分类的?阶跃型光纤和渐变型光纤的折射率分布是如何表示的?答:(1)按照截面上折射率分布的不同可以将光纤分为阶跃型光纤和渐变型光纤;按光纤中传输的模式数量,可以将光纤分为多模光纤和单模光纤;按光纤的工作波长可以将光纤分为短波长光纤、长波长光纤和超长波长光纤;按照ITU-T 关于光纤类型的建议,可以将光纤分为G .651光纤(渐变型多模光纤)、G.652光纤(常规单模光纤)、G.653光纤(色散位移光纤)、G .654光纤(截止波长光纤)和G .655(非零色散位移光纤)光纤;按套塑(二次涂覆层)可以将光纤分为松套光纤和紧套光纤。
(2)阶跃型光纤的折射率分布 () 21⎩⎨⎧≥<=ar n ar n r n 渐变型光纤的折射率分布 () 2121⎪⎩⎪⎨⎧≥<⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∆-=ar n a r a r n r n cm α 3.阶跃型光纤和渐变型光纤的数值孔径N A是如何定义的?两者有何区别?它是用来衡量光纤什么的物理量?答:阶跃型光纤的数值孔径 2sin 10∆==n NA φ 渐变型光纤的数值孔径 ()() 20-0sin 220∆===n n n NA c φ两者区别:阶跃型光纤的数值孔径是与纤芯和包层的折射率有关;而渐变型光纤的数值孔径只与纤芯内最大的折射率和包层的折射率有关。
数值孔径是衡量光纤的集光能力,即凡是入射到圆锥角φ0以内的所有光线都可以满足全反射条件,在芯包界面上发生全反射,从而将光线束缚在纤芯中沿轴向传播。
4.简述光纤的导光原理。
答:光纤之所以能够导光就是利用纤芯折射率略高于包层折射率的特点,使落于数值孔径角)内的光线都能收集在光纤中,并在芯包边界以内形成全反射,从而将光线限制在光纤中传播。
5.什么是传导模?推导相位一致条件,并说明其物理意义。
答:(1)能在光纤中长距离传播的模式称之为传导模,简称导模。
(2)A2,1,0 2) =(则:若: N N B A BA π=Φ-ΦΦ=Φ''即: ()() 2,1,0 N 221010 =='--'N B B n k A A n k πδ 根据平面几何知识,可化简为:() 2,1,0 cos 210 ==-N N a n k πδθ(3)光波在有限空间传播时,形成驻波。
因此,当光波横向传播一个周期时,其波相位变化2π的整数倍,才会相干加强形成驻波,否则相干抵消。
6.在均匀光纤中,为什么单模光纤的芯径和相对折射率差Δ比多模光纤小?答:光纤单模传输的条件是光纤的归一化频率V 要小于次低阶模的归一化截止频率Vc ,即: Vc V <;当 Vc V >时,光纤进行多模传输。
而∆=∆=2221010a n a n k V λπ。
因此,单模光纤的芯径a和相对折射率差Δ比多模光纤小。
7.均匀光纤纤芯和包层的折射率分别为n 1=1.50,n 2=1.45,光纤的长度L=10Km。
试求:(1)光纤的相对折射率差Δ; (2)数值孔径NA ;(3)若将光纤的包层和涂敷层去掉,求裸光纤的NA和相对折射率差Δ。
解:(1)%3.31.5245.11.5 2n n -n 222212221=⨯-=∆=(2) 0.39 0.03321.521=⨯⨯=∆=n NA(3)若将光纤的包层和涂敷层去掉,则相当于包层的折射率n 2=1,则%1.281.5211.5 2n n -n 222212221=⨯-=∆=1.12 0.28121.521=⨯⨯=∆=n NA而 sin 0φ=NA 最大为1,所以说只要光纤端面的入射角在90O 以内,就可以在光纤中形成全反射。
8.已知阶跃型光纤,纤芯折射率n1=1.50,相对折射率差Δ=0.5%,工作波长λ0=1.31μm,试求:(1)保证光纤单模传输时,光纤的纤芯半径a应为多大? (2)若a =5μm ,保证光纤单模传输时,n 2应如何选择? 解:(1)因为是阶跃型光纤,所以归一化截止频率Vc =2.405;()m m n a a n V μπμπλλπ34.3231.1%5.0250.1405.222405.2 405.2220110=⨯⨯⨯=⨯∆<∴<∆=(2)若a =5μm,保证光纤单模传输时,4967.1%22.0215.121n n 0.22% 2n n -n %22.02231.1550.1405.222405.2 405.22212212221220110=⨯-⨯=∆->⇒<∆=⎪⎪⎭⎫ ⎝⎛⨯⨯=⎪⎪⎭⎫⎝⎛⨯<∆<∆==πμμπλλπm m a n a n V9.已知抛物线型渐变多模光纤,纤芯轴线处的最大折射率n(o)=1.50,相对折射率Δ=5%,纤芯半径2a =50μm,工作波长λ0=0.85μm 。
试求此光纤可传输的模式数。
解:因为:抛物线型渐变多模光纤,α=2所以: 3.4 221405.2 21405.2=+⨯=+⨯=αVc ()4.36.87%522550.185.022210>=⨯⨯⨯⨯=∆=m ma o n V μμπλπ所以该抛物线型渐变多模光纤为多模传输,可传输的模式数为:191826.87222 2222=⋅+=⋅+=V N αα10.证明:垂直极化波和水平极化波的反射系数和传递系数的表达式(略)。
垂直极化波:cos cos cos cos 22112211θθθθn n n n R +-=cos cos cos 2221111θθθn n n T +=水平极化波:cos cos cos cos 21122112θθθθn n n n R +-=cos cos cos 2211211θθθn n n T +=11.根据上题证明的结果,推导垂直极化波和水平极化波在全反射情况下介质1和介质2中场的表达式,并简要说明介质1和介质2中波的特点。
答:垂直极化波在全反射情况下1sin cos 122212-⎪⎪⎭⎫ ⎝⎛-=θθn n j 1cos cos cos cos cos sin sin 2221122111212⎥⎥⎦⎤⎢⎢⎣⎡-⋅+-=∴θθθθθθθc arctg j en n n n R = 令:12122211cos sin sin θθθcnn arctg -⎪⎪⎭⎫ ⎝⎛=Φ112Φ⋅=j e R 则 在介质1中,既有入射波,又有反射波,并且入射波和反射波电场方向相同,因此合成波可在直角坐标系下展开,并表示为:()()111111111012010111cos 2 Φ---Φ--Φ+=+='+=z k j x z jk x jk j z jk x jk z z x z x ex k E e e e E e e E E E E 所以,全反射情况下介质1中波的特点是沿X 方向按三角函数规律变化,说明能量在X方向上不传播,波呈驻波分布。
沿Z 方向呈行波状态,说明合成波是沿Z方向传播的,其相位传播常数为 sin 1101θβn k k z ==在介质2中只有传递波:cos 2cos cos cos 212122cos sin sin 2221112211112θθθθθθθcjarctgj en n n n n n e T T -Φ-=+==z jk x jk j z x e e e T E E 2222012--Φ=() 21201Φ---=z k j x z e e T E α由于:21212102202sin cos ⎪⎪⎭⎫⎝⎛--==n n n jk n k k xθθsin sin 11102202βθθ====z z k n k n k k所以:() 2121212102sin 012Φ--⎪⎪⎭⎫ ⎝⎛-⋅-=z k j nn n k x z e eT E E θ因此,全反射情况下介质2中波的特点是沿Z方向呈行波分布,且传播常数与介质1中的相同;随X 方向变化的因子是2121210sin ⎪⎪⎭⎫ ⎝⎛-⋅-nn n k x eθ,说明波的幅度随离开界面的距离按指数形式衰减,衰减的快慢由参数2121210sin ⎪⎪⎭⎫ ⎝⎛-nn n k θ决定。
12.简述TEM 波、TE 波、TM 波、EH 波和HE 波各自的特点。
弱导光纤中存在哪些类型的波?为什么不存在TEM 波? 答:(1)TEM 波的电场和磁场方向与波的传播方向垂直,即在传播方向上既没有磁场分量也没有电场分量,且三者两两相互垂直。
TE 波在传播方向上只有磁场分量而没有电场分量;TM 波在传播方向上只有电场分量而没有磁场分量;EH 波在传播方向上既有磁场分量又有电场分量,但以电场分量为主;HE 波在传播方向上既有磁场分量又有电场分量,但以磁场分量为主。
(2)在弱导光纤中存在TE 波、TM 波、EH 波和HE波四种波型。
(3)TE M波在传播方向(Z方向)上既没有电场分量,又没有磁场分量。
即Ez =0、H z=0。
如果光纤中存在TEM 波,则根据E z 、H z 的表达式可以得到A=B=0,从而得到E r、E φ、H r、Eφ都为零,即光纤中不存在电磁场,所以光纤中根本不存在TEM 波。
13.模的特性是用哪些参数来衡量的?各描述的是什么含义?答:模的特性可以用三个特征参数U 、W 和β来描述。
其中:U 表示导模场在纤芯内部的横向分布规律;W表示表示导模场在纤芯外部的横向分布规律;U 和W 结合起来,就可以完整地描述导模的横向分布规律。
β是轴向的相位传播常数,表明导模的纵向传输特性。
14.根据TE 0n 和TM 0n 模在弱导光纤中的特征方程()()()()W WK W K U UJ U J 0101=-证明TE 0n 和Tm 0n模在截止状态下有:() 00=c U J 证明:根据贝塞尔函数的性质,当W→0时,() 2ln0WW K = ()() W1 2!112111=⎪⎭⎫⎝⎛⋅-=W W K模式处于临界状态时,W =0,对应的径向归一化相位常数记为Uc 。
()()()()()01lim2ln1limlim 020001001=⇒∞==⋅==-→→→c c W W W c c c U J U W WW W W WK W K U J U U J 若Uc =0,则()()()()00000101-=⋅-=-J J U J U U J c c c ,成为不定型,所以Uc ≠0,只有() 00=c U J 15.根据HE mn 模在弱导光纤中的特征方程()()()()W WK W K U UJ U J m m m m 11--=试求:HE 11、H E12、HE 21和HE 22模的归一化截止频率Vc 。
