各种校验码校验算法分析
常见校验算法

常见校验算法一、校验算法奇偶校验MD5校验求校验和BCC(Block Check Character/信息组校验码),好像也是常说的异或校验方法CRC(Cyclic Redundancy Check/循环冗余校验)LRC(Longitudinal Redundancy Check/纵向冗余校验)二、奇偶校验内存中最小的单位是比特,也称为“位”,位有只有两种状态分别以1和0来标示,每8个连续的比特叫做一个字节(byte)。
不带奇偶校验的内存每个字节只有8位,如果其某一位存储了错误的值,就会导致其存储的相应数据发生变化,进而导致应用程序发生错误。
而奇偶校验就是在每一字节(8位)之外又增加了一位作为错误检测位。
在某字节中存储数据之后,在其8个位上存储的数据是固定的,因为位只能有两种状态1或0,假设存储的数据用位标示为1、1、1、0、0、1、0、1,那么把每个位相加(1+1+1+0+0+1+0+1=5),结果是奇数,那么在校验位定义为1,反之为0。
当CPU读取存储的数据时,它会再次把前8位中存储的数据相加,计算结果是否与校验位相一致。
从而一定程度上能检测出内存错误,奇偶校验只能检测出错误而无法对其进行修正,同时虽然双位同时发生错误的概率相当低,但奇偶校验却无法检测出双位错误三、MD5校验MD5的全称是Message-Digest Algorithm 5,在90年代初由MIT的计算机科学实验室和RSA Data Security Inc 发明,由MD2/MD3/MD4 发展而来的。
MD5的实际应用是对一段Message(字节串)产生fingerprint(指纹),可以防止被“篡改”。
举个例子,天天安全网提供下载的MD5校验值软件WinMD5.zip,其MD5值是1e07ab3591d25583eff5129293dc98d2,但你下载该软件后计算MD5 发现其值却是81395f50b94bb4891a4ce4ffb6ccf64b,那说明该ZIP已经被他人修改过,那还用不用该软件那你可自己琢磨着看啦。
CRC16、CRC32校验简单分析
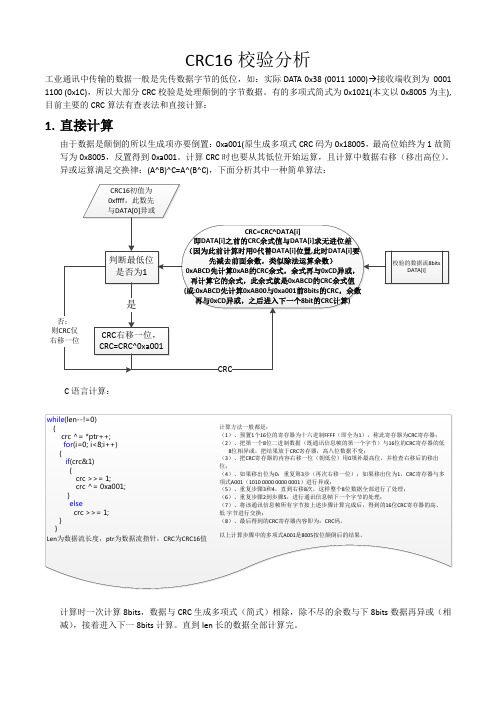
CRC16校验分析工业通讯中传输的数据一般是先传数据字节的低位,如:实际DATA 0x38 (0011 1000) 接收端收到为0001 1100 (0x1C),所以大部分CRC校验是处理颠倒的字节数据。
有的多项式简式为0x1021(本文以0x8005为主),目前主要的CRC算法有查表法和直接计算:1.直接计算由于数据是颠倒的所以生成项亦要倒置:0xa001(原生成多项式CRC码为0x18005,最高位始终为1故简写为0x8005,反置得到0xa001。
计算CRC时也要从其低位开始运算,且计算中数据右移(移出高位)。
异或运算满足交换律:(A^B)^C=A^(B^C),下面分析其中一种简单算法:C语言计算:计算时一次计算8bits,数据与CRC生成多项式(简式)相除,除不尽的余数与下8bits数据再异或(相减),接着进入下一8bits计算。
直到len长的数据全部计算完。
2.查表法:通过分别计算8bits(查表得到其余式)来实现逐个字节数据的CRC计算,直到全部字节数据计算完最后的余式就是CRC。
下面全是8bits查询表(256个余式的表),不过也可以4bits查询一次的计算(这样表里只需16个余式).先看程序的算法:r=0; //r是寄存器,先初始化为0//p0),t是查询表字节数据查询r高8位对应的余式,再与新得到的式子异或数据计算示意图:,之后再重复上面的步骤……若待测数据未扩展0,则此时还要计算4字节扩展0的CRC:构造CRC32查询表:一般来说,计算CRC是用“直驱表法”算法计算的,它与上面的算法非常相似,下面分析它的计算:计算步骤为(摘自文献):1. Shift the register left by one byte2. XOR the top byte just rotated out of the register with the next message byteto yield an index into the table ([0,255]).3. XOR the table value into the register.4. Goto 1 iff more augmented message bytes.C语言算法为:r=0; //r是寄存器,先初始化为0while (len--) //len是待测数据(不用扩展0)的字节长度r = (r<<8) ^ t[(r >> 24) ^ *p++]; //p是指向待测数据的指针,t是查询表相当于通过移位处理了8 个bit 的数据,相当于把之前的CRC 码的高字节(8bit)全部移出,与一个byte 的数据做XOR 运算,根据运算结果来选择一个值(称为余式),与原来的CRC 码再做一次XOR 运算,就可以得到新的CRC 码。
数字校验算法

数字校验算法数字校验算法是一种用于验证数据完整性和准确性的数学算法。
它通过对数据进行计算和比较,确定数据是否被篡改或损坏。
数字校验算法广泛应用于计算机网络、数据传输以及存储系统等领域,保证数据的可靠性和安全性。
本文将介绍几种常见的数字校验算法及其原理。
一、奇偶校验算法奇偶校验算法是最简单的数字校验算法之一。
它通过在数据位中添加一个奇偶位来确保数据的正确性。
具体操作是在数据中添加一个位,使得数据位和奇偶位的总位数为奇数或偶数。
接收端通过计算数据位和奇偶位的总位数是否为奇数或偶数来判断数据是否正确。
如果总位数不匹配,则说明数据传输中发生了错误。
二、循环冗余校验算法循环冗余校验算法(CRC)是一种常用的数字校验算法。
它通过对数据进行多项式的除法运算来生成校验码。
发送端首先将数据和生成多项式进行除法运算,得到余数作为校验码,然后将数据和校验码一起发送。
接收端将接收到的数据和生成多项式进行除法运算,如果余数为0,则说明数据传输正确;如果余数不为0,则说明数据传输错误。
三、哈希校验算法哈希校验算法是一种基于哈希函数的数字校验算法。
它通过对数据进行哈希运算,得到一个固定长度的校验值。
发送端将数据和校验值一起发送,接收端对接收到的数据进行相同的哈希运算,并将得到的校验值与接收到的校验值进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
四、消息认证码算法消息认证码算法(MAC)是一种常用的数字校验算法。
它通过对数据进行加密和认证来确保数据的完整性和真实性。
发送端使用密钥对数据进行加密和认证,并将加密后的数据和认证标签一起发送。
接收端使用相同的密钥对接收到的数据进行解密和认证,并将得到的认证标签与接收到的认证标签进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
五、数字签名算法数字签名算法是一种常用的数字校验算法。
它通过使用私钥对数据进行加密和签名,确保数据的完整性、真实性和不可抵赖性。
各种校验码校验算法分析

各种校验码校验算法分析校验码校验算法是一种用于数据传输或存储中验证数据完整性和准确性的技术,它能够检测出数据在传输或存储过程中是否发生了错误或损坏,从而确保数据的可靠性。
在实际应用中,校验码校验算法广泛应用于通信、网络传输、存储和数据处理等领域,其设计和选择对数据可靠性和安全性至关重要。
常见的校验码校验算法包括奇偶校验码、循环冗余校验码(CRC)、校验和、哈希校验码等。
下面将对这几种常见的校验码校验算法进行详细分析:1.奇偶校验码:奇偶校验码是最简单的一种校验码校验算法,它通过检测数据中的奇偶位来判断数据是否正确。
在奇偶校验中,通常规定数据中的位数为偶数个或奇数个,如果数据中出现奇数个1,则在校验位中加上1,使总的1的数量为偶数;如果数据中出现偶数个1,则在校验位中加上0,使总的1的数量仍为偶数。
在数据传输或存储中,接收方会通过比较校验位和数据位的和是否为偶数来判断数据的正确性。
奇偶校验码虽然简单易实现,但只能检测出奇数个错误位(例如一个错误的位),并不能检测出多个错误位或连续错误的情况。
因此,奇偶校验码一般用于对数据传输的基本错误进行检测。
2.循环冗余校验码(CRC):CRC是一种基于多项式除法的校验码校验算法,它通过对数据进行特定的多项式运算来计算出校验码。
接收方在收到数据后,也会对数据进行相同的多项式运算,然后比较计算出的校验码与发送方发送的校验码是否一致,从而判断数据是否正确。
CRC校验码具有较高的检错能力和容错率,能够有效地检测出多个位错误和定位错误的位置,因此广泛应用于计算机网络传输、磁盘存储、通信协议等领域。
3.校验和:校验和是一种简单的校验码校验算法,它通过对数据中所有位进行求和操作来计算出校验码。
接收方在接收到数据后,也会对数据进行相同的求和操作,然后比较计算出的校验和与发送方发送的校验和是否一致,从而判断数据是否正确。
校验和算法比较简单,计算速度较快,但只能检测出简单的错误情况,对于复杂的错误或多位错误检测能力有限。
12位条码计算校验码

12位条码计算校验码12位条码校验码是指在一个12位的条码号码中,通过一定的算法计算得出的最后一位校验码。
校验码的目的是为了验证条码的准确性和完整性,以防止错误的条码被误认为是正确的。
本文将从校验码的计算原理、应用领域以及常见的校验码算法等方面进行详细介绍。
一、校验码的计算原理校验码的计算原理是基于一种数学算法,通过对条码的其他位数进行运算,得出一个校验码。
这个校验码与条码的其他位数有一定的关联,一旦条码中的任意一位发生变化,校验码也会相应改变。
这样,通过对校验码的验证,就能判断条码是否正确。
二、校验码的应用领域校验码广泛应用于各个行业的条码系统中。
例如,在商品销售领域,校验码可以用于验证商品的真伪和有效性,以保证消费者的权益。
在物流管理领域,校验码可以用于追踪物流过程中的包裹,确保包裹的准确投递。
在图书馆管理领域,校验码可以用于管理图书的借阅和归还,防止图书遗失或错误归还。
三、常见的校验码算法1. 加权和校验码算法:将条码的每一位乘以一个固定的权重,然后将这些乘积相加,再取结果的个位数作为校验码。
2. 模10校验码算法:将条码的每一位从右往左依次乘以1、2、1、2、...,再将乘积的各位数相加,再将结果与10取模,然后用10减去模的结果作为校验码。
3. 模11校验码算法:将条码的每一位从右往左依次乘以2、3、4、5、6、7、8、9、2、3、4,再将乘积相加,再将结果除以11取余数,然后用11减去余数的结果作为校验码。
四、校验码的计算示例假设我们有一个12位的条码号码为123456789012,我们来演示一下校验码的计算过程。
对于加权和校验码算法,我们将每一位与固定的权重相乘,并将乘积相加:1*1 + 2*2 + 3*1 + 4*2 + 5*1 + 6*2 + 7*1 + 8*2 + 9*1 + 0*2 + 1*1 + 2*2 = 64。
然后取结果的个位数4作为校验码。
对于模10校验码算法,我们将每一位从右往左依次乘以1、2、1、2、...:2*1 + 1*2 + 0*1 + 9*2 + 8*1 + 7*2 + 6*1 + 5*2 + 4*1 + 3*2 + 2*1 + 1*2 = 39。
信息校验算法

信息校验算法
信息校验算法是一种用于检测数据完整性和准确性的技术。
常见的校验算法包括:
1. Checksum:一种简单的校验算法,通过将数据中的每个字节相加,然后取结果的最低有效字节,来检测数据是否在传输过程中发生了变化。
2. 奇偶校验:通过在数据中添加一个额外的位,使得整个数据(包括校验位)中的1的个数是偶数(偶校验)或奇数(奇校验)。
如果数据中的任何位发生变化,奇偶校验位的值也会发生变化,从而检测出错误。
3. 海明码校验:一种线性分组码,用于检测数据中的错误。
它将数据分成多个部分,并为每一部分添加冗余信息。
通过使用多个校验公式,海明码可以在多个位置检测到错误。
4. 循环冗余校验(CRC):一种用于检测错误的技术,它通过将数据视为多项式并计算其系数,然后添加一个额外的多项式作为校验码。
接收方使用相同的算法重新计算校验码,并与发送方的校验码进行比较。
如果两者匹配,则数据被认为是正确的;否则,数据被认为是有错误的。
5. 哈希算法:一种将任意大小的数据映射为固定大小散列值的算法。
常见的哈希算法包括MD系列和SHA系列。
哈希算法常用于验证数据的完整性和一致性,因为相同的输入总是产生相同的输出。
这些校验算法在不同的应用场景中都有其优势和局限性。
选择哪种算法取决于数据的性质、所需的错误检测能力以及计算和存储资源等因素。
16位CRC校验原理与算法分析

16位CRC校验原理与算法分析CRC(Cyclic Redundancy Check)是数据通信中常用的一种校验算法。
校验的目的是为了检测数据在传输过程中是否发生了错误或损坏。
CRC校验通过添加冗余数据(校验码)来实现错误检测。
一、CRC校验原理CRC校验通过生成一个多项式,将要传输的数据与该多项式进行除法运算,得到的余数作为校验码。
接收方收到数据后,也进行相同的除法运算,将得到的余数与发送方传来的校验码进行比较。
如果两者一致,说明数据在传输过程中没有发生错误;如果不一致,则说明数据发生了错误。
CRC校验原理可以通过以下步骤进行描述:1.选择一个固定的生成多项式。
常见的生成多项式有CRC-16、CRC-32等。
2.将要传输的数据(称为信息位)通过左移添加n个0来扩展为n+m 位,其中n为生成多项式的位数减1,m为校验码的位数。
这样做的目的是为了确保信息位和校验码可以做除法运算。
3.用生成多项式对扩展后的数据进行除法运算,得到的余数即为校验码。
4.将校验码附加到原始数据后面,形成完整的发送数据。
接收方收到数据后,也进行相同的除法运算,得到的余数与发送方传来的校验码进行比较。
如果两者一致,说明数据在传输过程中没有发生错误;如果不一致,则说明数据发生了错误。
二、CRC校验算法分析CRC校验算法的关键在于选择合适的生成多项式。
生成多项式的位数确定了校验码的位数,也决定了CRC校验的可靠性。
常见的生成多项式有CRC-16和CRC-32CRC-16:CRC-32:CRC校验算法实现时,通常使用查表法来加快计算速度。
预先计算所有2^8个字节的CRC余数后,将其存储在一个256个元素的表中。
每次对一个字节进行CRC运算时,只需要在表中查找对应的余数即可。
三、CRC校验应用CRC校验算法广泛应用于数据通信中,主要有以下几个方面:1.数据传输:在数据传输中,发送方将数据附加上CRC校验码,接收方收到数据后可以通过CRC校验码检查数据的完整性,防止传输错误。
各种条码的校验码算法(EAN13,COD128,GTIN,UCC等)

各种条码的校验码算法(EAN13,COD128,GTIN,UCC等)校验码是由编码⽅案决定的,所以在代码中是否使⽤校验码和条码基本⽆关,但商品条码除外。
今天给⼤家介绍⼏种校验码的计算⽅法。
⼀、商品条码:商品条码中需要计算校验码的有:EAN-8(8位),EAN-13(13位),UCC(UPC-A)(12位),GTIN-14(ITF-14)(14位),GLN(13位),SSCC(18位)等。
它们虽然位数不同,但计算校验码的⽅法完全相同。
1、包含校验码的所有数字从右向左编号,分别为1,2,3......18位;2、从第2位开始,所有偶数位的权数为3,从第3位开始,所有奇数位的权数为1;3、将对应位置的代码数字与权数相乘,参见下图(以SSCC的18位数字为例);4、将所有乘积相加求和;(结果为109)5、对第4步的和,求MOD 10运算(将和109除以10,取其余数9);6、如果余数为0,则校验码为0,否则,⽤10减去余数的差即为校验码。
(上例中校验码为1)⼆、⾝份证校验码:⾝份证校验码的计算⽐较复杂⼀些,参见下图:1、⾃右向左为⾝份证号编号1-18;2、确定各位数的权数,权数的计算公式为 2^(i-1) mod 11i—位数如第3位的权数为2^(3-1)=2^2=4, 4除以11,商0余4,则权数为4。
再如第5位的权数为2^(5-1)=2^4=16,16除以11,商1余5,则权数为5。
3、将权数与对应的⾝份证号数字相乘;4、将所有乘积相加求和;(⽰例中的184)5、将第4步的结果除以11,求余数(⽰例中的8)6、从下表的R值中找到第5步的结果,对应的C值即为校验码。
(⽰例中8对应的是4)三、CODE-128码的校验符:CODE-128码的校验符不会出现在数据中,也不⽤读出,这⾥仅介绍⼀下计算⽅法,实际使⽤中都是由条码软件⾃动⽣成的。
由于CODE-128码可以表⽰字母、符号、控制符,⽽这些字符不能直接参与计算,所以要为每个字符分配⼀个码值。
16位CRC校验原理与算法分析

16位CRC校验原理与算法分析2007-12-14 09:37这里,不讨论CRC的纠错原理以及为什么要选下面提及的生成多项式,只是针对以下的生成多项式,如何获得CRC校验码,作一个比较详细的说明。
标准CRC生成多项式如下表:名称生成多项式简记式* 标准引用CRC-4 x4+x+1 3ITU G.704CRC-8 x8+x5+x4+1 0x31CRC-8 x8+x2+x1+1 0x07CRC-8 x8+x6+x4+x3+x2+x1 0x5ECRC-12 x12+x11+x3+x+1 80FCRC-16 x16+x15+x2+1 8005 IBM SDLCCRC16-CCITT x16+x12+x5+1 1021 ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCSCRC-32 x32+x26+x23+...+x2+x+1 04C11DB7 ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCSCRC-32c x32+x28+x27+...+x8+x6+1 1EDC6F41 SCTP生成多项式的最高位固定的1,故在简记式中忽略最高位1了,如0x1021实际是0x11021。
I、基本算法(人工笔算):以CRC16-CCITT为例进行说明,CRC校验码为16位,生成多项式17位。
假如数据流为4字节:BYTE[3]、BYTE[2]、BYTE[1]、BYTE[0];数据流左移16位,相当于扩大256×256倍,再除以生成多项式0x11021,做不借位的除法运算(相当于按位异或),所得的余数就是CRC校验码。
发送时的数据流为6字节:BYTE[3]、BYTE[2]、BYTE[1]、BYTE[0]、CRC[1]、CRC[0];II、计算机算法1(比特型算法):1)将扩大后的数据流(6字节)高16位(BYTE[3]、BYTE[2])放入一个长度为16的寄存器;2)如果寄存器的首位为1,将寄存器左移1位(寄存器的最低位从下一个字节获得),再与生成多项式的简记式异或;否则仅将寄存器左移1位(寄存器的最低位从下一个字节获得);3)重复第2步,直到数据流(6字节)全部移入寄存器;4)寄存器中的值则为CRC校验码CRC[1]、CRC[0]。
【转】crc16几种标准校验算法及c语言代码

【转】crc16⼏种标准校验算法及c语⾔代码⼀、CRC16校验码的使⽤ 现选择最常⽤的CRC-16校验,说明它的使⽤⽅法。
根据Modbus协议,常规485通讯的信息发送形式如下: 地址功能码数据信息校验码 1byte 1byte nbyte 2byte CRC校验是前⾯⼏段数据内容的校验值,为⼀个16位数据,发送时,低8位在前,⾼8为最后。
例如:信息字段代码为: 1011001,校验字段为:1010。
发送⽅:发出的传输字段为: 1 0 1 1 0 0 1 1 0 10 信息字段校验字段 接收⽅:使⽤相同的计算⽅法计算出信息字段的校验码,对⽐接收到的实际校验码,如果相等及信息正确,不相等则信息错误;或者将接受到的所有信息除多项式,如果能够除尽,则信息正确。
⼆、CRC16校验码计算⽅法 常⽤查表法和计算法。
计算⽅法⼀般都是: (1)、预置1个16位的寄存器值0xFFFF,称此寄存器为CRC寄存器; (2)、把第⼀个8位⼆进制数据(既通讯信息帧的第⼀个字节)与16位的CRC寄存器的低 8位相异或,把结果放于CRC寄存器,⾼⼋位数据不变; (3)、把CRC寄存器的内容右移⼀位(朝⾼位)⽤0填补最⾼位,并检查右移后的移出位; (4)、如果移出位为0:重复第3步(再次右移⼀位);如果移出位为1,CRC寄存器与⼀多 项式(A001)进⾏异或; (5)、重复步骤3和4,直到右移8次,这样整个8位数据全部进⾏了处理; (6)、重复步骤2到步骤5,进⾏通讯信息帧下⼀个字节的处理; (7)、将该通讯信息帧所有字节按上述步骤计算完成后,得到的16位CRC寄存器的⾼、低 字节进⾏交换; (8)、最后得到的CRC寄存器内容即为:CRC码。
以上计算步骤中的多项式A001是8005按位颠倒后的结果。
查表法是将移位异或的计算结果做成了⼀个表,就是将0~256放⼊⼀个长度为16位的寄存器中的低⼋位,⾼⼋位填充0,然后将该寄存器与多项式0XA001按照上述3、4步骤,直到⼋位全部移出,最后寄存器中的值就是表格中的数据,⾼⼋位、低⼋位分别单独⼀个表。
16位循环冗余校验码_CRC_的原理和性能分析

16位循环冗余校验码_CRC_的原理和性能分析CRC(Cyclic Redundancy Check)是一种循环冗余校验码,常用来对数据进行校验,判断数据在传输过程中是否发生了错误。
原理:CRC是通过生成一个固定长度的校验码来判断数据是否出现错误。
它使用一个预定的生成多项式进行计算,并且利用位运算来对数据进行处理。
具体过程如下:1.选择一个合适的生成多项式,该多项式的位数决定了CRC的位数。
常见的生成多项式有CRC-8、CRC-16和CRC-32等。
2.将需要进行校验的数据以二进制形式表示,并在末尾添加相应个数的零。
添加的零的个数与生成多项式的位数相同。
3.将数据与生成多项式进行除法运算,得到的余数即为CRC校验码。
4.将CRC校验码附加在原始数据后面,形成带有校验码的数据。
接收方在接收到数据后,利用相同的生成多项式对数据进行除法运算,如果余数为零,则说明数据没有发生错误,否则说明数据出现了错误。
性能分析:1.安全性:CRC校验码主要用于检测数据在传输过程中是否出现了错误,能够有效检测大部分错误,但并不能保证100%的安全性。
如果数据发生错误,但计算出的CRC校验码与接收方计算出的不一致,此时无法判断数据是否真的发生了错误。
2.效率:CRC计算比较高效简单,可以实现硬件加速,其计算速度快。
3.适用范围:CRC适用于对数据进行简单校验的场景,例如网络传输、存储校验等。
但对于对数据完整性要求较高的场合,如加密算法等,CRC校验不够安全。
总结:CRC校验码是一种简单且高效的校验方法,适用于在数据传输中快速检测错误。
它的计算速度快、实现简单,但对于安全性要求较高的场合,CRC校验码不够安全可靠。
因此,根据实际需求,在选择校验方法时要综合考虑安全性和效率。
CRC32校验码算法

CRC32校验码算法CRC32(Cyclic Redundancy Check)校验码算法是一种错误检测算法,广泛应用于数据通信和数据存储中。
它基于多项式除法的原理,通过将要传输的数据进行计算,生成一个校验码,发送端和接收端对数据进行校验,以判断数据是否出现错误。
CRC32算法的基本原理是将要传输的数据看作是一个二进制数,除以一个固定的标准多项式(也称为生成多项式),并取余数作为校验码。
在CRC32算法中,标准多项式为0x04C11DB7,该多项式对应着一个32位的二进制数。
具体算法步骤如下:1.初始化:将校验寄存器的初始值设置为0xFFFFFFFF。
2.处理输入数据:从输入数据的最高位开始,依次进行以下操作:-将校验寄存器的最高位移出,与输入数据的当前位进行异或操作。
-如果校验寄存器的最低位为1,则将校验寄存器与标准多项式进行异或操作。
-将校验寄存器向右移动1位。
3.完成处理:当输入数据的所有位都处理完后,将校验寄存器取反作为最终的校验码。
1.算法简单:CRC32算法的实现逻辑相对简单,易于理解和实现。
2.高效性能:CRC32算法的计算速度较快,适用于高速传输和大批量数据校验。
3.强错误检测能力:CRC32算法在数据传输过程中,对于单一比特错误和双比特错误有较高的检测概率,可以有效减少数据传输中的误码率。
4.低冲突概率:CRC32算法生成的校验码具有较低的冲突概率,即不同的数据生成相同的校验码的概率较低。
然而,CRC32算法也存在一些缺点:1.弱错误检测能力:相比于MD5等哈希算法,CRC32算法的错误检测能力较弱,无法检测到所有的错误情况。
2.易被篡改:CRC32算法生成的校验码可以通过简单的替换操作来改变数据的校验结果,容易被恶意篡改。
3.无法纠错:CRC32算法只能检测错误,而无法纠正错误。
一旦数据出现错误,则需要重新传输或进行其他纠错处理。
校验码计算方法

校验码计算方法校验码的计算方法通常分为两种:奇校验和偶校验。
在这两种方法中,校验码的生成规则是相同的,都是根据特定的算法,对原始数据中的每一位进行特定的运算,得到的结果就是校验码。
1.奇校验(Odd parity):在奇校验中,校验码的位数与原始数据的位数相同。
对于原始数据中的每一位,如果该位是1,那么在计算校验码时,这一位的值就变为0;如果该位是0,那么在计算校验码时,这一位的值就变为1。
这样,原始数据中1的个数(包括校验码位)就总是奇数。
2.偶校验(Even parity):在偶校验中,校验码的位数与原始数据的位数相同。
对于原始数据中的每一位,如果该位是1,那么在计算校验码时,这一位的值就保持不变;如果该位是0,那么在计算校验码时,这一位的值就变为1。
这样,原始数据中1的个数(包括校验码位)就总是偶数。
这两种方法都有各自的优点和适用场景。
例如,偶校验在硬件错误检测中更为常见,因为这种错误通常是随机分布的,而奇校验则更适用于检测某些特定的错误模式。
除了奇校验和偶校验之外,还有其他的校验方法,如海明码(Hamming code)和循环冗余校验(CRC)等。
这些方法可以提供更高的错误检测能力,但实现起来更为复杂。
需要注意的是,无论采用哪种校验方法,都需要一个能够生成对应位数校验码的算法。
这个算法通常会根据数据的长度和校验码的长度来生成一个函数,用于计算每个位置上的校验码。
在实际应用中,还需要考虑到一些其他因素。
例如,如果原始数据中存在多个错误,那么校验码可能会失效。
在这种情况下,需要采取其他措施来处理这种情况。
此外,还需要考虑到数据的存储和传输效率。
如果数据量很大,那么使用复杂的校验方法可能会增加存储和传输的成本。
因此,在选择校验方法时,需要根据实际情况进行权衡。
总的来说,校验码是一种非常重要的数据完整性检查方法。
它可以有效地检测出数据传输或存储过程中可能出现的错误,从而保证数据的完整性和可靠性。
各种校验码校验算法分析

各种校验码校验算法分析校验码是一种用于验证数据完整性和准确性的算法。
在计算机科学中,常见的校验码算法包括纵向冗余校验(VRC),横向冗余校验(HRC),循环冗余校验(CRC),校验和和哈希校验等。
下面将对这些校验码算法进行分析。
VRC是一种最简单的校验码算法,它将数据位分为数据位和校验位两部分。
数据位按照一定的规则进行编码,校验位是根据数据位计算得到的。
当数据接收方收到数据后,它也会按照相同的规则计算校验位,并将计算得到的校验位与发送方传来的校验位进行比较,如果两者一致,则认为数据传输正确。
然而,VRC算法只能检测数据传输中的单比特错误,无法检测到多比特错误。
HRC是一种通过对数据进行按位求和来计算校验位的算法。
它与VRC算法类似,只是校验位的计算方法不同。
与VRC算法相比,HRC算法更加复杂,但也能检测到更多的错误。
然而,HRC算法仍然无法检测到多比特错误。
CRC是一种更为强大的校验码算法,它通过对数据进行除法运算来计算校验位。
CRC算法将数据视为二进制数,将除法运算看作一个模2整除的过程。
发送方在传输数据之前,计算数据的CRC校验位并将其附加在数据末尾。
接收方在接收数据后,也计算接收到的数据的CRC校验位,并与接收到的校验位进行比较。
如果两者一致,则认为数据传输正确。
与VRC和HRC算法相比,CRC算法具有更高的错误检测能力。
校验和是一种将数据按照一定规则进行求和来计算校验位的算法。
校验和算法将数据视为一系列数值,按照一定的规则进行求和,然后将求和结果的低位部分作为校验位。
校验和算法简单易实现,但其错误检测能力有限,无法检测到一些错误。
哈希校验是一种借助哈希函数来计算校验位的算法。
哈希函数将数据映射为一个固定长度的哈希值,该哈希值称为校验值。
发送方在发送数据之前,计算数据的哈希值并将其附加在数据末尾。
接收方在接收数据后,也计算接收到的数据的哈希值,并与接收到的校验值进行比较。
如果两者一致,则认为数据传输正确。
校验码的计算方法

校验码的计算方法校验码是指通过一定的算法对数据进行计算,以便在数据传输或存储过程中验证数据的完整性和准确性。
校验码的计算方法有多种,常见的包括奇偶校验、CRC校验、MD5校验等。
下面将分别介绍这些常见的校验码计算方法。
奇偶校验是一种简单的校验方法,适用于对数据位数进行校验。
其原理是通过统计数据中“1”的个数,如果“1”的个数为偶数,则校验位为0,如果“1”的个数为奇数,则校验位为1。
通过这种方法可以检测数据中是否存在奇数个的错误位。
奇偶校验适用于对单个字节或字符进行校验,但对于多字节或多字符的数据校验效果不佳。
CRC(Cyclic Redundancy Check)校验是一种基于多项式的校验方法,适用于对二进制数据进行校验。
CRC校验通过对数据进行多项式除法运算,得到余数作为校验码。
接收端同样对接收到的数据进行CRC校验,并将计算得到的校验码与接收到的校验码进行比对,从而验证数据的完整性。
CRC校验方法适用于数据传输过程中的错误检测,广泛应用于网络通信、存储系统等领域。
MD5(Message Digest Algorithm 5)是一种广泛应用的哈希函数,用于对任意长度的数据产生一个128位的哈希值。
MD5校验通过对数据进行哈希运算,得到固定长度的校验码。
MD5校验具有较高的安全性,不可逆性和唯一性,适用于对数据完整性和一致性进行验证。
MD5校验常用于文件完整性校验、数字签名等场景。
除了上述介绍的奇偶校验、CRC校验和MD5校验外,还有其他多种校验码的计算方法,如SHA-1、SHA-256等。
不同的校验方法适用于不同的场景,选择合适的校验方法可以提高数据的可靠性和安全性。
在实际应用中,校验码的计算方法需要根据具体的需求和场景进行选择。
在数据传输过程中,需要对数据进行校验以确保数据的完整性和准确性;在存储过程中,需要对数据进行校验以防止数据损坏或篡改。
因此,了解不同的校验码计算方法,并根据实际情况进行选择和应用,对保障数据的安全和可靠性具有重要意义。
CRC校验算法详解

CRC校验算法详解循环冗余校验(Cyclic Redundancy Check,CRC)是一种常用的错误校验算法,主要用于数据传输过程中的差错检测。
它将数据视为二进制数,通过生成多项式与数据进行异或运算,最后产生一个余数,将该余数作为校验码附加在数据末尾,接收方通过相同的生成多项式进行校验,如果余数为0,则认为数据传输无误。
CRC校验算法的基本原理是:通过生成多项式对整个数据进行模2除法运算,并得到一个余数作为校验码。
在数据传输过程中,发送方将原始数据和校验码一起发送给接收方,接收方利用相同的生成多项式对整个数据进行除法运算,并检查余数是否为0,来判断数据传输是否正确。
1.确定生成多项式:CRC校验算法中最重要的是生成多项式,它决定了校验能力的大小。
生成多项式通常在最高位和最低位都为1,其他位数也应该尽量选择为1、常用的生成多项式有CRC-8、CRC-16、CRC-32等,每种生成多项式的校验能力不同。
2.将生成多项式转换为二进制数:将生成多项式转换为二进制数表示,用多项式系数的二进制表示法来表示生成多项式。
3.将待发送的数据与校验码进行拼接:在发送数据的最后面添加足够位数的0,等于生成多项式次数减1,将生成多项式次方数减1的二进制表示添加到待发送的数据末尾。
4.进行模2除法运算:将待发送的数据与生成多项式进行模2除法运算,将得到的余数作为校验码。
5.发送数据与校验码:将原始数据与校验码一起发送给接收方,接收方接收到数据后利用相同的生成多项式进行除法运算。
6.检验余数是否为0:接收方进行除法运算后,检查得到的余数是否为0,如果余数为0,则认为数据传输无误;如果余数不为0,则认为数据传输存在错误。
CRC校验算法的优点是简单且高效,能够检测多位错误,且校验码的长度可以根据生成多项式的次方数来确定,可以根据不同的数据传输要求进行调整。
缺点则是无法纠正错误,只能检测错误的存在,需要额外的处理机制来进行纠正。
各种校验码校验算法分析

各种校验码校验算法分析二进制数据经过传送、存取等环节会发生误码1变成0或0变成1这就有如何发现及纠正误码的问题。
所有解决此类问题的方法就是在原始数据数码位基础上增加几位校验冗余位。
一、码距一个编码系统中任意两个合法编码码字之间不同的二进数位bit数叫这两个码字的码距而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
如图1所示的一个编码系统用三个bit来表示八个不同信息中。
在这个系统中两个码字之间不同的bit数从1到3不等但最小值为1故这个系统的码距为1。
如果任何码字中一位或多位被颠倒了结果这个码字就不能与其它有效信息区分开。
例如如果传送信息001而被误收为011因011仍是表中的合法码字接收机仍将认为011是正确的信息。
然而如果用四个二进数字来编8个码字那么在码字间的最小距离可以增加到2如图2的表中所示。
信息序号二进码字 a2 a1 a0 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 图 1 信息序号二进码字 a3 a2 a1 a0 0 0 0 0 0 1 1 0 0 1 2 1 0 1 0 3 0 0 1 1 4 1 1 0 0 5 0 1 0 1 6 0 1 1 0 7 1 1 1 1 图 2 注意图8-2的8个码字相互间最少有两bit 的差异。
因此如果任何信息的一个数位被颠倒就成为一个不用的码字接收机能检查出来。
例如信息是1001误收为1011接收机知道发生了一个差错因为1011不是一个码字表中没有。
然而差错不能被纠正。
假定只有一个数位是错的正确码字可以是100111110011或1010。
接收者不能确定原来到底是这4个码字中的那一个。
也可看到在这个系统中偶数个2或4差错也无法发现。
为了使一个系统能检查和纠正一个差错码间最小距离必须至少是“3”。
最小距离为3时或能纠正一个错或能检二个错但不能同时纠一个错和检二个错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各种校验码校验算法分析二进制数据经过传送、存取等环节会发生误码1变成0或0变成1这就有如何发现及纠正误码的问题。
所有解决此类问题的方法就是在原始数据数码位基础上增加几位校验冗余位。
一、码距一个编码系统中任意两个合法编码码字之间不同的二进数位bit数叫这两个码字的码距而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
如图1所示的一个编码系统用三个bit来表示八个不同信息中。
在这个系统中两个码字之间不同的bit数从1到3不等但最小值为1故这个系统的码距为1。
如果任何码字中一位或多位被颠倒了结果这个码字就不能与其它有效信息区分开。
例如如果传送信息001而被误收为011因011仍是表中的合法码字接收机仍将认为011是正确的信息。
然而如果用四个二进数字来编8个码字那么在码字间的最小距离可以增加到2如图2的表中所示。
信息序号二进码字 a2 a1 a0 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 图 1 信息序号二进码字 a3 a2 a1 a0 0 0 0 0 0 1 1 0 0 1 2 1 0 1 0 3 0 0 1 1 4 1 1 0 0 5 0 1 0 1 6 0 1 1 0 7 1 1 1 1 图 2 注意图8-2的8个码字相互间最少有两bit 的差异。
因此如果任何信息的一个数位被颠倒就成为一个不用的码字接收机能检查出来。
例如信息是1001误收为1011接收机知道发生了一个差错因为1011不是一个码字表中没有。
然而差错不能被纠正。
假定只有一个数位是错的正确码字可以是100111110011或1010。
接收者不能确定原来到底是这4个码字中的那一个。
也可看到在这个系统中偶数个2或4差错也无法发现。
为了使一个系统能检查和纠正一个差错码间最小距离必须至少是“3”。
最小距离为3时或能纠正一个错或能检二个错但不能同时纠一个错和检二个错。
编码信息纠错和检错能力的进一步提高需要进一步增加码字间的最小距离。
图8-3的表概括了最小距离为1至7的码的纠错和检错能力。
码距码能力检错纠错 1 2 3 4 5 6 7 0 0 1 0 2 或 1 2 加 1 2 加 2 3 加 2 3 加 3 图3 码距越大纠错能力越强但数据冗余也越大即编码效率低了。
所以选择码距要取决于特定系统的参数。
数字系统的设计者必须考虑信息发生差错的概率和该系统能容许的最小差错率等因素。
要有专门的研究来解决这些问题。
二、奇偶校验奇偶校验码是一种增加二进制传输系统最小距离的简单和广泛采用的方法。
例如单个的奇偶校验将使码的最小距离由一增加到二。
一个二进制码字如果它的码元有奇数个1就称为具有奇性。
例如码字“10110101”有五个1因此这个码字具有奇性。
同样偶性码字具有偶数个1。
注意奇性检测等效于所有码元的模二加并能够由所有码元的异或运算来确定。
对于一个n位字奇性由下式给出奇性a0⊕a1⊕a2⊕…⊕an 奇偶校验可描述为给每一个码字加一个校验位用它来构成奇性或偶性校验。
例如在图8-2中就是这样做的。
可以看出附加码元d2是简单地用来使每个字成为偶性的。
因此若有一个码元是错的就可以分辨得出因为奇偶校验将成为奇性。
奇偶校验编码通过增加一位校验位来使编码中1个个数为奇数奇校验或者为偶数偶校验从而使码距变为2。
因为其利用的是编码中1的个数的奇偶性作为依据所以不能发现偶数位错误。
再以数字0的七位ASCII码0110000为例如果传送后右边第一位出错0变成1。
接收端还认为是一个合法的代码0110001数字1的ASCII码。
若在最左边加一位奇校验位编码变为10110000如果传送后右边第一位出错则变成101100011的个数变成偶数就不是合法的奇校验码了。
但若有两位假设是第1、2位出错就变成101100111的个数为5还是奇数。
接收端还认为是一个合法的代码数字3的ASCII码。
所以奇偶校验不能发现。
奇偶校验位可由硬件电路异或门或软件产生偶校验位 an a0⊕a1⊕a2⊕…⊕an-1 奇校验位 an NOTa0⊕a1⊕a2⊕…⊕an-1。
在一个典型系统里在传输以前由奇偶发生器把奇偶校验位加到每个字中。
原有信息中的数字在接收机中被检测如果没有出现正确的奇、偶性这个信息标定为错误的这个系统将把错误的字抛掉或者请求重发。
在实际工作中还经常采用纵横都加校验奇偶校验位的编码系统--分组奇偶校验码。
现在考虑一个系统它传输若干个长度为m位的信息。
如果把这些信息都编成每组n个信息的分组则在这些不同的信息间也如对单个信息一样能够作奇偶校验。
图4中n个信息的一个分组排列成矩形式样并以横向奇偶HP及纵向奇偶VP的形式编出奇偶校验位。
m位数字横向奇偶位 n 个码字a1 a2 … am-1 am HP1 b1 b2 … bm-1 bm HP2 c1 c2 … cm-1 c m HP3 … … … … … … n1 n2 … nm-1 nm HPn VP1 VP2 … VPm-1 VPm HPn1 纵向奇偶位图 4 用综横奇偶校验的分组奇偶校验码研究图4可知分组奇偶校验码不仅能检测许多形式的错误。
并且在给定的行或列中产生孤立的错误时还可对该错误进行纠正。
在初级程序员试题中早期也出现在程序员试题中经常有综横奇偶校验的题目。
一般解法应该是这样先找一行或一列已知数据完整的确定出该行或列是奇校验还是偶校验。
并假设行与列都采用同一种校验这个假设是否正确在全部做完后可以得到验证。
然后找只有一个未知数的行或列根据校验性质确定该未知数这样不断做下去就能求出所有未知数。
【例】2001年初级程序员试题由 6 个字符的 7 位 ASCII 编码排列再加上水平垂直奇偶校验位构成下列矩阵最后一列为水平奇偶校验位最后一行为垂直奇偶校验位: 字符 7 位 ASCII 码 HP 3 0 X1 X2 0 0 1 1 0 Y1 1 0 0 1 0 0 X3 1 X4 1 0 1 0 1 1 0 Y2 0 1 X5 X6 1 1 1 1 D 1 0 0 X7 1 0 X8 0 0 X9 1 1 1 X10 1 1 VP 0 0 1 1 1 X11 1 X12 则 X1 X2 X3 X4 处的比特分别为 __36__ X5 X6X7 X8 处的比特分别为 ____ X9 X10 XI1 X12 处的比特分别为 __38__ Y1 和 Y2 处的字符分别为 __39__ 和__40__ 。
解从ASCII码左起第5列可知垂直为偶校验。
则从第1列可知X40从第3行可知水平也是偶校验。
从第2行可知X31从第7列可知X80从第8列可知X121 从第7行可知X111从第6列可知X100从第6行可知X91从第2列可知X11 从第1行可知X21从第3列可知X51从第4行可知X60 从第4列或第5行可知X70整理一下 36 X1X2X3X4 1110 37 X5X6X7X8 1000 38 X9X10X11X12 1011 39 由字符Y1的ASCII码100100149H知道Y1即是“I”由“D”的ASCII码是100010044H推得 40 由字符Y2的ASCII码011011137H知道Y2即是“7”由“3”的ASCII码是011001133H推得假如你能记住“0”的ASCII码是011000030H“A”的ASCII码是100000141H则解起来就更方便了。
三、海明校验我们在前面指出过要能纠正信息字中的单个错误所需的最小距离为3。
实现这种纠正的方法之一是海明码。
海明码是一种多重复式奇偶检错系统。
它将信息用逻辑形式编码以便能够检错和纠错。
用在海明码中的全部传输码字是由原来的信息和附加的奇偶校验位组成的。
每一个这种奇偶位被编在传输码字的特定位置上。
实现得合适时这个系统对于错误的数位无论是原有信息位中的还是附加校验位中的都能把它分离出来。
推导并使用长度为m位的码字的海明码所需步骤如下 1、确定最小的校验位数k将它们记成D1、D2、…、Dk每个校验位符合不同的奇偶测试规定。
2、原有信息和k个校验位一起编成长为mk位的新码字。
选择k 校验位0或1以满足必要的奇偶条件。
3、对所接收的信息作所需的k个奇偶检查。
4、如果所有的奇偶检查结果均为正确的则认为信息无错误。
如果发现有一个或多个错了则错误的位由这些检查的结果来唯一地确定。
校验位数的位数推求海明码时的一项基本考虑是确定所需最少的校验位数k。
考虑长度为m位的信息若附加了k个校验位则所发送的总长度为mk。
在接收器中要进行k个奇偶检查每个检查结果或是真或是伪。
这个奇偶检查的结果可以表示成一个k位的二进字它可以确定最多2k种不同状态。
这些状态中必有一个其所有奇偶测试试都是真的它便是判定信息正确的条件。
于是剩下的2k-1种状态可以用来判定误码的位置。
于是导出下一关系 2k-1≥mk 码字格式从理论上讲校验位可放在任何位置但习惯上校验位被安排在1、2、4、8、…的位置上。
图5列出了m4k3时信息位和校验位的分布情况。
码字位置 B1 B2 B3 B4 B5 B6 B7 校验位 x x x 信息位 x x x x 复合码字 P1 P2 D1 P3 D2 D3 D4 图5 海明码中校验位和信息位的定位校验位的确定 k个校验位是通过对mk位复合码字进行奇偶校验而确定的。
其中P1位负责校验海明码的第1、3、5、7、…P1、D1、D2、D4、…位包括P1自己 P2负责校验海明码的第2、3、6、7、...P2、D1、D3、D4、...位包括P2自己 P3负责校验海明码的第4、5、6、7、 (3)D2、D3、D4、…位包括P3自己对m4k3偶校验的例子只要进行式次偶性测试。
这些测试以A、B、C表示在图6所示各位的位置上进行。
奇偶条件码字位置 1 2 3 4 5 6 7 A B C x x x x x x x x x x x x 图6 奇偶校验位置因此可得到三个校验方程及确定校验位的三个公式 AB1⊕B3⊕B5⊕B70 得P1D1⊕D2⊕D4 BB2⊕B3⊕B6⊕B70 得P2D1⊕D3⊕D4 CB4⊕B5⊕B6⊕B70 得P3D2⊕D3⊕D4 若四位信息码为1001利用这三个公式可求得三个校验位P1、P2、P3值。
和海明码如图7则表示了信息码为1001时的海明码编码的全部情况。
而图8中则列出了全部16种信息D1D2D3D400001111的海明码。
码字位置 B1 B2 B3 B4 B5 B6 B7 码位类型 P1 P2 D1 P3 D2 D3 D4 信息码 - - 1 - 0 0 1 校验位 0 0 - 1 - - - 编码后的海明码 0 0 1 1 0 0 1 图7 四位信息码的海明编码 P1 P2 D1 P3 D2 D3 D4 0 0 0 0 00 0 1 1 0 1 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 1 0 0 11 0 0 0 1 0 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 1 1 1 10 0 0 0 0 0 1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 0 1 1 0 11 1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 图8 未编码信息的海明码上面是发送方的处理在接收方也可根据这三个校验方程对接收到的信息进行同样的奇偶测试 AB1⊕B3⊕B5⊕B70 BB2⊕B3⊕B6⊕B70 CB4⊕B5⊕B5⊕B70。
