§5.4两角和与差的余弦、正弦和正切(二)
两角和与差的正弦余弦正切公式

两角和与差的正弦余弦正切公式下面我们将分别介绍两角和与差的正弦、余弦和正切公式。
1.正弦的两角和与差公式:设角A和角B的正弦值分别为sinA和sinB,那么有:sin(A + B) = sinA * cosB + cosA * sinBsin(A - B) = sinA * cosB - cosA * sinB证明:我们考虑一个单位圆(半径为1),圆心为O,且角A对应的弧与x 轴的交点为点P,角B对应的弧与x轴的交点为点Q。
根据单位圆上的点的坐标表示,我们有:点P的坐标为(cosA, sinA)点Q的坐标为(cosB, sinB)以O为起点,连接OP和OQ,将其延长到圆的边缘,分别交于点M和点N。
由于所有的角度都是以弧度来表示的,因此我们可以使用三角函数的定义来表示OP和OQ的长度。
通过定义我们有:sinA = PMcosA = OMsinB = QNcosB = ON现在我们来计算sin(A + B)。
根据三角形的正弦定理,我们可以得到:sin(A + B) = PN(即三角形OPN的高)通过几何推导我们可以发现,三角形OPN的底边的长度为cosB * cosA。
同样地,通过几何推导我们可以发现,三角形OPN的高为sinA * cosB + cosA * sinB。
因此,我们得到sin(A + B) = sinA * cosB + cosA * sinB。
同理,可以推导得到sin(A - B) = sinA * cosB - cosA * sinB。
2.余弦的两角和与差公式:设角A和角B的余弦值分别为cosA和cosB,那么有:cos(A + B) = cosA * cosB - sinA * sinBcos(A - B) = cosA * cosB + sinA * sinB证明:我们考虑一个单位圆(半径为1),圆心为O,且角A对应的弧与x 轴的交点为点P,角B对应的弧与x轴的交点为点Q。
根据单位圆上的点的坐标表示,我们有:点P的坐标为(cosA, sinA)点Q的坐标为(cosB, sinB)以O为起点,连接OP和OQ,将其延长到圆的边缘,分别交于点M和点N。
两角和与差的正弦余弦和正切公式

利用三角函数的倍角公式推导
总结词
通过三角函数的倍角公式,我们可以推导出 两角和与差的正弦、余弦和正切公式。
详细描述
三角函数的倍角公式指出,对于任意角度α, sin(2α)、cos(2α)和tan(2α)的值可以通过
sin(α)、cos(α)、tan(α)的函数关系来表达。 利用这个公式,我们可以推导出两角和与差
总结词
通过三角函数的减法定理,我们可以推导出 两角和与差的正弦、余弦和正切公式。
详细描述
三角函数的减法定理指出,对于任意角度α、 β,sin(α-β)、cos(α-β)和tan(α-β)的值可 以通过sin(α)、cos(α)、sin(β)、cos(β)、 tan(α)和tan(β)的函数关系来表达。利用这 个定理,我们可以推导出两角和与差的正弦、 余弦和正切公式。
地理学问题
在地理学中,很多问题涉及到地 球的自转、公转等角度计算,如 时差、太阳高度角等,利用三角 函数公式可以方便地计算。
经济学问题
在经济学中,很多问题涉及到利 率、汇率等与角度相关的问题, 利用三角函数公式可以方便地描 述这些变化规律。
04
三角函数公式的扩展
利用三角函数的和差化积公式扩展
总结词
利用三角函数的积化和差公式扩展
总结词
利用三角函数的积化和差公式,可以将两角和与差的 正弦、余弦和正切公式进行扩展,得到更一般化的公 式形式。
详细描述
三角函数的积化和差公式可以将两个角度的正弦或余 弦的乘积转化为其他角度的正弦、余弦和正切的和或 差的形式,从而扩展了原有的公式。例如,利用积化 和差公式,可以将两角和的余弦表示为单个角度余弦 的函数,进一步推导得到更一般化的公式。
VS
详细描述
5.4 两角和与差的余弦、正弦和正切
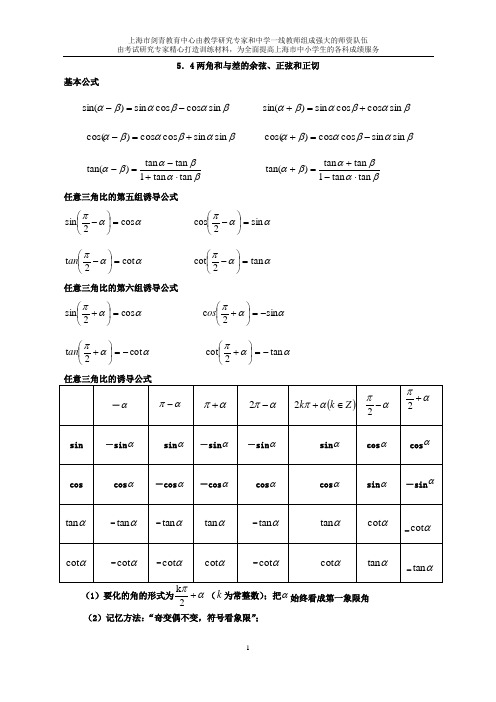
5.4两角和与差的余弦、正弦和正切基本公式βαβαβαsin cos cos sin )sin(-=- βαβαβαsin cos cos sin )sin(+=+βαβαβαsin sin cos cos )cos(+=- βαβαβαsin sin cos cos )cos(-=+βαβαβαtan tan 1tan tan )tan(⋅+-=- βαβαβαtan tan 1tan tan )tan(⋅-+=+ 任意三角比的第五组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛- ααπsin 2cos =⎪⎭⎫⎝⎛- ααπcot 2t =⎪⎭⎫ ⎝⎛-an ααπtan 2cot =⎪⎭⎫⎝⎛- 任意三角比的第六组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛+ ααπsin 2c -=⎪⎭⎫⎝⎛+os ααπcot 2t -=⎪⎭⎫ ⎝⎛+an ααπtan 2cot -=⎪⎭⎫⎝⎛+ 任意三角比的诱导公式(1)要化的角的形式为α+2(k 为常整数);把α始终看成第一象限角 (2)记忆方法:“奇变偶不变,符号看象限”;理解公式:a sin α+b cos α=22b a +sin (α+ϕ) (其中,ϕ通常取πϕ20<≤,2222sin ,cos b a b b a a +=+=ϕϕ,ab=ϕtan α为任意角). 例1.求证:)4cos(2)cos (sin 2)3()4sin(2sin cos )2()6sin(cos 21sin 23)1(ππθθθπααα-=++=++=+x x x例2.利用和(差)角公式化简:)3cos(66)3sin(62)4(cos sin 3)3(cos 53sin 153)2(cos 21sin 23)1(x x x x x x x x -+---+ππ)6sin(cos 21sin 23πααα+=+例3.求证:)4tan(cos sin cos sin π-=+-x xx x x例4.若0<α<β<4π,sin α+cos α=a ,sin β+cos β=b ,则( )A.ab <1B.a >bC.a <b D.ab >2 【当堂练习】1.化简)sin()sin()cos()cos(γββαγββα-----为 ( )A .)2sin(γβα+-B .)sin(γα- .cos()C αγ-D .)2cos(γβα+- 2.已知3tan =α,则αααα22cos 9cos sin 4sin 2-+的值为( )A .3B .2110C .13 D .1303.已知4sin 25α=-,(,)44ππα∈-,sin 4α的值为 ( )A .2425B .2425-C .45D .7254.已知sin αcos α=38,且4π<α<2π,则cos α-sin α的值为 ( ) A .12 B .—12 C .14- D .12±5.已知α+ β =3π, 则cos αcos β–sin αcos β–cos αsin β – sin αsin β 的值为( )A.B .–1C .1 D.6. 已知1tan 23α=,求tan α的值.7.已知4sin 5α=,(,)2παπ∈5cos 13β=-,β是第三象限角,求cos()αβ-的值.【家庭作业】 一、选择题1.tan 70°+tan 50°-3tan 70°·tan 50°= ( )A. 3B.33C .-33D .- 32.若3sin x -3cos x =23sin(x -φ),φ∈(-π,π),则φ=( )A .-π6 B.π6 C.5π6 D .-5π63.已知sin ⎝ ⎛⎭⎪⎫π4-x =35,则sin 2x 的值为( )A.725B.1625C.1425D.19254.已知cos ⎝ ⎛⎭⎪⎫π6-α=33,则sin2⎝ ⎛⎭⎪⎫α-π6-cos ⎝ ⎛⎭⎪⎫5π6+α的值是 ( )A.2+33B .-2+33C.2-33D.-2+33二、填空题5.函数y =2cos2x +sin 2x 的最小值是________.6.若0<α<π2<β<π,且cos β=-13,sin(α+β)=13,则cos α=________.7.已知α、β为锐角,且cos α=17,cos(α+β)=-1114,则β的值为________.三、解答题8.已知tan ⎝ ⎛⎭⎪⎫π4+α=12.(1)求tan α的值; (2)求sin 2α-cos2α1+cos 2α的值.【综合】 一、选择题1.有四个关于三角函数的命题:p1:∃x ∈R ,sin2x 2+cos2x 2=12; p2:∃x 、y ∈R ,sin(x -y)=sin x -sin y ;p3:∀x ∈[0,π],1-cos 2x 2=sin x ; p4:sin x =cos y ⇒x +y =π2. 其中的假命题是 ( )A .p1,p4B .p2,p4C .p1,p3D .p2,p4 二、填空题2. 3-sin 70°2-cos210°=________.3.若cos(α+β)=15,cos(α-β)=35,则tan α·tan β=________.三、解答题4.如图在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐 角α、β,它们的终边分别与单位圆相交于A 、B 两点.已 知A 、B 两点的横坐标分别为210、255. (1)求tan(α+β)的值; (2)求α+2β的大小.5.已知函数f(x)=4cos4x -2cos 2x -1cos 2x .(1)求f ⎝ ⎛⎭⎪⎫-1112π的值;(2)当x ∈⎣⎢⎡⎭⎪⎫0,π4时,求g(x)=f(x)+sin 2x 的最大值和最小值.6.sin14cos16cos14sin16︒︒+︒︒=7.比较大小:036cos 36sin + 038cos 38sin +;8.已知tan2α=2,求:(1)tan()4πα+的值; (2)6sin cos 3sin 2cos αααα+-的值.9.设α、β为锐角, sinα求α+β.10.(1) 已知tan (α+β)=1, tan α=3, 求tan β. (2) 设cos(α-2β)=19-, sin(2α-β)=23, 且2παπ<<, 0<β<2π,求cos(α+β).11.求值:(1) 已知sinθ=35, θ为锐角,求sin 2θ; (2) 已知sinθ=35,sin2θ<0, 求tan 2θ.参考答案:例1(1))6sin(cos 21sin 23πααα+=+ 证法一:左边=sin αcos 6π+cos αsin 6π=sin (α+6π)=右边 证法二:右边=sin αcos 6π+cos αsin 6π=23sin α+21cos α=左边 (2)cos θ+sin θ=2sin (θ+4π)证法一:左边=2(22cos θ+22sin θ)=2(sin 4πcos θ+cos 4πsin θ) =2sin (θ+4π)=右边证法二:右边=2(sin θcos 4π+cos θsin 4π)=2(22sin θ+22cos θ)=cos θ+sin θ=左边(3) 2(sinx+cosx )=2cos (x-4π)证法一:左边=2(sinx +cosx )=2(22sinx +22cosx )=2(cosxcos 4π+sinxsin 4π) =2cos (x -4π)=右边证法二:右边=2cos (x -4π)=2(cosxcos 4π+sinxsin 4π)=2(22cosx +22sinx )=2(cosx +sinx )=左边例2.解:(1) 23sinx +21cosx =sinxcos 6π+cosxsin 6π=sin (x +6π)或:原式=sinxsin 3π+cosxcos 3π=cos (x -3π)(2)315sinx -35cosx =65(23sinx -21cosx )=65(sinxcos 6π-cosxsin 6π) =65sin (x -6π)或:原式=65(sin 3πsinx -cos 3πcosx )=-65cos (x +3π)(3) 3sinx -cosx =2(23sinx -21cosx )=2sin (x -6π)=-2cos (x +3π)(4) 26sin (3π-x )+66cos (3π-x ) =32[21sin (3π-x )+23cos (3π-x )] =32[sin 6πsin (3π-x )+cos 6πcos (3π-x )] =32cos [6π-(3π-x )]=32cos (x -6π)或:原式=32[sin (3π-x )cos 3π+cos (3π-x )sin 3π]=32sin [(3π-x )+3π]=32sin(32π-x )例3证明:左边=)4tan()4cos(2)4sin(2πππ-=--x x x =右边或:右边=tan (x -4π)=xx xx x x x x x x cos sin cos sin 4sinsin 4cos cos 4sincos 4cos sin )4cos()4sin(+-=+-=--ππππππ=左边例4:解:sin α+cos α=2sin (α+4π)=a sin β+cos β=2sin (β+4π)=b 又∵0<α<β<4π∴0<α+4π<β+4π<2π∴sin (α+4π)<sin (β+4π) ∴a <b答案:C 当堂练习 1答案:C解析:利用两角差的余弦公式的逆用 2答案:B解析:二倍角的应用 3答案:B解析:三角函数基本关系式的平方关系的应用 4答案:B解析:平方关系、倍角公式的应用 5答案:B6解析:1tan 23α=,由此得2tan 6tan 10αα+-=解得tan 2α=-+tan 2α=-7答案:33cos()65αβ-=-解析:因为,(,)2παπ∈由此得4sin 5α=所以3cos 5α=-又因为5cos 13β=-,β是第三象限角,所以12sin 13β=-所以33cos()65αβ-=-家庭作业:1 解析:tan 70°+tan 50°-3tan 70°·tan 50° =tan 120°(1-tan 70°·tan 50°)-3tan 70°·tan 50° =- 3. 答案:D2 解析:23sin(x -φ)=23(sin xcos φ-cos xsin φ) =3sin x -3cos x ,∴cos φ=32,sin φ=12. 又φ∈(-π,π),∴φ=π6. 答案:B3 解析:sin 2x =cos ⎝ ⎛⎭⎪⎫π2-2x =cos 2⎝ ⎛⎭⎪⎫π4-x =1-2sin2⎝ ⎛⎭⎪⎫π4-x =1-2×⎝ ⎛⎭⎪⎫35 2=725. 答案:A 4 解析:sin2⎝ ⎛⎭⎪⎫α-π6-cos ⎝ ⎛⎭⎪⎫5π6+α =1-cos2⎝ ⎛⎭⎪⎫π6-α+cos ⎝ ⎛⎭⎪⎫π6-α=2+33.答案:A5 解析:y =(2cos2x -1)+sin 2x +1=cos 2x +sin 2x +1=2sin ⎝ ⎛⎭⎪⎫2x +π4+1 ∴y 的最小值为1- 2.答案:1- 26 解析:∵0<α<π2<β<π,∴π2<α+β<3π2, ∴sin β=223,cos(α+β)=-223,∴cos α=cos[(α+β)-β] =cos(α+β)cos β+sin(α+β)sin β =⎝ ⎛⎭⎪⎫-223×⎝ ⎛⎭⎪⎫-13+13×223 =49 2.答案:4297 解析:cos β=cos[(α+β)-α] =cos(α+β)cos α+sin(α+β)sin α =17×⎝ ⎛⎭⎪⎫-1114+437×5314=12. ∴β=π3. 答案:π38 解:(1)由tan ⎝ ⎛⎭⎪⎫π4+α=1+tan α1-tan α=12.解得tan α=-13. (2)sin 2α-cos2α1+cos 2α=2sin αcos α-cos2α2cos2α =tan α-12=-56.综合训练1 解析:p1:∃x ∈R ,sin2x 2+cos2x 2=12是假命题;p2是真命题,如x =y =0时成立;p3是真命题, ∵∀x ∈[0,π],sin x≥0, ∴1-cos 2x2=sin2x =|sin x|=sin x ;p4是假命题,如x =π2,y =2π时; sin x =cos y ,但x +y≠π2. 答案:A 2 解析:3-sin 70°2-cos210°=3-sin 70°2-1+cos 20°2=23-sin 70°3-cos 20°=23-cos 20°3-cos 20°=2. 答案:23 解析:∵cos(α+β)=cos αcos β-sin αsin β=15,cos(α-β)=cos αcos β+sin αsin β=35, ∴cos αcos β=25,sin αsin β=15. ∴sin αsin βcos αcos β=12,即tan α·tan β=12. 答案:124 解:(1)由已知条件及三角函数的定义可知,cos α=210,cos β =255.因为α为锐角,故sin α>0, 从而sin α=1-cos2α=7210,同理可得sin β=55,因此tan α=7,tan β=12. 所以tan(α+β)=tan α+tan β1-tan αtan β=7+121-7×12=-3. (2)tan(α+2β)=tan[(α+β)+β]=-3+121--3×12=-1. 又0<α<π2,0<β<π2,故0<α+2β<3π2,从而由tan(α+2β)=-1得α+2β=3π4. 5 解:f(x)=2cos2x -12cos2x +1-2cos2x cos 2x =cos 2x 2cos2x +1-2cos 2x cos 2x =2cos2x +1-2=2cos2x -1=cos 2x.(1)f ⎝ ⎛⎭⎪⎫-11π12=cos 2⎝ ⎛⎭⎪⎫-11π12=cos 11π6=cos π6=32. (2)g(x)=cos 2x +sin 2x =2sin ⎝⎛⎭⎪⎫2x +π4. 由0≤x<π4,故π4≤2x+π4<3π4, ∴22≤sin ⎝ ⎛⎭⎪⎫2x +π4≤1,1≤2sin ⎝⎛⎭⎪⎫2x +π4≤ 2.即g(x)的最小值是1,最大值是 2.6. 答案:12解析:sin14cos16cos14sin16︒︒+︒︒=sin 30︒=127. 答案:<8. 解析:(1)∵ tan 2α=2, ∴4tan 3α=-; 所以tan tan 4tan()41tan tan 4παπαπα++=-=17-; (2)由(1), 4tan 3α=-;6sin cos 6tan 173sin 2cos 3tan 26αααααα++==--. 9.答案:α+β=4π 解析:α、β为锐角, sinα∴ cosα, ∴cos(α+β)=cosαcosβ-sinαsinβ∴α+β=4π 10. 答案:tan β=12- cos(α+β) =239729- 解析:(1) ∵tan (α+β)=1, tan α=3,∴tan β=tan [(α+β)-β]=12-. (2) ∵cos(α-2β)=19-, sin (2α-β)=23, 且2παπ<<, 0<β<2π, ∴α-2β∈(4π, π), 2α-β∈(4π-, 2π), sin(α-2β)=92α-β)=3 ∴ cos 2αβ+=cos[(α-2β)-(2α-β)]+β)=2cos 22αβ+-1=239729- 11.答案:sin2θ==. t a n 32θ= 解析:(1) ∵sinθ=35, θ为锐角, ∴ cosθ=45, sin 2θ==. (2) ∵sinθ=35,sin2θ<0, ∴cosθ<0, cosθ=-45,tan 32θ=.。
两角和与差的正弦余弦正切公式

两角和与差的正弦余弦正切公式在三角函数中,我们经常需要计算两个角的和或差的正弦、余弦或正切值。
这些公式被广泛应用于数学、物理、工程等领域的问题求解中。
本文将详细介绍两角和与差的正弦、余弦和正切公式。
一、两角和与差的正弦公式首先,我们来讨论两个角的和的正弦公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道正弦的定义为一个角的对边与斜边之比,可以表示为sin(x)=opposite/hypotenuse。
根据这个定义,我们可以得到如下的两角和的正弦公式:sin(A+B) = sinA*cosB + cosA*sinB这个公式很重要,可以帮助我们计算两个角的和的正弦值。
在实际应用中,我们经常需要计算两个角的和的正弦,而不是两个角分别的正弦。
所以这个公式非常有用。
接下来,我们来讨论两个角的差的正弦公式。
设有两个角A和B,那么它们的差角记为(A-B)。
根据三角函数的定义,我们可以得到如下的两角差的正弦公式:sin(A-B) = sinA*cosB - cosA*sinB这个公式与两角和的正弦公式类似,也非常有用。
二、两角和与差的余弦公式类似于正弦公式,我们也可以推导出两角和与差的余弦公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道余弦的定义为一个角的邻边与斜边之比,可以表示为cos(x)=adjacent/hypotenuse。
根据这个定义,我们可以得到如下的两角和的余弦公式:cos(A+B) = cosA*cosB - sinA*sinB同样地,我们也可以得到两角差的余弦公式:cos(A-B) = cosA*cosB + sinA*sinB这两个公式和两角和与差的正弦公式一样重要,经常被应用于实际问题中。
三、两角和与差的正切公式最后,我们来讨论两角和与差的正切公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道正切的定义为一个角的对边与邻边之比,可以表示为tan(x)=opposite/adjacent。
两角和与差的余弦正弦和正切

10
10
10
D 、- 3 2 10
8、在 ABC 中,已知 sin Asin B
的形状是( ) A、等腰三角形 B 、直角三角形
sin Acos B cos Asin B cos A cos B 2 ,则
C 、等腰直角三角形 D 、等腰或直角三角形
ABC
9、计算: sin(54 x)cos(24 x) cos(54 x)sin(24 x) =
( 1) sin(
) sin cos cos sin
( 2) sin(
) sin cos cos sin
( 3) cos(
) cos cos cos sin
( 4) cos(
) cos cos cos sin
( 5) tan(
tan tan )
1 tan tan
( 6) tan(
tan tan )
1 tan tan
2
2
(2)若 为锐角,且 sin(
、- 2 2
D 、- 1 2
) 1 ,则 cos 等于( ) 63
2、 2 6 1 B 、 2 6 1 C 、 2 3 1
6
6
4
(7)下列等式成立的是(
)
D 、2 3 1 4
A、 sin( x) cos( x) B 、 sin(2x) sin x
cot( 3 2
) tan
-------------------------------------------------------------------------
【例题精讲 】
例 1、求 150 及 750 的 6 个三角比。
解:
--------------------------------------
0504两角和与差的余弦、正弦和正切(2)

5.4两角和与差的余弦、正弦和正切(2)教学目标:理解和掌握两角和与差的正弦和正切公式.能正确、熟练、灵活的运用公式进行三角变换,会应用于求值、化简、证明等有关问题.初步认识用“构造法”解决问题的思想.理解公式的来源,把握它们之间的内在关系和转化规律.体验“转化”的数学思想.重点难点:重点:两角和与差的余弦、正弦和正切公式.难点:两角和与差的余弦、正弦和正切公式.教学过程:1、 两角和与差的正弦公式下面我们来求两角和与差的正弦公式.sin(α+β)=cos[2π-(α+β)]=cos[(2π-α)-β]=cos(2π-α)cos β+sin(2π-α)sin β=sin αcos β+sin αcos β.即:sin(α+β)=sin αcos β+cos αsin β.它对于任意角α和β都成立.这个恒等式叫做两角和的正弦公式(sine formula of thesum between toe angles ).把上述公式中的β换成-β,得两角差的正弦公式:(sine formula of the difference between toe angles )sin(α-β)=sin αcos β-cos αsin β.例 1 求下列各三角比:(1)sin75°;(2)sin15°.例 2 求sin27°cos72°-cos63°sin18°的值.例 3 (课本P 55例6) 求5cos()cos()cos()cos()126123ππππαααα+⋅++−⋅−的值.例 4 (课本P 56例7)已知:cos α=53,α∈(0,2π),求sin(α-6π).例 5 (课本P56例8)求证:cos(α+β)cos(α-β)=cos 2α-sin 2β.练 1 (课本P 57练习5.4(2)/1、2、3、4、5)练 2 求证:sin(α+β)sin(α-β)=sin 2α-sin 2β.练 3 求证:2222sin()sin()1cot tan sin cos αβαβαβαα+−=−⋅⋅.例 6 (课本P 56例9)在△ABC 中,已知cos A =54,cos B =1312,求sin C 和cos C 的值.★在△ABC 中,有A +B +C =π,可有∠A 、∠B 、∠C 都大于0°小于180°,而且至多一个钝角(直角).★根据诱导公式又有:(1)sin C =sin[180°-(A +B )]=sin(A +B ),同样:cos C =-cos(A +B ),tan C =-tan(A +B );(2)sin 2C =sin[()22A B π+−]=cos(2A B +), 同样:cos2C =sin(2A B +),tan 2C =cot(2A B +). ☆上例改为(1)sin A =35,cos B =1312,求sin C 的值.(2)cos A =54,sin B =135,求sin C 的值.★注意两个解,以及两个解之后的检验.2、 两角和与差的正切公式应用两角和与差的正弦、余弦公式:sin(α+β)=sin αcos β+cos αsin β;cos(α+β)=cos α·cos β-sin α·sin β可以推得两角和与差的正切公式. 由sin()sin cos cos sin tan()cos()cos cos sin sin αβαβαβαβαβαβαβ+++==+−, 当cos α≠0,cos β≠0时,等式右边的分子分母都除以cos αcos β得两角和的正切公式tan tan tan()1tan tan αβαβαβ++=−⋅; 同理可得(或把上述公式中的β换成–β,的两角差的正切公式),tan tan tan()1tan tan αβαβαβ−−=+⋅. ★在两角和与差的正切公式中,α、β和α±β的值都不能取到2π+k π(k ∈Z ).例 7 (课本P 58例10) 已知tan α=31,tan β=-2,求下列三角比的值:(1)tan(α+β);(2)cot(α-β).例 8 (课本P 58例11) 运用两角和的正切公式,求1tan 751tan 75+−的值.例 9 (课本P 59例12)如图,等腰直角三角形ABC 中,∠C=90°,点D 、C 分别是BC 的三等分点, 求tan α、tan β、tan γ的值.练 4 (课本P 59练习5.4(3)/1、2、3、4)例 10 设tan α和tan β是一元二次方程3x 2+5x +1=0的两个根,求cot(α+β)的值.★要注意到两角和的正切公式与韦达定理的形似之处.练 5 已知tan θ和tan()4πθ−是方程x 2+px +q =0的两个根,求证:p -q +1=0.练 6 已知tan α,tan β是关于x 的一元二次方程x 2+px +2=0的两实根,求sin()cos()αβαβ+−值. ★体验推导两角和的正切的方法:分子分母都除以cos αcos β.3、 两角和与差的余弦、正弦和正切公式的混合应用,辅助角公式例 11 (1)已知cot α=2,tan(α-β)=25−,求tan(β-2α)的值; (2)已知sin(30°+α)=53,60°<α<150°,求tan(75°+α)的值.例 12 求值:练 7 在斜三角形△ABC 中,求证:tan A +tan B +tan C =tan A ·tan B ·tan C .练 8 若tan α=3x ,tan β=3x −,且α-β=6π,求x 的值.例 13 (课本P 60例13) 已知2sin 3α=,3cos 4β=−,且α∈(2π,π),β∈(2π,π). 求sin(α-β)和cos(α-β)的值,并判别α-β是第几象限的角.★(1)此题给我们提供了判断一个角在哪个象限的一个方法. ★(2)如果只求α-β所在的象限,还可以这样:∵β∈(2π,π),∴–β∈(-π,-2π),∴-2π<α-β<2π,又∵sin(α-β)=356+−<0,∴α-β∈(-2π,0).所以α-β为第四象限角.例 14 (课本P 60例14)把下列各式化为A sin(α+φ)(A>0)的形式:(1)2sin α+2cos α; (2)sin α-3cos α (3)a sin α+b cos α(a 、b 都不为0).★上述变形方法通常称之为:辅助角公式,常见的有:sin α±cos α=2sin(α±4π);3sin α±cos α=2sin(α±6π);sin α±3cos α=2sin(α±3π).。
两角和与差的正弦、余弦与正切公式

2
(sin
2
A.a>b>c
C.c>a>b
(2)已知
56°-cos 56°),c=
1-ta n 2 39°
,则 a,b,c 的大小关系是(
1+ta n 2 39°
B.b>a>c
D.a>c>b
π
cos(α-6 )+sin
4 3
α= 5 ,则
π
si(nα+6 )=
.
)
答案 (1)D
4
(2)
5
解析 (1)a=cos 50°cos 127°+cos 40°cos 37°
1
D.
2
.
答案 (1)B (2)D (3) 3
解析 (1)根据两角和的正弦公式展开得 sin
3
θ= sin
2
3
θ+ cos
2
θ=1,即
π
3sin(θ+ )=1,解得
6
π
θ+sin(θ+ )=sin
3
1
θ+ sin
2
π
3
sin(θ+ )= .故选
6
3
B.
(2)∵t=2sin 18°,
2cos2 27°-1
.
1+cos
5.积化和差公式
sin αcos
1
β=
2
sin( + ) + sin(-) ,
cos αsin
1
β=2
sin( + )-sin(-) ,
cos αcos
1
β=2
5.4(4)两角和与差的余弦、正弦和正切

cos( ) cos cos sin sin
tan( ) ?
能否用 tan , tan 表示 tan( )?
一、两角和与差的正切
sin cos cos sin sin( ) tan( ) cos( ) cos cos sin sin
1 1 证: tan , tan ,且 , (0, ) 2 2 3 tan tan tan( ) 1 1 tan tan , (0, ) (0, ) 2 在区间 (0, )内,正切值为1的角只有一个, 证毕 即 tan 1 ,因此 4 4
tan17 tan 43 (1) tan 75 (2) 1 tan17 tan 43 解: (1) tan 75 tan(45 30 ) 3 1 tan 45 tan 30 3 2 3 1 tan 45 tan 30 3 1 3 (2)原式= tan(17 43 ) tan 60 3
4
tan 5 cot 50 1 tan 75 (3) (1) tan15 (2) 1 tan 5 cot 50 1 tan 75 2.已知 tan( ) 2, tan 3 ,求 tan
3.在 ABC 中,若 tan A, tan B 是方程
课堂练习: 1. 求下列各式的精确值:
解毕
例2.已知 tan(
3 tan 3 2 解: tan( ) 6 3 1 tan 3 解得 tan 8 5 3
解法二:tan tan[(
5.4(5)两角和与差的余弦、正弦和正切

2
2
A 0 A a b
2
2
(3)a sin b cos (a、b都不为0). 解:a sin b cos a b 2 2 a b ( sin cos ) 2 2 2 2 a b a b a b 可设 cos , sin 2 2 2 2 a b a b 通常0 2,所以: a sin b cos
说明: 本系列课件,经多次使用,修改,其中有部分 来自网络,它山之石可以攻玉,希望谅解。 为了一个课件,我们仔细研磨; 为了一个习题,我们精挑细选; 为了一点进步,我们竭尽全力; 没有最好,只有更好! 制作水平有限,错误难免,请多指教: 28275061@
第五章 三角比
2 3 ex1、已知 sin , cos , ( , ), 3 4 2 ( , ),求 sin( )和 cos( ) 2 的值并判断 是第几象限的角. 6 35 解: sin( ) 0, 12 3 52 7 cos( ) 0 12
4 12 例1、 (2)在ABC 中,已知 sin A , cos B , 5 13 求 sin C和cosC;
12 5 3 解: cos B 0 sin B (2)当 cos A 时, 13 13 5 33 4 3 sin C 又 sin A cos A 65 5 5 56 3 cos C (1)当 cos A 时, 65 5 4 12 3 5 63 sin C sin( A B) 5 13 5 12 65 3 12 4 5 16 cos C cos( A B) 5 13 5 13 65
ABC中的重要结论:
两角和与差的正弦余弦正切公式及二倍角公式

两角和与差的正弦余弦正切公式及二倍角公式1.两角和的正弦公式:设角A和角B的正弦分别为sinA和sinB,则它们的和角C的正弦为sinC。
根据三角函数的定义,有sinA = a/c和sinB = b/c,其中a、b、c分别为三角形ABC的对边、邻边和斜边。
根据正弦公式,sinC = c/c =1、所以,两角和的正弦公式为sin(A + B) = sinC = 12.两角和的余弦公式:设角A和角B的余弦分别为cosA和cosB,则它们的和角C的余弦为cosC。
根据三角函数的定义,有cosA = b/c和cosB = a/c。
根据余弦公式,cosC = cos(A + B) = cos(AcosB - BsinA) = cosAcosB + sinAsinB = (b/c)(a/c) + (a/c)(b/c) = 2ab/c²。
3.两角和的正切公式:设角A和角B的正切分别为tanA和tanB,则它们的和角C的正切为tanC。
根据三角函数的定义,有tanA = a/b和tanB = b/a。
根据正切公式,tanC = tan(A + B) = (tanA + tanB) / (1 - tanAtanB) = (a/b + b/a) / (1 - (a/b)(b/a)) = (a² + b²) / (ab - ab) = a² + b² / ab。
4.两角差的正弦公式:设角A和角B的正弦分别为sinA和sinB,则它们的差角C的正弦为sinC。
根据三角函数的定义,有sinA = a/c和sinB = b/c。
根据差角公式,sinC = sin(A - B) = sin(AcosB + BsinA) = sinAcosB - cosAsinB = a/c(b/c) - (b/c)(a/c) = 2a b/c²。
5.两角差的余弦公式:设角A和角B的余弦分别为cosA和cosB,则它们的差角C的余弦为cosC。
两角和与差的正弦、余弦和正切(二倍角公式)

两角和与差的正弦、余弦和正切(二倍角公式)一.【学习目标】1、掌握并熟练使用两角和与差的余弦、正弦、正切进行证明、化简和求值;2、能针对不同情况进行寻找已知角之间的关系,灵活使用两角和与差的余弦、正弦、正切公式,二倍角公式进行证明、化简和求值.二.重点、难点、易错(混)点、常考点灵活使用两角和与差的余弦、正弦、正切进行证明、化简和求值三.【知识梳理】1.两角和与差的正弦、余弦、正切公式: C (),cos()αβαβ--= ; C (),cos()αβαβ++= S (),sin()αβαβ--= ; S (),sin()αβαβ++= . T (),tan()αβαβ++= 由T ()αβ+可得公式变形tan tan αβ+= T (),tan()αβαβ--=由T ()αβ-可得公式变形得:tan tan αβ-= 2. 二倍角的正弦、余弦、正切公式2:sin 2S ________________;2:tan 2T ________________。
2:cos 2C ________________=________________=________________;四.【基础题达标】 1.12cos312sinππ-=2.sin15°sin30°sin75°=__________.3.cos20°cos40°cos60°cos80° =4.),0(πθ∈,θθsin 1sin 1--+=5.313sin 253sin 223sin 163sin +的值等于 6.12cos312sinππ-=7.化简:x x sin 6cos 2-= 8.若51cos sin =+θθ,则θ2sin 的值 9.81cos sin =x x 且24ππ<<x ,则=-x x sin cos 10.),0(πθ∈,θθsin 1sin 1--+=11.函数)(2cos 21cos )(R x x x x f ∈-=的最大值为 12..若223tan 1tan 1+=-+αα,则=-αα2cos 2sin 113.50tan 10tan 350tan 10tan ++=14.化简:15tan 115tan 1-+=15.已知cos (6πα-)+sin α76)πα+的值是考点一: 运用公式求值、求角问题【例1】 (1)已知cos α=13,cos(α+β)=-13,且α,β∈⎝⎛⎭⎫0,π2,求cos(α-β)的值. (2)已知0<β<π2<α<π,且cos ⎝⎛⎭⎫α-β2=-19,sin ⎝⎛⎭⎫α2-β=23,求cos(α+β)的值; (3)已知π2<β<α<34π,sin(α-β)=1213,cos(α+β) =-35,求sin2α的值(3)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,求2α-β的值.【训练1】已知βα,是锐角且1010sin ,55sin ==βα,求βα+【训练2】(2012·江苏卷)设α为锐角,若cos ⎝⎛⎭⎫α+π6=45,则sin ⎝⎛⎭⎫2α+π12的值为________.考点二: 公式的变形应用【例2】已知:)tan(βα+=βtan 2。
两角和与差的正弦、余弦、正切公式及变形(最新整理)

两角和与差的正弦、余弦、正切公式及变形1.两角和与差的正弦、余弦、正切公式(1)公式①cos(α-β)=cos_αcos_β+sin_αsin_β(C (α-β))②cos(α+β)=cos_αcos_β-sin_αsin_β(C (α+β))③sin(α-β)=sin_αcos_β-cos_αsin_β(S (α-β))④sin(α+β)=sin_αcos_β+cos_αsin_β(S (α+β))⑤tan(α-β)=(T (α-β))tan α-tan β1+tan αtan β⑥tan(α+β)=(T (α+β))tan α+tan β1-tan αtan β(2)公式变形①tan α+tan β=tan(α+β)(1-tan αtan β).②tan α-tan β=tan(α-β)(1+tan αtan β).2.二倍角公式(1)公式①sin 2α=2sin_αcos_α,②cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α,③tan 2α=.2tan α1-tan 2α(2)公式变形①cos 2α=,sin 2α=;1+cos 2α21-cos 2α2②1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=sin .2)4(πα±3.判断下列结论的正误(正确的打“√”,错误的打“×”)(1)两角和与差的正弦、余弦公式中的角α,β是任意的.(√)(2)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.(√)(3)在锐角△ABC 中,sin A sin B 和cos A cos B 大小不确定.(×)(4)公式tan(α+β)=可以变形为tan α+tan β=tan(α+β)(1-tan αtan β),且对任意tan α+tan β1-tan αtan β角α,β都成立.(×)(5)二倍角的正弦、余弦、正切公式的适用范围是任意角.(×)(6)存在角α,使得sin 2α=2sin α成立.(√)(7)若α+β=,则(1+tan α)(1+tan β)=2.(√)π4(8)不存在实数α,β,使得cos(α+β)=sin α+cos β.(×)(9)存在实数α,使tan 2α=2tan α.(√)(10)y =的x 无意义.(×)1-2cos 2x考点一 三角函数式的给角求值命题点1.已知非特殊角求函数式的值2.已知含参数的角化简函数或求值[例1] (1)求值:-sin 10°;1+cos 20°2sin 20°)5tan 5tan 1(00-解:原式=-sin 10°2cos 210°2×2sin 10°cos 10°)5cos 5sin 5sin 5cos (0000-=-sin 10°·=-sin 10°·cos 10°2sin 10°cos 25°-sin 25°sin 5°cos 5°cos 10°2sin 10°cos 10°12sin 10°=-2cos 10°=cos 10°2sin 10°cos 10°-2sin 20°2sin 10°=cos 10°-2sin (30°-10°)2sin 10°===.cos 10°-2(12cos 10°-32sin 10°)2sin 10°3sin 10°2sin 10°32(2)化简:sin 2α·sin 2β+cos 2α·cos 2β-cos 2α·cos 2β.12解:法一:(复角→单角,从“角”入手)原式=sin 2α·sin 2β+cos 2α·cos 2β-·(2cos 2α-1)·(2cos 2β-1)12=sin 2α·sin 2β+cos 2α·cos 2β-·(4cos 2α·cos 2β-2cos 2α-2cos 2β+1)12=sin 2α·sin 2β-cos 2α·cos 2β+cos 2α+cos 2β-12=sin 2α·sin 2β+cos 2α·sin 2β+cos 2β-12=sin 2β+cos 2β-=1-=.121212法二:(从“名”入手,异名化同名)原式=sin 2α·sin 2β+(1-sin 2α)·cos 2β-cos 2α·cos 2β=cos 2β-sin 2α(cos 2β-sin 2β)-cos 2α·cos12122β=cos 2β-sin 2α·cos 2β-cos 2α·cos 2β12=cos 2β-cos 2β·)2cos 21(sin 2αα+=-cos 2β·1+cos 2β2[sin 2α+12(1-2sin 2α)]=-cos 2β=.1+cos 2β21212法三:(从“幂”入手,利用降幂公式先降次)原式=·+·-cos 2α·cos 2β1-cos 2α21-cos 2β21+cos 2α21+cos 2β212=(1+cos 2α·cos 2β-cos 2α-cos 2β)+(1+cos 2α·cos 2β+cos 2α+cos 2β)-·cos 2α·cos 2β141412=.12[方法引航] 给角求值问题往往给出的角是非特殊角,求值时要注意:(1)观察角,分析角之间的差异,巧用诱导公式或拆分.(2)观察名,尽可能使函数统一名称.(3)观察结构,利用公式,整体化简.1.求值sin 50°(1+tan 10°).3解:sin 50°(1+tan 10°)=sin 50°(1+tan 60°·tan 10°)3=sin 50°·cos 60°cos 10°+sin 60°sin 10°cos 60°cos 10°=sin 50°·====1.cos (60°-10°)cos 60°cos 10°2sin 50°cos 50°cos 10°sin 100°cos 10°cos 10°cos 10°2.在△ABC 中,已知三个内角A ,B ,C 成等差数列,则tan +tan +tan tan 的值为A 2C 23A 2C2________.解析:因为三个内角A ,B ,C 成等差数列,且A +B +C =π,所以A +C =,=,tan =,2π3A +C 2π3A +C23所以tan +tan +tan tanA 2C 23A 2C2=tan +tan tan22(C A +2tan 2tan 1(CA -3A 2C 2=+tan tan =.3)2tan 2tan1(CA -3A 2C 23考点二 三角函数式的给值求值命题点1.已知某角的三角函数值求其它的三角函数值2.已知某角的三角函数值,求三角函数的值3.已知三角函数式的值,求三角函数值[例2] (1)(2016·高考全国丙卷)若tan θ=-,则cos 2θ=( )13A .- B .-C. D.45151545解析:法一:cos 2θ=cos 2θ-sin 2θ=cos2θ-sin 2θcos 2θ+sin 2θ==.故选D.1-tan 2θ1+tan 2θ45法二:由tan θ=-,可得sin θ=±,因而cos 2θ=1-2sin 2θ=.1311045答案:D(2)已知tan =,且-<α<0,则等于( ))4(πα+12π2)4cos(2sin sin 22πααα-+A .-B .-C .-D.255351031010255解析:由tan ==,得tan α=-.)4(πα+tan α+11-tan α1213又-<α<0,所以sin α=-.π21010故==2sin α=-.)4cos(2sin sin 22πααα-+2sin α(sin α+cos α)22(sin α+cos α)2255答案:A(3)已知α∈,且2sin 2α-sin α·cos α-3cos 2α=0,则=________.)2,0(π12cos 2sin )4sin(+++ααπα解析:2sin 2α-sin αcos α-3cos 2α=0则(2sin α-3cos α)(sin α+cos α)=0,由于α∈,sin α+cos α≠0,)2,0(π则2sin α=3cos α.又sin 2α+cos 2α=1,∴cos α=,213∴==.12cos 2sin )4sin(+++ααπα22(sin α+cos α)(sin α+cos α)2+(-sin 2α+cos 2α)268答案:268[方法引航] 三角函数的给值求值,关键是把待求角用已知角表示:(1)已知角为两个时,待求角一般表示为已知角的和或差.(2)已知角为一个时,待求角一般与已知角成“倍”的关系或“互余互补”的关系.(3)已知三角函数时,先化简三角函数式,再利用整体代入求值.1.在本例(1)中,已知条件不变,求tan 的值.)6(θπ+解:tan ===.)6(θπ+tan π6+tan θ1-tan π6tan θ33-131+33×1353-6132.在本例(1)中,已知条件不变,求2sin 2θ-sin θcos θ-3cos 2θ的值.解:原式=2sin 2θ-sin θcos θ-3cos 2θsin 2θ+cos 2θ===-.2tan 2θ-tan θ-3tan 2θ+12×(-13)2+13-3(-13)2+11153.已知cos +sin =,则cos =________.)2(απ-)32(απ-23532(πα+解析:由cos +sin =,得)2(απ-)32(απ-235sin α+sin cos α-cos πsin α=∴sin α+cos α=,2π3232353232235即sin =,∴sin =,3)6(πα+2356(πα+25因此cos =1-2sin 2=1-2×=.)32(πα+6(πα+2)52(1725答案:1725考点三 已知三角函数式的值求角命题点1.利用弦函数值求角2.利用切函数值求角[例3] (1)已知cos α=,cos(α-β)=,0<β<α<,则β=________.171314π2解析:∵cos α=,0<α<.∴sin α=.17π2437又cos(α-β)=,且0<β<α<.∴0<α-β<,则sin(α-β)=.1314π2π23314则cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=×+×==,由于0<β<,所以β=.1713144373314497×1412π2π3答案:π3(2)已知α,β∈(0,π),且tan(α-β)=,tan β=-,则2α-β的值为________.1217解析:∵tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β==>0,∴0<α<.又∵tan 2α===>0,12-171+12×1713π22tan α1-tan 2α2)31(1312-⨯34∴0<2α<,∴tan(2α-β)===1.π2tan 2α-tan β1+tan 2αtan β34+171-34×17∵tan β=-<0,∴<β<π,-π<2α-β<0,∴2α-β=-π.17π234答案:-π34[方法引航] 1.解决给值求角问题应遵循的原则(1)已知正切函数值,选正切函数.(2)已知正、余弦函数值,选正弦函数或余弦函数,且①若角的范围是,选正、余弦皆可;②)2,0(π若角的范围是(0,π),选余弦较好;③若角的范围是,选正弦较好.)2,2(ππ-2.解给值求角问题的一般步骤(1)求角的某一个三角函数值.(2)确定角的范围.(3)根据角的范围写出所求的角.1.设α,β为钝角,且sin α=,cos β=-,则α+β的值为( )5531010A. B.C. D.或3π45π47π45π47π4解析:选C.∵α,β为钝角,sin α=,cos β=-,5531010∴cos α=,sin β=,∴cos(α+β)=cos αcos β-sin αsin β=>0.-255101022又α+β∈(π,2π),∴α+β∈,∴α+β=.)2,23(ππ7π42.已知tan α=-,cos β=,α∈,β∈,求tan(α+β)的值,并求出α+β的值.1355),2(ππ)2,0(π解:由cos β=,β∈,得sin β=,tan β=2.55)2,0(π255∴tan(α+β)===1.tan α+tan β1-tan αtan β-13+21+23∵α∈,β∈,∴<α+β<,∴α+β=.),2(ππ)2,0(ππ23π25π4[方法探究]三角恒等变换在化简、求值、证明中的综合应用三角恒等变换要重视三角函数的“三变”:“三变”是指“变角、变名、变式”;变角:对角的分拆要尽可能化成同名、同角、特殊角;变名:尽可能减少函数名称;变式:对式子变形一般要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的三角公式恒等变形.[典例] 某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:(1)sin 213°+cos 217°-sin 13°cos 17°;(2)sin 215°+cos 215°-sin 15°cos 15°;(3)sin 218°+cos 212°-sin 18°cos 12°;(4)sin 2(-18°)+cos 248°-sin(-18°)cos 48°;(5)sin 2(-25°)+cos 255°-sin(-25°)cos 55°.(Ⅰ)试从上述五个式子中选择一个,求出这个常数;(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.[解] (Ⅰ)选择(2)式,计算如下:sin 215°+cos 215°-sin 15°cos 15°=1-sin 30°=1-=.121434(Ⅱ)法一:三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-α)=.34证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos 30°cos α+sin 30°sin α)2-sin α(cos 30°cos α+sin 30°sin α)=sin 2α+cos 2α+sin αcos α+sin 2α-sin α·cos α-sin 2α=sin 2α+34321432123434cos 2α=.34法二:三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-α)=.34证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=+-sin α(cos 30°cos α+sin 1-cos 2α21+cos (60°-2α)230°sin α)=-cos 2α++(cos 60°cos 2α+sin 60°sin 2α)-sin αcos α-sin 2α=-cos 2α1212121232121212++cos 2α+sin 2α-sin 2α-(1-cos 2α)=1-cos 2α-+cos 2α=.121434341414141434[高考真题体验]1.(2016·高考全国甲卷)若cos =,则sin 2α=( ))4(απ-35A. B. C .-D .-7251515725解析:选D.因为cos =cos cos α+sin sin α=(sin α+cos α)=,所以sin α+cos α=)4(απ-π4π42235,所以1+sin 2α=,所以sin 2α=-,故选D.32518257252.(2016·高考全国丙卷)若tan α=,则cos 2α+2sin 2α=( )34A.B.C .1D.642548251625解析:选A.法一:由tan α==,cos 2α+sin 2α=1,得Error!或Error!,则sin 2α=2sin αcossin αcos α34α=,则cos 2α+2sin 2α=+=.2425162548256425法二:cos 2α+2sin 2α====.cos 2α+4sin αcos αcos 2α+sin 2α1+4tan α1+tan 2α1+31+91664253.(2015·高考课标全国卷Ⅰ)sin 20°cos 10°-cos 160°sin 10°=( )A .- B.C .- D.32321212解析:选D.sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin 30°=.124.(2014·高考课标全国卷Ⅰ)设α∈,β∈,且tan α=,则( ))2,0(π)2,0(π1+sin βcos βA .3α-β= B .2α-β=C .3α+β= D .2α+β=π2π2π2π2解析:选B.由条件得=,即sin αcos β=cos α(1+sin β),sin(α-β)=cos α=sin sin αcos α1+sin βcos β,因为-<α-β<,0<-α<,所以α-β=-α,所以2α-β=,故选B.)2(απ-π2π2π2π2π2π25.(2015·高考四川卷)已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________.解析:由sin α+2cos α=0,得tan α=-2.所以2sin αcos α-cos 2α==2sin αcos α-cos 2αsin 2α+cos 2α2tan α-1tan 2α+1==-1.-4-14+1答案:-16.(2016·高考四川卷)cos 2-sin 2=________.π8π8解析:由二倍角公式,得cos 2-sin 2=cos =.π8π8)82(π⨯22答案:22课时规范训练A 组 基础演练1.tan 15°+=( )1tan 15°A .2 B .2+C .4D.3433解析:选C.法一:tan 15°+=+1tan 15°sin 15°cos 15°cos 15°sin 15°===4.1cos 15°sin 15°2sin 30°法二:tan 15°+=+1tan 15°1-cos 30°sin 30°1sin 30°1+cos 30°=+==4.1-cos 30°sin 30°1+cos 30°sin 30°2sin 30°2.的值是( )2cos 10°-sin 20°sin 70°A. B.C.D.123232解析:选C.原式=2cos (30°-20°)-sin 20°sin 70°=2(cos 30°·cos 20°+sin 30°·sin 20°)-sin 20°sin 70°==.3cos 20°cos 20°33.已知θ∈(0,π),且sin =,则tan 2θ=( ))4(πθ-210A. B. C .-D.4334247247解析:选C.由sin =,得(sin θ-cos θ)=,所以sin θ-cos θ=.)4(πθ-2102221015解方程组Error!,得Error!或Error!.因为θ∈(0,π),所以sin θ>0,所以Error!不合题意,舍去,所以tan θ=,所以tan 2θ==432tan θ1-tan 2θ=-,故选C.2×431-(43)22474.若θ∈,sin 2θ=,则sin θ等于( )]2,4[ππ378A. B. C.D.35457434解析:选D.由sin 2θ=和sin 2θ+cos 2θ=1得387(sin θ+cos θ)2=+1=,3782)473(+又θ∈,∴sin θ+cos θ=.]2,4[ππ3+74同理,sin θ-cos θ=,∴sin θ=.3-74345.已知sin 2(α+γ)=n sin 2β,则的值为( )tan (α+β+γ)tan (α-β+γ)A.B.C.D.n -1n +1nn +1nn -1n +1n -1解析:选D.由已知可得sin[(α+β+γ)+(α-β+γ)]=n sin[(α+β+γ)-(α-β+γ)],则sin(α+β+γ)·cos(α-β+γ)+cos(α+β+γ)sin(α-β+γ)=n [sin(α+β+γ)cos(α-β+γ)-cos(α+β+γ)sin(α-β+γ)],即(n +1)cos(α+β+γ)sin(α-β+γ)=(n -1)sin(α+β+γ)cos(α-β+γ),所以=tan (α+β+γ)tan (α-β+γ),故选D.n +1n -16.若sin =,则cos 2θ=________.)2(θπ+35解析:∵sin =cos θ=,∴cos 2θ=2cos 2θ-1=2×-1=-.)2(θπ+352)53(725答案:-7257.若点P (cos α,sin α)在直线y =-2x 上,则sin 2α+2cos 2α=________.解析:∵点P (cos α,sin α)在直线y =-2x 上∴sin α=-2cos α,于是sin 2α+2cos 2α=2sin αcos α+2(2cos 2α-1)=-4cos 2α+4cos 2α-2=-2.答案:-28.设sin 2α=-sin α,α∈,则tan 2α的值是________.),2(ππ解析:∵sin 2α=-sin α,∴2sin αcos α=-sin α.∵α∈,sin α≠0,∴cos α=-.又∵α∈,∴α=π,),2(ππ12),2(ππ23∴tan 2α=tan π=tan =tan =.43)3(ππ+π33答案:39.化简:(0<θ<π).(1+sin θ+cos θ)(sin θ2-cosθ2)2+2cos θ解:由θ∈(0,π),得0<<,∴cos >0,θ2π2θ2∴==2cos .2+2cos θ4cos 2θ2θ2又(1+sin θ+cos θ)=)2cos 2(sinθθ-2cos 2)(sin 2cos 22cos 2sin 2(2θθθθθ-+=2cos θ2)2cos 2(sin 22θθ-=-2cos cos θ.故原式==-cos θ.θ2-2cos θ2cos θ2cosθ210.已知α∈,且sin +cos =.),2(ππα2α262(1)求cos α的值;(2)若sin(α-β)=-,β∈,求cos β的值.35),2(ππ解:(1)因为sin +cos =,两边同时平方,得sin α=.α2α26212又<α<π,所以cos α=-.π232(2)因为<α<π,<β<π,所以-π<-β<-,故-<α-β<.π2π2π2π2π2又sin(α-β)=-,得cos(α-β)=.3545cos β=cos[α-(α-β)=cos αcos(α-β)+sin αsin(α-β)=-×+×=-.324512)53(-43+310B 组 能力突破1.已知sin α+cos α=,则1-2sin 2=( )22)4(απ-A. B.C .-D .-12321232解析:选C.由sin α+cos α=,得1+2sin αcos α=,∴sin 2α=-.221212因此1-2sin 2=cos2=sin 2α=-.)4(απ-)4(απ-122.已知f (x )=2tan x -,则f 的值为( )2sin 2x2-1sin x 2cos x 2)12(πA .4B.C .4D .83833解析:选D.∵f (x )=2=2×=,)sin cos cos sin (2sin cos (tan xxx x x x x +⨯=+1cos x ·sin x 4sin 2x∴f ==8.)12(π4sin π63.已知sin α=,sin(α-β)=-,α,β均为锐角,则角β等于( )551010A. B. C. D.5π12π3π4π6解析:选C.∵α、β均为锐角,∴-<α-β<.π2π2又sin(α-β)=-,∴cos(α-β)=.101031010又sin α=,∴cos α=,55255∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=×-×=.5531010255)1010(-22∴β=.π44.若tan α=lg(10a ),tan β=lg ,且α+β=,则实数a 的值为________.1a π4解析:tan α+tan β=lg(10a )+lg =lg 10=1,1a∵α+β=,所以tan =tan(α+β)==,π4π4tan α+tan β1-tan αtan β11-tan αtan β∴tan αtan β=0,则有tan α=lg(10a )=0或tan β=lg =0.1a 所以10a =1或=1,即a =或1.1a 110答案:或11105.已知tan(π+α)=-,tan(α+β)=.13ααααπ2sin cos 10cos 4)2(2sin 22-+-(1)求tan(α+β)的值;(2)求tan β的值.解:(1)∵tan(π+α)=-,∴tan α=-.∵tan(α+β)=1313ααααπ2sin cos 10cos 4)2(2sin 22-+-===sin 2α+4cos 2α10cos 2α-sin 2α2sin αcos α+4cos 2α10cos 2α-2sin αcos α2cos α(sin α+2cos α)2cos α(5cos α-sin α)====.sin α+2cos α5cos α-sin αtan α+25-tan α-13+25-(-13)516(2)tan β=tan[(α+β)-α]===.tan (α+β)-tan α1+tan (α+β)tan α516+131-516×133143。
第3课时 两角和与差的正弦、余弦、正切公式(二)

1.存在 α,β∈R,使 tan (α+β)=tan α+tan β 吗?
tan α-tan β
2.对任意 α,β∈R,tan (α-β)=
吗?
1+tan αtan β
tan α+tan β
3.tan (α+β)=
等价于 tan α+tan β=tan (α+β)·(1-tan αtan β)?
1-tan αtan β
已知 tan α+π5 =37 ,tan 45π-β =25 ,则 tan (α-β)=________. 【解析】tan (α-β)=tan [π+(α-β)]
=tan α+π5+45π-β
=1t-antanα+α5π++π5ttaann
45π-β 45π-β
=1-37+37×2525
=1.
答案:1
1+tan 45°tan 21°
4.已知 A,B 都是锐角,且 tan A=13
,sin B=
5 5
,则
A+B=________.
【解析】因为 B 为锐角,sin B=
5 5
,所以 cos B=2 5 5
,
所以 tan B=12
tan A+tan B ,所以 tan (A+B)=
1-tan A tan B
-β)),三者知二可求出第三个.
(2)化简过程中注意“1”与“tan
π 4
”,“
3
”与“tan
π 3
”等特殊数与特殊角的函数值之间
的转化.
基础类型二 给值求值(数学运算)
【典例】已知 tan α=12 ,tan (α-β)=-25 ,那么 tan (2α-β)的值为( )
A.-34
B.98
C.-89
两角和与差的正弦余弦和正切

两角和与差的正弦余弦和正切首先,我们来看两角和的正弦公式。
假设有两个角A和B,它们的正弦分别为sin(A)和sin(B)。
那么它们的正弦和公式为:sin(A + B) = sin(A)cos(B) + cos(A)sin(B)这个公式告诉我们,两个角的正弦之和等于第一个角的正弦乘以第二个角的余弦,加上第一个角的余弦乘以第二个角的正弦。
我们可以用一个例子来理解这个公式。
假设A = 30°,B = 45°,那么sin(30°) = 0.5,sin(45°) = √2 / 2、将这些值代入公式:sin(30° + 45°) = sin(30°)cos(45°) + cos(30°)sin(45°)sin(75°) ≈ 0.5 × √2 / 2 + √3 / 2 × √2 / 2sin(75°) ≈ √2 / 4 + √6 / 4sin(75°) ≈ (√2 + √6) / 4可以看出,通过两角和公式,我们可以简化计算sin(75°)的过程。
接下来,我们来看两角和的余弦公式。
假设有两个角A和B,它们的余弦分别为cos(A)和cos(B)。
那么它们的余弦和公式为:cos(A + B) = cos(A)cos(B) - sin(A)sin(B)这个公式告诉我们,两个角的余弦之和等于第一个角的余弦乘以第二个角的余弦,减去第一个角的正弦乘以第二个角的正弦。
同样以前面的例子来说明,cos(30°) = √3 / 2,cos(45°) = √2 / 2、将这些值代入公式:cos(30° + 45°) = cos(30°)cos(45°) - sin(30°)sin(45°)cos(75°) ≈ √3 / 2 × √2 / 2 - √2 / 2 × √2 / 2cos(75°) ≈ √6 / 4 - 1 / 4cos(75°) ≈ (√6 - 1) / 4这个公式同样帮助我们简化了计算cos(75°)的过程。
【高中数学】两角和与差的正弦、余弦和正切公式及二倍角公式

两角和与差的正弦、余弦和正切公式及二倍角公式一、基础知识1.两角和与差的正弦、余弦、正切公式S (α±β):sin(α±β)=sin αcos β±cos αsin β.C (α±β):cos(α±β)=cos αcos β∓sin αsin β.T (α±β):tan(α±β),β,α±β≠π2+k π,k ∈两角和与差的正弦、余弦、正切公式的结构特征和符号特点及关系:C (α±β)同名相乘,符号反;S (α±β)异名相乘,符号同;T (α±β)分子同,分母反.2.二倍角公式S 2α:sin 2α=2sin αcos α.C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α.T 2α:tan 2α≠k π+π2且α≠k π2+π4,k ∈二倍角是相对的,例如,α2是α43α是3α2的二倍角.二、常用结论(1)降幂公式:cos 2α=1+cos 2α2,sin 2α=1-cos 2α2.(2)升幂公式:1+cos 2α=2cos 2α,1-cos 2α=2sin 2α.(3)公式变形:tan α±tan β=tan(α±β)(1∓tan αtan β).(4)辅助角公式:a sin x +b cos x =a 2+b 2sin(x +φsin φ=b a 2+b 2,cos φ考点一三角函数公式的直接应用[典例](1)已知sin α=35,αtan β=-12,则tan(α-β)的值为()A .-211B.211C.112D .-112(2)(2019·呼和浩特调研)若sin (π-α)=13,且π2≤α≤π,则sin 2α的值为()A .-229B .-429C.229D.429[解析](1)因为sin α=35,α所以cos α=-1-sin 2α=-45,所以tan α=sin αcos α=-34.所以tan(α-β)=tan α-tan β1+tan αtan β=-211.(2)因为sin(π-α)=sin α=13,π2≤α≤π,所以cos α=-1-sin 2α=-223,所以sin 2α=2sin αcos α=2×13×=-429.[答案](1)A(2)B[解题技法]应用三角公式化简求值的策略(1)首先要记住公式的结构特征和符号变化规律.例如两角差的余弦公式可简记为:“同名相乘,符号反”.(2)注意与同角三角函数基本关系、诱导公式的综合应用.(3)注意配方法、因式分解和整体代换思想的应用.[题组训练]1.已知sin α=13+cos α,且α,则cos 2α()A .-23B.23C .-13D.13解析:选A因为sin α=13+cos α,所以sin α-cos α=13,所以cos 2α=cos 2α-sin 2αsin αcos π4+cos αsin π4=(cos α-sin α)(cos α+sin α)22(sin α+cos α)=-1322=-23.2.已知sin α=45,且αsin α________.解析:因为sin α=45,且αα所以cos α=-1-sin 2α=-=-35.因为sin 2α=2sin αcos α=-2425,cos 2α=2cos 2α-1=-725.所以αsin 2αcos π3+cos 2αsin π3=-24+7350.答案:-24+7350考点二三角函数公式的逆用与变形用[典例](1)(2018·全国卷Ⅱ)已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=________.(2)计算:tan 25°+tan 35°+3tan 25°tan 35°=________.[解析](1)∵sin α+cos β=1,①cos α+sin β=0,②∴①2+②2得1+2(sin αcos β+cos αsin β)+1=1,∴sin αcos β+cos αsin β=-12,∴sin(α+β)=-12.(2)原式=tan(25°+35°)(1-tan 25°tan 35°)+3tan 25°·tan 35°=3(1-tan 25°tan 35°)+3tan 25°tan 35°=3.[答案](1)-12(2)3[解题技法]两角和、差及倍角公式的逆用和变形用的技巧(1)逆用公式应准确找出所给式子与公式的异同,创造条件逆用公式.(2)公式的一些常用变形:sin αsin β+cos(α+β)=cos αcos β;cos αsin β+sin(α-β)=sin αcos β;1±sin αsin α2±cos ;sin 2α=2sin αcos αsin 2α+cos 2α=2tan αtan 2α+1;cos 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α.[提醒](1)公式逆用时一定要注意公式成立的条件和角之间的关系.(2)tan αtan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β))三者中可以知二求一,且常与一元二次方程根与系数的关系结合命题.(3)注意特殊角的应用,当式子中出现12,1,32,3等这些数值时,一定要考虑引入特殊角,把“值变角”构造适合公式的形式.[题组训练]1.设a =cos 50°cos 127°+cos 40°cos 37°,b =22(sin 56°-cos 56°),c =1-tan 239°1+tan 239°,则a ,b ,c 的大小关系是()A .a >b >cB .b >a >cC .c >a >bD .a >c >b解析:选D由两角和与差的正、余弦公式及诱导公式,可得a =cos 50°cos 127°+cos40°cos 37°=cos 50°cos 127°+sin 50°sin 127°=cos(50°-127°)=cos(-77°)=cos 77°=sin 13°,b =22(sin 56°-cos 56°)=22sin 56°-22cos 56°=sin(56°-45°)=sin 11°,c =1-tan 239°1+tan 239°=1-sin 239°cos 239°1+sin 239°cos 239°=cos 239°-sin 239°=cos 78°=sin 12°.因为函数y =sin x ,x ∈0,π2为增函数,所以sin 13°>sin 12°>sin 11°,所以a >c >b .2.已知sin α=435,则________.解析:由sin α=435,可得32cos α+12sin α+sin α=435,即32sin α+32cos α=435,∴3sin =435,即=45.答案:453.化简sin sin sin 2α的结果是________.解析:sin 2α=1-12cos ααsin 2α=1-cos 2α·cos π3-sin 2α=1-cos 2α2-1-cos 2α2=12.答案:12考点三角的变换与名的变换考法(一)三角公式中角的变换[典例](2018·浙江高考改编)已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点-35,-若角β满足sin(α+β)=513,则cos β的值为________.[解析]由角α的终边过点-35,-得sin α=-45,cos α=-35.由sin(α+β)=513,得cos(α+β)=±1213.由β=(α+β)-α,得cos β=cos(α+β)cos α+sin(α+β)sin α,所以cos β=-5665或cos β=1665.[答案]-5665或1665[解题技法]1.三角公式求值中变角的解题思路(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,再应用诱导公式把“所求角”变成“已知角”.2.常见的配角技巧2α=(α+β)+(α-β),α=(α+β)-β,β=α+β2-α-β2,α=α+β2+α-β2,α-β2=考法(二)三角公式中名的变换[典例](2018·江苏高考)已知α,β为锐角,tan α=43,cos(α+β)=-55.(1)求cos 2α的值;(2)求tan(α-β)的值.[解](1)因为tan α=43,tan α=sin αcos α,所以sin α=43cos α.因为sin 2α+cos 2α=1,所以cos 2α=925,所以cos 2α=2cos 2α-1=-725.(2)因为α,β为锐角,所以α+β∈(0,π).又因为cos(α+β)=-55,所以α+β所以sin(α+β)=1-cos 2(α+β)=255,所以tan(α+β)=-2.因为tan α=43,所以tan 2α=2tan α1-tan 2α=-247.所以tan(α-β)=tan[2α-(α+β)]=tan 2α-tan (α+β)1+tan 2αtan (α+β)=-211.[解题技法]三角函数名的变换技巧明确各个三角函数名称之间的联系,常常用到同角关系、诱导公式,把正弦、余弦化为正切,或者把正切化为正弦、余弦.[题组训练]1.已知tan θ+1tan θ=4,则cos ()A.12B.13C.14D.15解析:选C由tan θ+1tan θ=4,得sin θcos θ+cos θsin θ=4,即sin 2θ+cos 2θsin θcos θ=4,∴sin θcos θ=14,∴cos =1-sin 2θ2=1-2sin θcos θ2=1-2×142=14.2.(2018·济南一模)若=7210A sin A 的值为()A.35B.45C.35或45D.34解析:选B ∵A A +π4∈∴=-210,∴sin A =-π4=cos π4-sin π4=45.3.已知sin α=-45,α∈3π2,2π,若sin (α+β)cos β=2,则tan(α+β)=()A.613B.136C .-613D .-136解析:选A ∵sin α=-45,α∈3π2,2π,∴cos α=35.又∵sin (α+β)cos β=2,∴sin(α+β)=2cos[(α+β)-α].展开并整理,得65cos(α+β)=135sin(α+β),∴tan(α+β)=613.[课时跟踪检测]A 级1.sin 45°cos 15°+cos 225°sin 165°=()A .1 B.12C.32D .-12解析:选B sin 45°cos 15°+cos 225°sin 165°=sin 45°·cos 15°+(-cos 45°)sin 15°=sin(45°-15°)=sin 30°=12.2.若2sin x +1,则cos 2x =()A .-89B .-79C.79D .-725解析:选C 因为2sin x +1,所以3sin x =1,所以sin x =13,所以cos 2x =1-2sin 2x =79.3.(2018·山西名校联考)若=-33,则cos α=()A .-223B .±223C .-1D .±1解析:选C cos α=12cos α+32sin α+cos α=32cos α+32sin α=3cos =-1.4.tan 18°+tan 12°+33tan 18°tan 12°=()A.3B.2C.22D.33解析:选D ∵tan 30°=tan(18°+12°)=tan 18°+tan 12°1-tan 18°tan 12°=33,∴tan 18°+tan 12°=33(1-tan 18°tan 12°),∴原式=33.5.若α3cos 2α=sin 2α的值为()A .-118B.118C .-1718D.1718解析:选C由3cos 2α=3(cos 2α-sin 2α)=22(cos α-sin α),又由α∈可知cos α-sin α≠0,于是3(cos α+sin α)=22,所以1+2sin αcos α=118,故sin 2α=-1718.6.已知sin 2α=13,则cos ()A .-13B.13C .-23D.23解析:选Dcos =12+12sin 2α=12+12×13=23.7.已知=12,α-π2,cos________.解析:由已知得cos α=12,sin α=-32,所以=12cos α+32sin α=-12.答案:-128.(2019·湘东五校联考)已知sin(α+β)=12,sin(α-β)=13,则tan αtan β=________.解析:因为sin(α+β)=12,sin(α-β)=13,所以sin αcos β+cos αsin β=12,sin αcos β-cosαsin β=13,所以sin αcos β=512,cos αsin β=112,所以tan αtan β=sin αcos βcos αsin β=5.答案:59.(2017·江苏高考)若=16,则tan α=________.解析:tan α=+π4=tanπ41-tan π4=16+11-16=75.答案:7510.化简:sin 235°-12cos 10°cos 80°=________.解析:sin 235°-12cos 10°cos 80°=1-cos 70°2-12cos 10°sin 10°=-12cos 70°12sin 20°=-1.答案:-111.已知tan α=2.(1)求tan(2)求sin 2αsin 2α+sin αcos α-cos 2α-1的值.解:=tan α+tan π41-tan αtan π4=2+11-2=-3.(2)sin 2αsin 2α+sin αcos α-cos 2α-1=2sin αcos αsin 2α+sin αcos α-(2cos 2α-1)-1=2sin αcos αsin 2α+sin αcos α-2cos 2α=2tan αtan 2α+tan α-2=2×222+2-2=1.12.已知α,β均为锐角,且sin α=35,tan(α-β)=-13.(1)求sin(α-β)的值;(2)求cos β的值.解:(1)∵α,β,∴-π2<α-β<π2.又∵tan(α-β)=-13<0,∴-π2<α-β<0.∴sin(α-β)=-1010.(2)由(1)可得,cos(α-β)=31010.∵α为锐角,且sin α=35,∴cos α=45.∴cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=45×31010+35×=91050.B 级1.(2019·广东五校联考)若4cos(2π-θ),|θ|<π2,则tan2θ=________.解析:∵4cos(2π-θ),∴cos θsin θ=4cos θ,又∵|θ|<π2,∴sin θ=14,∴0<θ<π2,cos θ=154,tan θ=sin θcos θ=115,从而tan 2θ=2tan θ1-tan 2θ=157.答案:1572.(2018·江西新建二中期中)已知A ,B 均为锐角,cos(A +B )=-2425,=35,则________.解析:因为A ,B 均为锐角,cos(A +B )=-2425,=35,所以π2<A +B <π,π2<B +π3<π,所以sin(A +B )=1-cos 2(A +B )=725,=-45,可得cos (A +B )=-2425×+725×35=117125.答案:1171253.(2019·石家庄质检)已知函数f (x )=x ∈R.(1)求f(2)若cos θ=45,θf θ解:(1)-π4+=-12.(2)θθ-π3+θ=22(sin 2θ-cos 2θ).因为cos θ=45,θsin θ=35,所以sin 2θ=2sin θcos θ=2425,cos 2θ=cos 2θ-sin 2θ=725,所以θ=22(sin 2θ-cos 2θ)=22×=17250.。
两角和与差的正弦余弦和正切公式及二倍角公式

(1)计算
sin110sin 20 cos2155 sin2155
的值为
(
)
A.- 1 B. 1 C. 3 D.- 3
2
2
2
2
(2)在△ABC中,若tan Atan B=tan A+tan B+1,则cos C的值为 ( )
A.- 2 B. 2 C. 1 D.- 1
2
2
2
2
答案 (1)B (2)B
2
2
α= 4 3 ,
5
即 3 cos α+ 3 sin α= 4 3 ,
2
2
5
所以
3 sin
2
α+
1 2
cos
α=sin
α
6
=
4 5
,
所以sin α
7 6
=-sin
α
6
=-
4 5
.
夯基提能作业 栏目索引
第五节 两角和与差的正弦、余弦 和正切公式及二倍角公式
解析
(1)
sin110sin 20 cos2155 sin2155
=
sin 70sin 20 cos 310
=
cos
20sin
20
=
1 2
sin
40
=
1
.
cos 50
sin 40 2
(2)由tan Atan B=tan A+tan B+1,
可得 tan A tan B =-1,
1 tan Atan B
教材研读
总纲目录
总纲目录 栏目索引
1.两角和与差的正弦、余弦、正切公式 2.二倍角的正弦、余弦、正切公式 3.有关公式的逆用、变形
两角和与差的正弦、余弦和正切公式

1
1
A.3
B.2
C.
2 2
√D.
3 3
∵cos α+cosα-π3=1, ∴cos α+12cos α+ 23sin α=32cos α+ 23sin α
=
3
3 2 cos
α+21sin
α
= 3cosα-π6=1,
∴cosα-π6= 33.
(2)化简:①sin x+ 3cos x= 2sinx+π3 .
∴β>α,而 α,β∈0,π2, ∴0<β-α<π2, ∴β-α=π3, 即选项D正确,C错误.
(2)在△ABC 中,C=120°,tan A+tan B=233,则 tan Atan B 的值为
1 A.4
√B.13
1
5
C.2
D.3
∵C=120°,∴tan C=- 3. ∵A+B=π-C, ∴tan(A+B)=-tan C. ∴tan(A+B)= 3, tan A+tan B= 3(1-tan Atan B), 又∵tan A+tan B=233, ∴tan Atan B=13.
A.a>b>c
B.b>a>c
C.c>a>b
√D.a>c>b
(sin2256°
由两角和与差的正、余弦公式及诱导公式,可得
a=cos 50°cos 127°+cos 40°cos 37°
=cos 50°cos 127°+sin 50°sin 127°
=cos(50°-127°)=cos(-77°)
=cos 77°=sin 13°,
第四章
考试要求
1.会推导两角差的余弦公式. 2.会用两角差的余弦公式推导出两角差的正弦、正切公式. 3.掌握两角和与差的正弦、余弦、正切公式,并会简单应用.
两角和与差的正弦余弦和正切公式及二倍角公式

两角和与差的正弦余弦和正切公式及二倍角公式1.两角和的正弦公式:sin(A + B) = sin A cos B + cos A sin B2.两角差的正弦公式:sin(A - B) = sin A cos B - cos A sin B3.两角和的余弦公式:cos(A + B) = cos A cos B - sin A sin B4.两角差的余弦公式:cos(A - B) = cos A cos B + sin A sin B5.两角和的正切公式:tan(A + B) = (tan A + tan B) / (1 - tan A tan B)6.两角差的正切公式:tan(A - B) = (tan A - tan B) / (1 + tan A tan B)二倍角公式:1.正弦的二倍角公式:sin(2A) = 2sin A cos A2.余弦的二倍角公式:cos(2A) = cos^2 A - sin^2 A = 2cos^2 A - 1 = 1 - 2sin^2 A 3.正切的二倍角公式:tan(2A) = (2tan A) / (1 - tan^2 A)这些公式在三角函数的学习中非常重要,可以用于简化计算,推导其他公式,解三角方程等。
以上是两角和与差的正弦、余弦和正切公式及二倍角公式的简要描述。
详细阐述这些公式需要更多的字数,下面将对每个公式进行更详细的解释。
1.两角和的正弦公式:sin(A + B) = sin A cos B + cos A sin B这个公式表示角A和角B的和的正弦等于角A的正弦乘以角B的余弦加上角A的余弦乘以角B的正弦。
2.两角差的正弦公式:sin(A - B) = sin A cos B - cos A sin B这个公式表示角A和角B的差的正弦等于角A的正弦乘以角B的余弦减去角A的余弦乘以角B的正弦。
3.两角和的余弦公式:cos(A + B) = cos A cos B - sin A sin B这个公式表示角A和角B的和的余弦等于角A的余弦乘以角B的余弦减去角A的正弦乘以角B的正弦。
