清华大学土木工程系结构力学(英)Chapter3_399306542
清华大学结构力学

38
3
目录
结构力学(II) 第十 章 矩阵位移法 第十三章 结构的动力计算 第十五章 结构的塑性分析与极限荷载
结构力学教程(I)、(II) 龙驭球 包世华 主编 龙驭球 包世华 匡文起 袁驷 编著
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如:房屋中的 框架结构、桥梁、大 坝等。
6
万里长城 7
天安门城楼
8
国家大剧院
9
三峡大坝
10
印度泰姬陵 11
意大利比萨斜塔
12
凯旋门
13
埃菲尔铁塔 14
吉隆坡石油双塔 15
桥梁 16
赵州桥
17
青马大桥
18
旧金山大桥
2)荷载作用下杆件截面存在弯矩、剪力和轴力。
33
3. 拱
FH FV
FP
三铰拱
FH
FV
拉杆
拉杆拱
拱的特点:
无铰拱
1) 拱的轴线为曲线,在竖向荷载作用下支座有
水平推力F(H 见图);
2) 水平推力大大改变了拱的受力特性。
34
4. 桁架和组合结构
静定桁架
超静定桁架 组合结构
35
特点:
1) 桁架由直杆组成,所有结点都是铰结点,当 荷载作用于结点时,各杆只受轴力;
一、支座和支座反力
支座定义:把结构与基础联结起来的装置。 1. 固定支座
B
A
实际形状
结构力学(英) Chapter2 Equilibrium and Geometric Stability PPT精品课件

P1 m
A
m
a
XA
l
YA V
M
N
YA
V
M N
P2 P3 B
YB
YB
6
Statically Determinate Structures
P
A
C
B
a
RA Pb l
Pb / l
b l
RB
Pa l
P
Pa / l
Shear Diagram
The equations of statics alone are sufficient to compute the reactions and the distribution of internal forces.
M1 M2
+ Mx = M1,x M2,x = 0
z
+ My = M1,y M2,y = 0
+ Mz = M1,z M2,z = 0
x
3
Equilibrium of Planar Structure
4
External Forces
External Forces are the actions of other bodies to the structure under consideration.
n = number of structural components r = number of unknown reaction components If r = 3n, the structure is statically determinate If r > 3n, the structure is statically indeterminate
清华大学结构力学下-矩阵位移法
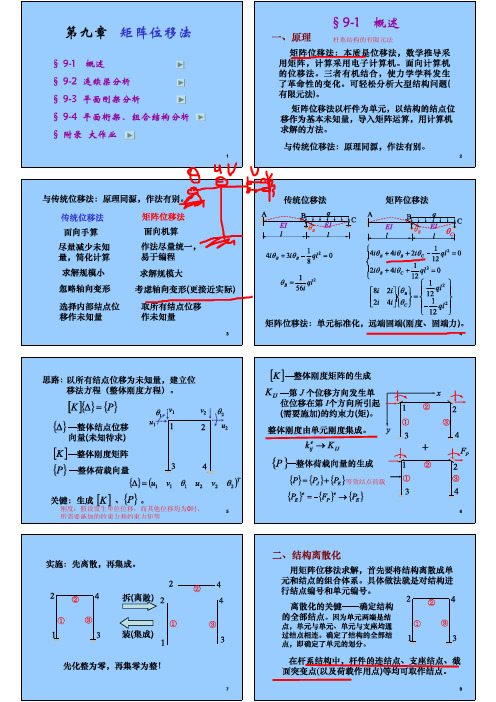
等效结点荷载
刚度:假设发生单位位移,而其他位移均为0时, 所需要施加的约束力和约束力矩等
只需要线位移,只有轴向位移,其他位移为整体的线位移
T是有整体到局部
整体系下的向量
局部坐标系的矩阵 转换矩阵
局部到整体要乘以转置矩阵
假设其他位移固定,发生某一个单一位移 那么会有一定相同的两列向量,综合,矩阵相同
单元是有方向的
位移协调条件
右端是直接的节点力,左边 是单元的杆断力
三个பைடு நூலகம்元的定位 向量
列对应单元的杆断位移(即这一列的元素都表示同一个位移引起的力),行对 应于杆断力(即这一行的元素表示所有位移引起的同一力)
放到第二行第一列
只管行码和列码都不为0的元素
对于单元是半正定,因为 可以发生刚体位移,整体正定 是因为变形储存的能量一定为正
横杆2处的左右转角相同,所以 只需要一个编码即可
因为是桁架单元, 所以为0
水平放置的原因
只是②上面有,因为桁架不考虑 且梁式杆中仅第二段有固端弯矩什么的
此处整体坐标和局部坐标是一样的
桁架单元的局部坐标杆断力
Δ1和Δ2的相关单元是①和②,所以单元1和单元2 中都会对K1,2有贡献额
将固端弯矩进行反向 得到等效结点荷载
在整体坐标系下面,顺时针方向为正的弯矩方向
原来本来就有的结点荷载向量
以局部坐标系规定的正方向为准
整体系下的杆断力
桁架中没有固断力的问题,所以去掉Fpe刚即可
不需要重码,因为只关注线位移 桁架中只有结点荷载
局部坐标的方向 外界应该施加的作用力或者作用弯矩
剪力为-(4+2)/l,逆时针, 方向向下,所以为正,此时 的正负是看与坐标轴方向的吻合与否 同一个杆端力在六种不同情况下的取值
3静定结构 (1)华科结构力学

Structural Mechanics
第三章 静定结构 第二章 第一章 几何构造分析 绪 论
Chapter2 Geometric construction analysis Chapter 3 Chapter Statically 1 Preface Determinate to Steel Structures Structure
X
q(x) p(x) q(x) dx
M x
F
0
M FN
F
Y
0
dx
M+dM FN+dFN直杆内力的 微分关系M 0结构力学
FQ p(x) FQ+dFQ
dFQ dM dFN 得: FQ , q ( y ), p( x) dx dx dx
Structural Mechanics 第4页
第三章 静定结构
Chapter 3 Statically Determinate Structures
1、梁的内力计算回顾 2、用区段叠加法画简支梁的弯矩图 3、斜梁及多跨静定梁 4、静定刚架与桁架 5、组合结构和三铰拱 6、静定结构的特性
结构力学 Structural Mechanics 第1页
第三章 静定结构 第二章 第一章 几何构造分析 绪 论
结构力学 Structural Mechanics 第2页
第三章 静定结构 第二章 第一章 几何构造分析 绪 论
Chapter2 Geometric construction analysis Chapter 3 Chapter Statically 1 Preface Determinate to Steel Structures Structure
无荷载区段 FQ图 水平线
清华大学土木工程系结构力学(英)Chapter7_812904391

Basic Concepts for the Force Method Construction of M,V,N diagrams
M - diag. 1) Direct-plotting 2) superposition
M M1 X 1 M 2 X 2 M P
V - diag. 1) Direct-plotting 2) Superposition N - diag. 1) Direct-plotting 2) Superposition
12
Basic Concepts for the Force Method
11 1n X1 D1P Flexibility matrix D NP n1 nn X N
q C
B
C
q
B X1
X2
Compatibility Equation:
A
A
Primary
D 1 11 X1 12 X 2 D 1 p 0 D 2 21 X1 22 X 2 D 2 p 0
Disp. due to X2 = 1
Disp. due to load
ij
— Non-diagonal coefficients
ij ji
Reciprocal theorem:
13
Basic Concepts for the Force Method
Several points:
(5) The force method = the method of consistent displacement
清华结构力学作业

程序结构力学期中大作业——平面刚架计算程序1、简要程序说明《结构力学求解器》教学版有前后处理界面,缺核心计算程序SM90.exe,本程序即编制核心计算程序SM90.exe。
1.1 处理范围限制荷载:支持所有结点荷载、包括杆端位移的四种单元荷载结点连接:支持所有非斜向的各种连接支座约束:支持除了斜支座之外的各种支座1.2 计算求解简要流程从文件“SM90.ipt”中读取、处理并储存结构的结点及单元信息。
使用矩阵位移法,首先集成整体总结点荷载向量P,集成整体刚度矩阵K,使用LDL T分解法求解得到整体结点位移向量∆,然后再根据∆先得到整体坐标下杆端位移向量∆e,再由杆端位移向量、局部单元刚度矩阵、单元固端力向量得到局部坐标系下杆端内力向量。
2、源代码模块及程序清单3、输入的结构数据信息3.1 结构、荷载数据及计算简图其它:柱刚度:EA=105().()kN m215104kN,EI=⨯⋅梁刚度:EA=106()kN m2.()kN,EI=⨯⋅10104支座沉降:c=001.()m3.2 输入数据文件内容(未处理)结点,1,0,0结点,2,0,5结点,3,6,0结点,4,6,4结点,5,6,8结点,6,6,12结点,7,6,16结点,8,13,0结点,9,13,4结点,10,13,8结点,11,13,12结点,12,13,16结点,13,16,0结点,14,16,2单元,1,2,1,1,0,1,1,1单元,2,5,1,1,1,1,1,0单元,3,4,1,1,1,1,1,1单元,4,5,1,1,1,1,1,1单元,5,6,1,1,1,1,1,1单元,6,7,1,1,1,1,1,0单元,4,9,1,1,1,1,1,1单元,5,10,1,1,1,1,1,1单元,6,11,1,1,1,1,1,1单元,7,12,1,1,1,1,1,1单元,8,9,1,1,0,1,1,1单元,9,10,1,1,1,1,1,1单元,10,11,1,1,1,1,1,1单元,11,12,1,1,1,1,1,1单元,9,14,1,1,0,1,1,1单元,13,14,1,1,1,1,1,1结点支承,1,4,0,0,0结点支承,3,6,0,0,0,0结点支承,8,4,0,0,0结点支承,13,6,0,0,0,0结点荷载,2,1,10,0结点荷载,7,1,40,0单元荷载,10,1,60,1/3,90单元荷载,10,1,60,2/3,90单元荷载,9,1,60,1/2,90单元荷载,8,3,5,0,1,90单元荷载,7,3,5,0,1,90单元荷载,5,3,2,0,1,90单元荷载,6,3,2,0,1,90单元荷载,15,3,3,0,1,90单元材料性质,1,1,100000,15000,0,0,-1单元材料性质,3,6,100000,15000,0,0,-1单元材料性质,11,14,100000,15000,0,0,-1单元材料性质,16,16,100000,15000,0,0,-1单元材料性质,2,2,1000000,10000,0,0,-1单元材料性质,15,15,1000000,10000,0,0,-1单元材料性质,7,10,1000000,10000,0,0,-1结点支承,3,6,0,0,0.01,03.3 输入数据文件内容(处理后:SM90.IPT)116 17 35 2 90.000000000000000E+000 0.000000000000000E+000 0 010.000000000000000E+000 5.00000000000000 2 346.00000000000000 0.000000000000000E+000 0 06.00000000000000 4.00000000000000 8 9106.00000000000000 8.00000000000000 5 676.00000000000000 8.00000000000000 5 6116.00000000000000 12.0000000000000 12 13146.00000000000000 16.0000000000000 15 16176.00000000000000 16.0000000000000 15 162713.0000000000000 0.000000000000000E+000 0 03113.0000000000000 4.00000000000000 18 192013.0000000000000 4.00000000000000 18 193213.0000000000000 8.00000000000000 21 222313.0000000000000 12.0000000000000 24 252613.0000000000000 16.0000000000000 28 293016.0000000000000 0.000000000000000E+000 0 016.0000000000000 2.00000000000000 33 34351 2 100000.000000000 15000.00000000002 5 1000000.00000000 10000.00000000003 4 100000.000000000 15000.00000000004 6 100000.000000000 15000.00000000006 7 100000.000000000 15000.00000000007 8 100000.000000000 15000.00000000004 11 1000000.00000000 10000.00000000006 13 1000000.00000000 10000.00000000007 14 1000000.00000000 10000.00000000009 15 1000000.00000000 10000.000000000010 11 100000.000000000 15000.000000000011 13 100000.000000000 15000.000000000013 14 100000.000000000 15000.000000000014 15 100000.000000000 15000.000000000012 17 1000000.00000000 10000.000000000016 17 100000.000000000 15000.00000000002 1 10.00000000000008 1 40.000000000000010 2 0.333333333333333 -60.000000000000010 2 0.666666666666667 -60.00000000000009 2 0.500000000000000 -60.00000000000008 1 1.00000000000000 -5.000000000000007 1 1.00000000000000 -5.000000000000005 1 1.00000000000000 -2.000000000000006 1 1.00000000000000 -2.0000000000000015 1 1.00000000000000 -3.000000000000003 3 0 1.000000000000000E-0024、计算结果4.1 输出数据文件内容(SMCAI90.OUT)10 00.000000000000000E+000 0.000000000000000E+000 -1.312320379407611E-002 5.560652234870134E-002 2.304558378405893E-004 -7.117505821068581E-003 5.560652234870134E-002 2.304558378405893E-004 -7.117505821068581E-003 5.278394963143841E-002 5.869045961093688E-003 4.968728206911202E-003 0.000000000000000E+000 0.000000000000000E+000 0.000000000000000E+000 6.134302073665104E-003 7.774337023929546E-003 -6.220921272818899E-003 6.134302073665104E-003 7.774337023929546E-003 -6.220921272818899E-0035.278394963143841E-002 5.869045961093688E-003 -1.281184195691321E-002 5.278394963143841E-002 5.869045961093688E-003 -1.281184195691321E-002 0.110389250192221 3.881789234098302E-003 -1.238265778050635E-002 0.110389250192221 3.881789234098302E-003 -1.238265778050635E-002 0.153055590585021 2.237297589939866E-003 -9.630770979269111E-0036.134302073665104E-0037.774337023929546E-003 -6.220921272818899E-003 5.841122486500181E-003 -5.232962938233666E-003 -5.246190249735726E-003 5.278394963143841E-002 5.869045961093688E-003 -1.281184195691321E-002 5.276332645090513E-002 -1.211203654567029E-002 -1.205485451586346E-002 0.110389250192221 3.881789234098302E-003 -1.238265778050635E-002 0.110502106300783 -1.732477981867489E-002 -1.117824150760299E-002 0.153055590585021 2.237297589939866E-003 -2.048707379649037E-002 0.152720805404088 -2.048028817451645E-002 -1.428627258452916E-003 0.000000000000000E+000 0.000000000000000E+000 4.326741924302934E-004 5.841122486500181E-003 -5.232962938233666E-003 -5.246190249735726E-003 5.841122486500181E-003 -5.232962938233666E-003 -5.246190249735726E-003 5.276332645090513E-002 -1.211203654567029E-002 -1.205485451586346E-002 5.276332645090513E-002 -1.211203654567029E-002 -1.205485451586346E-002 0.110502106300783 -1.732477981867489E-002 -1.117824150760299E-002 0.110502106300783 -1.732477981867489E-002 -1.117824150760299E-002 0.152720805404088 -2.048028817451645E-002 -1.428627258452916E-003 5.841122486500181E-003 -5.232962938233666E-003 3.549261962267918E-003 7.823052813148474E-003 -1.542869377984182E-003 -4.215008775865264E-003 0.000000000000000E+000 0.000000000000000E+000 0.000000000000000E+000 7.823052813148474E-003 -1.542869377984182E-003 -4.215008775865264E-003 4.60911675681179 7.20683756760904 2.842170943040401E-014 4.60911675681179 -7.20683756760904 36.0341878380452-0.437020751516684 -5.37165956799102 -36.0341878380452-0.437020751516684 5.37165956799102 -3.552713678800501E-015 -55.6415744017613 -17.7399575774232 -12.1514603817755-55.6415744017613 17.7399575774232 -58.8083699279173-47.6322765708965 24.1428405889943 73.0016337433423-47.6322765708965 -24.1428405889943 23.5697286126350-49.6814181748847 24.2958468042149 41.6489196135707-49.6814181748847 -16.2958468042149 39.5344676032887-41.1122911039609 0.173545581013641 -15.3058176759457-41.1122911039609 7.82645441898636 1.896260926059767E-013 -41.8827981664175 8.00929783086485 -14.1932638154252-41.8827981664175 26.9907021691352 -52.2416513685209-2.94616864761065 -6.65825836080036 -65.2186482262056-2.94616864761065 41.6582583608004 -103.88916029939716.1223012232022 8.56912707092378 -24.2286499273430 16.1223012232022 51.4308729290762 -125.787460576191-47.8264544189915 41.1122911039609 -3.197442310920451E-014-47.8264544189915 78.8877088960391 -132.213962272274-130.824073455842 -10.6478708290613 -2.842170943040401E-014 -130.824073455842 10.6478708290613 -42.5914833162452-171.976840185916 34.6503218433935 94.8331346847660-171.976840185916 -34.6503218433935 43.7681526888080-130.318581825115 31.7041531957828 60.1210076105888-130.318581825115 -31.7041531957828 66.6956051725423-78.8877088960390 47.8264544189804 59.0918554036481-78.8877088960390 -47.8264544189804 132.213962272274-110.338164658006 -8.33948062935629 -3.996802888650564E-015 -110.338164658006 19.1561344557483 -49.5684250198828-77.1434688992091 81.1809908388722 112.793556657862-77.1434688992091 -81.1809908388722 49.5684250198828 4.2 结构内力图12.15弯矩图x剪力图轴力图1314。
清华大学研究生院结构力学2007-2011考研真题

清华大学研究生院2007年考试科目:结构力学 题号:0901一.计算图1所示珩架指定杆的轴力()12,N N (10分)二.结构仅在ACB 部分温度升高t 度,并且在D 处作用外力偶M 。
试求图示刚架A,B 两点间水平向的相对位移。
已知:各杆的EI 为常值,α为线膨胀系数,h 为截面高度。
(20分)三.用力法分析图3所示结构,绘M 图。
计算时轴力和剪力对位移的影响略去不计。
各杆的EI 值相同。
(20分)半圆弧积分表:2211sin sin 2,cos sin 22424x x xdx x xdx x =-=+⎰⎰四.试用位移法求解图4所示刚架并绘M 图。
计算时不考虑轴力变形时对位移的影响。
(20分)杆端力公式:21,08f f AB BA ql M M =-=,53,88f f AB BA ql ql Q Q ==-一.试用力矩分配法计算图5所示连续梁并绘M 图。
(10分)二.求图示结构的自振频率和主振型,并作出振型图。
已知:122,,m m EI m m ===常数,忽略阻尼影响。
(20分)清华大学研究生院2008年招收硕士生入学试题考试科目:结构力学(包含结构动力学基础)题号:0901一.选择题:在正确答案处画“√”。
每题4分。
1.图示平面体系的几何组成性质是:A.几何不变且无多余联系的B.几何不变且有多余联系的C.几何可变的D.瞬变的2.图示结构A截面的剪力为:A. –PB. PC. P/2D. –P/23.图示珩架内力为零的杆为:A.3根B.6根C.8根D.7根3.图示结构的超静定次数为:A.6次B.4次C.5次D.7次4.图示梁当EI=常数时,B端的转角是:A. 3ql EI(顺时针)5/48B. 3ql EI(逆时针)5/48C. 37/48ql EI(逆时针)D. 3ql EI(逆时针)9/48二.计算题1.已知图示结构的M图,做Q.N图。
(10分)图(2.若P=1在梁AB上移动,试绘出M的影响线。
结构力学(英) Chapter4 Analysis of Statically Determinate Beam and Frame Structures PPT精品课件

MA 0:
YB
q0l 3
MB 0:
YA
q0l 6
11
Section Method for Internal Loadings
q0a l Vc
A
q0 B
Mc
c a
YA q0l
l
6
Vc
YA
1 2
q0a l
a
q0
l 2 3a2 6l
Mc
YA
a
1 2
•Axial Force:
+
NN
Positive axial force tends to elongate the segment.
9
Sign Convention (2)
•Shear Force:
+
VV
Positive shear force tends to rotate the segment clockwise.
Moment——Algebraic sum of moments against the considered point produced by loads acting to its left/right
(concave upward-positive, convex upward-negative)
q0 l
a
a
a 3
q0a
l2 a2 6l
12
Internal loadings over a beam
We frequently need to plot internal loading diagrams to describe the variation of shear and moment over a beam structure.
结构力学课件清华大学龙驭球版本

§2.3无多余约束几何不变体系的组成规则
图a为一无多余约束的几何不变体系 将杆AC,AB,BC均看成刚片,就成为三刚
A
图a
片组成的无多余约束的几何不变体系
一、三刚片以不在一条直线上的三铰 C
B
相联,组成无多余约束的几何不
变体系。
三铰共线瞬变体系
三刚片以三对平行链杆相联 瞬变体系
两平行链杆于两铰连线平行, 瞬变1体3 系
y x
yx 图a
yX
o
y
x
图b
四、约束:在体系内部加入的减少自由度的装置
多余约束:不减少体系自 由度的约束称为多余约束。
注意:多余约束将影响结构的 受力与变形。
a A
4
1、单链杆:仅在两处与其它物体用铰相连,不论其形 状和铰的位置如何。
一根链杆可以减少
体系一个自由度,相 当于一个约束。!
Ⅰ
15
3
4
几个基本概念 体系的计算自由度 无多余约束的几何不 变体系的组成规则 分析举例
1
§2.1构造分析的几个基本概念
一、构造分析的目的 1、研究结构 正确的连接方式,确保所设计的结构能承受
荷载,维持平衡,不至于发生刚体运动。 2、在结构计算时,可根据其几何组成情况,选择适当的
计算方法;分析其组成顺序,寻找简便的解题途径。 二、体系的分类:在忽略变形的前提下,体系可分为两类:
的内力, 故几何常变体系和几 何瞬变体系不能作为建筑结 构使用.
只有几何不变体系才 能作为建筑结构使用!!
β
PA
β
Δ是微量
P N
N
3
三、自由度:所谓体系的自由度是指体系运动时,可以 独立改变的几何参数的数目; 即确定体系位置所需独立坐 标的数目。
结构力学第3章

M图(kNm)
12
3-3 静定平面刚架
例
2kN/m
解
(1)求支反力
x xB yA
C
D
3m
F 0, F F 0, F M 0, M
y A
0 12 kN
A
12 kNm
A 12kNm 4m
B
1m
FxB=0
(2)作内力图
2m
FyA=12kN
3-3 静定平面刚架
8
4 12 12 4 16
例
l q
解
FP=ql
l ql
l/2
l/2 ql FN图 ql2/2 ql2/8
ql
ql
0
ql FQ图
ql2/2
M图
3-3 静定平面刚架
例 M M/2l M/2l l l 0 M/2 M/2l FN图 l l M/2l 解 M/2l
FQ图
M图
M/2
3-3 静定平面刚架
例 FP l FP l 0 Pl FP FPl FN图 解 FP
FP 2 FP FP 2
xB yA
FyA=FP /2
FP /2
(2)作内力图
FPa
FP /2
FN图
FP FQ图
M图
3-3 静定平面刚架
例
2FP A FyA=3FP/4 B FxB=2FP l C FP
解 (1)求支反力
l
(2)作内力图
l/2
FyC=7FP/4 FP
l/2
3FPa/4 F a/2 P FPa/4 FQ图 M图
R NC
FQ图
5kN
5kN
FN图
★取隔离体时: a:约束必须全部断开,用相应的约束反力来代替。 b:正确选择隔离体,标上全部荷载。
清华大学《结构力学习题集》

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
aa9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
qlll /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
ll l l /32 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m3m3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
清华大学考研结构力学2016-2020考研真题

清华大学考研结构力学2016-2020考研真题关键信息项:1、真题的年份范围:2016 2020 年2、真题所属科目:结构力学3、真题提供方与使用方11 协议目的本协议旨在规范关于清华大学考研结构力学 2016 2020 考研真题的使用、传播和相关责任。
111 定义在本协议中,以下术语具有以下含义:“真题”指清华大学结构力学考研在 2016 年至 2020 年期间的考试题目及相关资料。
112 协议范围本协议适用于所有获取、使用或传播上述真题的个人或组织。
12 真题提供提供方应确保所提供的真题完整、准确,且来源合法合规。
121 真题完整性提供的真题应包括完整的题目、答案(如有)、考试要求及相关说明。
122 准确性核实提供方应尽力核实真题的准确性,但不承担因不可抗力或其他无法预见、无法避免的因素导致的错误。
13 真题使用使用方应遵守以下规定:131 仅限个人学习使用真题仅供使用方个人学习之用,不得用于商业目的,不得向第三方出售、出租或转让。
132 保密义务使用方应妥善保管真题,不得将其公开在任何公共平台或向无关人员透露。
133 合理使用使用方应在合理范围内使用真题,不得进行恶意篡改、复制或抄袭。
14 知识产权真题的知识产权归清华大学所有,使用方不得以任何方式侵犯。
141 尊重版权使用方应充分尊重清华大学对真题的版权,不得未经授权进行任何形式的改编、出版或再创作。
15 责任与限制各方应承担以下责任和限制:151 提供方责任若因提供方原因导致真题存在严重错误或造成使用方损失,提供方应承担相应的赔偿责任,但赔偿上限不超过提供真题所获得的收益。
152 使用方责任若使用方违反本协议规定,应承担法律责任,并向提供方赔偿因此造成的一切损失。
153 不可抗力若因不可抗力因素导致无法履行本协议,各方互不承担责任,但应在合理期限内通知对方并提供相关证明。
16 协议变更与终止161 变更通知任何一方如需变更本协议条款,应提前书面通知对方,经双方协商一致后方可变更。
结构力学专业英语双语词汇

结构力学结构力学 structural mechanics结构分析 structural analysis结构动力学 structural dynamics拱 Arch三铰拱 three-hinged arch抛物线拱 parabolic arch圆拱 circular arch穹顶 Dome空间结构 space structure空间桁架 space truss雪载[荷] snow load风载[荷] wind load土压力 earth pressure地震载荷 earthquake loading弹簧支座 spring support支座位移 support displacement支座沉降 support settlement超静定次数 degree of indeterminacy机动分析 kinematic analysis结点法 method of joints截面法 method of sections结点力 joint forces共轭位移 conjugate displacement影响线 influence line三弯矩方程 three-moment equation单位虚力 unit virtual force刚度系数 stiffness coefficient柔度系数 flexibility coefficient力矩分配 moment distribution力矩分配法 moment distribution method力矩再分配 moment redistribution分配系数 distribution factor矩阵位移法 matri displacement method单元刚度矩阵 element stiffness matrix单元应变矩阵 element strain matrix总体坐标 global coordinates贝蒂定理 Betti theorem高斯--若尔当消去法 Gauss-Jordan elimination Method 屈曲模态 buckling mode复合材料力学 mechanics of composites复合材料 composite material纤维复合材料 fibrous composite单向复合材料 unidirectional composite泡沫复合材料 foamed composite颗粒复合材料 particulate composite层板 Laminate夹层板 sandwich panel正交层板 cross-ply laminate斜交层板 angle-ply laminate层片 Ply多胞固体 cellular solid膨胀 Expansion压实 Debulk劣化 Degradation脱层 Delamination脱粘 Debond纤维应力 fiber stress层应力 ply stress层应变 ply strain层间应力 interlaminar stress比强度 specific strength强度折减系数 strength reduction factor强度应力比 strength -stress ratio横向剪切模量 transverse shear modulus横观各向同性 transverse isotropy正交各向异 Orthotropy剪滞分析 shear lag analysis短纤维 chopped fiber长纤维 continuous fiber纤维方向 fiber direction纤维断裂 fiber break纤维拔脱 fiber pull-out纤维增强 fiber reinforcement致密化 Densification最小重量设计 optimum weight design网格分析法 netting analysis混合律 rule of mixture失效准则 failure criterion蔡--吴失效准则 Tsai-W u failure criterion达格代尔模型 Dugdale model断裂力学 fracture mechanics概率断裂力学 probabilistic fracture Mechanics格里菲思理论 Griffith theory线弹性断裂力学 linear elastic fracture mechanics, LEFM 弹塑性断裂力学 elastic-plastic fracture mecha-nics, EPFM 断裂 Fracture脆性断裂 brittle fracture解理断裂 cleavage fracture蠕变断裂 creep fracture延性断裂 ductile fracture晶间断裂 inter-granular fracture准解理断裂 quasi-cleavage fracture穿晶断裂 trans-granular fracture裂纹 Crack裂缝 Flaw缺陷 Defect割缝 Slit微裂纹 Microcrack折裂 Kink椭圆裂纹 elliptical crack深埋裂纹 embedded crack[钱]币状裂纹 penny-shape crack预制裂纹 Precrack短裂纹 short crack表面裂纹 surface crack裂纹钝化 crack blunting裂纹分叉 crack branching裂纹闭合 crack closure裂纹前缘 crack front裂纹嘴 crack mouth裂纹张开角 crack opening angle,COA裂纹张开位移 crack opening displacement, COD裂纹阻力 crack resistance裂纹面 crack surface裂纹尖端 crack tip裂尖张角 crack tip opening angle, CTOA裂尖张开位移 crack tip opening displacement, CTOD 裂尖奇异场 crack tip singularity Field裂纹扩展速率 crack growth rate稳定裂纹扩展 stable crack growth定常裂纹扩展 steady crack growth亚临界裂纹扩展 subcritical crack growth裂纹[扩展]减速 crack retardation止裂 crack arrest止裂韧度 arrest toughness断裂类型 fracture mode滑开型 sliding mode张开型 opening mode撕开型 tearing mode复合型 mixed mode撕裂 Tearing撕裂模量 tearing modulus断裂准则 fracture criterionJ积分 J-integralJ阻力曲线 J-resistance curve断裂韧度 fracture toughness应力强度因子 stress intensity factorHRR场 Hutchinson-Rice-Rosengren Field守恒积分 conservation integral有效应力张量 effective stress tensor应变能密度 strain energy density能量释放率 energy release rate内聚区 cohesive zone塑性区 plastic zone张拉区 stretched zone热影响区 heat affected zone, HAZ延脆转变温度 brittle-ductile transition temperature剪切带 shear band剪切唇 shear lip无损检测 non-destructive inspection双边缺口试件 double edge notched specimen, DEN specimen单边缺口试件 single edge notched specimen, SEN specimen三点弯曲试件 three point bending specimen, TPB specimen中心裂纹拉伸试件 center cracked tension specimen, CCT specimen 中心裂纹板试件 center cracked panel specimen, CCP specimen紧凑拉伸试件 compact tension specimen, CT specimen大范围屈服 large scale yielding小范围攻屈服 small scale yielding韦布尔分布 Weibull distribution帕里斯公式 paris formula空穴化 Cavitation应力腐蚀 stress corrosion概率风险判定 probabilistic risk assessment, PRA损伤力学 damage mechanics损伤 Damage连续介质损伤力学 continuum damage mechanics细观损伤力学 microscopic damage mechanics累积损伤 accumulated damage脆性损伤 brittle damage延性损伤 ductile damage宏观损伤 macroscopic damage细观损伤 microscopic damage微观损伤 microscopic damage损伤准则 damage criterion损伤演化方程 damage evolution equation损伤软化 damage softening损伤强化 damage strengthening损伤张量 damage tensor损伤阈值 damage threshold损伤变量 damage variable损伤矢量 damage vector损伤区 damage zone疲劳 Fatigue低周疲劳 low cycle fatigue应力疲劳 stress fatigue随机疲劳 random fatigue蠕变疲劳 creep fatigue腐蚀疲劳 corrosion fatigue疲劳损伤 fatigue damage疲劳失效 fatigue failure疲劳断裂 fatigue fracture疲劳裂纹 fatigue crack疲劳寿命 fatigue life疲劳破坏 fatigue rupture疲劳强度 fatigue strength疲劳辉纹 fatigue striations疲劳阈值 fatigue threshold交变载荷 alternating load交变应力 alternating stress应力幅值 stress amplitude应变疲劳 strain fatigue应力循环 stress cycle应力比 stress ratio安全寿命 safe life过载效应 overloading effect循环硬化 cyclic hardening循环软化 cyclic softening环境效应 environmental effect裂纹片 crack gage裂纹扩展 crack growth, crack Propagation 裂纹萌生 crack initiation循环比 cycle ratio实验应力分析 experimental stress Analysis 工作[应变]片 active[strain] gage基底材料 backing material应力计 stress gage零[点]飘移 zero shift, zero drift应变测量 strain measurement应变计 strain gage应变指示器 strain indicator应变花 strain rosette应变灵敏度 strain sensitivity机械式应变仪 mechanical strain gage直角应变花 rectangular rosette引伸仪 Extensometer应变遥测 telemetering of strain横向灵敏系数 transverse gage factor横向灵敏度 transverse sensitivity焊接式应变计 weldable strain gage平衡电桥 balanced bridge粘贴式应变计 bonded strain gage粘贴箔式应变计 bonded foiled gage粘贴丝式应变计 bonded wire gage桥路平衡 bridge balancing电容应变计 capacitance strain gage补偿片 compensation technique补偿技术 compensation technique基准电桥 reference bridge电阻应变计 resistance strain gage温度自补偿应变计 self-temperature compensating gage 半导体应变计 semiconductor strain Gage集流器 slip ring应变放大镜 strain amplifier疲劳寿命计 fatigue life gage电感应变计 inductance [strain] gage光[测]力学 Photomechanics光弹性 Photoelasticity光塑性 Photoplasticity杨氏条纹 Young fringe双折射效应 birefrigent effect等位移线 contour of equal Displacement暗条纹 dark fringe条纹倍增 fringe multiplication干涉条纹 interference fringe等差线 Isochromatic等倾线 Isoclinic等和线 isopachic应力光学定律 stress- optic law主应力迹线 Isostatic亮条纹 light fringe光程差 optical path difference热光弹性 photo-thermo -elasticity光弹性贴片法 photoelastic coating Method光弹性夹片法 photoelastic sandwich Method动态光弹性 dynamic photo-elasticity空间滤波 spatial filtering空间频率 spatial frequency起偏镜 Polarizer反射式光弹性仪 reflection polariscope残余双折射效应 residual birefringent Effect应变条纹值 strain fringe value应变光学灵敏度 strain-optic sensitivity应力冻结效应 stress freezing effect应力条纹值 stress fringe value应力光图 stress-optic pattern暂时双折射效应 temporary birefringent Effect脉冲全息法 pulsed holography透射式光弹性仪 transmission polariscope实时全息干涉法 real-time holographic interferometry网格法 grid method全息光弹性法 holo-photoelasticity全息图 Hologram全息照相 Holograph全息干涉法 holographic interferometry全息云纹法 holographic moire technique全息术 Holography全场分析法 whole-field analysis散斑干涉法 speckle interferometry散斑 Speckle错位散斑干涉法 speckle-shearing interferometry, shearography 散斑图 Specklegram白光散斑法 white-light speckle method云纹干涉法 moire interferometry[叠栅]云纹 moire fringe[叠栅]云纹法 moire method云纹图 moire pattern离面云纹法 off-plane moire method参考栅 reference grating试件栅 specimen grating分析栅 analyzer grating面内云纹法 in-plane moire method脆性涂层法 brittle-coating method条带法 strip coating method坐标变换 transformation of Coordinates计算结构力学 computational structural mechanics加权残量法 weighted residual method有限差分法 finite difference method有限[单]元法 finite element method配点法 point collocation里茨法 Ritz method广义变分原理 generalized variational Principle 最小二乘法 least square method胡[海昌]一鹫津原理 Hu-Washizu principle赫林格-赖斯纳原理 Hellinger-Reissner Principle 修正变分原理 modified variational Principle约束变分原理 constrained variational Principle 混合法 mixed method杂交法 hybrid method边界解法 boundary solution method有限条法 finite strip method半解析法 semi-analytical method协调元 conforming element非协调元 non-conforming element混合元 mixed element杂交元 hybrid element边界元 boundary element强迫边界条件 forced boundary condition自然边界条件 natural boundary condition离散化 Discretization离散系统 discrete system连续问题 continuous problem广义位移 generalized displacement广义载荷 generalized load广义应变 generalized strain广义应力 generalized stress界面变量 interface variable节点 node, nodal point[单]元 Element角节点 corner node边节点 mid-side node内节点 internal node无节点变量 nodeless variable杆元 bar element桁架杆元 truss element梁元 beam element二维元 two-dimensional element一维元 one-dimensional element三维元 three-dimensional element轴对称元 axisymmetric element板元 plate element壳元 shell element厚板元 thick plate element三角形元 triangular element四边形元 quadrilateral element四面体元 tetrahedral element曲线元 curved element二次元 quadratic element线性元 linear element三次元 cubic element四次元 quartic element等参[数]元 isoparametric element超参数元 super-parametric element亚参数元 sub-parametric element节点数可变元 variable-number-node element拉格朗日元 Lagrange element拉格朗日族 Lagrange family巧凑边点元 serendipity element巧凑边点族 serendipity family无限元 infinite element单元分析 element analysis单元特性 element characteristics刚度矩阵 stiffness matrix几何矩阵 geometric matrix等效节点力 equivalent nodal force节点位移 nodal displacement节点载荷 nodal load位移矢量 displacement vector载荷矢量 load vector质量矩阵 mass matrix集总质量矩阵 lumped mass matrix相容质量矩阵 consistent mass matrix阻尼矩阵 damping matrix瑞利阻尼 Rayleigh damping刚度矩阵的组集 assembly of stiffness Matrices 载荷矢量的组集 consistent mass matrix质量矩阵的组集 assembly of mass matrices单元的组集 assembly of elements局部坐标系 local coordinate system局部坐标 local coordinate面积坐标 area coordinates体积坐标 volume coordinates曲线坐标 curvilinear coordinates静凝聚 static condensation合同变换 contragradient transformation形状函数 shape function试探函数 trial function检验函数 test function权函数 weight function样条函数 spline function代用函数 substitute function降阶积分 reduced integration零能模式 zero-energy modeP收敛 p-convergenceH收敛 h-convergence掺混插值 blended interpolation等参数映射 isoparametric mapping双线性插值 bilinear interpolation小块检验 patch test非协调模式 incompatible mode节点号 node number单元号 element number带宽 band width带状矩阵 banded matrix变带状矩阵 profile matrix带宽最小化 minimization of band width波前法 frontal method子空间迭代法 subspace iteration method 行列式搜索法 determinant search method 逐步法 step-by-step method纽马克法 Newmark威尔逊法 Wilson拟牛顿法 quasi-Newton method牛顿-拉弗森法 Newton-Raphson method增量法 incremental method初应变 initial strain初应力 initial stress切线刚度矩阵 tangent stiffness matrix割线刚度矩阵 secant stiffness matrix模态叠加法 mode superposition method平衡迭代 equilibrium iteration子结构 Substructure子结构法 substructure technique超单元 super-element网格生成 mesh generation结构分析程序 structural analysis program 前处理 pre-processing后处理 post-processing网格细化 mesh refinement应力光顺 stress smoothing 组合结构 composite structure。
结构力学第三章习题及答案

静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。
解:首先分析几何组成:AB 为基本部分,EC 为附属部分。
画出层叠图,如图(b )所示。
按先属附后基本的原则计算各支反力(c)图。
之後,逐段作出梁的弯矩图和剪力图。
36.67KN15KN •m 20KNM 图(单位:KN/m )13.323.313.33F Q 图(单位:KN )3—3 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =48kN (→) M A =60 KN •m (右侧受拉) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—7 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =20kN (←) F AY =38kN(↑) F BY =62kN(↑) (2)逐杆绘M 图BCM 图(单位:KN/m ) F Q 图(单位:KN )3030F AX F N图(单位:60)20)(3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—9 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =0.75qL (←) F AY =-0.25qL( ) F BY =0.25qL(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—11试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F BX =40KN (←) F AY =30KN (↑) F BY =50kN(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)C(a )qBY 23—17 试求图示抛物线三铰拱的支座反力,并求截面D 和E 的内力。
清华大学2001年结构力学试卷
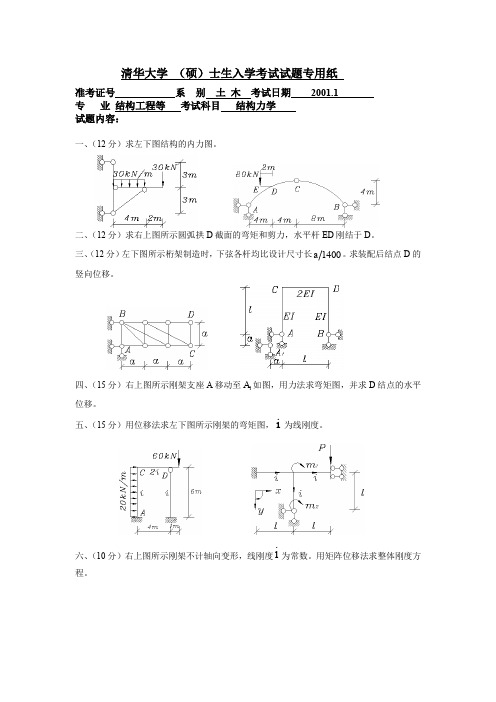
附录 固端弯矩表
m
F AB
ql 2 12
, mBFA
ql 2 12
不计轴向变形的弯曲单元的单元刚度 矩阵为
12i l 2 6i l 12i l 2 6i l4i6i l Nhomakorabea2i
对
12i l 2
称
4i
清华大学 (硕)士生入学考试试题专用纸
准考证号
系 别 土 木 考试日期
专 业 结构工程等 考试科目 结构力学
试题内容:
2001.1
一、(12 分)求左下图结构的内力图。
二、(12 分)求右上图所示圆弧拱 D 截面的弯矩和剪力,水平杆 ED 刚结于 D。
三、(12 分)左下图所示桁架制造时,下弦各杆均比设计尺寸长 a 1400 。求装配后结点 D 的
竖向位移。
四、(15 分)右上图所示刚架支座 A 移动至 A1 如图,用力法求弯矩图,并求 D 结点的水平
位移。
五、(15 分)用位移法求左下图所示刚架的弯矩图, i 为线刚度。
i 六、(10 分)右上图所示刚架不计轴向变形,线刚度 为常数。用矩阵位移法求整体刚度方
程。
七、(12 分)画出主梁反力 RB 、弯矩 M K , M B 、剪力 QB右 的影响线。
八、(12 分)左下图所示梁不计分布质量,集中质量为,简谐荷载 Pt F sin t ,不计阻
尼。
(1)求质体 m 的运动方程;
(2)若 m 0.5 t(吨),F 10kN, 1.25 ,( 为自振频率),EI 1.8 105 kN m2 , a 1m ,求 B 点振幅并画出最大动力弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Graphical Construction (1)
Ya 168kN
Find Reactions
Yb 392kN
Find shear forces at key points
Va 168kN
Vb,left 232kN Vb,right 160kN
33
Graphical Construction (2)
8
Sign Convention (1)
Over the years, structural engineers have adopted almost universally a sign convention for internal forces in beams to facilitate graphical construction.
wL/2
wL/2
V ( x) wL / 2 wx
x wx( L x) M ( x) ( wL / 2) x ( wx) 2 2
15
Internal Force Diagram (1)
Positive shear drawn above the axis.
Moment drawn on the tension side.
F V S ( x ) Const
— Shear diagram consists of horizontal lines
q(x)
F M Linear S ( x ) Const
F V S ( x) 0
P
F V S ( x) 0
V
M
30
Interpretations (3)
② q( x) Const
13
Example (2) Determine V&M at
A 3m YA=2kN
1 1 5m
5kN 2 2
B
sections 1-1 and 2-2
Sol.: (1)Shear 1-1Sec.: 2-2Sec.: (2) M
YB =3kN
(Left) F RA V S 1 Y A 2kN 1
24
25
Differential Equations
q(x)
26
Integral Equations (1)
q(x) q(x)
27
Integral Equations (2)
28
Interpretations (1)
q(x)
q (x )
q(x)
29
Interpretations (2) ① q ( x) 0
21
Free-Body of Small Beam Piece (1)
q(x)
q(x) c
M(x) V(x)
M(x)+dM(x)
V(x)+dV(x)
dx
Y 0 :
F VS ( x ) dF V VS ( x ) [F S ( x )] q ( x )dx 0
dF V S ( x) q( x ) dx
M C ,left 5kNm M C ,right 2.5kNm
5
M (kNm)
38
Superposition
q=5kN/m C A 7.5kNm 1m B 2.5m
7.5 2.5
5
M (kNm)
A
7.5kNm 1m B
C
7.5
2.5m
M1 (kNm)
15 2.5
A
q=5kN/m C 1m B 2.5m
q(x)
F Linear V S ( x ) Const
— Shear diagram consists of inclined straight lines
F M Parabola S ( x ) Const
( q(x)q
q(x)+
)
V
M
31
Procedures for Graphical Construction (1)
12
Section Method for Internal Forces
q0a l Vc
Mc YA
1 qa Vc YA 0 a 2 l
1 q0 a a M c YA a a 2 l 3
Shear——Algebraic sum of vertical force components acting to the left/right of the considered section (Left-Upward; Right-Downward) Moment——Algebraic sum of couples about the considered section produced by loads acting to the left/right (concave upward-positive, convex upward-negative)
Chapter 3 Analysis of Statically Determinate Beam and Frame Structures
1
Beam Structures
Beams are usually long slender members which resist large lateral load relative to their owe weight.
q0a l Vc
Mc YA Mc a Vc l
q0
YB
Y 0
Vc Y A
1 q0 a a 0 2 l
2
q 0 l 3a Vc 6l
2
M
c
0
1 q0 a a M c YA a a 0 2 l 3
q 0 al 2 3a 2 Mc 6l
16
Internal Force Diagram (2)
17
Concentrated Loads (1)
For x a : Pa V ( x) L Pb M ( x) x P( x a) L
18
Concentrated Loads (2)
“Jump” at each concent. load
RC: 3~5 times larger Steel: 8~10 times larger
The cross-section dimensions must be << than the length for the beam theory idealization to apply h < L/10
V (kN)
37
Example (3)
Construct V&M diagrams for the structure Solution:
(1) Reactions:
q=5kN/m C A 7.5kNm 1m B 2.5m
5
+
VA 5kN
M A 7.5kNm
7.5
V (kN)
2.5
(2) Moments at key points:
M2 (kNm)
39
Principle of Superposition
2
Beam Model
Simply-supported
Continuous
3
Simply-Supported Beam
4
Continuous Beam
5
Cantilever Beam
6
Beam Type
7
Internal Forces in Beams
Internal forces must be known to design correctly the cross section. The beam is a “shear-bending” member,
q0 l 2 (Resultant) q0
A a YA c l B
YB
q0l 2l M A 0 : YB l 2 3 0 q0l l M B 0 : YA l 2 3 0
q0l YB 3 q0l YA 6
11
Example (1)
(2)FBD: Segment AC will be considered since it yields the simplest solution
Construct V&M diagrams for the structure Solution:
(1) Reactions:
q=5kN/m C A 7.5kNm 1m B 2.5m
VA 5kN
M A 7.5kNm
5 +
(2) Shear forces at key points:
VC 5kN
Va 168kN
Vb,left 232kN
Vb,right 160kN
Ya 168kN
168
Yb 392kN
160
V(kN)
4.2m 232
34
Graphical Construction (3)
d
Hale Waihona Puke Ya 168kNYb 392kN
Find bending moments at key points
Ma 0
M b 320kNm
M c 0 M d 352.8kNm
35
Graphical Construction (3)
Ma 0
d
M b 320kNm
Yb 392kN
