15级高一数学二次函数在闭区间上的最值练习

合集下载

高一数学二次函数在闭区间上的最值

k
2
f(x)max=f(k)=k2-2k-3
5 10 15
f(x)min=f(k+2)=（k+2)2-2(k+2)-3 =k2+2k-3
4
6
8
4
x=1
2
k
10
k+2
当 k ＜1 ＜ k+2 时即-1 ＜k ＜1时 f(x)min=f(1)=- 4 当f(k)>f(k+2)时，
5 10 15
8 2
2 2
10 8
解：由图知，y=f(x)在[ 2，4 ]上为增函数故x=4时有最大值f(4)=5 x=2时有最小值f(2)=-3
10 5
6
4
2
x=1 2 4
5
2
4
6
例1、已知函数f(x)= x2 –2x – 3.
（1）若x∈[ –2，0]，求函数f(x)的最值；（2）若x∈[ 2，4]，求函数f(x)的最值；
4
10
8
6
4
当k ≥1
x=1 k k+2
5
时
2
f(x) max=f(k+2)=k2+2k-3
10 15
2
f(x) min=f(k)=k2-2k-3
4
6
8
10
例2:
6
6 2 求函数y=x -2x-3在x∈[k,k+2]时的最值
6
6
4
4
4
4
x=1
2
x=1 k+2
5
2
x=1
2
2
x=1
15
k
10

高一数学二次函数在闭区间上的最值

3 4
x
评注：例1属于“轴定区间变”的问题，看作动区间沿x轴移动的过程中，函数最值的变化，即动区间在定轴的左、右两侧及包含定轴的变化，要注意开口方向及端点情况。
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间 [–1，2]上的最值.
y
–1 0 1
2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间 [–1，2]上的最值.
函数f(x)的最值；
（5）若 x∈[t，t+2]时，求函数f(x)的最值.
t t +2 –1 0 1 2
3 4
x
例1、已知函数f(x)= x2 –2x – 3.
（1）若x∈[–2，0],求函数f(x)的最值；（2）若x∈[ 2，4]，求函数f(x)的最值；
1 5 （3）若x∈[ , ]，求函数f(x)的最值； 2 2 y 1 3 （4）若x∈[ , ]，求 2 2
二次函数在闭区间上的最值
复习：求给定区间x∈[m，n]的二次函数 y=f(x)=ax2+bx+c （a≠0）最值步骤（1）配方。（2）确定对称轴；（3）画图象。（4）讨论对称轴与区间的位置关系。（5）根据图象确定函数最值。（看所给区间内的最高点和最低点）
例1、已知函数f(x)= x2–2x –3. （1）若x∈[ –2，0 ], 求函数f(x)的最值；
y
–1
0
1
2
x
例3、已知函数f(x)=x2+ax+b，x∈[0,1]，试确定a、b,使f(x)的值域是[0,1].
y
–1
0
1
2
x
例3、已知函数f(x)=x2+ax+b，x∈[0,1]，试确定a、b,使f(x)的值域是[0,1].

二次函数在闭区间上的最值(详解)

二次函数在闭区间上的最值(详解)二次函数在闭区间上的最值一、知识要点：一元二次函数在闭区间上的最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论。

一般分为对称轴在区间的左边，中间，右边三种情况。

设函数f(x)=ax^2+bx+c(a≠0)，求f(x)在x∈[m,n]上的最大值与最小值。

分析：将f(x)配方，得顶点为(-b/2a,f(-b/2a))，对称轴为x=-b/2a。

当a>0时，它的图像是开口向上的抛物线，数形结合可得在[m,n]上f(x)的最值：1）当-b/2a∈[m,n]时，f(x)的最小值是f(-b/2a)，f(x)的最大值是max{f(m),f(n)}。

2）当-b/2a∉[m,n]时，若-b/2a<m，由f(x)在[m,n]上是增函数则f(x)的最小值是f(m)，最大值是max{f(-b/2a),f(n)}；若n<-b/2a，由f(x)在[m,n]上是减函数则f(x)的最大值是f(m)，最小值是min{f(-b/2a),f(n)}。

当a<0时，可类比得结论。

二、例题分析归类：一）、正向型是指已知二次函数和定义域区间，求其最值。

对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。

此类问题包括以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1.轴定区间定二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是“定二次函数在定区间上的最值”。

例1.函数y=-x^2+4x-2在区间[0,3]上的最大值是6，最小值是-2.练.已知函数f(x)=x^2+x+1(x≤3)，求函数f(x)的最值。

2、轴定区间变二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是“定函数在动区间上的最值”。

例2.如果函数f(x)=-x^2+2x+t在区间[t+1,t+2]上，求f(x)的最值。

例3.已知f(x)=-x^2-4x+3，当x∈[t,t+1](t∈R)时，求f(x)的最值。

15级高一数学二次函数在闭区间上的最值练习

3．已知函数 y x 2 2x 3 在闭区间[0, m] 上有最大值 3，最小值 2，则 m 的取值范围是
(A) [1,)
(B) [0,2]
(C) [1,2]
4．若函数 f (x) (a 2)x2 2(a 2)x 4 0对一切x R 恒成立，则 a 的取值范围（
（D） 1 , 3 4
(
2a
1 )x
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决，机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配，料置而试时且卷，可调需保控要障试在各验最类；大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安，与全要过，加度并强工且看作尽护下可关都能于可地管以缩路正小高常故中工障资作高料；中试对资卷于料连继试接电卷管保破口护坏处进范理行围高整，中核或资对者料定对试值某卷，些弯审异扁核常度与高固校中定对资盒图料位纸试置，卷.编保工写护况复层进杂防行设腐自备跨动与接处装地理置线，高弯尤中曲其资半要料径避试标免卷高错调等误试，高方要中案求资，技料编术试写5交、卷重底电保要。气护设管设装备线备置4高敷、调动中设电试作资技气高，料术课中并3试中、件资且卷包管中料拒试含路调试绝验线敷试卷动方槽设技作案、技术，以管术来及架避系等免统多不启项必动方要方式高案，中；为资对解料整决试套高卷启中突动语然过文停程电机中气。高课因中件此资中，料管电试壁力卷薄高电、中气接资设口料备不试进严卷行等保调问护试题装工，置作合调并理试且利技进用术行管，过线要关敷求运设电行技力高术保中。护资线装料缆置试敷做卷设到技原准术则确指：灵导在活。分。对线对于盒于调处差试，动过当保程不护中同装高电置中压高资回中料路资试交料卷叉试技时卷术，调问应试题采技，用术作金是为属指调隔发试板电人进机员行一，隔变需开压要处器在理组事；在前同发掌一生握线内图槽部纸内故资，障料强时、电，设回需备路要制须进造同行厂时外家切部出断电具习源高题高中电中资源资料，料试线试卷缆卷试敷切验设除报完从告毕而与，采相要用关进高技行中术检资资查料料和试，检卷并测主且处要了理保解。护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

二次函数在闭区间上的最值问题

如图1所示。函数的最大值为，最小值为。
图1
同步练习.已知，求函数的最值。
解：由已知，可得，即函数是定义在区间上的二次函数。将二次函数配方得，其对称轴方程，顶点坐标，且图象开口向上。显然其顶点横坐标不在区间内，如图2所示。函数的最小值为，最大值为。
图2
2、轴定区间变
二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是“定函数在动区间上的最值”。
1. 轴定区间定
二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是“定二次函数在定区间上的最值”。
例1.函数在区间[0，3]上的最大值是_________，最小值是_______。
解：函数是定义在区间[0，3]上的二次函数，其对称轴方程是，顶点坐标为（2，2），且其图象开口向下，显然其顶点横坐标在［0，3］上，
对二次函数的区间最值结合函数图象总结如下：
当时
当时
3、轴变区间定
二次函数随着参数的变化而变化，即其图象是运动的，但定义域区间是固定的，我们称这种情况是“动二次函数在定区间上的最值”。
例4.已知，且，求函数的最值。
解：由已知有，于是函数是定义在区间上的二次函数，将配方得：
二次函数的对称轴方程是顶点坐标为，图象开口向上
三、巩固训练
1．函数在上的最小值和最大值分别是（） 1 ,3 ,3（C） ,3（D） , 3
2．函数在区间上的最小值是（）
2
3．函数的最值为（）
最大值为8，最小值为0 不存在最小值，最大值为8
（C）最小值为0,不存在最大值不存在最小值，也不存在最大值
综上讨论，
图8
例3.已知，当时，求的最大值．

二次函数在闭区间上的最值问题练习题

二次函数在闭区间上的最值问题练习题11．函数y 12++=x x 在]1,1[-上的最小值和最大值分别是（）A 、1 ,3B 、43 ,3 C 、21- ,3 D 、41-, 3 2．函数242-+-=x x y 在区间]4,1[ 上的最小值是（）A 、7-B 、4-C 、2-D 、23．函数5482+-=x x y 的最值为（） A 、最大值为8，最小值为0 B 、不存在最小值，最大值为8C 、最小值为0, 不存在最大值D 、不存在最小值，也不存在最大值4．若函数]4,0[,422∈+--=x x x y 的取值范围是______________________5．已知函数f x ax a x a ()()()[]=+---22130322≠在区间，上的最大值是1，则实数a 的值为 6．如果实数y x ,满足122=+y x ，那么)1)(1(xy xy +-有（）A 、最大值为 1 , 最小值为21 B 、无最大值，最小值为43 C 、最大值为 1, 无最小值 D 、最大值为1，最小值为43 7．函数322+-=x x y 在区间],0[m 上有最大值3，最小值2，则m 的范围是（）A 、),1[+∞B 、]2,0[C 、]2,1[D 、]2,(-∞8、若12,0,0=+≥≥y x y x ，那么232y x +的最小值为__________________9．设21,,x x R m ∈是方程01222=-+-m mx x 的两个实根，则2221x x +的最小值_____10．设),](1,[,44)(2R t t t x x x x f ∈+∈--=求函数)(x f 的最小值)(t g 的解析式11．已知)(x f 22aax x +-=，在区间]1,0[上的最大值为)(a g ，求)(a g 的最小值。

12.设为实数，函数.(1)若，求的取值范围；(2)求的最小值；(3)设函数，直接写出．．．．(不需给出演算步骤)不等式的解集.13、函数()()2220f x ax ax b a =-++≠在[]2,3上有最大值5和最小值2，求,a b 的值。

二次函数求最值(动轴定区间、动区间定轴)

4
4
4
2 x=1
x=1
2
x=1
2
k+2
k k+2
k k+2
k 15
5
10
5
15
5 10
5
15
10
10
5
5
2
2
2
6
4
2 x=1
15
k 10
k+2 5
2
4
4
4
4
6
评注6：例1属于6“轴定区间动”的问题，看6 作动区
间沿8x轴移动的过8 程中，函数8 最值的变化，8 即动区
间在定轴的左、右两侧及包10含定轴的变化，要注
y 解： ⑴当
即a≥ 2时
y的最小值为f(-1)
O -1 1 x
=4-a
例3：若x∈
，求函数
•
y =x2+ax+3的最小值：
(2)当 1 < a 1
2
y
即-2≤ a<2时
y的最小值为
O
f( )=
-1 1 x
例2：若x∈
•
，求函数
y =x2+ax+3的最小值：
y
O -1 1
(3)当
即a<-2时
解：画出函数在定义域内的图像如图 8
对称轴为直线x=1
6
由图知，y=f(x)在[ 2，4 ]上为增函数
4
故x=4时有最大值f(4)=5
x=2时有最小值f(2)=-3
10
5
2 x=1 2
45
2
4
y = x2 2∙x 3
y = x2 2∙x 3

高一数学《二次函数在闭区间上的最值》练习题

第1课二次函数在闭区间上的最值之袁州冬雪创作一元二次函数的区间最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论.一般分为：对称轴在区间的左边，中间，右边三种情况. 设)0()(2≠++=a c bx ax x f ，求)(x f 在][n m x ，∈上的最大值与最小值. 分析：将)(x f 配方，得顶点为⎪⎪⎭⎫ ⎝⎛--a b ac a b 4422，、对称轴为a bx 2-= 当0>a 时，它的图象是启齿向上的抛物线，数形连系可得在[m ，n]上)(x f 的最值：（1）当[]n m a b ，∈-2时，)(x f 的最小值是a bac a b f 4422-=⎪⎭⎫ ⎝⎛-，)(x f 的最大值是)()(n f m f 、中的较大者.（2）当),(2m ab-∞∈-时，)(x f 在[]n m ，上是增函数则)(x f 的最小值是)(m f ，最大值是)(n f（3）当),(2+∞∈-n ab时，)(x f 在[]n m ，上是减函数则)(x f 的最大值是)(m f ，最小值是)(n f当0<a 时，可类比得结论.（一）、正向型是指已知二次函数和定义域区间，求其最值.对称轴与定义域区间的相互位置关系的讨论往往成为处理这类问题的关键.此类问题包含以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变.1. 轴定区间定二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是“定二次函数在定区间上的最值”.242-+-=x x y 在区间[0，3]上的最大值是_________，最小值是典型例题基础过关_______.操练. 已知x x 322≤，求函数1)(2++=x x x f 的最值.2、轴定区间变二次函数是确定的，但它的定义域区间是随参数而变更的，我们称这种情况是“定函数在动区间上的最值”.例2. 如果函数f x x ()()=-+112定义在区间[]t t ，+1上，求f x ()的最小值.例3. 已知32)(2+-=x x x f ，当]1,[+∈t t x ，()R t ∈时，求)(x f 的最大值．观察前两题的解法，为什么最值有时候分两种情况讨论，而有时候又分三种情况讨论呢？这些问题其实仔细思考就很容易处理.不难观察：二次函数在闭区间上的的最值总是在闭区间的端点或二次函数的顶点取到.第一个例题中，这个二次函数是启齿向上的，在闭区间上，它的最小值在区间的两个端点或二次函数的顶点都有能够取到，有三种能够，所以分三种情况讨论；而它的最大值不成能是二次函数的顶点，只能够是闭区间的两个端点，哪一个端点间隔对称轴远就在哪一个端点取到，当然也就根据区间中点与左右端点的远近分两种情况讨论.根据这个懂得，不难诠释第二个例题为什么这样讨论.对二次函数的区间最值连系函数图象总结如下：当a >0时⎪⎪⎩⎪⎪⎨⎧+<-+≥-=))((212)())((212)()(21max如图如图，，n m a b n f n m a b m f x f ⎪⎪⎪⎩⎪⎪⎪⎨⎧<-≤-≤->-=)(2)()(2)2()(2)()(543min如图如图如图，，，m a b m f n a b m a b f n a b n f x f当0<a 时⎪⎪⎪⎩⎪⎪⎪⎨⎧<-≤-≤->-=)(2)()(2)2()(2)()(876max如图如图如图，，，m a b m f n a b m a b f n a b n f x f f x f m b a m n f n b a m n ()()()()()()()min =-≥+-<+⎧⎨⎪⎪⎩⎪⎪，，如图如图212212910 3、轴变区间定二次函数随着参数的变更而变更，即其图象是运动的，但定义域区间是固定的，我们称这种情况是“动二次函数在定区间上的最值”.例4.. 例5.(1)求2f (x )x 2ax 1=++在区间[-1,2]上的最大值.(2) 求函数)(a x x y --=在]1,1[-∈x 上的最大值.4. 轴变区间变二次函数是含参数的函数，而定义域区间也是变更的，我们称这种情况是“动二次函数在动区间上的最值”. 例6. 已知)(42a x a y -=()0>a ，求()223y x u +-=的最小值.（二）、逆向型是指已知二次函数在某区间上的最值，求函数或区间中参数的取值.例7. 已知函数2()21f x ax ax =++在区间[3,2]-上的最大值为4，求实数a 的值.2()2x f x x =-+在区间[,]m n 上的最小值是3m 最大值是3n ，求m ，n 的值.评注：解法操纵闭区间上的最值不超出整个定义域上的最值，缩小了m ，n 的取值范围，避开了繁难的分类讨论，解题过程简洁、了然.2f (x )ax (2a 1)x 1=+-+在区间⎥⎦⎤⎢⎣⎡-2,23上的最大值为3，求实数a 的值.解后反思：若函数图象的启齿方向、对称轴均不确定，且动区间所含参数与确定函数的参数一致，可采取先斩后奏的方法，操纵二次函数在闭区间上的最值只能够在区间端点、顶点处取得，无妨令之为最值，验证参数的资格，停止取舍，从而避开繁难的分类讨论，使解题过程简洁、了然.1．函数12++=x x 在]1,1[-上的最小值和最大值分别是（）)(A 1,3 )(B 43 ,3 （C ）21- ,3 （D ）41-, 32．函数242-+-=x x y 在区间]4,1[ 上的最小值是（）)(A 7-)(B 4-)(C 2-)(D 23．函数5482+-=x x y 的最值为（）)(A 最大值为8，最小值为0)(B 不存在最小值，最大值为8（C ）最小值为0, 不存在最大值 )(D 不存在最小值，也不存在最大值4．若函数]4,0[,422∈+--=x x x y 的取值范围是______________________5．已知函数f x ax a x a ()()()[]=+---22130322≠在区间，上的最大值是1，则实数a 的值为6．如果实数y x ,知足122=+y x ，那末)1)(1(xy xy +-有（）(A)最大值为 1 , 最小值为21 (B)无最大值，最小值为43（C ）最大值为 1, 无最小值 (D)最大值为1，最小值为43巩固训练7．已知函数322+-=x x y 在闭区间],0[m 上有最大值3，最小值2，则(A) ),1[+∞ (B) ]2,0[ (C) ]2,1[ (D) ]2,(-∞ 8．若12,0,0=+≥≥y x y x ，那末232y x +的最小值为__________________ 9．设21,,x x R m ∈是方程01222=-+-m mx x 的两个实根，则2221x x +的最小值______ 10．设),](1,[,44)(2R t t t x x x x f ∈+∈--=求函数)(x f 的最小值)(t g 的解析式.11．已知)(x f 22a ax x +-=，在区间]1,0[上的最大值为)(a g ，求)(a g 的最小值.a 为实数，函数2()2()||f x x x a x a =+--.(1)若(0)1f ≥，求a 的取值范围；(2)求()f x 的最小值；(3)设函数()(),(,)h x f x x a =∈+∞，直接写出不等式()1h x ≥的解集(不需给出演算步调).第2课函数的定义域和值域一、定义域：1．函数的定义域就是使函数式的集合. 2．罕见的三种题型确定定义域： ①已知函数的解析式，就是.②复合函数)]([x g f 的有关定义域，就要包管内函数)(x g 的域是外函数)(x f 的域.③实际应用问题的定义域，就是要使得有意义的自变量的取值集合.二、值域： 1．函数)(x f y =中，与自变量x 的值的集合.2．求函数值域的常常使用方法：①观察法；②配方法；③反函数法；④不等式法；⑤单调性法； ⑥数形法；⑦辨别式法；⑧有界性法；⑨换元法例如：①221x y +=，可采取法；②2312++=x x y )32(-≠x ，可采取法或法；③c x bf x f a y ++=)()]([2，可采取法；④x x y --=1，可采取法；⑤21x x y --=，可采取法；⑥xxy cos 2sin -=可采取法等.基础过关典型例题例1. 求下列函数的定义域：（1）xx x y -+=||)1(0;(2)232531x x y -+-=;(3)1·1-+=x x y .变式训练1：求下列函数的定义域：（1）02)1(12)2lg(-+-+-=x x x x y ; (2)02)45()34lg(-++=x x x y ;2. 设函数)(x f y =的定义域为［0，1］，求下列函数的定义域.（1）)3(x f y =; （2）)1(xf y =;（3）)31()31(-++=x f x f y ;（4）)()(a x f a x f y -++=.变式训练2：若函数)(x f 的定义域是［0，1］，则)()(a x f a x f -⋅+（0＜a ＜21）的定义域是（） A.∅B.]1,[a a - C.]1,[a a +- D.［0，1］例3. 求下列函数的值域：（1）;122+--=x x xx y (2) x x y 21--=;(3)1e 1e +-=x x y .变式训练3：求下列函数的值域：（1）521+-=x xy ;(2)21x x y -⋅=.例4．若函数a x x x f +-=221)(的定义域和值域均为［1，b ］（b ＞1），求a 、b 的值.变式训练4：已知函数624)(2++-=a ax x x f (x∈R).（1）求函数的值域为［0，+∞)时的a 的值；（2）若函数的值均为非负值，求函数32)(+-=a a a f 的值域.第3课指数、对数和幂函数1．指数：(1) 规定：①a0＝(a≠0)；②a -p ＝；③(0,mn mn a a a m=>.(2) 运算性质：①a a a a s r s r ,0(>=⋅+(a>0,r 、∈s R)②a a a s r s r ,0()(>=⋅(a>0, r 、∈s R)③>>⋅=⋅b a b a b a r r r ,0()( 2．指数函数：①定义：函数称为指数函数，② 性质： 1) 函数的定义域为； 2) 函数的值域为； 3）恒过定点，4) 当________时函数为减函数，当_______时为增函数.③函数图象：3．对数：(1) 定义：如果Na b =)1,0(≠>a a 且，那末，其中a 称为对数的底，N 称为真数.(2) 基赋性质：①01log =a ； ②1log =a a ； ③Na Na=log．④m ab nlog = 换底公式log a N ＝4．对数函数： ①定义：函数称为对数函数，② 性质 1) 函数的定义域为； 2) 函数的值域为；3）恒过定点，4) 当______时，函数为减函数，当______时为增函数； 5) 函数x y a log =与函数)1,0(≠>=a a a y x 且互为反函数.③函数图象：5．幂函数：①定义：我们把形如的函数称为幂函数，其中是自变基础过关量，是常数；② 性质：（1）幂函数的图象都过点；（2）任何幂函数都不过象限；（3）当0α>时，幂函数在[0,)+∞上；当0α<时，幂函数在(0,)+∞上；（4）当2,2α=-时，幂函数是；当11,1,3,3α=-时，幂函数是．③函数图象：例 1.已知a=91,b=9. 求：（1）;315383327a a a a⋅÷-- （2）111)(---+ab b a . 变式训练1：化简下列各式（其中各字母均为正数）: （1）;)(65312121132b a ba b a ⋅⋅⋅⋅-- （2）.)4()3(6521332121231----⋅÷-⋅⋅b a b a b a例2.函数f(x)=x2-bx+c 知足f(1+x)=f(1-x)且f(0)=3,则f(bx)与f(cx)的大小关系是（）变式训练2：已知实数a 、b 知足等式11()()23a b =，下列五个关系式中，不成能成立的关系式有（）个①0＜b ＜a;②a＜b ＜0;③0＜a ＜b;④b＜a ＜0;⑤a=b.例3.求下列函数的定义域、值域及其单调区间：（1）f(x)=3452+-x x ;（2）g(x)=-11()4()542x x ++.变式训练3：求下列函数的单调递增区间：（1）y=(226)21x x -+;(2)y=262--x x .例4．设a ＞0,f(x)=e ex xaa +是R 上的偶函数.（1）求a 的值；（2）求证：f(x)在（0，+∞）上是增函数.变式训练4：已知定义在R 上的奇函数f(x)有最小正周期2即(2)()f x f x +=，且当x∈(0,1)时，f(x)=241xx +. （1）求f （x)在［-1，1］上的解析式；（2）证明：f(x)在（0，1）上是减函数. 例1计算：（1）23log (23)+-（2）2(lg 2)2+lg 2·lg5+2(lg 2)lg 21-+;变式训练1：化简求值.（1）(lg2)2+lg2·lg50+lg25;（2）(log32+log92)·(log43+log83).例2 比较下列各组数的大小.（1）log332与log556;（2）log与log1.20.7;变式训练2：已知0＜a ＜1,b ＞1,ab ＞1，则loga bb b ba1log ,log ,1的大小关系是（）bb b b a 1log log 1<< B.bb b b aa1log 1loglog << C.bb b a ba1log 1loglog << D.b bb a a blog 1log 1log<< 例3已知函数f(x)=logax(a ＞0,a≠1)，如果对于任意x∈［3，+∞）都有|f(x)|≥1成立，试求a 的取值范围.变式训练3：已知函数f （x ）=log2(x2-ax-a)在区间（-∞,1-3］上是单调递减函数.求实数a 的取值范围.例4已知函数131()log 1x f x x+=-．（1）求)(x f 的定义域；（2）断定)(x f 的奇偶性并予以证明；（3）若()0f x > 求实数x 的取值范围变式训练4已知).1,0(11log )(≠>-+=a a xx x f a （1）求f(x)的定义域;（2）断定f(x)的奇偶性并予以证明;（3）求使f(x)＞0的x 取值范围.例1.写出下列函数的定义域，并指出它们的奇偶性：（1）22y xx-=+（2）1122y xx-=+（3）1124()3()f x xx =+-变式训练1：讨论下列函数的定义域、值域，奇偶性与单调性：（1）43y x -= （2）54y x =（3）12y x -=例2比较大小：（1）11221.5,1.7（2）33( 1.2),( 1.25)--（3）1125.25,5.26,5.26---（4）30.530.5,3,log 0.5变式训练2：将下列各组数用小于号从小到大摆列：（1）2223332.5,( 1.4),(3)-- （2）3338420.16,0.5,6.25--（3）113323255(),(),log 333--例3已知幂函数223m m y x --=（m Z ∈）的图象与x 轴、y 轴都无交点，且关于原点对称，求m 的值．分析：幂函数图象与x 轴、y 轴都无交点，则指数小于或等于零；图象关于原点对称，则函数为奇函数．连系m Z ∈，即可逐步确定m 的值．变式训练3：证明幂函数12()f x x -=在(0,)+∞上是减函数．。

复合函数定义域、二次函数在闭区间上的最值

（对称轴固定，定义域
解析: 因为函数 f(x)=x2-2x-3=(x-1)2-4的对称轴为 x=1 固定不变,要求函数的最值,
即要看区间[t,t+2]与对称轴 x=1的位
置,则从以下几个方面解决如图:
t
t+2
X=1
则由上图知解为: 当t+2≤1(t≤-1)时 f(x)max=f(t)=t2-2t-3 f(x)min=f(t+2)=t2+2t+3 当 t＜1 ＜ t+2 时 f(x)max=max｛f(t),f(t+2)｝ (-1 ＜t＜1) f(x)min=f(1)=-4 当t ≥1 时 f(x) max=f(t+2)=t2+2t+3 f(x) min=f(t)=t2-2t-3
复合函数定义域
例1. 设函数 f ( x )的定义域为 [ 0 ,1 ] ，则（1）函数 f ( x 2 ) 的定义域为________ （2）函数 f ( x 2 ) 的定义域为__________
归纳:已知 f ( x ) 的定义域，求 f [ g ( x )] 的定义域
f [ g ( x )] 中其解法是：若 f ( x )的定义域为 a x b ，则
（5）若x∈[t，t+2]时，求函数f(x)的最值.
t
–1 0 1
t +2 2 3 4
x
例1、已知函数f(x)= x2 –2x – 3.
（1）若x∈[–2，0],求函数f(x)的最值；（2）若x∈[ 2，4]，求函数f(x)的最值； 1 5 （3）若x∈[ , ]，求函数f(x)的最值； 2 2 y 1 3 （4）若x∈[ , ]，求 2 2 函数f(x)的最值；

15级高一数学二次函数在闭区间上的最值练习

二次函数在闭区间上的最值、知识要点：一元二次函数的区间最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论。

般分为：对称轴在区间的左边，中间，右边三种情况时，它的图象是开口向上的抛物线，数形结合可得在［m ，n ］上设分析：将配方，得顶点为、对称轴为当的最(1)的最大值是中的较大(2 )当时大值是当 _______________ ■寸，可类比得结论。

、例题分析归类：）、正向型：是指已知二次函数和定义域区间，求其最值。

对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。

此类问题包括以下四种情形：（ 1）轴定,区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1.轴定区间定：二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是定二次函数在定区间上的最值，最小值是 ________上是增函数则上是减函数则的最的最例1.函数练习.已知2、轴定区间变：二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是定函数在动区间上的最值”。

2 _ _例3.已知f (x) = x -2x 3，当X • [t, t• 1](t R)时，求f (x)的最值.例2.如果函数当时:2例5.⑴求f (x ) = x - 2ax 1在区间［-1,2］上的最大值。

(2)求函数y 二-x(x -a)在［-1,1］上的最大值。

4.轴变区间变：二次函数是含参数的函数，而定义域区间也是变化的，我们称这种情况是动二次函数在动区间上的最值”。

例 6.已知 y 2 =4a(x_a)(a 0),，求 u =(x _3)2 ■ y 2 的最小值。

(二)、逆向型：是指已知二次函数在某区间上的最值，求函数或区间中参数的取值。

例7.已知函数f (x)二ax 2 2ax -1在区间［-3,2］上的最大值为4，则实数a 的值为 ______________ c3、轴变区间定：二次函数随着参数的变化而变化，即其图象是运动的，但定义域区间是固定的，我们称这种情况是f (n)，— ? >n(如图6) f(x)max 二 f (-■ — ), m_-— _ n(如图 7)f(x)mi i 2a 2a—:::m(如图8)2a f (m).min— 1f (m), (m n)(如图9)2a 2 — 1f(n)，—一< — (m + n)(如图10) . 2a 2例4.已知x2例8•已知函数f(x) x在区间［m, n］上的最小值是3m最大值是3n，求m，n的值。

【高中数学过关练习】过关练13-二次函数在闭区间上的最值问题

过关练13 二次函数在闭区间上的最值问题一、单选题1．（2022·山西运城·高一期末）已知二次函数()()2f x ax x c x =-+∈R 的值域为[)0,∞+，则41a c+的最小值为（） A ．16 B ．12 C ．10 D ．8【解析】由题意知0a >，140ac ∆=-=， ∴14ac =且0c >， ∴4148a c ac+≥=，当且仅当41a c=，即1a =，14c =时取等号.故选：D.2．（2022·全国·高一期末）若不等式220ax bx ++>的解集为{}21x x -<<，则二次函数224y bx x a =++在区间[]0,3上的最大值、最小值分别为（）A ．-1，-7B ．0，-8C ．1，-1D ．1，-7【解析】220ax bx ++>的解集为{}21x x -<<， 2∴-，1是方程220ax bx ++=的根，且0a <，∴21221b a a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，1a ∴=-，1b =-，则二次函数2224241y bx x a x x =++=-+-开口向下，对称轴1x =，在区间[]0,3上，当1x =时，函数取得最大值1，当3x =时，函数取得最小值7- 故选：D ．3．（2022·河南·信阳高中高一期末（理））函数()(||1)f x x x =-在[,]m n 上的最小值为14-，最大值为2，则n m -的最大值为（） A ．52B ．522+C ．32D ．2【解析】当x ≥0时，()()221111()244f x x x x x x ==-=--≥-﹣，当x ＜0时，()()22111()24f x x x x x x =-=--=-++，作出函数()f x 的图象如图：当0x ≥时，由()f x =22x x -=，解得x =2．当12x =时，()1124f =-．当x ＜0时，由21()4f x x x =--=-,即24410x x +=﹣，解得x 2444443244212-±+⨯-±-±-±===∴此时x 12-- ∵[,m n ]上的最小值为14-，最大值为2，∴n =21212m --≤≤， ∴n m -的最大值为1252222--=+，故选：B ．4．（2022·重庆巫山·高一期末）若函数234y x x =--的定义域为[]0,m ，值域为25,44⎡⎤--⎢⎥⎣⎦，则m 的取值范围是（） A ．(]0,4 B ．3,42⎡⎤⎢⎥⎣⎦C ．3,32⎡⎤⎢⎥⎣⎦D ．3,2⎡⎫+∞⎪⎢⎣⎭【解析】234y x x =--为开口方向向上，对称轴为32x =的二次函数 min 99254424y ∴=--=- 令2344x x --=-，解得：10x =，23x = 332m ∴≤≤即实数m 的取值范围为3,32⎡⎤⎢⎥⎣⎦故选：C5．（2022·浙江台州·高一期末）已知函数()22f x ax x =+的定义域为区间[m ，n ]，其中,,a m n R ∈，若f （x ）的值域为[-4，4]，则n m -的取值范围是（）A ．[4，42]B ．[22，82]C ．[4，82]D ．[42，8]【解析】若0a =，()2f x x =，函数为增函数，[,]x m n ∈时，则()24,()24f m m f n n ==-==，所以2(2)4n m -=--=，当0a >时，作图如下，为使n m -取最大，应使n 尽量大，m 尽量小，此时14a =，由22()424()424f n am m f m an n =⎧+=⎧⇒⎨⎨=+=⎩⎩，即2240ax x +-=，所以24,m n mn a a+=-=-，所以()22416482n m m n mn a a-=+-=+=82n m -≤ 当14a -<-时，即104a <<时，此时,m n 在对称轴同侧时n m -最小，由抛物线的对称性，不妨设,n m 都在对称轴右侧，则由22()24,()24f n an n f m am m =+==+=-，解得24162416a an m -++-+-==416416141441414141422a a a a n m a aa a+--+--∴-===++-++-，当且仅当1414a a +=- ,即0a =时取等号，但0a >，等号取不到，4n m ∴->，0a <时，同理，当14a =-时，max ()82n m -=14a >-时，()min 4n m ->，综上，n m -的取值范围是[4,82]，故选：C6．（2022·广东茂名·高一期末）已知函数2,02()34,23x x f x x x ⎧≤≤=⎨-<≤⎩，若存在实数1x ，2x （12x x <）满足12()()f x f x =，则21x x -的最小值为（） A ．712B ．22C ．23D ．1【解析】当0≤x ≤2时，0≤x 2≤4，当2<x ≤3时，2<3x －4≤5，则[0，4]∩(2，5]=(2，4]，令12()()f x f x ==t ∈(2，4]，则1x t 243t x +=， ∴2214143333t x x t tt -==， 32t ，即94t =时，21x x -有最小值712，故选：A.二、多选题7．（2022·新疆巴音郭楞·高一期末）定义在R 上的奇函数()f x 在(),0∞-上的解析式()()1f x x x =+，则()f x 在[)0,∞+上正确的结论是（）A ．()00f =B ．()10f =C ．最大值14D ．最小值14-【解析】由题可知，函数()f x 为定义在R 上的奇函数，则()()f x f x -=-，已知()f x 在(),0∞-上的解析式()()1f x x x =+，则当0x >时，0x -<，则()()()1f x x x f x -=--=-，所以当[)0,x ∈+∞时，()()2211124f x x x x x x ⎛⎫=-=-+=--+ ⎪⎝⎭，可知()00f =，()10f =，且最大值为14，无最小值，所以()f x 在[)0,∞+上正确的结论是ABC. 故选：ABC.8．（2022·贵州遵义·高一期末）设函数()21,21,ax x a f x x ax x a -<⎧=⎨-+≥⎩，()f x 存在最小值时，实数a 的值可能是（）A ．2B ．-1C ．0D ．1【解析】当x a ≥时，()()222211f x x ax x a a =-+=--+，所以当x a ≥时，()()2min 1f x f a a ==-+，若0a =，则()21,01,0x f x x x -<⎧=⎨+≥⎩，所以此时()min 1f x =-，即()f x 存在最小值，若0a >，则当x a <时，()1f x ax =-，无最小值，若0a <，则当x a <时，()1f x ax =-为减函数，则要使()f x 存在最小值时，则22110a a a ⎧-+≤-⎨<⎩，解得1a ≤-，综上0a =或1a ≤-. 故选：BC.三、填空题9．（2022·广西南宁·高一期末）已知函数2()25,[1,5]f x x x x =-+∈-．则函数的最大值和最小值之积为______【解析】因为22()25(1)4f x x x x =-+=-+，所以当1x =时，min ()(1)4f x f ==，当5x =时，2max ()(5)(51)420f x f ==-+=，所以最大值和最小值之积为42080⨯=.故答案为：8010．（2022·广东汕头·高一期末）函数()()()2f x x a bx a =++是偶函数，且它的值域为(],2-∞，则2a b +=__________．【解析】()()()()22222f x x a bx a bx a ab x a =++=+++为偶函数，所以20a ab +=，即0a =或2b =-，当0a =时，()2f x bx =值域不符合(],2-∞，所以0a =不成立；当2b =-时，()2222f x x a =-+，若值域为(],2-∞，则21a =，所以21a b +=-.故答案为：1-.11．（2022·广东·华南师大附中高一期末）对x ∀∈R ，不等式2430mx x m ++->恒成立，则m 的取值范围是___________；若2430mx x m ++->在()1,1-上有解，则m 的取值范围是___________.【解析】（1）关于x 的不等式函数2430mx x m ++->对于任意实数x 恒成立，则()204430m m m >⎧⎨∆=--<⎩，解得m 的取值范围是()4,+∞.（2）若2430mx x m ++->在()1,1-上有解，则2341x m x ->+在()1,1-上有解，易知当314x -<≤时23401xx -≥+，当314x <<时23401x x -<+，此时记34t x =-，则104t <<，()244253311624t g t t t t --==⎛⎫++++ ⎪⎝⎭，在10,4⎛⎫ ⎪⎝⎭上单调递减，故()12g t >-，综上可知，234112x x ->-+，故m 的取值范围是1,2⎛⎫-+∞ ⎪⎝⎭.故答案为：()4,+∞；1,2⎛⎫-+∞ ⎪⎝⎭四、解答题12．（2022·河南安阳·高一期末（文））已知二次函数()2f x ax bx c =++，满足()02f =，()()121f x f x x +-=-.(1)求函数()f x 的解析式； (2)求()f x 在区间[]1,2-上的值域. 【解析】（1）解：由()02f =可得2c =，()()()()221112f x a x b x c ax a b x a b c +=++++=+++++，由()()121f x f x x +-=-得221ax a b x ++=-，所以221a a b =⎧⎨+=-⎩，解得12a b =⎧⎨=-⎩，所以()222f x x x =-+.（2）解：由（1）可得：()()222211f x x x x =-+=-+，则()f x 的图象的对称轴方程为1x =，()11f =，又因为()15f -=，()22f =，所以，()f x 在区间[]1,2-上的值域为[]1,5.13．（2022·广东潮州·高一期末）()2f x x bx c =++，不等式()0f x ≤的解集为[]1,3．(1)求实数b ，c 的值；(2)[]0,3x ∈时，求()f x 的值域．【解析】(1)解：由题意，1和3是方程20x bx c ++=的两根，所以1313b c +=-⎧⎨⨯=⎩，解得4,3b c =-=；(2)解：由（1）知，22()43(2)1f x x x x =-+=--，所以当[]0,2x ∈时，()f x 单调递减，当[]2,3x ∈时，()f x 单调递增，所以min ()(2)1f x f ==-，max ()(0)3f x f ==，所以()f x 的值域为[1,3]-.14．（2022·广东湛江·高一期末）已知函数()223f x x ax =++，[]4,6x ∈-．(1)当2a =-时，求()f x 的最值；(2)若()f x 在区间[]4,6-上是单调函数，求实数a 的取值范围．【解析】（1）当2a =-时，()()224321f x x x x =-+=--， ∴()f x 在[]4,2-上单凋递减，在2,6上单调递增，∴()()min 21f x f ==-，()()()()2max 4444335f x f =-=--⨯-+=.（2）()()222233f x x ax x a a =++=++-，∴要使()f x 在[]4,6-上为单调函数，只需4a -≤-或6a -≥，解得4a ≥或6a ≤-． ∴实数a 的取值范围为(][),64,-∞-+∞．15．（2022·北京通州·高一期末）已知二次函数2()21f x ax ax =-+. (1)求()f x 的对称轴；(2)若(1)7f -=，求a 的值及()f x 的最值.【解析】(1)解：因为二次函数2()21f x ax ax =-+，所以对称轴212ax a-=-=． (2)解：因为(1)7f -=，所以217a a ++=. 所以2a =.所以2()241f x x x =-+．因为20a =>，所以()f x 开口向上，又2()241f x x x =-+对称轴为1x =，所以最小值为(1)1f =-，无最大值. 16．（2022·陕西·长安一中高一期末）函数2()22f x x x =-- (1)当[2,2]x ∈-时，求函数()f x 的值域； (2)当[,1]x t t ∈+时，求函数()f x 的最小值．【解析】(1)解：由题意，函数()22()2213f x x x x =--=--，可得函数()f x 在[]2,1-上单调递减，在[]12，上单调递增，所以函数()f x 在区间[]22-,上的最大值为(2)6f -=，最小值为(1)3f -=-，综上函数()f x 在上的值域为[]3,6-.(2)解：①当0t ≤时，函数在区间[],1t t +上单调递减，最小值为2(1)3f t t +=-； ②当01t <<时，函数在区间[],1t 上单调递减，在区间[]1,+1t 上单调递增，最小值为(1)3f =-；③当1t ≥时，函数在区间[],1t t +上单调递增，最小值为2()22f t t t =--，综上可得：当0t ≤时，函数()f x 的最小值为23t -；当01t <<，函数()f x 的最小值为3-；当1t ≥时，函数()f x 的最小值为222t t --.17．（2022·福建泉州·高一期末）已知函数2()4(0)f x ax ax b a =-+>在[0,3]上的最大值为3，最小值为1-． (1)求()f x 的解析式；(2)若(1,)∃∈+∞x ，使得()f x mx <，求实数m 的取值范围．【解析】（1）()f x 的开口向上，对称轴为2x =，所以在区间[]0,3上有：()()()()min max 2,0f x f f x f ==，即481133a a b a b b -+=-=⎧⎧⇒⎨⎨==⎩⎩，所以()243f x x x =-+.（2）依题意(1,)∃∈+∞x ，使得()f x mx <，即2343,4x x mx m x x-+<>+-，由于1x >，33424234x x x x+-≥⋅=，当且仅当33x x x=⇒=. 所以234m >.18．（2022·吉林·梅河口市第五中学高一期末）已知函数()()220f x mx mx n m =-+<在区间[]0,3上的最大值为5，最小值为1．(1)求m ，n 的值；(2)若正实数a ，b 满足2na mb -=，求114a b+的最小值．【解析】(1)由()()220f x mx mx n m =-+<，可得其对称轴方程为212mx m-=-=，所以由题意有(1)25(3)961f m m n f m m n =-+=⎧⎨=-+=⎩，解得1,4m n =-=.(2)由（1）2na mb -=为42a b +=，则111111171171725()()()(2)14242424848b a b a a b a b a b a b a b +=++=++≥+⨯=+=，（当且仅当25a b ==时等号成立）. 所以114a b +的最小值为258.19．（2022·山东日照·高一期末）已知函数()223f x x ax =--.(1)若1a =，求不等式()0f x ≥的解集；(2)已知()f x 在[)3,+∞上单调递增，求a 的取值范围； (3)求()f x 在[]1,2-上的最小值.【解析】（1）当1a =时，函数()223f x x x =--，不等式()0f x ≥，即223(1)(3)0x x x x --=+-≥，解得1x ≤-或3x ≥，即不等式()0f x ≥的解集为(,1][3,)-∞-+∞.（2）由函数()223f x x ax =--，可得()f x 的图象开口向上，且对称轴为x a =，要使得()f x 在[)3,+∞上单调递增，则满足3a ≤，所以a 的取值范围为(,3]-∞.（3）由函数()223f x x ax =--，可得()f x 的图象开口向上，且对称轴为x a =，当1a <-时，函数()f x 在[]1,2-上单调递增，所以()f x 最小值为()122f a -=-；当12a -≤≤时，函数()f x 在[]1,a -递减，在[],2a 上递增，所以()f x 最小值为()23f a a =--；当2a >时，函数()f x 在[]1,2-上单调递减，所以()f x 最小值为()214f a =-，综上可得，()f x 在[]1,2-上的最小值为()2min22,13,1214,2a a f x a a a a -<-⎧⎪=---≤≤⎨⎪->⎩. 20．（2022·江苏苏州·高一期末）已知函数f （x ）＝x |x ﹣m |＋n . (1)当f （x ）为奇函数，求实数m 的值；(2)当m ＝1，n ＞1时，求函数y ＝f （x ）在[0，n ]上的最大值. 【解析】(1)因为f （x ）为奇函数，所以f （﹣0）＝﹣f （0），所以f （0）＝0，即n ＝0，所以f （x ）＝x |x ﹣m |，又f （﹣1）＝﹣f （1），所以|1﹣m |＝|1＋m |，解得m ＝0，此时f （x ）＝x |x |，对∀x ∈R ，f （﹣x ）＝﹣x |x |＝﹣f （x ），所以f （x ）为奇函数,故m ＝0.(2)f （x ）＝x |x ﹣1|＋n ＝22,1,1x x n x x x n x ⎧-++⎨-+>⎩所以f （x ）在10,2⎡⎤⎢⎥⎣⎦和[1，n ]上单调递增，在1,12⎡⎤⎢⎥⎣⎦上单调递减，其中211(),()24f n f n n =+=，2111212()()()24f n f n n n n +--=--=，令214n n >+得，12n +>12n +>1()()2f n f >，2max ()f x n =.121n +<≤时1()()2f n f ≤，所以max 1()4f x n =+，因此y ＝f （x ）在[0，n ]上的最大值为2112,14212,n n n n ⎧++⎪⎪⎨+⎪⎪⎩. 21．（2022·天津市武清区杨村第一中学高一期末）已知函数()22f x x mx n =++的图象过点()1,1-，且满足()()23f f -=．(1)求函数()f x 的解析式：(2)求函数()f x 在[],2a a +上的最小值；(3)若0x 满足()00f x x =，则称0x 为函数()y f x =的不动点，函数()()g x f x tx t =-+有两个不相等且正的不动点，求t 的取值范围．【解析】（1）∵()f x 的图象过点()1,1-， ∴21m n ++=-① 又()()23f f -=， ∴82183m n m n -+=++② 由①②解2m =-，1n =-，∴()2221f x x x =--；（2）()2213221222f x x x x ⎛⎫=--=-- ⎪⎝⎭，[],2x a a ∈+，当122a +≤，即32a ≤-时，函数()f x 在[],2a a +上单调递减，∴()()2min 2263f x f a a a ⎡⎤=+=++⎣⎦；当122a a <<+，即3122a -<<时，函数()f x 在1,2a ⎡⎤⎢⎥⎣⎦上单调递减，在1,22a ⎡⎤+⎢⎥⎣⎦单调递增，∴()min1322f x f ⎛⎫⎡⎤==- ⎪⎣⎦⎝⎭；当12a ≥时，函数()f x 在[],2a a +上单调递增， ∴()()2min 221f x f a a a ⎡⎤==--⎣⎦．综上，()2min23263,,2331,,2221221,2a a a f x a a a a ⎧++≤-⎪⎪⎪⎡⎤=--<<⎨⎣⎦⎪⎪--≥⎪⎩．（3）设()()g x f x tx t =-+有两个不相等的不动点1x 、2x ，且1>0x ，20x >，∴()g x x =，即方程()22310x t x t -++-=有两个不相等的正实根1x 、2x ．∴()()21212Δ3810,30,2102t t t x x t x x ⎧⎪=+-->⎪+⎪+=>⎨⎪-⎪=>⎪⎩，解得1t >． 22．（2022·安徽合肥·高一期末）已知函数()22f x x mx =--.(1)若0m >且()f x 的最小值为3-，求不等式()1f x <的解集； (2)若当21x ≤时，不等式()20f x x -<恒成立，求实数m 的取值范围. 【解析】（1）解：()f x 的图象是对称轴为2mx =，开口向上的抛物线，所以，()222min2232424m m mm f x f ⎛⎫==--=--=- ⎪⎝⎭，因为0m >，解得2m =，由()1f x <得2230x x --<，即()()310x x -+<，得13x ，因此，不等式()1f x <的解集为()1,3-.（2）解：由21x ≤得11x -≤≤，设函数()()()2222g x f x x x m x =-=-+-，因为函数()g x 的图象是开口向上的抛物线，要使当21x ≤时，不等式()20f x x -<恒成立，即()0g x <在[]1,1-上恒成立，则()()1010g g⎧<⎪⎨-<⎪⎩，可得122010m m ---<⎧⎨+<⎩，解得3<1m -<-. 23．（2022·贵州毕节·高一期末）已知函数2()2(0)f x x ax a =->． (1)当3a =时，解关于x 的不等式5()7f x -<<；(2)函数()y f x =在[],2t t +上的最大值为0，最小值是4-，求实数a 和t 的值．【解析】（1）当3a =时，不等式5()7f x -<<，即为2567x x -<-<，即226756⎧-<⎪⎨-<-⎪⎩x x x x ，所以171,5或-<<⎧⎨<>⎩x x x ，所以11x -<<或57x <<，所以原不等式的解集为(1,1)(5,7)-⋃．（2）(0)(2)0f f a ==，由题意0=t 或22t a +=，这时24a -≤-解得2a ≥，若0=t ，则2t a +≤，所以()()2242f t f a +==-⇒=；若22t a +=，即22t a a =-≥，所以()()422f t f a =-=-，则2a =，综上，0,2t a ==或2,2t a ==．24．（2022·贵州·赫章县教育研究室高一期末）已知函数()2623f x ax x b =+-+（,a b 为常数），在1x =时取得最大值2. （1）求()f x 的解析式；（2）求函数()f x 在3,2上的单调区间和最小值.【解析】（1）由题意知6126232a ab ⎧-=⎪⎨⎪+-+=⎩,∴32a b =-⎧⎨=⎩ , ∴ ()2361f x x x =-+-.（2）∵()()()22321312f x x x x =---=--+，∴当[]3,2x ∈-时，()f x 的单调增区间为[]3,1-，单调减区间为[]1,2，又()()32718146,2121211f f -=---=-=-+-=-， ∴ ()f x 最小值为46-.25．（2022·广东·化州市第三中学高一期末）已知函数()22f x x mx =-+．（1）若()f x 在区间(],1-∞上有最小值为1-，求实数m 的值；（2）若4m ≥时，对任意的12,1,12m x x ⎡⎤∈+⎢⎥⎣⎦，总有()()21244mf x f x -≤-，求实数m 的取值范围．【解析】（1）可知()f x 的对称轴为2m，开口向上，当12m ≤，即2m ≤时，()2min 2124m m f x f ⎛⎫==-=- ⎪⎝⎭，解得23m =-23，∴23m =- 当12m>，即2m >时，()()min 131f x f m ==-=-，解得4m =，∴4m =．综上，23m =-4m =．（2）由题意得，对1,12m x ⎡⎤∈+⎢⎥⎣⎦，()()2max min 44m f x f x -≤-． ∵1,122m m ⎡⎤∈+⎢⎥⎣⎦，11222m m m⎛⎫-≥+- ⎪⎝⎭，∴()2min224m m f x f ⎛⎫==- ⎪⎝⎭，()()max 13f x f m ==-．∴()()22max min1444m m f x f x m -=-+≤-，解得5m ≥，∴5m ≥．26．（2022·黑龙江·鹤岗一中高一期末）已知二次函数()f x 满足()()12f x f x x +-=，且()01f =.(1)求函数()f x 在区间[]1,1-上的值域；(2)当x ∈R 时，函数y a =-与()3y f x x =-的图像没有公共点，求实数a 的取值范围.【解析】(1)解：设()()20f x ax bx c a =++≠､∴()1()22f x f x ax a b x +-=++=，∴220a a b =⎧⎨+=⎩，∴1a =，1b =-，又()01f =，∴1c =，∴()21f x x x =-+.∵对称轴为直线12x =，11x -≤≤，1324f ⎛⎫= ⎪⎝⎭，()13f -=， ∴函数的值域3,34⎡⎤⎢⎥⎣⎦.(2)解：由（1）可得：()2341y f x x x x =-=-+∵直线y a =-与函数()3y f x x =-的图像没有公共点∴()2min 41a x x -<-+，当2x =时，()2min 41=3x x -+-∴3a -<-，∴3a >.27．（2022·陕西安康·高一期末）已知二次函数()[]21,1,2f x x ax x =++∈-．(1)当1a =时，求()f x 的最大值和最小值，并指出此时x 的取值； (2)求()f x 的最小值，并表示为关于a 的函数()H a ．【解析】(1)当1a =时，()21f x x x =++，对称轴为12x =-，开口向上，所以()f x 在11,2⎡⎤--⎢⎥⎣⎦上单调递减，在1,22⎡⎤-⎢⎥⎣⎦上单调递增，()2min111312224f x f ⎛⎫⎛⎫⎛⎫=-=-+-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，()()2max 22217f x f ==++=.所以当12x =-时，()f x 的最小值为34，当2x =时()f x 的最大值为7.(2)()21f x x ax =++的对称轴为2a x =-，开口向上，当12a-≤-即2a ≥时，()21f x x ax =++在[]1,2-上单调递增， ()()()2min 1112f x f a a =-=--+=-，当122a -<-<即42a -<<时，()21f x x ax =++在1,2a ⎡⎤--⎢⎥⎣⎦上单调递减，在,22a ⎡⎤-⎢⎥⎣⎦上单调递增，此时()22min 112224a a a a f x f a ⎛⎫⎛⎫⎛⎫=-=-+⋅-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当22a-≥即4a ≤-时，()21f x x ax =++在[]1,2-上单调递减， ()()2min 222152f x f a a ==++=+，所以252,4()1,4242,2a a a H a a a a +≤-⎧⎪⎪=--<<⎨⎪-≥⎪⎩.28．（2022·北京平谷·高一期末）已知二次函数()()211f x ax a x =-++.(1)当对称轴为1x =-时，（i ）求实数a 的值；（ii ）求f （x ）在区间[]22-,上的值域. (2)解不等式()0f x ≥. 【解析】(1)解：（i ）由题得(1)(1)11,12,223a a a a a a a -++-==-∴+=-∴=-；（ii ）()212133f x x x =--+，对称轴为1x =-，所以当[]2,2x ∈-时，max 124()(1)1333f x f =-=-++=.min 445()(2)1333f x f ==--+=-.所以f （x ）在区间[]22-,上的值域为54[,]33-. (2)解：()2110ax a x -++≥，当0a =时，10,1x x -+≥∴≤；当0a >时，121(1)(1)0,0,1ax x x x a--≥∴=>=，当01a <<时，不等式的解集为1{|x x a≥或1}x ≤；当1a =时，不等式的解集为R ；当1a >时，不等式的解集为{|1x x ≥或1}x a≤；当0a <时，121(1)(1)0,0,1ax x x x a--+≤∴=<=，所以不等式的解集为1{|1}x x a≤≤. 综上，当0a =时，不等式的解集为{|1}x x ≤；当01a <<时，不等式的解集为1{|x x a≥或1}x ≤；当1a =时，不等式的解集为R ；当1a >时，不等式的解集为{|1x x ≥或1}x a≤；当0a <时，不等式的解集为1{|1}x x a≤≤. 29．（2022·重庆·高一期末）已知函数()29f x x ax a =-+-，a R ∈．(1)若()f x 在[]0,1上的值域为[]4,6，求a 的值；(2)若关于x 的不等式()0f x <只有一个正整数解，求a 的取值范围．【解析】(1)解：因为函数()29f x x ax a =-+-，a R ∈，对称轴2ax =，且()09f a =-，()1102f a =-，21924a f a a ⎛⎫=--+ ⎪⎝⎭，当02a<时，函数()f x 在0,1上单调递增，所以 ()()0416f f ⎧=⎪⎨=⎪⎩，即941026a a -=⎧⎨-=⎩，此时无解；当>12a时，函数()f x 在0,1上单调递减，所以 ()()0614f f ⎧=⎪⎨=⎪⎩，即961024a a -=⎧⎨-=⎩，解得3a =；当012a ≤≤，即02a ≤≤时，函数()f x 在2a x =取得最小值，所以42a f ⎛⎫= ⎪⎝⎭，即21944a a --+=，方程在02a ≤≤上无解，综上得：3a =；(2)解：关于x 的不等式()0f x <只有一个正整数解，等价于2+9>+1x a x 只有一个正整数解，令()2+9+1x g x x =，则()()()2+91010+1+22+12102+1+1+1g x x x x x x x ==-≥⋅=，当且仅当10+1+1x x =，即101x =， ()2+9+1x g x x =在(101⎤-⎦，上递减，在)101,⎡+∞⎣递增，而21013<，()21+9151+1g ==，()29g =，()2+913222+13g ==，()2+999133,5>>3+12233g ==，当a 13932⎛⎤∈ ⎥⎝⎦，不等式只有一个正整数解2x =，所以a 的取值范围为13932⎛⎤⎥⎝⎦，．30．（2022·河北秦皇岛·高一期末）已知函数()1f x x x=+，()21g x x ax a =-+-． (1)若()g x 的值域为[)0,∞+，求a 的值．(2)证明：对任意[]11,2x ∈，总存在[]21,3x ∈-，使得()()12f x g x =成立．【解析】(1)解：因为()g x 的值域为[)0,∞+，所以()()222414420a a a a a ∆=--=-+=-=，解得2a =．(2)证明：由题意，根据对勾函数的单调性可得()1111f x x x =+在[]1,2上单调递增，所以()152,2f x ⎡⎤∈⎢⎥⎣⎦．设()21g x x ax a =-+-在[]1,3-上的值域为M ，当12a≤-，即2a -时，()g x 在[1,3]-上单调递增，因为max ()(3)8212g x g a =-=，min ()(1)24g x g a -==-，所以2,52M ⎡⎤⊆⎢⎥⎣⎦；当32a，即6a 时，()g x 在[1,3]-上单调递减，因为max ()(1)212g x g a -==，min ()(3) 824g x g a =--=，所以2,52M ⎡⎤⊆⎢⎥⎣⎦；当132a -<<，即26a -<<时，22min 11()1(2)(4,0]244a g x g a a a ⎛⎫==-+-=--∈- ⎪⎝⎭，max ()max{2, 82}[4,12)g x a a =-∈，所以52,2M ⎡⎤⊆⎢⎥⎣⎦；综上，52,2M ⎡⎤⊆⎢⎥⎣⎦恒成立，即()f x 在[1,2]上的值域是()g x 在[1,3]-上值域的子集恒成立，所以对任意1[1,2]x ∈总存在2[1,3]x ∈-，使得()()12f x g x =成立.31．（2022·内蒙古赤峰·高一期末）已知函数2()21f x ax x a =-+-（a 为实常数）．（1）若0a >，设()f x 在区间[1,2]的最小值为()g a ，求()g a 的表达式：（2）设()()f x h x x=，若函数()h x 在区间[1,2]上是增函数，求实数a 的取值范围．【解析】（1）由于0a >，当[1,2]x ∈时，2211()212124f x ax x a a x a a a ⎛⎫=-+-=-+-- ⎪⎝⎭①若1012a <<，即12a >，则()f x 在[1,2]为增函数，()(1)32g a f a ==-； ②若1122a ≤≤，即1142a ≤≤时，11()2124g a f a a a ⎛⎫==-- ⎪⎝⎭；③若122a >，即104a <<时，()f x 在[1,2]上是减函数，()(2)63g a f a ==-；综上可得163,04111()21,442132,2a a g a a a a a a ⎧-<<⎪⎪⎪=--≤≤⎨⎪⎪->⎪⎩；（2）21()1a h x ax x-=+-在区间[1,2]上任取1212x x ≤<≤， ()()()212121211221212111a a a h x h x ax ax x x a x x x x ⎛⎫⎛⎫⎛⎫----=+--+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭[]211212(21)x x ax x a x x -=--（*） ()h x 在[1,2]上是增函数 ()()210h x h x ∴->∴（*）可转化为12(21)0ax x a -->对任意12,[1,2]x x ∈且12x x <都成立，即1221ax x a >- ①当0a =时，上式显然成立 ②12210,a a x x a ->>，由1214x x <<得211a a-≤，解得01a <≤； ③12210,a a x x a-<<，由1214x x <<得，214a a -≥，得102a -≤<，所以实数a 的取值范围是1,02⎡⎫-⎪⎢⎣⎭．。

专题25：二次函数在闭区间上的最值问题探讨(解析版)

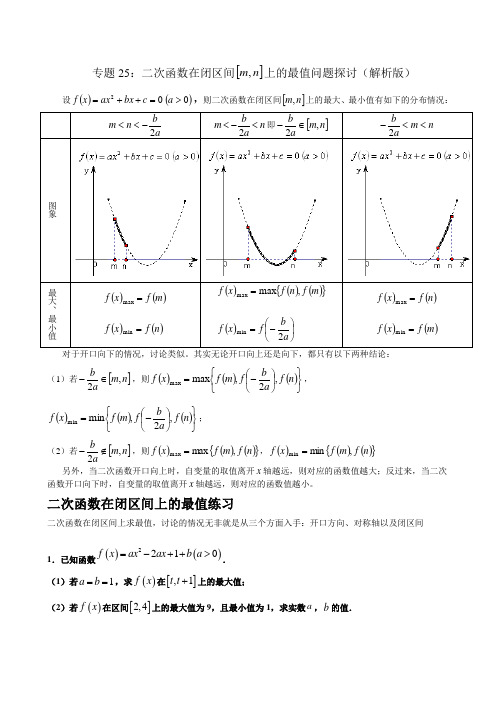
专题25：二次函数在闭区间[]n m ,上的最值问题探讨（解析版）设()()002>=++=a c bx ax x f ，则二次函数在闭区间[]n m ,上的最大、最小值有如下的分布情况：abn m 2-<< n a b m <-<2即[]n m ab ,2∈- n m ab<<-2 图象最大、最小值()()()()n f x f m f x f ==min max()()(){}()⎪⎭⎫⎝⎛-==a b f x f m f n f x f 2,max min max()()()()m f x f n f x f ==min max对于开口向下的情况，讨论类似。

其实无论开口向上还是向下，都只有以下两种结论：（1）若[]n m a b ,2∈-，则()()()⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛-=n f a b f m f x f ,2,max max ，()()()⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛-=n f a b f m f x f ,2,min min ；（2）若[]n m ab,2∉-，则()()(){}n f m f x f ,m ax max =，()()(){}n f m f x f ,m in min = 另外，当二次函数开口向上时，自变量的取值离开x 轴越远，则对应的函数值越大；反过来，当二次函数开口向下时，自变量的取值离开x 轴越远，则对应的函数值越小。

二次函数在闭区间上的最值练习二次函数在闭区间上求最值，讨论的情况无非就是从三个方面入手：开口方向、对称轴以及闭区间1．已知函数()()2210f x ax ax b a =-++>．（1）若1a b ==，求()f x 在[],1t t +上的最大值；（2）若()f x 在区间[]2,4上的最大值为9，且最小值为1，求实数a ，b 的值．【答案】（1）12t ≤时，最大值为222t t -+；12t >时，最大值为21t +；（2）10a b =⎧⎨=⎩．【分析】（1）根据题中条件，分别讨论112t +≤，112t +>两种情况，结合二次函数的性质，即可得出结果；（2）根据二次函数的性质，由函数在给定区间的最值，得到()()2114819f b f a b ⎧=+=⎪⎨=++=⎪⎩，求解，即可得出结果. 【详解】（1）()222f x x x =-+，[],1x t t ∈+因为对称轴1x =，而1122t t t ++=+，所以 ①112t +≤即12t ≤时，最大值()222f t t t =-+；②112t +>即12t >时，最大值()211f t t +=+；综上，12t ≤时，最大值为222t t -+；12t >时，最大值为21t +；（2）因为函数()f x 图像的开口方向向上，且对称轴方程为1x =，所以，函数()y f x =在区间[]2,4上为增函数，又因为函数()y f x =在区间[]2,4上的最大值为9，最小值为1，可得()()2114819f b f a b ⎧=+=⎪⎨=++=⎪⎩，解得1a b =⎧⎨=⎩．【点睛】思路点睛：求解二次函数在给定区间的最值问题时，通常需要根据二次函数的性质（开口方向、对称轴、单调性），由分类讨论的方法进行求解.2．已知一次函数()y f x =满足()12f x x a -=+， . 在所给的三个条件中，任选一个补充到题目中，并解答. ①()5f a =，②142a f ⎛⎫=⎪⎝⎭，③()()41226f f -=. （1）求函数()y f x =的解析式；（2）若()()()g x x f x f x x λ=⋅++在[]0,2上的最大值为2，求实数λ的值. 【答案】（1）()23f x x =+（2）2λ=- 【分析】利用待定系数法求出()22f x x a =++，（1）根据所选条件，都能求出1a =，可得()23f x x =+；（2）根据对称轴与区间中点值的大小分两种情况讨论求出最大值，结合已知最大值可求得λ的值. 【详解】设()f x kx b =+(0)k ≠，则(1)2k x b x a -+=+，即2kx k b x a -+=+，所以2k =，2b a ，所以()22f x x a =++，若选①，（1）由()5f a =得225a a ++=，得1a =，所以()23f x x =+. （2）()(23)(23)g x x x x x λ=++++=22(42)3x x λλ+++，区间[]0,2的中点值为1，对称轴为()22x λ+=-，当()212λ+-≤，即4λ≥-时，max()(2)8843716f x f λλλ==+++=+，所以7162λ+=，解得2λ=-；当()212λ+->，即4λ<-时，max()(0)3f x f λ==，所以32λ=，解得23λ=（舍），综上所述：2λ=-. 若选②，（1）由142a f ⎛⎫=⎪⎝⎭得14222a a =⨯++，解得1a =，所以()23f x x =+；（2）()(23)(23)g x x x x x λ=++++=22(42)3x x λλ+++，区间[]0,2的中点值为1，对称轴为()22x λ+=-，当()212λ+-≤，即4λ≥-时，max()(2)8843716f x f λλλ==+++=+，所以7162λ+=，解得2λ=-；当()212λ+->，即4λ<-时，max()(0)3f x f λ==，所以32λ=，解得23λ=（舍），综上所述：2λ=-. 若选③，（1）由()()41226f f -=得4(22)2(42)6a a ++-++=，解得1a =，所以()23f x x =+；（2）()(23)(23)g x x x x x λ=++++=22(42)3x x λλ+++，区间[]0,2的中点值为1，对称轴为()22x λ+=-，当()212λ+-≤，即4λ≥-时，max()(2)8843716f x f λλλ==+++=+，所以7162λ+=，解得2λ=-；当()212λ+->，即4λ<-时，max()(0)3f x f λ==，所以32λ=，解得23λ=（舍），综上所述：2λ=-. 【点睛】关键点点睛：第二问，讨论对称轴与区间中点值的大小求最大值是解题关键.3．对于函数f （x ），若存在0x R ∈，使得00()f x x =成立，则称0x 为函数f （x ）的不动点.已知二次函数2()4f x ax bx =+-有两个不动点－1和4.（1）求f （x ）的表达式；（2）求函数f （x ）在区间[,1]t t +上的最小值g （t ）的表达式；（3）在（2）的条件下，求不等式1(2)()02g x g x +->的解.【答案】（1）2()24f x x x =--；（2）()225,05,0124,1t t g t t t t t ⎧-≤⎪=-<<⎨⎪--≥⎩；（3）16x >或12x <-【分析】（1）由不动点定义可得()()11,44f f -=-=，代入表达式即可求解,a b ，进而得到()f x 表达式；（2）对参数t 进行分段讨论，分为0,01,1t t t ≤<<≥三段，分别结合对称轴与函数在定区间的单调性求解即可；（3）由()g x 表达式分析可知，()g x 图象关于12x =对称，则原不等式等价转化为1112222x x ⎛⎫+->- ⎪⎝⎭，解绝对值不等式即可. 【详解】（1）由题知()()1144f f ⎧-=-⎪⎨=⎪⎩得4116444a b a b --=-⎧⎨+-=⎩，解得1,2a b ==-，则2()24f x x x =--；（2）由2()24f x x x =--知()f x 对称轴为1x =，当11t +≤，即0t ≤时，()f x 在[],1t t +上单减，()()2min 15f x f t t =+=-；当1t ≥时，()f x 在[],1t t +上单增，()()2min 24f x f t t t ==--；当11t t <<+，即()0,1t ∈时，()()min 15f x f ==-，综上所述，()225,05,0124,1t t g t t t t t ⎧-≤⎪=-<<⎨⎪--≥⎩；（3）由（2）知()225,05,0124,1x x g x x x x x ⎧-≤⎪=-<<⎨⎪--≥⎩，画出函数图象，如图：显然函数()g x 图象关于12x =对称，则()()11111202222222g x g x g x g x x x ⎛⎫⎛⎫⎛⎫+->⇔+>⇒+->- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即()22122x x ⎛⎫>- ⎪⎝⎭，解得16x >或12x <-【点睛】关键点睛：（1）对于求解动区间上二次函数最值，需结合二次函数对称轴与参数值进行分段讨论；（2）对于存在对称轴x a =的函数，解决()()12f x f x >题型，长转化为12x a x a ->-或12x a x a -<-进行求解.4．已知二次函数()f x 的最小值为1，且(0)(2)3f f ==. （1）求()f x 的解析式；（2）若()f x 在区间[]2,1a a +上不单调，求实数a 的取值范围；（3）若()f x 在区间[1,]m -上的最小值为1，最大值为9，求实数m 的取值范围. 【答案】（1）2()243f x x x =-+；（2）102a <<；（3）13m ≤≤. 【分析】（1）用顶点式先设函数()f x 的解析式，再利用(0)3f =求解未知量即可；（2）只需保证对称轴落在区间内部即可；（3）分三种情况讨论，结合二次函数的单调性，分别求出最值，再判断是否符合条件即可. 【详解】（1）()f x 是二次函数，且(0)f f =（2）∴对称轴为1x =，又由函数最小值为1，设2()(1)1f x a x =-+，又(0)3f =2a ∴=22()2(1)1243f x x x x ∴=-+=-+（2）要使()f x 在区间[2a ，1]a +上不单调，则211a a <<+102a ∴<<；（3）因为2()243f x x x =-+，所以()(1)(3)9,11f f f -===，且()f x 的对称轴为1x =，若11m -<<，()f x 在区间[1-，]m 递减，()()()()max min ()19,11f x f f x f m f =-==>=，不合题意；若13m ≤≤，()f x 在区间[1-，1]递减，在区间[1，]m 递增，()()min11f x f ==，因为()()()31f m f f ≤=-，所以()max ()19,f x f =-=符合题意；若3m >，()f x 在区间[1-，1]递减，在区间[1，]m 递增，()()min 11f x f ==，因为()()39f m f >=，所以()max ()9,f x f m =>不合题意；综上，13m ≤≤. 【点睛】二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴定区间动，不论哪种类型，解决的关键是考查对称轴与区间的关系，当含有参数时，要依据对称轴与区间的关系进行分类讨论 5．已知函数2()23f x x ax =-+-．（Ⅰ）若函数()y f x =在(,1)-∞上是增函数，求实数a 的取值范围；（Ⅱ）求函数()f x 在[1,2]上的最大值．【答案】（Ⅰ）[1，＋∞）；（Ⅱ）答案见解析【分析】（Ⅰ）根据二次函数的图象和性质，可得函数2()23f x x ax =-+-的图象开口朝下，对称轴为直线x ＝a ，由函数()y f x =在(,1)-∞上是增函数，可得区间(,1)-∞完全在对称轴的左边，进而可得实数a 的取值范围；（Ⅱ）分a ≤1，1＜a ＜2时，a ≥2时三种情况，结合函数()f x 在[1，2]上的单调性求最大值．【详解】解：（Ⅰ）由已知得()222()233f x x ax x a a =-+-=--+-． ∴函数2()23f x x ax =-+-的图象是开口朝下，且对称轴为直线x ＝a 的抛物线，因为函数()y f x =在(,1)-∞上是增函数，所以a ≥1．故实数a 的取值范围是[1，＋∞）；（Ⅱ）①当a ≤1时，函数()y f x =在[1，2]上是减函数，于是()max 124y f a ==-；②当1＜a ＜2时，函数()y f x =在[1，a ]上是增函数，在（a ，2]上是减函数，于是()2max 3y f a a ==-；③当a ≥2时，函数()y f x =在[1，2]上是增函数，于是()max 247y f a ==-．【点睛】易错点睛：二次函数的最值一定要注意区间的限制，不要盲目配方求得结论，一定要讨论对称轴与区间的位置关系，确定单调性从而求出最值．6．已知二次函数()f x 满足(0)2,(2)()4=+-=f f x f x x ．（1）求函数()f x 的解析式；（2）求函数()f x 在[3,6]时的最值．【答案】（1）2()22f x x x =-+；（2）最小值为5，最大值为26 【分析】（1）设出二次函数()f x 的一般形式，根据条件利用待定系数法求解出()f x 的解析式；（2）根据二次函数的对称轴、开口方向，结合区间[3,6]，求解出()f x 的最值即可．【详解】（1）设2()(0)f x ax bx c a =++≠，因为(0)2f =，所以2c =，因为(2)()4f x f x x +-=，所以()22(2)(2)224⎡⎤++++-++=⎣⎦a x b x ax bx x ，所以4424ax a b x ++=，所以44420a a b =⎧⎨+=⎩，所以12a b =⎧⎨=-⎩，所以2()22f x x x =-+；（2）因为2()22,()=-+f x x x f x 的对称轴为1x =，且()f x 的开口向上，所以()f x 在[3,6]上递增，所以2min ()(3)32325==-⨯+=f x f ，2max ()(6)626226==-⨯+=f x f ．所以最小值为5，最大值为26．【点睛】本题考查根据待定系数法求解函数的解析式以及利用函数的单调性求解函数的最值，难度较易．（1）对于常见的一次函数、二次函数、反比例函数，求解析式时可采用待定系数法求解；（2）求解二次函数的值域时，注意借助二次函数的对称轴和开口方向进行分析． 7．已知函数()2f x x ax =-（1）若在区间[)1,+∞上是增函数，求实数a 的取值范围；（2）求函数()f x 在区间[]1,2上的最小值．【答案】（1）2a ≤；（2）分类讨论，答案见解析．【分析】（1）根据对称轴与区间的位置关系，即可得答案；（2）对称轴2ax =与区间[]1,2分三种位置关系进行讨论，即可得答案；【详解】解：（1）函数()2f x x ax =-的对称轴方程为2a x =，因为函数()f x 区间[)1,+∞上是增函数，所以12a≤ 所以2a ≤；（2）①当12a≤即2a ≤时，函数()f x 区间[]1,2上是增函数，所以()()min 11f x f a ==-； ②当22a≥即4a ≥时，函数()f x 区间[]1,2上是减函数，所以()()min 242f x f a ==-； ③当122a<<即24a <<时，函数()f x 区间1,2a ⎛⎫⎪⎝⎭上是减函数，在,22a ⎛⎫⎪⎝⎭上时增函数所以()2min24a a f x f ⎛⎫==- ⎪⎝⎭，综上所述：当2a ≤时，()()min 11f x f a ==-，当4a ≥时，()()min 242f x f a ==-；当24a <<时，()2min 24a a f x f ⎛⎫==- ⎪⎝⎭；【点睛】二次函数轴变区间定的问题，若是求最小值，一般是考虑对称轴在区间的三种位置关系即可.8．已知二次函数2()f x ax bx c =++，且满足(0)2f =，(1)()21f x f x x +-=+.（1）求函数()f x 的解析式；（2）若关于x 的方程()0f x m -=在[]1,2x ∈-上有解，求实数m 的取值范围；（3）当[],2()x t t t R ∈+∈时，求函数()f x 的最小值（用t 表示）.【答案】（1）2()2f x x =+；（2）[]2,6m ∈；（3）2min 22,0()2,1023,1t t f x t t t t ⎧+≥⎪=-<<⎨⎪++≤-⎩【分析】（1）根据题中条件，列出方程组求解，求出系数，即可得出结果；（2）根据二次函数的性质，求出()f x 在区间[]1,2-的值域，进而可得出结果；（3）分别讨论0t ≥，10t +≤，01t t <<+三种情况，结合二次函数的性质，即可得出结果.【详解】（1）因为二次函数2()f x ax bx c =++满足(0)2f =，(1)()21f x f x x +-=+，所以()()()2221121c a x b x c ax bx c x =⎧⎪⎨++++-++=+⎪⎩，即2221c ax b a x =⎧⎨++=+⎩，所以2221c a b a =⎧⎪=⎨⎪+=⎩，解得210c a b =⎧⎪=⎨⎪=⎩，因此2()2f x x =+；（2）由（1）知，2()2f x x =+是对称轴为0x =开口向上的二次函数，所以2()2f x x =+在[)1,0-上单调递减，在[]0,2上单调递增，因此min ()(0)2f x f ==，又(1)3f -=，(2)6f =，所以max ()(2)6f x f ==，即当[]1,2x ∈-时，[]()2,6f x ∈，为使关于x 的方程()f x m =在[]1,2x ∈-上有解，只需[]2,6m ∈；（3）因为2()2f x x =+是对称轴为0x =开口向上的二次函数，当0t ≥时，2()2f x x =+在[],2x t t ∈+上单调递增，则2min ())2(f x f t t =+=；当10t +≤，即1t ≤-时，2()2f x x =+在[],2x t t ∈+上单调递减，则()22min 2)23((1)1t f f t t t x =+=+=+++；当01t t <<+，即10t -<<时，min ()(0)2f x f ==；综上2min22,0()2,1023,1t tf x tt t t⎧+≥⎪=-<<⎨⎪++≤-⎩.【点睛】方法点睛：求二次函数()f x在区间[],a b上的最值时，一般用分类讨论的方法求解；分别讨论对称轴位于区间的左右两侧，以及位于给定区间内，结合二次函数的性质求解即可.。

二次函数求最值(动轴定区间、动区间定轴)

1 2
,
5 2
]（4）x6 ∈[
1 2
,
3] 2
6
6
4
4
4
x=1
2
0
10
-2
2
55
4
2 x=1
10 15
2
5
10
10
4 15
2
2 x=1
1
5
2
2
5
10 2
2
1 -2
5
15 2
x=1
3 2
10
4
4
4 4
6
思考6 ：通过以上几6 题，你发现二次6 函数在区间[m，n]
8
上的8 最值通常在哪8 里取到？
5 f(x)max=10f(k+2)=（1k5 +2)2-2(k+2)-3 =k2+2k-3
8
6
4
2 x=1 k
2
k+2 5
当k ≥1 时 f(x) max=f(k+2)=k2+2k-3
10
15
f(x) min=f(k)=k2-2k-3
4
6
8
10
8
例: 6求函数y=x2-62x-3在x∈[k,k6+2]时的最值
(3)已知函数 f(x)＝－x2＋2ax＋1－a 在 x∈[0,1]时有最大值 2，
求 a 的值．
(4)已知函数 f(x)＝－4x2＋4ax－4a－a2 在区间[0,1]内有一个最
大值－5，求 a 的值．
思考：如何求函数y=x2-2x-3在 x∈[k,k+2]时的最值?
解析: 因为函数 y=x2-2x-3=(x-1)2-4的对称轴为 x=1 固定不变,要求函数的最值, 即要看区间[k,k+2]与对称轴 x=1的位置,则从以下几个方面解决如图: