射线型布局算法简述
初二数学射线与线段位置关系

初二数学射线与线段位置关系在初中数学中,我们学习了很多与几何图形相关的内容,其中射线与线段的位置关系也是我们需要了解和掌握的知识点之一。
本文将介绍射线与线段的定义以及它们之间的位置关系。
一、射线的定义及特点射线是由一个起点和无限延伸的一条直线组成的图形。
在几何图形中,用大写字母表示射线,如射线AB可以表示为⇒AB。
射线具有以下特点:1. 起点:射线的起点是射线的起始位置,用大写字母表示。
2. 延伸:射线从起点开始向一个特定方向无限延伸。
二、线段的定义及特点线段是由两个点A和B确定的,由这两个点以及点A和点B之间的点组成的一条有限的直线部分。
线段通常用小写字母表示,如线段AB可以表示为AB。
线段具有以下特点:1. 两个端点:线段的两个端点是线段的起点和终点,用大写字母表示。
2. 有限长度:线段的长度是有限的,是由起点和终点之间的距离确定的。
三、射线与线段的位置关系当射线与线段相交时,我们可以根据它们的位置关系进行分类,并给出相应的例子。
1. 射线在线段之外:在这种情况下,射线的延长线与线段没有交点。
例如,射线AB与线段CD相交于C点(见下图)。
2. 射线与线段有一个公共点:在这种情况下,射线的延长线与线段有且只有一个交点。
例如,射线AB与线段CD相交于D点。
3. 射线在线段上:在这种情况下,射线的延长线与线段有无数个交点。
例如,射线AB与线段CD相交于CD的每一个点。
需要注意的是,射线与线段之间的位置关系是基于几何图形的定义和特点推断得出的。
在解题过程中,我们要灵活运用这些特性,观察图形并找到正确的答案。
综上所述,射线与线段是初中数学中重要的概念之一。
我们通过了解射线和线段的定义、特点以及它们之间的位置关系,可以更好地理解几何图形的相关知识和解答相关问题。
希望本文的介绍对你在初二数学学习中有所帮助。
小学数阵图的规律公式

小学数阵图的规律公式
将一些数按照一定的要求排列而成的某种图形,称之为数阵图。
数阵图是由幻方演化而来,但它的形状更加多样。
可以是三角形、多边形以及多个图形相结合。
数阵图一般可分为辐射型、封闭型以及复合型。
在数阵图中,重叠部分也称为阵眼,即使是同一个数阵,重叠数不一样,每条线上的和也会发生变化。
因此做数阵图,重叠部分是突破口,我们首要任务就是,先想办法确定重叠数。
辐射型数阵图相对来说简单一些,如果所填的数字是等差数列所构成,每一条线是奇数个数,可采用试算法。
重叠数可使用最大、最小以及最中间的数字,也就是等差数列的中间项进行试算。
这种方法有它的局限性,就是只适用于等差数列的数。
当然还有一种通用的方法:计算法。
计算法算出重叠部分,但还不能算完整地做完。
比如说没有给出每条线上的和,因为有时候计算出来的结果,不一定能成立,尤其是取最大值或最小值的时候,需要把数阵图填满,以检验是否有误。
这里有个重要公式。
总和=单条线和x线数=数字和+重叠数x(线数-1)。
判断一个点是否在指定区域内

判断一个点是否在指定区域内判断一个点是否在指定区域内在图像处理时,我们会经常需要判断一个点是否位于多边形区域内,这里介绍2种比较巧妙的算法。
射线法第一种是射线法,算法思想非常巧妙:从待判断的点向某一个方向引射线,计算和多边形交点的个数,如果个数是偶数或者0则点在多边形外,如果是奇数,则在多边形内,如下图:这里有二种特殊情况:1. 射线经过顶点:当射线经过顶点时,判断就会出现异常情况。
2. 点在边上:这种情况也不能用交点个数的奇偶性来判断了,要快速地判断这个点是否在边上。
C 的实现如下:参考自:Determining if a point lies on the interior of a polygon1 2 3 4 5 6 7 8 #define MIN(x,y) (x < y ? x : y)#define MAX(x,y) (x > y ? x : y)typedef struct {double x,y;} Point;int InsidePolygon(Point *polygon,int N,Point p)9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 {int counter = 0;int i;double xinters;Point p1,p2;p1 = polygon[0];for (i=1;i<=N;i++) {p2 = polygon[i % N];if (p.y > MIN(p1.y,p2.y)) { //低if (p.y <= MAX(p1.y,p2.y)) { //高if (p.x <= MAX(p1.x,p2.x)) { //右if (p1.y != p2.y) { //简单忽略平行X 轴这种情况 xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x; //交叉点坐标 参考if (p1.x == p2.x || p.x <= xinters) counter++;}}}}p1 = p2;}if (counter % 2 == 0)return 0;elsereturn 1;}再来个C#版的1 2 3 4 5 6 7 8 9 10 11 12 public static bool Contains( Point[] points, Point p ){bool result = false;for( int i = 0; i < points.Length - 1; i++ ){if( ( ( ( points[ i + 1 ].Y <= p.Y ) && ( p.Y < points[ i ].Y ) ) || ( ( points[ i ].Y <= p.Y ) && ( p.Y < points[ i + 1 ].Y ) ) ) && ( p.X < ( points[ i ].X - points[ i + 1 ].X ) * ( p.Y - points[ i + 1 ].Y ) / ( points[ i ].Y - points[ i + 1 ].Y ) + points[ i + 1 ].X ) ){result = !result;}}return result;}值得一提的是射线法对于带岛的多边形依然有效:改进:传统的射线法一开始就直接计算点和多边形的交点个数,这样的话,会花费大量的时间来作拓扑关系的判断,我们可以首先计算出最小外包矩形,迅速排除不在矩形内部的点,然后再做上面的判断。
第4讲 数阵图
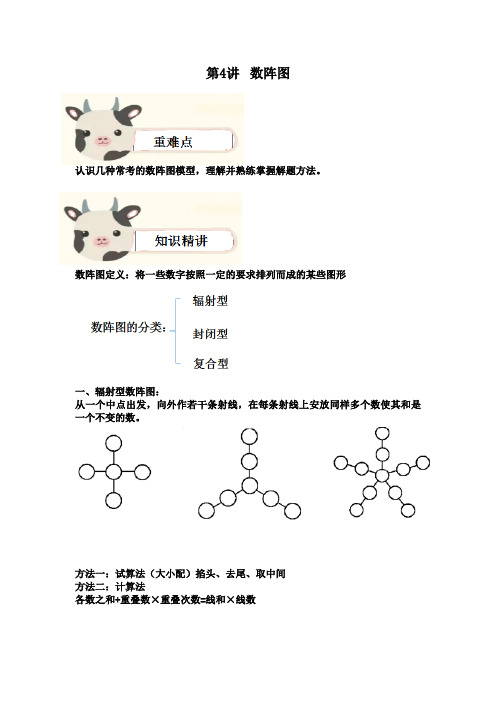
第4讲数阵图认识几种常考的数阵图模型,理解并熟练掌握解题方法。
数阵图定义:将一些数字按照一定的要求排列而成的某些图形一、辐射型数阵图:从一个中点出发,向外作若干条射线,在每条射线上安放同样多个数使其和是一个不变的数。
方法一:试算法(大小配)掐头、去尾、取中间方法二:计算法各数之和+重叠数×重叠次数=线和×线数二、封闭的数阵图:计算法各数之和+重叠数×重叠次数=线和×线数三、复合型数阵图即是辐射型数阵图,又是封闭型数阵图。
将1-7这7个数字分别填入图中各个○内,使每条线段上的三个○内的数之和等于14将1-11填入下图的各个圆圈内,使每条线段上的三个圆圈内的数之和相等。
1、将1-5分别填入圆圈内,使每条线上3个圆圈的数字之和都等于92.将1-9分别填入圆圈内,是每条线上的三个数之和相等将1-6六个数字分别填入下图6个圆圈内,使每条边上的和都等于11.把1-12这十二个数,分别填在如右图中正方形四条边上的十二个圆圈内,使每条边上四个圆圈内数的和都等于22,试求出一个基本解。
1.把1-9个数分别填入○中,使每条边上四个数的和相等于17.2.把1-8个数分别填入○中,使每条边上三个数的和相等12.(1)将1-7七个数字填入下图的七个圆圈内,使每个大圆圈和每条直线上的三个数字之和相等。
(2)将1-6这6个数字分别填入下图的6个圆圈内,使得三条线段上的数字之和都相等。
下图中,是有三个正三角形,将1-9分别填入9个圆圈内,使得三个正三角形三个顶点之和都相等,通过四个圆的每条线段之和也相等1.将1-5这五个数分别填入如果中的圆圈内,使每条线段上三个圆圈内的和相等。
2.将1-10这十个数分别填入下图中的十个○内,使每条线段上四个○内数的和相等,3.将1-9这九个数分别填入图中○内,使每条线段三个数相等.。
射线法_判断点和多边形的关系_概述说明以及解释

射线法判断点和多边形的关系概述说明以及解释1. 引言1.1 概述本文主要介绍了一种判断点和多边形关系的方法——射线法。
通过使用射线与多边形边界相交的方式,我们可以准确判断一个点是在多边形内部还是外部。
射线法是计算机图形学领域常用的算法之一。
1.2 文章结构本文将按照如下结构进行阐述:引言:对文章内容及目的进行简要介绍。
射线法判断点和多边形的关系:详细讲解射线法原理以及判断点在多边形内外部的方法。
示例与解释:通过实际示例来进一步说明射线法的运用和解释。
结论:总结射线法判断点和多边形关系的优劣势,并讨论应用场景与可能的限制条件。
结束语:对全文进行总结,并提出展望。
1.3 目的本文旨在为读者介绍射线法这种有效而常用的算法,并通过详细讲解和具体示例,帮助读者更好地理解和应用该方法。
同时,我们也希望能够探讨该方法的局限性以及适用范围,有助于读者在实际应用中做出合理选择。
通过阅读本文,读者将会对射线法的原理和应用有一个较为全面的了解。
2. 射线法判断点和多边形的关系:2.1 射线法原理:射线法是一种常用的方法,用于确定一个点是否在一个多边形内部。
其基本原理是通过从该点引出一条射线,然后计算与多边形各条边的交点个数。
如果交点个数为奇数,则说明该点在多边形内部;如果交点个数为偶数,则说明该点在多边形外部。
2.2 点在多边形内部的判断方法:要判断一个点是否在多边形内部,可以按照以下步骤进行:- 选择一条水平射线,起始位置与待判断的点相同。
- 遍历多边形的每条边,与水平射线进行相交计算。
- 如果相交,并且交点位于射线右侧,则将计数器加1。
- 最终检查计数器的值,如果是奇数,则表示该点在多边形内部;如果是偶数,则表示该点在多边形外部。
2.3 点在多边形外部的判断方法:同样地,要判断一个点是否在多边形外部,可以按照以下步骤进行:- 选择一条水平射线,起始位置与待判断的点相同。
- 遍历多边形的每条边,与水平射线进行相交计算。
射线法原理

射线法原理射线法是一种常用的图形学算法,用于模拟光线在三维空间中的传播和相交。
它是一种基于几何学的方法,通过追踪射线的路径来计算光线与物体的交点和光照效果。
射线法的原理可以简单概括为以下几个步骤:1. 发射射线:从相机或观察者的位置出发,向场景中的物体发射射线。
每条射线对应着图像上的一个像素点。
2. 确定交点:当射线与物体相交时,找到离观察者最近的交点。
这通常涉及到求解射线与物体表面的交点的问题。
3. 确定光照效果:根据交点的材质属性和光源位置,计算该点的光照效果。
这包括漫反射、镜面反射和阴影等。
4. 考虑反射和折射:如果物体是反射或折射的,就需要根据反射和折射定律计算出射线的方向,并继续追踪射线。
5. 重复追踪:根据需要,可以多次追踪射线,以模拟光线的继续传播和相交。
射线法的优点在于其灵活性和逼真度。
通过追踪射线的路径,可以模拟出真实世界中的光照效果,如阴影、反射、折射等。
这使得射线法在计算机图形学、虚拟现实、游戏开发等领域得到了广泛应用。
然而,射线法也存在一些挑战和限制。
首先,射线法需要对每条射线进行求交计算,这对于复杂的场景和大规模的物体来说是非常耗时的。
因此,射线法在实时渲染和动画等领域的应用受到了一定的限制。
其次,射线法只考虑了光线的传播和相交,对于光的衍射和色散等现象无法很好地模拟。
为了克服这些限制,研究人员提出了许多改进的射线法算法,如光线追踪、路径追踪、辐射度追踪等。
这些算法通过优化求交计算、引入随机采样和全局光照等技术,提高了射线法的效率和逼真度。
射线法是一种基于几何学的光线追踪算法,用于模拟光线在三维空间中的传播和相交。
它通过追踪射线的路径,计算光线与物体的交点和光照效果,实现了逼真的图形渲染。
尽管存在一些挑战和限制,但射线法仍然是计算机图形学领域中重要的算法之一,为实时渲染、虚拟现实和游戏开发等应用提供了有力支持。
2d 射线检测算法

2d 射线检测算法2D射线检测算法是计算机图形学中一种重要的算法,它被广泛应用于许多领域,例如计算机游戏、计算机辅助设计、计算机视觉等。
本文将介绍2D射线检测算法的原理、应用以及一些常见的优化技巧,旨在帮助读者更好地理解和应用该算法。
首先,让我们了解2D射线检测算法的原理。
该算法的核心思想是通过投射一条射线来判断该射线与图形中的物体是否相交。
射线可以看作是从某个点出发,沿着某个方向一直延伸的无限长线段。
算法首先确定射线的起点和方向,然后通过遍历所有可能与射线相交的物体,检测相交点,并判断是否存在相交。
在实际应用中,2D射线检测算法通常用于解决以下两个问题:点与物体的相交和线段与物体的相交。
点与物体的相交即判断某个点是否在物体内部或边界上,线段与物体的相交即判断线段是否与物体相交并求出相交点。
这些问题在计算机游戏中常常用于碰撞检测,例如判断游戏角色是否与墙壁、敌人等物体发生碰撞,以及计算游戏角色在地图中行走时与障碍物的交互。
为了提高算法的效率,我们可以采取一些优化技巧。
首先,我们可以通过空间分割技术,将场景划分为多个区域,减少需要遍历的物体数量。
常见的空间分割算法包括四叉树、网格划分等。
其次,我们可以使用快速排斥测试(AABB测试)来快速确定某个物体是否与射线相交。
AABB(Axis-Aligned Bounding Box)是指以物体的边界框为基础,以物体坐标系轴对齐的矩形框,通过判断射线与AABB是否相交,可以迅速排除掉一大部分不可能相交的物体。
此外,还有其他一些高级的算法优化方法,比如扫描线算法和分段线性插值等,可以进一步提高算法的效率和精度。
除了在游戏和计算机图形学领域广泛应用外,2D射线检测算法还在计算机辅助设计和计算机视觉领域有着重要的应用。
在计算机辅助设计中,该算法可以帮助设计师快速判断物体间的关系,提供实时的交互式设计工具。
在计算机视觉中,2D射线检测算法可以用于目标检测、轨迹跟踪等任务,为机器视觉系统提供更准确的信息。
射线的角度与长度计算公式

射线的角度与长度计算公式射线是一种特殊的直线,它具有起点和方向,可以延伸到无限远。
在几何学和物理学中,射线是一种重要的概念,它在描述光线、电磁波和其他形式的辐射时非常有用。
在本文中,我们将探讨射线的角度与长度的计算公式,并讨论其在实际应用中的意义。
首先,让我们来看一下射线的基本定义。
射线可以用一个起点和一个方向向量来描述,其中起点是射线的起始位置,方向向量则指示射线的延伸方向。
在二维空间中,一个射线可以用以下的参数方程来表示:P(t) = P0 + t v。
其中P(t)是射线上任意一点的位置向量,P0是射线的起点的位置向量,v是射线的方向向量,t是一个实数参数。
这个参数方程表明,射线上的任意一点都可以通过起点位置向量P0加上方向向量v乘以参数t来得到。
现在,让我们来考虑射线的角度与长度的计算。
射线的长度可以通过其起点和方向向量来计算。
假设我们有一个二维空间中的射线,其起点位置向量为P0 = (x0, y0),方向向量为v = (a, b)。
那么射线的长度可以通过以下的公式来计算:L = |v| = sqrt(a^2 + b^2)。
这个公式表明,射线的长度就是其方向向量的模长。
在三维空间中,这个公式可以推广为:L = |v| = sqrt(a^2 + b^2 + c^2)。
其中v = (a, b, c)是射线的方向向量。
接下来,让我们来考虑射线的角度。
射线的角度可以通过其方向向量来计算。
在二维空间中,射线的角度可以通过以下的公式来计算:θ = arctan(b/a)。
这个公式表明,射线的角度就是其方向向量的y分量与x分量的arctan值。
在三维空间中,射线的角度可以通过以下的公式来计算:θ = arccos(v1•v2 / |v1||v2|)。
其中v1和v2分别是两条射线的方向向量,•表示向量的点积。
这个公式表明,射线的角度就是其方向向量之间的夹角。
射线的角度与长度的计算公式在实际应用中具有广泛的意义。
射线跟踪光线跟踪RayCastingraytracing算法描述

3D 开端 RayCasting很佩服卡马克,他所独立研究出的图形学算法,几乎涉及图形学这门最令我头大的学科的各个领域。
是他将Wolfenstein 3D 搬上了286这样老古董的机型,是他将FPS 带入了我们的生活。
从1992年Wolfenstein 3D 发售至今10多年时间,仅凭一个人的力量就推动了图形学及计算机硬件的发展,他是美国创业梦及个人英雄主义的完美体现。
RayCasting 射线追踪从Wolfenstein 3D 到DOOM3,我又重玩了一遍,技术进步的轨迹清晰可见。
卡马克是个天才,但他技术的高楼并不是凭空建立,他的聪明才智加上他的专注造就了今天的卡马克及DOOM3。
追随他的足迹,我想探究天才造就的秘密,那就先从RayCasting 说起吧! 在当时286 386时代,CPU 速度的低下是不可能在实时的状态下运行真正的3D 引擎的,RayCasting 算法的出现是第一个解决之道。
由于它只需要对每条垂线进行必要的计算,所以它能够运行的很快。
Wolfenstein 3D 的射线追踪引擎非常的有限,所有的墙必须是相同的高度,而且在2D 平面他们必须是正方形的格子。
就像在Wolfenstein 3D 的地图编辑器里看到的那样。
像梯子,跳跃和高度差这样的东东在这个引擎里是不被实现的。
在DOOM里虽然也使用了射线追踪引擎,但是更高级一些,可以实现例如斜的墙,不同的高度,地板及天花板以及透明的墙等。
游戏里人物及物品等都使用了2D的贴图,就像公告牌一样。
这里说明一下RayCasting并不是RayTracing!RayCasting是一种伪3D技术,是使得3D场景可以在比较低速的CPU上运行的一种解决办法;而RayTracing是一种真实3D场景的实时渲染技术,在真实的3D场景里他被用作映像及阴影的计算,它需要很高速的CPU 才能完成计算。
主要思想:RayCasting的主要思想是:地图是2D的正方形格子,每个正方形格子用0代表没有墙,用1 2 3等代表特定的墙,用来做纹理映射。
小升初数学射线知识点总结

小升初数学射线知识点总结射线是平面几何中的一个重要概念,它是由一个端点和在这个端点上选择的一个方向上的无穷多个点所构成的。
这个方向上的点的集合就是射线。
射线通常用小写字母表示,其开始的端点用大写字母表示。
射线上的点都是与端点在同一条直线上的无穷多个点。
射线的记法为:→AB其中A是射线的起点,B是射线的方向。
为了更好地理解射线,我们先来看一下射线的性质:1. 射线没有长度。
因为它是由一个端点和端点上某一方向上的无穷多个点共同构成的,所以不可能用长度来度量它。
2. 一个射线包含无穷多个点。
这是射线的显著特征,因为射线是由端点向某一方向无限延伸的。
3. 射线的起点不能被改变。
因为射线是由一个端点和在这个端点上选择的一个方向上的无穷多个点所构成的,所以射线的起点(也就是端点)是不可改变的。
接下来,让我们来看一下射线的应用:1. 射线在几何形状的描述中起到了关键作用。
在平面几何中,我们常常需要描述直线、射线和线段,这些概念都是描述几何形状时非常有用的。
射线可以帮助我们更好地理解几何形状,并进行相关的计算。
2. 射线在物理学中也有重要应用。
在物理学中,射线可以用来描述光线、热线等。
光线在空间中传播时就可以看作是一条射线,这对我们理解光学原理及应用有很大的帮助。
3. 射线在几何题中也经常出现。
在数学考试中会出现各种与射线相关的计算题目,因此我们要熟练掌握射线的相关性质和计算方法,以帮助我们更好地解题。
总结:射线是数学中一个重要的概念,在几何学、物理学等领域都有重要的应用。
了解射线的基本概念和性质,掌握射线的相关计算方法,对我们理解几何形状、物理过程等都是非常有帮助的。
希望通过本文的介绍,大家对射线有了更深入的理解,能够更好地运用射线概念解决相关问题。
射线投影算法

射线投影算法
射线投影算法是一种用于计算三维物体在二维平面上的投影的方法。
它的基本原理是将每个像素点看作一个射线,从相机位置向物体发射。
当射线与物体相交时,用相交点的颜色来填充像素点。
这种算法通常用于计算计算机图形学中的三维渲染和医学图像处理中的CT和MRI扫描。
射线投影算法可以通过许多不同的实现方式来实现。
其中最常见的是光线跟踪(ray tracing)和光线追踪(ray casting)。
光线跟踪通常用于计算高质量的渲染图像,但需要耗费大量的计算资源。
光线追踪则更加快速,但不够精确。
射线投影算法在医学图像处理中也有广泛的应用。
它可以用于计算CT和MRI扫描的图像,以及计算机辅助诊断(CAD)系统中的肿瘤检测和图像分割。
总之,射线投影算法是一种基于射线的投影方法,适用于计算三维物体在二维平面上的投影。
它在计算机图形学和医学图像处理中有广泛的应用。
- 1 -。
分区多步快速行进法射线路径计算方法

分区多步快速行进法射线路径计算方法1.场景划分:首先将整个场景划分为多个分区,每个分区包含一定数量的物体。
划分的方法有很多种,可以根据场景的特点采用不同的划分策略,如均匀划分、树结构划分等。
2.射线投射:对于每一条射线,从相机的位置出发,依次经过每个分区,直到射线与物体相交或者射线超出场景范围。
在每个分区中,判断射线是否与该分区内的物体相交。
如果相交,记录相交点的位置和物体的相关信息。
3.优化行进:在计算射线路径时,可以根据需要进行一些优化,以提高计算效率。
例如,可以根据物体的边界框信息进行空间剪裁,排除不可能与射线相交的物体。
还可以使用加速结构,如包围盒树,对物体进行组织和,以减少相交计算的数量。
4.多步行进:在分区多步快速行进法中,射线的行进是分步进行的,即每次只前进一步。
在每个分区中,根据上一步的相交点和入射方向,计算射线在当前分区中的行进距离。
然后,在下一个分区中,以当前相交点为起点,按照之前的步骤计算新的相交点。
5.相交判断:在每个分区中,判断射线是否与该分区内的物体相交。
相交的判断方法可以根据物体的类型和形状采用不同的算法。
例如,对于球体,可以使用球-射线相交检测算法;对于三角形网格,可以使用莫勒-特鲁恩相交检测算法等。
6.相交点计算:如果射线与物体相交,需要计算射线与物体交点的位置和其他相关信息。
根据物体的形状和相交检测算法的具体实现,可以使用数学公式计算相交点的位置,并获取所需的信息,如法线、颜色等。
7.结果输出:对于每条射线,根据需要输出相交点的位置和其他相关信息,以及射线与场景中其他物体相交的次数。
可以将相交点的信息用于光线追踪渲染、碰撞检测等应用中。
总之,分区多步快速行进法是一种高效的射线路径计算方法,它通过将场景划分为多个分区,并将射线按照一定的顺序行进,以逐步快速地计算射线与物体的相交信息。
这种方法有效地减少了计算量,提高了计算效率,可以广泛应用于计算机图形学、游戏开发等领域中。
射线检测算法

射线检测算法射线检测算法是一种常用的计算机图形学算法,用于检测和判断射线与物体之间的交点。
它在计算机图形学中有着广泛的应用,如碰撞检测、物体投射等。
本文将介绍射线检测算法的原理、应用以及优缺点。
一、原理射线检测算法的基本原理是通过确定射线与物体之间的交点来判断射线是否与物体相交。
其核心思想是将射线视为一条直线,通过判断这条直线与物体的相交情况来确定射线的位置和方向。
射线检测算法的具体实现可以分为两步:首先是确定射线与物体的相交性,即判断射线是否与物体相交;其次是确定交点的位置,即确定射线与物体的交点坐标。
二、应用射线检测算法在计算机图形学中有着广泛的应用。
其中最常见的应用之一是碰撞检测。
在3D游戏开发中,为了实现真实的物理效果,需要检测游戏角色与场景中的物体是否发生碰撞。
射线检测算法可以用来判断射线与物体是否相交,从而判断游戏角色是否与物体发生碰撞。
射线检测算法还可用于物体投射。
在计算机图形学中,物体投射是一种常见的技术,用于在三维场景中生成阴影效果。
通过射线检测算法,可以确定射线与物体的交点,从而确定物体的投射位置和方向,实现真实的阴影效果。
三、优缺点射线检测算法具有以下优点:1. 算法简单易于实现。
射线检测算法的基本原理简单明了,实现起来比较容易。
2. 算法效率高。
射线检测算法可以通过一系列快速的计算和判断,快速确定射线与物体的相交性,提高算法的效率。
射线检测算法也存在一些缺点:1. 算法复杂度较高。
当场景中物体较多时,射线检测算法需要进行大量的计算和判断,导致算法复杂度增加。
2. 算法对物体形状敏感。
射线检测算法在处理复杂的物体形状时,可能会出现误判的情况,导致检测结果不准确。
四、总结射线检测算法是一种常用的计算机图形学算法,用于检测射线与物体之间的交点。
它在碰撞检测、物体投射等方面有着广泛的应用。
尽管射线检测算法具有一些优缺点,但在实际应用中,我们可以根据不同的需求选择合适的算法。
以上是关于射线检测算法的介绍,希望能对读者有所启发。
射线型布局算法简述

可视化布局算法布局算法是整个拓扑可视化系统的核心问题,选择合适的布局策略能够更好的切合用户需要解决的问题、能够更好的进行拓扑图形的绘制和实现。
布局算法主要需要解决的问题是如何确定和分配映射在显示界面上的几何图形的各个节点和边的以坐标表示的具体位置,简单的说也就是为可视化图形中的每一个节点和边分配其显示在界面上的坐标。
一个适合的良好的拓扑布局算法,能够有效地避免显示出来的拓扑结构图中节点的重叠,能够大大的减少拓扑结构图中边之间的交叉,能够更加美观大方的展示出要处理的网络的拓扑结构,能够使管理人员更方便的获取网络信息、进行网络管理。
拓扑绘图布局算法根据其作用和特征的不同可以分为很多不同的类别,这里从网络拓扑可视化的角度出发,将整个拓扑绘图布局算法分为物理布局算法和网络布局算法两类。
所谓物理布局,就是将节点的地理位置信息简单的解析为与其相对应的布局坐标,使得在拓扑图中能够清晰的发现节点的位置信息以及节点之间的相对位置和相对距离。
拓扑节点相关地理位置属性的映射和展示对于与地理位置相关的网络拓扑可视化来说有着极其重要的意义,但是也正是由于物理布局算法的这个特性使得这种方法相对来说更加适用于主干网络拓扑的可视化,而对于相对细致的局部网络或者主干网络之下的子网络的可视化则显得并不合适。
物理布局算法中最具代表性的方法是地理位置映射算法,很多以主干网络为研究对象的网络拓扑工具和网络拓扑系统都是采用这种算法,这其中比较著名的有以平面方式解析展示网络节点地理信息的和以及在三维球体上解析展示节点地理信息的。
逻辑布局算法与物理布局算法最大的不同就在于,逻辑布局算法不用去考虑节点在网络中的实际地理位置,只需要根据网络拓扑得到的具体节点的情况来设计分配节点的布局空间和布局策略。
逻辑布局算法让人们在设计实现布局的过程中,可以充分的针对现实问题分析解决办法,可以充分的利用图相关算法的技术和理论进行拓扑图的布局和绘制,可以不依赖网络节点物理位置的情况,更好的关心和研究网络节点的相互关系和网络拓扑图的内在特性。
射线法确定经纬度多边形

射线法确定经纬度多边形哎,说起这个射线法确定经纬度多边形啊,我得先给你唠唠啥是射线法,还有为啥咱们得用这个方法来确定经纬度多边形。
你看啊,咱们平时在地图上看到的那些区域,有圆的、方的、还有各种奇形怪状的,对吧?这些区域啊,其实都是由一个个的经纬度点围成的多边形。
就像咱们小时候玩的拼图,每一块都有它的边界,这些边界围起来就是一个形状。
那射线法呢,就像是咱们手里拿着一把神奇的尺子,从多边形的一个点开始,往四面八方画线。
这些线啊,就像是从这个点发射出去的射线,它们会碰到多边形的其他边。
咱们只要数一数这些射线被多边形边拦截了多少次,是奇数还是偶数,就能知道这个点是在多边形里面还是外面了。
为啥要用这个方法呢?因为啊,地图上的这些多边形区域,有时候会很复杂,有很多拐点,还有很多边。
如果咱们一个个地去比较点的位置,那实在是太麻烦了。
但是用射线法呢,就简单多了。
咱们只需要从这个点出发,画几条线,数一数就可以了。
就像咱们平时数数一样,简单又快捷。
好了,说了这么多,咱们来看看怎么用射线法来确定经纬度多边形吧。
首先呢,咱们得有一个多边形的经纬度点列表。
这些点就像是拼图上的那些小块,它们围在一起就形成了一个多边形。
然后啊,咱们再选一个点,这个点可以是多边形里面的,也可以是外面的,咱们要判断这个点到底是在里面还是外面。
接下来啊,咱们就从这个点出发,往一个方向画一条射线。
这条射线啊,就像是从这个点发射出去的一道光芒,它会穿过地图,碰到多边形的边。
咱们要做的就是,把这条射线碰到的每一条边都记录下来,然后数一数它到底碰到了多少次。
如果射线碰到的边数是奇数,那就说明这个点在多边形里面。
为啥呢?因为啊,当射线从多边形里面出发时,它会先碰到一条边,然后进入多边形内部,再碰到第二条边,然后又出来,如此反复。
所以,当它最后出来的时候,它碰到的边数一定是奇数。
而如果射线碰到的边数是偶数,那就说明这个点在多边形外面。
为啥呢?因为啊,当射线从多边形外面出发时,它会先穿过一条边进入多边形外部的一个区域,然后再穿过另一条边回到原来的位置。
放射式构图

放射式构图
放射式构图是以拍摄主体为核心,向四周扩散放射的构图方式。
主体核心与向心式构图相同,陪体则是背离主体,指向画外,还是举个例子,被一群拿着长矛围住的将军,突然将矛头指向身后,而背对将军,虽然还是将这位将军包围,但在方向性上最为明显的改变,也然整个局势发生了变化。
与向心式构图相同,放射式构图同样属于一种引导线构图,应用此方法拍摄的照片,同样具有将人的注意力集中在主体的效果,附加上其放射性,常常能给人以一种舒展、开阔、扩散的视觉感受。
放射式构图常用于需要突出展现主体而现场有较为混乱的场景中,常常需要人为对景物进行布置,如分散的花瓣、咖啡豆等,当然,也有本身具备放射式的景物,如烟花、耶稣光等,有时也运用使人物或景物在复杂的场景中,有时也运用于使人物或景物在复杂场景中显示出特殊效果的情况。
这是一种极其冷门的构图方法,在运用这种构图方法时,要注意主体的位置和背景之间的关系,协调好复杂的关系,更需要摄影师对景物的勘察,和精心的设计才能将放射式构图的优势发挥出来,最重要的是培养一双发现美的眼睛,也可以说是摄影眼,这需要大家坚持不懈的勤奋与练习,最后达到随心所欲、望眼欲穿的摄影水平。
(完整版)奥数知识点-简单数阵图

简单数阵图一、辐射型数阵图
从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和。
先求重叠数。
数总和 + 中心数×重复次数=公共的和×线数
重叠部分 = 线总和 - 数总和 / 线总和 = 公共的和×线数
数和:指所有要填的数字加起来的和
中心数:指中间那数字,即重复计算那数字(重叠数)
重复次数:中心数多算的次数,一般比线数少1
公共的和:指每条直线上几个数的和
线数:指算公共和的线条数
二、封闭型数阵图
多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
突破关键:确定顶点上的数字,公共的和。
数和+重叠数的和=公共的和×边数
数和:指所有要填的数字加起来的和
公共的和:指每条直线上几个数的和
重叠数和:指数阵图顶角重复算的数全加起来的和
边数:指封闭图形的边数。
射线相交算法

射线相交算法1. 简介射线相交算法是计算机图形学中常用的一种算法,用于确定一条射线与场景中的物体是否相交,并计算出相交点的位置。
该算法在计算机游戏、虚拟现实、计算机辅助设计等领域中广泛应用。
2. 基本原理射线相交算法基于光线追踪的思想,通过模拟光线从相机发出,与场景中的物体相交的过程来确定相交点的位置。
算法的基本原理如下:1.发射射线:从相机位置出发,沿着特定方向发射一条射线。
2.确定相交物体:遍历场景中的物体,判断射线与物体是否相交。
3.计算相交点:如果射线与物体相交,计算出相交点的位置。
4.确定最近相交点:遍历所有相交点,找到距离相机最近的相交点。
5.渲染物体:根据相交点的位置和相关属性,使用光照模型计算出物体的颜色,并渲染到屏幕上。
3. 具体实现射线相交算法的具体实现包括以下几个步骤:3.1 发射射线首先,需要确定相机的位置和方向。
一般情况下,相机位置为三维空间中的一个点,相机方向为一个单位向量,表示相机的朝向。
然后,根据相机位置和方向,可以计算出从相机发出的射线的方向。
射线的起点为相机位置,方向为相机方向。
3.2 确定相交物体对于场景中的每个物体,需要判断射线是否与物体相交。
常用的判断方法包括包围盒判断和精确相交判断。
包围盒判断是先判断射线是否与物体的包围盒相交,如果相交则进一步进行精确相交判断。
精确相交判断使用物体的几何形状和射线方程进行计算,判断射线是否与物体的表面相交。
3.3 计算相交点如果射线与物体相交,需要计算出相交点的位置。
对于几何形状简单的物体,如球体,可以使用解析解来计算相交点的位置。
对于复杂的物体,如多边形网格,常使用数值方法,如迭代求解或二分法,来逼近相交点的位置。
3.4 确定最近相交点遍历所有相交点,找到距离相机最近的相交点。
通常使用距离相机最近的相交点来进行渲染。
3.5 渲染物体根据相交点的位置和相关属性,使用光照模型计算出物体的颜色,并渲染到屏幕上。
4. 算法优化射线相交算法是计算密集型的算法,对于复杂的场景和大量的物体,计算量可能非常大。
射线投影算法

射线投影算法射线投影算法,是一种用于生成人工衍射图像的数学计算方法。
该算法使用一定数量的射线线性穿过物体,并在检测器上记录这些射线投影的结果。
这种方法既可以用于医学成像,也可以用于工业检测等领域。
射线投影算法是通过测量物体对射线的吸收程度来推断物体内部结构的。
当一束平行射线投射到物体上时,射线会以不同的强度通过不同的结构组织,并在另一侧的检测器上留下不同的影像。
这些影像反映了物体内部结构的变化,可以用于生成计算机重建图像。
射线投影算法广泛应用于医学成像、工业检测等领域。
例如,CT扫描就是一种基于射线投影算法的医学成像技术。
在CT扫描中,患者通过一个旋转的X射线机,将大量的X射线束穿过人体不同的部位。
检测器会记录每束射线的强度,从而得出一个射线投影图。
这些投影数据可以通过计算机算法进行重建,生成三维成像。
CT扫描可以帮助医生获得身体内部的详细信息,帮助诊断和治疗。
射线投影算法还可以应用于工业检测中。
例如,在金属检测中,射线投影可以帮助检测各种缺陷,如裂缝、气泡、夹杂等。
通过绘制物体各部位的X射线投影图,可以发现物体表面或内部的缺陷,帮助提高生产效率和降低成本。
1. 可以获得比较高的分辨率,可以检测到物体内部微小的变化。
2. 可以采集到数据,从而生成三维图像,给医生或工程师提供详细的信息。
3. 可以实现无损检测,避免对物体造成损伤。
1. 存在辐射危险,需要采取安全措施。
2. 需要较长的扫描时间,成像速度较慢。
3. 对比度较低,易受深度吸收的影响。
需要调整投影角度,进行多角度扫描,提高成像质量。
总结射线投影算法是一种常用的成像技术,可以在医学、工业检测等领域获得广泛的应用。
其基本原理是以线性方式穿过物体,通过记录射线的投影数据来重建三维成像。
由于其高精度、高分辨率等特点,被广泛应用于成像技术中,为医生和工程师提供了可靠的数据信息,使得检测和治疗更加精确和高效。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可视化布局算法
布局算法是整个拓扑可视化系统的核心问题,选择合适的布局策略能够更好的切合用户需要解决的问题、能够更好的进行拓扑图形的绘制和实现。
布局算法主要需要解决的问题是如何确定和分配映射在显示界面上的几何图形的各个节点和边的以坐标表示的具体位置,简单的说也就是为可视化图形中的每一个节点和边分配其显示在界面上的坐标。
一个适合的良好的拓扑布局算法,能够有效地避免显示出来的拓扑结构图中节点的重叠,能够大大的减少拓扑结构图中边之间的交叉,能够更加美观大方的展示出要处理的网络的拓扑结构,能够使管理人员更方便的获取网络信息、进行网络管理。
拓扑绘图布局算法根据其作用和特征的不同可以分为很多不同的类别,这里从网络拓扑可视化的角度出发,将整个拓扑绘图布局算法分为物理布局算法和网络布局算法两类。
所谓物理布局,就是将节点的地理位置信息简单的解析为与其相对应的布局坐标,使得在拓扑图中能够清晰的发现节点的位置信息以及节点之间的相对位置和相对距离。
拓扑节点相关地理位置属性的映射和展示对于与地理位置相关的网络拓扑可视化来说有着极其重要的意义,但是也正是由于物理布局算法的这个特性使得这种方法相对来说更加适用于主干网络拓扑的可视化,而对于相对细致的局部网络或者主干网络之下的子网络的可视化则显得并不合适。
物理布局算法中最具代表性的方法是地理位置映射算法,很多以主干网络为研究对象的网络拓扑工具和网络拓扑系统都是采用这种算法,这其中比较著名的有以平面方式解析展
示网络节点地理信息的和以及在三维球体上解析展示节点地理信息的。
逻辑布局算法与物理布局算法最大的不同就在于,逻辑布局算法不用去考虑节点在网络中的实际地理位置,只需要根据网络拓扑得到的具体节点的情况来设计分配节点的布局空间和布局策略。
逻辑布局算法让人们在设计实现布局的过程中,可以充分的针对现实问题分析解决办法,可以充分的利用图相关算法的技术和理论进行拓扑图的布局和绘制,可以不依赖网络节点物理位置的情况,更好的关心和研究网络节点的相互关系和网络拓扑图的内在特性。
逻辑拓扑布局算法是网络拓扑可视化过程中重要的实现方法,是研究网络拓扑可视化技术的重要工具,在逻辑拓扑布局算法的研究和开发过程中,产生了许多著名的布局算法,使得逻辑拓扑布局算法得到了巨大的发展。
射线型布局算法
射线型布局算法在一定程度上可以说是树型布局算法的极坐标形式,它要求在形成布局图之后,图中任意一个节点到中心节点的距离都是图形中两点之间的最短路径,也就是说在射线型布局算法中,中心点的选择会根据节点的度数和节点到叶节点的最短距离来综合考虑,一般会选择节点度数较大或者到叶节点最短距离最大的节点作为布局图的中心点。
使用射线型布局算法,设计实现比较简单,能够清晰的展示节点数目较多的网络拓扑结构,且设备的放置不易产生重复,空间利用率较高,生成的网络拓扑结构图效果比较好,但是同样存在的问题是这种布局算法也比较适合于中小型网络拓扑的绘图布局,而不太适合于大型网络拓扑的布局。
射线型布局算法在具体构图实现的时候首先找到根节点,也就是等级最高的节点,将它放置在整个图的中心位置上然后寻找此根节点的子节点,将这些子节点均匀分布在以根节点为圆心的圆上这些子节点若还有子节点,则将这些子节点以它们的父节点为圆心做均匀分布最后依次递归重复第三步直至所有的节点都被遍历之后整个算法结束,算法流程图如图所示
系统设计原则
1.清晰的网络层次
作为拓扑图显示介质的屏幕的大小是有限的,而需要表现的网络结构却是非
常复杂的,这使得在一张有限的画图上尽可能的展现网络拓扑的细节变的非常困
难,而清晰的网络层次却是认识网络结构的前提,所以在进行系统设计的时候,
更要注意对于图像层次性的把握和处理。
2.明确的连接关系
网络拓扑图应该具有良好的可读性,应该尽可能注意图中节点位置、距离等
因素,以求尽可能体现出实际网络的结构信息,减少节点连线间的交叉,考虑网
络中可能存在的环路情况,同时对于图中节点的类型和参数应该具有良好的表现,
应该明确体现出不同设备节点之间的区别和联系。
3.良好的操作性能
在一个拓扑可视化系统中应该具有良好的操作性,应该允许网络管理员或者
用户对于网络拓扑图的布局、连线等进行改动和调整,而且,这些手工的改动应
该能够被系统记录和保存,以保证拓扑图显示的一致性。
4.完善的交互功能
拓扑可视化系统作为网络管理系统中的一个可视化模块,负责将各种网络相
关信息以图形化的方式直接呈现给用户,是与用户交流较多的一个部分,一个较
好的拓扑可视化系统应该充分的考虑与用户的交流和反馈,应该具有良好的交互
模式和友善的操作界面。
射线型拓扑布局算法实现
射线型布局算法与树型布局算法有很多共同的地方,同树型布局算法一样,射线型布局算法,程序设计实现方面比较简单,能够清晰的展示节点数目较多的网络拓扑结构,在具体放置设备的时候不易产生重复,绘图空间利用率较高,它生成的网络拓扑结构图,结构清晰,层次分明,画面整洁,易于分析和理解整个网络拓扑结构。
但是同树型布局算法一样,射线型拓扑布局算法存在的问题也是比较适合于中小型网络拓扑的绘图布局,而当节点数量变得很多时,射线型布局算法就显得有些不合适了,产生的拓扑图也开始变得拥挤,大大降低了拓扑图的展示效果。
在射线型拓扑布局算法中,核心部分的节点坐标计算方法与树型拓扑布局算法中有所不同。
在射线型拓扑布局算法中,子节点不再排布在父节点的下方呈树型结构,而是排布在一个以父节点为圆心的圆上呈圆形结构,子节点的排布以父节点的坐标位置为基础和前提,并且还要兼顾整个图形的美观和协调。
为了使节点坐标计算和显示比较简单,在分配具体的坐标的时候都采用整型数据,当计算中出现非整型数据时将对其进行强制转换。
