2015年中考压轴题二次函数求最短距离
二次函数最短路径问题

例题:(2013滨州)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
跟踪练习:
1.(2015•甘肃武威)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
二次函数综合题
例题:(2013滨州)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
跟踪练习:
1.(2015•甘肃武威)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(2015湖南)如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
例题:已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.(1) 求抛物线的解析式;(2) 抛物线的对称轴上有一动点P,求出PA+PD的最小值;
二次函数压轴(最短路径).docx

26. (12分)(2015*天水)在平面直角坐标系屮,已知y= - 2x?+bx+c (b、c为常数)的顶2点为P,等腰直角三角形ABC的顶点A的坐标为((),・1),点C的坐标为(4, 3),直角顶点B在第四象限.(1)如图,若抛物线经过A、B两点,求抛物线的解析式.(2)平移(1)中的抛物线,使顶点P在直线AC±并沿AC方向滑动距离为返时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.(3)在(2)的情况卜,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q, 取BC的屮点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.考点:二次函数综合题.分析:(1)先求出点B的处标,然后利用待定系数法求出抛物线的函数表达式;(2)如答题图2,设顶点P在直线AC±并沿AC方向滑动距离迈吋,到达P',作P,M lly轴,PMIIx轴,交于M点,根据白线AC的斜率求得AP' PM是等腰直角三角形,进而求得抛物线向上平移1个单位,向右平移1个单位,从而求得平移后的解析式,进而求得为x轴的交点,与直线AC的交点,即可证得结论;(3)如答图3所示,作点B关于直线AC的对称点B',由分析可知,当B,、Q、F (AB 屮点)三点共线时,NP+BQ最小,最小值为线段B‘ F的长度.解答:解:(1)丁等腰直角三角形ABC的顶点A的处标为(0, - 1), C的坐标为(4, 3)二点B的坐标为(4, - 1).•••抛物线过A (0,・1), B (4,・1)两点,「c二 _]-2><16+4b+c二-1 'I 2解得:b=2, c= - 1,•••抛物线的函数表达式为:y=・-X2+2X - 1.2(2)如答题图2,设顶点P在直线AC ±并沿AC方向滑动距离返时,到达P',作P,Mlly轴,PMIIx轴,交于M点,•.•点A的坐标为(0, - 1),点C的坐标为(4, 3),・•・直线AC的解析式为y=x- 1,丁直线的斜率为1,PM是等腰直角三角形,•••PP' =V2,.-.P/ M=PM=1,.•.抛物线向上平移1个单位,向右平移1个单位,T+2X-1=4(X-2)2+B•••平移后的抛物线的解析式为y=-^ (x-3) ?+2,令y=0, 则F("2+2,解得X[ = l, X=52,•••平移后的抛物线与x轴的交点为(1, 0), (5, 0), 丨尸一1&-3)2+2 (x=i ( x=3解{ 2 ,得』或][尸x-l 1尸°1应二平移后的抛物线与AC的交点为(1, 0),•••平移后的抛物线与直线AC交于x轴上的同一点(1, 0).(3)如答图3,取点B关于AC的对称点B',易得点B'的坐标为(0, 3), BQ=B, Q, 取AB中点F, 连接QF, FN, QB',易得FNIIPQ,且FN二PQ,•••四边形PQFN为平行四边形./.NP=FQ.••.NP+BQ二FQ+B,Q>FB^ =^22+42=2Vl-.•.当B'、Q、F三点共线时,NP+BQ最小,最小值为2馅.点评:本题为二次函数中考压轴题,考查了二次函数的图彖与性质、待定系数法、一次函数、儿何变换(平移,对称)、等腰直角三角形、平行四边形、轴対称-最短路线问题等知识点,考查了存在型问题和分类讨论的数学思想,试题难度较大.28. (12分)(2015*西宁)如图,在平面直角坐标系xOy屮,以M为顶点的抛物线与x轴分别相交于B, C两点,抛物线上一点A的横处标为2,连接AB, AC,正方形DEFG的一边GF在线段BC上,点D, E在线段AB, AC ±, AK丄x轴于点K,交DE于点H,下表给出了这条抛物线X• • •-204810• • •y r0595P• • •(1)求出这条抛物线的解析式;(2)求正方形DEFG的边长;(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP 的周长最小?若存在,请求出P, Q两点的处标;若不存在,请说明理由.考点:二次函数综合题.分析:(1)利用已知表格中数据结合顶点式直接求出抛物线解析式即可;(2)百先得出四边形HEFK为矩形,再利用△ADE S/X ABC,得出正方形DEFG的边长;(3)首先求岀AB所在直线解析式,进而得出D点坐标,再求出直线A' D'的解析式得出Q'的坐标即可.解答:解:(1)由图表可得:抛物线的顶点坐标为:(4, 9),设函数解析式为:y=a (x - 4) 2+9 (a*0),把点(0, 5)代入尸a (x-4) 2+9,解得:a=-X4・••函数解析式为:y=--i (x-4) 2+9;(2)设正方形DEFG的边长为m,VAK±x$fll,・•・ ZAKC=90°,J ZDEF=ZEFG=90°,・・・四边形HEFK为矩形,.e.HK=EF=m,•・•点A在抛物线尸・* (x・4) ?+9上,横坐标为2,y= - — (x - 4) 2+9=8,4・••点A的坐标为:(2, 8),・•・AK=8,・•・AH=AK・HK=8・m,由题意可得:B ( - 2, 0), C (10, 0),・・・BC=12,•・・DE〃BC,A AADE^AABC,・AH_ DE••---- — -- 9AK BC•in•• ----- —-- 98 12…m=-——・・・正方形的边长为:単5(3)存在,理由:过顶点M作抛物线的对称轴直线1: x=4,设点A关于直线1: x=4对称点为A' , A'点的坐标为:(6, 8), ・•・设AB所在直线解析式为:y=kx+b,.(8=2k+b••(0=_2k+b,解得•・产◎[b二4・・・AB所在肓线解析式为:y=2x+4,•・・D在直线AB上,DG=—,5・・・点D的纵坐标为:単,5由2x+4=—,5解得:x=2,5・••点D的坐标为:G,竽),5 5设点D关于x轴对称点为D',则D'(辛,-单),5 5连接A' D z交对称轴于点P,交x轴于点Q,连接AP, DQ, 则四边形ADQP的周长最小,设总线A' D'的解析式为:尸k' x+b',[6k, +b,二8•••舍出二-学15 5K 7 解得:心・・・直线A' D f的解析式为:尸学X-卑,7 7当x=4 时,y=—x4 -—,・・・P (4, —),7 7 7 7当y=0 时,x=-,2・・・Q点坐标为:(号,0).。
二次函数典型例题——最短路径

二次函数典型例题——最短路径1、已知抛物线2:(1)1C y x m x =-++的顶点在坐标轴...上. (1)求m 的值;(2)0>m 时,抛物线C 向下平移n (n > 0)个单位后与抛物线C 1:c bx ax y ++=2关于y 轴对称,且1C 过点(n ,3),求C 1的函数关系式; (3)03<<-m 时,抛物线C 的顶点为M ,且过点P (1,y 0)问在直线1-=x 上是否存在一点Q 使得△QPM 的周长最小,如果存在,求出点Q 的坐标, 如果不存在,请说明理由.(1)m 的值=1,-1,-3;(2)C 1的函数关系式:22y x x =+;(3)Q 的坐标4(1,)3-.2、在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B .⑴直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3)已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值. 解:(1)21(2)4A n n +,,()B n n ,. (2) d =AB =A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+∴ 当14n =时,d 取得最小值18.当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB =PM . (如图10)(3) ∵ 对一切实数x 恒有 x ≤y ≤2124x +, ∴ 对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ① 图10xy111APBMO3、已知关于x 的一元二次方程()0312=-+--m x m x .(1)求证:不论m 取何值时,方程总有两个不相等的实数根.(2)若直线()31+-=x m y 与函数m x y +=2的图象1C 的一个交点的横坐标为2,求关于x 的一元二次方程()0312=-+--m x m x 的解.(3)在(2)的条件下,将抛物线()312-+--=m x m x y 绕原点旋转︒180,得到图象2C ,点P 为x 轴上的一个动点,过点P 作x 轴的垂线,分别与图象1C 、2C 交于N M 、两点,当线段MN 的长度最小时,求点P 的坐标.解:(1)证明:()[]()3412----=∆m m124122+-+-=m m m 1362+-=m m()432+-=m∵不论m 取何值时,()032≥-m ∴()0432>+-m ,即0>∆∴不论m 取何值时,方程总有两个不相等的实数根. (2)将2=x 代入方程()0312=-+--m x m x ,得3=m再将3=m 代入,原方程化为022=-x x , 解得2,021==x x . (3)将3=m 代入得抛物线:x x y 22-=,将抛物线x x y 22-=绕原点旋转︒180得到的图象2C 的解析式为:x x y 22--=.设()0,x P则()3,2+x x M ,()x x x N 2,2--()()25212322232222+⎪⎭⎫ ⎝⎛+=++=---+=x x x x x x MN∴当21-=x 时,MN 的长度最小,此时点P 的坐标为⎪⎭⎫⎝⎛-0,21(昌平)27.已知抛物线2y ax bx c =++经过原点O 及点A (-4,0)和点B (-6,3). (1)求抛物线的解析式以及顶点坐标;(2)如图1,将直线2y x =沿y 轴向下平移后与(1)中所求抛物线只有一个交点C ,平移后的直线与y 轴交于点D ,求直线CD 的解析式;(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离.yx图1BACD O yx图2CD O解:(1)∵ 抛物线经过()0,0,()4,0- ,()6,3-三点,∴ 01640,366 3.c a b a b =⎧⎪-=⎨⎪-=⎩ ………………………………………… 1分解得 1410a b c ⎧=⎪⎪=⎨⎪=⎪⎩,,. …………………………… 2分∴ 抛物线的解析式为214y x x =+.∵()()22211144421444y x x x x x =+=++-=+-∴抛物线的顶点坐标为()2,1-- ……………3分 (2)设直线CD 的解析式为2y x m =+,根据题意,得2124x x x m +=+, …………… 4分 化简整理,得2440x x m --=,由16160m ∆=+=,解得1m =-, ……………… 5分∴直线CD 的解析式为21y x =- .(3)点的坐标为()2,7, …………………………… 6分. ……………………… 7分。
点到二次函数的最短距离公式

点到二次函数的最短距离公式
二次函数是高中数学中的一个重要知识点,它在数学、物理、工程学等领域都有广泛的应用。
而当我们学习二次函数时,需要掌握的一个重要概念是“最短距离”。
那么,如何求解二次函数的最短距离呢?
首先,我们需要知道二次函数的一般式:y=ax^2+bx+c。
其中,a、b、c都是常数,x、y是变量。
我们假设点P(x0,y0)不在二次函数y=ax^2+bx+c上,而点Q(x,y)在该二次函数上,且点P到二次函数的最短距离为d。
接下来,我们可以通过以下公式来求解点P到二次函数的最短距离:
d=|a{x0^2-x^2}+b(x-x0)|/2|a|
其中,|...|表示绝对值。
这个公式的本质就是将点P到点Q的距离求导,使其等于0,从而得到最短距离。
需要注意的是,当a=0时,上述公式不适用。
此时,二次函数就成了一条直线,点P到该直线的最短距离可以通过求解点P到直线的垂线来求得。
掌握了二次函数的最短距离公式,我们便能够更加深入地理解二次函数的性质和应用。
- 1 -。
中考压轴题二次函数求最短距离

20XX 年中考数学二次函数求最短距离备考专题训练知识点:1.点到直线的距离直线外一点到直线的距离垂线段最短。
2.直线与直线的距离 两直线间垂线段最短。
3.在直线上找一点与直线同侧两点(不在直线上)的连线距离和最短的求法 首先找同侧两点中任一点关于该直线对称的点,再将同侧另一点与对称点连线,该连线与直线的交点即为所求。
中考真题训练1.如图,在锐角ABC △中,4245AB BAC =∠=,°,BAC ∠的平分线交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是___________ .ABCDN M(第1题图)2.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q 的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.3.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式;⑵动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标。
(第2题)4 x2 2A8 -2 O-2 -4 y 6B C D -444.如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t >,tan 3BAC ∠=,抛物线经过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点. (1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值;(3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.二次函数求最短距离参考答案1.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,OACBxy请说明理由.解:(1) 将点A (-4,8)的坐标代入2y ax =,解得12a =.……1分将点B (2,n )的坐标代入212y x =,求得点B 的坐标为(2,2),则点B 关于x 轴对称点P 的坐标为(2,-2). ……1分直线AP 的解析式是5433y x =-+.……1分 令y =0,得45x =.即所求点Q 的坐标是(45,0).……1分(2)① 解法1:CQ =︱-2-45︱=145,……1分故将抛物线212y x =向左平移145个单位时,A ′C +CB ′最短,……2分此时抛物线的函数解析式为2114()25y x =+.……1分解法2:设将抛物线212y x =向左平移m 个单位,则平移后A ′,B ′的坐标分别为A ′(-4-m ,8)和B ′(2-m ,2),点A ′关于x 轴对称点的坐标为A ′′(-4-m ,-8).直线A ′′B ′的解析式为554333y x m =+-. (1)分要使A ′C +CB ′最短,点C 应在直线A ′′B ′上, ……1分 将点C (-2,0)代入直线A ′′B ′的解析式,解得145m =.……1分故将抛物线212y x =向左平移145个单位时A ′C +CB ′最短,此时抛物线的函数解析式为2114()25y x =+.……1分② 左右平移抛物线212y x =,因为线段A ′B ′和CD 的长是定值,所以要使四边形A ′B ′CD 的周长最短,只要使A ′D +CB ′最短; ……1分第一种情况:如果将抛物线向右平移,显然有A ′D +CB ′>AD +CB ,因此不存在某个位置,使四边形A ′B ′CD 的周长最短.……1分第二种情况:设抛物线向左平移了b 个单位,则点A ′和点B ′的坐标分别为A ′(-4-b ,8)和B ′(2-b ,2).因为CD =2,因此将点B ′向左平移2个单位得B ′′(-b ,2),要使A ′D +CB ′最短,只要使A ′D +DB ′′最短. ……1分(第1题)4 x2 2A8 -2 O-2 -4 y 6 B CD -44(第1题(1)) 4 x2 2A8 -2 O -2 -4 y 6 BCD -44Q P (第1题(2)①)4 x2 2 A ′8-2 O -2 -4 y 6B ′ CD -4 4 A ′′(第1题(2)②)4 x 2 2A ′8-2 O-2 -4 y6B ′CD -4 4 A ′′B ′′点A ′关于x 轴对称点的坐标为A ′′(-4-b ,-8), 直线A ′′B ′′的解析式为55222y x b =++.要使A ′D +DB ′′最短,点D 应在直线A ′′B ′′上,将点D (-4,0)代入直线A ′′B ′′的解析式,解得165b =. 故将抛物线向左平移时,存在某个位置,使四边形A ′B ′CD 的周长最短,此时抛物线的函数解析式为2116()25y x =+.……1分2.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
2015中考数学真题分类汇编:二次函数压轴题(含答案解析可打印)

2015中考数学真题汇编:二次函数1.(13分)(2015•福州)如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.(1)这条抛物线的对称轴是,直线PQ与x轴所夹锐角的度数是;(2)若两个三角形面积满足S△POQ=S△PAQ,求m的值;(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.解答:解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,∴抛物线的对称轴是x=2,∵直线y=x+m,∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),∴交点到原点的距离相等,∴直线与坐标轴围成的三角形是等腰直角三角形,∴直线PQ与x轴所夹锐角的度数是45°,故答案为x=2、45°.(2)设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=S△PAQ不成立;①当点B落在线段OA上时,如图①,==,由△OBE∽△ABF得,==,∴AB=3OB,∴OB=OA,由y=x2﹣4x得点A(4,0),∴OB=1,∴B(1,0),∴1+m=0,∴m=﹣1;②当点B落在线段AO的延长线上时,如图②,同理可得OB=OA=2,∴B(﹣2,0),∴﹣2+m=0,∴m=2,综上,当m=﹣1或2时,S△POQ=S△PAQ;(3)①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形,∵∠CDQ=45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点出时,PM最大,此时PM=6,∴PH的最大值为6,即PD+DQ的最大值为6.②由①可知:PD+PH≤6,设PD=a,则DQ﹣a,∴PD•DQ≤a(6﹣a)=﹣a2+6a=﹣(a﹣3)2+18,∵当点P在抛物线的顶点时,a=3,∴PD•DQ≤18.∴PD•DQ的最大值为18.2.(10分)(2015•莆田)抛物线y=ax2+bx+c,若a,b,c满足b=a+c,则称抛物线y=ax2+bx+c 为“恒定”抛物线.(1)求证:“恒定”抛物线y=ax2+bx+c必过x轴上的一个定点A;(2)已知“恒定”抛物线y=x2﹣的顶点为P,与x轴另一个交点为B,是否存在以Q 为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.解答:(1)证明:由“恒定”抛物线y=ax2+bx+c,得:b=a+c,即a﹣b+c=0,∵抛物线y=ax2+bx+c,当x=﹣1时,y=0,∴“恒定”抛物线y=ax2+bx+c必过x轴上的一个定点A(﹣1,0);(2)解:存在;理由如下:∵“恒定”抛物线y=x2﹣,当y=0时,x2﹣=0,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=﹣,∴顶点P的坐标为(0,﹣),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,∴存在两种情况:①如图1所示:作QM⊥AC于M,则QM=OP=,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,﹣),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为y=a(x+2)2﹣,把点A(﹣1,0)代入得:a=,∴抛物线的解析式为:y=(x+2)2﹣,即y═x2+4x+3;②如图2所示:顶点Q在y轴上,此时点C与点B重合,∴点C坐标为(1,0),∵CQ∥PA,∴∠OQC=∠OPA,在△OQC和△OPA中,,∴△OQC≌△OPA(AAS),∴OQ=OP=,∴点Q坐标为(0,),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为y=ax2+,把点C(1,0)代入得:a=﹣,∴抛物线的解析式为:y=﹣x2+;综上所述:存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形,抛物线的解析式为:y=x2+4x+3,或y=﹣x2+.3.(13分)(2015•泉州)阅读理解抛物线y=x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.问题解决如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.(1)写出点C的坐标,并说明∠ECF=90°;(2)在△PEF中,M为EF中点,P为动点.①求证:PE2+PF2=2(PM2+EM2);②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.解答:解:(1)当x=0时,y=k•0+1=1,则点C的坐标为(0,1).根据题意可得:AC=AE,∴∠AEC=∠ACE.∵AE⊥EF,CO⊥EF,∴AE∥CO,∴∠AEC=∠OCE,∴∠ACE=∠OCE.同理可得:∠OCF=∠BCF.∵∠ACE+∠OCE+∠OCF+∠BCF=180°,∴2∠OCE+2∠OCF=180°,∴∠OCE+∠OCF=90°,即∠ECF=90°;(2)①过点P作PH⊥EF于H,Ⅰ.若点H在线段EF上,如图2①.∵M为EF中点,∴EM=FM=EF.根据勾股定理可得:PE2+PF2﹣2PM2=PH2+EH2+PH2+HF2﹣2PM2=2PH2+EH2+HF2﹣2(PH2+MH2)=EH2﹣MH2+HF2﹣MH2=(EH+MH)(EH﹣MH)+(HF+MH)(HF﹣MH)=EM(EH+MH)+MF(HF﹣MH)=EM(EH+MH)+EM(HF﹣MH)=EM(EH+MH+HF﹣MH)=EM•EF=2EM2,∴PE2+PF2=2(PM2+EM2);Ⅱ.若点H在线段EF的延长线(或反向延长线)上,如图2②.同理可得:PE2+PF2=2(PM2+EM2).综上所述:当点H在直线EF上时,都有PE2+PF2=2(PM2+EM2);②连接CD、PM,如图3.∵∠ECF=90°,∴▱CEDF是矩形,∵M是EF的中点,∴M是CD的中点,且MC=EM.由①中的结论可得:在△PEF中,有PE2+PF2=2(PM2+EM2),在△PCD中,有PC2+PD2=2(PM2+CM2).∵MC=EM,∴PC2+PD2=PE2+PF2.∵PE=PF=3,∴PC2+PD2=18.∵1<PD<2,∴1<PD2<4,∴1<18﹣PC2<4,∴14<PC2<17.∵PC>0,∴<PC<.4.(12分)(2015•福建)如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).(1)求抛物线的解析式;(2)求点O到直线AB的距离;(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB 相似时,请你直接写出点M的坐标.解答:解:(1)设抛物线的解析式为y=a(x﹣1)2﹣1,将B点坐标代入函数解析式,得(5﹣1)2a﹣1=3,解得a=.故抛物线的解析式为y=(x﹣1)2﹣1;(2)由勾股定理,得OA2=11+12=2,OB2=52+32=34,AB2=(5﹣1)2+(3+1)2=32,OA2+AB2=OB2,∴∠OAB=90°,O到直线AB的距离是OA=;(3)设M(a,b),N(a,0)当y=0时,(x﹣1)2﹣1=0,解得x1=3,x2=﹣1,D(3,0),DN=3﹣a.①当△MND∽△OAB时,=,即=,化简,得4b=a﹣3 ①M在抛物线上,得b=(a﹣1)2﹣1 ②联立①②,得,解得a1=3(不符合题意,舍),a2=﹣2,b=,M1(﹣2,),当△MND∽△BAO时,=,即=,化简,得b=12﹣4a ③,联立②③,得,解得a1=3(不符合题意,舍),a2=﹣17,b=12﹣4×(﹣17)=80,M2(﹣17,80).综上所述:当△DMN与△OAB相似时,点M的坐标(﹣2,),(﹣17,80).5.(14分)(2015•漳州)如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.(1)填空:点C的坐标为(0,3),点D的坐标为(1,4);(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t 之间的关系式,并直接写出当t为何值时S最大,最大值为多少?解答:解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴C(0,3),D(1,4),故答案为:0;3;1;4;(2)∵在三角形中两边之差小于第三边,∴延长DC交x轴于点P,设直线DC的解析式为y=kx+b,把D、C两点坐标代入可得,解得,∴直线DC的解析式为y=x+3,将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,如图1,点P(﹣3,0)即为所求;(3)过点C作CE∥x,交直线BD于点E,如图2,由(2)得直线DC的解析式为y=x+3,由法可求得直线BD的解析式为y=﹣2x+6,直线BC的解析式为y=﹣x+3,在y=﹣2x+6中,当y=3时,x=,∴E点坐标为(,3),设直线P′C′与直线BC交于点M,∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),∴直线P′C′的解析式为y=x+3﹣t,联立,解得,∴点M坐标为(,),∵B′C′∥BC,B′坐标为(3+t,0),∴直线B′C′的解析式为y=﹣x+3+t,分两种情况讨论:①当0<t<时,如图2,B′C′与BD交于点N,联立,解得,∴N点坐标为(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=×6×3﹣(6﹣t)×(6﹣t)﹣t×2t=﹣t2+3t,其对称轴为t=,可知当0<t<时,S随t的增大而增大,当t=时,有最大值;②当≤t<6时,如图3,直线P′C′与DB交于点N,立,解得,∴N点坐标为(,),S=S△BNP′﹣S△BMP′=(6﹣t)×﹣×(6﹣t)×=(6﹣t)2=t2﹣t+3;显然当<t<6时,S随t的增大而减小,当t=时,S=综上所述,S与t之间的关系式为S=,且当t=时,S 有最大值,最大值为.6.(12分)(2015•甘南州)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,﹣4),B(x1,0),C(x2,0)三点,且|x2﹣x1|=5.(1)求b,c的值;(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.解答:解:(1)∵抛物线y=﹣x2+bx+c,经过点A(0,﹣4),∴c=﹣4又∵由题意可知,x1、x2是方程﹣x2+bx﹣4=0的两个根,∴x1+x2=b,x1x2=6由已知得(x2﹣x1)2=25又∵(x2﹣x1)2=(x2+x1)2﹣4x1x2=b2﹣24∴b2﹣24=25解得b=±,当b=时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.∴b=﹣.(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,又∵y=﹣x2﹣x﹣4=﹣(x+)2+,∴抛物线的顶点(﹣,)即为所求的点D.(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(﹣6,0),根据菱形的性质,点P必是直线x=﹣3与抛物线y=﹣x2﹣x﹣4的交点,∴当x=﹣3时,y=﹣×(﹣3)2﹣×(﹣3)﹣4=4,∴在抛物线上存在一点P(﹣3,4),使得四边形BPOH为菱形.四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(﹣3,3),但这一点不在抛物线上7.(10分)(2015•酒泉)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C (5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解答:解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B(1,0)代入得,解得,∴y=x﹣,∵点P的横坐标为3,∴y=×3﹣=,∴P(3,).(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,t2﹣t+4)(0<t<5),如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣x+4,把x=t代入得:y=﹣t+4,则G(t,﹣t+4),此时:NG=﹣t+4﹣(t2﹣t+4)=﹣t2+4t,∵AD+CF=CO=5,∴S△ACN=S△ANG+S△CGN=AM×NG+NG×CF=NG•OC=×(﹣t2+4t)×5=﹣2t2+10t=﹣2(t﹣)2+,∴当t=时,△CAN面积的最大值为,由t=,得:y=t2﹣t+4=﹣3,∴N(,﹣3).8.(12分)(2015•兰州)已知二次函数y=ax2的图象经过点(2,1).(1)求二次函数y=ax2的解析式;(2)一次函数y=mx+4的图象与二次函数y=ax2的图象交于点A(x1、y1)、B(x2、y2)两点.①当m=时(图①),求证:△AOB为直角三角形;②试判断当m≠时(图②),△AOB的形状,并证明;(3)根据第(2)问,说出一条你能得到的结论.(不要求证明)解答:(1)解:∵y=ax2过点(2,1),∴1=4a,解得a=,∴抛物线解析式为y=x2;(2)①证明:当m=时,联立直线和抛物线解析式可得,解得或,∴A(﹣2,1),B(8,16),分别过A、B作AC⊥x轴,BD⊥x轴,垂足分别为C、D,如图1,∴AC=1,OC=2,OD=8,BD=16,∴==,且∠ACO=∠ODB,∴△ACO∽△ODB,∴∠AOC=∠OBD,又∵∠OBD+∠BOD=90°,∴∠AOC+∠BOD=90°,即∠AOB=90°,∴△AOB为直角三角形;②解:△AOB为直角三角形.证明如下:当m≠时,联立直线和抛物线解析式可得,解得或,∴A(2m﹣2,(m﹣)2),B(2m+2,(m+)2),分别过A、B作AC⊥x轴,BD⊥x轴,如图2,∴AC=(m﹣)2,OC=﹣(2m﹣2),BD=(m+)2,OD=2m+2,∴==,且∠ACO=∠ODB,∴△ACO∽△OBD,∴∠AOC=∠OBD,又∵∠OBD+∠BOD=90°,∴∠AOC+∠BOD=90°,即∠AOB=90°,∴△AOB为直角三角形;(3)解:由(2)可知,一次函数y=mx+4的图象与二次函数y=ax2的交点为A、B,则△AOB恒为直角三角形.(答案不唯一).9.(12分)(2015•天水)在平面直角坐标系中,已知y=﹣x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),点C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若抛物线经过A、B两点,求抛物线的解析式.(2)平移(1)中的抛物线,使顶点P在直线AC上并沿AC方向滑动距离为时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.(3)在(2)的情况下,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q,取BC的中点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.解答:解:(1)∵等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3)∴点B的坐标为(4,﹣1).∵抛物线过A(0,﹣1),B(4,﹣1)两点,∴,解得:b=2,c=﹣1,∴抛物线的函数表达式为:y=﹣x2+2x﹣1.(2)如答题图2,设顶点P在直线AC上并沿AC方向滑动距离时,到达P′,作P′M∥y轴,PM∥x轴,交于M点,∵点A的坐标为(0,﹣1),点C的坐标为(4,3),∴直线AC的解析式为y=x﹣1,∵直线的斜率为1,∴△P′PM是等腰直角三角形,∵PP′=,∴P′M=PM=1,∴抛物线向上平移1个单位,向右平移1个单位,∵y=﹣x2+2x﹣1=﹣(x﹣2)2+1,∴平移后的抛物线的解析式为y=﹣(x﹣3)2+2,令y=0,则0=﹣(x﹣3)2+2,解得x1=1,x=52,∴平移后的抛物线与x轴的交点为(1,0),(5,0),解,得或∴平移后的抛物线与AC的交点为(1,0),∴平移后的抛物线与直线AC交于x轴上的同一点(1,0).(3)如答图3,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q,取AB中点F,连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,∴四边形PQFN为平行四边形.∴NP=FQ.∴NP+BQ=FQ+B′Q≥FB′==2.∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2.10.(10分)(2015•酒泉)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解答:解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B(1,0)代入得,解得,∴y=x﹣,∵点P的横坐标为3,∴y=×3﹣=,∴P(3,).(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,t2﹣t+4)(0<t<5),如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣x+4,把x=t代入得:y=﹣t+4,则G(t,﹣t+4),此时:NG=﹣t+4﹣(t2﹣t+4)=﹣t2+4t,∵AD+CF=CO=5,∴S△ACN=S△ANG+S△CGN=AM×NG+NG×CF=NG•OC=×(﹣t2+4t)×5=﹣2t2+10t=﹣2(t﹣)2+,∴当t=时,△CAN面积的最大值为,由t=,得:y=t2﹣t+4=﹣3,∴N(,﹣3).11.(10分)(2015•佛山)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.解答:解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,故二次函数图象的最高点P的坐标为(2,4);(2)联立两解析式可得:,解得:,或.故可得点A的坐标为(,);(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×(+4)×(﹣2)﹣××=4+﹣=;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,∵P的坐标为(2,4),∴4=×2+b,解得b=3,∴直线PM的解析式为y=x+3.由,解得,,∴点M的坐标为(,).12.(14分)(2015•广州)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.(1)求点C的坐标;(2)当y1随着x的增大而增大时,求自变量x的取值范围;(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.解答:解:(1)令x=0,则y=c,故C(0,c),∵OC的距离为3,∴|c|=3,即c=±3,∴C(0,3)或(0,﹣3);(2)∵x1x2<0,∴x1,x2异号,①若C(0,3),即c=3,把C(0,3)代入y2=﹣3x+t,则0+t=3,即t=3,∴y2=﹣3x+3,把A(x1,0)代入y2=﹣3x+3,则﹣3x1+3=0,即x1=1,∴A(1,0),∵x1,x2异号,x1=1>0,∴x2<0,∵|x1|+|x2|=4,∴1﹣x2=4,解得:x2=﹣3,则B(﹣3,0),代入y1=ax2+bx+3得,,解得:,∴y1=﹣x2﹣2x+3=﹣(x+1)2+4,则当x≤﹣1时,y随x增大而增大.②若C(0,﹣3),即c=﹣3,把C(0,﹣3)代入y2=﹣3x+t,则0+t=﹣3,即t=﹣3,∴y2=﹣3x﹣3,把A(x1,0),代入y2=﹣3x﹣3,则﹣3x1﹣3=0,即x1=﹣1,∴A(﹣1,0),∵x1,x2异号,x1=﹣1<0,∴x2>0∵|x1|+|x2|=4,∴1+x2=4,解得:x2=3,则B(3,0),代入y1=ax2+bx+3得,,解得:,∴y1=x2﹣2x﹣3=(x﹣1)2﹣4,则当x≥1时,y随x增大而增大,综上所述,若c=3,当y随x增大而增大时,x≤﹣1;若c=﹣3,当y随x增大而增大时,x≥1;(3)①若c=3,则y1=﹣x2﹣2x+3=﹣(x+1)2+4,y2=﹣3x+3,y1向左平移n个单位后,则解析式为:y3=﹣(x+1+n)2+4,则当x≤﹣1﹣n时,y随x增大而增大,y2向下平移n个单位后,则解析式为:y4=﹣3x+3﹣n,要使平移后直线与P有公共点,则当x=﹣1﹣n,y3≥y4,即﹣(﹣1﹣n+1+n)2+4≥﹣3(﹣1﹣n)+3﹣n,解得:n≤﹣1,∵n>0,∴n≤﹣1不符合条件,应舍去;②若c=﹣3,则y1=x2﹣2x﹣3=(x﹣1)2﹣4,y2=﹣3x﹣3,y1向左平移n个单位后,则解析式为:y3=(x﹣1+n)2﹣4,则当x≥1﹣n时,y随x增大而增大,y2向下平移n个单位后,则解析式为:y4=﹣3x﹣3﹣n,要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4,即(1﹣n﹣1+n)2﹣4≤﹣3(1﹣n)﹣3﹣n,解得:n≥1,综上所述:n≥1,2n2﹣5n=2(n﹣)2﹣,∴当n=时,2n2﹣5n的最小值为:﹣.13.(2015•深圳)如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.解答:解:(1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),∴,解得,∴抛物线的解析式y=﹣x2﹣2x+3,(2)存在,当P在∠DAB的平分线上时,如图1,作PM⊥AD,设P(﹣1,m),则PM=PD•sin∠ADE=(4﹣m),PE=m,∵PM=PE,∴(4﹣m)=m,m=﹣1,∴P点坐标为(﹣1,﹣1);当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,设P(﹣1,n),则PN=PD•sin∠ADE=(4﹣n),PE=﹣n,∵PM=PE,∴(4﹣n)=﹣n,n=﹣﹣1,∴P点坐标为(﹣1,﹣﹣1);综上可知存在满足条件的P点,其坐标为(﹣1,﹣1)或(﹣1,﹣﹣1);(3)∵S△EBC=3,2S△FBC=3S△EBC,∴S△FBC=,过F作FQ⊥x轴,交BC的延长线于Q,如图3,∵S△FBC=FQ•OB=FQ=,∴FQ=9,∵BC的解析式为y=﹣3x+3,设F(x0,﹣x02﹣2x0+3),∴﹣3x0+3+x02+2x0﹣3=9,解得:x0=或(舍去),∴点F的坐标是(,).14.(9分)(2015•珠海)如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且=,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=﹣x2+x+c经过点E,且与AB边相交于点F.(1)求证:△ABD∽△ODE;(2)若M是BE的中点,连接MF,求证:MF⊥BD;(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.解答:(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,∴∠BDE=∠BCE=90°,∵∠BAD=90°,∴∠EDO+∠BDA=∠BDA+∠DAB=90°,∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,∴△ABD∽△ODE;(2)证明:∵=,∴设OD=4x,OE=3x,则DE=5x,∴CE=DE=5x,∴AB=OC=CE+OE=8x,又∵△ABD∽△ODE,∴==,∴DA=6x,∴BC=OA=10x,在Rt△BCE中,由勾股定理可得BE2=BC2+CE2,即(5)2=(10x)2+(5x)2,解得x=1,∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣x2+x+3,当x=10时,代入可得y=,∴AF=,BF=AB﹣AF=8﹣=,在Rt△AFD中,由勾股定理可得DF===,∴BF=DF,又M为Rt△BDE斜边上的中点,∴MD=MB,∴MF为线段BD的垂直平分线,∴MF⊥BD;(3)解:由(2)可知抛物线解析式为y=﹣x2+x+3,设抛物线与x轴的两个交点为H、G,令y=0,可得0=﹣x2+x+3,解得x=﹣4或x=12,∴H(﹣4,0),G(12,0),①当PD⊥x轴时,由于PD=8,DM=DN=8,故点Q的坐标为(﹣4,0)或(12,0)时,△PDQ是以D为直角顶点的等腰直角三角形;②当PD不垂直与x轴时,分别过P,Q作x轴的垂线,垂足分别为N,I,则Q不与G重合,从而I不与G重合,即DI≠8.∵PD⊥DQ,∴∠QDI=90°﹣∠PDN=∠DPN,∴Rt△PDN∽Rt△DQI,∵PN=8,∴PN≠DI,∴Rt△PDN与Rt△DQI不全等,∴PD≠DQ,另一侧同理PD≠DQ.综合①,②所有满足题设条件的点Q的坐标为(﹣4,0)或(12,0).15(12分)(2015•河池)如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.解答:解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴D(1,4),当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线l的解析式为y=kx+b,把C(0,3),E(4,0)分别代入得,解得,∴直线l的解析式为y=﹣x+3;(2)如图(1),当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),设直线BD的解析式为y=mx+n,把B(3,0),D(1,4)分别代入得,解得,∴直线BD的解析式为y=﹣2x+6,则P(x,﹣2x+6),∴S=•(﹣2x+6+3)•x=﹣x2+x(1≤x≤3),∵S=﹣(x﹣)2+,∴当x=时,S有最大值,最大值为;(3)存在.如图2,设Q(t,0)(t>0),则M(t,﹣t+3),N(t,﹣t2+2t+3),∴MN=|﹣t2+2t+3﹣(﹣t+3)|=|t2﹣t|,CM==t,∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,而QN∥y轴,∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,∴∠M′CN=∠CNM,∴∠M′CN=∠CNM′,∴CM′=NM′,∴NM=CM,∴|t2﹣t|=t,当t2﹣t=t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);当t2﹣t=﹣t,解得t1=0(舍去),t2=,此时Q点坐标为(,0),综上所述,点Q的坐标为(,0)或(4,0).16.(10分)(2015•南宁)在平面直角坐标系中,已知A、B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限,(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积.(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,A、B两点的横坐标的乘积是否为常数?如果是,请给予证明;如果不是,请说明理由.(3)在(2)的条件下,若直线y=﹣2x﹣2分别交直线AB,y轴于点P、C,直线AB交y 轴于点D,且∠BPC=∠OCP,求点P的坐标.解答:解:(1)如图1,∵AB与x轴平行,根据抛物线的对称性有AE=BE=1,∵∠AOB=90°,∴OE=AB=1,∴A(﹣1,1)、B(1,1),把x=1时,y=1代入y=ax2得:a=1,∴抛物线的解析式y=x2,A、B两点的横坐标的乘积为x A•x B=﹣1(2)x A•x B=﹣1为常数,如图2,过A作AM⊥x轴于M,BN⊥x轴于N,∴∠AMO=∠BNO=90°,∴∠MAO+∠AOM=∠AOM+∠BON=90°,∴∠MAO=∠BON,∴△AMO∽△BON,∴,∴OM•ON=AM•BN,设A(x A,y A),B(x B,y B),∵A(x A,y A),B(x B,y B)在y=x2图象上,∴,y A=,y B=,∴﹣x A•x B=y A•y B=•,∴x A•x B=﹣1为常数;(3)设A(m,m2),B(n,n2),如图3所示,过点A、B分别作x轴的垂线,垂足为E、F,则易证△AEO∽△OFB.∴,即,整理得:mn(mn+1)=0,∵mn≠0,∴mn+1=0,即mn=﹣1.设直线AB的解析式为y=kx+b,联立,得:x2﹣kx﹣b=0.∵m,n是方程的两个根,∴mn=﹣b.∴b=1.∵直线AB与y轴交于点D,则OD=1.易知C(0,﹣2),OC=2,∴CD=OC+OD=3.∵∠BPC=∠OCP,∴PD=CD=3.设P(a,﹣2a﹣2),过点P作PG⊥y轴于点G,则PG=﹣a,GD=OG﹣OD=﹣2a﹣3.在Rt△PDG中,由勾股定理得:PG2+GD2=PD2,即:(﹣a)2+(﹣2a﹣3)2=32,整理得:5a2+12a=0,解得a=0(舍去)或a=﹣,当a=﹣时,﹣2a﹣2=,∴P(﹣,).16.(2015•北海)如图1所示,已知抛物线y=﹣x2+4x+5的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.(1)直接写出D点和E点的坐标;(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,S△HGF:S△BGF=5:6?(3)图2所示的抛物线是由y=﹣x2+4x+5向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT 是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.解答:解:(1)∵抛物线y=﹣x2+4x+5=﹣(x﹣2)2+9∴D点的坐标是(2,9);∵E为对称轴上的一点,∴点E的横坐标是:﹣=2,设点E的坐标是(2,m),点C′的坐标是(0,n),∵将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上,∴△CEC′是等腰直角三角形,∴解得或(舍去),∴点E的坐标是(2,3),点C′的坐标是(0,1).综上,可得D点的坐标是(2,9),点E的坐标是(2,3).(2)如图1所示:令抛物线y=﹣x2+4x+5的y=0得:x2﹣4x﹣5=0,解得:x1=﹣1,x2=5,所以点A(﹣1,0),B(5,0).设直线C′E的解析式是y=kx+b,将E(2,3),C′(0,1),代入得,解得:,∴直线C′E的解析式为y=x+1,将y=x+1与y=﹣x2+4x+5,联立得:,解得:,,∴点F得坐标为(4,5),点A(﹣1,0)在直线C′E上.∵直线C′E的解析式为y=x+1,∴∠FAB=45°.过点B、H分别作BN⊥AF、HM⊥AF,垂足分别为N、M.∴∠HMN=90°,∠ADN=90°.又∵∠NAD=∠HNM=45°.∴△HGM∽△ABN∴,∵S△HGF:S△BGF=5:6,∴.∴,即,∴HG=5.设点H的横坐标为m,则点H的纵坐标为﹣m2+4m+5,则点G的坐标为(m,m+1),∴﹣m2+4m+5﹣(m+1)=5.解得:m1=,m2=.(3)由平移的规律可知:平移后抛物线的解析式为y=﹣(x﹣1)2+4(x﹣1)+5=﹣x2+6x.将x=5代入y=﹣x2+6x得:y=5,∴点T的坐标为(5,5).设直线OT的解析式为y=kx,将x=5,y=5代入得;k=1,∴直线OT的解析式为y=x,①如图2所示:当PT∥x轴时,△PTQ为等腰直角三角形,将y=5代入抛物线y=﹣x2+6x得:x2﹣6x+5=0,解得:x1=1,x2=5.∴点P的坐标为(1,5).将x=1代入y=x得:y=1,∴点Q的坐标为(1,1).②如图3所示:由①可知:点P的坐标为(1,5).∵△PTQ为等腰直角三角形,∴点Q的横坐标为3,将x=3代入y=x得;y=3,∴点Q得坐标为(3,3).③如图4所示:设直线PT解析式为y=kx+b,∵直线PT⊥QT,∴k=﹣1.将k=﹣1,x=5,y=5代入y=kx+b得:b=10,∴直线PT的解析式为y=﹣x+10.将y=﹣x+10与y=﹣x2+6x联立得:x1=2,x2=5∴点P的横坐标为2.将x=2代入y=x得,y=2,∴点Q的坐标为(2,2).综上所述:点Q的坐标为(1,1)或(3,3)或(2,2).17.(10分)(2015•贵港)如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y 轴交于点C(0,3),其对称轴I为x=﹣1.(1)求抛物线的解析式并写出其顶点坐标;(2)若动点P在第二象限内的抛物线上,动点N在对称轴I上.①当PA⊥NA,且PA=NA时,求此时点P的坐标;②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.解答:解:(1)∵抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴I为x=﹣1,∴,解得:.∴二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点坐标为(﹣1,4);(2)令y=﹣x2﹣2x+3=0,解得x=﹣3或x=1,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在y=﹣x2﹣2x+3上,∴设点P(x,﹣x2﹣2x+3)①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD即y=﹣x2﹣2x+3=2,解得x=﹣1(舍去)或x=﹣﹣1,∴点P(﹣﹣1,2);②∵S四边形BCPA=S△OBC+S△OAC=2+S△APC∵S△AOC=,S△OCP=x,S△OAP=•3•|y P|=﹣x2﹣3x+∴S△APC=S△OAP+S△OCP﹣S△AOC=x+(﹣x2﹣3x+)﹣=﹣x2﹣x=﹣(x﹣)2+,∴当x=﹣时,S△ACP最大值=,此时M(﹣,﹣),S四边形PABC最大=.18.(12分)(2015•桂林)如图,已知抛物线y=﹣x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O 时,点C、D停止运动.(1)直接写出抛物线的解析式:y=﹣x2+3x+8;(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.解答:解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣x2+bx+c得:,解得:b=3,c=8,∴抛物线的解析式为:y=﹣x2+3x+8,故答案为:y=﹣x2+3x+8;(2)∵点A(0,8)、B(8,0),∴OA=8,OB=8,令y=0,得:﹣x2+3x+8=0,解得:x18,x2=2,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=•DE•OC=•(10﹣t)•t=﹣t2+5t,即S=﹣t2+5t=﹣(t﹣5)2+,∴当t=5时,S最大=;(3)由(2)知:当t=5时,S最大=,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=,设直线CD的解析式为:y=kx+b,将C(0,5),D(3,0),代入上式得:k=﹣,b=5,∴直线CD的解析式为:y=﹣x+5,过E点作EF∥CD,交抛物线与点P,如图1,设直线EF的解析式为:y=﹣x+b,将E(﹣2,0)代入得:b=﹣,∴直线EF的解析式为:y=﹣x﹣,将y=﹣x﹣,与y=﹣x2+3x+8联立成方程组得:,解得:,,∴P(,﹣);过点E作EG⊥CD,垂足为G,∵当t=5时,S△ECD==,∴EG=,过点D作DN⊥CD,垂足为N,且使DN=,过点N作NM⊥x轴,垂足为M,如图2,可得△EGD∽△DMN,∴,即:,解得:DM=,∴OM=,由勾股定理得:MN==,∴N(,),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:y=﹣x+b,将N(,),代入上式得:b=,∴直线NH的解析式为:y=﹣x+,将y=﹣x+,与y=﹣x2+3x+8联立成方程组得:,解得:,,∴P(8,0)或P(,),综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P(,﹣)或P(8,0)或P(,).19.(14分)(2015•安顺)如图,抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S 取最大值时的点C的坐标.解答:解:(1)由题意得,解得:,∴y=﹣x2+2x+.(2)设直线AB解析式为:y=kx+b,则有,解得:,∴y=x+,则D(m,﹣m2+2m+),C(m,m+),CD=(﹣m2+2m+)﹣(m+)=﹣m2+m+2,∴S=(m+1)•CD+(4﹣m)•CD=×5×CD=×5×(﹣m2+m+2)=﹣m2+m+5∵﹣<0,∴当m=时,S有最大值,当m=时,m+=×+=,∴点C(,).20.(16分)(2015•毕节市)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.(1)求抛物线的解析式;(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.解答:解:(1)将A、B点坐标代入函数解析式,得,解得,抛物线的解析式y=x2﹣2x﹣3;(2)将抛物线的解析式化为顶点式,得y=(x﹣1)2﹣4,M点的坐标为(1,﹣4),M′点的坐标为(1,4),设AM′的解析式为y=kx+b,将A、M′点的坐标代入,得,解得,AM′的解析式为y=2x+2,联立AM′与抛物线,得,解得,C点坐标为(5,12).S△ABC=×4×12=24;(3)存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ 为正方形,由ABPQ是正方形,A(﹣1,0)B(3,0),得P(1,﹣2),Q(1,2),或P(1,2),Q(1,﹣2),①当顶点P(1,﹣2)时,设抛物线的解析式为y=a(x﹣1)2﹣2,将A点坐标代入函数解析式,得a(﹣1﹣1)2﹣2=0,解得a=,抛物线的解析式为y=(x﹣1)2﹣2,②当P(1,2)时,设抛物线的解析式为y=a(x﹣1)2+2,将A点坐标代入函数解析式,得a(﹣1﹣1)2+2=0,解得a=﹣,抛物线的解析式为y=﹣(x﹣1)2+2,综上所述:y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,使得四边形APBQ为正方形.21.(16分)(2015•六盘水)如图,已知图①中抛物线y=ax2+bx+c经过点D(﹣1,0),D (0,﹣1),E(1,0).(1)求图①中抛物线的函数表达式.(2)将图①中的抛物线向上平移一个单位,得到图②中的抛物线,点D与点D1是平移前后的对应点,求该抛物线的函数表达式.(3)将图②中的抛物线绕原点O顺时针旋转90°后得到图③中的抛物线,所得到抛物线表达式为y2=2px,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.(4)将图③中的抛物线绕原点O顺时针旋转90°后与直线y=﹣x﹣1相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.解答:解:(1)将D、C、E的坐标代入函数解析式,得,解得.图①中抛物线的函数表达式y=x2﹣1;(2)将抛物线的函数表达式y=x2﹣1向上平移1个单位,得y=x2,该抛物线的函数表达式y=x2;(3)将抛物线的函数表达式y=x2绕原点O顺时针旋转90°,得x=y2,图③中抛物线的函数表达式x=y2;(4)将图③中抛物线的函数表达式x=y2绕原点O顺时针旋转90°,得y=﹣x2,联立,。
二次函数压轴题专题一 最短路径问题

二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下 两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
例题导航例1:如图A 是锐角∠MON 内部任意一点,在∠MON 的两边OM ,ON 上各取一点B ,C ,组成三角形,使三角形周长最小.例:如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在何处才能使从A 到B 的路径AMNB 最短?(假设河的两岸是平行的直线,桥要与河垂直) 解:1.将点B 沿垂直与河岸的方向平移一个河宽到E , 2.连接AE 交河对岸与点M,则点M 为建桥的位置,MN 为所建的桥。
证明:由平移的性质,得 BN ∥EM 且BN=EM, MN=CD, BD ∥CE, BD=CE, 所以A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在CD 处,连接AC.CD.DB.CE, 则AB 两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE 中,∵AC+CE >AE, ∴AC+CE+MN >AE+MN,即AC+CD+DB >AM+MN+BN 所以桥的位置建在CD 处,AB 两地的路程最短。
例:如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
作法:作点B 关于直线 a 的对称点点C,连接AC 交直线a 于点D ,则点D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E ,连接AE.CE.BE.BD,··CDA BEa∵点B.C 关于直线 a 对称,点D.E 在直线 a 上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE 中,AE+EC >AC, 即 AE+EC >AD+DB所以抽水站应建在河边的点D 处,常见问题归纳“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DElBAllllBAOBOB+EF +CF 最小,则点E ,F 即为所求.⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y轴正半轴.点P 在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.二次函数中最短路径例题例1.(13广东)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BOB Oll练习1.(11菏泽)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.练习2.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.例2.(14海南)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由.【思路点拨】 (1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出; (3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5,∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN•MN -12OM •OE =12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1=-x 2+92x +92 =-(x -94)2+15316 ∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316). (3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1);作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图2练习3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.例4.(14福州)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了. (1)求点A ,B ,D 的坐标; (2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可.【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12 (x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).例5.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【解题过程】解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1; (2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ; (3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°.∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).l。
2015二次函数中考真题卷高难度专项练习及答案

组卷二次函数难题1-30一、选择题(共12小题)1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20 2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.45.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥36.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.17.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.89.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.二、填空题(共12小题)(除非特别说明,请填准确值)13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为_________、_________.14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过_________秒,四边形APQC的面积最小.15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是_________.16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=_________,公共部分面积y最大,y最大值=_________.17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为_________元/平方米.18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc_________0(填“>”或“<”);(2)a的取值范围是_________.19.(2009•包头)已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正确结论的个数是_________个.20.(2010•兰州)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为_________米.21.(2008•黄石)若实数a,b满足a+b2=1,则2a2+7b2的最小值是_________.22.(2009•包头)将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是_________cm2.23.(2008•长春)将抛物线y=ax2+bx+c(a≠0)向下平移3个单位,再向左平移4个单位得到抛物线y=﹣2x2﹣4x+5,则原抛物线的顶点坐标是_________.24.(2009•兰州)二次函数y=x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=_________;△A1B2A2的边长=_________;△A2007B2008A2008的边长=_________.三、解答题(共6小题)(选答题,不自动判卷)25.(2013•徐州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)请直接写出点D的坐标:_________;(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.26.(2013•雅安)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.27.(2013•烟台)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.28.(2013•新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.29.(2013•宜宾)如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.30.(2013•宜宾)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?【章节训练】第2章二次函数-3参考答案与试题解析一、选择题(共12小题)组卷二次函数难题61-90 难度 5 级1.(2011•包头)已知二次函数y=ax2+bx+c同时满足下列条件:对称轴是x=1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,则b的值是()A.4或﹣30 B.﹣30 C.4D.6或﹣20抛物线与x轴的交点;二次函数的性质;二次函数的最值.专题:压轴题;函数思想.分析:由在x=1时取得最大值15,可设解析式为:y=a(x﹣1)2+15,只需求出a即可,又与x轴交点横坐标的平方和为15﹣a,可求出a,所以可求出解析式得到b的值.解答:解:解法一:∵x轴上点的纵坐标是0,∴由题可设抛物线与x轴的交点为(1﹣t,0),(1+t,0),其中t>0,∵两个交点的横坐标的平方和等于15﹣a即:(1﹣t)2+(1+t)2=15﹣a,可得t=,由顶点为(1,15),可设解析式为:y=a(x﹣1)2+15,将(1﹣,0)代入可得a=﹣2或a=15(不合题意,舍去)∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13,∴b=4;解法二:∵对称轴是x=1,最值是15,∴设y=ax2+bx+c=a(x﹣1)2+15,∴y=ax2﹣2ax+15+a,设方程ax2﹣2ax+15+a=0的两个根是x1,x2,则x1+x2=﹣=2,x1•x2=,∵二次函数的图象与x轴有两个交点,其横坐标的平方和为15﹣a,(x1)2+(x2)2=(x1+x2)2﹣2x1x2=15﹣a,∴22﹣=15﹣a,a2﹣13a﹣30=0,a1=15(不合题意,舍去),a2=﹣2,∴y=﹣2(x﹣1)2+15=﹣2x2+4x+13;∴b=4.故选C.点评:本题考查了二次函数的最值及待定系数法求解析式,难度一般,关键算出a的值.组卷二次函数难题61-90 难度 4 级2.(2011•玉溪)如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,错误的是()A.顶点坐标为(﹣1,4)B.函数的解析式为y=﹣x2﹣2x+3C.当x<0时,y随x的增大而增大D.抛物线与x轴的另一个交点是(﹣3,0)考点:抛物线与x轴的交点;二次函数的性质.专题:计算题;压轴题.分析:由于y=﹣x2+bx+c的图象与x轴、y轴的交点分别为A(1,0),B(0,3),将交点代入解析式求出函数表达式,即可作出正确判断.解答:解:将A(1,0),B(0,3)分别代入解析式得,,解得,,则函数解析式为y=﹣x2﹣2x+3;将x=﹣1代入解析式可得其顶点坐标为(﹣1,4);当y=0时可得,﹣x2﹣2x+3=0;解得,x1=﹣3,x2=1.可见,抛物线与x轴的另一个交点是(﹣3,0);由图可知,当x<﹣1时,y随x的增大而增大.可见,C答案错误.故选C.点评:本题考查了抛物线与x轴的交点及二次函数的性质,利用待定系数法求出函数解析式是解题的关键,同时要注意数形结合.组卷二次函数难题61-90 难度 4 级3.(2010•钦州)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中错误的结论有()A.②③B.②④C.①③D.①④考点:二次函数图象与系数的关系.专题:压轴题.分析:①由二次函数y=ax2+bx+c(a≠0)的图象开口方向知道a<0,与y轴交点知道c>0,由此即可确定ac的符号;②由于当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,由此即可判定a﹣b+c的符号;③根据图象知道当x<﹣1时抛物线在x轴的下方,由此即可判定此结论是否正确;④根据图象与x轴交点的情况即可判定是否正确.解答:解:①∵二次函数y=ax2+bx+c(a≠0)的图象开口向下,∴a<0,∵与y轴交点在x轴上方,∴c>0,∴ac<0;②∵当x=﹣1时,y=a﹣b+c,而根据图象知道当x=﹣1时y<0,∴a﹣b+c<0;③根据图象知道当x<﹣1时抛物线在x轴的下方,∴当x<﹣1,y<0;④从图象可知抛物线与x轴的交点的横坐标都大于﹣1,∴方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.故错误的有①③.故选C.点评:此题主要考查了利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子,如:当x=1时,y>0,a+b+c>0;x=﹣1时,y<0,a﹣b+c<0.组卷二次函数难题61-90 难度4.5级4.(2010•柳州)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 0 1 2 …y …0 4 6 6 4 …从上表可知,下列说法正确的个数是()①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.A.1B.2C.3D.4考点:抛物线与x轴的交点.专题:压轴题;图表型.分析:从表中知道当x=﹣2时,y=0,当x=0时,y=6,由此可以得到抛物线与x轴的一个交点坐标和抛物线与y 轴的交点坐标,从表中还知道当x=﹣1和x=2时,y=4,由此可以得到抛物线的对称轴方程,同时也可以得到在对称轴左侧y随x增大而增大.解答:解:从表中知道:当x=﹣2时,y=0,当x=0时,y=6,∴抛物线与x轴的一个交点为(﹣2,0),抛物线与y轴的交点为(0,6),从表中还知道:当x=﹣1和x=2时,y=4,∴抛物线的对称轴方程为x=(﹣1+2)=0.5,同时也可以得到在对称轴左侧y随x增大而增大.所以①②④正确.故选C.点评:此题主要考查了抛物线与坐标轴的交点坐标与自变量和的函数值的对应关系,也考查了利用自变量和对应的函数值确定抛物线的对称轴和增减性.组卷二次函数难题61-90 难度4.5 级5.(2010•自贡)y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是()A.a≤﹣5 B.a≥5 C.a=3 D.a≥3考点:二次函数的最值.专题:压轴题.分析:由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,3]和对称轴在[1,3]内两种情况进行解答.解答:解:第一种情况:当二次函数的对称轴不在1≤x≤3内时,此时,对称轴一定在1≤x≤3的右边,函数方能在这个区域取得最大值,x=>3,即a>7,第二种情况:当对称轴在1≤x≤3内时,对称轴一定是在区间1≤x≤3的中点的右边,因为如果在中点的左边的话,就是在x=3的地方取得最大值,即:x=≥,即a≥5(此处若a取5的话,函数就在1和3的地方都取得最大值)综合上所述a≥5.故选B.点评:本题考查了二次函数的最值确定与自变量x的取值范围的关系,难度较大.组卷二次函数难题61-90 难度 4 级6.(2010•十堰)方程x2+2x﹣1=0的根可看出是函数y=x+2与y=的图象交点的横坐标,用此方法可推断方程x3+x ﹣1=0的实根x所在范围为()A.﹣B.C.D.1考点:二次函数的图象;反比例函数的图象.专题:压轴题.分析:首先根据题意推断方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,再根据四个选项中x 的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x3+x﹣1=0的实根x所在范围.解答:解:依题意得方程x3+x﹣1=0的实根是函数y=x2+1与y=的图象交点的横坐标,这两个函数的图象如图所示,∴它们的交点在第一象限,当x=1时,y=x2+1=2,y==1,此时抛物线的图象在反比例函数上方;当x=时,y=x2+1=1,y==2,此时反比例函数的图象在抛物线的上方;∴方程x3+x﹣1=0的实根x 所在范围为<x<1.故选C.点评:此题考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.组卷二次函数难题61-90 难度 4 级7.(2010•西宁)下列哪一个函数,其图象与x轴有两个交点()A.B.C.D.考点:抛物线与x轴的交点.专题:计算题.分析:由题意得,令y=0,看是否解出x值,对A,B,C,D,一一验证从而得出答案.解答:解:A、令y=0得,,移项得,,方程无实根;B、令y=0得,,移项得,,方程无实根;C、令y=0得,,移项得,,方程无实根;D、令y=0得,,移项得,,方程有两个实根.故选D.点评:此题考查二次函数的性质及与一元二次方程根的关系.(利用开口方向和顶点坐标也可解答)组卷二次函数难题61-90 难度 4.5 级8.(2010•台州)如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为()A.﹣3 B.1C.5D.8考点:二次函数综合题.专题:压轴题;动点型.分析:当C点横坐标最小时,抛物线顶点必为A(1,4),根据此时抛物线的对称轴,可判断出CD间的距离;当D点横坐标最大时,抛物线顶点为B(4,4),再根据此时抛物线的对称轴及CD的长,可判断出D点横坐标最大值.解答:解:当点C横坐标为﹣3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);由于此时D点横坐标最大,故点D的横坐标最大值为8;故选D.点评:能够正确地判断出点C横坐标最小、点D横坐标最大时抛物线的顶点坐标是解答此题的关键.组卷二次函数难题61-90 难度 4.5级9.(2010•东营)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx﹣ac 与反比例函数在同一坐标系内的图象大致为()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.专题:压轴题.分析:先根据二次函数y=ax2+bx+c的图象判断出a、b、c、a﹣b+c的符号,再用排除法对四个答案进行逐一检验.解答:解:由二次函数y=ax2+bx+c的图象开口向上可知,a>0,因为图象与y轴的交点在y轴的负半轴,所以c<0,根据函数图象的对称轴x=﹣>0,可知b<0,∵a>0,b<0,c<0,ac<0,∴一次函数y=bx﹣ac的图象过一、二、四象限,故可排除A、C;由函数图象可知,当x=﹣1时,y>0,即y=a﹣b+c>0,∴反比例函数的图象在一、三象限,可排除D选项,故选B.点评:此题比较复杂,综合考查了二次函数、一次函数及反比例函数图象的特点,锻炼了学生数形结合解题的思想方法.组卷二次函数难题61-90 难度4.5 级10.(2010•广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b<a+c;③2a+b=0;④a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.1个B.2个C.3个D.4个考点:二次函数图象与系数的关系.专题:压轴题.分析:①由抛物线开口向下a<0,抛物线和y轴的正半轴相交,c>0,﹣=1>0,b>0,②令x=﹣1,时y<0,即a﹣b+c<0,③﹣=1,即2a+b=0,④把x=m代入函数解析式中表示出对应的函数值,把x=1代入解析式得到对应的解析式,根据图形可知x=1时函数值最大,所以x=1对应的函数值大于x=m对应的函数值,化简得到不等式成立,故④正确.解答:解:①根据图象,a<0,b>0,c>0,故①错误;②令x=﹣1,时y<0,即a﹣b+c<0,故②错误;③∵﹣=1,∴2a+b=0,故③正确;④x=m对应的函数值为y=am2+bm+c,x=1对应的函数值为y=a+b+c,又x=1时函数取得最大值,∴a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),故④正确.故选B.点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.组卷二次函数难题61-90 难度 5 级11.(2010•丽水)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A.y=B.y=C.y=D.y=考点:根据实际问题列二次函数关系式.专题:压轴题.分析:四边形ABCD图形不规则,根据已知条件,将△ABC绕A点逆时针旋转90°到△ADE的位置,求四边形ABCD的面积问题转化为求梯形ACDE的面积问题;根据全等三角形线段之间的关系,结合勾股定理,把梯形上底DE,下底AC,高DF分别用含x的式子表示,可表示四边形ABCD的面积.解答:解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE∴∠BAC=∠DAE又∵AB=AD,∠ACB=∠E=90°∴△ABC≌△ADE(AAS)∴BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,在Rt△CDF中,由勾股定理得,CF2+DF2=CD2,即(3a)2+(4a)2=x2,解得:a=,∴y=S四边形ABCD=S梯形ACDE =×(DE+AC)×DF=×(a+4a)×4a=10a2=x2.故选C.点评:本题运用了旋转法,将求不规则四边形面积问题转化为求梯形的面积,充分运用了全等三角形,勾股定理在解题中的作用.组卷二次函数难题61-90 难度4.5级12.(2011•兰州)如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是()A.B.C.D.考点:二次函数的应用;全等三角形的判定与性质;勾股定理.专题:压轴题.分析:根据条件可知△AEH≌△BFE≌△CGF≌△DHG,设AE为x,则AH=1﹣x,根据勾股定理EH2=AE2+AH2=x2+(1﹣x)2,进而可求出函数解析式,求出答案.解答:解:∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,∴可证△AEH≌△BFE≌△CGF≌△DHG.设AE为x,则AH=1﹣x,根据勾股定理,得EH2=AE2+AH2=x2+(1﹣x)2即s=x2+(1﹣x)2.s=2x2﹣2x+1,∴所求函数是一个开口向上,对称轴是直线x=.∴自变量的取值范围是大于0小于1.故选B.点评:本题需根据自变量的取值范围,并且可以考虑求出函数的解析式来解决.二、填空题(共12小题)(除非特别说明,请填准确值)组卷二次函数难题61-90 难度5 级13.(2009•黄石)若抛物线y=ax2+bx+3与y=﹣x2+3x+2的两交点关于原点对称,则a、b 分别为、3.考点:二次函数图象与几何变换;关于原点对称的点的坐标.专题:压轴题.分析:有交点,可让两个抛物线组成方程组.解答:解:由题意可得,两个函数有交点,则y相等,则有ax2+bx+3=﹣x2+3x+2,得:(a+1)x2+(b﹣3)x+1=0.∵两交点关于原点对称,那么两个横坐标的值互为相反数;两个纵坐标的值也互为相反数.则两根之和为:﹣=0,两根之积为<0,解得b=3,a<﹣1.设两个交点坐标为(x1,y1),(x2,y2).这两个根都适合第二个函数解析式,那么y1+y2=﹣(x12+x 22)+3 (x 1+x2)+4=0,∵x1+x2=0,∴y1+y2=﹣(x1+x2)2+2x1x2+4=0,解得x1x 2=﹣2,代入两根之积得=﹣2,解得a=﹣,故a=﹣,b=3.另法:(若交点关于原点对称,那么在y=﹣x2+3x+2中,必定自身存在关于原点对称的两个点,设这两个点横坐标分别为k和﹣k,直接在y=﹣x2+3x+2代入k,然后相加两个式子﹣k2+3k+2=0与﹣k2﹣3k+2=0,可得出k为±,从而直接得到两个点,再待定系数法,将两点代入y=ax2+bx+3,直接可以得出a,b的值.点评:本题用到的知识点为:两个函数有交点,那么应让这两个函数图象组成方程组,而后根据根与系数的关系求解.组卷二次函数难题61-90 难度 4.5 级14.(2010•成都)如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s 的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B 同时出发,那么经过3秒,四边形APQC的面积最小.考点:二次函数的应用.专题:计算题.分析:根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系求最小值.解答:解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Smm2,则有:S=S△ABC﹣S△PBQ==4t2﹣24t+144=4(t﹣3)2+108.∵4>0∴当t=3s时,S取得最小值.点评:本题考查了函数关系式的求法以及最值的求法.组卷二次函数难题61-90 难度 5 级15.(2009•金华)如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是(3,),(,),(2,2),(,).考点:二次函数综合题.专题:压轴题.分析:在△AOH中,因为∠AOH=30°,所以A的纵坐标是横坐标的倍,若设A的坐标为(t,t),则Q、P 点坐标均可求出,然后根据全等三角形的判定,对应求解即可.解答:解:由题可得A的横坐标是纵坐标的倍,故设A的坐标为(t,t);则Q的坐标为(0,2t)或(0,t);可求得P点对应的坐标,解可得t的值有4个,为,,2,;故点A的坐标是(3,)、(,)、(2,2)、(,).点评:本题考查二次函数的有关性质,涉及图象与点的坐标的求法.组卷二次函数难题61-90 难度 4 级16.(2009•江津区)锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0),当x=3,公共部分面积y最大,y最大值=6.考点:二次函数的应用.专题:压轴题;动点型.分析:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.为正方形时可求出面积的值,为矩形时需求面积表达式再求最大值.解答:解:公共部分分为三种情形:在三角形内;刚好一边在BC上,此时为正方形;正方形有一部分在三角形外,此时为矩形.显然在内部时的面积比刚好在边上时要小,所以需比较后两种情形时的面积大小.(1)求公共部分是正方形时的面积,作AD⊥BC于D点,交MN于E点,∵BC=6,S△ABC=12,∴AD=4,∵MN∥BC,∴即,解得x=2.4,此时面积y=2.42=5.76.(2)当公共部分是矩形时如图所示:设DE=a,根据得=,所以a=4﹣x,公共部分的面积y=x(4﹣x)=﹣x2+4x,∵﹣<0,∴y有最大值,当x=﹣=3时,y最大值==6.综上所述,当x=3时,公共部分的面积y最大,最大值为6.点评:此题需分类讨论,综合比较后得结论.组卷二次函数难题61-90 难度4 级17.(2008•庆阳)兰州市“安居工程”新建成的一批楼房都是8层高,房子的价格y(元/平方米)随楼层数x(楼)的变化而变化(x=1,2,3,4,5,6,7,8);已知点(x,y)都在一个二次函数的图象上(如图所示),则6楼房子的价格为2080元/平方米.考点:二次函数的应用.专题:操作型;函数思想.分析:从图象中找出顶点坐标、对称轴,利用对称性即可解答.解答:解:由图象可知(4,2200)是抛物线的顶点,∵x=4是对称轴,∴点(2,2080)关于直线x=4的对称点是(6,2080).∴6楼房子的价格为2080元.点评:要求熟悉二次函数的对称性,并准确的找到所求的点与那个已知点是对称点,此题的关键是能找到顶点是(4,2200).组卷二次函数难题61-90 难度 5 级18.(2009•浙江)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则:(1)abc<0(填“>”或“<”);(2)a的取值范围是≤a≤.考点:二次函数综合题.专题:压轴题;动点型.分析:(1)观察图形发现,由抛物线的开口向下得到a<0,顶点坐标在第一象限得到b>0,抛物线与y轴的交点在y轴的上方推出c>0,由此即可判定abc的符号;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,可以知道顶点坐标为(1,3)且抛物线过(﹣1,0),则它与x轴的另一个交点为(3,0),由此可求出a;当顶点C与F点重合,顶点坐标为(3,2)且抛物线过(﹣2,0),则它与x轴的另一个交点为(8,0),由此也可求a,然后由此可判断a的取值范围.解答:解:(1)观察图形发现,抛物线的开口向下,∴a<0,∵顶点坐标在第一象限,∴﹣>0,∴b>0,而抛物线与y轴的交点在y轴的上方,∴c>0,∴abc <0;(2)顶点C是矩形DEFG上(包括边界和内部)的一个动点,当顶点C与D点重合,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3,由,解得﹣≤a≤﹣;当顶点C与F点重合,顶点坐标为(3,2),则抛物线解析式y=a(x﹣3)2+2,由,解得﹣≤a≤﹣;∵顶点可以在矩形内部,∴﹣≤a≤﹣.点评:本题主要考查了抛物线的解析式y=ax2+bx+c中a、b、c对抛物线的影响,在对于抛物线的顶点在所给图形内进行运动的判定,充分利用了利用形数结合的方法,展开讨论,加以解决.组卷二次函数难题61-90 难度 5.5 级。
2015中考数学二次函数压轴题题型归纳

2015中考二次函数综合压轴题型归类一、常考点汇总1、两点间的距离公式:()()22B A B A x x y y AB -+-=2、中点坐标:线段AB 的中点C 的坐标为:⎪⎭⎫⎝⎛++22B A B A y y x x , 直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系:(1)两直线平行⇔21k k =且21b b ≠ (2)两直线相交⇔21k k ≠ (3)两直线重合⇔21k k =且21b b = (4)两直线垂直⇔121-=k k3、一元二次方程有整数根问题,解题步骤如下:① 用∆和参数的其他要求确定参数的取值范围;② 解方程,求出方程的根;(两种形式:分式、二次根式)③ 分析求解:若是分式,分母是分子的因数;若是二次根式,被开方式是完全平方式。
例:关于x 的一元二次方程()01222=-m x m x ++有两个整数根,5<m 且m 为整数,求m 的值。
4、二次函数与x 轴的交点为整数点问题。
(方法同上)例:若抛物线()3132+++=x m mx y 与x 轴交于两个不同的整数点,且m 为正整数,试确定此抛物线的解析式。
5、方程总有固定根问题,可以通过解方程的方法求出该固定根。
举例如下:已知关于x 的方程23(1)230mx m x m --+-=(m 为实数),求证:无论m 为何值,方程总有一个固定的根。
解:当0=m 时,1=x ;当0≠m 时,()032≥-=∆m ,()m m x 213∆±-=,mx 321-=、12=x ;综上所述:无论m 为何值,方程总有一个固定的根是1。
6、函数过固定点问题,举例如下:已知抛物线22-+-=m mx x y (m 是常数),求证:不论m 为何值,该抛物线总经过一个固定的点,并求出固定点的坐标。
解:把原解析式变形为关于m 的方程()x m x y -=+-122;∴ ⎩⎨⎧=-=+-01 02 2x x y ,解得:⎩⎨⎧=-=1 1 x y ;∴ 抛物线总经过一个固定的点(1,-1)。
中考二次函数压轴题经典例题

中考二次函数压轴题经典例题
以下是一些中考二次函数压轴题的经典例题:
一、某商品原价为x元,打八折销售。
求让利额与x的关系。
分析:让利额是
指降低的价钱,原价x元打八折后,售价为0.8x元,让利额就是x-0.8x=0.2x。
答案:让利额与x的关系为y=0.2x。
二、已知函数y=ax²+bx+c(a≠0)的图象经过点(0,-1),(1,2)和(-1,0),求a、b、c的值。
解:由题意,将x=0,y=-1代入函数y=ax²+bx+c得到c=-1;将x=1,y=2代入函数得到a+b=-1;将x=-1,y=0代入函数得到a-b=1。
解这个二
元一次方程,得到a=1,b=-2。
答案:a=1,b=-2,c=-1。
三、某社团要举行一次活动,筹备的固定费用为200元,每增加一个参加人数,平均每人需支付的费用就会减少2元。
求参加人数x与每人需支付费用y的关系。
解:固定费用200元,每增加一个参会人数,平均每人需支付的费用就会减少2元,所以每个人需支付的费用为200/x。
而x每增加1,支付费用减少2元,所以
y=200/x-2。
答案:参加人数x与每人需支付费用y的关系为y=200/x-2。
以上就是一些中考二次函数压轴题的经典例题。
中考压轴题中的二次函数(三)带答案和详细解析30道解答题.docx

中考压轴题中的二次函数⑶一.解答题(共3()小题)1.(2015*雅安校级一模)己知:如图,抛物线y= - x'+bx+c与x轴,y轴分别相交于点A (-1, 0),B (0, 3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;(3)AAOB与ABDE是否和似?如果相似,请予以证明;如果不相似,请说明理由.2.(2()15・余姚市模拟)如果抛物线©的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C]上,那么,我们称抛物线C|与C2关联.(1)已知抛物线①y=x2+2x - 1,判断下列抛物线②y=- X2+2X+1; ®y=x2+2x+l与已知抛物线①是否关联,并说明理由.(2)抛物线C】:y=| (x+1) —2,动点P的坐标为(t, 2),将抛物线绕点P (t, 2)旋转180。
得到抛物线C2,若抛物线Ci与C2关联,求抛物线C2的解析式.(3)A为抛物线Ci: y=g(x+l)2-2的顶点,B为与抛物线0关联的抛物线顶点,是否8存在以AB为斜边的等腰直角AABC,使其直角顶点C在y轴上?若存在,求出C点的坐标;若不存在,请说明理由.3.(2015*临淄区校级模拟)设抛物线y=ax2+bx・2与x轴交于两个不同的点A (・1, 0)、B (m, 0),与y轴交于点C.且ZACB=90度.(1)求m的值;(2)求抛物线的解析式,并验证点D (1, -3)是否在抛物线上:(3)已知过点A的直线y=x+l交抛物线于另一点E.问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与AAEB相似?若存在,请求出所有符合耍求的点P的坐标;若4.(2015*营口模拟)如图,二次函数尸-丄,+bx+c的图象经过点A (4, 0), B (・4,-4),且与y轴交于点C.(1)试求此二次函数的解析式;(2)试证明:ZBAO=ZCAO(H屮O是原点);(3)若P是线段AB±的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图彖及x轴于Q、H两点,试问:是否存在这样的点P,便PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.5.(2()15・杭州模拟)己知经过原点的抛物线y=・2X2+4X(如图所示)与x的另一交点为A 现将它向右平移m (m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P (1)求点P的坐标(可用含m式子表示);(2)设APCD的面积为s,求s关于m关系式;(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、0、A、F为顶点的四边形为平行四边形?若存在,求出m的值;若不存在,6.(2()15・温州模拟)如图,已知抛物线y=ax2+bx+c经过A (0, 4), B (4, 0), C (・1, 0)三点.过点A作垂直于y轴的直线1.在抛物线上有一动点P,过点P作直线PQ平行于y轴交直线1于点Q ・连接AP.(1)求抛物线y=ax2+bx+c的解析式;(2)是否存在点P,使得以A、P、Q三点构成的三角形与AAOC相似?如果存在,请求出点P的坐标;若不存在,请说明理由;(3)当点P位于抛物线y=ax2+bx+c的对称轴的右狈9.若将AAPQ沿AP对折,点Q的对7.(2015*來凤县二模)如图1,在平面直角坐标系xOy屮,直线1: y=-|x+K与x轴、y轴分别交于点A和点B (0,・1),抛物线尸吉,+bx+c经过点B,且与直线1的另一个交点乙(2) 点D 在抛物线上,且点D 的横坐标为t (0<t<4).。
二次函数压轴题

2015年中考压轴题说明:由于中考所考内容为初中大部分内容∴关于二次函数的压轴题很少会单纯的考二次函数,必定结合几何内容,故部分试题会结合几何内容·在平面直角坐标系x O y中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+b x+c经过点A,B.(1)求点A,B的坐标;(2)求抛物线C1的表达式及顶点坐标;(3)若抛物线C2:y=a x2(a≠0)与线段A B恰有一个公共点,结合函数的图象,求a的取值范围.·如图1,在平面直角坐标系中,抛物线y=a x2+b x+3交x轴于A(-1,0)和B(5,0)两点,交y轴于点C.点D是线段O B上一动点,连接C D,将线段C D绕点D顺时针旋转90°得到线段D E.过点E作直线l⊥x轴于点H,过点C作C F⊥l于点F.(1)求抛物线解析式.(2)如图2,当点F恰好在抛物线上时,求线段O D的长.(3)在(2)的条件下:①连接D F,求t a n∠F D E的值.②试探究在直线l上,是否存在点G,使∠E D G=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.·如图,一次函数y=k x+2与反比例函数(x>0)的图象交于点A,与y轴交于点M,与x轴交于点N,且A M︰M N=1︰2,则k=________.·小明开了一家网店,计划经销甲、乙两种商品,若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件,为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲=________,y乙=________.(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式.如果每周甲商品的销售量不低于乙商品的销售量的,那么当x定为多少时,才能使小明每周销售甲、乙两种商品获得的总利润最大?·如图,已知经过点D(2,)的抛物线(m为常数,且m>0)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C.(1)填空:m的值为________,点A的坐标为________.(2)根据下列描述,用尺规完成作图(保留作图痕迹,不写作法):连接A D,在x轴上方作射线A E,使∠B A E=∠BA D,过点D作x轴的垂线交射线A E于点E.(3)动点M,N分别在射线A B,A E上,求M E+M N的最小值.(4)l是过点A平行于y轴的直线,P是抛物线上一点,过点P作l的垂线,垂足为点G.请你探究:是否存在点P,使以P,G,A为顶点的三角形与△A B D相似?若存在,求出点P的坐标;若不存在,说明理由.·如图,在平面直角坐标系中,抛物线y=a x2+b x+c(a,b,c为常数,a≠0)与x轴、y轴分别交于A,B,C三点.已知点A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点D 出发沿线段D B向终点B运动.(1)求抛物线的解析式和顶点D的坐标.(2)过点E作E F⊥y轴于点F,交抛物线对称轴左侧的部分子点G,交直线B C于点H,过点H作H P⊥x轴于点P,连接P F,求当线段P F最短时点G的坐标.(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,且速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为ts,试问存在几个t值能使△B E Q 为等腰三角形?并直接写出相应t值.·如图,一次函数y1=x与二次函数y2=a x2+b x+c图象相交于P、Q两点,则函数y=a x2+(b-1)x+c的图象可能是()A.B.C.D.·如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.(1)填空:点C的坐标为(________,________),点D的坐标为(________,________);(2)设点P的坐标为(a,0),当|P D-P C|最大时,求a的值并在图中标出点P的位置;(3)在(2)的条件下,将△B C P沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△B CD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值是S最大,最大值为多少?·抛物线上任意一点到点(0,1)的距离与到直线y=-1的距离相等.你可以利用这一性质解决问题.问题解决如图,在平面直角坐标系中,直线y=k x+1与y轴交于C点,与函数的图象交于A、B两点,分别过A、B两点作直线y=-1的垂线,交于E、F两点.(1)写出点C的坐标,并说明∠E C F=90°;(2)在△P E F中,M为E F中点,P为动点.①求证:P E2+P F2=2(P M2+E M2);②已知P E=P F=3,以E F为一条对角线作平行四边形C E D F,若1<P D<2,试求C P的取值范围.·如图,已知点D在双曲线(x>0)的图象上,以D为圆心的⊙D 与y轴相切于点C(0,4),与x轴交于A,B两点;抛物线y=a x2+b x+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与B C 所在直线有交点Q.(1)写出点D的坐标并求出抛物线的解析式;(2)证明∠A C O=∠O B C;(3)探究是否存在点P,使点Q为线段A P的四等分点?若存在,求出点P的坐标;若不存在,请说明理由.·如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.(1)这条抛物线的对称轴是_____,直线P Q与x轴所夹锐角的度数是____;(2)若两个三角形的面积满足,求m的值;(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线A C与直线P Q交于点D,求:①P D+D Q的最大值;②P D·D Q的最大值.·如图,已知二次函数L1:y=a x2-2a x+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.(1)函数y=a x2-2a x+a+3(a>0)的最小值为________;当二次函数L 1,L2的y值同时随着x的增大而减小时,x的取值范围是________;(2)当E F=M N时,求a的值,并判断四边形E N F M的形状;(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△A M N为等腰三角形时,求方程-a(x+1)2+1=0的解.·已知抛物线y=-m x2+4x+2m与x轴交于点A(α,0),B(β,0),且.(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l 的对称点为 E.是否存在x轴上的点M、y轴上的点N,使四边形D N M E 的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.·如图是抛物线y1=a x2+b x+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=m x+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②a b c>0;③方程a x2+b x+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1.其中正确的是____.·如图,抛物与直线交于A,B两点,交x 轴与D,C两点,连接A C,B C,A(0,3),C(3,0).(Ⅰ)求抛物线的解析式和t a n∠B A C的值;(Ⅱ)在(Ⅰ)条件下:(1)P为y轴右侧抛物线上一动点,连接P A,过点P作P Q⊥P A 交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△A C B相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.(2)设E为线段A C上一点(不含端点),连接D E,一动点M从点D出发,沿线段D E以每秒一个单位速度运动到E点,再沿线段E A以每秒个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?·在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.(1)求过A,B,C三点的抛物线的解析式;(2)P为抛物线上一点,它关于原点的对称点为Q.①当四边形P BQ C为菱形时,求点P的坐标;②若点P的横坐标为t(-1<t<1),当t为何值时,四边形P B Q C面积最大,并说明理由.·如图,在平面直角坐标系中,抛物线y=a x2+b x+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且A D为⊙M的直径点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥A D于点H,且F H=1.5.(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△P E F的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△Q C M是等腰三角形?如果存在,清直接写出点Q的坐标;如果不存在,请说明理由.·如图,在平面直角坐标系中,抛物线y=m x2-8m x+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线A D∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线A D的交点分别为P、Q.(1)求抛物线的解析式;(2)当0<t≤8时,求△A P C面积的最大值;(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△A O B相似?若存在,求出此时t的值;若不存在,请说明理由.·已知:抛物线l1:y=-x2+b x+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,).(1)求抛物线l2的函数表达式;(2)P为直线x=1上一动点,连接P A,P C,当P A=P C时,求点P的坐标;(3)M为抛物线l2上一动点,过点M作直线M N∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段M N长度的最大值.·如图,边长为8的正方形O A B C的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作P F⊥B C于点 F.点D、E的坐标分别为(0,6),(-4,0),连接P D,P E,D E.(1)请直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,P D与P F的差为定值.进而猜想:对于任意一点P,P D与P F的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△P D E的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△P D E的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△P D E的周长最小时“好点”的坐标.·已知抛物线C1:(a≠0)经过点A(-1,0)和B(3,0).(1)求抛物线C1的解析式,并写出其顶点C的坐标;(2)如图1,把抛物线C1沿直线A C方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴下方,若△D E F是以E F为底的等腰直角三角形,求点F的坐标;(3)如图2,在(2)的条件下,设点M是线段B C上一动点,E N⊥E M交直线B F于点N,点P为线段M N的中点.当点M从点B向点C运动时:①t a n∠E N M的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.·如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m 的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=a t2+5t+c,已知足球飞行0.8s时,离地面的高度为 3.5m.(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t.已知球门的高度为 2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?·如图,已知抛物线与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,C D∥x轴交抛物线于点D,M为抛物线的顶点.(1)求点A、B、C的坐标;(2)设动点N(-2,n),求使M N+B N的值最小时n的值;(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△A B D相似(△P A B与△A B D不重合)?若存在,求出点P的坐标;若不存在,请说明理由.·如图是二次函数y=a x2+b x+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4a c②2a+b=0③a+b+c>0④若点B(,y1)、C(,y2)为函数图象上的两点,则y1<y2.其中正确结论是________.·已知抛物线与x轴交于A(-1,0),B两点,交y轴于点 C.(1)求抛物线的解析式(2)点E(m,n)是第二象限内一点,过点E作E F⊥x轴交抛物线于点F,过点F作F G⊥y轴于点G,连接C E、C F,若∠C E F=∠C F G,求n的值并直接写出m的取值范围(利用图1完成你的探究)(3)如图2,点P是线段O B上一动点(不包括点(O、B),P,P M⊥x轴交抛物线于点M,∠O BQ=∠O M P,B Q交直线P M于点Q,设点P的横坐标为t,求△P B Q的周长.·边长为2的正方形O A B C在平面直角坐标系中的位置如图所示,点D是边O A的中点,连接C D,点E在第一象限,且D E⊥D C,D E=D C.以直线A B为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线C B以每秒1个单位长度的速度运动,运动时间为t秒,过点P作P F⊥C D于点F,当t为何值时,以点P,F,D为顶点的三角形与△C O D相似?(3)点M为直线A B上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.·如图,二次函数y=a x2+b x+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且O A=O C.则下列结论:①a b c<0;②;③a c-b+1=0;④.其中正确结论的个数是__________.·在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.(1)求抛物线的解析式;(2)在A C上方的抛物线上有一动点P.①如图(1),当点P运动到某位置时,以A P,A O为邻边的平行四边形的第四个顶点恰好也在抛物线上,求出此时点P的坐标;②如图(2),过点O,P的直线y=k x交A C于点E,若P E︰O E=3︰8,求k的值.·如图是二次函数y=a x2+b x+c的图象,下列结论:①二次三项式a x2+b x+c的最大值为4;②4a+2b+c<0;③一元二次方程a x2+b x+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数是_________.·如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).(1)求抛物线的表达式;(2)证明:四边形A OB C的两条对角线互相垂直;(3)在四边形A O B C的内部能否截出面积最大的□D E F G?(顶点D,E,F,G分别在线段A O,O B,B C,C A上,且不与四边形A O B C的顶点重合)若能,求出□D E F G的最大面积,并求出此时点D的坐标;若不能,请说明理由.·如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接A M,B M.(1)求抛物线的函数关系式;(2)判断△A B M的形状,并说明理由;(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.·若关于x的二次函数y=a x2+b x+c(a>0,c>0,a,b,c是常数)与x轴交于两个不同的点A(x1,0),B(x2,0),(0<x1<x2),与y轴交于点P,其图象顶点为点M,点O为坐标原点.(1)当x1=c=2,时,求x2与b的值;(2)当x1=2c时,试问△A B M能否为等边三角形?判断并证明你的结论;(3)当x1=m c(m>0)时,记△M A B,△P A B的面积分别为S1,S2,若△B P O∽△P A O,且S1=S2,求m的值.·已知抛物线的表达式为y=-x2+6x+c.(1)若抛物线与x轴有交点,求c的取值范围;(2)设抛物线与x轴两个交点的横坐标分别为x1、x2,若,求c的值;(3)若P、Q是抛物线上位于第一象限的不同两点,P A、Q B都垂直于x轴,垂足分别为A、B,且△O P A与△O Q B全等,求证:.·已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A,B关于y轴的对称点分别为点A′,B′.(1)求m的值及抛物线E2所表示的二次函数的表达式.(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q,B,B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接O P并延长与抛物线E2相交于点P′,求△P A A′与△P′B B′的面积之比.·如图1,关于x的二次函数y=-x2+b x+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,D E为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)D E上是否存在点P到A D的距离与到x轴的距离相等?若存在,求出点P,若不存在,请说明理由;(3)如图2,D E的左侧抛物线上是否存在点F,使2S△F B C=3S△E B C?若存在,求出点F的坐标,若不存在,请说明理由.·如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿O A方向以每秒1个单位长度移动,动点D从点B开始沿B O方向以每秒1个单位长度移动,动点C、D 同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式:________.(2)求△C E D的面积S与D点运动时间t的函数解析式;当t为何值时,△C E D的面积最大?最大面积是多少?(3)当△C E D的面积最大时,在抛物线上是否存在点P(点E除外),使△P C D的面积等于△C E D的最大面积,若存在,求出P点的坐标;若不存在,请说明理由.·如图,反比例函数的图象经过二次函数y=a x2+b x图象的顶点(,0)(m>0),则有()A.a=b+2k B.a=b-2k C.k<b<0D.a<k<0。
二次函数压轴题(含答案)

面积类1.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M 的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m 的值;若不存在,说明理由.考点:二次函数综合题.专题:压轴题;数形结合.分析:(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.解答:解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)设直线BC的解析式为:y=kx+b,则有:,解得;故直线BC的解析式:y=﹣x+3.已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).(3)如图;∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,∴S△BNC=(﹣m2+3m)•3=﹣(m﹣)2+(0<m<3);∴当m=时,△BNC的面积最大,最大值为.2.如图,抛物线的图象与x轴交于A、B两点,与y轴交于C 点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M 点的坐标.考点:二次函数综合题..专题:压轴题;转化思想.分析:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.(3)△MBC的面积可由S△MBC=BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.解答:解:(1)将B(4,0)代入抛物线的解析式中,得:0=16a﹣×4﹣2,即:a=;∴抛物线的解析式为:y=x2﹣x﹣2.(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);∴OA=1,OC=2,OB=4,即:OC2=OA•OB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;所以该外接圆的圆心为AB的中点,且坐标为:(,0).(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;∴4﹣4×(﹣2﹣b)=0,即b=﹣4;∴直线l:y=x﹣4.所以点M即直线l和抛物线的唯一交点,有:,解得:即M(2,﹣3).过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×(2+3)+×2×3﹣×2×4=4.平行四边形类3.如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.(1)分别求出直线AB和这条抛物线的解析式.(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.考点:二次函数综合题;解一元二次方程-因式分解法;待定系数法求一次函数解析式;待定系数法求二次函数解析式;三角形的面积;平行四边形的判定..专题:压轴题;存在型.分析:(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n 与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=时,PM最长为=,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.解答:解:(1)把A(3,0)B(0,﹣3)代入y=x2+mx+n,得解得,所以抛物线的解析式是y=x2﹣2x﹣3.设直线AB的解析式是y=kx+b,把A(3,0)B(0,﹣3)代入y=kx+b,得,解得,所以直线AB的解析式是y=x﹣3;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),因为p在第四象限,所以PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,当t=﹣=时,二次函数的最大值,即PM最长值为=,则S△ABM=S△BPM+S△APM==.(3)存在,理由如下:∵PM∥OB,∴当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,①当P在第四象限:PM=OB=3,PM最长时只有,所以不可能有PM=3.②当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3,解得t1=,t2=(舍去),所以P点的横坐标是;③当P在第三象限:PM=OB=3,t2﹣3t=3,解得t1=(舍去),t2=,所以P 点的横坐标是.所以P点的横坐标是或.4.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B 的两条性质.考点:二次函数综合题..专题:压轴题.分析:(1)利用旋转的性质得出A′(﹣1,0),B′(0,2),再利用待定系数法求二次函数解析式即可;(2)利用S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,再假设四边形PB′A′B的面积是△A′B′O面积的4倍,得出一元二次方程,得出P点坐标即可;(3)利用P点坐标以及B点坐标即可得出四边形PB′A′B为等腰梯形,利用等腰梯形性质得出答案即可.解答:解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).方法一:设抛物线的解析式为:y=ax2+bx+c(a≠0),∵抛物线经过点A′、B′、B,∴,解得:,∴满足条件的抛物线的解析式为y=﹣x2+x+2.方法二:∵A′(﹣1,0),B′(0,2),B(2,0),设抛物线的解析式为:y=a(x+1)(x﹣2)将B′(0,2)代入得出:2=a(0+1)(0﹣2),解得:a=﹣1,故满足条件的抛物线的解析式为y=﹣(x+1)(x﹣2)=﹣x2+x+2;(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=﹣x2+x+2.连接PB,PO,PB′,∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,=×1×2+×2×x+×2×y,=x+(﹣x2+x+2)+1,=﹣x2+2x+3.∵A′O=1,B′O=2,∴△A′B′O面积为:×1×2=1,假设四边形PB′A′B的面积是△A′B′O面积的4倍,则4=﹣x2+2x+3,即x2﹣2x+1=0,解得:x1=x2=1,此时y=﹣12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.(3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②P A′=B′B;③B′P∥A′B;④B′A′=PB.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)5.如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD 的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题;分类讨论.分析:(1)先根据抛物线的解析式得出其对称轴,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标.(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,即①AD PB、②AB PD,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.解答:解:(1)∵顶点A的横坐标为x=﹣=1,且顶点A在y=x﹣5上,∴当x=1时,y=1﹣5=﹣4,∴A(1,﹣4).(2)△ABD是直角三角形.将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,∴y=x2﹣2x﹣3,∴B(0,﹣3)当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3∴C(﹣1,0),D(3,0),BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,BD2+AB2=AD2,∴∠ABD=90°,即△ABD是直角三角形.(3)存在.由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)∴OE=OF=5,又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l,即P A∥BD则构成平行四边形只能是P ADB或P ABD,如图,过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.设P(x1,x1﹣5),则G(1,x1﹣5)则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|P A=BD=3由勾股定理得:(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或4∴P(﹣2,﹣7)或P(4,﹣1),存在点P(﹣2,﹣7)或P(4,﹣1)使以点A、B、D、P为顶点的四边形是平行四边形.周长类6.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.(1)求抛物线对应的函数关系式;(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S 和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)根据抛物线y=经过点B(0,4),以及顶点在直线x=上,得出b,c 即可;(2)根据菱形的性质得出C、D两点的坐标分别是(5,4)、(2,0),利用图象上点的性质得出x=5或2时,y的值即可.(3)首先设直线CD对应的函数关系式为y=kx+b,求出解析式,当x=时,求出y即可;(4)利用MN∥BD,得出△OMN∽△OBD,进而得出,得到ON=,进而表示出△PMN的面积,利用二次函数最值求出即可.解答:解:(1)∵抛物线y=经过点B(0,4)∴c=4,∵顶点在直线x=上,∴﹣=﹣=,∴b=﹣;∴所求函数关系式为;(2)在Rt△ABO中,OA=3,OB=4,∴AB=,∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,∴C、D两点的坐标分别是(5,4)、(2,0),当x=5时,y=,当x=2时,y=,∴点C和点D都在所求抛物线上;(3)设CD与对称轴交于点P,则P为所求的点,设直线CD对应的函数关系式为y=kx+b,则,解得:,∴,当x=时,y=,∴P(),(4)∵MN∥BD,∴△OMN∽△OBD,∴即得ON=,设对称轴交x于点F,则(PF+OM)•OF=(+t)×,∵,S△PNF=×NF•PF=×(﹣t)×=,S=(﹣),=﹣(0<t<4),a=﹣<0∴抛物线开口向下,S存在最大值.由S△PMN=﹣t2+t=﹣(t﹣)2+,∴当t=时,S取最大值是,此时,点M的坐标为(0,).等腰三角形类7.如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题;分类讨论.分析:(1)首先根据OA的旋转条件确定B点位置,然后过B做x轴的垂线,通过构建直角三角形和OB的长(即OA长)确定B点的坐标.(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式.(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP 三种情况分类讨论,然后分辨是否存在符合条件的P点.解答:解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,∵∠AOB=120°,∴∠BOC=60°,又∵OA=OB=4,∴OC=OB=×4=2,BC=OB•sin60°=4×=2,∴点B的坐标为(﹣2,﹣2);(2)∵抛物线过原点O和点A、B,∴可设抛物线解析式为y=ax2+bx,将A(4,0),B(﹣2.﹣2)代入,得,解得,∴此抛物线的解析式为y=﹣x2+x(3)存在,如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD==,∴∠POD=60°,∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上,∴y=2不符合题意,舍去,∴点P的坐标为(2,﹣2)②若OB=PB,则42+|y+2|2=42,解得y=﹣2,故点P的坐标为(2,﹣2),③若OP=BP,则22+|y|2=42+|y+2|2,解得y=﹣2,故点P的坐标为(2,﹣2),综上所述,符合条件的点P只有一个,其坐标为(2,﹣2),8.在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(﹣1,0),如图所示:抛物线y=ax2+ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y轴的距离,即B的坐标;(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.解答:解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCD=∠CAO,(1分)又∵∠BDC=∠COA=90°,CB=AC,∴△BCD≌△CAO,(2分)∴BD=OC=1,CD=OA=2,(3分)∴点B的坐标为(﹣3,1);(4分)(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),则得到1=9a﹣3a﹣2,(5分)解得a=,所以抛物线的解析式为y=x2+x﹣2;(7分)(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,(8分)过点P1作P1M⊥x轴,∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC.(10分)∴CM=CD=2,P1M=BD=1,可求得点P1(1,﹣1);(11分)②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,(12分)过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,(13分)∴NP2=OA=2,AN=OC=1,可求得点P2(2,1),(14分)经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y=x2+x﹣2上.(16分)9.在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示,抛物线y=ax2﹣ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:代数几何综合题;压轴题.分析:(1)首先过点B作BD⊥x轴,垂足为D,易证得△BDC≌△COA,即可得BD=OC=1,CD=OA=2,则可求得点B的坐标;(2)利用待定系数法即可求得二次函数的解析式;(3)分别从①以AC为直角边,点C为直角顶点,则延长BC至点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,去分析则可求得答案.解答:解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠AC0+∠OAC=90°,∴∠BCD=∠CAO,又∵∠BDC=∠COA=90°,CB=AC,∴△BDC≌△COA,∴BD=OC=1,CD=OA=2,∴点B的坐标为(3,1);(2)∵抛物线y=ax2﹣ax﹣2过点B(3,1),∴1=9a﹣3a﹣2,解得:a=,∴抛物线的解析式为y=x2﹣x﹣2;(3)假设存在点P,使得△ACP是等腰直角三角形,①若以AC为直角边,点C为直角顶点,则延长BC至点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,如图(1),∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC,∴CM=CD=2,P1M=BD=1,∴P1(﹣1,﹣1),经检验点P1在抛物线y=x2﹣x﹣2上;②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,如图(2),同理可证△AP2N≌△CAO,∴NP2=OA=2,AN=OC=1,∴P2(﹣2,1),经检验P2(﹣2,1)也在抛物线y=x2﹣x﹣2上;③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,如图(3),同理可证△AP3H≌△CAO,∴HP3=OA=2,AH=OC=1,∴P3(2,3),经检验P3(2,3)不在抛物线y=x2﹣x﹣2上;故符合条件的点有P1(﹣1,﹣1),P2(﹣2,1)两点.综合类10.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.考点:二次函数综合题..专题:压轴题.分析:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,运用待定系数法即可求出直线BC的解析式;同理,将B(5,0),C(0,5)两点∑的坐标代入y=x2+bx+c,运用待定系数法即可求出抛物线的解析式;(2)MN的长是直线BC的函数值与抛物线的函数值的差,据此可得出一个关于MN的长和M点横坐标的函数关系式,根据函数的性质即可求出MN的最大值;(3)先求出△ABN的面积S2=5,则S1=6S2=30.再设平行四边形CBPQ的边BC上的高为BD,根据平行四边形的面积公式得出BD=3,过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.证明△EBD 为等腰直角三角形,则BE=BD=6,求出E的坐标为(﹣1,0),运用待定系数法求出直线PQ的解析式为y=﹣x﹣1,然后解方程组,即可求出点P的坐标.解答:解:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,得,解得,所以直线BC的解析式为y=﹣x+5;将B(5,0),C(0,5)两点的坐标代入y=x2+bx+c,得,解得,所以抛物线的解析式为y=x2﹣6x+5;(2)设M(x,x2﹣6x+5)(1<x<5),则N(x,﹣x+5),∵MN=(﹣x+5)﹣(x2﹣6x+5)=﹣x2+5x=﹣(x﹣)2+,∴当x=时,MN有最大值;(3)∵MN取得最大值时,x=2.5,∴﹣x+5=﹣2.5+5=2.5,即N(2.5,2.5).解方程x2﹣6x+5=0,得x=1或5,∴A(1,0),B(5,0),∴AB=5﹣1=4,∴△ABN的面积S2=×4×2.5=5,∴平行四边形CBPQ的面积S1=6S2=30.设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD.∵BC=5,∴BC•BD=30,∴BD=3.过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.∵BC⊥BD,∠OBC=45°,∴∠EBD=45°,∴△EBD为等腰直角三角形,BE=BD=6,∵B(5,0),∴E(﹣1,0),设直线PQ的解析式为y=﹣x+t,将E(﹣1,0)代入,得1+t=0,解得t=﹣1∴直线PQ的解析式为y=﹣x﹣1.解方程组,得,,∴点P的坐标为P1(2,﹣3)(与点D重合)或P2(3,﹣4).11.如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x 轴正半轴上,且OD=OC.(1)求直线CD的解析式;(2)求抛物线的解析式;(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P 点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法求出直线解析式;(2)利用待定系数法求出抛物线的解析式;(3)关键是证明△CEQ与△CDO均为等腰直角三角形;(4)如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小.如答图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值.解答:解:(1)∵C(0,1),OD=OC,∴D点坐标为(1,0).设直线CD的解析式为y=kx+b(k≠0),将C(0,1),D(1,0)代入得:,解得:b=1,k=﹣1,∴直线CD的解析式为:y=﹣x+1.(2)设抛物线的解析式为y=a(x﹣2)2+3,将C(0,1)代入得:1=a×(﹣2)2+3,解得a=.∴y=(x﹣2)2+3=x2+2x+1.(3)证明:由题意可知,∠ECD=45°,∵OC=OD,且OC⊥OD,∴△OCD为等腰直角三角形,∠ODC=45°,∴∠ECD=∠ODC,∴CE∥x轴,则点C、E关于对称轴(直线x=2)对称,∴点E的坐标为(4,1).如答图①所示,设对称轴(直线x=2)与CE交于点M,则M(2,1),∴ME=CM=QM=2,∴△QME与△QMC均为等腰直角三角形,∴∠QEC=∠QCE=45°.又∵△OCD为等腰直角三角形,∴∠ODC=∠OCD=45°,∴∠QEC=∠QCE=∠ODC=∠OCD=45°,∴△CEQ∽△CDO.(4)存在.如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′;而F′C″+F′P′+P′C′是点C′,C″之间的折线段,由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,即△P′CF′的周长大于△PCE的周长.)如答图③所示,连接C′E,∵C,C′关于直线QE对称,△QCE为等腰直角三角形,∴△QC′E为等腰直角三角形,∴△CEC′为等腰直角三角形,∴点C′的坐标为(4,5);∵C,C″关于x轴对称,∴点C″的坐标为(0,﹣1).过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,在Rt△C′NC″中,由勾股定理得:C′C″===.综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为.12.如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标.(2)试判断△BCD的形状,并说明理由.(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法即可求得函数的解析式;(2)利用勾股定理求得△BCD的三边的长,然后根据勾股定理的逆定理即可作出判断;(3)分p在x轴和y轴两种情况讨论,舍出P的坐标,根据相似三角形的对应边的比相等即可求解.解答:解:(1)设抛物线的解析式为y=ax2+bx+c由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.把点A(1,0)、点B(﹣3,0)代入,得解得a=﹣1,b=﹣2∴抛物线的解析式为y=﹣x2﹣2x+3.∵y=﹣x2﹣2x+3=﹣(x+1)2+4∴顶点D的坐标为(﹣1,4);(2)△BCD是直角三角形.理由如下:解法一:过点D分别作x轴、y轴的垂线,垂足分别为E、F.∵在Rt△BOC中,OB=3,OC=3,∴BC2=OB2+OC2=18在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,∴CD2=DF2+CF2=2在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,∴BD2=DE2+BE2=20∴BC2+CD2=BD2∴△BCD为直角三角形.解法二:过点D作DF⊥y轴于点F.在Rt△BOC中,∵OB=3,OC=3∴OB=OC∴∠OCB=45°∵在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1∴DF=CF∴∠DCF=45°∴∠BCD=180°﹣∠DCF﹣∠OCB=90°∴△BCD为直角三角形.(3)①△BCD的三边,==,又=,故当P是原点O时,△ACP∽△DBC;②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3﹣a,=,即=,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3﹣b,则=,即=,解得:b=﹣,故P是(0,﹣)时,则△ACP∽△CBD一定成立;④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).则AP=1﹣d,当AC与CD是对应边时,=,即=,解得:d=1﹣3,此时,两个三角形不相似;⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).则AP=1﹣e,当AC与DC是对应边时,=,即=,解得:e=﹣9,符合条件.总之,符合条件的点P的坐标为:.对应练习13.如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.考点:二次函数综合题..专题:代数几何综合题;压轴题.分析:(1)利用待定系数法求二次函数解析式解答即可;(2)利用待定系数法求出直线AC的解析式,然后根据轴对称确定最短路线问题,直线AC 与对称轴的交点即为所求点D;(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.解答:解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴,解得,所以,抛物线的解析式为y=x2﹣4x+3;(2)∵点A、B关于对称轴对称,∴点D为AC与对称轴的交点时△BCD的周长最小,设直线AC的解析式为y=kx+b(k≠0),则,解得,所以,直线AC的解析式为y=x﹣1,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,当x=2时,y=2﹣1=1,∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小;(3)如图,设过点E与直线AC平行线的直线为y=x+m,联立,消掉y得,x2﹣5x+3﹣m=0,△=(﹣5)2﹣4×1×(3﹣m)=0,即m=﹣时,点E到AC的距离最大,△ACE的面积最大,此时x=,y=﹣=﹣,∴点E的坐标为(,﹣),设过点E的直线与x轴交点为F,则F(,0),∴AF=﹣1=,∵直线AC的解析式为y=x﹣1,∴∠CAB=45°,∴点F到AC的距离为×=,又∵AC==3,∴△ACE的最大面积=×3×=,此时E点坐标为(,﹣).14.如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的解析式及它的对称轴方程;(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;(3)试判断△AOC与△COB是否相似?并说明理由;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.考点:二次函数综合题..专题:压轴题.分析:(1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=求出对称轴方程;(2)在抛物线解析式中,令x=0,可求出点C坐标;令y=0,可求出点B坐标.再利用待定系数法求出直线BD的解析式;(3)根据,∠AOC=∠BOC=90°,可以判定△AOC∽△COB;(4)本问为存在型问题.若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.解答:解:(1)∵抛物线y=﹣x2+bx+4的图象经过点A(﹣2,0),∴﹣×(﹣2)2+b×(﹣2)+4=0,解得:b=,∴抛物线解析式为y=﹣x2+x+4,又∵y=﹣x2+x+4=﹣(x﹣3)2+,∴对称轴方程为:x=3.(2)在y=﹣x2+x+4中,令x=0,得y=4,∴C(0,4);令y=0,即﹣x2+x+4=0,整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2,∴A(﹣2,0),B(8,0).设直线BC的解析式为y=kx+b,把B(8,0),C(0,4)的坐标分别代入解析式,得:,解得k=,b=4,∴直线BC的解析式为:y=x+4.(3)可判定△AOC∽△COB成立.理由如下:在△AOC与△COB中,∵OA=2,OC=4,OB=8,∴,又∵∠AOC=∠BOC=90°,∴△AOC∽△COB.(4)∵抛物线的对称轴方程为:x=3,可设点Q(3,t),则可求得:AC===,AQ==,CQ==.i)当AQ=CQ时,有=,25+t2=t2﹣8t+16+9,解得t=0,∴Q1(3,0);ii)当AC=AQ时,有=,t2=﹣5,此方程无实数根,∴此时△ACQ不能构成等腰三角形;iii)当AC=CQ时,有=,整理得:t2﹣8t+5=0,解得:t=4±,∴点Q坐标为:Q2(3,4+),Q3(3,4﹣).综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+),Q3(3,4﹣).15.如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx﹣2的图象过C点.(1)求抛物线的解析式;(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3)点P是抛物线上一动点,是否存在点P,使四边形P ACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.考点:二次函数综合题..专题:压轴题.分析:如解答图所示:(1)首先构造全等三角形△AOB≌△CDA,求出点C的坐标;然后利用点C的坐标求出抛物线的解析式;(2)首先求出直线BC与AC的解析式,设直线l与BC、AC交于点E、F,则可求出EF 的表达式;根据S△CEF=S△ABC,列出方程求出直线l的解析式;(3)首先作出▱P ACB,然后证明点P在抛物线上即可.解答:解:(1)如答图1所示,过点C作CD⊥x轴于点D,则∠CAD+∠ACD=90°.∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,∴∠OAB=∠ACD,∠OBA=∠CAD.∵在△AOB与△CDA中,∴△AOB≌△CDA(ASA).∴CD=OA=1,AD=OB=2,∴OD=OA+AD=3,∴C(3,1).∵点C(3,1)在抛物线y=x2+bx﹣2上,∴1=×9+3b﹣2,解得:b=﹣.∴抛物线的解析式为:y=x2﹣x﹣2.(2)在Rt△AOB中,OA=1,OB=2,由勾股定理得:AB=.∴S△ABC=AB2=.设直线BC的解析式为y=kx+b,∵B(0,2),C(3,1),∴,解得k=﹣,b=2,。
二次函数压轴题最短路径问题

最短路径问题一一和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题)•如图所示,在直线 丨上找一点P 使得P%PB 最小•当点P 为直线AB 与直线丨的交点时,PA + PB 最小.B-r | P ,B'B4 P .B'③如图所示,在/ AOB 勺边AO B0上分别找一点 C D 使得PO C 戻PD 最小•过点P 分别作关于 AO BO 的对称点E ,F ,连接EF,并与AO B0分别交于点C, D,此时PO C 戻PD 最小,则点C D 即为所求.④如图所示,在/ AOB 勺边AO BO 上分别找一点 E F 使得D 可EF + CF 最小•分别过点 C , D 作关于AO BO 的对称点D ; C ;连接DC,并与AO BC 分别交于点E, F ,此时DE^EF + CF 最小,则点E, F 即为所求.⑤如图所示,长度不变的线段 CD 在直线丨上运动,在直线丨上找到使得AO BD 最小的CD 的位置•分别过 点A ,D 作AA// CD DA// AC AA 与 DA 交于点A ;再作点B 关于直线丨的对称点B',连接A'B 与直线丨交于【方法归纳】在直线丨上找一点B 使得线段AB 最小•过点A 作AB1丨,垂足为B,则线段AB 即为所求.在直线 ②如图所示,点P ,此时PA^ PB 最小,则点P 即为所求.丨上找一点P 使得PA^ PB 最小•过点B 作关于直线丨的对称点B',BB'与直线丨交于BFB点D ,此时点D 即为所求.1⑥如图所示,在平面直角坐标系中,点P 为抛物线(y = 4X 1 2)上的一点,点A ( 0, 1)在y 轴正半轴.点P在什么位置时PA+PB 最小?过点B 作直线I : y =— 1的垂线段BH, BH 与抛物线交于点 P ,此时PA+ PB最小,则点P 即为所求.【思路点拨】 (1)由二次函数的图象经过坐标原点 0(0,0),直接代入求出 m 的值即可;1 (13广东)已知二次函数 y = x2 — 2m 灶卅一1. (1)当二次函数的图象经过坐标原点 0(0, 0)时,求二次函数的解析式;(2) 如图,当m= 2时,该抛物线与y 轴交于点C ,顶点为D 求C 、D 两点的坐标;(3) 在(2)的条件下,x 轴上是否存在一点 P ,使得PO PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BBB'(2) 把m= 2代入求出二次函数解析式,令 X = o ,求出y 的值,得出点C 的坐标;利用配方法或顶点坐标 公式求岀顶点坐标即可; (3) 根据当P C 、D 共线时根据"两点之间,线段最短"得出PC +PD 最短,求出CD 的直线解析式,令y=0,求出x 的值,即可得出P 点的坐标. 【解题过程】解:(1)T 二次函数的图象经过坐标原点0(0,0),•••代入二次函数y = X 3 4 5-2m 对m — 1,得出:m — 1 = 0,解得:m=± 1, •••二次函数的解析式为:y =x 2— 2x 或y = X 2 + 2x ;(2) v m= 2, •二次函数 y = x 2 — 2m 灶 m - 1 得:y = x 2— 4x + 3=( x — 2) 2 — 1,•抛物线的顶点为:D (2,— 1),当 x = 0 时,y = 3,• C 点坐标为:(0, 3),• C (0, 3)、D( 2,— 1 ); (3) 当P 、C D 共线时PO PD 最短,【方法一】:C ( 0, 3)、D( 2,— 1),设直线CD 的解析式为y = kx + 3,代入得:2k + 3=— 1 ,• k =— 2, • y = — 2x + 3, 3 3当y = 0时,一2x + 3= 0,解得x = 2,二PO PD 最短时,P 点的坐标为:P ( 2,0). 【方法二】过点D 作DEL y 轴于点E ,3• PO PD 最短时,P 点的坐标为:P (2,0).12. (11菏泽)如图,抛物线 y = 2x 2 + bx - 2与x 轴交于A , B 两点,与y 轴交于C 点,且A (- 1, 0).3 求抛物线的解析式及顶点 D 的坐标;4 判断△ ABC 勺形状,证明你的结论;5 点M(m 0)是x 轴上的一个动点,当 M G MD 的值最小时,求 m 的值.v PO/ DEPO =CODE" CE P0=32 = 4,解得:3 P0=2,【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标;(2) 观察发现A ABC 是直角三角形,可以通过勾股定理的逆定理证明. 由抛物线的解析式,分别求出点B , C 的坐标,再得出AB AC BC 的长度,易得AC + BC = AB ,得出△ ABC 是直角三角形; (3) 作出点C 关于x 轴的对称点C ;连接C D 交x 轴于点M 根据“两点之间,线段最短”可知 MO MD 的值最小•求岀直线 C D 的解析式,即可得岀点 M 的坐标,进而求岀 m 的值. 【解题过程】1 2 1 23解:(1) v 点 A (- 1, 0)在抛物线 y =於 + bx — 2 上, /• 2^ (- 1 ) + b x (- 1) — 2= 0,解得 b =- ,1 2 31 32 25 一3 25二抛物线的解析式为 y =—必—2= 2 (x — 2)— 8,二顶点D 的坐标为 (2,— 8)•(2)当 x = 0 时 y = — 2,「. C (0,— 2),OC= 2•, 亠 1 2 3当 y = 0 时,2X — q x — 2 = 0,二 X 1=— 1, X 2= 4,•: B (4, 0),「• OA= 1, OB= 4, AB= 5.V A B = 25, A C = oA + oC = 5, B C = OC + OB = 20,「. A C + B C = A B • •••△ ABO 直角三角形. (3) 作出点C 关于x 轴的对称点C',则C'(0, 2), OC = 2,连接C'D 交x 轴于点M 根据轴对称性及两点之间线段最短可知, MO MD 勺值最小.【方法一】设直线C'D 的解析式为y = kx +n ,则3丄=_ 25,解得:2k + n = — ~8 41 24 24.当 y = 0 时,一12x + 2 = 0, x = 41 • . n== 41 • 【方法二】设抛物线的对称轴交x 轴于点E.v ED/ y 轴,OCM=/ EDM /C‘OM= / DEM .△ C’Og DEM .OM =OC . = 2 . 24…EM = E D 3 = 25,n 41 •2 — m 百n = 2十4141 .. y = — —x + 2 k =— • y 12x 十 23. (11福州)已知,如图,二次函数 y = ax 2+ 2ax - 3a (a H))图象的顶点为 H,与x 轴交于A B 两点(B 在A 点右侧),点H B 关于直线丨:y=£x +冷3对称.(1 )求A 、B 两点坐标,并证明点 A 在直线丨上; (2) 求二次函数解析式;(3) 过点B 作直线BK// AH 交直线丨于K 点,M N 分别为直线AH 和直线丨上的两个动点,连接 HN NM MK 求HN^ NMF MK 和的最小值.【思路点拨】(1 )二次函数y = ax 2+ 2ax - 3a(a 旳)中只有一个未知参数 a ,令y = 0,解出方程ax 2 + 2ax - 3a = 0(a ^D ), 即可得到点A ,B 的坐标•把点A 的坐标代入直线丨的解析式即可判断 A 是否在直线上;(2) 根据点H B 关于过A 点的直线丨:y = jx + 3对称,得出AH= AB= 4,过顶点H 作HCL AB 交AB 于1C 点,得AC= 2AB= 2,利用勾股定理求出 HC 的长,即可得出点 H 的坐标,代入二次函数解析式,求出 a ,即可得到二次函数解析式;(3) 直线BK// AH 易得直线BK 的解析式,联立直线 丨的解析式方程组,即可求出 K 的坐标•因为点 H B 关于直线AK 对称,所以HN= BN 所以根据“两点之间,线段最短"得出 HN b MN 的最小值是MB 作点K 关 于直线AH 的对称点Q 连接QK 交直线AH 于 E ,所以Ql = KM 易得BW MK 的最小值为BQ 即BQ 的长是 HN F NMF MK 勺最小值,求出 QB 的长即可. 【解题过程】解:(1)依题意,得 ax' + 2ax - 3a = 0 ( a®,解得 X 1=- 3,X 2 = 1,v B 点在A 点右侧,A 点坐标为(-3,0),B 点坐标为(1,0),丁直线丨:y =3,当x =- 3时,y = X - 3) + 3 = 0,点A 在直线丨上.过顶点 H 作 HCLAB 交 AB 于 C 点,贝U AC= 2AB= 2, HC= 2 3, 顶点H ( — 1, 2寸3),代入二次函数解析式,解得 a =—芈 二次函数解析式为y = — 2^x 2 — ^ 3x + ~2^,(2) v 点H 、B 关于过A 点的直线丨:二 AH= AB= 4,(3)直线AH 的解析式为y = »:;3x + 3 3,直线BK 的解析式为y =-J 3x + 3寸3, 由y=老X 十护,解得x- 3即K ( 3, 2、0,则BK= 4,y - 3x - 3 y - 6 7 3T 点H B 关于直线 AK 对称,••• HW M N 勺最小值是 MB KD= KE - 2*3,过点K 作直线AH 的对称点 Q 连接QK 交直线AH 于巳_则QM= MK QE F EK= ^-3, AE 1QK 二B 冊 MK 勺最小值是 BQ 即BQ 的长是HN b NM- MK 勺最小值, v BK// AHBK —/HE(- 90° ° 由勾股定理得 QB= 8 , 二HN - NM- MK 勺最小值为8.当a -1时,求四边形 MEFP 勺面积的最大值,并求此时点 P 的坐标;若厶PCM!以点P 为顶点的等腰三角形,求 a 为何值时,四边形 PMEF 周长最小?请说明理由.(2) (3)4. (14海南) 如图,对称轴为直线x - 2的抛物线经过A (- 1 , 0), C(0 , 5)两点,与x 轴另一交点为 B-已知 M (0, 1),E (a , 0),F (a +1, 0),点P 是第一象限内的抛物线上的动点.(1) 求此抛物线的解析式;【思路点拨】(1 )由对称轴为直线x = 2,可以得出顶点横坐标为 2,设二次函数的解析式为 y = a (x -2) 2+ k ,再把点 A , B 的代入即可求出抛物线的解析式; (2) 求四边形MEF 的面积的最大值,要先表示出四边形MEF 面积•直接求不好求,可以考虑用割补法来求,过点P 作PN4L y 轴于点N,由S 四边形MEFP = S 梯形OFP — S ^PM — S OM 即可得出;(3) 四边形PMEF 勺四条边中,线段 PM EF 长度固定,当M H PF 取最小值时,四边形 PMEF 勺周长取得最 小值•将点M 向右平移1个单位长度(EF 的长度),得到点M (1,1),作点M 关于x 轴的对称点M (1, —1),连接PM ,与x 轴交于F 点,此时MB PF = PM 最小.【解题过程】解:(1 )v 对称轴为直线x = 2,.••设抛物线解析式为 y = a (x — 2) °+ k .2 2.y = —( x — 2) + 9= — x +4x + 5.(2)当 a = 1 时,E (1 , 0) , F ( 2, 0) , OE= 1 , OF= 2•设 P( x , — x 2 + 4x + 5), 如答图2,过点P 作PNL y 轴于点N,则PNhx , O = — x 2+ 4x + 5,.Mf = ONF OM= — x 2 + 4x + 4.1 1 1MEF= S梯形 OFP— S A PM — ® OM =2 ( PI H OF ?O — 2PN?M — 2OMOE1 1 1=2 (x + 2) (— x +4x + 5) — ?x ?( — x + 4x + 4) —1 X 19 153 9 153•••当x = 4时,四边形MEFP 勺面积有最大值为16,此时点P 坐标为(4, 16 .(3)v M( 0, 1), C (0, 5) ,△ PCM!以点P 为顶点的等腰三角形,•点 P 的纵坐标为3 . 令 y =— X 2 + 4X + 5 =3,解得 x = 2± 6.T 点 P 在第一象限,• P (2 + 6, 3). 四边形PMEF 勺四条边中,PM EF 长度固定, 因此只要MH PF 最小,则PMEF 勺周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M (1, 1); 作点M 关于x 轴的对称点M ,则M (1,- 1);连接PM,与x 轴交于 F 点,此时 M 曰PF = PM 最小.设直线PM 的解析式为y = m>H n ,将P(2 + 6, 3) , M ( 1,- 1)代入得:将 A (— 1, 0), C (0, 5 )代入得:9a + k = 04a + k = 5,解得a =— 1 k = 9 S四边形9 =-(X -4)153 16(m +n =6—T n = 3,解得:m =呼6+ 5当y = 0时,解得x = 4,0). 丁 a +1 =•斗咛1时,四边形PME 周长最小.4 6+ 4 n =5 ,顶点为D 了.(1) 求点A B , D 的坐标;(2) 连接CD 过原点O 作O 吐CD 垂足为H, OE 与抛物线的对称轴交于点 E,连接AE AD 求证:/ AEO=Z ADC(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点 切点为Q,当PQ 的长最小时,求点 P 的坐标,并直接写岀点 Q 的坐标.【思路点拨】1(1) 由顶点式直接得出点 D 的坐标,再令y = 0,得2(x 3)2 1 = 0解出方程,即可得出点 A B 的坐标; (2) 设HD 与AE 相交于点F ,可以发现厶ADF 组成一个“ 8字型” •对顶角/ HFE=Z AFD 只要/ FHE=/FAD 即可•因为/ EHF= 90 °,只需证明/ EAD= 90°即可•由勾股定理的逆定理即可得出△ ADE 为 直角三角形,得/FHE=Z FAD= 90°即可得出结论;(3) 先画出图形.因为PQ 为。
中考二次函数压轴题解题技巧

中考二次函数压轴题解题技巧在解题过程中,我们需要借助函数解析式来表示动点坐标。
首先,我们可以设定动点P在某条直线上,其坐标为(t,f(t))。
然后,我们可以通过计算两个线段的长度,利用代数式证明它们相等。
这种方法适用于各种类型的线段相等问题,如求证两个三角形的周长相等等。
2.求解“定三角形内一点到三边距离之和〞的问题:对于定三角形内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到定理的结论。
这种方法适用于各种类型的定三角形内点距离之和问题。
3.求解“定直线与定点之间的距离〞的问题:对于一个定点A和一条定直线L,我们可以利用点到直线的距离公式来求解它们之间的距离。
具体来说,我们可以设定一个动点P在直线L上,然后计算点P到点A的距离,即可得到定点与定直线之间的距离。
这种方法适用于各种类型的定直线与定点之间的距离问题。
4.求解“定点到定线段的最短距离〞的问题:对于一个定点A和一条定线段BC,我们可以利用点到线段的最短距离公式来求解它们之间的最短距离。
具体来说,我们可以设定一个动点P在线段BC上,然后计算点A到线段BP和线段CP的距离,取其中较小值即可得到定点到定线段的最短距离。
这种方法适用于各种类型的定点到定线段的最短距离问题。
5.求解“动三角形内一点到三边距离之和〞的问题:对于一个动三角形ABC内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到结论。
这种方法适用于各种类型的动三角形内点距离之和问题。
1.证明两线段相等的方法:首先确定两线段的距离类型(点点距离、点轴距离或点线距离),然后利用距离公式计算出两线段的长度,并进行化简,从而证明它们相等。
2.平行于y轴的动线段长度的最大值问题:对于平行于y轴的线段,可以利用端点的函数图象解析式,将两个端点的纵坐标表示为含有字母t的代数式。
中考二次函数压轴题经典例题

中考二次函数压轴题经典例题一、一类中考二次函数高分难题:如考题:“某费用与生产成本的平方成正比,生产成本为每件5元时,总费用为125元,生产成本为每件10元时,总费用为多少元?”解:依题意可知费用与生产成本的平方之间的关系式为y=kx²,经过点(5,125),代入上式得k=5。
于是,当生产成本为每件10元时,总费用y=5x²=5×10²=500元。
二、二次函数的解析式与图像:题目:“已知函数y = ax² + bx + c(a ≠ 0)如果x1、x2是y = 0的解,试求函数的解析式。
”解:如果已知x1、x2是y=0的解,那么二次函数的解析式可以表示为y=a(x-x1)(x-x2)。
对x进行配平方,得y=ax²-(x1+x2)ax+ax1x2,与y=ax²+bx+c相比,可以得出b=-(x1+x2)a, c=ax1x2。
由此可以看出,二次函数的系数与其解之间存在着规律性的联系。
三、二次函数的最值问题:题目:“设函数y=ax²+bx+c,在点(0,c)处取得最值,已知a,c>0, c是常数,求a,b 的取值范围。
”解:本题主要考查了函数的极值点。
首先明确这样一个概念:一个函数在它的极值点处的导数等于0。
设二次函数y=ax²+bx+c的极值点为x0,将它代入导数等于0的方程式得到x0=-b/2a,所以二次函数的对称轴为x=-b/2a。
因为函数在点(0,c)处取得最值,那么有x0=0,将x0=0代入上式,解得b=0。
又因为a,c>0,且当a>0时,抛物线开口朝上,函数的最小值点在对称轴上,与题意相符。
故a>0,所以a,b的取值范围是:a>0,b=0。
中考复习之二次函数中问题综合-几何旋转问题[1]
![中考复习之二次函数中问题综合-几何旋转问题[1]](https://img.taocdn.com/s3/m/b24e1dfabcd126fff6050b9c.png)
最短距离问题分析最值问题是初中数学的重要内容,也是一类综合性较强的问题,它贯穿初中数学的始终,是中考的热点问题,它主要考察学生对平时所学的内容综合运用,无论是代数问题还是几何问题都有最值问题,在中考压轴题中出现比较高的主要有利用重要的几何结论(如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等)。
利用一次函数和二次函数的性质求最值。
一、“最值”问题大都归于两类基本模型:Ⅰ、归于函数模型:即利用一次函数的增减性和二次函数的对称性及增减性,确定某范围内函数的最大或最小值Ⅱ、归于几何模型,这类模型又分为两种情况:(1)归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
(2)归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
一)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:A、A’是关于直线m的对称点。
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:mmABmAB mnmn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点:n mAnnnm(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:m n Am nm nmmmmA m(1)点A 、B 在直线m 同侧:(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’如图1,正方形ABCD 的边长为2,E 为AB 的中点, P 是AC 上一动点.连结BD ,由正方形对称性可知, B 与D 关于直线AC 对称.连结ED 交AC 于P ,则 PB PE +的最小值是___________;2.如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE +的和最小,则这个最小值为( )A .B .C .3 DBAm A B E CBD 图1A D EPB C二次函数常见压轴y=322--x x (以下几种分类的函数解析式就是这个)和最小,差最大 在对称轴上找一点P ,使得PB+PC 的和最小,求出P 点坐标在对称轴上找一点P ,使得PB-PC 的差最大,求出P 点坐标求面积最大 连接AC,在第四象限找一点P ,使得ACP ∆面积最大,求出P 坐标讨论直角三角连接AC,在对称轴上找一点P ,使得ACP ∆为直角三角形,求出P 坐标 或者在抛物线上求点P ,使△ACP 是以AC 为直角边的直角三角形.因动点产生的三角形相似问题例1.(2013•南平)如图,已知点A(0,4),B(2,0).(1)求直线AB的函数解析式;(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.①求线段AC的长;(用含m的式子表示)②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.例2.如图,直线3y x=-+与x轴,y轴分别相交于点B,点C,经过B C,两点的抛物线2y ax bx c=++与x轴的另一交点为A,顶点为P,且对称轴是直线2x=.(1)求A点的坐标;(2)求该抛物线的函数表达式;(3)连结AC.请问在x轴上是否存在点Q,使得以点P B Q,,为顶点的三角形与ABC△相似,若存在,请求出点Q的坐标;若不存在,请说明理由.练习:如图,在直角坐标系中,O为原点,抛物线23y x bx=++与x轴的负半轴交于点A,与y轴的正半轴交于点B,tan∠ACO=31.(1)求抛物线的解析式;(2)若直线:(0)l y kx k=≠与线段BC交于点D(不与点B C,重合),则是否存在这样的直线l,使得以B O D,,为顶点的三角形与BAC△相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由.A BCPOxy2x=AOBCxy和最小差最大如图,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)(1)求抛物线的解析式(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线M N∥BD,交线段AD 于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.面积问题:例题1:如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,3-),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.(1)求该二次函数的解析式;(2)若设点P的横坐标为m,试用含m的代数式表示线段PF的长;(3)求△PBC面积的最大值,并求此时点P的坐标.yxBA FPx=1CO例题2:在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.例3:已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标. (3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.讨论直角三角例1:已知:如图一次函数y =21x +1的图象与x 轴交于点A ,与y 轴交于点B ;二次函数y =21x2+bx +c 的图象与一次函数y =21x +1的图象交于B 、C 两点,与x 轴交于D 、E 两点且D 点坐标为(1,0) (1)求二次函数的解析式; (2)求四边形BDEC 的面积S ;(3)在x 轴上是否存在点P ,使得△PBC 是以P 为直角顶点的直角三角形?若存在,求出所有的点P ,若不存在,请说明理由.例2:如图,抛物线与x 轴交于A (-1,0)、B (3,0)两点,与y 轴交于点C (0,-3),设抛物线的顶点为D .(1)求该抛物线的解析式与顶点D 的坐标;(2)以B 、C 、D 为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCD 相似?若存在,请指出符合条件的点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.二次函数中四边形存在问题研究一、已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足)例1.【08湖北十堰】已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0),与y 轴的正半轴交于点C .⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标;⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.解:1.如图,抛物线y =-x 2+bx +c 与直线221+=x y 交于C 、D 两点,其中点C 在y 轴上,点D 的坐标为)27 3(,. 点P 是y 轴右侧的抛物线上一动点,过点P 作PE ⊥x 轴于点E ,交CD 于点F . (1)求抛物线的解析式;(2)若点P 的横坐标为m ,当m 为何值时,以O 、C 、P 、F 为顶点的四边形是平行四边形?请说明理由.PEOFCDBAxyOCDBA 备用图yx二、已知两个定点,再找两个点构成平行四边形①确定两定点连接的线段为一边,则两动点连接的线段应和已知边平行且相等)例1.【09福建莆田】已知,如图抛物线23(0)=++>与y轴交于C点,与x轴交于A、By ax ax c a两点,A点在B点左侧。
二次函数线段和最值--最短路径
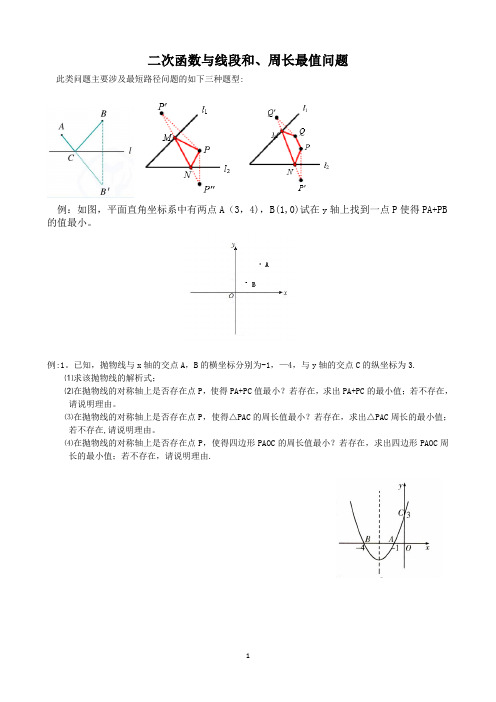
二次函数与线段和、周长最值问题此类问题主要涉及最短路径问题的如下三种题型:例:如图,平面直角坐标系中有两点A(3,4),B(1,0)试在y轴上找到一点P使得PA+PB 的值最小。
例:1。
已知,抛物线与x轴的交点A,B的横坐标分别为-1,—4,与y轴的交点C的纵坐标为3.⑴求该抛物线的解析式;⑵在抛物线的对称轴上是否存在点P,使得PA+PC值最小?若存在,求出PA+PC的最小值;若不存在,请说明理由。
⑶在抛物线的对称轴上是否存在点P,使得△PAC的周长值最小?若存在,求出△PAC周长的最小值;若不存在,请说明理由。
⑷在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长值最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.2。
如图,直线5+-=x y 与x 轴交于点B ,与y 轴交于点C,抛物线c bx x y ++-=2与直线5+-=x y 交于B 、C 两点.已知点D 的坐标为(0,3).⑴求该抛物线的解析式;⑵点M 、N 分别是直线BC 和x 轴上的动点,则当△DMN 的周长最小时,求点M ,N 的坐标,并写出△DMN 周长的最小值.3。
如图,二次函数)0(2>++=a c bx ax y 图像的顶点为D ,与x 轴的交点为A (—1,0),B(3,0),与y 轴负半轴交于点C.⑴若△ABD 为等腰直角三角形,求该抛物线的解析式; ⑵在⑴的条件下,抛物线与直线4-45x y =交于M 、N 两点(点M 在点N 的左侧),动点P 从M 点出发,先到达抛物线对称轴上的某点E ,再到达x 轴上的某点F ,最后运动到点N ,若使点P 运动的总路径最短,求点P 运动的总路径的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年中考数学二次函数求最短距离备考专题训练知识点:1.点到直线的距离直线外一点到直线的距离垂线段最短。
2.直线与直线的距离 两直线间垂线段最短。
3.在直线上找一点与直线同侧两点(不在直线上)的连线距离和最短的求法 首先找同侧两点中任一点关于该直线对称的点,再将同侧另一点与对称点连线,该连线与直线的交点即为所求。
中考真题训练1.如图,在锐角ABC △中,4245AB BAC =∠=,°,BAC ∠的平分线交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是___________ .ABCDN M(第1题图)2.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q 的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.3.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式;⑵动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标。
(第2题)4 x2 2A8 -2 O-2 -4 y 6B C D -444.如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t >,tan 3BAC ∠=,抛物线经过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点. (1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值;(3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.二次函数求最短距离参考答案1.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,OACBxy请说明理由.解:(1) 将点A (-4,8)的坐标代入2y ax =,解得12a =.……1分将点B (2,n )的坐标代入212y x =,求得点B 的坐标为(2,2),则点B 关于x 轴对称点P 的坐标为(2,-2). ……1分直线AP 的解析式是5433y x =-+.……1分 令y =0,得45x =.即所求点Q 的坐标是(45,0).……1分(2)① 解法1:CQ =︱-2-45︱=145,……1分故将抛物线212y x =向左平移145个单位时,A ′C +CB ′最短,……2分此时抛物线的函数解析式为2114()25y x =+.……1分解法2:设将抛物线212y x =向左平移m 个单位,则平移后A ′,B ′的坐标分别为A ′(-4-m ,8)和B ′(2-m ,2),点A ′关于x 轴对称点的坐标为A ′′(-4-m ,-8).直线A ′′B ′的解析式为554333y x m =+-. (1)分要使A ′C +CB ′最短,点C 应在直线A ′′B ′上, ……1分 将点C (-2,0)代入直线A ′′B ′的解析式,解得145m =.……1分故将抛物线212y x =向左平移145个单位时A ′C +CB ′最短,此时抛物线的函数解析式为2114()25y x =+.……1分② 左右平移抛物线212y x =,因为线段A ′B ′和CD 的长是定值,所以要使四边形A ′B ′CD 的周长最短,只要使A ′D +CB ′最短; ……1分第一种情况:如果将抛物线向右平移,显然有A ′D +CB ′>AD +CB ,因此不存在某个位置,使四边形A ′B ′CD 的周长最短.……1分第二种情况:设抛物线向左平移了b 个单位,则点A ′和点B ′的坐标分别为A ′(-4-b ,8)和B ′(2-b ,2).因为CD =2,因此将点B ′向左平移2个单位得B ′′(-b ,2),要使A ′D +CB ′最短,只要使A ′D +DB ′′最短. ……1分(第1题)4 x2 2A8 -2 O-2 -4 y 6 B CD -44(第1题(1)) 4 x2 2A8 -2 O -2 -4 y 6 BCD -44Q P (第1题(2)①)4 x2 2 A ′8-2 O -2 -4 y 6B ′C D-4 4 A ′′(第1题(2)②)4 x 2 2A ′8-2 O-2 -4 y6B ′CD -4 4 A ′′B ′′点A ′关于x 轴对称点的坐标为A ′′(-4-b ,-8), 直线A ′′B ′′的解析式为55222y x b =++.要使A ′D +DB ′′最短,点D 应在直线A ′′B ′′上,将点D (-4,0)代入直线A ′′B ′′的解析式,解得165b =. 故将抛物线向左平移时,存在某个位置,使四边形A ′B ′CD 的周长最短,此时抛物线的函数解析式为2116()25y x =+.……1分2.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式;⑵动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标。
解:(1)将A (0,1)、B (1,0)坐标代入212y x bx c =++得1102c b c =⎧⎪⎨++=⎪⎩解得321b c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解折式为213122y x x =-+…(2分) (2)设点E 的横坐标为m ,则它的纵坐标为213122m m -+ 即 E 点的坐标(m ,213122m m -+)又∵点E 在直线112y x =+上∴213111222m m m -+=+ 解得10m =(舍去),24m = ∴E 的坐标为(4,3) (Ⅰ)当A 为直角顶点时过A 作AP 1⊥DE 交x 轴于P 1点,设P 1(a,0) 易知D 点坐标为(-2,0) 由Rt △AOD ∽Rt △POA 得DO OA OA OP =即211a=,∴a =21 ∴P 1(21,0) (Ⅱ)同理,当E 为直角顶点时,P 2点坐标为(112,0)……(6分)(Ⅲ)当P 为直角顶点时,过E 作EF ⊥x 轴于F ,设P 3(b 、3)由∠OPA+∠FPE =90°,得∠OPA =∠FEP Rt △AOP ∽Rt △PFE由AO OP PF EF =得143bb =- 解得13b =,21b =∴此时的点P 3的坐标为(1,0)或(3,0)……综上所述,满足条件的点P 的坐标为(21,0)或(1,0)或(3,0)或(112,0)(Ⅲ)抛物线的对称轴为32x =…(9分)∵B 、C 关于x =23对称 ∴MC =MB要使||AM MC -最大,即是使||AM MB -最大由三角形两边之差小于第三边得,当A 、B 、M 在同一直线上时||AM MB -的值最大.(10分)易知直线AB 的解折式为1y x =-+∴由132y x x =-+⎧⎪⎨=⎪⎩ 得3212x y ⎧=⎪⎪⎨⎪=-⎪⎩ ∴M (23,-21)……3如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t >,tan 3BAC ∠=,抛物线经过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点.(1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值;(3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.解:(1)由A (-1,0)知AO=1,由tan ∠BAC=3,得CO=3AO=3,∴t=3 设抛物线的解析式为)3)(1(-+=x x a y , 将点C (0,3)坐标代入得1-=a∴所求解析式为322++-=x x y (2)332222=+⨯+-=m ,P (2,3)动点Q (1,n )在直线x =1上运动,点B (3,0)关于直线x =1的对称点为A (-1,0) ∴PQ+QB=PQ+QA∴PQ+QB 的最小值为PA=233)]1(2[22=+-- (3)将点P (2,3)的坐标代入)1(+=x k y 得1=k∴直线l 的解析式为1+=x y ∴AP 在l 上.设M (x ,322++-x x ),过M 作y 轴的平行线交AP 于D ,则D (x ,x +1),MD=322++-x x 2)1(2++-=+-x x xS △AMP =S △AMD +S △PMD =)2)(2(21)1)(2(2122x x x x x x -++-++++-=)2(232++-x x (9分) ∴AP S h AMP ∆=2)2(2223)2(322++-=++-=x x x x=]49)21([222+--x ∴当21=x 时,h 的最大值为829OACBxy。
