北京市顺义区2016届高三上学期期末统一测试数学(理)试题_Word版含答案

北京市顺义区2016届高三上学期期末统一测试化学试卷.pdf

（1）在元素周期表中的位置是
。
（2）A与可形成既含极性键又含非极性键的化合物W。W的水溶液呈弱酸性，常用作无污染的消毒杀菌剂。W的电子
式为_________。
（3）W溶液中ZE3，会消弱W的消毒杀菌能力，。用化学方程式表示其原因______。
由A、、D三种元素组成的两种强电解质甲和乙，它们的水溶液均呈酸性甲抑制水的电离，则甲的化学式为
（）已知：N2(g)+3H2(g) 2NH3(g) ΔH=－92.4 kJ/mol
2H2(g)+O2(g)2H2O(g) ΔH=－483.6kJ/mol
氨气完全燃烧生成气态水的热化学方程式_________。
氨燃料电池具有很大的发展潜力。氨氧燃料
电池
① a电极的电极反应式________；
C．用装置乙、丁收集和检验SO2的漂白性
D．用装置甲、丁制备和探究SO2的漂白性
. 肼（N2H4）是火箭燃料，常温下为液体，其球棍模型如下图所示。肼能与双氧水发生反应：N2H4 + 2H2O2===N2
+ 4H2O。下列说法正确的是
11.2 L N2中含电子总数为7
B. 3.2 g N2H4中含有共价键的总数为6
ΔH=－92.4kJ/mol。在500℃、20MPa时，将N2和H2通入到体积为 L的密闭容器中，反应过程中各种物质的量变化如图所
示:
（1）min内用H3表示该反应的平均速率v（H3）=。
（填字母）
a.加了催化剂 b. 降低温度
c.增加NH3的物质的量
（3）该可逆反应达到平衡的标志是钾溶液吸收CO2
（2）该富液中的溶质是__________（填化学式）。
（3）该富液中是________。

北京市顺义区高三数学第一次统练(一模)试题文

北京市顺义区2016届高三数学第一次统练（一模）试题文第Ⅰ卷（选择题共40分）一、选择题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项.1.设i 为虚数单位，则(1)+=i i ( ) （A ） 1-i （B ）1-+i （C ）1--i （D ）1+i2.已知集合2{|1}=<A x x ，{|21}=<x B x ，则A B =I （）（A ）(1,0)- （B ）(1,1)- （C ）(,0]-∞（D ）(,1)-∞3.下列函数在其定义域内既是奇函数又是增函数的是（）（A ）2-=x y （B ）3=+y x x （C ）1=-y x（D ）ln =y x 4.已知点(2,1)-P 为圆22(1)25-+=x y 的弦AB 的中点,则直线AB 的方程为（）（A ）30--=x y（B ）230+-=x y（C ）10+-=x y（D ）250--=x y5.执行如图所示的程序框图，输出的结果是 ( ) A. 15 B. 21 C. 24 D. 356.已知,∈a b R ，则“2≥ab ”是“224+≥a b ”成立的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分又不必要条件7.在平面直角坐标系中，若不等式组10,10,10+-≥⎧⎪-≤⎨⎪-+≥⎩x y x ax y （a 为常数）表示的区域面积等于3，则a 的值为（）（A ） 5- （B ） 2- （C ）2 （D ）5 8.如图，矩形ABCD 与矩形ADEF 所在的平面互相垂直，将DEF V 沿FD 翻折，翻折后的点E (记为点P )恰好落在BC 上. 设1=AB ，=FA x (1)>x ，=AD y .则以下结论正确的是（）（A ）当2=x 时，y 有最小值433 （B ）当2=x 时，y 有最大值 433（C ）当2=x 时，y 有最小值 2 （D ）当2=x 时，y 有最大值 2第Ⅱ卷（非选择题共110分）二、填空题共6小题，每小题5分，共30分.9.已知向量(2,1)=r a ，(1,)+=r ra b k ，若⊥r r a b ，则实数_________.=k10.抛物线28=y x 的准线与双曲线22:184-=x y C 的两条渐近线所围成的三角形面积为_________.11.在V ABC 中，角,,A B C 所对的边分别为,,a b c ，若2sin =a b A ，则___________.=B 12.已知某几何体的三视图如图,正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是________（单位:2cm ）.13.国家新能源汽车补贴政策，刺激了电动汽车的销售.据市场调查预测，某地区今年Q 型电动汽车的的销售将以每月10%的增长率增长；R 型电动汽车的销售将每月递增20辆.已知该地区今年1 月份销售Q 型和R 型车均为50辆，据此推测该地区今年Q 型汽车销售量约为_______辆；这两款车的销售总量约为_______辆.（参考数据：111.1 2.9,≈121.1 3.1,≈ 131.1 3.5≈）14.设集合3|12⎧⎫+≤≤≤⎨⎬⎩⎭b a b a 中的最大和最小元素分别是M m 、,则__,=M __=m . 三、解答题共6小题，共80分. 解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）已知函数2()sin 22cos =-f x x x ，∈x R . （Ⅰ）求函数()f x 的最小正周期；（Ⅱ）求函数()f x 在[0,]2π上的最大值与最小值.16.（本小题满分13分）某农业科研实验室，对春季昼夜温差大小与某蔬菜种子发芽多少之间的关系进行研究，分别记录了3月1日至3月6日的每天昼夜温差与实验室每天每100粒种子浸泡后的发芽数，得到如下数据：日期 3月1日3月2日3月3日3月4日3月5日3月6日昼夜温差()︒C 9 11 13 12 8 10 发芽数（粒）232530261624（Ⅰ）求此种蔬菜种子在这6天的平均发芽率；（Ⅱ）从3月1日至3月6日这六天中,按照日期顺序从前往后任选2天，记发芽的种子数分别为,m n ，用(,)m n 的形式列出所有基本事件，并求满足25302530≤≤⎧⎨≤≤⎩m n 的事件A 的概率. 17.（本小题满分13分 )已知等差数列{}n a ，23=a ，59=a . （Ⅰ）求数列{}n a 的通项公式n a ；（Ⅱ）令=n a n b c ，其中c 为常数，且0>c ，求数列{}n b 的前n 项和n S .18.（本小题满分13分）如图，已知⊥AB 平面ACD ，⊥DE 平面ACD ， V ACD 是等边三角形，22===AD DE AB ， ,F G 分别为,AD DC 的中点. （Ⅰ）求证：⊥CF 平面ABED ；（Ⅱ）求四棱锥-C ABED 的体积；（Ⅲ）判断直线AG 与平面BCE 的位置关系，并加以证明.19.（本小题满分14分 )已知函数2()21=+++x f x xe ax x 在1=-x 处取得极值. （Ⅰ）求函数()f x 的单调区间；（Ⅱ）若函数()1=--y f x m 在[2,2]-上恰有两个不同的零点，求实数m 的取值范围.20.（本小题满分14分 )已知椭圆:E 22221x y a b+=(0)a b >>的一个焦点(2,0)F ，点A 为椭圆上一点.（Ⅰ）求椭圆E 的方程；（Ⅱ）设,M N 为椭圆上两点，若直线AM 的斜率与直线AN 的斜率互为相反数. 求证：直线MN 的斜率为定值；（Ⅲ）在（Ⅱ）的条件下,V AMN 的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由.顺义区2016届高三第一次统练数学试卷（文科）参考答案及评分标准一、选择题：本大题共8小题，每小题5分，共40分.1. B ；2. A ；3. B ；4. A ；5. C ；6. A ；7. D ；8. C.二、填空题：本大题共6小题，每小题5分，共30分. 9. 3； 10.22；11.6π或 56π ; 12. 43+π ； 13.1050,2970；14. 5,23 三、解答题：本大题共6小题，共80分. 15.（本小题满分13分）解：（Ⅰ）由已知2()sin 22cos =-f x x x sin 2cos 212sin(2)14=--=--x x x π【4分】∴()f x 的最小正周期为π 【6分】（Ⅱ）02π≤≤Q x ，32444πππ∴-≤-≤x ，【7分】 ∴当244ππ-=-x ，即0=x 时， min ()2=-f x 【10分】当242ππ-=x ，即38π=x 时， max ()21=-f x 【13分】16.（本小题满分13分）解：（Ⅰ）这6天的平均发芽率为：232530261624100100100100100100100%24%6+++++⨯=，∴这6天的平均发芽率为 24% 【6分】（Ⅱ）(,)m n 的取值情况有(23,25),(23,30),(23,26),(23,16),(23,24),(25,30),(25,26),(25,16),(25,24),(30,26),(30,16),(30,24),(26,16),(26,24),(16,24),事件数为15 【9分】设25302530≤≤⎧⎨≤≤⎩m n 为事件A ，则事件A 包含的基本事件为(25,30),(25,26)(30,26)∴所求概率31155==P 【13分】17.（本小题满分13分）解：（Ⅰ）由已知11349+=⎧⎨+=⎩a d a d ，【2分】解得12,1==d a 【4分】∴数列{}n a 的通项公式为21=-n a n . 【6分】（Ⅱ）由（Ⅰ）知21-==na n nb cc 【7分】当 1=c 时，1=n b ， ∴.=n S n 【9分】当 1≠c 时，Q121+-+==n n a a n nb c c b ， ∴{}n b 是1=b c ，公比为2c 的等比数列；【11分】 ∴22(1)1-=-n n c c S c 【13分】 18.（本小题满分13分）解：（Ⅰ）Q F 为等腰V ACD 的边AD 的中点，∴⊥CF AD Q ⊥AB 平面ACD ，⊂AB 平面ABED ∴ 平面⊥ACD 平面ABED ，且交线为AD .由⊂CF 平面ACD ， ⊥CF AD ，∴⊥CF 平面ABED 【4分】（Ⅱ）Q 1(21)232=⋅+⋅=V ABED S ，3=CF ∴133-=⋅=C ABEF ABEF V S CF 【8分】（Ⅲ）结论：直线AG ∥平面BCE . 证明：取CE 的中点H ，连结,GH BH ， Q G 是CD 的中点， ∴GH ∥DE ，且 GH =12DE 由已知⊥AB 平面ACD ，⊥DE 平面ACD ，∴GH ∥AB ，且GH =1=AB ，∴四边形ABHG 为平行四边形，【11分】∴AG ∥BH ，又⊄AG 平面BCE ，⊂BH 平面BCE∴AG ∥平面BCE . 【13分】19.解：（本小题满分14分）（Ⅰ）'()22=+++x xf x e xe ax ，Q ()f x 在处取得极值，∴'(1)0-=f ，解得1=a .经检验1=a 适合.【2分】∴2()21=+++x f x xe x x ，'()(1)(2)=++x f x x e当(,1)∈-∞-x 时， '()0<f x ，∴()f x 在(,1)-∞-递减；当(1)∈-+∞x 时， '()0>f x ，∴()f x 在(1,)-+∞递增. 【6分】（Ⅱ）函数()1=--y f x m 在[2,2]-上恰有两个不同的零点，等价于220++-=x xe x x m 在[2,2]-上恰有两个不同的实根，等价于22++=x xe x x m 在[2,2]-上恰有两个不同的实根. 【8分】令2()2=++x g x xe x x ，∴'()(1)(2)=++x g x x e ，由（Ⅰ）知()g x 在(,1)-∞-递减；在(1,)-+∞递增.()g x 在[2,2]-上的极小值也是最小值；min 1()(1)1=-=--g x g e . 【11分】又22(2),-=-g e2(2)82(2)=+>-g e g∴2121--<≤-m e e ，即212(1,]∈---m e e【14分】20.（本小题满分14分）解：（Ⅰ）由已知2=C ，Q A 在椭圆上， ∴22421+=a b ，【2分】又 222=+a b c ，解得224,8==b a ，∴所求椭圆方程为22184+=x y 【4分】（Ⅱ）设1122(,),(,)M x y N x y ，直线AM 的斜率为k ，则直线AN 的斜率为-k ，∴22(2)184⎧-=-⎪⎨+=⎪⎩y k x x y 消去y得2222(12)(8)840+--+--=k x k x kQ 曲线E 与直线l 只有两个公共点，∴0>V ，【6分】且1,2x是方程的二根，∴21284212--=+kxk，∴2124212--=+kxk，∴21124(2)12-==-+-++ky k xk【7分】同理2224212+-=+kxk，222412++=-kyk∴21212-===-MNy ykx x为定值. 【9分】( Ⅲ )不妨设过,M N的直线方程为：=+y x m由222184⎧=+⎪⎪⎨⎪+=⎪⎩y x mx y，消去y得2240+-=x m，由0>V，解得28<m，12,+=x x2124=-x x m，计算得：A点到直线MN的距离=d∴1||2=⋅⋅=V AMNS d MN12==∴当24,=m即2=±m时，max()=AMNSV【14分】。

2016年北京高考真题数学理(含解析)

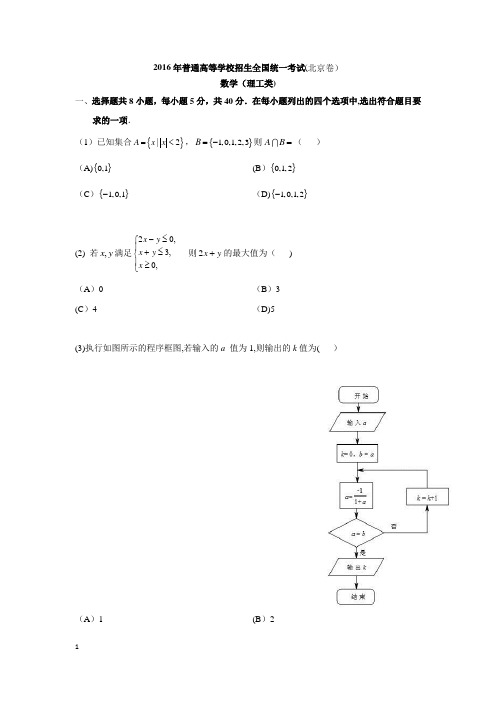
2016年普通高等学校招生全国统一考试(北京卷）数学（理工类)一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中,选出符合题目要求的一项．（1）已知集合{}|2A x x =<，{}1,0,1,2,3B =-则A B =（）（A){}0,1 (B ）{}0,1,2 （C ）{}1,0,1- （D){}1,0,1,2-(2) 若,x y 满足20,3,0,x y x y x -≤⎧⎪+≤⎨⎪≥⎩ 则2x y +的最大值为（ )（A ）0 （B ）3 (C ）4 （D)5(3)执行如图所示的程序框图,若输入的a 值为1,则输出的k 值为( ）（A ）1(B ）2（C)3 (D）4(4)设a,b是向量，则“a b="是“+a b a b=-”的( ）（A）充分而不必要条件(B）必要而不充分条件(C）充分必要条件（D）既不充分也不必要条件（5）已知,x y∈R，且0x y>>，则（）（A）11x y->(B）sin sin0x y->（C）1122x y⎛⎫⎛⎫-<⎪ ⎪⎝⎭⎝⎭（D）ln ln0x y+>(6）某三棱锥的三视图如图所示，则三棱锥的体积为( ）（A)16（B）13（C)12（D）1（7）将函数πsin23y x⎛⎫=-⎪⎝⎭图像上的点π,4P t⎛⎫⎪⎝⎭向左平移()0s s>个单位长度得到点P'．若P'位于函数sin2y x=的图像上，则( )（A)12t=，s的最小值为π6（B）3t,s的最小值为π6（C）12t=，s的最小值为π3（D）3t=,s的最小值为π3（8) 袋中装有偶数个球，其中红球，黑球各占一半，甲 ,乙，丙是三个空盒，每次从袋中随意取出两个球，将期中一个球放入甲盒，如果这个球是红球,就将另一个球放入乙盒，否则放入丙盒，重复上述过程，直到袋中所有球都被放入盒中,则( )．（A ）乙盒中黑球不多于丙盒中黑球（B ）乙盒中红球与丙盒中黑球一样多（C ）乙盒中的红球不多于丙盒中红球（D ）乙盒中黑球与丙盒中红球一样多二、填空题共6题，每小题5分,共30分．（9）设a ∈R ，若复数()()1i i a ++在复平面内对应的点位于实轴上，则a =__________．（10）在()612x -的展开式中，2x 的系数为__________．（11)在极坐标系中，直线cos sin 10ρθθ-=与圆2cos ρθ=交于,A B 两点，则AB = __________．(12）已知{}n a 为等差数列，n S 为其前n 项和．若1356,0a a a =+=，则6S =__________．（13）双曲线()222210,0x y a b a b-=>>的渐近线为正方形OABC 的边,OA OC 所在的直线，点B为该双曲线的焦点，若正方形OABC 的边长为2,则a =__________． (14)设函数()33,2,x x f x x ⎧-=⎨-⎩,,x a x a ≤>①若0a =，则()f x 的最大值__________．②若()f x 无最大值，则实数a 的取值范围是__________．三、解答题：本大题共6小题,共80分．解答应写出文字说明，演算步骤或证明过程．15. （本小题13分)在ABC △中，222a c b +=+ （1）求B ∠的大小．（2） cos A C +的最大值．16. (本小题13分)A ，B ，C 三班共有100名学生，为调查他们的体育锻炼情况，通过分层（Ⅰ）试估计班的学生人数；（Ⅱ)从A 班和C 班抽出的学生中，各随机选取一人，A 班选出的人记为甲，C 班选出的人记为乙，假设所有学生的锻炼时间相互独立,求该周甲的锻炼时间比乙的锻炼时间长的概率；（Ⅲ）再从A ，B ，C 三班中个随机抽取抽取一名学生，题目该周期的锻炼时间分别是7，9，8.25（单位：小时）,这3个新数据与表格构成的新样本的平均数记为1μ,表格中的数据的平均数记为0μ，试判断0μ和1μ的大小．（结论不要求证明）17. （本小题14分）如图，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =,AB AD ⊥，1AB =,2AD =，5AC CD ==．（Ⅰ）求证：PD ⊥平面PAB ；（Ⅱ）求直线PB 与平面PCD 所成角的正弦值；（Ⅲ)在棱PA 上是否存在点M ，使得BM ∥平面PCD ？若存在，求AMAP的值;若不存在，说明理由．（18）（本小题13分)设函数()a x f x xe bx -=+，曲线()y f x =在点()()2,2f 处的切线方程为()14y e x =-+. (1）求,a b 的值；（2）求()f x 的单调区间。

北京市东城区2016届高三上学期期末教学统一检测数学(理科)试卷_Word版含有答案

北京市东城区2015-2016学年第一学期期末教学统一检测高三数学（理科） 2016.1本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项. （1）已知集合{1,2,3,4}U =，集合{1,3,4}A =，{2,4}B =，那么集合()U C A B =I（A ）{2} （B ）{4} （C ）{1,3} （D ）{2,4} （2）已知某三棱锥的三视图(单位：cm)如图所示，那么该三棱锥的体积等于侧（左）视图俯视图（A ）32cm 3 （B ）2 cm 3 （C ）3 cm 3 （D ）9 cm 3 （3）设i 为虚数单位，如果复数z 满足(12)5i z i -=，那么z 的虚部为（A ）1- （B ）1 （C ） i （D ）i - （4）已知(0,1)m ∈，令log 2m a =，2b m =，2mc =，那么,,a b c 之间的大小关系为（A ）b c a << （B ）b a c << （C ）a b c << （D ）c a b << （5）已知直线l 的倾斜角为α，斜率为k ，那么“3πα>”是“k >（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（6）已知函数11,02()ln ,2x f x x x x ⎧+<≤⎪=⎨⎪>⎩，如果关于x 的方程()f x k =有两个不同的实根，那么实数k 的取值范围是3（7）过抛物线220)y px p =>（的焦点F 的直线交抛物线于,A B 两点，点O 是原点，如果3BF =，BF AF >，23BFO π∠=，那么AF 的值为 ()A 1 ()B 32()C 3 （D ） 6 （8）如图所示，正方体ABCD A B C D ''''-的棱长为1, ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，)1,0(∈x ，给出以下四个命题： ① 四边形MENF 为平行四边形；② 若四边形MENF 面积)(x f s =,)1,0(∈x ,则)(x f 有最小值；③ 若四棱锥A MENF 的体积)(x p V =，)1,0(∈x ，则)(x p 常函数；④ 若多面体MENF ABCD -的体积()V h x =，1(,1)2x ∈，则)(x h 为单调函数．其中假．命题．．为 ()A ①()B ②()C ③（D ）④第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分.（9）在ABC ∆中，a b 、分别为角A B 、的对边，如果030B =，0105C =，4a =，那么b = .（10）在平面向量a,b 中，已知(1,3)=a ，(2,y)=b .如果5⋅=a b ，那么y = ；如果-=a +b a b ，那么y = .（11）已知,x y 满足满足约束条件+10,2,3x y x y x ≤⎧⎪-≤⎨⎪≥⎩，那么22z x y =+的最大值为___.（12）如果函数2()sin f x x x a =+的图象过点(π,1)且()2f t =．那么a = ； ()f t -= ．（13）如果平面直角坐标系中的两点(1,1)A a a -+，(,)B a a 关于直线l 对称，那么直线l 的方程为__.（14）数列{}n a 满足：*112(1,)n n n a a a n n N -++>>∈，给出下述命题：①若数列{}n a 满足：21a a >，则*1(1,)n n a a n n N ->>∈成立； ②存在常数c ，使得*()n a c n N >∈成立；③若*(,,,)p q m n p q m n N +>+∈其中，则p q m n a a a a +>+； ④存在常数d ，使得*1(1)()n a a n d n N >+-∈都成立．上述命题正确的是____．(写出所有正确结论的序号)三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．（15）（本小题共13分）设{}n a 是一个公比为(0,1)q q q >≠等比数列，1234,3,2a a a 成等差数列,且它的前4项和415s =. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令2,(1,2,3......)n n b a n n =+=,求数列{}n b 的前n 项和.（16）（本小题共13分）已知函数22()sincos cos ()f x x x x x x =+-∈R ．（Ⅰ）求()f x 的最小正周期和在[0,π]上的单调递减区间；（Ⅱ）若α为第四象限角，且3cos 5α=，求7π()212f α+的值.（17）（本小题共14分）如图，在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥底面ABCD ，AB AP =,E 为棱PD 的中点.（Ⅰ）证明:AE CD ⊥；（Ⅱ）求直线AE 与平面PBD 所成角的正弦值；（Ⅲ）若F 为AB 中点，棱PC 上是否存在一点M ，使得FM AC ⊥，若存在，求出PMMC的值，若不存在，说明理由.（18）（本小题共13分）已知椭圆22221x y a b +=（0a b >>）的焦点是12F F 、，且122F F =，离心率为12．（Ⅰ）求椭圆C 的方程；（Ⅱ）若过椭圆右焦点2F 的直线l 交椭圆于A ，B 两点，求22||||AF F B g 的取值范围．（19）（本小题共14分）已知函数()(ln )xe f x a x x x=--．（Ⅰ）当1a =时，试求()f x 在(1,(1))f 处的切线方程；（Ⅱ）当0a ≤时，试求()f x 的单调区间；（Ⅲ）若()f x 在(0,1)内有极值，试求a 的取值范围．（20）（本小题共13分）已知曲线n C 的方程为：*1()nnx y n N +=∈.（Ⅰ）分别求出1,2n n ==时，曲线n C 所围成的图形的面积;（Ⅱ）若()n S n N *∈表示曲线n C 所围成的图形的面积，求证：()n S n N *∈关于n 是递增的;(III) 若方程(2,)n n n x y z n n N +=>∈，0xyz ≠，没有正整数解，求证：曲线(2,)n C n n N *>∈上任一点对应的坐标(,)x y ，,x y 不能全是有理数.东城区2015-2016学年第一学期期末教学统一检测参考答案高三数学（理科） 2016.1学校___________班级_____________姓名____________考号___________本试卷共5页，150分。

北京市部分区2016届高三上学期期中期末数学理试题分类汇编：数列

北京部分区2016届高三上学期期中期末考试数学理试题分类汇编数列一、选择题1、（昌平区2016届高三上学期期末）已知函数f (x ) 的部分对应值如表所示. 数列{}n a 满足11,a =且对任意*n ∈N ，点1(,)n n a a +都在函数()f x 的图象上，则2016a 的值为x1 2 3 4 ()f x3124A . 1 B.2 C. 3 D. 42、（朝阳区2016届高三上学期期中）已知等差数列{}n a 的公差为2，若124, , a a a 成等比数列，那么1a 等于（）A. 2B. 1C. 1-D. 2- 3、（东城区2016届高三上学期期中）在等差数列{}n a 中，，前n 项和Sn＝100，则公差d 和项数n 为A 、d ＝12，n ＝4B 、d ＝－18，n ＝2C 、d ＝16，n ＝3D 、d ＝16，n ＝44、（丰台区2016届高三上学期期末）已知数列{}n a 中，1111,1n na a a +==+，若利用下面程序框图计算该数列的第2016项，则判断框内的条件是（A ）2014≤n （B ）2016n ≤（C ）2015≤n （D ）2017n ≤5、（海淀区2016届高三上学期期中）数列的前n 项和为，则的值为A ．1B ．3C ．5D ．66、（石景山区2016届高三上学期期末）已知数列{}n a 是等差数列，348,4a a ==，则前n 项和n S 中最大的是（）A.3SB.4S 或5S？结束输出A 否是A =1A +1n =n +1n =1,A =1开始C.5S 或6SD.6S7、（西城区2016届高三上学期期末）在数列{}n a 中，“对任意的*n ∈N ，212n n n a a a ++=”是“数列{}n a 为等比数列”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件参考答案1、B2、A3、D4、C5、C6、B7、B二、填空题1、（朝阳区2016届高三上学期期末）在各项均为正数的等比数列{}n a 中，若22a =，则132a a +的最小值是2、（大兴区2016届高三上学期期末）已知数列{}n a 是等差数列，公差0d ≠，11a =，1a ，3a ，6a 成等比数列，则数列{}n a 的公差d 等于；前n 项和n S 等于 .3、（东城区2016届高三上学期期末）数列{}n a 满足：*112(1,)n n n a a a n n N -++>>∈，给出下述命题：①若数列{}n a 满足：21a a >，则*1(1,)n n a a n n N ->>∈成立； ②存在常数c ，使得*()n a c n N >∈成立；③若*(,,,)p q m n p q m n N +>+∈其中，则p q m n a a a a +>+；④存在常数d ，使得*1(1)()n a a n d n N >+-∈都成立．上述命题正确的是____．(写出所有正确结论的序号) 4、（东城区2016届高三上学期期中）在数列{}n a 中，5、（丰台区2016届高三上学期期末）设等差数列{}n a 的前n 项和为n S ，若7=42S ,则237a a a ++= .6、（海淀区2016届高三上学期期末）已知等比数列{}n a 的公比为2，若234a a +=，则14___.a a +=7、（海淀区2016届高三上学期期中）已知等差数列的公差，且39108a a a a +=-．若na ＝0 ，则n ＝参考答案1、422、217,48n n +3、①④4、121)2n -（ 5、186、67、5三、解答题1、（朝阳区2016届高三上学期期末）已知有穷数列：*123,,,,(,3)k a a a a k k ∈≥N L 的各项均为正数，且满足条件： ①1k a a =；②11212(1,2,3,,1)n n n n a a n k a a +++=+=-L ．（Ⅰ）若13,2k a ==，求出这个数列；（Ⅱ）若4k =，求1a 的所有取值的集合；（Ⅲ）若k 是偶数，求1a 的最大值（用k 表示）．2、（朝阳区2016届高三上学期期中）已知等差数列{}n a 的首项11a =，公差1d =，前n 项和为n S ，且1n nb S =. （Ⅰ）求数列{}n b 的通项公式；（Ⅱ）求证：1232n b b b b ++++<L .3、（东城区2016届高三上学期期末）设{}n a 是一个公比为(0,1)q q q >≠等比数列，1234,3,2a a a 成等差数列,且它的前4项和415s =.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令2,(1,2,3......)n n b a n n =+=,求数列{}n b 的前n 项和.4、（东城区2016届高三上学期期中）设数列{}n a 的前n 项和Sn ＝（I ）求（II ）求证：数列{}n a 为等比数列5、（丰台区2016届高三上学期期末）已知数列{}n a 的各项均为正数，满足11a =，1k k i a a a +-=.,1,2,i k k ≤=（3,,1)n -L（Ⅰ）求证：111,2,3,,1)k k a a k n +-≥=-L （；（Ⅱ）若{}n a 是等比数列，求数列{}n a 的通项公式；（Ⅲ）设数列{}n a 的前n 项和为n S ，求证：12)1(21-≤≤+n n S n n .6、（海淀区2016届高三上学期期末）若实数数列{}n a 满足*21()n n n a a a n ++=-∈N ，则称数列{}n a 为“P 数列”.（Ⅰ）若数列{}n a 是P 数列，且140,1a a ==，求3a ，5a 的值；(Ⅱ) 求证：若数列{}n a 是P 数列，则{}n a 的项不可能全是正数，也不可能全是负数； (Ⅲ) 若数列{}n a 为P 数列，且{}n a 中不含值为零的项，记{}n a 前2016项中值为负数的项的个数为m ，求m 所有可能取值.7、（海淀区2016届高三上学期期中）已知等比数列的公比，其n 前项和为（Ⅰ）求公比q 和a 5的值；（Ⅱ）求证：8、（石景山区2016届高三上学期期末）给定一个数列{}n a ，在这个数列里，任取*(3,)m m m N ≥∈项，并且不改变它们在数列{}n a 中的先后次序，得到的数列称为数列{}n a 的一个m阶子数列．已知数列{}n a 的通项公式为1n a n a=+（*,n N a ∈为常数），等差数列236,,a a a 是数列{}n a 的一个3阶子数列．（Ⅰ）求a 的值；（Ⅱ）等差数列12,,...,m b b b 是{}n a 的一个*(3,)m m m N ≥∈ 阶子数列，且11b k=(k 为常数，*,2)k N k ∈≥，求证：1m k ≤+；（Ⅲ）等比数列12,,...,m c c c 是{}n a 的一个*(3,)m m m N ≥∈ 阶子数列，求证：1211......22m m c c c -+++≤-．11、（西城区2016届高三上学期期末）参考答案1、解：（Ⅰ）因为13,2k a ==，由①知32a =；由②知，21211223a a a a +=+=，整理得，2222310a a -+=．解得，21a =或212a =．当21a =时，不满足2323212a a a a +=+，舍去；所以，这个数列为12,,22． …………………………………………………3分（Ⅱ）若4k =，由①知4a =1a ．因为11212(1,2,3)n n n n a a n a a +++=+=，所以111(2)(1)0n n n n a a a a ++--=．所以112n n a a +=或11(1,2,3)n n a n a +==．如果由1a 计算4a 没有用到或者恰用了2次11n na a +=，显然不满足条件；所以由1a 计算4a 只能恰好1次或者3次用到11n na a +=，共有下面4种情况：（1）若211a a =，3212a a =，4312a a =，则41114a a a ==，解得112a =；（2）若2112a a =，321a a =，4312a a =，则4111a a a ==，解得11a =；（3）若2112a a =，3212a a =，431a a =，则4114a a a ==，解得12a =；（4）若211a a =，321a a =，431a a =，则4111a a a ==，解得11a =；综上，1a 的所有取值的集合为1{,1,2}2． ………………………………………………8分（Ⅲ）依题意，设*2,,m 2k m m =∈≥N ．由（II ）知，112n n a a +=或11(1,2,3,21)n na n m a +==-L ．假设从1a 到2m a 恰用了i 次递推关系11n n a a +=，用了21m i --次递推关系112n n a a +=，则有(1)211()2itm a a -=⋅，其中21,t m i t ≤--∈Z ．当i 是偶数时，0t ≠，2111()2tm a a a =⋅=无正数解，不满足条件；当i 是奇数时，由12111(),21222t m a a a t m i m -=⋅=≤--≤-得22211()22t m a -=≤，所以112m a -≤．又当1i =时，若213221222211111,,,,222m m m m a a a a a a a a ---====L ，有222111()2m m a a --=⋅，222112m m a a a -==，即112m a -=．所以，1a 的最大值是12m -．即1212ka -=．…………………………………13分2、3、解：（Ⅰ）因为{}n a 是一个公比为(0,1)q q q >≠等比数列，所以11n n a a q -=．因为1234,3,2a a a 成等差数列，所以213642,a a a =+即2320q q -+=．解得2,1()q q ==舍.又它的前4和415s =，得41(1)15(0,1)1a q q q q-=>≠-，解得11a = ．所以12n n a -= . …………………9分（Ⅱ）因为2n n b a n =+，所以11122(n 1)1n n nn i i i i i b a i n ====+=++-∑∑∑． ………………13分4、5、（Ⅰ）证明：因为1,1,2,3,,1)k k i a a a i k k n +-=>≤=-L 0（，所以数列{}n a 是递增数列，即231n a a a <<<<L .又因为11,1,2,3,,1)k k i a a a i k k n +-=≥≤=-L （，所以111,2,3,,1)k k a a k n +-≥=-L （. …………………………3分（Ⅱ）解：因为211a a a -=，所以212a a =；因为{}n a 是等比数列，所以数列{}n a 的公比为2.因为1,1,2,3,,1)k k i a a a i k k n +-=≤=-L （，所以当=i k 时有1=2k k a a +.这说明在已知条件下，可以得到唯一的等比数列.所以12n n a -=. …………………………8分（Ⅲ）证明：因为11=1a =，22=2a =，2332a ≤≤， 3442a ≤≤… 12n n n a -≤≤ 由上面n 个式子相加，得到：0121123+2+3++2+2+2++2n n n a a a a -≤++++≤L L L 1，化简得1231))(21)2n n n n a a a a +<++++<-L （（所以12)1(21-≤≤+n n S n n . ………13分 6、（Ⅰ）因为{}n a 是P 数列，且10a =，所以3202||||a a a a =-=，所以43222a a a a a =-=-, 所以221a a -=，解得212a =-, …………………………….1分所以354311,||22a a a a ==-=. …………………………….3分(Ⅱ) 假设P 数列{}n a 的项都是正数，即120,0,0n n n a a a ++>>>，所以21n n n a a a ++=-，3210n n n n a a a a +++=-=-<，与假设矛盾. 故P 数列{}n a 的项不可能全是正数,…………………………….5分假设P 数列{}n a 的项都是负数，则0,n a <而210n n n a a a ++=->,与假设矛盾,…………………………….7分故P 数列{}n a 的项不可能全是负数.(Ⅲ)由(Ⅱ)可知P 数列{}n a 中项既有负数也有正数，且最多连续两项都是负数，最多连续三项都是正数. 因此存在最小的正整数k 满足10,0k k a a +<>（5k ≤）. 设1,(,0)k k a a a b a b +=-=>，则2345,,,k k k k a b a a a a b a b a ++++=+==-=-.678910,,,,k k k k k a b a b a b a a a a b a a a b +++++=-+=-+=-=-=,故有9k k a a +=, 即数列{}n a 是周期为9的数列…………………………….9分由上可知18,,,k k k a a a ++⋅⋅⋅这9项中4,k k a a +为负数，5,8k k a a ++这两项中一个为正数，另一个为负数，其余项都是正数. 因为20169224=⨯,所以当1k =时，2243672m =⨯=;当25k ≤≤时，121,,,k a a a -⋅⋅⋅这1k -项中至多有一项为负数，而且负数项只能是1k a -, 记12016,,,k k a a a +⋅⋅⋅这2007k -项中负数项的个数为t ，当2,3,4k=时，若10,k a -<则11k k k k b a a a a a +-==->=，故8k a +为负数，此时671t =，671+1=672m =；若10,k a ->则11k k k k b a a a a a +-==-<=，故5k a +为负数. 此时672t =，672m =，当5k =时，1k a -必须为负数，671t =，672m =,…………………………….12分综上可知m 的取值集合为{672}.…………………………….13分 7、解：（Ⅰ）法一：因为{}n a 为等比数列，且3244a a a =，所以2334a a =，所以34a =，因为233141a a q a ===，所以2q =±. 因为0n a >，所以q >，即2q =---------------------------3分所以45116a a q ==.--------------------------6分法二：因为{}n a 为等比数列，且3244a a a =，所以24114a q a q =，所以24q =，所以2q =±, 因为n a >，所以0q >，即2q =---------------------------3分所以45116a a q ==.--------------------------6分（Ⅱ）法一：因为2q =，所以1112n n n a a q --==,--------------------------８分因为1(1)211n n n a q S q-==--,--------------------------10分所以11211222n n n n n S a ---==-,因为1102n ->，所以11222n n n S a -=-<.--------------------------13分法二：因为2q =，所以1112n n n a a q --==,--------------------------８分所以1(1)211n n n a q S q -==--, --------------------------10分所以11202n n n S a --=-<，所以2n n S a <.--------------------------13分法三：因为2q =，所以1112n n n a a q --==, --------------------------８分所以1(1)211n n n a q S q -==--. --------------------------10分要证2n nS a <，只需2n n S a <，只需212n n -< 上式显然成立，得证.--------------------------13分8、解：（1）因为236,,a a a 成等差数列，所以2336a a a a -=-．又因为212a a =+，313a a =+，616a a=+，代入得11112336a a a a-=-++++，解得0a =． ………………3分（2）设等差数列12,,,m a a a L 的公差为d ．因为11b k =，所以211b k ≤+，从而211111(1)d b b k k k k =-≤-=-++．所以111(1)(1)m m b b m d k k k -=+-≤-+． ………………5分又因为0m b >，所以110(1)m k k k -->+．即11m k -<+．所以2m k <+．又因为*,m k N ∈，所以1m k ≤+． ………………8分（3）设11c t= (*t N ∈)，等比数列123,,m c c c c L 的公比为q ．因为211c t ≤+，所以211c t q c t =≤+．从而11*111()(1,)1n n n c c q n m n N t t --=≤≤≤∈+． ………………9分所以1211231111()()()111m m t t t c c c c t t t t t t t -++++≤++++++L L ＝1[1()]1m t t t t +-+ ＝11()1m t t t t -+-+．设函数*11(),(3,)m f x x m m N x -=-≥∈．当(0,)x ∈+∞时，函数11()m f x x x -=-为单调增函数．因为当*t N ∈，所以112t t+<≤．所以111()22m t f t -+≤-．即1211......22m m c c c -+++≤-． ………………13分。

北京顺义区第三中学高三数学理上学期期末试卷含解析

北京顺义区第三中学高三数学理上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 某校高二年级共有六个班级，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为（A）（B）（C）（D）参考答案：答案：C2. 对于定义在R上的奇函数A．0 B．—1 C．3 D．2参考答案：A3. 某位股民购进某只股票，在接下来的交易时间内，他的这只股票先经历了5次涨停（每次上涨10%），又经历了5次跌停（每次下跌10%），则该股民这只股票的盈亏情况（不考虑其他费用）为（）A．略有盈利B．略有亏损C．没有盈利也没有亏损D．无法判断盈亏情况参考答案：B【考点】函数的值．【分析】由题意设股民购进某只股票价值为1个单位，根据题意列出解析式化简后比较即可．【解答】解：由题意设股民购进某只股票价值为1个单位，则最后为：y=（1+10%）5（1﹣10%）5=0.995＜1．所以该股民这只股票的盈亏情况是略有亏损．故选：B．4. 若x∈A，则∈A，就称A是伙伴关系集合，集合M=的所有非空子集中具有伙伴关系的集合的个数是（）A．31 B．7 C．3 D．1参考答案：B【考点】12：元素与集合关系的判断．【专题】49 ：综合法；4R：转化法；5J ：集合．【分析】利用x∈A，则∈A，即可判断出集合A的伙伴关系集合个数．【解答】解：集合M=的所有非空子集中具有伙伴关系的集合为：{﹣1}，{，2}，{，3}，{﹣1，，2}，{﹣1，，3}，{，2，，3}，{﹣1，，2，，3}，故选：B．5. 在△ABC中， =，则△ABC是（）A．等腰三角形B．直角三角形C．等腰或直角三角形D．等边三角形参考答案：C【考点】三角函数中的恒等变换应用．【分析】利用正弦定理把题设等式中的边转化成角的正弦，进而化简整理求得sin2A=sin2B，进而推断出A=B或A+B=90°，进而可推断出三角形的形状．【解答】解：由正弦定理可得=∵=∴=，求得sinAcosA=sinBcosB即sin2A=sin2B∴A=B或2A+2B=180°，A+B=90°∴三角形为等腰或直角三角形．故选C【点评】本题主要考查了三角函数恒等变换的应用，三角形形状的判断．解题的关键是通过正弦定理把边转化为角的问题，利用三角函数的基础公式求得问题的解决．6. 对于实数a，b，c，下列命题正确的是（）A．若a＞b，则ac2＞bc2 B．若a＜b＜0，则a2＞ab＞b2C．若a＜b＜0，则D．若a＜b＜0，则参考答案：B7. 在直角梯形中，，，,，点在线段上，若，则的取值范围是（A）（B）（C）（D）参考答案：C略8. 已知，其中为虚数单位，则（）A.－1 B．1 C．2D．3参考答案：A略9. 图是计算函数的值的程度框图，在①、②、③处应分别填入的是（）A．y=ln（﹣x），y=0，y=2x B．y=ln（﹣x），y=2x，y=0C．y=0，y=2x，y=ln（﹣x）D．y=0，y=ln（﹣x），y=2x参考答案：B【分析】此题是一个计算函数的值的问题，由于函数是一个分段函数，故根据自变量的取值选取正确的解析式代入求值，由此对选择结构的空填数即可．【解答】解：由题意，本流程图表示的算法是计算分段函数的函数值的，结合框图可知，在①应填ln（﹣x）；在②应填y=2x；在③应填y=0故选：B10. 函数在的图像大致为（）A. B.C. D.参考答案：D【分析】根据函数的奇偶性和特殊值可判断.【详解】解：因为，所以为奇函数，关于原点对称，故排除，又因为，，，，故排除、,故选：D.【点睛】本题考查函数图象的识别，根据函数的性质以及特殊值法灵活判断，属于基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 若复数是纯虚数，则实数a 的值为．参考答案：1【考点】复数代数形式的乘除运算．【分析】利用两个复数代数形式的乘除法法则求得z 的值，再根据它是纯虚数，求得实数a 的值．【解答】解：∵复数==为纯虚数，故有a ﹣1=0，且a+1≠0，解得a=1，故答案为：1．【点评】本题主要考查复数的基本概念，两个复数代数形式的乘除法，虚数单位i 的幂运算性质，属于基础题．12. 方程有实根的概率为．参考答案：13. 设为抛物线的焦点，点在抛物线上，O为坐标原点，若，且，则抛物线的焦点到准线的距离等于 .参考答案：4略14. B(?－2，0)，C(2，0)，A为动点，△ABC的周长为10，则点A的轨迹的离心率为参考答案：.2/3略15. 在的展开式中，的系数为.参考答案：分析：由题意结合二项式定理展开式的通项公式得到r的值，然后求解的系数即可.详解：结合二项式定理的通项公式有：，令可得：，则的系数为：.16. 数列是等差数列，若，且它的前n项和有最大值，那么当取得最小正值时， .参考答案：19略17. 设m，n是两条不同的直线，，，是三个不同的平面，给出下列命题：①若，，则；②若，，则；③若，，则；④若，，，则．上面命题中，真命题的序号是▲（写出所有真命题的序号）．参考答案：略三、解答题：本大题共5小题，共72分。

北京市顺义区2016届高三上学期期末物理试卷Word版含解析

2015-2016学年北京市顺义区高三（上）期末物理试卷一、选择题（共16小题，每小题3分，满分48分）1．一列横波沿水平方向传播，某一时刻的波形如图所示，则图中a、b、c、d四点在此时刻具有相同运动方向的是（）A．a和c B．a和d C．b和c D．b和d2．地球上站立着两位相距非常远的观察者，发现自己的正上方有一颗人造地球卫星相对自己静止不动，则这两位观察者及两颗卫星到地球中心的距离是（）A．一个人在南极，一个人在北极，两卫星到地球中心的距离一定相等B．两人都在赤道上，两卫星到地球中心的距离一定相等C．一个人在南极，一个人在北极，两卫星到地球中心的距离可以不相等D．两人都在赤道上，两卫星到地球中心的距离可以不相等3．如图所示，是描述对给定的电容器充电时电荷量Q、电压U、电容C之间相互关系的图象，其中正确的是（）A．B．C．D．4．如图所示，质量为m的金属环用线悬挂起来，金属环有一半处于水平且与环面垂直的匀强磁场中，从某时刻开始，磁感应强度均匀减小，则在磁感应强度均匀减小的过程中，关于线拉力大小的下列说法中正确的是（）A．大于环重力mg，并逐渐减小B．始终等于环重力mgC．小于环重力mg，并保持恒定D．大于环重力mg，并保持恒定5．如图所示，质量分别为m和M的两物块紧挨着放在水平地面上，且M＞m．当用水平恒力F向右的推物块m时，两物块能在水平面上加速向右滑行，两物块的加速度大小为a，两物块间的作用力大小为T．如果用同样大小的水平恒力F 向左推木块M时，加速度大小为a′，物块间的作用力大小为T′，以下判断正确的是（）A．a′=a，T′＞T B．a′＜a，T′=T C．a′＞a，T′=T D．a′=a，T′＜T6．一物体悬挂在气球下面，与气球一起沿竖直方向匀速上升，某时刻该物体脱落，并从此时开始计时．已知气球和物体所受空气阻力大小不变．在下图中①代表气球运动的v﹣t图线，②代表物体运动的v﹣t图线．以下四个v﹣t图象中最接近真实情况的是（）A．B．C．D．7．如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑，通过轨道最低点时（）A．小球对轨道的压力相同B．小球对两轨道的压力不同C．此时小球的速度相等D．此时小球的向心加速度相等8．如图所示，质量为m的物体P放在光滑的倾角为θ的直角劈上，同时用力F 向右推劈，使P与劈保持相对静止，在前进的水平位移为s的过程中，劈对P做的功为（）A．F•s B．C．mgcosθ•s D．mgtanθ•s9．甲、乙两物体分别在恒力F1、F2的作用下，沿同一直线运动，它们的动量随时间变化的关系如图所示，设甲在t1时间内所受的冲量为I1，乙在t2时间内所受的冲量为I2，则F1、F2，I1、I2的大小关系是（）A．F1＞F2，I1=I2 B．F1＜F2，I1＜I2C．F1＞F2，I1＞I2D．F1=F2，I1=I2 10．如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球．支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动．开始时OB位于竖直方向．放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（）A．B球向左摆动所能达到的最高位置应高于A球开始运动时的高度B．当支架从左向右回摆时，A球不能回到起始高度C．A球机械能减少量大于B球机械能增加量D．A球到达最低点时速度为零11．如图所示，虚线a、b、c代表电场中三个等势面，相邻等势面之间的电势差相等，U ab=U bc，实线为一带正电的粒子仅在电场力作用下通过该区域时的运动轨迹，P、Q是这条轨迹上的两点，据此可知下列说法中正确的是（）A．三个等势面中，a的电势最低B．带电粒子通过P点时的动能比通过Q点时的动能大C．带电粒子通过P点时的加速度比通过Q点时加速度大D．带电粒子在P点具有的电势能比在Q点具有的电势能小12．如图所示，一物体以初速度v0冲向光滑斜面AB，并能沿斜面升高h后恰好到达B端，下列说法中正确的是（）A．若把斜面从C点锯断或弯成如图中的AB′线所示的圆弧状，物体都不能升高h，因为机械能不守恒B．若把斜面弯成如图中的AB′线所示的圆弧状或从C点开始锯掉CB段，物体都不能升高h，但机械能仍守恒C．若把斜面从C点开始锯掉CB段，由机械能守恒定律知，物体冲出C点后仍能升高hD．若把斜面弯成如图中的AB′线所示的圆弧形，物体仍能沿AB′升高h13．如图所示，水平向右方向的匀强电场和垂直纸面向外的匀强磁场互相垂直，竖直的绝缘杆上套一带负电荷小环并置于场中．小环由静止开始下落的过程中，小环的加速度（）A．不断减小最后为零B．不断增大后来不变C．先减小后增大，最后不变D．先增大后减小，最后不变14．一个自感系数很大的线圈，用如图所示的电路测量它的直流电阻，闭合电键S1与S2待稳定后．读出电压表与电流表的示数．下列说法正确的是（）①线圈电阻的测量值等于电压表示数与电流表示数的比值②线圈电阻的真实值小于电压表示数与电流表示数的比值③在测量完毕拆卸电路时，应先断开S1，后断开S2④在测量完毕拆卸电路时，应先断开S2后断开S l．A．①③B．①④C．②③D．②④15．如图所示，两个相邻的有界匀强磁场区，方向相反，且垂直纸面，磁感应强度的大小均为B，以磁场区左边界为y轴建立坐标系，磁场区在y轴方向足够长，在x轴方向宽度均为a．矩形导线框ABCD 的CD边与y轴重合，AD边长为a．线框从图示位置水平向右匀速穿过两磁场区域，且线框平面始终保持与磁场垂直．以逆时针方向为电流的正方向，线框中感应电流i与线框移动距离x的关系图象正确的是图中的（以逆时针方向为电流的正方向）（）A． B． C．D．16．电磁轨道炮工作原理如图所示．待发射弹体可在轨道沿伸方向自由移动，并与轨道保持良好接触．电流I从一条轨道流入，通过导电弹体后从另一条轨道流回．轨道电流可在弹体附近形成垂直于轨道面的磁场（可视为匀强磁场），磁感应强度的大小与I成正比．通电的弹体在轨道上受到安培力的作用而高速射出．现欲使弹体的出射动量增加至原来的2倍，理论上可采用的办法是（）A．只将电流I增加至原来的2倍B．只将弹体质量增加至原来的2倍C．只将轨道长度L增加至原来的2倍D．将电流，和轨道长度己均增加至原来的2倍，其它量不变二、非选择题（共7小题，满分72分）17．根据单摆周期公式，可以通过实验测量当地的重力加速度．以下是实验过程中的一些做法，其中正确的有（）A．摆线要选择细些的、伸缩性小些的，并且尽可能长一些B．摆球尽量选择质量大些、体积小些的C．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆球相距平衡值置有较大的角度D．拉开摆球到某一位置释放，第一次经平衡位置时开始计时，第二次经平衡位置时停止计时，此时间间隔t即为单摆周期T18．在《验证力的平行四边形定则》的实验中，首先用两只弹簧秤分别钩住细绳套，互成角度地拉橡皮条，使结点伸长到某一位置O，此时必须记录的是（）A．O点的位置B．橡皮条固定端位置C．两只弹簧秤的读数两条细绳套的方向D．橡皮条的伸长长度19．如图甲、乙是两组同样的器材实物图，用来测量待测电阻R的阻值，每组器材中包括：电池，电键，变阻器，电压表，电流表，等测电阻R，若干导线．（1）如果待测电阻R的阻值比电压表的内阻不是小很多，但R的阻值比电流表的内阻大很多，试在图甲中连线使之成为测量电路；如果待测电阻R的阻值比电流表的内阻不是大很多，但R的阻值比电压表的内阻小很多，试在图乙中连线使之成为测量电路．（2）如果已知上述电压表的内阻R V和电流表的内阻R A，对图甲和图乙中连成的测量电路，分别写出计算待测电阻的公式（用测得的量和给出的电表内阻来表示）．20．如图所示AB为半径R=0.45m的四分之一光滑圆弧轨道，底端距水平地面的高度h=0.45m．一质量m=l．Okg的小滑块从圆弧轨道顶端A由静止释放，到达轨道底端B点时水平飞出．不计空气的阻力，g取lOm/s2求：（1）小滑块滑到圆弧轨道底端B点时的速度v；（2）小滑块滑到圆弧轨道底端B点时对轨道的压力F N；（3）小滑块落地点与B点的水平距离x．21．对于长度为l、横截面积为S，单位体积自由电子数为n的均匀导体，若在其两端加上电压U，就会在导体中有匀强电场产生，此时导体内移动的自由电子受匀强电场作用而加速．在运动过程中又与做热运动的阳离子碰撞而减速，这样边反复进行碰撞边向前移动，可以认为阻碍电子运动的阻力大小与电子移动的平均速度成正比，其比例系数为k．已知自由电子的电荷量为e，求：（1）电场力和碰撞的阻力相平衡时，电子在导体中运动的平均速率v；（2）自由电子在导体中以平均速率v运动时，该导体中的电流I；（3）该导体的电阻值R．22．如图所示，一质量M=1．Okg的沙摆，用轻绳悬于天花板上O点．另有一玩具枪能连续发射质量m=0.01kg．速度v=4．Om/s的小钢珠．现将沙摆拉离平衡位置，由高h=0.20m处无初速度释放，恰在沙摆向右摆到最低点时，玩具枪发射的第一颗小钢珠水平向左射入沙摆，二者在极短时间内达到共同速度．小钢珠射入沙摆的过程中，沙摆的质量保持不变，不计空气阻力，g取lOm/s2（1）求第一颗小钢珠射入沙摆前的瞬间，沙摆的速度大小v0；（2）求第一颗小钢珠射入沙摆后，沙摆和小钢珠的共同速度（3）从第二颗小钢球开始，沙摆向左运动到最低点时打入小钢球．若使沙摆被小钢珠射入后摆起的最大高度超过h，则射入沙摆的小钢球的颗数应满足什么条件．23．示波管、电视机显像管、电子显微镜中常用到一种叫静电透镜的元件，它可以把电子聚焦在中心轴上的一点F，静电透镜的名称由此而来．它的结构如图所示，K为平板电极，G为中央带圆孔的另一平行金属板，现分别将它们的电势控制在一定数值．图中的数据的单位为V，其中K板的电势为120V．根据由实验测得的数据，在图中画出了一些等势面，如图中虚线所示．从图中可知G板圆孔附近的等势面不再是平面，而是向圆孔的右侧凸出来的曲面，所以圆孔附近右侧的电场不再是匀强电场．（1）题中已画出一条水平向右的电场线，请你在原电场线上下画出对称的一对电场线；（2）分析静电透镜为何对自K电极出发的电子束有会聚作用；（3）分析一个电子自K电极以一定的速度出发，运动到F点（电势为30.1V）的过程中，电子的加速度如何变化并求出电场力做了多少功．（设电子电量e=1.6×10﹣19C）2015-2016学年北京市顺义区高三（上）期末物理试卷参考答案与试题解析一、选择题（共16小题，每小题3分，满分48分）1．一列横波沿水平方向传播，某一时刻的波形如图所示，则图中a、b、c、d四点在此时刻具有相同运动方向的是（）A．a和c B．a和d C．b和c D．b和d【考点】横波的图象；波长、频率和波速的关系．【分析】根据波的传播方向，通过上下坡法得出质点的振动方向，从而确定哪些点运动方向相同．【解答】解：若波向右传播，根据上下坡法知，a、d质点振动方向向上，b、c 质点振动方向向下，故B、C正确，A、D错误．故选：BC．2．地球上站立着两位相距非常远的观察者，发现自己的正上方有一颗人造地球卫星相对自己静止不动，则这两位观察者及两颗卫星到地球中心的距离是（）A．一个人在南极，一个人在北极，两卫星到地球中心的距离一定相等B．两人都在赤道上，两卫星到地球中心的距离一定相等C．一个人在南极，一个人在北极，两卫星到地球中心的距离可以不相等D．两人都在赤道上，两卫星到地球中心的距离可以不相等【考点】同步卫星．【分析】地球同步卫星即地球同步轨道卫星，又称对地静止卫星，是运行在地球同步轨道上的人造卫星，星距离地球的高度约为36000 km，卫星的运行方向与地球自转方向相同、运行轨道为位于地球赤道平面上圆形轨道、运行周期与地球自转一周的时间相等，即23时56分4秒，卫星在轨道上的绕行速度约为3.1公里/秒，其运行角速度等于地球自转的角速度．【解答】解：发现自己正上方有一颗人造地球卫星相对自己静止不动，说明此卫星为地球同步卫星，运行轨道为位于地球赤道平面上圆形轨道，距离地球的高度约为36000 km，所以两个人都在赤道上，两卫星到地球中心的距离一定相等．故ACD错误，B正确故选B．3．如图所示，是描述对给定的电容器充电时电荷量Q、电压U、电容C之间相互关系的图象，其中正确的是（）A．B．C．D．【考点】电容．【分析】电容器的电容由本身的性质决定，与Q和U无关，根据Q=CU，知Q 与U成正比．【解答】解：是电容的定义式，电容器电容的大小与电容的带电量Q以及电容器两极板之间的电压无关，电容器电容的决定式为：，只要电容器不变其电容就不发生变化，故A错误，BD正确；根据可有：Q=CU，由于电容器不变，因此电量Q和电压U成正比，故C正确；故选BCD．4．如图所示，质量为m的金属环用线悬挂起来，金属环有一半处于水平且与环面垂直的匀强磁场中，从某时刻开始，磁感应强度均匀减小，则在磁感应强度均匀减小的过程中，关于线拉力大小的下列说法中正确的是（）A．大于环重力mg，并逐渐减小B．始终等于环重力mgC．小于环重力mg，并保持恒定D．大于环重力mg，并保持恒定【考点】法拉第电磁感应定律；楞次定律．【分析】磁感应强度均匀减小，穿过回路的磁通量均匀减小，回路中产生恒定的电流，由左手定则可确定安培力的方向，再根据安培力F=BIL，分析安培力的变化，由平衡条件即可求解．【解答】解：磁感应强度均匀减小，穿过回路的磁通量均匀减小，根据法拉第电磁感应定律得知，回路中产生恒定的电动势，感应电流也恒定不变．由楞次定律可知，感应电流方向：顺时针，再由左手定则可得，安培力的合力方向：竖直向下．ab棒所受的安培力F=BIL，可知安培力F均匀减小，且方向向下，金属环ab 始终保持静止，则拉力大于重力，由于磁感应强度均匀减小．所以拉力的大小也逐渐减小，故A正确，BCD均错误．故选：A．5．如图所示，质量分别为m和M的两物块紧挨着放在水平地面上，且M＞m．当用水平恒力F向右的推物块m时，两物块能在水平面上加速向右滑行，两物块的加速度大小为a，两物块间的作用力大小为T．如果用同样大小的水平恒力F 向左推木块M时，加速度大小为a′，物块间的作用力大小为T′，以下判断正确的是（）A．a′=a，T′＞T B．a′＜a，T′=T C．a′＞a，T′=T D．a′=a，T′＜T【考点】牛顿第二定律；物体的弹性和弹力．【分析】A、B具有相同的加速度可以视为整体，根据牛顿第二定律分别求出水平面光滑和粗糙时的加速度，隔离对B分析，求出弹力的大小，从而进行比较．【解答】解：如果水平面光滑整体根据牛顿第二定律可得：a=a′=；向右运动时对M分析：T=Ma=，向左运动时对m分析：T′=ma′=，由于m＜M，则T′＜T，D正确；如果接触面粗糙时，设动摩擦因数为μ，整体分析可得：F﹣μ（m+M）g=（m+M）a解得：，同理可得a′=a；向右运动时对M分析：T﹣μMg=Ma，解得：T=，向左运动时对m分析：T′﹣μmg=ma′，解得：T′=，由于m＜M，则T′＜T，D正确；故选：D．6．一物体悬挂在气球下面，与气球一起沿竖直方向匀速上升，某时刻该物体脱落，并从此时开始计时．已知气球和物体所受空气阻力大小不变．在下图中①代表气球运动的v﹣t图线，②代表物体运动的v﹣t图线．以下四个v﹣t图象中最接近真实情况的是（）A．B．C．D．【考点】匀变速直线运动的图像；匀变速直线运动的速度与时间的关系．【分析】刚开始，物体和气球一起匀速上升，受力平衡，某时刻该物体脱落后，分别对气球和物体受力分析，根据牛顿第二定律列式求出加速度，分析物体的运动情况，从而选择图象即可．【解答】解：设气球的质量为M，物体的质量为m，气球受到的空气阻力为f1，物体受到的空气阻力为f2，一起匀速运动的速度为v，刚开始，物体和气球一起匀速上升，根据平衡条件有：F﹣Mg﹣mg﹣f1﹣f2=0某时刻该物体脱落后，对气球受力分析，根据牛顿第二定律得：＞0，向上做匀加速直线运动，且初速度不为零，所以气球运动的v ﹣t图线是一条倾斜的直线且在v轴上有截距，对物体，脱落后继续向上做匀减速直线运动，根据牛顿第二定律得：加速度，速度减为零后，反向加速，加速度，则a2＞a3，故C正确．故选：C7．如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑，通过轨道最低点时（）A．小球对轨道的压力相同B．小球对两轨道的压力不同C．此时小球的速度相等D．此时小球的向心加速度相等【考点】向心力；机械能守恒定律．【分析】小球从与球心在同一水平高度的A、B两点由静止开始自由下滑过程中，受到重力和支持力作用，只有重力做功，机械能守恒，由机械能守恒定律可求出小球到最低点的速度，然后由向心加速度公式求向心加速度，由牛顿第二定律求出支持力，进而来比较向心加速度大小和压力大小．【解答】解：设半圆轨道的半径为r，小球到最低点的速度为v，由机械能守恒定律得：mgr=，得：v=，可见，小球到达最低点的速度不等．小球的向心加速度为：a n=，联立两式解得：a n=2g，与半径无关，因此此时小球的向心加速度相等，故C错误，D正确．在最低点，由牛顿第二定律得：F N﹣mg=m，联立解得：F N=3mg，即得小球对轨道的压力为3mg，也与半径无关，所以小球对轨道的压力相同．故A正确，B 错误．故选：AD8．如图所示，质量为m的物体P放在光滑的倾角为θ的直角劈上，同时用力F向右推劈，使P与劈保持相对静止，在前进的水平位移为s的过程中，劈对P做的功为（）A．F•s B．C．mgcosθ•s D．mgtanθ•s【考点】功的计算．【分析】m与楔形物体相对静止，二者必定都向右加速运动．即m的合外力方向水平向右，画出m的受力图，求出楔形物体对小物体的作用力，根据功的公式即可求解．【解答】解：m与楔形物体相对静止，二者必定都向右加速运动．即m的合外力方向水平向右，画出m的受力图，根据几何关系得：N=所以支持力做的功为：W=Ns•sinθ=mgtanθ•s故选：D9．甲、乙两物体分别在恒力F1、F2的作用下，沿同一直线运动，它们的动量随时间变化的关系如图所示，设甲在t1时间内所受的冲量为I1，乙在t2时间内所受的冲量为I2，则F1、F2，I1、I2的大小关系是（）A．F1＞F2，I1=I2 B．F1＜F2，I1＜I2C．F1＞F2，I1＞I2D．F1=F2，I1=I2【考点】动量定理．【分析】根据图象，结合初末状态的动量比较动量变化量的大小，从而结合动量定理得出冲量的大小关系以及力的大小关系．【解答】解：由图象可知，甲乙两物体动量变化量的大小相等，根据动量定理知，冲量的大小相等，即I1=I2，根据I=Ft知，冲量的大小相等，作用时间长的力较小，可知F1＞F2．故A正确，B、C、D错误．故选：A．10．如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球．支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动．开始时OB位于竖直方向．放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（）A．B球向左摆动所能达到的最高位置应高于A球开始运动时的高度B．当支架从左向右回摆时，A球不能回到起始高度C．A球机械能减少量大于B球机械能增加量D．A球到达最低点时速度为零【考点】共点力平衡的条件及其应用；物体的弹性和弹力．【分析】在不计任何阻力的情况下，整个过程中A、B组成的系统机械能守恒，据此列式判断即得．【解答】解：因为在整个过程中系统机械能守恒，故有：A、因为B球质量小于A球，故B上升高度h时增加的势能小于A球减少的势能，故当B和A球等高时，仍具有一定的速度，即B球继续升高，故A正确；B、因为不计一切阻力，系统机械能守恒，故当支架从左到右加摆时，A球一定能回到起始高度，故B错误；C、因为系统机械能守恒，即A、B两球的机械能总量保持不变，故A球机械能的减少量等于B球机械能的增加量，故C错误；D、若当A到达最低点时速度为0，则A减少的重力势能等于B增加的重力势能，只有A与B的质量相等时才会这样．又因A、B质量不等，故D错误．故选：A11．如图所示，虚线a、b、c代表电场中三个等势面，相邻等势面之间的电势差相等，U ab=U bc，实线为一带正电的粒子仅在电场力作用下通过该区域时的运动轨迹，P、Q是这条轨迹上的两点，据此可知下列说法中正确的是（）A．三个等势面中，a的电势最低B．带电粒子通过P点时的动能比通过Q点时的动能大C．带电粒子通过P点时的加速度比通过Q点时加速度大D．带电粒子在P点具有的电势能比在Q点具有的电势能小【考点】电势差与电场强度的关系；电势．【分析】带电粒子只受电场力作用，根据运动轨迹可知电场力指向运动轨迹的内侧即斜向右下方，由于粒子带正电，因此电场线方向也指向右下方；电势能变化可以通过电场力做功情况判断；电场线和等势线垂直，且等势线密的地方电场线密，电场强度大．【解答】解：A、带电粒子所受电场力指向轨迹弯曲的内侧，电场线与等势面垂直，且由于带电粒子带正电，因此电场线指向右下方，根据沿电场线电势降低，可知a等势线的电势最高，c等势线的电势最低，故A错误；BD、根据带电粒子受力情况可知，若粒子从P到Q过程，电场力做正功，动能增大，电势能减小，故带电粒子通过P点时的动能比通过Q点时的动能小，在P 点具有的电势能比在Q点具有的电势能大，故BD错误；C、等差等势线密的地方电场线密场强大，故P点电场强度较大，电场力较大，根据牛顿第二定律，加速度也较大，故C正确．故选：C12．如图所示，一物体以初速度v0冲向光滑斜面AB，并能沿斜面升高h后恰好到达B端，下列说法中正确的是（）A．若把斜面从C点锯断或弯成如图中的AB′线所示的圆弧状，物体都不能升高h，因为机械能不守恒B．若把斜面弯成如图中的AB′线所示的圆弧状或从C点开始锯掉CB段，物体都不能升高h，但机械能仍守恒C．若把斜面从C点开始锯掉CB段，由机械能守恒定律知，物体冲出C点后仍能升高hD．若把斜面弯成如图中的AB′线所示的圆弧形，物体仍能沿AB′升高h【考点】机械能守恒定律．【分析】物体上升过程中只有重力做功，机械能守恒；斜抛运动运动最高点，速度不为零；AD轨道最高点，合力充当向心力，速度也不为零．【解答】解：1、若把斜面从C点锯断，物体冲过C点后做斜抛运动，由于物体机械能守恒，同时斜抛运动运动到最高点，速度不为零，故不能到达h高处；2、若把斜面弯成圆弧形AB′，如果能到圆弧最高点，即h处，由于合力充当向心力，速度不为零，故会得到机械能增加，矛盾，所以物体不能升高h．故B正确，ACD错误；故选：B13．如图所示，水平向右方向的匀强电场和垂直纸面向外的匀强磁场互相垂直，。

2016年北京市顺义区高考一模数学试卷(理科)【解析版】

2016年北京市顺义区高考数学一模试卷（理科）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．（5分）已知i为虚数单位，则i（2i+1）＝（）A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i2．（5分）已知集合A＝{x|x2＜1}，B＝{x|log2x＜1}，则A∩B＝（）A．{x|﹣1＜x＜1}B．{x|0＜x＜1}C．{x|0＜x＜2}D．{x|﹣1＜x＜2} 3．（5分）下列函数在其定义域内既是奇函数又是增函数的是（）A．y＝2x B．y＝x3+x C．D．y＝﹣log2x 4．（5分）执行如图所示的程序框图，输出的结果是（）A．15B．21C．24D．355．（5分）已知向量，，其中x∈R．则“x＝2”是“”成立的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分又不必要条件6．（5分）直线l：（t为参数）与圆C：（θ为参数）的位置关系是（）A．相离B．相切C．相交且过圆心D．相交但不过圆心7．（5分）在平面直角坐标系中，若不等式组（a为常数）表示的区域面积等于1，则a的值为（）A．B．C．D．18．（5分）如图，已知平面α∩平面β＝l，α⊥β．A、B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，DA＝4，AB＝6，CB＝8．P是平面α上的一动点，且有∠APD＝∠BPC，则四棱锥P﹣ABCD体积的最大值是（）A．48B．16C．D．144二、填空题共6小题，每小题5分，共30分.9．（5分）（x2+）6的展开式中x3的系数是．（用数字作答）10．（5分）抛物线y2＝﹣8x的准线与双曲线的两条渐近线所围成的三角形面积为．11．（5分）已知某几何体的三视图如图，正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是（单位：cm2）．12．（5分）已知函数f（x）＝，则＝；f（x）的最小值为．13．（5分）某慢性疾病患者，因病到医院就医，医生给他开了处方药（片剂），要求此患者每天早、晚间隔12小时各服一次药，每次一片，每片200毫克．假设该患者的肾脏每12小时从体内大约排出这种药在其体内残留量的50%，并且医生认为这种药在体内的残留量不超过400毫克时无明显副作用．若该患者第一天上午8点第一次服药，则第二天上午8点服完药时，药在其体内的残留量是毫克，若该患者坚持长期服用此药明显副作用（此空填“有”或“无”）．14．（5分）设A1，A2，A3，A4，A5是空间中给定的5个不同的点，则使成立的点M的个数有个．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．（13分）已知函数，x∈R．（Ⅰ）求函数f（x）的最大值；（Ⅱ）若，求函数f（x）的单调递增区间．16．（13分）在某班级举行的“元旦联欢会”有奖答题活动中，主持人准备了A，B两个问题，规定：被抽签抽到的答题同学，答对问题A可获得100分，答对问题B可获得200分，答题结果相互独立互不影响，先回答哪个问题由答题同学自主决定；但只有第一个问题答对才能答第二个问题，否则终止答题．答题终止后，获得的总分决定获奖的等次．若甲是被抽到的答题同学，且假设甲答对A，B问题的概率分别为．（Ⅰ）记甲先回答问题A再回答问题B得分为随机变量ξ，求ξ的分布列和数学期望；（Ⅱ）你觉得应先回答哪个问题才能使甲的得分期望更高？请说明理由．17．（13分）如图，在四棱锥P﹣ABCD中，等边△P AD所在的平面与正方形ABCD 所在的平面互相垂直，O为AD的中点，E为DC的中点，且AD＝2．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求二面角P﹣EB﹣A的余弦值；（Ⅲ）在线段AB上是否存在点M，使线段PM与△P AD所在平面成30°角．若存在，求出AM的长，若不存在，请说明理由．18．（13分）已知函数f（x）＝x2﹣lnx．（Ⅰ）求曲线y＝f（x）在点（1，f（1））处的切线方程；（Ⅱ）设g（x）＝x2﹣x+t，若函数h（x）＝f（x）﹣g（x）在上（这里e≈2.718）恰有两个不同的零点，求实数t的取值范围．19．（14分）已知椭圆E：（a＞b＞0）的离心率，且点在椭圆E上．（Ⅰ）求椭圆E的方程；（Ⅱ）直线l与椭圆E交于A、B两点，且线段AB的垂直平分线经过点．求△AOB（O为坐标原点）面积的最大值．20．（14分）在数列{a n}中，a1＝0，，其中m∈R，n∈N*．（Ⅰ）当m＝1时，求a2，a3，a4的值；（Ⅱ）是否存在实数m，使a2，a3，a4构成公差不为0的等差数列？证明你的结论；（Ⅲ）当m＞时，证明：存在k∈N*，使得a k＞2016．2016年北京市顺义区高考数学一模试卷（理科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．（5分）已知i为虚数单位，则i（2i+1）＝（）A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i【解答】解：由题意，i（2i+1）＝i×2i+i＝﹣2+i故选：C．2．（5分）已知集合A＝{x|x2＜1}，B＝{x|log2x＜1}，则A∩B＝（）A．{x|﹣1＜x＜1}B．{x|0＜x＜1}C．{x|0＜x＜2}D．{x|﹣1＜x＜2}【解答】解：集合A＝{x|x2＜1}＝{x|﹣1＜x＜1}，B＝{x|log2x＜1}＝{x|0＜x＜2}，则A∩B＝{x|0＜x＜1}，故选：B．3．（5分）下列函数在其定义域内既是奇函数又是增函数的是（）A．y＝2x B．y＝x3+x C．D．y＝﹣log2x 【解答】解：A．y＝2x的图象不关于原点对称，不是奇函数，∴该选项错误；B．y＝x3+x的定义域为R，且（﹣x）3+（﹣x）＝﹣（x3+x）；∴该函数为奇函数；y＝x3和y＝x在R上都是增函数；∴y＝x3+x在R上是增函数，∴该选项正确；C．反比例函数在定义域上没有单调性，∴该选项错误；D．y＝﹣log2x的定义域为（0，+∞），不关于原点对称，不是奇函数，∴该选项错误．故选：B．4．（5分）执行如图所示的程序框图，输出的结果是（）A．15B．21C．24D．35【解答】解：模拟执行程序，可得S＝0，i＝1T＝3，S＝3，i＝2不满足i＞4，T＝5，S＝8，i＝3不满足i＞4，T＝7，S＝15，i＝4不满足i＞4，T＝9，S＝24，i＝5满足i＞4，退出循环，输出S的值为24．故选：C．5．（5分）已知向量，，其中x∈R．则“x＝2”是“”成立的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分又不必要条件【解答】解：∵，∴x2﹣4＝0，解得x＝±2．∴“x＝2”是“”成立的充分不必要条件．故选：A．6．（5分）直线l：（t为参数）与圆C：（θ为参数）的位置关系是（）A．相离B．相切C．相交且过圆心D．相交但不过圆心【解答】解：把圆的参数方程化为普通方程得：（x﹣2）2+（y﹣1）2＝4，∴圆心坐标为（2，1），半径r＝2，把直线的参数方程化为普通方程得：x﹣y+1＝0，∴圆心到直线的距离d＝＜r＝2，又圆心（2，1）不在直线x﹣y+1＝0上，则直线与圆的位置关系为相交但不过圆心．故选：D．7．（5分）在平面直角坐标系中，若不等式组（a为常数）表示的区域面积等于1，则a的值为（）A．B．C．D．1【解答】解：不等式组所围成的区域如图ABCD所示，∵其面积为1，A（2，2a+1），B（2，0），C（1，），D（1，a+1）∴S ABCD＝＝1，解得a＝．故选：B．8．（5分）如图，已知平面α∩平面β＝l，α⊥β．A、B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，DA＝4，AB＝6，CB＝8．P是平面α上的一动点，且有∠APD＝∠BPC，则四棱锥P﹣ABCD体积的最大值是（）A．48B．16C．D．144【解答】解：∵平面α∩平面β＝l，α⊥β，DA⊥l，CB⊥l，DA⊂平面β，CB⊂平面β，∴DA⊥平面α，CB⊥平面α，∵P A⊂平面α，PB⊂平面α，∴DA⊥P A，CB⊥PB．∵∠APD＝∠BPC，∴，即，∴PB＝2P A．以直线l为x轴，AB的中点为坐标原点建立平面直角坐标系，则A（﹣3，0），B（3，0）．设P（x，y），则P A＝，PB＝，∴2＝，整理得（x+5）2+y2＝16（y＞0）．∴P点的轨迹为以（﹣5，0）为圆心，以4为半径的半圆．∴当P到直线l的距离h＝4时，四棱锥P﹣ABCD体积取得最大值．∴棱锥的体积最大值为V＝＝＝48．故选：A．二、填空题共6小题，每小题5分，共30分.9．（5分）（x2+）6的展开式中x3的系数是20．（用数字作答）【解答】解：由于（x2+）6的展开式的通项公式为T r+1＝•x12﹣3r，令12﹣3r＝3，解得r＝3，故展开式中x3的系数是＝20，故答案为：20．10．（5分）抛物线y2＝﹣8x的准线与双曲线的两条渐近线所围成的三角形面积为2．【解答】解：抛物线y2＝﹣8x的准线为x＝2，双曲线的两条渐近线为y＝±x，可得两交点为（2，），（2，﹣），即有三角形的面积为×2×2＝2．故答案为：2．11．（5分）已知某几何体的三视图如图，正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是3π+4（单位：cm2）．【解答】解：根据三视图可知几何体是半个圆柱，且正视图是底面，∴底面圆的半径是1cm，母线长是2cm，∴几何体的表面积S＝π×12+π×1×2+2×2＝3π+4（cm2），故答案为：3π+4．12．（5分）已知函数f（x）＝，则＝1；f（x）的最小值为0．【解答】解：f（﹣）＝log33＝1，则f（1）＝1+2﹣2＝1，即＝1，当x≥1时，f（x）＝x+﹣2≥2﹣2＝2﹣2，当且仅当x＝，即x＝时取等号，当x＜1时，f（x）＝log3（x2+1）≥log31＝0；故函数f（x）的最小值为0，故答案为：1，0．13．（5分）某慢性疾病患者，因病到医院就医，医生给他开了处方药（片剂），要求此患者每天早、晚间隔12小时各服一次药，每次一片，每片200毫克．假设该患者的肾脏每12小时从体内大约排出这种药在其体内残留量的50%，并且医生认为这种药在体内的残留量不超过400毫克时无明显副作用．若该患者第一天上午8点第一次服药，则第二天上午8点服完药时，药在其体内的残留量是350毫克，若该患者坚持长期服用此药无明显副作用（此空填“有”或“无”）．【解答】解：设该生第n次服药后，药在他体内的残留量为a n毫克，则：a1＝200，a2＝200+a1×（1﹣50%）＝200×1.5＝300，a3＝200+a2×（1﹣50%）＝200+200×1.5×0.5＝350 （4分）故第二天早间，他第三次服空药后，药在他体内的残留量为350毫克．该运动员若长期服用此药，则此药在体内残留量为＝400（1﹣0.5n），当n→+∞时，药在体内残留量无限接近400∴长期服用此药，不会产生副作用，即该生长期服用该药，不会产生副作用．故答案为：350，无．14．（5分）设A1，A2，A3，A4，A5是空间中给定的5个不同的点，则使成立的点M的个数有1个．【解答】解：设A1（x1，y1，z1），A2（x2，y2，z2），A3（x3，y3，z3），A4（x4，y4，z4），A5（x5，y5，z5）；再设M（a，b，c），则可得＝（x1﹣a，y1﹣b，z1﹣c），＝（x2﹣a，y2﹣b，z2﹣c），＝（x3﹣a，y3﹣b，z3﹣c），＝（x4﹣a，y4﹣b，z4﹣c），＝（x5﹣a，y5﹣b，z5﹣c），∵＝成立，∴，解得，因此，存在唯一的点M，使＝成立．故答案为：1．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．（13分）已知函数，x∈R．（Ⅰ）求函数f（x）的最大值；（Ⅱ）若，求函数f（x）的单调递增区间．【解答】解：（Ⅰ）由三角函数公式化简可得＝＝sin2x+cos2x＝sin（2x+）当即，k∈z时，；（Ⅱ）∵当时，f（x）递增，即，令k＝0，且注意到，∴函数f（x）的递增区间为16．（13分）在某班级举行的“元旦联欢会”有奖答题活动中，主持人准备了A，B两个问题，规定：被抽签抽到的答题同学，答对问题A可获得100分，答对问题B可获得200分，答题结果相互独立互不影响，先回答哪个问题由答题同学自主决定；但只有第一个问题答对才能答第二个问题，否则终止答题．答题终止后，获得的总分决定获奖的等次．若甲是被抽到的答题同学，且假设甲答对A，B问题的概率分别为．（Ⅰ）记甲先回答问题A再回答问题B得分为随机变量ξ，求ξ的分布列和数学期望；（Ⅱ）你觉得应先回答哪个问题才能使甲的得分期望更高？请说明理由．【解答】（本小题满分13分）解：（Ⅰ）ξ的可能取值为0，100，300．（2分），，，（5分）∴ξ的分布列为：．（7分）（Ⅱ）设先回答问题B，再回答问题A得分为随机变量η，则η的可能取值为0，200，300．∴，，，（10分）η的分布列为：．（12分）∵Eξ＞Eη，∴应先回答A所得分的期望值较高．（13分）17．（13分）如图，在四棱锥P﹣ABCD中，等边△P AD所在的平面与正方形ABCD 所在的平面互相垂直，O为AD的中点，E为DC的中点，且AD＝2．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求二面角P﹣EB﹣A的余弦值；（Ⅲ）在线段AB上是否存在点M，使线段PM与△P AD所在平面成30°角．若存在，求出AM的长，若不存在，请说明理由．【解答】解：（Ⅰ）∵△P AD是等边三角形，O为AD的中点，∴PO⊥AD，∵平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，PO⊂平面P AD，∴PO⊥平面ABCD．（Ⅱ）取BC的中点F，∵底面ABCD是正方形，∴OF⊥AD，∴PO，OF，AD两两垂直．以O为原点，以OA、OF、OP为坐标轴建立空间直角坐标系如图：则O（0，0，0），P（0，0，），B（1，2，0），E（﹣1，1，0），∴＝（1，﹣1，），＝（2，1，0），＝（0，0，）．显然平面EBA的法向量为＝（0，0，）．设平面PBE的法向量为＝（x，y，z），则，∴，令x＝1，得＝（1，﹣2，﹣）．∴＝﹣3，||＝2，||＝，∴cos＜＞＝﹣．∵二面角P﹣EB﹣A为锐角，∴二面角P﹣EB﹣A的余弦值为．（Ⅲ）设在线段AB上存在点M（1，x，0）（0＜x≤2）使线段PM与平面P AD 所在平面成30°角，∵平面P AD的法向量为＝（0，2，0），＝（1，x，﹣），∴cos＜，＞＝＝．∴sin30°＝＝，解得，符合题意．∴在线段AB上存在点M，当线段时，PM与平面P AD所在平面成30°角．18．（13分）已知函数f（x）＝x2﹣lnx．（Ⅰ）求曲线y＝f（x）在点（1，f（1））处的切线方程；（Ⅱ）设g（x）＝x2﹣x+t，若函数h（x）＝f（x）﹣g（x）在上（这里e≈2.718）恰有两个不同的零点，求实数t的取值范围．【解答】解：（Ⅰ）函数定义域为（0，+∞），f′（x）＝2x﹣，∴f′（1）＝1，又f（1）＝1，∴所求切线方程为y﹣1＝x﹣1，即：x﹣y＝0；（Ⅱ）函数h（x）＝f（x）﹣g（x）＝﹣lnx+x﹣t在上恰有两个不同的零点，等价于﹣lnx+x﹣t＝0在上恰有两个不同的实根，等价于t＝x﹣lnx在上恰有两个不同的实根，令k（x）＝x﹣lnx，则，∴当时，k′（x）＜0，∴k（x）在递减；当x∈（1，e]时，k′（x）＞0，∴k（x）在（1，e]递增，故k min（x）＝k（1）＝1，又，∵，∴，∴，即．19．（14分）已知椭圆E：（a＞b＞0）的离心率，且点在椭圆E上．（Ⅰ）求椭圆E的方程；（Ⅱ）直线l与椭圆E交于A、B两点，且线段AB的垂直平分线经过点．求△AOB（O为坐标原点）面积的最大值．【解答】解：（Ⅰ）由已知，e＝＝，a2﹣b2＝c2，∵点在椭圆上，∴，解得a＝2，b＝1．∴椭圆方程为；（Ⅱ）设A（x1，y1），B（x2，y2），∵AB的垂直平分线过点，∴AB的斜率k存在．当直线AB的斜率k＝0时，x1＝﹣x2，y1＝y2，＝•2|x1|•|y1|＝|x1|•∴S△AOB＝≤•＝1，当且仅当x12＝4﹣x12，取得等号，）max＝1；∴时，（S△AOB当直线AB的斜率k≠0时，设l：y＝kx+m（m≠0）．消去y得：（1+4k2）x2+8kmx+4m2﹣4＝0，由△＞0可得4k2+1＞m2①，x1+x2＝﹣，x1x2＝，可得，，∴AB的中点为，由直线的垂直关系有，化简得1+4k2＝﹣6m②由①②得﹣6m＞m2，解得﹣6＜m＜0，又O（0，0）到直线y＝kx+m的距离为，，＝，∵﹣6＜m＜0，∴m＝﹣3时，．由m＝﹣3，∴1+4k2＝18，解得；即时，（S）max＝1；△AOB）max＝1．综上：（S△AOB20．（14分）在数列{a n}中，a1＝0，，其中m∈R，n∈N*．（Ⅰ）当m＝1时，求a2，a3，a4的值；（Ⅱ）是否存在实数m，使a2，a3，a4构成公差不为0的等差数列？证明你的结论；（Ⅲ）当m＞时，证明：存在k∈N*，使得a k＞2016．【解答】解：（Ⅰ）∵a1＝0，，其中m∈R，n∈N*．当m＝1时，a2＝0+1＝1，同理可得a3＝2，a4＝5．（Ⅱ）假设存在实数m，使a2，a3，a4构成公差不为0的等差数列，则a3﹣a2＝a4﹣a3，即﹣a2＝+m﹣a3，∴，即（a3﹣a2）（a3+a2﹣1）＝0．∵a3﹣a2≠0，∴a3+a2﹣1＝0．将a2＝m，a3＝m2+m代入上式，解得m＝﹣1．经检验，此时a2，a3，a4构成公差不为0的等差数列．∴存在得m＝﹣1，使a2，a3，a4构成公差不为0的等差数列．（Ⅲ）∵a n+1﹣a n＝+m﹣a n＝+≥m﹣，又，∴令d＝m﹣＞0．≥d，由a n﹣a n﹣1a n﹣1﹣a n﹣2≥d，…a2﹣a1≥d，将上述不等式相加，得a n﹣a1≥（n﹣1）d，即a n≥（n﹣1）d．取正整数，就有a k≥（k﹣1）d＞＝2016．。

北京市顺义区2016届高三数学下学期第一次统练试题理

顺义区2016届高三第一次统练数学试卷（理科）第Ⅰ卷（选择题共40分）一、选择题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1.设i 为虚数单位，则(21)i i += ( ) （A ） 2i + （B ） 2i - （C ）2i -+ （D ）2i -- 2.已知集合2{|1}=<A x x ，2{|log 1}=<B x x ，则=A B （）（A ）{|11}-<<x x（B ）{|01}<<x x（C ）{|02}<<x x （D ）{|12}-<<x x3.下列函数在其定义域内既是奇函数又是增函数的是（）（A ）2=x y （B ）3=+y x x （C ）1=-y x（D) 2log =-y x 4.执行如图所示的程序框图，输出的结果是 ( ) （A ）15 （B ）21 （C ）24 （D ） 355.已知向量(,1)=-a x ，(,4)=b x ，其中∈x R .则“2=x ”是“⊥a b ”成立的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分又不必要条件6.直线l ：212222⎧=+⎪⎪⎨⎪=+⎪⎩x ty t （t 为参数）与圆C ：22cos 12sin =+⎧⎨=+⎩x y θθ（θ为参数）的位置关系是 ( ) （A ）相离（B ）相切（C) 相交且过圆心（D ）相交但不过圆心7.在平面直角坐标系中，若不等式组22,12,10+≥⎧⎪≤≤⎨⎪-+≥⎩x y x ax y （a 为常数）表示的区域面积等于1，则a 的值为 ( )（A ） 16-（B ） 16 （C ）12 （D ）18.如图，已知平面α平面β=l ，⊥αβ.A B 、是直线l 上的两点，D C 、是平面β内的两点，且⊥DA l ，⊥CB l ，4,=DA 6=AB ，8=CB .P 是平面α上的一动点，且有∠=∠APD BPC ，则四棱锥-P ABCD 体积的最大值是（）（A ）48 （B ） 16 （C ）243 （D ）144第Ⅱ卷（非选择题共110分）二、填空题共6小题，每小题5分，共30分.9.261()+x x的展开式中3x 的系数为______（用数字作答).10.抛物线28=-y x 的准线与双曲线22:184-=x y C 的两条渐近线所围成的三角形面积为_________.11.已知某几何体的三视图如图,正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是________（单位:2cm ）.12.已知函数2322,1()log (1).1⎧+-≥⎪=⎨⎪+<⎩x x f x xx x 则((2))______;-=f f ()f x 的最小值为．13.某慢性疾病患者，因病到医院就医，医生给他开了处方药（片剂),要求此患者每天早、晚间隔12小时各服一次药，每次一片，每片200毫克．假设该患者的肾脏每12小时从体内大约排出这种药在其体内残留量的50%，并且医生认为这种药在体内的残留量不超过400毫克时无明显副作用.若该患者第一天上午8点第一次服药，则第二天上午8点服完药时．．．．，药在其体内的残留量是_______毫克，若该患者坚持长期服用此药________明显副作用（此空填“有”或“无”）.14..设12345,,,,A A A A A 是空间中给定的5个不同的点，则使510==∑kk MA成立的点M 的个数有_________ 个.三、解答题共6小题，共80分. 解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）已知函数21()cos()cos sin 22=--+f x x x x π，∈x R . （Ⅰ）求函数()f x 的最大值；（Ⅱ）若[,]63∈-x ππ，求函数()f x 的单调递增区间. 16.（本小题满分13分）在某班级举行的“元旦联欢会”有奖答题活动中，主持人准备了A B ，两个问题，规定：被抽签抽到的答题同学，答对问题A 可获得100分，答对问题B 可获得200分，答题结果相互独立互不影响，先回答哪个问题由答题同学自主决定；但只有第一个问题答对才能答第二个问题，否则终止答题.答题终止后，获得的总分决定获奖的等次.若甲是被抽到的答题同学，且假设甲答对A B ，问题的概率分别为 1124， .（Ⅰ）记甲先回答问题A 再回答问题B 得分为随机变量ξ，求ξ的分布列和数学期望；（Ⅱ）你觉得应先回答哪个问题才能使甲的得分期望更高？请说明理由.17.（本小题满分13分）如图，在四棱锥-P ABCD 中，等边PAD 所在的平面与正方形ABCD 所在的平面互相垂直,O 为AD 的中点，E 为DC 的中点，且 2.=AD（Ⅰ）求证：⊥PO 平面ABCD ；（Ⅱ）求二面角--P EB A 的余弦值；（Ⅲ）在线段AB 上是否存在点M ，使线段PM 与PAD 所在平面成30︒角.若存在，求出AM 的长,若不存在，请说明理由. 18.（本小题满分13分）已知函数2()ln =-f x x x .（Ⅰ）求曲线()=y f x 在点(1,(1))f 处的切线方程；（Ⅱ）设2()=-+g x x x t ，若函数()()()=-h x f x g x 在1[,]e e上(这里 2.718≈e ）恰有两个不同的零点,求实数t 的取值范围. 19.（本小题满分14分）已知椭圆:E 22221x y a b+=(0)a b >>的离心率3=e ，且点3在椭圆E 上.（Ⅰ）求椭圆E 的方程；(Ⅱ)直线l 与椭圆E 交于A 、B 两点，且线段AB 的垂直平分线经过点1(0,)2. 求AOB （O 为坐标原点)面积的最大值. 20.（本小题满分14分）在数列{}n a 中，10=a ，21+=+n n a a m ，其中∈m R ，*∈n N . （Ⅰ）当1=m 时，求234,,a a a 的值；（Ⅱ）是否存在实数m ，使234,,a a a 构成公差不为0的等差数列？证明你的结论；（Ⅲ）当14>m 时，证明：存在*∈k N ，使得2016>k a .顺义区2016届高三第一次统练数学试卷（理科）参考答案及评分标准一、选择题：本大题共8小题，每小题5分，共40分.1. C ；2. B ；3. B ；4. C ；5. A ；6. D ；7. B ； 8 . A.二、填空题：本大题共6小题，每小题5分，共30分.9. 20; 10.22; 11. 43+π; 12.1,0 ； 13.350 , 无. 14. 1. 三、解答题：本大题共6小题，共80分. 15.（本小题满分13分）解：（Ⅰ）由已知21()cos()cos sin 22=--+f x x x x π1cos 21sin cos 22-=-+x x x 【3分】112sin 2cos 2sin(2)2224=+=+x x x π【6分】当 2242+=+x k πππ ，即8=+x k ππ，∈k z 时，max 2()2=f x 【7分】（Ⅱ)当222242-≤+≤+k x k πππππ时，()f x 递增【9分】即388-≤≤+k x k ππππ，令0=k ，且注意到[,]63∈-x ππ ∴函数()f x 的递增区间为[,]68-ππ【13分】16.（本小题满分13分）（Ⅰ）ξ的可能取值为0,100.300. 【2分】∴0111(0=()(1)222=⋅-=P ξ），113(100=(1)248=⋅-=P ξ），111(300=248=⋅=P ξ）【5分】分布列为： ξ 0 100 300 P12 3818600758==E ξ. 【7分】（Ⅱ）设先回答问题B ，再回答问题A 得分为随机变量η，则η的可能取值为0,200.300.∴13(0=(1)44=-=P η），111(200=(1)428=⋅-=P ξ），111(300=428=⋅=P ξ），【10分】分布列为： η 0 200 300P34 181862.58==E η. 【12分】>E E ξη∴应先回答A 所得分的期望值较高. 【13分】17.（本小题满分13分）解：（Ⅰ）PAD 是等边三角形，O 为AD 的中点, ∴⊥PO AD平面⊥PAD 平面ABCD ，AD 是交线，⊂PO 平面PAD∴⊥PO 平面ABCD . 【4分】（Ⅱ）取BC 的中点F ，底面ABCD 是正方形，∴⊥OF AD ，∴,PO OF AD ，两两垂直.分别以OA OF OP 、、的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则3),(1,2,0),(1,2,0),(1,0,0),(1,0,0),(1,1,0)---P B C D A E 【5分】(1,0,3)=-PA ，(2,1,0,)=-AE ，(1,13)=-EP ，(2,1,0,)=EB设平面PBE 的法向量为(,,)=n x y z ，∴00⎧⋅=⎪⎨⋅=⎪⎩n PE n EB ，∴(,,)(1,3)0(,,)(2,1,0)0⎧⋅-=⎪⎨⋅=⎪⎩x y z x y z∴020⎧-=⎪⎨+=⎪⎩x y z x y ，∴123⎧=⎪=-⎨⎪=-⎩x y z ，∴(1,2,3)=--n平面EBA 的法向量即为平面ABCD 的法向量(0,0,3,)=OP . 由图形可知所求二面角为锐角，∴6cos ,||4||||⋅<>==n OP n OP n OP 【9分】 (Ⅲ)方法1：设在线段AB 上存在点(1,,0)M x ，(02)<≤x ，使线段PM 与PAD 所在平面成030角，平面PAD 的法向量为(0,2,0)，(1,,3)=-PM x ，∴0221sin 30||2244===++x x ，解得233=x ，适合∴在线段AB 上存在点M ，当线段23=AM 时，与PAD 所在平PM 面成030角. 【13分】方法2：由（Ⅰ）知⊥PO 平面ABCD ， ⊥BA AD ，⊥BA PO ,=PO AD O∴⊥BA 平面POD .设在线段AB 上存在点M 使线段PM 与PAD 所在平面成030角，连结PM ，由线面成角定义知：∠MPA 即为PM 与PAD 所在平面所成的角,023tan 30=⋅=AM PA ,当线段23=AM PAD 所在平PM 面成030角.18.（本小题满分13分）解：（Ⅰ）函数定义域为(0,)+∞ 【1分】1'()2=-f x x x，∴'(1)1=f 【2分】又(1)1=f ，∴所求切线方程为11-=-y x ，即0-=x y 【5分】（Ⅱ）函数()()()ln =-=-+-h x f x g x x x t 在1[,]e e上恰有两个不同的零点，等价于ln 0-+-=x x t 在1[,]e e上恰有两个不同的实根，【8分】等价于ln =-t x x 在1[,]e e上恰有两个不同的实根，令()ln ,=-k x x x 则11'()1-=-=x k x x x∴当1(,1)∈x e时，'()0<k x ，∴()k x 在1(,1)e 递减；当(1,]∈x e 时，'()0>k x ，∴()k x 在(1,]e 递增. 故min ()(1)1==k x k ，又11()1,()1=+=-k k e e e e. 【11分】 11()()20-=-+<k k e e e e ，∴1()()<k k e e ，∴1(1)()<≤k t k e即1(1,1]∈+t e【13分】 19.（本小题满分14分）解：（Ⅰ）由已知 221314=-=e a ，∴24=a 【2分】点3(1,2在椭圆上，∴221314+=a b ，解得2,1==a b .∴所求椭圆方程为2214+=x y 【4分】(Ⅱ)设11(,)A x y ，22(,)B x y ，AB 的垂直平分线过点1(0,2）, ∴AB 的斜率k 存在. 当直线AB 的斜率0=k 时， ∴1212,=-=x x y y∴2112|||||||||124=⋅==-AOBx Sx y x y x 222211114(4)1222+-=-≤⋅=x x x x ""=当且仅当22114,=-x x ∴12=±x max()1=AOB S【6分】当直线AB 的斜率0≠k 时，设:=+AB l y kx m (0)≠m .∴2214=+⎧⎪⎨+=⎪⎩y kx mx y 消去y 得：222(14)8440+++-=k x kmx m 由0∆>.2241+>k m ① 【8分】∴2121222844,1414-+=-=++km m x x x x k k ， ∴1224,214+=-+x x kmk ∴121222214++=+=+y y x x m k m k ，∴AB 的中点为224(,)1414-++km mk k由直线的垂直关系有2211421414-+⋅=--+m k k km k ，化简得2146+=-k m ② 由①②得26,60->∴-<<m m m 【10分】又(0,0)O 到直线=+y kx m 的距离为21=+dk，2222122214||1||14(14)+-=+-=+⋅⋅+k m AB k x x k k 【12分】2222221114||1422(14)1+-==+⋅⋅⋅++AOBk m SAB d k k k 222612||(3)9363--==-++m m m m m 60-<<m ，∴3=-m 时，max1()313=⨯=AOB S. 由3=-m ，∴21418+=k ，解得17=±k ；即172=±k 时，max()1=AOB S ；综上：max()1=AOB S；【14分】20.（本小题满分14分）解：（Ⅰ）21=a ，32=a ，45=a . 【3分】（Ⅱ）234,,a a a 成等差数列，∴3243-=-a a a a ，即 222233+-=+-a m a a m a ，∴ 223232()()0---=a a a a ，即()()323210-+-=a a a a .320-≠a a ，∴3210+-=a a .将2=a m ，23=+a m m 代入上式，解得12=-±m . 【7分】经检验，此时234,,a a a 的公差不为0.∴存在12=-±m 234,,a a a 构成公差不为0的等差数列. 【8分】（Ⅲ） 221111()()244+-=+-=-+-≥-n n n n n a a a m a a m m , 又 14>m ，∴ 令104=->d m . 【10分】由 1--≥n n a a d ， 12---≥n n a a d ，…… 21-≥a a d ，将上述不等式相加，得 1(1)-≥-n a a n d ，即(1)≥-n a n d . 【12分】取正整数20161>+k d ，就有2016(1)()2016≥->⋅=k a k d d d. 【14分】。

北京市顺义区2016届高三上学期期末统一测试理科数学试题及答案

顺义区2016届高三年级期末统一测试数学试卷（理科）第Ⅰ卷（选择题共40分）一、选择题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1．已知集合{|210}A x x =+<，{|10}B x x =-<<，那么A B = （）（A ）1{|}2x x <- （B ）{|0}x x <（C ）1{|1}2x x -<<-（D ）1{|0}2x x -<<2.下列函数中为偶函数的是（）（A ）2sin y x x =⋅（B ）cos y x x =⋅ （C ）ln ||y x =（D ）21xy =-3.某学校共有师生4000人.现用分层抽样的方法，从所有师生中抽取一个容量为200的样本，调查师生对学校食堂就餐问题的建议.已知从学生中抽取的人数为190人，那么该校的教师人数为（）（A ）100人（B ）150人（C ）200人（D ）250人4.极坐标方程分别是2cos ρθ=和2sin ρθ=的两个圆的圆心距是（）（A ）2（B（C ）1（D5.在ABC 中，角,,A B C 所对的边分别为,,a b c ，且1c =，045A ∠=，2ABC S = ，则a =（A ）5 （B ）25 （C ）（D ）6.对于非零向量,a b，“230a b += ”是“a ∥b ”成立的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分又不必要条件8.设函数()|21|,xf x c b a =-<<，且()()()f c f a f b >>，则下列关系式正确的是（）（A ）0a c +≤ （B ）0a c +> （C ）0a c +≤ （D ）0a c +<第Ⅱ卷（非选择题共110分）二、填空题共6小题，每小题5分，共30分. 9．复数1i__________.1i-+=+ 10．123123,2,log 3-三个数中最大的数是_________.11.设双曲线2222:1(0,0)x y C a b a b-=>>的一个顶点为(1,0),它的一个焦点与抛物线28y x =的焦点相同，则双曲线C 的方程为__________,离心率为_________.12.若,x y 满足约束条件10302x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩，则2z x y =-+的最大值为_______.13.已知函数1(0,1)x y aa a -=>≠的图象恒过定点A ，若点A 在一次函数y mx n =+的图象上，其中0,0m n >>，则mn 的最大值为_________.14.某大众创业公司，2015年底共有科研人员10人，公司全年产品总产值500万元,从2016年起该公司计划产品的年产值每年增加100万元,为扩大规模，科研人员每年净增a 人，设从2016年起的第x 年（*,x N ∈2016年为第一年），该公司科研人员人均产值y 万元，则y 与x 之间的函数关系式为____________；为使该公司的人均产值每年都不低于前一年的人均产值，7.如下程序框图中，当*(1)n N n ∈>时，函数()n f x 表示函数1()n f x -的导函数，即1()'()n n f x f x -=.若输入函数1()sin cos f x x x =+，则输出的函数()n f x 为 ( )（A)4x π+（B）)4x π+ （C)4x π- （D）)4x π-那么该公司每年增加的科研人员不能超过________人.三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）已知函数21()sin 22x f x x =+-．（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）求函数()f x 的单调递增区间. 16.（本小题满分13分）已知函数()||f x x a =-,2()21g x x ax =++(a 为正常数),且函数()f x 和()g x 的图像与y 轴相交于同一点. （Ⅰ）求a 的值；（Ⅱ）求函数()()f x g x +在[1,2]上的最大值与最小值． 17.（本小题满分13分）某班级举行一次“科普知识”竞赛活动，活动分为初赛和决赛两个阶段.现将初赛答卷成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表（Ⅰ）填写频率分布表中的空格；（Ⅱ）决赛规则如下：参加决赛的每位同学从给定的5道小题中依次口答，答对3道题就终止答题并获一等奖；如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛，每道题答对的概率均为 0.5.①求该同学恰好答满5道题并获一等奖的概率；②记该同学决赛中答题的个数为X ，求X 的分布列及数学期望.18.（本小题满分13分）已知函数()ln f x x =,(),(0)kg x k x=-≠ （Ⅰ）求曲线()y f x =在(,())e f e 处的切线方程；（Ⅱ）求函数()()()h x f x g x =-的单调递增区间；（Ⅲ）若对(,0)(0,)x ∀∈-∞+∞ 都有(||)(||)f x g x ≥成立，试确定实数k 的取值范围.19.（本小题满分14分）已知椭圆:E 22221x y a b +=(0)a b >>的一个顶点(0,1)A，离心率e =.（Ⅰ）求椭圆E 的方程；(Ⅱ)过右焦点F 作斜率为k 的直线l 与椭圆E 交于M 、N 两点.若在x 轴上存在点(,0)P m ，使得以,PM PN 为邻边的平行四边形是菱形，试求出m 的取值范围. 20.（本小题满分14分）2*(4,)n n n N ≥∈个正数排成一个n 行n 列的数阵，1112131412122232423132333431234n n n n n n n nn a a a a a a a a a a A a a a a a a a a a a ⋅⋅⋅⎛⎫⎪⋅⋅⋅ ⎪⎪=⋅⋅⋅ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅⎝⎭其中(1,1)ij a i n j n ≤≤≤≤表示该数阵中位于第i行第j 列的数，已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，且22336,16a a ==. (Ⅰ) 求11a 和i j a ；(Ⅱ)设12(1)3(2)1n n n n n A a a a a --=+++⋅⋅⋅⋅⋅⋅+. ①求n A ；②证明：当n 是3的倍数时，n A n +能被21整除.顺义区2016届高三期末统一测试（理科）参考答案及评分标准2016.1一、选择题：本大题共8小题，每小题5分，共40分.1. B ；2. C ；3. C；4. B；5. A；6. A；7. C ；8 . D.二、填空题：本大题共6小题，每小题5分，共30分.9. 10.11.，12.，13.14.三、解答题：本大题共6小题，共80分.15.（本小题满分13分）解：（Ⅰ）由已知【3分】【6分】的最小正周期为. 【7分】（Ⅱ）由（Ⅰ）知当时递增【10分】即函数的递增区间为【13分】16.（本小题满分13分）解：（Ⅰ）函数和的图像与轴相交于同一点，解得. 【4分】（Ⅱ）令，【8分】的对称轴为，当时，单调递增。

(全优试卷)北京市顺义区高三数学第一次模拟考试试卷理(含解析)

北京市顺义区2016届高三第一次模拟考试理科数学试卷一、单选题1.设为虚数单位，则（）A． B． C． D．【知识点】复数乘除和乘方【试题解析】故答案为：C【答案】C2.已知集合，，则（）A．B．C．D．【知识点】集合的运算【试题解析】所以。

故答案为：B【答案】B3.下列函数在其定义域内既是奇函数又是增函数的是（）A． B． C． D．【知识点】函数的单调性与最值函数的奇偶性【试题解析】若函数是奇函数，则故排除A、D；对C：在（-和（上单调递增，但在定义域上不单调，故C错；故答案为：B【答案】B4.执行如图所示的程序框图，输出的结果是（）A．15 B．21 C．24 D．35【知识点】算法和程序框图【试题解析】否，否，否，是，则输出S=24．故答案为：C【答案】C5.已知向量，，其中．则“”是“”成立的（）A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分又不必要条件【知识点】平面向量坐标运算【试题解析】若，则成立；反过来，若，则或所以“”是“”成立的充分而不必要条件。

故答案为：A【答案】A6.直线：（为参数）与圆：（为参数）的位置关系是（）A．相离 B．相切 C．相交且过圆心 D．相交但不过圆心【知识点】直线与圆的位置关系参数和普通方程互化【试题解析】将参数方程化普通方程为：直线：圆：圆心（2,1），半径2．圆心到直线的距离为：，所以直线与圆相交。

又圆心不在直线上，所以直线不过圆心。

故答案为：D【答案】D7.在平面直角坐标系中，若不等式组（为常数）表示的区域面积等于，则的值为（）A． B． C． D．【知识点】线性规划【试题解析】作可行域：由题知：所以故答案为：B【答案】B8.如图，已知平面=，．是直线上的两点，是平面内的两点，且，，，．是平面上的一动点，且有，则四棱锥体积的最大值是（）A． B． C． D．【知识点】空间几何体的表面积与体积【试题解析】由题知：是直角三角形，又，所以。

2016北京市顺义区高三(一模)数学(理)

2016北京市顺义区高三（一模）数学（理）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．（5分）已知i为虚数单位，则i（2i+1）=（）A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i2．（5分）已知集合A={x|x2＜1}，B={x|log2x＜1}，则A∩B=（）A．{x|﹣1＜x＜1} B．{x|0＜x＜1} C．{x|0＜x＜2} D．{x|﹣1＜x＜2}3．（5分）下列函数在其定义域内既是奇函数又是增函数的是（）A．y=2x B．y=x3+x C．D．y=﹣log2x4．（5分）执行如图所示的程序框图，输出的结果是（）A．15 B．21 C．24 D．355．（5分）已知向量，，其中x∈R．则“x=2”是“”成立的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分又不必要条件6．（5分）直线l：（t为参数）与圆C：（θ为参数）的位置关系是（）A．相离 B．相切C．相交且过圆心 D．相交但不过圆心7．（5分）在平面直角坐标系中，若不等式组（a为常数）表示的区域面积等于1，则a的值为（）A．B．C．D．18．（5分）如图，已知平面α∩平面β=l，α⊥β．A、B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，DA=4，AB=6，CB=8．P是平面α上的一动点，且有∠APD=∠BPC，则四棱锥P﹣ABCD体积的最大值是（）A．48 B．16 C．D．144二、填空题共6小题，每小题5分，共30分.9．（5分）（x2+）6的展开式中x3的系数是．（用数字作答）10．（5分）抛物线y2=﹣8x的准线与双曲线的两条渐近线所围成的三角形面积为．11．（5分）已知某几何体的三视图如图，正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是（单位：cm2）．12．（5分）已知函数f（x）=，则= ；f（x）的最小值为．13．（5分）某慢性疾病患者，因病到医院就医，医生给他开了处方药（片剂），要求此患者每天早、晚间隔12小时各服一次药，每次一片，每片200毫克．假设该患者的肾脏每12小时从体内大约排出这种药在其体内残留量的50%，并且医生认为这种药在体内的残留量不超过400毫克时无明显副作用．若该患者第一天上午8点第一次服药，则第二天上午8点服完药时，药在其体内的残留量是毫克，若该患者坚持长期服用此药明显副作用（此空填“有”或“无”）．14．（5分）设A1，A2，A3，A4，A5是空间中给定的5个不同的点，则使成立的点M的个数有个．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.15．（13分）已知函数，x∈R．（Ⅰ）求函数f（x）的最大值；（Ⅱ）若，求函数f（x）的单调递增区间．16．（13分）在某班级举行的“元旦联欢会”有奖答题活动中，主持人准备了A，B两个问题，规定：被抽签抽到的答题同学，答对问题A可获得100分，答对问题B可获得200分，答题结果相互独立互不影响，先回答哪个问题由答题同学自主决定；但只有第一个问题答对才能答第二个问题，否则终止答题．答题终止后，获得的总分决定获奖的等次．若甲是被抽到的答题同学，且假设甲答对A，B问题的概率分别为．（Ⅰ）记甲先回答问题A再回答问题B得分为随机变量ξ，求ξ的分布列和数学期望；（Ⅱ）你觉得应先回答哪个问题才能使甲的得分期望更高？请说明理由．17．（13分）如图，在四棱锥P﹣ABCD中，等边△PAD所在的平面与正方形ABCD所在的平面互相垂直，O为AD的中点，E为DC的中点，且AD=2．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求二面角P﹣EB﹣A的余弦值；（Ⅲ）在线段AB上是否存在点M，使线段PM与△PAD所在平面成30°角．若存在，求出AM的长，若不存在，请说明理由．18．（13分）已知函数f（x）=x2﹣lnx．（Ⅰ）求曲线y=f（x）在点（1，f（1））处的切线方程；（Ⅱ）设g（x）=x2﹣x+t，若函数h（x）=f（x）﹣g（x）在上（这里e≈2.718）恰有两个不同的零点，求实数t的取值范围．19．（14分）已知椭圆E：（a＞b＞0）的离心率，且点在椭圆E上．（Ⅰ）求椭圆E的方程；（Ⅱ）直线l与椭圆E交于A、B两点，且线段AB的垂直平分线经过点．求△AOB（O为坐标原点）面积的最大值．20．（14分）在数列{a n}中，a1=0，，其中m∈R，n∈N*．（Ⅰ）当m=1时，求a2，a3，a4的值；（Ⅱ）是否存在实数m，使a2，a3，a4构成公差不为0的等差数列？证明你的结论；（Ⅲ）当m＞时，证明：存在k∈N*，使得a k＞2016．数学试题答案一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项. 1．【解答】由题意，i（2i+1）=i×2i+i=﹣2+i故选C．2．【解答】集合A={x|x2＜1}={x|﹣1＜x＜1}，B={x|log2x＜1}={x|0＜x＜2}，则A∩B={x|0＜x＜1}，故选：B．3．【解答】A．y=2x的图象不关于原点对称，不是奇函数，∴该选项错误；B．y=x3+x的定义域为R，且（﹣x）3+（﹣x）=﹣（x3+x）；∴该函数为奇函数；y=x3和y=x在R上都是增函数；∴y=x3+x在R上是增函数，∴该选项正确；C．反比例函数在定义域上没有单调性，∴该选项错误；D．y=﹣log2x的定义域为（0，+∞），不关于原点对称，不是奇函数，∴该选项错误．故选：B．4．【解答】模拟执行程序，可得S=0，i=1T=3，S=3，i=2不满足i＞4，T=5，S=8，i=3不满足i＞4，T=7，S=15，i=4不满足i＞4，T=9，S=24，i=5满足i＞4，退出循环，输出S的值为24．故选：C．5．【解答】∵，∴x2﹣4=0，解得x=±2．∴“x=2”是“”成立的充分不必要条件．故选：A．6．【解答】把圆的参数方程化为普通方程得：（x﹣2）2+（y﹣1）2=4，∴圆心坐标为（2，1），半径r=2，把直线的参数方程化为普通方程得：x﹣y+1=0，∴圆心到直线的距离d=＜r=2，又圆心（2，1）不在直线x﹣y+1=0上，则直线与圆的位置关系为相交但不过圆心．故选：D．7．【解答】不等式组所围成的区域如图ABCD所示，∵其面积为1，A（2，2a+1），B（2，0），C（1，），D（1，a+1）∴S ABCD==1，解得a=．故选：B．8．【解答】∵平面α∩平面β=l，α⊥β，DA⊥l，CB⊥l，DA⊂平面β，CB⊂平面β，∴DA⊥平面α，CB⊥平面α，∵PA⊂平面α，PB⊂平面α，∴DA⊥PA，CB⊥PB．∵∠APD=∠BPC，∴，即，∴PB=2PA．以直线l为x轴，AB的中点为坐标原点建立平面直角坐标系，则A（﹣3，0），B（3，0）．设P（x，y），则PA=，PB=，∴2=，整理得（x+5）2+y2=16（y＞0）．∴P点的轨迹为以（﹣5，0）为圆心，以4为半径的半圆．∴当P到直线l的距离h=4时，四棱锥P﹣ABCD体积取得最大值．∴棱锥的体积最大值为V===48．故选：A．二、填空题共6小题，每小题5分，共30分.9．【解答】由于（x2+）6的展开式的通项公式为 T r+1=•x12﹣3r，令12﹣3r=3，解得r=3，故展开式中x3的系数是=20，故答案为：20．10．【解答】抛物线y2=﹣8x的准线为x=2，双曲线的两条渐近线为y=±x，可得两交点为（2，），（2，﹣），即有三角形的面积为×2×2=2．故答案为：2．11．【解答】根据三视图可知几何体是半个圆柱，且正视图是底面，∴底面圆的半径是1cm，母线长是2cm，∴几何体的表面积S=π×12+π×1×2+2×2=3π+4（cm2），故答案为：3π+4．12．【解答】f（﹣）=log33=1，则f（1）=1+2﹣2=1，即=1，当x≥1时，f（x）=x+﹣2≥2﹣2=2﹣2，当且仅当x=，即x=时取等号，当x＜1时，f（x）=log3（x2+1）≥log31=0；故函数f（x）的最小值为0，故答案为：1，0．13．【解答】设该生第n次服药后，药在他体内的残留量为a n毫克，则：a1=200，a2=200+a1×（1﹣50%）=200×1.5=300，a3=200+a2×（1﹣50%）=200+200×1.5×0.5=350 （4分）故第二天早间，他第三次服空药后，药在他体内的残留量为350毫克．该运动员若长期服用此药，则此药在体内残留量为=400（1﹣0.5n），当n→+∞时，药在体内残留量无限接近400∴长期服用此药，不会产生副作用，即该生长期服用该药，不会产生副作用．故答案为：350，无．14．【解答】设A1（x1，y1，z1），A2（x2，y2，z2），A3（x3，y3，z3），A4（x4，y4，z4），A5（x5，y5，z5）；再设M（a，b，c），则可得=（x1﹣a，y1﹣b，z1﹣c），=（x2﹣a，y2﹣b，z2﹣c），=（x3﹣a，y3﹣b，z3﹣c），=（x4﹣a，y4﹣b，z4﹣c），=（x5﹣a，y5﹣b，z5﹣c），∵=成立，∴，解得，因此，存在唯一的点M，使=成立．故答案为：1．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.15．【解答】（Ⅰ）由三角函数公式化简可得==sin2x+cos2x=sin（2x+）当即，k∈z时，；（Ⅱ）∵当时，f（x）递增，即，令k=0，且注意到，∴函数f（x）的递增区间为16．【解答】（Ⅰ）ξ的可能取值为0，100，300．（2分），，，（5分）∴ξ的分布列为：ξ 0 100 300 P．（7分）（Ⅱ）设先回答问题B，再回答问题A得分为随机变量η，则η的可能取值为0，200，300．∴，，，（10分）η的分布列为：η 0 200 300 P．（12分）∵Eξ＞Eη，∴应先回答A所得分的期望值较高．（13分）17．【解答】（Ⅰ）∵△PAD是等边三角形，O为AD的中点，∴PO⊥AD，∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PO⊂平面PAD，∴PO⊥平面ABCD．（Ⅱ）取BC的中点F，∵底面ABCD是正方形，∴OF⊥AD，∴PO，OF，AD两两垂直．以O为原点，以OA、OF、OP为坐标轴建立空间直角坐标系如图：则O（0，0，0），P（0，0，），B（1，2，0），E（﹣1，1，0），∴=（1，﹣1，），=（2，1，0），=（0，0，）．显然平面EBA的法向量为=（0，0，）．设平面PBE的法向量为=（x，y，z），则，∴，令x=1，得=（1，﹣2，﹣）．∴=﹣3，||=2，||=，∴cos＜＞=﹣．∵二面角P﹣EB﹣A为锐角，∴二面角P﹣EB﹣A的余弦值为．（Ⅲ）设在线段AB上存在点M（1，x，0）（0＜x≤2）使线段PM与平面PAD所在平面成30°角，∵平面PAD的法向量为=（0，2，0），=（1，x，﹣），∴cos＜，＞==．∴sin30°==，解得，符合题意．∴在线段AB上存在点M，当线段时，PM与平面PAD所在平面成30°角．18．【解答】（Ⅰ）函数定义域为（0，+∞），f′（x）=2x﹣，∴f′（1）=1，又f（1）=1，∴所求切线方程为y﹣1=x﹣1，即：x﹣y=0；（Ⅱ）函数h（x）=f（x）﹣g（x）=﹣lnx+x﹣t在上恰有两个不同的零点，等价于﹣lnx+x﹣t=0在上恰有两个不同的实根，等价于t=x﹣lnx在上恰有两个不同的实根，令k（x）=x﹣lnx，则，∴当时，k′（x）＜0，∴k（x）在递减；当x∈（1，e]时，k′（x）＞0，∴k（x）在（1，e]递增，故k min（x）=k（1）=1，又，∵，∴，∴，即．19．【解答】（Ⅰ）由已知，e==，a2﹣b2=c2，∵点在椭圆上，∴，解得a=2，b=1．∴椭圆方程为；（Ⅱ）设A（x1，y1），B（x2，y2），∵AB的垂直平分线过点，∴AB的斜率k存在．当直线AB的斜率k=0时，x1=﹣x2，y1=y2，∴S△AOB=•2|x1|•|y1|=|x1|•=≤•=1，当且仅当x12=4﹣x12，取得等号，∴时，（S △AOB）max=1；当直线AB的斜率k≠0时，设l：y=kx+m（m≠0）．消去y得：（1+4k2）x2+8kmx+4m2﹣4=0，由△＞0可得4k2+1＞m2①，x1+x2=﹣，x1x2=，可得，，∴AB的中点为，由直线的垂直关系有，化简得1+4k2=﹣6m②由①②得﹣6m＞m2，解得﹣6＜m＜0，又O（0，0）到直线y=kx+m的距离为，，=，∵﹣6＜m＜0，∴m=﹣3时，．由m=﹣3，∴1+4k2=18，解得；即时，（S△AOB）max=1；综上：（S△AOB）max=1．20．【解答】（Ⅰ）∵a1=0，，其中m∈R，n∈N*．当m=1时，a2=0+1=1，同理可得a3=2，a4=5．（Ⅱ）假设存在实数m，使a2，a3，a4构成公差不为0的等差数列，则a3﹣a2=a4﹣a3，即﹣a2=+m﹣a3，∴，即（a3﹣a2）（a3+a2﹣1）=0．∵a3﹣a2≠0，∴a3+a2﹣1=0．将a2=m，a3=m2+m代入上式，解得m=﹣1．经检验，此时a2，a3，a4构成公差不为0的等差数列．∴存在得m=﹣1，使a2，a3，a4构成公差不为0的等差数列．（Ⅲ）∵a n+1﹣a n=+m﹣a n=+≥m﹣，又，∴令d=m﹣＞0．由 a n﹣a n﹣1≥d，a n﹣1﹣a n﹣2≥d，…a2﹣a1≥d，将上述不等式相加，得 a n﹣a1≥（n﹣1）d，即a n≥（n﹣1）d．取正整数，就有a k≥（k﹣1）d＞=2016．。

2016届海淀区高三期末数学(理)答案

π ，海淀区高三年级第一学期期末练习参考答案数学（理科） 2016.1阅卷须知:1. 评分参考中所注分数，表示考生正确做到此步应得的累加分数。

2. 其它正确解法可以参照评分标准按相应步骤给分。

一、选择题：本大题共 8 小题，每小题 5 分，共 40 分. 题号 1 2 3 4 5 6 7 8 答案ABDCACDD题号 9101112 1314 答案2 ; 515 6 2 3-4②； 45三、解答题: 本大题共 6 小题，共 80 分.15. 解：（Ⅰ）因为 f (x ) = 2 2 cos x s in( x - π) +14= 2 2 cos x [ 2(sin x - cos x )] +12…………………………….1 分= 2cos x (sin x -cos x ) +1= 2cos x sin x - 2cos 2 x +1= sin 2x -cos2x…………………………….5 分（两个倍角公式，每个各 2 分）= 2 sin(2x - π)4…………………………….6 分所以函数 f (x ) 的最小正周期T =2π | ω |= π ...................................................................................... 7 分（Ⅱ）因为x ∈[ π π]，所以2x ∈[ π π] ，所以(2x - π) ∈[- π ，π ] .................................. 8 分，， 12 6 6 34 12 12 当2x - π = - π 4 12 时，函数 f (x ) 取得最小值 2 sin(- π) ; .............................................................. 10 分12 当2x - π = π 时，函数 f (x ) 取得最大值 2 sin π, ...................................................................... 12 分4 12 12因为 2 sin(- π) + 2 sin( ) = 0 ,12 12所以函数 f (x ) 在区间[ π π] 上的最大值与最小值的和为0 .................................................... 13 分12 616. 解：（Ⅰ）设持续i 天为事件 A i ,i = 1,2,3,4 ，用药持续最多一个周期为事件 B ， .............. 1 分所以 P ( A ) = 1，P ( A ) = 1 ⋅ 2，P ( A ) = 1 ⋅ ( 2)2，P ( A ) = 1 ⋅ ( 2)3 ， ................ 5 分1 323 3 3 3 3 43 3则 P (B ) = P ( A ）+ P ( A ) + P ( A ) + P ( A ) = 65 ........................................................................6 分1 2 3 4 81法二：设用药持续最多一个周期为事件 B ，则 B 为用药超过一个周期， ..................1 分所以P (B ) = ( 2)4 = 16, .............................................................................................................. 3 分 3 81 所以 P (B ) = 1- ( 2)4 = 65 ......................................................................................................6 分3 81（Ⅱ）随机变量η 可以取 1, 2 ， .................................................... 7 分所以 P (η = 1) = C 3 (1)3 2 + (1)4 = 1 , P (η = 2) = 1- 1 = 8 , ......................................................... 11 分 43 3 3 9 9 9所以 E η = 1⋅ 1 + 2 ⋅ 8 = 17 .............................................................................................................13 分9 9 9n , m >=n ⋅ m = - 1 HFA17. 解：P（Ⅰ）过点 F 作 FH AD ，交 PA 于 H ,连接 BH , 因为PF = 1 PD ，所以 HF = 1 AD = BC .............................................. 1 分 3 3 D又FH AD ， AD BC ，所以 HF BC .…………………………….2 分 BC所以 BCFH 为平行四边形, 所以CF.…………………………….3 分又 BH ⊂ 平面 PAB ， CF ⊄ 平面 PAB , ........................................ 4 分（一个都没写的，则这 1 分不给）所以CF 平面 PAD ....................................................................................5 分（Ⅱ）因为梯形 ABCD 中， AD BC ， AD ⊥ AB , 所以BC ⊥ AB . P因为 PB ⊥ 平面 ABCD ，所以 PB ⊥ AB ，PB ⊥ BC , 如图，以 B 为原点，BBC , B A , B P 所在直线为x , y , z 轴建立空间直角坐标系, ................................................................. 6 分所以C (1,0,0), D (3,3,0), A (0,3,0), P (0,0,3) .设平面 BPD 的一个法向量为n = (x , y , z ) ，平面 APD 的一个法向量为m = (a ,b ,c ) , 因为 PD = (3,3, -3), BP = (0,0,3),⎧⎪PD ⋅ n = 0 ⎧3x + 3y - 3z = 0 所以⎨BP ⋅ n = 0 ，即⎨3z = 0 ， ............................................ 7 分 ⎩⎪ ⎩ 取x = 1 得到n = (1, -1,0) ,..................................................................................................................... 8 分同理可得m = (0,1,1) , ............................................................................................................................ 9 分所以cos < | n || m |2 , ........................................................................................................ 10 分因为二面角 B - PD - A 为锐角，π所以二面角 B - PD - A 为 .…………………………….11 分3（Ⅲ）假设存在点 M ，设 PM = λ PD = (3λ,3λ, -3λ) ，所以CM = CP + λ P M = (-1+ 3λ,3λ,3 - 3λ) , .............................................................................. 12 分所以 PA ⋅ C M = -9λ + 3(3 - 3λ) = 0 ，解得λ = 1, ......................................................................... 13 分2 所以存在点 M ，且 PM = 1 PD =3 3 ..........................................................................................14 分 2 2BH zFyDACx2 18．解：（Ⅰ）因为 f (x ) = kx - (k +1) ln x - 1,xk +1 1 kx 2 - (k + 1)x + 1所以 f '(x ) = k - + = ， ..................................... 1 分x x 2 x 21 1( x - 2)( x -1) 当k = 时， f '( x ) = 2 ............................................................................................ 2 分 x21( x - 2)( x -1) 令 f '( x ) = 2 = 0 x2，得 x 1 = 1, x 2 = 2 ，............................... 3 分所以 f '(x ), f (x ) 随 x 的变化情况如下表：分所以 f (x ) 在 x = 1 处取得极大值 f (1) = - 1，2在 x = 2 处取得极小值 f (2) = 1 - 3ln 2 ...................................................................................... 7 分2 2函数 f (x ) 的单调递增区间为(0,1) ，(2, +∞) , （Ⅱ）证明：f (x ) 的单调递减区间为(1, 2)............................. 8 分不等式 f (x ) > 1在区间[1,e] 上无解，等价于 f (x ) ≤ 1在区间[1,e] 上恒成立，即函数 f (x ) 在区间[1,e] 上的最大值小于等于 1.k ( x - 1)( x -1)因为 f '( x ) = k ，x 2令 f '(x ) = 0 ，得 x = 1, x = 1 .......................................................................................................... 9 分1 k2因为0 < k < 1时，所以 1> 1 .k当 1≥ e 时， f '(x ) ≤ 0 对 x ∈[1,e]成立，函数 f (x ) 在区间[1, e ]上单调递减， ........... 10 分k所以函数 f (x ) 在区间[1, e]上的最大值为 f (1) = k -1 < 1,所以不等式 f (x ) > 1在区间[1, e] 上无解； ........................................... 11 分当1< e 时，f '(x), f (x) 随x 的变化情况如下表：k所以函数f (x) 在区间[1, e]上的最大值为f (1) 或f (e) ............................................................. 12 分此时 f (1) =k -1 <1, f (e) =k e - (k + 1) -1 ，e所以 f (e) -1 =k e - (k + 1) -1 -1e=k(e -1) - 2 -1< (e -1) - 2 -1= e - 3 -1< 0 .e e e综上，当0 <k <1时，关于x 的不等式f (x) >1在区间[1,e] 上无解..................... 13 分16 1+ k 2 y 1 19. 解：（Ⅰ）因为椭圆W 的左顶点 A 在圆O : x 2 + y 2= 16 上，令 y = 0 ，得 x = ±4 ，所以a = 4 ..................................................................................................... 1 分又离心率为3，所以e = c = 3，所以c = 2 , .......................................................................... 2 分 2 a 2所以b 2 = a 2 - c 2 = 4 , ........................................................................................................................ 3 分所以W 的方程为 x2 + = 1 ............................................................................................................4 分（Ⅱ）16 4法一：设点 P (x 1, y 1 ),Q (x 2 , y 2 ) ，设直线 AP 的方程为y = k (x + 4) ， ..................... 5 分 ⎧ y = k ( x + 4)⎪与椭圆方程联立得⎨ x 2 + y 2 = ,⎩16 4化简得到(1+ 4k 2 )x 2 + 32k 2 x + 64k 2-16 = 0 , .................................................................................... 6 分-32k 2 因为-4 为上面方程的一个根，所以 x 1 + (-4) = 1+ 4k2 ，所以 x 1 = 4 -16k 21 + 4k2 . …………………………….7 分所以| AP | . …………………………….8 分因为圆心到直线 AP 的距离为d = ， ........................................... 9 分所以| AQ |= 2 2= 8 , .................................................................................... 10 分因为| PQ | = | AQ | - | AP | = | AQ | -1 ， ............................................ 11 分| AP | | AP | | AP || PQ | = 1 + k 2- = 1 + 4k 2 - = 3k 2 = - 3 代入得到 | AP | 1 8 1 + k 2 21 + k2 1 1 + k 23 1 + k 2 .......................................................................................... 13 分显然3 -法二：3 1 + k 2≠ 3 ，所以不存在直线 AP ，使得| PQ | = 3 ..............................................................14 分 | AP | 设点 P (x 1, y 1 ),Q (x 2 , y 2 ) ，设直线 AP 的方程为 x = my - 4 ， ............................ 5 分⎧ x = my - 4⎪ 与椭圆方程联立得⎨ x 2 + y 2 = ⎪⎩16 4 13 8 1 + k 2 k 2+ 116 - d 21+ k 22化简得到(m 2 + 4) y 2- 8my = 0 , 由∆ = 64m 2> 0 得 m ≠ 0 ............................................................ 6 分显然0 是上面方程的一个根，所以另一个根，即 y 1 = 8mm 2+ 4. …………………………….7 分由| AP |y 1 - 0 |， .............................................8 分因为圆心到直线 AP 的距离为d =........................................... 9 分所以| AQ |===…………………………….10 分因为| PQ | = | AQ | - | AP | = | AQ | -1 ， ............................................ 11 分| AP | | AP | | AP || PQ | = = m 2 + 4 - = 3代入得到| AP | 1 1 + m 2 1 1 + m 2 , ................................................................ 13 分若 3 1 + m 2= 3 ，则m = 0 ，与m ≠ 0 矛盾，矛盾，所以不存在直线 AP ，使得| PQ |= 3 ............................................................................................... 14 分 | AP |法三：假设存在点 P ，使得| PQ | = 3 ，则 | AQ |= 4 ，得| y Q | = 4 .............................................. 5 分 | AP | | AP | | y P | 显然直线 AP 的斜率不为零，设直线 AP 的方程为x = my - 4 ， ........................... 6 分 ⎧ x = my - 4⎪由⎨ x 2 + y 2 = ，得(m 2 + 4) y 2 - 8my = 0 ,⎪⎩16 4由∆ = 64m 2 > 0 得m ≠ 0 ， .......................................................... 7 分所以 y P = 8mm 2+ 4. …………………………….9 分同理可得 y Q = 8mm 2+1， ............................................................ 11 分所以由 | y Q | = 4 得 | y P | m 2 + 4 m 2 +1= 4 ， ..................................................... 13 分则 m = 0 ，与 m ≠ 0 矛盾，所以不存在直线 AP ，使得| PQ |= 3 ..............................................................................................14 分 | AP |11 20. 解：（Ⅰ）因为{a n } 是 P 数列，且a 1 = 0 所以a 3 =| a 2 | -a 0 =| a 2 |，所以a 4 = a 3 - a 2 = a 2 - a 2 ,所以 a - a = 1，解得a = - 1, ............................................................................................... 1 分22 22所以a = 1, a =| a | -a =3分 325 4 32(Ⅱ) 假设 P 数列{a n } 的项都是正数，即a n > 0, a n +1 > 0, a n +2 > 0 ，所以a n +2 = a n +1 - a n ， a n +3 = a n +2 - a n +1 = -a n < 0 ，与假设矛盾.故 P 数列{a n } 的项不可能全是正数, ................................................................................................ 5 分假设 P 数列{a n } 的项都是负数，则a n < 0, 而a n +2 = a n +1 - a n > 0 ,与假设矛盾, ...........................................................................7 分故 P 数列{a n } 的项不可能全是负数.(Ⅲ)由(Ⅱ)可知 P 数列{a n } 中项既有负数也有正数，且最多连续两项都是负数，最多连续三项都是正数. 因此存在最小的正整数k 满足a k < 0, a k +1 > 0 （ k ≤ 5）. 设a k = -a , a k +1 = b (a ,b > 0)，则a k +2 =b + a , a k +3 = a , a k +4 = -b , a k +5 = b - a .a k +6 =b - a + b , a k +7 = b - a + a ,a k +8 = a - b ,a k +9 = -a ,a k +10 = b ,故有a k = a k +9 , 即数列{a n } 是周期为 9 的数列 ....................................... 9 分由上可知a k , a k +1,⋅⋅⋅, a k +8 这 9 项中a k , a k +4 为负数，a k +5,a k +8 这两项中一个为正数，另一个为负数，其余项都是正数. 因为2016 = 9 ⨯ 224 ,所以当k = 1时， m = 224 ⨯ 3 = 672 ;当2 ≤ k ≤ 5 时， a 1, a 2 ,⋅⋅⋅, a k -1 这k -1项中至多有一项为负数，而且负数项只能是a k -1 , 记a k , a k +1,⋅⋅⋅, a 2016 这2007 - k 项中负数项的个数为t ，当k = 2,3, 4 时，若a k -1 < 0, 则b = a k +1 = a k - a k -1 > a k = a ，故a k +8 为负数，此时t = 671， m = 671+1=672 ；若a k -1 > 0, 则b =a k +1 =a k -a k -1 <a k =a ，故a k +5 为负数.此时t = 672 ，m = 672 ，当k = 5 时，a k -1 必须为负数，t = 671，m = 672 , ................................................................. 12 分综上可知m 的取值集合为{672}...................................................................................................... 13 分说明：1. 正确给出m 的值，给1 分2.证明中正确合理地求出数列{a n } 的周期给2 分，但是通过特例说明的不给分3.正确合理说明m 取值情况给2 分。

北京市顺义区届高三第一次统练考试数学(理)试题.pdf

n
（A）若 n 为偶数，则集合 M 的个数为 22 个；
n
（B）若 n 为偶数，则集合 M 的个数为 22 −1个；
n−1
（C）若 n 为奇数，则）若 n 为奇数，则集合 M 的个数为 2 2 个.
二.填空题(本大题共 6 个小题,每小题 5 分,共 30 分)
9. 已知 i 为虚数单位，在复平面内复数 2i 对应点的坐标为 __________. 1+ i
10.一个几何体的三视图如图所示，
则这个几何体的体积是___________．
3
4 主视图
侧（左）视图
俯视图
2
11. ( x − 1)6 的展开式中，常数项是______________. x
12.已知抛物线 y2 = 2 px（ p 0）的焦点为 F ，准线为 l ，P 为抛物线上一点，PA ⊥ l ，垂足为 A .如果 APF 是边长为 4 的正三角形，则此抛物线的焦点坐标为__________, 点 P 的横坐标 xP = ______.
0)
满足对任意实数
x1
x2
，都有
f (x2 ) − f (x1) 0 成立，则 a 的取值范围是 x2 − x1
（A） (0,1) （B） (1, +)
（
C）
1,
5 3
8.设非空集合 M 同时满足下列两个条件：
① M 1, 2,3,, n −1 ；
（
D）
5 3
,
2
②若 a M ，则 n − a M ， (n 2, n N + ) .则下列结论正确的是
4x − 3y + 4 0
13.
设
x,
y
满足约束条件

北京市顺义区2016届高三上学期期末物理试卷含解析精

2015-2016学年北京市顺义区高三（上）期末物理试卷一、选择题（共16小题，每小题3分，满分48分）1．一列横波沿水平方向传播，某一时刻的波形如图所示，则图中a、b、c、d四点在此时刻具有相同运动方向的是（）A．a和c B．a和d C．b和c D．b和d2．地球上站立着两位相距非常远的观察者，发现自己的正上方有一颗人造地球卫星相对自己静止不动，则这两位观察者及两颗卫星到地球中心的距离是（）A．一个人在南极，一个人在北极，两卫星到地球中心的距离一定相等B．两人都在赤道上，两卫星到地球中心的距离一定相等C．一个人在南极，一个人在北极，两卫星到地球中心的距离可以不相等D．两人都在赤道上，两卫星到地球中心的距离可以不相等3．如图所示，是描述对给定的电容器充电时电荷量Q、电压U、电容C之间相互关系的图象，其中正确的是（）A．B．C．D．4．如图所示，质量为m的金属环用线悬挂起来，金属环有一半处于水平且与环面垂直的匀强磁场中，从某时刻开始，磁感应强度均匀减小，则在磁感应强度均匀减小的过程中，关于线拉力大小的下列说法中正确的是（）A．大于环重力mg，并逐渐减小B．始终等于环重力mgC．小于环重力mg，并保持恒定D．大于环重力mg，并保持恒定5．如图所示，质量分别为m和M的两物块紧挨着放在水平地面上，且M＞m．当用水平恒力F向右的推物块m时，两物块能在水平面上加速向右滑行，两物块的加速度大小为a，两物块间的作用力大小为T．如果用同样大小的水平恒力F 向左推木块M时，加速度大小为a′，物块间的作用力大小为T′，以下判断正确的是（）A．a′=a，T′＞T B．a′＜a，T′=T C．a′＞a，T′=T D．a′=a，T′＜T6．一物体悬挂在气球下面，与气球一起沿竖直方向匀速上升，某时刻该物体脱落，并从此时开始计时．已知气球和物体所受空气阻力大小不变．在下图中①代表气球运动的v﹣t图线，②代表物体运动的v﹣t图线．以下四个v﹣t图象中最接近真实情况的是（）A．B．C．D．7．如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑，通过轨道最低点时（）A．小球对轨道的压力相同B．小球对两轨道的压力不同C．此时小球的速度相等D．此时小球的向心加速度相等8．如图所示，质量为m的物体P放在光滑的倾角为θ的直角劈上，同时用力F 向右推劈，使P与劈保持相对静止，在前进的水平位移为s的过程中，劈对P做的功为（）A．F•s B．C．mgcosθ•s D．mgtanθ•s9．甲、乙两物体分别在恒力F1、F2的作用下，沿同一直线运动，它们的动量随时间变化的关系如图所示，设甲在t1时间内所受的冲量为I1，乙在t2时间内所受的冲量为I2，则F1、F2，I1、I2的大小关系是（）A．F1＞F2，I1=I2 B．F1＜F2，I1＜I2C．F1＞F2，I1＞I2D．F1=F2，I1=I2 10．如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球．支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动．开始时OB位于竖直方向．放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（）A．B球向左摆动所能达到的最高位置应高于A球开始运动时的高度B．当支架从左向右回摆时，A球不能回到起始高度C．A球机械能减少量大于B球机械能增加量D．A球到达最低点时速度为零11．如图所示，虚线a、b、c代表电场中三个等势面，相邻等势面之间的电势差相等，U ab=U bc，实线为一带正电的粒子仅在电场力作用下通过该区域时的运动轨迹，P、Q是这条轨迹上的两点，据此可知下列说法中正确的是（）A．三个等势面中，a的电势最低B．带电粒子通过P点时的动能比通过Q点时的动能大C．带电粒子通过P点时的加速度比通过Q点时加速度大D．带电粒子在P点具有的电势能比在Q点具有的电势能小12．如图所示，一物体以初速度v0冲向光滑斜面AB，并能沿斜面升高h后恰好到达B端，下列说法中正确的是（）A．若把斜面从C点锯断或弯成如图中的AB′线所示的圆弧状，物体都不能升高h，因为机械能不守恒B．若把斜面弯成如图中的AB′线所示的圆弧状或从C点开始锯掉CB段，物体都不能升高h，但机械能仍守恒C．若把斜面从C点开始锯掉CB段，由机械能守恒定律知，物体冲出C点后仍能升高hD．若把斜面弯成如图中的AB′线所示的圆弧形，物体仍能沿AB′升高h13．如图所示，水平向右方向的匀强电场和垂直纸面向外的匀强磁场互相垂直，竖直的绝缘杆上套一带负电荷小环并置于场中．小环由静止开始下落的过程中，小环的加速度（）A．不断减小最后为零B．不断增大后来不变C．先减小后增大，最后不变D．先增大后减小，最后不变14．一个自感系数很大的线圈，用如图所示的电路测量它的直流电阻，闭合电键S1与S2待稳定后．读出电压表与电流表的示数．下列说法正确的是（）①线圈电阻的测量值等于电压表示数与电流表示数的比值②线圈电阻的真实值小于电压表示数与电流表示数的比值③在测量完毕拆卸电路时，应先断开S1，后断开S2④在测量完毕拆卸电路时，应先断开S2后断开S l．A．①③B．①④C．②③D．②④15．如图所示，两个相邻的有界匀强磁场区，方向相反，且垂直纸面，磁感应强度的大小均为B，以磁场区左边界为y轴建立坐标系，磁场区在y轴方向足够长，在x轴方向宽度均为a．矩形导线框ABCD 的CD边与y轴重合，AD边长为a．线框从图示位置水平向右匀速穿过两磁场区域，且线框平面始终保持与磁场垂直．以逆时针方向为电流的正方向，线框中感应电流i与线框移动距离x的关系图象正确的是图中的（以逆时针方向为电流的正方向）（）A． B． C．D．16．电磁轨道炮工作原理如图所示．待发射弹体可在轨道沿伸方向自由移动，并与轨道保持良好接触．电流I从一条轨道流入，通过导电弹体后从另一条轨道流回．轨道电流可在弹体附近形成垂直于轨道面的磁场（可视为匀强磁场），磁感应强度的大小与I成正比．通电的弹体在轨道上受到安培力的作用而高速射出．现欲使弹体的出射动量增加至原来的2倍，理论上可采用的办法是（）A．只将电流I增加至原来的2倍B．只将弹体质量增加至原来的2倍C．只将轨道长度L增加至原来的2倍D．将电流，和轨道长度己均增加至原来的2倍，其它量不变二、非选择题（共7小题，满分72分）17．根据单摆周期公式，可以通过实验测量当地的重力加速度．以下是实验过程中的一些做法，其中正确的有（）A．摆线要选择细些的、伸缩性小些的，并且尽可能长一些B．摆球尽量选择质量大些、体积小些的C．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆球相距平衡值置有较大的角度D．拉开摆球到某一位置释放，第一次经平衡位置时开始计时，第二次经平衡位置时停止计时，此时间间隔t即为单摆周期T18．在《验证力的平行四边形定则》的实验中，首先用两只弹簧秤分别钩住细绳套，互成角度地拉橡皮条，使结点伸长到某一位置O，此时必须记录的是（）A．O点的位置B．橡皮条固定端位置C．两只弹簧秤的读数两条细绳套的方向D．橡皮条的伸长长度19．如图甲、乙是两组同样的器材实物图，用来测量待测电阻R的阻值，每组器材中包括：电池，电键，变阻器，电压表，电流表，等测电阻R，若干导线．（1）如果待测电阻R的阻值比电压表的内阻不是小很多，但R的阻值比电流表的内阻大很多，试在图甲中连线使之成为测量电路；如果待测电阻R的阻值比电流表的内阻不是大很多，但R的阻值比电压表的内阻小很多，试在图乙中连线使之成为测量电路．（2）如果已知上述电压表的内阻R V和电流表的内阻R A，对图甲和图乙中连成的测量电路，分别写出计算待测电阻的公式（用测得的量和给出的电表内阻来表示）．20．如图所示AB为半径R=0.45m的四分之一光滑圆弧轨道，底端距水平地面的高度h=0.45m．一质量m=l．Okg的小滑块从圆弧轨道顶端A由静止释放，到达轨道底端B点时水平飞出．不计空气的阻力，g取lOm/s2求：（1）小滑块滑到圆弧轨道底端B点时的速度v；（2）小滑块滑到圆弧轨道底端B点时对轨道的压力F N；（3）小滑块落地点与B点的水平距离x．21．对于长度为l、横截面积为S，单位体积自由电子数为n的均匀导体，若在其两端加上电压U，就会在导体中有匀强电场产生，此时导体内移动的自由电子受匀强电场作用而加速．在运动过程中又与做热运动的阳离子碰撞而减速，这样边反复进行碰撞边向前移动，可以认为阻碍电子运动的阻力大小与电子移动的平均速度成正比，其比例系数为k．已知自由电子的电荷量为e，求：（1）电场力和碰撞的阻力相平衡时，电子在导体中运动的平均速率v；（2）自由电子在导体中以平均速率v运动时，该导体中的电流I；（3）该导体的电阻值R．22．如图所示，一质量M=1．Okg的沙摆，用轻绳悬于天花板上O点．另有一玩具枪能连续发射质量m=0.01kg．速度v=4．Om/s的小钢珠．现将沙摆拉离平衡位置，由高h=0.20m处无初速度释放，恰在沙摆向右摆到最低点时，玩具枪发射的第一颗小钢珠水平向左射入沙摆，二者在极短时间内达到共同速度．小钢珠射入沙摆的过程中，沙摆的质量保持不变，不计空气阻力，g取lOm/s2（1）求第一颗小钢珠射入沙摆前的瞬间，沙摆的速度大小v0；（2）求第一颗小钢珠射入沙摆后，沙摆和小钢珠的共同速度（3）从第二颗小钢球开始，沙摆向左运动到最低点时打入小钢球．若使沙摆被小钢珠射入后摆起的最大高度超过h，则射入沙摆的小钢球的颗数应满足什么条件．23．示波管、电视机显像管、电子显微镜中常用到一种叫静电透镜的元件，它可以把电子聚焦在中心轴上的一点F，静电透镜的名称由此而来．它的结构如图所示，K为平板电极，G为中央带圆孔的另一平行金属板，现分别将它们的电势控制在一定数值．图中的数据的单位为V，其中K板的电势为120V．根据由实验测得的数据，在图中画出了一些等势面，如图中虚线所示．从图中可知G板圆孔附近的等势面不再是平面，而是向圆孔的右侧凸出来的曲面，所以圆孔附近右侧的电场不再是匀强电场．（1）题中已画出一条水平向右的电场线，请你在原电场线上下画出对称的一对电场线；（2）分析静电透镜为何对自K电极出发的电子束有会聚作用；（3）分析一个电子自K电极以一定的速度出发，运动到F点（电势为30.1V）的过程中，电子的加速度如何变化并求出电场力做了多少功．（设电子电量e=1.6×10﹣19C）2015-2016学年北京市顺义区高三（上）期末物理试卷参考答案与试题解析一、选择题（共16小题，每小题3分，满分48分）1．一列横波沿水平方向传播，某一时刻的波形如图所示，则图中a、b、c、d四点在此时刻具有相同运动方向的是（）A．a和c B．a和d C．b和c D．b和d【考点】横波的图象；波长、频率和波速的关系．【分析】根据波的传播方向，通过上下坡法得出质点的振动方向，从而确定哪些点运动方向相同．【解答】解：若波向右传播，根据上下坡法知，a、d质点振动方向向上，b、c 质点振动方向向下，故B、C正确，A、D错误．故选：BC．2．地球上站立着两位相距非常远的观察者，发现自己的正上方有一颗人造地球卫星相对自己静止不动，则这两位观察者及两颗卫星到地球中心的距离是（）A．一个人在南极，一个人在北极，两卫星到地球中心的距离一定相等B．两人都在赤道上，两卫星到地球中心的距离一定相等C．一个人在南极，一个人在北极，两卫星到地球中心的距离可以不相等D．两人都在赤道上，两卫星到地球中心的距离可以不相等【考点】同步卫星．【分析】地球同步卫星即地球同步轨道卫星，又称对地静止卫星，是运行在地球同步轨道上的人造卫星，星距离地球的高度约为36000 km，卫星的运行方向与地球自转方向相同、运行轨道为位于地球赤道平面上圆形轨道、运行周期与地球自转一周的时间相等，即23时56分4秒，卫星在轨道上的绕行速度约为3.1公里/秒，其运行角速度等于地球自转的角速度．【解答】解：发现自己正上方有一颗人造地球卫星相对自己静止不动，说明此卫星为地球同步卫星，运行轨道为位于地球赤道平面上圆形轨道，距离地球的高度约为36000 km，所以两个人都在赤道上，两卫星到地球中心的距离一定相等．故ACD错误，B正确故选B．3．如图所示，是描述对给定的电容器充电时电荷量Q、电压U、电容C之间相互关系的图象，其中正确的是（）A．B．C．D．【考点】电容．【分析】电容器的电容由本身的性质决定，与Q和U无关，根据Q=CU，知Q 与U成正比．【解答】解：是电容的定义式，电容器电容的大小与电容的带电量Q以及电容器两极板之间的电压无关，电容器电容的决定式为：，只要电容器不变其电容就不发生变化，故A错误，BD正确；根据可有：Q=CU，由于电容器不变，因此电量Q和电压U成正比，故C正确；故选BCD．4．如图所示，质量为m的金属环用线悬挂起来，金属环有一半处于水平且与环面垂直的匀强磁场中，从某时刻开始，磁感应强度均匀减小，则在磁感应强度均匀减小的过程中，关于线拉力大小的下列说法中正确的是（）A．大于环重力mg，并逐渐减小B．始终等于环重力mgC．小于环重力mg，并保持恒定D．大于环重力mg，并保持恒定【考点】法拉第电磁感应定律；楞次定律．【分析】磁感应强度均匀减小，穿过回路的磁通量均匀减小，回路中产生恒定的电流，由左手定则可确定安培力的方向，再根据安培力F=BIL，分析安培力的变化，由平衡条件即可求解．【解答】解：磁感应强度均匀减小，穿过回路的磁通量均匀减小，根据法拉第电磁感应定律得知，回路中产生恒定的电动势，感应电流也恒定不变．由楞次定律可知，感应电流方向：顺时针，再由左手定则可得，安培力的合力方向：竖直向下．ab棒所受的安培力F=BIL，可知安培力F均匀减小，且方向向下，金属环ab 始终保持静止，则拉力大于重力，由于磁感应强度均匀减小．所以拉力的大小也逐渐减小，故A正确，BCD均错误．故选：A．5．如图所示，质量分别为m和M的两物块紧挨着放在水平地面上，且M＞m．当用水平恒力F向右的推物块m时，两物块能在水平面上加速向右滑行，两物块的加速度大小为a，两物块间的作用力大小为T．如果用同样大小的水平恒力F 向左推木块M时，加速度大小为a′，物块间的作用力大小为T′，以下判断正确的是（）A．a′=a，T′＞T B．a′＜a，T′=T C．a′＞a，T′=T D．a′=a，T′＜T【考点】牛顿第二定律；物体的弹性和弹力．【分析】A、B具有相同的加速度可以视为整体，根据牛顿第二定律分别求出水平面光滑和粗糙时的加速度，隔离对B分析，求出弹力的大小，从而进行比较．【解答】解：如果水平面光滑整体根据牛顿第二定律可得：a=a′=；向右运动时对M分析：T=Ma=，向左运动时对m分析：T′=ma′=，由于m＜M，则T′＜T，D正确；如果接触面粗糙时，设动摩擦因数为μ，整体分析可得：F﹣μ（m+M）g=（m+M）a解得：，同理可得a′=a；向右运动时对M分析：T﹣μMg=Ma，解得：T=，向左运动时对m分析：T′﹣μmg=ma′，解得：T′=，由于m＜M，则T′＜T，D正确；故选：D．6．一物体悬挂在气球下面，与气球一起沿竖直方向匀速上升，某时刻该物体脱落，并从此时开始计时．已知气球和物体所受空气阻力大小不变．在下图中①代表气球运动的v﹣t图线，②代表物体运动的v﹣t图线．以下四个v﹣t图象中最接近真实情况的是（）A．B．C．D．【考点】匀变速直线运动的图像；匀变速直线运动的速度与时间的关系．【分析】刚开始，物体和气球一起匀速上升，受力平衡，某时刻该物体脱落后，分别对气球和物体受力分析，根据牛顿第二定律列式求出加速度，分析物体的运动情况，从而选择图象即可．【解答】解：设气球的质量为M，物体的质量为m，气球受到的空气阻力为f1，物体受到的空气阻力为f2，一起匀速运动的速度为v，刚开始，物体和气球一起匀速上升，根据平衡条件有：F﹣Mg﹣mg﹣f1﹣f2=0某时刻该物体脱落后，对气球受力分析，根据牛顿第二定律得：＞0，向上做匀加速直线运动，且初速度不为零，所以气球运动的v ﹣t图线是一条倾斜的直线且在v轴上有截距，对物体，脱落后继续向上做匀减速直线运动，根据牛顿第二定律得：加速度，速度减为零后，反向加速，加速度，则a2＞a3，故C正确．故选：C7．如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑，通过轨道最低点时（）A．小球对轨道的压力相同B．小球对两轨道的压力不同C．此时小球的速度相等D．此时小球的向心加速度相等【考点】向心力；机械能守恒定律．【分析】小球从与球心在同一水平高度的A、B两点由静止开始自由下滑过程中，受到重力和支持力作用，只有重力做功，机械能守恒，由机械能守恒定律可求出小球到最低点的速度，然后由向心加速度公式求向心加速度，由牛顿第二定律求出支持力，进而来比较向心加速度大小和压力大小．【解答】解：设半圆轨道的半径为r，小球到最低点的速度为v，由机械能守恒定律得：mgr=，得：v=，可见，小球到达最低点的速度不等．小球的向心加速度为：a n=，联立两式解得：a n=2g，与半径无关，因此此时小球的向心加速度相等，故C错误，D正确．在最低点，由牛顿第二定律得：F N﹣mg=m，联立解得：F N=3mg，即得小球对轨道的压力为3mg，也与半径无关，所以小球对轨道的压力相同．故A正确，B 错误．故选：AD8．如图所示，质量为m的物体P放在光滑的倾角为θ的直角劈上，同时用力F向右推劈，使P与劈保持相对静止，在前进的水平位移为s的过程中，劈对P做的功为（）A．F•s B．C．mgcosθ•s D．mgtanθ•s【考点】功的计算．【分析】m与楔形物体相对静止，二者必定都向右加速运动．即m的合外力方向水平向右，画出m的受力图，求出楔形物体对小物体的作用力，根据功的公式即可求解．【解答】解：m与楔形物体相对静止，二者必定都向右加速运动．即m的合外力方向水平向右，画出m的受力图，根据几何关系得：N=所以支持力做的功为：W=Ns•sinθ=mgtanθ•s故选：D9．甲、乙两物体分别在恒力F1、F2的作用下，沿同一直线运动，它们的动量随时间变化的关系如图所示，设甲在t1时间内所受的冲量为I1，乙在t2时间内所受的冲量为I2，则F1、F2，I1、I2的大小关系是（）A．F1＞F2，I1=I2 B．F1＜F2，I1＜I2C．F1＞F2，I1＞I2D．F1=F2，I1=I2【考点】动量定理．【分析】根据图象，结合初末状态的动量比较动量变化量的大小，从而结合动量定理得出冲量的大小关系以及力的大小关系．【解答】解：由图象可知，甲乙两物体动量变化量的大小相等，根据动量定理知，冲量的大小相等，即I1=I2，根据I=Ft知，冲量的大小相等，作用时间长的力较小，可知F1＞F2．故A正确，B、C、D错误．故选：A．10．如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球．支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动．开始时OB位于竖直方向．放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（）A．B球向左摆动所能达到的最高位置应高于A球开始运动时的高度B．当支架从左向右回摆时，A球不能回到起始高度C．A球机械能减少量大于B球机械能增加量D．A球到达最低点时速度为零【考点】共点力平衡的条件及其应用；物体的弹性和弹力．【分析】在不计任何阻力的情况下，整个过程中A、B组成的系统机械能守恒，据此列式判断即得．【解答】解：因为在整个过程中系统机械能守恒，故有：A、因为B球质量小于A球，故B上升高度h时增加的势能小于A球减少的势能，故当B和A球等高时，仍具有一定的速度，即B球继续升高，故A正确；B、因为不计一切阻力，系统机械能守恒，故当支架从左到右加摆时，A球一定能回到起始高度，故B错误；C、因为系统机械能守恒，即A、B两球的机械能总量保持不变，故A球机械能的减少量等于B球机械能的增加量，故C错误；D、若当A到达最低点时速度为0，则A减少的重力势能等于B增加的重力势能，只有A与B的质量相等时才会这样．又因A、B质量不等，故D错误．故选：A11．如图所示，虚线a、b、c代表电场中三个等势面，相邻等势面之间的电势差相等，U ab=U bc，实线为一带正电的粒子仅在电场力作用下通过该区域时的运动轨迹，P、Q是这条轨迹上的两点，据此可知下列说法中正确的是（）A．三个等势面中，a的电势最低B．带电粒子通过P点时的动能比通过Q点时的动能大C．带电粒子通过P点时的加速度比通过Q点时加速度大D．带电粒子在P点具有的电势能比在Q点具有的电势能小【考点】电势差与电场强度的关系；电势．【分析】带电粒子只受电场力作用，根据运动轨迹可知电场力指向运动轨迹的内侧即斜向右下方，由于粒子带正电，因此电场线方向也指向右下方；电势能变化可以通过电场力做功情况判断；电场线和等势线垂直，且等势线密的地方电场线密，电场强度大．【解答】解：A、带电粒子所受电场力指向轨迹弯曲的内侧，电场线与等势面垂直，且由于带电粒子带正电，因此电场线指向右下方，根据沿电场线电势降低，可知a等势线的电势最高，c等势线的电势最低，故A错误；BD、根据带电粒子受力情况可知，若粒子从P到Q过程，电场力做正功，动能增大，电势能减小，故带电粒子通过P点时的动能比通过Q点时的动能小，在P 点具有的电势能比在Q点具有的电势能大，故BD错误；C、等差等势线密的地方电场线密场强大，故P点电场强度较大，电场力较大，根据牛顿第二定律，加速度也较大，故C正确．故选：C12．如图所示，一物体以初速度v0冲向光滑斜面AB，并能沿斜面升高h后恰好到达B端，下列说法中正确的是（）A．若把斜面从C点锯断或弯成如图中的AB′线所示的圆弧状，物体都不能升高h，因为机械能不守恒B．若把斜面弯成如图中的AB′线所示的圆弧状或从C点开始锯掉CB段，物体都不能升高h，但机械能仍守恒C．若把斜面从C点开始锯掉CB段，由机械能守恒定律知，物体冲出C点后仍能升高hD．若把斜面弯成如图中的AB′线所示的圆弧形，物体仍能沿AB′升高h【考点】机械能守恒定律．【分析】物体上升过程中只有重力做功，机械能守恒；斜抛运动运动最高点，速度不为零；AD轨道最高点，合力充当向心力，速度也不为零．【解答】解：1、若把斜面从C点锯断，物体冲过C点后做斜抛运动，由于物体机械能守恒，同时斜抛运动运动到最高点，速度不为零，故不能到达h高处；2、若把斜面弯成圆弧形AB′，如果能到圆弧最高点，即h处，由于合力充当向心力，速度不为零，故会得到机械能增加，矛盾，所以物体不能升高h．故B正确，ACD错误；故选：B13．如图所示，水平向右方向的匀强电场和垂直纸面向外的匀强磁场互相垂直，。

北京市部分区2016届高三上学期期中期末考试数学文分类汇编：数列含答案

北京市部分区2016届高三上学期期末考试数学理试题分类汇编数列一、选择题1、（东城区2016届高三上学期期中）等差数列{}na 的前n 项和为nS ,已知3103,10aa ==,则S 7的值是A 、30B 、29C 、28D 、272、(海淀区2016届高三上学期期末)已知数列{}na 是公比为2的等比数列，且满足432aa a-=，则4a 的值为A 。

2B 。

4C 。

8D 。

16 3、（海淀区2016届高三上学期期中）数列{｝的前项和,若－2－1(≥2），且3，则1的值为A ．0B ．1C ．3D ．5参考答案1、C2、C3、A二、填空题1、（朝阳区2016届高三上学期期中)设等差数列{}na 的前n 项和为nS ,若3612aa +=，48S =,则9a 的值是．2、（东城区2016届高三上学期期中)在数列{}na 中，－3、（丰台区2016届高三上学期期末)设等差数列{}na 的前n 项和为nS ，若9=72S ,则249++a a a =______ .4、(海淀区2016届高三上学期期中）若等差数列{}na 满足14a =-,39108a a a a +=-,则n a = ______。

5、（海淀区2016届高三上学期期中)对于数列{}na ，若m ∀，()n Nm n *∈≠，均有()为常数mnaa t t m n-≥-,则称数列{}n a 具有性质()P t 。

(i ）若数列{}na 的通项公式为2nan =，且具有性质()P t ,则t 的最大值为____；（ii)若数列{}na 的通项公式为2na an n=-，且具有性质(7)P ，则实数a 的取值范围是____.参考答案1、152、123、244、5n -5、 3；[12,)+∞三、解答题1、（昌平区2016届高三上学期期末)在等差数列{}na 中,241, 5.aa（I)求数列{}na 的通项公式；（II)设数列nn n c a b =+，且数列{}n c 是等比数列.若123,b b 求数列{}n b 的前n 项和nS .2、（朝阳区2016届高三上学期期末）已知数列{}na 是等差数列,数列{}nb 是各项均为正数的等比数列,且113ab ==,2214a b +=，3453a a a b ++=．(Ⅰ）求数列{}na 和{}nb 的通项公式；（Ⅱ）设*,nn n ca b n =+∈N ,求数列{}n c 的前n 项和．3、(朝阳区2016届高三上学期期中）设等差数列{}na 的前n 项和为n S ,n *∈N ，公差30,15,d S ≠=已知1341,,a a a 成等比数列.（Ⅰ）求数列{}na 的通项公式；（Ⅱ)设2nnba =，求数列{}nb 的前n 项和nT 。

2016年秋高三(上)期末测试卷(理科数学)试题和参考答案

2016年秋高三(上)期末测试卷(理科数学)试题和参考答案2016年秋高三(上)期末测试卷理科数学一、选择题1.已知$a+2i$，其中$i$是虚数单位，则$ab=b+i$，其中$a$，$b$是实数。

(C)2.已知某品种的幼苗每株成活率为$p$，则栽种3株这种幼苗恰好成活2株的概率为$p^2(1-p)$。

(D)3.已知集合$A=\{1,2,3,4\}$，$B=\{xy=2x,y\in A\}$，则$A\cap B=\{2\}$。

(A)4.命题$p$：甲的数学成绩不低于100分，命题$q$：乙的数学成绩低于100分，则$p\lor(\neg q)$表示甲、乙两人至少有一人数学成绩不低于100分。

(D)5.在平面直角坐标系$xOy$中，不等式组$\begin{cases}-1\leq x\leq 3\\ x+y-1\geq x-y-1\end{cases}$表示的平面区域的面积为$12$。

(C)6.我国古代数学算经十书之一的《九章算术》有一衰分问题：今有北乡八千一百人，西乡七千四百八十八人，南乡六千九百一十二人，凡三乡，发役三百人，则北乡遣$120$人。

(D)7.执行如图所示的程序框图，若分别输入1，2，3，则输出的值得集合为$\{1,3\}$。

(D)8.设曲线$x=2y-y^2$上的点到直线$x-y-2=0$的距离的最大值为$a$，最小值为$b$，则$a-b$的值为$2$。

(B)9.函数$y=\sin x-\frac{1}{2}$的图像大致是$\begin{cases}y=\sin x-\frac{1}{2},-\pi\leq x\leq \pi\\ y=-\frac{1}{2}\end{cases}$。

(A)10.已知$\triangle ABC$的外接圆半径为$2$，$D$为该圆上一点，且$AB+AC=AD$，则$\triangle ABC$的面积的最大值为$4\sqrt{3}$。

(D)A）设定义在R上的函数f(x)的导函数为f'(x)，且满足f(2-x)=f(x)，x1+x22>2，x1<x2，则（）B）f(x1)=f(x2)C）f(x1)>f(x2)D）f(x1)与f(x2)的大小不能确定答案：（C）改写后：设在定义在实数集上的函数f(x)的导数为f'(x)，且满足f(2-x)=f(x)，当x1+x22>2，x1f(x2)。