土木工程测量1绪论
合集下载
土木工程测量(精)
第一章：绪论
一、 土木工程测量学的任务：测定、测设、监测 二、 地面点位的确定：
确定地面点的位置的 三要素：水平角、水平距离、高差
1、 水准面（人为规定的水平面）有无数个；大地水准面（海平面的平均高度）只有一个
2、 大地水准面和铅垂线是测量专业所依据的基准面和基准线
3、 常用的坐标系有：
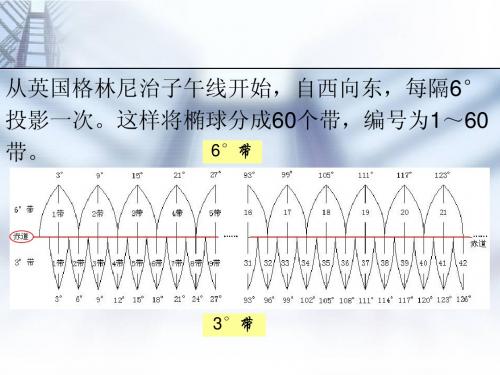
大地坐标系（1980西安坐标系或1980国家坐标系）； 高斯平面投影直角坐标系 6°带：中央子午线经度为 3°带：中央子午线经度为 独立平面直角坐标系 4、 高程系统（目前采用 绝对高程（海拔）：地面点到大地水准面的铅锤距离；
相对高程：到任意水准面的铅锤距离 水准面以上的高程为正，反之为负
5、 半径小于10km 的区域内（普通测量），地球曲率对水平距离的影响可以忽略，用水平面 代替水准面 三、 测量工作的基本原则：
测量工作的组织原则：
7C
第二章：水准仪及水准测量
一、高程测量分为 水准测量、三角高程测量和气压高程测量 水准测量的基本原理： 高差=后视读数-前视读数（
h
AB = a - b ）
a?b 时高差为正，B 点比A 点高，反之成立
1水准仪的基本构造 （三部分）望远镜、水准器、基座 2、水准测量的一般方法：
3、 水准尺和尺垫
尺垫的作用：防止水准尺的位置和高度发生变化而影响水准测量的精度 尺垫的位置：在起点和终点不能放尺垫而中间测点（
转点）必须要放
4、 水准点分为永久性和临时性（BM:已知高程的永久水准点） 二、水准路线：单一水准路线和水准网
1、 单一水准路线： 附合水准路线、闭合水准路线、支水准路线
测绘讲义土木工程测量-第一章绪论
1.3.3 高斯平面直角坐标系
3°带 是在6°带基础上划分的，其中央子午线在奇数带时与 6°带中央子午线重合，每隔3°为一带，共120带，各带中央子午 线经度为：
各带中央子午线经度(L03)按下式计算：
L30 3n'
(1-5)
已知某点大地经度L，可按下式计算所属的带号：
n' L 1.5 (的整数商)+1(有余数时) 3
xx’’pp==44442299775577.0.07755mm y在y’’p2p==0-带-5588中2266高99..5斯5993直3mm角坐 标为： xxp=p=44442299775577.0.07755mm 工y程ypp=测=22量004学44411773300.4.40077mm
§1 绪1.3 论 测量常用的坐标系统
要将球面上的大地坐标按一定数学法则归算到平面上，即采用 地图投影的理论绘制地形图，才能用于规划建设。
地图投影有等角投影、等面积投影和任意投影三种。
等角投影又称正形投影，它保证在椭球体面上的微分图形投影 到平面后将保持相似。这是地形图的基本要求。正投影有两个基本 条件：
①保角条件，即投影后角度大小不变。 ②长度变形固定性，即长度投影后会变形，但在一点上各个方 向的微分线段变形比m是个常数k:
②投影后赤道是一 直线，并与中央子午线 正交。
③离开赤道的纬线 是工弧程线测，量凸学向赤道。
土木工程测量_第三版_覃辉_课后答案(1-4章)
hAB = a − b ， H i = H A + a ， H B = H A + hAB = H i − b 。
[题 2-7] 与普通水准仪比较，精密水准仪有何特点？ [解]：精密水准仪的特点是：① 望远镜的放大倍数大、分辨率高；② 管水准器格式小，τ=10"，精平 精度高；③ 望远镜物镜的有效孔径大，亮度好；④ 望远镜外表材料采用受温度变化小的铟瓦合金钢，以 减小环境温度变化的影响；⑤ 采用平板玻璃测微器读数，读数误差小；⑥ 配备铟瓦水准尺。 [题 2-8] 用两次变动仪器高法观测一条水准路线，其观测成果标注于图 2-52 中，图中视线上方的数字 为第二次仪器高的读数，试计算高差 hAB。
参考椭球面——为了解决投影计算问题，通常选择一个与大地水准面非常接近的、能用数学方程表示
的椭球面作为投影的基准面，这个椭球面是由长半轴为 a 、短半轴为 b 的椭圆 NESW 绕其短轴 NS 旋转而
成的旋转椭球面，旋转椭球又称为参考椭球，其表面称为参考椭球面。
法线——垂直于参考椭球面的直线。
[题 1−3] 绝对高程和相对高程的基准面是什么？
一 3°投影带中的带号范围。
[解]：在统一 6°投影带的带号范围，计算公式 N = Int( L + 3 + 0.5) 6
N1
=
Int(109.65 6
+
[题 2-7] 与普通水准仪比较，精密水准仪有何特点？ [解]：精密水准仪的特点是：① 望远镜的放大倍数大、分辨率高；② 管水准器格式小，τ=10"，精平 精度高；③ 望远镜物镜的有效孔径大，亮度好；④ 望远镜外表材料采用受温度变化小的铟瓦合金钢，以 减小环境温度变化的影响；⑤ 采用平板玻璃测微器读数，读数误差小；⑥ 配备铟瓦水准尺。 [题 2-8] 用两次变动仪器高法观测一条水准路线，其观测成果标注于图 2-52 中，图中视线上方的数字 为第二次仪器高的读数，试计算高差 hAB。
参考椭球面——为了解决投影计算问题，通常选择一个与大地水准面非常接近的、能用数学方程表示
的椭球面作为投影的基准面，这个椭球面是由长半轴为 a 、短半轴为 b 的椭圆 NESW 绕其短轴 NS 旋转而
成的旋转椭球面，旋转椭球又称为参考椭球，其表面称为参考椭球面。
法线——垂直于参考椭球面的直线。
[题 1−3] 绝对高程和相对高程的基准面是什么？
一 3°投影带中的带号范围。
[解]：在统一 6°投影带的带号范围，计算公式 N = Int( L + 3 + 0.5) 6
N1
=
Int(109.65 6
+
土木工程测量第1章绪论(莫PPT-1)
∴该点位于六度带的第20带。(y坐标中去 掉十万位及其以后的所有数字,剩下的数字即 为带号) ⑵∵我国陆地国土主要位于北半球，x坐 标恒为“+”（正） ∴该点位于赤道的北面 该点的纵坐标(即x的坐标) =4271817.800m
⑶∵该点的y=20317897.338m
∴去掉带号20,再减去500km,即点的横坐 标Y值： ∴Y=317897.338－500000
（三）、绝对高程----是以大地水准面为高程基 准面，即地面任意一点沿铅垂线到大地水准面的 距离，也称为海拔 高（正高），用H表示，一地 H A、H B 面点对应一个绝对高程，如PPT26图所示： 海水面由于受潮汐、风浪的影响，是个动态曲 面。所谓静止海水面是不存在的，常用平均海水面 代替，即在海边设立验潮站，进行长期潮汐观测， 取海水面平均高度作为高程零点，即绝对高程为 零。
黄海高程系
国家高程基准
水准原点
建国后，我国采用青岛验潮站长期观 测资料求得黄海平均海水面作为我国高程基 准面，称为“1956年黄海高程系”。在青岛 市观象山建立水准原点，其高程为72.289m。
水准原点
后又将1953年到1979年验潮资料进行归算，推 算青岛国家水准原点高程为72.260m，（海水上 涨）称为“1985年国家高程基准”。1987年我国 开始启用这个基准。 水准原点作用：作为高程的起始点/起算数据。
土木工程测量课件绪论
高斯投影带划分
6º带与3º带中央子午线之间的关系如图:
3º带的中央子午线与6º带中央子午线及分带 子午线重合，减少了换带计算。 工程测量采用3 º带，特殊工程可采用1.5 º带 或任意带。
按照6º带划分的规定，第1带中央子午线的经 度为3º，其余各带中央子午线经度与带号的关系 是： L。=6ºN－3º （N为6º带的带号）
二、测量学科的分支
• 大地测量学
研究和测定地球的形状、大小、重力场 和地面点几何位置及其变化的理论和技术 的学科。地球的形状大小以大地水准面为 代表。大地点的定位，用经纬度或空间直 角坐标，定位方法有几何法大地测量、物 理法大地测量和近代的卫星法大地测量。
世界屋脊 - 珠穆朗玛峰的高程测定
摄影测量与遥感学
第一章 绪论
§1.1 测量学的研究对象及其作用 §1.2 地面点位的确定 §1.3 用水平面代替水准面的限度 §1.4 测量工作概述
一、测量学的概念
测量学是研究地球的形状、大小以及地表(包括地 面上各种物体）的几何形状及其空间位置的科学。
测量工作的基本任务： 确定地面点在规定坐标系中的
坐标值（X，Y，Z）。
导航、惯性组合导航、天文测量、水 声定位系统、水下摄影量测等。
地图制图学
研究模拟地图和数字地图的设计、 编绘、复制的理论和方法的科学。主 要内容：
地图投影 地图编绘 地图整饰 地图出版
土木工程测量笔记
土木工程测量
第一章绪论
1．测量学研究的对象是什么？
地球及其表面的各种形态。
2．测量学依据任务不同如何分类？
①大地测量学②摄影测量学③工程测量学④海洋测量学⑤地图制图学
3．大地水准面的概念及有关说明？
人们设想把平均静止的海水面向陆地延伸而形成的封闭水面称为大地水准面。
说明：①大地水准面所包围的球体可以代表整个地球的形状。
②大地水准面是一个略有起伏的不规则曲面。
③大地水准面处处与铅垂线方向垂直。
④大地水准面是测量学的基准面。铅垂线是测量学的基准线。
（注：铅垂线并非处处指向球心。）
4．确定地面点位有哪两个要素？
①点到大地水准面的铅垂距离（绝对高程）
②点在大地水准面上的投影位置
5．绝对高程的概念？
地面点到大地水准面的垂线长。
6．地面点的平面位置有哪些表达方法？
①地理坐标②高斯坐标
7．高斯平面直角坐标系的建立过程？
①分带：在地球表面沿着赤道进行分带，每隔6°或3°分带，共分60带或120带。
②假想用一个大圆柱去套地球。（大圆柱要与中央子午线相切，若有60带则套60次）注：中央子午线指每一带最中间的那根子午线。
③投影
④展开
8．1985年国家高程基准的概念？
以用青岛验潮站1956~1979年观测的潮位成果进行计算，引测出青岛水准原点的高程为72.260m，由此建立的高程系统称为“1985国家高程基准”。
9．用水平面代替水准面对水平距离和高程有何影响？
在半径小于10km的区域内，地球曲率对水平距离的影响可以忽略不计。
对高程测量来说，不能忽视地球曲率对高程的影响。
10．测量有哪些原则？
①测量一定是由高级到低级，先控制后碎部，由整体到局部。
土木工程测量：第1章 绪论
1.5.3碎部测量(detail survey) 在控制测量的基础上就可以进行碎部测量。碎 部测量就是以控制点为依据，测定控制点至碎 部点（地形的特征点）之间的水平距离、高差 及其相对于某一已知方向的角度来确定碎部点 的位置，应用碎部测量的方法，在测区内测定 一定数量的碎部点位置后，按一定的比例尺将 这些碎部点标绘在图纸上，绘制成图。
“1985国家高程基准”的国家水准基点高程为： H=72.260 m
1.4 水平面代替水准面的影响
1.4.1 水平面代替水准面对距离的影响
D=Rθ
D′=R tanθ
△D=D′-D=R(tanθθ)=D3/3R2
△D/D=(D/R)2/3
结论：影响较小，通常在半径 10km 测量范围内，可以用水 平面代替大地水准面。
→地理信息管理GIS 人造卫星的发明 →遥感RS
→全球定位系统GPS
全站仪ETS ( Electronic Total Station )
(4)目前:测量界最先进的理论和技术是3S，即:
全球卫星定位系统 GPS ( Global Positioning System ) 地理信息系统 GIS ( Geographic Information System ) 遥感 RS ( Remote Sensing )
(2)测设
测设（放样）是指用一定的测量方法，按要求 的精度，把设计图纸上规划设计好的建（构）筑 物的平面位置和高程标定在实地上，作为施工的 依据。（图纸、数据→地面点位）
土木工程概论 第1章 绪论1
秦皇陵 兵马俑
（ 公元前 200年左右 )
阵势宏伟、规模庞大，7000多军俑、车马阵列 有序、军容威严，被称为世界第八大奇迹
中国古代优秀建筑杰作 —— 水利工程
京杭(北京—杭州)大运河 (公元600年隋朝时开凿修建)
全长2500 公里 世界历史上最长的 运河 至今仍是江浙段重 要的水运通道
中国古代优秀建筑杰作--- 砖石结构
防灾减灾与防护防御工程等
按国际惯例也包括 运河、水渠、水库、堤坝、灌渠等水利工程
土 木 工 程 范 围 —— 非常广泛
基本建设（Caipisal Construction)：
二十世纪五十年代我国第一个五年计划期间、对重点建设 的一汽、一拖等数百重点基础性建设项目给出
统指：工厂、矿井、铁道、公路、桥梁、农田水利、
活 离
“行”则需要建造铁道、公路、机场、码头等交通土木建 筑工程，直接有关
不
开 “食”需打井取水，筑渠灌溉，建水库蓄水，建粮食加工
衣
厂，粮食储仓等，间接有关
、
食
“衣”的纺纱、 织布、制衣要在工厂内进行，间接有关
、
住
各种工业生产要建厂房
、 航天要建发射塔架和航天基地 行
土木工程对人类生存、国民经济、社会文明举足轻重
形成全国交通网：
以咸阳为中心 通往全国各郡县 的驰道 主要干道宽59步
土木测量学第1章 绪论1解剖
但大地水准面是野外测量统一的基准面。与其垂直的铅垂线则 是野外测量的基准线。
大地水准面所包围的形体—大地体，则是多年来大地测量工作 者研究的对象，认为它能代表地球的实际形状。
3）旋转椭球（地球椭球）
大地体接近于一个具有极小扁率的旋转椭球（由椭圆NWSE绕 其短轴NS旋转而成）。椭球面是一个规则的数学曲面。一般用长 半径a和扁率α(或长、短半径a、b)两个椭球体参数表示椭球的形 状和大小。
各国为处理其大地测量成果，往往根据本国及 其他国家所进行的天文、大地、重力测量资料， 采用适合本国领土范围的椭球参数并将其定位。 我国在解放前采用海福特椭球，解放后曾 一度采 用克拉索夫斯基椭球。我国目前采用的两种椭球 （ 1 ） 1975 年 “ 国 际 大 地 测 量 与 地 球 物 理 联 合 会” 推荐的 “1975国际椭球” ，其大地原点位
（3）高程系统
1） 绝对高程
地面点到大地水准面的铅垂距离，称为该点的绝对高程 (elevation)或海拔。用“H”表示。高程值有正有负，在基准面 以上的点，其高程值为正，反之为负。两点间的高程之差，称为 高差(difference in elevation)。 用“h”表示。hAB=HB-HA。
测设(也称放样)：就是把图上设计好的建筑物和构筑物的 位置标定到实地上去，以便于施工。
地面
测定 测设
图纸
1.1测量学的任务及其在工程中的作用
大地水准面所包围的形体—大地体，则是多年来大地测量工作 者研究的对象，认为它能代表地球的实际形状。
3）旋转椭球（地球椭球）
大地体接近于一个具有极小扁率的旋转椭球（由椭圆NWSE绕 其短轴NS旋转而成）。椭球面是一个规则的数学曲面。一般用长 半径a和扁率α(或长、短半径a、b)两个椭球体参数表示椭球的形 状和大小。
各国为处理其大地测量成果，往往根据本国及 其他国家所进行的天文、大地、重力测量资料， 采用适合本国领土范围的椭球参数并将其定位。 我国在解放前采用海福特椭球，解放后曾 一度采 用克拉索夫斯基椭球。我国目前采用的两种椭球 （ 1 ） 1975 年 “ 国 际 大 地 测 量 与 地 球 物 理 联 合 会” 推荐的 “1975国际椭球” ，其大地原点位
（3）高程系统
1） 绝对高程
地面点到大地水准面的铅垂距离，称为该点的绝对高程 (elevation)或海拔。用“H”表示。高程值有正有负，在基准面 以上的点，其高程值为正，反之为负。两点间的高程之差，称为 高差(difference in elevation)。 用“h”表示。hAB=HB-HA。
测设(也称放样)：就是把图上设计好的建筑物和构筑物的 位置标定到实地上去，以便于施工。
地面
测定 测设
图纸
1.1测量学的任务及其在工程中的作用
《土木工程测量》第1章教案1
– 1) 高斯平面坐标系
– 高斯投影是高斯在1820~1830年间，为解决德国汉诺威地区大地测量投影问题而 提出的一种投影方法。1912年起，德国学者克吕格(Kruger)将高斯投影公式加以 整理和扩充并推导出了实用计算公式。 – 高斯投影是将地球按经线划分成带，称为投影带，投影带是从首子午线起，每 隔经度6°划分为一带(称为统一6°带)，自西向东将整个地球划分为60个带。带 号从首子午线开始，用阿拉伯数字表示。
同济大学出版社 制作 覃辉
– 《城市测量规范》规定，当长度变形值不大于2.5cm/km时，应采用高斯投影统 一3°带的平面直角坐标系统； – 当长度变形值大于2.5cm/km时，可依次采用①投影于抵偿高程面上的高斯投影 统一3°带的平面坐标系；②高斯投影任意带的平面坐标系，投影面可用黄海平 均海水面或城市平均高程面；③假定平面直角坐标系。 – 所谓抵偿高程面，就是当城市所处的统一3°带平面坐标系的高斯投影距离变形 值大于2.5cm/km时，通过适当选择距离投影的高程面，使计算出的K值仍能满足 小于2.5cm/km的要求。其高程Hm称为抵偿高程面。 – §1.3.2确定点的高程系 – 地面点沿铅垂线到大地水准面的距离称为该点的绝对高程或海拔，简称高程 (height)，通常用加点名作下标表示,如HA、HB。
同济大学出版社 制作 覃辉
测量在国民经济建设中的应用： (1) 城市规划、给水排水、煤气管道、工业厂房和高层建筑建设的测量工作
工程测量第一章绪论
近代
17-20世纪初
现代
20世纪至今
将来
2011年3月2日星期三
数字地球
天津城市建设学院土 木 工 程 系
2011年3月2日星期三
天津城市建设学院土 木 工 程 系
2011年3月2日星期三
天津城市建设学院土 木 工 程 系
三维激光扫描系统
2011年3月2日星期三
天津城市建设学院土 木 工 程 系
天津城市建设学院土 木 工 程 系
一、地球形状和大小
1.地球自然表面 地球是一个表面起伏较大的椭球 地球表面最高峰： 8844.43m 海洋底部最深处: 11022.00m 地球表面最大高差近20km 地球又是一个近似光滑的水球 大陆面积: 占29% 海洋面积: 占71 %
2011年3月2日星期三
•1956黄海高程系：H。=72.289m •1985国家高程基准：H。=72.260m，相差29mm
笛卡尔坐标系
天津城市建设学院土 木 工 程 系
（4）假定平面直角坐标系 《城市测量规范》（CJJ8-99）规定， 面积小于25km2的城镇，可不经投影采用假 定平面直角坐标系在平面上直接计算。
以南北方向作为X轴，向
x 北为正；其东西方向为Y 轴，向东为正。 测区 坐标原点选在测区西南角。 o
2011年3月2日星期三
Y(E)
天津城市建设学院土 木 工 程 系
工程测量 第一章绪论
（3）、高斯平面直角坐标系 高斯投影的概念 高斯投影是一种等角投影。它是由德国数学家高斯 (Gauss，1777~1855)提出，后经德国大地测量学家克吕 格(Kruger，1857～1923)加以补充完善，故又称“高斯—
克吕格投影”，简称“高斯投影”。
测量对地图投影的要求： ①测量中大量的角度观测元素，在投影前后保持不变， 这样免除了大量投影计算工作； ②保证在有限范围内使得地图上图形同椭球上原形保持
返回
1.2地面点位的确定
一. 地球的形状和大小
1．地球自然形体：是一个不规则的几何体。 海洋面积约占地球表面的71%。
陆地
高山 丘陵 海洋
大地水准面：设想处于完全静止的平均海水面向陆地和岛屿 延伸所形成的闭合曲面。 大地体：大地水准面所包围的代表地球形状和大小的形体。
由于大地水准面是一个不规则的曲面，不能用数学公式 表述，因而需要寻找一个理想的几何体代表地球的形状和 大小。 该几何体必须满足两个条件： ① 形状接近地球自然形体； ② 可以用简单的数学公式表示。 2．参考椭球体及参考椭球面 参考椭球体： 一个非常接近大地体，并可用数学式表示
若已知某点的经度为L，则该点的6º 带的带号N由 下式计算：
N＝
L （取整）+1 6
若已知某点的经度为L，则该点所在3º 带的带号按 下式计算： n＝
L （四舍五入） 3
高教《土木工程测量》习题解答
《土木工程测量》习题解答
第一章 绪论
1、解：
∵y a =20882365.30m ，∴N =20； A 点所在6°带中央子午线的经度为：
λ0=6°N-3°=6°×20-3°=117°。
A 点的自然值为：Y a =882365.30-500000.00=382365.30m ，故A 点在中央子午线以
东382365.30m 处。 2、解：
∵已知点的经度λ=116°28′，则
201682116=⎥⎦
⎤⎢⎣⎡+'=
INT N 391303182116=⎥
⎦
⎤⎢⎣⎡+'-'=
INT n
于是：λ6=6°N -3°=6°×20-3°=117° λ3=3°n =3°×39=117°
∴ 该点在中央子午线以西，其横坐标自然值为：
()
m
km km km Y 00.592002.59111533333.011111782116-=-=⨯-=⨯-'=
故，该点在6°带中的横坐标通用值为：
y 6=20(500000.00-59200.00)=20440800.00m 该点在3°带中的横坐标通用值为：
y 3=39(500000.00-59200.00)=39440800.00m 。 3、解：
按式(1.3)计算对距离的影响为：
mm km R D D 0082.010*********.063713/13/2222==⨯==∆
按式(1.5)计算对高差的影响为：
mm km R D h 48.7800007848.063712/12/22==⨯==∆
∴ 95700082.0/48.78/==∆∆mm mm D h 即 地球曲率对高程的影响是对距离影响的9570倍。 4、解：
土木工程概论——1绪论
1906年美国旧金山大地震，1923年日本关东大地震， 这些自然灾害推动了结构动力学和工程抗震技术的发 展。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
2.3 现代土木工程
第二节 土木工程历史简介
2.3.2 城市建设立体化 20世纪中叶以来，城市建设有三个趋势： （1）高层建筑的大量兴起。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
（2）地下工 程发展迅速。 如地铁、商 业街、体育 馆、影剧院、 地下仓库等。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
2.3.3 交通运输高速化
（1）高速公路大规模修建
据不完全统计，至1993年底， 全世界有50多个国家和地区拥 有高速公路，其中有近20个国 家和地区拥有1000km以上。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
（3）设计理论的精确化、科学化
主要表现在理论分析又线性到非线性分析；由平面分析到空间 分析；由单个到系统的综合整体分析；由静态到动态分析；由经验定 值分析到随机分析；由数值分析到模拟实验分析，由人工手算、人工 做比较方案、人工制图到计算机辅助设计、计算机优化设计、计算机 制图等。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
2.3 现代土木工程
第二节 土木工程历史简介
2.3.2 城市建设立体化 20世纪中叶以来，城市建设有三个趋势： （1）高层建筑的大量兴起。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
（2）地下工 程发展迅速。 如地铁、商 业街、体育 馆、影剧院、 地下仓库等。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
2.3.3 交通运输高速化
（1）高速公路大规模修建
据不完全统计，至1993年底， 全世界有50多个国家和地区拥 有高速公路，其中有近20个国 家和地区拥有1000km以上。
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
第二节 土木工程历史简介
（3）设计理论的精确化、科学化
主要表现在理论分析又线性到非线性分析；由平面分析到空间 分析；由单个到系统的综合整体分析；由静态到动态分析；由经验定 值分析到随机分析；由数值分析到模拟实验分析，由人工手算、人工 做比较方案、人工制图到计算机辅助设计、计算机优化设计、计算机 制图等。
东北大学土木工程测量学1
16
1.2.1 地球的认识
中国 “天似穹窿” -----“天圆地方” 。 西方 “地如盘状，浮于无垠海洋之上”。 到公元前6世纪后半叶，毕达哥拉斯提出了地为圆球的说法。 公元前4世纪亚里士多德根据月食等自然现象也认识到大地是球
形，并接受其老师柏拉图的观点，发表了“地球”的概念，但都
没有得到可靠的证明。
3）会测量方法：掌握测量操作技能和方法；
4）会识图、用图，测图； 能识别地形图和地形图的应用了解大例尺地形图的
图原理和方法；
5）会施工测量。 东北大学
14
1.2 地球的形状、大小
❖1.2.1 地球的认识 ❖1.2.2 大地水准面和基准线 ❖1.2.3 参考椭球
东北大学
15
1.2.1 地球的认识
东北大学
基准线：铅垂线； 基准面：大地水准面
东北大学
35
1.3.1 地面点高程
1、地面点的高程
地面点到大地水准面的铅垂距离，称为该点的绝对高程 或海拔，简称高程。在下图中地面点A、B的绝对高程分别
为Ha、Hb。
东北大学
36
2、相对高程
当在局部地区进
行高程测量时，地面 点到假定水准面的铅 垂距离称为假定高程 或相对高程。在右图 中，A、B两点的相 对高程为Ha Hb。
大地水准面 铅垂线
地球 大地水准面所包围
土木工程测量-测量学绪论提纲资料
•12
亚里士多德（Aristotle） 作了进 一步论证 ，支持这一学说。又一世纪 后 ，埃拉托斯特尼（Eratosthenes） 用在南北两地同时观测日影的办法,首 次推算出地球子午圈的周长。
我国唐代僧人一行根据天文观测， 计算出地球子午线1°的长度。
测绘地图是地球表面形态认识的开 始。晋代裴秀总结出“制图六体”，
•15
三、测量学科的分支
大地测量学
研究和测定地球的形状、大小、重 力场和地面点几何位置及其变化的理论 和技术的学科。地球的形状大小以大地 水准面为代表。大地点的定位，用经纬 度或空间直角坐标，定位方法有几何法 大地测量、物理法大地测量和近代的卫 星法大地测量。
•16
用经纬仪作三角高程测量
•17
用水准Hale Waihona Puke Baidu作精密水准测量
•7
工程的竣工和变形监测 为了保障建筑物的施工和运行
时的安全，需要测量工作者以技术 上可行的最高精度，监测建筑物的 变形量和变形的发展情况。经常需 要在一段时间内进行连续观测，为 此要使用自动化的监测和记录的测
量仪器，在各种工程建设中的应 用愈来愈广泛。
•8
§1-2 测绘学科的内涵 和发展简史
一、测绘学科的定义和内涵 二、测绘科学的历史和近代发展 三、测绘学科的分支
•6
(四) 测量学在工程建设中的作用
亚里士多德（Aristotle） 作了进 一步论证 ，支持这一学说。又一世纪 后 ，埃拉托斯特尼（Eratosthenes） 用在南北两地同时观测日影的办法,首 次推算出地球子午圈的周长。
我国唐代僧人一行根据天文观测， 计算出地球子午线1°的长度。
测绘地图是地球表面形态认识的开 始。晋代裴秀总结出“制图六体”，
•15
三、测量学科的分支
大地测量学
研究和测定地球的形状、大小、重 力场和地面点几何位置及其变化的理论 和技术的学科。地球的形状大小以大地 水准面为代表。大地点的定位，用经纬 度或空间直角坐标，定位方法有几何法 大地测量、物理法大地测量和近代的卫 星法大地测量。
•16
用经纬仪作三角高程测量
•17
用水准Hale Waihona Puke Baidu作精密水准测量
•7
工程的竣工和变形监测 为了保障建筑物的施工和运行
时的安全，需要测量工作者以技术 上可行的最高精度，监测建筑物的 变形量和变形的发展情况。经常需 要在一段时间内进行连续观测，为 此要使用自动化的监测和记录的测
量仪器，在各种工程建设中的应 用愈来愈广泛。
•8
§1-2 测绘学科的内涵 和发展简史
一、测绘学科的定义和内涵 二、测绘科学的历史和近代发展 三、测绘学科的分支
•6
(四) 测量学在工程建设中的作用
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
38
1.3.1 坐标系统
1.地理坐标 (L, B )的定义
土木工程测量学的任务 地球的形状和大小 测量常用的坐标系统（重点） 用水平面代替水准面的限度 测量的基本工作和原则（重点）
1.1 土木工程测量学的任务
+ 1.1.1 测量学的定义 + 1.1.2 测量学任务 + 1.1.3 测量学作用 + 1.1.4 本课程要求
1.1.1 测量学的定义
一、测量学的定义
海拔高程 8844.43m
图9：马里亚纳海沟 － 斐查兹海渊剖面图
1.2.1 地球的认识 高山
海洋
陆地 丘陵
36
大地水准面：设想处于完全静止的平均海水面向 陆地和岛屿延伸所形成的闭合曲面。
大地体：大地水准面所包围的代表地球形状和大小 的形体。
1.3 测量常用的坐标系统
• 1.3.1 坐标系统 • 1.3.2 高程系统
（1）掌握测量仪器设备的原理和使用方法；熟 悉测量仪器
（2）研究测绘地形图的理论和方法；测图 （3）研究应用地形图的基本原理和方法；用图 （4）研究建、构筑物施工放样、质量检验的技 术和方法；放样 （5）研究大型建筑物的变形监测。变形观测
22
测量学的基本任务 （1）测定： （地面
图纸）测绘
（2）测设：（图纸 地面）放样
图3：渠道水位监测
图4：场地平整
•12
图5：大桥变形监测
•13
图6：隧道工程测量
•110
•14
图6：道路工程测量
•110
•15
海 底 地 形 测 量
德国汉堡的一个集装箱码头。日耳曼民族严谨、守时举世闻名
美 国 五 角 大 楼
东北大学
行 政 区 划 图
施 工 测 量
变 形 观 测
1.1.2 土木工程测量学的任务
24
1.1.3 测量学的作用
2、铁路、公路建设的测量工作
1) 确定一条最经济合理的路线；
2) 当路线跨越河流时，必须建造桥梁；
地形图 河流的水位、流速、流量和河床地形图 桥梁轴线长度等
设计阶段
桥台、桥墩的位置实地标定；---施工阶段
3) 当路线穿过山地需要开挖隧道。 计算隧道的长度和方向； 指示开挖方向，保证其正确贯通。
研究地球的形状和大小 以及确定地面点位的科学。
空中、地下和海底 （海陆空）
二、测绘学学科分类
普通测量学
大地测量学
测绘学
摄影测量学 海洋测量学 工程测量学
土木工程测量 矿山工程测量
铁道工程测量
1975年精确得到珠峰高 度为8848．13米
2005年5月22日测绘
2005年10月9日公布
珠穆朗玛峰峰顶岩石面 海拔高程8844.43米。
29
1.2.1 地球的认识
1969年7月20日，美国登月宇宙飞船“阿波罗”11号的宇航员 登上月球的时候，就看到了带蓝色的浑圆的地球，有如在地球 上观月亮一样。科学家们根据以往资料和宇航员拍下的像片， 认为最好把地球看作是一个“不规则的球体”。
至此，人类对地球形状的认识是否完成了呢？还没有。这是 因为地球实在太大了！而且无时无刻都在不停地运转着、变化 着。
参数：珠穆朗玛峰峰顶 岩石面高程测量精度
±0.21米；峰顶冰雪深 度3.50米。
6个交会点通过经纬仪、 激光测距仪等设备连续进 行48小时测量。峰顶测 量队员进行GPS高精度 定位，雷达探测仪对觇标 处冰雪层厚度进行测量。
图1：摄影测量学
图 2： 海 洋 测 量 a
图 2： 海 洋 测 量 b
土木工程测量学:研究在土木工程建设的勘测、规划、 设计、施工、竣工和运营管理各阶段中所需测量工 作的理论和方法，是工程测量学学科的重要组成部 分。
25
1.1.4 本课程要求
一知四会
1）知原理；
2）会用仪器：熟悉水准仪、经纬仪、全站仪等仪器； 3）会测量方法：掌握测量操作技能和方法； 4）会识图、用图，测图；
能识别地形图和地形图的应用了解大例尺地形图的 成图原理和方法； 5）会施工测量。
26
1.2 地球的形状和大小
• 1.2.1 地球的认识 • 1.2.2 大地水准面和基准线 • 1.2.3 参考椭球
27
1.2.1 地球的认识
公元8世纪的20年代，唐朝高僧在河南平原进行了弧度测量，
其距离和纬差都是实地测量的，这在世界尚属首次。并由此得 出地球子午线1度弧长为132.3公里，比现代精确值大21公里。
直到1522年，航海家麦哲伦率领船队从西班牙出发，一直向西
航行，经过大西洋、太平洋和印度洋，最后又回到了西班牙， 才得以事实证明，地球确确实实是一个球体。
30
1.2.1 地球的认识
31
1.2.2 大地水准面与基准线
地球自然表面是极不规则的，有高山、深谷、江河 湖海，不能用简单的数学关系来表达。 水七陆三 ，人们习惯上把海水所包围的地球形体视 为地球的的形状----水球。
1873年，德国的大地测量学家利斯廷创立了大地水 准面概念
32
图8：地球的制高点 － 珠穆朗玛峰
《土木工程测量》特点Βιβλιοθήκη Baidu
（1）实质上就是一门几何学，是平面和高程 分开计算的几何。 （2）根据已知点的坐标（及测量的角度和距 离）计算未知点的坐标；根据已知点的高程 （及测量的高差）计算未知点的高程。 （3）不同点：起始方向不同；角度值不同； 必要的检核条件。
第一章 绪论
❖1.1 ❖1.2 ❖1.3 ❖1.4 ❖1.5
1.1.3 测量学的作用
1、城市规划、给水排水、煤气管道、工业厂房和高层建 筑建设
1)设计阶段：测绘各种比例尺的地形图，供结构物的 平面及竖向设计使用；
2) 施工阶段：将设计结构物的平面位置和高程在实 地标定出来，作为施工的依据；
3)工程完工后：测绘竣工图，供日后扩建、改建、维修 和城市管理应用，对某些重要的建筑物或构筑物在建设 中和建成以后都需要进行变形观测，以保证建筑物的安 全。
28
1.2.1 地球的认识
但是，人类对地球的认识并未就此结束。随着科学技术的发展 和大地测量学科的形成与丰富，人们观测和认识地球形状的方 法和手段越来越多。三角测量、重力测量、天文测量等等都是 重要手段。近代科学家牛顿曾仔细研究了地球的自转，得出地 球是赤道凸起，两极扁平的椭球体，形状像个桔子。 到20世纪50年代末期，人造地球卫星发射成功，通过卫星观测 发现，南北两个半球是不对称的。南极离地心的距离比北极短 40米。因此，又有人把地球描绘成梨形。
1.3.1 坐标系统
1.地理坐标 (L, B )的定义
土木工程测量学的任务 地球的形状和大小 测量常用的坐标系统（重点） 用水平面代替水准面的限度 测量的基本工作和原则（重点）
1.1 土木工程测量学的任务
+ 1.1.1 测量学的定义 + 1.1.2 测量学任务 + 1.1.3 测量学作用 + 1.1.4 本课程要求
1.1.1 测量学的定义
一、测量学的定义
海拔高程 8844.43m
图9：马里亚纳海沟 － 斐查兹海渊剖面图
1.2.1 地球的认识 高山
海洋
陆地 丘陵
36
大地水准面：设想处于完全静止的平均海水面向 陆地和岛屿延伸所形成的闭合曲面。
大地体：大地水准面所包围的代表地球形状和大小 的形体。
1.3 测量常用的坐标系统
• 1.3.1 坐标系统 • 1.3.2 高程系统
（1）掌握测量仪器设备的原理和使用方法；熟 悉测量仪器
（2）研究测绘地形图的理论和方法；测图 （3）研究应用地形图的基本原理和方法；用图 （4）研究建、构筑物施工放样、质量检验的技 术和方法；放样 （5）研究大型建筑物的变形监测。变形观测
22
测量学的基本任务 （1）测定： （地面
图纸）测绘
（2）测设：（图纸 地面）放样
图3：渠道水位监测
图4：场地平整
•12
图5：大桥变形监测
•13
图6：隧道工程测量
•110
•14
图6：道路工程测量
•110
•15
海 底 地 形 测 量
德国汉堡的一个集装箱码头。日耳曼民族严谨、守时举世闻名
美 国 五 角 大 楼
东北大学
行 政 区 划 图
施 工 测 量
变 形 观 测
1.1.2 土木工程测量学的任务
24
1.1.3 测量学的作用
2、铁路、公路建设的测量工作
1) 确定一条最经济合理的路线；
2) 当路线跨越河流时，必须建造桥梁；
地形图 河流的水位、流速、流量和河床地形图 桥梁轴线长度等
设计阶段
桥台、桥墩的位置实地标定；---施工阶段
3) 当路线穿过山地需要开挖隧道。 计算隧道的长度和方向； 指示开挖方向，保证其正确贯通。
研究地球的形状和大小 以及确定地面点位的科学。
空中、地下和海底 （海陆空）
二、测绘学学科分类
普通测量学
大地测量学
测绘学
摄影测量学 海洋测量学 工程测量学
土木工程测量 矿山工程测量
铁道工程测量
1975年精确得到珠峰高 度为8848．13米
2005年5月22日测绘
2005年10月9日公布
珠穆朗玛峰峰顶岩石面 海拔高程8844.43米。
29
1.2.1 地球的认识
1969年7月20日，美国登月宇宙飞船“阿波罗”11号的宇航员 登上月球的时候，就看到了带蓝色的浑圆的地球，有如在地球 上观月亮一样。科学家们根据以往资料和宇航员拍下的像片， 认为最好把地球看作是一个“不规则的球体”。
至此，人类对地球形状的认识是否完成了呢？还没有。这是 因为地球实在太大了！而且无时无刻都在不停地运转着、变化 着。
参数：珠穆朗玛峰峰顶 岩石面高程测量精度
±0.21米；峰顶冰雪深 度3.50米。
6个交会点通过经纬仪、 激光测距仪等设备连续进 行48小时测量。峰顶测 量队员进行GPS高精度 定位，雷达探测仪对觇标 处冰雪层厚度进行测量。
图1：摄影测量学
图 2： 海 洋 测 量 a
图 2： 海 洋 测 量 b
土木工程测量学:研究在土木工程建设的勘测、规划、 设计、施工、竣工和运营管理各阶段中所需测量工 作的理论和方法，是工程测量学学科的重要组成部 分。
25
1.1.4 本课程要求
一知四会
1）知原理；
2）会用仪器：熟悉水准仪、经纬仪、全站仪等仪器； 3）会测量方法：掌握测量操作技能和方法； 4）会识图、用图，测图；
能识别地形图和地形图的应用了解大例尺地形图的 成图原理和方法； 5）会施工测量。
26
1.2 地球的形状和大小
• 1.2.1 地球的认识 • 1.2.2 大地水准面和基准线 • 1.2.3 参考椭球
27
1.2.1 地球的认识
公元8世纪的20年代，唐朝高僧在河南平原进行了弧度测量，
其距离和纬差都是实地测量的，这在世界尚属首次。并由此得 出地球子午线1度弧长为132.3公里，比现代精确值大21公里。
直到1522年，航海家麦哲伦率领船队从西班牙出发，一直向西
航行，经过大西洋、太平洋和印度洋，最后又回到了西班牙， 才得以事实证明，地球确确实实是一个球体。
30
1.2.1 地球的认识
31
1.2.2 大地水准面与基准线
地球自然表面是极不规则的，有高山、深谷、江河 湖海，不能用简单的数学关系来表达。 水七陆三 ，人们习惯上把海水所包围的地球形体视 为地球的的形状----水球。
1873年，德国的大地测量学家利斯廷创立了大地水 准面概念
32
图8：地球的制高点 － 珠穆朗玛峰
《土木工程测量》特点Βιβλιοθήκη Baidu
（1）实质上就是一门几何学，是平面和高程 分开计算的几何。 （2）根据已知点的坐标（及测量的角度和距 离）计算未知点的坐标；根据已知点的高程 （及测量的高差）计算未知点的高程。 （3）不同点：起始方向不同；角度值不同； 必要的检核条件。
第一章 绪论
❖1.1 ❖1.2 ❖1.3 ❖1.4 ❖1.5
1.1.3 测量学的作用
1、城市规划、给水排水、煤气管道、工业厂房和高层建 筑建设
1)设计阶段：测绘各种比例尺的地形图，供结构物的 平面及竖向设计使用；
2) 施工阶段：将设计结构物的平面位置和高程在实 地标定出来，作为施工的依据；
3)工程完工后：测绘竣工图，供日后扩建、改建、维修 和城市管理应用，对某些重要的建筑物或构筑物在建设 中和建成以后都需要进行变形观测，以保证建筑物的安 全。
28
1.2.1 地球的认识
但是，人类对地球的认识并未就此结束。随着科学技术的发展 和大地测量学科的形成与丰富，人们观测和认识地球形状的方 法和手段越来越多。三角测量、重力测量、天文测量等等都是 重要手段。近代科学家牛顿曾仔细研究了地球的自转，得出地 球是赤道凸起，两极扁平的椭球体，形状像个桔子。 到20世纪50年代末期，人造地球卫星发射成功，通过卫星观测 发现，南北两个半球是不对称的。南极离地心的距离比北极短 40米。因此，又有人把地球描绘成梨形。