上海民办新黄浦实验学校八年级数学下册第二单元《勾股定理》测试(有答案解析)

合集下载

初二下学期勾股定理练习题(含答案)

勾股定理练习题

一、基础达标:

1. 下列说法正确的是（）

A.若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2；

B.若 a 、b 、c 是Rt△ABC 的三边，则a 2＋b 2＝c 2；

C.若 a 、b 、c 是Rt△ABC 的三边， 90=∠A ，则a 2＋b 2＝c 2；

D.若 a 、b 、c 是Rt△ABC 的三边， 90=∠C ，则a 2＋b 2＝c 2．

2. Rt △ABC 的三条边长分别是a 、b 、c ，则下列各式成立的是（）

A ．c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+

3．如果Rt △的两直角边长分别为k 2－1，2k （k >1），那么它的斜边长是（）

A 、2k

B 、k+1

C 、k 2－1

D 、k 2+1 4. 已知a ，b ，c 为△ABC 三边，且满足(a 2－b 2)(a 2+b 2－c 2)＝0，则它的形状为（）

A.直角三角形

B.等腰三角形

C.等腰直角三角形

D.等腰三角形或直角三角形 5．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）

A ．121

B ．120

C ．90

D ．不能确定 6． △ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（） A ．42 B ．32 C ．42 或 32 D ．37 或 33 7.※直角三角形的面积为S ，斜边上的中线长为d ，则这个三角形周长为（）

（A 2d （B d

八年级数学下勾股定理_单元测试题(带答案)

(第6题)

B D C

（第12题）

7米5米

八年级下勾股定理测试题

一、耐心填一填每小题3分,共36分

1、在Rt △ABC 中,∠C=90°,AC=3,BC=4,则AB=___________；

2、如图,小明的爸爸在院子的门板上钉了一个加固板,从数学的角度看, 这样做的道理

是 .

3、小明同学要做一个直角三角形小铁架,他现有4根长度分别为4cm 、6cm 、8cm 、10cm 的

铁棒,可用于制作成直角三角形铁架的三条铁棒分别是________________________；

4、若三角形三条边的长分别为7,24,25,则这个三角形的最大内角是度.

5、在△ABC 中,∠C ＝90°,若c ＝10,a ∶b ＝3∶4,则ab ＝．

6、如图,在等腰△ABC 中,AB=AC=10,BC=12,则高AD=________；

7、等腰△ABC 的面积为12cm 2

,底上的高AD ＝3cm, 则它的周长为________．

8、在Rt △ABC 中,斜边AB ＝2,则AB 2

+BC 2

+CA 2

＝________．

9、有一个三角形的两边长是4和5,要使这个三角形成为直角三角形,则第三边长为；

10、有两棵树,一棵高6米,另一棵高3米,两树相距4米．一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了________米．

11、一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是________． 12、如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米, 则这棵大树折断前有__________米保留到0.1米; 二、精心选一选每小题4分,共24分

八年级数学-勾股定理-经典单元测试题(含答案)

八年级数学-勾股定理-经典单元测试题

(含答案)

1、能构成直角三角形的组合是A：4，5，6和C：6，8，11.

2、根据勾股定理，c的长为20，选项C。

3、根据勾股定理，OP的长为5，选项C。

4、根据正切函数，tanB=b/a=1，可得a=c/√2=5，选项A。

5、根据正弦函数，h=5*sin30°+5=7.5，选项B。

6、根据勾股定理，斜边长为√1800=30√2，选项B。

7、将长方形折叠成三角形ABE和ADE，根据勾股定理

可得AE=√90=3√10，△ABE的面积为1/2*3*3√10=4.5√10，选项B。

8、等边三角形的面积为√3/4*a^2，代入a=2可得面积为

√3，选项B。

9、根据勾股定理，BC的长为√(15^2-12^2)=9，三角形的

周长为15+13+9=37，选项D。

10、等腰三角形的底边上的高等于底边长的一半，即6，

选项A。

11、根据勾股定理，BC的长为√(15^2-12^2)=9，选项A。

12、设另一直角边为b，则斜边长为√(11^2+b^2)，周长为11+b+√(11^2+b^2)，因为周长为整数，所以b为60，周长为121，选项A。

二、填空题

1、等腰三角形。因为c-a=b，根据等腰三角形的定义可知，a=b。

八年级初二数学勾股定理测试试题含答案

一、选择题

1．如图，等边ABC ∆的边长为1cm ，D ，E 分别是AB ，AC 上的两点，将ADE ∆沿直线DE 折叠，点A 落在点'A 处，且点'A 在ABC ∆外部，则阴影部分图形的周长为（）

A ．1cm

B ．1.5cm

C ．2cm

D ．3cm 2．如图，在ABC 中，,904C AC ︒∠==cm ，3BC =cm ，点D 、

E 分别在AC 、BC

上，现将DCE 沿DE 翻折，使点C 落在点'C 处，连接AC '，则AC '长度的最小值（）

A ．不存在

B ．等于 1cm

C ．等于 2 cm

D ．等于 2.5 cm

3．如图，□ABCD 中，对角线AC 与BD 相交于点E ，∠AEB=45°，BD=2，将△ABC 沿AC 所在直线翻折180°到其原来所在的同一平面内，若点B 的落点记为B′，则DB′的长为（）

A ．1

B 2

C ．32

D 34．如图，已知直线a ∥b ，且a 与b 之间的距离为4，点A 到直线a 的距离为2，点B 到直线b 的距离为3，AB 30=a 上找一点M ，在直线b 上找一点N ，满足MN ⊥a 且AM +MN +NB 的长度和最短，则此时AM +NB ＝（）

A．6 B．8 C．10 D．12

5．圆柱形杯子的高为18cm，底面周长为24cm，已知蚂蚁在外壁A处（距杯子上沿2cm）发现一滴蜂蜜在杯子内（距杯子下沿4cm），则蚂蚁从A处爬到B处的最短距离为（）

A．813B．28 C．20 D．122

6．在平面直角坐标系内的机器人接受指令“[α，A]”(α≥0，0°＜A＜180°)后的行动结果为：在原地顺时针旋转A后，再向正前方沿直线行走α.若机器人的位置在原点，正前方为y轴的负半轴，则它完成一次指令[4，30°]后位置的坐标为( )

初中数学八年级下册《勾股定理》测试卷(附参考答案解析)

八年级数学下册《勾股定理》测试卷

班级考号姓名总分

一、选择题

1．下列各组数中，以a，b，c为边的三角形不是直角三角形的是（）

A．a=1.5，b=2，c=3 B．a=7，b=24，c=25C．a=6，b=8，c=10 D．a=3，b=4，c=5

2．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（）

A．25 B．14 C．7 D．7或25

3．正方形的面积是4，则它的对角线长是（）

A．2 B．C．D．4

4．如果直角三角形两直角边为5：12，则斜边上的高与斜边的比为（）

A．60：13 B．5：12 C．12：13 D．60：169

5．如下图，△ABC中AD⊥BC于D，AB=3，BD=2，DC=1，则AC等于（）

5题图 6题图 8题图A．6 B．C．D．4

6．已知，如上图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）A．25海里 B．30海里 C．35海里 D．40海里

7．三角形的三边长为a，b，c，且满足（a+b）2=c2+2ab，则这个三角形是（）

A．等边三角形 B．钝角三角形 C．直角三角形 D．锐角三角形

8．如上图，将一个边长分别为4，8的长方形纸片ABCD折叠，使C点与A点重合，则BE的长是（）

A．3 B．4 C．5 D．6

二、填空题

9．在直角三角形中，若两直角边的长分别为1cm，2cm，则斜边长为（）．

10．在△ABC中，∠C=90°，AB=5，则AB2+AC2+BC2=（）．

八年级数学下册《勾股定理》单元测试卷(带答案解析)

一、单选题

1.如图，在△ABC中，∠C=90°，AC=3，点D在BC上，∠ADC=2∠B，AD=√10，则BC的长为()

A. 3√3

B. √5+1

C. √10−1

D. √10+1

2.下列长度的线段中，能组成直角三角形的一组是()

A. 1，√3，2

B. 2，3，4

C. 4，5，6

D. 5，6，7

3.如图，在ΔABC中，三边a，b，c的大小关系是()

A. a

B. c

C. c

D. b

4.下列各组数中，能成为直角三角形的三条边长的是()

A. 3，5，7

B. 5，7，8

C. 4，6，7

D. 1，√3，2

，则AC的长为()

5.如图，点A，B都在格点上，点C在线段AB上，每个小格长度为1，若BC=2√13

A. √13

B. 4√13

C. 2√13

D. 3√13

6.如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、BD于M、N两点．若AM=√2，则线段BN的长为()

B. √2

C. 1

D. 2−√2

A. √2

7.在平面直角坐标系中，点A、B的坐标分别是(0,3)、(−4,0)，则原点到直线AB的距离是()

A. 2

B. 2.4

C. 2.5

D. 3

8.等腰三角形的一边长为4，另一边长为6，则这个等腰三角形的面积是()

A. 3√7

B. 8√2

C. 6√7

D. 3√7或8√2

9.如图，一只蚂蚁从长宽高分别是3，2，6的长方体纸箱的A点沿纸箱表面爬到B点，那么它所行的最短路线的长是()

A. √61

B. 11

C. 7

D. 8

10.若一个三角形的三边长分别为a，b，c，满足(a−3)2+√b−4+|c−5|=0，则这个三角形的形状是()

八年级数学(下)《勾股定理习题》练习题含答案

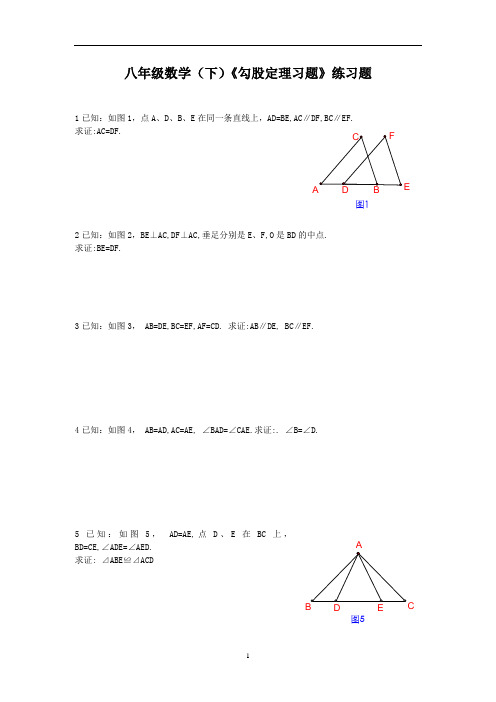
图1

八年级数学（下）《勾股定理习题》练习题

1已知：如图1，点A 、D 、B 、E 在同一条直线上，AD=BE,AC∥DF,BC∥EF.

求证:AC=DF.

2已知：如图2，BE⊥AC,DF⊥AC,垂足分别是E 、F,O 是BD 的中点. 求证:BE=DF.

3已知：如图3， AB=DE,BC=EF,AF=CD. 求证:AB∥DE, BC∥EF.

4已知：如图4， AB=AD,AC=AE, ∠BAD=∠CAE.求证:. ∠B=∠D.

5已知：如图5， AD=AE,点D 、E 在BC 上，

BD=CE,∠ADE=∠AED.

求证: ⊿ABE≌⊿ACD

图5

6已知：如图6，已知AC、BD相交于点O，AB∥CD, OA=OC.

求证: AB=CD

7已知：如图7，已知AC∥DF，BC=EF，∠C=∠F.

求证: ⊿ABC≌⊿DEF.

8已知：如图8，已知AC=AE，AB=AD.

求证: OB=OD.

9在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是

1、2、3,正放置的四个正方形的面积依次是S

1、S

、S

,则S

= .

S4 S3

图1

L 3

2 1

C 图

之间的关系，并分别用含n 的代数式表示a 、b 、c ：a= ，b= ，c= ；（2）猜想以a 、b 、c 为边的三角形是否为直角三角形，并验证你的猜想.

11分析：这是一道结论开放题，据题意经过分析，符合要求的点C 有多个，如图2所示，1C ，

2C ，3C ，4C ，5C ，6C 都是符合要求的点.

(人教版)上海市八年级数学下册第二单元《勾股定理》测试(含答案解析)

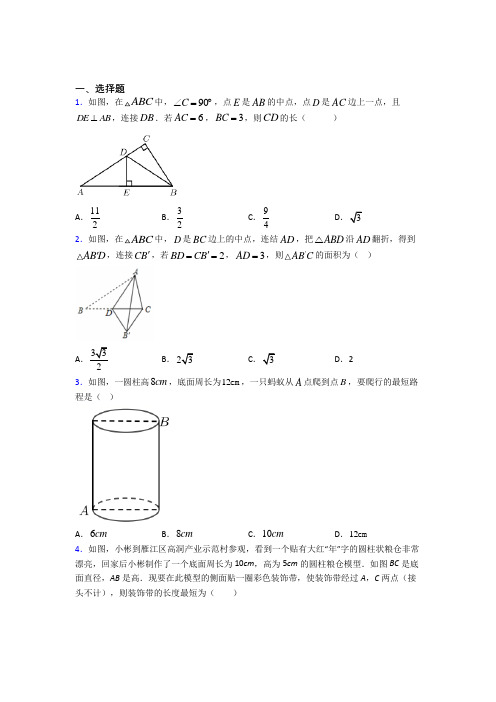
一、选择题

1．如图，在ABC 中，90C ∠=︒，点E 是AB 的中点，点D 是AC 边上一点，且DE AB ⊥，连接DB ．若6AC =，3BC =，则CD 的长（）

A ．112

B ．32

C ．94

D ．3

2．如图，在ABC 中，D 是BC 边上的中点，连结AD ，把ABD △沿AD 翻折，得到AB D '，连接CB '，若2BD CB '==，3AD =，则AB C '的面积为（）

A ．33

B ．23

C ．3

D ．2

3．如图，一圆柱高8cm ，底面周长为12cm ，一只蚂蚁从A 点爬到点B ，要爬行的最短路程是（）

A ．6cm

B ．8cm

C ．10cm

D ．12cm 4．如图，小彬到雁江区高洞产业示范村参观，看到一个贴有大红“年”字的圆柱状粮仓非常漂亮，回家后小彬制作了一个底面周长为10cm ，高为5cm 的圆柱粮仓模型．如图BC 是底面直径，AB 是高．现要在此模型的侧面贴一圈彩色装饰带，使装饰带经过A ，C 两点（接头不计），则装饰带的长度最短为（）

A ．10πcm

B ．20πcm

C ．102cm

D ．52cm 5．如图，在Rt ABC ∆中，90,45,2B BCA AC ︒︒∠=∠==，点D 在BC 边上，将ABD ∆沿直线AD 翻折，点B 恰好落在AC 边上的点

E 处，若点P 是直线AD 上的动点，连接,PE PC ，则PEC ∆的周长的最小值为（）

A ．22-

B ．2

C ．21+

D ．1

6．如图所示，在Rt ABC 中，90,3,5C AC BC ∠=︒==，分别以点A 、B 为圆心，大于

人教版初中数学八年级数学下册第二单元《勾股定理》检测题(包含答案解析)(1)

一、选择题

1．如图，在数轴上，点A ，B 对应的实数分别为1，3，BC AB ⊥，1BC =，以点A 为圆心，AC 为半径画弧交数轴正半轴于点P ，则P 点对应的实数为（）

A ．51+

B ．5

C ．53+

D ．45- 2．ABC 中，A ∠，B ，C ∠的对边分别记为a ，b ，c ，由下列条件不能判定ABC 为直角三角形的是（）

A ．A

C =+∠∠∠

B ．::1:1:2A B

C ∠∠∠= C ．222b a c =+

D ．::1:1:2a b c = 3．下列各组数中，以a ，b ，c 为边的三角形不是直角三角形的是（） A ．a ＝7，b ＝25，c ＝24

B ．a ＝11，b ＝41，c ＝40

C ．a ＝12，b ＝13，c ＝5

D ．a ＝8，b ＝17，c ＝15 4．如图，△ABC 中，∠ACB =90°，∠B =60°，CD ⊥AB 于点D ，△ABC 的面积为120，则

△BCD 的面积为（）

A ．20

B ．24

C ．30

D ．40

5．如图，△ABC 中，∠BAC=90°，AB=8，将△ABC 沿直线BC 向右平移，得到△EDF ，连接AD ，若四边形ACFD 为菱形，EC=4，则平移的距离为（）

A ．4

B ．5

C ．6

D ．8

6．如图①，直角三角形纸片的两直角边长分别为6、8，按如图②方式折叠，使点A 与点CB 重合，折痕为DE ，则BCE 与ADE 的面积之比为（）

A ．2:3

B ．4:9

C ．9:25

D ．14:25 7．《九章算术》是我国古代最重要的数学著作之一，它的出现标志着中国古代数学形成了完整的体系．“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”翻译成数学问题是：如图所示，ABC 中，90ACB ∠=︒，10AC AB +=尺，4BC =尺，求AC 的长．则AC 的长为（）

八年级数学下册勾股定理习题(附答案)(含答案)

勾股定理评估试卷（1）

一、选择题（每小题3分，共30分）

1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定

2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长

（A ）4 cm

（B ）8 cm （C ）10 cm

（D ）12 cm

3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（）（A ）25

（B ）14

（C ）7

（D ）7或25

4. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）64

5. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）

1524

20715

2024

157

257

202415

(A)

(B)

(C)

(D)

6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )

（A ）钝角三角形（B ）锐角三角形（C ）直角三角形（D ）等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) （A ） 25 （B ） 12.5 （C ） 9 （D ） 8.5 8. 三角形的三边长为ab c b a 2)(2

+=+,则这个三角形是( ) （A ）等边三角形（B ）钝角三角形（C ）直角三角形（D ）锐角三角形.

9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（）. （A ）50a 元（B ）600a 元（C ）1200a 元（D ）1500a 元 10.如图，A B ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.

上海民办新华初级中学八年级数学下册第二单元《勾股定理》检测(答案解析)

一、选择题

1．如图，2×2的方格中，小正方形的边长是1，点A 、B 、C 都在格点上，则ABC 中AB 边上的高长为（）

A ．355

B ．255

C ．3510

D ．322

2．如图，在Rt △ABC 中，∠ACB ＝90°，AB ＝10，AC ＝8，AB 的垂直平分线DE 交BC 的延长线于点E ，则DE 的长为（）

A ．103

B ．256

C ．203

D ．154

3．如图，△ABC 中，∠ACB =90°，∠B =60°，CD ⊥AB 于点D ，△ABC 的面积为120，则△BCD 的面积为（）

A ．20

B ．24

C ．30

D ．40 4．如图，在△ABC 中，AB ＝6，AC ＝9，AD ⊥BC 于D ，M 为AD 上任一点，则MC 2－MB 2

等于（）

A ．29

B ．32

C ．36

D ．45

5．如图，在长方形ACD 中，3AB cm =，9AD cm =，将此长方形折叠，便点D 与点B 重合，折痕为EF ，则ABE △的面积为（）2cm ．

A ．12

B ．10

C ．6

D ．15

6．如图，在ABC 中，点D 是BC 上一点，连结AD ，将ACD △沿AD 翻折，得到AED ，AE 交BD 于点F ．若2BD DC =，AB AD =，2AF EF =，2CD =，DFE △的面积为1，则点D 到AE 的距离为（）

A ．1

B ．65

C ．5

D ．2

7．在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几．”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离AB 长度为1尺．将它往前水平推送10尺时，即A C '＝10尺，则此时秋千的踏板离地距离A D '就和身高5尺的人一样高．若运动过程中秋千的绳索始终拉得很直，则绳索OA 长为（）

八年级数学下册《勾股定理》单元测试卷含答案

八年级数学下册《勾股定理》单元测试卷

（总分：100分，考试时间：60分钟）

一、选择题（共10小题，每小题3分，满分30分）

1．一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）A．4 B．8 C．10 D．12

2．小丰的妈妈买了一部29英寸（74cm）的电视机，下列对29英寸的说法中正确的是（） A．小丰认为指的是屏幕的长度B．小丰的妈妈认为指的是屏幕的宽度

C．小丰的爸爸认为指的是屏幕的周长D．售货员认为指的是屏幕对角线的长度

3．如图中字母A所代表的正方形的面积为（）

A．4 B．8 C．16 D．64

4．将直角三角形的三条边长同时扩大同一倍数，得到的三角形是（）

A．钝角三角形B．锐角三角形C．直角三角形D．等腰三角形

5．直角三角形的一直角边长是7cm，另一直角边与斜边长的和是49cm，则斜边的长（）A．18cm B．20cm C．24cm D．25cm

6．适合下列条件的△ABC中，直角三角形的个数为（）

①a=，b=，c=②a=6，∠A=45°；③∠A=32°，∠B=58°；

④a=7，b=24，c=25 ⑤a=2，b=2，c=4

A．2个B．3个C．4个D．5个

7．在△ABC中，若a=n2﹣1，b=2n，c=n2+1，则△ABC是（）

A．锐角三角形B．钝角三角形C．等腰三角形D．直角三角形

8．直角三角形斜边的平方等于两条直角边乘积的2倍，这个三角形有一个锐角是（）A．15°B．30°C．45°D．60°

9．已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）

八年级数学下册勾股定理习题(附答案)(含答案)

勾股定理评估试卷（1）

一、选择题（每小题3分，共30分）

1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定

2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长

（A ）4 cm

（B ）8 cm （C ）10 cm

（D ）12 cm

3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（）（A ）25

（B ）14

（C ）7

（D ）7或25

4. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）64

5. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）

1524

20715

2024

157

257

202415

(A)

(B)

(C)

(D)

6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )

+=+,则这个三角形是( ) （A ）等边三角形（B ）钝角三角形（C ）直角三角形（D ）锐角三角形.

八年级数学-勾股定理-经典单元测试题(含答案)

勾股定理单元测试题

一、选择题

1、下列各组数中，能构成直角三角形的是（）

A：4，5，6 B：1，1， C：6，8，11 D：5，

12，23

2、在Rt△ABC中，∠C＝90°，a＝12，b＝16，则c的长为（）

A：26 B：18 C：20 D：21

3、在平面直角坐标系中，已知点P的坐标是(3,4)，则OP的长为（）

A：3 B：4 C：5 D：

4、在Rt△ABC中，∠C＝90°，∠B＝45°,c＝10，则a的长为（

）

A：5 B： C： D：

5、等边三角形的边长为2，则该三角形的面积为（）

A、 B、 C、 D、3

6、若等腰三角形的腰长为10，底边长为12，则底边上的高为（）

A、6

B、7

C、8

D、9

7、已知，如图长方形ABCD中，AB=3cm，

第7题图

AD=9cm，将此长方形折叠，使点B与点D重合，

折痕为EF，则△ABE的面积为（）

A、3cm2

B、4cm2

C、6cm2

D、12cm2

8、若△ABC中，，高AD=12,则BC的长为（）

A、14

B、4

C、14或4

D、以上都不对

二、填空题

1、若一个三角形的三边满足，则这个三角形是。

2、木工师傅要做一个长方形桌面，做好后量得长为80cm，宽为60cm，对

角线为100cm，则这个桌面。（填“合格”或“不合格”

）

3、直角三角形两直角边长分别为3和4，则它斜边上的高为

__________。

4、如右图所示的图形中，所有的四边形都是正方形，

所有的三角形都是直角三角形，其中最大的正

方形的边长为5，则正方形A，B，C，D的

面积的和为。

八年级初二数学勾股定理测试试题含答案

一、选择题

1．如图：在△ABC 中，∠B=45°，D 是AB 边上一点，连接CD ，过A 作AF ⊥CD 交CD 于G ，交BC 于点F ．已知AC=CD ，CG=3，DG=1，则下列结论正确的是（）

①∠ACD=2∠FAB ②27ACD S ∆= ③272CF

=- ④ AC=AF A ．①②③ B ．①②③④ C ．②③④ D ．①③④

2．如图，等腰直角△ABC 中，∠C ＝90°，点F 是AB 边的中点，点D 、E 分别在AC 、BC 边上运动，且∠DFE ＝90°，连接DE 、DF 、EF ，在此运动变化过程中，下列结论：①图中全等的三角形只有两对；②△ABC 的面积是四边形CDFE 面积的2倍；③CD +CE ＝2FA ；④AD 2+BE 2＝DE 2．其中错误结论的个数有（）

A ．1个

B ．2个

C ．3个

D ．4个

3．如图，四边形ABCD 中，AC ⊥BD 于O ，AB ＝3，BC ＝4，CD ＝5，则AD 的长为（）

A ．1

B ．2

C ．4

D ．34．如图，已知直线a ∥b ，且a 与b 之间的距离为4，点A 到直线a 的距离为2，点B 到直线b 的距离为3，AB 30=a 上找一点M ，在直线b 上找一点N ，满足MN ⊥a 且AM +MN +NB 的长度和最短，则此时AM +NB ＝（）

A．6 B．8 C．10 D．12

5．如图，正方形ABCD和正方形CEFG边长分别为a和b，正方形CEFG绕点C旋转，给出下列结论：①BE=DG；②BE⊥DG；③DE2+BG2=2a2+2b2，其中正确结论有（）

勾股定理-单元测试题(含答案)

勾股定理单元测试题

一、选择题

1、下列各组数中，能构成直角三角形的是（）

A ：4，5，6

B ：1，1

：6，8，11 D ：5，12，23 2、在Rt △ABC 中，∠C ＝90°，a ＝12，b ＝16，则c 的长为（） A ：26 B ：18 C ：20 D ：21

3、在平面直角坐标系中，已知点P 的坐标是(3,4)，则OP 的长为（） A ：3 B ：4 C ：5 D ：7

4、在Rt △ABC 中，∠C ＝90°，∠B ＝45°,c ＝10，则a 的长为（） A ：5 B ：10 C ：25 D ：5

5、等边三角形的边长为2，则该三角形的面积为（）

、

、、3

6、若等腰三角形的腰长为10，底边长为12，则底边上的高为（）

A 、6

B 、7

C 、8

D 、9 7、已知，如图长方形ABCD 中，AB=3cm ， AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△AB

E 的面积为（） A 、3cm 2

B 、4cm 2

C 、6cm 2

D 、12cm 2

8、若△ABC 中，13,15AB cm AC cm ==，高AD=12,则BC 的长为（） A 、14 B 、4 C 、14或4 D 、以上都不对二、填空题

1、若一个三角形的三边满足2

c a b -=，则这个三角形是。

2、木工师傅要做一个长方形桌面，做好后量得长为80cm ，宽为60cm ，对角线为100cm ，则这个桌面。（填“合格”或“不合格” ）

3、直角三角形两直角边长分别为3和4，则它斜边上的高为__________。