第十八章检测卷
第十八章《电功率》单元检测卷(提高班)2021-2022学年人教版物理九年级全一册( 含答案)

第十八章《电功率》单元检测卷(提高班)一.选择题(共15小题)1.小明家记录5月初电能表示数为1432.7度,电能表的部分示数及6月初的示数如图所示,下列说法正确的是()A.电能表是测量用电器电功率的仪表B.此电能表适用于电流方向一秒钟改变50次的交流电路C.小明家5月初至6月初消耗的电能是105kW•hD.若电能表转盘在10min内转过250转,则用电器的总功率为1kW2.甲、乙两个用电器的电压之比为2:1,电流之比为1:2,通电时间之比为5:4,则两个用电器消耗的电能之比为()A.5:1 B.5:4 C.4:5 D.5:83.小红同学家的电冰箱正常工作时电流大约是1A,则它正常工作10h所消耗的电能是()A.2200J B.1.32×105J C.7.92×105J D.7.92×106J4.甲、乙两只灯泡,其I﹣U关系图象如图所示。
现将甲、乙两灯串联在电路中,当甲灯两端的电压为2V 时,乙灯消耗的功率是()A.1.2W B.0.8W C.2W D.3W5.一只电阻两端的电压由3V增大到4V时,通过该电阻的电流增加了0.25A,则该电阻消耗的电功率增加了()A.0.25W B.1.75W C.0.75W D.1W6.把标有“12V12W”的灯L1和“12V6W”的灯L2串联起来接在电源电压为12V的电路中,下列说法正确的是()A.两灯均不能正常发光,但L1灯较亮B.两灯均不能正常发光,但L2灯较亮C.两灯均能正常发光D.把电源电压提高到24V,两灯都能正常发光7.如图所示的电路中,电源电压不变,开关S闭合,滑动变阻器滑片P在a端时,电流表的示数为2.4A,电压表的示数为12V;滑片P移动到中点时,R1消耗的功率为P1;滑片P移到b点时,R1消耗的功率为P1′,P1:P1′=25:9,滑片P在中点和在b端时,R2消耗的功率之比为()A.1:2 B.5:3 C.25:9 D.25:188.如图甲所示,R1的阻值是20Ω,滑动变阻器R2消耗的功率P与其电阻R2的关系图像如图乙所示,则R2消耗的最大功率是()A.0.45W B.0.50W C.0.80W D.0.90W9.在“测定小灯泡的功率”的实验中,某同学电路连接正确,闭合开关,灯泡发光,但无论怎样调节滑动变阻器,电压表的示数虽然有变化,却始终达不到灯泡的额定电压。
人教版九年级下册物理第十八章《电功率》测试卷(含答案)

人教版九年级下册物理第十八章《电功率》测试卷(含答案)一、选择题(每题3分,共30分)1.下列用电器正常工作时,功率接近1 200 W的是( )A.白炽灯 B.空调 C.电视机 D.洗衣机2.夏天到了,相比于空调,使用电风扇更节能环保。
如图所示的是一款电风扇的“挡位”旋钮,当由2挡位调至3挡位时,能够吹出更强劲的风,则相较于2挡,下列关于3挡的说法正确的是( )A.消耗电能更多B.消耗电能更快C.消耗电能更少D.消耗电能更慢3.下列属于防止电流热效应产生危害的实例是( )A.家里使用电热水壶烧水B.利用电视机后盖的小孔散热C.家里使用电饭锅煮饭D.小佳妈妈使用电熨斗熨衣服4.a、b、c三盏灯分别标有“110 V20 W”“220 V40 W”“36 V350 W”字样,若三盏灯都正常发光,则它们的亮度情况是( )A.a灯最亮 B.b灯最亮 C.c灯最亮 D.三盏灯一样亮5.定值电阻R1标有“10 Ω 1 A”字样,R2标有“15 Ω0.6 A”字样,将R1、R2接入由一个开关和电压恒定的电源组成的电路,在保证电路安全的情况下,下列说法正确的是( )A.R1、R2并联时,通过干路的最大电流为1.6 AB.R1、R2并联时,R2的最大功率为9 WC.R1、R2串联时,电源电压最大为19 VD.R1、R2串联时,R1的最大功率为3.6 W6.如图所示的为明明家的电能表,他将新买的电水壶单独接入电路时,发现电能表的转盘在1 min内转了6 r。
下列关于电能表和电水壶的说法正确的是( )A.电能表应接在家庭电路的总开关之后B.为了不损坏电能表,明明家同时使用的用电器的总功率不能超过2 200 W C.电水壶的实际功率为600 WD.该电能表此时的读数为11 234 kW·h7.有一个定值电阻R和一只小灯泡L,流过它们的电流与其两端电压的关系如图甲所示,把它们并联在电路中,如图乙所示。
闭合开关S,这时电流表示数为0.6 A,则电源电压和小灯泡的电功率分别是( )A.2 V 0.3 W B.2 V 0.4 W C.1.5 V 1.75 W D.1.5 V 0.6 W 8.探究“小灯泡的电功率”的实验电路如图甲所示,实验中选择规格为“2.5 V”的小灯泡,得到的U-I图象如图乙所示。
九年级物理上册《第十八章电功率》单元检测卷及答案(人教版)

九年级物理上册《第十八章电功率》单元检测卷及答案(人教版)一、选择题(每题3分,共12分)1.如表是一种常见电器的铭牌,它可能是( )额定电压/频率220 V/50 Hz额定功率 1 800 W生产日期见商品外包装A.日光灯 B2.节能灯已成为家庭照明的主要选择,一个11 W的节能灯和一个40 W的白炽灯在正常工作时的照明亮度是相同的,如图所示,以下说法不正确的是( )A.节能灯每秒消耗11 J电能B.节能灯每秒产生的内能大于白炽灯C.两灯正常工作所需电压是相同的D.用节能灯替代白炽灯有助于节省电能3.四根电阻丝a、b、c、d由同种材料做成,其横截面积相同,但绕不同的圈数(每圈的长度相等,a、c圈数相同,b、d圈数相同),如图连接,通电后在相同的时间内,它们产生的热量由多到少的顺序是( )A.a、b、d、c B.a、c、b、dC.b、d、a、c D.d、c、b、a4.[2022·深圳盐田区期末改编]小灯泡L1与L2串联(灯丝电阻不变),其中L2的电功率为4 W,且L1比L2亮,使用一段时间后,L2突然熄灭,L1的亮度明显变亮,此时L1的功率为25 W,则L2发生的电路故障及L 2未熄灭之前L1的电功率为( )A.短路;1 W B.短路;9 W C.短路;16 W D.断路;18 W二、填空题(每空1分,共9分)5.小建家里买了一个家用电暖器,电暖器的工作原理是将电能转化为________,将电暖器单独接在220 V的电路中,电流为2 A,工作1 min后,该电暖器消耗的电能为________ J,1度电可以供给这个电暖器正常使用________h。
(结果保留2位小数)6.生活中灯泡“闪”了,一般发生在开灯的瞬间,这是由于开灯瞬间灯丝的温度_______,电阻较_______,通过它的电流________的缘故。
7.如图所示为电能表的面板示数,该家庭电路消耗的电能是________kW·h;根据电流规格参数表明,确定电能表有关特性的电流值是________A,家庭电路接入用电器的最高功率为________W。
人教版数学八年级下册:第十八章检测卷(附答案)

20.(8 分)如图,E 是▱ ABCD 的边 AD 的中点,连接 CE 并延长交 BA 的延长线于点 F.若 CD=6,求 BF 的长. 解析:∵E 是▱ ABCD 的边 AD 的中点, ∴AE=DE.(2 分) ∵四边形 ABCD 是平行四边形, ∴AB=CD=6,AB∥CD. ∴∠F=∠DCE.(4 分)
24.(10 分)如图,在▱ ABCD 中,对角线 AC,BD 交于点 O,过点 B 作 BE⊥CD 于点 E,延长 CD 到 点 F,使 DF=CE,连接 AF. (1)求证:四边形 ABEF 是矩形; (1)证明:在▱ ABCD 中, AD∥BC,且 AD=BC, ∴∠ADF=∠BCE.
在△ADF 和△BCE 中, AD=BC, ∠ADF=∠BCE, DF=CE, ∴△ADF≌△BCE(SAS).(3 分) ∴AF=BE,∠AFD=∠BEC=90°. ∴AF∥BE. ∴四边形 ABEF 是矩形.(5 分)
(2)求 DM 的长. (2)解:∵△ADB≌△ADE, ∴AE=AB=12, ∴EC=AC-AE=8. ∵M 是 BC 的中点,BD=DE, ∴DM=1EC=4.(10 分)
2
23.(10 分)如图,P 是正方形 ABCD 对角线 BD 上 一点,PE⊥DC,PF⊥BC,点 E,F 分别是垂足. (1)求证:AP=PC;
3.如图,点 P 是菱形 ABCD 对角线 BD 上一点, PE⊥AB 于点 E,若∠BPE=60°,则∠ADC 的度数 为( A ) A.60° B.65° C.70° D.75°
4.如图,在 Rt△ABC 中,∠ACB=90°,点 H、E、 F 分别是边 AB、BC、CA 的中点.若 EF+CH=8, 则 CH 的长为( B ) A.3 B.4 C.5 D.6
第18章《勾股定理》单元检测试卷(含答案)

第18章勾股定理单元测试一、选择题1.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是().A. 1、2、3B. 2、3、4C. 3、4、5D. 4、5、62.一个直角三角形中,两直角边长分别为3和4,下列说法正确的是()A. 斜边长为25B. 三角形周长为25C. 斜边长为5D. 三角形面积为203.如图,已知O为圆锥的顶点,MN为圆锥底面的直径,一只蜗牛从M点出发,绕圆锥侧面爬行到N点时,所爬过的最短路线的痕迹(虚线)在侧面展开图中的位置是()A. B.C. D.4.如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用()A. 9mB. 7mC. 5mD. 3m5.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则BC的长为()A. ﹣1B. +1C. ﹣1D. +16.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是()A. 0B. 1C.D.7.适合下列条件的△ABC中,直角三角形的个数为()①a=3,b=4,c=5;②a=6,∠A=45°;③a=2,b=2,c=2 ;④∠A=38°,∠B=52°.A. 1个B. 2个C. 3个D. 4个8.如图字母B所代表的正方形的面积是()A. 12B. 13C. 144D. 1949.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A. 24cm2B. 36cm2C. 48cm2D. 60cm210.如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.20B.25C.30D.3211.如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程是(◆)A. 40 cmB. cmC. 20 cmD. cm二、填空题12.如图,有一圆柱体,它的高为8cm,底面周长为12cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是________ cm.13.请写出两组勾股数:________、________.14.如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是________.15. 北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,下列说法:①a2+b2=13;②b2=1;③a2﹣b2=12;④ab=6.其中正确结论序号是________16.已知甲、乙两人在同一地点出发,甲往东走4km,乙往南走了3km,这时甲、乙两人相距________ km.17.一根旗杆在离底部4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆折断前高为________18.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为________ .19.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!20.如图,长为12cm的弹性皮筋直放置在x轴上,固定两端A和B,然后把中点C向上拉升8cm至D点,则弹性皮筋被拉长了________.21. 在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是25,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)2的值为________三、解答题22.如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.23.如图,四边形ABCD中,∠B=90°,AB=6,BC=8,CD=24,AD=26,求四边形ABCD的面积.24.在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.25.我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(ab),即(a+b)2=c2+4(ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.参考答案一、选择题C CD D D C C C A B C二、填空题12.1013.3、4、5;6、8、1014.15.①④16.5km17.12米18.42或3219.420.8cm21.49三、解答题22.解:如图,连接AC.在△ACD中,∵AD=4米,CD=3米,∠ADC=90°,∴AC=5米,又∵AC2+BC2=52+122=132=AB2,∴△ABC是直角三角形,∴这块地的面积=△ABC的面积﹣△ACD的面积= ×5×12﹣×3×4=24(平方米).23.解:连结AC,在△ABC中,∵∠B=90°,AB=6,BC=8,∴AC= =10,S△ABC= AB•BC= ×6×8=24,在△ACD中,∵CD=24,AD=26,AC=10,∴CD2+AC2=AD2,∴△ACD是直角三角形,∴S△ACD= AC•CD= ×10×24=120.∴四边形ABCD的面积=S△ABC+S△ACD=24+120=144.24.解:如图,在△ABC中,AB=15,BC=14,AC=13,设BD=x,则有CD=14﹣x,由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,∴152﹣x2=132﹣(14﹣x)2,解之得:x=9,∴AD=12,∴S△ABC= BC•AD= ×14×12=8425.(1)解:S阴影=4×ab,S阴影=c2﹣(a﹣b)2,∴4×ab=c2﹣(a﹣b)2,即2ab=c2﹣a2+2ab﹣b2,则a2+b2=c2;(2)解:如图所示,大正方形的面积为x2+4y2+4xy,也可以为(x+2y)2,则(x+2y)2=x2+4xy+4y2.。
第18章 平行四边形 达标测试卷(含答案) 华师大版数学八年级下册

第18章平行四边形达标测试卷一、选择题(本题共10小题,每小题5分,共50分)1.在▱ABCD中,∠A∶∠B∶∠C∶∠D可以是()A.1 ∶2 ∶3 ∶4 B.1 ∶2 ∶1 ∶2C.1 ∶1 ∶2 ∶2 D.1 ∶2 ∶2 ∶12.将一副三角板在平行四边形ABCD中按如图摆放,则∠α=() A.55°B.65°C.75°D.85°(第2题) (第3题) (第4题)3.如图,在四边形ABCD中,CE平分∠BCD交AD于点E,DE=CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是()A.AD=BC B.AB=CDC.CE=BC D.∠A=∠D4.如图,▱ABCD的周长为32,对角线AC与BD相交于点O,AC⊥AB,△BCO 的周长比△ABO的周长长4,则BO的长为()A.52B.13 C.4 D.55.如图,直线AB∥CD,P是AB上的动点,当点P从左向右运动时,△PCD的面积将()A.变大B.变小C.不变D.无法确定(第5题) (第6题) (第7题)6.如图,在▱ABCD 中,∠BDC =47°42′,依据尺规作图的痕迹,计算∠α的度数是( ) A .67°29′B .67°9′C .66°29′D .66°9′7.如图,在▱ABCD 中,将△ADC 沿AC 折叠后,点D 恰好落在DC 的延长线上的点E 处.若∠B =60°,AB =3,则△ADE 的周长为( ) A .12B .15C .18D .218.平移、旋转与轴对称都是图形之间的一些主要变换,为了得到▱ABCD (如图),下列说法错误的是( )A .将线段AB 沿BC 的方向平移至DC ,连结BC ,AD 可以得到▱ABCD B .将△ABC 绕边AC 的中点O 旋转180°可以得到▱ABCDC .将△AOB 绕点O 旋转180°得到△COD ,连结BC ,AD 可以得到▱ABCD D .将△ABC 沿AC 翻折可以得到▱ABCD9.如图,在平面直角坐标系中,平行四边形ABCD 的顶点A ,B ,C 的坐标分别是(1,0)、()6,0、()8,5,则顶点D 的坐标是( ) A .(5,5)B .(5,3)C .(2,5)D .(3,5)(第8题) (第9题) (第10题)10.如图,四边形ABCD 是平行四边形,E 是边CD 上一点,且BC =EC ,CF ⊥BE 交AB 于点F ,P 是EB 延长线上一点,下列结论:①BE 平分∠CBF ;②CF 平分∠DCB ;③BC =FB ;④PF =PC ,其中正确结论的个数为( ) A .1B .2C .3D .4二、填空题(本题共6小题,每小题5分,共30分)11.在四边形ABCD 中,(1)若AB =3,BC =4,CD =3,要使该四边形是平行四边形,则AD =________;(2)若∠A =60°,∠B =120°,则当∠D =________时,四边形ABCD 是平行四边形.12.如图,在▱ABCD 中,AC 与BD 交于点O ,AE ⊥BD 于点E ,BD =20,BE =7,AE=4,则AC的长等于________.(第12题)(第13题)13.如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1处,折痕为EF,若∠BAE=55°,则∠D1AD=________.14.如图,在▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE 与DF交于点H,则∠BHF=________.15.如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为________.(第14题)(第15题)16.在平面直角坐标系中,有A(2,5),B(5,1),C(m,-m),D(m-3,-m+4)四个点,当四边形ABCD的周长最小时,m的值为________.三、解答题(本题共6小题,共70分)17.(8分)如图,已知▱ABCD的对角线AC,BD相交于点O,AD=12,BD=10,AC=26.(1)求△ADO的周长;(2)求证:△ADO是直角三角形.3(第17题)18.(10分)已知:如图所示,在平行四边形ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,分别交AB,CD于点E,F,连结BD,EF.求证:BD,EF互相平分.(第18题) 19.(12分)如图,在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连结GE,EH,HF,FG.求证:四边形GEHF是平行四边形.(第19题)20.(12分)如图,在四边形ABCD中,∠ADB=∠CBD=90°,BE∥CD交AD于点E,且EA=EB.若AB=80,DB=4.求四边形ABCD的面积.(第20题)21.(14分)如图,在平行四边形ABCD中,AB= 2 cm,BC=12 cm,∠B=45°,5点P在边BC上,由点B向点C运动,速度为2 cm/s,点Q在边AD上,与点P同时出发,由点D向点A运动,速度为1 cm/s,连结PQ,设运动时间为t s.(1)当t为何值时,四边形ABPQ为平行四边形?(2)设四边形ABPQ的面积为y cm2,请用含有t的代数式表示y;(不必写出t的取值范围)(3)当点P运动至何处时,四边形ABPQ的面积是▱ABCD面积的34(第21题)22.(14分)在▱ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.(第22题)(1)如图①,求证:BP=DQ;(2)由图①易得BP+BQ=BC,请分别写出图②,图③中BP,BQ,BC三者之间的数量关系,并选择一个关系进行证明;(3)在(1)和(2)的条件下,若DQ=1,DP=3,请直接写出BC的长.7答案一、1.B 2.C 3.A 4.A 5.C 6.D7.C8.D9.D 10.D二、11.(1)4(2)120°12.1013.55°14.61°15.616.2三、17.(1)解:∵四边形ABCD是平行四边形,∴OA=OC=12AC,OB=OD=12BD.∵AC=26,BD=10,∴OA=13,OD=5.∵AD=12,∴△ADO的周长=5+12+13=30.(2)证明:由(1)知OA=13,OD=5,AD=12,∴在△AOD中,AD2+DO2=122+52=169,AO2=132=169,∴AD2+DO2=AO2,∴△AOD是直角三角形.18.证明:∵DE,BF分别是∠ADC和∠ABC的平分线,∴∠ADE=∠CDE,∠CBF=∠ABF.∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC.∴∠AED=∠CDE,∠CFB=∠ABF.∴∠AED=∠ADE,∠CFB=∠CBF.∴AE=AD,CF=CB.∴AE=CF.∴AB-AE=CD-CF,即BE=DF.∵DF∥BE,∴四边形DEBF是平行四边形.∴BD,EF互相平分.19.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠GBE=∠HDF.∵AG=CH,∴AB+AG=CD+CH,即BG=DH.又∵BE=DF,∴△GBE≌△HDF.∴GE=HF,∠GEB=∠HFD.∴∠GEF=∠HFE.∴GE∥HF.∴四边形GEHF是平行四边形.20.解:∵∠ADB=∠CBD=90°,∴DE∥CB.9 ∵BE ∥CD ,∴四边形BEDC 是平行四边形. ∴BC =DE .在Rt △ABD 中,由勾股定理得AD =AB 2-DB 2=(80)2-42=8. 设DE =x ,则EA =8-x ,∴EB =EA =8-x . 在Rt △BDE 中,由勾股定理得 DE 2+DB 2=EB 2, ∴x 2+42=(8-x )2.解得x =3.∴BC =DE =3,∴S 四边形ABCD =S △ABD +S △BDC =12AD ·DB +12DB ·BC =16+6=22.21.解:(1)由已知可得BP =2t cm ,DQ =t cm ,AD =BC =12 cm ,∴AQ =(12-t )cm.∵四边形ABPQ 为平行四边形, ∴BP =AQ ,即12-t =2t ,∴t =4, ∴当t =4时,四边形ABPQ 为平行四边形. (2)过点A 作AE ⊥BC 于点E .在Rt △ABE 中,∠AEB =90°,∠B =45°,∴AE =BE . 由勾股定理可知AB 2=AE 2+BE 2,∴AE =1 cm. ∴S 四边形ABPQ =12(BP +AQ )·AE =12(12+t )cm 2, 即y =12(12+t )=12t +6.(3)S ▱ABCD =1×12=12(cm 2).由题意得34×12=12t +6,∴t =6.∴BP =2×6=12(cm).此时BP =BC ,∴当点P 运动至点C 处时,四边形ABPQ 的面积是▱ABCD 面积的34.22.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴∠ADB =∠CBD . ∵AP ∥CQ ,∴∠APQ =∠CQB .∴△ADP ≌△CBQ . ∴DP =BQ .∴BQ -PQ =PD -PQ ,即BP =DQ . (2)解:图②:BQ -BP =BC ,证明: ∵AP ∥CQ ,∴∠APB =∠CQD .∵AB∥CD,∴∠ABD=∠CDB.∴∠ABP=∠CDQ. ∵AB=CD,∴△ABP≌△CDQ.∴BP=DQ.∴BC=AD=BD=BQ-DQ=BQ-BP. 图③:BP-BQ=BC,证明略.(3)解:BC=2或4.。
人教版数学八年级下册第18章平行四边形达标检测卷4份含答案

人教版数学八年级下册第18章平行四边形达标检测卷4份第18章单元测试(1)班级姓名成绩一、选择题(3′×10=30′)1.下列性质中,平行四边形具有而非平行四边形不具有的是().A.内角和为360° B.外角和为360° C.不确定性 D.对角相等2.□ ABCD中,∠A=55°,则∠B、∠C的度数分别是().A.135°,55° B.55°,135° C.125°,55° D.55°,125°3.下列正确结论的个数是().①平行四边形内角和为360°;②平行四边形对角线相等;③平行四边形对角线互相平分;④平行四边形邻角互补.A.1 B.2 C.3 D.44.平行四边形中一边的长为10cm,那么它的两条对角线的长度可能是().A.4cm和6cm B.20cm和30cm C.6cm和8cm D.8cm和12cm 5.在□ABCD中,AB+BC=11cm,∠B=30°,S ABCD=15cm2,则AB与BC的值可能是().A.5cm和6cm B.4cm和7cm C.3cm和8cm D.2cm和9cm 6.在下列定理中,没有逆定理的是().A.有斜边和一直角边对应相等的两个直角三角形全等;B.直角三角形两个锐角互余;C.全等三角形对应角相等;D.角平分线上的点到这个角两边的距离相等.7.下列说法中正确的是().A.每个命题都有逆命题 B.每个定理都有逆定理C.真命题的逆命题是真命题 D.假命题的逆命题是假命题8.一个三角形三个内角之比为1:2:1,其相对应三边之比为().A.1:2:1 B.1:1 C.1:4:1 D.12:1:29.一个三角形的三条中位线把这个三角形分成面积相等的三角形有()个. A.2 B.3 C.4 D.510.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=•14,•AC=19,则MN的长为().A.2 B.2.5 C.3 D.3.5二、填空题(3′×10=30′)11.用14cm长的一根铁丝围成一个平行四边形,短边与长边的比为3:4,短边的比为________,长边的比为________.12.已知平行四边形的周长为20cm,一条对角线把它分成两个三角形,•周长都是18cm,则这条对角线长是_________cm.13.在□ABCD中,AB的垂直平分线EF经过点D,在AB上的垂足为E,•若□ABCD•的周长为38cm,△ABD的周长比□ABCD的周长少10cm,则□ABCD的一组邻边长分别为______.14.在□ABCD中,E是BC边上一点,且AB=BE,又AE的延长线交DC的延长线于点F.若∠F=65°,则□ABCD的各内角度数分别为_________.15.平行四边形两邻边的长分别为20cm,16cm,两条长边的距离是8cm,•则两条短边的距离是_____cm.16.如果一个命题的题设和结论分别是另一个命题的______和_______,•那么这两个命题是互为逆命题.17.命题“两直线平行,同旁内角互补”的逆命题是_________.18.在直角三角形中,已知两边的长分别是4和3,则第三边的长是________.19.直角三角形两直角边的长分别为8和10,则斜边上的高为________,斜边被高分成两部分的长分别是__________.20.△ABC的两边分别为5,12,另一边c为奇数,且a+b+•c•是3•的倍数,•则c•应为________,此三角形为________三角形.三、解答题(6′×10=60′)21.如右图所示,在□ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,求ABCD的周长.22.如图所示,在□ABCD 中,E 、F 是对角线BD 上的两点,且BE=DF.求证:(1)AE=CF ;(2)AE ∥CF .23.如图所示,□ABCD 的周长是,AB 的长是DE ⊥AB 于E ,DF ⊥CB 交CB•的延长线于点F ,DE 的长是3,求(1)∠C 的大小;(2)DF 的长.24.如图所示,□ABCD 中,AQ 、BN 、CN 、DQ 分别是∠DAB 、∠ABC 、∠BCD 、•∠CDA 的平分线,AQ 与BN 交于P ,CN 与DQ 交于M ,在不添加其它条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程(要求:•推理过程中要用到“平行四边形”和“角平分线”这两个条件).FCDAEB25.已知△ABC的三边分别为a,b,c,a=n2-16,b=8n,c=n2+16(n>4).求证:∠C=90°.26.如图所示,在△ABC中,AC=8,BC=6,在△ABE中,DE⊥AB于D,DE=12,S =60,•求∠C的度数.△ABE27.已知三角形三条中位线的比为3:5:6,三角形的周长是112cm,•求三条中位线的长.28.如图所示,已知AB=CD,AN=ND,BM=CM,求证:∠1=∠2.29.如图所示,△ABC的顶点A在直线MN上,△ABC绕点A旋转,BE⊥MN于E,•CD•⊥MN于D,F为BC中点,当MN经过△ABC的内部时,求证:(1)FE=FD;(2)当△ABC继续旋转,•使MN不经过△ABC内部时,其他条件不变,上述结论是否成立呢?30.如图所示,E是□ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S .△EFC答案:一、1.D 2.C 3.C 4.B 5.A 6.C 7.A 8.B 9.C 10.C二、11.3cm 4cm 12.8 13.9cm和10cm 14.50°,130°,50°,130°• •15.10 16.结论题设 17.同旁内角互补,两直线平行18.5..13 直角三、21.□ABCD的周长为20cm 22.略24.略23.(1)∠C=45°(2)DF=225.•略 26.∠C=90° 27.三条中位线的长为:12cm;20cm;24cm 28.提示:连结BD,取BD•的中点G,连结MG,NG29.(1)略(2)结论仍成立.提示:过F作FG⊥MN于G 30.略第18章单元测试(2)班级姓名成绩一、选择题(3′×10=30′)1.下列判断四边形是平行四边形的是().A.两组角相等的四边形; B.对角线平分的四边形; C.一组对边相等,一组对角相等的四边形; D.两组对边分别相等的四边形2.根据下列条件,能作出平行四边形的是().A.两组对边长分别是3cm和7cm;B.相邻两边的边长分别是2cm和4cm,一条对角线长是7cm;C.一条边长为6cm,另一条对角线长为10cm,一条边长为8cm;D.一条边长为7cm,两条对角线长为6cm和8cm3.如图1所示,在□ABCD中,EF∥GH∥AB,MN∥BC,则图中的平行四边形的个数为(• ).A.12个 B.16个 C.14个 D.18个(1) (2) (3) 4.已知下列四个命题:①一组对边平行且相等的四边形;②两组对角分别相等的四边形;③对角线相等的四边形;④对角线互相平分的四边形.•其中能判断是平行四边形的命题个数为().A.1个 B.2个 C.3个 D.4个5.以不共线的三点为平行四边形的其中三个顶点作平行四边形,•一共可作平行四边形的个数是().A.2个 B.3个 C.4个 D.5个6.平行四边形的一边为32,则它的两条对角线长不可能是().A.20和40 B.30和50 C.40和50 D.20和607.如图2所示,EF过□ABCD对角线的交点O,分别交AD于E,交BC于点F,若OE=5,四边形CDEF的周长为25,则□ABCD的周长为().A.20 B.30 C.40 D.508.在□ABCD中,∠A:∠B:∠C:∠D的值可以是().A.1:2:3:4 B.1:3:4:2 C.1:1:2:2 D.3:4:3:49.已知O为□ABCD对角线的交点,且△AOB的周长为1,则□ABCD的面积为() A.1 B.2 C.3 D.410.已知O为□ABCD对角线的交点,且△AOB的周长比△BOC的周长多23,则CD-AD•的值为().A.23B.32C.2 D.3二、填空题(3′×10=30′)11.□ABCD中,∠A:∠B=7:2,则∠C=______.12.如图3所示,在□ABCD中,CM⊥AD于M,CN⊥AB于N,若∠B=50°,则∠MCN=_____.13.若平行四边形的周长为40cm,对角线AC、BD•相交于点O,•△BOC•的周长比△AOB的周长大2cm,则AB=________.14.若平行四边形的周长为56cm,相邻两边的长度比为3:4,则四边形的四边长分别为_____________.15.如果□ABCD和□ABEF有公共边AB,那么四边形DCEF是_________.16.四边形ABCD中,∠ADC=∠ABC,要判断这个四边形是平行四边形,•只需判断出__________即可,根据是________________.17.已知一个四边形的边长依次分别为a,b,c,d,且a2+b2+c2+d2=2ac+2bd,•则此四边形为___________.18.过平行四边形对角线的交点,且与一组边平行的直线将平行四边形分成的两个四边形________平行四边形.(填“是”或“不是”)19.四边形ABCD中,AC、BD交于点O,且OA=OC,OB=•OD,•∠ABC=•80•°,•则∠ADC=_____.20.已知:四边形ABCD中,AD∥BC,要使四边形ABCD为平行四边形,•需要增加条件________.(只需填写一个你认为正确的即可)三、解答题(共60′)21.(6′)如右图所示,在□ABCD中,AE、CF分别是∠DAB、∠BCD的平分线,求证:四边形AFCE是平行四边形.22.(6′)如右图所示,O为等边△ABC内任意一点,OD∥BC,OE∥AC,OF∥AB,•并且D、E、F分别在AB、BC、AC上,求证:OD+OE+OF=BC.23.(8′)如下图所示,已知平行四边形ABCD的周长是36cm,由钝角顶点D向AB、•BC引两条高DE、DF,且,cm,求平行四边形ABCD的面积.24.(8′)如下图所示,□ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=•60•°,BE=2,CF=1,连结DE,求△DEC的面积.25.(8′)求证:顺次连结四边形各边中点所得的四边形是平行四边形.26.(8′)如右图所示,△ABC中,CD是△ABC的角平分线,AE⊥CD于E,F为AC的中点,试问EF∥BC吗?为什么?27.(8′)已知□ABCD中,E、F分别是BC、CD的中点,AE、AF分别交BD于M、N.求证:BM=MN=ND.28.(8′)已知如下图所示,在□ABCD中,∠A=60°,E、F分别是AB、CD•的中点,•且AB=2AD.(1)求证:EF:(2)试判断EF与BD的位置关系?答案:一、1.D 2.A 3.D 4.C 5.B 6.A 7.B 8.D 9.D 10.A二、11.140° 12.50° 13.9cm 14.12cm,16cm,12cm,16cm 15.•平行四边形16.∠BAD=∠BCD 两组对角分别相等,则四边形是平行四边形 17.•平行四边形 •18.是 19.80° 20.AB∥DC三、21.略 22.略 23.2 24..提示:连结AC 26.略27.略28.(1)提示:连结DE (2)EF⊥BD第18章单元测试(3)一、选择题.(每小题4分,共32分)1.一个平行四边形的两条对角线的长分别为8和10,则这个平行四边形边长不可能是()A.2B.5C.8D.102.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为()A.75°B.65°C.55°D.50°第2题图第3题图3.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为()A.3B.3.5C.2.5D.2.84. 下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形5.如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=()A.2B.3C.4D.6第5题图第6题图第7题第8题6.如图所示,将□ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC,②MN=AM,下列说法正确的是()A.①②都对B.①②都错C.①对②错D.①错②对7.如图所示,在正方形ABCD中,点E、F分别在CD,BC上,且BF=CE,连接BE,AF相交于点G,则下列结论不正确的是()A.BE=AFB.∠DAF=∠BECC.∠AFB+∠BEC=90°D.AG⊥BE8. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO,若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE ∶S△BCM=2∶3.其中正确结论的个数是()A.4个B.3个C.2个D.1个二、填空题.(每小题4分,共32分)9.如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F= .第9题图第10题图10.如图所示,在R t△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线;②只填一个符合要求的条件)11.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=8,BC=10,则EF的长为 .第11题图第12题图12. 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE 的对角线,若∠D=60°,BC=2,则点D的坐标是 .13.已知一个平行四边形的一条对角线将其分为两个全等的等腰直角三角形,且这条对角线的长为6,则另一条对角线的长为 .14. 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为 cm.15.如图,已知点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接PA、EF.则线段PA与EF之间的大小关系是 .第15题图第16题图16.如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,BC=8,则GH等于 .三、解答题.(共56分)17.(8分)如图所示,一根长2.5m的木棍(AB)斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7m,设木棍的中点为P.若木棍顶端A沿墙下滑,且底端B沿地面向右滑行.(1)如果木棍的顶端A沿墙下滑0.4 m,那么木棍的底端B向外移动了多少距离?(2)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.18.(8分)如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别在OD,OC上,且DE=CF,连接DF,AE,AE的延长线交DF于点M.求证:AM⊥DF.19.(8分)如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得到△GFC.(1)求证:BE=DG;(2)若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.20.(8分)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A出发沿AD边向D以1cm/s的速度运动,点Q从点C出发沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t s.求:(1)当t为何值时,四边形ABQP为矩形?(2)当t为何值时,四边形PQCD为平行四边形?21.(12分)(2016·湖北十堰)如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为G,H,折痕分别与边BC,AD相交于点E,F.(1)判断四边形CEGF的形状,并证明你的结论;(2)若AB=3,BC=9,求线段CE的取值范围.22.(12分)如图①,菱形ABCD对角线AC,BD的交点O是四边形EFGH 对角线FH的中点,四个顶点A,B,C,D分别在四边形EFGH的边EF,FG,GH,HE 上.(1)求证:四边形EFGH是平行四边形;(2)如图②,若四边形EFGH是矩形,当AC与FH重合时,已知ACBD=2,且菱形ABCD的面积是20,求矩形EFGH的长与宽.答案第十八章达标检测卷一、选择题(每题3分,共30分)1.如图,▱ABCD中,AC=3 cm,BD=5 cm,则边AD的长可以是() A.3 cm B.4 cm C.5 cm D.6 cm2.如图,D,E分别是△ABC的边AB,AC上的点,且AD=DB,AE=EC.若DE =4,则BC的长为()A.2 B.4 C.6 D.83.如图,在▱ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则▱ABCD的周长是()A.20 cm B.21 cm C.22 cm D.23 cm4.下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形5.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD 一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形6.如图,在矩形ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为()A.12 B.18 C.24 D.307.平行四边形ABCD的对角线交于点O,有五个条件:①AC=BD,②∠ABC =90°,③AB=AC,④AB=BC,⑤AC⊥BD,则下列哪个组合可判定这个四边形是正方形?()A.①②B.①③C.①④D.④⑤8.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B. 2 C.4-2 2 D.3 2-49.如图,在菱形ABCD中,AB=2,∠A=120°,P,Q,K分别为线段BC,CD,BD上的任意一点,则P K+Q K的最小值为()A.1 B. 3 C.2 D.3+110.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.若第一个矩形的面积为1,则第n个矩形的面积为()A.14 B.14n-1C.14n D.14n+1二、填空题(每题3分,共30分)11.如图,在▱OABC中,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(4,2),则点C的坐标为__________.12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.13.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED等于________.14.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=10,则EC的长度是________.15.如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是线段AO,BO的中点.若AC+BD=30 cm,△OAB的周长为23 cm,则EF的长为__________.16.如图,在▱ABCD中,点E为BC边上一点(不与端点重合),若AB=AE,且AE平分∠DAB,则有下列结论:①∠B=60°;②AC=BC;③∠AED=∠ACD;④△ABC≌△EAD.其中正确的是__________(在横线上填所有正确结论的序号).17.如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上的点C′处,得到经过点D的折痕DE.则∠DEC的大小为________.18.菱形ABCD在平面直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,3),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2 020 s 时,点P的坐标为__________.19.如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为________.20.正方形ABCD的边长是4,点P是AD边的中点,点E是正方形边上的一点,若△PBE是等腰三角形,则腰长为____________________.三、解答题(21题8分,26题12分,其余每题10分,共60分)21.如图,在▱ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于点E,F.求证AE=CF.22.如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点.(1)求证△ADE≌△ABF;(2)求△AEF的面积.23.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交AB于点G,交CB的延长线于点F,连接AF,BE.(1)求证△AGE≌△BGF;(2)试判断四边形AFBE的形状,并说明理由.24.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC 于点E,O,F,连接CE和AF.(1)求证:四边形AECF为菱形;(2)若AB=4, BC=8,求菱形AECF的周长.25.如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD 的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF是平行四边形.(2)①当四边形CEDF是矩形时,求AE的长;②当四边形CEDF是菱形时,求AE的长.26.如图,在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图①;(2)若∠P AB=20°,求∠ADF的度数;(3)如图②,若45°<∠P AB<90°,用等式表示线段AB,EF,FD之间的数量关系,并证明.答案一、1.A 2.D 3.C 4.C5.D 点拨:运用三角形的中位线定理和矩形的性质解答.6.C 点拨:根据题意易知△COF 的面积与△AOE 的面积相等,阴影部分的面积为矩形面积的四分之一.7.C8.C 点拨:由题易得∠ABD =∠ADB =45°,再求出∠DAE 的度数.根据三角形的内角和定理求∠AED ,从而得到∠DAE =∠AED ,再根据等角对等边得到AD =DE ,然后求出正方形的对角线BD ,再求出BE ,进而在等腰直角三角形中利用勾股定理求出EF 的长.9.B10.B 点拨:第一个矩形的面积为1,易知第二个矩形的面积为14,第三个矩形的面积是116……故第n 个矩形的面积为14n -1. 二、11.(1,2) 12.30 13.65° 14.2.515.4 cm16.①③④ 点拨:∵四边形ABCD 为平行四边形,∴AB ∥CD ,AD =BC ,AD ∥BC .∴∠DAE =∠AEB .∵AE 平分∠DAB ,∴∠DAE =∠BAE .∴∠BAE =∠AEB .∴AB =BE .又AB =AE ,∴AB =AE =BE .∴△ABE 为等边三角形.∴∠B =∠BAE =60°.∴∠B =∠DAE .∵∠BAC =∠BAE +∠EAC =60°+∠EAC >∠B ,∴BC >AC .在△ABC 和△EAD 中,⎩⎨⎧AB =EA ,∠ABC =∠EAD ,BC =AD ,∴△ABC ≌△EAD (SAS ).∴∠BAC=∠AED.∵AB∥CD,∴∠BAC=∠ACD.∴∠AED=∠ACD.故正确的是①③④.17.75°点拨:如图,连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形.由P为AB的中点,利用等腰三角形三线合一的性质得到∠ADP=30°.由题意易得∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出∠DEC=75°.18.(0,3)19.16点拨:∵四边形ABCD是矩形,AB=x,AD=y,∴CD=AB=x,BC=AD=y,∠BCD=90°.又∵BD⊥DE,点F是BE的中点,DF=4,∴BF=DF=EF=4.∴CF=BF-BC=4-y.在Rt△DCF中,DC2+CF2=DF2,即x2+(4-y)2=42=16,∴x2+(y-4)2=16.20.25或52或652三、21.证明:∵四边形ABCD为平行四边形,∴AD=BC,∠D=∠B,∠BAD=∠BCD.又∵AE平分∠BAD,CF平分∠BCD,∴∠DAE=12∠BAD,∠BCF=12∠BCD.∴∠DAE=∠BCF.在△DAE和△BCF中,⎩⎨⎧∠D =∠B ,DA =BC ,∠DAE =∠BCF ,∴△DAE ≌△BCF (ASA ).∴AE =CF .22.(1)证明:∵四边形ABCD 为正方形,∴AB =AD =DC =CB ,∠D =∠B =90°.∵E ,F 分别为DC ,BC 的中点,∴DE =12DC ,BF =12BC .∴DE =BF .在△ADE 和△ABF 中,⎩⎨⎧AD =AB ,∠D =∠B ,DE =BF ,∴△ADE ≌△ABF (SAS ).(2)解:由题易知△ABF ,△ADE ,△CEF 均为直角三角形,且AB =AD =4,DE =BF =CE =CF =12×4=2,∴S △AEF =S 正方形ABCD -S △ADE -S △ABF -S △CEF =4×4-12×4×2-12×4×2-12×2×2=6.23.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC .∴∠AEG =∠BFG .∵EF 垂直平分AB ,∴EF ⊥AB ,AG =BG .在△AGE 和△BGF 中,⎩⎨⎧∠AEG =∠BFG ,∠AGE =∠BGF ,AG =BG ,∴△AGE ≌△BGF (AAS ).(2)解:四边形AFBE 是菱形.理由如下:∵△AGE ≌△BGF ,∴AE =BF .∵AD ∥BC ,∴四边形AFBE 是平行四边形.又∵EF ⊥AB ,∴四边形AFBE 是菱形.24.(1)证明:∵EF 是AC 的垂直平分线,∴AO =OC ,∠AOE =∠COF =90°.∵四边形ABCD 是矩形,∴AD ∥BC .∴∠EAO =∠FCO .在△AEO 和△CFO 中,⎩⎨⎧∠EAO =∠FCO ,AO =CO ,∠AOE =∠COF ,∴△AEO ≌△CFO (ASA ).∴OE =OF .∵OA =OC ,∴四边形AECF 是平行四边形.又∵EF ⊥AC ,∴四边形AECF 是菱形.(2)解:设AF =x .∵EF 是AC 的垂直平分线,∴AF =CF =x ,∴BF =8-x .在Rt △ABF 中,由勾股定理得:AB 2+BF 2=AF 2,即42+(8-x )2=x 2,解得x =5.∴AF =5.∴菱形AECF 的周长为20.25.(1)证明:∵四边形ABCD 是平行四边形,∴CF ∥ED .∴∠FCG =∠EDG .∵G 是CD 的中点,∴CG =DG .在△FCG 和△EDG 中,⎩⎨⎧∠FCG =∠EDG ,CG =DG ,∠CGF =∠DGE ,∴△FCG ≌△EDG (ASA ).∴FG =EG .∵CG =DG ,∴四边形CEDF 是平行四边形.(2)解:①∵四边形ABCD 是平行四边形,∴∠CDA =∠B =60°,DC =AB =3 cm ,BC =AD =5 cm .∵四边形CEDF 是矩形,∴∠CED =90°.在Rt △CED 中,易得ED =12CD =1.5 cm ,∴AE =AD -ED =3.5(cm).故当四边形CEDF 是矩形时,AE =3.5 cm.②若四边形CEDF 是菱形,则CE =ED .由①可知∠CDA =60°,∴△CED 是等边三角形.∴DE =CD =3 cm.∴AE =AD -DE =5-3=2(cm).故当四边形CEDF 是菱形时,AE =2 cm.点拨:在判定三角形全等时,关键是选择恰当的判定条件,有时还需添加适当的辅助线构造全等三角形.同时全等三角形也为平行四边形、矩形、菱形的判定构筑了重要的平台和保障.26.解:(1)如图①所示.(2)如图②,连接AE.∵点E是点B关于直线AP的对称点,∴∠P AE=∠P AB=20°,AE=AB.∵四边形ABCD是正方形,∴AE=AB=AD,∠BAD=90°.∴∠AED=∠ADE,∠EAD=∠DAB+∠BAP+∠P AE=130°.∴∠ADF=180°-130°2=25°.(3)EF2+FD2=2AB2.证明:如图③,连接AE,BF,BD,由轴对称和正方形的性质可得EF=BF,AE =AB=AD,易得∠ABF=∠AEF=∠ADF,又∵∠BAD=90°,∴∠ABF+∠FBD+∠ADB=90°.∴∠ADF+∠ADB+∠FBD=90°.∴∠BFD=90°.在Rt△BFD中,由勾股定理得BF2+FD2=BD2;在Rt△ABD中,由勾股定理得BD2=AB2+AD2=2AB2,∴EF2+FD2=2AB2.。
八年级数学下册《第18章平行四边形》单元评价检测试卷含解析.doc

单元评价检测(三)(第十八章)(45分钟100分)一、选择题(每小题4分,共28分)1.下列语句正确的是()A.对角线互相垂直的四边形是菱形B.有两边及一角对应相等的两个三角形全等C.矩形的対角线相等D.平行四边形是轴对称图形【解题指南】由菱形的判定方法得岀选项A错误;由全等三角形的判定方法得出选项B错误;由矩形的性质得出选项0正确;由平行四边形的性质得出选项D错误;即可得出结论.【解析】选C.对角线互相垂直且平分的四边形是菱形,故A错;两边及其夹角对应相等的两个三角形全等, 故B错;矩形的对角线相等,故C正确;平行四边形是屮心对称图形,故D错.【变式训练】下列命题:①平行四边形的对边相等;②对角线相等的四边形是矩形;③正方形既是轴对称图形,乂是中心对称图形;④一条对角线平分一组对角的平行四边形是菱形.其屮真命题的个数是()A.1B. 2C. 3D.4【解析】选C.平行四边形的对边相等,①正确;对角线相等的平行四边形是矩形,②错误;正方形既是轴对称图形,又是中心对称图形,③正确;一条对角线平分一组对角的平行四边形是菱形,④正确,所以有3个真命题.2.(2017 •黔东南州模拟)如图,在口ABCD中,AD=8,点E, F分别是BD, CD的中点,则EF等于()【解析】选C.・・•四边形ABCD 是平行四边形,・・・BC 二AD 二8.・・•点E, F 分别是BD, CD 的中点,1 1AEF =2BC =2X 8=4.3. (2017・衢州中考)如图,矩形纸片ABCD 中,AB=4, BC=6,将△ ABC 沿AC 折叠,使点B 落在点E 处,CE 交AD 于点F,则DF 的反等于() 3 5A. 5B. 3【解题指南】根据折亞的性质得到AE 二AB, ZE 二ZB 二90° ,易证Rt AAEF^Rt ACDF,即可得到结论EF 二DF;易 得 FC 二FA,设 FA 二x,则 FC 二x, FD 二6-x,在RtACDF 中利用勾股定理得到关于x 的方程X 2=42+(6-X )2,解方程求出x.【解析】选B.・・•矩形ABCD 沿对角线AC 对折,使AABC 落在AAEC 的位置,AAE=AB, ZE=ZB=90° ,又・・•四边形ABCD 为矩形,・・・AB 二CD,・・・AE 二DC,而 ZAFE 二 ZCFD, •・•在AAEF 与Z\CDF 中,(Z-AFE = Z-CFD, 厶E = e IAE = CD, AAAEF^ACDF(AAS),・•・ EF 二 DF.E.A. 2B. 3C.4D. 5・・•四边形ABCD为矩形,・・・AD二BC二6, CD二AB二4,VRtAAEF^RtACDF, ・・・FC二FA,设 FA=x,则 FC=x, FD二6-x,在 RtACDE 中,C『二CD'+DF;13即X2=42+(6-X)2,解得 x二3 ,5则 FD二6-x=>4.(2017・北流市一模)如图,四边形ABCD是菱形,A(3, 0) ,B(0, 4),则点C的坐标为( )A. (-5, 4)B. (-5, 5)C. (-4, 4)D. (-4, 3)【解析】选 A. J A (3, 0), B(0, 4),・・・ 0A=3, OB=4,・・・AB二J%' + °B2二5,・・•四边形ABCD是菱形,・・・BC=AD=AB=5, A点C的坐标为(-5, 4).5.顺次连接矩形ABCD各边中点,所得四边形必定是()A.邻边不等的平行四边形B.矩形C.正方形D. 菱形【解析】选D.如图,E, F, G, H 为矩形各边的屮点,连接AC, BD.根据三角形屮位线定理, 1得 EF 〃AC, EF=2AC ,HG 〃AC,1 1HG 二2A C, EH 二2BD .・・・EF 〃HG, EF 二HG, ・・・四边形EFGH 为平行四边形.又TAOBD, ・・・EF 二EH.・・・四边形EFGH 为菱形.6. (2017・威海模拟)在矩形ABCD 中,AB 二2, AD 二4, E 为CD 的中点,连接AE 交BC 的延长线于F 点,P 为BC 上 一点,当ZPAE=ZDAE 时,AP 的长为 (179 A.4 B. 4 C. 2【解析】选 B. VAD/7BC, A ZDAE=ZF,又 V ZPAE=ZDAE, A ZPAE^ZF,・・・PA 二PF. TE 为DC 中点,・・・DE 二CE.又T ZAED=ZFEC,AAADE^AFCE, .\CF=AD=4,设 CP=x, PA 二PF 二x+4, BP 二4-x,在直角 AABP 中,22+(4-X )2=(X +4)2,1解得:x=4,17・・・AP 的长为4.【变式训练】如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B'处,若AE=2, DE 二6, ZEFB 二60° ,则矩形ABCD 的面积是( )DGC【解析】选D.由两直线平行内错角相等,知ZDEF=ZEFB=60° , A ZAEF=8二16\/37. 如图所示,R, F 分别是正方形ABCD 的边CD, AD 上的点,且CE=DF, AE, BF 相交于点0,下列结论①AE 二BF;② AE 丄 BF;③AO 二0E ; ®S A AOB =S 四边形DEOF 中,错误的有( )【解析】选A. T 四边形ABCD 是正方形「.CD 二AD. VCE=DF, ADE=AF,又TAD 二AB, ZBAF=ZD, AAADE^ABAF, •••①AE 二BF, S AADE =S ABAF ,ZDEA-ZAFB, ZEAD-ZFBA,@S AAOB -S 四边形 DEOI :・•••ZABF+ZAFB 二ZDAE+ZDEA 二90° ,A ZAFB+ZEAF=90° ,・••②AE 丄BF —定成立.错误的结论是:③A0二0E.二、填空题(每小题5分,共25分)8. (2017 •徐州中#) AABC 中,点D,E 分别是AB, AC 的中点,DE 二7,则BC= ____【解析1 VD, E 分别是AABC 的边AB 和AC 的中点,DE 是AABC 的中位线,VDE=7, ABC=2DE=14.A. 1个 ,ZK 9 EF=120° …••ZA'EIT =60° , A , E-AE-2,求得 A'B',・・・AB 二矩形//CD 的面积为S=2\^ X B .2个C ・3个D.4个2 11 c JDA\答案:149. 已知矩形的对角线AC 与BD 相交于点0,若A0二1,那么BD 二【解析】在矩形ABCD 中, ・・•对角线AC 与BD 相交于点0, A0=l, ・•・ A0二CO 二B0二DO 二 1, A BD=2. 答案:210. (2017・连云港中考)如图,在口ABCD 中,AE 丄BC 于点E,AF 丄CD 于点F.若ZEAF 二56°,则ZB 二 _【解析】TAE 丄BC,AF 丄CD,A ZAEC=ZAFC=90° ,在四边形 AECF 中,ZC=360° -ZEAF-ZAEC-ZAFC=360° -56° -90° -90° =124° , 在Q ABCD 中,ZB=180° -ZC=180° -124° 二56° .答案:56°11. (2017・乌鲁木齐中考)如图,在菱形ABCD 中,ZDAB=60° ,AB=2,则菱形ABCD 的面积为—【解析】•・•菱形 ABCD, AAD=AB, OD=OB, 0A=0C, V ZDAB=60° , A AABD 为等边三角形,ABD=AB=2, A0D=l,在_________ 1RtAAOD 中,根据勾股定理得:A0二「.AC 二则S 菱形磁尸?AC ・BD=2A^.D答案:2&12.(2017 •安顺中考)如图所示,正方形ABCD的边长为6, AABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为___________・【解析】设BE与AC交于点P,连接BD,・・•点B与D关于AC对称,・・・PD二PB,・・・PD+PE二PB+PE二BE最小.即P在AC与BE的交点上时,PD+PE最小,为BE的长度;•・•正方形ABCD的边长为6,・・・AB二6.乂•••△ABE是等边三角形,ABE=AB=6.故所求最小值为6.答案:6 D三、解答题(共47分)13.(10分)如图,在口ABCD中,DE丄AB, BF丄CD,垂足分别为E, F.⑴求证:△ADE9ACBF.⑵求证:四边形BFDE为矩形.【证明】(1) VDE丄AB,BF丄CD,A ZAED=ZCFB=90° ,・・•四边形ABCD为平行四边形,・・・AD=BC, ZA=ZC,(/-AED =乙CFB,厶1 = zC,在Z\ADE 和Z\CBF 屮,I A。
2022年九年级物理下册第十八章家庭电路与安全用电达标检测卷新版粤教沪版

第十八章达标检测卷一、选择题(每题3分,共36分)1.家庭电路是最常见、最基本的实用电路,我国家庭电路的电压是( ) A.380 V B.220 V C.110 V D.36 V2.关于家庭电路和安全用电,下列说法准确的是( )A.控制各灯具的开关都应该安装在零线上B.有金属外壳的用电器都使用两脚插头C.应该定期对漏电保护器进行检查D.不接触高压设备就不会引起触电事故3.现在一般标准住宅户内配电系统都使用了空气开关、漏电保护器、三孔插座等设备,有一配电系统如图所示,其中各个设备的特征是( )A.电能表上可以直接读出应该交的电费B.空气开关的作用与保险丝的作用完全相同C.三孔插座正中间的插孔应接三脚插头的最长的那只脚D.漏电保护器用于当灯泡的灯丝烧断时,将电流导入大地4.某同学家的电灯均正常工作,当他把“220 V16 W”的台灯插入插座后,闭合台灯开关,室内电灯全部熄灭。
发生这一现象的原因可能是( )A.插座处短路B.台灯灯头处短路C.插座处断路D.台灯灯头处断路5.高压输电线路的铁塔顶端有一条(或两条)比下面输电线细的金属线,它的作用是( ) A.加强铁塔的稳定性B.传输零线的电流C.防雷电起到避雷针的作用D.作为备用线,供输电线断开时应急使用6.图中多孔插座冒烟的原因是由于电路中( )A.总电流过大B.总电阻过大C.总电压过高D.总电功过大7.下列图中符合安全用电与保护原则的是( )8.下列四种情况中,人相对安全的是(请同学们千万不要尝试做本实验)( )9.下列措施中不属于节约用电的是( )A.电视机不用时切断电源B.离开教室随手关灯C.夏天用空调时把温度调得很低D.用节能灯代替白炽灯10.某天,溧阳赵先生家中井水突然变热至47 ℃,让人恐慌。
维修电工访谈得知:水井内有抽水泵(电动机),原来可以正常工作,井水温度也正常;自从水泵坏了之后,开关S 就一直断开,但井水温度从此明显变高,电工检测发现:开关处确实断开,但水泵和井水都带电。
九年级物理第十八章《电功率》综合测试卷-人教版(含答案)

九年级物理第十八章《电功率》综合测试卷-人教版(含答案)一、选择题(本大题共12小题)1.如图所示电路的电源电压保持不变,闭合开关S后,将滑动变阻器的滑片向左移动的过程中()A.电流表示数变小B.电压表示数不变C.两表示数之比不变D.电阻R1的功率变小2.下列用电器利用电流热效应工作的是()A.平板电脑B.智能手机C.电视机D.电热毯3.从发电站到用电地区,通常都有一段相当长的距离。
根据焦耳定律,目前采用高压输电的方式可以减少远距离输电中的电能损失,因为这样减小了输电线中的()A.电压B.电流C.电阻D.通电时间4.将两只分别标有“6V 3W”和“3V 3W”的小灯泡L1和L2串联接在电源电压恒为6V的电路中,设两只小灯泡电阻不变,则()A.两只小灯泡的电阻之比R1:R2=2:1B.两只小灯泡的实际功率之比P1:P2=4:1C.小灯泡L1可以正常发光D.电路消耗的总功率为3W5.我国对超导体新材料的研究被收录在《改革开放先锋创新发展引擎﹣﹣中国科学院改革开放四十年》一书中,并高居榜首。
超导现象指的是某些物质在很低的温度时,如铝在﹣271.76℃以下,铅在﹣265.95℃以下,电阻就变成了0。
假如某种超导体新材料已经可以在常温下使用,你认为这种材料最适合用来做()A.保险丝B.电炉丝C.输电导线D.灯丝6.如图所示是定值电阻R和小灯泡L的U﹣I图像,下列依据图像信息的判断正确的是()A.当通过R的电流为0.1A时,它两端的电压为1VB.当L两端电压为2.5V时,其电阻为10ΩC.将R和L串联,若电流为0.3A,则电路消耗的总功率为0.6WD.将R和L并联,若电压为1V,则电路的总电流为0.4A7.如图所示的仪表装在家庭电路中,它是用来测量整个家庭电路中所有用电器在一段时间内消耗的()A.电能B.电流C.电功率D.电压8.如图所示,电源电压保持12V不变,小灯泡L上标有“6V 3W”字样,滑动变阻器最大阻值R=60Ω。
第十八章 能源与可持续发展 单元自测卷

第十八章能源与可持续发展单元自测卷满分:100分时间:90分钟一、选择题(每小题3分,共48分)1.能源危机是人类社会面临的一个重大问题.有的能源消耗完了以后,不可能在短期内从自然界得到补充,我们称此类能源为“不可再生能源”.下列各种能源中,属于“不可再生能源”的是( )A.太阳能B.水能C.风能D.化石能源2. (2010.天津)人类大量使用下列能源,会造成空气污染加剧的是( )A.化石能源B.太阳能C.风能D.地热能3.太阳能可以直接利用,下列装置中,把太阳能间接转化成电能的是( ) A.硅光电池B.植物进行光合作用C.太阳能集热器D.太阳能热电站4.为缓解电力紧张的状况,开发利用新能源,我国陆续建成了一些核电站.关于核电站,下列说法中正确的是( )A.核电站使用的核燃料是石油或天然气B.核反应堆中发生的是不可控制的核裂变C.核电站发电的能量转化过程是:核能——内能——机械能——电能D.核电站产生的核废料可以像生活垃圾那样被处理或进行二次加工利用5.利用焚烧垃圾来发电,此过程中的能量转化过程是( )A.化学能——内能——电能B.太阳能——内能——电能C.核能——内能——电能D.电能——太阳能——内能6.关于能源和能源的利用,下列说法中正确的是( )A.因为能量是守恒的,所以不存在能源危机B.太阳能无法被人类直接利用C.天然气可以直接从自然界获取,是一次能源D.温室效应使全球气温上升,对人类非常有利7.为缓解现在的能源危机,下列措施中不可行的是( )A. 大力开发新能源B.只要人类不使用能,量就可以了C.大量利用水能、风能D.采用新技术、新设备,更新落后的技术装备8.(2010.鸡西)关于能源的描述,下列说法中正确的是( )9.小明学习了本章的知识后,做了如下总结,其中有一条总结的内容有错误,请你帮他超出来( )A.现在人类社会使用的能源主要是煤、石油和天然气B.电能是最重要的二次能源C.木材、草类、肉类等由生命物质提供的能源称为生物质能D.地热能是不可再生能源的典型例子10.(2010·成都)下列关于杠杆或能量守恒的说法中,不正确的是( ) A.在使用杠杆的过程中,不可能既省力又省距离B.天平是等臂杠杆,既不省力又不省距离C.由能量守恒定律可知,永动机总是可以制造成功的D.由能量守恒定律可知,滑轮组的机械效率不可能达到100%11.学习了内能及能量的转化和守恒定律后,同学们在一起梳理知识时交流了以下想法.你认为其中不正确的是( )A.做功改变物体的内能是不同形式的能的相互转化B.热传递改变物体的内能是不同形式的能的相互转化C.各种形式的能在一定条件下都可以相互转化D.能量在转化和转移的过程中总会有损耗,但能量的总量保持不变12.(2010·连云港)目前,“低碳”、“绿色”等词语逐渐成为人们日常生活中谈论的热门话题,各级政府对此高度重视,并采取了一系列措施.下列措施中不符合“低碳”、“绿色”要求的是( )A.大力发展风力发电B.倡导多乘公交车,少开私家车C.大力发展火力发电D.加大对污染企业的减排监管力度13.下列关于“能量转化”的说法中,正确的是( )A.奥运冠军刘翔在110 m栏比赛的奔跑中,不断将他的内能转化为机械能B.汽车发动机熄火后,在继续前进的过程中,内能转化为机械能C.巨大的海浪在高速行进中,伴随着动能与势能的相互转化D.电源种类很多,工作时都是不断将机械能转化为电能14.关于能源与环境,下列说法中正确的是( )A.光的应用不会造成环境污染,城市建筑可以随意使用玻璃幕墙B.彩电、空调、手机等家用电器在使用中,对人和环境不会产生任何不利的影响C.石油、煤、天然气的开采和使用不会造成环境污染和生态破坏D.太阳能是一种既无污染,又取之不尽的新能源15.如图所示是一种在阳光下能不断摇摆的塑料小花.花盆表面的太阳能电板在光照下,产生电流驱动电动机,使小花左右摆动.下列有关该小花摆动过程中能量转化的描述,正确的是( )A.叶片将光能转化为化学能B.电动机将机械能转化为电能C.太阳能电板将太阳能转化为电能D.小花将动能转化为化学能16.(2010·哈尔滨)物理学是一门认识世界、改变世界的科学,它的发展对改变世界的贡献有下列说法,其中不正确的是( )A.蒸汽机推动了第一次工业革命B.电磁感应现象使人类社会进入了电气化时代C.信息技术改变着我们的科技、经济和生活D.新能源是不可再生的能源,它促进了世界的可持续发展二、填空题(每空1分,共28分)17.绿色植物通过光合作用将太阳能转化成________ (内能/化学能).为开发新能源,人类已能够把油菜子、蓖麻、大豆等农作物加工转化成“生物燃料”,“生物燃料”属于________________ (可再生能源/不可再生能源).18.(2010·泰州)如图所示表示白炽电灯将电能转化为光能和内能的大致比例,由此可以计算出,白炽电灯的发光效率为________ .一般节能灯的发光效率为30%,它只要有W 的功率就可以达到60 W的白炽灯的亮度.19.(2010·广东)如图所示是太阳能LED照明路灯,它主要由太阳能电池板、LED灯头等部分构成.LED是一种发光二极管,通过电流能够发光,可以把电能直接转化成________能.太阳能是________ (一次/二次)能源,清洁无污染,它是在太阳内部,氢原子核发生________ (裂变/聚变)释放出的核能.20.(2010·莆田)为了响应国家节能减排的号召,莆田市大力加快能源产业建设,并划分出四大基地:(1)福建液化天然气(LNG)及冷能利用生产基地.①纯净天然气是无色、无味的气体,使用前通常在天然气中加人有特殊气味的气体,以便泄漏时能及时察觉到.人能闻到这种气味.说明分子在永不停息地________.②液化天然气使用前要变成气体,这个过程叫________ (填物态变化的名称),在这个过程中,液化天然气要________热.③天然气的热值约为8×107 J/m3,完全燃烧3 m3的天然气能放出约________J的热量.(2)兴化湾风力发电生产基地.风力发电机是根据________________原理工作的.(3)仙游水力发电生产基地.利用水力发电时,是将水的________能转化为电能.(4)莆田高新技术同区太阳能光伏产业生产基地.利用太阳能的优点之一是:____________________________________________________________________________。
2023年人教版九年级物理全册第18章【电功率】复习检测卷及答案

2023年九年级物理全册第18章【电功率】复习检测卷一、选择题。
1、两个定值电阻R1、R2分别接入各自的电源使用时,通过各个电阻的电流I1=I2,如图所示,已知R1=2R2,当通电时间相等时每个电阻消耗电能W1、W2,则()A.W1=2W2B.W1=4W2C.W1=W2D.W1<W22、小科为探究“电压一定时,电流与电阻之间的关系”,设计了如图实验。
先在AB间接入10欧的定值电阻R1,移动滑片P,读取电压表、电流表示数并记录;然后用15欧的定值电阻R2替换R1后,接下来的操作和操作后的电路详解正确的是()A.注视电压表,并向左调节滑片B.注视电流表,并向右调节滑片C.操作后,电路消耗的电功率减小D.操作后,电路消耗的电功率保持不变3、老师要求同学们只能用电压表的“0—3V”量程测量额定电压为3.8V小灯泡的额定功率,所给电源的电压恒为6V,其他器材均符合实验要求。
如图是同学们设计的四种实验电路图,则能完成实验的电路图是()4、将规格都是“220V180W”的一台电冰箱、一台电脑和一床电热毯,分别接入同一家庭电路中,若通电时间相同,则下列说法正确的是()A.电冰箱产生的热量最多B.电脑产生的热量最多C.电热毯产生的热量最多D.三者产生的热量一样多5、如图所示为探究“焦耳定律”的实验装置。
两个透明容器中密封着等量的空气,U型管中液面高度的变化反映密闭空气温度的变化。
将容器中的电阻丝R1、R2串联在电路中,且R1<R2。
下列说法正确的是()A.该实验装置用于探究“电压和通电时间一定时,电热与电阻的关系”B.闭合开关后,通过R1的电流大于R2的电流C.闭合开关后,甲管中液面上升比乙慢D.闭合开关后,要使电流增大,应将滑动变阻器滑片P向左移动6、小明家中的电能表如图3所示,下列说法中不正确的是()A.每消耗1kW·h电能,电能表的转盘转了2500转B.电能表的额定电压为220V,允许通过的最大电流为10AC.小明家中“220V7A”的电烤炉和“220V5A”的电热壶可以同时正常工作D.电能表读数的单位是kW·h7、如图所示,电源电压保持不变闭合开关S,灯泡正常发光(假设灯丝电阻不变),在滑动变阻器滑片P 从中点向下滑动的过程中()A.两电流表示数均变小,灯泡变暗B.电路中的总功率变大C.电流表A1示数变小,电压表V示数变大,灯泡变亮D.电流表A2示数变小,电压表V示数不变,灯泡亮度不变8、要测量小灯泡的电功率,必须要测的物理量是()A.电流和电阻B.电流和电压C.电阻和电压D.电功和电流9、对下列四幅图的分析正确的是()A.图中蓝牙耳机是通过超声波与手机进行信号传输的B.如图装置可用来探究电流产生的热量与通电时间的关系C.图中电路能探究电磁铁磁性强弱与电流大小关系D.图中电路可以探究导体电阻与导体材料的关系10、有两个电阻,R1<R2,采用下列几种方式分别接到电压为U的电源上,在相同时间内电流做功最少的连接方式是()A.R1、R2并联B.R1、R2串联C.只接入R1D.只接入R211、如图所示,电源电压恒为4.5V,电流表的量程为“0~0.6A”,电压表的量程为“0~3V”,灯泡L标有“2.5V 1.25W”字样(设灯丝电阻不变),滑动变阻器R的规格为“20Ω1A”。
人教版初二数学8年级下册 第18章(平行四边形)达标测试卷(含答案)

第十八章平行四边形达标测试卷一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【广州期中】矩形具有而平行四边形不一定具有的性质是( )A.对边相等B.对角相等C.对角线相等D.对角线互相平分2.【广州天河区校级期中】下列条件中,能使菱形ABCD为正方形的是( ) A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD 3.【广东】如图,在△ABC中,BC=4,点D,E分别是AB,AC的中点,则DE=( )A.14B.12C.1 D.24.如图,在▱ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则BC的长是( )A.6 cm B.6.5 cm C.7 cm D.7.5 cm5.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )A.67.5° B.22.5° C.30° D.45°6.【中山期中】如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AD的长为( )A.4B.5C.3 D.4 37.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件后,不能判定四边形ABCD为菱形的是( )A.AC⊥BD B.AB=ADC.AC=BD D.∠ABD=∠CBD8.【教材P50习题T8变式】如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为( )A.(2,3) B.(3,2) C.(3,3) D.(3,3)9.如图,在△ABC中,AC=3,AB=4,BC=5,P为BC上一动点,PG⊥AC于点G,PH⊥AB于点H,M是GH的中点,P在运动过程中PM的最小值为( ) A.2.4B.1.4C.1.3 D.1.210.【教材拓展】如图,点A,B为定点,定直线l∥AB,P是l上一动点,M,N 分别为PA,PB的中点,下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是( )A.②③B.②⑤C.①③④D.④⑤二、填空题:本大题共5小题,每小题3分,共15分.11.【广州花都区期末】若直角三角形的两条直角边的长分别是3和4,则斜边上的中线长为________.12.【教材P57练习T2改编】如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.13.如图,▱ABCD的对角线AC,BD相交于点O,E是AB的中点,△BEO的周长是8,则△BCD的周长为________.14.【东莞期中】如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加______________条件,才能保证四边形EFGH是矩形.15.如图,在正方形ABCD中,AB=3,点E在边CD上,且DE=1,将△ADE沿AE折叠到△AFE,延长EF交边BC于点G,连接AG,CF. 则CG的长为________.三、解答题(一):本大题共3小题,每小题8分,共24分.16.【广州天河区期末】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,AC=CD=1,求BC的长.17.如图,在▱ABCD中,AE平分∠BAD,交CD于点E,CF平分∠BCD,交AB 于点F.求证:AE=CF.18.【汕头潮南区期中】已知:如图,在矩形ABCD中,E,F分别是边CD,AD 上的点,AE⊥BF,且AE=BF.求证:矩形ABCD是正方形.四、解答题(二):本大题共3小题,每小题9分,共27分.19.如图,在△ABC中,∠ACB=90°,点D是AB的中点,连接CD,过点D作DE ⊥AC于点E,延长DE到点F,使得EF=DE,连接AF,CF.(1)根据题意,补全图形;(2)求证:四边形ADCF是菱形.20.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD=________°时,四边形BECD是矩形.21.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G 在AB上,EF⊥AB,OG∥EF,连接OE.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.五、解答题(三):本大题共2小题,每小题12分,共24分.22.【惠州惠城区一模】如图,正方形ABCD中,AB=6,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED交BC于点F,以DE、EF为邻边作矩形DEFM,连接CM.(1)求证:矩形DEFM是正方形;(2)求CE+CM的值.23.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.(1)当点E在线段BC的延长线上时,如图②,猜想AB,CG,CE之间的关系并证明;(2)当点E在线段CB的延长线上时,如图③,直接写出AB,CG,CE之间的关系.答案一、1.C 2.B 3.D 4.C 5.B 6.D 7.C 8.D9.D 点拨: 连接PA ,如图.∵AC =3,AB =4,BC =5,∴AC 2+AB 2=BC 2,∴△ABC 是直角三角形,∠BAC =90°.∵PG ⊥AC 于点G ,PH ⊥AB 于点H ,∴∠PGA =∠PHA =90°,∴四边形AGPH 为矩形,∴AP 与GH 互相平分且相等.∵M 是GH 的中点,∴M 是AP 的中点.当AP ⊥BC 时,AP 最小,此时,△ABC 的面积为12BC ·AP =12AC ·AB ,则AP =AC ·AB BC =3×45=2.4,∴PM =12AP =1.2.即PM 的最小值为1.2.10.B 点拨:∵点A ,B 为定点,M ,N 分别为PA ,PB 的中点,∴MN 是△PAB的中位线.∴MN =12AB ,即线段MN 的长度不变.∵PA ,PB 的长度随点P 的移动而变化,∴△PAB 的周长会随点P 的移动而变化.∵MN 的长度不变,点P 到MN 的距离等于l 与AB 的距离的一半,∴△PMN 的面积不变.直线MN ,AB 之间的距离不随点P 的移动而变化.∠APB 的大小随点P 的移动而变化.综上所述,会随点P 的移动而变化的是②⑤.二、11.2.5 12.30 13.16 14. AC ⊥BD (答案不唯一)15.32 点拨:∵四边形ABCD 为正方形,∴AD =AB =BC =CD =3,∠BAD =∠B =∠BCD =∠D =90°,由折叠可知,AF =AD =3,∠AFE =∠D =90°,DE =EF =1,∴AB =AF =3,CE =2,∠AFG =90°.又∵AG =AG ,∴Rt △ABG ≌Rt △AFG ,∴BG =FG .设CG =x ,则BG =FG =3-x ,∴EG =4-x .在Rt △EGC 中,(4-x )2=x 2+22,解得x =32.∴CG =32.三、16.解:在Rt △ABC 中,∠ACB =90°,CD 是斜边AB 上的中线,则AB =2CD=2,由勾股定理得BC =AB 2-AC 2=22-12=3.17.证明:∵四边形ABCD 为平行四边形,∴AD =BC ,∠D =∠B ,∠BAD =∠BCD .又∵AE 平分∠BAD ,CF 平分∠BCD ,∴∠DAE =12∠BAD ,∠BCF =12∠BCD .∴∠DAE =∠BCF .在△DAE 和△BCF 中,{∠D =∠B ,DA =BC ,∠DAE =∠BCF ,∴△DAE ≌△BCF .∴AE =CF .18.证明:∵四边形ABCD 是矩形,∴∠BAD =∠ADE =90°,∴∠ABF +∠AFB =90°.∵AE⊥BF,∴∠DAE+∠AFB=90°,∴∠ABF=∠DAE.在△ABF和△DAE中.{∠ABF=∠DAE,∠BAF=∠ADE=90°,BF=AE,∴△ABF≌△DAE,∴AB=AD,∴矩形ABCD是正方形.四、19.(1)解:补全图形如图.(2)证明:∵DE⊥AC,∴∠AED=90°=∠ACB,∴DE∥BC.∵D是AB的中点,∴DE是△ABC的中位线,∴AE=EC.又∵ED=EF,∴四边形ADCF是平行四边形.∵AC⊥DE,即AC⊥DF,∴四边形ADCF是菱形.20.(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC.∴∠OEB=∠ODC.∵O为BC的中点,∴BO=CO.在△BOE和△COD中,{∠OEB=∠ODC,∠BOE=∠COD,BO=CO,∴△BOE≌△COD.∴OE=OD.又∵BO=CO,∴四边形BECD是平行四边形.(2)10021.(1)证明:∵四边形ABCD是菱形,∴BD⊥AC,OB=OD.∵E是AD的中点,∴AE=DE,∴OE是△ABD的中位线,∴OE∥FG.又∵OG∥EF,∴四边形OEFG是平行四边形.∵EF⊥AB,∴∠EFG=90°,∴四边形OEFG是矩形.(2)解:∵四边形ABCD是菱形,∴BD⊥AC,AB=AD=10,∴∠AOD=90°.∵E是AD的中点,∴OE=AE=12AD=5.由(1)知,四边形OEFG是矩形,∴FG=OE=5.∵AE=5,EF=4,∴AF=AE2-EF2=3,∴BG=AB-AF-FG=10-3-5=2.五、22.(1)证明:如图,作EG⊥CD于点G,EH⊥BC于点H.∵四边形ABCD是正方形,∴∠BCD=90°,∠ACB=∠ACD.∵EG⊥CD,EH⊥BC,∴∠EGC=90°,∠EHC=90°,EG=EH,∴∠EGC=∠EHC=∠BCD=90°,∴四边形EGCH是正方形,∴∠GEH=90°.∵四边形DEFM是矩形,∴∠DEF=90°.∴∠DEG=∠FEH.又∵EG=EH,∠EGD=∠EHF=90°,∴△EGD≌△EHF,∴ED=EF.∴矩形DEFM是正方形.(2)解:∵四边形DEFM是正方形,四边形ABCD是正方形,∴DE=DM,AD=CD=AB=6,∠ADC=∠EDM=90°,∴∠ADE=∠CDM,∴△ADE≌△CDM,∴AE =CM .∴CE +CM =CE +AE =AC =AD 2+CD 2=62+62=6 2.23.解:(1)AB =CG -CE .证明:∵四边形ABCD 是菱形,∴AB =BC .又∵∠BAC =60°,∴△ABC 是等边三角形.∴AB =AC .∵∠EAG =60°,∴∠BAC =∠EAG .∴∠BAC +∠CAE =∠EAG +∠CAE ,即∠BAE =∠CAG .又∵四边形AEFG 是菱形,∴AE =AG .在△ABE 和△ACG 中,{AB =AC ,∠BAE =∠CAG ,AE =AG ,∴△ABE ≌△ACG .∴BE =CG .∵AB =BC =BE -CE ,∴AB =CG -CE .(2)AB =CE -CG .。
九年级物理全一册第十八章《电功率》综合检测卷-人教版(含答案)

九年级物理全一册第十八章《电功率》综合检测卷-人教版(含答案)时间:60分钟总分:100分一、选择题(每小题4分,共20分)1. 小明家上次查看电能表示数为 ,本次查看时电能表读数如图所示,则下列说法正确的是( )A.他家在这段时间内消耗的电能为903 kW·hB.电能表是测量电功率的仪表C.若只让一个标有“220 V 1 000 W”的电热水器正常工作10 min,则电能表的铝盘转600转D.这个电能表的额定功率为2 200 W2. 根据额定电压为 2.5 V的小灯泡的I-U图像(如图所示)分析,下列结论正确的是( )A.当小灯泡两端的电压为0 V时,其电阻为0 ΩB.当通过小灯泡的电流为0.1 A时,其实际功率为0.1 WC.通过小灯泡的电流与其两端的电压成正比D.小灯泡的额定功率为0.625 W3. 将规格为“2.5 V0.3 A”的小灯泡L1和规格为“3.8 V0.3 A”的小灯泡L2串联,接在3 V的电源上,忽略灯丝电阻随温度的变化,下列判断正确的是 ( )A.L1的电阻大于L2的电阻B.L1的亮度比L2的亮度更小C.两只灯泡都正常发光D.两只灯泡实际功率相等4. 在如图甲所示的电路中,分别把定值电阻R1、R2(R1>R2)接入A、B之间进行实验,并根据电流表和电压表示数画出A、B之间电阻的P-U图像,如图乙所示.如果把R1和R2并联后接入A、B之间进行实验,同理,可以在图乙中画出A、B之间电阻的P-U图像③.则图像①所对应的电阻和图像③所在的区域分别是 ( )A.R1和ⅠB.R1和ⅢC.R2和ⅠD.R2和Ⅲ5. 如图,电源电压恒为4.5 V, 的量程为“0~0.6 A”, 的量程为“0~3 V”,灯泡上标有“2.5 V 1.25 W”(不考虑灯丝电阻变化),滑动变阻器R的规格为“20 Ω 1 A”.闭合开关,在保证电路安全的情况下,移动滑片P的过程中( )A. 的示数最大为0.6 AB.灯泡的最小功率为0.12 WC.电路的最大总功率为2.7 WD.滑动变阻器接入电路的最小电阻为4 Ω二、填空题(每空2分,共20分)6. 如图所示,电热水壶上标有“220 V 1 800 W”,小明发现烧水过程中热水壶的发热体部分很快变热,但连接的电线却不怎么热,这是因为导线的电阻比发热体的电阻.在额定电压下,烧开一壶水用时3 min 20 s,这段时间内电热水壶发热体产生的热量为J.7. 某手机电池的容量为4 200 mA·h,电压为3.7 V.用一个标有“输出5 V 4 A”的快速充电器,将手机电池从零电量充满,充电效率为84%,需要min.快充充电线比普通手机充电线要粗一些,这是因为正常工作时,通过快充充电线的较大. 8. 如图,灯L标有“4 V 2 W”,R=20 Ω,闭合开关S时,灯L正常发光(灯丝的电阻不受温度影响),电流表示数为A,通电1 min 电路中产生的热量为J.9. 灯A标有“220 V100 W”字样,灯B标有“220 V25 W”字样,设它们的电阻不随温度的变化而变化,如果将它们串联起来,接在220 V的电路中,A灯两端的电压为V,A与B的电功率之和为W.10. 如图甲所示的电路中,电源电压保持不变,闭合开关S,滑动变阻器的滑片P从a端移动到b端的整个过程中,电流表示数I与电压表示数U的关系图像如图乙所示.则定值电阻R1的阻值为Ω;当变阻器的滑片P处于a端时,定值电阻R1的电功率为W.三、实验探究题(第11小题9分,第12小题14分,第13小题14分,共37分)11. 某科学小组对电流通过导体产生热的多少与哪些因素有关进行了研究.装置如图,甲、乙两个烧瓶内装满煤油,瓶塞上各插1根玻璃管,瓶内各装1根阻值不同的电阻丝R R乙.甲和猜想一:通电时间相同时,电热跟电流的大小有关,电流越大电热越多.猜想二:通电时间相同时,电热跟导体的电阻大小有关,电阻越大电热越多.为验证猜想一,设计以下方案:①将电阻丝R甲和R乙串联在电路中,标出2根玻璃管内液面的位置,闭合开关记下电流表的读数I1,经过一段时间后标出2根玻璃管内液面的位置;②断开开关,当2根玻璃管中的液面降到原来的高度后,减小滑动变阻器接入电路的阻值,闭合开关,记下电流表的读数I2,经过相同时间后标出2根玻璃管内液面的位置.请回答下列问题:(1)为使实验现象明显,经常会采用转换或放大的思想,为比较电热丝产生热量的多少,实验中体现这些思想的设计有(写出一条即可).(2)为验证猜想一,必须比较同一个烧瓶中前后两次玻璃管内液面上升的高度,原因是.(3)科学研究倡导有依据的猜想,请说出生活中支持猜想二的一个实例: .12. 在“探究小灯泡在不同电压下工作时的电功率是否相同”实验中,实验室提供了如下器材:电源(电压U恒为8 V),滑动变阻器(规格为“20 Ω 2 A”),小灯泡(额定电压U额= 2.5 V,额定功率小于1.2 W),两个阻值分别为10 Ω、20 Ω的定值电阻(定值电阻用R0表示).(1)为使小灯泡两端电压有一较大的调节范围,小聪设计了如图甲所示的电路,请用笔画线代替导线,完成图乙中实物电路的连接.(2)正确连接电路后,进行实验,记录的数据如下表所示.当电压表示数为2.5 V时,电流表示数如图丙所示,小灯泡的额定功率为W.(3)分析表中数据可得出结论:小灯泡工作时,电功率随电压的增大而.根据数据还可判断出,小聪在实验中选用的是R0= Ω的定值电阻.(4)完成实验后,爱动脑筋的小聪又想出一种测量小灯泡额定功率的方法,设计了如图丁所示的电路,所用电压表量程为“0~15 V”,请将以下实验步骤补充完整.①检查电路无误后,闭合开关S,将开关S1拨至“1”,调节滑动变阻器滑片直至电压表示数为;②滑片不动,再将开关S1拨至“2”,读出电压表示数为U0;③小灯泡的额定功率:P额= .(用U额、U0、R0表示)若步骤②中,在将开关S1拨至“2”时,不小心将滑片向右移动了少许,其他操作正确,则测出的小灯泡额定功率(填“偏大”或“偏小”).13. “西电东送”是将我国西部发电厂发出的电传输到我国东部.由发电厂输出的电功率是一定的,它取决于发电机组的发电能力.根据P=UI中发电机的功率不变效应,若提高输电线路中的电压U,那么线路中的电流I一定会减小;反之亦然.输电线路的电能损耗主要是输电线的电流热效应,输电线损失的热功率P=I2R,所以采用的输电线的电阻要尽量小.如果线路中电流降低到原来的12,那么线路中损失的热功率就减小为原来的14,因此提高电压可以很有效地降低输电线路中的热功率损失.设发电厂的输出电功率P0=1.1×108 W,输电线路上的总电阻为10 Ω.(1)若采用110 kV的高压输送电能,输电线路的电流I1= A,输电线路损失的热功率P1= W,其与发电厂的输出电功率P0之比P1∶P0= .(2)若采用1100 kV超高压输送电能,输电线路损失的热功率P2= W,其与高压输送电能损失的热功率P1之比P2∶P1= ,所以采用超高压远距离输电可以大大降低输电线路的的损失.(3)若想使输电线路中的热功率损耗为零,还可以采用作为输电线材料.四、计算题(第14小题10分,第15小题13分,共23分)14. 如图所示是某型号的爆米花机的电路图,该爆米花机具有制作和保温的功能.只闭合开关S1时,R1加热,电动机搅拌,开始制作爆米花;只闭合开关S2时,R2保温,防止爆米花变凉.爆米花机的铭牌如表所示.[c玉米=1.2×103J/(kg·℃)](1)将100 g、20 ℃的玉米粒加热到300 ℃成为爆米花时,求玉米粒需要吸收的热量;(2)电阻R1发热,把100 g、20 ℃的玉米粒加热成为爆米花,需要用时5 min,求R1的加热效率;(3)求保温电阻R2的阻值.15. 如图所示,电源电压恒为4.5 V,灯泡L上标有“3 V 1.5 W”字样,滑动变阻器R2上标有“15 Ω 1 A”字样,定值电阻R1的阻值为10 Ω,电流表量程为0~3 A,电压表量程为0~3 V,不计温度对灯丝电阻的影响.求:(1)灯泡正常工作时的电阻.(2)当开关S、S1、S2闭合,S3断开时,电路的最小总功率.(3)当开关S、S3闭合,S1、S2断开时,在确保电路元件安全的情况下,滑动变阻器R2的取值范围.参考答案一、选择题1.C 电能表的两次示数之差就是小明家在这段时间所消耗的电能,W=8 633.5 kW·h-8 543.2 kW·h=90.3 kW·h,A错;电能表是测量家用电器消耗的电能的仪表,B错;“220 V1 000 W”的电热水器正常工作10 min 消耗的电能W'=Pt =1 000 W×10×60 s=6×105J,根据电能表上的参数“3 600 r/(kW·h)”可知,电能表的铝盘转动一转表示用电器消耗的电能W 1=13 600×3.6×106 J=1×103 J,所以该电能表的铝盘转动的转数n =6×105J1×103J =600,C 正确;该电能表所在电路允许同时工作的用电器的总功率P'=UI =220 V×10 A=2 200 W,但这不是电能表的额定功率,D 错.2.D 导体的电阻是导体本身的一种性质,当导体两端的电压为0时,导体的电阻不会为0,故A 错;由题图知,当通过小灯泡的电流为0.1 A 时,小灯泡两端的电压为0.5 V,其实际功率P 实=IU =0.1 A×0.5 V=0.05 W,故B 错;由题图可知,小灯泡的I-U 图像不是一条直线,所以通过小灯泡的电流与其两端的电压不成正比,C 错误;小灯泡的额定电压为2.5 V,由图像可知此时通过小灯泡的电流为0.25 A,故小灯泡的额定功率为P 额=I 额U 额=0.25 A×2.5 V=0.625 W,故选D.3.B 根据R=U I ,可知L 1的电阻小于L 2的电阻,A 错误;两灯串联在3 V 的电源两端时,通过计算可知电路中的电流小于0.3 A,因此两灯均不能正常发光,C 错误;根据P=I 2R 可知,L 1的实际功率小于L 2的实际功率,因此L 1的亮度比L 2的亮度更小,B 正确,D 错误.4.C A 、B 之间电阻的电功率P=U 2R ,当电压U 相等时,由于R 1>R 2,则P 1<P 2,故①表示R 2的P-U 图像,②表示R 1的P-U 图像;当将R 1与R 2并联后接入A 、B 间进行实验时,A 、B 间的电阻R 并<R 2<R 1,当电压U 相等时,P 并>P 2>P 1,故将A 、B 并联后,A 、B 间电阻的P-U 图像在Ⅰ区域.故选C.5.D 由灯泡的铭牌信息知,灯泡的额定电流I额=P 额U 额=1.25 W2.5 V=0.5 A,灯丝的电阻R L =U 额2P 额=(2.5 V)21.25 W =5 Ω.分析电路图知,灯泡与滑动变阻器串联,电压表测量灯泡两端电压,电流表测电路中的电流,电流表选用0~0.6 A 量程,滑动变阻器允许通过的最大电流为1 A,故电路中允许通过的最大电流为0.5 A,即电流表的最大示数为0.5 A,A 错误;电路的最大总功率P 总=UI最大=4.5 V×0.5 A=2.25 W,C 错误;电路中电流最大时,滑动变阻器连入电路的电阻最小为4.5 V0.5 A -5 Ω=4 Ω,D 正确;滑动变阻器连入电路的阻值最大为20 Ω,电路中的总电阻最大为R 总=R L +R 变=5 Ω+20 Ω=25 Ω,电路中的最小电流I 小=U R 总=4.5 V25 Ω=0.18A,灯泡的最小电功率P 小=I 小2R L =(0.18 A)2×5 Ω=0.162 W,B 错误.二、填空题6.【答案】 小 3.6×105【解析】 用电热水壶烧水时,发热体部分和连接的电线串联,电流相等,通电时间相等,电线不怎么热,即Q 较小,由Q=I 2Rt 可知,导线的电阻小.电热水壶发热体产生的热量Q=W=Pt =1 800 W×(3×60 s+20 s)=3.6×105 J.7.【答案】 55.5 电流【解析】 电池充满电时储存的电能W 储=3.7 V×4 200×10-3 A×3 600 s=55 944 J,由充电效率η=84%可得,充电器消耗的电能W充=W 储η=55 944J84%=6.66×104J ,由W=UIt 可得,选用快速充电器将电池从零电量充满需要的时间t=W 充UI=6.66×104 J5V×4 A =3 330 s =55.5 min .正常工作时,通过快充充电线的电流较大,由于导线有电阻,因此充电过程中导线会产生热量,快充充电线做得粗一些,目的是减小充电线的电阻,使充电过程中导线产生的热量少一些.8.【答案】 0.7 168【解析】 闭合开关S 时,L 和R 并联,电流表测干路中的电流,由L 正常发光可知U=U R =U L =4 V,电流表示数I=I R +I L =U R +P L U L=4 V 20 Ω+2 W4 V =0.7 A;通电1 min 电路中产生的热量Q=W=UIt =4 V×0.7 A×60 s=168 J.9.【答案】 44 20 【解析】 灯A 的电阻R A =U 2P A=(220 V)2100 W =484 Ω,灯B 的电阻R B =U 2P B=(220 V)225 W =1 936 Ω,两灯串联接在220 V 的电路中,灯A 两端的电压U A =R A R A +R B U =484 Ω484 Ω+1 936 Ω×220 V=44 V;A 和B的电功率之和P=U 2R A +R B=(220 V)2484 Ω+1 936 Ω=20 W. 10.【答案】 10 0.1【解析】 闭合开关S,R 1与R 2串联,电流表测电路中的电流,电压表测R 1两端的电压.滑片从a 端向b 端移动的过程中,滑动变阻器连入电路中的电阻变小,故电路中电流变大,电压表示数变大,由题中的I-U 图像可知,当滑片P 在b 端时,电压表的示数为3 V,电流表的示数为0.3 A,则R 1=3 V0.3 A =10 Ω;当滑片P 在a 端时,电压表的示数为1 V,电流表的示数为0.1 A,则此时R 1的电功率为P 1=1 V×0.1 A=0.1 W. 三、实验探究题11.【答案】 (每空3分)(1)通过玻璃管内液面上升的高度来反映电热丝产生热量的多少(答案合理即可) (2)保持前后两次电阻的大小相同 (3)相同时间内电水壶中的发热体比连接电水壶的导线放热多(答案合理即可) 12.【答案】 (每空2分)(1)如图所示.(2)1.05 (3)增大10 (4)①5.5 V(或U-U额) ③U额U0R0偏小【解析】(2)由题图丙知,电流表的示数为0.42 A,小灯泡的额定功率为P=UI=2.5 V×0.42 A=1.05 W.(3)由P=UI和表中数据可得出结论:小灯泡工作时,电功率随电压的增大而增大.当小灯泡两端的电压为3.0 V时,滑动变阻器和定值电阻的总阻值为R'=U′I′=8V−3.0V0.44A≈11.4 Ω,因为R'<20 Ω,所以选用的定值电阻应为10 Ω的.(4)①闭合开关S,将开关S1拨至“1”时,小灯泡、R0与滑动变阻器串联,电压表测R0和滑动变阻器两端的总电压,调节滑动变阻器直至电压表示数为5.5 V时,小灯泡两端的电压为8 V-5.5 V=2.5 V=U额,此时小灯泡正常发光;②滑片不动,再将开关S1拨至“2”,读出电压表示数为U0,此时电路中的电流I0=I额=U0R0;③小灯泡的额定功率P额=U额I额=U额×U0R0=U额U0R0.若在步骤②中不小心将滑片向右移动了少许,则电路中的总电阻变大,电流变小,R0两端电压变小,使测得的U0偏小,则测得的额定功率偏小.13.【答案】(每空2分)(1)1 000 1×1071∶11(2)1×1051∶100热功率(3)超导体【解析】(1)由P=UI,可知I1=P0U =1.1×108W110×103V=1 000 A;根据P=I2R可得P1=I12R=(1 000 A)2×10 Ω=1×107 W,则热功率与发电厂的输出功率之比P1∶P0=1∶11.(2)由P=UI可知I2=P0U′=1.1×108W1100×103V=100 A;根据P=I2R可得P2=I22R=(100 A)2×10 Ω=1×105W,则P2∶P1=1∶100,采用超高压远距离输电可以大大降低损失功率,从而降低输电线路的热功率的损失.(3)根据P=I2R可知,如果输电线路的电阻为0,不存在热功率损耗,可采用超导体作为输电线材料.四、计算题14.解:(1)玉米粒需要吸收的热量Q吸=c玉米mΔt=1.2×103J/(kg·℃)×0.1 kg×(300 ℃-20 ℃)=3.36×104 J;(2)W=P加热t时=200 W×5×60 s=6×104 J,η=Q 吸W ×100%=3.36×104 J6×104J ×100%=56%; (3)R 2=U 2P 保温=(220V)222 W =2 200 Ω.15.解:(1)灯泡正常工作时的电阻R L =U 额2P 额=(3 V)21.5 W =6 Ω.(2)当开关S 、S 1、S 2闭合,S 3断开时,灯泡L 被短路,定值电阻R 1与滑动变阻器R 2并联,当滑动变阻器R 2连入电路的阻值最大为15 Ω时,电路中的总电流最小,电路的总功率最小,此时通过R 1的电流I 1=U R 1=4.5 V10 Ω=0.45 A,通过滑动变阻器R 2的电流I 2=U R 2=4.5 V15 Ω=0.3 A, 电路的最小总功率P 最小=U ×(I 1+I 2)=4.5 V×(0.45 A+0.3 A)=3.375 W.(3)当开关S 、S 3闭合,S 1、S 2断开时,R 1断路,灯泡L 与滑动变阻器R 2串联,电压表测滑动变阻器R 2两端电压, 灯泡的额定电流I 额=P 额U 额=1.5 W3 V =0.5 A, 因为灯泡的额定电流I 额=0.5 A,电流表量程为0~3 A,滑动变阻器标有“15 Ω 1 A”字样,所以在确保电路元件安全的情况下,电路中的最大电流为I 最大=0.5 A,此时滑动变阻器连入电路的阻值最小, 电路最小总电阻R 最小=UI最大=4.5 V0.5 A =9 Ω,滑动变阻器R 2连入电路的最小阻值R 2最小=R 最小-R L =9 Ω-6 Ω=3 Ω,因为电压表量程为0~3 V,所以在确保电路元件安全的情况下,滑动变阻器两端电压最大为U R 2=3 V 时,滑动变阻器连入电路的阻值最大, 此时电路中电流最小,为I 最小=U−U R 2R L =4.5 V−3 V6 Ω=0.25 A, 滑动变阻器R 2连入电路的最大阻值R 2最大=U R 2I 最小=3 V0.25 A =12 Ω,综上所述,滑动变阻器R 2的取值范围为3~12 Ω.。
第18章 全等三角形 单元测试卷2021-2022学年人教版(五四制)七年级下册数学( 含答案)
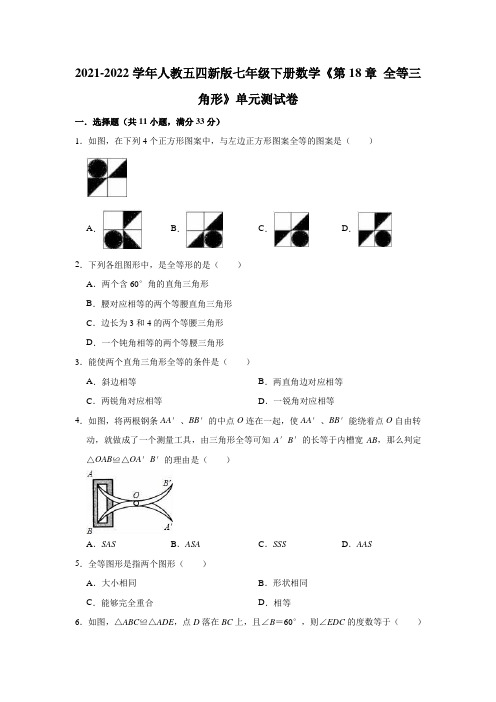
2021-2022学年人教五四新版七年级下册数学《第18章全等三角形》单元测试卷一.选择题(共11小题,满分33分)1.如图,在下列4个正方形图案中,与左边正方形图案全等的图案是()A.B.C.D.2.下列各组图形中,是全等形的是()A.两个含60°角的直角三角形B.腰对应相等的两个等腰直角三角形C.边长为3和4的两个等腰三角形D.一个钝角相等的两个等腰三角形3.能使两个直角三角形全等的条件是()A.斜边相等B.两直角边对应相等C.两锐角对应相等D.一锐角对应相等4.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是()A.SAS B.ASA C.SSS D.AAS5.全等图形是指两个图形()A.大小相同B.形状相同C.能够完全重合D.相等6.如图,△ABC≌△ADE,点D落在BC上,且∠B=60°,则∠EDC的度数等于()A.45°B.30°C.60°D.75°7.如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是()A.AD∥BC B.DF∥BE C.∠D=∠B D.∠A=∠C8.如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC 的面积是()A.30cm2B.40cm2C.50cm2D.60cm29.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为()A.90°B.105°C.120°D.135°10.如图,已知BC=BD,那么添加下列一个条件后,仍无法判定△ABC≌△ABD的是()A.AC=AD B.∠ABC=∠ABD C.∠C=∠D=90°D.∠CAB=∠DAB 11.如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为()A.21B.24C.27D.30二.填空题(共10小题,满分30分)12.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是.13.如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC 全等的图形是.14.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与对应;B与对应;C与对应;D与对应.15.如图,已知△ABC≌△DCB,∠BDC=35°,∠DBC=50°,则∠ABD=.16.如图,已知∠1=∠2,要判定△ABD≌△ACD,请你添加一个条件,是.(写出一个条件即可)17.如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件:.18.如图,在由6个相同的小正方形拼成的网格中,∠2﹣∠1=°.19.如图,∠A=∠B=90°,AB=100,E,F分别为线段AB和射线BD上的一点,若点E 从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为2:3,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为.20.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4.则两条凳子的高度之和为.21.如图,在△ACD中,∠CAD=90°,AC=6,AD=8,AB∥CD,E是CD上一点,BE 交AD于点F,若EF=BF,则图中阴影部分的面积为.三.解答题(共6小题,满分57分)22.已知,如图,△ABC≌△DEF,求证:AC∥DF.23.如图,AB=AC,请你添加一个条件,使△ABE≌△ACD,(1)你添加的条件是;(2)根据上述添加的条件证明△ABE≌△ACD.24.如图所示,CD=CA,∠1=∠2,EC=BC,求证:△ABC≌△DEC.25.如图所示,△ABC≌△ADE,且∠CAD=10°,∠D=25°,∠EAB=120°,求∠DFB 的度数.26.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′(1)其中,符合要求的条件是.(直接写出编号)(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.27.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE 长.参考答案与试题解析一.选择题(共11小题,满分33分)1.解:能够完全重合的两个图形叫做全等形.A、B、D图案均与题干中的图形不重合,所以不属于全等的图案,C中的图案旋转180°后与题干中的图形重合.故选:C.2.解:A、两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;B、腰对应相等的两个等腰直角三角形,符合AAS或ASA,或SAS,是全等形;C、边长为3和4的两个等腰三角形有可能是3,3,4或4,4,3不一定全等对应关系不明确不一定全等;D、一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.故选:B.3.解:A选项,无法证明两条直角边对应相等,因此A错误.C、D选项,在全等三角形的判定过程中,必须有边的参与,因此C、D选项错误.B选项的根据是全等三角形判定中的SAS判定.故选:B.4.解:∵O是AA′、BB∴AO=A′O,BO=B′O,在△OAB和△OA′B′中,∴△OAB≌△OA′B′(SAS),故选:A.5.解:全等图形是指两个图形的形状和大小都相等,故选:C.6.解:∵△ABC≌△ADE,∴∠B=∠ADE=60°,AB=AD,∴∠ADB=∠B=60°,∴∠EDC=60°.故选:C.7.解:∠D=∠B,理由是:∵在△ADF和△CBE中∴△ADF≌△CBE(SAS),即选项C正确;具备选项A、选项B,选项D的条件都不能推出两三角形全等,故选:C.8.解:过P作PD⊥AC于D,∵点P是∠BAC的平分线上一点,PB⊥AB于B,∴PD=PB=5cm,=AC•PD=12×5=30cm2,∴S△APC故选:A.9.解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°,故选:D.10.解:A、添加AC=AD,根据SSS,能判定△ABC≌△ABD,故A选项不符合题意;B、添加∠ABC=∠ABD,根据SAS,能判定△ABC≌△ABD,故B选项不符合题意;C、添加∠C=∠D=90°时,根据HL,能判定△ABC≌△ABD,故C选项不符合题意;D、添加∠CAB=∠DAB,SSA不能判定△ABC≌△ABD,故D选项符合题意;故选:D.11.解:如图,在AB上截取BE=BC,连接DE,∵BD 平分∠ABC ,∴∠ABD =∠CBD ,在△CBD 和△EBD 中,,∴△CBD ≌△EBD (SAS ),∴∠CDB =∠BDE ,∠C =∠DEB ,∵∠C =2∠CDB ,∴∠CDE =∠DEB ,∴∠ADE =∠AED ,∴AD =AE ,∴△ABC 的周长=AD +AE +BE +BC +CD =AB +AB +CD =27,故选:C .二.填空题(共10小题,满分30分)12.解:过O 作OE ⊥AB 于E ,OF ⊥AC 于F ,连接OA ,∵OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC ,∴OE =OD ,OD =OF ,即OE =OF =OD =4,∴△ABC 的面积是:S △AOB +S △AOC +S △OBC =×AB ×OE +×AC ×OF +×BC ×OD =×4×(AB +AC +BC ) =×4×21=42,故答案为:42.13.解:已知图①的△ABC 中,∠B =62°,BC =a ,AB =c ,AC =b ,∠C =58°,∠A =60°,图②中,甲:只有一个角和∠B相等,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;乙:只有一个角和∠B相等,还有一条边,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;丙:符合AAS定理,能推出两三角形全等;故答案为:丙.14.解:由全等形的概念可知:A是三个三角形,与M对应;B是一个三角形和两个直角梯形,与N对应;C是一个三角形和两个四边形,与Q对应;D是两个三角形和一个四边形,与P对应故分别填入M,N,Q,P.15.解:∵∠BDC=35°,∠DBC=50°,∴∠BCD=180°﹣∠BDC﹣∠DBC=180°﹣35°﹣50°=95°,∵△ABC≌△DCB,∴∠ABC=∠BCD=95°,∴∠ABD=∠ABC﹣∠DBC=95°﹣50°=45°.故答案为:45°.16.解:判断△ABD≌△ACD,已知的条件是:∠1=∠2,AD=AD,因而根据SAS,可以添加条件:AB=AC;根据AAS,可以添加条件:∠B=∠C;根据ASA可以添加∠ADB=∠ADC.故答案是:AB=AC或∠B=∠C或∠ADB=∠ADC.17.解:在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL),故答案为:BC=EF18.解:如图所示:由图可知△ABF与△CED全等,∴∠BAF=∠ECD,∴∠2﹣∠1=90°,故答案为:90.19.解:设BE=2t,则BF=3t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:情况一:当BE=AG,BF=AE时,∵BF=AE,AB=100,∴3t=100﹣2t,解得:t=20,∴AG=BE=2t=2×20=40;情况二:当BE=AE,BF=AG时,∵BE=AE,AB=100,∴2t=100﹣2t,解得:t=25,∴AG=BF=3t=3×25=75,综上所述,AG=40或AG=75.故答案为:40或75.20.解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,则∠DAC=∠BCE,在△ACD和△CBE中,,∴△ACD≌△CBE(AAS),故DC=BE=3,AD=CE=4,则两条凳子的高度之和为:3+4=7.故答案为:7.21.解:∵AB ∥CD ,∴∠BAD =∠D ,在△BAF 和△EDF 中,,∴△BAF ≌△EDF (ASA ),∴S △BAF =S △DEF ,∴图中阴影部分的面积=S 四边形ACEF +S △AFB =S △ACD ===24.故答案为:24.三.解答题(共6小题,满分57分)22.证明:∵△ABC ≌△DEF ,∴∠ACB =∠DFE ,∴AC ∥DF .23.解:(1)添加的条件是∠B =∠C 或AE =AD .故答案为:AD =AE 或∠B =∠C (答案不唯一);(2)若添加∠B =∠C ,在△ABE 和△ACD 中 ∵, ∴△ACD ≌△ABE (ASA ).24.证明:∵∠1=∠2,∴∠ACB =∠DCE ,在△ABC 和△DEC 中,,∴△ABC ≌△DEC (SAS ).25.解:∵△ABC ≌△ADE ,∠D =25°,∴∠B=∠D=25°,∠EAD=∠CAB.∵∠EAB=∠EAD+∠CAD+∠CAB=120°,∠CAD=10°,∴∠CAB=(120°﹣10°)÷2=55°,∴∠FAB=∠CAB+∠CAD=55°+10°=65°.又∵∠DFB是△ABF的外角,∴∠DFB=∠B+∠FAB,∴∠DFB=25°+65°=90°.26.解:(1)符合要求的条件是①②④,故答案为:①②④;(2)选④,证明:连接AC、A′C′,在△ABC与△A′B′C′中,,∴△ABC≌△A′B′C′(SAS),∴AC=A′C′,∠ACB=∠A′C′B′,∵∠BCD=∠B′C′D′,∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,∴∠ACD=∠A′C′D′,在△ACD和△A′C′D中,,∴△ACD≌△A′C′D′(SAS),∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,即∠BAD=∠B′A′D′,∴四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,∴四边形ABCD≌四边形A′B′C′D′.27.(1)证明:∵BE⊥EA,CF⊥AF,∴∠BAC=∠BEA=∠CFE=90°,∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,∴∠CAF=∠EBA,在△ABE和△AFC中,∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,∴△BEA≌△AFC(AAS).∴EA=FC,BE=AF.∴EF=EB+CF.(2)解:∵BE⊥EA,CF⊥AF,∴∠BAC=∠BEA=∠CFE=90°,∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,∴∠CAF=∠ABE,在△ABE和△AFC中,∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,∴△BEA≌△AFC(AAS).∴EA=FC=3,BE=AF=10.∴EF=AF﹣CF=10﹣3=7.。
人教版九年级物理第十八章《电功率》检测题(含答案)

人教版九年级物理第十八章《电功率》检测题(含答案)一、填空题1.实验中测小灯泡功率的原理是________,也就是说用_________测出所需的物理量,然后计算出灯泡的功率。
2.一个灯泡上标有“PZ220-100”,它正常工作时的电阻是________Ω,如果把它接入一个110V的电路中,它消耗的功率是________w,与接在220V电路中相比,这时灯泡的亮度要_______一些。
(填“亮”或“暗”)3.小明家新买了一个自动电饭锅,铭牌上部分数据如图所示,正常工作2h耗电_______kW﹒h,合_______J。
4.灯泡Ll标有“6V 3W”的字样,灯泡L2标有“6V 6W”的字样,将它们串联在电路中,要使每个灯泡都不损坏,这段电路两端所加最大电压为______V;灯L 3标有“220V 25W”的字样,灯L4标有“220 V 60W”的字样,将L3、L4两灯串联接到220V的电路中,灯______更亮些。
5.如图电路中,R1=10Ω、R2=20Ω,开关闭合后,电压表示数为6V,则A1的示数是_______A,A2的示数是______A。
5minR2的电功率是______W,R1消耗的电能______J。
6.甲、乙两盏灯分别接在110 伏和220 伏的电路中,则每通过1 库仑电荷量时,甲、乙两灯消耗的电功之比为________;通电时间相等则甲、乙两灯消耗的电功率之比为________,电流之比为________。
二、选择题7.家用的手电筒用干电池作电源,正常发光时电流为0.32A。
小灯泡的电功率接近()A.1W B.10W C.0.1KW D.1KW8.有甲、乙两盏电灯,甲灯上标有“36V 60W”,乙灯上标有“220V 60W”,当它们分别在其额定电压下工作发光时,其亮度是()A.乙灯比甲灯更亮 B.甲灯比乙灯更亮C.两盏灯一样亮 D.无法判定哪盏灯更亮9.一个大功率的用电器,用铝导线连接到电源上,工作时发现铝导线过热,为了使导线不过热,下列不可行的办法是()A.改用粗细相同的铜导线B.将原铝导线加长1倍C.将原铝导线减短些D.改用较粗的铝导线10.如图所示的电路中,电源电压恒定不变,当开关K闭合时()A.电压表示数变小,电流表示数变小,灯变暗B.电压表示数变大,电流表示数变大,灯变亮C.电压表示数不变,电流表示数不变,灯的亮度不变D.电压表示数不变,电流表示数变小,灯变暗11.小红同学在做“探究串联电路的电压规律”实验时,接通开关后,发现L 1亮度较大,L2亮度较小,对这一现象以下分析合理的是()A.灯泡L2发生了短路B.灯泡L2发生了断路C.灯泡L1两端的电压大于L2两端的电压D.灯泡L2两端的电压大于L1两端的电压12.一个标有“220V 600W”的电炉,想把它接在110伏的电源上使用,而保持原来的电功率不变,下列采取的措施中,正确的是()A.把电炉丝截去一半B.把电炉丝截成等长的两段再并联C.找一根同样的电炉丝跟原来的串联D.找一根同样的电炉丝跟原来的并联三、实验与探究题(13小题6分,14小题15分,共21分)13.如图为小明同学连接的测量小灯泡额定功率的电路图,图中使用了三节干电池作电源,已知小灯泡的额定电压为3.8V,额定功率大约为1.2W。
