实验三：用R软件进行方差分析

合集下载

统计软件R及其在_生物统计学_实验教学中的应用(1)

如下：
〉ｘ＜－ｓｅｑ（０．５，１．４，ｌｅｎｇｔｈ＝１００）＃给定ｘ的取值范围
〉ｙ＜－ｓｅｑ（０．０１，０．０８，ｌｅｎｇｔｈ＝１００）＃给定ｙ的取值范围
〉ｒ＜－ｆｕｎｃｔｉｏｎ（ｘ，ｙ）
｛
－０．７２５１＋１．６３３５＊ｘ＋９．９９３２＊ｙ－０．７１２１＊ｘ＊ｘ－９０．５６０２＊ｙ＊ｙ－
一、Ｒ软件及其特点
Ｒ是属于ＧＮＵ系统的自由、免费、源代码开放的软件，它是一个用于统计计算和统计制图的优秀工具。由于其开放性和自由灵活的特点，在国内外的学术界得到了广泛的应用。与国内目前大量采用的各种统计软件相比较，利用Ｒ进行科研和教学具有如下优势：
教学参考
统计软件Ｒ及其在《生物统计学》实验教学中的应用
文／程新魏赛金江莉涂国全
摘要：自由软件Ｒ是一种在统计学及其他科研领域应用非常广泛的软件。自２００５年开始，在生物工程与生物技术专业的学生的生物统计学课程中采用自由软件Ｒ作为教学辅助工具。结果表明，采用Ｒ进行教学，激发了学生的学习积极性，提高了学生掌握统计学知识的能力，教学效果比以前有了显著提高。因此，在统计学教学中采用自由软件Ｒ作为教学辅助工具，值得推广。
表１
２００５－２００６年本学院《生物统计学》课程考试成绩
２００３级生物技术专业
２００４级生物技术专业
２００３级生物工程专业
本科阶段，生物工程和生物技
使用软件ＳＰＳＳ
使用软件Ｒ
使用软件Ｒ
术专业学生《生物统计学》课程一共成绩人数百分比（％）成绩人数百分比（％）成绩人数百分比（％）

R语言学习系列27-方差分析

R语言学习系列27-方差分析(总21页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--22. 方差分析一、方差分析原理1. 方差分析概述方差分析可用来研究多个分组的均值有无差异，其中分组是按影响因素的不同水平值组合进行划分的。

方差分析是对总变异进行分析。

看总变异是由哪些部分组成的，这些部分间的关系如何。

方差分析，是用来检验两个或两个以上均值间差别显著性（影响观察结果的因素：原因变量（列变量）的个数大于2，或分组变量（行变量）的个数大于1）。

一元时常用F检验（也称一元方差分析），多元时用多元方差分析（最常用Wilks’∧检验）。

方差分析可用于：（1）完全随机设计（单因素）、随机区组设计（双因素）、析因设计、拉丁方设计和正交设计等资料；（2）可对两因素间交互作用差异进行显著性检验；（3）进行方差齐性检验。

要比较几组均值时，理论上抽得的几个样本，都假定来自正态总体，且有一个相同的方差，仅仅均值可以不相同。

还需假定每一个观察值都由若干部分累加而成，也即总的效果可分成若干部分，而每一部分都有一个特定的含义，称之谓效应的可加性。

所谓的方差是离均差平方和除以自由度，在方差分析中常简称为均方（Mean Square）。

2. 基本思想基本思想是，将所有测量值上的总变异按照其变异的来源分解为多个部份，然后进行比较，评价由某种因素所引起的变异是否具有统计学意义。

根据效应的可加性，将总的离均差平方和分解成若干部分，每一部分都与某一种效应相对应，总自由度也被分成相应的各个部分，各部分的离均差平方除以各自的自由度得出各部分的均方，然后列出方差分析表算出F检验值，作出统计推断。

方差分析的关键是总离均差平方和的分解，分解越细致，各部分的含义就越明确，对各种效应的作用就越了解，统计推断就越准确。

效应项与试验设计或统计分析的目的有关，一般有：主效应（包括各种因素），交互影响项（因素间的多级交互影响），协变量（来自回归的变异项），等等。

r语言三组间两两比较方法

在R语言中，有多种方法可以进行三组间的两两比较。

以下是一些常见的方法：1. t检验（pairwise.t.test）：当数据满足正态性和方差齐性假设时，可以使用t检验来进行两两比较。

该函数会对每对组进行t检验，计算出每对之间的差异显著性水平和置信区间。

```Rpairwise.t.test(data$group, data$value, p.adjust.method = "bonferroni")```2. 方差分析（ANOVA）：如果数据不满足t检验的假设条件，可以使用方差分析来进行两两比较。

可以使用ANOVA函数进行方差分析，然后使用posthoc函数进行多重比较。

```Rmodel <- aov(value ~ group, data = data)posthoc <- TukeyHSD(model)```3. 非参数检验（Kruskal-Wallis检验）：当数据不满足正态性和方差齐性假设时，可以使用非参数方法进行两两比较，如Kruskal-Wallis检验。

可以使用kruskal.test函数进行Kruskal-Wallis检验，然后使用pairwise.wilcox.test函数进行多重比较。

```Rkruskal.test(value ~ group, data = data)pairwise.wilcox.test(data$value, data$group, p.adjust.method = "bonferroni")```这些方法都可以用于进行三组间的两两比较，具体应该根据数据的性质和实验设计来选择合适的方法。

在进行多重比较时，通常需要考虑到多重比较校正以控制错误率。

常见的多重比较校正方法包括Bonferroni校正、Holm校正等。

方差分析的基本思想和应用

方差分析的基本思想和应用方差分析（ANOVA，Analysis of Variance）是统计学中的一种重要方法，主要用于研究多个样本之间的均值是否存在显著性差异。

方差分析将总的变异分解为几个部分，从而判断这些部分是否具有统计学意义。

本文将详细介绍方差分析的基本思想、类型及应用。

一、方差分析的基本思想方差分析的基本思想是将总的变异分为两部分：组内变异和组间变异。

组内变异是指每个样本内部的变异，组间变异是指不同样本之间的变异。

通过比较组间变异和组内变异的大小，可以判断样本之间的均值是否存在显著性差异。

二、方差分析的类型根据实验设计的不同，方差分析可分为以下几种类型：1. 单因素方差分析（One-Way ANOVA）单因素方差分析是指只有一个因素（或称自变量）影响实验结果的情况。

在这种实验设计中，将样本分为若干个组别，每组只有一种水平的因素。

单因素方差分析的目的是检验这个因素的不同水平是否会导致实验结果的显著性差异。

2. 多因素方差分析（Multi-Way ANOVA）多因素方差分析是指有两个或两个上面所述的因素同时影响实验结果的情况。

在这种实验设计中，需要考虑多个因素之间的交互作用。

多因素方差分析的目的是检验这些因素及其交互作用是否会导致实验结果的显著性差异。

3. 重复测量方差分析（Repeated Measures ANOVA）重复测量方差分析是指在同一组样本中，对同一因素进行多次测量的情况。

这种实验设计适用于研究因素对样本的影响随时间变化的情况。

重复测量方差分析的目的是检验这个因素在不同时间点上是否会导致实验结果的显著性差异。

三、方差分析的应用方差分析在实际应用中具有广泛性，以下列举几个常见领域的应用：1. 生物学领域在生物学研究中，方差分析常用于比较不同物种、品种或组织类型的生物学特性。

例如，研究不同植物品种的生长速度、不同动物种群的繁殖能力等。

2. 医学领域在医学研究中，方差分析可用于比较不同治疗方法的疗效。

r软件实训内容

r软件实训内容
R软件是一种用于统计计算和可视化的编程语言和软件环境。

以下是一些可能的R软件实训内容：
1. R语言基础：学习R语言的语法、变量、数据结构、控制流、函数等基础知识。

2. 数据导入和整理：学习如何从各种数据源导入数据到R中，并掌握数据清洗、数据转换和数据重塑等技术。

3. 数据可视化：学习如何使用R中的各种可视化包（如ggplot2、lattice 等）创建各种图表和图形，以更好地理解数据。

4. 统计分析：学习如何使用R进行各种统计分析，如描述性统计、参数检验、非参数检验、回归分析、方差分析等。

5. 机器学习和数据挖掘：学习如何使用R中的各种机器学习包（如caret、randomForest、e1071等）进行数据挖掘和机器学习。

6. 实践项目：通过实际项目，将所学的R知识和技能应用到实际问题中，提高解决实际问题的能力。

以上是一些常见的R软件实训内容，具体实训内容可能会根据课程要求和实际需求而有所不同。

实验三用Excel进行方差分析实验报告

3.多重比较采用q法，3种课程训练销售记录平均数多重比较表如下
3种课程训练平均销售记录多重比较表
课程 B课程 A课程 C课程
平均数 x i 2928 2228.8 1951.6
x i 1951 6 . 976.4 277.2
x i 2228.8 699.2
因为MSe 3992323, n 5, 所以标准误 x 为 . s
的提高无显著影响，不同改革方
q0.01 6.93 5.95 5.41
LSR0.05 1.6996 1.5288 1.4280
LSR0.01 3.0356 2.6063 2.3698
进一步对改革方案各水平平均经
3.多重比较
品种小麦收获量极显著高于B4品种，但B1、B2和B3品
方案
B2 B3
B1
式为
F值 1.61 20.49**
自由度df 均方MS 4 3.5245 3 44.8818 12 2.1902 19
SS B
1 1 x2j C 3 2 (20 an
2415655 2411208 444
SSAB SSAB SSA SSB 469
因为MSe 3992323, n 5, 所以标准误 x 为 . s
s x MSe / n 3992323 / 5 282.5712 .
q值与LSR值
dfe
12
秩次距 2 3
q0.05 3.08 3.77
q0.01 4.32 5.05
LSR0.05 870.3193 1065.2934
A2
单个观测值试验资料。A因素有5个水平，即a=5
b=5× 4=20个观测值。方差分析如下：

R语言实战（五）方差分析与功效分析

R语⾔实战（五）⽅差分析与功效分析本⽂对应《R语⾔实战》第9章：⽅差分析；第10章：功效分析====================================================================⽅差分析：回归分析是通过量化的预测变量来预测量化的响应变量，⽽解释变量⾥含有名义型或有序型因⼦变量时，我们关注的重点通常会从预测转向组别差异的分析，这种分析⽅法就是⽅差分析（ANOVA）。

因变量不只⼀个时，称为多元⽅差分析（MANOVA）。

有协变量时，称为协⽅差分析（ANCOVA）或多元协⽅差分析（MANCOVA）。

#基本格式aov(formula, data = dataframe)基本表达式符号参考回归中的表格研究设计的表达式下表中，⼩写字母表⽰定量变量，⼤写字母表⽰组别因⼦，Subject是对被试者独有的标识变量设计表达式单因素ANOVA y ~ A含单个协变量的单因素ANCOVA y ~ x + A双因素ANOVA y ~ A * B含两个协变量的ANCOVA y ~ x1 + x2 + A*B随机化区组y ~ B + A （B是区组因⼦）单因素组内ANOVA y ~ A + Error(Subject/A)含单个组内因⼦（W）和单个组间因⼦（B）的重复测量ANOVA y ~ B * W + Error(Subject/W)表达式中的各项顺序：有两种情况会造成影响：（1）因⼦不⽌⼀个，并且是⾮平衡设计；（2）存在协变量。

出现任意⼀种情况时，等式右边的变量都与其他每个变量相关，此时我们⽆法清晰地划分它们对因变量的影响。

例如，对于双因素⽅差分析，若不同处理⽅式中的观测数不同，那么模型y ~ A * B与模型y ~ B * A的结果不同R默认类型1（序贯型）⽅法计算ANOVA效应。

第⼀个模型可以这样写：y ~ A + B + A : BR中的ANOVA表的结果将评价：1. A对y的影响2. 控制A时，B对y的影响3. 控制A和B的主效应时，A与B的交互效应顺序很重要当⾃变量与其他⾃变量或者协变量相关时，没有明确的⽅法可以评价⾃变量对因变量的贡献。

实验三-ANOVA方差分析

实验三――ANOV A方差分析在现实生活中影响一事物的因素往往很多，我们常常需要确定哪些因素的影响值是显著的，方差分析就是解决这一问题的有效方法。

Spss进行方差分析时，单因素方差分析用compare mean 中的one-way ANOV A过程来完成，双因素方差分析则用GLM-General Factorial 过程来完成。

一、单因素方差分析过程one-way ANOV A1.选择Analyze compare mean one way anova 打开主对话框。

把因变量放入因变量栏dependent list ，影响因素放入因素变量栏factor。

2.单因素方差分析过程包含3个子对话框：contrast, post hoc及options●contrast 一般取默认值●post hoc multiple- comparisons多重比较子对话框，进行多重比较时有假定方差齐性equal variances assumed和不假定方差非齐性equal variances not assumed两种条件比较。

●options 包括描述统计量和缺省值的处理办法二、单变量方差分析过程（univariate）1.点击Analyze genera linear model univariate，把数据导入spss。

将因变量放入dependent，将影响因素放入fix factor(s)下。

2.有5个子对话框：model设定模型：分析所有因素影响，包括主效应因素和交互效应因素影响。

选full factorial continuecontrast对照plot绘图使用少，一般选默认值save变量储存options选择项3.ok例题1等重复每一类数据表示不同仓库中牛奶中细菌含量，要检验不同仓库中牛奶中细菌含量是否相等。

样本（细菌含量）123456仓库号1241521273323 214712171416 31197131218 477471218 5192419151020步骤：定义变量x和g，x代表细菌含量，g代表仓库号。

[整理]SPSS处理多元方差分析例子.

实验三多元方差分析一、实验目的用多元方差分析说明民族和城乡对人均收入和文化程度的影响。

二、实验要求调查24个社区，得到民族与城乡有关数据如下表所示，其中人均收入为年均，单位百元。

文化程度指15岁以上小学毕业文化程度者所占百分比。

试依此数据通过方差分析说明民族和城乡对人均收入和文化程度的影响。

三、实验内容1．依次点击“分析”---- “常规线性模型”----“多变量”，将“人均收入”和“文化程度”加到“因变量”中，将“民族”和“居民”加到“固定因子”中，如下图一所示。

民族农村城市人均收入文化程度人均收入文化程度1 46，50，60，68 70，78，90，93 52，58，72，75 82，85，96，982 52，53，63，71 71，75，86，88 59，60，73，77 76，82，92，933 54，57，68，69 65，70，77，81 63，64，76，78 71，76，86，90【图一】2.点击“选项”，将“输出”中的相关选项选中，如下图二所示：【图二】3.点击“继续”，“确定”得到如下表一的输出：【表一】常规线性模型主体间因子值标签N民族 1.00 1 82.00 2 83.00 3 8居民 1.00 农村122.00 城市12描述性统计量民族居民均值标准差N人均收入 1 农村56.00009.93311 4 城市64.250011.026484 总计60.1250 10.6695582 农村59.7500 8.99537 4城市67.2500 9.10586 4总计63.5000 9.28901 8 3 农村62.0000 7.61577 4城市70.2500 7.84750 4总计66.1250 8.40812 8 总计农村59.2500 8.45442 12 城市67.2500 8.89458 12总计63.2500 9.41899 24文化程度1 农村82.7500 10.68878 4城市90.2500 7.93200 4总计86.5000 9.59166 8 2 农村80.0000 8.28654 4城市85.7500 8.18026 4总计82.8750 8.21910 8 3 农村73.2500 7.13559 4城市80.7500 8.77021 4总计77.0000 8.41767 8 总计农村78.6667 9.00841 12 城市85.5833 8.53291 12总计82.1250 9.27977 24协方差矩阵等同性的 Box 检验(a)Box 的 M 12.397F .587df1 15df2 1772.187Sig. .887检验零假设，即观测到的因变量的协方差矩阵在所有组中均相等。

R语言总和性试验

中北大学理学院实验报告实验课程名称：R语言与统计分析实验类别：验证型专业：应用统计学班级： 13080441学号： ***********名：***中北大学理学院R语言与统计分析综合实验【实验类型】验证性【实验目的】（1）掌握利用R语言实现数据处理并进行严格的统计分析；（2）学会运用R语言进行程序的编写；（3）熟练掌握R语言绘图功能；（4）掌握R语言统计分析中的“参数估计”，“假设检验”，“方差分析”，“回归分析”，等基本分析函数。

【实验要求】（1）实验过程要求用R软件完成；（2）实验结果逐个导入Word文档，并按问题作出解释；（3）实验报告按照既定格式书写。

【实验仪器与软件平台】计算机 R软件【实验前的预备知识】1、实验室电脑要求安装有R软件；2、上实验课程的学生要对涉及到的统计概念有所了解；3、要求学生事先查阅并熟悉R的相关命令。

【实验内容】第二章：1、用rep()构造一个向量x，它由3个3,4个2,5个1构成。

x<-rep(c(3,2,1),c(3,4,5))2、由1.2...16构成两个方阵，其中矩阵A按列输入，矩阵B按行输入，并计算以下：A<-matrix(1:16,4,4)B<-matrix(1:16,4,4,byrow=TRUE)1、C=A+B2、> D=A*B3、> E=A%*%B4、F<-A[-3,][,1] [,2] [,3] [,4][1,] 1 5 9 13 [2,] 2 6 10 14 [3,] 4 8 12 16> G<-B[,-3][,1] [,2] [,3][1,] 1 2 4[2,] 5 6 8[3,] 9 10 12[4,] 13 14 16> H=F%*%G3、函数solve()有两个作用；solve（A,b）可用于求解线性方程组Ax=b,solve(A)可用于求解矩阵A的逆，用两种方法编程求解方程组Ax=b的解。

三水平试验方差分析

适用性广
三水平试验方差分析适用于多种数据类型，如连续型、分类型和有序分类型数据，具有广泛的适用性。
缺点
01
复杂性
三水平试验方差分析涉及多个处理水平，导致模型复杂度高，对数据的要求也较高。
02
对数据的要求
03
对软件的要求
该方法要求数据具有正态分布、同方差性和独立性等假设，否则可能导致分析结果的不准确。
5. 检验假设
检验组间方差与组内方差的差异是否显著，以确定处理因素是否对响应变量有显著影响。
6. 解释结果
解释方差分析的结果，并得出结论。
方差分析的假设检验
01
假设检验是方差分析的核心部分，用于确定处理因素对响应变量的影响是否显著。
02
它基于以下假设：组间方差与组内方差不相等，表示处理因素对响应变量有显著影响；组间方差与组内方差相等，表示处理因素对响应变量没有显著影响。
实验结果的解释与讨论
结果解释
根据方差分析的结果，结合专业知识，对实验结果进行解释，并探讨其实际意义和影响。
结果讨论
对实验结果进行深入讨论，包括结果的可靠性、稳定性、推广性等方面，并提出可能的改进和完善建议。
文献综述
查阅相关文献，了解同类研究的现状和进展，对比和评价本研究的优缺点和创新点。
选择实验对象和样本量
根据研究问题和实验目的选择适当的实验对象和样本量。
确定实验处理和变量
根据研究问题和实验目的确定适当的实验处理和变量，并设计合理的实验程序。
实施实验
按照实验设计进行实验，并记录实验数据。
分析实验数据
对实验数据进行分析，包括数据的整理、描述性统计、方差分析等。
解释和撰写实验结果

统计学实践教学的软件(3篇)

第1篇摘要：随着统计学在我国教育领域的广泛应用，统计学实践教学的重要性日益凸显。

本文旨在探讨统计学实践教学软件的应用，分析其特点、功能以及在实际教学中的应用效果，以期为我国统计学实践教学提供参考。

一、引言统计学作为一门应用性较强的学科，其实践教学对于提高学生的实际操作能力、培养数据分析思维具有重要意义。

随着计算机技术的飞速发展，统计学实践教学软件应运而生，为统计学实践教学提供了有力支持。

本文将分析统计学实践教学软件的特点、功能及其在实际教学中的应用效果。

二、统计学实践教学软件的特点1. 实用性强：统计学实践教学软件紧密结合实际应用，为学生提供丰富的数据资源和案例，有助于学生将理论知识与实际操作相结合。

2. 操作简便：软件界面友好，操作步骤简单明了，学生可以快速上手，降低学习门槛。

3. 功能丰富：软件集成了多种统计分析方法，包括描述性统计、推断性统计、时间序列分析等，满足不同层次学生的需求。

4. 可视化效果：软件提供多种可视化图表，如柱状图、饼图、折线图等，有助于学生直观地理解数据和分析结果。

5. 案例教学：软件内置大量案例，学生可以跟随案例进行操作，加深对统计方法的理解。

6. 个性化定制：软件支持用户自定义分析参数，满足不同教学需求。

三、统计学实践教学软件的功能1. 数据处理：软件提供数据导入、数据清洗、数据转换等功能，方便学生进行数据处理。

2. 描述性统计：软件支持计算均值、方差、标准差等描述性统计量，帮助学生了解数据的基本特征。

3. 推断性统计：软件提供t检验、方差分析、相关分析等推断性统计方法，帮助学生进行数据推断。

4. 时间序列分析：软件支持时间序列数据的建模、预测和分析，帮助学生了解经济、金融等领域的时间序列分析。

5. 图表制作：软件提供多种图表制作工具，如柱状图、饼图、折线图等，方便学生展示分析结果。

6. 案例教学：软件内置大量案例，学生可以跟随案例进行操作，加深对统计方法的理解。

四、统计学实践教学软件在实际教学中的应用效果1. 提高学生学习兴趣：统计学实践教学软件将理论知识与实际操作相结合，激发学生的学习兴趣。

实验三__方差分析

[实验项目]实验三方差分析[教学时数]2课时。

[实验目的与要求]掌握使用Excel电子表格和统计分析软件进行方差分析的方法。

[实验材料与设备]计算机；有关数据资料。

[实验内容]1、掌握用Excel中的数据分析工具进行方差分析的方法。

2、学习用统计分析软件进行方差分析的方法。

[实验方法]1、用Excel中的数据分析工具进行方差分析的方法。

（1）工具的安装。

（2）工具的使用。

①单因子方差分析。

②两因子无重复资料的方差分析。

③两因子有重复资料的方差分析。

④两因子系统资料的方差分析。

⑤多因子方差分析。

2、用统计分析软件进行方差分析的方法。

（1）单因子方差分析（2）两因子方差分析（3）两因子系统资料的方差分析（4）多因子方差分析[指导与训练方案]1、将本次实验内容整理成实验报告。

2、练习：1、在同样饲养管理条件下，三个品种猪的增重如下表，试对三个品种增重差异是否显著进行检验。

品种增重x ij(kg)A116 12 18 18 13 11 15 10 17 18A210 13 11 9 16 14 8 15 13 8A311 8 13 6 7 15 9 12 10 11 (MS e=8.57,F=6.42)2、用三种酸类处理某牧草种子，观察其对牧草幼苗生长的影响(指标：幼苗干重，单位：mg)。

试验资料如下：处理幼苗干重(mg)对照 4.23 4.38 4.10 3.99 4.25HCl 3.85 3.78 3.91 3.94 3.86丙酸 3.75 3.65 3.82 3.69 3.73丁酸 3.66 3.67 3.62 3.54 3.71(1)进行方差分析(不用LSD法、LSR进行多重比较，F=33.86**)(2)对下列问题通过单一自由度正交比较给以回答：①酸液处理是否能降低牧草幼苗生长?②有机酸的作用是否不同于无机酸?③两种有机酸的作用是否有差异?(F1=86.22**,F2=13.13**,F3=2.26)3、为了比较4种饲料(A)和猪的3个品种(B)，从每个品种随机抽取4头猪(共12头)分别喂以4种不同饲料。

应用统计学与R语言建模教学大纲

《应用统计学与R语言建模》教学大纲一、课程说明《应用统计学与R语言建模》是数据科学与大数据技术专业的核心课程之一，属于专业选修课，是一门运用统计学的原理和方法，研究各领域有关数据收集、整理和分析的学科。

本课程基于R语言，系统地介绍了常见的统计分析方法，如描述性统计分析、参数估计与假设检验、方差分析、线性回归、逻辑回归、降维分析等及其在R语言中的实现，包含理论教学和实践操作两个部分。

课程用大量实例来说明常用统计分析方法的具体应用，目的是培养学生解决实际问题的能力。

学生通过学习本课程后，应系统掌握各种基本的统计数据分析方法，能运用R语言对统计数据进行处理和分析，能综合运用统计学和计算机科学方法去认识客观世界。

学习这门课程的目标是培养学生掌握统计学的原理和方法以及利用R语言进行数据建模和分析的能力。

培养学生理论与实际应用并重的能力、问题解决能力、团队协作与沟通能力、批判性思维以及持续学习的态度，为学生在数据科学领域的进一步发展做好准备。

先修课程：《高等数学A》《高等数学B》《线性代数》《概率论与数理统计》《计算思维Ⅰ（C）》《计算思维Ⅰ（C）实验》二、课程目标三、课程目标对毕业要求的支撑关系矩阵四、理论教学内容、要求、教学方法与学时五、实验（实践、上机）教学内容、基本要求与学时分配六、考核及成绩评定方式本课程最终成绩由平时考核、期中考核、期末考核三部分构成。

课程的总评成绩=平时成绩×40%+期中成绩×10%+期末成绩×50%。

其中，平时考核由课堂表现、课后作业和实验报告三个部分组成。

课程平时成绩=课堂表现得分×40%+课后作业得分×30%+实验报告得分×30%。

期中成绩由期中考试卷面成绩（随堂测验、百分制）按参考答案及评分标准批阅得出。

期末成绩由数据分析报告的撰写和答辩陈述的表现等按百分制综合折算得出，具体见7.3节内容。

各项课程目标分数分配见下表：七、考核标准7.1平时考核课程平时成绩=课堂表现得分×40%+课后作业得分×30%+实验报告得分×30%。

R语言单因素方差分析

R语言单因素方差分析单因素方差分析是一种用于比较不同组之间平均数是否有显著差异的统计方法。

它可以用来分析一个自变量对一个连续型因变量的影响。

在R 语言中进行单因素方差分析，可以通过使用内置的函数或者额外的包来实现。

下面将介绍如何使用R进行单因素方差分析的步骤及示例代码。

步骤一：安装和加载R语言的额外包，比如"lmtest"和"car"包。

```install.packages("lmtest")install.packages("car")library(lmtest)library(car)```步骤二：准备数据。

这里我们以一个虚拟的示例数据为例，假设有一个实验研究了三种不同处理对一些指标的影响，每种处理都有10个观测值。

数据存储在一个数据框中，变量名为“处理”（treatment）和“指标”（score）。

```treatment <- c(rep("A", 10), rep("B", 10), rep("C", 10))score <- c(1.7, 2.9, 2.3, 1.8, 3.1, 2.4, 2.2, 2.5, 2.8, 1.9, 4.2, 3.9, 4.0, 3.7, 3.2, 3.5, 3.6, 4.3, 3.0, 3.8, 2.1, 2.6, 2.7, 2.0, 2.3, 2.1, 2.4, 2.7, 2.5, 2.8)data <- data.frame(treatment, score)```步骤三：进行方差分析。

使用`aov(`函数创建一个方差分析模型，并用`summary(`函数查看分析结果。

```model <- aov(score ~ treatment, data=data)summary(model)```分析结果将输出方差分析表，包括误差平方和（SS）、均方（MS）、F值和p值等信息。

r分组计算方差

在统计学和数据分析中，你可以使用 R 语言来计算数据集的方差。

假设你有一个数据集，想要计算其方差，可以使用 R 中的内置函数 `var()`。

假设你的数据集存储在一个向量或数据框中，例如：
```R
创建一个示例数据集
data <- c(5, 8, 6, 10, 7)
使用 var() 函数计算方差
variance <- var(data)
print(variance)
```
如果你有一个包含多列的数据框，并想要计算特定列的方差，可以指定列名或索引号：
```R
创建一个示例数据框
data_frame <- data.frame(A = c(5, 8, 6, 10, 7), B = c(9, 12, 10, 15, 11))
计算特定列的方差
variance_A <- var(data_frame$A) # 使用列名
variance_B <- var(data_frame[, "B"]) # 使用列索引
print(variance_A)
print(variance_B)
```
请确保在实际使用中，对应的数据类型和数据结构与你的需求一致，并适当地调整函数的输入参数。

`var()` 函数将会返回所计算数据的方差值。

(新)方差分析操作步骤详解

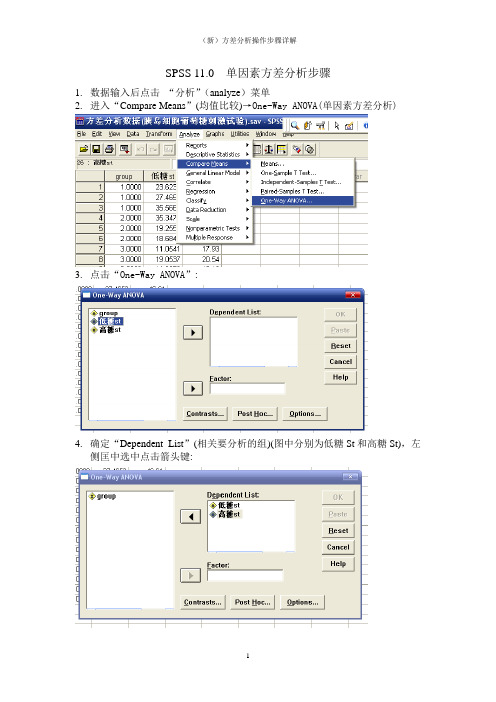
SPSS 11.0 单因素方差分析步骤1.数据输入后点击“分析”（analyze）菜单2.进入“Compare Means”(均值比较)→One-Way ANOVA(单因素方差分析)3.点击“One-Way ANOVA”:4.确定“Dependent List”(相关要分析的组)(图中分别为低糖St和高糖St)，左侧匡中选中点击箭头键:5．确定“Factor”(因素)(图中为group):5. Contrast子对话框：该对话框有两个用途：对均数的变动趋势进行趋势检验：定义根据研究目的需要进行的某些精确两两比较。

由于该对话框太专业，也较少用，这里只做简单介绍，在综合实例中会结合具体例题讲解。

1). Polynomial：定义是否在方差分析中进行趋势检验，即随着组别的变化，各组均数是否呈现某种变化趋势。

2)．Degree下拉列表：和Polynomial复选框配合使用，用于定义需检验的趋势曲线的最高次方项，可选择从线性趋势一直到五次方曲线。

如果你选择了高次方曲线，系统会给出所有相应各低次方曲线的拟合优度检验结果(比如选择3次方曲线时，系统会给出线性、二次方、三次方三个结果)，以供你选择。

3)．Coefficients框：精确定义某些组间均数的比较。

这里按照分组变量升序给每组一个系数值，注意最终所有系数值相加应为o。

比如说在上例中要对第一、三组进行单独比较，则在这里给三组分配系数为1、0、-1，就会在结果中给出相应的检验内容。

6.点击“Post Hoc…”确定两两比较方法（当各组方差齐时适用）:equal variances assume复选框：方差齐时比较结果有效，根据需要选择，通常选LSD、Tukey 等, 点击“Contimue”返回。

EqualVariancesNotAssumed复选框组：提供了方差不齐时可以采用的两两比较方法，共有四种可以选择，一般认为是Games-Howell法稍好一些，推荐使用。