MATLAB课件·第2章 信号与系统的建模与仿真
信号与系统_MATLAB ppt课件

矩形脉冲信号
y = rectpuls(t,width)
三角波脉冲信号 y = tripuls(t,width,skew) %skew:斜度
PPT课件
24
一、基本信号的MATLAB表示
%decaying exponential t=0:001:10; A=1; a=-0.4; ft=A*exp(a*t); plot(t,ft)
MATLAB简介
( Matrix Laboratory )
MATLAB的工作方式 如何获取帮助
表达式——变量、数值、算数运算符、 关系运算符、逻辑运算符、冒号运算符
数组及其运算
函数文件
循环(FOR、 WHILE 循环) 基本绘图语句
PPT课件
2
一、MATLAB的工作方式
(1)窗口命令方式 (2)运行以 .M 为扩展名磁盘文件
值为0时表示逻辑假(F),其它任何非零值表示 逻辑真。
PPT课件
9
三、表达式
运算符号
关系运算符 A<B A>B A <= B A >= B A == B A ~= B
小于 大于 小于等于 大于等于 等于 不等于
PPT课件
10
三、表达式
运算符号
冒号运算符
表达式 1:10 表示产生一个行向量,它的值为 1 2 3 4 5 6 7 8 9 10
0.8 0.7
0.6
delta=[zeros(1,50),1,zeros(1,50)]; 0.5
0.4
stem(k,delta)
0.3
0.2
function [f,k]=impseq(k0,k1,k2)
0.1 0 -50 -40 -30 -20 -10
《信号与系统》MATLAB仿真实验讲义

《信号与系统》MATLAB仿真实验讲义(第二版)肖尚辉编写宜宾学院电信系电子信息教研室《信号与系统》课程2004年3月 宜宾使用对象:电子专业02级3/4班(本科)实验一 产生信号波形的仿真实验一、实验目的:熟悉MATLAB软件的使用,并学会信号的表示和以及用MATLAB来产生信号并实现信号的可视化。
二、实验时数:3学时+3学时(即两次实验内容)三、实验内容:信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。
对信号进行时域分析,首先需要将信号随时间变化的规律用二维曲线表示出来。
对于简单信号可以通过手工绘制其波形,但对于复杂的信号,手工绘制信号波形显得十分困难,且难以绘制精确的曲线。
在MATLAB中通常用三种方法来产生并表示信号,即(1)用MATLAB软件的funtool符合计算方法(图示化函数计算器)来产生并表示信号;(2)用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)来产生并表示信号;(3)用MATLAB软件的仿真工具箱Simulink中的信号源模块。
(一) 用MATLAB软件的funtool符合计算方法(图示化函数计算器)来产生并表示信号在MATLAB环境下输入指令funtool,则回产生三个视窗。
即figure No.1:可轮流激活,显示figure No.3的计算结果。
figure No.2:可轮流激活,显示figure No.3的计算结果。
figure No.3:函数运算器,其功能有:f,g可输入函数表达式;x是自变量,在缺省时在[-2pi,2pi]的范围内;自由参数是a;在分别输入完毕后,按下面四排的任一运算操作键,则可在figure No.1或figure No.2产生相应的波形。
学生实验内容:产生以下信号波形3sin(x)、5exp(-x)、sin(x)/x、1-2abs(x)/a、sqrt(a*x)(二) 用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)来产生并表示信号一种是用向量来表示信号,另一种则是用符合运算的方法来表示信号。
Matlab与信号与系统的应用.ppt

二、线性卷积及其MATALB实现
多项式乘法
y1 [am am1 ... a0 ] y2 [an an1 ... a0 ] y1* y2 conv( y1, y2)
注意:y1和y2的幂次是按照降幂顺序排列的, 这样a0对应的幂次为0,因此如果多项式没有 常数项,则多项式也要写出a0的取值为0
y(-1)=3*2+ (-3) *(-5)+7*0+0*3+(-1)*2=19 由右下图k=-2: 2五个点上的x和h乘积之和,得到
y(2)=7*1+0*2+(-1)*(-5)+5*0+2*3=18 对每一个n值,都要这样运算y(n),很繁。
序列的卷积运算算例
7
3
5 23 2 21
0 -1 -3
-5
相关函数与线性卷积的关系
n
卷积:y(k) x(n)h(k n) n
注意:计算相关性时,两个序列都不翻转,只是将h(k)移动后对应相 乘再相加;卷积时,要将其中一个序列翻转后再移动;
相关表示两个信号之间的关联性,与系统无关,卷积则表示的是 时不变系统中输入、单位响应和输出之间的关系
三、系统描述与转换
K为系统增益,zi为零点,pj为极点。 零极点增益模型用[z,p,K]矢量组表示,即:
z=[z1,z2,…,zm]’ p=[p1,p2,...,pn]’ K=[k] 注意:这里的零点、极点都是列向量表示
零极点增益模型
G(s) 0.5
s(s 6)(s 5)
(s 1)(s 2)(s 3 4 j)(s 3 4 j)
Matlab与信号与系统的应用
提纲
一、信号系统的MATLAB表示 二、线性卷积及MATALB实现 三、系统描述与转换 四、时域分析 五、频域分析
matlab应用(信号与系统)课件

代码: y=fliplr(x)
5)累加求和
n2
y(n) x(n)
n n1
代码: y=sum(x(n1:n2));
6)信号能量和功率
Ex | x(n) |2
n
Px
1
N 1
| x(n) |2
N n0
代码: Ex=sum(abs(x).^2)); Px= sum(abs(x).^2))/N;
x=sin(2*pi*t);
序列的运算
1)信号加 x(n) x1(n) x2(n)
代码: x=x1+x2;
x1和x2长度相同,位置对应才能相加,否则应作处理。如:
function [y,n]=sigadd(x1,n1,x2,n2)
n_min=min(min(n1),min(n2));
n_max=max(max(n1),max(n2));
n=n_min:n_max;
y1=zeros(1,length(n)); y2=y1;
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;
y=y1+y2;
例如 n1=-2:1; x1=1:4; n2=-1:2; x2=1:4;
解:首先用解析的方法求出信号的离散傅里叶变换为
X (e jw )
x(n)e jwn
e jw e jw 0.5
再画出相应的图形,代码如下:
w=[0:1:500]*pi/500; X=exp(j*w)./(exp(j*w)-0.5); magX=abs(X); angX=angle(X); realX=real(X); imagX=imag(X) ; subplot(2,2,1);plot(w/pi,magX);grid xlabel('freqency in pi units');ylabel('Magnitude'); subplot(2,2,3);plot(w/pi,angX);grid xlabel('freqency in pi units');ylabel('Angle') subplot(2,2,2);plot(w/pi,realX);grid xlabel('freqency in pi units');ylabel('Real') subplot(2,2,4);plot(w/pi,imagX);grid xlabel('freqency in pi units');ylabel('Image')
MATLAB仿真实例ppt课件

精选PPT课件
41
3.1 工具箱介绍
控制系统工具箱将大量函数分成若干 类,以方便按功能查找,以下列出主要的 类。 ➢ 一般工具(General) ➢ 线 性 模 型 创 建 ( Creating Linear Models)
精选PPT课件
42
➢ 数据提取(Data Extraction) ➢ 变换工具(Conversions) ➢ 系统互连(System Interconnections) ➢ 系 统 增 益 和 特 性 ( System Gain and
?一般工具general?线性模型创建creatinglinearmodels42ppt课件?数据提取dataextraction?变换工具conversions?系统互连systeminterconnections?系统增益和特性systemgainanddynamics?时域分析timedomainanalysis43ppt课件?频域分析frequencydomainanalysis?经典设计classicaldesign?极点配置poleplacement?最优设计lqrlqgdesign?状态模型statespacemodel?时延timedelays44ppt课件?模型维数和特性modeldimensionsandcharacteristics?重载的数学运算overloadedandarithmeticoperators?矩阵方程求解器matrixequationsolvers?命令行绘图工具commandlineplotcustomization45ppt课件32实例ss22transferfcnttoworkspaceytoworkspacestep0clock46ppt课件运行该模型并在命令窗口输入如下代码
MATLAB实现“信号与系统”课程可视化建模及仿真 精品

第1章绪论宇宙中的一切事物都在不停地运动中,物质的一切运动或状态的变化,广义地说都是一种信号(signal),即信号是物质运动的表现形式。
在通信技术中,一般将语言、文字、图像或数据等统称为消息(Message)。
在消息之中包含有一定数量的信息(Information),通信的目的就是从一方向另一方传送消息,给对方以信息。
但是,消息的传送一般都不是直接的,必须借助于一定形式的信号(光信号、电信号等)才能远距离快速传输和进行各种处理。
因而,信号是消息的表现形式,它是通信传输的客观对象;而消息则是信号的具体内容,它蕴藏在信号之中。
我们目前广泛应用的是电信号,电信号通常是随时间变化的电压或电流,在某些情况下,也可以是电荷或磁通。
由于信号是随时间而变化的,在数学上它可以用时间t的函数来表示,因此,习惯上常常交替地使用“信号”与“函数”两个名词。
系统的主要任务是对信号进行传输与处理,信号与系统之间有着十分密切的联系,分析系统的功能和特性必然要涉及到对信号的分析,因此对信号的分析是非常重要的。
信号的特性可以从两个方面描述,即时间特性和频率特性。
信号是时间t的函数,它具有一定的波形,因而表现出一定的时间特性,如出现时间的先后、持续时间的长短、重复周期的大小以及随时间变化的快慢等。
另外,任意信号总可以分解为许多不同频率的正弦分量,即具有一定的频率成分,因而表现出一定的频率特性,如各频率分量的相对大小,主要频率分量占有的范围等。
信号的形式之所以不同,就在于他们各自有不同的时间特性和频率特性,信号的时间特性和频率特性有着密切的关系,不同的时间特性将导致不同的频率特性。
各种变化着的信号从来不是孤立存在的,信号总是在系统中产生又在系统中不断传递。
所谓系统(system),是有若干相互联系,相互作用的单元组成的具有一定功能的有机整体。
系统的种类很多,如通信系统、计算机系统、自动控制系统、生态系统、经济系统、社会系统等。
如通信系统包括接收机、发射机和计算机等,它们是通信系统的组成单元,它们本身又是一个较小的系统,称为子系统;而一个电容元件具有存储电容元件具有储存电荷的功能,也可以把它看作一个小系统。
《MATLAB与系统仿真》PPT课件

模型的表达形式有物理模型和数学模型两类。
数学模型是系统的某种特征本质的数学表达式, 是用数学公式来描述所研究的客观对象或系统中 的某一方面的问题。
数
静态模型
学
连续系统模型
模
动态模型 离散系统模型
型
编辑版ppt
15
三、系统仿真
一个较流行于工程技术界的定义是:仿真是 通过对系统模型的实验去研究一个存在的或设计 中的系统。这种定义适用于概括了所有工程的 (技术的)或非工程的(非技术的)系统。
30
工程实际对仿真技术提出的新需求:
1、减少模型的开发时间; 2、提高模型建立的精度和实验的精度; 3、改进人与人、人与计算机的通信。
编辑版ppt
31
本课程主要讲授内容 1、系统建模的基本方法与模型处理技术 2、连续系统的数字仿真程序通用算法
-数值积分仿真方法学 3、连续系统模型的离散化处理技术 4、计算机仿真软件-MATLAB
动而发生变化的系统进行仿真称为离散事件系统 仿真。其数学模型多用流程图或网络图来描述。
(3)混合系统仿真:
当系统的数学模型是由上述两类模型混合 构成时,称为混合系统仿真。其仿真方法是将 上述两类方法综合于一体。
(4)系统动力学仿真: 当对象的数学模型是用系统动力学方程式来
描述时,该系统的仿真称为系统动力学仿真。
法。模拟计算机由一些基本的模拟运算部件组成, 这些运算部件有:积分器、加法器、系数器、函 数发生器、乘法器等。
模拟计算机是并行运算的,运算速度快,但 精度不高,由于它可以实现传递函数为1/s的积 分运算,可以方便地求解微分方程。
编辑版ppt
24
(2)数字计算机仿真:
MATLAB仿真课件第2章

8
2020/11/23
第2章 MATLAB基础及其使用初步
2)MATLAB 界面 1º MATLAB主界面
图2-1 MATLAB主界面
9
2020/11/23
第2章 MATLAB基础及其使用初步 2º MATLAB程序编辑器
图2-2 MATLAB程序编辑器
10
2020/11/23
第2章 MATLAB基础及其使用初步 3º MATLAB的图形界面
7
2020/11/23
第2章 MATLAB基础及其使用初步
2º Simulink 是MATLAB软件的扩展,用于动态系统仿真的交互式系统。Simulink 允许用户在屏幕上绘制框图来模拟一个系统,并能够动态地控制该 系统。Simulink 采用鼠标驱动方式,能够处理线性、非线性、连续、 离散、多变量以及多级系统。此外,Simulink 还为用户提供了两个 附加功能项:Simulink 扩展和模块集; 3º MATLAB 是 MATLAB 用来解决各个领域特定问题的函数库,是开放式的--可 以拿来就用,也可以根据自己的需要进行扩展。MATLAB提供的工 具箱为用户提供了丰富而实用的资源,涵盖了科学研究的很多门类。 目前,已经涉及到数学、控制、通信、信号处理、图像处理、经济、 医学等多种学科。
建模培训matlab使用PPT课件

在信号处理中的应用
信号滤波
MATLAB提供了丰富的信号滤波频谱分析
利用MATLAB的FFT(快速傅里叶 变换)函数,可以对信号进行频谱 分析,提取信号的特征信息。
信号调制与解调
MATLAB可以用于信号的调制与解 调过程,实现信号的传输与处理。
在控制系统中的应用
系统建模
利用MATLAB的Simulink工具箱,可以对控制系 统进行建模,并进行仿真分析。
控制算法设计
MATLAB提供了多种控制算法,如PID控制、模糊 控制等,可用于设计控制系统。
系统稳定性分析
通过MATLAB的稳定性分析工具,可以对控制系 统进行稳定性评估和优化。
在机器学习中的应用
数据预处理
实时仿真
通过MATLAB与Simulink的集成,可以实现实时仿真和测试,提高开发效率。
与C/C的交互
MATLAB Coder
使用MATLAB Coder,可以将MATLAB代码转换为C/C代码,以便 在嵌入式系统或高性能计算环境中运行。
调用C/C代码
通过MATLAB的MEX函数或MATLAB引擎API,可以在MATLAB中 调用C/C代码,实现混合编程。
编写单元测试用例,对代码进行测试和验证,确保代码的正确
性和稳定性。
性能分析和优化
分析代码性能
使用MATLAB的性能分析工具,如Profiler,分析代码运行时间、 内存占用等性能指标。
优化算法
根据性能分析结果,优化算法和数据结构,提高代码执行效率。
并行计算
利用MATLAB的并行计算工具箱,实现多核处理器上的并行计算, 加速代码运行。
1980年代中
推出MATLAB 1.0,成为商业 化的数学软件。
信号与系统MATLAB文件及仿真

2.2 离散时间序列卷积离散时间序列卷积和的定义为:∑∞-∞=-=*=m m n f m f n f n f n f )()()()()(2121设序列f 1(n)在区间n 1~ n 2非零,f 2(n) 在区间m 1~ m 2非零,则f 1(n)的时域宽度为L 1= n 2 - n 1+1,f 2(n)的时域宽度为L 2= m 2 - m 1+1。
由卷积和的定义可得,卷积后的序列f (n)的宽度为L = L 1 + L 2 -1,且。
,只在区间n 1 +m 1~ n 1 +m 1+ L 1 + L 2 –2非零。
因此对于f 1(n)和f 2(n)均为有限期间非零的情况,只需计算在区间n 1 +m 1~ n 1 +m 1+ L 1 + L 2 –2的序列值即可。
MATLAB 的conv()函数可以快速求出两个离散序列卷积和,conv()函数的调用格式为: ∙ f=conv(f1,f2)其中f1为包含序列f 1(n)的非零样值点的行向量,f2为包含序列f 2(n)的非零样值点的行向量,向量f 则返回序列f (n)= f 1(n)* f 2(n)的所有非零样值点的行向量。
但是函数conv()不需要给出序列f 1(n)和f 2(n)非零样值点的时间序列,也不返回卷积后序列非零样值点的时间序号。
为此编制出如下求离散序列卷积和的通用函数dconv()。
function[f,n]=dconv(f1,f2,n1,n2)%f:卷积和序列f(n)对应的非零样值向量%n:序列f(n)对应的序号向量%f1:序列f1(n)的非零样值向量%f2:序列f2(n)的非零样值向量%n1:序列f1(n)对应的序号向量%n2:序列f2(n)对应的序号向量f=conv(f1,f2);%计算序列f1与f2的卷积和fn0=n1(1)+n2(1);%计算序列f 非零样值点的起始位置n3=length(f1)+length(f2)-2;%计算卷积和f 非零样值的宽度n=n0:n0+n3;%确定卷积和f 非零样值的序号向量subplot(2,2,1)stem(n1,f1,'filled')title('f1(n)')xlabel('n')ylabel('f1(n)')subplot(2,2,2)stem(n2,f2,'filled')title('f2(n)')xlabel('n')ylabel('f2(n)')subplot(2,2,3)stem(n,f,'filled')title('f1(n)与f2(n)的卷积和f(n)')xlabel('n')ylabel('f(n)')h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) %将第三个子图的横坐标范围扩为原来的2.5倍例1:⎩⎨⎧≤≤=elsen n f 0201)(1 ⎪⎪⎩⎪⎪⎨⎧====else n n n n f 0332211)(2求:)()()(21n f n f n f *=f1=ones(1,3);f2=0:3;f=conv(f1,f2)结论:f = 0 1 3 6 5 3例2: ⎪⎪⎩⎪⎪⎨⎧==-==else n n n n f 0110211)(1, ⎩⎨⎧≤≤-=e l s e n n f 0221)(2 求:)()()(21n f n f n f *=n1=[-1 0 1];f1=[1 2 1];n2=-2:2;f2=ones(1,5);[f,n]=dconv(f1,f2,n1,n2)结论:f = 1 3 4 4 4 3 1n = -3 -2 -1 0 1 2 3例3:)4()()(1--=n u n u n f 、)3()()(2--=n u n u n f求:)()()(21n f n f n f *=n1=0:3;f1=ones(1,4);n2=0:2;f2=ones(1,3);[f,n]=dconv(f1,f2,n1,n2)结论:f = 1 2 3 3 2 1n = 0 1 2 3 4 52.1 连续时间信号卷积连续时间信号卷积的定义为:⎰∞-∞=-=*=ττττd t f f t f t f t f )()()()()(2121用MA TLAB 实现上述卷积积分运算实际上是采用分段求和的方法来实现的。
信号与系统的MATLAB仿真
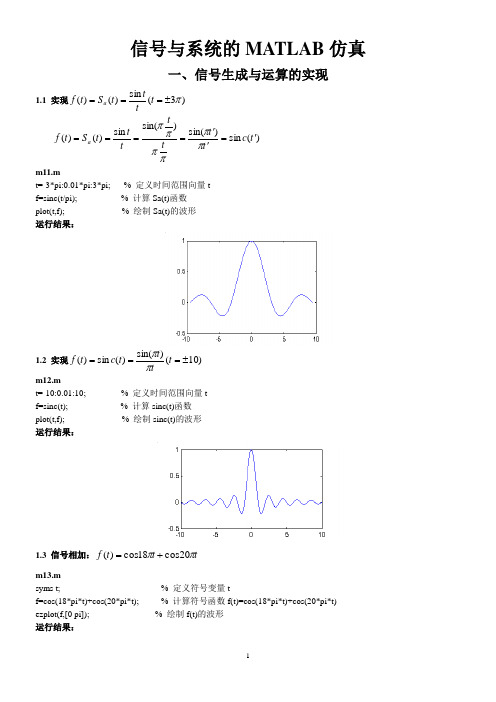
信号与系统的MATLAB 仿真一、信号生成与运算的实现1.1 实现)3(sin )()(π±===t ttt S t f a )(sin )sin()sin(sin )()(t c t t t t t t t S t f a '=''====ππππππ m11.mt=-3*pi:0.01*pi:3*pi; % 定义时间范围向量t f=sinc(t/pi); % 计算Sa(t)函数 plot(t,f); % 绘制Sa(t)的波形 运行结果:1.2 实现)10()sin()(sin )(±===t tt t c t f ππ m12.mt=-10:0.01:10; % 定义时间范围向量t f=sinc(t); % 计算sinc(t)函数plot(t,f); % 绘制sinc(t)的波形 运行结果:1.3 信号相加:t t t f ππ20cos 18cos )(+=m13.msyms t; % 定义符号变量tf=cos(18*pi*t)+cos(20*pi*t); % 计算符号函数f(t)=cos(18*pi*t)+cos(20*pi*t) ezplot(f,[0 pi]); % 绘制f(t)的波形 运行结果:1.4 信号的调制:t t t f ππ50cos )4sin 22()(+=m14.msyms t; % 定义符号变量tf=(2+2*sin(4*pi*t))*cos(50*pi*t) % 计算符号函数f(t)=(2+2*sin(4*pi*t))*cos(50*pi*t) ezplot(f,[0 pi]); % 绘制f(t)的波形 运行结果:1.5 信号相乘:)20cos()(sin )(t t c t f π⋅=m15.mt=-5:0.01:5; % 定义时间范围向量f=sinc(t).*cos(20*pi*t); % 计算函数f(t)=sinc(t)*cos(20*pi*t) plot(t,f); % 绘制f(t)的波形 title('sinc(t)*cos(20*pi*t)'); % 加注波形标题 运行结果:二、系统时域的仿真分析2.1 实现卷积)(*)(t h t f ,其中:)2()()()],1()([2)(--=--=t t t h t t t f εεεε m21.mp=0.01; % 取样时间间隔 nf=0:p:1; % f(t)对应的时间向量 f=2*((nf>=0)-(nf>=1)); % 序列f(n)的值nh=0:p:2; % h(t)对应的时间向量 h=(nh>=0)-(nh>=2); % 序列h(n)的值 [y,k]=sconv(f,h,nf,nh,p); % 计算y(t)=f(t)*h(t) subplot(3,1,1),stairs(nf,f); % 绘制f(t)的波形 title('f(t)');axis([0 3 0 2.1]);subplot(3,1,2),stairs(nh,h); % 绘制h(t)的波形 title('h(t)');axis([0 3 0 1.1]);subplot(3,1,3),plot(k,y); % 绘制y(t)=f(t)*h(t)的波形 title('y(t)=f(t)*h(t)');axis([0 3 0 2.1]);子程序 sconv.m% 此函数用于计算连续信号的卷积y(t)=f(t)*h(t) function [y,k]=sconv(f,h,nf,nh,p)% y:卷积积分y(t)对应的非零样值向量 % k:y(t)对应的时间向量 % f:f(t)对应的非零样值向量 % nf:f(t)对应的时间向量 % h:h(t)对应的非零样值向量 % nh:h(t)对应的时间向量 % p:取样时间间隔y=conv(f,h); % 计算序列f(n)与h(n)的卷积和y(n) y=y*p; % y(n)变成y(t)left=nf(1)+nh(1) % 计算序列y(n)非零样值的起点位置 right=length(nf)+length(nh)-2 % 计算序列y(n)非零样值的终点位置 k=p*(left:right); % 确定卷积和y(n)非零样值的时间向量 运行结果:2.2 实现卷积)(*)(t h t f ,其中:)()()],2()([2)(t e t h t t t f tεεε-=--= m22.mp=0.01; % 取样时间间隔 nf=0:p:2; % f(t)对应的时间向量 f=2*((nf>=0)-(nf>=2)); % 序列f(n)的值nh=0:p:4; % h(t)对应的时间向量 h=exp(-nh); % 序列h(n)的值 [y,k]=sconv(f,h,nf,nh,p); % 计算y(t)=f(t)*h(t) subplot(3,1,1),stairs(nf,f); % 绘制f(t)的波形 title('f(t)');axis([0 6 0 2.1]);subplot(3,1,2),plot(nh,h); % 绘制h(t)的波形 title('h(t)');axis([0 6 0 1.1]);subplot(3,1,3),plot(k,y); % 绘制y(t)=f(t)*h(t)的波形 title('y(t)=f(t)*h(t)');axis([0 6 0 2.1]);运行结果:2.3 设方程 )(2)(6)(5)('''t e t y t y t y tε-=++,试求零状态响应)(t y m23.m :yzs=dsolve('D2y+5*Dy+6*y=2*exp(-t)','y(0)=0,Dy(0)=0') ezplot(yzs,[0 8]); 运行结果:yzs =exp(-t)+exp(-3*t)-2*exp(-2*t) 即:)()2()(32t e e et y t t tε---+-=2.4 已知二阶系统方程)(1)(1)()('''t LCt u LC t u L R t u c c δ=++对下列情况分别求)(t h ,并画出其波形。
MATLAB语言与系统仿真ppt资料

3、混合仿真:结合了模拟仿真与数字仿真。 4、现代计算机仿真:采用先进的微型计算机,基于
专用的仿真软件、仿真语言来实现,其数值计算 功能强大,使用方便,易学。80年代以来
第十页,编辑于星期五:十三点 五十分。
第三节 仿真技术的应用与发展
一、仿真技术在工程中的应用
1、模型的定义
• 模型是对现实系统有关结构信息和行为的某种形式
的描述,是对系统的特征与变化规律的一种定量抽 3、分布式数字仿真:充分利用网络技术,协调合作,投资少,效果好。
指根据系统的数学模型,用仿真语言转化为计算机可以实施的模型。
象,是人们认识事物的一种手段或工具。 仿真是在模型上进行的,建立系统的模型是仿真的关键内容。
提高设计效率:比如电路设计,服装设计等等。 第九页,编辑于星期五:十三点 五十分。
第宏七观页 经,济编与辑商于业星策期略•五的:研指十究三不点 五以十分人。 的意志为转移的客观存在的实体,如:飞行器研
制中的飞行模型;船舶制造中的船舶模型等。 第一节
计算机仿真和辅助设计的基本概念
1、PSPICE、ORCAD:通用的电子电路仿真软件,适合于元件级仿真。
四、计算机仿真的三要素及基本步骤(内容)
1、三要素
(1)系统:研究的对象 (2)模型:系统的抽象
(3)计算机:工具与手段
系统
建立数学模型
仿真实验
模型
计算机
建立仿真模型
图1.1 计算机仿真三要素关系图
结果分析
第五页,编辑于星期五:十三点 五十分。
2、基本步骤
• 包括三个基本的内容:建模 仿真实验
问题的阐述
1、航空与航天工业
• 飞行器设计中的三级仿真体系:纯数学模拟(软件)、 半实物模拟、实物模拟或模拟飞行实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章信号与系统的建模与仿真教学目标通过本章的学习,了解Simulink的基本功能,熟练掌握Simulink模块的基本操作、Simulink仿真参数的设置;掌握连续系统和离散系统的数学模型以及建模与仿真的方法。
Simulink是MATLAB的重要组成部分,提供建立系统模型、选择仿真参数和数值算法、启动仿真程序对该系统进行仿真、设置不同的输出方式来观察仿真结果等功能。
Simulink既适用于线性系统,也适用于非线性系统;既适用于连续系统,也适用于离散系统和连续与离散混合系统;既适用于定常系统,也适用于时变系统。
Simulink提供图形用户界面,用户可以用鼠标操作,从模块库中调用标准模块,将它们适当地连接起来以构成动态系统模型,并且用各模块的参数对话框为系统中各模块设置参数。
当各模块的参数设置完成后,即建立起该系统的模型。
如果对某一模块没有设置参数,那就意味着使用Simulink预先为该模块设置的默认参数值作为该模块的参数。
Simulink模块库内容十分丰富,除包括输入信号源模块库(Sources)、输出接收模块库(Sinks)、连续系统模块库(Continuous)、离散系统模块库(Discrete)数学运算模块库(Math Operations)等许多标准模块外,用户还可以自定义和创建模块。
系统的模型建立后,选择仿真参数和数值算法,便可以启动仿真程序对该系统进行仿真,这种操作可以用Simulink菜单,也可以用MATLAB命令实现。
菜单方式对于交互式运行特别方便,而命令方式对于运行一批仿真时很有用。
在仿真过程中,用户可以设置不同的输出方式来观察仿真结果。
例如,使用Sinks模块库中的Scope模块或其他显示模块来观察有关信号的变化曲线,也可以将结果存放在MATLAB工作空间中,供以后处理和使用。
根据仿真结果,用户可以调整系统参数,观察分析仿真结果的变化,从而获得更加理想的仿真结果。
2.1 Simulink模块库简介2.1.1 常用模块库常用模块库(Commonly Used Blocks)是为了加快建模速度、节省建模过程中寻找模块的时间而将最常用的基本模块集中放在一起形成的。
在Simulink Library Browser (Simulink 模块库浏览器)窗口中,单击Libraries列表框中的Commonly Used Blocks选项,即可在窗口右侧展开Commonly Used Blocks(常用模块库)标签,如图2.1所示。
也可以右击Libraries列表框中的Commonly Used Blocks选项,在弹出的快捷菜单中选择Open Commonly Used Block Library命令,这时系统将弹出独立的Library:Simulink/Commonly Used Blocks窗口,如图2.2所示。
46MATLAB在电气信息类专业中的应用图2.1 Simulink Library Browser窗口图2.2 Library:Simulink/Commonly Used Blocks窗口常用模块库包括以下内容。
第2章信号与系统的建模与仿真471.总线信号生成器与总线信号选择器模块Bus Creator(总线信号生成器)模块用于将多个信号合成一个总线信号,常用于子系统接口信号传递;Bus Selector(总线信号选择器)模块用来选择总线信号中的一个或多个。
2.信号合成器与信号分离器模块Mux(信号合成器)模块和Demux(信号分离器)模块的功能看似与总线信号生成模块和总线信号选择模块的功能相似,但是信号合成器与信号分离器模块是对所有信号进行合成与分离的,而总线信号选择模块可以任意选择总线上的信号进行输出。
3.数据类型转换模块Data Type Conversion(数据类型转换)可将输入数据转换为指定输出类型,具体选择有Inherit(与输入数据保持一致)、Double(双精度类型)、Single(单精度)、int8(8位整数数据)、uint8(无符号8位整数数据)等。
在输入/输出数据上可选择Real World Value(实数值相等)或者Stored Integer(存储整数相等)。
同时可以选择取整的方向,如选择Round Integer Calculations toward为Zero时,表示向零取整;选择Nearest时,表示向最接近的整数取整;选择Floor时,表示向负无穷取整;选择Ceiling时,表示向正无穷取整。
4.积分模块Integrator(积分)模块为连续时间积分单元。
5.离散时间积分模块Discrete-Time Integrator(离散时间积分)模块可完成离散系统积分作用。
6.乘法与加法模块Product(乘法器)模块可用来求输入信号的乘积,双击Product模块可修改输入信号的端口数。
Sum(加法器)模块可用来求输入信号的加法、减法操作。
双击Sum模块打开参数设置对话框,在List of signs符号列表框可修改加、减法符号,改变符号列表栏“|”位置,可改变加、减法符号的位置,在Icon shape列表框中可选择加法器模块的外部形状为圆形或方形。
7.关系操作与逻辑操作模块Relational Opetator(关系操作)模块可用来比较两个输入信号的大小关系,双击Relational Opetator模块,可设置输入信号的比较关系。
关系操作可选择大于等于(>=)、小于等于(<=)、不等于(~=)、等于(==)、大于(>)、小于(<)。
Logic operator(逻辑操作)模块可用来求取两输入变量的逻辑操作关系,双击Logic operator模块,打开Logic operator模块参数对话框,逻辑操作具体有AND(与)、OR (或)、NOT(非)、XOR(异或)、NAND(与非)、NOR(或非)操作。
8.增益模块Gain(增益)模块可用来设置信号放大倍数,在Simulink动态仿真中使用频繁。
双击Gain模块打开参数设置对话框,在Gain文本框中可设置具体信号放大倍数。
48MATLAB在电气信息类专业中的应用9.输入/输出接口及子系统模块In1(输入)模块在建立子系统时作为输入信号的接口。
Out1(输出)模块在建立子系统时作为输出信号的接口。
Subsystem(子系统)模块可用来将复杂系统的全部或局部生成为一个子系统,这样便于简化Simulink模型结构。
10.终端模块Terminator(终端)模块可用来连接没有与其他模块相连的输出端口,在Simulink模型中,如果有输出端口没有连接,运行仿真时,在MATLAB窗口将显示警告信息,使用终端模块可以避免这类警告信息的出现。
2.1.2 连续系统模块库Continuous(连续系统)模块库提供了连续系统Simulink建模与仿真的基本模块。
在Simulink模块库浏览器中,单击Libraries列表框中的Continuous选项选项,可打开连续系统模块库;也可以用右击Continuous选项,在弹出的快捷菜单中选择Open Continuous Library选项,系统弹出独立的Library:simulink/Continuous窗口,如图2.3所示。
图2.3 Library:simulink/Continuous窗口连续系统模块库包括以下内容。
1.微积分模块使用Derivative(微分)模块、Integrator(积分)模块可建立各种各样的控制器及控制系统动态仿真模型。
微分模块的作用是将输入端的信号经过一阶数值微分,在输出端输出。
双击Derivative模块,打开微分环节线性化设置对话框。
系统默认的微分环节线性化时间常数为inf(无穷大),用户可根据需要自行设定。
积分模块的作用是将输入信号经过数值积分,在输出端直接反映出来。
在将常微分方第2章 信号与系统的建模与仿真 49程转换为图形表示时也必须使用该模块。
2.状态空间模型使用Simulink 动态仿真模型,可使用State-Space (状态空间)模块,双击State-Space 模块,系统弹出参数设置对话框,在这里可设定状态空间模型的系数矩阵及初始状态。
3.传输延迟及可变传输延迟如果控制系统模型里含有纯延迟环节,用户可使用Simulink 连续系统模块库提供的Transport Delay(传输延迟)模块来建立仿真模型。
双击Transport Delay 模块,系统弹出参数设置对话框,在Time Delay 文本框中输入需要延迟的时间数值。
同时,在Pade Order 文本框中输入纯延迟环节线性化处理的近似多项式阶数。
Variable Time Delay (可变时间延迟)模块与Variable Transport Delay (可变传输延迟)模块在Simulink 连续系统模块库里以两个模块的形式出现,但它们可以通过选择模型属性的Select Delay Type 属性值来相互转换。
传输延迟模块应用在传输的延迟时间与被控对象传输速度有关的系统建模中。
4.传递函数模块与零极点增益模型传递函数是频域中常用的描述线性微分方程的一种方法,通过引入Laplace 变换可以将原来的线性微分方程在初始条件下变换为代数的形式,从而以多项式的比值形式描述系统。
传递函数的一般形式为:11211121()()()m m m n n n b s b s b num s G s den s a s a s a −+−++++==+++ (2-1) Transfer Fcn (传递函数)模块可以用来建立连续系统传递函数的Simulink 仿真模型,双击Transfer Fcn 模块,打开参数设置对话框。
在Numerator coefficient 文本框中定义分子多项式系数向量,在Denominator coefficient 文本框中定义分母多项式系数向量,从而建立传递函数的Simulink 仿真模型。
将传递函数模型的分子和分母分别进行因式分解,则可以将其变换为1212()()()()()()()m n s z s z s z G s k s p s p s p −−−=−−− (2-2) 式(2-2)中,k 为系统增益,(1,2,,)i z i m = 为系统的零点,(1,2,,)i p i n = 为系统的极点。
如果已知系统的零点、极点和增益,可以使用连续系统的Zero-Pole(零极点)增益模型来建立Simulink 仿真模型。
双击Zero-Pole 模块,打开零极点增益模型的参数设置对话框,在指定的零点、极点、增益文本框中输入相应的数据,然后单击OK 按钮即可完成零极点增益模型的Simulink 建模。
