第二章 计算机中信息的表示1
第2章计算机中的信息表示习题参考答案-汇编语言与计算机组成原理 答案
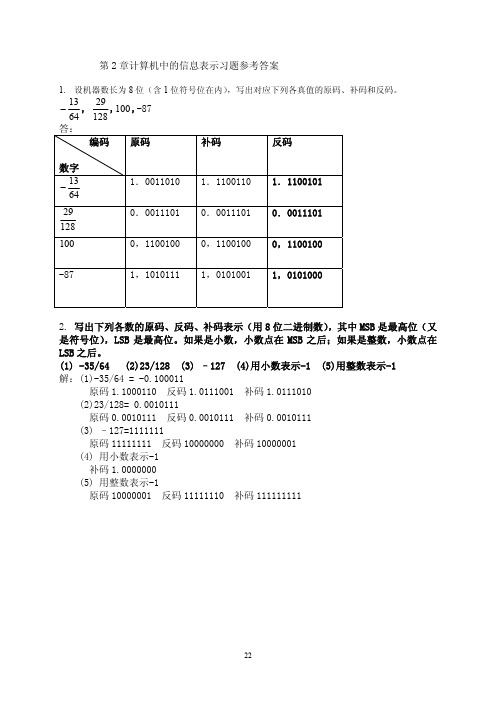
第2章计算机中的信息表示习题参考答案1. 设机器数长为8位(含1位符号位在内),写出对应下列各真值的原码、补码和反码。
6413−, 12829,100,-872. 写出下列各数的原码、反码、补码表示(用8位二进制数),其中MSB 是最高位(又是符号位),LSB 是最高位。
如果是小数,小数点在MSB 之后;如果是整数,小数点在LSB 之后。
(1) -35/64 (2)23/128 (3) –127 (4)用小数表示-1 (5)用整数表示-1 解:(1)-35/64 = -0.100011原码1.1000110 反码1.0111001 补码1.0111010(2)23/128= 0.0010111原码0.0010111 反码0.0010111 补码0.0010111 (3) –127=1111111原码11111111 反码10000000 补码10000001 (4) 用小数表示-1 补码1.0000000 (5) 用整数表示-1原码10000001 反码11111110 补码1111111113. 己知[X],求[X]和X .补原4. 当十六进制数9B和FF分别表示为原码、补码、反码、移码和无符号数时,所对应的十进制数各为多少(设机器数采用一位符号位)。
答:5. 有一个字长为32位的浮点数,符号位1位,阶码8位,用移码表示,尾数23位,用补码表示;基数为2。
请写出:(1)最大数的二进制表示;(2)最小数的二进制表示; (3)规格化数所能表示数的范围。
解:用IEEE754格式(E的取值范围:1~254,留出全0和全1分别表示0和无穷大)31 30 23 22 20 0S E M(1) 最大数的二进制表示:0 11111110 11111111111111111111111即 2127(2-2-23)(2) 最小数的二进制表示:1 11111110 11111111111111111111111即 - 2127(2-2-23)(3) 规格化数所能表示数的范围:最小的正数:0 00000001 00000000000000000000001 即2-126(1+2-23)绝对最小的负数:1 00000001 00000000000000000000001 即-2-126(1+2-23)所以范围是: -2127(2-2-23)至-2-126(1+2-23) ,2-126(1+2-23)至2127(2-2-23)6. 将下列十进制数表示成IEEE754标准的32位浮点规格化数。
第二章 计算机中的信息表示 2.1 数在计算机中的表示

(e)八进制和二进制之间的转换 1、为什么要有八进制和十六进制 2、二进制到八进制之间的转换 八进制的特征:有0-7八个数,逢八进一 二进制和八进制之间的转换 例: (10100.1011)2——(?)8 010 100 . 101 100 2 4 . 说明划分时的注意事项 5 4
3、八进制和二进制之间的转换 例: (326.125)8——(?)2 3 2 6 . 1 2
011 010 110 . 001 010
5
101
(f)二进制和十六进制之间的转换 十六进制的特征: 二进制和十六进制之间的转换
(11010111100.11011)2 = (0110 1011 1100.1101 1000)2 = (6BC.D8)16 (F28)16=(1111 0010 1000)2
在原码中0有两种表示: [+0]=00000000 [-0]=10000000
原码能够表示的数的范围:
特点: (1)直观,与真值转换很方便; (2)进行乘、除运算方便 (3)加、减运算比较麻烦,比如:一 个正数和一个负数相加必须要考虑符 号问题。
(f)反码:
规则:对于正数,其反码与原码相同, 对于负数,符号位为1,其数值位X的 绝对值取反 例:[+2]反=00000010 [-2]反=11111101 [+0] 反=00000000 [-0] 反=11111111
2 信息的表示 2.1 信息在计算机中的表示
为什么要采用二进制
1、电路简单: 2、工作可靠: 3、简化运算: 4、逻辑性强:
2.1.1 数制及其转换
1)数制 ①什么是进位计数制 一般而言,对于任意的R进制数 An-1An-2......A1A0A-1A-2A-3.......A-m (其中n为整数位 数,m为小数位数) 其值可以表示为: An-1×Rn-1+An-2×Rn-2......A1×R1+A0×R0+ A1×R-1+A-2×R-2+A-3×R-3.......A-m×R-m
计算机组成原理考试大纲

《计算机组成原理》考试大纲第一章概论一、知识要点冯.诺依曼体制;信息的数字化表示方法;存储程序工作方式;计算机系统的层次结构;计算机的主要特点;计算机的主要性能指标。
二、要求1、理解和掌握计算机的基本组成及各部分功能。
2、理解和掌握冯.诺依曼体制的要点和核心。
3、理解信息的数字化表示方法。
4、理解和掌握存储程序工作方式的过程。
5、理解计算机的主要特点。
6、理解和掌握计算机的主要性能指标。
7、理解计算机系统的层次结构。
第二章计算机中的信息表示一、知识要点进位计数制概念,二进制、八进制、十进制、十六进制之间的转换;机器数概念,原码、补码、真值之间的转换;定点数与浮点数的表示范围;字符编码与汉字编码;指令的基本形态、操作码表示与扩展、地址结构的简化;常见寻址方式的含义、特点与应用;各类指令的特点和设置方法。
二、要求1、理解进位计数制的基数r和权值ir的概念,能实现各进位制间的相互转换。
2、理解机器数的概念,知道原码、补码表示方法及表示范围;掌握原码、补码、真值之间的转换方法。
3、知道定点数和浮点数的表示方法、典型值和表示范围。
4、理解指令中应给出哪些基本信息,知道指令按地址结划分有哪些类指令格式,知道简化地址结构的途径,知道计算机指令中操作码怎么表示。
5、理解常见寻址方式的含义(包括立即寻址、直接寻址、寄存器寻址、间接寻址、寄存器间址及其变型、变址寻址、相对寻址),给出地址或数据信息能寻址找出操作数。
6、掌握堆栈的定义、用途、基本组成及各部分的作用。
7、理解RISC和C ISC指令的基本特点。
8、理解指令分类方法,按功能划分有哪几类指令及其设置方法,掌握I/O设备的编址方式。
第三章CP U子系统一、知识要点CP U各组成部分的基本功能;同步控制方式和异步控制方式的基本概念;补码加减运算方法;溢出判断方法;原码一位乘法和补码一位乘法的运算规则;浮点加减运算流程;模型机指令类型和寻址方式;模型机数据通路结构;组合逻辑控制的基本思想;模型机组合逻辑控制器的三级时序系统和各类指令流程与操作时间表,微程序控制的基本思想;微指令的编码方法和微地址形成方式。
计算机系统导论——读书笔记——第二章信息的表示和处理

计算机系统导论——读书笔记——第⼆章信息的表⽰和处理第⼆章信息的表⽰和处理2.1 信息存储2.1.1 ⼗六进制2.1.2 字数据⼤⼩2.1.3 寻址和字节顺序1.地址:对象所使⽤的字节中最⼩的地址2.⼤端法:最⾼有效字节在前⼩端法:最低有效字节在前(⼤多Intel兼容机使⽤)3.发送⽅机器(内部代码)——>⽹络应⽤程序(⽹络标准)——>接收⽅机器(内部代码)4.⼩程序——打印程序对象的字节表⽰1 #include <stdio.h>2using namespace std;34 typedef unsigned char * byte_pointer;//定义类型:指向unsigned char的指针56void show_byte(byte_pointer start, size_t len){7 size_t i;8for(i = 0; i < len; ++i)9 printf(" %.2x", start[i]);//%.2x表⽰整数必须⽤⾄少两个数字的⼗六进制格式输出10 printf("\n");11 }1213void show_int(int x){14 show_byte((byte_pointer) &x, sizeof(int));15 }1617void show_float(float x){18 show_byte((byte_pointer) &x, sizeof(float));19 }2021void show_double(double x){22 show_byte((byte_pointer) &x, sizeof(double));23 }2425void show_pointer(void * x){//void*是特殊类型的指针,没有相关联的类型信息26 show_byte((byte_pointer) &x, sizeof(void *));27 }2829int main(){30int x;31float y;32double z;33while(scanf("%d %f %lf", &x, &y, &z)){34 show_int(x);35 show_float(y);36 show_double(z);37 show_pointer(&x);38 show_pointer(&y);39 show_pointer(&z);40 }41return0;42 }输⼊111-1-1.0-1.0123451.0011.001输出01 00 00 0000 00 80 3f00 00 00 00 00 00 f0 3f98 f5 bf ef fe 7f 00 0094 f5 bf ef fe 7f 00 0088 f5 bf ef fe 7f 00 00ff ff ff ff00 00 80 bf00 00 00 00 00 00 f0 bf98 f5 bf ef fe 7f 00 0094 f5 bf ef fe 7f 00 0088 f5 bf ef fe 7f 00 0039 30 00 00c5 20 80 3f6a bc 74 93 18 04 f0 3f98 f5 bf ef fe 7f 00 0094 f5 bf ef fe 7f 00 0088 f5 bf ef fe 7f 00 00我的电脑是MaxOS,可以看出它是64位系统,采⽤⼩端法表⽰5.可以通过在终端(mac是terminal,windows是命令⾏⼯具)执⾏命令man ascii得到⼀张ASCII字符码表,回车后运⾏结果如下ASCII(7) BSD Miscellaneous Information Manual ASCII(7)NAMEascii -- octal, hexadecimal and decimal ASCII character setsDESCRIPTIONThe octal set:000 nul 001 soh 002 stx 003 etx 004 eot 005 enq 006 ack 007 bel010 bs 011 ht 012 nl 013 vt 014 np 015 cr 016 so 017 si020 dle 021 dc1 022 dc2 023 dc3 024 dc4 025 nak 026 syn 027 etb030 can 031 em 032 sub 033 esc 034 fs 035 gs 036 rs 037 us040 sp 041 ! 042 " 043 # 044 $ 045 % 046 & 047 '050 ( 051 ) 052 * 053 + 054 , 055 - 056 . 057 /060 0 061 1 062 2 063 3 064 4 065 5 066 6 067 7070 8 071 9 072 : 073 ; 074 < 075 = 076 > 077 ?100 @ 101 A 102 B 103 C 104 D 105 E 106 F 107 G110 H 111 I 112 J 113 K 114 L 115 M 116 N 117 O120 P 121 Q 122 R 123 S 124 T 125 U 126 V 127 W130 X 131 Y 132 Z 133 [ 134 \ 135 ] 136 ^ 137 _140 ` 141 a 142 b 143 c 144 d 145 e 146 f 147 g150 h 151 i 152 j 153 k 154 l 155 m 156 n 157 o160 p 161 q 162 r 163 s 164 t 165 u 166 v 167 w170 x 171 y 172 z 173 { 174 | 175 } 176 ~ 177 delThe hexadecimal set:00 nul 01 soh 02 stx 03 etx 04 eot 05 enq 06 ack 07 bel08 bs 09 ht 0a nl 0b vt 0c np 0d cr 0e so 0f si10 dle 11 dc1 12 dc2 13 dc3 14 dc4 15 nak 16 syn 17 etb18 can 19 em 1a sub 1b esc 1c fs 1d gs 1e rs 1f us20 sp 21 ! 22 " 23 # 24 $ 25 % 26 & 27 '28 ( 29 ) 2a * 2b + 2c , 2d - 2e . 2f /30 0 31 1 32 2 33 3 34 4 35 5 36 6 37 738 8 39 9 3a : 3b ; 3c < 3d = 3e > 3f ?40 @ 41 A 42 B 43 C 44 D 45 E 46 F 47 G48 H 49 I 4a J 4b K 4c L 4d M 4e N 4f O50 P 51 Q 52 R 53 S 54 T 55 U 56 V 57 W58 X 59 Y 5a Z 5b [ 5c \ 5d ] 5e ^ 5f _60 ` 61 a 62 b 63 c 64 d 65 e 66 f 67 g68 h 69 i 6a j 6b k 6c l 6d m 6e n 6f o70 p 71 q 72 r 73 s 74 t 75 u 76 v 77 w78 x 79 y 7a z 7b { 7c | 7d } 7e ~ 7f delThe decimal set:0 nul 1 soh 2 stx 3 etx 4 eot 5 enq 6 ack 7 bel8 bs 9 ht 10 nl 11 vt 12 np 13 cr 14 so 15 si16 dle 17 dc1 18 dc2 19 dc3 20 dc4 21 nak 22 syn 23 etb24 can 25 em 26 sub 27 esc 28 fs 29 gs 30 rs 31 us32 sp 33 ! 34 " 35 # 36 $ 37 % 38 & 39 '40 ( 41 ) 42 * 43 + 44 , 45 - 46 . 47 /48 0 49 1 50 2 51 3 52 4 53 5 54 6 55 756 8 57 9 58 : 59 ; 60 < 61 = 62 > 63 ?64 @ 65 A 66 B 67 C 68 D 69 E 70 F 71 G72 H 73 I 74 J 75 K 76 L 77 M 78 N 79 O80 P 81 Q 82 R 83 S 84 T 85 U 86 V 87 W88 X 89 Y 90 Z 91 [ 92 \ 93 ] 94 ^ 95 _96 ` 97 a 98 b 99 c 100 d 101 e 102 f 103 g104 h 105 i 106 j 107 k 108 l 109 m 110 n 111 o112 p 113 q 114 r 115 s 116 t 117 u 118 v 119 w120 x 121 y 122 z 123 { 124 | 125 } 126 ~ 127 delFILES/usr/share/misc/asciiHISTORYAn ascii manual page appeared in Version 7 AT&T UNIX.BSD June 5, 1993 BSD(END)2.1.4 表⽰字符串1.⼗进制数字‘y’的ascii码正好是0x3y2.strlen(str)函数不计算终⽌的空字符(ascii码为0x00)3.字符编码⽅式:(1)ASCII (American Standard Code for Information interchange)(2)Unicode (Unique Code)(3)UTF-8 / UTF-16 / UFT-32 (Unicode Transformation Format)2.1.5 表⽰代码2.1.6 布尔代数(Boolean Algebra)简介1.布尔运算&对|有分配律:a&(b|c) = (a&b)|(a&c)布尔运算|对&有分配律:a|(b&c) = (a|b)&(a|c)2.位向量:长度为w,由0和1组成的串应⽤:表⽰有限集合/压位运算(例:[01101010]表⽰集合{1,3,5,6}),位向量掩码/屏蔽信号3.布尔环(Boolean ring),类似于整环/整数环“加法”逆元:^类似于+; 每个整数x有加法逆元-x使得x+(-x)=0,类似地,每个布尔元素a都有“加法逆元”a使得a^a=0; 有趣的性质:(a^b)^a=b 1//这是⼀个不需要第三个量的交换函数,不过它并没有性能上的优势2void inplace_swap(int *x, int *y){//*x = a, *y = b3 *x = *x ^ *y;//*x = a^b, *y = b4 *y = *x ^ *y;//*x = a^b, *y = a5 *x = *x ^ *y;//*x = b, *y = a6 }2.1.7 C语⾔中的位级运算:&, |, ^, ~2.1.8 C语⾔中的逻辑运算: &&, ||, !2.1.9 C语⾔中的移位运算:>>, <<1.逻辑右移(⾼位补0,⽆符号数进⾏逻辑右移)算数右移(⾼位补符号位,有符号数进⾏算数右移)(1)初级运算符[]().->(2)单⽬运算符(3)算数运算符(4)移位运算符(5)关系运算符(6)位级运算符(7)逻辑运算符(8)赋值运算符2.2 整数表⽰2.2.1 整形数据类型2.2.2 ⽆符号数的编码(unsigned)2.2.3 补码编码(two's-complement)1.<limits.h>库:INT_MIN, INT_MAX, UINT_MAX<stdint.h>库:intN_t, UintN_t (t = 16,32,64等)(我在xcode上没有include这两个库也能直接使⽤INT_MIN、int32_t等)2.有符号数的表⽰⽅法(1)补码(two's-complement):最⾼位权重为-2^(w-1)(2)反码(ones' complement):最⾼位权重为-(2^(w-1)-1)(3)原码(sign-magnitude):最⾼位为1表⽰所有其他位权重为负注:(2)(3)中0的表⽰法不唯⼀,有+0和-0两种2.2.4 有符号数和⽆符号数之间的转换(可能)改变数值,但不改变位表⽰1.补码转换为⽆符号数(w位):TMin <= x < 0, T2U(x) = x + 2^w0 <= x <= TMax, T2U(x) = x2.⽆符号数转换为有符号数(w位):0 <= x <= TMax, U2T(x) = xTMax < x <= UMax, U2T(x) = x - 2^w2.2.5 C语⾔中的有符号数和⽆符号数1.数字常量默认为有符号数,加上后缀u或U可创建⽆符号数常量2.类型转换的⽅式:(1)显式:强制类型转换(2)隐式:不同类型变量间赋值3.%d有符号⼗进制,%u⽆符号⼗进制,%o⼋进制,%x⼗六进制4.C语⾔对于同时包含有符号数和⽆符号数的表达式,会隐式地将有符号数转换为⾮负的⽆符号数 1/*2这是⼀个测试函数3注:TMin写成-2147483647-1⽽⾮-21474836484是因为limits.h中定义INT_MIN=-INT_MAX-1,以规避某些奇怪的现象5*/6 #include <cstdio>7using namespace std;89int main(){10 printf("-1 < 0u = %d\n", -1 < 0u);11 printf(" -1 = 0x%x \n", -1);12 printf(" 0u = 0x%x\n\n", 0u);1314 printf("2147483547 > (int)2147483648u = %d\n", 2147483547 > (int)2147483648u);15 printf(" 2147483547 = 0x%x \n", 2147483547);16 printf(" (int)2147483648u = 0x%x\n\n", (int)2147483648u);1718 printf("-2147483647-1u < 2147483647 = %d\n", -2147483647-1u < 2147483647);19 printf(" -2147483647-1u = 0x%x \n", -2147483647-1u);20 printf(" 2147483647 = 0x%x\n\n", 2147483647);2122 printf("-2147483647-1u < -2147483647 = %d\n", -2147483647-1u < -2147483647);23 printf(" -2147483647-1u = 0x%x \n", -2147483647-1u);24 printf(" -2147483647 = 0x%x\n\n", -2147483647);25return0;26 }运⾏结果如下-1 < 0u = 0-1 = 0xffffffff0u = 0x02147483547 > (int)2147483648u = 12147483547 = 0x7fffff9b(int)2147483648u = 0x80000000-2147483647-1u < 2147483647 = 0-2147483647-1u = 0x800000002147483647 = 0x7fffffff-2147483647-1u < -2147483647 = 1-2147483647-1u = 0x80000000-2147483647 = 0x800000012.4 浮点数2.4.1 ⼆进制⼩数2.4.2 IEEE浮点表⽰1.表⽰形式:(1)符号(sign)s: 表⽰+-(2)尾数(significand)M:⼆进制⼩数,取值范围为[1,2)或[0,1)(3)阶码(exponent)E:对浮点数加权,权重为2的E次幂2.编码:s编码符号sign s,exp编码阶码exponent E,frac编码尾数significand M3.三种情况(1)规格化的(noemalized): exp!=00...0 && exp!=11 (1)i. 阶码 E = exp - bias, bias = 2^(k-1)-1, k=exp的位数ii. 尾数 M = 1.xx...x = 1.frac的位(隐含的以1开头的表⽰)(2)⾮规格化的(denormalized): exp == 00 0i. 阶码 E = 1 - bias, bias = 2^(k-1)-1, k=exp的位数ii. 尾数 M = 0.xx...x = 0.frac的位iii.注意:0.0有两种表⽰⽅法+0.0和-0.0,符号位分别为0或1,其他位全部为0(3)特殊值: exp == 11 (1)i. ⽆穷:frac = 00...0, s=0或1表⽰+∞或-∞,能够表⽰溢出的运算结果,如x/0 ii. Nan(not a number): frac != 00...0, 表⽰⾮实数的运算结果,如根号-1,∞-∞4.三种情况的数字分布⾮规格化数字的阶码定义为E=1-bias可以补偿⾮规格化的尾数没有隐含的开头1,有助于数字表⽰的平滑转变;否则,在绝对值最⼤的⾮规格化数字(其⼆进制表⽰为0 00...0 11...1)和绝对值最⼩的规格化数字(其⼆进制表⽰为0 00...01 00...0)之间将存在跳跃2.4.3 数字⽰例1. 处理正浮点数时,若按照⽆符号整数解释他们的⼆进制表⽰,则可以发现它们的⼤⼩顺序不变;负浮点数只需要倒序。
第二章 计算机中信息的表示习题及答案

第二章一、选择题1.下列数中,最小的数是 A 。
8A.(101001)2B.(52) C.(2B)16D.452.下列数中,最大的数是 D 。
A.(101001)2B.(52)8C.(2B)16 D.453.计算机中表示地址时使用__ _D___A.原码B.补码C.反码D.无符号数4.字长16位,用定点补码小数表示时,一个字能表示的范围是__D___ 1-2-15A.-1~()B.0~(1-2-15)1-2-15C.-1~+1 D.-()~(1-2-15)5.若X补=10000000,则十进制真值为___ C___。
A、-0B、-127C、-128D、-16.定点整数16位,含1位符号位,原码表示,则最大正数为___C ___A、216B、215C、215-1D、216-17.当-1<x<0时,[x]原=___B___A.xB.1-xC.4+xD.(2-2n)-1*18.8位反码表示数的最小值为_______,最大值__ A___。
A.-127,+127B.-128,+128C.-256,+256D.-255,+2559.N+1位二进制正整数的取值范围是____D ___A.0~2n-1 B.1~2n-1C.0~2n+1-1 D.1-2n+1-110.浮点数的表示范围和精度取决于___ A____A.阶码的位数和尾数的位数B.阶码的位数和尾数采用的编码C.阶码采用的编码和尾数采用的编码D.阶码采用的编码和尾数的位数11.在浮点数编码表示中,___ C___在机器数中不出现,是隐含的。
A.尾数B.符号C.基数D.阶码12.移码和补码比较,只有____ C___不同,其他都相同。
A.正号 B.负号C.符号 D.标志13.一个24×24点阵的汉字,需要___ _B____字节的存储空间。
A.62 B.72C.64 D.3214.62个汉字的机内码需要 CA.62字节 B.32字节C.124字节 D.248字节15.ASCII码是对____ A____进行编码的一种方案A.字符、图形符号 B.汉字C.数字 D.声音16.D/A转换是___ C___A.把计算机输出的模拟量转化为数字量B.把模拟量转化为数字量,把数字量输入到计算机C.把数字量转化为模拟量,把转化结果输出计算机D.把计算机输出的模拟量转为数字量17.在大量数据传送中常用且有效的检验法是__ D___A.奇偶校验法 B.海明码校验C.判别校验 D.CRC校验二、填空题1.二进制中的基数为 2,十进制中的基数为 10 ,八进制中的基数为8 ,十六进制中的基数为 16 。
02 计算机内信息的数字化表示

示例: 示例:
(1011.1) 2 = 1×23+0×22 + 1×21 + 1 ×20 +1 × 2-1 +0× 1×
= 8 + 0 + 2 + 1 + 0.5 = (11.5)10
编码和数制
八与十六进制之间的转换
整数从右向左 小数从左向右
三位并一位
二进制
一位拆三位 四位并一位
八进制
二进制
一位拆四位
Word) 字(Word) 一条指令或一个数据信息,称为一个字。 字是计算机进行信息交换、处理、存储的 基本单元。计算机一次能处理的二进制数 计算机一次能处理的二进制数 字长 CPU中每个字所包含的二进制代码的位数, 称为字长。字长是衡量计算机性能的一个 重要指标。
四、常见名词
指令 指挥计算机执行某种基本操作的命令称为指 令。一条指令规定一种操作,由一系列有序 指令组成的集合称为程序。 容量 容量是衡量计算机存储能力常用的一个名词, 主要指存储器所能存储信息的字节数。常用 的容量单位有B、KB、MB、GB,它们之间 的关系是:1KB=1024B,1MB=1024KB, 1GB=1024MB。
十六进制
编码和数制
示例: 示例: 100 110 110 111 . 010 100
(4
6
6
7 . 2 4 )8
Hale Waihona Puke 0001 1011 0111.0100 ( 1 B 7 . 4 )16
三、计算机采用二进制的好处
1. 2. 3. 4.
技术上容易实现。 运算规则简单。 可以方便的进行逻辑运算。 与十进制之间关系简单,转换容易 实现。
二、进位计数制
2计算机信息表示

41
计算机编码_数值
小数的表示
✓ 浮点数:小数点的位置不固定。由阶码和尾数组 成
✓ 阶码:指数部分,是一个整数 ✓ 尾数:数的有效数值,整数或纯小数两种形式
42
计算机编码_字符
字符编码
✓ 如何表示A、B、C等字母? ✓ 如何表示句号、逗号等? ✓ 如何表示回车、换行等?
9
1001
11
不同数制值之间的关系
12
二进制运算
算术运算规则: 0+0=0 0+1=1 0*0=0 0*1=0
1+0=1 1*0=0
1+1=10 1*1=1
110 + 011
1001
011 + 011
110
13
二进制运算
逻辑运算规则: 与 / :或 / : 非:
0
1
0
1
110001 011111
✓ 一个字节可有256个值 ✓ 可存放一个半角英文字符(ASCII码)。两
个或四个字节存放一个汉字编码
26
数据的计算机存储
位: b 字节:B
1B=8b
1KB = 1024 B=210B 1MB = 1024KB =220B 1GB = 1024MB =230B 1TB = 1024GB =240B
5
1 数制
数制(number system)
✓ 用一组固定的数字(数码符号)和一套 统一的规则来表示数值的方法。也叫计 数制
6
数制
几种常用进位计数制。
✓ 十位制(Decimal notation) D –十个手指 ✓ 24进制(一天);60进制(秒、分、时) ✓ 二进制(Binary notation) B ✓ 八进制(Octal notation) O ✓ 十六进制数(Hexadecimal notation) H ✓ 古巴比伦人-60进制 ✓ 玛雅人-20进制
计算机中数据信息的表示

1.3 计算机中数值的表示
1.3.1 机器数的编码表示
正数的补数即该正数本身。 一个正数和一个负数互为补数时,它们绝对值之和即为模数。 一个负数可用它的正补数来代替,而这个正补数可以用模加上负
101001010 =01001010;(只有八位,最高位第九位自然丢失) 即验证了正数的补码为该正数本身。
1.3 计算机中数值的表示
1.3.1 机器数的编码表示
[Y]原=11001010 [Y]补=11001010+模=11001010+100000000=100000000+11001010
=100000000+(-1001010)=11111111+1-1001010 =(11111111-1001010)+1 可以看出,上式中(11111111-1001010)符号位为1,数值位为各位取 反,即有: [Y]补=10110101+1=10110110 其中(10110101)我们对(-1001010)定义为反码,即符号位为1,数值位 各位取反。
1.2 进位计数制及其相互转换
1.1.4 二进制与十进制间的相互转换
二级制转换为十进制 二进制各位的权为2i ,将二进制数按权展开,相加即得十 进制数。
十进制转换为二进制 二进制各位的权为2i ,将十进制数按权对应展开,即得二 进制数。
1.3 计算机中数值的表示
1.3.1 机器数的编码表示
1. 原码表示法 整数的最高位用于符号位,规定0表示“+”号,1表示“-”
计算机中信息的表示

128瓦
64瓦
32瓦
16瓦
8瓦
4瓦
2瓦
1瓦
1
1
1
0
1
0
1
0
不论指令还是数据,若想存入计算机中,都必须采 用二进制编码形式 , 在二进制系统中只有两个数 0 和 1, 即便是多媒体信息 ( 声音、图形等 ) 也必须转 换成二进制的形式 , 才能存入计算机 , 一个二进制 数在计算机中是以电子器件的两个物理状态来表 示。
数制基础
位权值:处在不同位置上的数字所代表的值不同。一个数 字在某个固定位置上所代表的值是确定的, 这个固定位 上的值称为位权。位权与基数的关系是:各进位制中位 权的值是基数的若干次幂。任何一种数制表示的数都可 以写成按位权展开的多项式之和。
例:666.66 = 6×102+6×101+6×100+6×10-1+6×10-2 例:(101101.11) 2 = 1×25+1×24+1×23+1×22+ 0×21+1×20+1×2-1+1×2-2 32 + 0 + 8 + 4 + 0 +1 + 0.5 + 0.25
1. 0000 …… 整数部分为1
低位
计算机中的常用计数制及转换
* 2、 十六进制
十六进制数:逢 16 进一,基数为 16 ,权为 16 的 若干次幂。16个数字符号:0,1,2,3,4,5, 6,7,8,9,A,B,C,D,E,F 一.十六进制转换为十进制(按权展开) (1CB)16 =1×162+12×161+11×160 =(459)10 (FF)16 =15×161+15×160 =(255)10
* 八进制(举例)
二.十进制转换为八进制
计算机中信息的表示方法

“假”相对应,为计算机实现逻辑运算和程序中逻辑判断提
供了便利条件。
A B F=A+B
00 0
1、逻辑或运算:or v +
01 1
10 1
11 1
A B F=A ·B
2、逻辑与运算: and ^ ·
00 0 01 0
10 011ຫໍສະໝຸດ 13、逻辑非运算: not —
A F=A 01 10
3.进位计数制之间的转换方法 (1)十进制数转换成J进制数
十进制实数既有整数部分,又有小数部分,其转换方法是将整 数部分和小数部分分别转换,然后将这两部分拼起来即可。
整数部分:除以 J取余数,直到商为0,余数从右到左排列。
小数部分:乘以 J取整数,整数从左到右排列。
~ 例 100.345(D)=1100100.01011(B)
100(D)=144(Q)=64(H) 八进制
数据
数值数据 非数值数据
有符号数
无符号数 文字、字符 图形、图像 声音
数据类型
2.1 数值数据的表示
2.2.1进位计数制及其相互转换
1.进位计数制
按照一定进位方法进行计数的数制称为进位计数制, 简称进制。
在日常生活中,人们习惯使用的进制是十进制 (Decimal),但在计算机内部采用的进制却是二进制 (Binary)。由于用二进制表示的数的位数长,书写不便, 为了便于书写常采用八进制(Octal [Q])和十六进制 (Hexadecimal)作为中间进制。
第2章 计算机数据表示
计算机要对各种信息或数据进行处理, 首先遇到的问题是必须将各种信息以计算 机可以识别的方式表示,并且以一定的形 式存储在计算机中。现代计算机大都是以 二进制表示的数字计算机。
计算机组成原理第02章 计算机中的信息表示

2.1 数值型数据的表示方法
2.1.2 带符号数的表示 2. 补码表示法 ⑴ 补码定义 ·通式 [X]补=M+X (mod M) 数X对模M 的补 数称作其补码 X>0, 作为正常溢出量可以舍去。 若X>0,则模 M 作为正常溢出量可以舍去。 因而正数的补码就是其本身, 因而正数的补码就是其本身,形式上与原码 相同。 相同。
2.1 数值型数据的表示方法
2.1.3 数的定点表示与浮点表示 2. 浮点表示法 浮点数格式(原理性) ⑴ 浮点数格式(原理性) N =±RE×M 其中: 其中: N :真值 RE :比例因子 E :阶码 R :阶码的底 M :尾数 一般采取规格化的约定 一般采取规格化 规格化的约定
Ef Em
…
E2 E1 Mf M1 M2
2.1 数值型数据的表示方法
2.1.3 数的定点表示与浮点表示 ⑵ 带符号定点整数 设代码序列为: ……X 设代码序列为:XnXn-1……X1X0 ,Xn为符号位
原码 典型值 真值 最大正数 非零最小正数
2n-1 1
补码 真值
2n-1 1 -2n -1
代码序列
01…… ……11 …… 00…… ……01 ……
第2章 计算机中的信息表示
重点:定点、浮点数的表示; 重点:定点、浮点数的表示;操作码扩展技 术;指令系统的设计 难点:浮点数的IEEE754格式表示, 难点:浮点数的IEEE754格式表示,定点和 IEEE754格式表示 浮点数的表示范围,浮点数的规格化问题, 浮点数的表示范围,浮点数的规格化问题, 操作码扩展技术,指令系统的设计 操作码扩展技术,
2.1 数值型数据的表示方法
2.1.2 带符号数的表示 3. 反码表示法 若定点小数的反码序列为X ·若定点小数的反码序列为X0.X1X2……Xn,则 X X 1>X≥0 [X]反= 0>X≥2-2-n+X 0>X≥-1 若定点整数的反码序列为X ·若定点整数的反码序列为XnXn-1……X1X0,则 X X 2n>X≥0 [X]反= 0>X≥2n+1-1+X 0>X≥-2n
第二章 汉字信息在计算机内部的表示

0
1
2
3
4
5
6
7
ASCII码字符标准中用7 ASCII码字符标准中用7位 码字符标准中用 二进制数定义了128个字符, 128个字符 二进制数定义了128个字符, 其中94个为图形字符, 94个为图形字符 其中94个为图形字符,32 个为控制字符, 个为控制字符,1个为空格 字符和一个Del Del键 字符和一个Del键。 ASCII的编码空间如图所示, ASCII的编码空间如图所示, 的编码空间如图所示 图中把7位二进制数分为高 图中把7位二进制数分为高 位作为列号, 3位作为列号,低4位作为 行号,并用十六进制表示, 行号,并用十六进制表示, 从而组成了一个ASCII编码 从而组成了一个ASCII编码 ASCII 空间。 空间。
7.代码页 代码页 不同国家的人使用着不同语言的操作系统。然而, 不同国家的人使用着不同语言的操作系统。然而,操 作系统厂商若要根据各个国家和地区使用不同语言文字的 人开发不同的操作系统,在成本、 人开发不同的操作系统,在成本、系统维护与升级等方面 的开销太大。为此,微软公司在开发MS DOS和 MS的开销太大。为此,微软公司在开发MS-DOS和Windows3.1 的各种产品时, 的各种产品时,进一步将依赖于各具体平台的各文种的字 符集加以整理,并对各个具体的代码页都赋予一个代号, 符集加以整理,并对各个具体的代码页都赋予一个代号, 称作“代码页ID ID”。 称作“代码页ID 。
0 0 1 2 3 4 5 6 7 8 9 A B C D E F
1
2
3
4
5
6
7
8
9
A
B
C
D
E
Fቤተ መጻሕፍቲ ባይዱ
C0控制 字符区
1-2、计算机中信息的表示及其运算

(3) 求补码的快捷方式
设 x = 1010 时
则[x]补 = 24+1 1010 = 100000 1010 = 1,0110
又[x]原 = 1,1010
= 11111 + 1 1010 = 11111 + 1 1010 10101 + 1 = 1,0110
当真值为 负 时,补码 可用 原码除符号位外 每位取反,末位加 1 求得
[x]补 = 27+1 +( 1011000 ) = 100000000 1011000 1,0101000
小数
x [x]补 =
x 为真值 如 x = + 0.1110 [x]补 = 0.1110 x = 0.1100000
1>x ≥0 0 > x ≥ 1(mod 2)
2+x
[x]补 = 2+( 0.1100000 ) = 10.0000000 0.1100000 1.0100000 用 小数点 将符号位
真值
[x]补
[x]原
0,1000110 1,1000110 0.1110 1.1110 0.0000 1.0000
不能表示
x = + 70 = 1000110 0, 1000110 x = –70 = – 1000110 1, 0111010 x = 0.1110 0.1110 x = 0.1110 1.0010 x = 0.0000 [+ 0]补 = [ 0]补 0.0000 x = 0.0000 0.0000 x = 1.0000 1.0000 由小数补码定义
1.
不带符号的整数
数的表示范围: 4位: 0000B ~ 1111B, 0H ~ FH,0D ~ 15D; 8位: 00000000B ~ 11111111B, 00H ~ FFH, 0D ~ 255D; 16位: 0000H ~ FFFFH, 0D ~ 65535D; n位数:0D ~ (2n-1)D
1.2计算机中信息的表示与存储教学设计河南大学出版社、河南电子音像出版社七年级信息技术上册
-重点知识点:位、字节、KB、MB、GB、TB的层次关系、存储单位的应用场景、存储容量对计算机性能的影响
-重点词:位、字节、KB、MB、GB、TB、存储容量、计算机性能
⑤数据安全与保护
-重点知识点:数据安全的重要性、常见的数据保护措施、计算机病毒的原理与防范
-重点词:数据安全、加密、备份、防病毒、计算机病毒
6.数据安全与保护
-数据安全的重要性
-常见的数据保护措施:加密、备份、防病毒等
-计算机病毒的原理与防范
7.二进制逻辑运算
-二进制逻辑运算的基本概念:与、或、非、异或
-逻辑运算在计算机中的运用:条件判断、位操作等
-逻辑运算的真值表与逻辑表达式
8.计算机信息处理流程
-计算机如何通过二进制数据进行信息处理
-信息处理的基本流程:输入、处理、存储、输出
- CPU与内存协同工作原理
9.信息技术在日常生活中的应用
-计算机信息表示与存储技术在现实生活中的应用案例
-信息技术对社会发展的影响与贡献
-未来信息技术发展趋势与展望
典型例题讲解
例题1:将十进制数200转换为二进制数。
解答:
步骤1:200 ÷ 2 = 100 ... 0
-举例:讲解存储器中的地址是如何用来定位和访问特定数据的。
(3)信息存储的层次结构:学生需要理解从位到字节、从KB到TB的信息存储层次结构,以及它们之间的换算关系。
-举例:解释1KB等于多少字节,以及1MB、1GB、1TB分别代表多大的存储容量。
教学资源
1.软硬件资源
-计算机
-投影仪
-教学软件(二进制转换工具、内存管理模拟器)
过程:
各组代表依次上台展示讨论成果,包括主题的现状、挑战及解决方案。
信息在计算机中的表示

注意:十进制小数不一定能转换成完全等值的其他进制
小数。遇到这种情况时,根据精度要求,取近似值。
11
例:
(100.345)10(1100100.01011)2 2 2 2 2 2 2 2 100 50 25 12 6 3 1 0 0.345 2 0.690 2 1.380 2 0.760 2 1.520 2 1.040 (100)10=(144)8=(64)16 8 100 8 12 8 1 0 16 100 16 6 0
3
1、进位记计数制的概念
• 十进制(D) 十种状态,逢十进一, (0,1,2,3,4,5,6,7,8,9) • 二进制(B) 两种状态,逢二进一,(0,1) • 八进制(Q) 八种状态,逢八进一,(0,1,2,3,4,5,6,7) • 十六进制(H) 十六种状态,逢十六进一 (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
逻辑性强
二进制的两种状态正好与逻辑代数中的真和假相对 应,可以方便地进行逻辑运算。
2
1、进位记计数制的概念
进位计数制(简称数制)就是按进位的方法计数。 在不同的数制中,把某一进位计数制中涉及的数字符号
的个数称为基数,用R表示,一个具体的数用(S)R的形式
表示。计算机中经常用到的数制有十进制、二进制、十 六进制和八进制。
汉字的机内表示:机内码 汉字的输出:字形码(字库
输入码
Font)
字形 检索 程序
字形码
键盘
键盘 处理 程序
代码 转换 程序
机内码
储存、加工
输出设备
码表
字模库
25
汉字输入编码
汉字输入编码的实质就是用字母、数字和一些符号代码 的组合来描述汉字。目前,汉字编码的方案有很多种,主要 可分为四种:数字编码、字音编码、字形编码、音形编码。 数字码 (利用一串数字代表一个汉字) 如:电报码、区位码、纵横码 字音码 (用汉语拼音代表一个汉字) 如:全拼、双拼、微软拼音 字形码 (根据汉字结构或笔画用字母或数字表示汉字) 如:五笔字型 音形码 (根据汉语拼音和字形结构规定汉字编码) 如:声形码、王林快码
第2章 计算机中数据信息表示法_1

28
§2.2 机器数的编码表示
例2:写出机器字长8位,反码表示时所对应的 十进制整数和小数的表示范围。
反码表示:同原码表示(一一对应)
整数范围:-127≤x ≤ +127
小数范围:-(1-2-7 ) ≤ x ≤ 1 -2-7
29
1.三种机器数的比较 1)对于正数它们都等于真值本身,但对于负数各有不同 的表示。 2)最高位都表示符号位,补码的符号位可作为数值位的 特殊部分同数值位—起参加运算;而原码和反码的符号位不 允许和数值位同等看待,必须分开进行处理。 3)对于值0,原码和反码各有正负2种不同的表示形式, 只有补码有惟一的表示形式。 4)原码、反码表示的正、负数范围是对称的,而补码表 示的范围要宽,能多表示一个最负的数(绝对值最大的负 数)。
30
§2.2 机器数的编码表示
原、反、补码表示举例: 求下列各数的原、反、补码(设机器字长5位)
大 x=+1101
[x]原=0,1101 [x]反=0,1101 [x]补=0,1101
X=+0.1001 [x]原=0.1001 [x]反=0.1001 [x]补=0.1001 X=-0.0101 [x]原=1.0101 [x]反=1.1010 [x]补=1.1011
真值 原 码 反 码 补码 移码
+0
-0
00000000 00000000 00000000 10000000
10000000 11111111 00000000 10000000
+(27-1) 01111111 01111111 01111111 11111111
-1 10000001 11111110 11111111 01111111
计算机信息的表示形式

02
03
01
可见,二进制数码个数比较少,因此比较简单,容易实现(但肯定也会带来问题)
二进制运算规则也很简单:0+0,1+0,(交换律)0+1,与十进制都一样。但1+1=0,此时将进位
乘法与十进制完全相同
下面我们来比较下十进制数和二进制数:
(见教科书表1-7)
*
二、八、十、十六进制之间关系对照
十进制 二进制 十六进制 八进制 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 8 10 9 1001 9 11 10 1010 A 12 11 1011 B 13 12 1100 C 14 13 1101 D 15 14 1110 E 16 15 1111 F 17
*
计算机中的数据
1
计算机为什么采用二进制?
二进制只有2个数码,0或1,即2个状态
在现实世界中,表示2个状态的电子逻辑器件很容易实现。
*
计算机中的数据
例如:
1
灯泡的亮和暗;
2
开关的开和关等
3
在计算机中,一般采用电子开关,用电子器件实现,如电子管、晶体管等
4
*
关于进位计数制的概念
一般的计数方法都采用进位计数制,人,习惯使用十进制
01
在某一位,当计数满后,清0,并向高位进位
02
一个数字,有多位,某数码在不同的位置表示不同的数值,即不同数位的数字有不同的权值
03
*
关于进位计数制的概念
对于十进制,当数到9时必须进位,这就是进位计数制。对于二进制来说,概念相同
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.计算机的数据单位 计算机的数据单位 • 计算机采用的是二进制数字系统,任何信息必须转换成二 进制数据后才能由计算机进行处理、存储和传输。
1.什么是数据? 什么是数据 广义上的数据是指表达现实世界中各种信息的一组可以记录和识别的标 记或符号,它是信息的载体,是信息的具体表现形式。在计算机领域中, 记或符号,它是信息的载体,是信息的具体表现形式。在计算机领域中, 狭义的数据是指能够被计算机处理的数字、字母和符号等信息的集合, 狭义的数据是指能够被计算机处理的数字、字母和符号等信息的集合, 一切可以被计算机加工、处理的对象都可被称之为数据。 一切可以被计算机加工、处理的对象都可被称之为数据。 计算机要处理信息,首先要将信息表示成具体的数据形式。 计算机要处理信息,首先要将信息表示成具体的数据形式。
3. 字 (Word)
计算机一次可以同时处理的二进制数称为一个“ 计算机一次可以同时处理的二进制数称为一个“字”。字的长度 称为字长。一个字由若干个字节组成,用于表示数据或信息的长度。 称为字长。一个字由若干个字节组成,用于表示数据或信息的长度。 常用的字长有8位 位等。 常用的字长有 位、16位、32位、64位等。字长越长的计算机的运算速 位 位 位等 度越快,精度也越高。字长通常成为一个计算机性能的标志。 度越快,精度也越高。字长通常成为一个计算机性能的标志。
二进制数: 二进制数:
小数点左边:从右向左, 小数点左边:从右向左,每一位对应权值分别为 20、21、22、23、24 小数点右边:从左向右,每一位对应的权值分别为2 小数点右边:从左向右,每一位对应的权值分别为 -1、2-2 、2-3、2-4
例: (100101.01)2
(100101.01)2 =1×25+0×24+0×23+1×22+0×21+1×20+0×2-1+1×2-2 × × × × × × × ×
尽管计算机可以处理各种数据和信息,但是计算机内部使用的是二进制数, 尽管计算机可以处理各种数据和信息,但是计算机内部使用的是二进制数, 二进制并不符合人们的习惯,计算机中采用二进制只要原因有: 二进制并不符合人们的习惯,计算机中采用二进制只要原因有: 一、物理实现 简单 计算机采用物理原件的状态来表示计数制中各位的值和位权, 计算机采用物理原件的状态来表示计数制中各位的值和位权,绝大多数物理 元件都只有两种状态,如果计算机中采用十进制, 元件都只有两种状态,如果计算机中采用十进制,势必要求计算机有能够识别 0~9共10种状态的装置。在实际工作中,是很难找到能表示 种不同稳定状态的 种状态的装置。 共 种状态的装置 在实际工作中,是很难找到能表示10种不同稳定状态的 电子器件的。虽然可以用电子线路组合来表示,但是线路非常复杂, 电子器件的。虽然可以用电子线路组合来表示,但是线路非常复杂,所需的设备 量大,而且十分不可靠。而二进制中只有0和 两个数字符号 两个数字符号, 量大,而且十分不可靠。而二进制中只有 和1两个数字符号,可以用电子器件的 两种不同状态来表示一位二进制数。例如,可以用晶体管的截止和导通表示1和 两种不同状态来表示一位二进制数。例如,可以用晶体管的截止和导通表示 和 0,或者用电平的高和低表示 和0等。所以,在数字系统中普通采用二进制。 ,或者用电平的高和低表示1和 等 所以,在数字系统中普通采用二进制。
通过本章的学习,掌握各种进位计数制的进位数、 通过本章的学习,掌握各种进位计数制的进位数、计算机的进位制和 不不同进制之间的转换的方法以及计算机的数据单位。 不不同进制之间的转换的方法以及计算机的数据单位。
1.计算机的数据单位 计算机的数据单位 2.各种进位计数制 各种进位数制 3. 计算机中的进位制 4. 不用进制之间的转换
2.1计算机中常用的计数制 计算机中常用的计数制
1.十进制(D) .十进制( ) 日常生活中最常见的是十进制数,用十个不同的符号来表示:0、1、2、 日常生活中最常见的是十进制数,用十个不同的符号来表示: 3、4、5、6、7、8、9,称为代码。 称为代码。 2. 二进制数(B) 二进制数( )
① 由两个不同的数字符号组成,即0和1; ② 逢二进位。 二进制加法运算: 0+0=0 0+1=1 1+1=10 例: (0101)2+(0011) 2 =(1000) 2 二进制乘法运算: 0*0=0 0*1=0 1*1=1 例: (1101) 2 *(1010) 2 =(10000010) 2
第二章 计算机中信息的表示
回顾
通过上次课的学习,掌握计算机发展、 通过上次课的学习,掌握计算机发展、计算机的特点和分类以及 计算机的常识。 计算机的常识。
回顾1 回顾 回顾2 回顾 回顾3 回顾
计算机的分类 计算机的发展 计算机的组成
计算机的发展
1、巨型机 、
5、微型机(PC) 、微型机( )
2、大型机 、
位权
一个数码处在不同位置上所代表的值不同 。每个数码所表示的数值等于该数码乘以 一个与数码所在位置相关的常数叫位权。 一个与数码所在位置相关的常数叫位权。
数的十进制、二进制、 数的十进制、二进制、八进制和十六进制表示对照表
在同一进位制中,不同位置上的同一个数字符号所代表的值是不同的。例如: 在同一进位制中,不同位置上的同一个数字符号所代表的值是不同的。例如:
2.各种进位计数制 各种进位计数制
十进制: 个记数符号 个记数符号, 、 十进制:10个记数符号,0、 1、2、……、9。每一个数码 、 、 、 。 符号根据它在这个数中所在 的位置(数位 数位), 的位置 数位 ,按“逢十进 来决定其实际数值。 一”来决定其实际数值。基 数为10。 数为 。 二进制:基数为2。 个记 二进制:基数为 。2个记 数符号, 和 。 数符号,0和1。按“逢二进 来决定其实际数值。 一”来决定其实际数值。 八进制:基数为8。8个记 八进制:基数为 。 个记 数符号, 、 、 、 数符号,0、1、2、……7。 。 逢八进一” 按“逢八进一”来决定其实 际的数值。 际的数值。 十六进制:基数为16。 十六进制:基数为 。16 个记数符号,0-9,A,B,C 个记数符号, , , , ,D,E,F。其中 , , 。其中A-F对应 对应 十进制的10-15。按“逢十六 十进制的 。 进一” 进一”来决定其实际的数值
二、运算规则简单 二进制数只有0和 两个数字符号 因此运算规则比十进制简单很多。 两个数字符号, 二进制数只有 和1两个数字符号,因此运算规则比十进制简单很多。 二进制的加减乘除运算规则表
三、适合逻辑运算 逻辑是指条件与结论之间的关系。因此, 逻辑是指条件与结论之间的关系。因此,逻辑运算是指对因果关系进行分析 的一种运算,运算结果并不表示数值大小,而是表示逻辑概念, 的一种运算,运算结果并不表示数值大小,而是表示逻辑概念,即成立还是不成 计算机的逻辑关系是一种二值逻辑,二值逻辑可以用二进制的1和 表示 表示, 立。计算机的逻辑关系是一种二值逻辑,二值逻辑可以用二进制的 和0表示,例 表示“ 表示“ 如:1表示“成立”、“是”或“真”,0表示“不成立”、“否”或“假”等。 表示 成立” 表示 不成立” 逻辑运算只要包括3种基本运算 逻辑加法(又称“ 种基本运算: 运算)、 )、逻辑乘法 逻辑运算只要包括 种基本运算:逻辑加法(又称“或”运算)、逻辑乘法 又称“ 运算)和逻辑否定(又称“ 运算)。此外, 异或” )。此外 (又称“与”运算)和逻辑否定(又称“非”运算)。此外,“异或”运算也很有作用 1)、逻辑加法(“或”运算) 运算) 、逻辑加法( 逻辑加法通常用符号“ 或 表示。逻辑加法运算规则如下: 逻辑加法通常用符号“+”或“∨”表示。逻辑加法运算规则如下: 0+0=0,0∨0=0 , ∨ 总结: 总结:在“或”运算逻 0+1=1,0∨1=1 , ∨ 辑变量中只要有一 者是真, 者是真,其结果都 1+0=1,1∨0=1 , ∨ 为真 1+1=1,1∨1=1 , ∨
一般而言,对于任意的 R 进制数 (其中 n 为整数 位数 ,m 为小数位数): an-1an-2 … a1a0a-1 … a-m 可以表示为以下和式:
an-1×Rn-1+an-2×Rn-2+ … +a1×R1+a0×R0+a-1×R-1+ … +a-m×R-m
( 其中 R 为基数 )
3. 计算机中的进位制
常见进位计数制的基数和数码表 进位制 二进制 八进制 十进制 基数 2 8 10 数字符号 0,1 0,1,2,3,4,5,6,7 0,1,2,3,4,5,6,7,8, 9 0,1,2,3,4,5,6,7,8, 9, A,B,C,D,E,F 标识 B O或Q D
十六进制
16
H
不同的进制由于其进位的基数不同权值是不同的。
进位 数制
一种按进位方式实现计数的制度,简称 一种按进位方式实现计数的制度, 进制制。 进制制。
进位 计数制
按照进位方式计数的数制。如十进制、 按照进位方式计数的数制。如十进制、 二进制、十六进制等。 二进制、十六进制等。 指该进制中允许选用的基本数码的个数. 指该进制中允许选用的基本数码的个数
基数
字节换算关系
1B=8bit ;(1B=1个英文字母 个数字 1个汉字 个英文字母=1个数字 个汉字 ( 个英文字母 个数字; 个汉字=2B) )
位是计算机的最小 数据单位, 数据单位,字节是 计算机中的基本信 息单位。 息单位。
1KB=1024B=210B 1MB=1024KB=210 KB=220 B=1024B×1024B × 1GB=1024MB=210MB=220KB=230B=10243B 1TB=1024GB=210GB=220MB=230KB=240B=10244B
数据的单位
1. 位 (bit)
计算机中最小的数据单位是二进制的一个数位,简称为位 英文 计算机中最小的数据单位是二进制的一个数位,简称为位(英文 名称为bit,读音为比特)。计算机中最直接、 名称为 ,读音为比特 。计算机中最直接、最基本的操作就是对 二进制位的操作。 二进制位的操作。
