人教版六年级数学上册《扇形的认识》同步练习
【分层作业】5.4 扇形(同步练习) 六年级上册数学同步课时练 (人教版,含答案)

第五单元圆5.4 扇形【基础巩固】一、选择题1.下面各圆中的涂色部分,()是扇形。
A.B.C.2.如图中涂色部分的面积和半圆的面积相比,()。
A.涂色部分的面积大B.半圆的面积大C.涂色部分的面积和半圆的面积相等3.如图,在钟面上分针从12点整起,走15分钟经过的部分可以看作()。
A.圆形B.扇形C.三角形D.梯形4.在同一个圆中,扇形的大小与这个扇形的()有关。
A.圆心角B.半径C.直径5.如果两个扇形的半径之比为1∶2,圆心角之比也为1∶2,那么它们的面积之比为()。
A.1∶2 B.1∶4 C.1∶1 D.1∶8二、填空题6.如图,这是一个( ),已知它的周长是28.56dm,它的弧长(AB)是( )dm,面积是( )dm2。
(π取3.14)7.把一张圆形纸片对折三次(如图),此时圆心角是( )。
量得弧长是6.28cm,这张圆形纸片的直径是( )cm。
8.图中阴影部分的面积之和是( )cm2。
9.如图,一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为______平方厘米。
10.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。
在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
三、作图题11.画一个半径2厘米的圆,并用字母标出圆的半径和直径;再在圆中画出一个扇形并涂色。
四、图形计算题12.求涂色部分的面积。
13.求阴影部分的面积(如下图,红色的部分是一个扇形)。
【能力提升】五、解答题14.在比赛中,铅球投掷的落点区域是一个14圆,某运动员最远投掷距离为16米,铅球可能的落点区域面积是多少?15.一个挂钟的时针长5厘米,分针长8厘米,从中午12时到下午3时,分针尖端“走了”多少厘米?时针“扫过”的面积是多少平方厘米?【拓展实践】16.下图每个方格边长表示为1厘米,图中是一个梯形,按要求完成下面两个问题∶(1)计算梯形面积。
【分层作业】5.4 扇形(同步练习) 六年级上册数学同步课时练 (人教版,含答案)

第五单元圆5.4 扇形【基础巩固】一、选择题1.下面各圆中的涂色部分,()是扇形。
A.B.C.2.如图中涂色部分的面积和半圆的面积相比,()。
A.涂色部分的面积大B.半圆的面积大C.涂色部分的面积和半圆的面积相等3.如图,在钟面上分针从12点整起,走15分钟经过的部分可以看作()。
A.圆形B.扇形C.三角形D.梯形4.在同一个圆中,扇形的大小与这个扇形的()有关。
A.圆心角B.半径C.直径5.假如两个扇形的半径之比为1∶2,圆心角之比也为1∶2,那么它们的面积之比为()。
A.1∶2 B.1∶4 C.1∶1 D.1∶8二、填空题6.如图,这是一个( ),已知它的周长是28.56dm,它的弧长(AB)是( )dm,面积是( )dm2。
(π取3.14)7.把一张圆形纸片对折三次(如图),此时圆心角是( )。
量得弧长是6.28cm,这张圆形纸片的直径是( )cm。
8.图中阴影部分的面积之和是( )cm2。
9.如图,一把折扇的骨架长是30厘米,扇面宽为20厘米,完全开放时圆心角为135°,扇面的面积为______平方厘米。
10.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。
在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
三、作图题11.画一个半径2厘米的圆,并用字母标出圆的半径和直径;再在圆中画出一个扇形并涂色。
四、图形计算题12.求涂色部分的面积。
13.求阴影部分的面积(如下图,红色的部分是一个扇形)。
【力量提升】五、解答题14.在竞赛中,铅球投掷的落点区域是一个14圆,某运动员最远投掷距离为16米,铅球可能的落点区域面积是多少?15.一个挂钟的时针长5厘米,分针长8厘米,从中午12时到下午3时,分针尖端“走了”多少厘米?时针“扫过”的面积是多少平方厘米?【拓展实践】16.下图每个方格边长表示为1厘米,图中是一个梯形,按要求完成下面两个问题∶(1)计算梯形面积。
人教版六年级数学上册《第五单元圆- 扇形的认识》单元测试卷带答案

人教版六年级数学上册《第五单元圆-扇形的认识》单元测试卷带答案一、填空。
1.如图,圆上A、B两点之间的部分叫做( ),读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做()。
图中涂色部分就是扇形。
像∠AOB 这样,顶点在圆心的角叫做( )。
可以发现:在同一个圆中,扇形的大小与这个扇形的( )的大小有关。
2. 把一个圆平均分成4 份,其中每份都是一个扇形,一个扇形的面积是圆面积。
的( )( )3. 把一个周长为628 cm的圆平均分成4个大小相同的扇形,每个扇形的周长是( ) cm。
二、判断。
(对的打“√”,错的打“×”)1.扇形的面积比圆的面积小。
( )2.在一个圆内,过圆心剪去一个扇形后,剩下的部分仍是扇形。
( )3.扇形是轴对称图形,有1条对称轴。
( )4.顶点在圆心的角一定是圆心角。
( )5.在同一个圆中,圆心角越大,扇形的面积越大。
( )三、下面图形中阴影部分是扇形的画“√”。
( )( )( )( )( )( )四、下面图形中哪些角是圆心角? 是的打“√”,不是的打“×”。
( )( )( )( )( )( )( )( )五、画一个半径为1.5cm的圆,再在圆中画一个圆心角是70°的扇形。
六、在括号里写出下面各扇形(涂色部分)圆心角的度数。
( )( )( )七、画一个直径为2cm的圆,再在圆中画一个圆心角为100°的扇形。
八、你能求出下面各扇环的面积吗?九、用一张长方形纸制作一把扇子的扇面,如图,扇面的环宽是纸张宽度的一半,这个扇面的面积是多少平方分米?十、如图,是块扇形形状的披萨,求出这块披萨的面积。
(单位: cm)参考答案一、1.弧扇形圆心角圆心角2. 143.3.357二、1.× 2.√ 3.√ 4.× 5.√三、(√)(√)( )(√) (√) ( )四、(√)(√)( √)(×)(×) (√) (×) (×) (√)五、略六、180°120°270°七、八、[3.14×82-3.14×(8-3)2]×14=30.615(cm2)[3.14×52-3.14×(5-1)2×12=14.13(cm2)九、2÷2=1(dm)3.14x(22-12)÷2=4.71(dm2)十、3.14 ×52×30360=15724(cm2)。
数学六年级上册《扇形》同步练习题(含答案)
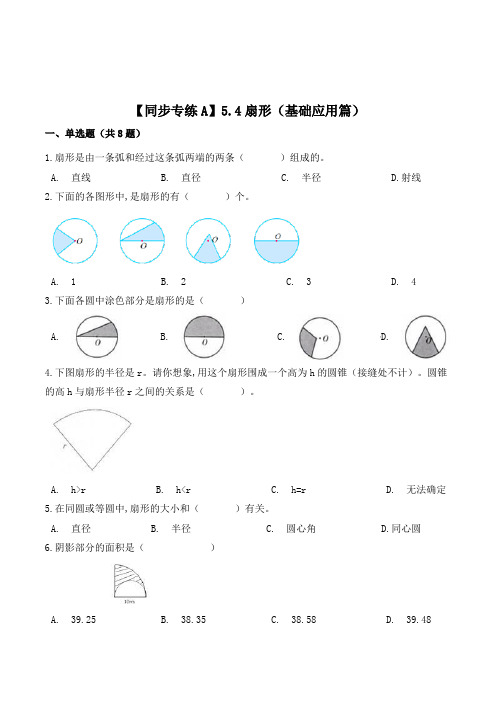
【同步专练A】5.4扇形(基础应用篇)一、单选题(共8题)1.扇形是由一条弧和经过这条弧两端的两条()组成的。
A. 直线B. 直径C. 半径D.射线2.下面的各图形中,是扇形的有()个。
A. 1B. 2C. 3D. 43.下面各圆中涂色部分是扇形的是()A. B. C. D.4.下图扇形的半径是r。
请你想象,用这个扇形围成一个高为h的圆锥(接缝处不计)。
圆锥的高h与扇形半径r之间的关系是()。
A. h>rB. h<rC. h=rD. 无法确定5.在同圆或等圆中,扇形的大小和()有关。
A. 直径B. 半径C. 圆心角D.同心圆6.阴影部分的面积是()A. 39.25B. 38.35C. 38.58D. 39.487.把一个圆平均分成10个扇形,圆心角都是( )。
A. 90°B. 36°C. 18°D. 70°8.在一个圆内最多可以画出( )个相等的扇形。
A. 180B. 无数C. 360D. 90二、填空题(共8题)9.如图,圆上A、B两点之间的部分叫做________,读作________。
10.扇形是由________围成的,扇形的角的顶点在________。
11.扇形是________图形,它有________条对称轴。
12.如果弧所对的圆心角为60°,弧长为8πcm,那么该弧所在扇形的面积是________(结果保留π)13.如图,王师傳从一张三角形铁皮上剪下3个半径都是2厘米的扇形,这3个扇形的面积和是________平方厘米。
14.如图这个三角形中三个阴影部分面积的积是________.15.以圆为弧的扇形的圆心角是________度,它的面积是所在圆面积的________。
16.圆心角是60°,扇形面积是所在圆面积的________三、判断题(共8题)17.扇形的两条直边可以不是圆的半径。
( )18.在一个圆内,剪去一个扇形后,剩下的部分仍是扇形。
人教版数学六年级上册同步习题5-4 扇形
3.顶点在圆上的角是圆心角。( )
【答案】×
【解析】
【分析】圆心角是顶点在圆心的角,据此判断。
【详解】圆心角的顶点在圆心,不是在圆上。
故答案为:×
【点睛】掌握圆心角的含义是此此题的关键。
4.因为扇形是它所在圆的一部分,那么圆的一部分一定是扇形.( )
A.只与圆心角大小有关B.只与半径长短有关
C.与半径长短无关D.与圆心角大小、半径的长短都有关
【答案】D
【解析】
【分析】扇形的面积= π ,n表示扇形圆心角的大小,据此判断。
【详解】因为扇形的面积= π ,所以扇形面积的大小与圆心角大小、半径的长短都有关。
故答案为:D。
【点睛】解题的关键是掌握扇形的面积公式。
()()()()
()()()()
【答案】
【解析】
【分析】扇形是由两条半径和一段曲线组成的,它有一个角,并且角的顶点在圆心,据此解答即可。
【详解】
【点睛】掌握扇形的含义是此题的关键。
2.判断下面各个角是不是圆心角,并说出理由。
【答案】 ,是顶点在圆心的角,是圆心角;
,顶点在圆上,不是圆心,不是圆心角;
第5课时 认识扇形
本课导学
本课知识点:认识弧、圆心角以及他们间 对应关系,在此基础上认识扇形,并能准确判断圆心角和扇形。
特别提醒:明确扇形是由两条半径和圆上 一段曲线围成的图形。扇形都有一个角,角的顶点在圆心。理解扇形概念知道扇形有一条对称轴以及圆心角的大小决定扇形面积。
【快乐训练营】
1.请在下面阴影部分是扇面的图形下面画“√”。
7.半圆也是一个扇形.( )
【答案】√
【解析】
六年级上册扇形练习题及答案

六年级上册扇形练习题
及答案
TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】
5.4扇形一、用心填一填。
1.扇形是由()和()围成的。
2.扇形都有一个角,角的顶点在()。
二、细心来判断。
1.圆的一部分就是扇形。
()
2.扇形有无数条对称轴。
()
3.把一个圆分成5份,每一份都一定是个扇形。
()三、下面哪个图形的涂色部分是扇形?请在下面的括号里画
“√”。
()()()
()
四、选择题。
(把正确答案的序号填在括号里)
1.在一个圆内最多可以画出()个相等的扇形。
B.无数
2.把一个圆平均分成10个扇形,圆心角都是()。
°°°°
3.下列图形中,阴影部分不是扇形的是()。
A. B.
C. D.
4.下列图形中,阴影部分是扇形的是()。
A. B.
C. D.
答案:
一、1. 半径弧 2. 圆心
二、1. × 2. × 3.×
三、
四、 1. B 2. B 3. B 4. A。
六年级数学上册《扇形》课后练习

人教版•六年级数学上册
六年级数学上册《扇形》课后练习
一、单选题
1.下面图形中,涂色部分不是扇形的是()。
A. B. C. D.
2.下面图中有扇形的是( )。
A.B.C.D.
3.下列图形中相同圆的涂色部分,是扇形并且扇形的面积最小的一个是()。
A.B.C.D.
4.在圆内剪去一个圆心角为 45 度的扇形,余下部分的面积是剪去部分面积的()倍。
A.6 B.7 C.8 D.9
5.扇形的大小,()。
A.只跟圆心角有关 B.只跟半径有关 C.跟圆心角和半径都有关
二、判断题
6.一个扇形的圆心角不变,半径越大,弧就越长。
()
7.顶点在圆内的角一定是圆心角。
()
8.用2个圆心角是180°的扇形,可以拼成一个圆。
()
9.下面两图中的阴影部分都是扇形。
()
人教版•六年级数学上册
10.下图中,∠OAB是圆心角。
()
三、填空题
11.把一个圆平均分成份,每一份所对的角的大小是1度。
那么180°所对的角是角。
12.如下图,等边三角形的边长是20cm,阴影部分的面积是cm²。
13.如图。
线段OB是圆的.一般用字母表示,用字母表示半径与直径之间的关系是;图中阴影部分是一个,∠AOB是,AB之间的曲线叫做。
14.如下图,一个正方形的内部有一个四分之一圆(空白部分)。
已知正方形的面积是10cm2,那么阴影部分的面积是cm2。
15.扇形是由围成的,扇形的角的顶点在。
【分层作业】5.4 扇形(同步练习) 六年级上册数学同步课时练 (人教版,含答案)

第五单元圆5.4 扇形【基础巩固】一、选择题1.下面各圆中的涂色部分,()是扇形。
A.B.C.2.如图中涂色部分的面积和半圆的面积相比,()。
A.涂色部分的面积大B.半圆的面积大C.涂色部分的面积和半圆的面积相等3.如图,在钟面上分针从12点整起,走15分钟经过的部分可以看作()。
A.圆形B.扇形C.三角形D.梯形4.在同一个圆中,扇形的大小与这个扇形的()有关。
A.圆心角B.半径C.直径5.如果两个扇形的半径之比为1∶2,圆心角之比也为1∶2,那么它们的面积之比为()。
A.1∶2 B.1∶4 C.1∶1 D.1∶8二、填空题6.如图,这是一个( ),已知它的周长是28.56dm,它的弧长(AB)是( )dm,面积是( )dm2。
(π取3.14)7.把一张圆形纸片对折三次(如图),此时圆心角是( )。
量得弧长是6.28cm,这张圆形纸片的直径是( )cm。
8.图中阴影部分的面积之和是( )cm2。
9.如图,一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为______平方厘米。
10.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。
在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
三、作图题11.画一个半径2厘米的圆,并用字母标出圆的半径和直径;再在圆中画出一个扇形并涂色。
四、图形计算题12.求涂色部分的面积。
13.求阴影部分的面积(如下图,红色的部分是一个扇形)。
【能力提升】五、解答题14.在比赛中,铅球投掷的落点区域是一个14圆,某运动员最远投掷距离为16米,铅球可能的落点区域面积是多少?15.一个挂钟的时针长5厘米,分针长8厘米,从中午12时到下午3时,分针尖端“走了”多少厘米?时针“扫过”的面积是多少平方厘米?【拓展实践】16.下图每个方格边长表示为1厘米,图中是一个梯形,按要求完成下面两个问题∶(1)计算梯形面积。
新人教版六年级上册《第6课时-扇形的认识》同步练习卷

新人教版六年级上册《第6课时扇形的认识》2017年同步练习卷一、我会填.1.一条________和经过这条________两端的两条________所围成的图形叫做________.2.顶点在________的角叫圆心角.3.在同一圆中,扇形的大小与这个扇形的________的大小有关.4.以半圆为弧的扇形的圆心角是________度,以1圆为弧的扇形的圆心角是________度.4二、我会判断.5.圆的一部分就是扇形.________ (判断对错)6.顶点在圆内的角叫做圆心角________.(判断对错)7.在一个圆中,扇形的大小是由圆心角决定的.________.(判断对错)8.扇形有无数条对称轴.________.三、画图.9.画一个半径是1厘米的圆,再在圆中画一个圆心角是60度的扇形.四、选择题10.下列图形中的角,是圆心角的个数是( )ﻫA.1个B.2个C.3个五、求面积11.求阴影部分的面积.ﻫ六、求面积12.求阴影部分的面积.七、求面积13.求阴影部分的面积.(单位:厘米)14.口算1.63+2.3=25÷14=480×13=29−0.6=0.85+0.15=8×14=59×3=4×56=325×5=6×38=答案1. 【答案】弧,弧,半径,扇形【解析】根据扇形的意义:一条弧弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此解答.【解答】解:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形.ﻫ故答案为:弧,弧,半径,扇形.2.【答案】圆心上,由两条半径围成【解析】根据圆心角的定义知,顶点在圆心上,并且由两条半径围成的角是圆心角;据此解答即可.【解答】解:由分析可知:顶点在圆心上,由两条半径围成的角叫圆心角.ﻫ故答案为:圆心上,由两条半径围成.3.【答案】圆心角【解析】在同一个圆里,1∘的圆心角的扇形面积占圆面积的1360,90∘的圆心角的扇形面积占圆面积的14,因此同一圆内圆心角的大小决定扇形的大小;据此解答.【解答】解:在同一圆中,扇形的大小与这个扇形的圆心角的大小有关;ﻫ故答案为:圆心角.4. 【答案】180,90【解析】因为圆周长是360度,所以以半圆为弧的扇形的圆心角是圆周角的一半,14圆为弧的扇形的圆心角是360∘×14=90∘;据此解答.【解答】解:360×12=180(度);ﻫ360×14=90(度);ﻫ答:以半圆为弧的扇形的圆心角是180度,以1圆为弧的扇形的圆心角是90度.ﻫ故答案为:180,90.45. 【答案】×【解析】根据扇形的定义是以圆心角的两条半径和之间的弧所围成的闭合图形,即可得出答案.【解答】解:可以说扇形是圆的一部分,但不能说圆的一部分是扇形.ﻫ严格地说扇形是以圆心角的两条半径和之间的弧所围成的闭合图形.故答案为:×.6. 【答案】×【解析】依据圆心角的概念进行解答即可,即顶点在圆心的角叫做圆心角.【解答】解:因为顶点在圆心的角叫做圆心角,所以题干的说法是错误的.ﻫ故答案为:×.7.【答案】√【解析】在同圆或等圆中,圆心角大,与它对应的扇形的面积就大,圆心角小,与它对应的扇形的面积就小,所以在同圆或等圆中,扇形的大小与它对应的圆心角的大小有关.【解答】解:在同圆或等圆中,扇形的大小与它对应的圆心角的大小有关,所以本题说法正确;故答案为:√.8. 【答案】错误【解析】根据轴对称图形的定义,找出扇形所有的对称轴,即可作出判断.【解答】解:扇形只有一条对称轴,是圆心角的角平分线所在的直线,ﻫ所以原题说法错误. 故答案为:错误.9. 【答案】解:先画出圆,再画一个圆心角为60∘,半径为1厘米的扇形(下图绿色部分):【解析】首先确定一点O为圆心,然后再以O为圆心,以半径为1厘米(圆规两脚间的距离为1厘米)画圆即可;然后在圆内画一圆心角为60∘的扇形即可.【解答】解:先画出圆,再画一个圆心角为60∘,半径为1厘米的扇形(下图绿色部分):10. 【答案】B【解析】根据圆心角的含义:顶点在圆心的角是圆心角;由此进行判断即可.【解答】解:根据圆心角的含义可知:第一个和第二个图中的角是圆心角;故选:B.11. 【答案】阴影部分的面积是21.5cm2..正方形的边长或者说【解析】阴影部分是正方形面积减去半径为正方形边长的圆面积的14圆半径已知,根据正方形面积计算公式“S=a2”、圆面积计算公式“S=πr2”即可解答. 【解答】解:10×10=100(cm2)3.14×100×1 4=314×1 4=78.5(cm2)ﻫ100−78.5=21.5(cm2)12. 【答案】阴影部分的面积是28.26cm2.【解析】阴影部分是一个外圆半径为10厘米,内圆半径为8厘米的环形的14,根据环形面积计算公式“S=π(R2−r2)”及分数乘法的意义即可解答.【解答】解:3.14×(102−82)×14=3.14×(100−64)×1 4=3.14×36×1 4=3.14×(36×1 4 )=3.14×9ﻫ=28.26(cm2)13. 【答案】阴影部分的面积是21.192平方厘米.【解析】梯形的内角和是360度,然后用360减去90度就是三个阴影部分的内角和,即360−90=270(度),这样阴影部分的面积就等于圆心角是270度,半径3厘米的圆的面积,然后根据圆的面积公式解答即可.【解答】解:360−90=270(度)ﻫ270360×3.14×32=34×28.26=21.195(平方厘米) 14.【答案】解:1.63+2.3=3.9325÷14=85480×13=16029−0.6=28.40.85+0.15=18×14=259×3=534×56=103325×5=356×38=94【解析】根据小数、分数加减乘除法运算的计算法则计算即可求解. 【解答】解:1.63+2.3=3.9325÷14=85480×13=16029−0.6=28.40.85+0.15=18×14=259×3=534×56=103325×5=356×38=94。
2022-2023学年人教版数学六年级上册认识扇形练习题(含解析)
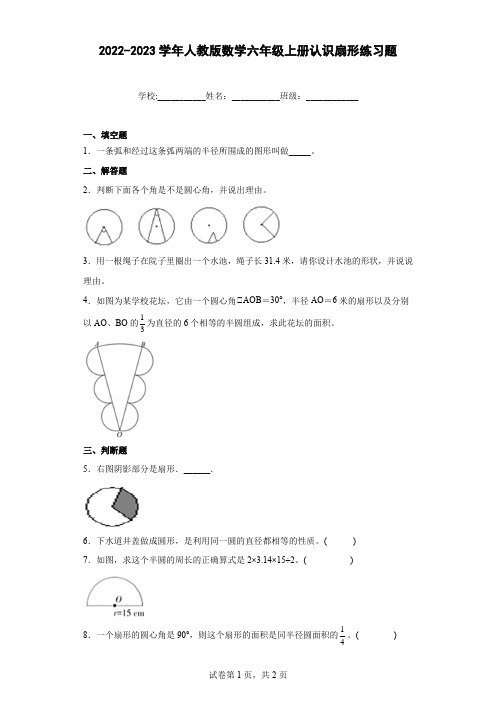
2022-2023学年人教版数学六年级上册认识扇形练习题学校:___________姓名:___________班级:____________一、填空题1.一条弧和经过这条弧两端的半径所围成的图形叫做_____。
二、解答题2.判断下面各个角是不是圆心角,并说出理由。
3.用一根绳子在院子里圈出一个水池,绳子长31.4米,请你设计水池的形状,并说说理由。
4.如图为某学校花坛,它由一个圆心角∠AOB=30°,半径AO=6米的扇形以及分别以AO、BO的13为直径的6个相等的半圆组成,求此花坛的面积。
三、判断题5.右图阴影部分是扇形.______.6.下水道井盖做成圆形,是利用同一圆的直径都相等的性质。
( ) 7.如图,求这个半圆的周长的正确算式是2×3.14×15÷2。
( )8.一个扇形的圆心角是90°,则这个扇形的面积是同半径圆面积的14。
( )9.扇形是轴对称图形,对称轴有无数条.( )10.是轴对称图形。
( )11.在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
( )四、选择题12.下列说法正确的有()句。
∠4个圆心角是90°的扇形可以拼成一个圆。
∠数a(a不为0)除以一个真分数,商一定大于a。
∠百分数既可以表示两个量之间的关系,也可以表示一个具体量。
∠3米的110与1米的310是相等的。
A.1B.2C.3D.413.扇形面积的大小()。
A.只与圆心角大小有关B.只与半径长短有关C.与半径长短无关D.与圆心角大小、半径的长短都有关五、作图题14.按要求在如图作图.(1)画一个半径是2厘米的圆;(2)标出圆心、半径和直径;(3)在圆中画一个圆心角是120°的扇形.六、图形计算15.看图计算下列图形的面积。
16.计算下图的周长和面积。
参考答案:1.扇形【详解】根据扇形的意义:由两条半径,和连接两条半径的一段弧围成的图形叫做扇形。
人教版2024-2025学年六年级数学上册5.4扇形的面积同步练习(附答案解析)

人教版2024-2025学年六年级数学上册5.4 扇形的面积同步练习班级:姓名:亲爱的同学们:练习开始了,希望你认真审题,细致做题,不断探索数学知识,领略数学的美妙风景。
运用所学知识解决本练习,祝你学习进步!一、单选题1.下面各圆中的阴影部分,()是扇形。
A.B.C.D.2.下面图形中,涂色部分不是扇形的是()。
A.B.C.D.3.如图,在钟面上分针从12点整起,走15分钟经过的部分可以看作()。
A.圆形B.扇形C.三角形D.梯形4.下面四个图形中,空白部分与阴影部分的周长和面积分别相等的是()A.B.C.D.5.下面四幅由实线围成的图形中,()不是扇形。
A.B.C.D.二、判断题6.扇形是轴对称图形。
()7.用4个圆心角是90°的扇形,一定可以拼成一个圆。
()8.两个扇形,圆心角大的面积就大。
()9.圆心角60°的扇形一定比圆心角40°的扇形面积大。
()10.扇形的圆心角越大,扇形就越大。
( )三、填空题11.如下图,等腰直角三角形中阴影部分的面积是(π取3.14)。
12.如图。
线段OB是圆的.一般用字母表示,用字母表示半径与直径之间的关系是;图中阴影部分是一个,∠AOB是,AB之间的曲线叫做。
13.一个钟表的分针长10cm,从“12”走到“9”,分针针尖走过了cm,分针扫过的面积是cm2。
14.如下图是半径为6厘米的半圆,让这个半圆绕A点按顺时针方向旋转30°此时B点移动到B’点,则阴影部分的面积是平方厘米。
15.如下图,等边三角形的边长是20cm,阴影部分的面积是cm²。
16.如下图,把一张圆形的纸片对折三次后,得到的角的度数是。
四、计算题17.如图,长方形ABCD的长为3,宽为2.求阴影部分的面积。
(结果保留π)五、作图题18.先画一个 d=2cm 的圆,并用 O、r、d 标出圆心、半径和直径,再在圆中画一个圆心角是120° 的扇形。
人教版数学六年级上册 第五单元 扇形 同步练习(含答案)

人教版六年级上册 5.4 扇形同步练习一、选择题1.一条弧和经过这条弧两端的两条半径所围成图形叫做()。
A.圆心角B.扇形C.弧形2.在同一个圆中,扇形的大小与()的大小有关。
A.这个扇形的圆心角B.这个圆的半径C.这个圆的直径3.下面各图中,阴影部分是扇形的是()。
A.B.C.D.4.在一个圆中14,以圆为弧的扇形的圆心角是()。
A.360度B.180度C.90度D.45度5.明明、丁丁、圆圆分别从同样大的正方形中剪掉了涂色部分的图形(如下图),他们剩下部分的面积相比,()。
A.明明剩下的面积大B.丁丁剩下的面积大C.只有丁丁和圆圆剩下的面积一样大D.三个人剩下的面积一样大二、填空题6.当扇形的圆心角等于( )度时,扇形就是一个整圆。
7.把一个圆平均分成10个扇形,圆心角都是( )。
8.下图是直径6cm的圆。
其中阴影扇形的半径是( )厘米,圆心角是( )度,弧AB长( ) cm。
9.如图,一个圆的半径是4cm,它的直径是( )cm,周长是( )cm,面积是( )cm2。
在这个圆中有一个圆心角为90°的扇形,这个扇形的面积是( )cm2。
10.如图:一个三角形的三个顶点分别为三个半径为4厘米的圆的圆心,则图中阴影部分的面积是( )平方厘米。
三、判断题11.两个扇形,圆心角大的扇形就大。
( )12.用两个圆心角是180°的扇形,一定可以拼成一个圆。
( )13.圆心角的度数越大,扇形的面积就越大。
( )14.用四个圆心角都是90°的扇形,正好拼成一个圆。
( )15.两条线段和一段弧所围成的图形叫做扇形。
( )四、解答题16.朱婷婷正在制作一张六(1)班同学喜欢各类运动的扇形统计图。
已知六(1)班共有同学63人,最喜欢踢球的同学有14人,那么在这张扇形统计图上表示最喜欢踢球同学的扇形圆心角应该画多少度?17.(1)画一个直径是4厘米的圆,标上圆心O,画出一条直径并标出数据。
人教版六年级数学上册第五单元第9课时《扇形》课后练习题(附答案)
人教版六年级数学上册
第五单元第9课时《扇形》课后练习题(附答案)
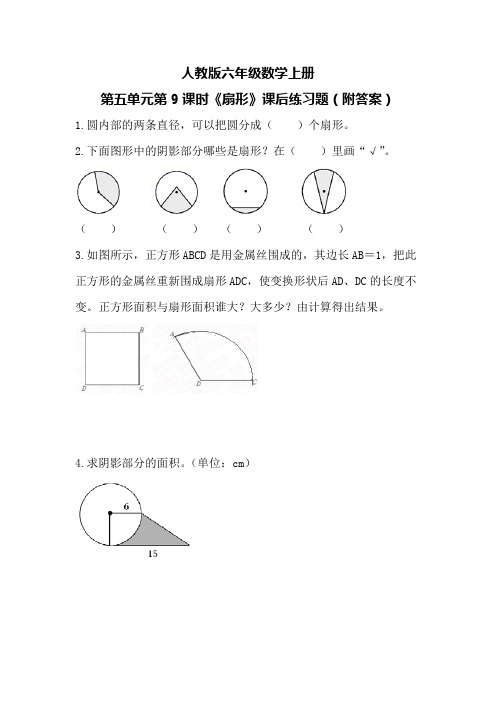
1.圆内部的两条直径,可以把圆分成()个扇形。
2.下面图形中的阴影部分哪些是扇形?在()里画“√”。
()()()()
3.如图所示,正方形ABCD是用金属丝围成的,其边长AB=1,把此正方形的金属丝重新围成扇形ADC,使变换形状后AD、DC的长度不变。
正方形面积与扇形面积谁大?大多少?由计算得出结果。
4.求阴影部分的面积。
(单位:cm)
参考答案
1.4
2. (√)()()()
3.正方形的面积:1²=1
扇形的面积:(1×2)÷(3.14×1×2)×3.14×1²=1 正方形面积=扇形面积
答:正方形面积与扇形面积一样大。
4.(6+15)×6÷2-3.14×6²÷4=34.74(cm²)
答:阴影部分的面积是34.74cm²。
小学数学六年级上册《扇形的认识》课时练习题

第6课时扇形的认识学习目标:1.认识扇形,掌握扇形的特征,了解扇形的各部分名称,会用字母表示各部分名称。
2.培养自己的观察、分析、综合、概括及动手操作能力。
学习重点:认识扇形,掌握扇形的特征,了解扇形的各部分名称。
学具准备:准备折扇或贝壳使用说明及学法指导:1.先自学教材P75页,然后自主完成导学案的自主与合作学习部分,找出疑难问题,准备与组内同学交流。
展示时要结合文字、图形和学具熟练地介绍圆的有关特征。
2.带★的可以选做。
知识储备用字母表示圆的周长计算公式:用字母表示圆的面积计算公式:自主与合作学习展示同学们搜集到的扇形物体,有:小组内观察比较,找到这些物体的相同点:用圆规在纸上画一个圆,用涂色的方法表示出扇形,并标出各部分名称,再与同学互相说一说。
如左图,圆上A、B两点之间的部分叫做(),读作();一条弧和经过这条弧两端的两条半径所围成的图形叫做()(涂色表示);像∠AOB这样,顶点在圆心的角叫做()。
我发现:扇形的大小与()有关。
达标测评1.下面图形中哪些角是圆心角?2.填空(1)以半圆为弧的扇形的圆心角是()度。
(2)以四分之一圆为弧的扇形的圆心角是()度。
3.画一个半径是2厘米的圆,再在圆中画一个圆心角是100度的扇形。
像下面这样一个圆环被截得的部分叫做扇环,求出下面各扇环的面积。
★一只挂钟的分针长20厘米,经过30分钟后,分针所扫过的钟面面积是多大?45分钟呢?课后反思:为什么要规定“先乘除后加减”?对于这个问题,我们分两层来谈。
第一层先谈谈规定运算顺序的必要性,第二层再谈谈为什么要规定“先乘除后加减”。
(1)规定运算顺序的必要性。
先举两个例子予以说明。
例1 小勇买了一块橡皮,价18分,又买了3支铅笔,每支12分,一共多少钱?综合算式18+12×3=18+36=54(分)=5角4分根据题意,这道题先算乘法后算加法是合情合理的。
例2 小春有18分钱,小敏有12分钱,小冬的钱数是他们俩人钱数之和的3倍,问小冬有多少钱?解答这道题的时候应该先求出小春与小敏两人钱数之和,即求出(18+12=)30分,然后再求出30分的3倍,即(30×3=)90分。
人教版六年级数学上册《扇形》课后练习

人教版六年级数学上册《扇形》课后练习一、填空题1.在同一个圆中,扇形的大小与这个扇形的的大小有关。
2.如下图中,圆上A、B两点之间的部分叫做,读作。
3.一个扇形的圆心角为90°,它所在圆的半径为6cm,这个扇形的面积是cm2。
4.如图,圆周上A、B两点之间的部分叫做,由半径OA、OB和弧AB。
围成的阴影部分面积是圆面积的()()5.有一把折扇完全打开后是一个圆心角为180°的扇形,它的周长是51.4厘米,它的面积是平方厘米。
6.在面积为20cm2的正方形内画一个面积最大的扇形,这个扇形的面积是m2。
7.一条弧和经过这条弧两端的两条所围成的图形叫做。
8.扇形是由两条和的一段围成的。
9.圆形钟表时针长6dm,从12点到21点,它走过了dm,扫过的面积是dm2。
10.王老师用扇形统计图反映学校的学生和老师情况,表示男生和女生的扇形圆心角度数比是6:5,表示老师的扇形圆心角度数是30°。
那么男生的扇形圆心角为。
11.一个圆可以平均分成个圆心角是60°的扇形。
12.把一个圆平均分成六个相等的扇形,每个扇形的圆心角是度。
13.如图所示,直角三角形AOB的面积为6平方厘米,图中阴影部分的面积是平方厘米。
(π取3.14)14.(如图)正方形的边长是8cm,正方形内有一个最大的扇形。
图中阴影部分的面积是cm2.15.如图这个三角形中三个阴影部分面积的积是。
参考答案一、填空题1.圆心角 2.弧弧AB 3.28.26 4.弧15.157 6.0.0015767.半径扇形 8.半径圆上曲线 9.28.26 84.78 10.180度11.6 12.60 13.3.42 14.13.76 15.6.28。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《扇形的认识》同步练习
一、填空。
1、圆上两点间的部分叫做()。
2、一条()和经过这条弧两端的两条()所围成的图形叫做()。
3、顶点在()的角叫圆心角。
4、如果两个圆同样大,()越大,扇形的面积越大。
如果圆心角同样大,()越长,扇形的面积越大。
5、一个圆环被截一部分叫()。
二、判断。
1、顶点在圆上的角叫圆心角。
()
2、扇形是圆的一部分,所以扇形的面积小于圆的面积。
()
3、扇形是圆的一部分,圆的一部分就是扇形。
()
4、半圆也是一个扇形。
()
5、一个圆内剪与一个扇形,剩下的部分还是扇形。
()
三、选择题。
1、扇形是轴对称图形,对称轴有()条。
A 2
B 1
C 无数
2、一个半圆形花圃,在花圃周围围上篱笆。
篱笆的长度是()。
A 21
B 22.3
C 23.6
D 25.7
3、如图阴影部分的面积是()
A 39.55
B 38.35
C 38.58
D 39.48
四、画图题。
画一个半径是3厘米,圆心角是1200的扇形。
五、解决问题。
1、把一张圆纸片三次对折,并量得曲线的长(如图)。
那么,圆纸片的直径是多少厘米?
2、下图空白你部分的面积是800平方厘米,求阴影部分的面积是多少平方厘米?
参考答案
一、填空。
1、弧
解析:弧的定义:圆上两点间的部分叫做弧。
2、弧半径扇形
解析:扇形的定义。
解析:扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
3、圆心
解析:圆心角的定义:顶点在圆心的角叫圆心角。
4、圆心角半径
解析:扇形的大小是又圆心角和半径两个因素决定的。
圆心角大,扇形就大,半径长,扇形也大。
5、扇环
解析:扇环的定义:一个圆环被截一部分叫扇环。
二、判断。
1、√
解析:顶点在圆心的角叫圆心角。
所以命题错误。
2、×
解析:虽然扇形是圆的一部分,但是在同一个圆内扇形的面积才小于圆的面积。
否则不能保证。
所以命题错误。
3、×
解析:扇形是圆的一部分,但圆的一部分不一定是扇形。
4、√
解析:半圆也是由一条弧和经过这条弧两端的两条半径所围成的图形,所以也是扇形。
5、×
解析:因为只有当剪去的扇形和余下的部分是同一个圆心时,余下的部分才能成为扇形。
三、选择题。
2、D
解析:篱笆的长度就是半圆的周长,半圆的周长就是圆周长的一半加上半圆的直径。
列式为:
3.14×10÷2+10=25.7米。
3、 A
解析:阴影部分的面积等于外面大扇形的面积减去半圆的面积。
大扇形的面积=3.14×102
÷4=78.5(cm 2),半圆的面积=3.14×52÷2=39.25平方厘米。
两部分相减得到阴影部分的面积是39.15平方厘米。
所以A 正确。
四、 画图题。
五、解决问题。
1、1.57×8÷3.14=4(厘米)
答:圆纸片的直径是4厘米。
解析:把一张圆纸片三次对折,折后的部分相当与原来的81,弧长也相当于圆周长的8
1。
所以1.57÷8
1
就是圆的周长,根据d=C ÷π。
计算得到直径为4厘米。
2、3.14×800÷2-800=456(平方厘米)
答:阴影部分的面积是456平方厘米。
解析:根据题意,空白部分的面积是800平方厘米,即:2r ×r ÷2=r 2=800。
又因为阴影不分的面积=半圆的面积=三角形的面积。
半圆的面积=3.14×800÷2=1256,所以阴影部分的面积是456平方厘米。
