时间序列分析实验报告

合集下载

时间序列分析实例研究报告

时间序列分析实例研究报告实例研究背景：某大城市的人口数量变化首先，我们选取了某大城市的人口数量变化作为实例进行分析，以了解该城市的人口发展趋势和变化规律。

1. 数据收集和观察我们首先收集了过去十年该城市每年的人口数据，从2009年到2019年的数据。

通过观察这些数据，我们可以初步了解人口数量的增减情况。

2. 数据预处理在进行时间序列分析之前，需要对数据进行预处理。

首先，我们要检查数据是否存在异常值或缺失值，并进行处理。

其次，我们要对数据进行平滑处理，以减少异常波动对分析结果的影响。

常见的平滑方法有均值平滑和移动平均法。

3. 时间序列分解接下来，我们使用时间序列分解方法，将人口数据分解为趋势、季节和随机成分。

- 趋势分析：通过一系列统计方法，了解人口数量的长期变化趋势。

可以使用简单平均法或线性回归模型等方法。

- 季节分析：通过统计周期性规律，了解人口数量的季节性变化。

可以使用季节指数法或移动平均法等方法。

- 随机分析：通过统计残差项，了解人口数量的随机波动情况。

可以使用ARIMA模型等方法。

4. 模型拟合和预测在分析了趋势、季节和随机成分之后，我们可以选择适当的模型进行拟合和预测。

- 趋势预测：可以根据趋势分析的结果选择合适的趋势预测模型，如线性趋势模型、指数平滑模型等。

- 季节预测：可以根据季节性分析的结果选择合适的季节预测模型，如季节指数法、季节ARIMA模型等。

- 随机预测：可以使用时间序列模型进行随机成分的预测，如ARIMA模型等。

5. 模型评估和调整在完成模型拟合和预测后，我们需要对模型进行评估和调整，以提高模型的准确性和可靠性。

常见的评估指标有均方误差、平均绝对误差等。

如果模型评估结果不理想，需要调整模型参数或选择其他模型进行尝试。

6. 结果分析和讨论最后，我们对时间序列分析的结果进行分析和讨论。

通过对人口数量的趋势、季节和随机成分的分析，我们可以对该城市的人口发展趋势和变化规律进行深入理解。

时间序列分析试验报告

时间序列分析试验报告
一、试验简介
本次试验旨在探索时间序列分析，以分析日期变化的影响与规律。

时
间序列分析是数据分析的一种，目的是预测未来正确的趋势，并且分析既
有趋势的影响及其变化。

二、试验材料
本次试验使用的资料为最近12个月（即2024年1月到2024年12月）的电子商务网站销售数据。

该电子商务网站以每月总销售量、每月总销售
额及每月交易次数三个变量作为试验数据。

三、试验方法
1．首先，收集2024年1月到2024年12月的电子商务销售数据，记
录每月总销售量、总销售额及交易次数。

2．然后，编制时间序列分析图表，反映每月总销售量、总销售额及
交易次数的变化情况。

3．最后，分析每月的变化趋势，比较每月的销售数据，并进行相关
分析推断。

四、实验结果
1．通过时间序列分析图表可以看出，每月总销售量、总销售额及交
易次数均呈现出稳定上升趋势。

2．从图表中可以推断，在2024年底到2024年底，当月的总销售量、总销售额及交易次数均较上月有所增加。

3．从表中可以推断，每月的总销售量、总销售额及交易次数都在逐渐增加，最终在2024年末达到高峰。

五、结论
通过本次实验可以得出结论。

时间序列实验报告心得

在本次时间序列实验中，我深刻体会到了时间序列分析在解决实际问题中的重要作用。

通过对时间序列数据的收集、处理、分析和预测，我学会了如何运用时间序列分析方法解决实际问题，以下是我在实验过程中的心得体会。

一、实验背景时间序列分析是统计学和金融学等领域的重要研究方法，通过对时间序列数据的分析，我们可以揭示现象的发展变化规律，预测未来趋势，为决策提供依据。

本次实验以我国某地区1980年1月至1995年8月每月屠宰生猪数量为研究对象，运用时间序列分析方法进行建模和预测。

二、实验步骤1. 数据收集与处理：首先，收集了某地区1980年1月至1995年8月每月屠宰生猪数量数据。

然后，对数据进行初步处理，包括去除异常值、缺失值等。

2. 时间序列图绘制：运用Excel或R等软件绘制时间序列图，观察数据的变化趋势，为后续建模提供依据。

3. 平稳性检验：对时间序列数据进行平稳性检验，以确定是否可以直接进行建模。

常用的平稳性检验方法有ADF检验、KPSS检验等。

4. 模型选择与参数估计：根据时间序列图和平稳性检验结果，选择合适的模型进行拟合。

本次实验选择了ARIMA模型，并对模型参数进行估计。

5. 模型预测与结果分析：利用估计出的模型对未来的数据进行预测，并对预测结果进行分析，评估模型的准确性。

三、实验心得1. 时间序列分析的重要性：通过本次实验，我深刻认识到时间序列分析在解决实际问题中的重要性。

在实际工作中，许多现象都呈现出时间序列特征，运用时间序列分析方法可以揭示现象的发展变化规律，为决策提供依据。

2. 数据处理的重要性：在实验过程中，数据预处理是至关重要的。

只有保证数据的准确性和完整性，才能得到可靠的实验结果。

3. 平稳性检验的必要性：时间序列建模的前提是数据平稳。

通过对数据平稳性进行检验，可以确保模型的准确性。

4. 模型选择与参数估计的重要性：选择合适的模型和参数对于时间序列分析至关重要。

不同的模型适用于不同类型的数据，需要根据实际情况进行选择。

统计实验报告时间序列

一、实验背景时间序列分析是统计学中的一个重要分支，它主要研究如何对时间序列数据进行建模、预测和分析。

本实验旨在通过实际数据的时间序列分析，了解时间序列的基本特性，掌握时间序列建模的方法，并尝试进行未来趋势的预测。

二、实验目的1. 理解时间序列的基本概念和特征。

2. 掌握时间序列数据的可视化方法。

3. 学习并应用时间序列建模的基本方法，如自回归模型（AR）、移动平均模型（MA）和自回归移动平均模型（ARMA）。

4. 尝试进行时间序列数据的预测。

三、实验数据本实验选用某城市过去一年的月度降雨量数据作为分析对象。

数据包括12个月的降雨量，单位为毫米。

四、实验步骤1. 数据预处理- 读取数据：使用Python的pandas库读取降雨量数据。

- 数据检查：检查数据是否存在缺失值或异常值。

- 数据清洗：如果存在缺失值或异常值，进行相应的处理。

2. 数据可视化- 使用matplotlib库绘制降雨量时间序列图，观察数据的趋势和季节性特征。

3. 时间序列建模- 自回归模型（AR）：根据自回归模型的理论，建立AR模型，并通过AIC（赤池信息量准则）和SC（贝叶斯信息量准则）进行模型选择。

- 移动平均模型（MA）：建立MA模型，并使用同样的准则进行模型选择。

- 自回归移动平均模型（ARMA）：结合AR和MA模型，建立ARMA模型，并选择最佳模型。

4. 模型验证与预测- 使用历史数据进行模型验证，比较不同模型的预测精度。

- 对未来几个月的降雨量进行预测。

五、实验结果与分析1. 数据可视化通过时间序列图可以看出，降雨量存在明显的季节性特征，每年的夏季降雨量较多。

2. 时间序列建模- AR模型：通过AIC和SC准则，选择AR（2）模型作为最佳模型。

- MA模型：同样通过AIC和SC准则，选择MA（3）模型作为最佳模型。

- ARMA模型：结合AR和MA模型，选择ARMA（2，3）模型作为最佳模型。

3. 模型验证与预测- 模型验证：通过比较实际值和预测值，可以看出ARMA（2，3）模型的预测精度较高。

实验报告-时间序列

实验报告----平稳时间序列模型的建立08经济统计I60814030王思瑶一．实验目的从观察到的化工生产过程产量的70个数据样本出发，通过对模型的识别、模型的定价、模型的参数估计等步骤建立起适合序列的模型。

以下是化工生产过程的产量数据：obs BF obs BF1 47 36582 64 37453 23 38544 71 39365 38 40546 64 41487 55 42558 41 43459 59 445710 48 455011 71 466212 35 474413 57 486414 40 494315 58 505216 44 513817 80 525918 55 535519 37 544120 74 555321 51 564922 57 573423 50 583524 60 595425 45 604526 57 616827 50 623828 45 635029 25 646030 59 653931 50 665932 71 674033 56 685734 74 695435 50 7023可以明显看出序列均值显著非零，所以用样本均值作为其估计对序列进行零均值化。

obs BF 零均值化后的数据Y obs BF零均值化后的数据Y1 47 -4.12857 3658 6.871432 64 12.87143 3745-6.128573 23 -28.12857 3854 2.871434 71 19.87143 3936-15.128575 38 -13.12857 4054 2.871436 64 12.87143 4148-3.128577 55 3.87143 4255 3.871438 41 -10.12857 4345-6.128579 59 7.87143 4457 5.8714310 48 -3.12857 4550-1.1285711 71 19.87143 466210.8714312 35 -16.12857 4744-7.1285713 57 5.87143 486412.8714314 40 -11.12857 4943-8.1285715 58 6.87143 50520.8714316 44 -7.12857 5138-13.1285717 80 28.87143 52597.8714318 55 3.87143 5355 3.8714319 37 -14.12857 5441-10.1285720 74 22.87143 5553 1.8714321 51 -0.12857 5649-2.1285722 57 5.87143 5734-17.1285723 50 -1.12857 5835-16.1285724 60 8.87143 5954 2.8714325 45 -6.12857 6045-6.1285726 57 5.87143 616816.8714327 50 -1.12857 6238-13.1285728 45 -6.12857 6350-1.1285729 25 -26.12857 64608.8714330 59 7.87143 6539-12.1285731 50 -1.12857 66597.8714332 71 19.87143 6740-11.1285733 56 4.87143 6857 5.8714334 74 22.87143 6954 2.8714335 50 -1.12857 7023-28.12857二．实验步骤1.模型识别零均值平稳序列的自相关函数与偏相关函数的统计特性如下：模型 AR(n) MA(m) ARMA(n,m)自相关函数拖尾截尾拖尾偏自相关函数截尾拖尾拖尾所以，作零均值化后数据的自相关函数与偏自相关函数图Date: 04/25/11 Time: 22:35Sample: 2001 2070Included observations: 70Autocorrelation Partial Correlation AC PAC Q-Stat Prob***| . | ***| . | 1 -0.382 -0.382 10.638 0.001. |** | . |** | 2 0.325 0.209 18.444 0.000**| . | . | . | 3 -0.193 -0.018 21.234 0.000. |*. | . | . | 4 0.090 -0.049 21.857 0.000.*| . | .*| . | 5 -0.162 -0.126 23.900 0.000. | . | .*| . | 6 0.014 -0.094 23.916 0.001. | . | . | . | 7 0.012 0.065 23.928 0.001.*| . | .*| . | 8 -0.085 -0.079 24.519 0.002. | . | . | . | 9 0.039 -0.051 24.644 0.003. | . | . |*. | 10 0.033 0.080 24.736 0.006. |*. | . |*. | 11 0.090 0.125 25.426 0.008.*| . | . | . | 12 -0.077 -0.054 25.942 0.011. | . | . | . | 13 0.063 -0.045 26.291 0.016. | . | . |*. | 14 0.051 0.134 26.524 0.022. | . | . |*. | 15 -0.006 0.079 26.528 0.033. |*. | . |*. | 16 0.126 0.145 28.016 0.031.*| . | . | . | 17 -0.090 -0.040 28.792 0.036. | . | .*| . | 18 0.017 -0.084 28.820 0.051.*| . | . | . | 19 -0.099 -0.017 29.795 0.054. | . | . | . | 20 0.006 -0.036 29.798 0.073. | . | . | . | 21 0.015 0.055 29.820 0.096. | . | . | . | 22 -0.037 -0.015 29.968 0.119. | . | . | . | 23 0.013 -0.051 29.985 0.150. | . | . | . | 24 0.010 0.010 29.997 0.185. | . | . | . | 25 0.015 -0.016 30.023 0.223. | . | . | . | 26 0.036 0.023 30.172 0.261. | . | . | . | 27 -0.016 -0.036 30.202 0.305. | . | . | . | 28 0.033 0.030 30.335 0.347. | . | . | . | 29 -0.057 -0.015 30.735 0.378. | . | . | . | 30 0.051 -0.003 31.064 0.412.*| . | . | . | 31 -0.070 -0.053 31.706 0.431. | . | . | . | 32 0.057 -0.003 32.141 0.460由上图可知Autocorrelation与Partial Correlation序列均有收敛到零的趋势，可以认为Y的自相关函数与偏自相关函数均是拖尾的，所以初步判断该序列适合ARMA模型。

时间序列分析实验报告

引言概述：
时间序列分析是一种用于研究时间数据的统计方法，主要关注数据随时间的变化趋势、季节性和周期性等特征。

时间序列分析应用广泛，可以用于金融预测、经济分析、气象预测等领域。

本实验报告旨在介绍时间序列分析的基本概念和方法，并通过实例分析来展示其应用。

正文内容：
1.时间序列分析基本概念
1.1时间序列的定义
1.2时间序列的模式
1.3时间序列分析的目的
2.时间序列分析方法
2.1随机游走模型
2.2移动平均模型
2.3自回归移动平均模型
2.4季节性模型
2.5ARCH和GARCH模型
3.时间序列数据预处理
3.1数据平稳性检验
3.2数据平滑
3.3缺失值填补
3.4离群值检测
3.5数据变换
4.时间序列模型建立与评估
4.1模型的选择
4.2参数估计
4.3拟合优度检验
4.4模型诊断
4.5预测准确性评估
5.实例分析：某公司销售数据时间序列分析
5.1数据收集与预处理
5.2模型建立与评估
5.3预测分析与结果解释
5.4预测精度评估
5.5结果讨论与进一步改进方向
总结：
时间序列分析是一种重要的统计方法，可用于预测和分析时间相关的数据。

本报告介绍了时间序列分析的基本概念和方法，并通
过实例分析展示了其应用过程。

通过时间序列分析，可以更好地理解数据的趋势和周期性，并进行准确的预测。

时间序列分析也面临着多样的挑战，如数据质量问题和模型选择困难等。

因此，在实际应用中，需要综合考虑多种因素，灵活运用合适的方法和技巧，以提高预测准确性和分析可靠性。

时间序列期末实验报告10

时间序列分析实验报告一、实验主题对“2001年至2009年每个月发电量”序列进行分析预测，并得出其发展趋势的结论。

二、实验内容1、数据的平稳性检验。

2、数据的平稳化处理。

（差分消除方法）3、根据平稳序列的自-偏自相关图确定模型类型。

4、模型阶数的确定。

5、模型的建立。

（参数显著性、残差检验）6、模型的预测。

三、实验步骤：1、数据录入打开Eviews软件，选择“File”菜单中的“New--Workfile”选项，在“Workfile structure type”栏选择“Dated –regular frequency”，在“Date specification”栏中选择“Mouthly”，分别在起始年输入2001M01，终止年输入2009M11，点击ok，见图1，这样就建立了一个工作文件。

点击File/Import，找到相应的Excel数据集，导入即可。

图1 建立工作文件2、作出序列的时序图对“2001年至2009年每个月发电量”序列y作时序图，观察数据的形态，双击序列y，点击View/Graph，出现图2的时序图：5001,0001,5002,0002,5003,0003,500图2 序列y 时序图从时序图上可以看出，发电量有季节变动的因素影响，以一个年度为周期呈现循环上升的趋势，看出序列不平稳。

欲对其进行分析，需先平稳化。

3、差分法消除增长趋势除了周期性波动外，序列呈现出上升趋势，利用差分方法消除增长趋势，在命令栏里输入series x=y-y(-1)，见图3，就得到一个不再有长期趋势的序列x ，时序图见图4：图3 一阶差分-600-400-200200400600图4 序列x 时序图4、季节差分法消除季节变动经过一阶差分过的时序图4显示出序列不再有明显的上升趋势，但有明显的季节变动，现在通过4步差分来消除季节变动，在命令栏里输入series xt=x-x(-4)，得到消除季节变动的序列时序图见图5：-600-400-2000200400600800XT图5 序列xt 时序图经过一阶差分消除增长趋势和经过4步差分消除季节变动的序列围绕0上下波动，看起来是平稳的，但需要通过统计检验进一步证实这个结论。

时间序列分析实训报告心得

时间序列分析实训报告心得1. 引言时间序列分析是一种重要的统计分析方法，可以用于研究时间序列数据的变化规律、预测未来趋势以及分析影响因素等。

在本次时间序列分析实训中，我们通过实际数据的分析和建模，深入学习了时间序列的基本理论和方法，并运用所掌握的知识解决了实际问题。

在本文中，我将分享我的实训心得和体会。

2. 数据获取与初步分析在时间序列分析的实训中，首先需要获取相关的时间序列数据，并进行初步的数据分析。

我们可以使用Python编程语言和相关的库来获取和处理数据。

通过对实际数据的初步观察和描述性统计分析，可以对数据的特征有一个初步的了解。

3. 数据预处理时间序列数据可能存在缺失值、异常值以及非平稳性等问题，因此在进行时间序列分析之前需要对数据进行预处理。

我们可以使用插值法来填充缺失值，使用平滑法或者移动平均法来处理异常值，使用差分法来消除非平稳性等。

4. 时间序列模型的选择与建立选择适当的时间序列模型是时间序列分析的关键步骤之一。

常见的时间序列模型包括ARMA模型、ARIMA模型、ARCH模型等。

根据实验要求和数据特点，我们可以选择合适的模型，并通过参数估计来建立模型。

5. 模型诊断与验证建立时间序列模型后，需要进行模型的诊断和验证。

通过残差的自相关图和偏自相关图，可以判断模型是否符合ARMA(p, q)模型的要求。

同时，还可以通过计算残差的百分比误差、平均绝对百分比误差等指标来评估模型的拟合效果。

6. 模型用于预测与应用时间序列模型的主要应用之一是预测未来的数值。

在选定合适的模型后，可以使用模型对未来的数据进行预测。

同时，时间序列模型还可以用于分析影响因素、判断趋势变化等。

通过对模型的应用，可以得到一些有价值的结论和洞察。

7. 总结与展望通过本次时间序列分析实训，我不仅深入了解了时间序列分析的理论和方法，还学会了使用Python编程语言和相关的库对时间序列数据进行分析和建模。

实践中遇到的问题和挑战也锻炼了我的动手能力和解决问题的能力。

时间序列法实验报告

一、实验目的1. 了解时间序列分析方法的基本原理和应用。

2. 学习如何使用时间序列分析方法对实际数据进行预测和分析。

3. 通过实验，提高对时间序列数据处理的实际操作能力。

二、实验内容本次实验选取了一组某城市过去三年的月均降雨量数据，旨在通过时间序列分析方法预测未来一个月的降雨量。

三、实验步骤1. 数据预处理- 读取实验数据，确保数据格式正确。

- 检查数据是否存在缺失值，如有，进行插补处理。

- 对数据进行初步的描述性统计分析，了解数据的分布情况。

2. 时间序列平稳性检验- 对原始数据进行ADF（Augmented Dickey-Fuller）检验，判断时间序列是否平稳。

- 若不平稳，进行差分处理，直至序列平稳。

3. 时间序列建模- 根据平稳时间序列的特点，选择合适的模型进行拟合。

- 本实验选取ARIMA模型进行拟合，其中AR项数为1，MA项数为1，差分次数为1。

4. 模型参数估计- 使用最小二乘法对模型参数进行估计。

5. 模型检验- 对拟合后的模型进行残差分析，检查是否存在自相关或异方差。

- 若存在自相关或异方差，对模型进行修正。

6. 预测- 使用拟合后的模型对未来一个月的降雨量进行预测。

四、实验结果与分析1. 数据预处理- 实验数据共有36个观测值，无缺失值。

- 描述性统计分析结果显示，降雨量数据呈正态分布。

2. 时间序列平稳性检验- 对原始数据进行ADF检验，结果显示P值小于0.05，拒绝原假设，说明原始数据不平稳。

- 对数据进行一阶差分后，再次进行ADF检验，结果显示P值小于0.05，接受原假设，说明一阶差分后的数据平稳。

3. 时间序列建模- 根据平稳时间序列的特点，选择ARIMA(1,1,1)模型进行拟合。

4. 模型参数估计- 使用最小二乘法对模型参数进行估计，得到AR系数为0.8，MA系数为-0.9。

5. 模型检验- 对拟合后的模型进行残差分析，发现残差序列存在自相关，但不存在异方差。

- 对模型进行修正，加入自回归项，得到修正后的ARIMA(1,1,1,1)模型。

时间序列分析试验报告【范本模板】

所以得：，
这时，趋势项的估计值是回归直线：
，
利用原始数据减去趋势项的估计后得到的数据基本只含有季节项和随机项了。
分解季节项：用第k季度的平均值作为季节项的估计。如果用分别表示第j年第k个季度的数据和趋势项，则时刻（j,k)的时间次序指标为。
在Matlab命令窗口中继续输入下列命令：
dx=B(：）'-(5780.1+21.9*(1：24））
C=[dx(：，1:4)；dx（:,5：8)；dx(：，9：12)；dx（：,13:16）；dx(：，17：20）;dx（:，21：24）];
s=mean(C）%季节项估计
则得
s = 1.0e+003 *
1。0371 —0.3936 —1。1552 0.5110
即季节项估计为
分解随机项：利用原始数据减去趋势项的估计和季节项的估计后得到的数据就是随机项的估计 .
在Matlab命令窗口中继续输入下列命令：
for j=1:6
for k=1：4
St(k+4＊（j—1)）=s（k);％求季节项值St
end
end
Rt=dx-St;%求随机项估计
plot（1:24,St，'＊—’,1：24，Rt，'〈-')％画出季节项和随机项图形
图2季节项和随机项散点图
预测:为得到1997年的预报值，可以利用公式
表7.1.1某城市居民季度用煤消耗量（单位：吨）
年份
1季度
2季度
3季度
4季度
年平均
1991
6878.4
5343.7
4847.9
6421.9
5873.0
1992

计量时间序列实验报告

一、实验背景时间序列分析是统计学和数据分析领域中一个重要的分支，广泛应用于经济、金融、气象、医学等领域。

通过对时间序列数据的分析，我们可以了解现象的发展变化规律，预测未来趋势，为决策提供科学依据。

本实验旨在通过实际操作，学习时间序列分析的基本方法，并运用相关软件进行时间序列分析。

二、实验目的1. 理解时间序列的基本概念和特点；2. 掌握时间序列数据的收集和整理方法；3. 学会运用时间序列分析方法对数据进行处理和分析；4. 培养运用相关软件进行时间序列分析的能力。

三、实验内容1. 数据收集本次实验采用我国某城市近10年的居民消费水平数据作为研究对象。

数据来源于国家统计局。

2. 数据整理对收集到的数据进行整理，剔除异常值和缺失值，将数据转换为适合时间序列分析的形式。

3. 时间序列分析（1）描述性分析对整理后的数据进行描述性统计分析，包括均值、标准差、最大值、最小值等。

（2）平稳性检验运用ADF（Augmented Dickey-Fuller）检验方法对时间序列数据进行平稳性检验。

（3）自相关性分析运用自相关函数（ACF）和偏自相关函数（PACF）对时间序列数据进行自相关性分析。

（4）模型选择根据自相关性分析结果，选择合适的模型对时间序列数据进行拟合。

本次实验采用ARIMA模型。

（5）模型参数估计运用最小二乘法估计模型参数，包括自回归项、移动平均项和差分阶数。

（6）模型检验运用残差分析、AIC准则等对模型进行检验。

（7）预测根据拟合的模型，对未来一段时间内的居民消费水平进行预测。

四、实验结果与分析1. 描述性分析根据描述性统计分析，我国某城市近10年的居民消费水平呈上升趋势，但波动较大。

2. 平稳性检验运用ADF检验方法对时间序列数据进行平稳性检验，结果显示该时间序列在5%的显著性水平下是平稳的。

3. 自相关性分析运用ACF和PACF对时间序列数据进行自相关性分析，发现自回归项和移动平均项的阶数分别为1和1。

时间序列分析实验报告

时间序列分析实验报告一、实验目的时间序列分析是一种用于处理和分析随时间变化的数据的统计方法。

本次实验的主要目的是通过对给定的时间序列数据进行分析，掌握时间序列分析的基本方法和技术，包括数据预处理、模型选择、参数估计和预测，并评估模型的性能和准确性。

二、实验数据本次实验使用了一组某商品的月销售量数据，数据涵盖了过去两年的时间范围，共 24 个观测值。

数据的具体形式为一个时间序列，其中每个观测值表示该商品在相应月份的销售量。

三、实验方法1、数据预处理首先，对数据进行了可视化，绘制了时间序列图，以便直观地观察数据的趋势、季节性和随机性。

然后，对数据进行了平稳性检验。

采用了 ADF（Augmented DickeyFuller）检验来判断数据是否平稳。

如果数据不平稳，则需要进行差分处理，使其达到平稳状态。

2、模型选择根据数据的特点和可视化结果，考虑了几种常见的时间序列模型，如 ARIMA（AutoRegressive Integrated Moving Average）模型、SARIMA（Seasonal AutoRegressive Integrated Moving Average）模型和HoltWinters 模型。

通过对不同模型的参数进行估计，并比较它们在训练数据上的拟合效果和预测误差，选择了最适合的模型。

3、参数估计对于选定的模型，使用最大似然估计或最小二乘法等方法来估计模型的参数。

通过对参数的估计值进行分析，判断模型的合理性和稳定性。

4、预测使用估计得到的模型参数，对未来一段时间内的销售量进行预测。

为了评估预测的准确性，采用了均方根误差（RMSE）、平均绝对误差（MAE）等指标来衡量预测值与实际值之间的差异。

四、实验过程1、数据可视化通过绘制时间序列图，发现数据呈现出明显的季节性和上升趋势。

同时，数据的波动范围也较大，存在一定的随机性。

2、平稳性检验对原始数据进行 ADF 检验，结果表明数据是非平稳的。

实验报告关于时间序列(3篇)

第1篇一、实验目的1. 了解时间序列的基本概念和特性；2. 掌握时间序列的常用分析方法；3. 学会运用时间序列分析方法解决实际问题。

二、实验内容1. 时间序列数据收集2. 时间序列描述性分析3. 时间序列平稳性检验4. 时间序列模型构建5. 时间序列预测三、实验方法1. 时间序列数据收集：通过查阅相关文献、统计数据网站等方式获取实验所需的时间序列数据。

2. 时间序列描述性分析：对时间序列数据进行统计分析，包括均值、标准差、偏度、峰度等。

3. 时间序列平稳性检验：运用单位根检验（ADF检验）判断时间序列的平稳性。

4. 时间序列模型构建：根据时间序列的平稳性，选择合适的模型进行构建，如ARIMA模型、季节性分解模型等。

5. 时间序列预测：利用构建好的时间序列模型进行预测，并评估预测结果的准确性。

四、实验步骤1. 数据收集：选取我国某地区近十年的GDP数据作为实验数据。

2. 描述性分析：计算GDP数据的均值、标准差、偏度、峰度等统计量。

3. 平稳性检验：对GDP数据进行ADF检验，判断其平稳性。

4. 模型构建：根据ADF检验结果，选择合适的模型进行构建。

5. 预测：利用构建好的模型对GDP数据进行预测，并评估预测结果的准确性。

五、实验结果与分析1. 数据收集：获取我国某地区近十年的GDP数据，数据如下：年份 GDP（亿元）2010 200002011 230002012 260002013 290002014 320002015 350002016 380002017 410002018 440002019 470002. 描述性分析：计算GDP数据的均值、标准差、偏度、峰度等统计量，结果如下：均值：39600亿元标准差：4900亿元偏度：-0.2峰度：-1.83. 平稳性检验：对GDP数据进行ADF检验，结果显示ADF统计量在1%的显著性水平下拒绝原假设，说明GDP数据是非平稳的。

4. 模型构建：由于GDP数据是非平稳的，我们可以对其进行差分处理，使其变为平稳序列。

时间序列实验报告

一、实验目的本次实验旨在通过时间序列分析方法，对一组实际数据进行建模、分析和预测。

通过学习时间序列分析的基本理论和方法，提高对实际问题的分析和解决能力。

二、实验内容1. 数据来源及预处理本次实验所使用的数据集为某地区近十年的年度GDP数据。

数据来源于国家统计局，共包含10年的数据。

2. 数据可视化首先，我们将使用Excel软件绘制年度GDP的时序图，观察数据的基本趋势和周期性特征。

3. 平稳性检验根据时序图，我们可以初步判断数据可能存在非平稳性。

为了进一步验证，我们将使用ADF（Augmented Dickey-Fuller）检验对数据进行平稳性检验。

4. 模型选择由于数据存在非平稳性，我们需要对数据进行差分处理，使其变为平稳序列。

然后，根据自相关函数（ACF）和偏自相关函数（PACF）图，选择合适的模型。

5. 模型参数估计使用最大似然估计法（MLE）对所选模型进行参数估计。

6. 模型拟合与检验将估计出的模型参数代入模型，对数据进行拟合，并计算残差序列。

接着，使用Ljung-Box检验对残差序列进行白噪声检验，以验证模型的有效性。

7. 预测利用拟合后的模型，对未来几年的GDP进行预测。

三、实验过程及结果1. 数据可视化通过Excel绘制年度GDP时序图，发现数据呈现明显的上升趋势，但同时也存在一定的波动性。

2. 平稳性检验对数据进行一阶差分后，使用ADF检验进行平稳性检验。

结果显示，差分后的序列在5%的显著性水平下拒绝原假设，说明序列是平稳的。

3. 模型选择根据ACF和PACF图，选择ARIMA(1,1,1)模型。

4. 模型参数估计使用MLE法对ARIMA(1,1,1)模型进行参数估计，得到参数值：- AR系数：-0.864- MA系数：-0.652- 常数项：392.4765. 模型拟合与检验将估计出的模型参数代入模型，对数据进行拟合，并计算残差序列。

使用Ljung-Box检验对残差序列进行白噪声检验，结果显示在5%的显著性水平下拒绝原假设，说明模型拟合效果较好。

时间序列分析实验报告

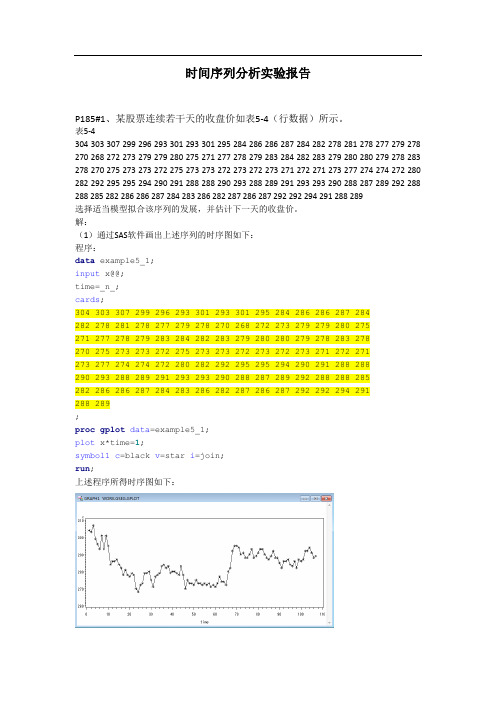
时间序列分析实验报告P185#1、某股票连续若干天的收盘价如表5-4（行数据）所示。

表5-4304 303 307 299 296 293 301 293 301 295 284 286 286 287 284 282 278 281 278 277 279 278 270 268 272 273 279 279 280 275 271 277 278 279 283 284 282 283 279 280 280 279 278 283 278 270 275 273 273 272 275 273 273 272 273 272 273 271 272 271 273 277 274 274 272 280 282 292 295 295 294 290 291 288 288 290 293 288 289 291 293 293 290 288 287 289 292 288 288 285 282 286 286 287 284 283 286 282 287 286 287 292 292 294 291 288 289选择适当模型拟合该序列的发展，并估计下一天的收盘价。

解：（1）通过SAS软件画出上述序列的时序图如下：程序：data example5_1;input x@@;time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292 294 291288 289;proc gplot data=example5_1;plot x*time=1;symbol1c=black v=star i=join;run;上述程序所得时序图如下：上述时序图显示，该序列具有长期趋势又含有一定的周期性，为典型的非平稳序列。

时间序列_实验报告

一、实验目的1. 了解时间序列分析的基本原理和方法；2. 掌握时间序列数据的平稳性检验、模型识别和参数估计等基本操作；3. 通过实例，学习使用ARIMA模型进行时间序列预测。

二、实验环境1. 操作系统：Windows 102. 软件环境：EViews 9.0、R3.6.1三、实验数据1. 数据来源：某城市1980年1月至2020年12月每月的GDP数据；2. 数据格式：Excel表格。

四、实验步骤1. 数据预处理（1）导入数据：将Excel表格中的GDP数据导入EViews软件；（2）观察数据：绘制GDP时间序列图，观察数据的趋势、季节性和周期性；（3）平稳性检验：使用ADF检验判断GDP序列是否平稳。

2. 模型识别（1）自相关函数（ACF）和偏自相关函数（PACF）图：观察ACF和PACF图，初步确定ARIMA模型的阶数；（2）模型选择：根据ACF和PACF图，选择合适的ARIMA模型。

3. 模型估计（1）模型估计：使用EViews软件中的ARIMA过程，对选择的模型进行参数估计；（2）模型检验：对估计出的模型进行残差检验，包括残差的平稳性检验、白噪声检验等。

4. 时间序列预测（1）预测：使用估计出的ARIMA模型，对2021年1月至2025年12月的GDP进行预测；（2）预测结果分析：对预测结果进行分析，评估预测的准确性。

五、实验结果与分析1. 数据预处理（1）导入数据：将Excel表格中的GDP数据导入EViews软件；（2）观察数据：绘制GDP时间序列图，发现GDP序列存在明显的上升趋势和季节性；（3）平稳性检验：使用ADF检验，发现GDP序列在5%的显著性水平下拒绝原假设，序列是平稳的。

2. 模型识别（1）自相关函数（ACF）和偏自相关函数（PACF）图：根据ACF和PACF图，初步确定ARIMA模型的阶数为（1，1，1）；（2）模型选择：根据ACF和PACF图，选择ARIMA（1，1，1）模型。

时间序列分析实验报告 (4)

基于matlab的时间序列分析在实际问题中的应用时间序列分析(Time series analysis)是一种动态数据处理的统计方法。

该方法基于随机过程理论和数理统计学方法，研究随机数据序列所遵从的统计规律，以用于解决实际问题。

时间序列分析不仅可以从数量上揭示某一现象的发展变化规律或从动态的角度刻画某一现象和其他现象之间的内在的数量关系及其变化规律性，而且运用时间序列模型可以预测和控制现象的未来行为，以达到修正或重新设计系统使其达到最优状态。

时间序列是指观察或记录到的一组按时间顺序排列的数据。

如某段时间内。

某类产品产量的统计数据，某企业产品销售量，利润，成本的历史统计数据；某地区人均收入的历史统计数据等实际数据的时间序列。

展示了研究对象在一定时期内的发展变化过程。

可以从中分析寻找出其变化特征，趋势和发展规律的预测信息。

时间序列预测方法的用途广泛，它的基本思路是，分析时间序列的变化特征，选择适当的模型形式和模型参数以建立预测模型，利用模型进行趋势外推预测，最后对模型预测值进行评价和修正从而得到预测结果。

目前最常用的拟合平稳序列模型是ARMA模型，其中AR和MA模型可以看成它的特例。

一．时间序列的分析及建模步骤（1）判断序列平稳性，若平稳转到（3），否则转到（2）。

平稳性检验是动态数据处理的必要前提，因为时间序列算法的处理对象是平稳性的数据序列，若数据序列为非平稳，则计算结果将会出错。

在实际应用中，如某地区的GDP，某公司的销售额等时间序列可能是非平稳的，它们在整体上随着时间的推移而增长，其均值随时间变化而变化。

通常将GDP等非平稳序列作差分或预处理。

所以获得一个时间序列之后，要对其进行分析预测，首先要保证该时间序列是平稳化的。

平稳性检验的方法有数据图、逆序检验、游程检验、自相关偏相关系数、特征根、参数检验等。

本实验中采用数据图法，数据图法比较直观。

（2）对序列进行差分运算。

一般而言，若某序列具有线性趋势，则可以通过对其进行一次差分而将线性趋势剔除掉。

时间应用序列实验报告

一、实验背景时间序列分析是统计学和数据分析领域的一个重要分支，广泛应用于经济、金融、气象、生物等多个领域。

本实验旨在通过实际案例，学习时间序列分析方法，并运用相关模型进行预测和解释。

二、实验目的1. 掌握时间序列数据的基本特征和常见模型。

2. 学习时间序列数据的平稳性检验、模型识别和参数估计。

3. 熟悉时间序列预测方法，并进行实际应用。

三、实验数据本次实验选用某城市近五年月均气温数据作为研究对象，数据来源为气象局官方网站。

四、实验步骤1. 数据预处理- 将数据导入统计软件，进行数据清洗和整理。

- 绘制时间序列图，观察数据的基本特征，如趋势、季节性、周期性等。

2. 平稳性检验- 对数据进行单位根检验（ADF检验），判断数据是否平稳。

- 对非平稳数据，进行差分处理，使其达到平稳。

3. 模型识别- 根据时间序列图和自相关图、偏自相关图，初步判断模型类型。

- 对候选模型进行参数估计，比较不同模型的拟合优度。

4. 模型验证- 对模型进行残差分析，检验模型是否合适。

- 利用预测指标（如均方误差、均方根误差等）评估模型的预测性能。

5. 模型应用- 利用训练好的模型，对未来一段时间内的气温进行预测。

- 分析预测结果，解释气温变化趋势和原因。

五、实验结果与分析1. 数据预处理- 数据清洗：删除异常值，填补缺失值。

- 数据整理：将数据转换为时间序列格式。

2. 平稳性检验- 对原始数据进行ADF检验，结果显示P值小于0.05，拒绝原假设，说明数据是非平稳的。

- 对数据进行一阶差分，再次进行ADF检验，结果显示P值大于0.05，接受原假设，说明一阶差分后的数据是平稳的。

3. 模型识别- 根据时间序列图和自相关图、偏自相关图，初步判断模型为ARIMA模型。

- 对ARIMA模型进行参数估计，比较不同模型的拟合优度，最终选择ARIMA(1,1,1)模型。

4. 模型验证- 对模型进行残差分析，发现残差基本符合正态分布，说明模型合适。

时间序列分析报告心得

时间序列分析报告心得一、引言时间序列分析是一门研究按一定时间顺序排列的数据并通过统计方法对其进行建模、预测和分析的方法。

在时间序列分析的过程中，我们运用了各种统计技术，比如平均数、标准差等，通过对历史数据的分析，我们可以预测未来一段时间内的数据变化趋势和规律。

本篇报告主要总结了我对时间序列分析的学习和实践的心得体会。

二、学习过程在学习时间序列分析的过程中，我首先了解了时间序列分析的基本概念和常用的方法。

我了解到，时间序列分析的目标是通过分析时间序列的内在规律，对未来的发展趋势进行预测。

同时，时间序列分析也可以揭示时间序列中的周期性变化、趋势性变化和季节性变化。

我学习了一些时间序列分析的基本概念，比如平稳性、自相关函数、移动平均、自回归等。

在学习过程中，我尝试了不同的学习方法。

首先，我阅读了一些经典的时间序列分析教材和文献，掌握了基本的理论知识。

其次，我通过在线课程和视频教程学习了时间序列分析的实践技巧。

最后，我参与了一些实际项目，应用时间序列分析模型对数据进行预测和分析。

三、实践应用在时间序列分析的实践应用中，我主要应用了Python编程语言和一些常用的时间序列分析工具包，比如pandas和statsmodels。

通过这些工具，我可以对时间序列数据进行读取、处理、分析和可视化。

我首先通过pandas库读取了时间序列数据，并进行了数据的预处理工作。

预处理包括填充缺失值、平滑数据、去除异常点等步骤，这可以使得模型更准确地反映数据的真实情况。

然后，我使用了statsmodels库来构建时间序列分析模型。

statsmodels库提供了丰富的时间序列模型类和函数，比如ARIMA模型、SARIMA模型等。

通过这些模型，我可以对时间序列数据进行建模和预测。

最后，我使用了matplotlib库对分析结果进行可视化。

可视化可以帮助我们更直观地理解数据的规律和趋势，以及模型的预测效果。

四、心得体会通过学习和实践时间序列分析，我深刻体会到了时间序列分析在实际应用中的重要性和价值。