【知识学习】--县1%人口抽样调查工作方案

合集下载

2024年贵阳市南明区永乐第一中学中考第二次模拟测试数学试卷

2024年贵阳市南明区永乐第一中学中考第二次模拟测试数学试卷(限时：120分钟　总分：150分)一、选择题(每小题3分，共36分．每小题均有A，B，C，D四个选项，其中只有一个选项正确)1．在－3，2，0，－1四个数中，最小的数是( )A．－3 B．2 C．0 D．－12．如图所示几何体的主视图为( )第2题图 A B C D3．据贵阳文化和旅游局统计，2023年五一期间，贵阳44个重点景区景点(其中41个A级景区、3个景点)累计接待游客105万人次，其中1 050 000用科学记数法表示应为( )A．10.5×105 B.1.05×105 C.1.05×106 D.0.105×1064．估计15的值在( )A．1和2之间 B.2和3之间 C.3和4之间 D.4和5之间5．如图，在Rt△ABC中，D，E分别为边BC，AC上的点，连接DE，将△ABC沿DE折叠，使点C与点A 重合，若AD＝5，AE＝4，则AB的长为( )第5题图A．4 B.6 C.8 D.106．如图，数轴上有四个点A，B，C，D分别对应四个有理数，若点B，D表示的有理数互为相反数，则图中表示绝对值最小的数的点是( )第6题图A．点A B.点B C.点C D.点D7．风铃，又称铁马，古称“铎”，常见于中国传统建筑屋檐下(如图①)，如图②是六角形风铃的平面示意图，其底部可抽象为正六边形ABCDEF，连接CF，则∠AFC的度数为( )第7题图A．30° B.45° C.60° D.75°8．小星所在班级10名同学的身高数据如下表所示．编号12345678910身高(cm)165158168162174168162165168170下列统计量中，不能够描述这组数据集中趋势的是( )A ．平均数 B.方差 C.众数 D.中位数9．如图，在△ABC 中，AB ＝AC ，按以下步骤作图：①以点A 为圆心，任意长为半径作弧，分别交AB ，AC 于点D 和点E ；②以点B 为圆心，AD 长为半径作弧，交AB 于点F ；③以F 为圆心，DE 长为半径作弧，在∠ABC 内部交前面的弧于点G ；④过点G 作射线BG 交AC 于点H .若BC ＝6，∠A ＝36°，则AH 的长为( )第9题图 A ．4 B.5 C.6 D.710．关于x 的方程1x －2＋a －22－x＝1的解是正数，则a 的取值范围是( )A ．a ＞5 B.a ＜5C ．a ＞5且a ≠7D.a ＜5且a ≠311．如图，在菱形ABCD 中，AC ＝8，BD ＝6，DE ⊥AB ，垂足为E ，DE 与AC 交于点F ，则sin ∠DFC 的值为( )第11题图　A ．34 B.43 C.35 D.4512．已知二次函数y ＝－x 2＋ax ＋3图象的对称轴为直线x ＝2，关于x 的方程－x 2＋ax ＋3－m ＝0(m 为实数)在－1＜x ＜3的范围内有实数根，则m 的取值范围是( )A ．6≤m ＜7 B.m ＜7 C ．－2≤m ＜6 D.－2＜m ≤7二、填空题(每小题4分，共16分)13．如图是反比例函数y ＝m －4x图象的一支，根据图象可知常数m 的取值范围是________．第13题图14．某校九年级选出三名同学参加学校组织的“防溺水知识竞赛”．比赛规定，以抽签方式决定每个人的出场顺序，主持人将表示出场顺序的数字1，2，3分别写在3张同样的纸条上，并将这些纸条放在一个不透明的盒子中，搅匀后从中任意抽出一张，小星第一个抽，则小星第一个上场的概率是________．15．某车间有20名工人，每人每天可以生产600个螺母或900个螺丝．一个螺丝需要配两个螺母，为使每天生产的螺丝与螺母刚好配套，设安排x名工人生产螺母，根据题意可列方程为________．16．如图，四边形ABCD中，∠A＝∠C＝90°，点M、N分别是BC、AB边上的动点，∠B＝56°，当△DMN 的周长取最小值时，则∠MDN的度数是________．第16题图三、解答题(本大题共9题，共98分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本题满分12分)如图是三张写有整式的卡片A，B，C，小芳发现A，B，C之间其中两个整式相加等于第三个整式，但B卡片中一单项式不小心被墨水污染了．(1)小芳推测B＋C＝A，请你帮助小芳判断她的推测是否正确，并说明理由；(2)根据三个整式，求出被墨水污染的部分．第17题图18．(本题满分10分)2023年6月6日是第28个“全国爱眼日”．某初级中学为了解本校学生的视力情况，从本校学生中随机抽取100名学生进行问卷调查，并将调查结果用统计图描述如下：调查问卷1．你近视吗？近视的度数x(度)为A.不近视　B．100≤x＜200　C．200≤x＜300　D．300≤x＜400　E．x≥4002．你近视的主要原因是什么？a.先天遗传　b．过度使用电子产品　c．长期在过明或过暗的环境下用眼　d．距离书本太近或躺着看书　e．作息不规律或睡眠不足　f．户外活动时间太短　g．其他100名学生近视度数扇形统计图　图①100名学生近视主要原因条形统计图　图②第18题图根据以上信息，解答下列问题：(1)本次调查中，被调查学生的近视度数的中位数落在________(填字母)，近视度数在200度及以上的学生人数占被调查人数的百分比为________；(2)小明同学帮助学校绘制100名学生近视原因条形统计图时，发现被调查人数之和远远超出100人，经核实，小明绘制的条形统计图无误，请帮助小明解释出现该情况的原因？(3)若该校学生共有2 200人，请估计全校近视的学生有多少人？并给现在学生保护眼睛提一条意见．19．(本题满分10分)如图，在正方形ABCD中，E是边CD的中点，点P是边AD上一点(与点A，D不重合)，射线PE与BC的延长线交于点Q.(1)求证：△PDE≌△QCE；(2)过点E作EF∥BC交PB于点F，连接AF，当PB＝PQ时．求证：四边形AFEP是平行四边形．第19题图20．(本题满分10分)如图，一次函数y1＝k1x＋2(k1≠0)经过点B(1，0)且与反比例函数y2＝k2x(k2≠0)的图象交于点C(a，－2).(1)求一次函数和反比例函数的表达式；(2)根据函数图象观察，直接写出当x>0时，y1与y2的大小关系；(3)若一次函数y＝mx＋b的图象过点A，且与反比例函数y2＝k2x的图象有且仅有一个交点，求m的值．第20题图21．(本题满分10分)贵阳乌当惜字塔位于贵阳市乌当区，它是贵阳当地历史悠久的古塔之一，也是唯一一座与爱惜文字有关的古塔．某校九年级的一个班级利用周末时间开展“测量乌当惜字塔高度”的实践活动，想得到乌当惜字塔的高度．如图．乌当惜字塔AB垂直于地面，在塔的两侧不远处取C，D两点，C，D两点之间的距离为22 m，并测量出∠ACB＝45°，∠ADB＝42°.(参考数据：sin 42°≈0.67，cos 42°≈0.74，tan 42°≈0.90，sin 25°≈0.42，cos 25°≈0.90，tan 25°≈0.47，2≈1.41，结果保留一位小数．)(1)求乌当惜字塔的高度；(2)同学们发现，在塔身第三层的位置镌嵌着“过”、“化”、“存”、“神”四个大字，于是在D点观察第三层时测量到∠EDB＝25°，求四个大字所在的第三层距离地面的高度．第21题图22．(本题满分10分)遵义某校准备组织师生共60人，从遵义乘动车前往贵阳参加夏令营活动，动车票价如表所示：(教师按成人票价购买，学生按学生票价购买).若师生均购买二等座票，则共需2 750元．运行区间成人票价(元/张)学生票价(元/张)出发站终点站一等座二等座二等座遵义贵阳705045(1)参加活动的教师、学生各有多少人？(2)由于部分教师需提早前往做准备工作，这部分教师均购买一等座票，而后续前往的教师和学生均购买二等座票，设提早前往的教师有x人，购买一、二等座票全部费用为y元．①求y关于x的函数解析式；②若购买一、二等座票全部费用不多于2 800元，则提早前往的教师最多只能多少人？23．(本题满分12分)如图，AB是⊙O的一条弦，⊙O的直径CD⊥AB于点E，连接AC，BO，延长BO交AC于点F，交⊙O于点G，连接AG.(1)求证：△AGF∽△COF；(2)若劣弧AB对应的圆心角的度数为120°，求∠ACD的度数；(3)若tan ∠CAE＝2，探究线段AE，OE之间的数量关系，并说明理由．第23题图24．(本题满分12分)已知抛物线y＝ax2＋bx＋3的对称轴为直线x＝2.(1)求抛物线顶点M的坐标和b的值(用含a的代数式表示)；(2)已知点A(0，y1)，B(1，y2)都在此抛物线上，点P为对称轴上一动点，求PA＋PB的值最小时，P点的坐标；(3)若自变量x的值满足－1≤x≤1，与其对应的函数的最大值为6a，求b的值．第24题图25．(本题满分12分)综合与实践问题情境：在综合与实践课上，老师要求同学们以“折纸中的数学”为主题开展活动．独立思考：(1)如图①，将三角形纸片ABC沿DE折叠，使点A落在四边形BCDE内点A′的位置，则∠A 与∠1＋∠2之间的数量关系为________，请说明理由；深入探究：(2)如图②，若点A′落在四边形BCDE的边CD下方时，试猜想此时∠A与∠1，∠2之间的数量关系，并说明理由；结论运用：(3)如图③，在四边形ABCD中，∠A＝∠C＝90°，E，F分别是AB，CD边上的一点，沿EF将四边形ABCD折叠，点A的对应点G恰好落在BC边上，且∠1＝75°，∠2＝15°.①∠B的度数为________；②若BE＝22，AD＝12AE，求点H到BC的距离．第25题图。

部编版二年级下册写字表字帖

生字表
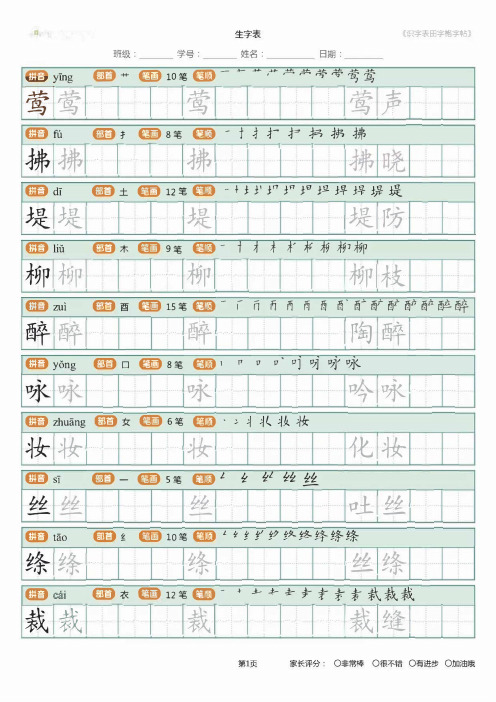
《识字表田字格字帖》
班级：
学号：
姓名：
日期：
I: I :·I··I莺I :-+··I···I--: I莺声 mymg
萄莺
m m -++-
10笔。一七廿户乒乒茅苛莺莺
：
才m弗mI才弗Im-- : I才…。 - I -8笔I。才弗:. •一 ' ' ' ' 寸才扩护把招拂
fiDdi
m m + 土 €i)12 笔》- 1 扩尸尸尸乒坢焊埽j是
裹襄
裹
I ·I ,. I·: I寄I : ·I,·I· ·I ·I iDji
m 笔。. ,· 占 @11
产,""中中主客客字寄
穿寄 -!
! 邮寄
Sju
m 尸。 7笔。勹
刁
尸局局局局
局局I i I , I : I局I i I : I : I I I棍局
第3页
家长评分： O非常棒 O很不错 O有进步 O加油哦
户
K
音符 f 应吐矨泸庐符符
．
| |
第2页
家长评分： O非常堵 O很不错 O有进步 O加油哦
生字表
《识字表田泗字帖》
班级：
学号：
姓名：
日期：
cmljie
&角f!D13 笔- 丿力 f 介弁肖俞旷你勹铲胪解解
1 俞，畔开，解解，．
．．，刀牛 I ．
I
触 1 I : I : I·I触I I ; I : I 飞如角 f «iDchu 回D 角 fmD13笔-/ 力
性�, 懊 …|、·:--
15 笔.,,、 ,t

三国志姜维传完美攻略

辘度：逗一-☆i三二-★ 腭利修件：全;威敢人印授修件：辗友隼撤退 iS三-：一^5始全窜麻癖+降防，姜雉符超霎挑掉彳麦就解;夬那群小兵。 jg撵二：典超霎军挑彳麦起雪降防及hp-100（不撤退），小兵曾追著尹赏打。三K:注意一始和超霎罩挑彳度有iS撵是否要JE级穗果，明Ii冕。&A。第二^天水之戟军挑：姜雉VS.袁^姜雉VS.魏延三BS：姜雉-孟琰姜雉-Ig葛亮鞋度：JS☆Jg二-★ 瞒利修件：迤入冀城印授修件：斶赞所有罩挑三三-:首先姜雉先聘袁^挑掉，然彳爰解决那群崎兵。遇槁之彳爰魏延出现，挑掉彳爰解，夬那群崎兵就能迤城。第10回合孟琰部除出擎,靠近Ig葛亮即全里出擎。遇^容易，i⅛在拿智慧果和全;威。 iSJ三⊂：流程相同，但是城F号多三彳固步兵守衢，l⅛葛亮裴^^物。
I三：ii一—★il二-★★
腭利修件：擎退曹真
失败修件：澳中防⅛a被攻破
印授修件：一-我隼和友窜辗人撤退（吴班除外）
二-懒彝所有舆竦到有BS的封^
il三-:一^始斜谷道前绛敝窜混阖L,而子午谷道敲窜移Ii力下降。超廉挑完^^彳爰先守住北方^卡，等姜雉部消滋斜谷道前^彳爰再去接替。榻赢可先去右很IJM忙防守，也易引彝和她有信舶勺封IS。第八回合张郃部优中央营地出现，吴班曾因^事件而撤退。第12回合李殿和竦到前来支援，我里攻擎、防梁、士氟上升。第16回合司焉懿部曾徙右很IJ管地出现，注意^葛亮和司禹懿的塞^舌是11^拿Jl羽扇的前置修件。曹真那Jl敲人少於一定程度曾斶樊趣限崎兵的增援，翥早卡住有利位置2£擎退他。
鞋度：逗一-☆ig二-★★ 腭利修件：司焉懿撤退印授修件：一-斶彝全部罩挑和封言舌二-全滋敲人出戟限制：本Ba南中^I■不能出埸。 iSJ三-：夏侯兄弟先曾先出擎，之彳麦敲窜曾一波一波接著出擎，利用栅橄伟睡来抵搐攻擎,第六回合王平、吴班、竦式曾来增援。第12回合假的B⅛葛亮出现，敲人全罩混第L3£且不曾攻擎我窜。 iS三三：要小心敲人可是来势;就匈，彳度方的武衢管和强弓手更是一大威膏。 l三葛果入除她自带白羽扇第十二g∣魏延制伐戟罩挑：超统VS.魏容三三VS.魏昌禹岱VS.魏延（魏延如果死在禹岱手上，就没有五槿果子和印授） ⅛t三S：姜雉-魏延王平-魏延l⅛葛果-魏延句扶-魏延重要物品：印授腭利修件：全;威敲隼印授修件：一-擎退魏延

福建省泉州市(新版)2024高考数学部编版质量检测(提分卷)完整试卷

福建省泉州市（新版）2024高考数学部编版质量检测(提分卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题如图，圆为的外接圆，，为边的中点，则（）A．10B．13C．18D．26第(2)题记全集，设集合则（）A．B．C．D．第(3)题加斯帕尔-蒙日是1819世纪法国著名的几何学家．如图，他在研究圆锥曲线时发现：椭圆的任意两条互相垂直的切线的交点都在同一个圆上，其圆心是椭圆的中心，这个圆被称为“蒙日圆”．若长方形的四边均与椭圆相切，则下列说法错误的是（）A．椭圆的离心率为B．椭圆的蒙日圆方程为C．若为正方形，则的边长为D．长方形的面积的最大值为18第(4)题在的展开式中，含的项的系数为（）A．8B．28C．56D．70第(5)题若函数f（x）满足f（1－ln x）＝，则f（2）＝（）A．B．eC．D．－1第(6)题函数在开区间的零点个数为（）A．B．C．D．第(7)题“”是“方程表示的曲线为双曲线”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件第(8)题攒尖是古代中国建筑中屋顶的一种结构形式．宋代称为撮尖，清代称攒尖．依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，也有单檐和重檐之分，多见于亭阁式建筑．如图所示，某园林建筑为六角攒尖，它的主要部分的轮廓可近似看作一个正六棱锥，若此正六棱锥的侧面等腰三角形的底角为a，则侧棱与底面外接圆半径的比为（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知是定义在上的函数的导数，且，则下列不等式一定成立的是（）A．B．C．D．第(2)题已知椭圆的左、右焦点分别为，是上的两个动点，则（）A．存在点，使得B．若，则的面积为C．记的上顶点为，若轴，则直线AP与AQ的斜率之积为D．若是的上顶点，则的最大值为第(3)题下列说法正确的有（）A．若，则B．若，则C．若，则D．若，则三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题如图伪代码的输出结果为________.第(2)题已知函数的图象如图所示，点M和N分别是最低点和最高点，P是的图象与x轴的一个交点，轴于点Q，O为坐标原点，若且，则A=___________.第(3)题已知，是两条不同的直线，，是两个不同平面，则以下命题不成立的是__（1）若，，，则（2）若，，则（3）若，，则（4）若，，，则四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知函数．（Ⅰ）求函数的单调区间；（Ⅱ）设，为函数的两个极值点，求证．第(2)题如图，已知四棱锥的底面ABCD为菱形，平面平面ABCD，，E为CD的中点.(1)求证：；(2)若，，求平面PBC与平面PAE所成锐二面角的余弦值.第(3)题已知函数．（Ⅰ）设，求的单调区间；（Ⅱ）设在区间中至少有一个极值点，求a的取值范围．第(4)题已知，，直线，相交于点，且它们的斜率之积是.（1）求点的轨迹的方程；（2）过点的直线与轨迹交于点，与交于点，过作的垂直线交轴于点，求证：.第(5)题已知函数．(1)设a＝0．①求曲线在点处的切线方程．②试问有极大值还是极小值？并说明理由．(2)若在上恰有两个零点，求a的取值范围．。

(完整版)古诗十九首原文(注音版)

1、《行行重行行》X 1 ngx I ngch δ ng ι ng× ι ngy U 与j U n君Sh e n∣gi e I i离。

行行重行行，生别Xi a ngq U Wa n y u I i g e Z a i ti a n y i y a 相去万余里，各在天——涯；d αO I U Z U qie Ch a ng hu i mi a n an k e Zh 1 道路阻且长，会面安可知？h U ma y i b e i f e ng yu ( ≡ rd a0 Ch a( )n a n Zh 1 胡马依北风，越鸟巢南枝。

Xi a ngq U r i y i yu a n y i d a i r 1 y i h u a n 相去日已远，衣带日已缓；f U y u n b i b a i r i y δ uz i bug U fan 浮云蔽白日，游子不顾反。

S 1 j U n I i ngr e n I a O SU 1 yu e h U y i Wan 思君令人老，岁月忽已晚。

q 1 ju a n Wu f U ClaO n U I i Ji a Can fan弃2、捐勿复《青青河畔草》道，努力加餐饭！q I ngq i ngh e Pan CaO y U y U yu a n Zh δ∏S U 青青河畔草，郁郁园中柳。

y 1 ngy i ngl δ ιu Sh a ng U ji a Oji a Oda n gch u C In g δ u 盈盈楼上女，皎皎当窗牖e e h 6 n gf e n ZhU a ng Xi a n xi a n chυi S U sh δ u娥娥红粉妆，纤纤出素手X 1 Wei Ch α n⅛ and j InWeida f U昔为倡家女，今为荡子妇。

d a n@ i han @ tIgUl k o n ghu an g a n d u sh δ u荡子行不归，空床难独守3、《青青陵上柏》q 1 ngq ι n© ι ngsh a nig a i I e il e i ji a n zh o ngh i青青陵上柏，磊磊涧中石r e nsh e n® a nd i ji a n h U r U yu a n X i ngk e人生天地间，忽女口远行客d δ u ji U Xi a r⅛g u Ie Ii a o h δ u b U W e i b a o斗酒相娱乐，聊厚不为薄q U Ch e C e nCιma you X 1 Wan y u IU δ驱车策弩马，游戏宛与洛Iu δ zh δ r⅛ e y U y U gu a n d a i Z i Xian^Jo洛中何郁郁，冠带自相索ChangtI IU δ ji a Xi a ng W a ngh δ U du o Cl i Zh a i 长衢罗夹巷，王侯多第宅Ii a n®o ngy a o xi a ng a ng ShU a ngu e b a i y U Ch i 两宫遥相望，双阙百余尺。

部编版六上语文知训答案

• （二）1．B
• 2．画“——”的句子：众人先是发怔，后来一想，上上下下都一齐哈哈大笑起来。
• 画“∽∽”的句子：湘云撑不住，一口茶都喷出来。黛玉笑岔了气，伏着桌子只叫“哎哟！”宝玉滚到贾母怀里，贾母笑的搂着叫“心肝”，王夫人笑的用手指着凤姐，却说不出话来。薛姨妈也撑不住，口里的茶喷了探春一裙子。探春的茶碗都合在迎春身上。惜春离了座位，拉着他的奶母，叫“揉揉肠子”。地下无一个不弯腰屈背，也有躲出去笑去的，也有忍着笑上来替他姐妹换衣裳的。
材料一材料二
（3）（3）⑥ (答案供参考，学生所选合理即可)
我最感兴趣的研究任务是第个（填序号），为了完成它，我还可以这样做：查找更多关于故宫的新闻或故事，游故宫时除了讲解建筑特点，再讲讲与建筑有关的故事，一定会更有意思。(答案供参考，学生所答合理即可)
• 二、1．C 2．B
• 单元自测三
了关键信息，帮我理解了鸟类的灭绝与动植物生存之间的关系密切。 • ⑤这段举例进一步说明鸟类能维护生物的多样性，没有了渡渡鸟，大颅榄树会渐渐消失。 • ⑥鸟类为人类提供生活之需，略读。 • ⑦用列数字的方法说明鸟类濒临灭绝的原因，与我想要探究的问题关系不大，略读。
• 11* 故宫博物院
• 【基础训练】
1、草原
• 基础训练
• 一、绿毯、陈旧、衣裳、彩虹、
•
马蹄、豆腐、羞涩、微笑
• 二、C
三、A
• 能力提升
• 一、喜迎远客图、依依惜别图
• 二、1、在天底下，一碧千里，而并不茫茫。
2、C
3、C
拓展延伸
• 1、C
• 2、B A
• 3、它红似晚霞，可比晚霞要红得纯正；它红似枫叶，可比枫叶红得刺眼。

01.数字码序(1-3d)3077.P0241-0260.P1046汉字基本集V186

01.數字碼序(1-3d)
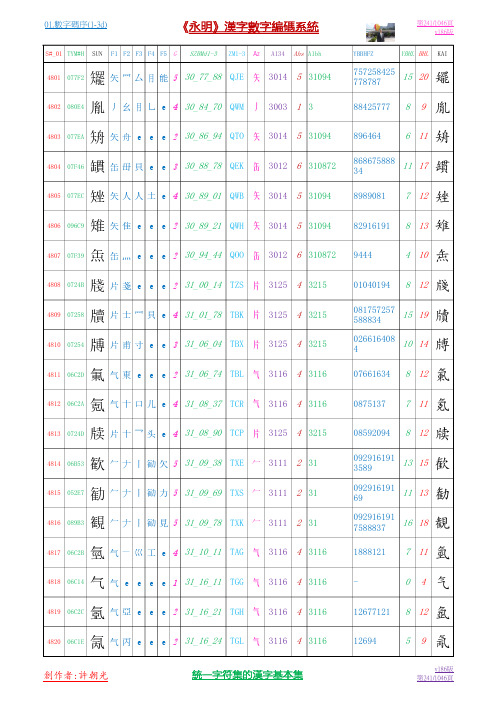
《永明》漢字數字編碼系統
F1 F2 F3 F4 F5 G
第241/1046頁 v186版 YBBHFZ
S#_01 TYM#H
SUN
SZBMd1-3
ZM1-3
Az
A134
Ahs A1bh
YBHL BHL
KAI
4801 077F2
矲胤矪罆矬雉缹牋牘牔氭氪牍歓勧観氫气氬氞
4822 06C29
4823 0520F
4824 06C19
4825 05C13
4826 07247
4827 0516A
4828 06C1D
4829 065A4
4830 06C18
4831 06C1A
4832 07248
4833 06C1B
4834 06C21
4835 07250
9 13 4 8
4836 06B23
S#_01 TYM#H
SUN
SZBMd1-3
ZM1-3
Az
A134
Ahs A1bh
YBHL BHL
KAI
4821 09880
颀氩刏氙尓片兪氝斤氘氚版氛氡牐欣氣牖牓牑
斤页 e e e 2 31_17_39 TFW 斤 3132 4 3312 气亚 e e e 2 31_17_71 TFH 气 3116 4 3116 气刂 e e e 2 31_22_22 TJJ 气 3116 4 3116 气山 e e e 2 31_22_72 TJJ 气 3116 4 3116 �� 小 e e e 2 31_24_34 TLW �� 3111 2 31 片 e e e e 1 31_25_12 TMF 片 3125 4 3215 �� ⺝巜 e e 3 31_27_88 TJE �� 3191 3 391 气内 e e e 2 31_29_64 TLS 气 3116 4 3116 斤 e e e e 1 31_32_13 TRD 斤 3132 4 3312 气介 e e e 2 31_32_22 TRJ 气 3116 4 3116 气川 e e e 2 31_32_72 TRJ 气 3116 4 3116 片⺁又 e e 3 31_33_65 TEA 片 3125 4 3215 气八刀 e e 3 31_34_53 TWC 气 3116 4 3116 气夂⺀ e e 3 31_35_92 TQU 气 3116 4 3116 片千臼 e e 3 31_38_36 TET 片 3125 4 3215 斤欠 e e e 2 31_38_59 TEX 斤 3132 4 3312 气米 e e e 2 31_40_34 TPW 气 3116 4 3116 片户甫 e e 3 31_41_06 TYB 片 3125 4 3215 片亠丷冖方 5 31_41_45 TYP 片 3125 4 3215 片户 �� e e 3 31_41_76 TYH 片 3125 4 3215

中职语文-基础模块-字音字形1

中职语文-基础模块-字音字形1-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN字音字形（基础模块）上册刮痧[shā] 敷衍[fū yǎn] 窘迫[jiǒng ] 供给[gōng jǐ] 家当[dàng] 燠热[yù rè] 证券[zhèng quàn] 污秽[huì] 笨拙[zhuō] 抽噎[ch ōu yē] 踽踽独行[jǔ] 黑黢黢[qū]箢篼[yuān dōu] 眉黛[dài] 翩然[piān ] 宁谧[mì]缥缈[piāo miǎo] 尸骸[hái] 沙砾[lì] 逶迤[wēi yí]阿訇[hōng] 苍穹[qióng] 憩息[qì] 遒劲[qiú jìng]毛骨悚然[sǒng] 饿殍[piǎo] 推搡[sǎng]寒伧[hán chen] 吮吸[shǔn ] 泅水[qiú shuǐ]围剿[wéi jiǎo]膝盖[xī gài]撅嘴[juē zuǐ]惦记[diàn jì]吆喝[yāo he]包裹[bāo guǒ]凫水[fú ] 打烊[yàng]睿智[ruì] 大抵[dǐ] 自诩[xǔ]残羹冷炙[gēng zhì]冠冕[guān miǎn] 脑髓[nǎo suǐ]蹩[bié] 炼字[liàn zì] 咬文嚼字[yǎo wén jiáo zì]憎恶[zēng wù] 孱头[càn tou] 锱铢必较[zī zhū bì jiào]岑寂[cén jì] 慰藉[wèi jiè] 刀枪剑戟[jǐ] 雾霭[wùǎi] 虹霓[hóng ní] 稠密[chóu ] 惊诧[ chà] 殷红[yān]萦绕[yíng] 不落窠臼[kē jiù] 懊丧[ào sàng] 笑靥[yè]2。

新教材苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数知识点考点重点难点归纳总结

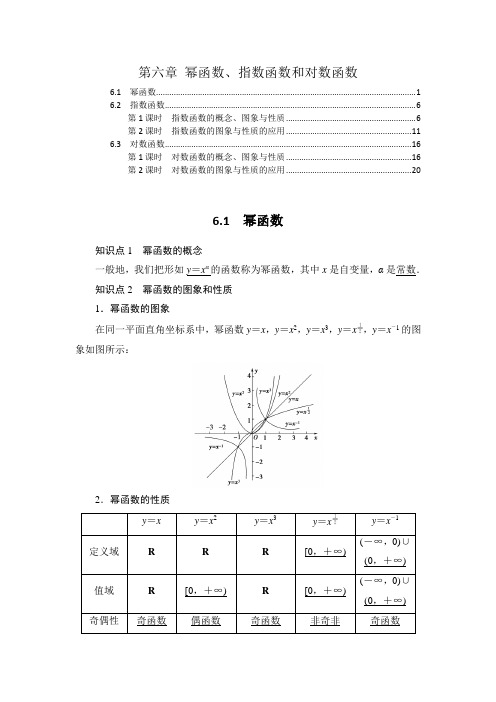
第六章幂函数、指数函数和对数函数6.1幂函数 (1)6.2指数函数 (6)第1课时指数函数的概念、图象与性质 (6)第2课时指数函数的图象与性质的应用 (11)6.3对数函数 (16)第1课时对数函数的概念、图象与性质 (16)第2课时对数函数的图象与性质的应用 (20)6.1幂函数知识点1幂函数的概念一般地，我们把形如y＝xα的函数称为幂函数，其中x是自变量，α是常数．知识点2幂函数的图象和性质1．幂函数的图象在同一平面直角坐标系中，幂函数y＝x，y＝x2，y＝x3，y＝x，y＝x－1的图象如图所示：2．幂函数的性质y＝x y＝x2y＝x3y＝x y＝x－1定义域R R R[0，＋∞)(－∞，0)∪(0，＋∞)值域R[0，＋∞)R[0，＋∞)(－∞，0)∪(0，＋∞)奇偶性奇函数偶函数奇函数非奇非奇函数偶函数单调性在(－∞，＋∞)上单调递增在(－∞，0]上单调递减，在[0，＋∞)上单调递增在(－∞，＋∞)上单调递增在[0，＋∞) 上单调递增在(－∞，0)上单调递减，在(0，＋∞)上单调递减定点(1,1)，(0,0)(1,1)，(0,0) (1,1)，(0,0) (1,1)，(0,0)(1,1)考点类型1 幂函数的概念【例1】 (1)下列函数：①y ＝x 3；②y ＝⎝ ⎛⎭⎪⎫12x；③y ＝4x 2；④y ＝x 5＋1；⑤y ＝(x －1)2；⑥y ＝x ；⑦y ＝a x (a >1)．其中幂函数的个数为( )A ．1B ．2C ．3D ．4(2)已知y ＝(m 2＋2m －2)x m2－2＋2n －3是幂函数，求m ，n 的值．(1)B [幂函数有①⑥两个．] (2)[解] 由题意得⎩⎨⎧m 2＋2m －2＝1，2n －3＝0，解得⎩⎪⎨⎪⎧m ＝－3，n ＝32或⎩⎪⎨⎪⎧m ＝1，n ＝32.所以m ＝－3或1，n ＝32.1．幂函数y ＝x α满足的三个特征 (1)幂x α前系数为1；(2)底数只能是自变量x ，指数是常数； (3)项数只有一项．2．求幂函数解析式时常用待定系数法，即设解析式为f (x )＝x α，根据条件求出α.类型2 比较大小【例2】比较下列各组数中两个数的大小： (1)⎝ ⎛⎭⎪⎫13与⎝ ⎛⎭⎪⎫14；(2)⎝ ⎛⎭⎪⎫－23－1与⎝ ⎛⎭⎪⎫－35－1； (3)0.25与6.25；(4)1.20.6与0.30.4；(5)(－3)与(－2).[思路点拨] 可以借助幂函数y ＝x 2的单调性或化为同指数或借助于中间量进行比较．[解] (1)∵y ＝x 是[0，＋∞)上的增函数，且13>14， ∴⎝ ⎛⎭⎪⎫13>⎝ ⎛⎭⎪⎫14. (2)∵y ＝x －1是(－∞，0)上的减函数，且－23<－35，∴⎝ ⎛⎭⎪⎫－23－1>⎝ ⎛⎭⎪⎫－35－1. (3)0.25＝⎝ ⎛⎭⎪⎫14＝2，6．25＝2.5.∵y ＝x 是[0，＋∞)上的增函数，且2<2.5， ∴2<2.5，即0.25<6.25.(4)由幂函数的单调性，知1.20.6>10.6＝1,0.30.4<10.4＝1，从而0.30.4<1.20.6. (5)由幂函数的奇偶性，(－3)＝3>0，(－2)＝－2<0，所以(－3)>(－2).比较幂值的大小，关键在于构造适当的函数(1)若指数相同而底数不同，则构造幂函数；若指数相同、底数不在同一单调区间，则用奇偶性；(2)若指数与底数都不同，需考虑是否能把指数化为相同，是否可以引入中间量．类型3 幂函数的图象及应用【例3】点(2，2)与点⎝ ⎛⎭⎪⎫－2，－12分别在幂函数f (x )，g (x )的图象上，问当x 为何值时，有：(1)f (x )>g (x )；(2)f (x )＝g (x )；(3)f (x )<g (x )． [解] 设f (x )＝x α，g (x )＝x β. ∵(2)α＝2，(－2)β＝－12， ∴α＝2，β＝－1，∴f (x )＝x 2，g (x )＝x －1.分别作出它们的图象，如图所示．由图象知，(1)当x ∈(－∞，0)∪(1，＋∞)时，f (x )>g (x )； (2)当x ＝1时，f (x )＝g (x )； (3)当x ∈(0,1)时，f (x )<g (x )．1．解决幂函数图象问题应把握研究一般的方法 (1)求幂函数的定义域，再判定奇偶性；(2)先研究第一象限的图象与性质，再根据奇偶性(对称性)研究其它象限的图象．2．幂函数在第一象限的图象与性质(1)α>0，幂函数的图象恒经过(0,0)，(1,1)，在[0，＋∞)是增函数． (2)α<0，幂函数的图象恒经过(1,1)，在(0，＋∞)上是减函数． 3．幂函数图象在第一象限内随指数变化而变化的规律(1)在第一象限内直线x ＝1的右侧，图象从上到下，相应的指数由大变小；(2)在第一象限内直线x ＝1的左侧，图象从下到上，相应的指数由大变小．类型4 幂函数性质的综合应用【例4】已知幂函数y ＝x 3m －9(m ∈N *)的图象关于y 轴对称，且在(0，＋∞)上单调递减，求满足(a ＋1)<(3－2a )的a 的取值范围．1．函数图象关于y 轴对称，函数有怎样的奇偶性？ [提示] 偶函数． 2．x>y时，x 、y 与0的大小关系有多少种？[提示] 0<x <y ，x <y <0，x >0>y .[解] ∵函数在(0，＋∞)上递减，∴3m －9<0，解得m <3. 又m ∈N *，∴m ＝1,2.又函数图象关于y 轴对称，∴3m －9为偶数，故m ＝1. ∴有(a ＋1)<(3－2a ).∵y ＝x在(－∞，0)，(0，＋∞)上均递减，∴a ＋1>3－2a >0或0>a ＋1>3－2a ，或a ＋1<0<3－2a ，解得23<a <32或a <－1. 所以a 的取值范围为(－∞，－1)∪⎝ ⎛⎭⎪⎫23，32.1．本题在解答过程中易出现忽略对底数的分类讨论而产生漏解． 2．求解此类题目的关键是弄清幂函数的概念及幂函数的性质．解决此类问题可分为两大步：第一步，研究幂函数的奇偶性(图象对称性)、第一象限的图象的单调性求出m 的值或范围；第二步，利用分类讨论的思想，结合函数的图象求出参数a 的取值范围．6.2指数函数第1课时指数函数的概念、图象与性质知识点1指数函数的概念一般地，函数y＝a x(a>0，a≠1)叫作指数函数，它的定义域是R.知识点2指数函数的图象和性质a>10<a<1图象性质定义域R值域(0，＋∞)定点图象过点(0,1)，图象在x轴的上方函数值的变化x>0时，y>1；x<0时，0<y<1x>0时，0<y<1；x<0时，y>1单调性在(－∞，＋∞)上是增函数在(－∞，＋∞)上是减函数奇偶性非奇非偶函数1.指数函数y＝a x(a>0且a≠1)的图象“升”“降”主要取决于什么？[提示]指数函数y＝a x(a>0且a≠1)的图象“升”“降”主要取决于字母a.当a>1时，图象具有上升趋势；当0<a<1时，图象具有下降趋势．2.为什么底数应满足a>0且a≠1?[提示]①当a≤0时，a x可能无意义；②当a>0时，x可以取任何实数；③当a＝1时，a x＝1(x∈R)，无研究价值．因此规定y＝a x中a>0，且a≠1.考点类型1指数函数的概念【例1】(1)下列函数中，是指数函数的个数是()①y＝(－8)x；②y＝2x2－1；③y＝a x；④y＝2·3x.A ．1B ．2C ．3D ．0(2)已知函数f (x )为指数函数，且f ⎝ ⎛⎭⎪⎫－32＝39，则f (－2)＝________.(1)D (2)19 [(1)①中底数－8<0，所以不是指数函数； ②中指数不是自变量x ，而是x 的函数，所以不是指数函数；③中底数a ，只有规定a >0且a ≠1时，才是指数函数； ④中3x 前的系数是2，而不是1，所以不是指数函数，故选D.(2)设f (x )＝a x (a >0且a ≠1)，由f ⎝ ⎛⎭⎪⎫－32＝39得a －32＝39，所以a ＝3，又f (－2)＝a －2，所以f (－2)＝3－2＝19.]1．判断一个函数是否为指数函数，要牢牢抓住3点 (1)底数是大于0且不等于1的常数；(2)指数函数的自变量必须位于指数的位置上； (3)a x 的系数必须为1.2．求指数函数的解析式常用待定系数法．类型2 利用单调性比较大小【例2】比较下列各组数的大小： (1)⎝ ⎛⎭⎪⎫34－1.8与⎝ ⎛⎭⎪⎫34－2.6；(2)⎝ ⎛⎭⎪⎫58与1； (3)0.6－2与⎝ ⎛⎭⎪⎫43；(4)⎝ ⎛⎭⎪⎫130.3与3－0.2；(5)0.20.6与0.30.4；(6) ⎝ ⎛⎭⎪⎫23，⎝ ⎛⎭⎪⎫23，⎝ ⎛⎭⎪⎫25.[思路点拨] 观察底数是否相同(或能化成底数相同)，若相同用单调性，否则结合图象或中间值来比较大小．[解] (1)∵0<34<1，y ＝⎝ ⎛⎭⎪⎫34x在定义域R 内是减函数，－1.8>－2.6， ∴⎝ ⎛⎭⎪⎫34－1.8<⎝ ⎛⎭⎪⎫34－2.6.(2)∵0<58<1，∴y ＝⎝ ⎛⎭⎪⎫58x在定义域R 内是减函数．又∵－23<0， ∴⎝ ⎛⎭⎪⎫58>⎝ ⎛⎭⎪⎫580＝1， ∴⎝ ⎛⎭⎪⎫58>1.(3)∵0.6－2>0.60＝1，⎝ ⎛⎭⎪⎫43<⎝ ⎛⎭⎪⎫430＝1， ∴0.6－2>⎝ ⎛⎭⎪⎫43.(4)∵⎝ ⎛⎭⎪⎫130.3＝3－0.3，y ＝3x 在定义域R 内是增函数，又∵－0.3<－0.2， ∴3－0.3<3－0.2，∴⎝ ⎛⎭⎪⎫130.3<3－0.2.(5)由幂函数的单调性，知0.20.6<0.30.6，又y ＝0.3x 是减函数，∴0.30.4>0.30.6，从而0.20.6<0.30.4.(6)∵f (x )＝⎝ ⎛⎭⎪⎫23x 在R 上为减函数，∴⎝ ⎛⎭⎪⎫23<⎝ ⎛⎭⎪⎫23， ∵f (x )＝x 在(0，＋∞)上为增函数，∴⎝ ⎛⎭⎪⎫23>⎝ ⎛⎭⎪⎫25，所以⎝ ⎛⎭⎪⎫23>⎝ ⎛⎭⎪⎫23>⎝ ⎛⎭⎪⎫25.在进行指数式的大小比较时，可以归纳为以下3类 (1)底数同、指数不同：利用指数函数的单调性解决． (2)底数不同、指数同：利用幂函数的单调性解决．(3)底数不同、指数也不同：采用介值法．以其中一个的底为底，以另一个的指数为指数．比如a c 与b d ，可取a d ，前者利用单调性，后者利用图象．类型3 利用指数函数的单调性解不等式【例3】 (1)解不等式⎝ ⎛⎭⎪⎫123x －1≤2；(2)已知ax 2－3x ＋1<a x ＋6(a >0，且a ≠1)． [解] (1)∵2＝⎝ ⎛⎭⎪⎫12－1，∴原不等式可以转化为⎝ ⎛⎭⎪⎫123x －1≤⎝ ⎛⎭⎪⎫12－1. ∵y ＝⎝ ⎛⎭⎪⎫12x在R 上是减函数，∴3x －1≥－1，∴x ≥0，故原不等式的解集为{x |x ≥0}． (2)分情况讨论①当0<a <1时，函数f (x )＝a x (a >0，a ≠1)在R 上为减函数， ∴x 2－3x ＋1>x ＋6， ∴x 2－4x －5>0，根据相应二次函数的图象可得x <－1或x >5.②当a >1时，函数f (x )＝a x (a >0，a ≠1)在R 上是增函数． ∴x 2－3x ＋1<x ＋6，∴x 2－4x －5<0. 根据相应二次函数的图象可得－1<x <5，综上所述当0<a <1时，x <－1或x >5，当a >1时，－1<x <5.1．形如a x >a y 的不等式，借助y ＝a x 的单调性求解，如果a 的取值不确定，需分a ＞1与0＜a ＜1两种情况讨论．2．形如a x ＞b 的不等式，注意将b 化为以a 为底的指数幂的形式，再借助y ＝a x 的单调性求解．类型4 图象变换及其应用【例4】 (1)函数y ＝3－x 的图象是________．(填序号)(2)已知0＜a ＜1，b ＜－1，则函数y ＝a x ＋b 的图象必定不经过第________象限．(3)函数f (x )＝2a x ＋1－3(a ＞0且a ≠1)的图象恒过定点________． [思路点拨] 题(1)中可将y ＝3－x转化为y ＝⎝ ⎛⎭⎪⎫13x.题(2)中，函数y ＝a x ＋b 的图象过点(0,1＋b )，因为b ＜－1，所以点(0,1＋b )在y 轴负半轴上．题(3)应该根据指数函数经过定点求解．(1)② (2)一 (3)(－1，－1) [(1)y ＝3－x ＝⎝ ⎛⎭⎪⎫13x 为单调递减的指数函数，其图象为②.(2)函数y ＝a x (0＜a ＜1)在R 上单调递减，图象过定点(0,1)，所以函数y ＝a x ＋b 的图象在R 上单调递减，且过点(0,1＋b )．因为b ＜－1，所以点(0,1＋b )在y 轴负半轴上，故图象不经过第一象限．(3)令x ＋1＝0，得x ＝－1，此时y ＝2a 0－3＝－1，故图象恒过定点(－1，－1)．]1．处理函数图象问题的策略(1)抓住特殊点：指数函数的图象过定点(0,1)．(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)． (3)利用函数的性质：奇偶性与单调性． 2．指数型函数图象过定点问题的处理方法求指数型函数图象所过的定点时，只要令指数为0，求出对应的y 的值，即可得函数图象所过的定点．第2课时指数函数的图象与性质的应用知识点指数型函数形如y ＝ka x (k ∈R ，且k ≠0，a >0且a ≠1)的函数是一种指数型函数，这是一种非常有用的函数模型．设原有量为N ，每次的增长率为p ，经过x 次增长，该量增长到y ，则y ＝N (1＋p )x (x ∈N )．考点类型1 求函数的定义域、值域【例1】求下列函数的定义域和值域： (1)y ＝2；(2)y ＝1－2x；(3)y ＝⎝ ⎛⎭⎪⎫12x 2－2x －3；(4)y ＝4x ＋2x ＋2－3.[解] (1)由x －4≠0，得x ≠4，故y ＝2的定义域为{x |x ≠4}．又1x －4≠0，即2≠1，故y ＝2的值域为{y |y >0，且y ≠1}．(2)由1－2x ≥0，得2x ≤1，∴x ≤0， ∴y ＝1－2x 的定义域为(－∞，0]．由0<2x ≤1，得－1≤－2x <0， ∴0≤1－2x <1，∴y ＝1－2x 的值域为[0,1)． (3)y ＝⎝ ⎛⎭⎪⎫12x 2－2x －3的定义域为R .∵x 2－2x －3＝(x －1)2－4≥－4， ∴⎝ ⎛⎭⎪⎫12 x 2－2x －3≤⎝ ⎛⎭⎪⎫12－4＝16. 又∵⎝ ⎛⎭⎪⎫12x 2－2x －3>0，故函数y ＝⎝ ⎛⎭⎪⎫12x 2－2x －3的值域为(0,16]．(4)函数 y ＝4x ＋2x ＋2－3的定义域为R .设t ＝2x ，则t >0.所以y ＝t 2＋4t －3＝(t ＋2)2－7，t >0. 因为函数y ＝t 2＋4t －3＝(t ＋2)2－7在(0，＋∞)为增函数，所以y >－3，即函数的值域为(－3，＋∞)．1．若将本例(2)中函数换为y ＝⎝ ⎛⎭⎪⎫13x－1，求其定义域． [解] 由⎝ ⎛⎭⎪⎫13x －1≥0得⎝ ⎛⎭⎪⎫13x ≥⎝ ⎛⎭⎪⎫130，∴x ≤0即函数的定义域为(－∞，0]．2．若将本例(4)增加条件“0≤x ≤2”再求函数的值域．[解] 由于x ∈[0,2]则2x ＝t ∈[1,4]，所以y ＝t 2＋4t －3＝(t ＋2)2－7.t ∈[1,4]，∵函数y ＝t 2＋4t －3＝(t ＋2)2－7在[1,4]为增函数．故y ∈[2,29]．1．对于y ＝a f (x )这类函数(1)定义域是指使f (x )有意义的x 的取值范围． (2)值域问题，应分以下两步求解： ①由定义域求出u ＝f (x )的值域；②利用指数函数y ＝a u 的单调性或利用图象求得函数的值域．2．对于y ＝m (a x )2＋n (a x )＋p (m ≠0)这类函数值域问题，利用换元法，借助二次函数求解．类型2 指数型函数的应用题【例2】某市现有人口总数为100万人，如果年平均增长率为1.2%，试解答下列问题：(1)试写出x 年后该城市人口总数y (万人)与年份x (年)之间的函数关系式； (2)计算10年后该城市人口总数(精确到1万人)．(参考数据：1.01210≈1.127) [思路点拨] 本题考查有关增长率的问题，若设原来人口总数为N ，年平均增长率为p ，则对于x 年后的人口总数y ，可以用y ＝N (1＋p )x 表示．[解] (1)1年后城市人口总数为： y ＝100＋100×1.2%＝100(1＋1.2%)．2年后城市人口总数为：y ＝100×(1＋1.2%)＋100×(1＋1.2%)×1.2% ＝100(1＋1.2%)2，同理3年后城市人口总数为y ＝100(1＋1.2%)3， …故x 年后的城市人口总数为y ＝100(1＋1.2%)x . (2)10年后该城市人口总数为：y ＝100(1＋1.2%)10＝100×1.01210≈100×1.127 ≈113(万人)．故10年后该城市人口总数约为113万人．解决实际应用题的步骤(1)领会题意，并把题中的普通语言转化为数学语言；(2)根据题目要求，分析量与量之间的关系，建立恰当的函数模型，并注意对变量的限制条件，加以概括；(3)对已经“数学化”的问题用所学的数学知识处理，求出解；(4)检验：将数学问题的解代入实际问题检查，舍去不符合题意的解，并作答．类型3 指数函数性质的综合应用【例3】已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋a 是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围； (3)求f (x )在[－1,2]上的值域．[思路点拨] (1)根据奇函数的定义，求出a ，b .(2)利用单调性和奇偶性去掉“f ”解不等式求k 的范围．(3)利用(2)中单调性求f (x )的值域．[解] (1)∵函数y ＝f (x )是定义域R 上的奇函数， ∴⎩⎨⎧f (0)＝0，f (－1)＝－f (1)，∴⎩⎪⎨⎪⎧－1＋b 2＋a ＝0，－2－1＋b 20＋a ＝－－21＋b 22＋a ，∴b ＝1，a ＝2.(2)由(1)知f (x )＝1－2x 2(2x ＋1)＝－12＋12x ＋1，设x 1，x 2∈R 且x 1<x 2，则f (x 2)－f (x 1)＝12x 2＋1－12x 1＋1＝2x 1－2x 2(2x 2＋1)(2x 1＋1)<0， ∴f (x )在定义域R 上为减函数，由f (t 2－2t )＋f (2t 2－k )<0恒成立，可得f (t 2－2t )<－f (2t 2－k )＝f (k －2t 2)， ∴t 2－2t >k －2t 2， ∴3t 2－2t －k >0恒成立，∴Δ＝(－2)2＋12k <0，解得k <－13， ∴k 的取值范围为⎝ ⎛⎭⎪⎫－∞，－13.(3)由(2)知f (x )在R 上单调递减， ∴f (x )在[－1,2]上单调递减，∴f (x )max ＝f (－1)＝－12＋11＋12＝16，f (x )min ＝f (2)＝－12＋14＋1＝－310，∴f (x )的值域为⎣⎢⎡⎦⎥⎤－310，16.与指数函数有关的综合应用问题往往涉及到指数函数的定义域、值域、单调性、奇偶性、最值(值域)等问题，求解时可充分借助已学的知识逐项求解．类型4 复合函数的单调性【例4】判断f (x )＝⎝ ⎛⎭⎪⎫13x 2－2x的单调性，并求其值域．y ＝⎝ ⎛⎭⎪⎫13x与y ＝x 2－2x 的单调性分别如何？ [提示] y ＝⎝ ⎛⎭⎪⎫13x单调递减．y ＝x 2－2x 在(－∞，1]上单调递减，在[1，＋∞)上单调递增．[解] 令u ＝x 2－2x ，则原函数变为y ＝⎝ ⎛⎭⎪⎫13u.∵u ＝x 2－2x ＝(x －1)2－1在(－∞，1]上递减，在[1，＋∞)上递增，又∵y ＝⎝ ⎛⎭⎪⎫13u在(－∞，＋∞)上递减，∴y ＝⎝ ⎛⎭⎪⎫13x 2－2x 在(－∞，1]上递增，在[1，＋∞)上递减．∵u ＝x 2－2x ＝(x －1)2－1≥－1， ∴y ＝⎝ ⎛⎭⎪⎫13u，u ∈[－1，＋∞)，∴0<⎝ ⎛⎭⎪⎫13u ≤⎝ ⎛⎭⎪⎫13－1＝3，∴原函数的值域为(0,3]．1．关于指数型函数y ＝a f (x )(a >0，且a ≠1)，它由两个函数y ＝a u ，u ＝f (x )复合而成．其单调性由两点决定，一是底数a >1还是0<a <1；二是f (x )的单调性．2．求这种指数型函数的单调区间，首先求出函数的定义域，然后把函数分解成y ＝f (u )，u ＝φ(x )，通过考查f (u )和φ(x )的单调性，求出y ＝f (φ(x ))的单调性，其规则是“同增异减”．6.3对数函数第1课时对数函数的概念、图象与性质知识点1对数函数的概念一般地，函数y＝log a x(a>0，a≠1)叫作对数函数，它的定义域是(0，＋∞)．1.函数y＝2log3x，y＝log3(2x)是对数函数吗？[提示]不是，其不符合对数函数的形式．知识点2对数函数的图象与性质a>10<a<1图象性质定义域：(0，＋∞)值域：R图象过定点(1,0)在(0，＋∞)上是增函数当0<x<1时，y<0；当x>1时，y>0在(0，＋∞)上是减函数当0<x<1时，y>0；当x>1时，y<02.对数函数的“上升”或“下降”与谁有关？[提示]底数a与1的关系决定了对数函数的升降．当a>1时，对数函数的图象“上升”，当0<a<1时，对数函数的图象“下降”．知识点3反函数(1)对数函数y＝log a x(a>0，a≠1)和指数函数y＝a x(a>0，a≠1)互为反函数，它们的图象关于y＝x对称．(2)一般地，如果函数y＝f(x)存在反函数，那么它的反函数记作y＝f－1(x)．(3)互为反函数的两个函数的图象关于直线y＝x对称．(4)原函数y＝f(x)的定义域是它的反函数y＝f－1(x)的值域；原函数y＝f(x)的值域是它的反函数y＝f－1(x)的定义域．考点类型1对数函数的概念【例1】判断下列函数是否是对数函数？并说明理由．(1)y＝log a x2(a＞0，且a≠1)；(2)y＝log2x－1；(3)y＝2log8x；(4)y＝log x a(x＞0，且x≠1)．[思路点拨]依据对数函数的定义来判断．[解](1)中真数不是自变量x，∴不是对数函数；(2)中对数式后减1，∴不是对数函数；(3)中log8x前的系数是2，而不是1，∴不是对数函数；(4)中底数是自变量x，而不是常数a，∴不是对数函数．一个函数是对数函数，必须是形如y＝log a x(a＞0且a≠1)的形式，即必须满足以下条件：(1)系数为1；(2)底数为大于0且不等于1的常数；(3)对数的真数仅有自变量x.类型2对数函数的定义域【例2】求下列函数的定义域．(1)f(x)＝1log12x＋1；(2)f(x)＝12－x＋ln(x＋1)；(3)f(x)＝log(2x－1)(－4x＋8)；(4)f (x )＝x ln(1－2x )．[解] (1)要使函数f (x )有意义，则log 12 x ＋1>0，即log 12 x >－1，解得0<x <2，即函数f (x )的定义域为(0,2)．(2)要使函数式有意义需满足⎩⎨⎧ x ＋1>0，2－x >0，即⎩⎨⎧x >－1，x <2，解得－1<x <2，故函数的定义域为(－1,2)．(3)由题意得⎩⎨⎧－4x ＋8>0，2x －1>0，2x －1≠1，解得⎩⎪⎨⎪⎧x <2，x >12，x ≠1，故函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <2，且x ≠1. (4)由题意知⎩⎨⎧x ≥0，1－2x >0，解得0≤x <12，∴定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0≤x <12.求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数；三是按底数的取值应用单调性，有针对性地解不等式．类型3 比较对数式的大小【例3】比较下列各组值的大小： (1)log 534与log 543； (2)log 13 2与log 15 2；(3)log 23与log 54.[解] (1)法一(单调性法)：对数函数y ＝log 5x 在(0，＋∞)上是增函数，而34<43，所以log 534<log 543.法二(中间值法)：因为log 534<0，log 543>0，所以log534<log543.(2)法一(单调性法)：由于log132＝1log213，log152＝1log215，又因对数函数y＝log2x在(0，＋∞)上是增函数，且13>15，所以0>log213>log215，所以1log213<1log215，所以log132<log152.法二(图象法)：如图，在同一坐标系中分别画出y＝log13x及y＝log15x的图象，由图易知：log132<log152.(3)取中间值1，因为log23>log22＝1＝log55>log54，所以log23>log54.比较对数值大小的常用方法(1)同底数的利用对数函数的单调性．(2)同真数的利用对数函数的图象或用换底公式转化．(3)底数和真数都不同，找中间量．提醒：比较数的大小时先利用性质比较出与零或1的大小．第2课时对数函数的图象与性质的应用知识点图象变换(1)平移变换当b＞0时，将y＝log a x的图象向左平移b个单位，得到y＝log a(x＋b)的图象；向右平移b个单位，得到y＝log a(x－b)的图象．当b＞0时，将y＝log a x的图象向上平移b个单位，得到y＝log a x＋b的图象，将y＝log a x的图象向下平移b个单位，得到y＝log a x－b的图象．(2)对称变换要得到y＝log a 1x的图象，应将y＝log a x的图象关于x轴对称．考点类型1与对数函数相关的图象【例1】作出函数y＝|log2 (x＋2)|＋4的图象，并指出其单调增区间．[解]步骤如下：(1)作出y＝log2x的图象，如图(1)．(2)将y＝log2x的图象沿x轴向左平移2个单位得到y＝log2 (x＋2)的图象，如图(2)．(3)将y＝log2(x＋2)的图象在x轴下方的图象以x轴为对称轴翻折到x轴的上方，得到y＝|log2 (x＋2)|的图象，如图(3)．(4)将y＝|log2(x＋2)|的图象沿y轴方向向上平移4个单位，得到y＝|log2(x ＋2)|＋4的图象，如图(4)．由图可知，函数的单调增区间为[－1，＋∞)．1．已知y＝f(x)的图象，求y＝|f(x＋a)|＋b的图象步骤如下：y＝f(x)→y＝f(x＋a)→y＝|f(x＋a)|→y＝|f(x＋a)|＋b.2．已知y＝f(x)的图象，求y＝|f(x＋a)＋b|的图象，步骤如下：y＝f(x)→y＝f(x＋a)→y＝f(x＋a)＋b→y＝|f(x＋a)＋b|.以上可以看出，作含有绝对值号的函数图象时，先将绝对值号内部的图象作出来，再进行翻折，内部变换的顺序是先变换x，再变换y.类型2值域问题x的定义域为[2,4]，则函数f(x)的值域是【例2】(1)已知函数f(x)＝2log12________．(2)求函数f(x)＝log2(－x2－4x＋12)的值域．x在定义域[2,4]上为减函数求解．[思路点拨](1)中利用f(x)＝2log12(2)中注意考虑真数－x2－4x＋12的范围．x在[2,4]上为减函数，(1)[－4，－2][∵f(x)＝2log122＝－2；∴x＝2时，f(x)max＝2log124＝－4.x＝4时，f(x)min＝2log12∴f(x)的值域为[－4，－2]．](2)[解]∵－x2－4x＋12＞0，又∵－x2－4x＋12＝－(x＋2)2＋16≤16，∴0＜－x2－4x＋12≤16，故log2(－x2－4x＋12)≤log216＝4，∴函数的值域为(－∞，4]．求函数值域或最大(小)值的常用方法(1)直接法根据函数解析式的特征，从函数自变量的变化范围出发，通过对函数定义域、性质的观察，结合解析式，直接得出函数值域．(2)配方法当所给的函数是二次函数或可化为二次函数形式的(形如y ＝a [f (x )]2＋bf (x )＋c )，求函数值域问题时，可以用配方法．(3)单调性法根据在定义域(或定义域的某个子集)上的单调性，求出函数的值域．(4)换元法求形如y ＝log a f (x )型函数值域的步骤：①换元，令u ＝f (x )，利用函数图象和性质求出u 的范围；②利用y ＝log a u 的单调性、图象，求出y 的取值范围．类型3 对数函数的综合问题【例3】已知函数f (x )＝lg (2－x )－lg (2＋x )．(1)求值：f ⎝ ⎛⎭⎪⎫12 021＋f ⎝ ⎛⎭⎪⎫－12 021； (2)判断f (x )的奇偶性；(3)判断函数的单调性并用定义证明．[思路点拨] (1)利用代入法求解，(2)(3)用定义法判断奇偶性和单调性．[解] (1)f ⎝ ⎛⎭⎪⎫12 021＋f ⎝ ⎛⎭⎪⎫－12 021＝lg ⎝ ⎛⎭⎪⎫2－12 021－lg ⎝ ⎛⎭⎪⎫2＋12 021＋lg ⎝ ⎛⎭⎪⎫2＋12 021－lg ⎝ ⎛⎭⎪⎫2－12 021＝0. (2)由题知⎩⎨⎧2－x >0，2＋x >0⇒－2<x <2，又f (－x )＝lg (2＋x )－lg (2－x )＝－f (x )，∴f (x )为奇函数．(3)设－2<x 1<x 2<2，f (x 1)－f (x 2)＝lg 2－x 12＋x 1－lg 2－x 22＋x 2＝lg (2－x 1)(2＋x 2)(2＋x 1)(2－x 2)， ∵(2－x 1)(2＋x 2)－(2＋x 1)(2－x 2)＝4(x 2－x 1)>0.又(2－x 1)(2＋x 2)>0，(2＋x 1)(2－x 2)>0，∴(2－x 1)(2＋x 2)(2＋x 1)(2－x 2)>1，∴lg (2－x 1)(2＋x 2)(2＋x 1)(2－x 2)>0.从而f (x 1)>f (x 2)，故f (x )在(－2,2)上为减函数．对数函数性质的综合应用(1)常见的命题方式对数函数常与函数的奇偶性、单调性、最大(小)值以及不等式等问题综合命题，求解中通常会涉及对数运算．(2)解此类问题的基本思路首先要将所给的条件进行转化，然后结合涉及的知识点，明确各知识点的应用思路、化简方向，与所求目标建立联系，从而找到解决问题的思路．类型4 解对数不等式【例4】解下列关于x 的不等式： (1)log 17 x >log 17(4－x )； (2)log a (2x －5)>log a (x －1)．[解] (1)由题意可得⎩⎨⎧ x >0，4－x >0，x <4－x ，解得0<x <2.所以原不等式的解集为{x |0<x <2}．(2)当a >1时，原不等式等价于⎩⎨⎧ 2x －5>0，x －1>0，2x －5>x －1.解得x >4. 当0<a <1时，原不等式等价于⎩⎨⎧ 2x －5>0，x －1>0，2x －5<x －1，解得52<x <4. 综上所述，当a >1时，原不等式的解集为{x |x >4}；当0<a <1时，原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 52<x <4.对数不等式的三种考查类型及解法(1)形如log a x>log a b的不等式，借助y＝log a x的单调性求解，如果a的取值不确定，需分a>1与0<a<1两种情况进行讨论．(2)形如log a x>b的不等式，应将b化为以a为底数的对数式的形式(b＝log a a b)，再借助y＝log a x的单调性求解．(3)形如log f(x)a>log g(x)a(f(x)，g(x)>0且不等于1，a>0)的不等式，可利用换底公式化为同底的对数进行求解，或利用函数图象求解．。

民国时期云南省昆明市历任市长生平述略

返故里。于１４年４月２１日逝世。终年６岁。２９２第十七任昆明市政府市长 — — 熊从周熊从周（７ — １４年）心畲，南玉溪新侣８９６字云
地，培养农政人才奠定基础。曾兼任成德中学校为
校，孙中山革命思想影响，在校编写《命军周受曾革
刊》，又联络同学发起组织《范学报》，统３年后师宣
（９参加云南 “ 九 ” 义。１１１１１）重起９３年毕业后，祥偕云杨文清赴北京考入农商部农政专ｆ２学校农政系，
禺县县长、南盐津、平、安（水）江川、良云新临建、陆
县县长，３Ｔ４月至１３年７月任昆明市市１１ｚ－９－３９
长。
修筑乡村道路，立青年会、女会、耆老会，成妇考移风易＇，办集体婚礼，导妇女留短发，缠足，Ｎ－举倡禁戒赌博，吸烟（片）建体育场，展体育活动，禁鸦，开
于初勘中熟界情，辞令，识面广，华超人，善知才国民政府即简任其继任中国委员（使级）为中方全大，
权代表率云南为之专配的护卫部队腾永独立营及随员，班洪与英方委员会晤。会勘中，方证据确赴中

“12371党建信息平台”网上组织转接简要指南

“12371党建信息平台”⽹上组织转接简要指南12371党建信息平台”⽹上组织转接简要指南1党员本⼈申请党员从12371⾸页进⾏登录，进⼊我的⽀部，按钮，点击之后右侧页⾯如下：点击.S≡皱珈按钮，跳转到如下页⾯:样爼奴矣蒋—性创碧碍菲党内娈考鮭⼿机13933937^67 甩话所在⽀理?≡ESJ??≡S⼯作单位liE正就员许翱?^≡' il-Z rr_?冃的Jt区去庆市J iflj?∣S⽬的轴區⾃的盍带 1 √ iB??扎⽬的⽀部St α.ooDfl(^? 已率轉I H Φ?ifrΛ LCS0■ ?tS^??(SΞ然后点击ι-S?r?fiι??≡PjaLS:-各舷部和貫裘退⾏审批芫举3.覚超IJ⽬的覚⽀部报到注册填写相关信息，点击“提交”完成操作2组织关系代转在党员不便上⽹的情况下，⽀部管理员可代党员提出转接申请。

管理员使⽤“组织关系-> 组织关系代转”打开如下界⾯:选詹宾员…】兌员貴Si 正戲甜 I t SJ 與Ai 送徉⽬的地区affifcci SsSni爭孟.≠r；恃总刁 2.?F∏O JX ：-j≤'l填写相关信息，点击“提交”完成操作3组织关系审批管理员接⼊后台，点击“组织关系-> 组织关系审批”，如下:l^*l?丰机号码宝空市tt 1E?E 兌资般列背⽆器亞记⽰狀j?i?认<∣ ffiβΛS 的⽀部SKAASI 正式兌贯ft 射宜期?!春暫⽆ X^gP 中#匾庄市剝I 胞地⽅l?春后机⾐登员合侃关⼀吏忠 Ift*β⼿机号码恥系电话 RS 地JItl?ffi??SJ 由∣?ft市內转细观丢系A ^Si?λ.科箍■动正式覓员中共更伕芾永.IM 电HJ ⽅乐欝.甌展密员童中??≡r∏?J ∣IE?⽅寝黔冏机壬竟员誉机关*：中共■佞帛感中共盲冏∣≡J 颐关⼯⽫需站 Q斎险⽬的圍⽬如価底市】IS ⽆致雷记录因⼯IEi 聊畑堀坦去蒂从永川区抱⽅幅社員机关蚕昂芒机Λ-修到曲共⽣庶市百厲机J ；⼯作委E 主J?1?S 因fi?*?中≡?i ∣≡?J ∣ IEiesi??l3t ∣l≠S⁄3.?Λ?-≡S - [2o ια⁄7Λ?J ：同倉谗岡斓坝关来MifdIl 区地⽅視箝smfi?fi?-??κ ?≡?±t??i? ⼝ IS 机夬⼯作吾番员合中 ?SF?r1i?Jι∣ lEJ?Kfi?ISWl≠? 员合 [5QiaZ7⁄l^] S 冋:S 上J ra?本镇意⽫J iSW≡W^S!?l[ 办I a LhlK??H?可辱岀介铝f? [ 是⾈⼆j如审批通过，点击页⾯下⽅的“办理”按钮通过审批，办j ??1F中币JJai !宙Qr HriHil?1Π?1*Φcπ? ?r=mrιrIil型⼖S= i 坤呻氓gw JPN lul ~ I-—点击待审批记录上的“进⾏审批”按钮，如下:申清审批I1党员粪怕⽀器⽬的粗级±-WΦ?申请⽇期 Sir■'正式党中共≡∣A≡永H I 区地⽅稅劳局机美委中共垂底击亘屋机关⼯中共垂丽永川区地万稅劳局员员敬关⼀芟制作?ra ?机关鑒员会19接⼊审批页⾯如下:亟回咒员详博pχ3?j?s理结束后可导出介绍信（需要安装 PDF 浏览器，主要⽤于市外转接），反之则点击“退办”按钮。

36孤立奇点的分类

解析，则称∞点为f(z)的一个孤立奇点。
可令 1
z
则
f
(z)
f
1
(
)
→在ξ平面上，ξ=0为φ(ξ)的孤立奇点
f
(z) ak zk
k
k
ak
1
k
bk k
k
( )
其中 ak=b-k
即 φ(ξ)在原点去心邻域展开式中的负幂项系数 = f(z)在无穷远点去心邻域展开式中的正幂项系数
→ ∞点为本性奇点， a-1=0→留数为零
五、支点
对于多值函数，在支点处各单值分支值相同，则在支点的邻域内无法将各单值分支分开，即支点的导数无法定义，所以，支点必是奇点。
正幂部分称为解析(正则)部分，负幂部分称为主要 (无限)部分：
特别地：a-1称为f(z)在z0点的留数。
1)无主要部分：z0称为f(z)的可去奇点；
2)有限项主要部分：z0称为f(z)的极点，若主要部
分为
am (z z0 )m ... a2 (z z0 )2 a1(z z0 )1
则z0称为m阶极点； 3)无限多项主要部分：z0称为本性奇点；
am 0
f (z) am (z z0 )m ... a1(z z0 )1 a0 a1(z z0 ) ...
(zLeabharlann 1 z0 )mam ... a1(z z0 )m1 a0 (z z0 )m ...
(z)
(z z0 )m
则(z0 ) am 0
3) 极点处 lim f (z) zz0
如： f (z) sin z 1 z2 z4 ... (0 | z | )
z
3! 5!
sin z
f1(z)

专题07 函数中的双变量问题(学生版) -2025年高考数学压轴大题必杀技系列导数

专题7 函数中的双变量问题函数与导数一直是高考中的热点与难点, 近几年高考试卷及各地模拟试卷中常出现在函数背景下借组导数处理含有两个变量的等式与不等式问题,这类问题由于变量多,不少同学不知如何下手,其实如能以函数思想为指导,把双变量问题转化为一个或两个一元函数问题,再利用导数就可有效地加以解决.(一) 与函数单调性有关的双变量问题此类问题一般是给出含有()()1212,,,x x f x f x 的不等式,若能通过变形,把不等式两边转化为同源函数,可利用函数单调性定义构造单调函数,再利用导数求解.常见结论：(1)若对任意12,x x D Î,当12x x ¹时恒有()()12120f x f x x x ->-,则()y f x =在D 上单调递增；(2)若对任意12,x x D Î,当12x x ¹时恒有()()1212f x f x k x x ->-,则()y f x kx =-在D 上单调递增；(3)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x kx x x x ->-,则()k y f x x =+在D 上单调递增；(4)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x x x x x ->+-,则()2y f x x =-在D 上单调递增.【例1】（2024届四川省仁寿第一中学校高三上学期调研）已知函数212ln ()xf x x +=．(1)求()f x 的单调区间；(2)存在12,(1,)x x Î+¥且12x x ¹，使()()1212ln ln f x f x k x x -³-成立，求k 的取值范围．【解析】（1）由题意得()34ln xf x x -¢=，令()0f x ¢=得1x =，(01),x Î时，()0f x ¢>，()f x 在(0,1)上单调递增；,(1)x Î+¥时，()0f x ¢<，()f x 在(1,)+¥上单调递减；综上，()f x 单调递增区间为(0,1)，单调递减区间为(1,)+¥．（2）由题意存在12,(1,)x x Î+¥且12x x ¹，不妨设121x x >>，由（1）知,(1)x Î+¥时，()f x 单调递减．()()1212ln ln f x f x k x x -³-等价于()()()2112ln ln f x f x k x x -³-，即()()2211ln ln f x k x f x k x +³+，即存在12,(1,)x x Î+¥且12x x >，使()()2211ln ln f x k x f x k x +³+成立．令()()ln h x f x k x =+，则()h x 在(1,)+¥上存在减区间．即234ln ()0kx x h x x-¢=<在(1,)+¥上有解集，即24ln x k x <在(1,)+¥上有解，即2max 4ln x k x æö<ç÷èø，(1,)x Î+¥；令()24ln x t x x =，(1,)x Î+¥，()()3412ln x t x x -¢=，(x Î时，()0t x ¢>，()t x在(上单调递增，)x ¥Î+时，()0t x ¢<，()t x在)+¥单调递减，∴max 2()e t x t ==，∴2ek <． (二) 与极值点有关的双变量问题与极值点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x ¢=的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数，此外若题中含有参数也可考虑把所给式子转化为关于参数的表达式.【例2】（2024届黑龙江省双鸭山市高三下学期第五次模拟）已知函数2()ln (1)(R)f x x a x a x=+-+Î.(1)当1a =-时，讨论()f x 的单调性；(2)若()1212,x x x x <是()f x 的两个极值点，证明：()()21f x f x -<【解析】（1）当1a =-时，2()ln 1,()f x x x f x x=+++的定义域为(0,)+¥，所以2222122(2)(1)()1x x x x f x x x x x¢+-+-=-+==，令()0f x ¢=，解得1x =，当(0,1)x Î时，()0f x ¢<，当(1,)x Î+¥时，()0f x ¢>，故()f x 在(0,1)上单调递减，在(1,)+¥上单调递增．（2）222122()ax x f x a x x x ¢-+-=--=，由题意可知，()1212,x x x x <是方程220ax x -+-=的两根，则102180a a ì>ïíïD =->î，解得108a <<，所以121x x a +=，122x x a =，要证()()21f x f x -<====即证()()22112122ln 1ln 1x a x x a x x x éù+-+-+-+êúëû只需证()()122211122lnx x x a x x x x x -+--<需证()()212211122ln2x x x a x x x x x -<-=++令21(1)x t t x =>，则需证2(1)ln 1t t t -<++，设()ln 1)g t t t =>，则2111111442222111(1)11222()02t t t t t t t g t t t tt---¢æö-ç÷----+èø=-==-<，所以函数()g t 在(1,)+¥上单调递减，所以()(1)0g t g <=，因此ln t <由1t >得，2(1)01t t ->+，所以2(1)ln 1t t t -<+，故()()21f x f x -<,【例3】（2023届云南省曲靖市高三下学期第二次联考）已知函数()()21ln 402f x x a x x a =+->.(1)当3a =时，试讨论函数()f x 的单调性；(2)设函数()f x 有两个极值点()1212,x x x x <，证明：()()12ln 10f x f x a +>-.【解析】（1）当3a =时，()213ln 42f x x x x =+-定义域为()0,x Î+¥，()()()2133434x x x x f x x x x x---+=+-==¢，令()0f x ¢=解得1x =或3，且当01x <<或3x >时，()0f x ¢>，当13x <<时，()0f x ¢<，所以当01x <<或3x >时，()f x 单调递增，当13x <<时，()f x 单调递减，综上()f x 在区间()0,1，()3,+¥上单调递增，()f x 在区间()1,3单调递减.（2）由已知()21ln 42f x x a x x =+-，可得()244a x x af x x x x-+=+-=¢，函数()f x 有两个极值点()1212,x x x x <，即240x x a -+=在()0,¥+上有两个不等实根，令()24h x x x a =-+，只需()()00240h a h a ì=>ïí=-<ïî，故04a <<，又124x x +=，12x x a =，所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--，要证()()12ln 10f x f x a +>-，即证ln 8ln 10a a a a -->-，只需证()1ln 20a a a -+-<，令()()1ln 2m a a a a =-+-，()0,4a Î，则()11ln 1ln a m a a a a a-=-++=-¢，令()()n a m a ¢=，则()2110n a a a¢=--<恒成立，所以()m a ¢在()0,4a Î上单调递减，又()110m ¢=>，()12ln202m =-<¢，由零点存在性定理得，()01,2a $Î使得()00m a ¢=，即001ln a a =，所以()00,a a Î时，()0m a ¢>，()m a 单调递增，()0,4a a Î时，()0m a ¢<，()m a 单调递减，则()()()()0000000max 00111ln 2123m a m a a a a a a a a a ==-+-=-+-=+-，又由对勾函数知0013y a a =+-在()01,2a Î上单调递增，所以00111323022a a +-<+-=-<，所以()0m a <，即()()12ln 10f x f x a +>-得证.(三) 与零点有关的双变量问题与函数零点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x =的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数,有时也可转化为关于12x x -的函数,若函数中含有参数,可考虑把参数消去,或转化为以参数为自变量的函数.【例4】（2024届四川省南充高中高三下学期月考）已知函数())ln 2f x x a =-ÎR .(1)讨论函数()f x 的单调性，并求()f x 的极值；(2)若函数()f x 有两个不同的零点12,x x （12x x <），证明：1e a<<.【解析】（1）函数()f x 的定义域为(0,)+¥，由题意，()1f x x ==¢，当0a £时，()0f x ¢>，函数()f x 在(0,)+¥单调递增，无极值.当0a >时，令()0f x ¢=，得21x a =∴()f x 在210,a æöç÷èø单调递增，在21,a ¥æö+ç÷èø单调递减，所以函数()f x 在21x a =时取极大值，极大值为212ln 2f a a æö=--ç÷èø，无极小值.x210,a æöç÷èø21a 21,a ¥æö+ç÷èø()f x ¢+-()f x 递增极大值递减（212t t ==，且12x x <，则有1122ln ln t at t at =ìí=î，两式相减可得，1212ln ln t t a t t-=-1a <.12121ln ln t t a t t-<=-12ln 0t t Û>，令u =121ln02ln 0(01)t u u u t u >Û-+><<，设()12ln g u u u u =-+，则()222212110u u g u u u u -+-=--=<¢，所以()g u 在()0,1上单调递减，所以()()10g u g >=1a<.1122ln ln t at t at =ìí=î，两式子相加得，()1212ln t t a t t =+e >，即证212e t t >，由上式只需证()122a t t +>，即证()1121212112221ln ln 2ln 201t t t t t t t t t t t t --×+>Û-<-+，令12t v t =，11212211ln 20ln 20(01)11t t t v v v t t v t --æö-<Û-<<<ç÷+èø+，设()()1ln 2011v h v v v v -æö=-<<ç÷+èø，则()22(1)0(1)v h v v v +¢-=>，所以()h v 在()0,1上单调递增，所以()()10h v h <=e >.综上：1e a<<. (四) 独立双变量,各自构造一元函数此类问题一般是给出两个独立变量,通过变形,构造两个函数,再利用导数知识求解.【例5】（2024届陕西省宝鸡实验高中高三一模）已知函数2()ln (,,1)x f x a x x a b a b R a =+--Î>，e 是自然对数的底数.(1)当e,4a b ==时，求整数k 的值，使得函数()f x 在区间(,1)k k +上存在零点；(2)若存在12,[1,1],x x Î-使得12|()()|e 1f x f x -³-，试求a 的取值范围.【解析】（1）2()e 4x f x x x =+--，()e 21x f x x ¢\=+-，(0)0f ¢\=当0x >时，e 1x >，()0f x ¢\>，故()f x 是(0,)+¥上的增函数，同理()f x 是(,0)-¥上的减函数，2(0)30,(1)e 40,(2)e 20f f f =-<=-<=->，且2x >时，()0f x >，故当0x >时，函数()f x 的零点在()1,2内，1k \=满足条件．同理，当0x <时，函数()f x 的零点在()2,1--内，2k \=-满足条件，综上1,2k =-．（2）问题Û当[1,1]x Î-时，max min max min |()()|()()e 1f x f x f x f x -=-³-，()ln 2ln 2(1)ln x x f x a a x a x a a ¢=+-=+-，①当0x >时，由1a >，可知10,ln 0,()0x a a f x ¢->>\>；②当0x <时，由1a >，可知10,ln 0,()0x a a f x ¢-<>\<；③当0x =时，()0f x ¢=，()f x \在[1,0]-上递减，[0,1]上递增，\当[1,1]x Î-时，min max ()(0),()max{(1),(1)}f x f f x f f ==-，而1(1)(1)2ln f f a a a--=--，设1()2ln (0),g t t t t t =-->22121()1(1)0g t t t t¢=+-=-³Q （仅当1t =时取等号），()g t \在(0,)+¥上单调递增，而(1)0g =，\当1t >时，()0g t >即1a >时，12ln 0a a a-->，(1)(1),(1)(0)e 1f f f f \>-\-³-即ln e 1e ln e a a -³-=-，构造()ln (1)h a a a a =->，易知()0¢>h a ，()h a \在(1,)+¥递增，e a \³，即a 的取值范围是[e,)+¥．(五) 构造一元函数求解双变量问题当两个以上的变元或是两个量的确定关系在解题过程中反复出现.通过变量的四则运算后,把整体处理为一个变量,从而达到消元的目的.【例6】（2024届山东省菏泽市高考冲刺押题卷）已知函数2()ln 1(02)f x tx x x t =-+<£．(1)求函数()f x 的单调区间(2)若0a b >>，证明:2244a b a b <-．【解析】（1）()ln 2,0f x t x t x x ¢=+->，令()()ln 2g x f x t x t x ¢==+-，所以()2,0tg x x x¢=->，由()0g x ¢>可得02t x <<，由()0g x ¢<可得2t x >，所以()f x ¢在(0,)2t 上单调递增，在(,)2t+¥上单调递减，所以max ()(ln ln 222t t tf x f t t t t ¢¢==+-=.又因为02t <£，所以ln02t£，即()0f x ¢£，且()f x ¢至多在一个点处取到0.所以()f x 在(0,)+¥上单调递减，故()f x 的单调递减区间为()0,+¥，没有单调递增区间.（2）证明2244a b a b <-，只需证：22222222222222+)))()11((ln 24(a b a b a b a b a b a b --<-++-，即证：2222222222222ln a b a b a b a b a b a b ++-<---+，令2222,0a b x a b a b +=>>-，所以1x >，只需证：12ln x x x<-，即证：22ln 10x x x -+<，由（1）知，当2t =时，2()2ln 1f x x x x =-+在(0,)+¥上单调递减，1x >()(1)0f x f <=，即22ln 10x x x -+<，所以2244a b a b<-.(六) 独立双变量,把其中一个变量看作常数若问题中两个变量没有明确的数量等式关系,有时可以把其中一个当常数,另外一个当自变量【例7】已知函数，(1)若函数在处的切线也是函数图像的一条切线，求实数a 的值；(2)若函数的图像恒在直线的下方，求实数a 的取值范围；(3)若，且，证明：>【解析】 (1)，在处切线斜率，，所以切线，又，设与相切时的切点为，则斜率，则切线的方程又可表示为，由，解之得．(2)由题可得对于恒成立，即对于恒成立，令，则，由得，x20,e a æöç÷èø2e a2e a æö+¥ç÷èø，()h x ¢+0-()h x ↗极大值↘则当时，，由，得：，即实数的取值范围是．(3)由题知，由得，当时，，单调递减，因为，所以，即，所以，①同理，②①+②得，()ln (0)af x x a x=×>()e xg x =0x =()f x ()f x 10x y -+=12,(,)e 2a a x x Î12x x ¹412()x x +212a x x ()e xg x ¢=()g x 0x =()01k g ¢==()01g =:1l y x =+()ln1af x x =¢-l ()f x 000,ln a x x x æöç÷èø()00ln 1a k f x x ¢==-l ()000000ln 1ln ln 1a a ay x x x x x x x x æöæö=--+=-+ç÷ç÷èøèø00ln 111ax x ì-=ïíï=î2e a =()10f x x --<0x >ln 10ax x x--<0x >()ln 1a h x x x x =--()ln 2ah x x =¢-()0h x ¢=2ea x =0x >()22max 1e ea a h x h æö==-ç÷èø210e a -<20e a <<a ()20,e ()ln 1af x x=¢-()0f x ¢=e a x =e a x a <<()0f x ¢<()()ln 0af x x a x=>112x x x a +<<()()112f x f x x >+()112112ln ln a ax x x x x x >++121112lnln x x a a x x x x +>+122212ln ln x x a ax x x x +>+1212121212lnln ln x x x x a a ax x x x x x æöç÷èø>+++++因为，由得，即，所以，即，所以．(七) 双变量,通过放缩消元转化为单变量问题此类问题一般是把其中一个变量的式子放缩成常数,从而把双变量问题转化为单变量问题【例8】（2024届河北省衡水市高三下学期联合测评）过点(),P a b 可以作曲线e x y x =+的两条切线，切点为,A B .(1)证明：()1ea b a ->-；(2)设线段AB 中点坐标为()00,x y ，证明：00a y b x +>+.【解析】（1）证明：设切点(),e tA t t +，1e xy ¢=+，所以e 1e t tPAt bk t a+-=+=-，即关于t 的方程()1e 0tt a b a --+-=有两个不相等的实数根.设()()1e t f t t a b a =--+-，则()()e 0tf t t a =-=¢，t a =.当t a <时，()0f t ¢<，则()f t 在(),a ¥-上单调递减；当t a >时，()0f t ¢>，则()f t 在(),a ¥+上单调递增，所以()f t 在t a =处取值得最小值，即()e af a b a =--.当t ®+¥时，()f t ¥®+，当t ®-¥时，()f t b a ®-，若满足方程有两个不相等的实数根，则0e 0ab a b a ->ìí--<î，于是0e a b a <-<，即()ln b a a -<，得()()()ln b a b a b a a --<-,设()ln g x x x =，()ln 10g x x +¢==，得1ex =，在10,e æöç÷èø上，()0g x ¢<，则()g x 单调递减，在1,e ¥æö+ç÷èø上，()0g x ¢>，则()g x 单调递增，所以()ln g x x x =，在1e x =处取得最小值，即11e e g æö=-ç÷èø，所以()1e a b a ->-.（2）证明：设()()1122,,,A x y B x y ，则()()12012011e e 22x x y y y x =+=++，即()()12001211e e 22x x y x y y -=+=+，121221121224x x x x x x x x x x +++=++³12x x a +<121a x x +>12ln 0ax x >+1212ln ln 4ln a a a x x x x +>+421212a a x x x x æö>ç÷+èø()421212x x a x x +>在点()()1122,,,A x y B x y 处的切线方程都过(),P a b ，于是，由()()1111e 1e x xb x a x --=+-，得()1110e x b a x a --++=，由()()2222e 1e x xb x a x --=+-，得()2210e x b a x a --++=两式相减整理得：()121212e e e x x x x x x b a +--=-，()()()()1212121200e 1e ee e 2x x x x x x x x b a y x +----=-+-()()121212122212e e e 2e 2e e x x x x x x x x x x ++éù-=--êú-ëû()()1212121212e 12e e 2e e x x x x x x x x x x +--éù=--+êú-ëû，不妨设1212,0x x m x x >=->，所以()1212e 02e e x x x x +>-，则()12e e m mh m m =-+，()12e 220e m mh m ¢=--£-=，所以()h m 在()0,¥+上单调递减，于是()()00h m h <=，于是()()000b a y x ---<，即00a y b x +>+.【例1】（2024届陕西省西安市一中高三考前模拟）已知函数()2e 2xx f x a =++.(1)若4a =-，求()f x 的极值；(2)若0a >，不相等的实数,m n 满足()()228f m f n m n +=++，求证：0m n +<.【解析】（1）依题意，()2e 42x f x x =-+，则()2e 4xf x =¢-，令()0f x ¢=，解得ln 2x =，故当(),ln 2x ¥Î-时，()0f x ¢<，当()ln 2,x ¥Î+时，()0f x ¢>，故函数()f x 在(),ln 2¥-上单调递减，在()ln 2,¥+上单调递增，故函数()f x 的极小值为()ln 244ln 2264ln 2f =-+=-，无极大值；（2）令()()222e 2x g x f x x ax x =-=+-+，则()2e 2xg x x a =¢-+，令()e xt x x =-，则()e 1x t x ¢=-，当0x <时，()0t x ¢<，当0x >时，()0t x ¢>，所以函数()t x 在(),0¥-上单调递减，在()0,¥+上单调递增，所以()()e 010x t x x t =-³=>，又0a >，所以()()2e 0xg x x a =-+>¢，所以()g x 在R 上单调递增，()()228f m f n m n +=++，即()()8g m g n +=，因为()04g =，所以,0m n ¹，要证0m n +<，即证n m <-，只需证()()g n g m <-，即()()8g m g m -<-，即()()8g m g m +->，令函数()()()22e 2e 24x x h x g x g x x -=+-=+-+，则()2e 2e 4x x h x x -=--¢，令()()x h x j =¢，则()2e 2e 40xx x j -=-¢+³，所以()h x ¢为R 上的增函数，当0x <时，()()00h x h ¢¢<=，当0x >时，()()00h x h ¢¢>=，所以()h x 在(),0¥-上单调递减，在()0,¥+上单调递增，所以对任意0m ¹，都有()()()()08h m g m g m h =+->=，从而原命题得证.【例2】（2024届河北省衡水市部分示范性高中高三下学期三模）已知()e xf x x =-．(1)求()f x 的单调区间和最值；(2)定理：若函数()f x 在(,)a b 上可导，在[]a b ，上连续，则存在(,)a b x Î，使得()()()f b f a f ξb a-¢=-．该定理称为“拉格朗日中值定理”，请利用该定理解决下面问题：若0m n <<，求证：()2e e 111m n m n m n m æö-<+-ç÷èø．【解析】（1）()e 1x f x ¢=-，令()0f x ¢=，解得0x =，当(,0)x Î-¥时，()0,()¢<f x f x 单调递减；当,()0x Î+¥时，()0,()¢>f x f x 单调递增．当0x =时，()f x 取得最小值1，无最大值；（2）要证2e e 11(1)m n m n m n m æö-<+-ç÷èø，只需证2e e (1)()m n m n m m n -<+-，因为0m n <<，故只需证2e e (1)m nm n m m n->+-．令()e (0)x g x x x =>，显然()g x 在(,)m n 上可导，在[]m n ，上连续，故由拉格朗日中值定理知存在(,)m n x Î，使得e e()m nm n g m nx ¢-=-，而()(1)e 0,()x g x x g x ¢¢=+>在(0,)+¥上单调递增，因为m n x <<，故()()g g m x ¢¢>，即()(1)e m g m x ¢>+，故只需证2(1)e (1)m m m +³+即可，因为0m >，故只需证e 1m m ³+．由（1）知e 1x x ³+恒成立，因此原命题得证．【例3】（2024届天津市部分区高三二模）已知,R a b Î，函数()sin ln f x x a x b x =++．(1)当0,1a b ==-时，求()f x 的单调区间；(2)当1,02a b =-¹时，设()f x 的导函数为()f x ¢，若()0f x ¢>恒成立，求证：存在0x ，使得()01f x <-；(3)设01,0a b <<<，若存在()12,0,x x Î+¥，使得()()()1212f x f x x x =¹>．【解析】（1）由函数()sin ln f x x a x b x =++，可得其定义域为()0,¥+，当0,1a b ==-时，可得()ln f x x x =-，则()111x f x x x¢-=-=，当()0,1x Î时，可得()0f x ¢<，()f x 单调递减；当()1,x ¥Î+时，可得()0f x ¢>，()f x 单调递增，\函数()f x 的单调递增区间为()1,¥+，单调递减区间为()0,1．（2）当1,02a b =-¹时，可得()1sin ln 2f x x x b x =-+，则()11cos 2bf x x x =-+¢，Q ()0f x ¢>恒成立，即11cos 02b x x -+>恒成立，令()11cos ,02bh x x x x=-+>，若0b <，则0b x <，存在2b x =-，使得111cos 21cos 022222b b b h æöæöæö-=---=---<ç÷ç÷ç÷èøèøèø，即()0f x ¢<，不符合题意，>0b \，取30e bx -=，则001x <<，可得()3301esin e 312bb f x --=--<-，即存在0x ，使得()01f x <-．（3）由函数()sin ln f x x a x b x =++，可得()1cos bf x a x x ¢=++，设12x x <，由()()12f x f x =，可得111222sin ln sin ln x a x b x x a x b x ++=++，则()()()22121211sin sin ln ln lnx x x a x x b x x b x -+-=--=-，又由sin y x x =-，可得'1cos 0y x =-³，\函数sin y x x =-为单调递增函数，\2211sin sin x x x x ->-，即2121sin sin x x x x -<-，\()()2211ln1x b a x x x -<+-，设()1ln 21x h x x x -=-´+，可得()()()()222114011x h x x x x x -=-=+¢³+，\当1x >时，()()10h x h >=，即ln 2x >\2>即ln 4x =>\21ln 44x x >=代入可得：()()()()21411b a x x a ×-<+-=+，则()241b a -×<++，\>【例4】（2024届四川省百师联盟高三联考三）已知函数()214ln 2f x x x a x =-+.(1)当1a =时，求曲线()f x 在点()()1,1f 处的切线方程；(2)设函数()y f x =有两个不同的极值点1x ，2x .证明：()()2121135ln 244f x f x a a +--≥.【解析】（1）当1a =时()214ln 2x f x x x =-+，()14f x x x ¢=-+，()171422f =-=-，()14121f ¢=-+=-，则切线方程为()7212y x +=--，化简得4230x y ++=.（2）证明：由题()244a x x af x x x x=¢-+=-+，函数()f x 有两个极值点1x ，2x ，即240x x a -+=在()0,¥+上有两个不等实根，令()24h x x x a =-+，只需故()()00240h a h a ì=>ïí=-<ïî，故04a <<.又124x x +=，12x x a =，所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--.若证()()2121135ln 244f x f x a a +--≥，即证21135ln 8ln 244a a a a a ----≥，即2113ln ln 0244a a a a a --++≥.令()2113ln ln 244x x x x x x j =--++，()0,4x Î，()11ln 2x x xx j æö¢=+-ç÷èø，则()x j ¢在()0,4上递增，且有()01j ¢=，当()0,1x Î时，()0x j ¢<，所以()x j 在()0,1上递减；当()1,4x Î时，()0x j ¢>，所以()x j 在()1,4上递增；所以()()113ln11ln101244x j j =--++=≥，()0,4x Î.即()()2121135ln 244f x f x a a +--≥得证.【例5】（2024陕西省西安八校高三下学期联考）已知函数的图象在处的切线过原点．(1)求的值；(2)设，若对总，使成立，求整数的最大值．【解析】（1）易知的定义域为，又，的图象在处的切线方程为，将代入，得；（2）．当时，取得最小值，．由（1）知，．，得的定义域为．则，易知单调递增，又．即在上有唯一解，故．()()()e ln 1R ,xf x m x x m f x =-+-Î()()1,1f m ()()()2,2g x f x x h x x x a =-=-+()10,x ¥"Î+2x $ÎR ()1g x >()2h x a ()f x ()()0,,1e f ¥+=()()e 1,1e 1x mf x f m x¢¢=-+=-+()f x \()()1,1f ()()e e 11y m x -=-+-0,0x y ==1m =()222(1)1h x x x a x a =-+=-+-\1x =()h x ()()min []11h x h a ==-1m =()e ln 1x f x x x \=-+-()()e ln 1,x g x x g x =--()0,¥+()1e xg x x =¢-()1e 0xy x x=->()120,1e 102g g æö¢¢=-ç÷èø()0g x ¢=1,12æöç÷èø0x 000011e ,e x x x x ==于是当时，在上单调递减；当时，在上单调递增．在处取得极小值也是最小值．则，对总，使成立，只需，得．故整数的最大值为．1．（2024届广东省汕头市第二次模拟）设M 是由满足下列条件的函数()f x 构成的集合：①方程()0fx x-=有实根；②()f x 在定义域区间D 上可导，且()f x ¢满足()01f x ¢<<.(1)判断()ln 322x xg x =-+，()1,x Î+¥是否是集合M 中的元素，并说明理由；(2)设函数()f x 为集合M 中的任意一个元素，证明：对其定义域区间D 中的任意a 、b ，都有()()a b a b -£-f f .2．（2024届山东省滨州市高三下学期二模）定义：函数()f x 满足对于任意不同的12,[,]x x a b Î，都有()()1212f x f x k x x -<-，则称()f x 为[],a b 上的“k 类函数”．(1)若2()13x f x =+，判断()f x 是否为[]1,3上的“2类函数”；(2)若2()(1)e ln 2xx f x a x x x =---为[1,e]上的“3类函数”，求实数a 的取值范围；(3)若()f x 为[1,2]上的“2类函数”，且(1)(2)f f =，证明：1x "，2[1,2]x Î，()()121f x f x -<．3．（2024届辽宁省沈阳市第一二〇中学高三最后一卷）设函数()21ln 2f x x x x ax =--的两个极值点分别为()1212,x x x x <．(1)求实数a 的取值范围；(2)若不等式()12a x x l <+恒成立，求正数l 的取值范围（其中e 271828=L ．为自然对数的底数）．00x x <<()()0,g x g x ¢<()00,x 0x x >()()0,g x g x ¢>()0,x ¥+()g x \0x x =()000min 015e ln 112,2xg x x x x æö=--=+-Îç÷èø\()10,x ¥"Î+2x $ÎR ()()12g x h x >11a ³-2a £a 24．（2024届湖南省高三“一起考”大联考下学期模拟）已知函数()2f x ax =，()lng x x =，函数()f x ，()g x 有两条不同的公切线（与()f x ，()g x 均相切的直线）1l ，2l .(1)求实数a 的取值范围；(2)记1l ，2l 在y 轴上的截距分别为1d ，2d ，证明：121d d +<-.5．（2024届天津市民族中学高三下学期4月模拟）已知函数()()22ln 0f x x x a x a =-+>．(1)当2a =时，试求函数图象在点()()1,1f 处的切线方程；(2)若函数()f x 有两个极值点1x 、()212x x x <；（ⅰ）求a 的取值范围；（ⅱ）不等式()12f x mx ³恒成立，试求实数m 的取值范围．6．（2024届陕西省部分学校（菁师联盟）高三下学期5月份高考适应性考试）已知函数()2ln f x x x x =-.(1)求曲线()y f x =在2e x =处的切线方程；(2)若()()12f x f x =，且12x x <.求证：212e x x +<.7．（2024届广东省广州市二模）已知函数()()21e x f x a x x -=++．(1)讨论()f x 的零点个数；(2)若()f x 存在两个极值点，记0x 为()f x 的极大值点，1x 为()f x 的零点，证明：0122x x ->．8．（2024届重庆市名校联盟高三下学期全真模拟）T 性质是一类重要的函数性质，具有T 性质的函数被称为T 函数，它可以从不同角度定义与研究.人们探究发现，当()y f x =的图像是一条连续不断的曲线时，下列两个关于T 函数的定义是等价关系．定义一：若()y f x =为区间(),a b 上的可导函数，且()y f x ¢=为区间(),a b 上的增函数，则称()y f x =为区间(),a b 上的T 函数．定义二：若对()12,,x x a b "Î，()0,1l "Î，都有()()()()121211f x x f x f x l l l l éù+-£+-ëû恒成立，则称()y f x =为区间(),a b 上的T 函数．请根据上述材料，解决下列问题：(1)已知函数()πtan 02f x x x æö=Îç÷èø，,．①判断()y f x =是否为π0,2x æöÎç÷èø上的T 函数，并说明理由；②若π0,2a b æöÎç÷èø，且π22a b +=，求()()2f f a b +的最小值(2)设11111m n m n >>+=，，，当00a b >>，时，证明：11m na b ab m n+³．9．（2024届河南省九师联盟高三下学期5月联考）已知函数1()ln (0)f x a x a x=+¹．(1)若()f x a >对,()0x Î+¥恒成立，求a 的取值范围；(2)当3a =时，若关于x 的方程211()42f x x x b x =-++有三个不相等的实数根1x ，2x ，3x ，且1x <23x x <，求b 的取值范围，并证明：314x x -<．10．（2024届湖北省宜荆荆随恩高三5月联考）设函数，(1)讨论的单调性．(2)若函数存在极值，对任意的，存在正实数，使得（ⅰ）证明不等式．（ⅱ）判断并证明与的大小．11．（2024届江西省上饶市六校高三5月第二次联合考试）已知函数．(1)若，求的极值；(2)若，求的最大值．12．（2024届山西省临汾市高三下学期考前适应性训练）已知函数．(1)求在处的切线方程；(2)若曲线与直线有且仅有一个交点，求的取值范围；(3)若曲线在处的切线与曲线交于另外一点，求证：．13．（2024届江苏省扬州市仪征市四校高三下学期4月联合学情检测）已知函数．()()24ln 42f x x ax a x =-+-a ÎR()f x ()f x 120x x <<0x ()()()()21021f x f x f x x x ¢-=-212121ln ln 2x x x x x x ->-+122x x +0x ()()ln ,,0f x x a x b a b a =--Î¹R 1a b ==()f x ()0f x ³ab ()()21ln 12=++f x x x ()f x 0x =()y f x =y ax =a ()y f x =()()(),0m f m m >()y f x =()(),n f n 21mm n m -<<-+()()()ln 0f x mx x m =->(1)若恒成立，求的取值范围；(2)若有两个不同的零点，证明．14．（2024届河北省保定市高三下学期第二次模拟）已知函数为其导函数．(1)若恒成立，求的取值范围；(2)若存在两个不同的正数，使得，证明：．15．（2024届云南省高中毕业生第二次复习统一检测）已知常数，函数.(1)若，求的取值范围;(2)若、是的零点，且，证明:.()0f x £m ()f x 12,x x 122x x +>()ln ,()f x ax x x f x ¢=-()1f x £a 12,x x ()()12f x f x=0f ¢>0a >221()2ln 2f x x ax a x =--20,()4x f x a ">>-a 1x 2x ()f x 12x x ¹124x x a +>。

双曲线方程知识点详细总结

双曲线方程 1.双曲线的第一定义：呼\卜更』二加叱厅兰工方程为洩曲线严j-丹■，卜加卜卩丈,氏軌迹昭1|_严沪血=町^附1^的_牛端烂的一^播 y 2 y 2 i 1飞―分g”明刍— ⑴①双曲线标准方程：口] --' 一般方程：.=「_「—：. ⑵①i.焦点在x 轴上：・=±兰 3"顶点：W 叽 ^焦点： ' ' " ' ii.焦点在尸轴上：顶点: 4 4=o，参数方程:y=±?L—….焦点：（叭g 町.准线方程：匚x- a&eoO4 q±±_0渐近线方程：或asccQ②轴兀卅为对称轴，实轴长为 2a,虚轴长为2b,焦距2c. 0 g =l通径 .⑤参数关系 .⑥焦点半径公式: 线的左、右焦点或分别为双曲线的上下焦点）长加短减”原则： [MFjwai.+iH [AfFj |=—ff ■f ■-:构成满足亠 ■ 焦半径不同，椭圆焦半径要带符号计算，而双曲线不带符号） \MP^\~ay t ^a|4fFi|=-ffyi +€J }|--ayi -a ③离心率口.④准线距心 ^__y^_=x对于双曲线方程<（两准线的距离）；片宀分别为双曲（与椭圆⑶等轴双曲线：双曲线 w 称为等轴双曲线，其渐近线方程为•亠，离心率*・. ⑷共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲互为共轭双曲线，它们具有共同的渐近线：的渐近线方程为川 -j-=^ -线. 与 ⑸共渐近线的双曲线系方程: —±Z -=0 如果双曲线的渐近线为厘时，它的双曲线方程可设为「厂且过心丿 1_，求双曲线的方程？.1- 得囊匕例如：若双曲线一条渐近线为 Jr= # 可 P>_—）解：令双曲线的方程为： 4 ，代入 1 ⑹直线与双曲线的位置关系：区域①：无切线，2条与渐近线平行的直线，合计 2条；区域②：即定点在双曲线上，1条切线，2条与渐近线平行的直线，合计区域③：2条切线，2条与渐近线平行的直线，合计 4条；区域④：即定点在渐近线上且非原点，1条切线，1条与渐近线平行的直线，合计 2条；区域⑤：即过原点，无切线，无与渐近线平行的直线.小结：过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有0、2、3、4条.（2）若直线与双曲线一支有交点，交点为二个，求确定直线的斜率可用代入"△"法与渐近线求交和两根之和与两根之积同号•⑺若P在双曲线. ，则常用结论1： P到焦点的距离为 m = n,则P到两准线的距离比为m : n.简证：=丹.常用结论2:从双曲线一个焦点到另一条渐近线的距离等于 b.双曲线的标准方程和简单几何性质4、点訊心片）和败側r=1 > 0,6 >0）的位盖关丟口- D“求汉曲线的方程，用待定系频法、先宦位「后定星"常见考法在段考中，多以选择题、填空题和解答题的形式考查双曲线的简单几何性质。

求数列通项公式的十种方法,例题答案详解

求数列通项公式的十一种方法(方法全，例子全，归纳细)总述：一.利用递推关系式求数列通项的11种方法：累加法、累乘法、待定系数法、阶差法(逐差法)、迭代法、对数变换法、倒数变换法、换元法(目的是去递推关系式中出现的根号) 、数学归纳法、不动点法(递推式是一个数列通项的分式表达式) 、特征根法二。

四种基本数列：等差数列、等比数列、等和数列、等积数列及其广义形式。

等差数列、等比数列的求通项公式的方法是：累加和累乘，这二种方法是求数列通项公式的最基本方法。

三.求数列通项的方法的基本思路是：把所求数列通过变形，代换转化为等差数列或等比数列。

四.求数列通项的基本方法是：累加法和累乘法。

五.数列的本质是一个函数，其定义域是自然数集的一个函数。

一、累加法1.适用于：%+ =% + f(n) -------- 这是广义的等差数列累加法是最基本的二个方法之一。

2.若an+ -a n = f (n) (n >2),a2 -4=f(1)则出一包="2)III IHa n 1 -a n = f (n)两边分别相加得a n1._.a1 == f (n)k 4例1已知数列｛a n｝满足an4 =a n +2n +1, & =1,求数列｛a n｝的通项公式。

解：由an_1 =an+2n+1 得an邛一an = 2n+1 则n n n na n =(a n -a n。

(a n」- a n- IM (a3 -a2)(a2 -a1)&= [2(n-1) 1] [2(n-2) 1] |H (2 2 1) (2 1 1) 1= 2[(n -1) (n -2) ||| 2 1] (n -1) 1= 2(n 21)n (n -1) 1=(n -1)(n 1) 12 二n所以数列｛a n｝的通项公式为a n =n2。

例2已知数列｛a n｝满足a n+ =a n +2父3n +1, a1 =3 ,求数列｛a n｝的通项公式。

肌电图课件大全

异常肌电图
针电极插入及肌肉放松时的异常肌电图
➢ 插入电位延长：针极插入、挪动时骤然出现电位排放，针极挪动停止后电位并不立即消失，但数量、频率逐渐减少以至消失，挪动针极后又重新出现。病理意义：插入电位延长常见于神经源性疾病，在周围神经损伤中最常见，肌炎、肌强直中也可见到
➢ 纤颤电位：单根肌纤维自发性收缩产生的电位，以起始为正向、短时限、低电压节律较整齐为其特点。时限大多<3.0ms，电压<300uv 病理意义：失神经支配；电解质改变；肌炎；肌纤维的破坏等
➢ 临床意义：主要是检测小纤维特别是C类无髓小纤维的电生理特点，是客观评价自主神经系统功能的检测方法之一，最常用于糖尿病周围神经病和痛性周围神经病的诊断和研究。糖尿病周围神经病可表现为潜伏期延长，波幅降低或分化不良，严重者无波形。
正常肌电图
➢ 针电极插入及肌肉放松时的肌电图
1 插入电位：指针电极插入挪动和叩击时，因针电极对肌肉纤维或神经的机械刺激及损伤作用而猝发的电位正常肌肉插入电位持续时间短，针电极一旦停止移动，插入电位迅速消失
影响神经传导速度的技术和生理因素
➢ 技术因素 ➢ 温度：皮肤温度降低时，传导速度减慢、潜伏期延长 ➢ 年龄：老年人传导速度下降、波幅降低 ➢ 上肢神经的运动传导速度比下肢快，近端神经传导速度
比远端快、感觉神经传导速度比运动神经快
影响神经传导速度的病理因素
➢ 髓鞘脱失：传导速度减慢 ➢ 神经轴突直径改变：
的信息，准确反映患者的病变范围。（2）检查者应将丰富的临床经验与电生理结合
➢ 重视病变随时间演变的过程根据疾病发生发展的过程，动态分析不同阶段的电生
理特点 ➢ 注意不同检测内容的严重程度和特点以及与临床的相关性，

普通话考试：舌头大战

普通话考试：舌头大战1、你不认识的单音节字��(三个土，读音yáo，意：山高，多用於人名。

)��(三条牛，读音bēn，意：同“奔”，急走，跑，紧赶，逃跑等。

) 聂(三只耳朵，读音niè)磊(三块石头，读音lěi，本义:石头多)�Y(三条小狗，读音biāo )�F(三个宝贝，读音bì )虫(3个虫重叠，读音chong ) (虫的繁体)奸(三个女字重叠,读音jian) (奸的繁体)�U(上只下要，读音jiào )��(两个喜字，每个喜字31口，共六十二口，读音xǐ )�~(上功下夫，读音bū)�h(上好下心，读音hào )孬(上不下好,读音nao)�T(上天下明，读音wěng)��(上不下要，读音biáo，意：不要 )�Q(三匹马，读音piāo )��(三个吉，读音zhé)�n(三个言，读音tà )�p(三条舌头，读音qì )�a(三只眼，读音mò )�Q(三只香，读音xīn)��(三条泉水，读音xún )�h(三个响雷，读音bìng)��(三个条田，读音léi)轰(三个车，读音hōng )�~(三个白，读音xiǎo)��(三颗心，读音suǒ )��(三个小，读音mó)��(三个鹿，读音cū )��(三个龙，读音dá ，意古同“��”，龙腾飞的样子。

)票(三个票，读音piāo，意通“飘”。

轻举的样子)鑫(三个金，读音xīn，意旧时商店字号、人名用字,取其金多兴旺之意)森(三个木，读音sēn，意稠密)2、鲜为人知的多音节字觊觎jìyú 龃龉jǔyǔ 囹圄língyǔ魍魉wǎngliǎng痤疮cuóchuāng鳜鱼guìyú 耄耋màodié 饕餮tāotiè纨绔wánkù踟躇chíchú 倥偬kǒn��zǒn��倥侗念kōngdòng彳亍chìchù谄媚chǎnmèi 女红nǚgōng 古同“工”佝偻gōulóu 龟裂guīliè 蓓蕾bèilěi蹀躞diéxiè 迤逦yǐlǐ 呷茶xiāchá狡黠jiǎoxiá 猥亵wěixiè猥狎wěixiá (怀疑是否有这个词)委蛇wēiyí 蟾蜍chánchú 迷惘míwǎn��趔趄lièqie 窥觑kuīqù 肄业yìyè叱咤chìzhà 绸缪chóumóu 纶巾guānjīn咄嗟duōjiē 罹难línàn 龌龊wòchuò促狭cùxiá 皈依guīyī 旮旯gālá戛然jiárán 参差cēncī 鳏夫guānfū 髑髅dúlóu 皴裂cūnliè 妊娠rènshēn 老鸨lǎobǎo 东莞dōngguǎn 孑孓jiéjué逡巡qūnxún 趑趄zīqiè 斡旋wòxuán 弹劾tánhé 旌旗jīngqí 沟壑gōuhè 交媾jiāogòu 菁华jīnghuá 毓婷yùtíng 拈花niānhuā 旖旎yǐnǐ 褴褛lánlǚ 蒯草kuǎicǎo 执拗zhíniù匍匐púfú阿訇āhōng 暴殄bàotiǎn拥趸yōngdǔn 氤氲yīnyūn 鹄的gǔdì 整饬zhěngchì 北京话里常念轻声。

微机原理键盘控制与显示实验报告

课程名称： __________ 微机原理（实验） _________________ 指导老师： _徐习东 _______________ 成绩： _______________________ 实验名称： _________ 键盘控制与显示 ___________ 实验类型： _______ 软件实验 __________ 同组学生姓名： _______________ 七、讨论、心得【实验目的】1. 通过实验掌握TMS320F2812 通用输入/输出管脚直接控制外围设备的方法2. 了解发光二极管的控制编程方法。

3. 了解SPI 的使用。

4. 了解如何使用GpioA 口进行数据的锁存5. 通过实验掌握TMS320F2812 的扩展端口接收外围设备信息的方法6.了解键盘的使用原理及编程方法【实验内容】1. 按键显示程序，对按键记录次数，以二进制显示在16个LED 上。

2.定时器编程，并用按键控制各位时分秒，使其能完成加减操作【实验仪器】TMS320F2812 数字信号处理器与学生用集成板。

【实验步骤】1. 撰写代码2. 调试代码3.实现功能別f 尹丿占实验报告专业: 姓名:学号: 日期: 地点:电气工程及其自动化一、实验目的和要求（必填）三、主要仪器设备（必填）五、实验数据记录和处理二、实验内容和原理（必填）四、操作方法和实验步骤六、实验结果与分析（必填）【实验代码】、疋时器① 宏定义和全局变量定义R 犍蛊控制曲钟nclude "DSP281x_De (vic« .h" 卍枝键对应值Uint16 LEEReg;UintlS KeyReg 1:Uitit321 = 0;Uint16Ctrl ; int 16Sec=0;1 Tltl6M IL =0;int 16 Hor-Cl ; UintlSLight[3];秒，按键编码，LED 编码和控制位。

② 共阳字形码O K jOOO.Oxf 900, OxA4OO J .0iBDOO,0x9900,0x5200, OMfl^OD^OxFSOD, O K B000y0x9000.0zBBOO,Oz3300,OxcEDO,Oxa IDO,OxB&OD^OssEciOO , 0x5G (J0,Uxbf DU,Osa7UQ,OzffOa,0x4000,CK79Da,DM240D r Dx^ 000, 0 itl900, O K ISOQ, 0s DEOO,Oz 7000,030000,0x1000);分析：由于这次实验要用到数码管，所以我们要定义一个数码管共阳端字形码，使每一个代码对应一种显示状态。