【配套K12】2018版高中数学第二章点直线平面之间的位置关系2.22.2.1直线与平面平行的判定2
高中数学第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.1.3-2.1

2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.3-2.1.4 平面与平面之间的位置关系优化练习新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.3-2.1.4 平面与平面之间的位置关系优化练习新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.3-2.1.4 平面与平面之间的位置关系优化练习新人教A版必修2的全部内容。
2.1。
3—2。
1。
4 平面与平面之间的位置关系[课时作业][A组基础巩固]1.如果直线l在平面α外,那么直线l与平面α()A.没有公共点B.至多有一个公共点C.至少有一个公共点D.有且只有一个公共点解析:当直线l与平面α平行时,没有公共点;当直线l与平面α相交时,有且只有一个公共点.答案:B2.下列说法中,正确的是( )①若一个平面内的任何直线都与另一个平面无公共点,则这两个平面平行;②过平面外一点有且仅有一个平面和已知平面平行;③过平面外两点不能作平面与已知平面平行;④若一条直线和一个平面平行,经过这条直线的任何平面都与已知平面平行.A.①③ B.②④C.①②D.②③④解析:①②正确;③中,两点所在直线与平面平行时可以;④中,经过这条直线的平面与已知平面可能相交.答案:C3.如果两条直线a∥b,且a∥平面α,那么b和平面α的位置关系是( )A.相交B.b∥αC.b⊂αD.b∥α或b⊂α解析:当直线b⊄α时,b∥α;b⊂α也有可能成立.答案:D4.若直线a⊄α,则下列结论中成立的个数是( )(1)α内的所有直线与a异面;(2)α内的直线与a都相交;(3)α内存在唯一的直线与a平行;(4)α内不存在与a平行的直线.A.0 B.1 C.2 D.3解析:∵直线a⊄α,∴a∥α或a∩α=A。
教育最新K122018版高中数学第二章点直线平面之间的位置关系2.12.1.3空间中直线与平面之间的位置关系2.1.4平

2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系目标定位 1.掌握直线与平面之间的三种位置关系,会用图形语言和符号语言表示.2.掌握平面与平面之间的两种位置关系,会用图形语言和符号语言表示.自主预习1.直线与平面的位置关系2.1.判断题(1)若直线a在平面α外,则直线a∥α.(×)(2)若平面α内存在直线与平面β无交点,则α∥β.(×)(3)若平面α内的任意直线与平面β均无交点,则α∥β.(√)(4)与两相交平面的交线平行的直线必平行于这两个相交平面.(×)提示(1)直线a在平面α外,则直线a∥α或a与α相交.(2)α与β可能平行,也可能相交.(4)若α∩β=b,且a∥b,则有a∥α且a∥β,或a⊂α,或a⊂β.2.若直线l与平面α不平行,则( )A.l与α相交B.l⊂αC.l与α相交或l⊂αD.以上结论都不对解析若l与α不平行,则l与α相交或l⊂α.答案 C3.若两个平面互相平行,则其中一个平面内的一条直线与另一个平面的位置关系是( )A.线面平行B.线面相交C.线在面内D.无法确定解析两面平行时,两个平面没有公共点,在一个平面的直线与另一个平面也没有公共点,所以它们平行.答案 A4.两条直线不相交,则两条直线可能平行或者异面;如果两个平面不相交,则两个平面________.解析两个平面之间的位置关系有且只有两种:平行或相交.答案平行类型一直线与平面的位置关系(互动探究)【例1】以下命题(其中a,b表示直线,α表示平面),①若a∥b,b⊂α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b⊂α,则a∥b.其中正确命题的个数是( )A.0B.1C.2D.3[思路探究]探究点一空间中直线与平面的位置关系有哪几种?提示空间中直线与平面只有三种位置关系:直线在平面内,直线与平面相交,直线与平面平行.探究点二判断直线与平面的位置关系的策略是什么?提示判断直线与平面的位置关系时可借助几何模型判断,通过特例排除错误命题.对于正确命题,根据线、面位置关系的定义或反证法进行判断.要注意多种可能情形.解析如图所示在长方体ABCD-A′B′C′D′中,AB∥CD,AB⊂平面ABCD,但CD⊂平面ABCD,故①错误;A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故②错误;AB∥A′B′,A′B′∥平面ABCD,但AB⊂平面ABCD,故③错误;A′B′∥平面ABCD,BC⊂平面ABCD,但A′B′与BC异面,故④错误.答案 A规律方法 1.本题在求解时,常受思维定势影响,误以为直线在平面外就是直线与平面平行.2.判断直线与平面位置关系的问题,其解决方式除了定义法外,还可以借助模型(如长方体)和举反例两种行之有效的方法.【训练1】下列命题:①若直线l平行于平面α内的无数条直线,则l∥α②若直线a在平面α外,则a∥α③若直线a∥b,直线b⊂α,则a∥α④若直线a∥b,直线b⊂α,那么直线a就平行于平面α内的无数条直线其中假命题的序号是________.解析对于①,∵直线l虽与平面α内无数条直线平行,但l有可能在平面α内,∴l不一定平行于α,∴①是假命题;对于②,∵直线a在平面α外包括两种情况:a∥α和a 与α相交,∴a和α不一定平行,∴②是假命题;对于③,∵直线a∥b,b⊂α,则只能说明a和b无公共点,但a可能在平面α内,∴a不一定平行于α,∴③是假命题;对于④,∵a∥b,b⊂α,那么a⊂α或a∥α,所以a可以与平面α内的无数条直线平行,∴④是真命题.答案①②③类型二平面与平面的位置关系【例2】给出的下列四个命题中,其中正确命题的个数是( )①平面α内有两条直线和平面β平行,那么这两个平面平行;②平面α内有无数条直线和平面β平行,则α与β平行;③平面α内△ABC的三个顶点到平面β的距离相等,则α与β平行;④若两个平面有无数个公共点,则这两个平面的位置关系是相交或重合. A.0 B.1 C.3 D.4解析如图,在正方体ABCD-A1B1C1D1中,对于①,在平面A1D1DA中,AD∥平面A1B1C1D1,分别取AA1、DD1的中点E,F,连接EF,则知EF∥平面A1B1C1D1.但平面AA1D1D与平面A1B1C1D1是相交的,交线为A1D1,故命题①错;对于②,在正方体ABCD-A1B1C1D1的面AA1D1D中,与A1D1平行的直线有无数条,但平面AA1D1D 与平面A1B1C1D1不平行,而是相交于直线A1D1,故②是错误的;对于③,在正方体ABCD-A1B1C1D1中,分别取AA1,DD1,BB1,CC1的中点E,F,G,H,A1,B,C到平面EFHG的距离相等,而△A1BC与平面EFHG相交,故③是错误的;对于④,两平面位置关系中不存在重合,若重合则为一个平面,故命题④错. 答案 A规律方法 (1)判断两平面的位置关系或两平面内的线线,线面关系,我们常根据定义,借助实物模型“百宝箱”长方体(或正方体)进行判断. (2)反证法也用于相关问题的证明.【训练2】 如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是( ) A.平行 B.相交 C.平行或相交D.不能确定解析 如图所示,由图可知C 正确.答案 C [课堂小结]1.空间中直线与平面的位置关系有两种分类方式(1)按公共点的个数分类⎩⎪⎨⎪⎧直线与平面平行(直线与平面没有公共点)直线与平面不平行⎩⎪⎨⎪⎧直线与平面相交(直线与平面有唯 一公共点)直线在平面内(直线与平面有无数公共点)(2)按是否在平面内分类⎩⎪⎨⎪⎧直线在平面内直线在平面外⎩⎪⎨⎪⎧直线与平面相交直线与平面平行2.判断直线与平面及平面与平面位置关系常用定义和反证法.1.如果直线a ∥平面α,那么直线a 与平面α内的( ) A.一条直线不相交 B.两条直线不相交 C.无数条直线不相交 D.任意一条直线不相交解析 直线a ∥平面α,则a 与α无公共点,与α内的直线当然均无公共点. 答案 D2.若M ∈平面α,M ∈平面β,则α与β的位置关系是( ) A.平行B.相交C.异面D.不确定解析 ∵M ∈平面α,M ∈平面β,∴α与β相交于过点M 的一条直线.答案 B3.下列命题:①两个平面有无数个公共点,则这两个平面重合;②若l,m是异面直线,l∥α,m∥β,则α∥β.其中错误命题的序号为________.解析对于①,两个平面相交,则有一条交线,也有无数多个公共点,故①错误;对于②,借助于正方体ABCD-A1B1C1D1,AB∥平面DCC1D1,B1C1∥平面AA1D1D,又AB与B1C1异面,而平面DCC1D1与平面AA1D1D相交,故②错误.答案①②4.如图所示,平面ABC与三棱柱ABC-A1B1C1的其他面之间有什么位置关系?解∵平面ABC与平面A1B1C1无公共点,∴平面ABC与平面A1B1C1平行.∵平面ABC与平面ABB1A1有公共直线AB,∴平面ABC与平面ABB1A1相交.同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.基础过关1.若a,b是异面直线,且a∥平面α,则b与α的位置关系是( )A.b∥αB.相交C.b⊂αD.b⊂α、相交或平行解析如图所示,选D.答案 D2.如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是( )A.平行B.相交C.平行或相交D.AB⊂α解析结合图形可知选项C正确.答案 C3.α、β是两个不重合的平面,下面说法正确的是( )A.平面α内有两条直线a、b都与平面β平行,那么α∥βB.平面α内有无数条直线平行于平面β,那么α∥βC.若直线a与平面α和平面β都平行,那么α∥βD.平面α内所有的直线都与平面β平行,那么α∥β解析A、B都不能保证α、β无公共点,如图①;C中当a∥α,a∥β时,α与β可能相交,如图②;只有D说明α、β一定无公共点,故选D.答案 D4.若a与b异面,则过a与b平行的平面有________个.解析当a与b异面时,如图,过a上任意一点M作b′∥b,则a与b′确定了唯一的平面α,且b∥α,故过a与b平行的平面有1个.答案 15.空间三个平面如果每两个都相交,那么它们的交线有________条.解析以打开的书页或长方体为模型,观察可得结论.答案1或36.如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是A1B1和BB1的中点,则下列直线与平面的位置关系是什么?(1)AM所在的直线与平面ABCD的位置关系;(2)CN所在的直线与平面ABCD的位置关系;(3)AM所在的直线与平面CDD1C1的位置关系;(4)CN所在的直线与平面CDD1C1的位置关系.解(1)AM所在的直线与平面ABCD相交.(2)CN所在的直线与平面ABCD相交.(3)AM所在的直线与平面CDD1C1平行.(4)CN所在的直线与平面CDD1C1相交.7.已知一条直线与一个平面平行,求证:经过这个平面内的一点与这条直线平行的直线必在这个平面内.解已知:a∥α,A∈α,A∈b,b∥a.求证:b⊂α.证明如图,∵a∥α,A∈α,∴A∉a,∴由A和a可确定一个平面β,则A∈β,∴α与β相交于过点A的直线,设α∩β=c,由a∥α知,a与α无公共点,而c⊂α,∴a与c无公共点.∵a⊂β,c⊂β,∴a∥c.又已知a∥b,且A∈b,A∈c,∴b与c重合.∴b⊂α.能力提升8.以下四个命题:①三个平面最多可以把空间分成八部分;②若直线a⊂平面α,直线b⊂平面β,则“a与b相交”与“α与β相交”等价;③若α∩β=l,直线a⊂平面α,直线b⊂平面β,且a∩b=P,则P∈l;④若n条直线中任意两条共面,则它们共面.其中正确的是( )A.①②B.②③C.③④D.①③解析对于①,正确;对于②,逆推“α与β相交”推不出“a与b相交”,也可能a∥b;对于③,正确;对于④,反例:正方体的侧棱任意两条都共面,但这4条侧棱却不共面,故④错.所以正确的是①③.答案 D9.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有( )A.2个B.3个C.4个D.5个解析如图所示,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.答案 B10.如果空间的三个平面两两相交,则下列判断正确的是________(填序号).①不可能只有两条交线②必相交于一点③必相交于一条直线④必相交于三条平行线解析空间的三个平面两两相交,可能只有一条交线,也可能有三条交线,这三条交线可能交于一点.答案①11.如图,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l 不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.解平面ABC与β的交线与l相交.证明如下:∵AB与l不平行,且AB⊂α,l⊂α,∴AB与l一定相交.设AB∩l=P,则P∈AB,P∈l.又∵AB⊂平面ABC,l⊂β,∴P∈平面ABC,P∈β.∴点P是平面ABC与β的一个公共点,而点C也是平面ABC与β的一个公共点,且P,C是不同的两点,∴直线PC就是平面ABC与β的交线,即平面ABC∩β=PC,而PC∩l=P,∴平面ABC与β的交线与l相交.探究创新12.试画图说明三个平面可把空间分成几个部分?解三个平面可把空间分成4(如图①)、6(如图②③)、7(如图④)或8(如图⑤)个部分.。
高中数学第二章点、直线、平面之间的位置关系2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂

2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定检测新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定检测新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定检测新人教A版必修2的全部内容。
2。
3。
1 直线与平面垂直的判定A级基础巩固一、选择题1.下列说法中正确的个数是()①如果直线l与平面α内的两条相交直线都垂直,则l⊥α;②如果直线l与平面α内的任意一条直线垂直,则l⊥α;③如果直线l不垂直于α,则α内没有与l垂直的直线;④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直.A.0 B.1 C.2 D.3解析:由直线和平面垂直的定理知①正确;由直线与平面垂直的定义知,②正确;当l与α不垂直时,l可能与α内的无数条直线垂直,故③错误,④正确.答案:D2.直线l⊥平面α,直线m⊂α,则l与m不可能( )A.平行B.相交C.异面D.垂直解析:若l∥m,l⊄α,m⊂α,则l∥α,这与已知l⊥α矛盾.所以直线l与m不可能平行.答案:A3.如果一条直线垂直于一个平面内的下列各种情况,能保证该直线与平面垂直的是()①三角形的两边②梯形的两边③圆的两条直径④正六边形的两条边A.①③B.②C.②④D.①②③解析:由线面垂直的判定定理可知①③是正确的,而②中线面可能平行、相交.④中由于正六边形的两边不一定相交,所以也无法判定线面垂直.答案:A4。
2018版人教A版高中数学必修二同步学习讲义:第二章 点、直线、平面之间的位置关系2-2-4 含答案 精品

2.2.4平面与平面平行的性质学习目标 1.掌握平面与平面平行的性质,并会应用性质解决问题.2.知道直线与直线、直线与平面、平面与平面之间的平行关系可以相互转化.知识点平面与平面平行的性质观察长方体ABCD-A1B1C1D1的两个面:平面ABCD及平面A1B1C1D1.思考1平面A1B1C1D1中的所有直线都平行于平面ABCD吗?答案是的.思考2若m⊂平面ABCD,n⊂平面A1B1C1D1,则m∥n吗?答案不一定,也可能异面.思考3过BC的平面交面A1B1C1D1于B1C1,B1C1与BC是什么关系?答案平行.梳理类型一面面平行的性质定理的应用命题角度1由面面平行的性质定理求线段长例1如图,平面α∥β,A、C∈α,B、D∈β,直线AB与CD交于S,且AS=8,BS=9,CD=34,求CS的长.证明 设AB ,CD 共面γ,因为γ∩α=AC ,γ∩β=BD ,且α∥β, 所以AC ∥BD ,所以△SAC ∽△SBD ,所以SC SC +CD =SASB ,即SC SC +34=89,所以SC =272.引申探究若将本例改为:点S 在平面α,β之间(如图),其他条件不变,求CS 的长.解 设AB ,CD 共面γ,γ∩α=AC ,γ∩β=BD . 因为α∥β,所以AC 与BD 无公共点,所以AC ∥BD , 所以△ACS ∽△BDS ,所以AS BS =CSDS .设CS =x ,则x 34-x =89,所以x =16,即CS =16.反思与感悟 应用平面与平面平行性质定理的基本步骤跟踪训练1 如图所示,平面α∥平面β,△ABC ,△A ′B ′C ′分别在α,β内,线段AA ′,BB ′,CC ′共点于O ,O 在平面α和平面β之间,若AB =2,AC =2,∠BAC =60°,OA ∶OA ′=3∶2,则△A ′B ′C ′的面积为________.答案439解析 AA ′,BB ′相交于O ,所以AA ′,BB ′确定的平面与平面α,平面β的交线分别为AB ,A ′B ′,有AB ∥A ′B ′,且OA OA ′=AB A ′B ′=32,同理可得OA OA ′=AC A ′C ′=32,OAOA ′=BC B ′C ′=32,所以△ABC ,△A ′B ′C ′面积的比为9∶4,又△ABC 的面积为3,所以△A ′B ′C ′的面积为439.命题角度2 利用面面平行证明线线平行例2 如图所示,平面四边形ABCD 的四个顶点A ,B ,C ,D 均在平行四边形A ′B ′C ′D ′外,且AA ′,BB ′,CC ′,DD ′互相平行,求证:四边形ABCD 是平行四边形.证明 ∵四边形A ′B ′C ′D ′是平行四边形, ∴A ′D ′∥B ′C ′.∵A ′D ′⊄平面BB ′C ′C ,B ′C ′⊂平面BB ′C ′C , ∴A ′D ′∥平面BB ′C ′C . 同理AA ′∥平面BB ′C ′C .∵A ′D ′⊂平面AA ′D ′D ,AA ′⊂平面AA ′D ′D , 且A ′D ′∩AA ′=A ′,∴平面AA ′D ′D ∥平面BB ′C ′C .又∵AD ,BC 分别是平面ABCD 与平面AA ′D ′D ,平面BB ′C ′C 的交线,∴AD ∥BC . 同理可证AB ∥CD .∴四边形ABCD 是平行四边形.反思与感悟 本例充分利用了▱A ′B ′C ′D ′的平行关系及AA ′,BB ′,CC ′,DD ′间的平行关系,先得出线面平行,再得面面平行,最后由面面平行的性质定理得线线平行. 跟踪训练2 如图,已知E ,F 分别是正方体ABCD -A 1B 1C 1D 1的棱AA 1,CC 1的中点,求证:四边形BED 1F 是平行四边形.证明如图,连接AC,BD,交点为O,连接A1C1,B1D1,交点为O1,连接BD1,EF,OO1,设OO1的中点为M,由正方体的性质可得四边形ACC1A1为矩形.又因为E,F分别为AA1,CC1的中点,所以EF过OO1的中点M,同理四边形BDD1B1为矩形,BD1过OO1的中点M,所以EF与BD1相交于点M,所以E,B,F,D1四点共面.又因为平面ADD1A1∥平面BCC1B1,平面EBFD1∩平面ADD1A1=ED1,平面EBFD1∩平面BCC1B1=BF,所以ED1∥BF.同理,EB∥D1F.所以四边形BED1F是平行四边形.类型二平行关系的综合应用例3设AB,CD为夹在两个平行平面α,β之间的线段,且直线AB,CD为异面直线,M,P分别为AB,CD的中点.求证:MP∥平面β.证明如图,过点A作AE∥CD交平面β于点E,连接DE,BE.∵AE∥CD,∴AE,CD确定一个平面,设为γ,则α∩γ=AC,β∩γ=DE.又α∥β,∴AC∥DE(面面平行的性质定理),取AE 的中点N ,连接NP ,MN , ∴M ,P 分别为AB ,CD 的中点, ∴NP ∥DE ,MN ∥BE .又NP ⊄β,DE ⊂β,MN ⊄β,BE ⊂β, ∴NP ∥β,MN ∥β,∵NP ∩MN =N ,∴平面MNP ∥β. ∵MP ⊂平面MNP ,MP ⊄β, ∴MP ∥β.反思与感悟 线线平行、线面平行、面面平行是一个有机的整体,平行关系的判定定理、性质定理是转化平行关系的关键,其内在联系如图所示:跟踪训练3 如图所示,在正方体ABCD -A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,且CM =DN .求证MN ∥平面AA 1B 1B .证明 如图,作MP ∥BB 1交BC 于点P ,连接NP ,∵MP ∥BB 1,∴CM MB 1=CPPB .∵BD =B 1C ,DN =CM , ∴B 1M =BN . ∴CP PB =DNNB,∴NP ∥CD ∥AB . ∵NP ⊄平面AA 1B 1B ,AB ⊂平面AA 1B 1B , ∴NP ∥平面AA 1B 1B .∵MP ∥BB 1,MP ⊄平面AA 1B 1B ,BB 1⊂平面AA 1B 1B , ∴MP ∥平面AA 1B 1B ,又∵MP⊂平面MNP,NP⊂平面MNP,MP∩NP=P,∴平面MNP∥平面AA1B1B.∵MN⊂平面MNP,∴MN∥平面AA1B1B.1.已知平面α与平面β平行,a⊂α,则下列命题正确的是()A.a与β内所有直线平行B.a与β内的无数条直线平行C.a与β内的任何一条直线都不平行D.a与β内的一条直线平行答案 B解析若α∥β,a⊂α,则a与β内的部分直线平行,所以A、C、D均不正确,B正确.2.若平面α∥平面β,直线a⊂α,点M∈β,过点M的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.有且只有一条与a平行的直线答案 D解析由于α∥β,a⊂α,M∈β,过M有且只有一条直线与α平行,故D项正确.3.平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是()A.互相平行B.交于一点C.相互异面D.不能确定答案 A解析由平面与平面平行的性质定理知,a∥b,a∥c,b∥d,c∥d,所以a∥b∥c∥d,故选A.4.过正方体ABDC—A1B1C1D1的三顶点A1、C1、B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是________.答案平行解析因平面ABCD∥平面A1B1C1D1,平面ABCD∩平面A1C1B=l,平面A1B1C1D1∩平面A1C1B=A1C1,所以l∥A1C1(面面平行的性质定理).5.已知AB,CD是夹在两个平行平面α,β之间的线段,A,B,C,D四点共面,M,N分别为AB,CD的中点,求证:MN∥平面α.证明平面ABDC与α,β的交线为AC,BD.因为α∥β,所以AC∥BD.又M,N分别为AB,CD的中点,所以MN∥BD,所以MN∥AC.又AC⊂平面α,所以MN∥平面α.1.常用的面面平行的其他几个性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面之间的平行线段长度相等.(3)经过平面外一点有且只有一个平面与已知平面平行.(4)两条直线被三个平行平面所截,截得的对应线段成比例.(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.2.空间中各种平行关系相互转化关系的示意图课时作业一、选择题1.如果平面α平行于平面β,那么()A.平面α内任意直线都平行于平面βB.平面α内有两条相交直线平行于平面βC.平面α内任意直线都平行于平面β内的任意直线D.平面α内的直线与平面β内的直线不能垂直答案 A2.已知α∥β,a⊂α,那么a与β的关系是()A.平行B.相交C.在面内D.垂直答案 A解析平面与平面平行,两个平面没有公共点,所以直线和平面没有公共点,直线与平面平行,故选A.3.下列命题:①一条直线与两个平行平面中的一个平面相交,必与另外一个平面相交;②如果一个平面平行于两个平行平面中的一个平面,必平行于另一个平面;③夹在两个平行平面间的平行线段相等. 其中正确的是命题的个数为( ) A .1 B .2 C .3 D .0 答案 C解析 根据面面平行的性质知①②③正确,故选C.4.如图所示,P 是三角形ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段P A 、PB 、PC 于A ′、B ′、C ′,若P A ′∶AA ′=2∶3,则S △A ′B ′C ′∶S △ABC 等于( )A .2∶25B .4∶25C .2∶5D .4∶5答案 B解析 ∵平面α∥平面ABC ,平面P AB 与它们的交线分别为A ′B ′,AB ,∴AB ∥A ′B ′, 同理B ′C ′∥BC ,易得△ABC ∽△A ′B ′C ′, S △A ′B ′C ′∶S △ABC =(A ′B ′AB )2=(P A ′P A )2=425.5.α,β,γ为三个不重合的平面,a ,b ,c 为三条不同的直线,则下列命题中不正确的是( ) ①⎭⎪⎬⎪⎫a ∥c b ∥c ⇒a ∥b; ②⎭⎪⎬⎪⎫a ∥γb ∥γ⇒a ∥b ; ③⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β; ④⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β; ⑤⎭⎪⎬⎪⎫α∥c a ∥c ⇒α∥a; ⑥⎭⎪⎬⎪⎫α∥γa ∥γ⇒a ∥α. A .④⑥ B .②③⑥ C .②③⑤⑥ D .②③答案 C解析 由公理4及平行平面的传递性知①④正确.举反例知②③⑤⑥不正确.②中a ,b 可以相交,还可以异面;③中α,β可以相交;⑤中a 可以在α内;⑥中a 可以在α内. 6.下列命题中,错误的是( )A .平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行B .平行于同一个平面的两个平面平行C .若两个平面平行,则位于这两个平面内的直线也互相平行D .若两个平面平行,则其中一个平面内的直线平行于另一个平面 答案 C解析 由面面平行的判定定理和性质知A 、B 、D 正确.对于C ,位于两个平行平面内的直线也可能异面.7.设α∥β,A ∈α,B ∈β,C 是AB 的中点,当A 、B 分别在平面α、β内运动时,得到无数个AB 的中点C ,那么所有的动点C ( ) A .不共面B .当且仅当A 、B 分别在两条直线上移动时才共面C .当且仅当A 、B 分别在两条给定的异面直线上移动时才共面D .不论A 、B 如何移动,都共面 答案 D解析 如图所示,A ′、B ′分别是A 、B 两点在α、β上运动后的两点,此时AB 中点C 变成A ′B ′的中点C ′,连接A ′B ,取A ′B 的中点E .连接CE 、C ′E 、AA ′、BB ′、CC ′,则CE ∥AA ′,∴CE ∥α.又C ′E ∥BB ′,∴C ′E ∥β. 又∵α∥β,∴C ′E ∥α.∵C ′E ∩CE =E ,∴平面CC ′E ∥平面α, ∴CC ′∥平面α.∴不论A 、B 如何移动,所有的动点C 都在过C 点且与α、β平行的平面上. 二、填空题8.如图所示,平面四边形ABCD 所在的平面与平面α平行,且四边形ABCD 在平面α内的平行投影A 1B 1C 1D 1是一个平行四边形,则四边形ABCD 的形状一定是________.答案 平行四边形解析 由夹在两平行平面间的平行线段相等可得.9. 如图,在长方体ABCD -A 1B 1C 1D 1中,过BB 1的中点E 作一个与平面ACB 1平行的平面交AB 与M ,交BC 与N ,则MNAC=________.答案 12解析 ∵平面MNE ∥平面ACB 1,由面面平行的性质定理可得EN ∥B 1C ,EM ∥B 1A , 又∵E 为BB 1的中点,∴M ,N 分别为BA ,BC 的中点, ∴MN =12AC .即MN AC =12.10.如图,已知α∥β,GH ,GD ,EH 分别交α,β于A ,B ,C ,D ,E ,F ,且GA =9,AB =12,BH =16,则ACBD=________.答案 37解析 因为α∩平面GAC =AC ,β∩平面GBD =BD ,且α∥β, 所以AC ∥BD ,同理可证AE ∥BF . 又因为∠EAC 与∠FBD 的两边同向, 所以∠EAC =∠FBD .又因为GA =9,AB =12,AC ∥BD , 所以AC BD =GA GB =99+12=37.11.已知平面α∥β,P ∉α且P ∉β,过点P 的直线m 与α,β分别交于点A ,C ,过点P 的直线n 与α,β分别交于点B ,D ,且P A =6,AC =9,PD =8,则BD 的长为________. 答案245或24 解析 如图①所示,∵AC ∩BD =P ,∴经过直线AC 与BD 可确定平面PCD .∵α∥β,α∩平面PCD =AB ,β∩平面PCD =CD ,∴AB ∥CD .∴P A AC =PB BD ,即69=8-BD BD ,∴BD =245. 如图②所示,同理可证AB ∥CD ,∴P A PC =PB PD , 即63=BD -88,∴BD =24. 综上所述,BD 的长为245或24. 12.已知l ,m ,n 是互不相同的直线,α,β,γ是三个不同的平面,给出下列命题: ①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β;②若α∥β,l ⊂α,m ⊂β,则l ∥m ;③若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n .其中所有真命题的序号为________.答案 ③解析 ①中α可能与β相交;②中直线l 与m 可能异面;③中根据线面平行的性质定理可以证明m ∥n .三、解答题13.如图,在三棱柱ABC -A 1B 1C 1中,M 是A 1C 1的中点,平面AB 1M ∥平面BC 1N ,AC ∩平面BC 1N =N .求证:N 为AC 的中点.证明 ∵平面AB 1M ∥平面BC 1N ,平面ACC 1A 1∩平面AB 1M =AM ,平面BC 1N ∩平面ACC 1A 1=C 1N ,∴C 1N ∥AM ,又AC ∥A 1C 1,∴四边形ANC 1M 为平行四边形,∴AN =C 1M =12A 1C 1=12AC , ∴N 为AC 的中点.14.如图,在长方体ABCD -A 1B 1C 1D 1中,E 是BC 上一点,M ,N 分别是AE ,CD 1的中点,AD =AA 1=a ,AB =2a ,求证:MN ∥平面ADD 1A 1.证明 如图,取CD 的中点K ,连接MK ,NK .因为M ,N ,K 分别是AE ,CD 1,CD 的中点, 所以MK ∥AD ,NK ∥DD 1.又MK ⊄平面ADD 1A 1,AD ⊂平面ADD 1A 1, 所以MK ∥平面ADD 1A 1.同理NK ∥平面ADD 1A 1.又MK ∩NK =K ,所以平面MNK ∥平面ADD 1A 1, 又MN ⊂平面MNK ,所以MN ∥平面ADD 1A 1.四、探究与拓展15.如图所示,在三棱柱ABC -A 1B 1C 1中,D 是棱CC 1的中点,问在棱AB 上是否存在一点E ,使DE ∥平面AB 1C 1?若存在,请确定点E 的位置;若不存在,请说明理由.解 存在点E ,且E 为AB 的中点时,DE ∥平面AB 1C 1. 证明如下:如图,取BB 1的中点F ,连接DF ,则DF ∥B 1C 1,因为AB 的中点为E ,连接EF ,则EF∥AB1,B1C1∩AB1=B1,EF∩DF=F,所以平面DEF∥平面AB1C1.又DE⊂平面DEF,所以DE∥平面AB1C1.。
【配套K12】2018版高中数学第二章点直线平面之间的位置关系2.22.2.3直线与平面平行的性质2

2.2.3 直线与平面平行的性质2.2.4 平面与平面平行的性质目标定位 1.证明并掌握直线与平面平行、平面与平面平行的性质定理.2.能应用文字语言、符号语言、图形语言准确描述直线与平面平行,两平面平行的性质定理.3.能用两个性质定理,证明一些空间线面平行关系的简单问题.自 主 预 习1.判断题(1)一条直线如果和一个平面平行,它就和这个平面内的无数条直线平行.(√) (2)如果直线a ∥平面α,直线b ⊂α,则a 与b 平行.(×)(3)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(√) (4)过直线外一点,有且只有一个平面和已知直线平行.(×) 提示 (2)a 与b 平行或异面.(4)过直线外一点可以作一条直线与已知直线平行,但过直线外一点可以作无数个平面与已知直线平行.2.如图所示,过正方体ABCD -A 1B 1C 1D 1的棱BB 1作一平面交平面CDD 1C 1于EE 1,则BB 1与EE 1的位置关系是( )A.平行B.相交C.异面D.不确定解析BB1∥平面CDD1C1,平面BB1E1E∩平面CDD1C1=E1E,BB1⊂平面BB1E1E,由线面平行的性质定理知,BB1∥EE1.答案 A3.若平面α∥平面β,直线a⊂α,点B∈β,则在β内过点B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行C.存在无数多条直线与a平行D.存在唯一一条直线与a平行解析设点B与直线a确定一平面为γ,γ∩β=b,∴a∥b.答案 D4.已知直线l∥平面α,l⊂平面β,α∩β=m,则直线l,m的位置关系是________. 解析由直线与平面平行的性质定理知l∥m.答案平行类型一线面平行性质定理的应用【例1】求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行. 解已知直线a,l,平面α,β满足α∩β=l,a∥α,a∥β.求证:a∥l.证明:如图所示,过a作平面γ交平面α于b,∵a∥α,∴a∥b.同样过a作平面δ交平面β于c,∵a∥β,∴a∥c.则b∥c.又∵b⊄β,c⊂β,∴b∥β.又∵b⊂α,α∩β=l,∴b∥l.又∵a∥b,∴a∥l.规律方法在空间平行关系中,交替使用线线平行、线面平行的判定定理与性质定理是解决此类问题的关键.【训练1】若两个相交平面分别过两条平行直线,则它们的交线和这两条平行直线平行. 解已知:a∥b,a⊂α,b⊂β,α∩β=l.求证:a∥b∥l.证明:如图所示,∵a∥b,b⊂β,a⊄β,∴a∥β,又a⊂α,α∩β=l,∴a∥l,又a∥b,∴a∥b∥l.类型二面面平行性质定理的应用【例2】已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面α.证明(1)若AB、CD在同一平面内,则平面ABDC与α、β的交线为BD、AC.∵α∥β,∴AC∥BD.又M、N为AB、CD的中点,∴MN∥BD.又BD⊂平面α,MN⊄平面α,∴MN∥平面α.(2)若AB、CD异面,如图,过A作AE∥CD交α于E,取AE中点P,连接MP、PN、BE、ED.∵AE∥CD.∴AE、CD确定平面AEDC.则平面AEDC与α、β的交线分别为ED、AC,∵α∥β,∴ED∥AC.又P、N分别为AE、CD的中点,∴PN∥ED,又ED⊂平面α,PN⊄平面α,∴PN∥平面α.同理可证MP∥BE,又MP⊄平面α,BE⊂平面α,∴MP∥平面α,∵AB、CD异面,∴MP、NP相交.∴平面MPN∥平面α.又MN⊂平面MPN,∴MN∥平面α.规律方法 1.利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作是平面的交线,往往需要有三个平面,即有两平面平行,再构造第三个面与两平行平面都相交. 2.面面平行⇒线线平行,体现了转化思想与判定定理的交替使用,可实现线线、线面及面面平行的相互转化.【训练2】如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.(1)求证:AC ∥BD ;(2)已知PA =4 cm ,AB =5 cm ,PC =3 cm ,求PD 的长.(1)证明 ∵PB ∩PD =P ,∴直线PB 和PD 确定一个平面γ,则α∩γ=AC ,β∩γ=BD .又α∥β,∴AC ∥BD . (2)解 由(1)得AC ∥BD ,∴PA AB =PC CD ,∴45=3CD, ∴CD =154(cm),∴PD =PC +CD =274(cm).类型三 平行关系的综合应用(互动探究)【例3】 如图所示,四边形ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH ,求证:GH ∥平面PAD . [思路探究]探究点一 证明平行关系的基本思路是什么?提示 证明平行关系时,应综合应用线线平行、线面平行及面面平行之间的相互转化. 探究点二 解本题的关键是什么?提示 关键是连接AC 交BD 于O ,结合PC 中点M ,利用中位线,进行平行转化,进而作出判断.证明 如图所示,连接AC 交BD 于点O ,连接MO .∵ABCD 是平行四边形,∴O 是AC 的中点,又M 是PC 的中点, ∴PA ∥MO ,而AP ⊄平面BDM ,OM ⊂平面BDM , ∴PA ∥平面BMD ,又∵PA ⊂平面PAHG , 平面PAHG ∩平面BMD =GH ,∴PA ∥GH .又PA⊂平面PAD,GH⊄平面PAD,∴GH∥平面PAD.规律方法 1.本题证明线面平行,利用了线面平行的性质定理和判定定理进行转化,即线线平行⇒线面平行⇒线线平行⇒线面平行.2.在将线面平行转化为线线平行时,注意观察图形中是否是性质定理中符合条件的平面. 【训练3】在长方体ABCD-A1B1C1D1,E为棱DD1上的点,试确定点E的位置,使B1D∥平面A1C1E.解如图,连接B1D1,设A1C1∩B1D1=M,连接ME.若B1D∥平面A1C1E,则B1D平行于过B1D的平面与平面A1C1E的交线.由于B1D⊂平面B1DD1,平面B1DD1∩平面A1C1E=ME,所以B1D∥ME.又因为M为B1D1的中点,所以E为DD1的中点.[课堂小结]1.三种平行关系可以任意转化,其相互转化关系如图所示:2.证明线与线、线与面的平行关系的一般规律是:“由已知想性质,由求证想判定”,是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.1.已知:α∩β=b,a∥α,a∥β,则a与b的位置关系是( )A.a∥bB.a⊥bC.a,b相交但不垂直D.a,b异面解析利用结论:若一直线与两个相交平面平行则此直线与交线平行.答案 A2.已知a,b表示直线,α、β、γ表示平面,下列推理正确的是( )A.α∩β=a,b⊂α⇒a∥bB.α∩β=a,a∥b⇒b∥α且b∥βC.a∥β,b∥β,a⊂α,b⊂α⇒α∥βD.α∥β,α∩γ=a,β∩γ=b⇒a∥b解析由面面平行的性质定理知D正确.答案 D3.过两平行平面α,β外的点P 的两条直线AB 与CD ,它们分别交α于A ,C 两点,交β于B ,D 两点,若PA =6,AC =9,PB =8,则BD 的长为________. 解析 两条直线AB 与CD 相交于P 点,所以可以确定一个平面,此平面与两平行平面α,β的交线AC ∥BD ,所以PA PB =ACBD,又PA =6,AC =9,PB =8,故BD =12.答案 124.如图,已知E ,F 分别是长方体ABCD -A 1B 1C 1D 1的棱A 1B 1、CC 1的中点,过D 1、E 、F 作平面D 1EGF 交BB 1于G .求证:EG ∥D 1F .证明 在长方体ABCD -A 1B 1C 1D 1中,因为平面ABB 1A 1∥平面DCC 1D 1,平面D 1EGF ∩平面ABB 1A 1=EG ,平面D 1EGF ∩平面DCC 1D 1=D 1F ,∴EG ∥D 1F .基 础 过 关1.a ∥α,b ∥β,α∥β,则a 与b 位置关系是( ) A.平行 B.异面C.相交D.平行或异面或相交解析 如图(1),(2),(3)所示,a 与b 的关系分别是平行、异面或相交.答案 D2.已知直线l ∥平面α,P ∈α,那么过点P 且平行于l 的直线( ) A.只有一条,不在平面α内 B.只有一条,在平面α内 C.有两条,不一定都在平面α内 D.有无数条,不一定都在平面α内 解析 如图所示,∵l ∥平面α,P ∈α,∴直线l 与点P 确定一个平面β, α∩β=m ,∴P ∈m ,∴l ∥m 且m 是唯一的. 答案 B3.如图,四棱锥P -ABCD 中,M ,N 分别为AC ,PC 上的点,且MN ∥平面PAD ,则( )A.MN ∥PDB.MN ∥PAC.MN ∥ADD.以上均有可能解析 ∵MN ∥平面PAD ,MN ⊂平面PAC , 平面PAD ∩平面PAC =PA ,∴MN ∥PA . 答案 B4.过正方体ABCD -A 1B 1C 1D 1的三个顶点A 1、C 1、B 的平面与底面ABCD 所在平面的交线为l ,则l 与A 1C 1的位置关系是________.解析 由面面平行的性质可知第三平面与两平行平面的交线是平行的. 答案 平行5.如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.解析 ∵在正方体ABCD -A 1B 1C 1D 1中,AB =2,∴AC =2 2.又E 为AD 的中点,EF ∥平面AB 1C ,EF ⊂平面ADC ,平面ADC ∩平面AB 1C =AC , ∴EF ∥AC ,∴F 为DC 的中点, ∴EF =12AC = 2.答案26.如图所示,在三棱柱ABC -A 1B 1C 1中,过A 1,B ,C 1的平面与平面ABC 的交线为l ,试判断l 与直线A 1C 1的位置关系,并给以证明.解 l ∥A 1C 1证明 在三棱柱ABC -A 1B 1C 1中,A 1C 1∥AC ,A 1C 1⊄平面ABC ,AC ⊂平面ABC , ∴A 1C 1∥平面ABC .又∵A 1C 1⊂平面A 1BC 1,且平面A 1BC 1∩平面ABC =l , ∴A 1C 1∥l .7.如图,在正方体ABCD -A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,且CM =DN ,求证:MN ∥平面AA 1B 1B .证明 如图,作MP ∥BB 1交BC 于点P ,连接NP . ∵MP ∥BB 1,∴CM MB 1=CP PB.∵BD =B 1C ,DN =CM ,∴B 1M =BN ,∴CM MB 1=DN NB, ∴CP PB =DN NB,∴NP ∥CD ∥AB .∵NP ⊄平面AA 1B 1B ,AB ⊂平面AA 1B 1B ,∴NP ∥平面AA 1B 1B . ∵MP ∥BB 1,MP ⊄平面AA 1B 1B ,BB 1⊂平面AA 1B 1B ,∴MP ∥平面AA 1B 1B .又∵MP ⊂平面MNP ,NP ⊂平面MNP ,MP ∩NP =P , ∴平面MNP ∥平面AA 1B 1B .∵MN ⊂平面MNP ,∴MN ∥平面AA 1B 1B .能 力 提 升8.下列说法正确的是( )A.平行于同一条直线的两个平面平行B.平行于同一个平面的两个平面平行C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行D.若三直线a ,b ,c 两两平行,则在过直线a 的平面中,有且只有一个平面与b ,c 均平行 解析 平行于同一条直线的两个平面可以平行也可以相交,所以A 错;B 正确;C 中没有指明这三个点在平面的同侧还是异侧,不正确;D 不正确,因为过直线a 的平面中,只要b ,c 不在其平面内,则与b ,c 均平行. 答案 B9.过平面α外的直线l ,作一组平面与α相交,如果所得的交线为a ,b ,c ,…,则这些交线的位置关系为( ) A.都平行B.都相交且一定交于同一点C.都相交但不一定交于同一点D.都平行或交于同一点解析 ∵l ⊄α,∴l ∥α或l 与α相交.(1)若l ∥α,则由线面平行的性质可知l ∥a ,l ∥b ,l ∥c ,… ∴a ,b ,c ,…这些交线都平行.(2)若l 与α相交,不妨设l ∩α=A ,则A ∈l ,又由题意可知A ∈a ,A ∈b ,A ∈c ,…,∴这些交线交于同一点A .综上可知D 正确. 答案 D10.如图,P 是△ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段PA 、PB 、PC 于A ′、B ′、C ′,若PA ′∶AA ′=2∶3,则S △A ′B ′C ′S △ABC=________.解析 由平面α∥平面ABC ,得AB ∥A ′B ′,BC ∥B ′C ′,AC ∥A ′C ′, 由等角定理得∠ABC =∠A ′B ′C ′, ∠BCA =∠B ′C ′A ′,∠CAB =∠C ′A ′B ′, 从而△ABC ∽△A ′B ′C ′,△PAB ∽△PA ′B ′,S △A ′B ′C ′S △ABC =⎝ ⎛⎭⎪⎫A ′B ′AB 2=⎝ ⎛⎭⎪⎫PA ′PA 2=425. 答案42511.如图所示,已知P是▱ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=l.(1)求证:l∥BC;(2)MN与平面PAD是否平行?试证明你的结论.法一(1)证明因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD.又因为平面PBC∩平面PAD=l,所以BC∥l.(2)解平行.证明如下:取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,又因为MN⊄平面APD,AE⊂平面APD,所以MN∥平面APD.法二(1)证明由AD∥BC,AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.又因为平面PBC∩平面PAD=l,所以l∥AD,l∥BC.(2)解平行.证明如下:设Q是CD的中点,连接NQ,MQ,则MQ∥AD,NQ∥PD,而MQ∩NQ=Q,所以平面MNQ∥平面PAD.MN⊂平面MNQ,所以MN∥平面PAD.探究创新12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.小初高试卷教案类K12小学初中高中解 能.取AB ,C 1D 1的中点M ,N ,连接A 1M ,MC ,CN ,NA 1, ∵A 1N ∥PC 1且A 1N =PC 1,PC 1∥MC ,PC 1=MC ,A 1N 綉MC , ∴四边形A 1MCN 是平行四边形,又∵A 1N ∥PC 1,A 1M ∥BP ,A 1N ∩A 1M =A 1,C 1P ∩PB =P , ∴平面A 1MCN ∥平面PBC 1,因此,过点A 1与截面PBC 1平行的截面是平行四边形. 连接MN ,作A 1H ⊥MN 于点H , ∵A 1M =A 1N =5,MN =22,∴A 1H = 3.∴S △A 1MN =12×22×3= 6. 故S ▱A 1MCN =2S △A 1MN =2 6.。
完整版高中数学必修2《点、直线、平面之间位置关系》知识点
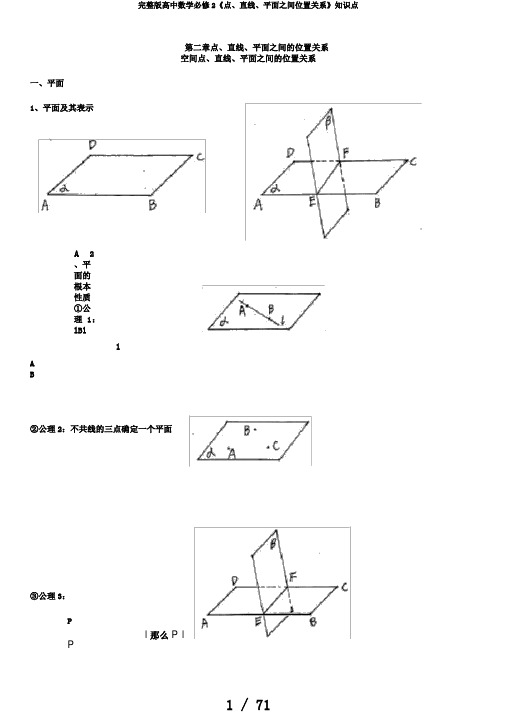
第二章点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示A2、平面的根本性质①公理1:lBllAB②公理2:不共线的三点确定一个平面③公理3:Pl那么P lP二、点与面、直线位置关系1、A1、点与平面有2种位置关系2、B1、A l2、点与直线有2种位置关系2、B l三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系相交共面平行异面3、公理4和定理公理4:l1Pl3l1Pl2l2Pl3定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤:①作:作平行线得到相交直线; ②证:证明作出的角即为所求的异面直线所成的角;③构造三角形求出该角。
提示:1、作平行线常见方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是 00,900。
四、空间中直线与平面之间的位置关系位置关系 直线a 在平面内 直线a 与平面相交直线a 与平面 平行 公共点 有无数个公共点 有且只有一个公共点 没有公共点 符号表示a aI A aP 图形表示 五、空间中平面与平面之间的位置关系位置关系 两个平面平行 两个平面相交公共点 没有公共点有一条公共直线 符号表示 P I a图形表示直线、平面平行的判定及其性质一、线面平行1、判定:b a bPbPa〔线线平行,那么线面平行〕2、性质:aPaP abb〔线面平行,那么线线平行〕二、面面平行1、判定:aba b P PPbP〔线面平行,那么面面平行〕2、性质1:PI a aPbI b〔面面平行,那么线面平行〕性质2:PmPm〔面面平行,那么线面平行〕说明〔1〕判定直线与平面平行的方法:①利用定义:证明直线与平面无公共点。
②利用判定定理:从直线与直线平行等到直线与平面平行。
③利用面面平行的性质:两个平面平行,那么其中一个平面内的直线必平行于另一个平面。
2〕证明面面平行的常用方法利用面面平行的定义:此法一般与反证法结合。
2018版高中数学必修二同步讲义(人教A版)第二章点、直线、平面之间的位置关系2.2.2Word版含答案

2.2.2平面与平面平行的判定学习目标 1.通过直观感知、操作确认,归纳出平面与平面平行的判定定理.2.掌握平面与平面平行的判定定理,并能初步利用定理解决问题.知识点平面与平面平行的判定定理思考1三角板的一条边所在平面与平面α平行,这个三角板所在平面与平面α平行吗?答案不一定.思考2三角板的两条边所在直线分别与平面α平行,这个三角板所在平面与平面α平行吗?答案平行.思考3如图,平面BCC1B1内有多少条直线与平面ABCD平行?这两个平面平行吗?答案无数条.不平行.梳理面面平行的判定定理类型一面面平行的判定定理例1下列四个命题:(1)若平面α内的两条直线分别与平面β平行,则平面α与平面β平行;(2)若平面α内有无数条直线分别与平面β平行,则平面α与平面β平行;(3)平行于同一直线的两个平面平行;(4)两个平面分别经过两条平行直线,这两个平面平行.其中正确的个数是______________.答案0反思与感悟在判定两平面是否平行时,一定要强调一个平面内的“两条相交直线”这个条件,线不在多,相交就行.跟踪训练1设直线l, m, 平面α,β,下列条件能得出α∥β的有()①l⊂α,m⊂α,且l∥β,m∥β;②l⊂α,m⊂α,且l∥m,l∥β,m∥β;③l∥α,m∥β,且l∥m;④l∩m=P, l⊂α,m⊂α,且l∥β,m∥β.A.1个B.2个C.3个D.0个答案 A解析①错误,因为l, m不一定相交;②错误,一个平面内有两条平行直线平行于另一个平面,这两个平面可能相交;③错误,两个平面可能相交;④正确.类型二平面与平面平行的证明例2如图所示,在正方体AC1中,M,N,P分别是棱C1C,B1C1,C1D1的中点,求证:平面MNP∥平面A1BD.证明如图,连接B1C.由已知得A1D∥B1C,且MN∥B1C,∴MN∥A1D.又∵MN⊄平面A1BD,A1D⊂平面A1BD,∴MN∥平面A1BD.连接B1D1,同理可证PN∥平面A1BD.又∵MN⊂平面MNP,PN⊂平面MNP,且MN∩PN=N,∴平面MNP∥平面A1BD.引申探究若本例条件不变,求证:平面CB1D1∥平面A1BD.证明因为ABCD-A1B1C1D1为正方体,所以DD1綊BB1,所以BDD1B1为平行四边形,所以BD∥B1D1.又BD⊄平面CB1D1,B1D1⊂平面CB1D1,所以BD∥平面CB1D1,同理A1D∥平面CB1D1.又BD∩A1D=D,所以平面CB1D1∥平面A1BD.反思与感悟判定平面与平面平行的四种常用方法(1)定义法:证明两个平面没有公共点,通常采用反证法.(2)利用判定定理:一个平面内的两条相交直线分别平行于另一个平面.证明时应遵循先找后作的原则,即先在一个平面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β.(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.跟踪训练2如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分別是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EF A1∥平面BCHG.证明(1)因为G,H分别是A1B1,A1C1的中点,所以GH是△A1B1C1的中位线,所以GH∥B1C1.又因为B1C1∥BC,所以GH∥BC,所以B,C,H,G四点共面.(2)因为E,F分别是AB,AC的中点,所以EF∥BC.因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF∥平面BCHG.因为A1G∥EB,A1G=EB,所以四边形A1EBG是平行四边形,所以A1E∥GB.因为A1E⊄平面BCHG,GB⊂平面BCHG,所以A1E∥平面BCHG.因为A1E∩EF=E,所以平面EF A1∥平面BCHG.类型三线线平行与面面平行的综合应用命题角度1线线、线面、面面平行的相互转化的证明问题例3如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点,求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.证明(1)如图,连接SB.∵E,G分别是BC,SC的中点,∴EG∥SB.又∵SB⊂平面BDD1B1,EG⊄平面BDD1B1,∴EG∥平面BDD1B1.(2)连接SD.∵F,G分别是DC,SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴FG∥平面BDD1B1.又EG∥平面BDD1B1,且EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.反思感悟解决线线平行与面面平行的综合问题的策略(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的.(2)线线平行――→判定线面平行――→判定面面平行所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.跟踪训练3 如图所示,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G ,H 分别为BC ,CC 1,C 1D 1,A 1A 的中点.求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面HB 1D 1.证明 (1)如图,取BB 1的中点M ,连接C 1M ,HM ,易知HMC 1D 1是平行四边形,∴HD 1∥MC 1, 又由已知可得MC 1∥BF ,∴BF ∥HD 1.(2)取BD 的中点O ,连接OE ,D 1O ,则OE 綊12DC .又D 1G 綊12DC ,∴OE 綊D 1G ,∴四边形OEGD 1是平行四边形,∴GE ∥D 1O . 又D 1O ⊂平面BB 1D 1D ,EG ⊄平面BB 1D 1D , ∴EG ∥平面BB 1D 1D .(3)由(1)知HD 1∥BF ,又BD ∥B 1D 1,B 1D 1,HD 1⊂平面HB 1D 1,BF ,BD ⊂平面BDF , 且B 1D 1∩HD 1=D 1,BD ∩BF =B , ∴平面BDF ∥平面HB 1D 1.命题角度2 线线与面面平行的探索性问题例4 如图所示,在正方体ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,问:当点Q 在什么位置时,平面D 1BQ ∥平面P AO ?解 当Q 为CC 1的中点时,平面D 1BQ ∥平面P AO .∵Q 为CC 1的中点,P 为DD 1的中点,连接PQ ,如图,易证四边形PQBA 是平行四边形,∴QB ∥P A .又∵AP ⊂平面APO ,QB ⊄平面APO ,∴QB ∥平面APO .∵P ,O 分别为DD 1,DB 的中点,∴D 1B ∥PO . 同理可得D 1B ∥平面P AO , 又D 1B ∩QB =B , ∴平面D 1BQ ∥平面P AO .反思感悟 对于探索性问题,一是可直接运用题中的条件,结合所学过的知识探求;二是可先猜想,然后证明猜想的正确性.跟踪训练4 在底面是平行四边形的四棱锥P -ABCD 中,点E 在PD 上,且PE ∶ED =2∶1,M 为PE 的中点,在棱PC 上是否存在一点F ,使平面BFM ∥平面AEC ?并证明你的结论.解 当F 是棱PC 的中点时,平面BFM ∥平面AEC . ∵M 是PE 的中点,∴FM ∥CE . ∵FM ⊄平面AEC ,CE ⊂平面AEC , ∴FM ∥平面AEC . 由EM =12PE =ED ,得E 为MD 的中点,连接BM ,BD ,如图所示,设BD∩AC=O,则O为BD的中点.连接OE,则BM∥OE.∵BM⊄平面AEC,OE⊂平面AEC,∴BM∥平面AEC.又∵FM⊂平面BFM,BM⊂平面BFM,FM∩BM=M,∴平面BFM∥平面AEC.1.下列命题中正确的是()A.一个平面内两条直线都平行于另一平面,那么这两个平面平行B.如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行C.平行于同一直线的两个平面一定相互平行D.如果一个平面内的无数多条直线都平行于另一平面,那么这两个平面平行答案 B解析如果一个平面内任何一条直线都平行于另一个平面,即两个平面没有公共点,则两平面平行,所以B正确.2.在正方体中,相互平行的面不会是()A.前后相对侧面B.上下相对底面C.左右相对侧面D.相邻的侧面答案 D解析由正方体的模型知前后面、上下面、左右面都相互平行,所以选D.3.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G答案 A解析如图,∵EG∥E1G1,EG⊄平面E1FG1,E1G1⊂平面E1FG1,∴EG∥平面E1FG1.又G1F∥H1E,同理可证H1E∥平面E1FG1,又H1E∩EG=E,∴平面E1FG1∥EGH1.4.如图,已知在三棱锥P-ABC中,D,E,F分别是棱P A,PB,PC的中点,则平面DEF 与平面ABC的位置关系是________.答案平行解析在△P AB中,因为D,E分别是P A,PB的中点,所以DE∥AB.又DE⊄平面ABC,因此DE∥平面ABC.同理可证EF∥平面ABC.又DE∩EF=E,所以平面DEF∥平面ABC.5.如图,在正方体ABCD-A1B1C1D1中,P为DD1中点.能否同时过D1,B两点作平面α,使平面α∥平面P AC?证明你的结论.解能作出满足条件的平面α,其作法如下:如图,连接BD1,取AA1的中点M,连接D1M,。
高中数学第二章点、直线、平面之间的位置关系2.32.3.2平面与平面垂直的判定学案新人教A版必修2

(浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.3 2.3.2 平面与平面垂直的判定学案新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.3 2.3.2 平面与平面垂直的判定学案新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.3 2.3.2 平面与平面垂直的判定学案新人教A版必修2的全部内容。
2.3.2 平面与平面垂直的判定目标定位1。
了解二面角及其平面角的概念,会求简单的二面角的大小.2.通过直观感知、操作确认,归纳平面与平面垂直的判定定理.3.能运用判定定理证明一些空间位置关系的简单命题。
自主预习1.二面角(1)二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
这条直线叫做二面角的棱.这两个半平面叫做二面角的面。
如图(1)可记作:二面角α-l-β或P-AB-Q或P-l-Q。
如图(2)对二面角α-l-β若有:①O∈l;②OA⊂α,OB⊂β;③OA⊥l,OB⊥l.则∠AOB就叫做二面角α-l-β的平面角。
2.平面与平面的垂直(1)定义:如果两个平面相交,且它们所成的二面角是直二面角,就说这两个平面互相垂直。
(2)画法:记作:α⊥β。
(3)面面垂直的判定定理文字语言:一个平面过另一个平面的垂线,则这两个平面垂直。
图形语言:如图所示符号语言:错误!⇒α⊥β。
即时自测1.判断题(1)若α∩β=a,b⊂α,a⊥b,则α⊥β.(×)(2)若直线l⊥平面α,l⊂平面β,则α与β相交且垂直。
高中数学第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.1.1平面检测

2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面检测新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面检测新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面检测新人教A版必修2的全部内容。
2.1.1 平面A级基础巩固一、选择题1.下列图形均表示两个相交平面,其中画法正确的是()解析:A中图形没有画出两平面的交线,故不正确;B,C中图形的实、虚线没有按照画法原则去画,也不正确.答案:D2.空间不共线的四点,可以确定平面的个数是( )A.0 B.1C.1或4 D.无法确定解析:若有三点共线,则由直线与直线外一点确定一个平面,得不共线的四点,可以确定平面的个数为1个;若任意三点均不共线,则空间不共线的四点,可以确定平面的个数是4,故空间不共线的四点,可以确定平面的个数是1或4。
故选C。
答案:C3.下列图形中,不一定是平面图形的是( )A.三角形B.菱形C.梯形D.四边相等的四边形解析:三角形有两条相交直线,梯形和菱形中都有两条平行直线,所以它们均为平面图形,而四边相等的四边形不一定是平面图形.答案:D4.如果直线a⊂平面α,直线b⊂平面α,M∈a,N∈b,M∈l,N∈l,则 ( )A.l⊂αB.l⊄αC.l∩α=M D.l∩α=N解析:因为M∈l,N∈l,且M∈α,N∈α,所以l⊂α。
2018年秋人教A版高中数学必修2课件 第二章 点、直线、平面之间的位置关系 2.2.1、2 精品
[类题通法] 两个平面平行的判定定理是确定面面平行的重要方法.解 答问题时一定要寻求好判定定理所需要的条件,特别是相交的 条件,即与已知平面平行的两条直线必须相交,才能确定面面 平行.
[活学活用] 如右图所示,已知四棱锥PABCD的底面ABCD为矩形, E,F,H分别为AB,CD,PD的中点. 求证:平面AFH∥平面PCE.
(2)连接 SD.∵F,G 分别是 DC,SC 的中点,∴FG∥SD. 又∵SD⊂平面 BDD1B1,FG⊄平面 BDD1B1, ∴FG∥平面 BDD1B1. 又 EG∥平面 BDD1B1, 且 EG⊂平面 EFG,FG⊂平面 EFG, EG∩FG=G, ∴平面 EFG∥平面 BDD1B1.
4.探索点的位置问题
因为四边形 C1CDD1 与 B1BCC1 都是正方形,F,G 分别为 C1D1 和 CD 的中点,所以 FG∥C1C∥B1B,且 FG=C1C=B1B. 因此四边形 B1BGF 是平行四边形,所以 B1F∥BG.而 B1F⊄平面 A1BE,BG⊂平面 A1BE,故 B1F∥平面 A1BE.
应用 落实体验
[活学活用] 如右图所示,在正方体ABCDA1B1C1D1中,S是B1D1的中 点,E,F,G分别是BC,DC,SC的中点. 求证:(1)直线EG∥平面BDD1B1; (2)平面EFG∥平面BDD1B1.
证明:(1)如图,连接 SB. ∵E,G 分别是 BC,SC 的中点, ∴EG∥SB. 又∵SB⊂平面 BDD1B1, EG⊄平面 BDD1B1. ∴直线 EG∥平面 BDD1B1.
连接 BD,则 O∈BD, 又∵O 为 DB 的中点,P 为 D1D 的中点, ∴PO∥D1B.(8 分) 又∵PO⊂平面 PAO,D1B⊄平面 PAO, ∴D1B∥平面 PAO.(10 分) 又∵D1B∩BQ=B, ∴平面 D1BQ∥平面 PAO.(12 分)
高中数学第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.1.1平面优化

2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面优化练习新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面优化练习新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面优化练习新人教A版必修2的全部内容。
2。
1。
1 平面[课时作业][A组基础巩固]1.平行六面体ABCD。
A1B1C1D1中,既与AB共面又与CC1共面的棱的条数为( )A.3 B.4 C.5 D.6解析:依题意,与AB和CC1都相交的棱有BC;与AB相交且与CC1平行的棱有AA1,BB1;与AB平行且与CC1相交的棱有CD,C1D1,故符合条件的棱共有5条.答案:C2.下列命题:①圆上三点可以确定一个平面;②圆心和圆上两点可以确定一个平面;③四条平行线不能确定五个平面;④不共线的五点,可以确定五个平面,必有三点共线.其中假命题的个数为( )A.1 B.2 C.3 D.4解析:由公理可知,①显然正确;若圆上两点为直径的两个端点,则圆心和圆上两点不能确定一个平面,②不正确;四条平行线只能确定一个,四个或六个平面,③正确;④不共线的五点,可以确定五个平面,必有三点共线,不正确,比如四棱锥.故选B.答案:B3.在空间四边形ABCD的边AB,BC,CD,DA上分别取点E,F,G,H,若EF与HG交于点M,则()A.M一定在直线AC上B.M一定在直线BD上C.M可能在直线AC上,也可能在直线BD上D.M不在直线AC上,也不在直线BD上解析:由题意得EF在平面ABC内,HG在平面ACD内,∴EF与HG交于点M一定落在面ABC与面ACD的交线AC上.答案:A4.已知下列三个命题:①若点P不在平面α内,A,B,C三点都在平面α内,则P,A,B,C 四点不在同一平面内;②两两相交的三条直线在同一平面内;③两组对边分别相等的四边形是平行四边形.其中真命题的个数是()A.0 B.1 C.2 D.3解析:当A,B,C三点都在平面α内,且三点共线时,P,A,B,C四点在同一个平面内,故①不是真命题;三棱锥的三条侧棱所在的直线两两相交,但三条直线不在同一平面内,故②不是真命题;两组对边分别相等的四边形也可能是空间四边形,故③不是真命题.答案:A5.用一个平面截正方体所得的截面图形不可能是( )A.六边形B.五边形C.菱形D.直角三角形解析:可用排除法,正方体的截面图形可能是六边形、五边形、菱形,故选D。
2018秋新版高中数学人教A版必修2:第二章点、直线、平面之间的位置关系 本章整合2

12345
2(2016·全国高考甲卷)α,β是两个平面,m,n是两条直线,有下列四个
命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m⊂α,那么m∥β.
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
专题一 专题二 专题三 专题四 专题五
专题五 空间角 空间角包括:异面直线所成的角、直线与平面所成的角以及二面 角.这些角是对点、直线、平面所组成的空间图形的位置关系进行 定性分析和定量计算的重要组成部分,学习时要深刻理解它们的含 义,并能综合应用空间各种角的概念和平面几何的知识熟练解题. 求异面直线所成的角常用平移法(转化为两条相交直线的夹角). 求直线与平面所成的角常需先作出这个线面角,再在三角形中求 解. 求二面角常需先作出二面角的平面角.作平面角的常用方法有三 种:定义法、垂线法、垂面法. 总之,求空间角的大小一般都转化为平面角来计算.其计算步骤 为:一作二证三计算.
(1)判定:
������ ∥ ������,������ ∥ ������ ① ������ ⊂ ������,������ ⊂ ������
������⋂������ = ������
⇒α∥β,②
������ ������
∥ ∥
������ ������
⇒α∥β.
(2)性质:
������ ∥ ������ ① ������⋂������ =
正确,故正确命题的编号有②③④.
答案:②③④
12345
3
(2016·全国高考丙卷)如图,在四棱锥P-ABCD中,PA⊥底面 ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一 点,AM=2MD,N为PC的中点. (1)证明MN∥平面PAB; (2)求四面体N-BCM的体积.
2018学年高中数学必修二教师用书配套课件:第二章 点、直线、平面之间的位置关系 2.3.2 精品

(2)因为AD⊥BD,EF∥AD,所以EF⊥BD. 因为CB=CD,F是BD的中点,所以CF⊥BD. 又EF∩CF=F,所以BD⊥平面EFC. 因为BD⊂平面BCD,所以平面EFC⊥平面BCD.
类型三:垂直关系的综合应用
【典例3】(2016·四川高考)如图,在四
棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=
【解题指南】(1)要证明线面平行可利用面面平行加以 证明.(2)过H点向AC作垂线,垂足为M,过M点向GF作垂 线,垂足为N,连接HN.求出∠MNH即可.
【解析】(1)因为DEF-ABC是三棱台,且AB=2DE, 所以BC=2EF,AC=2DF. 因为点G,H分别是AC,BC的中点,所以GH∥AB, 因为AB⊄平面FGH,GH⊂平面FGH,所以AB∥平面 FGH.
A.30° B.45° C.60° D.90°
【解析】选B.因为∠D1CD为二面角D1-BC-D的平面角, 而∠D1CD=45°.
2.直线l⊥α,l⊂β,则α与β的位置关系是( )
A.平行
B.可能重合
C.相交且垂直
D.相交不垂直
【解析】选C.由平面与平面垂直的判定定理,得α与
β垂直.
3.过两点与一个已知平面垂直的平面 ( )
【规律总结】求二面角的平面角的步骤 (1)作:找出或作出二面角的平面角. (2)证:证明所找或作的角就是二面角的平面角. (3)求:在三角形中解出角的大小.
【巩固训练】如图,四边形ABCD是正方形,PA⊥平面 ABCD,且PA=AB.求二面角B-PC-D的大小.
【解题指南】作BE⊥PC,连接DE,证明DE⊥PC,确定 二面角B-PC-D的平面角,解三角形求解.
【规律总结】证明面面垂直的两个方法及实质 (1)定义法:证明二面角的平面角为直角. 步骤:①找出两个相交平面的平面角;②证明这个平 面角是直角;③根据定义,说明这两个平面互相垂直.
【配套K12】2018版高中数学第二章点直线平面之间的位置关系2.32.3.3直线与平面垂直的性质2

2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质目标定位 1.证明并掌握直线与平面、平面与平面垂直的性质定理,并能用文字、符号和图形语言描述定理.2.能运用性质定理证明一些空间位置关系的简单命题.3.理解“平行”与“垂直”之间的相互转化.自 主 预 习1.直线与平面垂直的性质定理2.1.判断题(1)两条平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.(√) (2)垂直于同一平面的两个平面平行.(×)(3)如果两个平面垂直,那么经过第一个平面内一点且垂直于第二个平面的直 线在第一个平面内.即α⊥β,A ∈α,A ∈b ,b ⊥β⇒b ⊂α.(√)(4)如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β.(×)提示(2)垂直于同一平面的两个平面可以相交也可以平行.(4)直线与平面β位置关系不确定.2.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( )A.相交B.异面C.平行D.不确定解析因为l⊥AB,l⊥AC,AB⊂α,AC⊂α且AB∩AC=A,所以l⊥α,同理可证m⊥α,所以l∥m.答案 C3.在长方体ABCD-A1B1C1D1的棱AB上任取一点E,作EF⊥A1B1于F,则EF与平面A1B1C1D1的关系是( )A.平行B.EF⊂平面A1B1C1D1C.相交但不垂直D.相交且垂直解析在长方体ABCD-A1B1C1D1中,平面A1ABB1⊥平面A1B1C1D1且平面A1ABB1∩平面A1B1C1D1=A1B1,又EF⊂面A1ABB1,EF⊥A1B1,∴EF⊥平面A1B1C1D1,答案D正确.答案 D4.已知a、b为直线,α、β为平面.在下列四个命题中,正确的命题是________(填序号).①若a⊥α,b⊥α,则a∥b;②若a∥α,b∥α,则a∥b;③若a⊥α,a⊥β,则α∥β;④若α∥b,β∥b,则α∥β.解析由“垂直于同一平面的两直线平行”知①真;由“平行于同一平面的两直线平行或异面或相交”知②假;由“垂直于同一直线的两平面平行”知③真;易知④假.答案①③类型一直线与平面垂直的性质及应用【例1】如图,正方体ABCD-A1B1C1D1中,EF与异面直线AC、A1D都垂直相交.求证:EF∥BD1.证明如图所示,连接AB1、B1D1、B1C、BD,∵DD1⊥平面ABCD,AC⊂平面ABCD,∴DD1⊥AC.又AC⊥BD,DD1∩BD=D,∴AC⊥平面BDD1B1,又BD1⊂平面BDD1B1,∴AC⊥BD1.同理可证BD1⊥B1C,又AC∩B1C=C,∴BD1⊥平面AB1C.∵EF⊥A1D,A1D∥B1C,∴EF⊥B1C.又∵EF⊥AC,AC∩B1C=C,∴EF⊥平面AB1C,∴EF∥BD1.规律方法证明线线平行常有如下方法:(1)利用线线平行定义:证共面且无公共点;(2)利用三线平行公理:证两线同时平行于第三条直线;(3)利用线面平行的性质定理:把证线线平行转化为证线面平行;(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直;(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.【训练1】如图,已知平面α∩平面β=l,EA⊥α,垂足为A,EB⊥β,垂足为B,直线a⊂β,a⊥AB.求证:a∥l.证明因为EA⊥α,α∩β=l,即l⊂α,所以l⊥EA.同理l⊥EB,又EA∩EB=E,所以l⊥平面EAB.因为EB⊥β,a⊂β,所以EB⊥a,又a⊥AB,EB∩AB=B,所以a⊥平面EAB.因此,a∥l.类型二平面与平面垂直的性质及应用【例2】已知:α、β、γ是三个不同平面,l为直线,α⊥γ,β⊥γ,α∩β=l.求证:l⊥γ.证明法一设α∩γ=a,β∩γ=b,在γ内任取一点P,过P在γ内作直线m⊥a,n ⊥b,如图.∵α⊥γ,β⊥γ,∴m⊥α,n⊥β,又∵α∩β=l,∴m⊥l,n⊥l,又m∩n=P,∴l⊥γ.法二如图,α∩γ=a,β∩γ=b,在α内作m⊥a,在β内作n⊥b.∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ,∴m∥n.又∵n⊂β,m⊄β,∴m∥β,又α∩β=l,m⊂α,∴m∥l,∴l⊥γ.规律方法 1.证明或判定线面垂直的常用方法有:(1)线面垂直的判定定理;(2)面面垂直的性质定理;(3)若a∥b,a⊥α则b⊥α;(a,b为直线,α为平面).(4)若a⊥α,α∥β则a⊥β;(a为直线,α,β为平面).2.两平面垂直的性质定理告诉我们要将面面垂直转化为线面垂直,方法是在其中一个面内作(找)与交线垂直的直线.【训练2】设平面α⊥平面β,点P在平面α内,过点P作平面β的垂线a,试判断直线a与平面α的位置关系.解如图,设α∩β=c,过点P在平面α内作直线b⊥c.根据平面与平面垂直的性质定理有b⊥β.因为过一点有且只有一条直线与平面β垂直,所以直线a与直线b重合,因此a⊂α.类型三线线、线面、面面垂直的综合应用(互动探究)【例3】如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.[思路探究]探究点一运用面面垂直的性质定理的一般策略是什么?提示运用面面垂直的性质定理时,一般要作辅助线:过其中一个平面内一点作交线的垂线.这样就把面面垂直转化成线面垂直或线线垂直了.探究点二线线、线面、面面垂直关系之间有怎样的转化关系?提示证明(1)∵在菱形ABCD中,∠DAB=60°,∴△ABD为正三角形,又G为AD的中点,∴BG⊥AD.又平面PAD⊥平面ABCD,BG⊂平面ABCD,平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.(2)连接PG,如图,∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.由(1)知BG⊥AD,PG∩BG=G,∴AD⊥平面PGB,∵PB⊂平面PGB,∴AD⊥PB.规律方法证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理.本题已知面面垂直,故可考虑面面垂直的性质定理.利用面面垂直的性质定理.证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.【训练3】如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC =PB=PC=2CD,侧面PBC⊥底面ABCD.PA与BD是否相互垂直?请证明你的结论.解PA与BD相互垂直.证明如下:如图,取BC的中点O,连接PO、AO.∵PB=PC,∴PO⊥BC,又侧面PBC⊥底面ABCD,平面PBC∩平面ABCD=BC,∴PO⊥底面ABCD,又BD⊂平面ABCD.∴PO⊥BD,在直角梯形ABCD中,易证△ABO≌△BCD,∠BAO=∠CBD,∠CBD+∠ABD=90°,∴∠BAO+∠ABD=90°,∴AO⊥BD,又PO∩AO=O,∴BD⊥平面PAO,∴BD⊥PA,即PA与BD相互垂直.[课堂小结]1.线面垂直的性质定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“垂直”与“平行”关系相互转化的依据.2.面面垂直的性质定理揭示了“面面垂直、线面垂直及线线垂直”间的内在联系,体现了数学中的转化与化归思想,其转化关系如下:1.下列说法正确的是( )A.垂直于同一条直线的两直线平行B.垂直于同一条直线的两直线垂直C.垂直于同一个平面的两直线平行D.垂直于同一条直线的一条直线和平面平行解析由线面垂直的性质定理知C正确.答案 C2.设α-l-β是直二面角,直线a⊂α,直线b⊂β,a,b与l都不垂直,那么( )A.a与b可能垂直,但不可能平行B.a与b可能垂直,也可能平行C.a与b不可能垂直,但可能平行D.a与b不可能垂直,也不可能平行解析当a,b都与l平行时,则a∥b,所以A、D错,如图,若a⊥b过a上一点P在α内作a′⊥l,因为α⊥β,所以a′⊥β,又b⊂β,∴a′⊥b,∴b⊥α,而l⊂α,∴b⊥l,与b和l不垂直矛盾,所以B错.答案 C3.如图,在三棱锥P-ABC内,侧面PAC⊥底面ABC,且∠PAC=90°,PA=1,AB=2,则PB =________.解析∵侧面PAC⊥底面ABC,交线为AC,∠PAC=90°(即PA⊥AC),PA⊂平面PAC,∴PA ⊥平面ABC,又AB⊂平面ABC,∴PA⊥AB,∴PB=PA2+AB2=1+4= 5.答案 54.如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,求证:平面SCD⊥平面SBC.证明∵底面ABCD是矩形,∴BC⊥CD.又∵平面SDC⊥平面ABCD,平面SDC∩平面ABCD=CD,BC⊂平面ABCD,∴BC⊥平面SCD.又∵BC⊂平面SBC,∴平面SCD⊥平面SBC基础过关1.下列命题中错误的是( )A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β解析由平面与平面垂直的有关性质可以判断出D项错误.答案 D2.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD 折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析如图,在平面图形中CD⊥BD,折起后仍然满足CD⊥BD,由于平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,CD⊂平面BCD,故CD⊥平面ABD,又AB⊂平面ABD,CD⊥AB.又AB⊥AD,AD∩CD=D,故AB⊥平面ADC,又AB⊂平面ABC,所以平面ADC⊥平面ABC.答案 D3.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β解析如图,在长方体ABCD-A1B1C1D1中,平面BCC1B1⊥平面ABCD,BC1⊂平面BCC1B1,BC⊂平面ABCD,而BC1不垂直于BC,故A错误.平面A1B1C1D1∥平面ABCD,B1D1⊂平面A1B1C1D1,AC⊂平面ABCD,但B1D1和AC不平行,故B错误.AB⊥A1D1,AB⊂平面ABCD,A1D1⊂平面A1B1C1D1,但平面A 1B 1C 1D 1∥平面ABCD ,故C 错误.故选D.答案 D4.a ,b 是两条不同直线,α为平面,以下命题中正确的是________(填序号).①⎩⎪⎨⎪⎧a ⊥b ,b ⊥α⇒a ∥α;②⎩⎪⎨⎪⎧a ∥α,a ⊥b ⇒b ⊥α;③⎩⎪⎨⎪⎧a ⊥α,b ⊥α⇒a ∥b ; ④⎩⎪⎨⎪⎧a ∥b ,a ⊥α⇒b ⊥α.解析 ①中a 可能在α内;②中b 也可能与α平行,③④正确 . 答案 ③④5.若α⊥β,α∩β=AB ,a ∥α,a ⊥AB ,则a 与β的关系为________. 解析 如图,过a 作平面γ,设γ∩α=b , ∵a ∥α,∴a ∥b .又∵a ⊥AB ,∴b ⊥AB .又∵α⊥β,α∩β=AB ,b ⊂α,∴b ⊥β,∴a ⊥β.答案 a ⊥β6.如图三棱锥P -ABC 中,已知△ABC 是等腰直角三角形,∠ABC =90°,△PAC 是直角三角形,∠PAC =90°,∠ACP =30°,平面PAC ⊥平面ABC .求证:平面PAB ⊥平面PBC .证明 ∵平面PAC ⊥平面ABC , 平面PAC ∩平面ABC =AC ,PA ⊥AC ,PA ⊂平面PAC ,∴PA ⊥平面ABC .又BC ⊂平面ABC ,∴PA ⊥BC .又∵AB ⊥BC ,AB ∩PA =A ,∴BC ⊥平面PAB . 又BC ⊂平面PBC ,∴平面PAB ⊥平面PBC .7.如图,在四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面PAD ⊥底面ABCD ,PA ⊥AD ,E 和F 分别是CD 和PC 的中点.求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.证明(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,PA⊂平面PAD,所以PA⊥底面ABCD.(2)因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE.所以四边形ABED为平行四边形.所以BE∥AD.又因为BE⊄平面PAD,AD⊂平面PAD,所以BE∥平面PAD.(3)因为AB⊥AD,而且四边形ABED为平行四边形,所以BE⊥CD,AD⊥CD.由(1)知PA⊥底面ABCD,CD⊂平面ABCD,所以PA⊥CD.又PA∩AD=A,所以CD⊥平面PAD.又PD⊂平面PAD,所以CD⊥PD.因为E和F分别是CD和PC的中点,所以PD∥EF.所以CD⊥EF.又因为CD⊥BE,EF∩BE=E,所以CD⊥平面BEF.又CD⊂平面PCD,所以平面BEF⊥平面PCD.能力提升8.如图所示,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则点C1在底面ABC上的射影H必在( )A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析连接AC1,∠BAC=90°,即AC⊥AB,又AC⊥BC1,AB∩BC1=B,所以AC⊥平面ABC1.又AC⊂平面ABC,于是平面ABC1⊥平面ABC,且AB为交线,因此,点C1在平面ABC上的射影必在直线AB上,故选A.答案 A9.如图,正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,现在沿SE、SF、EF把这个正方形折成一个四面体,使G1、G2、G3重合,重合后的点记为G.给出下列关系:①SG⊥平面EFG;②SE⊥平面EFG;③GF⊥SE;④EF⊥平面SEG.其中成立的有( )A.①与②B.①与③C.②与③D.③与④解析由SG⊥GE,SG⊥GF,GE∩GF=G,得SG⊥平面EFG,排除C、D;若SE⊥平面EFG,则SG∥SE,这与SG∩SE=S矛盾,排除A,故选B.答案 B10.如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.若CD=2,平面ABCD⊥平面DCEF,则线段MN的长等于________.解析取CD的中点G,连接MG,NG.因为ABCD,DCEF为正方形,且边长为2,所以MG⊥CD,MG=2,NG= 2.因为平面ABCD⊥平面DCEF,平面ABCD∩平面DCEF=CD,所以MG⊥平面DCEF,由于GN⊂平面CDEF,可得MG⊥NG,所以MN=MG2+NG2= 6.答案 611.如图所示,在平行四边形ABCD中,已知AD=2AB=2a,BD=3a,AC∩BD=E,将其沿对角线BD折成直二面角.求证:(1)AB⊥平面BCD;(2)平面ACD⊥平面ABD.证明(1)在△ABD中,AB=a,AD=2a,BD=3a,∴AB2+BD2=AD2,∴∠ABD=90°,AB⊥BD.又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,∴AB⊥平面BCD.(2)∵折叠前四边形ABCD是平行四边形,且AB⊥BD,∴CD⊥BD.∵AB⊥平面BCD,CD⊂平面BCD.∴AB⊥CD.∵AB∩BD=B,∴CD⊥平面ABD.又∵CD⊂平面ACD,∴平面ACD⊥平面ABD.探究创新12.在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.(1)证明因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB,AA1⊥AC.因为AB,AC为平面ABC内两条相交的直线,所以AA1⊥平面ABC.因为直线BC⊂平面ABC,所以AA1⊥BC.又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条的相交直线,所以BC⊥平面ACC1A1. (2)解取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.由已知,O 为AC 1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC 1的中位线,所以MD 綉12AC ,OE 綉12AC , 因此MD 綉OE .连接OM ,从而四边形MDEO 为平行四边形, 则DE ∥MO .因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC , 所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点), 使直线DE ∥平面A 1MC .。
高中数学第二章点、直线、平面之间的位置关系2.22.2.1直线与平面平行的判定2.2.2平面与平面

(浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.2 2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定学案新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.2 2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定学案新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(浙江专用)2018版高中数学第二章点、直线、平面之间的位置关系2.2 2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定学案新人教A版必修2的全部内容。
2.2。
1 直线与平面平行的判定2。
2。
2 平面与平面平行的判定目标定位1。
通过直观感知、操作确认,归纳出直线与平面、平面与平面平行的判定定理.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用。
3。
能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题。
自主预习1.直线与平面平行的判定定理语言叙述符号表示图形表示平面外的一条直线与此平面内的一条错误!⇒a∥α直线平行,则该直线与此平面平行2语言叙述符号表示图形表示平面内的两条相交直线与另一个平面平行,则这两个平面错误!⇒α∥β平行即时自测1.判断题(1)直线l平行于平面α内的无数条直线,则l∥α.(×)(2)若直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.(√)(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行。
高中数学 第二章 点、直线、平面之间的位置关系 2.2.1 直线方程的概念与直线的斜率教学设计 新

江苏省苏州市高中数学第二章点、直线、平面之间的位置关系2.2.1 直线方程的概念与直线的斜率教学设计新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省苏州市高中数学第二章点、直线、平面之间的位置关系2.2.1 直线方程的概念与直线的斜率教学设计新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省苏州市高中数学第二章点、直线、平面之间的位置关系2.2.1 直线方程的概念与直线的斜率教学设计新人教A版必修2的全部内容。
§2.2.1 直线方程的概念与直线的斜率一【教材分析】本节课选自《普通高中课程标准实验教课书数学必修2(B版)》第二章第二节第一课时,直线方程的概念与直线的斜率,教学内容有直线方程的概念、直线倾斜角、斜率以及直线倾斜角与直线斜率的关系等概念.直线的倾斜角和斜率都描述了直线的倾斜程度,倾斜角从几何角度刻画了直线的倾斜程度,斜率是从数量关系上刻画了直线的倾斜程度.直线的倾斜角是几何概念,它主要起过渡作用,是联系新旧知识的纽带;而斜率则是代数量,建立斜率公式的过程,体现了解析法的基本思想:把几何问题代数化,通过代数运算研究几何图形的性质,而且它在以后建立直线方程、通过直线方程研究几何问题时也起到核心作用,是本节课的重点.同时,本节课是第一次用方程研究直线,为后续研究曲线起到一个示范作用。
二【目标分析】(1)、理解直线的倾斜角和斜率的定义;掌握斜率公式,并会求直线的斜率.(2)、通过直线倾斜角概念的引入和直线倾斜角与斜率关系的揭示,以提高学生分析、比较、概括、化归的数学能力,使学生初步了解用代数方程研究几何问题的思路,培养学生综合运用知识解决问题的能力.(3)、帮助学生进一步了解分类讨论思想、数形结合思想,在教学中充分揭示“数”与“形”的内在联系,体现数、形的统一美,激发学生学习数学的兴趣.三。
高中数学 第二章 点、直线、平面之间的位置关系 2.2 直线、平面平行的判定及其性质(第1课时)教学

高中数学第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质(第1课时)教学设计新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质(第1课时)教学设计新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质(第1课时)教学设计新人教A版必修2的全部内容。
直线与平面平行的判定一、教学内容分析:本节教材选自人教A版数学必修②2.2第一节课,本节内容在立体几何学习中起着承上启下的作用,具有重要的意义与地位。
本节课是在前面已学空间点、线、面位置关系的基础作为学习的出发点,结合有关的实物模型,通过直观感知、操作确认,归纳出直线与平面平行的判定定理。
本节课的学习对培养学生空间感与逻辑推理能力起到重要作用,特别是对面面平行的判定的学习作用重大。
二、学生学习情况分析:任教的学生是普理和理科特长生,学生数学基础很薄弱,语言表达能力也欠佳,学习兴趣不高,学习立体几何所具备的语言表达及空间感与空间想象能力相对不足,学习方面有一定困难。
三、教学目标知识与能力目标理解并掌握直线与平面平行的判定定理,进一步培养学生观察和发现的能力及空间想象能力。
过程与方法目标通过直观感知——观察——操作确认的认识方法掌握直线与平面平行的画法并能准确使用数学符号语言、文字语言表述判定定理。
情感态度与价值观目标让学生在观察、探究、发现中学习,在自主合作、交流中体验创造的激情,享受成功的喜悦,感受数学的魅力。
教育最新K122018版高中数学第二章点直线平面之间的位置关系2.22.2.3直线与平面平行的性质2.2.4平面与平面平

2.2.3 直线与平面平行的性质2.2.4 平面与平面平行的性质目标定位 1.证明并掌握直线与平面平行、平面与平面平行的性质定理.2.能应用文字语言、符号语言、图形语言准确描述直线与平面平行,两平面平行的性质定理.3.能用两个性质定理,证明一些空间线面平行关系的简单问题.自 主 预 习1.判断题(1)一条直线如果和一个平面平行,它就和这个平面内的无数条直线平行.(√) (2)如果直线a ∥平面α,直线b ⊂α,则a 与b 平行.(×)(3)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(√) (4)过直线外一点,有且只有一个平面和已知直线平行.(×) 提示 (2)a 与b 平行或异面.(4)过直线外一点可以作一条直线与已知直线平行,但过直线外一点可以作无数个平面与已知直线平行.2.如图所示,过正方体ABCD -A 1B 1C 1D 1的棱BB 1作一平面交平面CDD 1C 1于EE 1,则BB 1与EE 1的位置关系是( )A.平行B.相交C.异面D.不确定解析BB1∥平面CDD1C1,平面BB1E1E∩平面CDD1C1=E1E,BB1⊂平面BB1E1E,由线面平行的性质定理知,BB1∥EE1.答案 A3.若平面α∥平面β,直线a⊂α,点B∈β,则在β内过点B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行C.存在无数多条直线与a平行D.存在唯一一条直线与a平行解析设点B与直线a确定一平面为γ,γ∩β=b,∴a∥b.答案 D4.已知直线l∥平面α,l⊂平面β,α∩β=m,则直线l,m的位置关系是________. 解析由直线与平面平行的性质定理知l∥m.答案平行类型一线面平行性质定理的应用【例1】求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行. 解已知直线a,l,平面α,β满足α∩β=l,a∥α,a∥β.求证:a∥l.证明:如图所示,过a作平面γ交平面α于b,∵a∥α,∴a∥b.同样过a作平面δ交平面β于c,∵a∥β,∴a∥c.则b∥c.又∵b⊄β,c⊂β,∴b∥β.又∵b⊂α,α∩β=l,∴b∥l.又∵a∥b,∴a∥l.规律方法在空间平行关系中,交替使用线线平行、线面平行的判定定理与性质定理是解决此类问题的关键.【训练1】若两个相交平面分别过两条平行直线,则它们的交线和这两条平行直线平行. 解已知:a∥b,a⊂α,b⊂β,α∩β=l.求证:a∥b∥l.证明:如图所示,∵a∥b,b⊂β,a⊄β,∴a∥β,又a⊂α,α∩β=l,∴a∥l,又a∥b,∴a∥b∥l.类型二面面平行性质定理的应用【例2】已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面α.证明(1)若AB、CD在同一平面内,则平面ABDC与α、β的交线为BD、AC.∵α∥β,∴AC∥BD.又M、N为AB、CD的中点,∴MN∥BD.又BD⊂平面α,MN⊄平面α,∴MN∥平面α.(2)若AB、CD异面,如图,过A作AE∥CD交α于E,取AE中点P,连接MP、PN、BE、ED.∵AE∥CD.∴AE、CD确定平面AEDC.则平面AEDC与α、β的交线分别为ED、AC,∵α∥β,∴ED∥AC.又P、N分别为AE、CD的中点,∴PN∥ED,又ED⊂平面α,PN⊄平面α,∴PN∥平面α.同理可证MP∥BE,又MP⊄平面α,BE⊂平面α,∴MP∥平面α,∵AB、CD异面,∴MP、NP相交.∴平面MPN∥平面α.又MN⊂平面MPN,∴MN∥平面α.规律方法 1.利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作是平面的交线,往往需要有三个平面,即有两平面平行,再构造第三个面与两平行平面都相交. 2.面面平行⇒线线平行,体现了转化思想与判定定理的交替使用,可实现线线、线面及面面平行的相互转化.【训练2】如图,已知α∥β,点P是平面α、β外的一点(不在α与β之间),直线PB、PD分别与α、β相交于点A、B和C、D.(1)求证:AC ∥BD ;(2)已知PA =4 cm ,AB =5 cm ,PC =3 cm ,求PD 的长.(1)证明 ∵PB ∩PD =P ,∴直线PB 和PD 确定一个平面γ,则α∩γ=AC ,β∩γ=BD .又α∥β,∴AC ∥BD . (2)解 由(1)得AC ∥BD ,∴PA AB =PC CD ,∴45=3CD, ∴CD =154(cm),∴PD =PC +CD =274(cm).类型三 平行关系的综合应用(互动探究)【例3】 如图所示,四边形ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH ,求证:GH ∥平面PAD . [思路探究]探究点一 证明平行关系的基本思路是什么?提示 证明平行关系时,应综合应用线线平行、线面平行及面面平行之间的相互转化. 探究点二 解本题的关键是什么?提示 关键是连接AC 交BD 于O ,结合PC 中点M ,利用中位线,进行平行转化,进而作出判断.证明 如图所示,连接AC 交BD 于点O ,连接MO .∵ABCD 是平行四边形,∴O 是AC 的中点,又M 是PC 的中点, ∴PA ∥MO ,而AP ⊄平面BDM ,OM ⊂平面BDM , ∴PA ∥平面BMD ,又∵PA ⊂平面PAHG , 平面PAHG ∩平面BMD =GH ,∴PA ∥GH .又PA⊂平面PAD,GH⊄平面PAD,∴GH∥平面PAD.规律方法 1.本题证明线面平行,利用了线面平行的性质定理和判定定理进行转化,即线线平行⇒线面平行⇒线线平行⇒线面平行.2.在将线面平行转化为线线平行时,注意观察图形中是否是性质定理中符合条件的平面. 【训练3】在长方体ABCD-A1B1C1D1,E为棱DD1上的点,试确定点E的位置,使B1D∥平面A1C1E.解如图,连接B1D1,设A1C1∩B1D1=M,连接ME.若B1D∥平面A1C1E,则B1D平行于过B1D的平面与平面A1C1E的交线.由于B1D⊂平面B1DD1,平面B1DD1∩平面A1C1E=ME,所以B1D∥ME.又因为M为B1D1的中点,所以E为DD1的中点.[课堂小结]1.三种平行关系可以任意转化,其相互转化关系如图所示:2.证明线与线、线与面的平行关系的一般规律是:“由已知想性质,由求证想判定”,是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.1.已知:α∩β=b,a∥α,a∥β,则a与b的位置关系是( )A.a∥bB.a⊥bC.a,b相交但不垂直D.a,b异面解析利用结论:若一直线与两个相交平面平行则此直线与交线平行.答案 A2.已知a,b表示直线,α、β、γ表示平面,下列推理正确的是( )A.α∩β=a,b⊂α⇒a∥bB.α∩β=a,a∥b⇒b∥α且b∥βC.a∥β,b∥β,a⊂α,b⊂α⇒α∥βD.α∥β,α∩γ=a,β∩γ=b⇒a∥b解析由面面平行的性质定理知D正确.答案 D3.过两平行平面α,β外的点P 的两条直线AB 与CD ,它们分别交α于A ,C 两点,交β于B ,D 两点,若PA =6,AC =9,PB =8,则BD 的长为________. 解析 两条直线AB 与CD 相交于P 点,所以可以确定一个平面,此平面与两平行平面α,β的交线AC ∥BD ,所以PA PB =ACBD,又PA =6,AC =9,PB =8,故BD =12.答案 124.如图,已知E ,F 分别是长方体ABCD -A 1B 1C 1D 1的棱A 1B 1、CC 1的中点,过D 1、E 、F 作平面D 1EGF 交BB 1于G .求证:EG ∥D 1F .证明 在长方体ABCD -A 1B 1C 1D 1中,因为平面ABB 1A 1∥平面DCC 1D 1,平面D 1EGF ∩平面ABB 1A 1=EG ,平面D 1EGF ∩平面DCC 1D 1=D 1F ,∴EG ∥D 1F .基 础 过 关1.a ∥α,b ∥β,α∥β,则a 与b 位置关系是( ) A.平行 B.异面C.相交D.平行或异面或相交解析 如图(1),(2),(3)所示,a 与b 的关系分别是平行、异面或相交.答案 D2.已知直线l ∥平面α,P ∈α,那么过点P 且平行于l 的直线( ) A.只有一条,不在平面α内 B.只有一条,在平面α内 C.有两条,不一定都在平面α内 D.有无数条,不一定都在平面α内 解析 如图所示,∵l ∥平面α,P ∈α,∴直线l 与点P 确定一个平面β, α∩β=m ,∴P ∈m ,∴l ∥m 且m 是唯一的. 答案 B3.如图,四棱锥P -ABCD 中,M ,N 分别为AC ,PC 上的点,且MN ∥平面PAD ,则( )A.MN ∥PDB.MN ∥PAC.MN ∥ADD.以上均有可能解析 ∵MN ∥平面PAD ,MN ⊂平面PAC , 平面PAD ∩平面PAC =PA ,∴MN ∥PA . 答案 B4.过正方体ABCD -A 1B 1C 1D 1的三个顶点A 1、C 1、B 的平面与底面ABCD 所在平面的交线为l ,则l 与A 1C 1的位置关系是________.解析 由面面平行的性质可知第三平面与两平行平面的交线是平行的. 答案 平行5.如图,在正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.解析 ∵在正方体ABCD -A 1B 1C 1D 1中,AB =2,∴AC =2 2.又E 为AD 的中点,EF ∥平面AB 1C ,EF ⊂平面ADC ,平面ADC ∩平面AB 1C =AC , ∴EF ∥AC ,∴F 为DC 的中点, ∴EF =12AC = 2.答案26.如图所示,在三棱柱ABC -A 1B 1C 1中,过A 1,B ,C 1的平面与平面ABC 的交线为l ,试判断l 与直线A 1C 1的位置关系,并给以证明.解 l ∥A 1C 1证明 在三棱柱ABC -A 1B 1C 1中,A 1C 1∥AC ,A 1C 1⊄平面ABC ,AC ⊂平面ABC , ∴A 1C 1∥平面ABC .又∵A 1C 1⊂平面A 1BC 1,且平面A 1BC 1∩平面ABC =l , ∴A 1C 1∥l .7.如图,在正方体ABCD -A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,且CM =DN ,求证:MN ∥平面AA 1B 1B .证明 如图,作MP ∥BB 1交BC 于点P ,连接NP . ∵MP ∥BB 1,∴CM MB 1=CP PB.∵BD =B 1C ,DN =CM ,∴B 1M =BN ,∴CM MB 1=DN NB, ∴CP PB =DN NB,∴NP ∥CD ∥AB .∵NP ⊄平面AA 1B 1B ,AB ⊂平面AA 1B 1B ,∴NP ∥平面AA 1B 1B . ∵MP ∥BB 1,MP ⊄平面AA 1B 1B ,BB 1⊂平面AA 1B 1B ,∴MP ∥平面AA 1B 1B .又∵MP ⊂平面MNP ,NP ⊂平面MNP ,MP ∩NP =P , ∴平面MNP ∥平面AA 1B 1B .∵MN ⊂平面MNP ,∴MN ∥平面AA 1B 1B .能 力 提 升8.下列说法正确的是( )A.平行于同一条直线的两个平面平行B.平行于同一个平面的两个平面平行C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行D.若三直线a ,b ,c 两两平行,则在过直线a 的平面中,有且只有一个平面与b ,c 均平行 解析 平行于同一条直线的两个平面可以平行也可以相交,所以A 错;B 正确;C 中没有指明这三个点在平面的同侧还是异侧,不正确;D 不正确,因为过直线a 的平面中,只要b ,c 不在其平面内,则与b ,c 均平行. 答案 B9.过平面α外的直线l ,作一组平面与α相交,如果所得的交线为a ,b ,c ,…,则这些交线的位置关系为( ) A.都平行B.都相交且一定交于同一点C.都相交但不一定交于同一点D.都平行或交于同一点解析 ∵l ⊄α,∴l ∥α或l 与α相交.(1)若l ∥α,则由线面平行的性质可知l ∥a ,l ∥b ,l ∥c ,… ∴a ,b ,c ,…这些交线都平行.(2)若l 与α相交,不妨设l ∩α=A ,则A ∈l ,又由题意可知A ∈a ,A ∈b ,A ∈c ,…,∴这些交线交于同一点A .综上可知D 正确. 答案 D10.如图,P 是△ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段PA 、PB 、PC 于A ′、B ′、C ′,若PA ′∶AA ′=2∶3,则S △A ′B ′C ′S △ABC=________.解析 由平面α∥平面ABC ,得AB ∥A ′B ′,BC ∥B ′C ′,AC ∥A ′C ′, 由等角定理得∠ABC =∠A ′B ′C ′, ∠BCA =∠B ′C ′A ′,∠CAB =∠C ′A ′B ′, 从而△ABC ∽△A ′B ′C ′,△PAB ∽△PA ′B ′,S △A ′B ′C ′S △ABC =⎝ ⎛⎭⎪⎫A ′B ′AB 2=⎝ ⎛⎭⎪⎫PA ′PA 2=425. 答案42511.如图所示,已知P是▱ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=l.(1)求证:l∥BC;(2)MN与平面PAD是否平行?试证明你的结论.法一(1)证明因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD.又因为平面PBC∩平面PAD=l,所以BC∥l.(2)解平行.证明如下:取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,又因为MN⊄平面APD,AE⊂平面APD,所以MN∥平面APD.法二(1)证明由AD∥BC,AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.又因为平面PBC∩平面PAD=l,所以l∥AD,l∥BC.(2)解平行.证明如下:设Q是CD的中点,连接NQ,MQ,则MQ∥AD,NQ∥PD,而MQ∩NQ=Q,所以平面MNQ∥平面PAD.MN⊂平面MNQ,所以MN∥平面PAD.探究创新12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.小学+初中+高中小学+初中+高中解 能.取AB ,C 1D 1的中点M ,N ,连接A 1M ,MC ,CN ,NA 1, ∵A 1N ∥PC 1且A 1N =PC 1,PC 1∥MC ,PC 1=MC ,A 1N 綉MC , ∴四边形A 1MCN 是平行四边形,又∵A 1N ∥PC 1,A 1M ∥BP ,A 1N ∩A 1M =A 1,C 1P ∩PB =P , ∴平面A 1MCN ∥平面PBC 1,因此,过点A 1与截面PBC 1平行的截面是平行四边形. 连接MN ,作A 1H ⊥MN 于点H , ∵A 1M =A 1N =5,MN =22,∴A 1H = 3.∴S △A 1MN =12×22×3= 6. 故S ▱A 1MCN =2S △A 1MN =2 6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定目标定位 1.通过直观感知、操作确认,归纳出直线与平面、平面与平面平行的判定定理.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题.自 主 预 习1.直线与平面平行的判定定理即时自测1.判断题(1)直线l平行于平面α内的无数条直线,则l∥α.(×)(2)若直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.(√)(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.(×)(4)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行.(√)提示(1)直线l可以在平面α内.(3)如果一个平面内的两条相交直线分别平行于另一个平面,则这两个平面平行.2.三棱台ABC-A1B1C1中,直线AB与平面A1B1C1的位置关系是( )A.相交B.平行C.在平面内D.不确定解析AB∥A1B1,AB⊄平面A1B1C1,A1B1⊂平面A1B1C1,∴AB∥平面A1B1C1.答案 B3.点P是平面α外一点,过P作直线a∥α,过P作直线b∥α,且直线a,b确定一个平面β,则( )A.α∥βB.α与β相交C.α与β异面D.α与β的位置关系不确定解析a∩b=P,a⊂β,b⊂β,b∥α,a∥α,∴α∥β.答案 A4.平面α内任意一条直线均平行于平面β,则平面α与平面β的位置关系是________. 解析平面α内任意一条直线均平行于平面β,所以平面α与平面β无公共点,所以平面α与平面β平行.答案平行类型一线面平行判定定理的应用【例1】如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.证明(1)∵EH为△ABD的中位线,∴EH∥BD.∵EH⊄平面BCD,BD⊂平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊄平面EFGH,EH⊂平面EFGH,∴BD∥平面EFGH.规律方法 1.利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.2.证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.【训练1】如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.证明连接AC交BD于点O,连接OM.∵M为SC的中点,O为AC的中点,∴OM∥SA∵OM⊂平面MDB,SA⊄平面MDB,∴SA∥平面MDB.类型二面面平行判定定理的应用【例2】如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.证明由棱柱性质知,B1C1∥BC,B1C1=BC,又D,E分别为BC,B1C1的中点,所以C1E綉DB,则四边形C1DBE为平行四边形,因此EB∥C1D,又C1D⊂平面ADC1,EB⊄平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1綉BD,所以四边形EDBB1为平行四边形,则ED綉B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED綉A1A,则四边形EDAA1为平行四边形,所以A1E∥AD,又A1E⊄平面ADC1,AD⊂平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1,A1E⊂平面A1EB,EB⊂平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.规律方法 1.要证明两平面平行,只需在其中一个平面内找到两条相交直线平行于另一个平面.2.判定两个平面平行与判定线面平行一样,应遵循先找后作的原则,即先在一个面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.【训练2】如图,三棱锥P-ABC中,E,F,G分别是AB,AC,AP的中点.证明平面GFE∥平面PCB.证明因为E,F,G分别是AB,AC,AP的中点,所以EF∥BC,GF∥CP.因为EF,GF⊄平面PCB,BC,CP⊂面PCB.所以EF∥平面PCB,GF∥平面PCB.又EF∩GF=F,所以平面GFE∥平面PCB.类型三线面平行、面面平行判定定理的综合应用(互动探究)【例3】如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC 的中点,求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.[思路探究]探究点一 判定线面平行与面面平行的思路原则是什么?提示 判定线面平行与面面平行的思路原则是找作一条直线与平面平行或在一个面内找作两条与另一个平面平行的相交直线,应遵循先找后作的原则,若找不到再作辅助线. 探究点二 如何判定(2)中平面EFG ∥平面BDD 1B 1?提示 根据面面平行的判定定理,结合(1)的结论,故在平面EFG 内找到另一条直线与平面BDD 1B 1平行即可.证明 (1)如图,连接SB ,∵E ,G 分别是BC ,SC 的中点,∴EG ∥SB . 又∵SB ⊂平面BDD 1B 1,EG ⊄平面BDD 1B 1, ∴EG ∥平面BDD 1B 1. (2)连接SD ,∵F ,G 分别是DC ,SC 的中点,∴FG ∥SD . 又∵SD ⊂平面BDD 1B 1,FG ⊄平面BDD 1B 1, ∴FG ∥平面BDD 1B 1.又EG ∥平面BDD 1B 1,且EG ⊂平面EFG ,FG ⊂平面EFG ,EG ∩FG =G , ∴平面EFG ∥平面BDD 1B 1.规律方法 要证明面面平行,由面面平行的判定定理知需在某一平面内寻找两条相交且与另一平面平行的直线.要证明线面平行,又需根据线面平行的判定定理,在平面内找与已知直线平行的直线,即:【训练3】 如图,S 是平行四边形ABCD 在平面外一点,M ,N 分别是SA ,BD 上的点,且AMSM=DN NB.求证:MN ∥平面SBC .证明 连接AN 并延长交BC 于P ,连接SP ,因为AD ∥BC ,所以DN NB =ANNP ,又因为AM SM =DN NB, 所以AM SM =AN NP,所以MN ∥SP .又MN ⊄平面SBC ,SP ⊂平面SBC ,所以MN ∥平面SBC . [课堂小结]1.直线与平面平行的关键是在已知平面内找一条直线和已知直线平行,即要证直线和平面平行,先证直线和直线平行,即由立体向平面转化,由高维向低维转化.2.证明面面平行的一般思路:线线平行⇒线面平行⇒面面平行.3.准确把握线面平行及面面平行两个判定定理,是对线面关系及面面关系作出正确推断的关键.1.能保证直线a 与平面α平行的条件是( ) A.b ⊂α,a ∥bB.b ⊂α,c ∥α,a ∥b ,a ∥cC.b ⊂α,A 、B ∈a ,C 、D ∈b ,且AC =BDD.a ⊄α,b ⊂α,a ∥b解析 A 错误,若b ⊂α,a ∥b ,则a ∥α或a ⊂α;B 错误,若b ⊂α,c ∥α,a ∥b ,a ∥c ,则a ∥α或a ⊂α;C 错误,若满足此条件,则a ∥α或a ⊂α或a 与α相交;D 正确.答案 D2.在正方体EFGH -E 1F 1G 1H 1中,下列四对截面彼此平行的一对是( ) A.平面E 1FG 1与平面EGH 1 B.平面FHG 1与平面F 1H 1G C.平面F 1H 1H 与平面FHE 1 D.平面E 1HG 1与平面EH 1G解析 如图,∵EG ∥E 1G 1,EG ⊄平面E 1FG 1,E 1G 1⊂平面E 1FG 1, ∴EG ∥平面E 1FG 1,又G 1F ∥H 1E ,同理可证H 1E ∥平面E 1FG 1, 又H 1E ∩EG =E ,∴平面E 1FG 1∥平面EGH 1.答案 A3.梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α的位置关系是________.解析因为AB∥CD,AB⊂平面α,CD⊄平面α,由线面平行的判定定理可得CD∥α.答案CD∥α4.如图所示,E,F分别为三棱锥A-BCD的棱BC,BA上的点,且BE∶BC=BF∶BA=1∶3.求证:EF∥平面ACD.证明在△BEF和△BCA中,∵BE∶BC=BF∶BA=1∶3,∴EF∥AC.又EF⊄平面ACD,AC⊂平面ACD,∴EF∥平面ACD基础过关1.下列图形中能正确表示语句“平面α∩β=l,a⊂α,b⊂β,a∥β”的是( )解析A中不能正确表达b⊂β;B中不能正确表达a∥β;C中也不能正确表达a∥β.D正确.答案 D2.已知三个平面α,β,γ,一条直线l,要得到α∥β,必须满足下列条件中的( )A.l∥α,l∥β,且l∥γB.l⊂γ,且l∥α,l∥βC.α∥γ,且β∥γD.l与α,β所成的角相等解析⎭⎪⎬⎪⎫α∥γ⇒α与γ无公共点β∥γ⇒β与γ无公共点⇒α与β无公共点⇒α∥β.答案 C3.在正方体ABCD -A 1B 1C 1D 1中,M 是棱CD 上的动点,则直线MC 1与平面AA 1B 1B 的位置关系是( ) A.相交 B.平行 C.异面D.相交或平行解析 如图,MC 1⊂平面DD 1C 1C ,而平面AA 1B 1B ∥平面DD 1C 1C ,故MC 1∥平面AA 1B 1B .答案 B4.若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系为________. 解析 三条平行线段共面时,两平面可能平行也可能相交,当三条平行线段不共面时,两平面一定平行. 答案 平行或相交5.给出下列结论:①若直线a 上有无数个点不在平面α内,则a ∥α;②若直线a 与平面α内的无数条直线平行,则a ∥α;③若平面α,β都与直线a 平行,则α∥β;④若平面α内存在无数条直线平行于平面β,则α∥β.其中错误的是______(填序号). 解析 ①中直线a 与平面α可能相交;②中直线a ∥α或a ⊂α;③中,α∥β或α与β相交;④中,平面α内无数条直线互相平行时,α∥β或α与β相交 .故①②③④均错误.答案 ①②③④6.如图所示的几何体中,△ABC 是任意三角形,AE ∥CD ,且AE =AB =2a ,CD =a ,F 为BE 的中点,求证:DF ∥平面ABC .证明 如图所示,取AB 的中点G ,连接FG ,CG ,∵F ,G 分别是BE ,AB 的中点, ∴FG ∥AE ,FG =12AE .又∵AE =2a ,CD =a ,∴CD =12AE .又AE ∥CD ,∴CD ∥FG ,CD =FG ,∴四边形CDFG 为平行四边形,∴DF ∥CG .又CG ⊂平面ABC ,DF ⊄平面ABC , ∴DF ∥平面ABC .7.如图在正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别为棱AB ,CC 1,AA 1,C 1D 1的中点.求证:平面CEM ∥平面BFN .证明 因为E ,F ,M ,N 分别为其所在各棱的中点,如图连接CD 1,A 1B ,易知FN ∥CD 1. 同理,ME ∥A 1B .易证四边形A 1BCD 1为平行四边形,所以ME ∥NF . 连接MD 1,同理可得MD 1∥BF .又BF ,NF 为平面BFN 中两相交直线,ME ,MD 1为平面CEM 中两相交直线,故平面CEM ∥平面BFN .能 力 提 升8.点E ,F ,G ,H 分别是空间四边形ABCD 的边AB ,BC ,CD ,DA 的中点,则空间四面体的六条棱中与平面EFGH 平行的条数是( )A.0B.1C.2D.3解析如图,由线面平行的判定定理可知,BD∥平面EFGH,AC∥平面EFGH.答案 C9.已知直线l,m,平面α,β,下列命题正确的是( )A.l∥β,l⊂α⇒α∥βB.l∥β,m∥β,l⊂α,m⊂α⇒α∥βC.l∥m,l⊂α,m⊂β⇒α∥βD.l∥β,m∥β,l⊂α,m⊂α,l∩m=M⇒α∥β解析如图所示,在正方体ABCD-A1B1C1D1中,AB∥CD,则AB∥平面DC1,AB⊂平面AC,但是平面AC与平面DC1不平行,所以A错误;取BB1的中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面AC.EF⊂平面BC1,B1C1⊂平面BC1,但是平面AC与平面BC1不平行,所以B错误;可证AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,又平面AC与平面BC1不平行,所以C错误;很明显D是面面平行的判定定理,所以D正确.答案 D10.如图是正方体的平面展开图.在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是________.解析以ABCD为下底面还原正方体,如图:则易判定四个命题都是正确的.答案 ①②③④11.在如图所示的几何体中,四边形ABCD 为平行四边形,EF ∥AB ,FG ∥BC ,EG ∥AC ,AB =2EF ,M 是线段AD 的中点,求证:GM ∥平面ABFE .证明 因为EF ∥AB ,FG ∥BC ,EG ∥AC ,所以△ABC ∽△EFG ,由于AB =2EF ,因此BC =2FG .如图,连接AF ,由于FG ∥BC ,FG =12BC ,在▱ABCD 中,M 是线段AD 的中点,则AM ∥BC ,且AM =12BC , 因此FG ∥AM 且FG =AM ,所以四边形AFGM 为平行四边形,因此GM ∥FA .又FA ⊂平面ABFE ,GM ⊄平面ABFE ,所以GM ∥平面ABFE .探 究 创 新12.如图,在正方体ABCD -A 1B 1C 1D 1中,点E 是棱A 1B 1的中点.(1)求证:A 1C ∥面BEC 1.(2)求异面直线A 1C 与B 1C 1所成的角的正切值.(1)证明 连接B 1C ,交BC 1于点O ,连接OE ,如图.因为几何体是正方体, 所以O 是B 1C 的中点. 又点E 是棱A 1B 1的中点,所以OE ∥A 1C . 因为OE ⊂平面BEC 1,A 1C ⊄平面BEC 1, 所以A 1C ∥平面BEC 1.(2)解 连接A 1B ,因为BC ∥B 1C 1, 所以异面直线A 1C 与B 1C 1所成的角为∠BCA 1. 因为几何体是正方体, 所以BC ⊥A 1B , 所以tan ∠BCA 1=A 1B BC = 2.。
