全等三角形练习10(45道基础证明题)

合集下载

全等三角形经典题型50题(有答案)

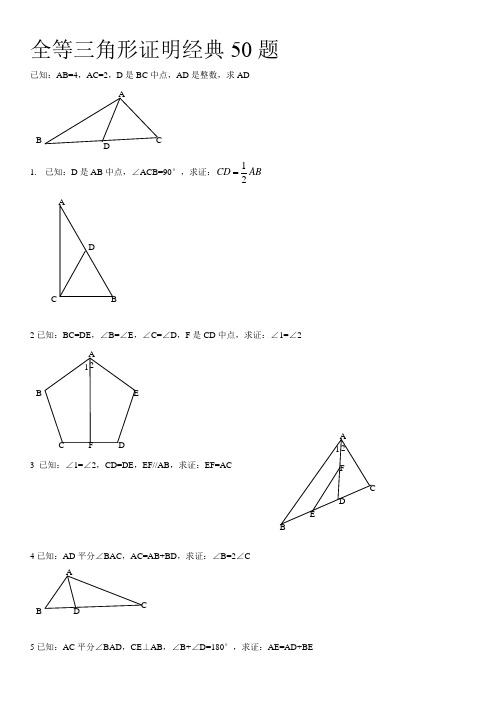
全等三角形证明经典50题已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD1. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB2已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BEADBCCDB ABA CDF2 1 E12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. 已知：AB=CD ，∠A=∠D ，求证：∠B=∠C15. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB16. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE17. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DCDCB A FE P D ACB FAE DCB18．（5分）如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ． 19．（5分）如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA 20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．（6分）如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠BPED CBA D CBA22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．23．（7分）已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）： 24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．25、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。

全等三角形证明经典100题

全等三⾓形证明经典100题1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2已知：∠1=∠2，CD=DE ，EF BCDF ADB CBC B A CDF2 1 ECDB A12CD AB如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：A B C D EF 21 A DBCDABC BA C2 1 ECDB ABC=AB+DC 。

13.已知：AB园⾥有⼀条“Z”字形道路ABCD ，如图所⽰，其DC BAFE ABCDP DACBFAED C BPEDCBAO E DCBCB ADCBA MFECBAFE DCBA DCBA F DCBA F ED CB A中AB ∥CD ，在AB ，CD ，BC 三段路旁各有⼀只⼩⽯凳E ，F ，M ，且BE ＝CF ，M 在BC 的中点，试说明三只⽯凳E ，F ，M 恰好在⼀条直线上.31．已知：点A 、F 、E 、C 在同⼀条直线上， AF ＝CE ，BE∥DF，BE ＝DF ．求证：△ABE≌△CDF．32.已知：如图所⽰，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证： AE ＝AF 。

33．如图，在四边形ABCD 中，E 是AC 上的⼀点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．34．已知AB ∥DE ，BC ∥EF ，D ，C 在AF 上，且AD ＝CF ，求证：△ABC ≌△DEF ．DB654321E DCBADCBAE35．已知：如图，AB =AC ，BDAC ，CE AB ，垂⾜分别为D 、E ，BD 、CE 相交于点F ，求证：BE =CD ．36、如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F 。

全等三角形经典题型50题[含答案解析]

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2ADBC证明：连接BF 和EF 。

因为BC=ED,CF=DF,∠BCF=∠EDF。

所以三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF。

又因为 ∠ABC=∠AED。

所以 ∠ABE=∠AEB。

所以 AB=AE 。

在三角形ABF和三角形AEF中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。

所以三角形ABF 和三角形AEF 全等。

所以∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA，∠DGE=∠2又∵CD=DE ∴⊿ADC≌⊿GDE（AAS）BACDF2 1 E∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE 证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE⊥AB所以∠CEB＝∠CEF＝90° 因为EB ＝EF ，CE ＝CE ，所以△CEB≌△CEF所以∠B ＝∠CFE因为∠B ＋∠D ＝180°，∠CFE＋∠CFA＝180° 所以∠D＝∠CFA 因为AC 平分∠BAD所以∠DAC＝∠FAC又因为AC ＝AC所以△ADC≌△AFC（SAS ）所以AD ＝AF 所以AE ＝AF ＋FE ＝CDB AAD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形经典题型50题(含答案)

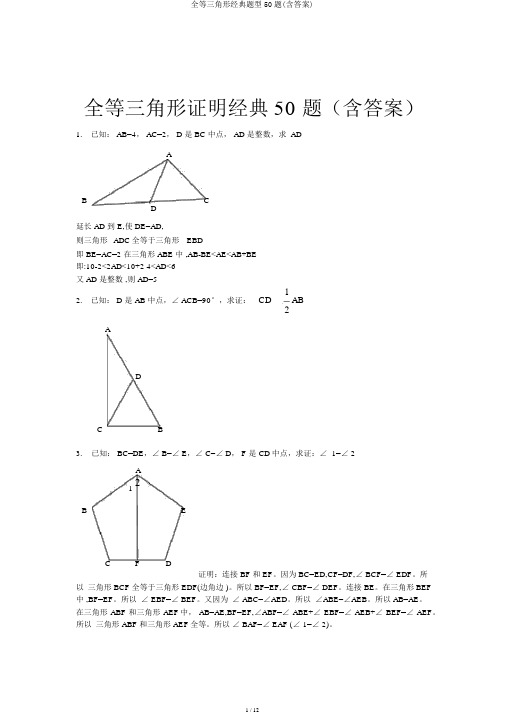
全等三角形证明经典50 题（含答案）1. 已知： AB=4， AC=2， D 是 BC 中点， AD 是整数，求ADAB CD延长 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知： D 是 AB 中点，∠ ACB=90°，求证：CD AB2ADC B3.已知： BC=DE，∠ B=∠ E，∠ C=∠ D， F 是 CD中点，求证：∠ 1=∠ 2A21B EC F D证明：连接 BF 和 EF。

因为 BC=ED,CF=DF,∠ BCF=∠ EDF。

所以三角形 BCF 全等于三角形 EDF(边角边 )。

所以 BF=EF,∠ CBF=∠ DEF。

连接 BE。

在三角形BEF 中 ,BF=EF。

所以∠ EBF=∠ BEF。

又因为∠ ABC=∠AED。

所以∠ABE=∠AEB。

所以 AB=AE。

在三角形 ABF 和三角形 AEF中， AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。

所以三角形 ABF 和三角形 AEF全等。

所以∠ BAF=∠ EAF (∠ 1=∠ 2)。

A4. 已知：∠ 1=∠ 2， CD=DE， EF//AB，求证： EF=AC 1 2证明：过 E 点，作 EG//AC，交 AD 延长线于 G 则∠ DEG=∠ DCA，F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE（AAS）∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知：AD平分∠ BAC，AC=AB+BD，求证：∠B=2∠C ACB D证明：在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB，连接（SASED∵ AD）平分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB，，DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知： AC 平分∠ BAD，CE⊥ AB，∠ B+∠ D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接 CF 因为 CE⊥AB 所以∠CEB＝∠ CEF＝ 90 °因为 EB＝ EF， CE＝ CE，所以△CEB≌△CEF 所以∠B ＝∠ CFE 因为∠ B＋∠ D＝ 180 ，°∠CFE＋∠ CFA＝ 180°所以∠ D＝∠ CFA 因为AC 平分∠ BAD 所以∠ DAC＝∠ FAC 又因为AC＝ AC所以△ ADC≌ △ AFC（ SAS）所以 AD＝ AF 所以 AE＝ AF＋ FE＝ AD＋ BE12.如图，四边形 ABCD 中， AB∥ DC， BE、 CE 分别平分∠ ABC、∠ BCD，且点 E 在 AD 上。

全等三角形练习10(45道基础证明题)

全等三角形练习10(45道基础证明题)本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March全等三角形的判定1．已知AD 是⊿ABC 的中线，BE ⊥AD ，CF ⊥AD ，问BE =CF 吗？说明理由。

2．已知AC =BD ，AE =CF ，BE =DF ，问AE ∥CF 吗？3．已知AB =CD ，BE =DF ，AE =CF ，问AB∥CD 吗？4．已知在四边形ABCD 中，AB =CD ，AD =CB ，问AB ∥CD 吗？说明理由。

5．已知∠BAC =∠DAE ，∠1=∠2，BD =CE ，问ABD ≌⊿ACE .吗为什么6．已知CD ∥AB ，DF ∥EB ，DF =EB ，问AF =CE 吗说明理由。

A B C D F E A C DEF D C FE A B A D E B C1 2 A D C EF B7．已知BE =CF ，AB =CD ， ∠B =∠C .问AF =DE 吗A C DBE F8．已知AD =CB ， ∠A =∠C ，AE =CF ，问EB ∥DF 吗？说明理由。

9．已知，M 是AB 的中点，∠1=∠2，MC =MD ，问∠C =∠D 吗？说明理由。

10．已知，AE =DF ，BF =CE ，AE ∥DF ，问AB =CD 吗？说明理由。

11．已知∠1=∠2，∠3=∠4，问AC =AD 吗？说明理由。

12．已知∠E =∠F ，∠1=∠2，AB =CD ，问AE =DF 吗？说明理由。

13．已知ED ⊥AB ，EF ⊥BC ，BD =EF ，问BM =ME 吗？说明理由。

ACD B 1 2 3 4 A B C DE F1 2 B AD F ECM A B C D 1 2 D C F E A B14．在⊿ABC 中，高AD 与BE 相交于点H ，且AD =BD ，问⊿BHD ≌⊿ACD ，为什么？15．已知∠A =∠D ，AC ∥FD ，AC =FD ，问AB ∥DE 吗？说明理由。

全等三角形证明经典30题

全等三角形证明经典30题1. 根据SSS全等定理，如果两个三角形的三边分别相等，则这两个三角形全等。

2. 根据SAS全等定理，如果两个三角形的两边和它们夹角相等，则这两个三角形全等。

3. 根据ASA全等定理，如果两个三角形的两角和它们夹边相等，则这两个三角形全等。

4. 根据AAS全等定理，如果两个三角形的两角和一边或两边相等，则这两个三角形全等。

5. 根据HL全等定理，如果两个右三角形的一条直角边和斜边长度相等，则这两个三角形全等。

6. 根据正弦定理和余弦定理，如果两个三角形的三条边的比例相等，则这两个三角形全等。

7. 如果三角形的两边相等，则它们所对的角也相等。

8. 如果三角形的两角相等，则它们所对的边也相等。

9. 如果一个三角形的两边和夹角分别等于另一个三角形的两边和夹角，则这两个三角形相似。

10. 如果一个三角形的两角和一边与另一个三角形的两角和一边成比例，则这两个三角形相似。

11. 如果一个三角形的两边成比例，且这两个三角形所夹的角也成比例，则这两个三角形相似。

12. 如果一个三角形的一边与另一个三角形的一边成比例，且这两个三角形所对的角也成比例，则这两个三角形相似。

13. 如果两个三角形有一个角相等，则这两个三角形的相似比例等于这个角的正弦值。

14. 如果两个三角形的对角线成比例，则这两个三角形相似。

15. 如果两个三角形有两条相似的边，则这两个三角形相似。

16. 如果两个三角形的高成比例，则这两个三角形相似。

17. 如果两个三角形的中线成比例，则这两个三角形相似。

18. 如果两个三角形的内切圆半径成比例，则这两个三角形相似。

19. 如果两个三角形的外接圆半径成比例，则这两个三角形相似。

20. 如果两个三角形的垂心、重心、外心、内心在同一条直线上，则这两个三角形相似。

21. 如果两个三角形的面积成比例，则这两个三角形相似。

22. 如果一个三角形的内角平分线与另一个三角形的内角平分线成比例，则这两个三角形相似。

(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB15. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BED C B A FE PD A CB16. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．19．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．F AEDCB P E D CB A DC B A23．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．证明：25、如图：DF=CE ，AD=BC ，∠D=∠C 。

全等三角形证明经典50题

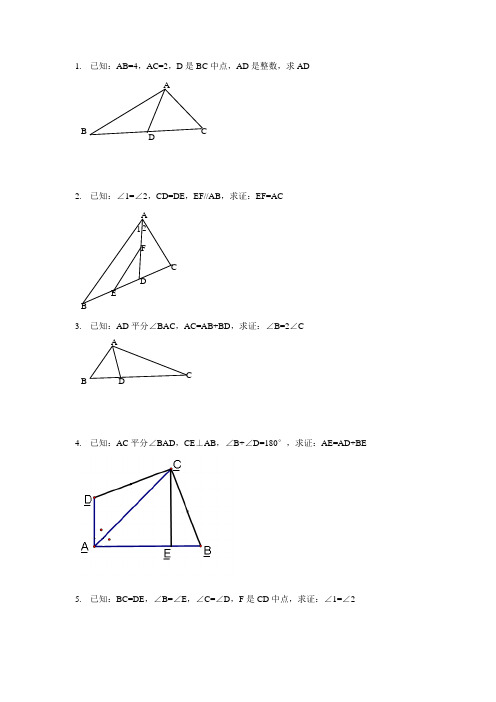
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC3. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C4. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE5. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2ADBCBA CDF2 1 ECDB A6. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. 已知：AB=CD ，∠A=∠D ，求证：∠B=∠CA BC DEF 21 BA CDF2 1 EDCBAFE15. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE16. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．（5分）如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ． 19．（5分）如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBAAB CDFAED C B20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．（6分）如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．23．（7分）已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：PE D C B AOEDCBAD CBA24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．25、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。

八年级全等三角形简单证明题及答案(15道)

∴BC=ED．
全等三角形的判定与性质．
01
如图，在△ABC中， ∠C=90°，点D是AB边上的一点，DM⊥AB，且 DM=AC，过点M作 ME∥BC交AB于点E．求证： △ABC≌△MED。
02
证明：∵MD⊥AB，
∴∠MDE=∠C=90°，
∵ME∥BC，
∴∠B=∠MED，
在△ABC与△MED中， ∠B=∠MED ∠C=∠EDM DM=AC ，
∠D=∠B ， ∴△ADF≌△CBE（ASA）， ∴AF=CE， ∴AF+EF=CE+EF，即
AE=CF．
全等三角形的判定与性质．
11.在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．求证： Rt△ABE≌Rt△CBF；
证明：∵∠ABC=90°，
角平分线的性质；全等三角形的判定与性质．
全等三角形的判定．
如图，在△ABC中， AB=AC，AD平分 ∠BAC．求证： ∠DBC=∠DCB．
解：∵AD平分∠BAC， ∴∠BAD=∠CAD． ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD
AD=AD ， ∴△ACD≌△ABD， ∴BD=CD， ∴∠DBC=∠DCB．
：∵AC平分∠BAD，
∴∠BAC=∠DAC，
在△ABC和△ADC中， AB=AD ∠BAC=∠DAC AC=AC ，
∴△ABC≌△ADC．
全等三角形的判定．
9.如图，已知点E，C在线段
BF上， BE=CF， AB∥DE， ∠ACB=∠F．
求证： △ABC≌△DEF
．
证明：∵AB∥DE，
∴∠B=∠DEF．
全等三角形的判定与性质．

全等三角形证明经典10题((含答案)

全等三角形证明经典10题(含答案)1 如图,已知: AD 是BC 上的中线 ,且DF=DE ．求证:BE ∥CF ．2.如图，在ΔABC 中，D 是边BC 上一点，AD 平分∠BAC ，在AB 上截取AE=AC ，连结DE ，已知DE=2cm ，BD=3cm ，求线段BC 的长。

3.已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=24.已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2ADBCA BCDE1. 证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

5.已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC证明：过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角） ∴△EFD ≌△CGD EF ＝CG ∠CGD ＝∠EFD又，EF ∥AB ∴，∠EFD ＝∠1 ∠1=∠2 ∴∠CGD ＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CGBA CDF2 1 EEDC B A F∴EF ＝AC6.已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：延长AB 取点E ，使AE ＝AC ，连接DE ∵AD 平分∠BAC ∴∠EAD ＝∠CAD ∵AE ＝AC ，AD ＝AD ∴△AED ≌△ACD （SAS ） ∴∠E ＝∠C ∵AC ＝AB+BD ∴AE ＝AB+BD ∵AE ＝AB+BE ∴BD ＝BE ∴∠BDE ＝∠E ∵∠ABC ＝∠E+∠BDE ∴∠ABC ＝2∠E ∴∠ABC ＝2∠C7.如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.8.如图(1), 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD ⊥AE 于D, CE ⊥AE 于E 试说明: BD=DE+CE9已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE证明：在AC上取一点D，使得角DBC=角C∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C；∵∠ADB=∠C+∠DBC=2∠C;∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD中，AE是角BAD的角平分线，∴AE垂直BD∵BE⊥AE∴点E一定在直线BD上，在等腰三角形ABD中，AB=AD，AE垂直BD ∴点E也是BD的中点∴BD=2BE∵BD=CD=AC-AB∴AC-AB=2BE22．（6分）如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．（1）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，∴∠DEC=∠BFA=90°，DE∥BF，在Rt△DEC和Rt△BFA中，∵AF=CE，AB=CD，∴Rt△DEC≌Rt△BFA（HL），∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF；（2）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，∴∠DEC=∠BFA=90°，DE∥BF，在Rt△DEC和Rt△BFA中，∵AF=CE，AB=CD，∴Rt△DEC≌Rt△BFA（HL），∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF．欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求。

全等三角形证明经典50题

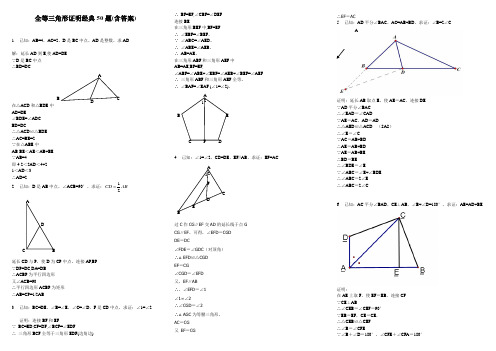
全等三角形证明经典50题(含答案)1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=22.已知：D是AB中点，∠ACB=90°，求证：12 CD AB延长CD与P，使D为CP中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边) ∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。

∴∠BAF=∠EAF (∠1=∠2)。

4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠C证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°AD BCBACDF21EA∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ） ∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：1CD ABAD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=29. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

全等三角形证明经典40题含答案(供参考)

1.已知：AB=4, AC=2, D是BC中点，AD是整数，求AD的长.解：延长AD到E使AD=DEYD是BC中点ABD=DC^EAACD和厶BDE中AD=DEZBDE=ZADCBD=DCAAACD^ABDEAAC=BE=2•••在△ ABE 中AB-BE<AE<AB+BEVAB=4即4・2V2ADV4+21<AD<3AAD=22.已知：BC=ED, ZB二ZE, ZC=ZD, F 是CD 中点，求证：Z1 = Z2证明：连接BF和EF••• BC=ED.CF=DE ZBCF=ZEDF・•.三角形BCF全等于三角形EDF(边角边)••• BF=EEZCBF=ZDEF连接BE在三角形BEF中,BF=EF••• ZEBF=ZBEFo••• ZABC=ZAEDc••• ZABE=ZAEBo/. AB=AEo在三角形ABF和三角形AEF中AB=AE.BF=EEZABF=ZABE+ZEBF=ZAEB+ZBEF=ZAEF ・•.三角形ABF和三角形AEF全等。

••• ZBAF=ZEAF(Zl=Z2)o3.已知：Z1=Z2, CD=DE, EF//AB,求证：EF=AC过C作CG〃EF交AD的延长线于点GCG/7EF,可得，ZEFD=CGDDE=DCZFDE=ZGDC (对顶角)•••△ EFD^ACGDEF=CGZCGD=ZEFD又，EF〃AB•••, ZEFD=Z1Z1=Z2AZCGD=Z2・•・△ AGC为等腰三角形，AC=CG又EF=CG・・・EF=AC4.已知：AD 平分ZBAC, AC=AB+BD,求证：ZB=2ZC证明：延长AB取点E,使AE=AC,连接DE TAD 平分ZBAC •••ZEAD=ZCADVAE=AC, AD=ADAAAED^AACD (SAS)AZE=ZCVAC=AB+BDAAE = AB+BDVAE = AB+BE•••BD = BEAZBDE=ZEAZABC=2ZEAZABC=2ZC5.已知：AC 平分ZBAD, CE丄AB, ZB+ZD=180° ,求证：AE=AD+BE证明：在AE上取F,使EF=EB,连接CFICE丄ABAZCEB = ZCEF=90°VEB=EF, CE=CE,AACEB^ACEF(SAS)AZB = ZCFEVZB4-ZD=180° , ZCFE+ZCFA=180°AZD=ZCFAVAC 平分ZBADAZDAC=ZFACVAC=ACAAADC^AAFC (SAS)•••AD = AF•••AE=AF+FE=AD+BE6.如图，四边形ABCD中，AB〃DC, BE、CE分别平分ZABC、ZBCD,且点E在AD 上。

全等三角形证明题及答案(15道)

1.已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证： BC=ED．
证明：∵∠1=∠2， ∴∠1+∠BAD=∠2+∠BAD，即：∠EAD=∠BAC，在△EAD和△BAC中 ∠B=∠E AB=AE ∠BAC=∠EAD ， ∴△ABC≌△AED（ASA）， ∴BC=ED．全等三角形的判定与性质．
全等三角形的判定．

4.如图，点E、F分别是AD上的两点，AB∥CD， AB=CD，AF=DE．问：线段CE、BF有什么数量关系和位置关系？并加以证明．
• • • • 证明：∵AB∥CD， ∴∠A=∠D， ∵在△ABF和△DCE中 AB=CD ∠A=∠D AF=DE ， • ∴△ABF≌△DCE， • ∴CE=BF， ∠AFB=∠DEC， • ∴CE∥BF，即CE和BF的数量关系是 CE=BF，位置关系是 CE∥BF．．
如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F，BE=CF．求证：AD是△ABC的角平分线．
证明：∵DE⊥AB，DF⊥AC， ∴Rt△BDE=Rt△DCF=90°． BD=DC BE=CF ， ∴Rt△BDE≌Rt△DCF（HL）， ∴DE=DF，又∵DE⊥AB，DF⊥AC， ∴AD是角平分线．角平分线的性质；全等三角形的判定与性质
直角三角形全等的判定
如图，△ABC中，∠ABC=∠BAC=45°，点 P在AB上，AD⊥CP，BE⊥CP，垂足分别为D， E，已知DC=2，求BE的长．
∵∠ABC=∠BAC=45° ∴∠ACB=90°，AC=BC ∵∠DAC+∠ACD=90°，∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2．

全等三角形经典题型50题(有答案)

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以三角形BCF全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC 5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C 6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ，所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ）所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE 12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形证明经典50题(含答案)

1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2) 4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC ∠FDE ＝∠GDC （对顶角） ∴△EFD ≌△CGD EF ＝CG ∠CGD ＝∠EFD 又，EF ∥AB ∴，∠EFD ＝∠1 ∠1=∠2 ∴∠CGD ＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：延长AB 取点E ，使AE ＝AC ，连接DE ∵AD 平分∠BAC ∴∠EAD ＝∠CAD ∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）A C DEF 21 ADBCDABBA CDF2 1 EA∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF ∴AE＝AF＋FE＝AD＋BE12. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

全等三角形证明100题（经典）

全等三角形证明100题（经典）1：已知：AB=4，AC=2，D 是BC 中点， AD 是整数，求AD 长。

2：已知：D 是AB 中点，∠ACB=90°，求证：12CD AB:3：已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2:4：已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACADB CBA CDF2 1 E5：已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE :6：.:如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

7：P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<ac-ab< p="">8：已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BEP D ACB9：已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC10：如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．11：如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA :FA ED C B12：如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．13：已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：14：如图：DF=CE ，AD=BC ，∠D=∠C 。

全等三角形经典题型50题(含答案)

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ，所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ）所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。