fisher算法及其matlab实现
matlab fisher最优分割 时间序列

在MATLAB中,可以使用以下步骤来实现Fisher最优分割算法对时间序列进行聚类:1. 确定聚类数:使用Fisher最优分割算法对时间序列进行聚类,需要先确定聚类数。
可以通过交叉验证等方法来选择最优的聚类数。
2. 建立Fisher矩阵:使用MATLAB中的Fisher矩阵函数可以快速计算出Fisher矩阵。
Fisher 矩阵是一个方阵,其中每个元素表示两个变量之间的相关性。
可以使用以下代码来计算Fisher矩阵:定义时间序列数据data = [1 2 3 4 5; 6 7 8 9 10; 11 12 13 14 15];计算Fisher矩阵F = fisher(data, 'Distance', 'euclidean');在这个示例中,我们使用Fisher函数计算Fisher矩阵,并将'euclidean'作为距离度量方式。
3. 计算最优分割点:使用MATLAB中的fminsearch()函数可以找到Fisher矩阵的最小值。
可以使用以下代码来计算最优分割点:定义最小值搜索函数fun = (x) -sum(x.*F);计算最小值x0 = [0.5 0.5];x = fminsearch(fun, x0);输出最优分割点disp(['最优分割点为:', num2str(x(1)) ', ', num2str(x(2))]);在这个示例中,我们将Fisher矩阵作为输入,并使用fminsearch()函数找到Fisher矩阵的最小值。
最终,我们将得到最优分割点,并将其打印出来。
4. 对时间序列进行聚类:使用MATLAB中的cluster()函数可以将时间序列聚类到相应的聚类中。
可以使用以下代码来进行聚类:定义聚类函数clustFunc = (x) cluster(x, x(1), x(2));对时间序列进行聚类clustLabels = cluster(data, x(1), x(2));输出聚类标签disp(['时间序列的聚类标签为:', num2str(clustLabels)]);在这个示例中,我们将时间序列数据和最优分割点作为输入,并使用cluster()函数将时间序列聚类到相应的聚类中。
Fisher线性分类器通俗解释及MATLAB、Python实现

Fisher线性分类器通俗解释及MATLAB、Python实现⼀、通俗的解释:问题提出:还是以iris的数据为例,有A、B、C三种花,每⼀类的特征都⽤4维特征向量表⽰。
现在已知⼀个特征向量,要求对应的类别,⽽我们⼈可以直接通过眼睛看⽽作出分类的是在⼀维⼆维三维空间,⽽不适应这样的四维数据。
启⽰:假设有这样的⼀个⽅向向量,其与特征向量进⾏内积运算(即向⽅向向量的投影)后,结果为⼀个数值,若同类的特征向量投影后聚集在⼀起,不同类的特征投影后相对分散,那么,我们的⽬的就达到了。
⽬标:这样就有了⽅向,即要寻找⼀个独特的⽅向,使其达到我们的要求。
注:具体的推导过程,参看教科书,另外,在求解极值的时候,利⽤了矩阵论中的向量导数运算。
⼆、MATLAB程序:clearA=[5.1,3.5,1.4,0.24.9,3.0,1.4,0.24.7,3.2,1.3,0.24.6,3.1,1.5,0.25.0,3.6,1.4,0.25.4,3.9,1.7,0.44.6,3.4,1.4,0.35.0,3.4,1.5,0.24.4,2.9,1.4,0.24.9,3.1,1.5,0.15.4,3.7,1.5,0.24.8,3.4,1.6,0.24.8,3.0,1.4,0.14.3,3.0,1.1,0.15.8,4.0,1.2,0.25.7,4.4,1.5,0.45.4,3.9,1.3,0.45.1,3.5,1.4,0.35.7,3.8,1.7,0.35.1,3.8,1.5,0.35.4,3.4,1.7,0.25.2,4.1,1.5,0.15.5,4.2,1.4,0.24.9,3.1,1.5,0.15.0,3.2,1.2,0.25.5,3.5,1.3,0.24.4,3.2,1.3,0.25.0,3.5,1.6,0.6 5.1,3.8,1.9,0.44.8,3.0,1.4,0.35.1,3.8,1.6,0.24.6,3.2,1.4,0.25.3,3.7,1.5,0.2 5.0,3.3,1.4,0.2 7.0,3.2,4.7,1.4];B=[6.4,3.2,4.5,1.5 6.9,3.1,4.9,1.55.5,2.3,4.0,1.36.5,2.8,4.6,1.55.7,2.8,4.5,1.36.3,3.3,4.7,1.6 4.9,2.4,3.3,1.0 6.6,2.9,4.6,1.3 5.2,2.7,3.9,1.4 5.0,2.0,3.5,1.05.9,3.0,4.2,1.56.0,2.2,4.0,1.0 6.1,2.9,4.7,1.45.6,2.9,3.6,1.36.7,3.1,4.4,1.4 5.6,3.0,4.5,1.55.8,2.7,4.1,1.06.2,2.2,4.5,1.5 5.6,2.5,3.9,1.15.9,3.2,4.8,1.86.1,2.8,4.0,1.3 6.3,2.5,4.9,1.5 6.1,2.8,4.7,1.25.5,2.4,3.8,1.1 5.5,2.4,3.7,1.05.8,2.7,3.9,1.26.0,2.7,5.1,1.65.4,3.0,4.5,1.56.0,3.4,4.5,1.6 6.7,3.1,4.7,1.5 6.3,2.3,4.4,1.3 5.6,3.0,4.1,1.3 5.5,2.5,4.0,1.35.5,2.6,4.4,1.26.1,3.0,4.6,1.4 5.8,2.6,4.0,1.2 5.0,2.3,3.3,1.0 5.6,2.7,4.2,1.3 5.7,3.0,4.2,1.25.7,2.9,4.2,1.36.2,2.9,4.3,1.3 5.1,2.5,3.0,1.1 5.7,2.8,4.1,1.3];C=[6.3,3.3,6.0,2.5 5.8,2.7,5.1,1.9 7.1,3.0,5.9,2.1 6.3,2.9,5.6,1.86.5,3.0,5.8,2.27.6,3.0,6.6,2.1 4.9,2.5,4.5,1.7 7.3,2.9,6.3,1.86.7,2.5,5.8,1.87.2,3.6,6.1,2.5 6.5,3.2,5.1,2.0 6.4,2.7,5.3,1.97.7,2.6,6.9,2.36.0,2.2,5.0,1.56.9,3.2,5.7,2.35.6,2.8,4.9,2.07.7,2.8,6.7,2.06.3,3.4,5.6,2.46.4,3.1,5.5,1.86.0,3.0,4.8,1.86.9,3.1,5.4,2.16.7,3.1,5.6,2.46.9,3.1,5.1,2.35.8,2.7,5.1,1.96.8,3.2,5.9,2.36.7,3.3,5.7,2.56.7,3.0,5.2,2.36.3,2.5,5.0,1.96.5,3.0,5.2,2.06.2,3.4,5.4,2.35.9,3.0,5.1,1.8];%⽅法⼀:先将A作为⼀类,BC作为⼀类NA=size(A,1);NB=size(B,1);NC=size(C,1);A_train=A(1:floor(NA/2),:);%训练数据取1/2(或者1/3,3/4,1/4)B_train=B(1:floor(NB/2),:);C_train=C(1:floor(NC/2),:);A_test=A((floor(NA/2)+1):end,:);B_test=B((floor(NB/2)+1):end,:);C_test=C((floor(NC/2)+1):end,:);A_train=A_train;D_train=[B_train;C_train];A_test=A_test;D_test=[B_test;C_test];for i=1:size(A_train,1)S1=S1+(A_train(i,:)-u1)'*(A_train(i,:)-u1);endfor i=1:size(D_train,1)S2=S2+(D_train(i,:)-u2)'*(D_train(i,:)-u2);endSw=S1+S2;w1=(inv(Sw)*(u1-u2)')';w1=w1./norm(w1);y0=w1*(u1+u2)'/2;% a1=w*u1'% d1=w*u2'r1=0;for i=1:size(D_test,1)if w1*D_test(i,:)'<y0r1=r1+1;endendrate_D=r1/size(D_test,1)r2=0;for i=1:size(A_test,1)if w1*A_test(i,:)'>y0r2=r2+1;endendrate_A=r2/size(A_test,1)三、Python程序:from sklearn import discriminant_analysisfrom sklearn.model_selection import train_test_splitimport numpydata = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(0,1,2,3)) target = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(4), dtype=str) t = numpy.zeros(len(target))t[target == 'setosa'] = 1t[target == 'versicolor'] = 2t[target == 'virginica'] = 3#print(clf.predict([data[3]]))。
FISHER线性判别MATLAB实现

Fisher线性判别上机实验报告班级:学号:姓名:一.算法描述Fisher 线性判别分析的基本思想:选择一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起,不同类的样本相隔尽可能地远。
Fisher 线性判别分析,就是通过给定的训练数据,确定投影方向W 和阈值w0, 即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
线性判别函数的一般形式可表示成0)(w X W X g T += 其中⎪⎪⎪⎭⎫⎝⎛=d x x X 1 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=d w w w W 21Fisher 选择投影方向W 的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求。
如下为具体步骤:(1)W 的确定样本类内离散度矩阵i和总类内离散度矩阵w S12w S S S =+Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵b S在投影后的一维空间中,各类样本均值Tiim '= Wm样本类内离散度和总类内离散度 T Ti i ww S ' = W S W S ' = W S W 样本类间离散度Tbb S ' = W S W Fisher 准则函数为 max 2221221~~)~~()(S S m mW J F +-=(2)阈值的确定w 0是个常数,称为阈值权,对于两类问题的线性分类器可以采用下属决策规则: 令)()()(21x x x g g g -=则:如果g(x)>0,则决策w x 1∈;如果g(x)<0,则决策w x 2∈;如果g(x)=0,则可将x 任意分到某一类,或拒绝。
(3)Fisher 线性判别的决策规则 Fisher 准则函数满足两个性质:1.投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
费舍变换 matlab

费舍变换 matlab费舍变换(Fisher's linear discriminant analysis)是一种经典的监督学习算法,用于特征提取和数据降维。
在MATLAB中,你可以使用`fitcdiscr`函数来实现费舍变换。
这个函数可以用于训练一个线性判别分析器,并且返回一个分类器对象。
你可以使用这个分类器对象来进行预测和特征提取。
下面是一个简单的示例代码,演示如何在MATLAB中使用`fitcdiscr`函数进行费舍变换:matlab.% 生成一些示例数据。
X = [randn(100,2); randn(100,2)+2];Y = [ones(100,1); 2ones(100,1)];% 使用fitcdiscr函数训练一个线性判别分析器。
classifier = fitcdiscr(X, Y);% 使用训练好的分类器对象进行预测。
predictedY = predict(classifier, X);% 获取费舍变换后的特征。
transformedX = X classifier.Coeffs(1, 2).Linear; % 可视化原始数据和变换后的数据。
figure;scatter(X(:,1), X(:,2), 20, Y, 'filled');title('Original Data');xlabel('Feature 1');ylabel('Feature 2');figure;scatter(transformedX, zeros(length(transformedX),1), 20, Y, 'filled');title('Transformed Data');xlabel('Transformed Feature');在这个示例中,我们首先生成了一些示例数据,然后使用`fitcdiscr`函数训练了一个线性判别分析器。
Fisher分类器(算法及程序)
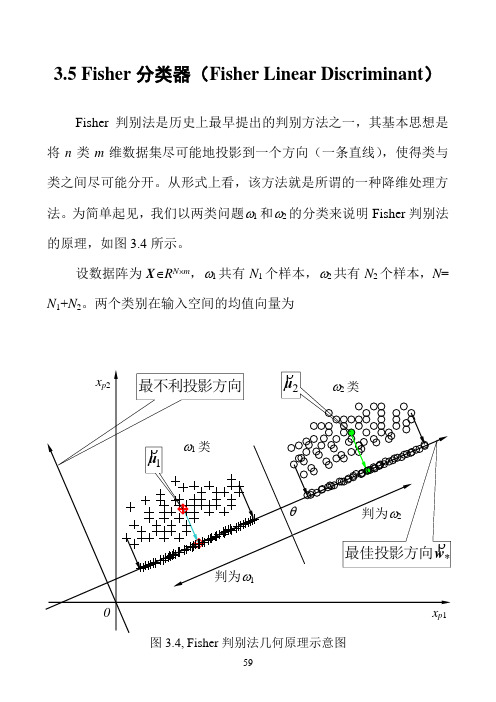
3.5 Fisher分类器(Fisher Linear Discriminant)Fisher判别法是历史上最早提出的判别方法之一,其基本思想是将n类m维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题ω1和ω2的分类来说明Fisher判别法的原理,如图3.4所示。
设数据阵为X∈R N⨯m,ω1共有N1个样本,ω2共有N2个样本,N= N1+N2。
两个类别在输入空间的均值向量为图3.4, Fisher判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μρρρρρρ设有一个投影方向()mT m R w w w ∈=,,,21Λρw ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μρρρρρρρρρρρρ在w ρ方向,两均值之差为())39.3(~~2121μμw μμρρρρρ-=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μρρρρρ定义类间散度(Between-class scatter)平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμρρρρρρρρρρρρρρρρρρρρρρρρρρB T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS ρρρρρρρρρρρρ定义类ωj 的类内散度(Within-class scatter)平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw ρρρρρρρ两个类的总的类内散度误差平方和为()()())44.3(2121221wS w w μμw μw w ρρρρρρρρρρρρW T j Np T jp j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS ρρρρ我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w w ρρρρρW T B T WBSS SS J ==图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义。
fisher算法及其matlab实现

Fisher判别法讲解以及matlab代码实现两类的线形判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。
过这个预置点且与投影方向垂直的超平面就是两类的分类面。
第一个问题,如何确定投影方向?这里只讨论两类分类的问题.训练样本集是X={x1,x2...xn},每个样本是一个d维向量,其中第一类w1={ X i,x2 ... x ii},第二类w2={ x i ,x2 ... x?2 }。
我们要寻求一个投影方向w(w也是一个d维向量),投影以后样本变成:y i = W T X i(y 是一个标量),i=1...n在原样本空间中,类均值为:1m i —X j n i x j w ii=1,2(一共两类的均值)(ps.m i是一个d*1的矩阵,假设每个维度是一个变量值,mi中的每一维度就是这些变量值的均值,如下图所示:特别注明:有些例子给的矩阵是这样的:fisher算法公式的时候就会发现最后得到的矩阵维数不对。
定义各类类内的离散度矩阵为:(类内离散度矩阵其实就是类协方差矩阵,类在多于一个样本,且样本维度>1时是一个矩阵)S (X j m i)(X j mJ TX j w i(因为,Xj是一个d*1的矩阵,也可称作d维向量,m也是一个d*1的矩阵, 所以最后得到的S一定是一个d*d的矩阵)(在用matlab计算的时候直接用cov(wi)即可得到想要的协方差矩阵,故直接计算不探究细节时图2可直接cov算协方差,不用根据公式转置来转置去,不过matlab中算的协方差被缩小了(n 1-1)倍,计算时i=cov(w1)* (n 1-1))总的类内离散度矩阵:S w类间离散度矩阵定义为:S b (m i m 2)(m 1在投影以后的一维空间里,两类的均值分别是;将公式代入并通过拉格朗日求极值的方法,可得 投影方向:m iiNi y j w iy i丄N i xTw x jwTw m ii=1,2故类内离散度不再是一个矩阵,而是一个值S i(y i mJ 2y j W ii=1,2总类内离散度为:SwwS11S11类间离散度:(m ii mu)2要使得需求的方向投影能在投影后两类能尽可能的分开, 聚集,可表示成如下准则,即fisher 准则: 而各类内部又尽可能的max J (w)Sbb1w S w (m mJ(w是一个d*1的矩阵,或者说亦是一个d维向量)阈值可表示为:W。
LDA算法学习(Matlab实现)

LDA算法学习(Matlab实现)LDA算法对于两类问题的LDA(Matlab实现)1 function [ W] = FisherLDA(w1,w2)2 %W最⼤特征值对应的特征向量3 %w1 第⼀类样本4 %w2 第⼆类样本56 %第⼀步:计算样本均值向量7 m1=mean(w1);%第⼀类样本均值8 m2=mean(w2);%第⼆类样本均值9 m=mean([w1;w2]);%总样本均值1011 %第⼆步:计算类内离散度矩阵Sw12 n1=size(w1,1);%第⼀类样本数13 n2=size(w2,1);%第⼆类样本数14 %求第⼀类样本的散列矩阵s115 s1=0;16 for i=1:n117 s1=s1+(w1(i,:)-m1)'*(w1(i,:)-m1);18 end19 %求第⼆类样本的散列矩阵s220 s2=0;21 for i=1:n222 s2=s2+(w2(i,:)-m2)'*(w2(i,:)-m2);23 end24 Sw=(n1*s1+n2*s2)/(n1+n2);25 %第三步:计算类间离散度矩阵Sb26 Sb=(n1*(m-m1)'*(m-m1)+n2*(m-m2)'*(m-m2))/(n1+n2);27 %第四步:求最⼤特征值和特征向量28 %[V,D]=eig(inv(Sw)*Sb);%特征向量V,特征值D29 A = repmat(0.1,[1,size(Sw,1)]);30 B = diag(A);31 [V,D]=eig(inv(Sw + B)*Sb);32 [a,b]=max(max(D));33 W=V(:,b);%最⼤特征值对应的特征向量34 end测试:cls1_data=[2.95 6.63;2.53 7.79;3.57 5.65;3.16 5.47];cls2_data=[2.58 4.46;2.16 6.22;3.27 3.52];%样本投影前plot(cls1_data(:,1),cls1_data(:,2),'.r');hold on;plot(cls2_data(:,1),cls2_data(:,2),'*b');hold on;W=FisherLDA(cls1_data,cls2_data);%样本投影后new1=cls1_data*W;new2=cls2_data*W;k=W(2)/W(1);plot([0,6],[0,6*k],'-k');axis([2 6 0 11]);hold on;%画出样本投影到⼦空间点for i=1:4temp=cls1_data(i,:);newx=(temp(1)+k*temp(2))/(k*k+1);newy=k*newx;plot(newx,newy,'*r');end;for i=1:3temp=cls2_data(i,:);newx=(temp(1)+k*temp(2))/(k*k+1);newy=k*newx;plot(newx,newy,'ob');end; 结果:。
matlab中lsqcurvefit的用法

matlab中lsqcurvefit的用法摘要:I.引言- 介绍MATLAB 中的lsqcurvefit 函数II.lsqcurvefit 函数的基本用法- 函数定义与功能- 函数语法及参数说明III.lsqcurvefit 函数的应用实例- 实例1:非线性函数拟合- 实例2:多项式拟合- 实例3:指数拟合IV.lsqcurvefit 函数与其他拟合函数的比较- 与polyfit 函数的比较- 与cftool 函数的比较V.总结- 概括lsqcurvefit 函数的特点与优势- 指出lsqcurvefit 函数的适用场景正文:I.引言MATLAB 是一款功能强大的数学软件,广泛应用于科学计算、数据分析等领域。
在MATLAB 中,lsqcurvefit 函数是一个重要的拟合工具,可以用于对非线性数据进行最小二乘拟合。
本文将介绍MATLAB 中lsqcurvefit 函数的用法及应用实例。
II.lsqcurvefit 函数的基本用法lsqcurvefit 函数用于对非线性数据进行最小二乘拟合。
其函数定义如下:```matlabX = lsqcurvefit(FUN, X0, XDATA, YDATA)```其中,FUN 是函数句柄,X0 是初始参数向量,XDATA 和YDATA 分别是输入数据向量和输出数据向量。
函数返回拟合后的参数向量X。
lsqcurvefit 函数的语法及参数说明如下:- FUN:拟合函数的句柄。
可以是MATLAB 中的内置函数,如"poly1"、"exp1"等,也可以是用户自定义的函数。
- X0:初始参数向量。
用于初始化搜索算法,其元素数量应与拟合函数中参数的数量相同。
- XDATA:输入数据向量。
拟合函数的输入数据,其长度应与YDATA 相同。
- YDATA:输出数据向量。
拟合函数的输出数据,其长度应与XDATA 相同。
III.lsqcurvefit 函数的应用实例lsqcurvefit 函数可以应用于多种拟合场景,以下为三个实例:实例1:非线性函数拟合假设我们有一组非线性数据点,如下所示:```matlabx = [1, 2, 3, 4, 5];y = [2.1, 3.9, 6.2, 8.1, 10.5];```我们可以使用lsqcurvefit 函数对其进行拟合。
fisheriris数据集matlab中knn分类

fisheriris数据集matlab中knn分类fisheriris数据集是一个经典的模式识别数据集,常用于机器学习中的分类问题。
其中包含了150个样本,分为三类鸢尾花:Setosa、Versicolor和Virginica。
每个样本有四个特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。
本文将以fisheriris数据集和其中的k-最近邻(k-Nearest Neighbors, KNN)分类算法为主题,详细解释该算法的原理和实现过程。
一、数据集介绍Fisheriris数据集由英国生物统计学家罗纳德·费雪收集,用于分类问题的研究。
数据集中的每个样本都代表一朵鸢尾花,共有150朵花。
每朵花有四个特征值(花萼长度、花萼宽度、花瓣长度和花瓣宽度)以及一个类标签,用于表示该花属于鸢尾花的哪个类别。
鸢尾花共分为三个类别:Setosa、Versicolor和Virginica。
Fisheriris数据集可以在MATLAB的datasets 包中找到。
二、KNN算法概述KNN算法是一种基于实例的学习方法,用于解决分类和回归问题。
对于分类问题,KNN算法通过比较待分类样本与已知类别样本的特征相似度,将其归为相似度最高的k个样本所属的类别中出现次数最多的类别。
KNN算法的原理比较简单。
首先,计算待分类样本与已知样本之间的距离,常用的距离度量方法有欧氏距离、曼哈顿距离和闵可夫斯基距离等。
然后,根据距离的大小选择k个最近邻样本,并统计这k个样本中各个类别出现的次数。
最后,将待分类样本归为出现次数最多的类别所属。
三、KNN算法步骤详解1. 导入数据集首先,我们需要导入Fisheriris数据集并查看其中的数据。
在MATLAB中,可以直接使用load命令加载数据集。
Matlabload fisheriris2. 数据集预处理在使用KNN算法之前,我们需要进行数据集的预处理,包括数据归一化、划分训练集和测试集等操作。
模式识别fisher判别

论文(设计)《模式识别》题目Fisher线性判别的基本原理及应用Fisher判别准则一、基本原理思想Fisher线性判别分析的基本思想:通过寻找一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,并且要求变换后的一维数据具有如下性质:同类样本尽可能聚集在一起,不同类的样本尽可能地远。
Fisher线性判别分析,就是通过给定的训练数据,确定投影方向W和阈值y0,即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
二、算法的实现及流程图1 算法实现 (1)W 的确定x 1m x, 1,2ii X ii N ∈==∑各类样本均值向量mi样本类内离散度矩阵和总类内离散度矩阵Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵T1212S (m m )(m m )b =--在投影后的一维空间中,各类样本均值。
样本类内离散度和总类内离散度。
样本类间离散度。
Fisher 准则函数满足两个性质:·投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
·投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出W :。
(2)阈值的确定采取的方法:【1】【2】【3】(3)Fisher 线性判别的决策规则对于某一个未知类别的样本向量x ,如果y=W T·x>y0,则x ∈w1;否则x ∈w2。
2 流程图归一化处理载入训练数据三、实验仿真1.实验要求试验中采用如下的数据样本集:ω1类: (22,5),(46,33),(25,30),(25,8),(31, 3),(37,9),(46,7),(49,5),(51,6),(53,3)(19,15),(23,18),(43,1),(22,15),(20,19),(37,36),(22,22),(21,32),(26,36),(23,39)(29,35),(33,32),(25,38),(41,35),(33,2),(48,37)ω2类: (40,25),(63,33),(43,27),(52,25),(55,27),(59,22) ,(65,59),(63,27)(65,30),(66,38),(67,43),(52,52),(61,49) (46,23),(60,50),(68,55) (40,53),(60,55),(55,55) (48,56),(45,57),(38,57) ,(68,24)在实验中采用Fisher线性判别方法设计出每段线性判别函数。
fisher分布matlab函数

fisher分布matlab函数
在MATLAB中,Fisher分布可以使用`fpdf`函数来计算概率密度函数(PDF)和`fcdf`函数来计算累积分布函数(CDF)。
具体来说,`fpdf`函数用于计算Fisher分布的概率密度函数,其语法为:
matlab.
y = fpdf(x,v1,v2)。
其中,`x`是自变量,`v1`和`v2`分别是Fisher分布的自由度参数。
这个函数将返回Fisher分布在`x`处的概率密度值。
另外,`fcdf`函数用于计算Fisher分布的累积分布函数,其语法为:
matlab.
p = fcdf(x,v1,v2)。
其中,`x`是自变量,`v1`和`v2`分别是Fisher分布的自由度
参数。
这个函数将返回Fisher分布在`x`处的累积概率值。
除了这两个函数之外,MATLAB还提供了一系列用于处理Fisher 分布的函数,如`finv`用于计算Fisher分布的反函数,`fstat`用于计算Fisher分布的均值和方差等。
总之,在MATLAB中,可以使用这些函数来对Fisher分布进行各种计算和分析。
希望这些信息能够帮助到你。
matlab中lsqcurvefit的用法

MATLAB中lsqcurvefit的用法概述在M AT LA B中,`ls qc u rv ef it`是一个用于非线性最小二乘拟合的函数。
该函数可以求解一组非线性方程或拟合一组数据,以最小化残差平方和。
函数语法```m at la b[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(fu n,x0,x da ta,y da ta,l b,u b,o pt io ns)```参数说明-`fu n`:自定义函数句柄,用于计算模型预测值和实际观测值之间的残差。
该函数应接受参数x和xd at a作为输入,返回模型预测值。
-`x0`:拟合参数的初始猜测值。
-`xd at a`:实际观测值的自变量数据。
-`yd at a`:实际观测值的因变量数据。
-`lb`:拟合参数的下界限制。
-`ub`:拟合参数的上界限制。
-`op ti on s`:可选参数,用于指定拟合过程中的详细设置,如最大迭代次数、收敛容限等。
示例假设我们有一组数据,需拟合出一个指数函数模型。
首先定义自定义函数`e xp Fu nc`,用于计算指数函数的预测值和实际观测值之间的残差。
```m at la bf u nc ti on y=ex pF unc(x,xd at a)y=x(1)*e xp(x(2)*x d at a);e n d```然后,我们准备好数据和初始猜测值,并调用`l sq cu rv ef it`进行拟合。
```m at la bx d at a=[01234];y d at a=[12.66.714.529.6];x0=[11];[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(@e xp Fun c,x0,xd at a,yd ata);```输出结果-`x`:拟合出的参数值。
fisheriris数据集matlab中knn分类

fisheriris数据集matlab中knn分类鸢尾花数据集(Iris)是一个非常常用的用于模式识别和机器学习的数据集。
它包含了150个样本,每个样本有4个特征,分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度。
每个样本所属的类别有三个,分别是Setosa、Versicolor和Virginica。
我们可以使用k最近邻(k-nearest neighbors,KNN)算法对鸢尾花数据集进行分类。
KNN算法是一种监督学习算法,可以用于分类和回归任务。
在Matlab中,我们可以使用ClassificationKNN对象来实现KNN算法。
首先,我们需要加载鸢尾花数据集。
```matlabload fisheriris;```鸢尾花数据集加载后,可以用以下代码查看数据集的结构。
```matlabwhos```可以看到数据集有两个变量,一个是150x4的测量数据矩阵meas,另一个是150x1的类别标签矩阵species。
接下来,我们可以将数据集拆分为训练集和测试集。
训练集用于训练KNN模型,而测试集则用于评估模型的准确性。
```matlabcv = cvpartition(species,'Holdout',0.3); % 70%的数据作为训练集,30%的数据作为测试集dataTrain = meas(cv.training,:);speciesTrain = species(cv.training);dataTest = meas(cv.test,:);speciesTest = species(cv.test);```然后,我们可以创建一个ClassificationKNN对象,并使用训练集来训练模型。
```matlabknnModel = fitcknn(dataTrain, speciesTrain, 'NumNeighbors', 5);```在这个示例中,我们选择邻居数量为5。
fisher函数matlab实现

一、实验目的在UCI数据集上的Iris和sonar数据上验证算法的有效性;Iris数据3类,4维,150个数据;Sonar数据2类,60维,208个样本;二、实验说明1、本实验由MATLAB2014实现算法及验证。
2、训练和测试样本采用留1法划分三、在Iris上验证算法的代码及结果(1)代码1、function y=fisher_iris(SE,VE,VI)2、3、S_V=[SE;VE];4、5、ALL_1=[S_V;VI];6、7、for L=1:1508、 T=S_V;9、 P=VI;10、 sample=ALL_1(L,:);11、if L<=10012、 T(L,:)=[];13、else14、 P(L-100,:)=[];15、end16、17、 R1=size(T,1);18、 R2=size(P,1);19、20、 a1=mean(T);21、 a2=mean(P);22、23、 s1=cov(T)*(R1-1);24、 s2=cov(P)*(R2-1);25、26、 Sw=s1+s2;27、28、 w=inv(Sw)*(a1-a2)';29、30、 y1=mean(w'*a1');31、 y2=mean(w'*a2');32、33、 w0=1/2*(y1+y2);34、35、 y(L)=w'*sample';37、if y(L)>w0;38、 y(L)=0;39、40、for L_2=1:10041、 T_2=SE;42、 P_2=VE;43、 sample=S_V(L_2,:);44、if L_2<=5045、 T_2(L_2,:)=[];46、else47、 P_2(L_2-50,:)=[];48、end49、50、 R1=size(T_2,1);51、 R2=size(P_2,1);52、53、 a1_2=mean(T_2);54、 a2_2=mean(P_2);55、56、 s1_2=cov(T_2)*(R1-1);57、 s2_2=cov(P_2)*(R2-1);58、59、 Sw_2=s1_2+s2_2;60、61、 w_2=inv(Sw_2)*(a1_2-a2_2)';62、63、 y1_2=mean(w_2'*a1_2');64、 y2_2=mean(w_2'*a2_2');65、66、 w0=1/2*(y1_2+y2_2);67、68、 y(L_2)=w_2'*sample';69、70、if y(L_2)>w0;71、 y(L_2)=0;72、else73、 y(L_2)=1;74、end75、end76、77、78、else79、 y(L)=2;81、end(2)实验结果z四、在sonar上验证算法的代码及结果(1)代码1、function y=fisher_sonar(M,R)2、3、A=[M;R];4、for l=1:2085、 T=M;6、 P=R;7、 sample=A(l,:);8、if l<=1119、 T(l,:)=[];10、else11、 P(l-111,:)=[];12、end13、14、 R1=size(T,1);15、 R2=size(P,1);16、17、 a1=mean(T);18、 a2=mean(P);19、20、 s1=cov(T)*(R1-1);21、 s2=cov(P)*(R2-1);22、23、 Sw=s1+s2;24、25、 w=inv(Sw)*(a1-a2)';26、27、 y1=mean(w'*a1');28、 y2=mean(w'*a2');29、30、 w0=1/2*(y1+y2);31、32、 y(l)=w'*sample';33、34、if y(l)>w0;35、 y(l)=0;36、else37、 y(l)=1;38、end40、41、(2)实验结果>> fisher_sonar(M,R)ans =1 至 5 列1 0 1 1 16 至 10 列0 1 1 1 011 至 15 列0 1 1 0 016 至 20 列0 1 0 0 021 至 25 列0 0 0 0 026 至 30 列0 0 0 0 031 至 35 列1 1 0 0 036 至 40 列0 0 1 0 041 至 45 列0 0 0 0 00 0 0 0 0 51 至 55 列0 0 0 1 1 56 至 60 列0 1 1 1 0 61 至 65 列0 0 0 0 0 66 至 70 列0 1 0 1 0 71 至 75 列0 0 0 0 0 76 至 80 列0 0 0 0 0 81 至 85 列1 1 0 0 0 86 至 90 列0 0 0 0 0 91 至 95 列0 0 0 0 1 96 至 100 列0 1 1 0 00 0 0 0 0 106 至 110 列0 0 0 0 0 111 至 115 列0 1 1 0 0 116 至 120 列0 0 1 0 0 121 至 125 列1 1 1 1 1 126 至 130 列1 1 1 0 1 131 至 135 列0 0 0 1 1 136 至 140 列1 1 0 0 0 141 至 145 列1 1 1 1 0 146 至 150 列0 0 1 1 1 151 至 155 列1 1 1 1 10 0 0 0 1 161 至 165 列1 1 1 1 1 166 至 170 列1 1 1 1 1 171 至 175 列1 1 1 1 1 176 至 180 列1 1 1 1 1 181 至 185 列1 1 1 1 0 186 至 190 列1 1 1 1 1 191 至 195 列0 0 0 0 1 196 至 200 列1 1 1 1 0 201 至 205 列1 1 1 1 0 206 至 208 列1 1 1>>。
Python实现线性判别分析(LDA)的MATLAB方式

#计算第一类样本在直线上的投影点 xi=[] yi=[] for i in range(0,p):
y0=X1[i,1] x0=X1[i,0] x1=(k*(y0-b)+x0)/(k**2+1) y1=k*x1+b xi.append(x1) yi.append(y1) print(xi)
%3.2700 3.5200 1
X=load('22.txt'); pos0=find(X(:,3)==0); pos1=find(X(:,3)==1); X1=X(pos0,1:2); X2=X(pos1,1:2); hold on plot(X1(:,1),X1(:,2),'r+','markerfacecolor', [ 1, 0, 0 ]); plot(X2(:,1),X2(:,2),'b*','markerfacecolor', [ 0, 0, 1 ]);
plt.show()
以上这篇Python实现线性判别分析(LDA)的MATLAB方式就是小编分享给大家的全部内容了,希望能给大家一个参考, 也希望大家多多支持。
p=np.size(X1,0) print(p) q=np.size(X2,0)
print(q)
#第二步,求类内散度矩阵 S1=np.dot((X1-M1).transpose(),(X1-M1)) print(S1) S2=np.dot((X2-M2).transpose(),(X2-M2)) print(S2) Sw=(p*S1+q*S2)/(p+q)
Python实现线性判别分析(LDA)的MATLAB方式
matlab fisher最优分割 时间序列 -回复

matlab fisher最优分割时间序列-回复题目:使用Fisher最优分割方法进行时间序列分析引言:时间序列分析是用于研究时间相关数据的统计方法。
在金融、经济、天气和环境等领域,时间序列分析常被用于预测和理解数据的变化。
Fisher最优分割方法是一种常用的时间序列分析技术,通过对时间序列数据进行分割,将序列分为不同的子空间,从而更好地理解和预测数据。
第一部分:介绍Fisher最优分割方法(300字)Fisher最优分割方法是一种基于统计推断的时间序列分析技术,它主要用于发现序列中的重要转折点或显著变化。
该方法基于Fisher准则,通过最大化不同子序列之间的方差比率,将序列分割为两个或多个子序列。
在每个子序列中,数据具有不同的趋势或特征,因此可以更准确地分析和预测。
第二部分:Fisher最优分割方法的基本原理(400字)Fisher最优分割方法的基本原理是寻找最优分割点,该分割点应使得分割后的子序列之间的方差比率最大。
方差比率是Fisher准则的一个关键指标,它反映了分割点的重要性。
具体而言,Fisher最优分割方法的计算步骤如下:1. 计算整个序列的方差。
2. 选择一个可能的分割点,并将序列分割成两个子序列。
3. 计算每个子序列的方差。
4. 计算方差比率,即将每个子序列的方差除以整个序列的方差。
5. 循环步骤2和步骤3,直到找到使方差比率最大的最优分割点。
6. 将序列分割为最优分割点两侧的子序列。
通过上述步骤,Fisher最优分割方法可以将时间序列分割为多个子序列,每个子序列具有不同的属性。
这样的分割可以更好地理解和预测序列中的趋势和变化。
第三部分:应用Fisher最优分割方法进行时间序列分析(600字)1. 数据准备:首先,需要准备时间序列数据。
这些数据可以是经济指标、股票价格、天气数据等。
确保数据是按照时间顺序排列的。
2. 寻找最优分割点:使用Fisher最优分割方法,根据上述原理,寻找使方差比率最大的最优分割点。
matlab中的一些经典算法

matlab中的一些经典算法在MATLAB中,有许多经典算法可以用于各种数学和工程问题。
以下是一些常见的经典算法:1. 最小二乘法(Least Squares Method),用于拟合数据和解决过定系统的线性方程组。
MATLAB中的`polyfit`和`lsqcurvefit`函数可以实现最小二乘拟合。
2. 快速傅里叶变换(Fast Fourier Transform, FFT),用于信号处理和频域分析。
MATLAB中的`fft`函数可以对信号进行快速傅里叶变换。
3. 线性规划(Linear Programming),用于优化问题的求解,例如最大化/最小化线性目标函数的线性约束问题。
MATLAB中的`linprog`函数可以用于线性规划求解。
4. 非线性最小二乘法(Nonlinear Least Squares),用于拟合非线性模型到数据。
MATLAB中的`lsqnonlin`函数可以用于非线性最小二乘拟合。
5. 最优化算法(Optimization Algorithms),MATLAB提供了许多优化算法,包括梯度下降、共轭梯度、拟牛顿等算法,用于解决无约束和约束优化问题。
6. 插值算法(Interpolation),MATLAB中的`interp1`和`interp2`函数可以用于一维和二维数据的插值。
7. 微分方程求解(Differential Equation Solving),MATLAB中的`ode45`和`ode15s`等函数可以用于求解常微分方程和偏微分方程。
8. 图像处理算法(Image Processing Algorithms),MATLAB提供了丰富的图像处理工具箱,包括滤波、边缘检测、图像分割等经典算法。
以上列举的算法只是 MATLAB 中众多经典算法的一小部分,它们在数学建模、信号处理、优化、图像处理等领域有着广泛的应用。
希望这些信息能够帮助到你。
matlab 英文模糊匹配算法

matlab 英文模糊匹配算法在MATLAB中,模糊匹配算法主要用于在字符串处理和文本分析中找到与给定字符串相似的字符串。
以下是一些常见的MATLAB中用于模糊匹配的算法:1. Levenshtein 距离算法Levenshtein距离是一种用于计算两个字符串之间的编辑距离的算法,即通过插入、删除和替换操作,将一个字符串转换成另一个字符串所需的最小操作次数。
MATLAB中,可以使用editdist函数来计算Levenshtein距离。
str1='example';str2='exmple';distance=editdist(str1,str2);2. Jaccard 相似性算法Jaccard相似性是一种用于比较两个集合相似性的方法,可以应用于字符串的字符集。
在MATLAB中,可以使用jaccard函数来计算两个字符串之间的Jaccard相似性。
str1='example';str2='exmple';similarity=1-jaccard(str1,str2);3. Dice 系数算法Dice系数是一种用于计算两个集合相似性的方法,特别适用于字符集的相似性计算。
在MATLAB中,可以使用dice函数来计算两个字符串之间的Dice系数。
str1='example';str2='exmple';similarity=1-dice(str1,str2);4. 向量空间模型(Vector Space Model)向量空间模型通常用于文本相似性和匹配。
可以使用诸如cosine等函数来计算两个文本向量之间的余弦相似性。
doc1=tokenizedDocument("This is an example");doc2=tokenizedDocument("This is another example");vec1=doc2vec(bag,doc1);vec2=doc2vec(bag,doc2);similarity=cosine(vec1,vec2);以上是一些在MATLAB中用于模糊匹配的算法和函数的简单介绍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
页脚内容1
Fisher 判别法讲解以及matlab 代码实现
两类的线形判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。
过这个预置点且与投影方向垂直的超平面就是两类的分类面。
第一个问题,如何确定投影方向?
这里只讨论两类分类的问题.训练样本集是X ={x1,x2...xn},每个样本是一个d 维向量,其中第一类
w1={11x ,12x ...11n x },第二类w2={21x ,22x (2)
2n x }。
我们要寻求一个投影方向w (w 也是一个d 维向量),投影以后样本变成:i y =
i T x w (y 是一个标量),i=1...n 在原样本空间中,类均值为: ∑∈=
i j w x j i i x n m 1 i=1,2(一共两类的均值)
(ps.i m 是一个d*1的矩阵,假设每个维度是一个变量值,mi 中的每一维度就是这些变量值的均值,如下图所示:
图1
特别注明:有些例子给的矩阵是这样的:
页脚内容2
图2
这里的单个样本是1*d 的矩阵,要注意计算的时候将其转置,不然套用fisher 算法公式的时候就会发现最后得到的矩阵维数不对。
定义各类类内的离散度矩阵为:(类内离散度矩阵其实就是类协方差矩阵,类在多于一个样本,且样本维度>1时是一个矩阵)
∑∈--=
i j w x T i j i j i m x m x
S ))(( (因为,j x 是一个d*1的矩阵,也可称作d 维向量,i m 也是一个d*1的矩阵,所以最后得到的i S 一定是一个d*d 的矩阵)
(在用matlab 计算的时候直接用cov (wi )即可得到想要的协方差矩阵,故直接计算不探究细节时图2可直接cov 算协方差,不用根据公式转置来转置去,不过matlab 中算的协方差被缩小了(n1-1)倍,计算时i S =cov (w1)*(n1-1))
总的类内离散度矩阵:
页脚内容3 21S S S w +=
类间离散度矩阵定义为:
T
b m m m m S ))((2121--=
在投影以后的一维空间里,两类的均值分别是;
i
T
w x j T i w y i i ii m w x w N y N m i
j i j ===∑∑∈∈1
1
i=1,2
故类内离散度不再是一个矩阵,而是一个值
∑∈-=i
j w y ii i ii m y S 2
)
( i=1,2
总类内离散度为:
1111S S S ww +=
类间离散度:
页脚内容4 2
1111)(m m S bb -=
要使得需求的方向投影能在投影后两类能尽可能的分开,而各类内部又尽可能的聚集,可表示成如下准则,即fisher 准则:
ww bb S S w J =)(max
将公式代入并通过拉格朗日求极值的方法,可得投影方向:
)(211
m m S w w -=-
(w 是一个d*1的矩阵,或者说亦是一个d 维向量)
阈值可表示为: )(2
122110m m w +-= 最后将待确定样本代入
0)(w x w x g T
+=
判断)(x g 的符号和哪个类相同,确定其属于哪个类别。
例子(注意表格中所给的样本维度和公式中变量维度的问题)
代码已经运行无误
代码:
%读取excel中特定单元格的数据
w12=xlsread('E:\模式识别\理论学习\胃病分类问题.xls','C2:F16'); %分别选取类1和类2、测试样本的数据
w1=w12(1:5,:);
w2=w12(6:12,:);
sample=w12(13:15,:);
%计算类1和类2的样本数
页脚内容5
r1=size(w1,1);
r2=size(w2,1);
r3=size(sample,1);
%计算类1和类2的均值(矩阵)
m1=mean(w1);
m2=mean(w2);
%各类类内离散度矩阵(协方差矩阵)
s1=cov(w1)*(r1-1);
s2=cov(w2)*(r2-1);
%总类内离散度矩阵
sw=s1+s2;
%投影向量的计算公式
w=inv(sw)*(m1-m2)';
%计算投影后的一位空间内,各类的均值
y1=w'*m1';
y2=w'*m2';
%计算阈值
页脚内容6
w0=-1/2*(y1+y2);
%和类相同符号被归为同类
for i=1:r3
y(i)=sample(i,:)*w+w0;
if y(i)*(w'*w1(1,:)'+w0)>0
y(i)=1;
else
y(i)=2;
end
End
判断得出第一个待测样本属于类1,第二,三个待测样本属于类2
如果想进一步知道样本矩阵是如何转置得到最后结果的,可看下面这个例子,这个例子没有用到matlab 内置的cov协方差函数(用cov可以直接用样本数据直接进行矩阵运算,不用转置成样本维度向量),所以要进行转置后代入fisher准则公式求解.
页脚内容7
x=xlsread('E:\模式识别\理论学习\污染水域问题.xls','C3:F14'); x1=x(1:5,:)';
x2=x(6:10,:)';
sample=x(11:12,:)';
m1=zeros(size(x1,1),1);
% 求类内离散度矩阵
m1=mean(x1,2)
m2=mean(x2,2)
% 求类内离散度矩阵
s1=zeros(size(x1,1),size(x1,1));
for i=1:size(x1,2)
页脚内容8
s1=s1+(x1(:,i)-m1)*(x1(:,i)-m1)';
end
s2=zeros(size(x2,1),size(x2,1));
for i=1:size(x2,2)
s2=s2+(x2(:,i)-m2)*(x2(:,i)-m2)';
end
sw=s1+s2;
w=inv(sw)*(m1-m2);
y1=w'*m1;
y2=w'*m2;
w0=-1/2*(y1+y2);
for i=1:size(sample,2)
y(i)=w'*sample(:,i);
if y(i)+w0>0
y(i)=1;
else
y(i)=2;
页脚内容9
end
end
页脚内容10。
