边界条件
边界条件

边界条件边界条件有什么作用?•边界条件可以施加到模型的节点、边缘或表面。
边缘或表面边界条件会将节点边界条件施加到边缘或表面上的每个节点。
•当进行模型分析时,会为每个节点的每个自由度生成一个方程。
如果将边界条件施加到某个节点,那么,因为该节点不会经历平动或转动,所以不会为该节点生成方程。
•如果想构建悬臂梁模型,那么您会希望同时约束固定端的平动或和转动。
•如果想构建简支梁模型,那么您会希望仅约束固定端点的平动。
这种连接将允许该梁自由转动。
此连接也通称为平动约束连接。
•每种单元类型都支持确定的自由度。
如果您将边界条件施加到某个单元上的自由度,而该单元并不支持此自由度,那么该边界条件将被忽略。
例如,桁架单元用于构建平动约束连接的模型,因此,无法抗拒转动。
如果您将固定边界条件放置到桁架单元的一端,那么三个转动约束将被忽略。
施加边界条件如果您选择了节点、边缘或表面,可以右键单击显示区并选择“添加” 侧开菜单。
选择“节点边界条件...”、“边缘边界条件...”或“表面边界条件...”命令。
只能将边缘边界条件施加到由 CAD 实体模型生成的模型。
按“预定义”部分中的其中一个按钮,或者,激活“约束自由度”部分中的适当复选框。
“固定”按钮将激活所有六个复选框。
“自由”按钮将取消激活所有六个复选框。
“平动约束”按钮将激活“Tx”、“Ty”和“Tz”复选框。
“无转动”按钮将激活“Rx”、“Ry”和“Rz”复选框。
剩余六个按钮将施加对称或反对称边界条件。
刚性边界单元刚性边界单元有什么作用?•刚性边界单元可以施加到模型的节点、边缘或表面。
边缘或表面弹性边界单元会将节点弹性边界单元施加到边缘或表面上的每个节点。
•刚性边界单元会将刚度施加到节点,从而抗拒沿全局方向或绕全局方向进行平动或转动。
模型上实际添加了一个新节点。
此节点上限制了指定的自由度。
在此节点与施加节点刚性边界的模型节点之间,创建了一个新节点。
此单元位于施加刚性边界单元的全局轴上。
边界条件的定义

边界条件的定义
边界条件是指在计算机程序、数学模型或系统设计中,定义问题的输入、输出或操作所必须满足的条件。
这些条件是问题解决的关键因素,因为如果边界条件不正确或不完整,那么计算机程序或解决方案将无
法正确工作。
边界条件通常可分为两类:输入边界条件和输出边界条件。
输入边界
条件是指在程序中需要接收的输入信息,而输出边界条件是指在程序
运行完毕后需要输出的结果。
以下是边界条件的几个基本定义:
1. 最小值和最大值- 最小值和最大值是边界条件的基本概念。
在很多
问题中,最小和最大值是非常重要的因素。
例如,在一些排序算法中,最小和最大值可能直接影响算法的效率。
2. 边界顺序- 当问题有多个边界情况的时候,它们的顺序也非常的重要。
例如,在一些搜索算法中,问题的解可能受限于某个边界情况。
如果这个边界情况与其他条件冲突,那么这个算法将无法产生有效的
解决方案。
3. 特定的值- 在一些特定的问题中,特定的值可能会与边界条件有关。
例如,在寻找图像的边缘时,边缘的像素通常被视为边界条件。
除了输入和输出边界条件,还有一些其他的边界条件需要考虑。
例如,在计算机程序中,内存和时间通常是有限的资源。
因此,程序设计者
需要考虑程序可能需要运行的时间和内存使用量。
正如你所看到的,边界条件对于任何问题的解决方案都是至关重要的。
只有当问题的输入和输出的边界清晰明确时,我们才能保证程序的正
确性和解决方案的有效性。
因此,在分析问题时,我们应该非常注意问题的边界条件,并且确保它们被正确地定义和实现。
有限元边界条件定义

有限元边界条件定义有限元方法是一种常用的数值分析方法,用于解决工程和科学领域中的各种物理问题。
在使用有限元方法进行计算之前,需要定义适当的边界条件。
边界条件是指在计算区域的边界上所施加的约束条件,用于模拟真实世界中的物理现象。
本文将详细介绍有限元边界条件的定义和应用。
1. 强制边界条件强制边界条件是指在计算区域的边界上施加的已知值或已知函数。
这些边界条件通常是由实验数据、分析解或其他先验知识提供的。
强制边界条件可以是以下几种类型:1.1 固定边界条件固定边界条件是指在计算区域的边界上施加的位移或变形的已知值。
例如,当我们研究一个悬臂梁的弯曲问题时,可以将梁的一端固定在原点,这样就施加了一个固定边界条件。
1.2 力边界条件力边界条件是指在计算区域的边界上施加的外力或力密度的已知值。
例如,当我们研究一个杆件的拉伸问题时,可以在杆件的一端施加一个已知的拉力,这样就施加了一个力边界条件。
1.3 热边界条件热边界条件是指在计算区域的边界上施加的温度或热流的已知值。
例如,当我们研究一个热传导问题时,可以在物体的表面上施加一个已知的温度,这样就施加了一个热边界条件。
2. 自然边界条件自然边界条件是指在计算区域的边界上施加的无约束条件。
这些边界条件通常是由物理现象本身决定的,不需要额外的输入。
自然边界条件可以是以下几种类型:2.1 自由边界条件自由边界条件是指在计算区域的边界上不施加任何约束条件。
例如,当我们研究一个流体力学问题时,可以将流体的边界设置为自由边界,这样流体可以自由地进出计算区域。
2.2 绝缘边界条件绝缘边界条件是指在计算区域的边界上施加的无热流或无质量流的条件。
例如,当我们研究一个热传导问题时,可以将物体的边界设置为绝缘边界,这样热量不能通过边界传递。
2.3 对称边界条件对称边界条件是指在计算区域的边界上施加的关于某个轴对称的条件。
例如,当我们研究一个结构的弯曲问题时,可以将结构的边界设置为对称边界,这样只需要计算一半的结构即可。
材料力学边界条件

材料力学边界条件边界条件在材料力学中起到非常重要的作用,它们是物理现象或力学问题的解决方案的关键要素之一、边界条件确定了在研究区域边界上发生的物理过程和影响。
在材料力学中,常见的边界条件包括:1.位移边界条件:位移边界条件是指物体在边界上的位移情况。
常见的位移边界条件有固定边界条件、自由边界条件和摩擦边界条件等。
固定边界条件是指物体在其中一边界上的位移被限制为零,即该边界上的点不能发生位移。
自由边界条件是指物体在其中一边界上的位移没有任何限制,即该边界上的点可以自由运动。
摩擦边界条件是指物体在其中一边界上的位移受到边界面上的摩擦力所限制。
2.力边界条件:力边界条件是指物体在边界上受到的外力情况。
常见的力边界条件有固定力边界条件和自由力边界条件等。
固定力边界条件是指物体在其中一边界上受到的外力为零,即该边界上没有外力作用。
自由力边界条件是指物体在其中一边界上受到的外力没有任何限制,即该边界上的外力可以自由作用。
3.应力边界条件:应力边界条件是指物体在边界上的应力情况。
常见的应力边界条件有固定应力边界条件和自由应力边界条件等。
固定应力边界条件是指物体在其中一边界上的应力被固定为其中一个值,即该边界上的应力受到限制。
自由应力边界条件是指物体在其中一边界上的应力没有任何限制,即该边界上的应力可以自由变化。
边界条件的选择需要根据具体问题的要求和实际情况进行确定。
通常情况下,边界条件需要满足力学平衡条件、位移连续条件和应力连续条件等。
同时,边界条件的选择也需要考虑到物体的边界特性,比如是否有固定边界、自由边界或者摩擦边界等。
边界条件的正确选择对于力学问题的解决至关重要。
不恰当的边界条件会导致计算结果的不准确甚至错误。
因此,在进行模拟和计算时,需要仔细分析和确定边界条件,并考虑到实际问题的特点和要求。
总之,材料力学边界条件是研究区域边界上发生的物理过程和影响的要素,其正确选择对于解决力学问题具有重要作用。
在选择边界条件时,需要考虑到力学平衡、位移连续和应力连续等方面,以获得准确的计算结果。
数学物理方法三类边界条件

数学物理方法三类边界条件
在数学物理中,常常会遇到需要考虑边界条件的问题。
根据不同的情况,可以将数学物理方法中的边界条件分为三类,第一类边界条件、第二类边界条件和第三类边界条件。
1. 第一类边界条件(Dirichlet边界条件):
第一类边界条件是指在边界上给定了物理量的具体值。
例如,在一个热传导问题中,可以给定边界上的温度值。
在一个波动方程中,可以给定边界上的振幅值。
这类边界条件可以用数学上的等式或函数来表示。
2. 第二类边界条件(Neumann边界条件):
第二类边界条件是指在边界上给定了物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度(即温度梯度)。
在一个波动方程中,可以给定边界上的振幅的导数。
这类边界条件可以用数学上的导数来表示。
3. 第三类边界条件(Robin边界条件):
第三类边界条件是指在边界上给定了物理量的线性组合,其中既包括物理量的值,也包括物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度和温度的线性组合。
这类边界条件可以用数学上的线性组合来表示。
需要注意的是,以上分类只是一种常见的方式,具体问题中的边界条件可能会有其他形式。
此外,边界条件的选择和应用也取决于所研究的具体物理问题和数学模型。
在实际问题中,根据边界条件的具体形式,可以选择合适的数学方法和技巧来求解。
边界条件解析课件

目录
CONTENTS
• 边界条件概述 • 常见边界条件类型解析 • 边界条件的设置与调整 • 边界条件在各领域的应用 • 边界条件的未来发展与展望
01 边界条件概述
定义与分类
定义
边界条件是指在求解数学问题时,对所求问题的定义域或解的取值范围进行限 制的一些条件。
分类
根据不同的分类标准,边界条件可以分为多种类型,如根据约束类型可分为显 式和隐式边界条件,根据对解的影响可分为本质边界条件和非本质边界条件等。
详细描述
在物理、工程和自然界中,很多现象具有周期性变化的特性。 周期性边界条件是指在系统的边界上,变量的值按照一定的 时间或空间周期重复。这种边界条件通常用于模拟具有周期 性变化的现象,例如振动、波动等。
反射性边界条件
总结词
反射性边界条件是指系统在边界上的变量值被反射回来,不穿过边界。
详细描述
反射性边界条件通常用于模拟具有反射特性的现象,例如声音在硬表面上的反射、 光线在镜面上的反射等。在边界上,变量的值被反射回来,不穿过边界,保持了 系统的完整性。
总结词
在数据分析中,边界条件可以用来限制数据范围和分 析结果。
详细描述
在数据分析中,边界条件可以用来限制数据范围和分析 结果。例如,在统计分析中,边界条件可以用来排除异 常值和离群点,以确保分析结果的准确性和可靠性。此 外,在数据挖掘中,边界条件也可以用来限制搜索范围 和优化算法性能。
05 边界条件的未来发展与展 望
详细描述
常见的问题包括边界条件的设定不正确、不 合理或不符合实际情况等。针对这些问题, 可以采取相应的解决方案,如重新审查物理 定律和数学原理、增加额外的数据或信息来 源、寻求专业人士的帮助等。同时,应注意 及时总结和归纳经验教训,不断完善边界条 件的设置和调整过程。
第二章边界条件

第二章:边界条件这一章主要介绍使用边界条件的基本知识。
边界条件能够使你能够控制物体之间平面、表面或交界面处的特性。
边界条件对理解麦克斯韦方程是非常重要的同时也是求解麦克斯韦方程的基础。
§2.1 为什么边界条件很重要用Ansoft HFSS求解的波动方程是由微分形式的麦克斯韦方程推导出来的。
在这些场矢量和它们的导数是都单值、有界而且沿空间连续分布的假设下,这些表达式才可以使用。
在边界和场源处,场是不连续的,场的导数变得没有意义。
因此,边界条件确定了跨越不连续边界处场的性质。
作为一个 Ansoft HSS 用户你必须时刻都意识到由边界条件确定场的假设。
由于边界条件对场有制约作用的假设,我们可以确定对仿真哪些边界条件是合适的。
对边界条件的不恰当使用将导致矛盾的结果。
当边界条件被正确使用时,边界条件能够成功地用于简化模型的复杂性。
事实上,Ansoft HSS 能够自动地使用边界条件来简化模型的复杂性。
对于无源RF 器件来说,Ansoft HSS 可以被认为是一个虚拟的原型世界。
与边界为无限空间的真实世界不同,虚拟原型世界被做成有限的。
为了获得这个有限空间, Ansoft HSS使用了背景或包围几何模型的外部边界条件。
模型的复杂性通常直接与求解问题所需的时间和计算机硬件资源直接联系。
在任何可以提高计算机的硬件资源性能的时候,提高计算机资源的性能对计算都是有利的。
§2.2 一般边界条件有三种类型的边界条件。
第一种边界条件的头两个是多数使用者有责任确定的边界或确保它们被正确的定义。
材料边界条件对用户是非常明确的。
1、激励源波端口(外部)集中端口(内部)2、表面近似对称面理想电或磁表面辐射表面背景或外部表面3、材料特性两种介质之间的边界具有有限电导的导体§2.3 背景如何影响结构所谓背景是指几何模型周围没有被任何物体占据的空间。
任何和背景有关联的物体表面将被自动地定义为理想的电边界(Perfect E)并且命名为外部(outer)边界条件。
第四章,边界条件PPT讲解
计算流体与传热传质
压力边界条件
压力边界条件要求输入表压
( gauge pressure):
p p p absolute
gauge
operating
工作压力(Operating pressure)设置 :
Define Operating Conditions
适合压力边界条件设置的条件:
给定曲线分布的进口
用 UDF’s 定义边界条件. 曲线可以是空间变化,也可以 随时间变化.
读入: 从其它 CFD 软件模拟结果中读 入 产生一个格式文件,具有位置 及边界条件的信息。
可以处理曲线分布边界条件命令: Define Profiles
用 ‘hooks’把曲线加到边界条件中.
速度进口:Velocity Inlets
进口速度知道时,给定该条件 默认是均匀速度
针对不可压缩流动问题. 总(滞止)量(温度、压力 等)不定. 总(滞止)量不定用以调 节速度分布 如果用于可压缩流动,得 到的解不符合物理意义.
避免把速度进口放的太靠近障碍物.
计算流体与传热传质
Mass flux through boundary varies depending on interior solution and specified flow direction.
压力进口的地方可能会有流出情况出现. 流动方向由求解结果决定. Exhaust static pressure is defined by value specified for gauge total pressure wherever outflow occurs.
流体或固体材料 动坐标或滑移网格 源项 固定值 多孔介质区域 湍流(层流)
05边界条件

二维流动问题的边界条件
• 在进口边界AC上:u,v,和T 随着y的分布给定 • 固体壁面CDE上: • 在对称线AB上: • 在出口边界BE上:
• 在构造计算网格时,需考虑边界条件的给定方式。
要使用周期性边界条件,必须取流出循环边界 出口的所有流动变量的通量等于流入循环边界的 对应变量的通量。
5.3 使用边界条件的注意事项
边界条件的组合: 1) 只有壁面 2) 壁面、入口和至少一个出口 3) 壁面、入口和至少一个恒压边界 4) 壁面和恒压边界
14
15
流动出口边界位置的选择:如果流动出口边界 太靠近固体障碍物,流动可能尚未达到充分发展 的状态(在流动方向上梯度为零),这将导致相当 大的误差。 一般为了得到准确的结果,出口边界必须位于 最后一个障碍物后10倍于障碍物高度或更远的距 离。 对于更高精度要求,还要研究模拟结果对出口 位于不同距离时的影响的敏感程度,以保证内部 模拟不受出口位置选取的影响。
16
• 出流面位置的设置
17
3
近壁面网格:在CFD模拟时,为了获得较高的精 度,常需要加密计算网格,而在近壁面处为了快速 得到解,必须将湍流模型结合壁面函数一起使用。 要保证壁面函数法有效,需要使离壁面最近的一个 内节点位于湍流的对数律层之中,这就相当于给最 近壁面的网格到壁面的距离设定一个下限。
Elective Course for Graduate Students
5 边界条件
孙晓颖 Harbin Institute of Technology
5.1 概述
边界条件:是流场变量在计算边界上应该满足的数 学物理条件,指在求解域的边界上所求解的变量或其 一阶导数随地点及时间变化的规律。 边界条件的基本类型: 流动入口边界;流动出口边界;给定压力边界; 壁面边界;对称边界;周期性(循环)边界
弹性力学-边界条件

yx
x
P y
fx
n
l cosn, x cos m cosn, y sin
xy
由 x s m xy s f x xy s m y s f y
fy
x s cos yx s sin 0
h 2 h 2
h 2 h 2
f x ydy M
则边界条件可以写成(P.23 (b)):
x x l
dy Fx ,
xy x l
dy Fy ,
x x l
ydy M
悬臂梁的例子:
y
h 2 h 2
y y x
h 2 h 2
x
P
L
L
对边界条件的积分为: (P.23 (b)):
x yx
xy l fx y s m fy
x 上面:l=0,m=-1 左面: 右面: l=-1 l=1 m=0 m=0 下面:l=0,m=1 y
(2).上下两面 ( ) f l 0 m 1 ( ) f
二、应力边界条件 在边界上的楔形体(单位厚度)如图所示: 弹性体内单元体斜面上的 y 应力分量与坐标面应力的 yx 关系有(静力平衡) f xn X x p x x xy l p y m y yx
• 所得到的应力分量必须在所有边界上各点处严 格满足应力边界条件,才是所论问题的解答。 • 在小边界上,如果不能严格满足边界条件,可 以用圣维南原理在静力等效意义上满足(积分 意义上的)边界条件。 • 根据这个原理:两组面力其分布尽管不同,但 如果两者的合力与合力矩相同(静力等效),此 时它们所产生的作用结果仅仅在局部有比较大 的差异,远离这个局部,结果基本相同。
边界条件定义

边界条件定义边界条件是指在一个问题或系统中,所设定的特定条件或限制,用于测试或确定系统的行为。
边界条件在各个领域都有应用,例如软件开发、数学、物理学等等。
在软件开发中,边界条件是指在测试或运行程序时,需要考虑的各种极端情况。
下面将从不同领域的角度,讨论边界条件的定义和应用。
在数学中,边界条件是指在函数或方程中所设定的特定约束条件。
例如,在求解微分方程时,需要给定初始条件或边界条件,以确定唯一的解。
边界条件可以是函数在某一点的值,或者函数在某一区间的行为。
这些边界条件的设定,对于解的存在性和唯一性具有重要影响。
在物理学中,边界条件指的是在物理系统中所设定的限制条件。
例如,在求解波动方程时,需要考虑波函数在边界处的行为。
边界条件可以是波函数在某一点的值,或者波函数在某一区域的导数。
这些边界条件的设定,对于确定系统的行为和性质具有重要影响。
在计算机科学中,边界条件是指在程序设计或算法实现中所设定的特定限制条件。
例如,在编写排序算法时,需要考虑数组的边界条件,即数组的起始位置和结束位置。
边界条件的设定,可以避免数组越界和程序崩溃的情况发生。
边界条件的考虑也可以提高程序的效率和性能。
除了数学、物理学和计算机科学,边界条件在其他领域也有广泛的应用。
例如,在经济学中,边界条件是指经济模型中所设定的特定限制条件,用于分析和预测经济现象。
在生物学中,边界条件是指生物系统中所设定的特定约束条件,用于研究生物过程和现象。
边界条件的设定需要考虑到问题的特性和目标,以及系统的实际情况。
边界条件的选择应该合理、准确,能够准确反映问题的本质和复杂性。
同时,边界条件的设定也需要符合问题的要求和约束,以保证系统的稳定性和可靠性。
边界条件是问题或系统中所设定的特定条件或限制,用于测试或确定系统的行为。
边界条件的设定在各个领域都有重要的应用,对于解决问题和研究系统行为具有关键作用。
边界条件的设定需要考虑问题的特性和目标,以及系统的实际情况,从而保证系统的稳定性和可靠性。
自然边界条件的通俗解释

自然边界条件的通俗解释一、什么是自然边界条件在自然界中,各种物理现象和过程都受到一定的限制和规律,这些限制和规律常常被称为边界条件。
自然边界条件是指自然界中存在的各种限制和规律,它们能够影响物理过程的发生和发展,同时也限制了物理系统的行为。
自然边界条件包括了空气、水、地球表面等自然元素对物理过程的影响,它们决定了物理系统的行为与演化。
二、自然边界条件对物理过程的影响2.1温度和能量传输温度是自然界中一个重要的边界条件,在很多物理过程中起着关键作用。
热量的传输受到温度差异的影响,从高温向低温的传导、传感、辐射等方式都受到温度差的驱动。
自然界中的温度差异会引发大气冷暖空气的形成,导致大气环流的发生。
2.2湿度和气候变化湿度是描述空气中水汽含量的指标,它对气候变化起着重要作用。
空气中的湿度受到水汽的蒸发和降水的影响。
湿度的变化会影响大气的稳定性,进而影响气候的转变。
在自然边界条件的限制下,湿度决定了雨水的形成和分布,影响了地球上的水循环。
2.3地形和地质结构地形和地质结构也是自然边界条件的重要组成部分。
地球表面的起伏、山脉、河流等地理特征直接影响了大气和水体的流动。
山脉作为自然边界,影响着气候的形成和降水的分布。
地质结构则决定了地下水的蓄藏和流动,对水文循环和地下水资源的分布起到重要作用。
三、自然边界条件的意义自然边界条件对各种物理过程的发生和发展起到了制约和调控的作用,它们决定了物理系统的特性和演化。
自然边界条件的研究不仅有助于对地球环境和气象气候变化的理解,还能为生态保护、资源开发等方面提供科学依据。
在气候变化的背景下,深入研究自然边界条件对物理过程的影响,有助于我们更好地预测和应对自然灾害,也能为环境保护和可持续发展提供有益的指导。
四、自然边界条件的研究方法研究自然边界条件的方法多种多样,包括实地观测、数值模拟、实验室研究等。
通过实地观测可以获取地球表面的温度、湿度、地貌等数据,以及大气和水体的运动信息。
boundary condition 条件

boundary condition 条件边界条件(Boundary Conditions)是指在进行数学模型或物理模拟时,为了确定问题的解决方案而设定的特定条件。
边界条件在模拟过程中起着至关重要的作用,它们可以对问题的解决产生重大影响。
在这篇文章中,我们将讨论边界条件的定义、种类以及在不同领域中的应用。
边界条件可以分为以下几类:第一类是几何边界条件,即在模拟中给定的区域的边界上所设置的条件。
这些条件可以是给定的形状、大小、位置等。
例如,在流体力学的模拟中,我们可以设置一个固体壁面,从而确定流体在该壁面上的速度和压力分布。
第二类是物理边界条件,即在边界上给定的物理量值。
这些物理量可以是温度、浓度、吸收率等。
例如,在热传导问题中,我们可以给定热流的大小和方向,从而确定边界上的温度分布。
第三类是数值边界条件,即在数值模拟中为了保证计算的稳定性而设定的条件。
这些条件可以是数值格式所要求的数值限制,例如稳定性条件、收敛性条件等。
在计算流体力学的模拟中,我们常常需要考虑Courant-Friedrichs-Lewy(CFL)条件,以保证数值解的稳定性和收敛性。
边界条件在不同领域中扮演着重要的角色。
在物理学中,边界条件可以帮助我们理解问题的特定情况。
例如,在电磁场模拟中,我们可以设置给定位置处的电荷密度,以探索与该电荷密度相关的电场分布。
在天气模拟中,我们可以通过设置地表的气温和风速分布来预测不同地区的天气变化。
在工程学中,边界条件可以帮助我们优化设计和工艺。
例如,在建筑结构分析中,我们可以通过设置柱或梁的边界条件来确定结构的稳定性和安全性。
在流体管道系统的设计中,我们可以通过设置管道末端的边界条件来确定流体流动的特性,以便选择最合适的泵和阀门。
在计算机科学中,边界条件在算法设计和数据分析中也起着重要的作用。
例如,在图像处理中,我们可以通过在图像边界上设置边界条件来处理图像的边缘。
在机器学习中,我们可以通过定义特定的边界条件来训练和优化模型。
边界条件

如果方程要求未知量y(x)及其导数y′(x)在自变量的同一点x=x0取给定的值,即y(x0 )=y0,y′(x0)= y0′,则这种条件就称为初始条件,由方程和初始条件构成的问题就称为初值问题;
而在许多实际问题中,往往要求微分方程的解在某个给定区间a ≤ x ≤b的端点满足一定的条件,如y(a) = A, y(b) = B,则给出的在端点(边界点)的值的条件,称为边界条件,微分方程和边界条件构成数学模型就称为 边值问题。
边界条件数学ຫໍສະໝຸດ 语01 简介目录02 分类
边界条件,是指在求解区域边界上所求解的变量或其导数随时间和地点的变化规律。边界条件是控制方程有 确定解的前提,对于任何问题,都需要给定边界条件。边界条件的处理,直接影响了计算结果的精度。而解微分 方程要有定解,就一定要引入条件,这些附加条件称为定解条件。
简介
分类
边值问题中的边界条件的形式多种多样,在端点处大体上可以写成这样的形式,Ay+By'=C,若B=0,A≠0,则 称为第一类边界条件或狄里克莱(Dirichlet)条件;B≠0,A=0,称为第二类边界条件或诺依曼(Neumann)条件; A≠0,B≠0,则称为第三类边界条件或洛平(Robin)条件。
谢谢观看
总体来说, 第一类边界条件: 给出未知函数在边界上的数值; 第二类边界条件: 给出未知函数在边界外法线的方向导数; 第三类边界条件: 给出未知函数在边界上的函数值和外法线的方向导数的线性组合。 对应于comsol,只有两种边界条件: Dirichlet boundary(第一类边界条件)—在端点,待求变量的值被指定。
常微分方程的边界条件

常微分方程的边界条件常微分方程(ODE)就像是一道数学的难题,等着我们去破解。
而边界条件就像是这道题的“约束”,没有它,方程就像没有方向的船,飘荡在数学的海洋中。
好啦,今天就带大家一起聊聊这个话题,保证不让你觉得无聊,反正这事儿跟我们的生活也有些联系嘛!1. 什么是边界条件?边界条件,简单来说,就是给方程设置一些限制条件。
就像做菜,你不能随便往锅里扔一大堆材料,要有个先后顺序,要加盐要加醋,不能忽略了。
这些条件告诉你,方程在特定点上的值或者导数应该是什么样子。
比如说,假设你在追一个目标,边界条件就像是你设定的目标,告诉你该往哪儿去,怎么才能实现。
1.1 边界条件的类型边界条件大体上可以分为两种,一种叫“初值条件”,另一种叫“边值条件”。
初值条件就像你早上起床时给自己设定的目标,比如“今天一定要早起,吃一顿营养早餐!”这个条件一旦设定,你就得努力去实现。
而边值条件则有点像你在旅途中设定的终点,“我要去海边看日出!”这时候你就得计划好路线,确保每一步都朝着那个目标走去。
1.2 为什么边界条件重要?有了边界条件,我们的常微分方程才能真正“落地”。
没有边界条件,你的方程就像一场没有结束的马拉松,跑来跑去,却不知道目的地在哪。
边界条件不仅能帮助我们找到解,还能确保解是唯一的。
这就像你在比赛时,有了明确的目标,才能不迷失方向,一路跑到终点。
2. 如何选择边界条件?选择边界条件就像挑选食材,得看具体的菜式。
你不能随便拿个土豆就往汤里扔,得根据你要做的汤类型来决定。
常微分方程的边界条件选择也一样。
我们需要根据实际问题来设定,比如物理问题中的温度、速度,甚至是市场经济中的需求量。
这些因素都能影响我们方程的结果。
2.1 物理中的应用在物理学中,边界条件尤为重要。
想象一下你在研究一个弹簧的振动,初始时弹簧的长度、质量和弹性系数都是已知的。
那么这就是你的初值条件。
再想象一下,你希望弹簧的最大伸展长度不超过某个值,这就是你的边值条件。
化学反应的边界条件定义

化学反应的边界条件定义化学反应是物质发生变化的过程,其速率受到很多因素的影响。
边界条件是指影响化学反应进行的因素和条件,进一步影响反应速率和结果。
在化学反应中,边界条件可以分为温度、浓度、压力、催化剂等方面。
首先,温度是影响化学反应速率的重要因素之一。
在一定的温度下,反应速率会随着温度的升高而增加。
这是因为温度的提高会增加分子的平均动能,使得分子碰撞的频率和能量增加,从而促进反应进行。
而当温度过高时,反应速率可能会受到热能的影响而减慢或中断。
其次,浓度也是影响化学反应的边界条件之一。
一般来说,浓度越高,分子间的碰撞频率也越高,反应速率也更快。
这是因为在高浓度下,分子更容易相遇并发生反应。
而反之,浓度过低则会减缓反应速率,甚至导致反应无法进行。
此外,压力也是影响某些反应的边界条件。
在气相反应中,当压力升高时,气体分子之间的碰撞频率增加,反应速率也会相应提高。
这是因为高压条件下,气体分子的平均自由程较短,碰撞的频率增加。
但并非所有反应都受压力影响,只有涉及气态物质的反应才会受到压力的影响。
最后,催化剂是能够改变反应速率的物质,但并不改变反应的终点物质。
催化剂通常通过提供新的反应路径来降低反应的活化能,从而促进反应进行。
催化剂可以提高反应速率,降低反应温度要求,减少副反应产生等。
因此,在进行化学反应时,选择适当的催化剂也是十分重要的。
综上所述,化学反应的边界条件包括温度、浓度、压力和催化剂等多个方面。
了解这些边界条件对于控制反应速率和结果具有重要意义。
通过合理地控制这些边界条件,可以提高反应效率,减少能量消耗,并获得更好的反应产物。
因此,在进行化学反应时,需要认真考虑这些边界条件,以达到预期的反应目的。
第5讲 边界条件

en (D1 D2 ) S 同理 ,由 B dS 0
S
D1n D2n S
en (B1 B2 ) 0 或 B1n B2n
S en (J1 J 2 ) t
S
J dS
V
dV t
第5讲 边界条件
D H J t B E t B 0 D
J t
S
J dS
V
dV t
第5讲 边界条件
为什么要研究边界条件 ?
en
物理:由于在分界面两侧介质的特性 参数发生突变,场在界面两侧 也发生突变。麦克斯韦方程组 的微分形式在分界面上失去意 义,必须采用边界条件。
en ( H1 H 2 ) J S
en ( E1 E2 ) 0
B 0
D
J t
en (B1 B2 ) 0 en (D1 D2 ) S
S en (J1 J 2 ) t
第5讲 边界条件
为什么电场强度矢量的切向分量总是连续的? 当 当
D的法向分量连续 B的法向分量连续 E的切向分量连续 H的切向分量连续
第5讲 边界条件
场矢量的折射关系 在线性、各向同性的理想介质分界面上 电场矢量的折射关系
介质1 介质2
en
E2 2
1
E1
1
2
E1t / E1n tan 1 1 / D1n 1 tan 2 E 2t / E 2n 2 / D2n 2
8
s 0 时,为什么电位移矢量的法向分量不连续? s 0 时,为什么电位移矢量的法向分量是连续的?
三类边界条件推导
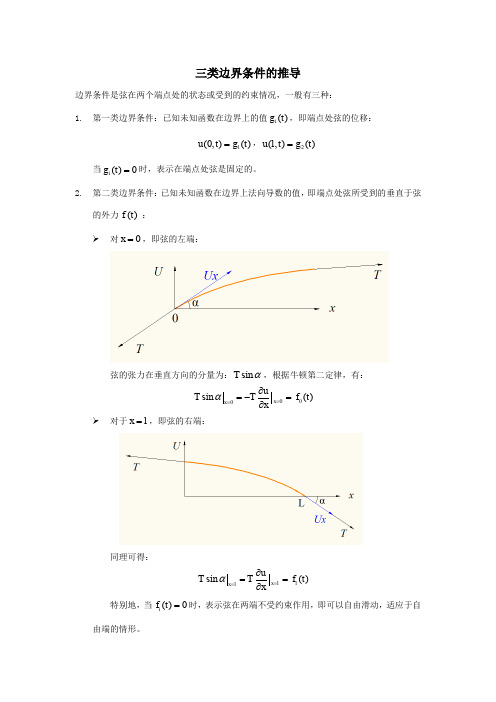
三类边界条件的推导边界条件是弦在两个端点处的状态或受到的约束情况,一般有三种:1. 第一类边界条件:已知未知函数在边界上的值()i g t ,即端点处弦的位移:1(0,)()u t g t =,2(,)()u l t g t =当()0i g t =时,表示在端点处弦是固定的。
2. 第二类边界条件:已知未知函数在边界上法向导数的值,即端点处弦所受到的垂直于弦的外力() f t :对0x =,即弦的左端:弦的张力在垂直方向的分量为:sin T α,根据牛顿第二定律,有:000sin () x x u T Tf t x α==∂=-=∂对于x l =,即弦的右端:同理可得:sin () x l l x l u T T f t x α==∂==∂特别地,当()0i f t =时,表示弦在两端不受约束作用,即可以自由滑动,适应于自由端的情形。
3. 第三类边界条件:又称混合边界条件,它给出了未知函数和它的法线方向上的导数的线性组合在边界上的值。
对弦的一维振动问题,即已知端点处弦的位移(引起弹性支撑的力)和所受的垂直于弦线的外力。
对0x =,即弦的左端:弦对支撑外力的垂直分量为:u T x∂∂,由胡克定律知: 000(t)x x u T ku f x==∂=+∂ 设k T σ=,()()f t v t T=,可以得到,弹性支撑条件下,弦振动的边界条件为: 0()()x u u v t xσ=∂-=∂ 对于x l =,即弦的右端:弦对支撑外力的垂直分量为:u Tx ∂-∂,由胡克定律知(t)x l x l l u T ku f x ==∂-=+∂此时得到的弦振动的边界条件为: ()()x l u u v t x σ=∂+=∂对于外力()0i f t =的特殊情况,即()0v t =,边界条件在弦的两端可统一简化为:()0 (0,)x a u u a a l x σ=∂===∂。
传热问题 三类边界条件

传热问题三类边界条件
在传热学中,边界条件是解决传热问题的关键因素之一。
通常,我们将边界条件分为以下三类:
1. 第一类边界条件:直接给出边界处的温度值。
这种边界条件简单直观,适用于导热问题等。
2. 第二类边界条件:告诉你边界处的温度梯度是多少。
这与物体内部温度的变化速率有关,常用于对流换热等问题。
3. 第三类边界条件:与前两类不同,它不仅给出了温度梯度,还与温度满足一个关系式。
这类边界条件更复杂,但在实际问题中非常常见,如自然对流传热和辐射传热等。
自然对流传热是由于流体中的温度差异形成的流动导致的传热现象,物体表面的温度和热流密度通常是随时间和位置变化的。
辐射传热则是物体通过辐射方式传递热量的现象,这也与物体表面的温度和热流密度有关,而这些参数通常是随时间和位置变化的。
边界条件的处理

可以采用虚拟点法。
虚拟点法:
在右边界外虚设一点M1+1,这 样节点M1就被视为内节点, 其 导数即可采用中心差分:
TM11 TM11 2x
qB
为消去TM1+1,由一维、稳态、含内热源的控 制方程可得在M1点的离散形式:
TM 11
2TM1
(x)2
TM 11
S
0
从以上两式消去TM1+1得,
TM 1
★两种处理方法的比较
大量数值实践表明,附加源项法比补充节点方 程的方法更为简洁、有效,主要体现在以下三个 方面: 1.有利于用统一模式来处理三种边界条件; 2.可以缩小计算区域; 3.采用补充节点方程方法时,如把求解代数方程 的区域也限在内节点,然后通过边界节点方程不 断更新边界节点上的值并以此作为下一次迭代计 算的边界条件,则附加源项法的计算时间可以比 这种边界值更新法大约节省一个数量级。
V [1 /
h
ATf
(
x)w
/
B
}V ]
其中:A是所研究控制容积在边界上的传热面积 V 为控制容积的体积
[aP
A
1/ h ( x)w
/ B
]TP
aETE
aNTN
aSTS
{SC
V [1/
h
ATf
(
x)w
/
}V
B ]
上式表明,对第三类边界条件,如果在边界控制容积中加 入一下附加源项:
S C ,ad
3.温度边界条件:
(1)规定了边界上的温度:tw=f1(τ)
(2)规定了边界上的热流密度:
qw
(
t n
)w
f2 ( )
(3)规定了边界上物体与周围流体间的表面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章:边界条件这一章主要介绍使用边界条件的基本知识。
边界条件能够使你能够控制物体之间平面、表面或交界面处的特性。
边界条件对理解麦克斯韦方程是非常重要的同时也是求解麦克斯韦方程的基础。
§2.1 为什么边界条件很重要用Ansoft HFSS求解的波动方程是由微分形式的麦克斯韦方程推导出来的。
在这些场矢量和它们的导数是都单值、有界而且沿空间连续分布的假设下,这些表达式才可以使用。
在边界和场源处,场是不连续的,场的导数变得没有意义。
因此,边界条件确定了跨越不连续边界处场的性质。
作为一个Ansoft HSS 用户你必须时刻都意识到由边界条件确定场的假设。
由于边界条件对场有制约作用的假设,我们可以确定对仿真哪些边界条件是合适的。
对边界条件的不恰当使用将导致矛盾的结果。
当边界条件被正确使用时,边界条件能够成功地用于简化模型的复杂性。
事实上,Ansoft HSS 能够自动地使用边界条件来简化模型的复杂性。
对于无源RF 器件来说,Ansoft HSS 可以被认为是一个虚拟的原型世界。
与边界为无限空间的真实世界不同,虚拟原型世界被做成有限的。
为了获得这个有限空间,Ansoft HSS使用了背景或包围几何模型的外部边界条件。
模型的复杂性通常直接与求解问题所需的时间和计算机硬件资源直接联系。
在任何可以提高计算机的硬件资源性能的时候,提高计算机资源的性能对计算都是有利的。
§2.2 一般边界条件有三种类型的边界条件。
第一种边界条件的头两个是多数使用者有责任确定的边界或确保它们被正确的定义。
材料边界条件对用户是非常明确的。
1、激励源波端口(外部)集中端口(内部)2、表面近似对称面理想电或磁表面辐射表面背景或外部表面3、材料特性两种介质之间的边界具有有限电导的导体§2.3 背景如何影响结构所谓背景是指几何模型周围没有被任何物体占据的空间。
任何和背景有关联的物体表面将被自动地定义为理想的电边界(Perfect E)并且命名为外部(outer)边界条件。
你可以把你的几何结构想象为外面有一层很薄而且是理想导体的材料。
如果有必要,你可以改变暴露于背景材料的表面性质,使其性质与理想的电边界不同。
为了模拟有耗表面,你可以重新定义这个边界为有限电导(Finite Conductivity )或阻抗边界(Impedance boundary)。
有限电导边界可以是一种电导率和导磁率均为频率函数的有耗材料。
阻抗边界默认在所有频率都具有相同的实数或复数值。
为了模拟一个允许波进入空间辐射无限远的表面,重新定义暴露于背景材料的表面为辐射边界(Radiation Boundary)。
背景能够影响你怎样给材料赋值。
例如,你要仿真一个充满空气的矩形波导,你可以创建一个具有波导形状特性为空气的简单物体。
波导表面自动被假定为良导体而且给出外部(outer)边界条件,或者你也可以把它变成有损导体。
§2.4 边界条件的技术定义激励(Excitation)——激励端口是一种允许能量进入或导出几何结构的边界条件。
理想电边界(Perfect E)——Perfect E是一种理想电导体或简称为理想导体。
这种边界条件的电场(E-Field)垂直于表面。
有两种边界被自动地赋值为理想电边界。
1、任何与背景相关联的物体表面将被自动地定义为理想电边界并且命名为outer的外部边界条件。
2、任何材料被赋值为PEC(理想电导体)的物体的表面被自动的赋值为理想电边界并命为smetal边界。
理想磁边界(Perfect H)——Perfect H是一种理想的磁边界。
边界面上的电场方向与表面相切。
自然边界(Natural)——当理想电边界与理想磁边界出现交叠时,理想磁边界也被称为Natural边界。
理想磁边界与理想电边界交叠的部分将去掉理想电边界特性,恢复所选择区域为它以前的原始材料特性。
它不会影响任何材料的赋值。
例如,可以用它来模拟地平面上的同轴线馈源图案。
有限电导率(Finite Conductivity)边界——有限电导率边界将使你把物体表面定义有耗(非理想)的导体。
它是非理想的电导体边界条件。
并且可类比为有耗金属材料的定义。
为了模拟有耗表面,你应提供以西门子/米(Siemens/meter)为单位的损耗参数以及导磁率参数。
计算的损耗是频率的函数。
它仅能用于良导体损耗的计算。
其中电场切线分量等于Zs(n xHtan)。
表面电阻(Zs)就等于(1+j)/(δσ)。
其中,δω是激励电磁波的频率.σ是导体的电导率µ是导体的导磁率阻抗边界(Impedance)——一个用解析公式计算场行为和损耗的电阻性表面。
表面的切向电场等于Zs(n xHtan)。
表面的阻抗等于Rs + jXs。
其中,Rs是以ohms/square为单位的电阻Xs 是以ohms/square为单位的电抗分层阻抗(Layered Impedance)边界——在结构中多层薄层可以模拟为阻抗表面。
使用分层阻抗边界条件进一步的信息可以在在线帮助中寻找。
集总RLC(Lumped RLC)边界——一组并联的电阻、电感和电容组成的表面。
这种仿真类似于阻抗边界,只是软件利用用户提供的R、L和C值计算出以ohms/square为单位的阻抗值。
无限地平面(Infinite Ground Plane)——通常,地面可以看成是无限的、理想电壁、有限电导率或者是阻抗的边界条件。
如果结构中使用了辐射边界,地面的作用是对远区场能量的屏蔽物,防止波穿过地平面传播。
为了模拟无限大地平面的效果,在我们定义理想电边界、有限电导或阻抗边界条件时,在无限大地平面的框子内打勾。
辐射边界(Radiation )——辐射边界也被称为吸收边界。
辐射边界使你能够模拟开放的表面。
即,波能够朝着辐射边界的方向辐射出去。
系统在辐射边界处吸收电磁波,本质上就可把边界看成是延伸到空间无限远处。
辐射边界可以是任意形状并且靠近结构。
这就排除了对球形边界的需要。
对包含辐射边界的结构,计算的S 参数包含辐射损耗。
当结构中包含辐射边界时,远区场计算作为仿真的一部分被完成。
§2.5 激励技术综述端口是唯一一种允许能量进入和流出几何结构的边界类型。
你可以把端口赋值给一个两维物体或三维物体的表面。
在几何结构中三维全波电磁场被计算之前,必须确定在每一个端口激励场的模式。
Ansoft HFSS 使用任意的端口解算器计算自然的场模式或与端口截面相同的传输线存在的模式。
导致两维场模式作为全三维问题的边界条件。
Ansoft HFSS 默认所有的几何结构都被完全装入一个导电的屏蔽层,没有能量穿过这个屏蔽层。
当你应用波端口(Wave Ports )于你的几何结构时,能量通过这个端口进入和离开这个屏蔽层。
作为波端口的替代品,你可以在几何结构内应用集中参数端口(Lumped Ports )。
集中参数端口在模拟结构内部的端口时非常有用。
§2.5.1 波端口(Wave Ports )端口解算器假定你定义的波端口连接到一个半无限长的波导,该波导具有与端口相同的截面和材料。
每一个端口都是独立地激励并且在端口中每一个入射模式的平均功率为1瓦。
波端口计算特性阻抗、复传播常数和S 参数。
波动方程在波导中行波的场模式可以通过求解Maxwell 方程获得。
下面的由Maxwell 方程推出的方程使用两维解算器求解。
021(,)(,)0r r E x y E x y κεμ⎛⎫∇⨯∇⨯-= ⎪⎝⎭其中:(,)E x y 是谐振电场的矢量表达式; 0κ是自由空间的波数;r μ是复数相对导磁率;r ε是复数相对介电常数。
求解这个方程,两维解算器得到一个矢量解(,)E x y 形式的激励场模式。
这些矢量解与z 和t 无关,只要在矢量解后面乘上z e γ-它们就变成了行波。
另外,我们注意到激励场模式的计算只能在一个频率。
在每一个感兴趣的频率,计算出的激励场模式可能会不一样。
§2.5.2 模式(Modes )对于给定横截面的波导或传输线,特定频率下有一系列的场模式满足麦克斯维方程组。
这些模式的线性叠加都可以在波导中存在。
模式转换某些情况下,由于几何结构的作用像一个模式变换器,计算中包括高阶模式的影响是必须的。
例如,当模式1(主模)从某一结构的一个端口(经过该结构)转换到另外一个端口的模式2时,我们有必要得到模式2下的S参数。
模式,反射和传播在单一模式的信号激励下,三维场的解算结果中仍然可能包含由于高频结构不均匀引起的高次模反射。
如果这些高次模反射回激励源端口,或者传输到下一个端口,那么和这些高次模相关的S参数就必须被考虑。
如果高次模在到达任何端口前,得到衰减(这些衰减由金属损耗或者传播常数中的衰减部分所造成),那么我们就可以不考虑这些高次模的S参数。
模式和频率一般来说,和每种模式相关的场模式也许会随频率的改变而变化。
然而,传播常数和特性阻抗总是随频率变化的。
因此,需要频扫时,在每一个频率点,都应有相应的解算。
通常,随着频率的增加,高次模出现的可能性也相应的增加。
模式和S参数当每个端口的定义都正确时,仿真中包括的每个模式,在端口处都是完全匹配的。
因此,每个模式的S参数和波端口,将会根据不同频率下的特性阻抗进行归一化。
这种类型的S 参数叫做广义的S参数。
实验测量,例如矢量网络分析仪,以及电路仿真器中使用的特性阻抗是常数(这使得端口在各个频率下不是完全匹配)。
为了使计算结果,和实验及电路仿真得到的测量结果保持一致,由HFSS得到的广义S 参数必须用常数特性阻抗进行归一化。
如何归一化,参看波端口校准。
注解:对广义S参数归一化的失败,会导致结果的不一致。
例如,既然波端口在每一个频点都完全匹配,那么S参数将不会表现出各个端口间的相互作用,而实际上,在为常数的特性阻抗端口中,这种互作用是存在的。
§2.5.3 波端口的边界条件:波端口边缘有以下所述的边界条件:理想导体或有限电导率边界—在默认条件下,波端口边缘的外部定义为理想导体。
在这种假设条件下,端口定义在波导之内。
对于被金属包裹传输线结构,这是没问题的。
而对于非平衡或者没被金属包围的传输线,在周围介质中的场必须被计算,不正确的端口尺寸将会产生错误的结果。
对称面——端口解算器可以理解理想电对称面(Perfect E symmetry)和理想磁对称面(Perfect H symmetry)面。
使用对称面时,需要填入正确的阻抗倍增数。
阻抗边界——端口解算将识别出端口边缘处的阻抗边界。
辐射边界——在波端口和辐射边界之间默认的设置是理想导体边界。
§2.5.4 波端口校准:一个添加到几何结构的波端口必须被校准以确保一致的结果。
为了确定场的方向和极性以及计算电压,校准是必要的。
